Abstract
Purpose
Roll compaction/dry granulation is established in manufacturing of solid oral dosage forms and, within the context of continuous manufacturing, it has sparked interest as material is fed, processed, and ejected continuously while also providing large possible throughputs. However, this amount of material has to be adequately controlled in real time to assure quality.
Methods
This research aimed at monitoring the critical quality attribute granule size distribution in continuous roll compaction/dry granulation (QbCon®; L.B. Bohle, Ennigerloh, Germany) using in-line and on-line laser diffraction. The influence of varying process parameters and excipient formulations was studied and evaluated with the prospect of using this technique to develop control loops. For this purpose, residence time parameters were assessed. In- and on-line data was compared with off-line laser diffraction and dynamic image analysis data.
Results
The system successfully monitored the granule size distribution in a variety of process parameters and throughputs (up to 27.5 kg/h). It was sensitive to changes in process parameters and changes in material blends, which could pose a potential threat to the final drug products’ quality. Average event propagation time from the compaction zone to the laser diffraction system of 17.7 s demonstrates the systems’ fast reaction time.
Conclusion
Results highlight laser diffraction as a valuable method of in- and on-line size determination and allow for the development of a control strategy using this principle.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Shifting the mindset from batch to continuous manufacturing (CM), the pharmaceutical industry is rather slow, compared with, e.g., the food industry, as the highest standard of quality must be met and documented for every product [1, 2]. However, the advantages of CM have been recognized and academic and industrial research efforts have increased [3,4,5,6]. Issues like proposing a new definition of a “batch” and traceability have been addressed [7]. Early in CM initiatives, proposals for continuous granulation were published [8]. The Food and Drug Administration (FDA) has been especially supportive of the CM approach [3, 5] and the International Council of Harmonization published quality guidance to help introducing advanced concepts [9, 10]. ICH Guideline Q13, Continuous Manufacturing, was also announced and is currently under construction. Currently, six small-molecule drug products are on the market that, at least to some extent, incorporate CM approaches [11].
An integral part of a functional CM manufacturing line is a detailed control strategy to assure that the resulting final drug product is matching all necessary quality requirements and to separate out-of-specification product from in-specification product. To achieve this, process analytical technologies (PAT) can be implemented. PAT tools are developed to monitor critical quality attributes (CQA) [12] of the intermediates and the final product and use these results to control the process in real time. The aim is to minimize the amount of product that is out-of-specification and, if all necessary CQAs can be controlled, real-time release of the final drug product. Various guidelines and experimental approaches to implementing PAT tools have been described in literature [3, 13,14,15,16,17].
Roll compaction/dry granulation (RCDG) is the favored continuous dry granulation method while twin-screw granulation is chosen if a wet granulation process is desired [18, 19]. RCDG is known for its high potential material throughput, comparably low production cost and the granulation method of choice if the bulk density of the material needs to be significantly increased [20,21,22]. The granule size distribution (GSD) of the resulting granules is a CQA [23, 24]. Therefore, development of in-line or on-line particle size measurements are of interest. Numerous techniques (e.g., dynamic image analysis (DIA), laser diffraction, focused beam reflectance measurement, spatial filtering technique) have been reported to be implemented in discontinuous or continuous processing of pharmaceuticals [25,26,27,28,29,30]. GSD monitoring for RCDG is impeded by the high throughput of the process, resulting in a high number of granules, and the broad size distribution that typically results from dry granulation. This results in difficulties to measure the full product flow as well as obtaining a representative sample to measure [20]. Therefore, limited research has been published on RCDG and in-line/on-line particle sizing [31,32,33].
Laser diffraction as means of particle size determination is based on the different behaviors of laser light that is diffracted at the surface of a particle. Larger particles diffract light at smaller angles and different intensities compared with smaller particles. The scattered light intensity is measured by circular detector plates and used to calculate the size of the particle that would be responsible for this scattering under certain assumptions (e.g., a spherical particle shape) [34]. Laser diffraction is widely used for off-line analytics in batch mode manufacturing, has been intensively studied [35,36,37], and was explored for process monitoring in pharmaceutical applications [26].
The aim of this study was to implement laser diffraction as a tool to monitor GSD in-line or on-line. The sensitivity of the tool with regard to a change in process parameters, excipients, and reproducibility was studied. Off-line laser diffraction was performed and compared with in-line/on-line data. In general, the applicability of the PAT tool with regard to continuous manufacturing of solid oral dosage forms with a throughput up to 27.5 kg/h was to be explored.
Materials and Methods
Materials
Microcrystalline cellulose (MCC, Vivapur® 102, JRS Pharma, Germany) was used as primary excipient in experiments studying varying process parameters.
Different placebo formulations were prepared. Excipients used were lactose (Granulac® 200, Meggle, Germany) and magnesium stearate (Parteck® LUB MST, Merck, Germany).
Continuous Roll Compaction/Dry Granulation
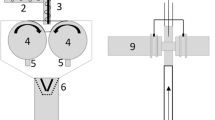
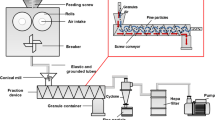
RCDG was performed on a QbCon® dry continuous manufacturing line using a commercially available roll compactor (BRC 25, L.B. Bohle GmbH, Germany). Filling of material, either pure MCC or a preblend, was conducted manually. The roll compactor was equipped with knurled surfaced rolls, a hybrid sealing system and a 360° rotating conical sieve (BTS 100, L.B. Bohle GmbH, Germany) equipped with a 1.0-mm rasp sieve. Specific compaction forces (SCF) between 2 and 7 kN/cm were applied. If not mentioned otherwise, the default gap width was 2.0 mm and the roll speed setting was 2 rpm. Below the sieve, a small buffer vessel was mounted with a suction shoe. On the other side, a plastic hose was attached (Fig. 1a). The hose was then attached either to the laser diffraction system itself or to a T-piece, if the bypass system was used. At the outlet of the laser diffraction system, a plastic hose was attached and connected to a vacuum receiver (Volkmann GmbH, Soest, Germany). If the fill grade of the vessel exceeded a certain level, the pump stopped for 10 s and the container was emptied. Afterwards, conveyance restarted.
Scheme of a RCDG, b in-line laser diffraction, c on-line laser diffraction. (1) powder inlet, (2) feeding auger, (3) tamping auger, (4) rolls, (5) scrapers, (6) conical sieve, (7) vessel, (8) hose, (9) laser diffraction system, (10) inlet for scavenging air, (11) T-piece, (12) pipe with angled opening, (13) venturi nozzle
Granule Size Determination Using Laser Diffraction
The granule size distribution was determined using Insitec® T laser diffraction system (Malvern Panalytical, United Kingdom). The system was equipped with a lens of 500-mm focal length, allowing the measurements of particles’ equivalence diameters up to 1600 μm. It consists of a red diode laser (670 nm), a 10.0-mm beam waist, and a circular detector with 33 detector plates. The scan rate was 2000 Hz. GSD parameters and transmission data were exported. The transmission is a value that describes how much of laser light passes through the measurement zone onto the detector. At 100% transmission, all laser light reaches the detector, while at 0% transmission, none of the laser light reaches the detector. It is therefore a value that can be used to estimate how many particles are in the measurement zone at a certain time frame. An initial update time of 5 s was chosen. Scavenging air of 10 Nm3/h was used to protect the lenses from window fouling and inserted on both, the laser and the detector lens. Window fouling was evaluated daily, as a blank measurement with a fouled window will lead to a decreased transmission and recording of granule size, while no particles are transported through the measurement zone. Measurements were performed only if the transmission during the blank was 100%. RTSizer® (Malvern Panalytical, United Kingdom) software was used to track and export GSD and transmission data.
For in-line laser diffraction, the whole product stream was passing the laser diffraction installation (Fig. 1b).
For on-line measurements, the product stream was directed through a T-piece, in which a metal pipe (10 mm) with an angled opening was inserted. The pipe was linked to a venturi nozzle to disperse the sample through the laser diffraction measurement zone with additional compressed air (4 Nm3/h). After measurement, the sample was reunited with the main fraction and conveyed into the storage vessel (Fig. 1c).
Off-line laser diffraction was conducted using the Mastersizer® 3000 (Malvern Panalytical, United Kingdom). Samples for off-line analysis were taken without the hose and vessel (nos. (7) and (8) in Fig. 1). Every sample was taken for 1 min, resulting in a sample mass between 50 and 275.8 g. Samples were split using a rotational sample divider (PT100, Retsch, Germany). They were measured at 0.8-bar dispersion pressure. The dispersion pressure was chosen to ensure that no granules are destroyed during dispersion based on expertise on laser diffraction measurement of dry granulated product. All off-line samples were measured at least in threefold.
In-line/On-line Data Analysis
For figures that show the granule size development over time, the key parameters D25, D50, and D75 are plotted instead of a full GSD curve. In all cases, the moving average over 30 s was calculated and plotted. Transmission values were plotted as individual values every 5 s. Process parameters were plotted as individual values every 10 s.
Detailed analysis of GSD curves is also included in this work. Data was only included in this analysis, if it was measured, when the system was in equilibrium. More specifically, if the set-specific compaction force (SCF) was met and the gap width only fluctuated between set gap width ± 0.1 mm. When the system was in equilibrium, the average of the last 30 s was taken as data point every minute.
Granule Size Determination Using Dynamic Image Analysis
There are many different methods to determine particle size. It is therefore interesting to compare the method of choice with at least one other method that provides additional information. A distinctive difference between laser diffraction and DIA is the role of particle shape and morphology. Laser diffraction does not provide information about particle shape and irregularly shaped particles will generate signals that might under- or overestimate their size. DIA typically records two-dimensional projections that are subsequently evaluated. It is possible to choose from a plethora of different size descriptors. It was therefore chosen as a comparative technique of size determination.
DIA was conducted using Haver CPA 2-1 (Haver&Boecker, Oelde, Germany). It scans the particle projection in free fall through a measurement zone that is equipped with a red LED light source and a CCD line scan camera. With a pixel size of 34 μm × 34 μm, it can measure particles between 24 μm (67% obscuration needed to measure a signal) and 25 mm. To allow a comparison to laser diffraction results, the equivalence diameter was chosen as a size descriptor. The equivalence diameter was calculated by measuring the projected area of each particle and determining the radius of a circle that would generate the same projected area.
Results and Discussion
GSD Determination at Varying SCF and Determination of Residence Time
Figure 2 displays results from two experiments with the same experimental scheme. GSD was determined in-line (Fig. 2a and b) and on-line (Fig. 2c and d) at four different SCFs. All three GSD parameters react to a change in SCF. They seem to reach a constant value, albeit fluctuations can be seen, especially in the D75 values. This constant level is reached after the SCF and gap width (see Fig. 2b and d) have reached an equilibrium. For both, in- and on-line analysis, returning to a SCF led to GSD parameters that do not differ significantly from different experiment timings in which the same parameters were chosen (e.g., 2 kN/cm at minutes 6–12 and 24–30). In this example, the average D25, D50, and D75 values were evaluated statistically. The arithmetic mean was chosen as parameter every 30 s. As stated before, data was only included in this analysis if the process was in equilibrium. In this example, 6 values for D25, D50, and D75 were taken into account for minutes 6–12 and 8 values for minutes 24–30. An F test was conducted comparing the variances of the recorded data (α = 0.05). Variances were similar for D25 and D50 (F values of 1.19 and 1.66 accordingly compared with the table value of F = 3.97) but varied for D75 (F value of 8.87). Afterwards, a t test (either for similar variances or varying variances) was conducted (α = 0.05). In all cases, the t test confirmed that the arithmetic means do not differ significantly (t value of 0.44 (D25), 1.77 (D50), and 2.05 (D75) were calculated and compared with the table values of t (2.18 for D25 and D50; 2.36 for D75). In both experiments, approximately at minutes 8.5 and 22.5 (Fig. 2a and b) and 8.5 and 23.5 (Fig. 2c and d), the collecting vessel was emptied, which can be seen in abrupt stop of all measurements. Afterwards, the conveying system restarted.
Plot of GSD parameters (dashed, D75; full, D50; dotted, D25) against time. a and c SCF is plotted in gray. b and d Gap width is plotted in gray. Constant settings: gap width 2 mm and roll speed 2 rpm. a and b In-line measurement, n = 1. c and d On-line measurement, n = 1. GSD data in moving average over 30 s
Using these results (Fig. 2), an analysis of the residence time from between the two rolls to the analysis in the laser diffraction system was performed. It has to be noted that this residence time does not only include the time a particle needs to move from the tightest place in the compaction gap to the laser diffraction measurement zone. It furthermore includes the time the roll compaction process needs to reach the equilibrium after the SCF was adjusted. The combination of particle movement and process equilibration was measured in this experiment. A change in specific compaction force was the step change input while the D50 value was chosen as response parameter. The defining D50 value for each step was calculated by averaging the D50 values of the last 20 s of each run (individual measurements), assuming the values are in equilibrium right before changing the SCF. Event propagation time (EPT) was determined by calculating the time in which 5% (EPT5), 50% (EPT50), and 95% (EPT95) of the step change were reached and were calculated for every step change (n = 4) and averaged (Table 1).
Despite the time delay implied by using the moving average, it can be seen that with a mean EPT50 of 17.7 s, the time between changing SCF and reaching a GSD plateau is short. The SCF is measured between the rolls while the GSD is measured in the laser diffraction setup. Although the distance was about 2 m, the pneumatic conveyance was fast. The slowest step is supposedly the milling process. As shown in literature, the MRT of the milling process varies with different SCF [38]. Therefore, a fluctuation in residence time parameters can be reasoned by varying residence time of the ribbons in the milling unit. Furthermore, to obtain reliable granule size, both, the SCF and the gap width, must be in equilibrium. A change in SCF results in fluctuating gap widths (Fig. 2b and d). The time that is needed to reach a constant gap width also influences the time that is needed to reach the plateau. Despite relevant standard deviations, the calculated residence time parameters underline a fast adaption of the system to changes in particle size generated by process parameters.
For both setups, the effect of a change in SCF was seen. Changing back to a previously used SCF leads to comparable GSD results (see also the “In-line vs. on-line GSD determination and repeatability of measurements” section). Concerning a change in SCF, laser diffraction is an appropriate monitoring tool. Residence times of under a minute highlight that the system is fast in measuring differences in particle size if they appear in the process and are therefore favorable if a control strategy is to be developed.
GSD Determination at Increasing Throughput
In Fig. 3, GSD data recorded at 2 kN/cm SCF, 2.0-mm gap width, and increasing roll speed is displayed. The GSD parameters fluctuate around a constant value. For in-line measurements (Fig. 3a), the fluctuation is higher at low roll speeds while it decreases with increasing roll speed. This could be true for on-line measurements as well; however, judgment here is impeded by the higher frequency of emptying the collection vessel. After each emptying, the recorded transmission (Fig. 3d) is zero, indicating an overload of material passing through the laser beam. The material that was produced in about 10 s (up to 76 g) is collected just below the compactor outlet and transported in a bulk when the conveying is restarted. The dispersion might not be sufficient to separate those granules. This could explain increased recorded particle size at low-transmission values. These disturbances are visible in the data and complicate the analysis.
Plot of GSD parameters (dashed, D75; full, D50; dotted, D25) against time. a and c Roll speed is plotted in gray. b and d Transmission is plotted in gray. Constant settings: gap width 2 mm and SCF 2 kN/cm. a and b In-line measurement, n = 1. c and d On-line measurement, n = 1. Transmission data in single values; GSD data in moving average over 30 s
Figure 3b additionally shows the current transmission every 5 s. The value of transmission depends on the size and number of particles in the measurement zone. As size is constant in this experiment, it is a measure of throughput. The actual throughput was determined off-line (Table 2). With increasing roll speed and throughput, the transmission is lowered. This is in accordance with the basic principle of laser diffraction. A decline in transmission can be a warning for the chances of multiple scattering increasing. This would be seen in varying GSD data. As the GSD data up to 16.6 kg/h is constant for the experiment, it can be concluded that no relevant multiple scattering effects take place. The in-line system can, in this case, be used for throughputs up to 16.6 kg/h (for pure MCC).
The on-line setup utilizes a bypass and, as not all material is conducted through the measurement zone, the transmission is lower for similar throughputs (Fig. 3d). Comparing the concentration values recorded by the laser diffraction system in parts per million, about 50% of material are directed through the bypass. Therefore, higher throughputs can be aimed at. Up to 27.5 kg/h, the measurements are fluctuating around similar values. A further increase of the throughput was feasible; however, the collection vessel filled up fast and the pneumatic conveyance was frequently stopped to empty the vessel so a continuous process with stable measurements was not possible.
In Fig. 3a and b, it can be seen that with increasing roll speed, fluctuations in the measurement seem to diminish. An explanation can be found in the hybrid sealing system that was implemented. Comparable with cheek plate sealing systems commonly found in RCDG, the hybrid sealing system leads to ribbons not sticking to the rolls after leaving the compaction zone. The ribbon is usually one continuous piece until it touches the milling unit and breaks. A slow roll speed leads to longer time between ribbon breakage than a high roll speed. Therefore, it could be observed that at 1 rpm, the mill is not filled with material constantly. A broken piece of the ribbon is completely milled down and before the next ribbon enters the milling unit, there is a certain time in which the mill is empty. This results in a fluctuating concentration of particles (Cv (ppm)) that is detected by the laser diffractometer (Fig. 4a).
a Plot of mass variation (g/5 s) (black) and concentration of particles (ppm) (gray), value saved every 10 s, against production time; n = 1. b Amplitude against frequency plot of the mass variation (fast Fourier transformation). c Amplitude against frequency plot of the Cv fluctuations (fast Fourier transformation) d Amplitude against frequency plot of the D50 fluctuations (fast Fourier transformation). Roll speed = 1 rpm; throughput = 3.0 kg/h
In a separate experiment, the mass produced using a BRC25 with similar setup and 1 rpm roll speed was tracked every 10 s. The fluctuations in the output of the sieve are evident (Fig. 4a). Both fluctuations show peaks in dominant frequencies after a fast Fourier transformation (FFT) (Fig. 4b and c) that lay around 0.035 Hz (≈ a surge of material output every 28 s). This fluctuation of material can be one reason for fluctuations in measured GSD. Another point that has to be considered is that a ribbon entering the milling unit will be milled down over a certain time. Thereby, there is an initial breakage of ribbons that has to be differentiated from breakage occurring later in the milling process. Milling of a single ribbon over a time period can lead to resulting granule sizes that differ in the beginning and in the end. This phenomenon disappears at higher throughput as ribbons are produced faster and an equilibrium fill level is reached in the mill. Granule sizes can be expected to show less fluctuations in these cases as shown in Fig. 3a minutes 20–35. Figure 4d shows FFT results of the D50 parameter. It was tracked every 5 s over a period of 1895 s (equaling 379 individual measurement points). There is a peak at 0.036 Hz indicating that the mass fluctuation in ribbon production is noticeable in the D50 variation. Further dominant frequencies exist and could indicate effects of the differing fill level in the sieve or further, so far undescribed, effects.
GSD determination can therefore be done in adequate throughputs for pharmaceutical manufacturing. For high throughputs, the on-line setup could be favorable. To reach constant granule sizes (produced and measured), a roll speed of 3 rpm and above is favorable. It is also possible to develop a bypass system in which the material is not continuously conveyed in the manufacturing line. Instead, the material could be collected in a vessel below the compactor outlet and then conveyed in bulk at predefined time points. Measurement details have to be adapted in such a system.
In-line vs. On-line GSD Determination and Repeatability of Measurements
Figure 5 shows a comparison of full GSD curves between in- and on-line measurements at various SCFs. The data is obtained partly from the experiment shown in Fig. 2. However, the experiment was repeated on a different day following the same experimental procedure. For Fig. 5, results of both experiments were merged. As 2 kN/cm was also the SCF used for further experiments (e.g., also part of the data shown in Fig. 3), there are additional measurements that were also taken into consideration for this specific SCF (also shown in Fig. 6). Judging from the low standard deviations in all cases, the repeatability of the system can be regarded as high.
Concerning the comparison of in-line and on-line measurements, at 2 kN/cm, the curves align well (full black lines). At higher SCFs, the on-line measurements repeatedly record smaller granule sizes compared with the same measurements in-line (in-line curves shifted to the left). Potentially, this difference is a product of non-representative sampling in the on-line setup that can only be seen for larger, more sluggish granules with a broader size distribution than that of the granules at 2 kN/cm. The fact that at increasing SCF, the size distributions get wider and the difference in D50 increases (4 μm at 2 kN/cm, 14.2 μm at 3 kN/cm, 100.1 μm at 4 kN/cm, and 219.2 μm at 5 kN/cm) supports this. The angled pipe might not isokinetically sample the granule stream representatively, as larger granules with a higher mass require a stronger intervention than the pressured air of the venturi nozzle to be distracted from their flow pattern.
Granules obtained at low SCF can be representatively separated using the bypass setup. For bigger granules and broader size ranges, the bypass does not sample representatively but favors the extraction of smaller granules (shift to the left in the GSD curve). In- and on-line data therefore show differences. The sensitivity of the system to changes in process parameters is not diminished. If key GSD parameters can be determined representatively, it can therefore still be used as a parameter for a control strategy.
Comparison to Off-line Data
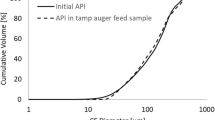
Figure 6 shows exemplary full GSD data for granules produced at 2 kN/cm and 5 kN/cm. As previously discussed, the in- and on-line measurements match well at 2 kN/cm but for larger SCF, they vary, with on-line data measuring smaller granule sizes. In the case of 2 kN/cm, off-line measurements match well with in/on-line data up to the D70 value. At higher size quantiles, off-line measurements record larger granule sizes. As a 1000-μm rasp sieve was used and granulation was performed at low SCF, it is unlikely that granules up to over 2000 μm were produced. Similar observations can be made for higher SCF (e.g., 5 kN/cm). The off-line measurement matches well with the on-line measurements up to 750 μm equaling about 60% of all material. Afterwards, it records larger granules up to a D99 of 2830 μm. About 10% of all granules are measured off-line with a granule size of 1600 μm and above. As mentioned above, this amount of granules larger than the rasp sieve size can be regarded as questionable.
Exemplarily, dynamic image analysis was conducted for the 5 kN/cm granules. The granule size distribution measured using DIA of the same material used for off-line laser diffraction is shown in Fig. 6b) (gray curve). A different curve shape when comparing laser diffraction and image analysis was expected and can be seen. However, the in/on-line laser diffraction data and image analysis data agree on a maximum granule size between 1400 and 1600 μm (D99). Larger granules (10% above 1600 μm in case of off-line laser diffraction) cannot be found by any other technique. As DIA also provides information on particle shape, the roundness according to DIN ISO 9276-6 (“Representation of results of particle size analysis – Part 6: Descriptive and quantitative representation of particle shape and morphology”) was evaluated. Ninety percent of all measured particles show a roundness of 0.65 or less (with 1.00 indicating a perfect circle projection of a particle). The particles are therefore irregularly shaped, which can shift laser diffraction particle size results and explain the observed deviations. It has to be kept in mind that the dispersion is 0.8 bar for off-line measurements. As the dispersion pressure is relatively low (up to 4 bars are possible), destruction of granules can be avoided. There was no hint of measuring agglomerates. It is however difficult to decide, whether smaller particle sizes are recorded at larger dispersion pressure due to destruction of granules or due to a previous lack of dispersion. As the 0.8-bar dispersion pressure is chosen routinely for characterization of dry granulated product [39], it was chosen for this study as well.
As expected, it is not possible to transfer GSD information from one analyzing system to another without any adjustments. This is also true for in/on-line and off-line laser diffraction. Since repeatability for in/on-line measurements is high (see Figs. 6 and 7), it might be advisable to conduct reference measurements in the same setup as used in development/manufacturing to avoid the usage of off-line measurement systems.
Ability of the System to Detect Faulty Excipient Blends
The ability to detect changes in the granule sizes, if process parameters do not adhere, is important to judge the system’s usefulness. Process parameters should themselves be monitored and incorporated into a control strategy. The information about GSD in this case is valuable to determine whether the product is still suitable for further processing despite an unexpected event in process parameters. It could avoid unnecessary discarding of material, however, especially unexpected events that might not be visible directly in the process parameters should be detectable by monitoring the granule size of the resulting granules.
In the following experiments, no process parameters were changed. However, excipient blends were fed into the system that were produced differently.
Figure 7 shows results of two experiments in which the same formulation (MCC 79%, lactose 20%, magnesium stearate 1%) was used. However, the material was prepared differently according to Table 3.
In the first experiment (Fig. 7a), blend B was compacted at a constant 7 kN/cm specific compaction force (minutes 0 to 11). Without any adjustments, at minute 11, blend A was manually fed into the inlet of the roll compactor. The material was introduced as soon as the feeding screw was visible. Immediate blending of the two materials in the feeding unit could not be inhibited, as the material could not be fed into the compaction zone directly. Therefore, a delay in response was expected. As expected, the over lubricated material led to smaller granules compared with the correctly blended mixture. All GSD key parameters (D25, D50, and D75) increase after the blend was switched.
Figure 7b shows results of a similar experiment in which at first blend A was compacted at 3 kN/cm and at minute two blend B was added. GSD parameters of blend A are well below the ones in the experiment shown in Fig. 7a. This can be explained by different applied SCFs. The resulting granules of blend B show smaller particle sizes. They are comparable with the granulation behavior at 7 kN/cm which can be reasoned by the impact of magnesium stearate as lubricant in compaction processes. At minute 10, pure MCC was added as excipient. About 30 s after addition, the gap width decreased as not enough material was fed into the gap to reach 3 kN/cm at a constant gap width. This resulted in a strong initial increase in granule size. Afterwards, the gap equilibrated around the desired 2 mm. The D75 was significantly increased compared with the over lubricated formulation as larger granules were produced. A high amount of fine material is typical for RCDG, especially at low SCF of 3 kN/cm. This amount is comparable with particle sizes resulting from an over lubricated formulation (D25 and D50).
The laser diffraction system was able to determine differences in GSD, if over lubricated material was delivered to the process. This should simulate a user error of incorrect blending of materials. A time delay was noticed as the material was fed into the hopper and not directly into the compaction zone.
Conclusions
An in- and on-line GSD monitoring system based on laser diffraction was implemented successfully in a RCDG process with up to 27.5 kg/h of material throughput. No window fouling was observed over the experiment time span of 2 weeks. The system detected changes in granule size based on varying process parameters or blend preparation methods. This can be utilized as the base to develop an integrated control strategy for continuous RCDG. Knowledge about possible parameters that can be used to control (feedback or feedforward control loops) needs to be identified and linked to information obtained by GSD measurements. Also, information about RTD in the RCDG needs to be cumulated and put into practice. On-line laser diffraction measurements are based on non-representative sampling; however, sensitivity of and relevance in measured GSD data is similar to in-line data. A control strategy could be based on this bypass setup if measurements are reproducible or the bypass could be improved in future research.
References
Plumb K. Continuous processing in the pharmaceutical industry - changing the mind set. Chem Eng Res Des. 2005;83(A6):730–8. https://doi.org/10.1205/cherd.04359.
Rantanen J, Khinast J. The future of pharmaceutical manufacturing sciences. J Pharm Sci. 2015;104(11):3612–38. https://doi.org/10.1002/jps.24594.
Lee SL. Current FDA Perspective for Continuous Manufacturing. US FDA Center for Drug Evaluation and Research, MIT-CMAC 2nd International Symposium on Continuous Manufacturing of Pharmaceuticals. 2016. http://iscmp.mit.edu/sites/default/files/documents/ISCMP%202016%20-%20FDA%20MIT-CMAC%20for%20CM%202016%20Ver6.pdf.
Lee SL, O’Connor TF, Yang XC, Cruz CN, Chatterjee S, Madurawe RD, et al. Modernizing pharmaceutical manufacturing: from batch to continuous production. J Pharm Innov. 2015;10(3):191–9. https://doi.org/10.1007/s12247-015-9215-8.
Lee SL. Quality Considerations for Continuous Manufacturing Guidance for Industry. Food and Drug Administration, Silver Spring. 2019. https://www.fda.gov/media/121314/download. Accessed 14.11.2019 14:48.
Garcia T, Cook G, Nosal R. PQLI key topics-criticality, design space, and control strategy. J Pharm Innov. 2008;3(2):60–8.
Engisch W, Muzzio F. Using residence time distributions (RTDs) to address the traceability of raw materials in continuous pharmaceutical manufacturing. J Pharm Innov. 2016;11(1):64–81. https://doi.org/10.1007/s12247-015-9238-1.
Betz G, Junker-Burgin P, Leuenberger H. Batch and continuous processing in the production of pharmaceutical granules. Pharm Dev Technol. 2003;8(3):289–97. https://doi.org/10.1081/pdt-120022157.
ICH Q8 (R2) Pharmaceutical development, (2014).
ICH Q10 Pharmaceutical Quality System, (2008).
Badman C, Cooney CL, Florence A, Konstantinov K, Krumme M, Mascia S, et al. Why we need continuous pharmaceutical manufacturing and how to make it happen. J Pharm Sci. 2019;108(11):3521–3. https://doi.org/10.1016/j.xphs.2019.07.016.
Hlinak AJ, Kuriyan K, Morris KR, Reklaitis GV, Basu PK. Understanding critical material properties for solid dosage form design. J Pharm Innov. 2006;1(1):12–7. https://doi.org/10.1007/bf02784876.
Laske S, Paudel A, Scheibelhofer O, Author T. A review of PAT strategies in secondary solid oral dosage manufacturing of small molecules. J Pharm Sci. 2017;106(3):667–712. https://doi.org/10.1016/j.xphs.2016.11.011.
U.S. Food & Drug Administration. Guidance for Industry, PAT - A Framework for Innovative Pharmaceutical Development, Manufacturing and Quality Assurance. 2004. https://www.fda.gov/media/71012/download.
Singh R, Ierapetritou M, Ramachandran R. An engineering study on the enhanced control and operation of continuous manufacturing of pharmaceutical tablets via roller compaction. Int J Pharm. 2012;438(1–2):307–26. https://doi.org/10.1016/j.ijpharm.2012.09.009.
Fonteyne M, Vercruysse J, De Leersnyder F, Van Snick B, Vervaet C, Remon JP, et al. Process analytical technology for continuous manufacturing of solid-dosage forms. Trac-Trend Anal Chem. 2015;67:159–66. https://doi.org/10.1016/j.trac.2015.01.011.
Tok AT, Goh X, Ng WK, Tan RB. Monitoring granulation rate processes using three PAT tools in a pilot-scale fluidized bed. AAPS PharmSciTech. 2008;9(4):1083–91. https://doi.org/10.1208/s12249-008-9145-6.
Leuenberger H. New trends in the production of pharmaceutical granules: batch versus continuous processing. Eur J Pharm Biopharm. 2001;52(3):289–96. https://doi.org/10.1016/s0939-6411(01)00199-0.
Vervaet C, Remon JP. Continuous granulation in the pharmaceutical industry. Chem Eng Sci. 2005;60(14):3949–57. https://doi.org/10.1016/j.ces.2005.02.028.
Parikh DM. Handbook of pharmaceutical granulation technology. Boca Raton: CRC Press; 2016.
Kleinebudde P. Roll compaction/dry granulation: pharmaceutical applications. Eur J Pharm Biopharm. 2004;58(2):317–26. https://doi.org/10.1016/j.ejpb.2004.04.014.
Shlieout G, Lammens RF, Kleinebudde P. Dry granulation with a roller compactor part I: the functional units and operation modes. Pharm Technol Eur. 2000;12(11):24–35.
Shekunov BY, Chattopadhyay P, Tong HH, Chow AH. Particle size analysis in pharmaceutics: principles, methods and applications. Pharm Res. 2007;24(2):203–27. https://doi.org/10.1007/s11095-006-9146-7.
Alderliesten M. Mean particle diameters. Part IV: empirical selection of the proper type of mean particle diameter describing a product or material property. Part Part Syst Charact. 2004;21(3):179–96. https://doi.org/10.1002/ppsc.200400917.
Madarasz L, Nagy ZK, Hoffer I, Szabo B, Csontos I, Pataki H, et al. Real-time feedback control of twin-screw wet granulation based on image analysis. Int J Pharm. 2018;547(1–2):360–7. https://doi.org/10.1016/j.ijpharm.2018.06.003.
Chan LW, Tan LH, Heng PWS. Process analytical technology: application to particle sizing in spray drying. AAPS PharmSciTech. 2008;9(1):259–66. https://doi.org/10.1208/s12249-007-9011-y.
Nalluri VR, Schirg P, Gao X, Virdis A, Imanidis G, Kuentz M. Different modes of dynamic image analysis in monitoring of pharmaceutical dry milling process. Int J Pharm. 2010;391(1–2):107–14. https://doi.org/10.1016/j.ijpharm.2010.02.027.
Greaves D, Boxall J, Mulligan J, Montesi A, Creek J, Sloan ED, et al. Measuring the particle size of a known distribution using the focused beam reflectance measurement technique. Chem Eng Sci. 2008;63(22):5410–9. https://doi.org/10.1016/j.ces.2008.07.023.
Närvänen T, Lipsanen T, Antikainen O, Räikkönen H, Heinämäki J, Yliruusi J. Gaining fluid bed process understanding by in-line particle size analysis. J Pharm Sci. 2009;98(3):1110–7.
Petrak D. Simultaneous measurement of particle size and particle velocity by the spatial filtering technique. Part Part Syst Charact. 2002;19(6):391–400. https://doi.org/10.1002/ppsc.200290002.
Mangal H, Derksen E, Lura A, Kleinebudde P. In-line particle size measurement in dry granulation: Evaluation of probe position. 10th World Meeting on Pharmaceutics, Biopharmaceutics and Pharmaceutical Technology. 2016.
Wilms A, Knop K, Kleinebudde P. Combination of a rotating tube sample divider and dynamic image analysis for continuous on-line determination of granule size distribution. Int J Pharm X. 2019;1:100029. https://doi.org/10.1016/j.ijpx.2019.100029.
McAuliffe MAP, O’Mahony GE, Blackshields CA, Collins JA, Egan DP, Kiernan L, et al. The use of PAT and off-line methods for monitoring of roller compacted ribbon and granule properties with a view to continuous processing. Org Process Res Dev. 2015;19(1):158–66. https://doi.org/10.1021/op5000013.
Allen T. Powder sampling and particle size determination. 1st ed. Amsterdam: Elsevier B.V; 2003.
Ma ZH, Merkus HG, de Smet JGAE, Verheijen PJT, Scarlett B. Improving the sensitivity of forward light scattering technique to large particles. Part Part Syst Charact. 1999;16(2):71–6. https://doi.org/10.1002/(Sici)1521-4117(199906)16:2<71::Aid-Ppsc71>3.0.Co;2-2.
Ma ZH, Merkus HG, Scarlett B. Extending laser diffraction for particle shape characterization: technical aspects and application. Powder Technol. 2001;118(1–2):180–7. https://doi.org/10.1016/S0032-5910(01)00309-6.
Ma Z, Merkus HG, van der Veen HG, Wong M, Scarlett B. On-line measurement of particle size and shape using laser diffraction. Part Part Syst Charact. 2001;18(5–6):243–7.
Mangal H, Kleinebudde P. Experimental determination of residence time distribution in continuous dry granulation. Int J Pharm. 2017;524(1–2):91–100. https://doi.org/10.1016/j.ijpharm.2017.03.085.
Wiedey R, Šibanc R, Wilms A, Kleinebudde P. How relevant is ribbon homogeneity in roll compaction/dry granulation and can it be influenced? Eur J Pharm Biopharm. 2018;133:232–9. https://doi.org/10.1016/j.ejpb.2018.10.021.
Acknowledgments
This work was supported by the Drug Delivery Innovation Center (DDIC), INVITE GmbH, Leverkusen.
Funding
Open Access funding provided by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wilms, A., Meier, R. & Kleinebudde, P. Development and Evaluation of an In-line and On-line Monitoring System for Granule Size Distributions in Continuous Roll Compaction/Dry Granulation Based on Laser Diffraction. J Pharm Innov 16, 247–257 (2021). https://doi.org/10.1007/s12247-020-09443-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12247-020-09443-3