1 Introduction

The recent impressive progress in wireless networking is mostly due to enhancements at the physical layer. As for MAC layer, the dominant paradigms can be cast into the big categories of reservation protocols and random access protocols. Reservation protocols rely heavily on signaling. Random access provides simplicity and robustness in uncertain environments characterized by high traffic burstiness.

Already existing multiple access schemes may not be applicable to exploit the full potential of next-generation wireless networks. This is attracting interest on re-thinking the design of Next Generation Multiple Access (NGMA) [1]. There exists a need for the development of innovative access schemes, to integrate and exploit the impressive progress of physical layer transceiver technology and signal processing techniques over the last decade.

A key feature offered by modern wireless transceivers is the ability to decode multiple superposed packets, i.e., Multi-Packet Reception (MPR). MPR can be implemented by leveraging on Successive Interference Cancellation (SIC) or other signal processing techniques [2, 3]. We aim to investigate the impact of SIC on multiple access, with emphasis on Internet of Things (IoT) scenarios. Multiple access in IoT systems is often ruled according to random access protocols, given the burstiness of traffic and the limited amount of data that devices usually communicate in each interaction.

An extensive literature has been growing on new multiple access techniques [1, 4, 5], specifically so-called Non-Orthogonal Multiple Access (NOMA), most suited for IoT scenarios. Specifically, innovative and powerful algorithms have been shown to improve Slotted ALOHA performance and random access schemes in general (see Section 2 for a review). In this paper, we define a general framework for random multiple access with SIC-based MPR, encompassing Slotted ALOHA and CSMA. We analyze several performance metrics, i.e., sum-rate, probability of success, energy consumption, and age of information. The perspective assumed in this work is to evaluate system performance as a function of the communication link spectral efficiency.

We provide the following two main original contributions:

  • We highlight the existence of two fundamental regimes: (i) high spectral efficiency, where CSMA is superior in terms of sum-rate and SIC gives little contribution to system performance; and (ii) low spectral efficiency, where the effect of MAC protocol is marginal and performance is dominated by SIC. This interpretation of the obtained results is new, to the best of the authors’ knowledge.

  • The low spectral efficiency sum-rate peak couples with fair sharing of the channel among contending nodes, while unfairness arises for high spectral efficiency regime. More in depth, fairness here means that the same probability of success and age of information performance are achieved by all nodes, irrespective of their distances from the base station, and in spite of limited transmission power range.

This paper extends and strengthens the preliminary model analysis and results presented in [6]. The major new contributions are (i) extension of the analytical model to evaluate mean energy consumption per delivered packet and mean age of information; (ii) new numerical results to assess energy consumption and AoI performance, both as global and individual node metrics.

The rest of the paper is organized as follows: An overview of related literature is presented in Section 2. Section 3 introduces the modeling approach and the main assumptions. The proposed model is analyzed in Section 4, where expressions of all considered performance metrics for the Slotted ALOHA and CSMA are derived. In Section 5, numerical results are provided, the model is validated against simulations, and the main outcomes of the model are discussed. Conclusions are drawn in Section 6, hinting also at future work.

2 Related work

The impact of MPR on the design and performance of MAC protocols represents an important field of research. It has been shown that interference cancellation has the potential to boost the performance [7, 8]. A first study of Slotted ALOHA stability under a general MPR model is presented in [9]. The throughput analysis for pure ALOHA with all-or-nothing MPR model that can decode successfully up to \(K=2\) received packets is given in [10]. A general K all-or-nothing model for Slotted ALOHA is analyzed in [11]. A thorough and very interesting analysis of the Slotted ALOHA and CSMA for an all-or-nothing MPR model is given in [12].

Several SIC models are proposed in [13], in which throughput is increased while maintaining low complexity. It is shown that both proposed models, so-called SA-NOMA-SIC and SA-NOMA-Joint Decoding (JD), suit the next generation IoT. Non-orthogonal multiple access-based collision resolution is investigated in [14] in a heterogeneous device environment. MAC layer perspective is the main focus in [13, 14]. The recent paper [15] on ALOHA-NOMA protocol shows a significant increase of throughput. However, the achieved performance depends critically on a number of assumptions, like ideal SIC, and perfect Channel State Information (CSI).

In case of heterogeneous IoT networks, strict slot synchronization might be a challenging problem. The Slotted-ALOHA NOMA protocol considered in [16] solves the problem of synchronization, assuming that the number of active devices is detected to adjust power levels. However, there exists an issue: achieved throughput is linked to picking distinct optimum power levels, which is done by repeated randomized attempts. Increasing the number of attempts introduces an increased delay in the system. An enhanced version of this protocol is studied in [17], where the receiver adaptively learns the number of active devices using multi-hypothesis testing. A comparison with CSMA shows that the Slotted ALOHA NOMA protocol performs better in a low transmission probability regime in terms of throughput [17]. A similar study for Slotted ALOHA is done in [18], to analyze sum-rate, with ordered and unordered SIC receivers.

A NOMA-based random access scheme is utilized in [19]. It maximizes the packet decoding probability, by using SIC. This requires that transmission power levels be fixed using channel state information.

The interplay between NOMA and other advanced physical layer techniques might help in a smooth transition toward next generation multiple access schemes. NOMA-based multi-antenna techniques are proposed in [4] for the evolution of next generation multiple access. A coded pilot random access scheme is proposed in [20] for massive Multiple-Input Multiple-Output (MIMO) systems. To deal with high spectral efficiency and large-scale connectivity, a power level-based NOMA modulation technique is proposed for NGMA in [21]. Extra information bits are encoded into the power levels. Different signal constellations are utilized for different power levels to help the receiver distinguish mixed signals.

An energy-efficient Slotted ALOHA protocol based on SIC is studied in [22]. The model assumed there is similar to that presented in this paper. The analysis proves that there exists a significant increase in throughput due to the SIC. A few other strategies are proposed in [23, 24] for energy-efficient wireless sensor networks (WSN). A cooperative Slotted ALOHA-based model is studied in [25] for throughput maximization.

Different power allocation methods have been proposed in [26, 27] based on NOMA along with SIC at the receiver side, both for uplink and downlink scenarios. A particle swarm optimization with a genetic algorithm is proposed in [26], which utilizes the channel state information to obtain better performance metrics, especially throughput and average consumed energy. A straightforward model of NOMA along with SIC is studied in [28], where the main parameter is the distance between the user and the base station. Bit Error Ratio (BER) performance of a downlink NOMA model is investigated in [29] with ideal and non-ideal SIC conditions.

Recently, age of information has been considered as a more relevant metric than throughput and delay in many multiple access applications, e.g., IoT and sensor networks. Age of information is analyzed in [30] for NOMA along with SIC. A comparison is done with Orthogonal Multiple Access (OMA) schemes, like Time Division Multiple Access (TDMA) and Frequency Division Multiple Access (FDMA). Two sensors are considered around the Access Point (AP), and it is seen that SIC-based NOMA outperforms the OMA schemes. A modified version of Slotted ALOHA is proposed in [31] to minimize the network-wide average age of information. It is named as Mini-Slotted Threshold ALOHA (MiSTA). A similar analytical study is done based on game theory for MAC layer protocol, Slotted ALOHA, in [32] with capture effect.

A CSMA-SIC-based study for a three-node network is presented in [33]. It shows that most of transmission opportunities provided by SIC are not exploited, even if CSMA is optimized. This proves that MAC protocols should be re-designed having in mind the potential of SIC. Along these lines, a SIC-based MAC-layer protocol in Wireless Local Area Network (WLAN) is defined in [34]. Also, a few strategies for maximizing the SIC-based gains are analyzed. A SIC-aware scheduling algorithm is developed in [34] for WLANs.

The perspective of this paper is broader than most literature contributions that deal with techniques to achieve practical SIC solutions. Instead, we highlight fundamental trade-offs in a general modeling framework of random multiple access with SIC. We aim at answering the following question: given new physical layer and signal processing techniques that boost the communication channel performance, and considering a random access-based IoT scenario, where should we spend most efforts for system performance improvement, physical or MAC layer? To explore this issue, we state a unifying model setting that encompasses both Slotted ALOHA and CSMA, SIC-based receiver as well as simple receiver that can only exploit capture effect.

3 System model

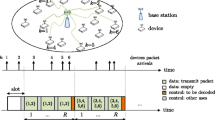
We consider n nodes sharing a communication channel. Nodes are scattered uniformly at random within a maximum distance R from a Base Station (BS). Nodes send update messages to the BS, that acts as a collector. We assume that the n nodes are saturated, i.e., they always have packets ready to send.

3.1 Spectral efficiency

Let W denote the bandwidth of the shared communication channel and \(\eta \) be the target spectral efficiency (bit/s/Hz) selected by the nodes, e.g., by properly setting the modulation and coding scheme of the communication link. The achieved data rate is \(\eta W\) bit per second.

We assume that the communication link can be modeled as an Additive White Gaussian Noise (AWGN) channel, i.e., the additive impairments, including noise and interference, are modeled as white Gaussian processes with zero mean. Then, the spectral efficiency \(\eta \) is related to the required level of Signal-to-Interference-plus-Noise Ratio (SINR) \(\gamma \) as follows:

$$\begin{aligned} \eta = \log _2 \left( 1 + \gamma \right) \end{aligned}$$
(1)

In the following, we assume that a block of data bits (packet) is decoded successfully if the average SINR at which the packet is received exceeds the threshold \(\gamma = 2^\eta - 1\).

3.2 SINR and path loss model

The SINR \(\Gamma \) at the receiver side is given by

$$\begin{aligned} \Gamma = \frac{ G P_{tx} }{ P_N+P_I } \end{aligned}$$
(2)

where we use the following definitions:

G:

path gain of the link between the transmitter and the receiver.

\(P_{tx}\):

transmitted power level.

\(P_N\):

background thermal noise power level.

\(P_I\):

interference power level.

We model the path gain, \(G = G_d G_s G_f\), as the product of a deterministic component \(G_d\), accounting for distance between the transmitter and the receiver, a log-normal random component \(G_s\), accounting for shadowing, and a negative exponential random component \(G_f\), accounting for multi-path Rayleigh fading.

The deterministic path gain \(G_d\) follows a power law: \(G_d = \kappa /d^\alpha \), where \(\kappa \) is a constant that depends on the carrier frequency and antenna gains, d is the distance between the transmitter and the receiver, and \(\alpha \) is the path gain exponent, typically in the range of 2 to 5.

The shadowing \(G_s\) is assumed to remain the same for a given node throughout its communication activity. It is given by \(G_s = 10^{ \sigma _s Z / 10 }\), where \(\sigma _s\) is the shadowing standard deviation in dB and Z is a standard Gaussian random variable (zero mean, unit variance).

The fading \(G_f\) depends on variability of the propagation scenario. It is sampled from a negative exponential probability distribution with unit mean, independently packet by packet. Hence, it is \(\mathcal {P}( G_f> x ) = e^{ - x }, \; x > 0\).

3.3 Power control and interference

Power control is in place, so that nodes aim at achieving an average target level of SNR at the receiving BS. We account for the limited power dynamic range of nodes by requiring that \(P_{\text {tx}} \in [ P_{\text {tx,min}} \; P_{\text {tx,max}} ]\). Let \(S_0\) denote the target SNR level. The node can estimate its deterministic and shadowing path gain components, e.g., by means of periodic pilot tones sent by the BS. Then, the node sets its transmission power level so as to compensate those two components (fast Rayleigh fading changes packet by packet and cannot be compensated by means of power control). Hence, transmission power is set as follows:

$$\begin{aligned} P_{tx} = \max \left\{ P_{\text {tx,min}} \;,\; \min \left\{ P_{\text {tx,max}} \;,\; S_0 \frac{ P_N }{ G_d G_s } \right\} \right\} \end{aligned}$$
(3)

The value of \(S_0\) is chosen as follows: The received SINR in case of no interference (single transmitter) is \(\Gamma = S_0 G_f\). Packet decoding is successful, if \(\Gamma > \gamma \), i.e., if \(G_f > \gamma /S_0\). Since \(G_f\) is a negative exponential random variable with mean 1, the probability of successful decoding, in case of a single transmitter (no interference), is \(e^{-\gamma /S_0}\). The level \(S_0\) is set so that this probability be at least \(1-\epsilon \), i.e., \(S_0 = -\gamma /\log (1-\epsilon )\).

Let us consider a reference node, say node 1. The interference power is the summation of power received from all nodes, transmitting at the same time as node 1. Generalizing to any node i, we can write the SINR for the i-th node as follows:

$$\begin{aligned} \Gamma _i \!=\! \frac{ G_{d,i} G_{s,i} G_{f,i} P_{tx,i} }{ P_N \!+\! \sum _{ j \ne i }{ G_{d,j} G_{s,j} G_{f,j} P_{tx,j}}} \!=\! \frac{ G_{f,i} \hat{S}_{0,i} }{ 1 \!+\! \sum _{ j \ne i }{ G_{f,j} \hat{S}_{0,j}}} \end{aligned}$$
(4)

where power control implies that

$$\begin{aligned} S_{0,j} \!=\! \max \left\{ \frac{ G_{d,j} G_{s,j} P_{\text {tx,min}} }{ P_N }, \min \!\left\{ \frac{ G_{d,j} G_{s,j} P_{\text {tx,max}} }{ P_N }, S_0 \!\right\} \!\right\} \end{aligned}$$
(5)

for \(j = 1,\dots ,n\).

3.4 Multi-packet reception

MPR is implemented thanks to SIC. Let us assume that k packets are received simultaneously and let \(S_j, \, j = 1,\dots ,k\) be their respective received power levels, normalized with respect to the background noise power level (hence, the \(S_i\)’s are non-dimensional). Assume they are ordered in descending order, i.e., \(S_1 \ge S_2 \dots \ge S_k\) (ties are broken at random). SIC works as follows: Provided decoding of packets \(1,\dots ,h-1\) be successful, packet h is decoded successfully if and only if the following inequality holds:

$$\begin{aligned} \frac{ S_h }{ 1 + \sum _{ r = h+1 }^{ k }{ S_r } } \ge \gamma \end{aligned}$$
(6)

Note that we assume perfect interference cancellation. Hence, the residual interference is due only to signals weaker than the h-th one.

For comparison purposes, we will also consider a plain receiver not endowed with SIC capability. In that case, MPR is still possible, thanks to capture effect. Specifically, packet h is successfully received if and only if its SINR exceeds \(\gamma \), which in case of capture only turns into the following inequality:

$$\begin{aligned} \frac{ S_h }{ 1 + \sum _{ r = 1, r \ne h }^{ k }{ S_r } } \ge \gamma \end{aligned}$$
(7)

The transmission time of a packet (including overhead) is denoted with T. Let L denote the packet length. Since the bit rate that a node can afford with a required SINR level of \(\gamma \) is \(W\log _2(1+\gamma )\), the packet transmission time and packet length are tied by the following relationship:

$$\begin{aligned} T = \frac{ L }{ W \log _2(1+\gamma ) } \end{aligned}$$
(8)

In case of Slotted ALOHA, it is assumed that the slot time is equal to T, i.e., one packet transmission fits exactly the slot time.

4 Model analysis

We define the following node-related performance metrics:

  • U(i), rate of node i, i.e., the mean number of bits delivered by node i per unit time, normalized by the channel bandwidth.

  • \(P_s(i)\), probability of successful packet delivery by node i.

  • E(i), mean energy consumed by node i per delivered packet.

  • A(i), mean age of information of node i.

The global sum-rate U is given by \(U = \sum _{ i = 1 }^{ n }{ U(i) }\). The overall success probability \(P_s\) is obtained by averaging the corresponding individual node metric, i.e., \(P_s = \frac{ 1 }{ n } \sum _{ i = 1 }^{ n }{ P_s(i) }\). The global energy consumption must be calculated by means of a weighted average, where the mean energy per delivered packet of each source node is weighted by the average rate of delivered packets of that source node. In other words, the global mean energy consumption is obtained as the ratio of the overall energy consumption of all nodes, divided by the overall number of correctly delivered packets. As for the age of information, the relevant global metric is obtained simply as an arithmetic average of individual values of each node.

In the following, we analyze these metrics in case of Slotted ALOHA and CSMA protocols.

4.1 Analysis of Slotted ALOHA

Time is slotted, and slot size equals the packet transmission time T. A station transmits in the current slot with probability p, while it defers to next slot with probability \(1-p\), where the same procedure is repeated.

The probability that k nodes transmit in a time slot is

$$\begin{aligned} w_k = \left( {\begin{array}{c}n\\ k\end{array}}\right) p^k (1-p)^{n-k} \end{aligned}$$
(9)

Let \(q_{h \mid k}\) be the conditional probability that h packets are decoded successfully, given that k nodes transmit simultaneously, for \(h = 0,1,\dots ,k\) and \(k \ge 1\). Let M denote the number of successfully decoded packets in a time slot. The mean number of successfully delivered packets in a time slot is

$$\begin{aligned} \textrm{E}[M] = \sum _{ k = 1 }^{ n }{ w_k \sum _{ h = 0 }^{ k }{ h q_{ h \mid k } } } = \sum _{ k = 1 }^{ n }{ m_k w_k } \end{aligned}$$
(10)

where \(m_k\) is the mean number of successfully decoded packets in a slot, conditional on k nodes attempting their transmissions. Let \(s_k(j)\) be the probability that node j is successful, given that it transmits in a slot along with k other nodes, \(0 \le k \le n-1\). It is easy to prove that

$$\begin{aligned} m_k = \frac{ k }{ n } \left[ s_{k-1}(1) + \dots + s_{k-1}(n) \right] \end{aligned}$$
(11)

for \(k = 1,\dots ,n\).

Let us consider a given scenario, with fixed nodes. The SNR of node j is denoted with \(S_{0,j}\). For \(k=1\), it is easy to verify that \(s_0(j) = e^{-\gamma /S_{0,j}}\). For larger values of k, the calculation depends on the way interference is dealt with (either capture or cancellation). As a matter of example, for given values of \(S_{0,j}, \, j = 1,\dots ,n\), in case of capture only (no SIC), a formal expression for \(s_k(j)\) is as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} s_0(j) \!=\! e^{ - \gamma / S_{0,j} } &{} k \!=\! 0 \\ s_k(j) \!=\! e^{ - \gamma / S_{0,j}}\! \sum _{ (i_1,\dots ,i_k) \in \mathcal {C}_{n-1,k} }{ \prod _{ h = 1 }^{ k }{ \frac{ 1 }{ 1 + \gamma S_{0,i_h} / S_{0,j}}}}\! &{} k \!=\! 1,\!\dots \!,n\!-\!1 \end{array}\right. } \end{aligned}$$
(12)

where \(\mathcal {C}_{n-1,k}\) is the set of all ways to select k indices from the set \(\{1,2,\dots ,n-1\}\), irrespective of the order. Note that the summation extends to \(\left( {\begin{array}{c}n-1\\ k\end{array}}\right) \) terms, so the expression above has little practical value for large values of n. No effective analytic closed formula has been found in case of SIC. Hence, we resort to ad hoc simulation to provide an accurate estimate of the \(s_k(j)\)’s for each given value of \(\gamma \).

4.1.1 Probability of success

The probability of success can vary from node to node, since power control is not perfect, i.e., the finite power dynamics can forbid some nodes from achieving the target SNR \(S_0\) at the receiver. The success probability of node j, given that it transmits, is obtained by weighting the conditional probability \(s_h(i)\) with the probability of the event that h nodes other than node i transmit in the same slot. Hence,

$$\begin{aligned} P_s(i) = \sum _{ h = 0 }^{ n-1 }{ s_h(i) { \left( {\begin{array}{c}n-1\\ h\end{array}}\right) } p^h (1-p)^{ n-1-h } } \end{aligned}$$
(13)

Note that \(\textrm{E}[M] = \sum _{ i = 1 }^{ n }{ p P_s(i) }\). We define an overall success probability as follows:

$$\begin{aligned} P_s = \frac{ 1 }{ n } \sum _{ i = 1 }^{ n }{ P_s(i) } \end{aligned}$$
(14)

4.1.2 Sum-rate

Let L be the number of bits in one packet. The amount of bits decoded successfully in a slot is \(L \textrm{E}[M]\), and the resulting delivered bit rate is \(R = L \textrm{E}[M]/T = W \log _2(1+\gamma ) \textrm{E}[M]\), where we have used Eq. (8). The overall sum-rate is \(U = R/W\), that is,

$$\begin{aligned} U = \log _2\left( 1 + \gamma \right) \sum _{ k = 1 }^{ n }{ m_k \left( {\begin{array}{c}n\\ k\end{array}}\right) p^k (1-p)^{n-k} } \end{aligned}$$
(15)

In the following, we set the transmission probability p to the value that maximizes the mean number of packets delivered per slot, namely, \(\textrm{E}[M]\), which also maximizes the sum-rate. Note that the optimal p is a function of \(\gamma \), since the \(m_k\)’s are.

We obtain the rate of node i as the product of the spectral efficiency \(\eta \), the probability p with which a node transmits, and \(P_s(i)\), the probability of success of node i, given that it transmits:

$$\begin{aligned} U(i)= & {} \log _2(1+\gamma ) p P_s(i) = \log _2(1+\gamma ) p \sum _{ h = 0 }^{ n - 1 } s_h(i) \nonumber \\{} & {} \quad \times { \left( {\begin{array}{c}n-1\\ h\end{array}}\right) } p^h (1-p)^{ n-1-h } \end{aligned}$$
(16)

It can be checked that \(U = \sum _{ i = 1 }^{ n }{ U(i) }\).

4.1.3 Energy

Let E denote the mean amount of energy per delivered packet. The mean energy consumed by node i in a slot is \(p P_{tx}(i) T\). The mean number of packets delivered by node i in a slot is \(p P_s(i)\). The mean required energy per delivered packet of node i is therefore given by

$$\begin{aligned} E(i) = \frac{ p P_{tx}(i) T }{ p P_s(i) } = \frac{ L }{ W \log _2(1+\gamma ) } \frac{ P_{tx}(i) }{ P_s(i) } \end{aligned}$$
(17)

Also in this case, we define a global metric by averaging E(i) over all nodes. The mean number of packets delivered successfully by node i over K slot times equals \(K p P_s(i)\). The average number of packets delivered successfully by all nodes over K slot times is \(K n p P_s\). Hence, the weight to be used for E(i) is \(w_i = K p P_s(i) / (K n p P_s ) = P_s(i) / ( n P_s )\). Then, the global average energy per successfully delivered packet is given by

$$\begin{aligned} E = \sum _{ i = 1 }^{ n }{ \frac{ P_s(i) }{ n P_s } E(i) } = \frac{ L }{ P_s W \log _2(1+\gamma ) } \, \frac{ 1 }{ n } \sum _{ i = 1 }^{ n }{ P_{\text {tx}}(i) } \end{aligned}$$
(18)

4.1.4 Age of information

The mean age of information can be defined as the mean age of updates collected at the BS from each individual node. Let us focus on node i, and let Y(i) be the number of slots separating the delivery of two consecutive successful packets of node i. It is easy to recognize that Y(i) is a Geometric random variable with ratio equal to \(p P_s(i)\). Then, it is \(\textrm{E}[ Y(i) ] = 1/(p P_s(i))\) and \(\textrm{E}[ Y(i)^2 ] = (2-p P_s(i) )/(p P_s(i))^2\). Therefore, for node i, we get

$$\begin{aligned} A(i)= & {} T \frac{ \textrm{E}[ Y(i)^2 ] }{ 2 \textrm{E}[ Y(i) ] } \!=\! T \left( \frac{ 1 }{ p P_s(i) } \!-\! \frac{ 1 }{ 2 } \right) \!=\! \frac{ L }{ W \log _2(1+\gamma ) }\nonumber \\{} & {} \quad \times \left( \frac{ 1 }{ p P_s(i) } - \frac{ 1 }{ 2 } \right) \end{aligned}$$
(19)

4.2 Analysis of CSMA

Let us define the back-off slot time as the time required to perform channel sensing. Let \(\delta \) denote the duration of the back-off slot time. A node sensing an idle back-off slot time starts transmitting with probability p. With probability \(1-p\), the node defers to next back-off slot, where the procedure is repeated. Transmission time lasts T.

We assume nodes can hear each other.Footnote 1 Therefore, back-off time slot boundaries are synchronized. We define the virtual slot time as the time elapsing between two consecutive idle back-off slot times. Let V denote the random variable representing the duration of a virtual slot time. V is either equal to \(\delta \), if no node transmits, or \(\delta +T\), if at least one node transmits. The probability that no node transmits in a slot is \((1-p)^n\). Then, the mean duration of the virtual slot is

$$\begin{aligned} \textrm{E}[V] \!=\! \delta (1-p)^n + (\delta +T ) [1-(1-p)^n] \!= \delta + T [1-(1-p)^n] \end{aligned}$$
(20)

For the renewal reward theorem, we can write the throughput in terms of packets per unit time as \(\Lambda = \frac{ \textrm{E}[M] }{ \textrm{E}[V] }\). Then, the normalized throughput \(\rho \) is

$$\begin{aligned} \rho = T \Lambda = \frac{ T \textrm{E}[M] }{ \textrm{E}[V] } = \frac{ T \sum _{ k = 0 }^{ n }{ w_k m_k } }{ \delta + T [1-(1-p)^n] } \end{aligned}$$
(21)

4.2.1 Sum-rate and probability of success

The average amount of bits delivered in a transmission time T is \(L \rho \). The average delivered bit rate is \(R = L \rho /T = W \log _2(1+\gamma ) \rho \), where we have used Eq. (8). The sum-rate is \(U = R/W\), that is,

$$\begin{aligned} U = \log _2\left( 1 + \gamma \right) \frac{ \sum _{ k = 1 }^{ n }{ w_k m_k } }{ \beta + 1-(1-p)^n } \end{aligned}$$
(22)

where \(\beta = \delta /T\) is the normalized back-off time slot duration. Note that we assume \(\delta \) is a constant and does not scale with \(\gamma \). As a consequence, \(\beta \) varies with \(\gamma \), since T varies with \(\gamma \).

Also with CSMA, we set the transmission probability p to the value that maximizes the sum-rate. The optimal p in case of CSMA takes a different value with respect to the optimal p with Slotted ALOHA. Expressions for the success probabilities \(P_s(i)\) in case of CSMA are the same as those holding for Slotted ALOHA. However, numerical values of success probability differ because of the different optimal p value of CSMA with respect to Slotted ALOHA.

4.2.2 Energy

The energy consumption is computed considering that a CSMA node can be in one of three states:

  1. 1.

    Transmitting, corresponding to power level \(P_0+P_{tx}(i)\) for node i.

  2. 2.

    Receiving/listening, corresponding to power level \(P_0\).

  3. 3.

    Sleeping (doze mode), where we assume that no power is consumed.

The logic is as follows: Maintaining an active transceiver chain costs a power consumption of \(P_0\). If in addition the node transmits, a power level \(P_{\text {tx}}\) adds to the baseline power consumption \(P_0\).

The metric E is defined as the mean consumed energy per delivered packet. We evaluate mean consumed energy and mean number of carried bits with reference to a virtual slot time. A virtual slot time lasts \(\delta \) if no node transmits (nodes only do sensing), or \(\delta +T\) if at least one node transmits. In the latter case, all nodes do sensing for a time \(\delta \), then some of them transmit for a time T, and the remaining ones listen to the channel (to check when it goes back to idle) over time T.

Let us focus on a given node i. The mean energy consumed in a virtual slot by node i is

$$\begin{aligned} E_{VS}(i) \!= \! (1-p) \left( P_0 \delta (1-p)^{n-1} + P_0 (\delta +T) [1-(1-p)^{n-1} ] \right) \nonumber \\ + p \left( P_0 \delta \!+\! [ P_0\!+\!P_{tx}(i) ] T \right) \end{aligned}$$
(23)

The mean number of packets sent by node i and successfully delivered in a virtual time slot is \(Q_{VS}(i) = p P_s(i)\), where \(P_s(i)\) is the success probability of node i. So the mean energy consumed by node i can be found as follows:

$$\begin{aligned} E(i)&= \frac{ E_{VS}(i) }{ Q_{VS}(i) } = \frac{ P_0 \delta + P_0 T [ 1 - (1-p)^n ] + p P_{tx}(i) T }{ p P_s(i) } \\&= \frac{ L }{ W \log _2(1+\gamma ) } \left( P_0 \frac{ \beta + 1 - (1-p)^n }{ p P_s(i) } + \frac{ P_{tx}(i) }{ P_s(i) } \right) \end{aligned}$$

Note that the average energy per packet for node i is the sum of two terms. One is the same as the energy per delivered packet in case of Slotted ALOHA. The other one is proportional to \(P_0\), and it is due to channel sensing.

We define a global metric E, as the average energy per successfully delivered packet belonging to any node. The mean number of packets delivered successfully by node i in a virtual slot time is \(p P_s(i)\). The mean number of packets delivered successfully by all nodes in a virtual slot time is \(n p P_s\). Hence, the weight of E(i) in the global metric E is given by \(w_i = p P_s(i) / (n p P_s ) = P_s(i) / ( n P_s )\). Then, the global average energy per successfully delivered packet is

$$\begin{aligned} E= & {} \sum _{ i = 1 }^{n}{\frac{ P_s(i)}{n P_s} E(i) } = \frac{ L }{ P_s W \log _2(1+\gamma ) } \, \Bigg ( P_0 \frac{ \beta + 1 - (1-p)^n }{ p }\nonumber \\{} & {} \quad + \frac{ 1 }{n} \sum _{ i = 1 }^{ n }{ P_{\text {tx}}(i) } \Bigg ) \end{aligned}$$
(24)

Note that the global average energy in case of CSMA is the sum of two terms. The first one accounts for energy dissipated during sensing of the channel (it is the term proportional to \(P_0\)). The second term is formally identical to the global average energy per delivered packet in case of Slotted ALOHA. Note however that the success probability \(P_s\) and the optimized probability of transmission p may take different values for CSMA and Slotted ALOHA. Therefore, CSMA does not require necessarily more energy per packet than Slotted ALOHA, in the considered setting (saturated stations).

4.2.3 Age of information

We consider the point of view of a node, say node i. Let V denote the duration of the virtual slot time seen by node i when it is idle, and let C denote the time required for a node to countdown idle back-off slots, until it attempts transmission. It is

$$\begin{aligned} V = {\left\{ \begin{array}{ll} \delta &{} \text { with probability } q, \\ \delta +T &{} \text { otherwise}. \end{array}\right. } \end{aligned}$$
(25)

where \(q = (1-p)^{n-1}\) is the probability that no node \(\ne i\) transmits. The Laplace Transform (LT) of the PDF of V is

$$\begin{aligned} \varphi _V(s) = \textrm{E}[ e^{ - s V } ] = e^{ - s \delta } q + e^{ - s ( \delta + T ) } ( 1 - q ) \end{aligned}$$
(26)

The time C is equal to

$$\begin{aligned} C = {\left\{ \begin{array}{ll} \delta +T &{} \text {if } K = 0, \\ \sum _{ k=1 }^{ K }{ V_k } + \delta +T &{} \text {if } K \ge 1. \end{array}\right. } \end{aligned}$$
(27)

where \(\mathcal {P}( K = h ) = (1-p)^h p, \; h \ge 0\). The LT of the PDF of C is given by

$$\begin{aligned} \varphi _C(s) = \textrm{E}[ e^{ - s C } ] = \frac{ p e^{ - s ( \delta + T ) } }{ 1 - (1-p) \varphi _V(s) } \end{aligned}$$
(28)

The time Y between two consecutive successful packet delivery from the considered node to the BS is given by

$$\begin{aligned} Y = \sum _{ k = 1 }^{ N }{ C_k } \end{aligned}$$
(29)

where \(\mathcal {P}( N = h ) = (1-P_s(i))^{h-1} P_s(i), \; h \ge 1\). Hence, the LT of the PDF of Y is given by

$$\begin{aligned} \varphi _Y(s) = \textrm{E}[ e^{ - s Y } ] = \frac{ P_s(i) \varphi _C(s) }{ 1 - (1-P_s(i)) \varphi _C(s) } \end{aligned}$$
(30)

Note that the transmission time T is tied to the SINR requirement \(\gamma \): \(T = \frac{ L }{ W_{ch} \log _2(1+\gamma ) }\), for a given value of the number L of bits in a packet.

The mean AoI of node i is given by

$$\begin{aligned} A(i) = \frac{ \textrm{E}[ Y^2 ] }{ 2 \textrm{E}[ Y ] } = \frac{ \textrm{E}[ C^2 ] }{ 2 \textrm{E}[ C ] } + \textrm{E}[ C ] \left( \frac{ 1 }{ P_s(i) } - 1 \right) \end{aligned}$$
(31)

It can be verified that

$$\begin{aligned}&\textrm{E}[ C ] = \frac{ 1-p }{ p } \textrm{E}[ V ] + \delta + T = T \frac{ \beta + 1 - (1-p)^n }{ p } \end{aligned}$$
(32)
$$\begin{aligned}&\textrm{E}[ C^2 ] = \frac{ 1-p }{ p } \textrm{E}[ V^2 ] + \left( \frac{ 1-p }{ p } \textrm{E}[ V ] \right) ^2 + \left( \textrm{E}[ C ] \right) ^2 \end{aligned}$$
(33)

where

$$\begin{aligned} \textrm{E}[ V ]&=\delta + T (1-q) = T ( \beta + 1 - q ) \end{aligned}$$
(34)
$$\begin{aligned} \textrm{E}[ V^2 ]&= \delta ^2 + 2 \delta T (1-q) + T^2 (1-q) \nonumber \\&= T^2 \left[ ( \beta + 1 - q )^2 + q ( 1-q ) \right] \\&= T^2 q ( 1-q) + ( \textrm{E}[ V ] )^2 \nonumber \end{aligned}$$
(35)

where \(q = (1-p)^{n-1}\) and \(\beta = \delta / T\).

5 Performance evaluation

The presented analytical models are validated against MATLAB simulations by implementing the MAC layer protocols Slotted ALOHA and CSMA, along with the system model defined in Section 3.

More in depth, the considered approach is semi-analytic. The mean number of correctly decoded packets given that k nodes transmit, \(m_k\), is estimated by mean of dedicated simulations. The estimated value is used in the analytic formulas introduced earlier. Also, the individual success probabilities \(P_s(i)\) are estimated by means of dedicated simulations and then fed into the analytic formulas.

In case of CSMA, it is assumed that all nodes hear each other, and hence back-off slot boundaries are synchronized. The performance metrics introduced in Section 4 are plotted as a function of the SINR threshold \(\gamma \). We consider a quite stretched range of values of \(\gamma \), mainly for the purpose of highlighting the existence of different operational regimes in the system. Numerical values assigned to system parameters are listed in Table 1. A quite large value has been considered for the back-off slot time of CSMA. They are generally targeted to low-bit rate applications, e.g., sensor networks. Note that, since the theoretical transmission rate is \(W \log _2(1+\gamma )\) and the length of messages is fixed to L, the time to transmit one message (slot time in Slotted ALOHA, transmission time in CSMA) is \(T = L/(W \log _2(1+\gamma ))\), hence it varies with \(\gamma \). Therefore, the ratio \(\beta = \delta /T\) is actually a function of \(\gamma \). For the lowest considered value of \(\gamma \), namely, \(\gamma = 0.01\), we have \(T \approx 139.3~ms\), hence \(\beta \approx 0.00072\). For the largest considered value of \(\gamma = 1000\), we have \(T \approx 0.2~ms\) and hence \(\beta \approx 0.5\).

Table 1 Numerical values used in the performance evaluation
Full size table
Fig. 1
figure 1

Mean number of correctly decoded packets conditional on k nodes transmitting, \(m_k\), as a function of SINR threshold \(\gamma \), in case of capture effect only

Full size image
Fig. 2
figure 2

Mean number of correctly decoded packets conditional on k nodes transmitting, \(m_k\), as a function of SINR threshold \(\gamma \), in case of SIC at the receiver

Full size image

Two kinds of plots are displayed: global metrics and individual performance indicators.

In each plot of the first kind, Slotted ALOHA and CSMA are compared with and without SIC (i.e., only capture effect is in place). Global metrics curves referring to Slotted ALOHA are colored in blue, and curves of CSMA are red. Curves referring to SIC are plotted as solid lines, capture only (without SIC) being plotted as dashed line curves. In case of per-node performance metrics, four different plots are reported, one for each case of Slotted ALOHA/CSMA without/with SIC, for a clearer vision of results. In each plot, ten curves are shown, one for each node.

Fig. 3
figure 3

Optimal value of the transmission probability p as a function of SINR threshold \(\gamma \). (SA, Slotted ALOHA)

Full size image

5.1 Mean number of successfully decoded packets

The mean number of correctly decoded packets in one transmission time, \(m_k\), conditional on k nodes transmitting, is shown in Fig. 1 in case of capture effect only (no SIC). Figure 2 shows \(m_k\) in case of SIC. Both these figures are shown for several values of k.

In both cases, \(m_k\) is monotonously decreasing with \(\gamma \), which is quite intuitive, based on the fact that the higher the \(\gamma \), the more difficult to decode correctly the superposed packets. Note that \(m_1\) decays as \(\gamma \) grows, since transmission power is limited to \(P_{\text {tx}}\). Another common feature of \(m_k\) plots with respect to capture and SIC is that for large values of \(\gamma \), \(m_1\) appears to be the strongest candidate, i.e., the less the number of superposed packets, the better for the success of decoding. On the contrary, for small \(\gamma \) values, the higher k, the better. In fact, for very low \(\gamma \) values, interference cancellation is quite effective and even capture works fine for many packets. This is not so counter-intuitive, if one thinks of what actually happens here, e.g., in case code division multiple access is used, or any other multiplexing technique which is robust against interference.

Fig. 4
figure 4

Sum-rate U as a function of SINR threshold \(\gamma \) for the optimized value of the transmission probability p. (SA, Slotted ALOHA)

Full size image
Fig. 5
figure 5

Slotted ALOHA probability of success of individual nodes as a function of SINR threshold \(\gamma \). (a) Without SIC; (b) with SIC

Full size image

The main difference between the results with and without SIC lies with the behavior of curves in the transition region, for intermediate values of \(\gamma \). The transition in case of SIC is much sharper than in the other case, denoting a sort of threshold effect.

5.2 Optimization of transmission probability and sum-rate

Figure 3 shows the optimal value of the transmission probability p as a function of \(\gamma \). For low SINR threshold values, physical layer (SIC) is mainly responsible for improving the system performance, while the role of MAC layer is negligible, because all the nodes are allowed to transmit simultaneously. This is derived by the fact that optimal probability is equal to 1 in low SINR regime. For large values of \(\gamma \), the MAC layer is the bottleneck, since collisions are the main responsible for performance degradation. Hence, the optimal value of p becomes smaller and smaller as \(\gamma \) grows. This effect is also clear in the sum-rate plot in Fig. 4.

The sum-rate plot in Fig. 4 is quite interesting, since it reveals that sum-rate has two peaks, one in the low \(\gamma \) range and another one in the high \(\gamma \) range.

As for capture only performance, the highest sum-rate is achieved for relatively high values of \(\gamma \), while low spectral efficiency operation leads to very low sum-rate values. Moreover, CSMA turns out to offer superior sum-rate performance with respect to Slotted ALOHA, which is a well-known classic result. In other words, when working in the high spectral efficiency regime (high values of \(\gamma \)), SIC provides little gain to random access protocols in terms of throughput. Note that the high spectral efficiency regime is the typical choice of cellular system as well as WiFi.

A second peak of sum-rate appears for lower values of \(\gamma \), i.e., when the system is operated in a low spectral efficiency regime. This is the region of choice of, e.g., spread-spectrum systems, or of some sensor network technology, e.g., LoRaWAN. The same optimized performance is achieved by Slotted ALOHA and CSMA at this left peak of sum-rate, which is consistent with the fact that the optimal value of the transmission probability is 1 or close to 1, so that the MAC protocol plays essentially no role. On the contrary, SIC has a major effect on performance. When only the capture effect is exploited (no SIC), the achieved sum-rate is very low, definitely worse than what can be achieved at high \(\gamma \) values. If SIC is in place, a strong improvement of sum-rate is obtained, even better than what is offered by the high spectral efficiency regime.

5.3 Probability of success

The probability of successful transmission per node is plotted in Fig. 5 (with and without SIC) in case of Slotted ALOHA. For low values of SINR threshold, there exists perfect fairness among the nodes, i.e., all of them experience the same probability of success. As \(\gamma \) grows, the near-far effect takes hold and unfairness shows up, since nodes farther away from the BS cannot compensate their attenuation due to the limited transmission power range.

Similar comments apply to Fig. 6a, where the probabilities of success for individual nodes are plotted as a function of \(\gamma \) in case of CSMA. Differently from Slotted ALOHA, in case of CSMA, a non-trivial behavior of the success probability is apparent (see the discussion at the end of this section, with reference to Fig. 7).

The probability of success for each node is different due to the fact that the dynamic range of the transmission power is limited. Hence, the nodes that experience a large attenuation cannot possibly make up for it, due to limitation of their maximum transmission power level. This limitation creates unfairness among the nodes. Nodes close to the BS experience high probability of success, while nodes far away experience low probability of success. This difference of probability of success among the nodes becomes significant in high \(\gamma \) regime, as the required SINR levels are high.

Fig. 6
figure 6

CSMA probability of success of individual nodes as a function of SINR threshold \(\gamma \). (a) Without SIC; (b) with SIC

Full size image
Fig. 7
figure 7

Overall probability of success \(P_s\) as a function of the SINR threshold \(\gamma \). (SA, Slotted ALOHA)

Full size image

A key finding of these results stems from a comparison of sum-rate and success probability plots. Focusing on the location of sum-rate peak in low threshold regime, it can be checked that it occurs for values of \(\gamma \) for which node individual success probabilities coincide, i.e., unfairness disappears. Exploiting SIC and operating the system at low spectral efficiency achieves apparently a double advantage: high sum-rate and removal of unfairness.

Figure 7 represents the overall probability of success as a function of \(\gamma \). In this plot, the analytical models are compared with simulations. Simulations correspond to circle markers. Simulation results match perfectly with the analytical expression curves.

Fig. 8
figure 8

Overall average energy per delivered packet E as a function of the SINR threshold \(\gamma \). (SA, Slotted ALOHA)

Full size image
Fig. 9
figure 9

Slotted ALOHA mean energy consumed by individual nodes per delivered packet, as a function of SINR threshold \(\gamma \). (a) Without SIC; (b) with SIC

Full size image
Fig. 10
figure 10

CSMA mean energy consumed by individual nodes per delivered packet, as a function of SINR threshold \(\gamma \). (a) Without SIC; (b) with SIC

Full size image
Fig. 11
figure 11

Slotted ALOHA age of information of individual nodes as a function of SINR threshold \(\gamma \). (a) Without SIC; (b) with SIC

Full size image

The probability of success is high for low threshold regime and low for high threshold regime. In between these two regions, there exists a quite interesting behavior. While the overall success probability is monotonously decreasing in case of Slotted ALOHA, a non-trivial behavior shows up for CSMA. This is due to the decreasing value of the optimal transmission probability as \(\gamma \) grows. Hence, the average number of concurring transmissions decreases, boosting the value of success probability. As \(\gamma \) grows further, success probability definitely falls down, since the effect of the limited maximum transmission power level prevails.

Fig. 12
figure 12

CSMA age of information of individual nodes as a function of SINR threshold \(\gamma \). (a) Without SIC; (b) with SIC

Full size image

5.4 Energy

The overall average energy per delivered packet E is plotted as a function of the SINR threshold \(\gamma \) in Fig. 8. It is assumed that the sensing energy (power level consumed by a node while listening to the channel) is \(P_0 = 0.7 \cdot P_{\text {tx}}\), i.e., 70% of the transmission power level.

In general, required energy per delivered packet has a monotonous trend for increasing values of \(\gamma \). This comes at no surprise, given that higher power levels should be adopted by nodes to meet the more stringent requirement on the SINR threshold. It is less obvious why the curve is not actually monotonous. On the contrary, local peaks appear. This is due to the interplay of several factors: (i) the varying optimal level of transmission probability, (ii) the varying value of \(\beta \) in case of CSMA, and (iii) the variability of success probability with \(\gamma \).

Slotted ALOHA turns out to be much more parsimonious with respect to CSMA. However, it is to be noted that we are addressing saturated nodes, thus a node that is not transmitting with CSMA is always busy doing sensing. Even if less extreme scenarios were considered, it could be expected that the weight of power consumption due to sensing would make CSMA more demanding in terms of energy required per delivered packet. This stems also from observing that, in the physical layer-dominated region, i.e., for low values of \(\gamma \), both MAC protocols Slotted ALOHA and CSMA achieve the same sum-rate and success probability with SIC. Hence, CSMA offers no incentive in the face of the increased demand of energy due to sensing.

It turns out that SIC provides energy saving. This is due to the definition of E, which is the average energy spent to deliver a packet with success. Since SIC improves the probability of success, less re-transmissions are required to deliver a packet, and hence energy is saved with respect to the case, without SIC.

The mean energy consumed per delivered packet by each node is plotted in Figs. 9 and 10 (without and with SIC) for Slotted ALOHA and CSMA, respectively. The results highlight that the unfairness in energy consumption is the price that we pay to maximize global sum-rate, while maintaining fairness among the nodes in terms of probability of success of individual nodes for low values of SINR threshold (see Figs. 5 and 6).

The unequal energy consumption of nodes stems from considering a given scenario, where nodes stay at fixed positions. Since it is required that all nodes set their transmission power so as to compensate the long-term average path loss (deterministic path loss plus shadowing), it is consequential that farther nodes spend more energy to achieve this target. It is interesting that the minimum energy budget is struck at low SINR threshold values. It grows slowly at the beginning, and it finally ramps up very quickly when we move to the high SINR threshold range. The main reason of this behavior is the sharp decrease of success probability when \(\gamma \) grows. Also, note the fast growth of the energy per packet is quite different from node to node. Some of them (the closest to the BS) exhibit a moderate growth.

The same qualitative behavior is found by the comparison of curves, in Figs. 9 and 10 for Slotted ALOHA and CSMA, respectively. Somewhat larger values of the energy budget are exhibited by CSMA with respect to Slotted ALOHA for each value of \(\gamma \), as already anticipated by the overall energy per delivered packet. In case of low values of the SINR threshold, all nodes are transmitting, and the probability of success for each node is almost \(1-\epsilon = 0.9\) in this regime, due to the low requirement of SINR threshold. For this reason, the transmission power required of each node can be easily matched. For high values of the SINR threshold, the nodes need higher levels of transmission power. Hence, we expect a smaller success rate due to the maximum power limit. As a result, the energy curves increase in this region.

5.5 Age of information

The mean Age of Information (AoI) of each individual node is plotted in Fig. 11 (with and without SIC) for Slotted ALOHA. Similar comments apply to Fig. 12, where the individual node mean AoI is plotted as a function of \(\gamma \) in case of CSMA.

In the low \(\gamma \) range, SIC brings a major performance advantage, leading to a local minimum of AoI. Moreover, AoI performance coincides for all nodes, i.e., full fairness is achieved. If only capture effect is exploited, the local minimum is much less pronounced. A wide plateau appears, where AoI is largely insensitive to the specific value of the SINR threshold. Fairness is achieved as well.

In the large \(\gamma \) range, a very different behavior is observed. The AoI values taken by each nodes differ significantly from each other, thus giving evidence of great unfairness. For some nodes (the farthest ones from the BS), the AoI  exhibits an extremely fast increase, due to the collapse of success probability, ultimately tied to the upper limit on the transmission power level. The nodes closest to the BS manage to keep AoI at low values, even for very high values of \(\gamma \). At least for the more lucky nodes, the mean AoI shows a local minimum also in this range. However, the value of the minimal AoI is different for different nodes, and it is attained at different values of \(\gamma \). Another important aspect here is that the local minima of AoI at high levels of \(\gamma \) are higher in value than the local minima of AoI at low levels of \(\gamma \).

Comparing sum-rate, energy per packet and AoI in case of SIC, irrespective whether Slotted ALOHA or CSMA is used, we see that all performance are optimized at approximately the same point, corresponding to the tip point where the optimal transmission probability starts falling down from 1. In other words, optimal performance is obtained by running the system with the largest \(\gamma \) value for which it is optimal having all nodes transmit simultaneously. This optimal level of \(\gamma \) is identified by the left peak of the sum-rate.

6 Conclusion

This study presents a comprehensive analysis of several performance metrics of Slotted ALOHA and CSMA with and without successive interference cancellation. Our focus is on optimization of multiple performance metrics, namely, the sum-rate, probability of success, energy required per delivered packet, and the mean age of information, as the required SINR level at the receiver is varied.

Based on the results, we identify two regimes: the low threshold regime and the high threshold regime. The analysis shows that the performance in the low threshold regime is dominated by the physical layer (SIC), while MAC layer protocol has no influence. In the high threshold regime, performance is mainly determined by MAC layer protocol, due to the high cost of collisions that cannot be properly solved by SIC, because of the large required SINR level. We observed that the local optimization achieved in the low SINR threshold regime achieves generally better performance targets than the optimal point in the high \(\gamma \) range. An important outcome is that unfairness among nodes arises in the high \(\gamma \) regime, while any unfairness disappears at low \(\gamma \) values for all metrics, except energy consumption. Adopting SIC and setting the target spectral efficiency to relatively low values, a double advantage is achieved, optimal performance sum-rate, and AoI fairness among nodes. We highlight that achieving fairness is not trivial, since we consider stationary nodes that maintain different distances from the BS and we account for power control with a limited dynamic range.

As future work, non-saturated nodes are to be considered to match a massive multiple access scenario. We aim also to define distributed adaptive algorithm able to adjust the transmission probability p and the target SINR \(\gamma \) to achieve the sum-rate peak as the load on the system varies.