Performance analysis of full-duplex decode-and-forward two-way relay networks with transceiver impairments

Abstract

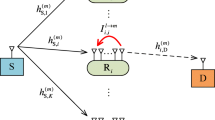
In this paper, we analyze the performance of an in-band full-duplex (IBFD) decode-and-forward (DF) two-way relay (TWR) system whose two terminal nodes exchange information via a relay node over the same frequency and time slot. Unlike the previous works on full-duplex two-way relay systems, we investigate the system performance under the impacts of both hardware impairments and imperfect self-interference cancellation (SIC) at all full-duplex nodes. Specifically, we derive the exact expression of outage probability based on the signal to interference plus noise and distortion ratio (SINDR), thereby determine the throughput and the symbol error probability (SEP) of the considered system. The numerical results show a strong impact of transceiver impairments on the system performance, making it saturate at even a low level of residual self-interference. In order to tackle with the impact of hardware impairments, we derive an optimal power allocation factor for the relay node to minimize the outage performance. Finally, the numerical results are validated by Monte Carlo simulations.

Appendices

Appendix A:: Detailed derivation of Theorem 1

• 1) Consider the case when $1 - {k_{1}^{2}}x \leqslant 0$ or $\lambda - k_{\mathrm {R}}^{2}y \leqslant 0$ or $1 - \lambda - k_{\mathrm {R}}^{2}x \leqslant 0$ or $1 - {k_{2}^{2}}y \leqslant 0$ or $(1 - {k_{1}^{2}}z \leqslant 0\& 1 - {k_{2}^{2}}z \leqslant 0)$, at least one of the five cases in Eq. 23, Eqs. 24, and 25 always occurs; therefore, $\mathcal {P}_{\text {out}} = 1$. For example, consider the probability of the first case in Eq. 23:

$$ \begin{array}{@{}rcl@{}} \begin{gathered} \text{Pr}\left\{ \gamma_{\mathrm{S}_{1}\mathrm{R}} < x \right\} = \text{Pr} \left\{ \frac{\rho_{1} P_{1}}{\sigma^{2}_{\mathrm{R}} + \sigma^{2}_{\mathrm{RSI_{R}}} + \rho_{1} {k_{1}^{2}} P_{1} + \rho_{2} {k_{2}^{2}} P_{2}} < x\right\} \\ \quad\quad\quad\quad\quad = \text{Pr}\{ \rho_{1} P_{1}(1 - {k_{1}^{2}}x) < t_{\mathrm{R}}x + \rho_{2} P_{2}{k_{2}^{2}}x\}. \\ \end{gathered} \end{array} $$

(55)

When $1 - {k_{1}^{2}}x \leqslant 0$, we always have $\rho _{1} P_{1}(1 - {k_{1}^{2}}x) < t_{\mathrm {R}}x + \rho _{2} P_{2} {k_{2}^{2}}x$. Thus, $\text {Pr}\{ \gamma _{\mathrm {S}_{1}\mathrm {R}} < x\} =1$. Therefore, OP of the system is given by $\mathcal {P}_{\text {out}} = 1$,

• 2) When all the conditions in 1) do not occur simultaneously, $\mathcal {P}_{\text {out}}$ is derived as follows:

• a) When $1 - {k_{1}^{2}}x > 0$ and $\lambda - k_{\mathrm {R}}^{2}y > 0$

$$ \begin{array}{@{}rcl@{}} \mathcal{P}_{\text{out}_{12}} = \int\limits_{0}^{\infty} \text{Pr}\{ \rho_{1} < \max (A_{1},A_{2})\}f_{\rho_{2}}(\rho_{2})d\rho_{2} \cdot \end{array} $$

(56)

where

$$ \begin{array}{@{}rcl@{}} A_{1} = \frac{t_{\mathrm{R}}x + \rho_{2} P_{2} {k_{2}^{2}}x}{P_{1}(1 - {k_{1}^{2}}x)}, A_{2} = \frac{t_{1}y}{P_{\mathrm{R}}(\lambda - k_{\mathrm{R}}^{2}y)} \cdot \end{array} $$

(57)

To determine the $\mathcal {P}_{\text {out}_{12}}$ from Eq. 56, we consider the case A₁ > A₂, thus

$$ \begin{array}{@{}rcl@{}} \frac{t_{\mathrm{R}}x + \rho_{2} P_{2} {k_{2}^{2}}x}{P_{1}(1 - {k_{1}^{2}}x)} > \frac{t_{1}y}{P_{\mathrm{R}}(\lambda - k_{\mathrm{R}}^{2}y)} \cdot \end{array} $$

(58)

Therefore, we have

$$ \begin{array}{@{}rcl@{}} \rho_{2} > \frac{P_{1} t_{1} y(1 - {k_{1}^{2}}x) - P_{\mathrm{R}} t_{\mathrm{R}}x(\lambda - k_{\mathrm{R}}^{2}y)}{P_{\mathrm{R}} P_{2} {k_{2}^{2}}x(\lambda - k_{\mathrm{R}}^{2}y)}. \end{array} $$

(59)

Set

$$ \begin{array}{@{}rcl@{}} A_{12} = \frac{P_{1} t_{1} y(1 - {k_{1}^{2}}x) - P_{\mathrm{R}} t_{\mathrm{R}} x(\lambda - k_{\mathrm{R}}^{2}y)}{P_{\mathrm{R}} P_{2} {k_{2}^{2}}x(\lambda - k_{\mathrm{R}}^{2}y)}, \end{array} $$

(60)

if ρ₂ > A₁₂, then A₁ > A₂, otherwise we have $A_{1} \leqslant A_{2}$. Thus, the expression (56) becomes

$$ \begin{array}{@{}rcl@{}} \begin{gathered} \mathcal{P}_{\text{out}_{12}} = \int\limits_{0}^{A_{12}} \text{Pr}\{ \rho_{1} < A_{2}\}f_{\rho_{2}}(\rho_{2})d\rho_{2} \\ \quad\quad\quad + \int\limits_{A_{12}}^{\infty} \text{Pr}\{ \rho_{1} < A_{1}\}f_{\rho_{2}}(\rho_{2})d\rho_{2} \cdot \\ \end{gathered} \end{array} $$

(61)

We now consider the condition for A₁₂ to derive the closed-form expression for Eq. 61.

• If $A_{12} \leqslant 0$, then

$$ \begin{array}{@{}rcl@{}} \lambda \geqslant k_{\mathrm{R}}^{2}y + \frac{P_{1} t_{1} y(1 - {k_{1}^{2}}x)}{P_{\mathrm{R}} t_{\mathrm{R}}x} = Y. \end{array} $$

(62)

Thus, the expression (61) becomes

$$ \begin{array}{@{}rcl@{}} \begin{gathered} \mathcal{P}_{\text{out}_{12}} = \int\limits_{0}^{\infty} \text{Pr}\{ \rho_{1} < A_{1}\}f_{\rho_{2}}(\rho_{2})d\rho_{2} \\ = 1 - Q_{1}. \\ \end{gathered} \end{array} $$

(63)

It is noted that the expression (63) is OP of the link from S₁ to R.

• If A₁₂ > 0 then λ < Y.

Thus, we can calculate the two integrals in Eq. 61 numerically as follows:

$$ \begin{array}{@{}rcl@{}} \begin{gathered} \mathcal{P}_{\text{out}_{12}} = \int\limits_{0}^{A_{12}} \text{Pr}\{ \rho_{1} < A_{2}\}f_{\rho_{2}}(\rho_{2})d\rho_{2} \\ \quad\quad\quad + \int\limits_{A_{12}}^{\infty} \text{Pr}\{ \rho_{1} < A_{1}\}f_{\rho_{2}}(\rho_{2})d\rho_{2} = 1 - Q_{2}. \\ \end{gathered} \end{array} $$

(64)

It is noted that expression (64) is OP of the links from R to S₁ and from S₁ to R. This differs from the ideal hardware system. For the ideal hardware system (k₁ = k₂ = k_R = 0) and expression (64) becomes OP of only the outage link from R to S₁.

Combining (63) with Eq. 64 we have OP of the links from S₁ to R and from R to S₁ as follows:

$$ \begin{array}{@{}rcl@{}} \mathcal{P}_{\text{out}_{12}} = \left\{ \begin{gathered} 1 - Q_{1}, \lambda \geqslant Y, \\ 1 - Q_{2},\lambda < Y. \\ \end{gathered} \right. \end{array} $$

(65)

• b) When $1 - \lambda - k_{\mathrm {R}}^{2}x > 0$ and $1 - {k_{2}^{2}}y > 0$, using the similar method, we have

$$ \begin{array}{@{}rcl@{}} \mathcal{P}_{\text{out}_{34}} = \int\limits_{0}^{\infty} \text{Pr}\{\rho_{2} < \max (A_{3},A_{4})\}f_{\rho_{1}}(\rho_{1})d\rho_{1} \end{array} $$

(66)

where

$$ \begin{array}{@{}rcl@{}} A_{3} = \frac{t_{\mathrm{R}}y + \rho_{1} P_{1} {k_{1}^{2}}y}{P_{2}(1 - {k_{2}^{2}}y)}, A_{4} = \frac{t_{2}x}{P_{\mathrm{R}}(1 - \lambda - k_{\mathrm{R}}^{2}x)}\cdot \end{array} $$

(67)

Therefore, OP of the links from S₂ to R and from R to S₂ are defined as follows

$$ \begin{array}{@{}rcl@{}} \mathcal{P}_{\text{out}_{34}} = \left\{ \begin{gathered} 1 - Q_{3}, \lambda \leqslant Z, \\ 1 - Q_{4}, \lambda > Z. \\ \end{gathered} \right. \end{array} $$

(68)

When $\lambda \leqslant Z$ we have $\mathcal {P}_{\text {out}_{34}} =1 - Q_{3}$ for the link from S₂ to R, and when λ > Z we have $\mathcal {P}_{\text {out}_{34}} = 1 - Q_{4}$ accounting for both the links from S₂ to R and from R to S₂.

• c) When the two conditions $1 - {k_{1}^{2}}z \leqslant 0$ and $1 - {k_{2}^{2}}z \leqslant 0$ are not simultaneously satisfied, we have:

  $$ \begin{array}{@{}rcl@{}} \mathcal{P}_{\text{out}_{5}} = \text{Pr}\{\mathcal{C}\} = \text{Pr}\{\gamma_{\text{sum}} < z\}. \end{array} $$

  (69)

Thus

$$ \begin{array}{@{}rcl@{}} \mathcal{P}_{\text{out}_{5}} = \text{Pr}\{ \rho_{1} P_{1}(1 - {k_{1}^{2}}z) + \rho_{2} P_{2}(1 - {k_{2}^{2}}z) < t_{\mathrm{R}}z\}. \end{array} $$

(70)

Therefore,

$$ \begin{array}{@{}rcl@{}} \mathcal{P}_{\text{out}_{5}} = 1 - Q_{5} \cdot \end{array} $$

(71)

Note that Q_i,i = 1 ÷ 5 in Eqs. 65, 68, and 71 are defined in Eqs. 30, 31, 32, 33, and 34, respectively. Combining (65), (68), and (71), and applying the following theorem in [36]:

$$ \begin{array}{@{}rcl@{}} \begin{gathered} \text{Pr}\{\mathcal{A} \cup \mathcal{B} \cup \mathcal{C} \} = \text{Pr}\{\mathcal{A}\} + \text{Pr}\{\mathcal{B}\} + \text{Pr}\{\mathcal{C}\} - \text{Pr}\{\mathcal{A} \cap \mathcal{B} \} \\ \quad\quad\quad\quad - \text{Pr}\{\mathcal{A} \cap \mathcal{C} \} - \text{Pr}\{\mathcal{B} \cap \mathcal{C} \} + \text{Pr}\{\mathcal{A} \cap \mathcal{B} \cap \mathcal{C} \} \\ \end{gathered} \end{array} $$

(72)

we can derive the exact expression of OP.

For example, for the outage links from R →S₁, and from S₁ → R, and from S₂ → R (case 1 in Table 1), the following conditions must be simultaneously satisfied

$$ \begin{array}{@{}rcl@{}} \left\{ \begin{gathered} 1 - {k_{1}^{2}}x > 0 \\ \lambda - k_{\mathrm{R}}^{2}y > 0 \\ 1 - \lambda - k_{\mathrm{R}}^{2}x > 0 \\ 1 - {k_{2}^{2}}y > 0 \\ \lambda < k_{\mathrm{R}}^{2}y + \frac{P_{1} t_{1} y(1 - {k_{1}^{2}}x)}{P_{\mathrm{R}} t_{\mathrm{R}} x} =Y \\ \lambda \leqslant 1 - k_{\mathrm{R}}^{2}x - \frac{P_{2} t_{2} x(1 - {k_{2}^{2}}y)}{P_{\mathrm{R}} t_{\mathrm{R}} y}=Z \\ \end{gathered}. \right. \end{array} $$

(73)

Therefore, the condition for power allocation factor λ becomes

$$ \begin{array}{@{}rcl@{}} \left\{ \begin{gathered} \lambda > k_{\mathrm{R}}^{2}y \\ \lambda < Y \\ \lambda \leqslant Z \\ \end{gathered}, \right. \end{array} $$

(74)

where the conditions $1 - {k_{1}^{2}}x > 0$ and $\lambda - k_{\mathrm {R}}^{2}y > 0$ are to guarantee that $\mathcal {P}_{\text {out}_{12}} \ne 1$ and Eq. 65 occurs; the conditions $1 - \lambda - k_{\mathrm {R}}^{2}x > 0$ and $1 - {k_{2}^{2}}y > 0$ are for $\mathcal {P}_{\text {out}_{34}} \ne 1$ and Eq. 68 occurs; the condition

$$ \begin{array}{@{}rcl@{}} \lambda < k_{\mathrm{R}}^{2}y + \frac{P_{1} t_{1} y(1 - {k_{1}^{2}}x)}{P_{\mathrm{R}} t_{\mathrm{R}}x} = Y \end{array} $$

(75)

is the the links from R →S₁ and S₁ → R, which is determined using Eq. 65; the condition

$$ \begin{array}{@{}rcl@{}} \lambda \leqslant 1 - k_{\mathrm{R}}^{2}x - \frac{P_{2} t_{2} x(1 - {k_{2}^{2}}y)}{P_{\mathrm{R}} t_{\mathrm{R}} y} = Z \end{array} $$

(76)

is for the link from S₂ → R, which is determined using Eq. 68. When all these conditions simultaneously occur, we can determine the condition $\mathcal {P}_{\text {out}_{5}} = 0$ for ${\gamma _{\text {sum}}} \geqslant z$ (i.e. outage does not occur). Therefore, the value of power allocation factor λ is determined as follows

$$ \begin{array}{@{}rcl@{}} \rho_{1} P_{1}(1 - {k_{1}^{2}}z) + \rho_{2} P_{2}(1 - {k_{2}^{2}}z) \geqslant t_{\mathrm{R}}z. \end{array} $$

(77)

After some straightforward manipulations, we get

$$ \begin{array}{@{}rcl@{}} \lambda \leqslant k_{\mathrm{R}}^{2}y + \frac{P_{1} t_{1} y[1 - {k_{2}^{2}}y - {k_{1}^{2}}(z - y)]}{P_{\mathrm{R}} t_{\mathrm{R}}(z - y)} =X. \end{array} $$

(78)

Combining these conditions (i.e. Eqs. 74 and 78), we have $k_{\mathrm {R}}^{2}y < \lambda < \min \limits \{ X, Y, Z\}$. Since X < Y, we have Case 1 in Table 1. When the reverse case in Eq. 78 occurs, it means λ > X, combining with Eq. 74, we obtain Case 2 in Table 1. Considering Case 3, the condition of λ for that outage occurs in the links from S₁ → R, and S₂ → R is as follows

$$ \begin{array}{@{}rcl@{}} \left\{ \begin{gathered} \lambda - k_{\mathrm{R}}^{2}y > 0 \\ 1 - \lambda - k_{\mathrm{R}}^{2}x > 0 \\ \lambda \geqslant Y \\ \lambda \leqslant Z \\ \end{gathered}. \right. \end{array} $$

(79)

Since

$$ \begin{array}{@{}rcl@{}} Y = k_{\mathrm{R}}^{2}y + \frac{P_{1} t_{1} y(1 - {k_{1}^{2}}x)}{P_{\mathrm{R}} t_{\mathrm{R}} x} > k_{\mathrm{R}}^{2}y, \end{array} $$

(80)

and

$$ \begin{array}{@{}rcl@{}} Z = 1 - k_{\mathrm{R}}^{2}x - \frac{P_{2} t_{2} x(1 - {k_{2}^{2}}y)}{P_{\mathrm{R}} t_{\mathrm{R}} y} < 1 - k_{\mathrm{R}}^{2}x. \end{array} $$

(81)

Therefore, the condition that outage occurs in the links from S₁ → R, and S₂ → R is determined as follows

$$ \begin{array}{@{}rcl@{}} Y \leqslant \lambda \leqslant Z. \end{array} $$

(82)

Under this condition, expression (25) is always satisfied and $\mathcal {P}_{\text {out}_{5}} \ne 0$. Therefore, we have case 3. Due to this reason, we do not have scenario that outage occurs from S₁ → R, S₂ → R but does not occur at R_sum. The remaining cases can be determined by the same method. Note that since T > Z so we always have $\max \limits \{Y, Z, T\} = \max \limits \{Y, T\}$ in case 7. Therefore, we have the result for this case. For case 4 and case 5, there is the same selection range λ but for each specific value of λ, only one of the two cases occurs. To have the outage links from R →S₁, S₁ → R, R →S₂ and S₂ → R the condition of λ must be satisfied:

$$ \begin{array}{@{}rcl@{}} \left\{ \begin{gathered} \lambda - k_{\mathrm{R}}^{2}y > 0 \\ \lambda < Y \\ 1 - \lambda - k_{\mathrm{R}}^{2}x > 0 \\ \lambda > Z \\ \end{gathered}. \right. \end{array} $$

(83)

Thus, the condition $\max \limits (k_{\mathrm {R}}^{2}y,Z) < \lambda < \min \limits (1 - k_{\mathrm {R}}^{2}x,Y)$ is the value of λ to outage links from from R →S₁, S₁ → R, R →S₂ and S₂ → R. To check the outage link at R_sum to choose case 4 or case 5, we need to determine the specific value of λ. After some transform, we get a quadratic equation, depending on the value of the roots of the quadratic equation

$$ \begin{array}{@{}rcl@{}} a \lambda^{2} + b\lambda + c = 0 \end{array} $$

(84)

to determine exactly case 4 or case 5, where a = P_Rt_Rz, $b = P_{2} t_{2} x(1 - {k_{2}^{2}}z) - P_{1} t_{1} y(1 - {k_{1}^{2}}z) - P_{\mathrm {R}} t_{\mathrm {R}} z(1 - k_{\mathrm {R}}^{2}x + k_{\mathrm {R}}^{2}y)$, and $c = P_{1} t_{1} y(1 - {k_{1}^{2}}z)(1 - k_{\mathrm {R}}^{2}x) - P_{2} t_{2} x k_{\mathrm {R}}^{2}y(1 - {k_{2}^{2}}z) + P_{\mathrm {R}} t_{\mathrm {R}} z k_{\mathrm {R}}^{2}y(1 - k_{\mathrm {R}}^{2}x)$. If the quadratic equation has no real roots or it has exactly one real root, we have $\mathcal {P}_{\text {out}_{5}} = 0$. Combining with the condition above, we have case 5. If the quadratic equation has two distinct real roots λ₁,λ₂, with λ₁ < λ < λ₂ then $\mathcal {P}_{\text {out}_{5}} \ne 0$. Thus, with this value of λ combining with the condition above, we have case 4. If the value of λ changes, it means λ < λ₁ or λ > λ₂, then $\mathcal {P}_{\text {out}_{5}} = 0$, combining with the condition above, we have case 5.

When k₁ = k₂ = k_R = 0, this system becomes an ideal hardware system, and the expression (29) becomes expression (14) in [5] and expression (19) in [6]. Thus, Table 1 in this paper becomes the Table I in [5] and the Table III in [6].

Appendix B

This appendix provide the detail for the optimal value of power allocation factor λ to minimize the OP of the system in the Theorem 2. Set $f(\lambda )=\mathcal {P}_{\text {out}}$ and use the derivation of the f(λ) respect to λ. For conveniently, we find the derivation of the sub-function in the OP as follows

$a^{\prime }_{12} = b^{\prime }_{12}=0, a^{\prime }_{34} = b^{\prime }_{34}=0, a^{\prime }_{5} = b^{\prime }_{5}=0, c^{\prime }_{12} ={\Omega }_{1}P_{\mathrm {R}}, c^{\prime }_{34}=-{\Omega }_{2}P_{\mathrm {R}},$

$$ \begin{array}{@{}rcl@{}} Q^{\prime}_{1} = Q^{\prime}_{3} =Q^{\prime}_{5} =0; \end{array} $$

(85)

$$ \begin{array}{@{}rcl@{}} Q^{\prime}_{2} =\frac{{\Omega}_{1}P_{\mathrm{R}}t_{1}y}{c_{12}^{2}} \exp\Big(\frac{-t_{1}y}{c_{12}}\Big) \Bigg[1-\exp\Big(\frac{xt_{\mathrm{R}}c_{12} - y t_{1}a_{12}}{b_{12}c_{12}}\Big)\Bigg]; \end{array} $$

(86)

$$ \begin{array}{@{}rcl@{}} Q^{\prime}_{4} =\frac{{\Omega}_{2}P_{\mathrm{R}}t_{2}x}{c_{34}^{2}} \exp\Big(\frac{-t_{2}x}{c_{34}}\Big) \Bigg[1-\exp\Big(\frac{yt_{\mathrm{R}}c_{34} - xt_{2}a_{34}}{b_{34}c_{34}} \Big)\Bigg]. \end{array} $$

(87)

In case 1, we have:

$$ \begin{array}{@{}rcl@{}} f^{\prime}(\lambda) = -Q^{\prime}_{2}Q_{3} - Q_{2}Q^{\prime}_{3} =- Q^{\prime}_{2}Q_{3}. \end{array} $$

(88)

Thus, $f^{\prime }(\lambda ) = 0$ when $1-\exp \Big (\frac {xt_{\mathrm {R}}c_{12} - y t_{1}a_{12}}{b_{12}c_{12}}\Big ) = 0$. After some manipulations, we get λ = Y. When λ < Y lead to $Q^{\prime }_{2} >0$, so $f^{\prime }(\lambda )<0$. When λ > Y, we have $f^{\prime }(\lambda )>0$. Therefore, λ = Y is the optimal value of λ to minimize the OP in case 1. Combine with the condition in the Table 1, we get case 1 in Eq. 54.

In case 2, similarly case 1, we have

$$ \begin{array}{@{}rcl@{}} f^{\prime}(\lambda) = -Q^{\prime}_{2}Q_{3}Q_{5} - Q_{2}Q^{\prime}_{3}Q_{5}- Q_{2}Q_{3}Q^{\prime}_{5} = -Q^{\prime}_{2}Q_{3}Q_{5}. \end{array} $$

(89)

From Eq. 89, the optimal value of the power allocation factor is λ = Y. Combine with the condition in the Table 1, we get case 2 in Eq. 54.

In case 3, we always have $f^{\prime }(\lambda )=0$. So the value of λ in the Table 1 is the optimal value.

In case 4, we find the sub-optimal power allocation for the OP. Firstly, we rewrite the OP in case 4 as follows

$$ \begin{array}{@{}rcl@{}} \text{OP} &=& 1 -Q_{2}Q_{4}Q_{5} = 1 - \exp\Big(-\frac{t_{1}y}{c_{12}} - \frac{t_{2}x}{c_{34}}\Big)Q_{5} \\ &\times& \Bigg[1 - \frac{b_{12}}{a_{12} + b_{12}}\exp\Big(\frac{xt_{\mathrm{R}}c_{12} - y t_{1}a_{12}}{b_{12}c_{12}}\Big)\Bigg] \\ &\times& \Bigg[1 - \frac{b_{34}}{a_{34} + b_{34}}\exp\Big(\frac{yt_{\mathrm{R}}c_{34} - xt_{2}a_{34}}{b_{34}c_{34}}\Big)\Bigg]. \end{array} $$

(90)

From Eq. 90, the sup-optimal for the OP is the value of λ to maximize $f_{4}=\exp \Big (-\frac {t_{1}y}{c_{12}} - \frac {t_{2}x}{c_{34}}\Big )$. After some mathematical manipulation, the critical point to maximize f₄ is

$$ \begin{array}{@{}rcl@{}} \lambda=\frac{(1 -k_{\mathrm{R}}^{2}x)\sqrt{{\Omega}_{2} t_{1} y} + k_{\mathrm{R}}^{2}y\sqrt{{\Omega}_{1} t_{2} x}}{ \sqrt{{\Omega}_{2} t_{1} y}+\sqrt{{\Omega}_{1} t_{2} x}} \cdot \end{array} $$

(91)

In case 5, similarly, we get the value of λ as Eq. 91.

In case 6, we have

$$ \begin{array}{@{}rcl@{}} f^{\prime}(\lambda) &=& -Q^{\prime}_{1}Q_{4}Q_{5} - Q_{1}Q^{\prime}_{4}Q_{5} -Q_{1}Q_{4}Q^{\prime}_{5}\\ &=&- Q_{1}Q^{\prime}_{4}Q_{5}. \end{array} $$

(92)

Set $f^{\prime }(\lambda ) = 0$ to find the optimal value of λ, it is the root of $Q^{\prime }_{4}=0$ we have $1-\exp \Big (\frac {yt_{\mathrm {R}}c_{34} - xt_{2}a_{34}}{b_{34}c_{34}}\Big ) = 0$. After some manipulations, the value λ = Z is the root of $Q^{\prime }_{4}=0$. When λ < Z lead to $Q^{\prime }_{4} >0$, so $f^{\prime }(\lambda )<0$. When λ > Z, we have $f^{\prime }(\lambda )>0$. Therefore, λ = Z is the optimal value of λ to minimize the OP in case 6. Due to the fact that, T > Z, so $\max \limits \{Y,Z,T\}=\max \limits \{Y,T\}$. Combine with the condition in the Table 1, we get case 6 in Eq. 54.

In case 7, similarly case 6, the optimal value of λ is λ = Z. Therefore, the proof is completely.