Joint azimuth, elevation, and time of arrival estimation of diffuse sources

Abstract

In this paper, we estimate the azimuth, the elevation, and the time of arrival of diffuse sources using the covariance matching estimator (COMET) algorithm. Previous works dealt with azimuth estimation of diffuse sources or azimuth and time of arrival estimation of point sources. However, in realistic situations, a tridimensional diffuse source localization is needed, which is the main objective of this paper. We show that the dimensionality of the COMET algorithm can be reduced by separating the estimation of the different source powers and the noise variance from that of the remaining parameters, namely the azimuth, the elevation, the time of arrival, and the corresponding angular and temporal spreads. As COMET still involves a multidimensional nonlinear optimization, we choose, in this purpose, the alternating projection algorithm to alleviate the corresponding complexity. The multiple signal classification (MUSIC) algorithm is processed to initialize the so-resulted algorithm. Simulations of the proposed algorithm are carried in different contexts and compared to the Cramér-Rao Bound, MUSIC algorithm, and dispersed signal parametric estimation simulation results.

Résumé

Dans cet article, nous utilisons l’algorithme “covariance matching estimator” (COMET) afin d’estimer l’azimut, l’élévation et le temps d’arrivé de sources diffuses. Les travaux antérieurs ont traité l’estimation de l’azimut de sources diffuses ou l’estimation de l’azimut et le temps d’arrivé de sources ponctuelles. Dans cet article, on s’intéresse à des scénarios réalistes nécessitant une localisation tridimensionnelle de sources diffuses. Nous montrons que la complexité de l’algorithme COMET peut être réduite en séparant l’estimation des puissances des diverses sources et la variance du bruit du reste des paramètres, à savoir l’azimut, l’élévation, le temps d’arrivé et les déviations angulaires et temporelles correspondantes. Etant donnée que l’algorithme COMET nécessite une optimization non linéaire multidimensionnelle, nous utilisons l’algorithme des projections alternées afin d’alléger sa complexité. L’algorithme MUSIC “MUltiple SIgnal Classification algorithm” est utilisé afin d’initialiser l’algorithme ainsi obtenu. Des résultats de simulations de l’algorithme proposé sont présentés dans divers contextes et comparés à la Borne de Cramer Rao (BCR) et à des résultats de simulations des algorithmes MUSIC et “dispersed signal parametric estimation” (DISPARE).

Contents

• I. Introduction

• II. Received signal model

• III. Space time manifold

• IV. Spatiotemporal correlation matrix

• V. The proposed algorithm

• VI. Simulation results

• VII. Conclusion

•  

  References (15 ref.)

1 Introduction

The problem of mobile localization has been largely dealt with in the past few decades as it uses the spatial diversity to increase the system capacity. Also, mobile localization is needed when seeking for lost and injured people. Mobile localization by means of a single base station (BS) is obtained by estimating both the time of arrival (TOA) and the angle of arrival (AOA) of the received waves. Estimating only the AOA or the TOA requires, respectively, two and three BSs. In this work, we focus on AOA and TOA estimation, which is usually obtained by using subspace algorithms such as “joint angle and delay estimation–multiple signal classification algorithm” (JADE–MUSIC) [1] and JADE–“estimation of signal parameter via rotational invariance techniques” (ESPRIT) [2–4].

Local scattering in the mobile vicinity results in angular and temporal spreading. In such situations, the rank of the spatiotemporal correlation matrix [1] is greater than the number of sources, which makes distinction between signal and noise subspaces difficult, leading then to a performance degradation of both MUSIC and ESPRIT.

Previous works on diffuse source localization dealt with only azimuth estimation and suppose that the sources are in the same plane. In [5], a distributed source was approximated by two point sources. Then, the AOA of the point sources were estimated using MUSIC or root-MUSIC [6]. The AOA of the distributed source was shown to be the middle of the point sources and the angle spread was related to the angular separation between them. In [7], the AOA and the angle spread were estimated using the maximum likelihood (ML) algorithm. Suboptimal but computationally more attractive techniques based on covariance matching estimator (COMET) were used in [7, 8]. Adaptation of subspace algorithms for scattered sources were proposed in [9–13]. In [9], a Taylor series approximation of the array manifold was used by the ESPRIT algorithm to estimate the AOA of the diffuse source. The obtained algorithm was called Taylor series–ESPRIT. Adaptation of MUSIC algorithm has given rise to “dispersed signal parametric estimation” (DISPARE) [10] and “distributed signal parameter estimation” [11]. In [12] and [13], the commonly used array manifold for point sources is generalized to include linear combinations of the nominal array response vector and their derivatives. The so-obtained generalized array manifold was used to derive better estimates of the nominal AOA by exploiting the orthogonality between signal and noise subspaces.

In this paper, we use the COMET algorithm to estimate the azimuth, the elevation, the TOA, and the corresponding temporal and angular spreads of the different sources. We show that the dimensionality of the COMET algorithm can be reduced by separating the estimation of the different source powers and the noise variance from that of the remaining parameters. Because COMET still involves a multidimensional nonlinear optimization, we use the alternating projection algorithm [14] to reduce its complexity. A theoretical expression of the asymptotic variance of COMET is given. Simulation results of the proposed algorithm are carried in different contexts and compared to the Cramér-Rao Bound (CRB), MUSIC and DISPARE simulation results.

The paper is organized as follows: The next section gives the received signal model. Section 3 introduces the notion of a space time manifold. Section  derives the theoretical expression of the spatiotemporal correlation matrix in the presence of dispersion in azimuth, elevation, and TOA. Section 5 describes the proposed algorithm. Section 6 comments on the simulation results. Finally, Section 7 gives our conclusions.

2 Received signal model

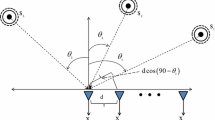
For a digital communication system and in the presence of dispersion in azimuth, elevation, and TOA, the received signal by an M-sensors antenna is given by

$${\mathbf{x}}(t)=\sum\limits_{l}s_{l}{\mathbf{h}}(t-lT_{s})+{\mathbf{n}}(t), \label{1} $$

(1)

where s _l is the l-th transmitted symbol; T _s is the symbol period; h(t) is the channel impulse response given by [1]

$$\label{2} {\mathbf{h}}(t)=\sum\limits_{i=1}^{Q}\sum\limits_{q=1}^{K}\beta _{i,q}(t){\mathbf{a}}\left( \theta _{i}\!+\!\widetilde{\theta }_{i,q},\Delta _{i}\!+\!\widetilde{\Delta } _{i,q}\right) g(t\!-\!\tau _{i}\!-\!\widetilde{\tau }_{i,q}); $$

(2)

Q is the number of paths (sources); K is the number of reflexions for each path; β _i,q is the path gain of q-th reflexion of the i-th path; θ _i , Δ _i , and τ _i are, respectively, the nominal azimuth, elevation, and TOA of the i-th path; $\widetilde{ \theta }_{i,q}$, $\widetilde{\Delta }_{i,q}$, and $\widetilde{\tau }_{i,q}$ are, respectively, the corresponding random, angular, and TOA deviation, g(t) is the shaping filter impulse response, which is a square root raised cosine filter with roll-off 0.22; and ${\mathbf{a}} \left( \theta ,\Delta \right)$ is the array manifold defined by

$$ \begin{array}{lll} && {\mathbf a}\left( \theta ,\Delta \right) \!=\!\left( \exp \left[\!-\frac{2\Pi j}{ \lambda }\cos \left( \Delta \right) \left( p_{x_{1}}\cos (\theta )\!+\!p_{y_{1}}\sin (\theta )\right) \right]\right. \\ &&{\kern43pt} \cdots ,\exp \left[ -\frac{2\Pi j}{\lambda }\cos \left( \Delta \right) \left( p_{x_{M}}\cos (\theta )\right.\right.\\ &&\left.\left.\left.{\kern81pt} +p_{y_{M}}\sin (\theta )\right) \right]\, \right) ^{T}\!, \end{array}\label{3} $$

(3)

where λ is the wavelength and $p_{x_{l}}$ and $p_{y_{l}}$ are the co ordinate of the l-th sensor in the antenna plane.

The noise n(t) is zero mean complex circular gaussian and is spatially and temporally white, i.e.,

$$ E\left( {\mathbf{n}}(t){\mathbf{n}}(s)^{H}\right) =\sigma ^{2}\;{\mathbf{I}} _{M}\;\delta (t,s), \label{4} $$

(4)

where H denotes the Hermitian transposition and δ the Kronecker symbol.

The path gains are assumed to be temporally white, independent from path to path, zero mean, and circularly symmetric, i.e,

$$ E\left( \beta _{i,q}(t)\beta _{n,l}^{\ast }(s)\right) =\frac{S_{i}}{K} \;\delta (t,s)\delta (i,n)\delta (q,l), \label{5} $$

(5)

$$ E\left( \beta _{i,q}(t)\right) =0, \label{6} $$

(6)

and

$$ E\left( \beta _{i,q}(t)\beta _{i,q}(s)\right) =0. \label{7} $$

(7)

3 Space time manifold

Let LT _s  = L _g T _s  + Δτ be the length of channel impulse response where L _g T _s is the length of the shaping filter impulse response and Δτ is the channel delay spread. The sampled version of x(t) at rate P/T _s , where P is the oversampling factor, over N symbol periods can be written as

$$ \mathbf{X}=\mathbf{HS}+\mathbf{N,} \label{8} $$

(8)

where

$$ {\mathbf{X}}=\left[ \begin{array}{c} {\mathbf{x}}(0) \\ \vdots \\ {\mathbf{x}}\left(\left( 1-\frac{1}{P}\right) T_{s}\right) \end{array} \begin{array}{c} \cdots \\ \vdots \\ \cdots \end{array} \begin{array}{c} {\mathbf{x}}((N-1)T_{s}) \\ \vdots \\ {\mathbf{x}}\left(\left( N-\frac{1}{P}\right) T_{s}\right) \end{array} \right] _{MP\times N}, $$

$$ {\mathbf{H}}=\left[ \begin{array}{c} {\mathbf{h}}(0) \\ \vdots \\ {\mathbf{h}}\left(\left( 1-\frac{1}{P}\right) T_{s}\right) \end{array} \begin{array}{c} \cdots \\ \vdots \\ \cdots \end{array} \begin{array}{c} {\mathbf{h}}((L-1)T_{s}) \\ \vdots \\ {\mathbf{h}}\left(\left( L-\frac{1}{P}\right) T_{s}\right) \end{array} \right] _{MP\times L}, $$

$$ {\mathbf{S}}=\left[ \begin{array}{c} s_{0} \\ s_{-1} \\ \vdots \\ s_{-L+1} \end{array} \begin{array}{c} s_{1} \\ s_{0} \\ \vdots \\ s_{-L+2} \end{array} \begin{array}{c} s_{N-1} \\ s_{N-2} \\ \vdots \\ s_{N-L} \end{array} \right] _{L\times N}, $$

and N is defined similarly to X.

The channel matrix, H, can be estimated slot by slot using N training symbols. The channel matrix can be estimated as follows:

$$ \begin{array}{lll} {\mathbf{H}}_{\mathrm{est}} &=&\mathbf{XS}^{\dag} \\ &=&\mathbf{H}+{\mathbf{V}}_{\mathrm{est}}, \end{array}\label{9} $$

(9)

where ${\mathbf{V}}_{\mathrm{est}}={\mathbf{NS}}^{\dag}$ and ${\mathbf{A}}^{\dag}={\mathbf{A}} ^{H}\left( {\mathbf{AA}}^{H}\right) ^{-1}$.

H _est can be written as

$${\mathbf{H}}_{\mathrm{est}}=\left[ \begin{array}{c} {\mathbf{h}}_{\mathrm{est}}(0) \\ \vdots \\ {\mathbf{h}}_{\mathrm{est}}\left(\left( 1-\frac{1}{P}\right) T_{s}\right) \end{array} \begin{array}{c} \cdots \\ \vdots \\ \cdots \end{array} \begin{array}{c} {\mathbf{h}}_{\mathrm{est}}((L-1)T_{s}) \\ \vdots \\ {\mathbf{h}}_{\mathrm{est}}\left(\left( L-\frac{1}{P}\right) T_{s}\right) \end{array} \right] . \label{11} $$

(10)

It will be convenient to rearrange H _est into

$$ \overline{{\mathbf{H}}}_{\mathrm{est}} =\left[ {\mathbf{h}}_{\mathrm{est}}(0)\;{\mathbf{h}}_{\mathrm{est}}\left(\! \frac{T_{s}}{P}\!\right)\,\cdots \,{\mathbf{h}}_{\mathrm{est}}\left(\left( L-\frac{1}{P}\right)\! T_{s}\right)\right] _{M\times PL} \label{12} $$

(11)

$$ \qquad=\overline{\mathbf{H}}+\overline{\mathbf{V}}_{\mathrm{est}}. \label{13} $$

(12)

Let ${\mathbf{y}}=vec\big(\overline{\mathbf{H}}_{\mathrm{est}}\big)$ be a column vector of length MPL obtained by taking the transpose of each row of matrix $\overline{{\mathbf{H}}}_{\mathrm{est}}$ and stacking it bellow the transpose of the previous row. Using Eq. 11, we obtain [1]

$${\mathbf{y}}=\sum\limits_{i=1}^{Q}\sum\limits_{q=1}^{K}\beta _{i,q}{\mathbf{u}}\left( \theta _{i}+\widetilde{\theta }_{i,q},\Delta _{i}+\widetilde{\Delta }_{i,q},\tau _{i}+\widetilde{\tau }_{i,q}\right) +\mathbf{v}, \label{14} $$

(13)

where ${\mathbf{v}}=vec\big(\overline{{\mathbf{V}}}_{\mathrm{est}}\big),$ ${\mathbf{u}}\left( \theta ,\Delta ,\tau \right) ={\mathbf{a}}\left( \theta ,\Delta \right) \otimes {\mathbf{g}}(\tau )$ is the space time array manifold,

$${\mathbf{g}}(\tau )=\left[ g\left( kT_{s}-\tau \right) \right] _{k=0,1/P,\cdots ,L-1/P} \label{15} $$

(14)

and ⊗ is the Kronecker product.

4 Spatiotemporal correlation matrix

Using a first order Taylor series expansion and assuming that the TOA deviation is centered and assuming independent deviations in azimuth, elevation and TOA, we can easily show that the spatiotemporal correlation matrix is given by

$${\mathbf{R}}_{y}=E\big({\mathbf{yy}}^{H}\big)=\sum\limits_{i=1}^{Q}S_{i}\;{\mathbf{B}}_{i}+\sigma _{b}^{2}\;{\mathbf{I}}_{MPL}, \label{16} $$

(15)

where B _i  = R _i  ⊙ F _i  ⊙ G _i  ⊙ H _i , ⊙ is the Schur-Hadamard product, $\sigma _{b}^{2}=\frac{\sigma ^{2}}{N}$,

$${\mathbf{R}}_{i}(l,n)=\exp \!\left[\! -\frac{2\Pi j}{\lambda }\cos \left( \Delta _{i}\right) \left( p_{x_{\ln }}{\kern-1pt}\cos (\theta _{i})+p_{y_{\ln }}{\kern-1pt}\sin (\theta _{i})\right) \!\right] , \label{17} $$

(16)

$$\label{18} \begin{array}{lll} {\mathbf{F}}_{i}(l,n)&=&\int f_{\theta _{i}}(\widetilde{\theta })\exp \left[ \frac{2\Pi j}{\lambda }\widetilde{\theta }\cos \left( \Delta _{i}\right) \left( p_{x_{\ln }}\sin (\theta _{i}) \right.\right. \\\\ &&\left.\left.{\kern54pt} -\,p_{y_{\ln }}\cos (\theta _{i})\right) \right] d\widetilde{ \theta } \end{array} $$

(17)

$$\label{19} \begin{array}{lll} {\mathbf{G}}_{i}(l,n)&=&\int f_{\Delta _{i}}(\widetilde{\Delta })\exp \left[ \frac{2\Pi j}{\lambda }\widetilde{\Delta }\sin \left( \Delta _{i}\right) \left( p_{x_{\ln }}\cos (\theta _{i})\right.\right. \\\\ &&{\kern60pt} \left.\left. +\,p_{y_{\ln }}\sin (\theta _{i})\right) \right] d\widetilde{ \Delta } \end{array} $$

(18)

$$ \begin{array}{lll} {\mathbf{H}}_{i}(l,n)&=&g\left( \frac{r_{l}T_{s}}{P}-\tau _{i}\right) g\left( \frac{r_{n}T_{s}}{P}-\tau _{i}\right) \\\\ &&+\,\sigma _{\tau _{i}}^{2}g^{\prime }\left( \frac{r_{l}T_{s}}{P}-\tau _{i}\right) g^{\prime }\left( \frac{r_{n}T_{s}}{P}-\tau _{i}\right) \end{array}\label{20} $$

(19)

where $p_{x_{\ln }}=p_{x_{\left\lfloor \frac{l}{LP}\right\rfloor }}-p_{x_{\left\lfloor \frac{n}{LP}\right\rfloor }},$ $p_{y_{\ln }}=p_{y_{\left\lfloor \frac{l}{LP}\right\rfloor }}\! -\!p_{y_{\left\lfloor \frac{n }{LP}\right\rfloor }},$ ${\kern-2.5pt} \left\lfloor .\right\rfloor$ is the integer part operator, $\sigma _{\tau _{i}}^{2}=E\big(\widetilde{\tau }_{i}^{2}\big)$, $g^{\prime }(t)=\frac{dg(t)}{dt}$, $r_{l}=l-\left\lfloor \frac{l}{LP}\right\rfloor LP$, S _i is the i-th source power, and $f_{\theta _{i}}(\widetilde{\theta })$ and $f_{\Delta _{i}}(\widetilde{ \Delta })$ are, respectively, the azimuth and elevation probability density function (pdf) of the i − th path.

For a gaussian distribution, we have

$$ \begin{array}{lll} {\mathbf{F}}_{i}(l,n)&=&\exp \left[ \frac{-2\Pi ^{2}}{\lambda ^{2}}\sigma _{\theta _{i}}^{2}\cos ^{2}\left( \Delta _{i}\right) \left( p_{x_{\ln }}\sin (\theta _{i})\right.\right. \\\\ &&{\kern18pt} \left.\left. -\,p_{y_{\ln }}\cos (\theta _{i})\right) ^{2}\right] \end{array}\label{21} $$

(20)

$$ \begin{array}{lll} {\mathbf{G}}_{i}(l,n)&=&\exp \left[ \frac{-2\Pi ^{2}}{\lambda ^{2}}\sigma _{\Delta _{i}}^{2}\sin ^{2}\left( \Delta _{i}\right) \left( p_{x_{\ln }}\cos (\theta _{i})\right.\right. \\\\ &&{\kern18pt}\left.\left. +\,p_{y_{\ln }}\sin (\theta _{i})\right)^2\right], \end{array}\label{22} $$

(21)

where $\sigma _{\theta _{i}}$ and $\sigma _{\Delta _{i}}$ are, respectively, the azimuth and elevation standard deviations (std) of the i-th path.

5 The proposed algorithm

In this section, we use the COMET algorithm to estimate the azimuth, the elevation, the TOA, and the corresponding temporal and angular spreads of the different sources. COMET estimates are obtained by minimizing the error between the theoretical and the sample correlation matrices. The determination of the spatiotemporal theoretical correlation matrix is based on a priori knowledge of the AOA pdf. COMET estimates are obtained by minimizing the following metric:

$$\label{jonel} \widehat{{\mathbf{v }}}= \underset{\mathbf{v }}{argmin} \left\{ J\left( {\mathbf{v }}\right) \right\} , $$

(22)

where

$$ \begin{array}{rll} {\mathbf{v}}&=&\left( S_{1},\theta _{1},\sigma _{\theta _{1}},\Delta _{1},\sigma _{\Delta _{1}},\tau_1,\sigma_{\tau_1},\cdots \right. \\[2pt] &&{\kern2pt} \left. \cdots ,S_{Q},\theta _{Q},\sigma _{\theta _{Q}},\Delta _{Q},\sigma _{\Delta _{Q}},\tau_Q,\sigma_{\tau_Q},\sigma _{b}^{2}\right) ^{T}, \\[6pt] J\left( {\mathbf{v }}\right) &=&Tr\left( \left( {\mathbf{R}}_{y}\left( {\mathbf{ v }}\right) -\widehat{{\mathbf{R}}}_{D}\right) {\mathbf{W}}\left( {\mathbf{R}} _y\left( {\mathbf{v }}\right) -\widehat{{\mathbf{R}}}_{D}\right) {\mathbf{W}} \right) , \end{array}\label{parbo} $$

(23)

$\widehat{{\mathbf{R}}}_{D}$ is the sample covariance matrix given by

$$ \widehat{{\mathbf{R}}}_{D}=\frac{1}{D}\sum\limits_{n=1}^{D}{\mathbf{y}}^{(n)}\;{\mathbf{y}} ^{(n)H}, \label{25} $$

(24)

D is the number of snapshots, and W is a positive definite weighting matrix.

5.1 Weighted least square algorithm

In [7], it is shown that the estimates obtained from Eq. 22 are asymptotically efficient for ${\mathbf{W=}}\widehat{{\mathbf{R}}}_{D}^{-1}.$ Hence, the corresponding algorithm, weighted least square (WLS), is asymptotically¹ equivalent to the ML estimator as it reaches the CRB given by

$$ E\left( \left(\, \widehat{{\mathbf{v }}}-{\mathbf{v }}\right) \left(\, \widehat{{\mathbf{v }}}-{\mathbf{v }}\right) ^{T}\right) \geq {\mathbf{FIM}} ^{-1}, \label{tigno} $$

(25)

where the ln-th element of the Fisher information matrix (FIM) is given by

$${\mathbf{FIM}}(l,n)=D\;Tr\left( {\mathbf{R}}_{y}^{-1}\frac{\partial {\mathbf{R}} _y}{\partial v _{l}}{\mathbf{R}}_{y}^{-1}\frac{\partial {\mathbf{R}}_{y}}{ \partial v _{n}}\right) . \label{27} $$

(26)

By using Eq. 23, we deduce the expression of the WLS metric

$$ \widehat{\mathbf{v}}=\underset{\mathbf{v}}{argmin}\text{ }Tr\left\{ \left( {\mathbf{R}}_{y}\left( {\mathbf{v}}\right) \widehat{{\mathbf{R}}}_{D}^{-1}-{\mathbf{ I}}\right) ^{2}\right\} . \label{WLS} $$

(27)

By differentiating the criterion Eq. 27 with respect to S _l and $\sigma_b^2$ and setting the result to zero, we have

$$ \begin{array}{lll} \sum\limits_{n=1}^{Q}\widehat{S}_{n}Tr\left({\mathbf{B}}_{n}\widehat{\mathbf{R}}_{D}^{-1}{\mathbf{B}}_{l} \widehat{\mathbf{R}}_{D}^{-1}\right) &=&Tr\left( \widehat{\mathbf{R}} _{D}^{-1}{\mathbf{B}}_{l}\right)\\\\ &&-\,\widehat{\sigma }_{b}^{2}Tr\left( \widehat{\mathbf{R}} _{D}^{-1}{\mathbf{B}}_{l}\widehat{\mathbf{R}}_{D}^{-1}\right), \end{array}\label{djs} $$

(28)

$$ \widehat{\sigma }_{b}^{2}=\frac{Tr\left( \widehat{\mathbf{R}} _{D}^{-1}\right) -\sum_{n=1}^{Q}\widehat{S}_{n}Tr\left( {\mathbf{B}}_{n}\widehat{ \mathbf{R}}_{D}^{-2}\right) }{Tr\left( \widehat{\mathbf{R}}_{D}^{-2}\right) } . \label{djb} $$

(29)

By replacing Eq. 29 in Eq. 28, we obtain the following linear system

$$ \mathbf{L}\widehat{\mathbf{S}}=\mathbf{c,} \label{MCPlin} $$

(30)

where

$$ \widehat{\mathbf{S}}=\left( \widehat{S}_{1},\widehat{S}_{2},...,\widehat{S} _{Q}\right) ^{T}, $$

$$ {\mathbf{L}}(l,n)=Tr\left( \widehat{\mathbf{R}}_{D}^{-2}\right) Tr\left( {\mathbf{B}}_{n}\widehat{ \mathbf{R}}_{D}^{-1}{\mathbf{B}}_{l}\widehat{\mathbf{R}}_{D}^{-1}\right) $$

$$ {\kern40pt} -Tr\left( {\mathbf{B}}_{n} \widehat{\mathbf{R}}_{D}^{-2}\right) Tr\left( {\mathbf{B}}_{l}\widehat{\mathbf{R}} _{D}^{-2}\right) , $$

$$ {\kern22.5pt} 1\leq l,n\leq Q, $$

and

$$ c_{l}=Tr\left( \widehat{\mathbf{R}}_{D}^{-2}\right) Tr\left( \widehat{ \mathbf{R}}_{D}^{-1}{\mathbf{B}}_{l}\right) $$

$$ {\kern19pt} -Tr\left( \widehat{\mathbf{R}} _{D}^{-1}\right) Tr\left( \widehat{\mathbf{R}}_{D}^{-2}{\mathbf{B}}_{l}\right) , $$

$$ {\kern1pt} 1\leq l\leq Q. $$

By substituting in the WLS criterion Eq. 27 $\sigma_{b}^2$ and {S _i }_{1 ≤ i ≤ Q} by their estimates Eqs. 29 and 30, we obtain

$$ \widehat{\mathbf{u}}=\underset{\mathbf{u}}{argmin}\text{ }Tr\left\{ \left[ \left( \sum\limits_{i=1}^{Q}\widehat{S}_{i}{\mathbf{B}}_{i}\left( {\mathbf{u}}_i\right) + \widehat{\sigma }_{b}^{2}{\mathbf{I}}_{MPL}\right) \right.\right. $$

$${\kern78pt} \times \widehat{\mathbf{R}}_{D}^{-1} -{\mathbf{I}}_{MPL}\Biggr] ^{2}\Biggr\}, \label{WLSm} $$

(31)

where

$$ {\mathbf{u}}_{i}=\left( \theta _{i},\sigma _{\theta _{i}},\Delta _{i},\sigma _{\Delta _{i}},\tau_{i},\sigma_{\tau_i}\right), $$

and

$$ {\mathbf{u}}=\left( {\mathbf{u}}_{1},\cdots ,{\mathbf{u}}_{Q}\right) . $$

Which clearly shows that the estimation of the different source powers and the noise variance can be separated from that of the remaining parameters. Consequently, the dimensionality of the COMET algorithm is reduced from 7Q + 1 to 6Q, the computational complexity then becomes lower than that of ML.

5.2 LS algorithm

To reduce metric computational complexity, least square (LS) algorithm can be also used by setting W =  I _MPL . However, the obtained estimator is not asymptotically efficient and the covariance matrix of LS estimates is given by [7]

$$ E\left( \left({\kern1.5pt} \widehat{{\mathbf{v }}}-{\mathbf{v }}\right) \left({\kern1.5pt} \widehat{{\mathbf{v }}}-{\mathbf{v }}\right) ^{T}\right) =\frac{1}{D}\; {\mathbf{J}}^{-1}{\mathbf{EJ^{-1}}}, \label{jona} $$

(32)

where

$$ {\mathbf{J}}(l,n)=2\;Tr\left( \frac{\partial {\mathbf{R}}_{y}}{\partial v _{n}}\frac{ \partial {\mathbf{R}}_{y}}{\partial v _{l}}\right) , $$

$$ {\mathbf{E}}(l,n)=4\;Tr\left( {\mathbf{R}}_{y}\frac{\partial {\mathbf{R}}_{y}}{\partial v _{l}}{\mathbf{R}}_{y}\frac{\partial {\mathbf{R}}_{y}}{\partial v _{n}} \right) . $$

By using Eq. 23, we deduce the expression of the LS metric

$$ \widehat{\mathbf{v}}=\underset{\mathbf{v}}{argmin}\text{ }Tr\left\{ \left( {\mathbf{R}}_{y}\left( \mathbf{v}\right) -\widehat{{\mathbf{R}}}_{D}\right) ^{2}\right\} . \label{LS} $$

(33)

Differentiating the criterion Eq. 33 with respect to S _l and $\sigma_b^2$ and setting the result to zero gives

$$ \sum\limits_{n=1}^{Q}\widehat{S}_{n}Tr\left( {\mathbf{B}}_{n}{\mathbf{B}}_{l}\right) =Tr\left( \widehat{ \mathbf{R}}_{D}{\mathbf{B}}_{l}\right) -\widehat{\sigma }_{b}^{2}MPL, \label{djs2} $$

(34)

$$ \widehat{\sigma }_{b}^{2}=\frac{Tr\left( \widehat{\mathbf{R}}_{D}\right) -MPL\sum_{n=1}^{Q}\widehat{S}_{n}}{MPL}. \label{djb2} $$

(35)

Substituting Eq. 35 in Eq. 34 leads to the following linear system:

$$ \mathbf{P}\widehat{\mathbf{S}}=\mathbf{d,} \label{MClin} $$

(36)

where

$$ {\mathbf{P}}(l,n)=Tr\left( {\mathbf{B}}_{l}{\mathbf{B}}_{n}\right) -MPL,\text{ }1\leq l,n\leq Q, $$

and

$$ d_{l}=Tr\left( \widehat{\mathbf{R}}_{D}{\mathbf{B}}_{l}\right) -Tr\left( \widehat{ \mathbf{R}}_{D}\right) ,\text{ }1\leq l\leq Q. $$

By substituting in the LS criterion Eq. 33 $\sigma_{b}^2$ and {S _i }_{1 ≤ i ≤ L} by their estimates Eqs. 35 and 36, we obtain

$$ \widehat{\mathbf{u}}=\underset{\mathbf{u}}{argmin}\text{ }Tr\left\{ \left[ \sum_{i=1}^{Q}\widehat{S}_{i}{\mathbf{B}}_{i}\left( {\mathbf{u}}_i\right) + \widehat{\sigma }_{b}^{2}{\mathbf{I}}_{MPL}-\widehat{{\mathbf{R}}}_{D}\right] ^{2}\right\} . $$

(37)

Notice that, similar to the WLS estimator, the dimensionality of the algorithm is reduced from 7Q + 1 to 6Q. The computational complexity is therefore lower than that of ML.

5.3 Complexity considerations and simplified COMET

The complexity of localization algorithms depends on metric computational complexity and the dimensionality of the problem. COMET metric is computationally less complex than that of ML, which requires the inversion of R _y . Moreover, we have shown in Sections 5.1 and 5.2 that the dimensionality of COMET algorithm is lower than that of ML. As for DISPARE [10] and MUSIC algorithms, they are less complex than COMET. However, as it will be shown in the next section, their performances are far from the CRB.

Since COMET algorithms still involve multidimensional nonlinear optimization, we propose to use the alternating projection technique [14] to reduce its complexity. This is an iterative technique for which the metric optimization is done with respect to a single parameter while all the others are held fixed at each iteration. The process is continued until convergence. This technique depends strongly on the initialization step and is subject, as most nonlinear optimization methods, to the problem of local minima. In our implementation, the minimum description length criterion is used to estimate the number of sources and the MUSIC algorithm is used to estimate the AOAs and TOAs. These values are used to initialize the alternating projection algorithm. As for the angular spread in azimuth and elevation of the different sources, they are initialized at 1°. The TOA spreads of the different sources are initialized to $0.1~\upmu$s

6 Simulation results

In this section, we compare the root mean square error (RMSE) performance of WLS, LS, MUSIC, and DISPARE algorithms. DISPARE is an adaptation of MUSIC to diffuse sources. If all the sources have the same AOA pdf, DISPARE estimates are obtained by determining the $\widehat{Q}$ minima of the following criterion [10]:

$$ \left( \widehat{\theta },\widehat{\sigma }_{\theta },\widehat{\Delta }, \widehat{\sigma }_{\Delta},\widehat{\tau },\widehat{\sigma_{\tau} }\right) =\underset{\left( \theta ,\sigma _{\theta },\Delta ,\sigma _{\Delta },\tau,\sigma_{\tau}\right) }{argmin}Tr\left( \widehat{\mathbf{V}}^{H} \mathbf{BB}^{H}\widehat{\mathbf{V}}\right), $$

(38)

where $\widehat{\mathbf{V}}$ is an estimate of the quasinoise subspace obtained from $\widehat{\mathbf{R}}_{D}$ as the set of eigenvectors whose eigenvalues’ energy is less than 5% of the total energy of the eigenvalues [10].

A five-element circular antenna array of radius λ/2 is used, on which the different sensors are uniformly placed. The number of local reflections is set to K = 20 and the RMSE simulation results are averaged over 100 independent Monte Carlo simulations. The shaping filter g(τ) is a square root raised cosine filter with roll-off 0.22, P = 4, and $T_s=10^{-3}$. The simulated AOA and TOA pdf is Gaussian. During these simulations, we noticed a rapid convergence to the global optimum of the alternating projection technique. The convergence is obtained after less than six iterations on all parameters.

6.1 Effects of angular and temporal spread

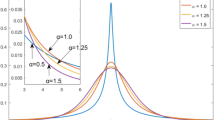
In Fig. 1, we study the effect of elevation spread, $\sigma_{\Delta_1}$, on the RMSE of elevation and elevation std estimates for a single source: SNR = 10 dB (S ₁ = 1, $\sigma _{b}^{2}=0.1$), $\Delta_1=40^\circ$, $\theta_1=-10^\circ$, $\sigma_{\theta_1}=5^{\circ}$, $\tau_1=1~\upmu$s, and $\sigma_{\tau_1}=0.2~\upmu$s. The number of snapshots is set to D = 100. We first notice that WLS and LS simulation results are close, respectively, to the CRB Eq. 25 and LS theoretical study Eq. 32. Moreover, they give better estimates than MUSIC, the performance of which degrades rapidly for elevation stds greater than 5°. This can be explained by the fact that, in the presence of dispersion, there is no possible distinction between signal and noise subspaces. DISPARE algorithm offers better performance than MUSIC since it takes into account of the presence of dispersion. However, DISPARE performance is worse than that of WLS since it fails to give consistent estimates [15].

Fig. 1

RMSE of elevation and elevation std estimates vs $\sigma_{\Delta_1}$: Q = 1, SNR = 10 dB, $\sigma_{\theta_1}=5^{\circ}$, $\sigma_{\tau_1}=0.2~\upmu$s.

Variation de la REQM de l’élévation et de l’écart type de l’élévation en fonction de $\sigma_{\Delta_1}$: Q = 1, SNR = 10 dB, $\sigma_{\theta_1}=5^{\circ}$, $\sigma_{\tau_1}=0.2~\upmu$s

In Fig. 2, we study the effect of azimuth spread, $\sigma_{\theta_1}$, on the RMSE of azimuth and azimuth std estimates for the same parameters as Fig. 1 and $\sigma_{\Delta_1}=5^{\circ}$. We notice that WLS offers better performance than LS, DISPARE, and MUSIC.

Fig. 2

RMSE of azimuth and azimuth std estimates vs $\sigma_{\theta_1}$: Q = 1, SNR = 10 dB, $\sigma_{\Delta_1}=5^{\circ}$, $\sigma_{\tau_1}=0.2~\upmu$s.

Variation de la REQM de l’azimut et de l’écart type de l’azimut en fonction de $\sigma_{\theta_1}$: Q = 1, SNR = 10 dB, $\sigma_{\Delta_1}=5^{\circ}$, $\sigma_{\tau_1}=0.2~\upmu$s

In Fig. 3, we study the effect of TOA spread, $\sigma_{\tau_1}$, on the RMSE of TOA and TOA std estimates for the same parameters as Fig. 1 and $\sigma_{\Delta_1}=\sigma_{\theta_1}=5^{\circ}$. We notice that MUSIC and DISPARE performance degrades for TOA spread greater than $0.2~\upmu$s. WLS offers better performance than LS, DISPARE, and MUSIC.

Fig. 3

RMSE of TOA and TOA std estimates vs $\sigma_{\tau_1}$: Q = 1, SNR = 10 dB, $\sigma_{\Delta_1}=5^{\circ}$, $\sigma_{\theta_1}=5^{\circ}$.

Variation de la REQM du temps d’arrivé et de l’écart type du temps d’arrivé en fonction de $\sigma_{\tau_1}$: Q = 1, SNR = 10 dB, $\sigma_{\Delta_1}=5^{\circ}$, $\sigma_{\theta_1}=5^{\circ}$

6.2 Effect of SNR

In Figs. 4, 5, and 6, we set Q = 1, $\Delta_1=40^\circ$, $\theta_1=-10^\circ$, $\sigma_{\theta_1}=5^{\circ}$, $\sigma_{\Delta_1}=5^{\circ}$, $\tau_1=1~\upmu$s, and $\sigma_{\tau_1}=0.2~\upmu$s, and the SNR is varied from 0 to 20 dB. We can see that, even for small SNRs, WLS and LS perform better than DISPARE and MUSIC.

Fig. 4

RMSE of elevation and elevation std estimates vs SNR: Q = 1, $\sigma_{\Delta_1}=5^{\circ}$, $\sigma_{\theta_1}=5^{\circ}$, $\sigma_{\tau_1}=0.2~\upmu$s.

Variation de la REQM de l’élévation et de l’écart type de l’élévation en fonction du SNR: Q = 1, $\sigma_{\Delta_1}=5^{\circ}$, $\sigma_{\theta_1}=5^{\circ}$, $\sigma_{\tau_1}=0.2~\upmu$s

Fig. 5

RMSE of azimuth and azimuth std estimates vs SNR: Q = 1, $\sigma_{\Delta_1}=5^{\circ}$, $\sigma_{\theta_1}=5^{\circ}$, $\sigma_{\tau_1}=0.2~\upmu$s.

Variation de la REQM de l’azimut et de l’écart type de l’azimut en fonction du SNR: Q = 1, $\sigma_{\Delta_1}=5^{\circ}$, $\sigma_{\theta_1}=5^{\circ}$, $\sigma_{\tau_1}=0.2~\upmu$s

Fig. 6

RMSE of TOA and TOA std estimates vs SNR: Q = 1, $\sigma_{\Delta_1}=5^{\circ}$, $\sigma_{\theta_1}=5^{\circ}$, $\sigma_{\tau_1}=0.2~\upmu$s.

Variation de la REQM du temps d’arrivé et de l’écart type du temps d’arrivé en fonction du SNR: Q = 1, $\sigma_{\Delta_1}=5^{\circ}$, $\sigma_{\theta_1}=5^{\circ}$, $\sigma_{\tau_1}=0.2~\upmu$s

Figure 7 shows the evolution of the probability of bad detection of the number of sources, P _bd , with respect to the SNR for the same parameters as Figs. 4, 5, 6. We verify that the probability of bad detection of the number of sources is very low.

Fig. 7

Probability of bad detection of the number of sources vs SNR: Q = 1, $\sigma_{\Delta_1}=5^{\circ}$, $\sigma_{\theta_1}=5^{\circ}$, $\sigma_{\tau_1}=0.2~\upmu$s.

Variation de la probabilité de mauvaise de détection du nombre de sources en fonction du SNR: Q = 1, $\sigma_{\Delta_1}=5^{\circ}$, $\sigma_{\theta_1}=5^{\circ}$, $\sigma_{\tau_1}=0.2~\upmu$s

6.3 Effect of S ₁/S ₂

Figures 8, 9, and 10 give the RMSE of the first source estimates in the presence of a second source for $\Delta _{1}=40^\circ$, $\theta _{1}=-10^\circ$, $\Delta _{2}=70^\circ$, $\theta _{2}=20^\circ$, $\sigma_{\theta_1}=\sigma_{\theta_2}=\sigma_{\Delta_1}=\sigma_{\Delta_2}=5^\circ$, $\tau_1=1~\upmu$s, $\tau_2=2~\upmu$s, $\sigma_{\tau_1}=\sigma_{\tau_2}=0.2~\upmu$s, and SNR₁ = 10 dB, and S ₁/S ₂ is varied from − 10 to 10 dB. We observe that WLS offers better performance than LS, DISPARE, and MUSIC for high and low interference levels (S ₁/S ₂). We emphasize on the fact that LS and DISPARE performance degradation, compared to WLS, increases in the presence of an interfering source.

Fig. 8

RMSE of elevation and elevation std estimates vs S ₁/S ₂ (dB): Q = 2, SNR₁ = 10 dB.

Variation de la REQM de l’élévation et de l’écart type de l’élévation en fonction de S ₁/S ₂ (dB): Q = 2, SNR₁ = 10 dB

Fig. 9

RMSE of azimuth and azimuth std estimates vs S ₁/S ₂ (dB): Q = 2, SNR₁ = 10 dB.

Variation de la REQM de l’azimut et de l’écart type de l’azimut en fonction de S ₁/S ₂ (dB): Q = 2, SNR₁ = 10 dB

Fig. 10

RMSE of TOA and TOA std estimates vs S ₁/S ₂ (dB): Q = 2, SNR₁ = 10 dB.

Variation de la REQM du temps d’arrivé et de l’écart type du temps d’arrivé en fonction de S ₁/S ₂ (dB): Q = 2, SNR₁ = 10 dB

7 Conclusion

In this paper, we treated the problem of tridimensional multiple diffuse source localization. We have used the COMET algorithm to estimate the different source powers, the noise variance, the azimuth, the elevation, the TOA, and the corresponding angular and temporal spreads. We have shown that the dimensionality of the COMET algorithm can be reduced by separating the estimation of the different source powers and the noise variance from that of the remaining parameters. Since COMET still involves multidimensional nonlinear optimization, we have used the alternating projection algorithm to alleviate its complexity. Within the class of COMET estimators, the WLS algorithm is shown to perform better than LS, DISPARE, and MUSIC. Also, simulation results of both WLS and LS are found to be close, respectively, to the CRB and LS theoretical results.