Abstract
Turbidity is an important habitat component in estuaries for many fishes and affects a range of other ecological functions. Decadal timescale declines in turbidity have been observed in the San Francisco Estuary (Estuary), with the declines generally attributed to a reduction in sediment supply to the Estuary and changes to the erodible sediment pool in the Estuary. However, we analyzed hourly wind data from 1995 through 2015 and found statistically significant declines of 13 to 48% in wind speed around the Estuary. This study applied a 3-D hydrodynamic, wave, and sediment transport model to evaluate the effects of the observed decrease in wind speed on turbidity in the Estuary. The reduction in wind speed over the past 20 years was predicted to result in a decrease in turbidity of 14 to 55% in Suisun Bay from October through January. These results highlight that the observed declines in both wind speed and sediment supply over the past 20 years have resulted in reduced turbidity in the San Francisco Estuary from October through January. This decline in turbidity in Suisun Bay potentially has negative effects on habitat for fish like the endangered Delta Smelt which are more commonly caught in relatively turbid water.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Motivation and Background
Water column turbidity is an important habitat component in many estuarine systems, and changes to turbidity can have significant management implications. In the San Francisco Estuary (Estuary), endangered Delta Smelt are more likely to be caught in relatively high-turbidity water (Feyrer et al. 2007; Sommer and Mejia 2013), and in the past, phytoplankton growth was light-limited (Cloern 1987; Alpine and Cloern 1988). Delta Smelt distribution and habitat influence management decisions for issues ranging from California water supply to dredging of harbors and channels. Reductions in observed turbidity in the San Francisco Estuary are of concern due to the potential importance of elevated turbidity to habitat for endangered fishes such as Delta Smelt.
Turbidity is a metric based on the optical properties of a water sample that act to scatter light at a specific angle emitted by an instrument (Davies-Colley and Smith 2001; Gray and Gartner 2009), and turbidity is correlated to the amount of sediment suspended in the water column in many coastal, estuarine, and riverine environments. The suspended sediment concentration (SSC) is defined as the mass of sediment in a given volume of water and is primarily driven by sediment resuspension from the seabed and upward mixing by turbulence, sediment settling and deposition on the seabed, and external sediment supply (e.g., river inflows) (Hill and MacCave 2001). SSC is often estimated by measuring the water turbidity and then converting the turbidity to SSC (see Schoellhamer et al. 2002; Fain et al., 2007; Gray and Gartner 2009; Buchanan and Morgan 2012; Nowacki and Ogston 2013). Turbidity is used as a surrogate for SSC because it is easy to observe and the emitted light is scattered primarily by sediment suspended within the water column (Davies-Colley and Smith 2001; Gray and Gartner 2009). As a result, there is a direct relationship between turbidity (nephelometric turbidity units, NTU) and SSC (mg/L), as long as the sediment size distribution at the sensor remains relatively constant. Turbidity is then converted to SSC using conversion curves (e.g., Ganju et al. 2007; Buchanan and Morgan 2012). Increases or decreases in SSC in these systems from changes to either sediment resuspension or sediment supply will result in corresponding changes in the turbidity. In this paper, “turbidity” refers to the NTU values based on the light-scattering properties of a water sample, while “SSC” refers to the mass of sediment suspended in a known volume of water.
Long-term decreases in the SSC and turbidity in the San Francisco Estuary (Estuary) are well documented. For example, Schoellhamer (2011) demonstrated a step decrease in the SSC in the Estuary in 1999. Schoellhamer (2011) attributed the step decrease to the crossing of a threshold from transport to supply regulation of sediment in the Estuary. This step decrease resulted in an abrupt decrease in SSC throughout the Estuary but cannot explain decadal timescale trends in SSC and turbidity. Observed declining trends in SSC and turbidity in the Estuary have generally been attributed to long-term declines in riverine sediment supply (e.g., Cloern and Jassby 2012; Hestir et al. 2016; Schoellhamer et al. 2014; Wright and Schoellhamer 2004). Schoellhamer et al. (2014) also observed a decline in September to October average SSC in Suisun Bay from 2000 to 2011, which was attributed to a range of possible contributing factors that would result in a decrease in sediment supply to the Estuary.
Even though reductions in sediment supply can impact turbidity, it is well documented that most of the time, tidal currents and wind-wave resuspension are the dominant processes resulting in sediment mobilization in the San Francisco Bay (Krone 1979; Lacy et al. 1996; Schoellhamer 2002, 2011; Brand et al. 2010) and shallow or estuarine systems in general (Weir and McManus 1987; Maceina and Soballe 1990; Sanford 1994; Fain et al. 2007; Friedrichs 2009). The cycle of sediment transport in the Estuary follows a strong seasonal pattern. Episodic pulses of sediment during elevated river discharge in the winter supply easily erodible sediment to the Estuary during an otherwise relatively low wind speed and low SSC seasonal period (Krone 1979; Schoellhamer 2002). Wind-wave resuspension resulting from increased wind speeds coupled with recently supplied easily erodible sediment increase SSC in the spring and summer, followed by a subsequent decrease in SSC in the fall as easily erodible sediment is winnowed from the surface of the sediment bed and wind speed decreases seasonally (Krone 1979; Ruhl et al. 2001; Schoellhamer 2002). The importance of waves and currents on seasonal SSC patterns suggests that a decrease in wind-wave resuspension resulting from a decrease in wind speed could also account for some of the observed decline in SSC and turbidity in the Estuary. This could be especially true in the fall, after easily erodible sediments supplied during the previous winter may have been winnowed from the shallows.
Study Area and Questions
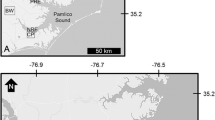
This study focuses on Suisun Bay, a subembayment within the Estuary, and the western portion of the Delta (Fig. 1). Suisun Bay includes two subembayments, Grizzly Bay and Honker Bay (Fig. 2). The water depth in Suisun Bay reaches 20 m in the channels, but Grizzly Bay and Honker Bay are typically less than 3 m deep. Suisun Bay has historically been considered favorable habitat for the endangered Delta Smelt when salinity is low and turbidity is high, with Delta Smelt predominantly caught in Suisun Bay in the fall and early winter before migrating upstream (Bennett 2005; Bever et al. 2016). Therefore, long-term changes in habitat quality resulting from changes to turbidity may be important in this region of the Estuary, especially during the fall to winter period. During the first large flows of the water year from the Delta tributaries, commonly referred to as the “first flush,” large amounts of sediment are supplied to the Estuary from tributaries, and SSC and turbidity in Suisun Bay are strongly influenced by riverine sediment supply (Ruhl and Schoellhamer 2004). However, turbidity returns to baseline levels within a month following the first flush and is driven by wind-wave resuspension and tidal currents during the remainder of the year (Ruhl and Schoellhamer 1999, 2004).
San Francisco Estuary. Orange lines delineate the wind regions. Wind data stations (squares) are identified by abbreviations spelled out in Table 1. Triangles show locations with field observations used to develop SSC to turbidity conversion curves
Suisun Bay and the western Delta with validation and analysis stations (circles) and analysis station (square) shown. The location of the Sacramento River at Freeport station is provided in Fig. 1
Wind speed over the Estuary is generally relatively low during the late fall and winter and then increases during the spring and summer before decreasing during the fall (Schoellhamer et al. 2016). Wind direction is strongly influenced by local orographic effects and predominantly from the west to southwest over the northern San Francisco Bay and the western Sacramento-San Joaquin Delta (Delta), with more variability in direction during the winter than during the summer (Conomos 1979). When episodic winter storms pass south of the Estuary, the winds are often from the east or southeast (Conomos 1979).
This study analyzed wind speed data to evaluate long-term trends at 11 stations around the Estuary and then investigated the influence of wind-wave resuspension on turbidity in Suisun Bay and the western Delta. The study demonstrates that decadal changes in wind speed affect turbidity, which in turn can affect estuarine habitat and ecology. Our approach combined the analysis of decadal-timescale trends in observed wind and sediment data with multiple year-long numerical model simulations. This study addressed the following main questions:
-
1.
Are there consistent decadal timescale trends in observed seasonal wind speed around the San Francisco Estuary?
-
2.
What is the effect of long-term trends in wind speed on the turbidity in Suisun Bay and the western Delta?
Methods
A combination of data analysis and 3-D numerical modeling was used to address the two main study questions. Twenty-one years of wind data from 11 stations were used to evaluate decadal timescale changes in wind speed around the Estuary. A coupled 3-D hydrodynamic, wave, and sediment transport model was then used to predict the effects of changes to wind speed on turbidity in the Estuary.
Decadal Wind Trend Analysis
Hourly wind data around the Estuary were obtained from the Bay Area Air Quality Management District (BAAQMD 2016) and the National Oceanic and Atmospheric Administration (NOAA 2014, 2016). Wind data from each station were initially visually screened for artificial changes to the wind speed time series, generally represented by a change in the minimum reported wind speed value, which Wan et al. (2010) demonstrated can have large effects on calculated trends. Stations that showed artificial changes in wind speed were not included in further analysis.
Wind speed trends were analyzed at seven BAAQMD stations around the Estuary using hourly data from 1995 through 2015 and at four NOAA stations using hourly data from 1995 through 2013 (Fig. 1; Table 1). Any periods with more than 10% missing data were not used in the trend analysis. A statistically significant trend in the wind speed was classified as having a Spearman rank correlation (Yue et al. 2002) p of less than 0.05. A non-parametric rank correlation was used to test for statistically significant trends because the non-parametric test does not include assumptions on data distribution inherent in a parametric test. The slope of the wind speed trend was calculated using the Theil-Sen non-parametric method (Theil 1950; Sen 1968; Gocic and Trajkovic 2013), commonly referred to as the Sen’s slope. The slope of the trend line represents the average change in wind speed per year (McVicar et al. 2012).
We first calculated trends in the monthly averaged wind speed at each station for each month of the year individually. This monthly analysis indicated that many stations had statistically significant declines in wind speed from October through January between 1995 and 2015. The months of February through September did not have the same consistency of statistically significant wind speed declines at the analysis stations as did October through January. Based on the consistent trends in the four consecutive months of October through January, we grouped the wind speed data into three 4-month averaging periods: October through January; February through May; and June through September. At each station, we then evaluated trends in the wind speed averaged over these three periods. The use of 4-month-average wind speed limited the influence on the trend analysis of episodic winter storms occurring in different months each year.
The wind trend line based on the Sen’s slope was used to estimate a percent decline in the wind speed from 1995 through 2015. The percentage decline in wind speed for each station was calculated using the change in wind speed from the trend lines over the 20-year period, rather than from differences between the individual years at the beginning and end of the period. The use of the trend lines in determining the percent decline in wind speed removed any influence of particularly high or low wind speed during the beginning or end years of the analysis period.
The Estuary was separated into five discrete regions for determining average wind speed trends throughout the system (Fig. 1; Table 1). The use of five regions ensured there are at least two wind speed stations in each region and that the analysis in a region was not dependent on only a single station. The percent changes in wind speed from 1995 through 2015 at the stations within each wind region were averaged to estimate a wind reduction within each of the five regions for each 4-month averaging period. Shell East, Port Chicago, and Fairfield were averaged for the Suisun Bay region; Rio Vista and Sacramento Executive Airport were averaged for the North Delta Region; Stockton Municipal Airport and Bethel Island were averaged for the South Delta region; Point San Pablo and Oakland International Airport were averaged for the Central Bay and San Pablo Bay region; and San Francisco International Airport and San Carlos were averaged for the South Bay region. If any station in a wind region had a non-significant trend during a 4-month averaging period, the analysis assumed no significant trend for that seasonal period for that region. Similarly, if two different stations in a region had positive and negative wind speed trends, the analysis assumed no significant trend for that seasonal period for that region. Thus, our approach only assumed the presence of a trend when all stations evaluated within a region showed consistent statistically significant trends over a 4-month period.
Long-term trends in wind direction were examined through evaluation of the dominant wind direction and wind roses for each 4-month averaging period for each water year. Wind direction at individual stations was binned into 20° bins and the dominant direction was identified as the directional bin with the highest occurrence in the hourly wind data over each 4-month averaging period. Wind roses were generated from the binned wind direction to visualize the predominant wind directions.
Turbidity Modeling
The Unstructured non-linear Tidal Residual Inter-tidal Mudflat (UnTRIM) Bay-Delta model (MacWilliams et al. 2015) was used to predict the effects of long-term trends in wind speed on turbidity in the Estuary, with focus on the region surrounding Suisun Bay and the Western Delta. In this modeling framework, the 3-D UnTRIM hydrodynamic model is coupled to the Simulated WAves Nearshore (SWAN) wave model and the SediMorph seabed morphology model and runs as a fully-coupled 3-D hydrodynamic, wave, and sediment transport model. Detailed descriptions of the UnTRIM Bay-Delta hydrodynamic model and the coupled hydrodynamic, wave, and sediment transport model are provided in MacWilliams et al. (2015) and Bever and MacWilliams (2013), respectively. Because the models are well documented in previous literature, this section only presents a general overview of the models.
UnTRIM Bay-Delta Model
The UnTRIM model solves the 3-D Navier-Stokes equations on an unstructured grid in the horizontal plane. The model uses a Z-layer vertical grid with layers at fixed elevations. Grid layer thickness can be varied vertically to provide increased resolution near the surface or other vertical locations. The numerical method in UnTRIM allows full wetting and drying. The governing equations are discretized using a finite difference–finite volume algorithm. A complete description of the governing equations, numerical discretization, and numerical properties of UnTRIM are described in Casulli and Zanolli (2002, 2005), Casulli (1999), and Casulli and Walters (2000) and are not reproduced here.
The UnTRIM San Francisco Bay-Delta model (UnTRIM Bay-Delta model) is an implementation of the UnTRIM hydrodynamic model which extends from the Pacific Ocean through San Francisco Bay and the entire Sacramento-San Joaquin Delta (MacWilliams et al. 2015; Fig. 3). The UnTRIM Bay-Delta model takes advantage of the grid flexibility allowed with an unstructured mesh by gradually varying grid cell sizes, beginning with large grid cells in the Pacific Ocean and gradually transitioning to finer grid resolution in the smaller channels of the Delta. The vertical grid resolution is 1 m to a depth of 20 m below the North American Vertical Datum of 1988 (NAVD88). Between 20 m below NAVD88 and 105 m below NAVD88, the vertical layer spacing gradually increases from 2 to 5 m.
UnTRIM San Francisco Bay-Delta model domain, bathymetry, and locations of model boundary conditions which include inflows, export facilities, intakes for the Contra Costa Water District (CCWD), wind stations from the Bay Area Air Quality Management District (BAAQMD), evaporation and precipitation from the California Irrigation Management System (CIMIS) weather stations, Delta Island Consumptive Use (DICU), and flow control structures
The salinity field for the Estuary portion of the UnTRIM Bay-Delta model is initialized based on observed profiles from transects spanning the length of the Bay (USGS 2016a). SSC in the water column is initialized to zero. Model simulations start about 2.5 months before the analysis period to allow for spin-up from the initial conditions. Observations of water surface elevation at the NOAA San Francisco station, located at Fort Point, near the southern end of the Golden Gate Bridge, are used to drive the tidal (ocean) boundary of the model domain. The river inflows to the model domain include tributary inflows to the Delta, discharges from water pollution control plants, and other tributaries of the Estuary (Fig. 3). Delta inflow values are obtained from daily-averaged flows estimated by the DAYFLOW program, made available by the California Department of Water Resources (CDWR 1986). The model also accounts for operable gates, temporary flow barriers, and Delta Island Consumptive Use (DICU) within the Delta (MacWilliams et al. 2015). The model has been extensively validated in previous studies and shown to accurately predict water level, current speeds, and salinity (e.g., MacWilliams et al. 2015) throughout the estuary under a wide range of conditions, and for waves and suspended sediment (e.g., Bever and MacWilliams 2013). Therefore, no further validation for hydrodynamic variables other than turbidity is presented here.
Wind forcing is applied at the water surface as a wind stress, with the drag coefficient varying based on local wind speed according to Large and Pond (1981). Observed hourly wind speed and direction from the BAAQMD were used to account for spatial variability in wind velocities (Fig. 3). For the model simulations, wind forcing within each region of the domain was based on a single BAAQMD station within that region following the approach used previously for specifying wind in the model (MacWilliams et al. 2015). The use of a single wind station to specify wind within each region in the model rather than the multiple wind stations used in the trend analysis is not likely to affect the study results because the wind trends are consistent between stations within each region. Wind data from San Carlos were used in South San Francisco Bay, wind data from Point San Pablo were used in Central San Francisco Bay and San Pablo Bay, and wind data from Pittsburg and Fairfield were used in Carquinez Strait and Suisun Bay. Wind data at Rio Vista were used in the northern and central portions of the Delta, and data at Bethel Island were used in the southern portion of the Delta.
Wave Modeling
The SWAN model was used to calculate the 2-D and time-dependent waves necessary for simulating wave-induced sediment resuspension. SWAN is a third-generation wave model based on the wave action balance equation which is formulated for use in coastal applications (Booij et al. 1999; SWAN Team 2016a). SWAN models the effects of wind wave generation, refraction, shoaling, dissipation by bottom friction, white capping, nonlinear wave-wave interactions, and ambient currents on the wave properties (SWAN Team 2016b).
The SWAN implementation used in this study is configured based on previous calibrations using UnTRIM and SWAN in Suisun Bay, to the west in San Pablo Bay, and in the South Bay (MacWilliams et al. 2012; Bever and MacWilliams 2013; Bever and MacWilliams 2014). Directional space is divided into 36 sections and frequency space is divided into 47 sections between a minimum of 0.0521 Hz and a maximum of 4.1774 Hz. The processes modeled include bottom friction based on Madsen et al. (1988) (see SWAN Team 2016b for details), wind generated waves, whitecapping, wave breaking, quadruplet wave-wave interactions, wave refraction, and the influence of the currents on the waves. A method from Rogers et al. (2003) was included in the SWAN modeling to limit the artificial reduction of lower frequency waves by dissipation. Wave refraction was limited based on the Courant–Friedrichs–Lewy (CFL) criteria to improve the calculations of wave period (Dietrich et al. 2013). SWAN was run hourly, corresponding to the use of hourly winds in the model.
Sediment Transport Modeling
SediMorph is a morphologic model that calculates erosion, deposition, net sediment flux at the seabed, and the adjustment and tracking of sediment parameters in the seabed. The physics modeled in SediMorph are described in detail by Malcherek (2001), Malcherek and Knock (2006), and Bever and MacWilliams (2013). SediMorph allows for multiple sediment classes, each with different settling velocity, critical shear stress, diameter, erosion rate parameter, and density. SediMorph keeps track of multiple seabed sediment layers, each of which can be composed of different fractions of each sediment class to allow for armoring of the seabed or the retention of fine sediment as thin, easily erodible layers. Erosion from a surface exchange layer is calculated according to Ariathurai and Arulanandan (1978). The surface exchange layer varies in thickness with the bed shear stress and seabed grain size, as in Harris and Wiberg (1997).
Four sediment classes, representing a range of sediment sizes and characteristics, are modeled in this application of the UnTRIM and SediMorph models. The four modeled sediment classes are silt, aggregated clay and silt which behave as flocculated particles (flocs), sand, and gravel (Table 2). In this way, the mud within the estuary is modeled using the silt and flocs classes. Aggregation and disaggregation processes are not included, and sediment mass cannot move between sediment classes. Gravel is transported only as bedload and the other three sediment classes are transported only as suspended load, because the model allows for each sediment class to be treated as either bedload or suspended load. Sediment class characteristics were determined based on available data (e.g., Kineke and Sternberg 1989; Smith and Friedrichs 2011) and model calibration throughout the Estuary. These sediment characteristics are consistent with the ranges of values used for sediment transport modeling within the Estuary (Ganju and Schoellhamer 2009; Van der Wegen et al. 2011; Van der Wegen and Jaffe 2013; Bever and MacWilliams 2013). The erosion rate parameter for each sediment class varied based on the wave-induced bed shear stress to improve predictions of wave-driven sediment resuspension in the Bay shallows. The erosion rate parameter increased linearly to four times the minimum erosion rate parameter from 0.0 Pa wave stress to 1.0 Pa wave stress. This increase in the erosion rate parameter is similar to Moriarty et al. (2014), who varied the erosion rate parameter as a function of water depth. An increase in the erosion rate parameter as stress increases is also consistent with erosion rate parameters estimated from experimental data (see Dickhudt 2008; Schoellhamer et al. 2017). Schoellhamer et al. (2017) hypothesize that the erosion rate parameter increases with increased stress because the surface area of the bed undergoing erosion increases as the stress increases and sediment is eroded.
The initial sediment bed grain size distribution in each model grid cell was determined based on over 1000 grain size distribution observations collected from at least as far back as 1992 until 2012 (not all data was provided with collection dates), as described by Bever and MacWilliams (2013). The thickness of the initial sediment bed was set to 1 m. Seabed elevation and depth-averaged current speed were used to help partition the mud fraction in the initial sediment bed into silt and floc classes. In this approach, the percentage of the silt class was increased relative to the flocs class as water depth and depth-averaged velocity decrease, representing the higher likelihood for single particle silts to settle from the water column and be present in the sediment bed in significant quantities in regions with relatively slower current speed (e.g., mudflats and breached salt ponds).
Model Scenarios
Eight model simulations, each spanning a 12-month period corresponding to a specific water year, were used to predict the effects of long-term trends in wind speed on turbidity in the vicinity of Suisun Bay and the western Delta (Table 3). Water years are defined as the period between October 1 of one year and September 30 of the next, such that water year 1992 spans from October 1, 1991 through September 30, 1992. By using water years instead of calendar years, all the water that falls with a single rainy season is captured in the same 12-month period. Similar long-term analyses (e.g., Schoellhamer 2011) are also based on water years. Four baseline scenarios simulated water years 1992, 1995, 2011, and 2015 using the observed wind speed and direction (Table 3). Water years 1992 and 1995 were selected to provide an evaluation of conditions during both a “wet” water year (1995), the wettest classification (CDWR 2016), and a “critical” water year (1992), the driest classification, during the 1990s, when the wind speed and sediment supply were higher than the present. Water years 2011 and 2015 were selected to provide an evaluation of conditions during both a wet water year (2011) and a critical water year (2015) during the 2010s under more recent conditions, which have lower wind speed and sediment supply than the early 1990s. The use of both critical and wet water years allows for the examination of the effects of wind speed trends on turbidity during both less stormy and low sediment supply years (critical) and more stormy and high sediment supply years (wet). The use of years from the 1990s and the 2010s allows for the comparison of the predicted effects on turbidity between years with relatively higher (1990s) and relatively lower (2010s) wind speed. These four base year scenarios were used for model validation, and as baseline conditions for comparisons to the four wind scenarios.
In the baseline scenarios, sediment is supplied to the system from six Delta, one North Bay, and four South Bay tributaries. Sediment is supplied to the Delta from the Sacramento River, Cosumnes River, Mokolumne River, Calaveras River, San Joaquin River, and the Yolo Bypass (Fig. 3). For the 1992 and 1995 scenarios, the SSC for the Sacramento River and San Joaquin River inflows were set based on U.S. Geological Survey (USGS) daily estimates (USGS 2016b), while the SSC for the Cosumnes River, Mokolumne River, and Calaveras River inflows were set based on rating curves (Wright and Schoellhamer 2005). For the 2011 and 2015 scenarios, SSC for the Sacramento River, Cosumnes River, Mokolumne River, Calaveras River, and San Joaquin River inflows were set based on USGS estimates of cross-sectional averaged concentration (USGS 2016b). The SSC for the Yolo Bypass inflows during all years is based on an updated rating curve provided by the USGS (Tara Morgan-King, USGS, Pers. Comm. 2013). Sediment is supplied to the North Bay by the Napa River. Sediment is supplied to the South Bay from Alameda Creek, San Lorenzo Creek, Coyote Creek, and Guadalupe River. For these North Bay and South Bay tributaries, the observed SSC from USGS was used to specify the inflow SSC when data were available (USGS 2016b), and rating curves were used to set inflow SSC when no observation data were available.
Four wind scenarios (Table 3, scenarios 5–8) use the baseline winds adjusted by the observed long-term trends to evaluate the effect of wind speed on turbidity. Water years 1992 and 1995 were simulated with a decrease in the wind speed, while 2011 and 2015 were simulated with an increase in the wind speed. The hourly wind speed in the model input files was increased and decreased by the long-term percentage change in each wind region and 4-month averaging period from the trend analysis (Table 4) to create model input files with increased wind speed and with decreased wind speed. The wind direction was not changed. The four wind scenarios were compared to the four baseline scenarios (Table 3, scenarios 1–4) to evaluate the effect of long-term trends in wind speed on turbidity in the Estuary.
Conversion of Modeled Suspended Sediment Concentration to Turbidity
The sediment transport model predicts the SSC in the water column and not the turbidity directly. SSC is simulated because there are well-established physics equations for predicting sediment erosion, deposition, and transport, and SSC is a conservative property. Turbidity is an optical property of the water (see Gray and Gartner 2009), resuspension effects on turbidity cannot be directly modeled using physics-based equations, and turbidity is not a conservative property. However, in systems where SSC is the primary driver of turbidity, conversion curves can be used to convert between turbidity and SSC. Due to the large number of available turbidity observations, and the widespread use of turbidity (rather than SSC) as a habitat indicator for many species, including Delta Smelt (e.g., Nobriga et al. 2008; Sommer and Mejia 2013; Bever et al. 2016), the model predictions of SSC were converted to turbidity using conversion curves developed from field observations. This allows for the inclusion of the physical processes driving the sediment transport and SSC into predictions of turbidity. The conversion of SSC to turbidity was appropriate for this study because suspended sediment is the largest component of water turbidity in the Estuary (Schoellhamer et al. 2002; Buchanan and Morgan 2012). Ganju et al. (2007) found that the conversion of SSC to turbidity is remarkably constant in the San Francisco Bay. However, our analysis based on USGS data showed a very large range in the conversion curves in the study area when the Delta is included (Fig. 4). Because of the large range in slopes of conversion curves, we used multiple SSC to turbidity conversion curves throughout the Estuary and interpolated spatially between these curves.
Available turbidity and SSC time series data (CDEC 2016; USGS 2016b) at 18 stations from Carquinez Strait through the Delta were used to estimate the relationships used to convert the observed turbidity into observed SSC. These curves were then used to convert predicted SSC into predicted turbidity. A linear interpolation from 0 NTU to 1 NTU was used at very low predicted SSC to prevent negative predicted turbidity, even though a very small amount of turbidity observations in the Delta are negative values. The conversion curves were assumed to be vertically uniform within each horizontal model grid cell. To account for the spatial variability in SSC to turbidity conversion curves (Fig. 4), an inverse distance-squared interpolation based on along-channel distance was used to develop weighting for each conversion curve at each model grid cell. The use of along-channel distance prevents interpolation across land and better represents the paths of water flow.
Model Validation
Model validation was conducted to demonstrate that the model captured the primary processes driving SSC and turbidity in the Estuary. The predicted SSC and turbidity were initially calibrated to observed data from water year 2011. Model predictions of turbidity were then validated against observed turbidity time series at nine stations in the vicinity of the study area for water year 2015 (Fig. 2), with two stations having sensors at two vertical locations in the water column. This resulted in a total of 11 time series validation comparisons at 9 locations. Water year 2015 was chosen for model validation because it has the highest number of continuous monitoring turbidity stations and is outside the main calibration period. The predicted turbidity was validated using methods detailed in MacWilliams et al. (2015), using the means and correlation of the observed and predicted turbidity, model skill (Willmott 1981), and target diagram statistics (Jolliff et al. 2009) to classify the accuracy of the model. Although Ralston et al. (2010) identified some shortcomings of the Willmott (1981) model skill metric, it has nevertheless been used to compare model predictions to observed data in numerous hydrodynamic modeling studies (e.g., Warner et al. 2005; Haidvogel et al. 2008; MacWilliams and Gross 2013).
The target diagram statistics determine how the mean and variability of the model predictions related to those of the observed data at numerous different times or locations. Jolliff et al. (2009) and Hofmann et al. (2011) provide detailed descriptions of target diagrams and their use in assessing model skill. This approach uses the bias and the unbiased root-mean-square difference (ubRMSD) between the observations and predictions, which are normalized by the standard deviation in the observations (biasN and ubRMSDN) to assess the accuracy of the model predictions. The ubRMSDN was multiplied by the sign of the difference in the observed and predicted standard deviations to indicate overprediction (positive) or underprediction (negative) of the observed variability. The radial distance from the origin to each data point is the normalized total root-mean-square difference (RMSDN, calculated as \( {\mathrm{RMSD}}_{\mathrm{N}}=\sqrt{{\mathrm{bias}}_N^2+ ub{\mathrm{RMSD}}_N^2} \)). Thresholds established by MacWilliams et al. (2015) were used to classify the accuracy of the model predictions, with an RMSDN less than 0.25 indicating very accurate predictions, 0.25 to 0.5 indicating accurate predictions, 0.5 to 1.0 indicating acceptable predictions, and greater than 1.0 indicating relatively poor agreement between the predictions and observations.
The spatial distribution in turbidity was validated using remote sensing data. The NASA Jet Propulsion Laboratory (JPL) used satellite data to estimate surface turbidity throughout Suisun Bay for August 12, 2015, at 10:45 am, a date that overlaps with the 2015 simulation. Surface turbidity was estimated using data from the Landsat-8 satellite (USGS 2018) following the method of Dogliotti et al. (2015), with an estimated relative error in the remotely sensed turbidity of 13.7%. This method uses the reflectance of 645 and 859 nm wavelengths to estimate surface turbidity up to 1000 Formazin Nephelometric Units (FNU). The model-predicted surface turbidity at the same date and time was compared to the remote-sensing-estimated turbidity to validate the surface turbidity pattern and magnitudes in the study location around Suisun Bay assuming FNU is equivalent to NTU. The model-predicted turbidity was interpolated onto the same 30-m by 30-m grid developed for the remote sensing data and validated using a map-based comparison and the same statistical approach used for the time series comparisons described above.
Results
Decadal Wind Speed Trends
Seasonal-average wind speed showed statistically significant (p < 0.05) declines at each station for the October through January averaging period (Fig. 5; Table 1). A similar result was obtained using the root mean square (RMS) wind speed over each 4-month period. The RMS wind speed trends are not discussed because they showed similar trends to the average wind speed, which are discussed in detail. Stations in the Suisun Bay region did not have statistically significant wind speed trends in the February through May or the June through September averaging periods. All the North Delta stations had statistically significant declines in wind speed for all three 4-month averaging periods. The South Delta, Central Bay, and South Bay regions all had stations both with and without statistically significant wind speed trends over the February through May and June through September averaging periods. The Bethel Island station for the June through September averaging period was the only station to have a statistically significant wind speed increase. The wind speed declines ranged from a high of 47.5% at the Sacramento Executive Airport during October through January to a low of 7.6% at San Carlos during February through May (Table 1).
The wind speed trends from each individual station in the five regions were averaged to determine an average wind speed trend during each time period. Region-wide wind speed declines ranged from 19.8 to 41.0% over the 20-year analysis period between 1995 and 2015 (Table 4). Only the October through January time period had a wind speed decline in all five regions. For the February through May and June through September periods, only the North Delta region had statistically significant wind speed declines at all stations. None of the regions had consistent statistically significant wind speed increases.
Plots of the dominant wind directions at stations around the Suisun Bay study area do not suggest a trend in the dominant wind direction over the October through January period when statistically significant wind speed declines were observed (Fig. 6). The Shell East, Fairfield, and Rio Vista stations had almost no annual variability in the dominant wind direction from October through January. The limited variability in the dominant wind direction can also be seen in wind roses. Wind roses show that Rio Vista generally has winds from three directions, but that those directions remain the same over the entire 1995 through 2015 period and the dominant direction is generally from the west-southwest (Fig. 7, left panels). The general pattern in the wind roses at Port Chicago of wind from the southwest or east-northeast is consistent between wet (Fig. 7e, g) and dry (Fig. 7f, h) water years. However, the dominant wind direction at the Port Chicago station varied by year (Fig. 6). Some of the interannual variability in the dominant wind direction at Port Chicago may be due to differences in wind between wet (generally more stormy) and dry (generally less stormy) years, because wind direction can be different during episodic storms than average October to January conditions (Conomos 1979).
Validation of Model-Predicted Turbidity
Time series observations of turbidity were used to validate that the model captured the variability in turbidity on multiple timescales at individual locations. Based on the target diagram accuracy classification RMSDN thresholds from MacWilliams et al. (2015), the model accurately predicted the turbidity at one location, acceptably predicted the turbidity at seven locations, and poorly predicted the turbidity at three locations in the study area (Table 5). The observation station in Grizzly Bay is located near the edge of expansive shallows, and turbidity at this location is influenced both by wind-wave resuspension in the shallows and relatively less turbid water from the main channel (see spatial validation of the predicted surface turbidity below). At the Grizzly Bay station, the model-predicted tidal timescale increases in turbidity at the same times as the observed turbidity increases (Fig. 8a). The model also captured the increases and decreases in turbidity occurring on an approximately 2-week spring-neap cycle (Fig. 8a, b) and the seasonal cycle of relatively low turbidity in the late fall and winter increasing in the spring through the summer and then decreasing into the late fall (Fig. 8b). The model tended to underpredict the peaks in the observed turbidity, resulting in a low slope of the best-fit line. This underprediction of turbidity may result from either an underprediction of sediment resuspension or from uncertainty in the conversion from SSC to turbidity. The Grizzly Bay station is approximately equidistant from Benicia and Mallard Island, which have markedly different conversion curves between SSC and turbidity (Fig. 4). For example, for a predicted SSC concentration of 100 mg/L, the Benicia Bridge curve would yield a turbidity value of approximately 66 NTU, whereas the Mallard Island curve yields a turbidity value of approximately 134 NTU (103% higher). Because the spatial conversion from SSC to turbidity weights the conversion curves for both these stations, there is significant uncertainty in the magnitude of the turbidity due to the difference between these two curves (Fig. 4). Thus, while the model accurately predicts the timing of individual peaks and longer term seasonal trends, uncertainty in the magnitude is introduced by applying SSC to turbidity conversions derived from data collected at other locations to this station.
Based on the target diagram accuracy classification RMSDN thresholds, the second poorest predictions of turbidity were at the Three Mile Slough Station (Fig. 9). The Three Mile Slough station is in the Delta between the Sacramento and San Joaquin Rivers, where turbidity is more strongly influenced by periods of elevated river discharge and junction dynamics than wind resuspension. Additionally, the SSC to turbidity conversion at this station most strongly weights the conversion curves for the Rio Vista and Jersey Point stations, which have markedly different conversion curves between SSC and turbidity (Fig. 4). For example, for a predicted SSC concentration of 100 mg/L, the Rio Vista curve would yield a turbidity value of approximately 71 NTU, whereas the Jersey Point curve yields a turbidity value of approximately 113 NTU (59% higher). This range of uncertainty may explain the wide range of slopes on the best fit lines between observed and predicted turbidity (Table 5), whereas the prediction of the timing and pattern of peaks in turbidity are accurate on both tidal (Fig. 9a) and seasonal (Fig. 9b) timescales. Both the observed and predicted turbidity showed two episodic increases as a result of two periods of elevated river discharge from winter storms (Fig. 9). The observed and predicted turbidity also both indicated relatively low turbidity with little variability before the elevated discharge, increasing turbidity and increasing tidal variability between December 10 and December 15, 2014, and then a large increase in turbidity and tidal variability between December 15 and December 20, 2014 (Fig. 9a). This large tidal-timescale variability during elevated discharge results from differences in flow direction through the junction between the turbid Sacramento River and the relatively clear San Joaquin River on a tidal-timescale. Following the elevated discharge, the observed and predicted turbidity both return to relatively lower turbidity and lower tidal variability. The modeled turbidity was overpredicted during the episodic events, resulting in the steep slope to the best fit line. However, some of this overprediction in turbidity may result from uncertainty in the SSC to turbidity conversion curves.
Remote sensing data was used to validate that the predicted turbidity captured spatial distributions in observed turbidity. The JPL remote sensing turbidity and the model predictions of turbidity both show the same spatial pattern in surface turbidity (Fig. 10). The model predictions and the estimates derived from satellite imagery both show relatively lower turbidity water throughout most of Suisun Bay and higher turbidity in the shallow portions of Grizzly Bay. Both estimates of turbidity show a sharp turbidity gradient between the high turbidity region in Grizzly Bay and the rest of Suisun Bay, which is much less turbid. The model predicted lower turbidity than estimated from remote sensing along the northwest shore of Suisun Bay. This difference in estimated turbidity is shown on the scatter plot (Fig. 10c) by an increase in the remote sensing turbidity from 200 to about 360 NTU, while the model predictions remain around 75 NTU. This area of very high remote sensing turbidity is localized to a relatively small area that is below the horizontal resolution of the model. Statistically, the model predicted average turbidity to be 7.8 NTU higher than the remote sensing estimate and acceptably predicted the remote sensing turbidity (RMSDN = 0.55; Table 5). When accounting for the estimated relative error in the remotely sensed turbidity estimates (13.7% from Dogliotti et al. 2015), the model bias over Suisun Bay is potentially reduced from 7.8 to 2.6 NTU.
The model predictions of the timing and magnitude of elevated turbidity on multiple timescales (tidal, fortnightly, and seasonal), as seen on Figs. 8 and 9, and the accurate prediction of spatial turbidity patterns (Fig. 10), demonstrates that the model is accurately capturing the dominant processes influencing sediment resuspension and transport and the resulting turbidity in the study area. Because the model captures the relevant processes, it is suitable for use in investigating the influence of the observed decline in wind speed on turbidity in the Estuary.
Effects of Wind Speed Trend
Four model scenarios evaluated the effect of long-term trends in wind speed (Table 3, scenarios 5 through 8). These scenarios indicated that the effect of the observed wind speed trend on waves was the largest in the open water regions of San Francisco Bay and decreased into the narrow channels of the Delta, where waves are generally small. Increasing or decreasing the wind speed by the observed long-term trend (Fig. 11a) resulted in corresponding changes to the size of the predicted waves. Reductions in wind speed resulted in reductions in wave height (Fig. 11b) and period, and increases in wind speed resulted in increases in wave height and period. Decreases in the predicted waves in Suisun Bay produced corresponding changes to the seabed shear stress (Fig. 11c), and increases in the waves resulted in increased seabed shear stress. The physical processes driving turbidity changes in the study area were the cascading effects of wind on waves and the nonlinear effect of waves on sediment resuspension from the Suisun Bay shallows (e.g., Grizzly Bay and Honker Bay). Sediment resuspension from the shallows was strongly influenced by the predicted bed shear stress during wind-wave resuspension events. Some of the sediment resuspended from the shallows was then advected to the main channels, resulting in an overall increase in turbidity throughout Suisun Bay. The effects of increasing or decreasing the wind speed on turbidity were not predicted to be uniform in time; rather, the majority of the differences in turbidity between the baseline (scenarios 1 through 4) and the wind scenarios (scenarios 5 through 8) occurred during wind-wave episodes and periods of elevated sediment resuspension (Fig. 11d). Following the periods of elevated resuspension, both the baseline and wind scenarios returned to similar background values.
a Suisun Bay wind speed used in the scenarios, b significant wave height, c wave and current combined seabed shear stress, and d turbidity at the Grizzly Bay monitoring station for the 1995 baseline and decreased wind scenarios. The shaded periods highlight resuspension events in the baseline scenario that were not predicted in the decreased wind scenario. The dashed line in (c) shows the critical shear stress of the flocs sediment class for reference
Figure 11d highlights periods of elevated sediment resuspension and turbidity that occurred in the baseline but were absent when the wind speed was decreased. This indicates that the decrease in wind speed decreased the waves over a large portion of the Grizzly Bay shallows such that the bed shear stress was below the critical shear stress of the modeled sediment classes, resulting in some of the relatively large resuspension events in the baseline not being predicted in the decreased wind scenario. The wind scenarios which applied the observed long-term trends in wind speed as wind speed increases predicted similar findings, with both higher turbidity during resuspension events and more resuspension events and turbidity peaks than the baseline.
Similar to the waves, the effect of the observed wind speed trend on turbidity was largest in the open water regions of San Francisco Bay and decreased into the narrow channels of the Delta (Fig. 12; Tables 6 and 7). The October through January period had the largest effect of changes to wind speed on turbidity (Tables 6 and 7). During the October through January period, the four wind scenarios (Table 3, scenarios 5 through 8) applied wind speed trends throughout the entire Estuary based on the observed trends at all stations during these months. For the remainder of the year, the wind scenarios applied the trend to wind speed only in the North Delta region (Table 4). The largest effects on turbidity due to decreasing wind speed for 1992 and 1995 (Table 6) and increasing wind speed for 2011 and 2015 (Table 7) are evident at the Grizzly Bay and Honker Bay stations in open water (Fig. 12). Averaged over October through January, during the water year 1992 (critical water year) wind scenario, the observed reduction in wind speed was predicted to decrease the turbidity by 55% in Grizzly Bay (Fig. 13a; Table 6) and had a smaller decrease of 26% at Sherman Island (Fig. 14a; Table 6). The 1995 (wet water year) scenario predicted similar results between Grizzly Bay (Fig. 13a; Table 6) and Sherman Island (Fig. 14a; Table 6) with decreases of 50 and 7%, respectively. During the 2011 (wet water year) scenario, an increase in the wind speed equal to the long-term trend resulted in an average increase in turbidity of 60% at the Grizzly Bay station (Fig. 13b; Table 7) and again less effect (4% increase) progressing up the Sacramento River at Sherman Island (Fig. 14b; Table 7). The water year 2015 (critical water year) scenario predicted similar results with comparatively larger effects of wind on turbidity during the October through January period at Grizzly Bay (Fig. 13b; Table 6) than at Sherman Island, with increases of 50 and 8%, respectively (Fig. 14b; Table 7). Somewhat smaller turbidity effects were predicted during this time period at the Benicia and Mallard Island stations relative to the Grizzly Bay station. At the Rio Vista and Freeport stations in the Delta, only very small effects on turbidity were predicted as a result of either increasing or decreasing winds between October and January.
During the February through May and June through September periods, when the wind trends were applied only in the North Delta, the effects on turbidity due to decreasing wind speed for 1992 and 1995 (Table 6) and increasing wind speed for 2011 and 2015 (Table 7) were relatively small for all the analysis stations except Jersey Point. The small change in turbidity relative to the period when the wind trends were applied throughout the study region is evidenced by the smaller changes predicted at the Grizzly Bay station between February and May (Fig. 13). The smaller effect of the wind trends during the February through May and June through September periods results because only the North Delta region had a statistically significant wind speed trend during these months (Table 4) and the effect on turbidity resulting from changes in wind speed from October through January throughout all five regions was largely confined to that time period. Turbidity in the North Delta region near large open-water areas was predicted to be more affected by wind speed trends from June through September than Suisun Bay. For example, the largest predicted declines in turbidity resulting from decline in wind speed trends in the North Delta during June and September were at Jersey Point (Tables 6 and 7).
The availability of easily erodible sediment on the seabed was increased when past resuspension and winnowing were decreased. This lead to changes in turbidity in the wind scenarios relative to the baseline outside of the time period when the winds were adjusted. For example, turbidity in Grizzly Bay was increased in the reduced wind scenarios relative to the baseline during some resuspension events in February through May 1992 and 1995 (Fig. 13a). This increase in turbidity relative to the baseline was because the reduction in wind-wave resuspension during October through January resulted in slightly more easily erodible sediment remaining at the bed surface following the end of the October through January period than in the baseline. The 2011 wind scenario shows similar results, with an increase in wind speed and wind-wave resuspension during October through January due to higher winds resulting in a slight decrease in fine sediment at the bed surface relative to the baseline and a general slight decrease in turbidity from February through May 2011 at the Grizzly Bay station (Fig. 13b).
Discussion
Decadal Reduction in Wind Speed
This study documented a statistically significant decline in wind speed throughout the Estuary from 1995 through 2015. However, there was interannual variability in the seasonally averaged wind speed around the long-term trend (Fig. 5). Because California was in a drought from water year 2013 through 2015, it was possible that multiple low storm years at the end of the 1995 through 2015 record, possibly corresponding to low average wind speed from October through January, could have caused the decline in wind speed to be statistically significant. However, when the average wind speed trends were recalculated using only the 1995 through 2012 data, the decline in average wind speed from October through January was still statistically significant at every station evaluated except one (Point San Pablo, p = 0.123). Also, 1995 through 2000 were all wet or above normal water years at the beginning of the analysis period, possibly corresponding to above-average wind speed from October through January. Excluding 1995 through 2000 from the analysis period, results in the analysis both starting and ending with dry or critical water years. After excluding 1995 through 2000 from the wind trend analysis, all stations evaluated except Point San Pablo (p = 0.081) and San Francisco Airport (p = 0.067) had statistically significant wind speed declines. This demonstrates that the cause of the decline in wind speed is likely a result of decadal changes in conditions driving the winds over the Estuary and not the sequence of wet versus critical (dry) water years during the 20-year time period evaluated.
It is unclear whether the observed decline in wind speed over the past 20 years will continue, whether future winds will remain at the current lower level, or whether this trend is cyclical and will reverse in the coming decades. While the available data from 1995 through 2015 was consistent in indicating wind speed declines in the fall, a similar analysis of the NOAA wind data around the Estuary from 1973 to 1994 indicated that three stations (Oakland International Airport, Sacramento Executive Airport, and Stockton Metropolitan Airport) did not have a statistically significant trend in wind speed and one station (San Francisco Airport) had a statistically significant increasing trend over the 20 years preceding the analysis period used in this study.
Previous studies have documented the influence of climate oscillations on wind speed and direction. For example, Scully (2010) showed that wind direction over the Chesapeake Bay is associated with the modified Bermuda high climate index, and that much of the decadal variability in the volume of hypoxic water is also associated with the modified Bermuda high index. Wei et al. (2016) showed a link between North Pacific sea surface temperature anomalies and wind over the ocean. The Pacific Decadal Oscillation (PDO) is a climate oscillation based on sea surface temperature anomalies in the northern Pacific and is itself a product of three different processes (Mantua and Hare 2002; Newman et al. 2016). The PDO underwent an increasing trend from the early 1970s until the mid-1980s and a decreasing trend from the mid-1980s until the mid-2010s. These trends in the PDO, or corresponding trends in the processes driving the PDO, could be influencing the observed wind speed trend from 1995 through 2015 and the absence of a wind speed trend when we analyzed the available wind data from 1973 through 1994. Further work to identify the mechanisms driving the observed wind speed trends would both improve the ability to forecast future wind speed trends (or the absence of trends) and improve the understanding of the mechanisms behind past trends.
Effect of Long-Term Declines in Wind Speed on Turbidity
The observed long-term decline in wind speed resulted in a large decrease in SSC and turbidity in the open-water areas of the Estuary from October through January when turbidity potentially provides an important habitat component for native fishes. This demonstrates that declines in observed SSC and turbidity in the Bay over the past 20 years are a product of both reduced sediment supply and reduced wind speed. Specifically, the trend in decreasing SSC in Suisun Bay from 2000 to 2011 identified by Schoellhamer et al. (2014) that was attributed to a decrease in sediment supply may result in part from a decline in wind speed. Even if the supply of sediment to the Estuary levels off, a continued decrease in wind speed could result in a continued decrease in turbidity. However, if the decrease in wind speed is cyclical, future increases in wind speed may result in increased turbidity, particularly in open water areas of the Estuary, such as Suisun Bay. If the sediment supply to the Estuary remains low and the shallows (e.g., Grizzly Bay) erode and deepen over time (Cappiella et al. 1999), then the effectiveness of wind waves at resuspending sediment and increasing turbidity will be reduced such that future increases in wind speed may not result in corresponding increases in turbidity.
The predicted magnitudes of the reduction in turbidity from October through January that resulted from a decline in wind speed are ecologically important, even if the magnitude of the turbidity decreases do not appear to be large (maximum of 12 NTU decrease when averaged over October through January; Tables 6 and 7). Because the SSC and turbidity during this portion of the year are already seasonally low, further decreases in turbidity may exacerbate any negative ecological effects of both the step decrease in turbidity in 1999 and the continued observed decline in turbidity since 1999. For example, Delta Smelt are more likely to be caught in the Estuary when the turbidity is relatively high, with a turbidity of less than 18 to 12 NTU considered unfavorable for Delta Smelt (Baskerville-Bridges et al. 2004; Sommer and Mejia 2013). Grizzly and Honker Bays are favorable habitat for Delta Smelt catch if the salinity is low and the turbidity is high (Bever et al. 2016). However, the scenarios evaluated here suggest that reductions in turbidity as a result of decreasing wind speed over the past 20 years have contributed to the more frequent occurrence of low turbidity levels considered unfavorable for Delta Smelt catch in Grizzly and Honker Bays.
While the analysis of wind direction did not suggest decadal trends in dominant wind direction, it is difficult to analyze long-term trends in wind direction. The analysis of wind direction suggested that during very stormy years, there is more variation in dominant wind direction than in less stormy years. This may have implications for turbidity because the Estuary is a fetch limited system, and winds of equal speed from one direction may result in much less sediment resuspension and increase in turbidity than winds from another. Further work is needed to more fully examine the influence of wind direction on turbidity in the Estuary.
Spatial Patterns in Turbidity in Suisun Bay
Spatial patterns in turbidity and continuous time series at discrete locations demonstrate that turbidity throughout Suisun Bay during periods of low river inflow is influenced by sediment resuspension from the shallows and the advection of resuspended sediment to the deeper channel areas. For example, Warner et al. (2004) found that tidal-timescale increases in turbidity near the outer edge of Grizzly Bay were the product of wind-wave resuspension at low tide and tidal advection of the resuspended sediment, a similar finding to that obtained by analyzing surface turbidity patterns (e.g., Fig. 10). This interplay of sediment resuspension from the shallows followed by advection by tidal currents results in turbidity signals at locations between the shallows and deeper channels that may not be intuitive. Because the Grizzly Bay monitoring station is located slightly west of the area of elevated turbidity in the shallows of Grizzly Bay seen in Fig. 10, the tidal timescale increases in turbidity at the Grizzly Bay monitoring station (e.g., Fig. 8) are primarily driven by the transport of sediment resuspended in the shallower areas of Grizzly Bay to the monitoring station, and not by local sediment resuspension at the monitoring station. The advection of sediment from shallow water has also been observed on other mudflats of the Estuary, for example by Lacy et al. (1996, 2014) in South San Francisco Bay. This implies that wind-wave resuspension plays a large role in turbidity throughout the San Francisco Bay, especially since about half of the Bay bathymetry is less than 2 m mean lower low water (Conomos 1979).
The interplay of wind-wave resuspension and tidal advection results in complex near-surface turbidity patterns that are time-varying and difficult to characterize with non-synoptic sampling (see Fig. 10 and Fichot et al. 2016). Using time-series SSC field observations at five locations, Ruhl and Schoellhamer (1999, 2004) found a large degree of spatial variability in SSC in Honker Bay that was related to the combined effects of wind-wave resuspension and advection of sediment from tidal currents. Fichot et al. (2016) used remote sensing to observe very complex surface turbidity patterns in Grizzly Bay. The model captures observed spatial turbidity patterns (Fig. 10) and provides information on the causes of the sharp gradients in turbidity, overall turbidity patterns, and timing of elevated turbidity at a continuous monitoring station. Because the model captured the observed patterns and the physical processes driving these patterns, these results demonstrate that both numerical models and remote sensing of turbidity can provide valuable insight into time-varying surface turbidity patterns that would be difficult to observe using non-synoptic point observations or only a few continuous monitoring locations. However, because remote sensing turbidity is only available at discrete times, models provide a valuable tool to understand the temporal variability in turbidity patterns over shorter time scales.
Applicability to Other Estuaries
This study demonstrates that long-term trends in average wind speed can have large effects on estuarine systems. The model scenarios which applied a decreasing trend in wind speed to 1992 and 1995 showed a similar effect of wind speed on turbidity to that predicted for the scenarios that applied an increasing trend in wind speed to 2011 and 2015. For example, a decrease in wind speed resulted in overall lower turbidity and the loss of some resuspension events on the shoals (Fig. 11), while an increase in wind speed resulted in an overall increase in turbidity and an increase in the number of resuspension events. In addition, the spatial variability in the percentage change in turbidity between the analysis stations was much larger than the variability between wet and critical water years (Tables 6 and 7). This consistency in findings between the scenarios which evaluated decreasing and increasing trends implies that the physical processes affecting turbidity changes are the same whether the observed trends were applied forward by decreasing wind speed from 1992 and 1995 levels or backward by increasing wind speed for 2011 and 2015. Because the underlying physical processes driving sediment transport and turbidity were included in the model, the findings of this study which demonstrate that long-term trends in average wind speed can have large effects on sediment transport and turbidity are broadly applicable to similar estuarine systems.
While decreases in turbidity are of concern in the San Francisco Estuary, decreases in turbidity have positive effects in other estuaries. For example, in the Chesapeake Bay, another large estuarine system, decreases in turbidity result in decreased light attenuation and increased growth of seagrass (Moore et al. 1996, 1997), an important habitat component for fishes and blue crabs (e.g., Schaffler et al. 2013; Lipcius et al. 2005). Reducing turbidity in the Chesapeake Bay through decreases in sediment supply is part of the bay-wide total maximum daily loads (TMDLs), which are designed to restore the health of the Chesapeake Bay ecosystem (USEPA 2010). Full implementation of the sediment and nutrient TMDLs is expected to cost in the tens of billions of dollars (Maryland 2012; Commonwealth of Virginia 2010).
Current research is focusing on the effects of infilling of the Conowingo Dam and the resulting increase in sediment supply to the Chesapeake Bay (Hirsch 2012; Zhang et al. 2013; Zhang and Blomquist 2018). However, there is much less work examining the effects of wind trends, either in speed or direction, on sediment transport and turbidity in Chesapeake Bay, even though previous studies have documented the importance of wind waves on SSC (e.g., Sanford 1994) and by correlation turbidity. Similar analyses, which examine wind data and the effects of any trends on SSC and turbidity, could provide insight into any decadal timescale changes in SSC and turbidity in other estuarine systems.
Conclusions
Wind data throughout the San Francisco Estuary showed statistically significant wind speed declines from 1995 through 2015 from October through January. All the analysis stations had statistically significant wind speed declines from October through January, even though the magnitude of the declines varied. Wind speeds averaged from October through January have declined by as much as 13 to 48% from 1995 to 2015 at the stations evaluated. For February through May and June through August averaging periods, only the North Delta had statistically significant declining wind trends at each station evaluated.
Analyses from this study demonstrate that the observed long-term reduction in wind speed has resulted in a reduction in turbidity in the Estuary. This reduction in turbidity has been the highest in the Suisun Bay portion of the study area and with smaller effects predicted in the Delta. Turbidity reductions have likely been the largest from October through January when the wind speed data had statistically significant wind speed declines at all the analysis stations. Turbidity was predicted to have declined by 14 to 55% throughout Suisun Bay from October through January as a result of the observed long-term decline in wind speed from 1995 through 2015. This decline in turbidity during an already seasonally low turbidity portion of the year has potential negative effects on habitat for endangered fish like the Delta Smelt which are more likely to be caught in relatively turbid water.
This study suggests that the long-term declines in wind speed and sediment supply have both resulted in reduced turbidity in the San Francisco Estuary over the past 20 years. Future work examining the cause of the long-term declines in observed wind speed would provide a greater understanding of whether the decline in wind speed over the past 20 years is due to cyclical processes and will increase in the future or if wind speed is expected to remain low or decrease further in the future.
References
Alpine, A.E., and J.E. Cloern. 1988. Phytoplankton growth rates in a light-limited environment, San Francisco Bay. Marine Ecology Progress Series 44: 167–173.
Ariathurai, C.R., and K. Arulanandan. 1978. Erosion rates of cohesive soils. Journal of the Hydraulics Division 104: 279–282.
[BAAQMD] Bay Area Air Quality Management District. 2016. Research and Data. http://www.baaqmd.gov/research-and-data. Accessed 1 December 2016.
Baskerville-Bridges, B., J.C. Lindberg, and S.I. Doroshow. 2004. The effect of light intensity, alga concentration, and prey density on the feeding behavior of delta smelt larvae. In Early life history of fishes in the San Francisco Estuary and Watershed. Ed. F. Freyer, L. Brown, R. Brown, and J. Orsi. American Fisheries Society, Symposium 39, Bethesda, MD. pp. 219–228.
Bennett, W.A. 2005. Critical assessment of the Delta smelt population in the San Francisco estuary, California. San Francisco Estuary and Watershed Science 3(2). https://escholarship.org/uc/item/0725n5vk. Accessed 1 December 2016.
Bever, A.J., and M.L. MacWilliams. 2013. Simulating sediment transport processes in San Pablo Bay using coupled hydrodynamic, wave, and sediment transport models. Marine Geology 345: 235–253. https://doi.org/10.1016/j.margeo.2013.06.012.
Bever, A.J., and M.L. MacWilliams. 2014. South San Francisco Bay sediment transport modeling. Prepared for the U.S. Army Corps of Engineers, San Francisco District. 242 pp.
Bever, A.J., M.L. MacWilliams, B. Herbold, L.R. Brown, and F.V. Feyrer. 2016. Linking hydrodynamic complexity to Delta smelt (Hypomesus transpacificus) distribution in the San Francisco estuary, USA. San Francisco Estuary and Watershed Science 14(1): 27 pp. https://doi.org/10.15447/sfews.2016v14iss1art3.
Booij, N., R.C. Ris, and L.H. Holthuijsen. 1999. A third-generation wave model for coastal regions 1. Model description and validation. Journal of Geophysical Research 104 (C4): 7649–7666. https://doi.org/10.1029/98JC02622.
Brand, A., J.R. Lacy, K. Hsu, D. Hoover, S. Gladding, and M.T. Stacy. 2010. Wind-enhanced resuspension in the shallow waters of South San Francisco Bay: Mechanisms and potential implications for cohesive sediment transport. Journal of Geophysical Research 115 (C11). https://doi.org/10.1029/2010JC006172.
Buchanan, P.A., and T.L. Morgan. 2012, Summary of suspended-sediment concentration data, San Francisco Bay, California, water year 2009: U.S. Geological Survey Data Series 744, 26 pp.
Cappiella, K., C. Malzone, R. Smith, and B.E. Jaffe. 1999. Sedimentation and Bathymetry Changes in Suisun Bay: 1867–1990. U.S. Geological Survey Open-File Report 99–563. https://pubs.usgs.gov/of/1999/0563/. Accessed 1 December 2016.
Casulli, V. 1999. A semi-implicit numerical method for non-hydrostatic free-surface flows on unstructured grid. In Numerical Modelling of Hydrodynamic Systems, ESF Workshop, Zaragoza, Spain, pp. 175–193.
Casulli, V., and R.A. Walters. 2000. An unstructured, three-dimensional model based on the shallow water equations. International Journal for Numerical Methods in Fluids 32 (2): 331–348. https://doi.org/10.1002/(SICI)1097-0363(20000215)32:3<331::AID-FLD941>3.0.CO;2-C.
Casulli, V., and P. Zanolli. 2002. Semi-implicit numerical modelling of non-hydrostatic free-surface flows for environmental problems. Mathematical and Computer Modelling 36 (9–10): 1131–1149. https://doi.org/10.1016/S0895-7177(02)00264-9.
Casulli, V., and P. Zanolli. 2005. High resolution methods for multidimensional advection-diffusion problems in free-surface hydrodynamics. Ocean Modelling 10 (1–2): 137–151. https://doi.org/10.1016/j.ocemod.2004.06.007.
[CDEC] California Data Exchange Center. 2016. Department of Water Resources. http://cdec.water.ca.gov/. Accessed 1 December 2016.
[CDWR] California Department of Water Resources. 1986. DAYFLOW program documentation and data summary user’s guide. Sacramento: California Department of Water Resources http://www.water.ca.gov/dayflow/docs/DAYFLOW_1986.pdf. Accessed 1 December 2016.
[CDWR] California Department of Water Resources. 2016. Chronological Reconstructed Sacramento and San Joaquin Valley Water Year Hydrologic Classification Indices. http://cdec.water.ca.gov/cgi-progs/iodir/wsihist. Accessed 1 December 2016.
Cloern, J.E. 1987. Turbidity as a control on phytoplankton biomass and productivity in estuaries. Continental Shelf Research 11 (12): 1367–1381. https://doi.org/10.1016/0278-4343(87)90042-2.
Cloern J.T., and A.D. Jassby. 2012. Drivers of change in estuarine-coastal ecosystems: discoveries from four decades of study in San Francisco Bay. Reviews of Geophysics 50(RG4001): 33 pp. https://doi.org/10.1029/2012RG000397.
Commonwealth of Virginia. 2010. Chesapeake Bay TMDL Phase I Watershed Implementation Plan: Revision of the Chesapeake Bay Nutrient and Sediment Reduction Tributary Strategy, 133 pp.
Conomos, T.J. 1979. Properties and circulation of San Francisco Bay waters. In San Francisco Bay: The Urbanized Estuary Investigations into the Natural History of San Francisco Bay and Delta With Reference to the Influence of Man. American Association for the Advancement of Science, Pacific Division, pp. 47–84.
Davies-Colley, R.J., and D.G. Smith. 2001. Turbidity, suspended sediment, and water clarity: a review. Journal of the American Water Resources Association 37 (5): 1085–1101. https://doi.org/10.1111/j.1752-1688.2001.tb03624.x.
Dickhudt, P.J. 2008. Controls on erodibility in a partially mixed estuary: York River, Virginia. Thesis. The College of William & Mary, Virginia Institute of Marine Science. 230 pp. http://web.vims.edu/library/Theses/Dickhudt08.pdf.
Dietrich, J.C., M. Zijlema, P.-E. Allier, L.H. Holthuijsen, N. Booij, J.D. Meixner, J.K. Proft, C.N. Dawson, C.J. Bender, A. Naimaster, J.M. Smith, and J.J. Westerink. 2013. Limiters for spectral propagation velocities in SWAN. Ocean Modelling 70: 85–102. https://doi.org/10.1016/j.ocemod.2012.11.005.
Dogliotti, A.I., K.G. Ruddick, B. Nechad, D. Doxran, and E. Knaeps. 2015. A single algorithm to retrieve turbidity from remotely-sensed data in all coastal and estuarine waters. Remote Sensing of Environment 156: 157–168. https://doi.org/10.1016/j.rse.2014.09.020.
Fain, A.M.V., A.S. Ogston, and R.W. Sternberg. 2007. Sediment transport event analysis on the western Adriatic continental shelf. Continental Shelf Research 27 (3-4): 431–451. https://doi.org/10.1016/j.csr.2005.03.007.
Feyrer, F., M. Nobriga, and T.R. Sommer. 2007. Multidecadal trends for three declining fish species: habitat patterns and mechanisms in the San Francisco estuary. Canadian Journal of Fisheries and Aquatic Sciences 64 (4): 723–734. https://doi.org/10.1139/F07-048.
Fichot, C.G., B.D. Downing, B.A. Bergamaschi, L. Windham-Meyers, M. Marvin-DiPasquale, D.T. Thompson, and M.M. Gierach. 2016. High-resolution remote sensing of water quality in the San Francisco Bay-Delta estuary. Environmental Science and Technology 50 (2): 573–583. https://doi.org/10.1021/acs.est.5b03518.
Friedrichs, C.T. 2009. York River physical oceanography and sediment transport. Journal of Coastal Research 57: 17–22. https://doi.org/10.2112/1551-5036-57.sp1.17.
Ganju, N.K., and D.H. Schoellhamer. 2009. Calibration of an estuarine sediment transport model to sediment fluxes as an intermediate step for simulation of geomorphic evolution. Continental Shelf Research 29 (1): 148–158. https://doi.org/10.1016/j.csr.2007.09.005.
Ganju, N.K., D.H. Schoellhamer, M.C. Murrell, J.W. Gartner, and S.A. Wright. 2007. Constancy of the relation between floc size and density in San Francisco Bay. In Estuarine and coastal fine sediment dynamics - INTERCOH 2003, ed. J.P. Maa, L.H. Sanford, and D.H. Schoellhamer, 75–91. Amsterdam: Elsevier.
Gocic, M., and S. Trajkovic. 2013. Analysis of changes in meteorological variables using Mann-Kendall and Sen’s slope estimator statistical tests in Serbia. Global and Planetary Change 100: 172–182. https://doi.org/10.1016/j.gloplacha.2012.10.014.
Gray, J.R., and J.W. Gartner. 2009. Technological advances in suspended-sediment surrogate monitoring. Water Resources Research 45 (4): 20 pp. https://doi.org/10.1029/2008WR007063.
Haidvogel, D.B., H. Arango, W.P. Budgell, B.D. Corulle, E. Curshitser, E.D. Lorenzo, K. Fennel, W.R. Geyer, A.J. Hermann, L. Lanerolle, J. Levin, J.C. McWilliams, A.J. Miller, A.M. Moore, T.M. Powell, A.F. Shchepetkin, C.R. Sherwood, R.P. Signell, J.C. Warner, and J. Wilkin. 2008. Ocean forecasting in terrain-following coordinates: Formulation and skill assessment of the Regional Ocean modeling system. Journal of Computational Physics 227 (2): 3595–3624. https://doi.org/10.1016/j.jcp.2007.06.016.
Harris, C.K., and P.L. Wiberg. 1997. Approaches to quantifying long-term continental shelf sediment transport with an example from the northern California STRESS mid-shelf site. Continental Shelf Research 17 (11): 1389–1418. https://doi.org/10.1016/S0278-4343(97)00017-4.
Hestir, E.L., D.H. Schoellhamer, J. Greenberg, T. Morgan-King, and S.L. Ustin. 2016. The effect of submerged aquatic vegetation expansion on a declining turbidity trend in the Sacramento-San Joaquin River Delta. Estuaries and Coasts 29 (4): 1100–1112. https://doi.org/10.1007/s12237-015-0055-z.
Hill, P.S., and I.N. MacCave. 2001. Suspended particle transport in benthic boundary layers. In The Benthic Boundary Layer, ed. B.P. Boudreau and B.B. Jorgensen, 78–103. Oxford University Press.
Hirsch, R.M. 2012. Flux of nitrogen, phosphorus, and suspended sediment from the Susquehanna River basin to the Chesapeake Bay during tropical storm Lee, September 2011, as an indicator of the effects of reservoir sedimentation on water quality. USGS scientific investigations report 2012-5185. 17 pp.
Hofmann, E.E., B. Cahill, K. Fennel, M.A.M. Friedrichs, K. Hyde, C. Lee, A. Mannino, R.G. Najjar, J.E. O’Reilly, J. Wilkin, and J. Xue. 2011. Modeling the dynamics of continental shelf carbon. Annual Review of Marine Science 3 (1): 93–122. https://doi.org/10.1146/annurev-marine-120709-142740.
Jolliff, J.K., J.C. Kindle, I. Shulman, B. Penta, M.A.M. Friedrichs, R. Helber, and R.A. Arnone. 2009. Summary diagrams for coupled hydrodynamic-ecosystem model skill assessment. Journal of Marine Systems 76 (1-2): 64–82. https://doi.org/10.1016/j.jmarsys.2008.05.014.
Kineke, G.C., and R.W. Sternberg. 1989. The effect of particle settling velocity on computed suspended sediment concentration profiles. Marine Geology 90 (3): 159–174. https://doi.org/10.1016/0025-3227(89)90039-X.
Krone, R.B. 1979. Sedimentation in the San Francisco Bay system. In San Francisco Bay: The Urbanized Estuary Investigations into the Natural History of San Francisco Bay and Delta With Reference to the Influence of Man. American Association for the Advancement of Science, Pacific Division. pp. 85–96.
Lacy, J.R., D.H. Schoellhamer, and J.R. Burau. 1996. Suspended-solids flux at a shallow water site in South San Francisco Bay, California. In Proceedings of the north American water and environment congress, June 23–28, 1996, ed. C.T. Bathala, 3357–3362. New York: American Society of Civil Engineers.
Lacy, J.R., S. Gadding, A. Brand, A. Collignon, and M. Stacy. 2014. Lateral baroclinic forcing enhances sediment transport from shallows to channel in an estuary. Estuaries and Coasts 37 (5): 1058–1077.
Large, W., and S. Pond. 1981. Open ocean momentum flux measurements in moderate to strong winds. Journal of Physical Oceanography 11 (3): 324–336. https://doi.org/10.1175/1520-0485(1981)011<0324:OOMFMI>2.0.CO;2.
Lipcius, R.N., R.D. Seitz, M.S. Seebo, and D. Colon-Carrion. 2005. Density, abundance and survival of the blue crab in seagrass and unstructured salt marsh nurseries of Chesapeake Bay. Journal of Experimental Biology and Ecology 319 (1–2): 69–80. https://doi.org/10.1016/j.jembe.2004.12.034.
Maceina, M., and D.M. Soballe. 1990. Wind-related limnological variation in Lake Okeechobee, Florida. Lake and Reservoir Management 6 (1): 93–100.
MacWilliams, M.L., and E.S. Gross. 2013. Hydrodynamic simulation of circulation and residence time in Clifton court Forebay. San Francisco Estuary and Watershed Science 11(2). https://doi.org/10.15447/sfews.2013v11iss2art1.
MacWilliams, M.L., A.J. Bever, and E.S. Gross. 2012. Three-dimensional sediment transport modeling for San Francisco Bay RDMMP. Prepared for the U.S. Army Corps of Engineers, San Francisco District. 190 pp.
MacWilliams, M.L., A.J. Bever, E.S. Gross, G.S. Ketefian, and W.J. Kimmerer. 2015. Three-dimensional modeling of hydrodynamics and salinity in the San Francisco estuary: An evaluation of model accuracy, X2, and the low–salinity zone. San Francisco Estuary and Watershed Science 13(1): 37 pp. https://doi.org/10.15447/sfews.2015v13iss1art2.
Madsen, O.S., Y.-K. Poon, and H.C. Graber. 1988. Spectral wave attenuation by bottom friction: Theory. Coastal Engineering Proceedings 21: 492–504. https://doi.org/10.9753/icce.v21.%25p.
Malcherek, A. 2001. Hydromechanik der Fließgewässer. Bericht Nr. 61, Institut für Strömungsmechanik and Elektron, Rechen im Bauwesen der Universität Hannover. Hannover: University of Hannover.
Malcherek, A., and D. Knock. 2006. The influence of waves on the sediment composition in a tidal bay. In Proceedings of the Ninth International Conference on Estuarine and Coastal Modeling. ASCE. October 31–September 2, 2005. Charleston, SC, pp. 842–859. https://doi.org/10.1061/40876(209)48.
Mantua, N.J., and S.T. Hare. 2002. The Pacific decadal oscillation. Journal of Oceanography 58 (1): 35–44. https://doi.org/10.1023/A:1015820616384.
Maryland. 2012. Maryland’s Phase II Watershed Implementation Plan for the Chesapeake Bay TMDL. NOAA Technical Report NOS CS 29, 84 pp.
McVicar, T.R., M.L. Roderick, R.J. Donohue, L.T. Li, T.G. Van Niel, A. Thomas, J. Grieser, D. Jhajharia, Y. Himri, N.M. Mahowald, A.V. Mescherskaya, A.C. Kruger, S. Rehman, and Y. Dinpashoh. 2012. Global review and synthesis of trends in observed terrestrial near-surface wind speeds: Implications for evaporation. Journal of Hydrology 416-417: 182–205. https://doi.org/10.1016/j.jhydrol.2011.10.024.
Moore, K.A., H.A. Neckles, and R.J. Orth. 1996. Zostera marina (eelgrass) growth and survival along a gradient of nutrients and turbidity in the lower Chesapeake Bay. Marine Ecology Progress Series 147: 247–259. https://doi.org/10.3354/meps142247.
Moore, K.A., R.L. Wetzel, and R.J. Orth. 1997. Seasonal pulses of turbidity and their relations to eelgrass (Zostera marina L.) survival in an estuary. Journal of Experimental Marine Biology and Ecology 219 (1): 115–134. https://doi.org/10.1016/S0022-0981(96)02774-8.
Moriarty, J.M., C.K. Harris, and M.G. Hadfield. 2014. A hydrodynamic and sediment transport model for the Waipaoa shelf, New Zealand: Sensitivity of fluxes to spatially-varying erodibility and model nesting. Journal of Marine Science and Engineering 2 (2): 336–369. https://doi.org/10.3390/jmse2020336.
Newman, M., M.A. Alexander, T.R. Ault, K.M. Cobb, C. Deser, E. Di Lorenzo, N.J. Mantua, A.J. Miller, S. Minobe, H. Nakamura, N. Schneider, D.J. Vimont, A.S. Phillips, J.D. Scott, and C.A. Smith. 2016. The pacific decadal oscillation, revisited. Journal of Climate 29 (12): 4399–4427. https://doi.org/10.1175/JCLI-D-15-0508.1.
[NOAA] National Oceanic and Atmospheric Administration. 2014. National Satellite and information service. National Climatic Data Center. https://www.nesdis.noaa.gov/. Accessed 1 December 2016.
[NOAA] National Oceanic and Atmospheric Administration. 2016. National Data Buoy Center. http://www.ndbc.noaa.gov/. Accessed 1 December 2016.
Nobriga, M.L., T.R. Sommer, F. Feyrer, and K. Fleming. 2008. Long-term trends in summertime habitat suitability for Delta smelt (Hypomesus transpacificus). San Francisco Estuary and Watershed Science 6(1). http://escholarship.org/uc/item/5xd3q8tx.
Nowacki, D.J., and A.S. Ogston. 2013. Water and sediment transport of channel-flat systems in a mesotidal mudflat: Willapa Bay, Washington. Continental Shelf Research 60 (S1): S111–S124. https://doi.org/10.1016/j.csr.2012.07.019.
Ralston, D.K., W.R. Geyer, and J.A. Lerczak. 2010. Structure, variability, and salt flux in a strongly forced salt wedge estuary. Journal of Geophysical Research 115 (C06005). https://doi.org/10.1029/2009JC005806.
Rogers, W.E., P.A. Hwang, and D.W. Wang. 2003. Investigation of wave growth and decay in the SWAN model: Three regional-scale applications. Journal of Physical Oceanography 33 (2): 366–389. https://doi.org/10.1175/1520-0485(2003)033<0366:IOWGAD>2.0.CO;2.
Ruhl, C.L., and D.H. Schoellhamer. 1999. Time series of suspended solids concentration in Honker Bay during water year 1997. In 1997 annual report of the regional monitoring program for trace elements, pp. 82–92. San Francisco Estuary Institute, Richmond, California. http://www.sfei.org/sites/default/files/biblio_files/1997_RMP_Annual_Report.pdf. Accessed 1 December 2016.
Ruhl, C.L., and D.H. Schoellhamer. 2004. Spatial and temporal variability of suspended-sediment concentration in a shallow estuarine environment. San Francisco Estuary and Watershed Science 2(2): 10 pp. http://escholarship.org/uc/item/1g1756dw. Accessed 1 December 2016.
Ruhl, C.L., D.H. Schoellhamer, R.P. Stumpf, and C.L. Lindsay. 2001. Combined use of remote sensing and continuous monitoring to analyse the variability of suspended-sediment concentrations in San Francisco Bay, California. Estuarine, Coastal and Shelf Science 53 (6): 801–812. https://doi.org/10.1006/ecss.2000.0730.
Sanford, L.P. 1994. Wave-forced resuspension of upper Chesapeake Bay muds. Estuaries 17 (1B): 148–165. https://doi.org/10.2307/1352564.
Schaffler, J.J., J. van Montfrans, C.M. Jones, and R.J. Orth. 2013. Fish species distribution in seagrass habitats of Chesapeake Bay are structured by abiotic and biotic factors. Marine and Coastal Fisheries 5 (1): 114–124. https://doi.org/10.1080/19425120.2013.804013.
Schoellhamer, D.H. 2002. Variability of suspended-sediment concentration at tidal to annual time scales in San Francisco Bay, USA. Continental Shelf Research 22 (11-13): 1857–1866. https://doi.org/10.1016/S0278-4343(02)00042-0.
Schoellhamer, D.H. 2011. Sudden clearing of estuarine waters upon crossing the threshold from transport to supply regulation of sediment transport as an erodible pool is depleted: San Francisco Bay, 1999. Estuaries and Coasts 34 (5): 885–899. https://doi.org/10.1007/s12237-011-9382-x.
Schoellhamer, D.H., P.A. Buchanan, and N.K. Ganju. 2002. Ten years of continuous suspended-sediment concentration monitoring in San Francisco Bay and Delta. In Turbidity and other Sediment Surrogates Workshop, April 30–May 2, 2002, Reno Nevada. https://water.usgs.gov/osw/techniques/TSS/schoelhamer.pdf. Accessed 1 December 2016.
Schoellhamer, D.H., T.L. Morgan-King, M.A. Downing-Kunz, S.A. Wright, and G.G. Shellenbarger. 2014. Appendix 5. U.S. Geological Survey sediment monitoring and analysis. In: Synthesis of Studies in the Fall Low-Salinity Zone of the San Francisco Estuary, September–December 2011. U.S. Geological Survey scientific investigations report 2015–4041, pp. 111–123.
Schoellhamer, D.H., G.G. Shellenbarger, M.A. Downing-Kunz, and A.J. Manning. 2016. Review of Suspended sediment in lower south Bay relevant to light attenuation and phytoplankton blooms. In Lower South Bay Nutrient Synthesis. San Francisco Estuary Institute & Aquatic Science Center, pp. 23–56.
Schoellhamer, D.H., A.J. Manning, and P.A. Work. 2017. Erosion characteristics and horizontal variability for small erosion depths in the Sacramento-San Joaquin Delta, California, USA. Ocean Dynamics 67 (6): 799–811. https://doi.org/10.1007/s10236-017-1047-2.
Scully, M.E. 2010. The importance of climate variability to wind-driven modulation of hypoxia in Chesapeake Bay. Journal of Physical Oceanography 40 (6): 1435–1440. https://doi.org/10.1175/2010JPO4321.1.
Sen, P.K. 1968. Estimates of the regression coefficient based on Kendall’s tau. Journal of the American Statistical Association 63 (324): 1379–1389. https://doi.org/10.2307/2285891.
Smith, S.J., and C.T. Friedrichs. 2011. Size and settling velocities of cohesive flocs and suspended sediment aggregates in a trailing suction hopper dredge plume. Continental Shelf Research 31 (10): 550–563. https://doi.org/10.1016/j.csr.2010.04.002.
Sommer, T. and F. Mejia. 2013. A place to call home: A synthesis of Delta smelt habitat in the upper San Francisco Estuary. San Francisco Estuary and Watershed Science 11(2): 25 pp. http://www.escholarship.org/uc/item/32c8t244. Accessed 1 December 2016.
SWAN Team. 2016a. SWAN user manual version 41.10. Delft, Netherlands: Delft University of Technology. http://swanmodel.sourceforge.net/download/zip/swanuse.pdf. Accessed 1 December 2016. 127 pp.
SWAN Team. 2016b. SWAN scientific and technical documentation 41.10. Delft, Netherlands: Delft University of Technology. http://swanmodel.sourceforge.net/download/zip/swantech.pdf. Accessed 1 December 2016. 132 pp.
Tara Morgan-King personal communication: Morgan-King, Tara (USGS), 2013. Personal communication with Michael MacWilliams and Aaron Bever (Delta Modeling Associates).
Theil, H. 1950. A rank-invariant method of linear and polynomial regression analysis. Part 3. Proceedings of Koninalijke Nederlandse Akademie van Weinenschatpen A 53: 1397–1412.
[USEPA] U.S. Environmental Protection Agency. 2010. Chesapeake Bay total maximum daily load for nitrogen, phosphorus, and sediment. U.S. Environmental Protection Agency Chesapeake Bay Program Office, Annapolis, Maryland. https://www.epa.gov/sites/production/files/2014-12/documents/cbay_final_tmdl_exec_sum_section_1_through_3_final_0.pdf. Accessed 1 December 2016.
[USGS] U.S. Geological Survey. 2016a. Water Quality of San Francisco Bay. http://sfbay.wr.usgs.gov/access/wqdata. Accessed 17 January 2016.
[USGS] U.S. Geological Survey. 2016b. National Water Information System. http://waterdata.usgs.gov/ca/nwis/. Accessed 1 December 2016.
[USGS] U.S. Geological Survey. 2018. EarthExplorer. https://earthexplorer.usgs.gov/. Accessed 2018.
Van der Wegen, M., and B.E. Jaffe. 2013. Towards a probabilistic assessment of process-based morphodynamic models. Coastal Engineering 75: 52–63. https://doi.org/10.1016/j.coastaleng.2013.01.009.
Van der Wegen, M., B.E. Jaffe, and J.A. Roelvink. 2011. Process-based, morphodynamic hindcast of decadal deposition patterns in San Pablo Bay, California, 1856–1887. Journal of Geophysical Research 116 (F02008). https://doi.org/10.1029/2009JF001614.
Wan, H., X.L. Wang, and V.R. Swail. 2010. Homogenization and trend analysis of Canadian near-surface wind speeds. Journal of Climate 23 (5): 1209–1225. https://doi.org/10.1175/2009JCLI3200.1.
Warner, J.C., D.H. Schoellhamer, C.A. Ruhl, and J.R. Burau. 2004. Floodtide pulses after low tides in shallow subembayments adjacent to deep channels. Estuarine, Coastal and Shelf Science 60 (2): 213–228. https://doi.org/10.1016/j.ecss.2003.12.011.
Warner, J.C., W.R. Geyer, and J.A. Lerczak. 2005. Numerical modeling of an estuary: a comprehensive skill assessment. Journal of Geophysical Research 110 (C05001). https://doi.org/10.1029/2004JC002691.
Wei, J., Q. Jin, Z-L. Yang, and P.A. Dirmeyer. 2016. Role of ocean evaporation in California droughts and floods. Geophysical Research Letters 43 (12): 6554–6562.
Weir, D.J., and J. McManus. 1987. The role of wind in generating turbidity maxima in the Tay estuary. Continental Shelf Research 7 (11/12): 1315–1318. https://doi.org/10.1016/0278-4343(87)90035-5.
Willmott, C. 1981. On the validation of models. Physical Geography 2: 184–194.
Wright, S.A., and D.H. Schoellhamer. 2004. Trends in the sediment yield of the Sacramento River, California, 1957-2001. San Francisco Estuary and Watershed. Science 2 (2): 14. http://escholarship.org/uc/item/891144f4.
Wright, S.A., and D.H. Schoellhamer. 2005. Estimating sediment budgets at the interface between rivers and estuaries with application to the Sacramento-San Joaquin River Delta. Water Resources Research 41 (9). https://doi.org/10.1029/2004WR003753.
Yue, S., P. Pilon, and G. Cavadias. 2002. Power of the Mann-Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series. Journal of Hydrology 259 (1-4): 254–271. https://doi.org/10.1016/S0022-1694(01)00594-7.
Zhang, Q.Z., and J.D. Blomquist. 2018. Watershed export of fine sediment, organic carbon, and chlorophyll-a to Chesapeake Bay: Spatial and temporal patterns in 1984-2016. Science of the Total Environment 619–620: 1066–1078. https://doi.org/10.1016/j.scitotenv.2017.10.279.
Zhang, Q., D.C. Brady, and W.P. Ball. 2013. Long-term seasonal trends of nitrogen, phosphorous, and suspended sediment load from non-tidal Susquehanna River basin to Chesapeake Bay. Science of the Total Environment 452–453: 208–221. https://doi.org/10.1016/j.scitotenv.2013.02.012.
Acknowledgements
Funding was provided by the Metropolitan Water District of Southern California. We thank Stephen Monismith, Jon Burau, Lenny Grimaldo, and Shawn Acuna for input on designing the study and David Schoellhamer, Neil Ganju, and an anonymous reviewer for their comments, which helped improve the manuscript. Christine Lee from the NASA Jet Propulsion Laboratory provided the remotely-sensed surface turbidity data. The UnTRIM code was developed and provided by Professor Vincenzo Casulli (University of Trento, Italy). We would like to thank the Bundesanstalt für Wasserbau (BAW), Holger Weilbeer (BAW), and the University of the German Federal Armed Forces for their collaboration on the use of the SediMorph model.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Carl T. Friedrichs
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bever, A.J., MacWilliams, M.L. & Fullerton, D.K. Influence of an Observed Decadal Decline in Wind Speed on Turbidity in the San Francisco Estuary. Estuaries and Coasts 41, 1943–1967 (2018). https://doi.org/10.1007/s12237-018-0403-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12237-018-0403-x