Quantifying the Effect of Salinity Stratification on Phytoplankton Density Patterns in Estuaries

Liu, Bo; de Swart, Huib E.

doi:10.1007/s12237-017-0276-4

Quantifying the Effect of Salinity Stratification on Phytoplankton Density Patterns in Estuaries

Open access
Published: 05 July 2017

Volume 41, pages 453–470, (2018)
Cite this article

Download PDF

You have full access to this open access article

Estuaries and Coasts Aims and scope Submit manuscript

Quantifying the Effect of Salinity Stratification on Phytoplankton Density Patterns in Estuaries

Download PDF

3209 Accesses
8 Citations
1 Altmetric
Explore all metrics

Abstract

To quantify the effect of salinity stratification on phytoplankton density (denoted as P) patterns, experiments were conducted with an idealised model that couples physical and biological processes. Results show that the idealised model is capable of capturing the main features of observed P patterns in the Columbia River estuary during the spring season: during weak stratification, P is almost vertically uniform with values decreasing towards the estuary mouth, whereas during strong stratification, high values of P extend further seawards but are confined to the upper layer. Sensitivity studies reveal that the strong vertical gradients of P can only occur if the intensity of turbulence (measured by depth-averaged values of vertical eddy viscosity and eddy diffusivity) is weak. The advection of P by subtidal currents is important in obtaining a smaller along-estuary gradient of P during weak stratification and in obtaining a smaller horizontal gradient and a larger vertical gradient of P during strong stratification. Accounting for stratification controlled vertical distribution of vertical eddy viscosity and eddy diffusivity is necessary for obtaining realistic P patterns if stratification is strong, but not if stratification is weak. A higher osmotic stress, which leads to faster loss of phytoplankton in salt water, results in a larger along-estuary gradient of P if stratification is weak and in a larger vertical gradient of P if stratification is strong.

Factors Controlling Seasonal Phytoplankton Dynamics in the Delaware River Estuary: an Idealized Model Study

Article Open access 07 August 2019

Effect of small scale transport processes on phytoplankton distribution in coastal seas

Article Open access 05 June 2018

Impact of critical eddy diffusivity on seasonal bloom dynamics of Phytoplankton in a global set of aquatic environments

Article Open access 10 October 2023

Use our pre-submission checklist

Avoid common mistakes on your manuscript.

Introduction

Phytoplankton density (viz, phytoplankton cell number density, hereafter denoted as P) in estuaries shows distinct spatial patterns for different strength of salinity stratification. It has been frequently observed that the vertical distribution of P is almost uniform under weakly stratified conditions, whereas if the water column is highly stratified, high densities are only found in the upper layer (Indrebø et al. 1979; Cloern 1996; Watanabe et al. 2014). Also, the horizontal distribution of P is remarkably different under different stratification conditions. A specific example is the Columbia River estuary, where in spring season P during spring tides (weak salinity stratification) significantly decreases along the estuary towards the mouth, whereas during neap tides (strong salinity stratification) high densities extend seawards in the upper layer (Roegner et al. 2011).

Salinity stratification affects vertical turbulent exchange processes, subtidal currents as well as the lysis rate of phytoplankton due to osmotic stress. The latter three aspects are likely to be closely linked to the observed P patterns in the Columbia River estuary. Cloern (1996) pointed out that in estuarine and coastal systems, a strong tidal stirring effectively mixes phytoplankton downward into the aphotic zone where net growth rate is negative, whereas a vertical stratification can isolate phytoplankton in the euphotic zone such that it allows P to increase. Roegner et al. (2011) related the isolation of phytoplankton in the upper low-salinity water during neap tides to the extension of the fluvial conditions to the estuary mouth during strong stratification. Lara-Lara et al. (1990) suggested that estuarine salinity variation also directly influences the P pattern, since it has been observed that a large number of freshwater phytoplankton lyse in low salinity (3–5 psu) regions.

Previous studies did not quantitatively explain the relative importance of the above-mentioned aspects in determining estuarine P patterns under different stratification conditions. In order to study this, account should be taken of the fact that with increasing stratification, the maximum values of eddy viscosity occur closer to the bottom (Geyer et al. 2000) because stratification limits the development of turbulence generated at the estuary bottom (Stacey and Ralston 2005). According to Munk and Anderson (1948), the qualitative behaviour of eddy diffusivity is similar to that of eddy viscosity, i.e. with increasing stratification the values of eddy diffusivity become smaller and their maxima are attained closer to the bed. The impact of the vertical distributions of turbulent exchange coefficients on P patterns, in relation to that of other factors, has not been quantified yet. Moreover, the vertical distribution of eddy viscosity directly impacts the magnitude and vertical structure of the subtidal current (Cheng et al. 2013), which affects the along-estuary distribution of P (Liu and de Swart 2015).

The fact that salinity stratification, vertical turbulent exchange processes and subtidal currents are mutually coupled leads to difficulty in understanding observed P patterns in stratified estuaries and in interpreting results of sophisticated numerical models. To reduce this gap in knowledge, this study is dedicated to quantify the effect of each of the above mentioned aspects on P patterns. Specifically, this is done by fulfilling four aims. The first is to examine the effect of vertical stratification, which largely affects the magnitudes and vertical distributions of eddy viscosity and eddy diffusivity, on the overall characteristics of P patterns, in particular their typical vertical and along-estuary gradients. The second aim is to quantify the importance of advection of phytoplankton and nutrients by subtidal currents on the spatial patterns of P. The third and fourth aims are to assess the sensitivity of the overall characteristics of P patterns to the vertical distributions of vertical eddy viscosity and eddy diffusivity and to the salinity-dependent loss rate, respectively.

To achieve these aims, an idealised model that couples physical and biological processes (Liu and de Swart 2015) was adapted in this study. The motivation to choose an idealised model is that it allows investigation of individual processes in isolation, thereby yielding fundamental insight into the dynamics of the system. Thus, an idealised model is suitable to identify and to analyse mechanisms through which the above-mentioned aspects influence P patterns in stratified estuaries. Moreover, idealised models, also referred to as exploratory models, are fast and flexible, and therefore suitable for sensitivity studies (Murray and Thieler 2004). Furthermore, the Columbia River estuary was chosen as the prototype estuary because sufficient data were available to check the performance of the model.

The hydrodynamic module, turbulence closure and biological module are introduced in “Material and Methods” section. Here, also two parameters are introduced that quantify the vertical and along-estuary gradients of P. In “Results” section, results are first shown for weakly and strongly stratified conditions and they are compared to field data of Roegner et al. (2011) to demonstrate that the model is capable of capturing main characteristics of the observed P patterns. Next, results of sensitivity experiments that relate to the last three research aims are presented. In “Discussion” section, key processes controlling phytoplankton density patterns are identified and results of sensitivity experiments are further analysed. Also, results of additional sensitivity studies (which concern other parameters and boundary conditions, see the Electronic Supplement) are briefly summarised and limitations of the model are discussed. Conclusions are given in “Conclusions” section.

Material and Methods

Model

The model used in this study consists of different modules and is an extended version of that of Liu and de Swart (2015). Estuarine subtidal currents are described by a hydrodynamic module. A turbulence closure module (details see “Turbulence Closure” section) that accounts for the dependence of the magnitudes and vertical distributions of eddy viscosity and eddy diffusivity on salinity stratification was adopted, which is one of the new aspects of the present model. Phytoplankton and nutrient dynamics are described in a biological module, which is coupled to the previous two modules.

Domain

The simplified estuarine geometry considered in this study is illustrated in Fig. 1, whose length is denoted by L. The cross section is assumed rectangular with a constant total water depth H and a constant width. A Cartesian coordinate system is used with the x-axis pointing from the estuary mouth (x = 0) to the riverine boundary (x = L) and the z-axis from the water surface (z = 0) downward to the bottom (z = H).

Hydrodynamic Module

In this study, the estuarine subtidal current model of Burchard and Hetland (2010) is adapted by extending the formulation of eddy viscosity such that it explicitly depends on the strength of salinity stratification. The width-averaged along-estuary velocity u(x,z) in the present study accounts for the river flow u _r induced by freshwater discharge and density-driven flow u _d due to along-estuary salinity gradient. The expressions of u _r and u _d are

$$ u_{r} = \gamma (z) U_{r}, $$

(1)

$$ \gamma (z) = \frac{H \displaystyle {{\int}_{z}^{H}} \frac{z^{\prime}}{A_{v}} \, \mathrm{d} z^{\prime}}{ \displaystyle {{\int}_{0}^{H}} {\int}_{z^{\prime}}^{H} \frac{z^{\prime\prime}}{A_{v}} \, \mathrm{d} z^{\prime\prime} \, \mathrm{d} z^{\prime}}, $$

(2)

$$ u_{d} = {{\int}_{z}^{H}} \mathcal{F} (z^{\prime}) \, \mathrm{d} z^{\prime} - \frac{\gamma(z)}{H} {{\int}_{0}^{H}} {\int}_{z^{\prime}}^{H} \mathcal{F} (z^{\prime\prime}) \,\mathrm{d} z^{\prime\prime} \,\mathrm{d} z^{\prime}, $$

(3)

$$ \mathcal{F} (\zeta) = - \frac {g}{\rho_{*}} \frac{\partial \rho}{\partial x} \frac{\zeta^{2}}{2A_{v}}. $$

(4)

In these expressions, U _r is the depth-averaged velocity of river flow, A _v is the tidally-averaged vertical eddy viscosity, $\rho _{*} = 10^{3} \text {kg~m}^{-3}$ is the density of fresh water and ρ is the density. The latter is related to salinity s by the equation of state:

$$ \rho = \rho_{*} \, (1 + \beta s), $$

(5)

where β is the coefficient of isohaline contraction.

Salinity s can be split into depth-averaged $\overline {s}$ and depth-varying $s^{\prime }$ parts, i.e. $s=\overline {s}+s^{\prime }$. Assuming that $\partial {s^{\prime }}/\partial {x} \ll \partial {\overline {s}}/\partial {x} $ (Pritchard 1952), only $\overline {s}$ is accounted for when calculating the density-driven flow u _d. The formulation for $\bar s$ follows that of Warner et al. (2005):

$$ \bar s(x) = \frac{1}{2} \,s_{0} \, [1-\tanh(\frac{x-x_{c}}{x_{\delta}})]. $$

(6)

Here, s ₀ is seawater salinity, x _c denotes the position where the salinity is 0.5 s ₀, and x _δ is the length scale over which $\bar s$ varies. At x = x _c, the along-estuary salinity gradient $\mathrm {d} \bar s / \mathrm {d} x$ reaches its maximum. Furthermore, (x _c + x _δ) is an estimate of tidally-averaged salt intrusion length.

The width-averaged vertical subtidal velocity w(x,z) is obtained by solving the continuity equation and it reads

$$ w = - {{\int}^{z}_{0}} \frac{\partial u}{\partial x} \mathrm{d} z^{\prime}. $$

(7)

Turbulence Closure

The formulation of eddy viscosity A _v is that of Chen and de Swart (2016) and it reads

$$ A_{v}= \kappa u_{*} H \, A_{z}, $$

(8)

in which κ = 0.41 is the von Karman’s constant, u _∗ is the tidally-averaged friction velocity, whose value is input into this model, and A _z describes the vertical distribution of A _v. Here, A _z is modelled as a piecewise function:

$$ A_{z}=\left\{ \begin{array}{lr} (A_{I}-A_{S}) |\frac{z}{z_{t}} |^{2} + A_{S}, & 0 \leq z \leq z_{t} ;\\ (\frac{H - z + z_{0}}{H}) (\frac{z - (H - h_{b})}{H} ), & z_{t} \leq z \leq H. \end{array} \right. $$

(9)

The vertical shape of A _z calculated by the above function is plotted in Fig. 2a. At z = z _t, which separates the two sub-domains, continuity of A _z requires $A_{I}=(\frac {H - z_{t} + z_{0}}{H}) (\frac {z_{t} - (H - h_{b})}{H} )$. The value of z _t is determined by requiring dA _z/dz to be continuous at z = z _t. The function of A _z contains three independent parameters. Parameter A _S is proportional to the value of A _v at the water surface, i.e. A _v|_z=0 = κ u _∗ H A _S. Furthermore, z ₀ is the bottom roughness length and h _b is a measure of the height of the turbulent bottom boundary layer. As shown in Fig. 2b, if h _b decreases, the maximum of A _z decreases and its location shifts closer to the bottom. The turbulent bottom boundary layer is represented by (H − h _b) ≤ z ≤ H (as shown by the grey areas in Fig. 2).

Note that if A _S equals the maximum of A _z and z _t = H, Eq. 9 yields a vertically constant eddy viscosity as was used in e.g. Hansen and Rattray (1965). Furthermore, the choice of A _S = 0 and z _t = 0 yields a parabolic shape of eddy viscosity used by Burchard and Hetland (2010). The latter two shapes are plotted in Fig. 2a as well.

In this study, A _S is tuned such that the amplitude of the modelled subtidal current agrees well with observations, and z ₀ is an input parameter whose value is obtained from previous studies. The turbulent bottom boundary layer height h _b is calculated from

$$ h_{b} = H\, [{\exp}(0.78 \,R^{0.36})]^{-1}, $$

(10)

where

$$ R = g \beta \mathrm{\Delta} s H / (\rho_{*} {U_{T}^{2}}). $$

(11)

Here, R is the bulk Richardson number (Dyer 1997), g = 9.81 m s⁻² is the gravitational acceleration, Δs is the tidally-averaged bottom-to-surface salinity difference and U _T is the amplitude of depth-averaged tidal current. Equation 10 was determined by Chen and de Swart (2016) by fitting Eq. 9 to field data of several estuaries. In this study, U _T and Δs are derived from field data.

The formulation of the vertical eddy diffusivity κ _v reads

$$ \kappa_{v} = A_{v} \frac{(1+3.33 R)^{-1.5}}{(1+10 R)^{-0.5}}. $$

(12)

The above expression is based on Munk and Anderson (1948), except that here the bulk Richardson number rather than the gradient Richardson number is used. Finally, the along-estuary turbulent diffusivity κ _h was assumed spatially constant.

Biological Module

The equations govern phytoplankton and nutrient dynamics are

$$\begin{array}{@{}rcl@{}} \frac{\partial P}{\partial t} &=& \mu P -mP -v \frac{\partial P}{\partial z} -u \frac{\partial P}{\partial x} -w \frac{\partial P}{\partial z} + \frac{\partial}{\partial x}(\kappa_{h}\frac{\partial P}{\partial x})\\ &&+ \frac{\partial}{\partial z}(\kappa_{v}\frac{\partial P}{\partial z}), \end{array} $$

(13)

$$\begin{array}{@{}rcl@{}} \frac{\partial N}{\partial t} &=& -\alpha \mu P + \epsilon \alpha mP - u \frac{\partial N}{\partial x} - w \frac{\partial N}{\partial z} + \frac{\partial}{\partial x}(\kappa_{h}\frac{\partial N}{\partial x})\\ && + \frac{\partial}{\partial z}(\kappa_{v}\frac{\partial N}{\partial z}). \end{array} $$

(14)

In the above equations, P = P(x,z,t) denotes the width-averaged phytoplankton density (cells m ⁻³) and N = N(x,z,t) is the width-averaged nutrient (e.g., phosphorus, nitrogen or silicon) concentration (mmol m ⁻³). Parameter μ is the specific growth rate of phytoplankton, m is the loss rate, v is the sinking velocity, α is the nutrient amount in each cell and 𝜖 is the proportion of dead phytoplankton that is recycled into nutrients.

The specific growth rate μ is constrained by local nutrient concentration N and light intensity I. The parameterisation for μ follows Huisman et al. (2006):

$$ \mu (N,I) = \mu_{{\max}} \, \min\left( \frac{N}{H_{N}+N}, \frac{I}{H_{I}+I}\right), $$

(15)

where $\mu _{{\max }}$ is the maximum specific growth rate, H _N and H _I are the half-saturation constant for nutrient-limited and light-limited growth, respectively, and $\min $ denotes the minimum function. Based on the above equation, a limitation index is defined as $\left (\frac {N}{H_{N}+N} - \frac {I}{H_{I}+I}\right )$. If this index has negative values, phytoplankton growth is nutrient-limited, whilst if the limitation index has positive values, the growth is light-limited.

The light is supplied at the water surface and its intensity decreases exponentially with depth according to Lambert-Beer’s law:

$$ I=I_{in}\exp\left( -k_{bg}z - k{{\int}^{z}_{0}}P(t,\theta)\mathrm{d}\theta \right). $$

(16)

Here, I _{i
n} is the incident light intensity, k _{b
g} is the light extinction coefficient due to absorption by water, coloured dissolved organic matter and suspended particulate material and k is the light absorption coefficient of phytoplankton.

The loss rate m of phytoplankton is assumed to depend on salinity. For freshwater phytoplankton, saltier water implies higher loss rate because of osmotic stress. In this study, m is modelled as

$$ m(s) = m_{L} + (\frac{m_{0} - m_{L}}{2}) [1+\tanh(\frac{s-s_{c}}{s_{\delta}})]. $$

(17)

In this expression, m _L and m ₀ are the loss rate of phytoplankton in fresh and salt water, respectively, s _c is the salinity where m = (m ₀ + m _L)/2 and s _δ defines the salinity scale over which m varies. Input parameters are m _L, m ₀, s _c and s _δ. An analytical shape of Eq. 17 is plotted in Fig. 3.

The boundary conditions at the water surface, the bottom and the estuary mouth are set as

$$ \left.(vP-\kappa_{v}\frac{\partial P}{\partial z})\right\vert_{z=0 \text{ and } z=H} \,=\,0, \quad \left.(\kappa_{v}\frac{\partial N}{\partial z})\right\vert_{z=0 \text{ and } z=H} \,=\,0, $$

(18)

$$ \left. \kappa_{h}\frac{\partial P}{\partial x}\right\vert_{x=0}=0, \quad \left. \kappa_{h}\frac{\partial N}{\partial x}\right\vert_{x=0}=0. $$

(19)

At the surface and the bottom, zero-flux conditions are applied to P and N Eq. 18. At the seaward boundary, zero diffusive flux is assumed for both P and N Eq. 19.

At the riverine boundary, the depth-averaged density $\overline P_{L} = (1/H) {{\int }_{0}^{H}} P|_{x=L}(z) \, \mathrm {d}z $ is imposed, and the vertical distribution of P|_{x = L}(z) obeys v P − κ _v ∂ P/∂ z = 0. This condition is motivated by field data in the Columbia River estuary that show freshwater phytoplankton are transported into the estuary from the river compartment. Furthermore, a vertically-constant nutrient concentration is imposed at x = L. In the initial state, P and N at each location along the estuary are set the same with their riverine boundary conditions, respectively.

Model Implementation and Verification

To solve the two nonlinear differential equations in the biological module, central finite difference schemes are employed for spatial discretisation, and a fourth-order Runge-Kutta scheme is used to discretise the time derivatives (Press et al. 1992). This numerical scheme was also used by Liu and de Swart (2015) and it has been verified against data from published studies, yielding good agreement. The hydrodynamic module is solved analytically.

Experimental Set-up

Research Aim 1

Two experiments were carried out to mimic the observed phytoplankton density patterns in the Columbia River estuary during weak stratification and strong stratification, respectively. The effect of vertical stratification (which affects the magnitudes and vertical distributions of vertical eddy viscosity and eddy diffusivity) on P patterns follows from the analysis of the differences between the results of these two cases. In the field data of Roegner et al. (2011), the stratification conditions mainly vary due to variation in tidal mixing during the spring-neap cycle, rather than due to variation in river discharge. These cases are referred to as DF-W and DF-S, i.e. the default cases representing weakly stratified conditions (spring tides) and strongly stratified conditions (neap tides), respectively.

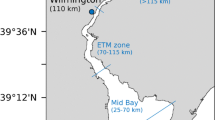
Figure 4 displays the map of the Columbia River estuary, in which sampling stations are indicated. The distance from sampling station SC16 to SC01 is 30 km. The length of the model domain is chosen as L = 45 km. The reason for selecting this length is that it allows an area for the impact of boundary conditions on P and N dynamics to diminish such that the modelled P patterns in 0 < x < 30 km are determined by internal dynamics.

At the riverine boundary x = 45 km, the same value of the depth-averaged density $\overline P_{L}$ has been used for both DF-W and DF-S. Moreover, for both cases, a vertically constant high value for eddy diffusivity $\kappa _{v} = 10^{-2} \text { m}^{2} \text { s}^{-1}$ at x = 45 km has been chosen such that P|_{x = L}(z) has little vertical variation. These choices for the riverine boundary condition of P guarantee that P patterns in DF-W and DF-S are not dictated by boundary conditions at the riverine boundary.

The total water depth H = 16 m, which is an estimate of the mean water depth in the area 0 < x < 30 km of the Columbia River estuary. A rectangular uniform grid system was used, with 41 × 201 grid nodes in the vertical and along-estuary direction, respectively. The time steps are 5 × 10⁻⁵ day and 2 × 10⁻⁴ day for DF-W and DF-S, respectively.

The values of parameters in the hydrodynamic module are listed in Table 1, including their sources. Here, x _c and x _δ were determined by fitting Eq. 6 to salinity data of Roegner et al. (2011). Furthermore, motivated by the success of earlier studies in explaining observed features of estuarine circulation (for instance, Hansen and Rattray 1965; Guha and Lawrence 2013), vertical eddy viscosity A _v and diffusivity κ _v are assumed longitudinally uniform. Accordingly, constant values of u _∗, z ₀, U _T and Δs are used. Specifically, the same values of friction velocity u _∗ and bottom roughness length z ₀ have been employed in DF-W and DF-S. These choices will be further discussed in “Insights from Additional Sensitivity Studies in the Electronic Supplement” section. Parameter U _T was estimated as the amplitude of depth-averaged tidal current at x = 11 km using field data of Chawla et al. (2008). The location x = 11 km (that is Station red26 in Chawla et al. 2008) was chosen to estimate U _T because its depth is approximately 16 m. Using the field data of Roegner et al. (2011), the tidally-averaged bottom-to-surface salinity difference Δs was also estimated at x = 11 km.

Table 1 Values of parameters in the hydrodynamic module for the default cases

Full size table

The isohalines have steep slopes under weakly stratified conditions. It is a fair estimate to assume that in this case the loss rate m depends on the depth-averaged salinities $\bar s$, i.e. m only varies in the along-estuary direction. On the contrary, isohalines are almost horizontal during strong stratification and m is assumed to vary only in the vertical direction. Specifically, in the latter case, m is a function of the length-averaged salinity that was obtained by averaging the field data of salinity along the estuary. For both DF-W and DF-S, s _c = 4 psu and s _δ = 0.8 psu were prescribed such that m increases from m _L to m ₀ when the depth-averaged (length-averaged) salinity increases from 3 to 5 psu.

In this study, phytoplankton considered in the biological module represent freshwater diatoms (Lara-Lara et al. 1990) and the depth-averaged density $ \overline P_{L}$ at the riverine boundary was set to 10⁹ cells m⁻³. Furthermore, based on the above-cited study, the nutrient that potentially limits phytoplankton growth in the Columbia River estuary is phosphorus, and the nutrient concentration at the riverine boundary $\left . N\right \vert _{x=L}=0.6 \text { mmol m}^{-3}$. Finally, the values of other parameters in the biological module are listed in Table 2, which were adopted from other studies that are cited in the footnote of this table.

Table 2 Biological and abiotic characteristics and parameters for the default cases DF-W (weak stratification) and DF-S (strong stratification)

Full size table

The following sensitivity experiments were further conducted to achieve the other three research aims. The set-ups of all the experiments are summarised in Table 3.

Table 3 Description of experiments

Full size table

Research Aim 2

To quantify the impact of subtidal currents u (which consists of river flow u _r and density-driven flow u _d) on P patterns, experiments were conducted in which the subtidal currents were completely switched off (u = 0). Because the structure of subtidal currents vary with stratification conditions, additional experiments were conducted in which u = u _r or u = u _d.

Research Aim 3

To assess the sensitivity of P patterns to the vertical distribution of vertical eddy viscosity A _v and eddy diffusivity κ _v, experiments were carried out with constant and parabolic vertical shapes of A _z, which are denoted by A _z|_const and A _z|_para, respectively. Note that a change in A _z affects A _v through Eq. 8 and κ _v through Eq. 12. Compared to the default vertical shape that depends on stratification (denoted by A _z|_DF), the former two shapes assume that the height of the turbulent bottom boundary layer equals the total water depth. Furthermore, the depth-averaged values of A _z|_const and A _z|_para are kept the same as that of A _z|_DF. Moreover, the value of A _S for A _z|_para is identical to that of A _z|_DF, as is illustrated in Fig. 2a.

Research Aim 4

To assess the influence of salinity-dependent loss on P patterns, experiments were conducted with the value of the loss rate m ₀ of phytoplankton in salt water halved and doubled, respectively, with respect to that of the default cases ($m_{0}|_{\text {DF}}=0.5 \text { day}^{-1}$). The former case mimics the behaviour of phytoplankton that are tolerant to the change of salinity, and the latter accounts for the high osmotic stress that freshwater species experience in salt water. Besides, experiments were conducted with a loss rate m|_const that is constant in space. Here, $m|_{\text {const}} = 0.4 \text { day}^{-1}$ is an approximation of the domain-averaged values of m in both DF-W and DF-S. A spatially constant m|_const mimics the case that the osmotic stress of freshwater phytoplankton is roughly accounted for by increasing the loss rate in the whole domain rather than by parameterising it as a function of salinity.

Finally, to test whether model results are qualitatively affected by the choices of boundary conditions in the biological module or by values of other model parameters (for instance, along-estuary turbulent diffusivity κ _h, nutrient input N|_{x = L}, maximum specific growth rate μ _{m
a
x}, half-saturation constant H _N for nutrient-limited growth, etc.), additional sensitivity experiments were carried out.

Analysis of Output

To facilitate comparison between model results and field data, spatial distributions of model results are shown in the area 0 ≤ x ≤ 30 km. Furthermore, two parameters are defined to quantify the overall vertical and along-estuary gradient of P in the area 0 ≤ x ≤ 30 km:

$$ \phi_{z} = (P^{u}_{\max}|_{x=0} - P^{l}_{\min}|_{x=0}) \,/ \, P^{u}_{\max}|_{x=30 \text{ km}}, $$

(20)

$$ \phi_{x} = (P^{u}_{\max}|_{x=30 \text{ km}} - P^{u}_{\max}|_{x=0}) \,/ \, P^{u}_{\max}|_{x=30 \text{ km}}. $$

(21)

Here, $P^{u}_{\max }|_{x=0}$ and $P^{l}_{\min }|_{x=0}$ are the maximum P in the upper layer and minimum P in the lower layer at the estuary mouth, respectively, and $P^{u}_{\max }|_{x=30 \text { km}}$ is the density at x = 30 km at the same depth as $P^{u}_{\max }|_{x=0}$. The definitions of the upper and lower layer are given in “Results” section. The above parameterisations are motivated by field data of Roegner et al. (2011). Furthermore, ϕ _z, being the fraction of the relative change of P between the upper and lower layer, is analogous to the salinity stratification indicator proposed by Guha and Lawrence (2013). Parameter ϕ _x is the fraction of the relative change of P along the estuary over a distance of 30 km. Higher values of ϕ _z (ϕ _x) indicate larger vertical (along-estuary) gradients of P. Comparison among the results of sensitivity experiments in this study are made in terms of ϕ _z and ϕ _x.

Results

In this section, first the output of the default cases DF-W and DF-S, for the weakly and strongly stratified conditions, respectively, are presented in “Default Cases Under Weakly and Highly Stratified Conditions” section. Next, results of sensitivity experiments listed in Table 3 are presented in “Sensitivity Experiments” section. For all default cases and sensitivity studies, equilibrium states of P are reached after several days starting from the given initial condition (the time evolution of P is not shown here). Results presented of sensitivity studies concern the values of ϕ _z and ϕ _x at equilibrium.

Default Cases Under Weakly and Highly Stratified Conditions

Figure 5 contains physical conditions estimated for DF-W and DF-S. The observed and parameterised along-estuary profiles of depth-averaged salinity $\bar s$ are shown in Fig. 5a, b for DF-W and DF-S, respectively. Clearly, the overall behaviour of the observed $\bar s$ is captured by the parameterisation of $\bar s$ used in this study. In case DF-W, the modelled salt intrusion length (x _c + x _δ) = 26 km, and in case DF-S (x _c + x _δ) = 63 km. These estimates for tidally-averaged salt intrusion length are consistent with those observed by Jay and Smith (1990). Interestingly, data observed by Roegner et al. (2011) show an oscillation in the salinity pattern during high stratification. The potential reason for the presence of this oscillation will be discussed in “Discussion” section.

The modelled vertical profiles of eddy viscosity A _v and diffusivity κ _v are displayed in Fig. 5c. The heights of turbulent boundary layer h _b are 8.6 and 3.6 m in DF-W and DF-S, respectively. The maximum of A _v for DF-W is 1.4 × 10⁻² m² s⁻¹, which is six times larger than that for DF-S. Similar to A _v, κ _v for DF-W has a significantly larger magnitude than that for DF-S. Contour plots of the width-averaged along-estuary subtidal current u for DF-W and DF-S are shown in Fig. 5d, e, respectively. Clearly, for DF-W, maximum velocities occur at x = 18 km, where the along-estuary salinity gradient $\mathrm {d} \bar s / \mathrm {d} x$ reaches its maximum. For DF-S, the magnitude of u is large throughout the domain. Both magnitudes and vertical profiles of the modelled u agree well with those of the observed subtidal current (Chawla et al. 2008).

The spatial distributions of phytoplankton density P at equilibrium for DF-W and DF-S are shown in Fig. 6a, b, respectively. For DF-W, the spatial pattern of P is characterised by little vertical variation and by a gradual longitudinal decline of density from about 10⁹ cells m⁻³ at the riverine boundary to about 0.24 × 10⁹ cells m⁻³ at the estuary mouth. In contrast, the spatial distribution of P for DF-S shows a two-layer vertical structure. Within a thickness of 6 m below the water surface, the values of P are significantly higher compared to those in the lower water column, and the maxima of P are located with in 1 < z < 2 m. Moreover, P shows less variability in the along-estuary direction for DF-S.

The modelled spatial distributions of P described above capture the main features of those observed by Roegner et al. (2011) (displayed in Fig. 6c, d). Specifically, in the field data, high values of P also occur in the region 0 < z < 6 m. In this study, “the upper layer” refers to 0 ≤ z ≤ 6 m, whereas “the lower layer” is 6 ≤ z ≤ 16 m. Locations of $P^{u}_{\max }|_{x=0}$, $P^{l}_{\min }|_{x=0}$ and $P^{u}_{\max }|_{x=30 \text { km}}$ are marked in Fig. 6a, b. Values of ϕ _z and ϕ _x are calculated using Eqs. 20 and 21. Here, ϕ _z = 0.01, ϕ _x = 0.64 in DF-W, and ϕ _z = 0.67, ϕ _x = 0.2 in DF-S.

The values of the limitation index (which is defined in “Biological Module” section) suggest that the growth of phytoplankton for both DF-W and DF-S is mostly light-limited (result not shown here). Nutrient limitation occurs only within 0 < z < 1 m where light intensity is high. The results of nutrient dynamics for DF-W and DF-S and those of sensitivity experiments concerning parameters directly related to nutrient dynamics are presented and discussed in the Electronic Supplement.

Sensitivity Experiments

Advection by Subtidal Currents

The values of ϕ _z and ϕ _x for the cases in which different subtidal current components are switched off are plotted in Fig. 7a. Under weakly stratified conditions, completely switching off advection of phytoplankton by the subtidal current u results in a negligible decrease in ϕ _z but a noticeable increase of ϕ _x (from 0.64 to 0.88). Furthermore, when the subtidal current only consists of river flow, i.e. u = u _r, ϕ _x = 0.68 is close to that of DF-W. In contrast, if only the density-driven flow component is accounted for, that is u = u _d, ϕ _x = 0.83 is evidently larger than that of DF-W.

Under strongly stratified conditions, switching off both u _r and u _d leads to large changes in both ϕ _z and ϕ _x. Specifically, ϕ _z decreases from 0.67 to 0.11 and ϕ _x increases from 0.2 to 0.79. If u = u _r, the value of ϕ _z is still much smaller than that of DF-S and the value of ϕ _x is much larger than that of DF-S. However, when u = u _d, values of both ϕ _z and ϕ _x are close to those of DF-S.

Vertical Shape of A _z

The values of ϕ _z and ϕ _x obtained for different vertical shapes of A _z are shown in Fig. 7b, c. For both weakly and strongly stratified conditions, when the default vertical shape A _z|_{D
F} is changed to a constant shape A _z|_const or to a parabolic shape A _z|_para, values of ϕ _z decrease and those of ϕ _x increase. Furthermore, values of ϕ _z and ϕ _x for A _z|_const differ marginally from those for A _z|_para. Moreover, the ranges over which ϕ _z and ϕ _x vary are much larger during strong stratification than those during weak stratification.

Osmotic Stress

The values of ϕ _z and ϕ _x for different values of loss rate m ₀ of phytoplankton in salt water and for a spatially-constant loss rate m|_const are plotted in Fig. 7d. Under weakly stratified conditions, as m ₀ increases, the value of ϕ _x increases from 0.39 to 0.85, whereas that of ϕ _z hardly changes. Furthermore, when the salinity-dependent loss rate in DF-W is replaced with m|_const, the value of $P^{u}_{\max }|_{x=0}$ (defined in “Analysis of Output” section) hardly change, whereas the value of $P^{u}_{\max }|_{x=30 \text { km}}$ slightly decreases (results not presented). Hence, according to Eq. 21, ϕ _x for m|_const is smaller than that of DF-W.

During strong stratification, as m ₀ increases, the value of ϕ _z increases from 0.48 to 0.76, and that of ϕ _x slightly increases from 0.16 to 0.21. When m|_const is used, ϕ _z = 0.57 and ϕ _x = 0.25 for m|_const.

Discussion

To understand the mechanisms underlying phytoplankton dynamics under different stratification conditions, at first, the observed P patterns in the Columbia River estuary are explained by quantifying the contribution of each factor to the local change of P (“Factors Contributing to Local Change of P ” section) for cases DF-W and DF-S. Next, the results of sensitivity studies are further analysed in “Sensitivity Experiments” section. Finally, results of additional experiments (that are described in the Electronic Supplement) and the model limitations are discussed in “Insights from Additional Sensitivity Studies in the Electronic Supplement” and “Limitations” sections, respectively.

Factors Contributing to Local Change of P

In the equation governing phytoplankton dynamics (13), the left-hand side term ∂ P/∂ t is the accumulation rate of phytoplankton density at a fixed position. The latter is a summation of contributions related to the net growth (viz., gross growth and loss), sinking, along-estuary and vertical advection, along-estuary and vertical mixing. Figure 8 contains the spatial distributions of these terms in the equilibrium state, when ∂ P/∂ t = 0.

Case DF-W

Due to light limitation, the net specific growth rate (μ − m) (results not shown) of phytoplankton is positive within a thickness of 2 m below the water surface. As a results, positive values of net growth (μ − m)P only occur in a thin layer close to the water surface, as is shown in Fig. 8a. If the vertical mixing is strong, phytoplankton cells produced in the euphotic zone are rapidly moved downward to the aphotic zone (Cloern 1996). This statement is confirmed by Fig. 8c, in which the vertical turbulent diffusion term persistently has negative values in the upper layer. As a result, P is vertically almost uniform (see Fig. 6a). Moreover, the strong vertical mixing results in negligible impact of the sinking of phytoplankton on the P pattern, as is illustrated by Fig. 8e.

High intensity of vertical turbulent mixing, together with light limitation on phytoplankton growth, results in an unproductive estuary (in which the domain integrated value of (μ − m)P is negative) regarding to pelagic phytoplankton production, as was concluded from field studies (Cloern 1987; Lara-Lara et al. 1990; Ragueneau et al. 1996). Consequently, phytoplankton observed in such estuaries are mostly imported from the river compartment rather than are in situ produced (Frey et al. 1983). This point is proven by the fact that the along-estuary advection term (see Fig. 8g) is positive in the upper layer and it generally compensates for the vertical mixing term. Since the depth-averaged (μ − m)P is negative, P gradually decreases as phytoplankton are advected seawards, as is seen in both model results and field data (Lara-Lara et al. 1990; Roegner et al. 2011).

The along-estuary turbulent diffusion term (Fig. 8i) only has large values in the vicinity of the estuary mouth, where the along-estuary advection term becomes zero due to imposed zero diffusive flux boundary condition (Eq. 19), and in the area 20 < x < 25 km, in which the increased loss rate causes increased ∂ P/∂ x. Moreover, the magnitude of longitudinal turbulent diffusion is much smaller than that of along-estuary advection. Thus, the along-estuary advection of P by subtidal currents has a much larger impact on P patterns than the longitudinal turbulent diffusion of P. The vertical advection term (see Fig. 8k) has a much smaller magnitude compared to that of the vertical turbulent mixing term and it only has noticeable impact in the area where vertical velocity w is large.

Case DF-S

Under strongly stratified conditions, the positive net growth of P is still restricted to a thin layer below the water surface (see Fig. 8b) although the loss rate of freshwater species is low in the surface fresh water. As shown in Fig. 8d, a weak vertical turbulent mixing is not efficient in reducing P in the surface layer. Therefore, high values of P are possible in the upper layer, which is consistent with field observations (such as Ragueneau et al. 1996; Roegner et al. 2011). Note that Huisman and Sommeijer (2002) argued that bloom development requires a minimal vertical turbulent mixing in the euphotic zone to prevent phytoplankton to sink downward into the aphotic zone. The vertical mixing in the upper layer in case DF-S is weak such that sinking of phytoplankton effectively removes phytoplankton from the surface productive layer, as is demonstrated in Fig. 8f.

Because of light limitation, weak vertical turbulent mixing and sinking of phytoplankton, during strong stratification, the prototype estuary is unproductive. Hence, phytoplankton abundance in the estuary domain again relies on the seaward advection of freshwater species by subtidal current, as is demonstrated in Fig. 8h. Furthermore, P slightly decreases towards the estuary mouth as phytoplankton gradually sink out of the upper layer.

The along-estuary turbulent diffusion term (Fig. 8j) is smaller than the longitudinal advection term in the most area of the domain. The former term only show high values in a narrow area close to the estuary mouth, where zero diffusive flux of P is imposed, and in the area x > 25 km, where ∂ P/∂ x is relatively high due to the constant phytoplankton density assumed at the riverine boundary (see “Biological Module” section). High values of the vertical advection term only occur in the areas where w is large, as is shown in Fig. 8l.