Modeling the Population Effects of Hypoxia on Atlantic Croaker (Micropogonias undulatus) in the Northwestern Gulf of Mexico: Part 1—Model Description and Idealized Hypoxia

Abstract

We developed a spatially explicit, individual-based model to analyze how hypoxia effects on reproduction, growth, and mortality of Atlantic croaker in the northwestern Gulf of Mexico lead to population-level responses. The model follows the hourly growth, mortality, reproduction, and movement of individuals on a 300 × 800 spatial grid of 1-km² cells for 140 years. Chlorophyll-a concentration, water temperature, and dissolved oxygen (DO) were specified daily for each grid cell and repeated for each year of the simulation. A bioenergetics model was used to represent growth, mortality was assumed stage- and age-dependent, and the movement behavior of juveniles and adults was modeled based on temperature and avoidance of low DO. Hypoxia effects were imposed using exposure effect submodels that converted time-varying exposures to low DO to reduced hourly growth, increased hourly mortality, and reduced annual fecundity. Results showed that 100 years of either mild or intermediate hypoxia produced small reductions in population abundance, while repeated severe hypoxia caused a 19% reduction in long-term population abundance. Relatively few individuals were exposed to low DO each hour, but many individuals experienced some exposure. The response was dominated by a 5% average reduction in annual fecundity of individuals. Under conditions of random sequences of mild, intermediate, and severe hypoxia years occurring in proportion to their historical frequency, the model predicted a 10% decrease in the long-term population abundance of croaker. A companion paper substitutes hourly DO values from a three-dimensional water quality model for the idealized hypoxia and results in a more realistic population reduction of about 25%.

Introduction

Anthropogenic eutrophication is increasing in coastal waters (Howarth et al. 2011) and has been implicated in causing changes to the ecological structure and functioning of semi-enclosed and coastal marine systems (Diaz and Rosenberg 2008). Ecosystem responses to eutrophication include shifts in energy flow among functional groups within the food web, changes in phytoplankton and fish community composition, declines in habitat quality for fish and other organisms, and increases in harmful algal blooms (Cloern 2001; Rabalais et al. 2002). Coastal hypoxia is commonly defined as dissolved oxygen (DO) concentration less than 2 mg l⁻¹, and is often associated with eutrophication. Increasing nutrient loadings trigger primary and secondary production that acts as fuel to decomposition processes in the bottom layer of stratified water columns (Cloern 2001; Breitburg 2002). However, the increased secondary production can also stimulate fish productivity (Grimes 2001; Nixon and Buckley 2002; Kemp et al. 2005). Efforts to reduce nutrient loadings to coastal waters are widespread (McCrackin et al. 2017). Eutrophication in coastal waters, and associated hypoxia, is expected to increase in the future due to increased human population and climate change (Rabalais et al. 2009).

Hypoxia clearly has detrimental effects on individual fish and on small spatial and temporal scales (i.e., localized effects). For example, laboratory and field experiments have shown that low DO can alter foraging behavior (Pihl et al. 1992; Baustian et al. 2009), reduce growth rate (McNatt and Rice 2004; Stierhoff et al. 2006), affect sex differentiation (Shang et al. 2006), and result in reproductive impairment (Thomas and Rahman 2009, 2012; Thomas et al. 2007, 2015; Murphy et al. 2009; Cheek et al. 2009). In field studies, low DO has been implicated in causing mass mortality (Thronson and Quigg 2008), altering spatial distributions (Eby and Crowder 2002; Tyler and Targett 2007; Switzer et al. 2009; Zhang et al. 2009; Roberts et al. 2009; Craig 2012), changing the vertical distribution and size structure of the zooplankton (Pierson et al. 2009; Roman et al. 2012), and causing a shift in the system from demersal to pelagic species (de Leiva Moreno et al. 2000; Chesney and Baltz 2001).

Knowing the likely ecological consequences of reducing nutrients on the system-level is critical to proper decision-making and public policy formulation (Vaquer-Sunyer and Duarte 2008; Bianchi et al. 2010; Task Force 2015). Reducing nutrient loadings in large coastal systems incurs high monetary costs (Butt and Brown 2000; Ribaudo et al. 2001; Rabotyagov et al. 2010). There is no doubt that reducing hypoxia benefits sessile species and has positive local effects on aquatic fauna, including large numbers of individuals (e.g., Roberts et al. 2009; Pollock et al. 2007). However, quantitative evidence that reducing hypoxia has positive population-level effects on coastal fish species is equivocal except for several well-studied systems (Rose et al. 2009). The reasons that detecting hypoxia effects is difficult include high variation in population dynamics from other sources, uncertainties in establishing hypoxia exposure and effects on individuals in the field, and general challenges in monitoring and modeling multiple life stages that use different habitats (Rose 2000; Rose et al. 2017a). We use the term “population level” here in the fisheries management sense of a fish stock: a stock is a group of reproducing individuals of the same species (at least semi-closed) that have similar life history parameters (Begg and Waldman 1999).

Caddy (1993) proposed a conceptual model for how eutrophication and hypoxia affect fish production. Caddy suggested that ecosystems reach a point where the negative effects of increasing enrichment (including hypoxia) result in declines of demersal and, eventually, pelagic fish species. In a subsequent paper, Caddy (2000) used several case studies (e.g., Black Sea, Baltic Sea) to illustrate how nutrient loadings and hypoxia affect fish populations. For example, hypoxia effects on the volume of reproductive habitat are one of several major factors implicated in a variety of analyses of Baltic Sea cod recruitment variability (Koster et al. 2005; Margonski et al. 2010; Tomczak et al. 2012; Casini et al. 2016). In another study, Huang et al. (2010) estimated that an average 13% decline in harvest of brown shrimp in North Carolina estuaries was attributed to hypoxia.

However, analyses of long-term fisheries landings and survey data have not found convincing widespread evidence of the negative effects of hypoxia on coastal fish populations. Breitburg et al. (2009a, b) analyzed the landings, nutrient loadings, and hypoxia conditions across a suite of estuarine and marine ecosystems and concluded “It is difficult to find compelling evidence for negative effects of hypoxia on fisheries for mobile species even in systems with extensive and persistent oxygen depletion if system-wide conditions and total landings are the focus of analyses.” Chesney et al. (2000) and Chesney and Baltz (2001) did not detect any obvious downward trends in long-term fishery-dependent and fishery-independent abundance indices for several species in Louisiana, and this period included a highly variable but increasing trend in hypoxia (see Obenour et al. 2013). An important caveat is that these statistical (correlative) analyses of fisheries time series data have low power to detect an effect at the population level given the high degree of variability in the available data and other covarying factors (e.g., harvest, climate) that also influence fish population dynamics (Diaz and Solow 1999; Chesney and Baltz 2001; Rose et al. 2017).

Analyses based on ecological and population models that included the Chesapeake Bay, Patuxent Estuary, Gulf of Mexico, and the Neuse River (Rose et al. 2009) suggest that the direct morality effects of hypoxia have small to moderate effects on fish populations, suggesting that population-level responses may result primarily from indirect or sublethal direct effects. Likely direct but sublethal effects are reductions in growth and reproduction. Indirect effects include displacement of individuals to inferior habitat or changes in predator-prey interactions that then result in slower growth or higher mortality. Rose et al. (2009) described a suite of population and community models used to investigate the effects of hypoxia. They concluded that the modeling evidence suggests that direct effects of hypoxia on coastal fish populations are generally small in most years; however, indirect effects coupled with the direct effects can result in large population-level responses under certain environmental and biological conditions. Rose et al. (2009) also noted that the seemingly small population-level responses to hypoxia predicted by the reviewed models may reflect the failure to include certain direct effects (e.g., reproductive impairment), the challenges dealing with modeling the effects of eutrophication (which increase fish production), and the high uncertainty in quantifying the degree of exposure to hypoxia. Modeling fish population responses to variation in environmental factors in general remains a challenge (Rose 2000).

In this paper, we present a spatially explicit, individual-based population dynamics model of Atlantic croaker (Micropogonias undulatus) in the northwestern Gulf of Mexico (NWGOM). We use the model to examine the effects of hypoxia on population-level responses. Atlantic croaker in the NWGOM is a good case study for investigating the population-level effects of hypoxia on a coastal fish species. Atlantic croaker is a demersal, estuarine-dependent sciaenid fish that frequently inhabits highly productive areas along the Texas-Louisiana shelf that are susceptible to hypoxia. Croaker dominate summer and fall surveys of groundfish on the Gulf of Mexico shelf and can be considered as an indicator species for the fish communities off of coastal Louisiana (Monk et al. 2015). Also, a relatively large database has accumulated on laboratory and field studies quantifying low DO effects on growth, mortality, reproduction, and movement of individual croaker and related species. The hypoxic zone in the NWGOM has been well monitored and varies in magnitude and duration from year to year (Rabalais et al. 2007). The hypoxia zone has also garnered a lot of scientific and public interest (National Research Council 2008), and various plans have been put forth for reducing the nutrient loadings from upstream in the Mississippi River watershed in order to reduce the degree of hypoxia in the Gulf of Mexico (Task Force 2008, 2015). Thus, modeling of croaker in the NWGOM offers an opportunity for quantitative evaluation of the population-level effects of hypoxia on a common coastal fish species in a system that experiences widespread and variable hypoxia and that is the focus of management actions to reduce nutrient loadings.

Croaker Life Cycle in the Northwest GOM

Atlantic croaker in the NWGOM spend much of their life on the Louisiana-Texas continental shelf, and are a dominate fish species by biomass in Louisiana waters (Monk et al. 2015). Spawning occurs offshore beginning in September, peaks in October, and sometimes persists into March (White and Chittenden 1977; Sheridan et al. 1984). About 75% of age 1, and all age 2 and older, individuals are mature. Spawners release about 12 batches per year over a few months and appear to exhibit some degree of indeterminate spawning (Barbieri et al. 1994), suggesting a mix of capital (energy stored prior) and income (energy gained during) spawning (see McBride et al. 2015). Eggs, yolk-sac larvae, and ocean larvae are transported from offshore to nearshore waters during late fall and winter (Hansen 1969; Rooker et al. 1998; Baltz and Jones 2003), and arrive in shallow coastal habitats and in estuaries as estuary larvae (typically 50–60 days of age, Table 1). Estuary larvae settle out of the plankton to shallow benthic habitats such as salt marshes and gradually move to deeper estuarine and nearshore waters as they transition to early juveniles. Juveniles begin “bleeding off” to the shelf (i.e., offshore) in early summer, with size-at-emigration increasing (e.g., 55 mm in March; 85 mm in July) as the summer season progresses (Yakupzack et al. 1977). Gonadal development in competent first year-of-life individuals and recrudescence in adults begins in the summer and early fall (Hansen 1969; White and Chittenden 1977; Sheridan et al. 1984; Thomas et al. 2007). Mortality is highly variable in early stages, and juveniles and adults are subject to mortality as bycatch in the shrimp fishery (Diamond et al. 1999, 2000). Juvenile and adult croaker consume a variety of benthic meiofauna and macrofauna (Nye et al. 2011).

Table 1 Mortality rate (day⁻¹), duration (days), entering lengths, and whether off or on the model grid for the egg, yolk-sac larva, ocean larva, estuary larva, early juvenile, late juvenile, and adult stages

Potential exposure of croaker to low DO occurs on the nearshore shelf, typically in waters <30 m, which is the primary habitat of croaker and many other demersal fishes during summer (Moore et al. 1970; Craig and Crowder 2005, Craig et al. 2010). Larvae and juveniles can be exposed to hypoxia in estuaries and on the shelf; juveniles are vulnerable as they move during the summer from the estuaries into progressively deeper shelf waters. Adult croaker may be exposed to hypoxia due to their seasonal nearshore-offshore migrations on the shelf associated with the summer growing and fall-winter spawning seasons (Darnell et al. 1983). Croaker generally prefer near-bottom conditions, and evidence suggests they move horizontally rather than vertically to avoid very low DO concentrations (Craig 2012; see summary in Rose et al. 2017a). Low DO has been shown to alter croaker densities and foraging dynamics in ways that may impair growth (Eby et al. 2005; Powers et al. 2005), and summer exposure to hypoxia can affect fecundity during the following fall spawning season (Thomas et al. 2007, Thomas and Rahman 2012). Exposure to DO less than 3.0 mg l⁻¹ reduced growth (McNatt and Rice 2004) and below about 1.5 mg l⁻¹ increased mortality (Shimps et al. 2005) in laboratory experiments with the closely related juvenile spot (Leiostomus xanthurus). Fecundity of croaker in the laboratory was sharply reduced as DO decreased below 4.0–4.5 mg l⁻¹ (Thomas et al. 2007). These DO concentrations that trigger sublethal effects in croaker are typical for many fish species (Vaquer-Sunyer and Duarte 2008). Whereas croaker typically avoid lethal DO, their avoidance thresholds based on field data are relatively low (1.7–2.7 mg l⁻¹; Eby and Crowder 2002; Craig and Crowder 2005; Craig 2012), and thus, they experience sublethal DO concentrations that are too high to trigger avoidance but sufficiently low to affect growth and reproduction.

Model Description

Overview

The model simulated the hourly growth, mortality, reproduction, and movement of thousands of individual croaker from fertilization until age 8 for a period of 140 years on a two-dimensional spatial grid. The grid domain roughly encompassed a rectangular area from Mobile Bay, AL, southwest to East Matagorda Bay, TX (28.00° N to 30.70° N and 87.60° W to 95.96° W). This domain corresponds to a broad area surrounding the hypoxic zone (i.e., beyond just local effects), and croaker are found most concentrated in the western GOM (Darnell 1990). Our model grid is centered on the coastal area of Louisiana to include both the hypoxic zone and the major habitat for croaker. The model year was 365 days long, beginning on September 1.

Daily water temperature and food availability were specified for each spatial cell for a typical year (climatological conditions), and these conditions were repeated year after year. The environmental conditions were specified to represent near-bottom conditions because croaker is a demersal species. The daily values were used for all hours in each day for growth, mortality, reproduction, and movement.

Growth was represented using a bioenergetics approach with temperature and food availability as inputs. Mortality was stage-dependent, whereas maturity and fecundity were size-dependent. Movement was based on both a kinesis approach with temperature as the cue for hourly behavioral movements and on a restricted area (neighborhood-based) search approach for avoidance of low DO. Movement determined the hourly position of each individual on the grid, and thus determined the exposure of each individual to temperature, food, and DO. Growth, mortality, and fecundity were reduced based on accumulated exposure to the hourly DO values using a set of exposure effect submodels specifically designed to deal with fluctuating exposures.

Grid Configuration and Environmental Variables

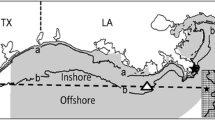
The two-dimensional grid was 300 × 800 cells, with each cell measuring 1 km² (Fig. 1). The depth of each cell was specified by linearly interpolating bottom elevations from 1″ resolution bathymetry data (http://topex.ucsd.edu/marine_topo/). The coastline was delineated within the grid based on 2″ resolution coastline data (http://www.ngdc.noaa.gov/mgg/shorelines/). All cells at or below mean sea level were considered aquatic habitat (i.e., water cells). Cell depths from shore to 100 m (the approximate shelf-slope break) were based on the actual bottom elevations, after which model cells were assumed to have a constant 100-m depth. Atlantic croaker is not typically found at depths greater than 100 m (Moore et al. 1970; Chittenden and Moore 1977).

Fig. 1

Model grid for the northwestern Gulf of Mexico showing the Louisiana and Texas portions of the grid (denoted by dashed line) and the areas that individuals are confined to according to life stage. Individuals were restricted to cells: within line a (depths <5 m) at the early juvenile stage, within line b (depths <20 m) at the late juvenile stage, and outside of line a (depths >5 m) as adults. A magnified 25 × 25 cell area of the grid (referenced by the solid star) is displayed in the lower right corner. Station C6, where DO is commonly monitored, is also shown (solid triangle)

Daily water temperature (°C) and chlorophyll-a concentration (mg m⁻³) were specified for each cell on the spatial grid for each day of the year using spatial and temporal interpolation of field or satellite data (ESM-1). Values on the middle day of each month are shown for temperature in Fig. 2 and for chlorophyll-a in Fig. 3. Surface chlorophyll-a concentration was assumed to be a reasonable index of food availability based on general correspondence between zooplankton growth rates and chlorophyll-a concentration (Peterson et al. 2002; Hirst and Bunker 2003), and reported empirical relationships between chlorophyll-a and fish distribution and production within systems (Cole and McGlade 1998; Ware and Thomson 2005) and across ecosystems (Ryther 1969). Further, the flux of organic matter to the bottom on the inner Louisiana shelf is positively correlated with the productivity of the overlying surface waters (Redalje and Fahnenstiel 1994; Wysocki et al. 2006), suggesting that surface chlorophyll-a may be a crude index of benthic secondary production that is then directly utilized by croaker in the GOM. Rose et al. (2017a) further discuss the use of surface chlorophyll as indicator of food for croaker.

Fig. 2

Snapshots of daily temperatures (°C) on the 15th day of each month used in model simulations

Fig. 3

Snapshots of daily chlorophyll-a concentrations (mg m⁻³; square root-transformed) on the 15th day of each month used in model simulations

Three hypoxia scenarios, classified by the areal extent (km²) of hypoxia (mild, intermediate, and severe), were simulated (Fig. 4). Normoxic conditions were defined by assigning a cell a DO value of 8.0 mg l⁻¹; this value was arbitrarily set to evoke no effects of hypoxia in the model. The three hypoxic conditions were represented by specifying DO values less than 8 mg l⁻¹ for specific cells and time periods during the summer. Low DO values for each cell were determined by analysis of a map depicting the frequency of occurrence of hypoxia off the Louisiana Coast during the last week of July (ESM-2). Average DO values within the entire hypoxic area (colored area in Fig. 4) under the mild, intermediate, and severe scenarios were 4.5, 2.2, and 1.1 mg l⁻¹.

Fig. 4

Maps showing the spatial distribution of DO (mg l⁻¹) for the mild (top), intermediate (middle), and severe (bottom) hypoxia scenarios used in model simulations. Numbers in upper left-hand corner correspond to the areal extent of hypoxia (DO <2.0 mg l⁻¹) in each scenario

DO concentration in each cell was linearly interpolated hourly from the normoxic conditions on June 1 to the target DO concentration in each cell (Fig. 4) over a 7-day period. The DO values were then maintained for the rest of the summer (June 8 to August 31). Time series plots of DO at a moored sampling station near the middle of the hypoxic zone (Station C6, Fig. 1) showed that about 5–10 days were needed for DO concentrations to decline from normoxia to hypoxia (Babin 2012). All cells return to normoxic on September 1, which is near the time that fall cold fronts and weakening solar insolation break down salinity stratification and remix the water column (Rabalais et al. 2001).

Life Stages

Simulated croaker individuals progressed through seven life stages (egg, yolk-sac larva, ocean larva, estuary larva, early juvenile, late juvenile, and adult), and were followed as adults until they reached their eighth birthday (the assumed maximum age of croaker; Barger 1985), when they were removed from the simulation. The birth date of all individuals was assumed to be September 1. Development through the egg, yolk-sac larva, ocean larva, and estuary larva stages was based on temperature. Transition between the early juvenile and late juvenile stages was length-dependent (97.5 mm); late juveniles became adults when their total length exceeded 180 mm (Diamond et al. 1999). Eggs, yolk-sac larvae, ocean larvae, and estuary larvae were followed as individuals, but were assumed to experience grid-wide averaged daily temperatures (i.e., they were not followed in a spatially explicit manner). Upon entering the early juvenile stage, each individual was assigned a weight and length (32-mm total length (TL) and 0.28 g), positioned randomly on the 2-D spatial grid, and then followed hourly as individuals through growth, mortality, reproduction, and movement through age 7. Early juveniles (including to their initial placement) were restricted to cells shallower than 5 m, late juveniles to cells shallower than 20 m, and adults were restricted to cells deeper than 5 m (lines a and b in Fig. 1). Individuals were allowed to move to any cells within their depth restrictions. Because the transition of late juveniles to adults was length-based, there were some age 1 juveniles (individuals <180 mm after September 1) and a few age 0 adults (individuals >180 mm in their first year before September 1).

Numerics

Due to the high spatial (1 km²) and temporal (1 h) resolution of the model, a super-individual approach was used to ensure reasonable memory usage and computational times (Scheffer et al. 1995, ESM-3). This approach follows a fixed number of super-individuals for each age class. Each super-individual is assigned an initial worth, which is the number of identical population individuals that it represents. Worth is used as a weighting factor (in the statistical sense) to scale up from the activities of the super-individual to the population level. Mortality operates to reduce the worth of each super-individual over time while never actually removing it from the population (the same number of super-individuals remains in the model throughout). When super-individuals reach their maximum age (age 8), they are removed from the simulated population and their places in the computer code are made available to house newly recruiting early juvenile individuals during the next year. The new early juveniles are the survivors that result from all of the eggs released in that year (ESM-3). All computations and output variables related to population-level metrics such as abundance, biomass, weight, fecundity, and spatial distributions are based on an individual’s attributes multiplied by its worth.

Development and Growth

Development of eggs, yolk-sac larvae, ocean larvae, and estuary larvae was temperature-dependent. Each hour, the stage-specific fractional development FD was computed as follows:

$$ FD=\left\{\begin{array}{c}\hfill \begin{array}{c}\hfill 0.0957\cdot {\mathrm{e}}^{0.06931\cdot \overline{T}(t)},\mathrm{for}\ \mathrm{eggs}\kern6.25em \hfill \\ {}\hfill 0.0610\cdot {\mathrm{e}}^{0.06931\cdot \overline{T}(t)},\mathrm{for}\ \mathrm{yolk}-\mathrm{sac}\ \mathrm{larvae}\kern1em \hfill \end{array}\hfill \\ {}\hfill \begin{array}{c}\hfill 0.0045\cdot {\mathrm{e}}^{0.06931\cdot \overline{T}(t)},\mathrm{for}\ \mathrm{ocean}\ \mathrm{larvae}\kern2.25em \hfill \\ {}\hfill 0.0082\cdot {\mathrm{e}}^{0.04055\cdot \overline{T}(t)},\mathrm{for}\ \mathrm{estuary}\ \mathrm{larvae}\kern1.25em \hfill \end{array}\hfill \end{array}\right. $$

(1)

The grid-wide average daily temperature [$\overline{T}(t)$ was used because these life stages were not spatially located in specific grid cells. The daily temperature was applied for each hour. A running sum of fractional developments was updated each hour, and when the summed value exceeded one, transition to the next life stage occurred. The same functional form was used for all stages, but each was calibrated to generate their target duration (Table 1) when exposed to the grid-wide daily temperatures starting at typical starting dates for each stage. All super-individuals created as eggs on the same day progressed through the life stages and transitioned to early juveniles on the same hour of the same day.

The growth of individual juvenile and adult croaker under normoxia was computed hourly using a bioenergetics model, with the temperature and chlorophyll-a concentration in their occupied cell. The bioenergetics model followed the Wisconsin formulation (Hanson et al. 1997):

$$ W\left( t+1\right)= W(t)+\left[ P-\kern-0.em value\cdot {C}_{\max }-\left( R+ SDA+ Eg+ Ex\right)\right]\cdot W(t)\cdot \frac{\rho_{\mathrm{p}}}{\rho_{\mathrm{f}}}\cdot \left(\frac{1}{24}\right) $$

(2)

where P-value is the fraction of maximum consumption (C _max) realized, R is the respiration, SDA is the specific dynamic action, Eg is the egestion, Ex is the excretion, and ρ _p and ρ _f are the energy densities (J g⁻¹) of consumed prey and of croaker. Maximum consumption and basal respiration rate were computed based on allometric functions of weight and of temperature. Egestion (Eg) was computed as a fraction of consumption, and SDA and excretion (Ex) were computed as fractions of consumption minus egestion. The final parameter values are shown in Table 2, and the detailed equations are in ESM-4.

Table 2 Parameter values used in the bioenergetics submodel for <9.0, 9.0–62.0, and >62 g Atlantic croaker

P-value was computed each hour from the average daily chlorophyll-a concentration Chl in each cell (denoted by column i and row j):

$$ P-{value}_{i, j}=0.8415+0.020\cdot \ln \left[\frac{Chl_{i, j}}{{\left(52-{Chl}_{i, j}\right)}^{3.83}}\right] $$

(3)

Each hour, a P-value was determined from the chlorophyll-a concentration in the cell, and daily growth in weight was computed and divided by 24 to obtain the change in weight for that hour.

TL (mm) was updated from weight (g) each hour by back-calculating from the length-weight relationship reported by Barger (1985):

$$ W=5.302\cdot {10}^{-6}\cdot {TL}^{3.134} $$

(4)

Individuals could lose weight but not length; maximum weight loss per hour was constrained to no more than 1% of their current weight. Weight loss rarely occurred because the P-values generated using the chlorophyll-a concentrations almost always resulted in a positive growth rate and individuals moved every hour frequently to new cells. Length was only updated if the individual was at the weight expected from its length, given the above length-weight relationship (Eq. 4).

Mortality

Background mortality and starvation-induced mortality, in addition to direct mortality from hypoxia exposure, were represented in the model. Background mortality rates (M) were specified by life stage and specific to Louisiana and Texas estuaries (Table 1). Murphy (2006) modified the mortality rates reported in Diamond et al. (1999, 2000) based on long-term field data to separate mortality rates for estuary larvae and juveniles by Texas versus Louisiana estuaries. Individuals west of 94° longitude (columns 1–200) were assigned Texas rates, and individuals east of 94° longitude (columns 201–800) were assigned Louisiana rates (Fig. 1). All mortality rates were converted to hourly rates for use in the simulations. Starvation occurred when an individual’s weight dropped below 50% of its expected weight based on its length. When a super-individual died due to starvation, the individual with all of its worth was removed from the simulation.

Background mortality of the late juvenile stage was density-dependent (Fig. 5). The juvenile stage is the likely stage for density dependence based on general theory of fish population dynamics (Rothschild 1986; Myers and Cadigan 1993; Cowan et al. 2000; Rose et al. 2001; Houde 2008). Further, Murphy (2006) showed a positive relationship between apparent loss rates (slope of log-transformed catch versus time) and average abundance of late juvenile croaker in long-term monitoring data from Texas, North Carolina, and Virginia estuaries. There is also evidence for density dependence during the juvenile stage in croaker from other systems (Eby et al. 2005) and from related species (e.g., juvenile spot, Craig et al. 2007). Each hour, abundance (sum of worths) of late juveniles in each cell (population-level abundance) was divided by a fixed value to obtain the standardized abundance, which was then used to determine the multiplier (Fig. 5). The multiplier was applied to the mortality rate for that individual (M) for that hour, which acted to reduce the worth of the super-individual. The specified abundance used to standardize late juvenile abundance was determined during calibration. The realism of the density-dependent effect on hourly mortality was assessed by generating spawner-recruit results from the model and comparing them to reported stock-recruitment relationships (ESM-5).

Fig. 5

Relationship between standardized abundance and the multiplier of daily mortality rate used to impose density-dependent mortality on late juvenile stage Atlantic croaker. Standardized abundance was the sum of the worths of all late juvenile super-individuals in a cell divided by 1803. The value of 1803 was determined by calibration

Reproduction

On September 1 of each year, all individuals were evaluated for maturity based on their length:

$$ {P}_{\mathrm{M}}=\frac{1}{1+1.572\cdot {10}^8\cdot {\mathrm{e}}^{-0.1156\cdot TL}} $$

(5)

Equation 5 results in 70% mature at the typical length of age 1 (about 180 mm) and complete maturity by age 2 (Hansen 1969; Barbieri et al. 1994; Diamond et al. 1999). For each individual, if a randomly generated value between 0 and 1 was less than P _M, then that individual was considered mature. All mature individuals on September 1 were then assigned a degree-days value from a triangular probability distribution with minimum, mode, and maximum values (20, 200, and 450) that determined when they would spawn within the year. Maturity and the assigned degree-days value were kept by individuals for the remainder of their life. Every mature individual spawned, but their egg production was multiplied by 0.5 to account for a 1:1 male to female sex ratio.

Day of spawning for each individual was determined by its assigned degree-days and its location and movements on the grid. Degree-days were computed each day for each mature individual starting on September 1 by summing the difference between the temperature in the occupied cell and a specified temperature threshold (17 °C) below which degree days were not accumulated. When an individual accumulated its assigned degree-days, it initiated spawning on that day. Each individual released 12 batches of eggs, one batch every 3 days over a consecutive 34-day period. Assuming that batches can be released every 3–7 days (Waggy et al. 2006), 12 batches would require an individual spawn over 2–3 months, which is consistent with Barbieri et al. (1994) for croaker in the Chesapeake Bay. Eggs per batch for each of the 12 batches were derived from a relationship between weight (W, g) and potential annual fecundity (F, eggs) reported by Sheridan et al. (1984):

$$ F=-3248+1179\cdot W $$

(6)

Each batch consisted of F/12 eggs multiplied by the worth of the spawning individual. Annual fecundity was recomputed using the weight on each day of a batch release during the 34 days. The total annual number of eggs spawned by each individual was the sum of the actual number of eggs spawned over all of its batches.

Movement

Hourly movement was modeled using a kinesis algorithm (Benhamou and Bovet 1989; Humston et al. 2004), unless interrupted by exposure to low DO that triggered avoidance. The position of each juvenile and adult individual was tracked in x-y continuous space (i.e., x and y distances in meters from the lower left corner of the grid) and in discrete grid space (i.e., cell number denoted by column i and row j). Kinesis uses the velocities of the individual in each of the x and y directions as the sum of two components: an inertial component based on the velocity in the previous hour (I, m h⁻¹) and a randomly generated velocity (D, m h⁻¹):

$$ \begin{array}{l} x\left( t+1\right)= x(t)+{I}_{\mathrm{x}}\cdot \varDelta t+{D}_{\mathrm{x}}\cdot \Delta t\\ {} y\left( t+1\right)= y(t)+{I}_{\mathrm{y}}\cdot \varDelta t+{D}_{\mathrm{y}}\cdot \Delta t\end{array} $$

(7)

where Δt is the time step (i.e., 1 h). I and D are shown with x and y subscripts to note that separate values are computed for each dimension. The inertial component dominates as the temperature in the occupied cell approaches the optimal temperature (T _opt), while movement becomes more random under suboptimal temperature conditions. This approach assumes that individuals do not have knowledge of their surrounding environment, but can evaluate conditions experienced in the occupied cell relative to some optimum and recall their movement from the previous time step (Watkins and Rose 2013).

The I and D functions included terms that determined the weighting of the inertial and random components based on how close water temperature was to optimal conditions:

$$ \begin{array}{l} I= v\left( t-1\right)\cdot {h}_1\cdot \left[{\mathrm{e}}^{-0.5\cdot {\left[\left( T-{T}_{\mathrm{opt}}\right)/{\sigma}_{\mathrm{T}}\right]}^2}\right]\\ {} D=\varepsilon \cdot \left[1-{h}_2\cdot \left({\mathrm{e}}^{-0.5\cdot {\left[\left( T-{T}_{\mathrm{opt}}\right)/{\sigma}_{\mathrm{T}}\right]}^2}\right)\right]\end{array} $$

(8)

where v(t − 1) is the velocity from the previous time step, T is water temperature in the occupied cell, T _opt is the specified optimal temperature, and ε is the random swim speed computed as a random deviate from a normal distribution with mean equal to distance swum in 1 h (km) at a swimming speed of 3 BL s⁻¹ (i.e., 3·TL · 10⁻⁶ ∙ 3600 · Δt) and SD equal to one half of that distance. The two height parameters (h ₁ and h ₂) and the optimal (T _opt) and variance (σ _T) temperature parameters in Eq. 8 were the same for early juveniles, late juveniles, and adults, but values were specific to certain time periods and were determined by calibration (Table 3). The generated random distance had an equal probability of being positive or negative. Once an individual’s new continuous x and y locations were determined, the individual’s cell location was then updated. Early juveniles could only move to cells with depths less than 5 m, late juveniles to cells with depths less than 20 m, and adults to cells with depths greater than 5 m.

Table 3 Description and values of parameters used in the kinesis movement model

Low DO avoidance behavior was simulated using a threshold DO level that induced movement with a restricted area search (Watkins and Rose 2013). Individuals that entered a cell due to kinesis movement with a DO value less than 2.0 mg l⁻¹ were assumed to go that cell and then immediately initiate horizontal avoidance behavior (i.e., they moved again before any exposure occurred). We used a threshold value of 2.0 mg l⁻¹ to trigger avoidance behavior because croaker in the NWGOM avoid DO concentrations of 1.2–2.7 mg l⁻¹ (Craig 2012). In the hour that avoidance was triggered, individuals evaluated DO concentrations and temperatures in a neighborhood of cells centered on their current cell and based on their length (5 × 5 for 96 to 111 mm, 7 × 7 for 111 to 140 mm, 9 × 9 for >140 mm). Individuals moved to the center of the cell within their neighborhood that had DO >2.0 mg l⁻¹ and whose temperature was closest to their T _opt. If DO was less than 2.0 mg l⁻¹ in all cells, then the individual moved to the cell within the same neighborhood that had the highest DO, regardless of temperature.

Exposure and Effects of Hypoxia

DO affected hourly growth, hourly mortality, and annual reproduction (fecundity). Individuals were exposed to time-varying DO values as the DO concentration in cells changed hourly during the 7-day setup period and the end of hypoxia and also as an individual moved from cell to cell every hour. Three exposure effect submodels were used that related reduced growth, increased mortality, and reduced annual fecundity to exposure to time-varying DO concentrations (Neilan and Rose 2014). Each hour, the immediate effect of low DO for that hour of exposure was computed for growth, reproduction, and survival used the same general formulation:

$$ f=\left\{\begin{array}{c}\hfill 1.0-\alpha \frac{{\left\{{DO}_{\mathrm{NE}}- DO(t)\right\}}^2}{{\left\{{DO}_{\mathrm{NE}}- DO(t)\right\}}^2+{\beta}^2}\kern0.3em \mathrm{if}\kern0.2em DO(t)\kern-0.1em <\kern-0.1em {DO}_{\mathrm{NE}}\hfill \\ {}\hfill 1.0\kern10.9em \mathrm{if}\kern0.2em DO(t)\ge {DO}_{\mathrm{NE}}\hfill \end{array}\right. $$

(9)

where DO(t) is the DO concentration in its cell at hour t and DO _NE is the DO threshold below which an effect occurs, and α and β are non-negative constants. The parameters DO _NE, α, and β were estimated separately for the growth (f _G), reproduction (f _R), and survival (f _S) exposure effect submodels using published laboratory experiments on spot and croaker (Table 4, ESM-6). The estimated no-effect thresholds (DO _NE) were 3.35 mg l⁻¹ for growth, 4.40 for reproduction, and 1.35 for mortality.

Table 4 Parameter values used in the exposure effect submodels

The values of f from Eq. 9 were then used to determine hourly reductions in growth and survival (V _G and V _S), and accumulated and applied once to reduce annual fecundity (V _R). For survival, V _S was simply set to f _S each hour and the worth of an individual was updated using the mortality rate (M) and V _S: worth(t + 1) = worth(t) ∙ e^−M ∙ V _s. For growth, V _G was updated each hour using f _G but with an additional adjustment for repair (sensu Mancini 1983): V _G(t + 1) = min(f _G, V _G(t) + 0.21). V _G immediately decreased as DO decreased (V _G was set to f _G each hour), and was limited to increasing by 0.21 per hour as DO increased. V _G was the reduction in instantaneous growth rate and was used to adjust the finite growth rate predicted from Eq. 2. V _G and V _S were reset to one at the beginning of each year (September 1). For reproduction, V _R was computed hourly as the average of the hourly f _R values over a 10-week period (June 23 to August 31) and then the fecundity of all batches (F in Eq. 6) was multiplied by this final V _R value. V _R was reset on June 1 to allow for summer exposure to affect fecundity during the subsequent fall.

The vitality variables were only imposed on late juveniles, age 1 adults, and age 2 adults. Early juveniles were restricted to the nearshore habitat (<5-m depth) and thus had very limited exposure to hypoxia on the shelf that we therefore ignored. Late juveniles were restricted to less than 20-m depth that overlapped with the hypoxia area. Based on GOM and mid-Atlantic Bight monitoring data, age 3 and older adult croaker are generally farther offshore than younger adults and juveniles (Jon Hare, pers. communication), and so probably only experience minimum exposure to low DO.

Initial Conditions

All model simulations began with 20,000 super-individuals per age class. All individuals within an age class were assigned a weight and length based on the mean length at age relationship (Table 1) and were randomly placed on the grid. The beginning worth of each super-individual was set to a worth specific to its age class, which was based on a specified total worth of entering age 1 individuals (1.5 million) that was then decreased for older ages using the adult mortality rate of 0.0012 day⁻¹. Initial worths by age ranged from 5.92 × 10⁶ for age 1 individuals to 4.28 × 10⁵ for age 7 individuals. The first 40 years of all simulations were ignored to minimize any effects of arbitrary initial conditions.

Design of Simulations

Calibration

Calibration was performed in a series of steps. First, the development rate functions were adjusted using grid-wide average daily temperatures until realistic stage durations of egg, yolk-sac larva, ocean larva, and estuary larva were obtained (target values in Table 1). As part of developing a life table for croaker, Diamond et al. (1999, 2000) used combinations of results reported in laboratory and field data to directly derive stage durations or used entering and exiting lengths, which, when combined with growth rates, enabled indirect estimation of durations. Second, bioenergetics parameters were adjusted using the time series of average daily temperatures and assumed typical consumption rates (P-values) until average stage durations of early and late juveniles and mean length at age of adults were within 5% of target values (Table 1). Third, optimal temperatures and σ _T values for movement were calibrated by following 1000 super-individuals over 8 years using the full model (i.e., two-dimensional grid) but without growth and mortality (i.e., individuals followed as moving particles). Fourth, the full model was run with all of the calibrated parameter values for 140 years, and final adjustments were made to ensure that the criteria met with off-grid calibration were still met in the full model. Finally, the normalizing abundance for density-dependent mortality of late juveniles was determined so a stable population of 1.5 million new age 1 individuals (i.e., summed worths on September 1 of their first year) was obtained, which corresponded to a total adult (entering age 2 and older on September 1) population abundance of about 10 million. Because we simulated an arbitrary population size benchmarked to its own normalizing abundance for density dependence, all comparisons of hypoxia effects were relative to the baseline (normoxic) and other hypoxia simulations.

Hypoxia Scenarios

Four scenarios of hypoxic conditions were performed using the calibrated model. Three scenarios consisted of single simulation each and were the mild, intermediate, or severe hypoxia, each repeated every year. The fourth scenario consisted of a set of 12 simulations that accounted for inter-annual variability in the severity of hypoxia. Twelve randomly generated time series sequences of mild, intermediate, and severe hypoxia years. In the time series scenario, there was a 0.18, 0.52, and 0.30 probability of each year being mild, intermediate, or severe. The probability of the severity of hypoxia was estimated by classifying each observed July area of hypoxia (areas noted in Fig. 4) as either mild (<10,000 km²), intermediate (10,000–20,000 km²), or severe (>20,000 km²) based on mapping surveys from 1985 to 2010 (Obenour et al. 2013).

Model Outputs

For all simulations, croaker population dynamics were simulated for 140 years assuming baseline conditions for the first 40 years, followed by hypoxic conditions imposed beginning in year 41. All model outputs presented are defined in Table 5. We plotted annual abundance of age 2 and older individuals over time for all simulations. Results of model calibration are shown for the final, full model simulation only. The outputs for calibration evaluation consisted of mean stage durations, monthly spatial distributions by life stage, mean lengths at age, and mean age 2 and older abundance over time.

Table 5 Model output variables and how they were calculated from the super-individuals

Aspects of the severe hypoxia applied every year scenario were examined in more detail because while unrealistic, the repetition of severe years allowed for clear model responses, including lagged effects into future years, to emerge. We used year 140 as representative of the hypoxia effects having reached steady state at the population level, and show spatial distributions, percent of individuals exposed to low DO averaged effects (V _S, V _G, and V _R) of the exposed individuals, mean length at age (growth effects), daily mortality, and reproduction information (percent of age 1 mature, averaged eggs per batch per individual and per gram). Finally, we examined a single replicate of the time series hypoxia simulations and reported a subset of the outputs reported for the severe scenario.

Results

Calibration and Baseline

The final baseline simulation showed a stable population abundance of age 2 and older individuals (top line Fig. 6). The average abundance during years 101 to 140 was 10 million and annual egg production averaged 2.19 trillion. The population stabilized as a result of the calibration and also due to the density-dependent mortality of the late juveniles. Steady-state (but model-generated) recruitment was simulated to help isolate the effects of hypoxia; in nature, croaker recruitment (late summer, 190–200 mm) varies with a year-to-year coefficient of variation (mean/SD) of about 0.5 to 1 for Louisiana coastal waters (Rose et al. 2017b).

Fig. 6

Average age 2 and older abundance of Atlantic croaker on September 1 of each year for baseline (normoxic), mild, intermediate, and severe hypoxia simulations

Simulated movement approximated the reported inshore-offshore seasonal migration patterns of Atlantic croaker in the Gulf of Mexico (ESM-7). Early juveniles were in the estuaries and nearshore areas (<5-m depth) of the grid from January through May, and late juveniles were distributed in deeper nearshore areas (<20-m depth) during April to October. Based on temperature, age 1 adults moved onto the shelf by October, spawning occurred in November, and then adults dispersed more widely to the mid and outer regions of the shelf by May, after which adults moved more inshore. Similar seasonal movements of adult croaker dispersed in winter and spring and more inshore in summer were reported by Moore et al. (1970), Hansen (1969), and Gutherz (1976), who also attributed it to changes in bottom temperature.

Average stage durations and length at age in the baseline simulation were comparable to literature values (Table 1). Average stage duration for years 101–140 in the baseline simulation was 2 days for eggs, 3 days for yolk-sac larvae, 45 days for ocean larvae, 54 days for estuary larvae, 75 days for early juveniles, and 168 days for late juveniles (close to target values in Table 1). In the full baseline model simulation, the bioenergetics submodel (Eq. 2), with the calibrated chlorophyll-a adjustment to consumption, resulted in mean lengths at age that when averaged over years 101–140 were within 5% of the reported values (Table 1).

Spawning peaked around October 1 and ended by the end of March in the calibrated baseline simulation. Approximately 71% of age 1 individuals (just had their first birthday) were mature on September 1 of each year, and all individuals were mature by age 2. Age 2 and age 3 individuals accounted for more than 40% of total annual egg production (Table 6). Average eggs per batch per gram of fish (EPG) were lowest for age 1, increased through age 3, and leveled off by age 4. Average eggs per batch per individual (EPI) were very low for age 1 (6793) because not all age 1 individuals were mature (immature individuals were still included in the average). EPI increased steadily with age for age 2 through age 7 (20,446 to 63,572) because all individuals were mature and fecundity increased with body weight.

Table 6 Averaged percent contribution of each age to total annual egg production, eggs per batch per gram (EPG), and eggs per batch per individual (EPI) in the baseline and severe simulations

Mild, Intermediate, and Severe Hypoxia Scenarios

Repeated exposure to low DO year after year resulted in small declines in average population abundance for the mild and intermediate hypoxia scenarios and a larger decline for the severe hypoxia scenario. The average abundance of age 2 and older croaker abundance for years 101–140 was 97% of baseline for the mild hypoxia scenario, 90% of baseline for the intermediate hypoxia, and 81% of baseline for the severe hypoxia scenario (Fig. 6).

Details of Severe Hypoxia Scenario

Exposure

Even under the severe hypoxia scenario, only a small percentage of individuals in the population were exposed to very low DO (DO <1.35 mg l⁻¹) in any given hour, but many individuals were exposed to nonlethal and moderately low DO (1.35 to 4.4 mg l⁻¹) for at least 1 h at some point during the summer. Hypoxia caused displacement from areas of preferred temperature, as abundance was typically highest in these regions under baseline conditions (Fig. 7). Avoidance resulted in the percentage of individuals exposed to DO <1.35 mg l⁻¹ (lethal) being very small and only within the first few days of hypoxia setup (rare black bars in June in Fig. 8). Individuals were effective at avoidance that was triggered when DO was less than 2.0 mg l⁻¹. Exposure to sublethal concentrations showed a peak of about 15% during hypoxia setup (Fig. 8a), which was a combination of age 0 individuals (Fig. 8b) and ages 1 and 2 being exposed (Fig. 8c). Once individuals either died or avoided the initial few days of the setup of hypoxia, exposure of about 5 to 10% to 1.35 to 3.35 mg l^-1 (growth and reproduction effects) and 3.35 to 4.40 mg l^-1 (reproduction effects only) persisted throughout the remainder of the hypoxic summer period (Fig. 8a). The majority of individuals exposed were age 1 and age 2 individuals (Fig. 8c) because age 0 individuals were restricted to shallower waters.

Fig. 7

Mid-monthly snapshots from model year 140 showing the spatial distribution of age 2 croaker in the baseline (normoxic) scenario in a June, c July, and e August and under the severe hypoxia scenario in b June, d July, and f August. Colored pixels represent the distribution of age 2 croaker abundance (ln-transformed) based on the integration of the model 1 × 1-km² grid cells to a 10 × 10-km² grid for mapping

Fig. 8

Stacked area plots showing the percentage of croaker exposed to 3.35 ≤ DO < 4.4 mg l⁻¹ (white), 1.35 ≤ DO < 3.35 mg l⁻¹ (gray), and DO <1.35 mg l⁻¹ (black) each hour in model year 140 in the severe hypoxia scenario for a ages 0 to 2, b age 0 only, and c ages 1 and 2 only

While the percentage of individuals that were exposed to hypoxia in any given hour was low, many individuals were exposed at some point over the summer. For years 101–140, the average percentage of surviving individuals on August 31 that had experienced at least 1 h of DO <4.4 mg l⁻¹ during that summer was 20% for age 0, 58% for age 1, and 55% for age 2.

Effects on Exposed Individuals

While only a small percentage of individuals in the population were exposed to hypoxia in any given hour, those that were exposed showed significant short-term reductions in their hourly survival and growth, as well as accumulated effects over the summer season that impaired reproduction (Fig. 9). On average, the relatively few individuals exposed to DO <1.35 mg l⁻¹ for the few days during hypoxia setup (Fig. 8a) showed reduced survival (V _S < 0.75 briefly in Fig. 9a). Individuals exposed to 1.35 to 3.35 mg l⁻¹ DO on each hour (Fig. 9b) showed an initial relatively large reduction in growth during the hypoxia setup and then a consistent 20–25% reduction (V _G = 0.75–0.80) for remainder of the summer as individuals avoided lethal concentrations but were continued to be exposed to sublethal concentrations. The effect of low DO exposure on reproduction (V _R) did not start until June 23 (i.e., 10 weeks prior to the September 1 spawning period). The average of V _R culminated in a 20% reduction in average batch fecundity of exposed individuals in the fall (Fig. 9b, c).

Fig. 9

Hourly mean effects (V _S = survival, V _g = growth, V _r = reproduction) from June 1 to August 31 for individuals exposed to a DO <1.35 mg l⁻¹, b 1.35 ≤ DO < 3.35 mg l⁻¹, and c 3.35 ≤ DO < 4.4 mg l⁻¹ in model year 140 in the severe hypoxia scenario

Population Responses

The effects of severe hypoxia on growth of individual croaker caused little population-level response, while small and consistent reductions in survival and fecundity of exposed individuals that accumulated year after year resulting in the 19% reduction in the long-term average abundance of age 2 and older croaker (Fig. 6). While many individuals were exposed and those exposed showed lower growth (V _G in Fig. 9), few individuals were exposed for sufficiently long periods of time to affect their length (and weight) at age. Mean length at age, and therefore percentage of age 1 fish that were mature, differed from baseline by less than 1%.

In contrast, direct mortality due to hypoxia removed a small percentage of individuals and reduced fecundity lowered the number of eggs per individual of spawners that, when combined, resulted in the nearly 20% reduction at the population level. Average daily mortality rate over years 101–140 for age 1 adults and age 2 adults, and this expressed as the annual fraction surviving, increased by about 1% under the severe hypoxia scenario. A 0.5% reduction in annual survival compounded over 40 years results in cumulative reduction of 20%. The change in age 0 mortality was negligible because of low or no exposure of some life stages and lower late juveniles leading to density-dependent decreases in mortality rate. Survival of age 3 and older individuals was not affected by DO conditions.

Reduced reproduction of the exposed individuals led to reduced EPG and EPI at the population level (Table 6). EPG decreased by about 5% from the average baseline values for age 2 (97 to 91.4) and age 3 (97.5 to 92.3) individuals. EPI decreased by about 8% from the average baseline values for age 2 (20,446 to 19,064) and age 3 (33,229 to 30,672). Total annual egg production during years 101–140 was, on average, 22% lower (1.708 × 10¹² versus 2.189 × 10¹²) under severe hypoxia.

Density-dependent mortality in the late juvenile stage (Fig. 5) offset some of the increased mortality and reduced fecundity from exposure to hypoxia. The population declined slowly each year as late juvenile mortality gradually decreased from 0.0200 day⁻¹ in year 40 to an average rate of 0.0195 day⁻¹ during years 101–140. These changes in mortality rate resulted in survival of the late juvenile stage increasing from 3.6% under baseline to 3.9% after years of exposure to severe hypoxia. However, the increased survival of late juveniles could only partially offset the hypoxia-induced increased mortality and reduced fecundity of age 1 and age 2 individuals.

Time Series Scenario

When hypoxia was simulated as a random time series of mild, intermediate, and severe years in proportion to their historical occurrence, the average abundance of age 2 and older croaker abundance for years 101–140 ranged from 88 to 90% of baseline or a reduction of 10–12% (Fig. 10). The relatively small amount of variation among replicates in the percentage decline compared to baseline was because the replicate simulations only differed by the random ordering of the mild, intermediate, and severe hypoxia years.

Fig. 10

Annual abundance of age 2 and older croaker in the 12 time series scenario replicates (the dashed line is the average over the replicate runs). The baseline (black line) age 2 and older total abundance is included for reference

Reproduction showed a clear decrease due to hypoxia, while annual survival showed a small but persistent response and growth showed little change from baseline. Total annual egg production averaged 2.19 trillion under the baseline scenario and 1.88 trillion under time series scenario, a 14% decline. V _R values on September 1 (after summer exposure) for all mature age 1 to 3 individuals (i.e., population level) averaged about 0.97. However, 41% of these mature age 1 to 3 individuals were exposed for at least 1 h, and their final averaged V _R value was 0.91. This exposure leads to an EPG for all age 2 croaker of 90.7 compared to 97.0 under baseline (a 6% decline) and a similar decrease for age 3. The decline in EPG was also reflected in EPI (19,023 versus 20,446 for age 2 and 30,802 versus 33,229 for age 3) between the baseline and time series scenarios. Daily mortality rates of age 1 and age 2 croaker (0.0012 day⁻¹) were seemingly unaffected, but age 1 and age 2 annual survival fractions, which extrapolate daily rates to 1 year, were slightly reduced (<1%). Mean lengths at age and fraction of age 1 mature were indistinguishable between the baseline and time series scenarios.

Discussion

Hypoxia Effects

Our strategy was to simulate quasi-realistic environmental conditions that croaker experience in the NWGOM and, by repeating the same conditions every year, allow for clear quantification of any long-term cumulative population-level effects of hypoxia. We used a spatially explicit, individual-based approach to allow for flexible, and hopefully more accurate, simulation of movement, hypoxia avoidance, and exposure to time- and space-varying abiotic (temperature, DO) and biotic (food) conditions. Hypoxia varies in time and space, as does the spatial distribution of croaker, creating a complicated situation of time-dependent exposures that then must be related to growth, mortality, and reproduction effects. The individual-based approach allows for the history of each individual to be followed over time and through space, which was critical for overlaying movement patterns onto the dynamic hypoxia and environmental conditions (see Hope et al. 2011). Furthermore, the reproduction effect required the accumulation of exposures over 10 weeks, which would be difficult to simulate without a Lagrangian-type approach.

Once we simulated exposure, we used a set of three exposure effect submodels to determine effects on the growth, survival, and reproduction of individuals. The exposure effect submodels had a strong empirical basis, as they were first developed from laboratory data and then tested on fluctuating DO treatments with multiple species prior to their use in the croaker population model (Neilan and Rose 2014). We represented low DO effects as multipliers of growth and fecundity because that was sufficient for the purposes of our modeling. One could have developed effects of low DO on the components (e.g., food intake, respiration) of growth (Vaquer-Sunyer and Duarte 2008); however, many laboratory results report growth only and there are no feedbacks of croaker on prey in the model so the simpler approach of directly adjusting growth is sufficient. Similarly, we have some information on the underlying endocrine mechanisms of how low DO reduces fecundity (Thomas and Rahman 2009, 2012) that could be used to derive a submodel (e.g., Murphy et al. 2005), but this added complexity is not needed to simulate the population responses that depend on croaker size (growth) and fecundity.

Our use of the same temperature, chlorophyll-a concentrations (food), and hypoxia conditions (i.e., mild, intermediate, or severe) year after year is clearly not a realistic simulation of the population dynamics of croaker or of hypoxia. However, the approach is ideal for isolating any potential population-level effects of hypoxia, which would then provide a minimum estimate of population effects and also provide information on the types of responses to be expected within the model and therefore easier to detect and quantify as more and more realistic conditions are added to the population model. In a companion paper (Rose et al. 2017a), we explore population responses of croaker under increased variability by using DO output from a hydrodynamics-water quality model, perform sensitivity analysis that varies some key model assumptions and values of inputs, and also perform simulations that also couple the severity of hypoxia to the availability of food for croaker. In a third paper (Rose et al. 2017b), we impose interannual variability on the simulated croaker population response to hypoxia to evaluate the ability of field sampling to detect a known population-level effect.

There are fishery-independent data available for croaker that could provide the basis for a traditional calibration exercise (Janssen and Heuberger 1995) of tuning our model to match features of the interannual variability in the data (e.g., coefficient of variation of recruitment). However, previous attempts were unsuccessful in relating indices of relative abundance and landings of fish species to hypoxia in the Gulf of Mexico (Chesney and Baltz 2001; Chesney et al. 2000) and across many coastal systems (Breitburg et al. 2009a, b). Thus, calibration of our model to mimic observed interannual variability is possible (e.g., add a random variation to egg mortality rate), although the data would already include the hypoxia effects and the results would be simply viewed as random variation around the population response to hypoxia. We opted instead to create (albeit idealistic) conditions to maximize our ability to isolate and understand how hypoxia effects on individuals scale up to population responses. Our approach of a constant climate (climatological environmental conditions) allowed for both short-term and long-term (multi-generational) population responses to be isolated. Our predictions are therefore very limited in terms of true forecasting (Clark et al. 2001) of likely future croaker population abundances, and our analysis is best considered as simulation experiments (Peck 2004).

Under the repeated environmental conditions, 100 years of either mild or intermediate seasonal hypoxia produced small reductions in population abundance. This was because after the initial development of hypoxia, most individuals successfully avoided the relatively small areas of low DO that caused mortality and the costs of brief exposure to mild or intermediate hypoxia were not particularly strong. In contrast, severe hypoxia caused a 19% reduction in long-term population abundance because low DO extended over much of the habitat that croaker typically occupy, and the costs of many individuals to some degree of exposure to sublethal DO concentrations resulted in reduced fecundity and to a lesser extent increased mortality.

The population response to repeated severe hypoxia years was the result of many individuals exposed briefly to low DO, and then the compounding effect over years of the resulting small immediate increases in mortality rate and lowered annual fecundity. In any given hour, only about 3–4% of the late juvenile, age 1, and age 2 individuals were exposed to low DO (<4.0 mg l⁻¹); however, 20–60% of the same individuals were exposed to at least 1 h of low DO each year. The 19% reduction in long-term population abundance under severe hypoxia was due to the accumulation over years of population-level effects occurring in any given single year. Under severe hypoxia, average length-age appeared unchanged and daily mortality rate (and annual survival) of age 1 and age 2 adults slightly reduced, while average eggs per individual of age 2 and age 3 croaker decreased by 6% (Table 6). These reproduction effects of severe hypoxia built up in the model over decades, with population abundance gradually declining for about 50 years before the 19% reduction was fully realized (Fig. 7). The average percentage relative to baseline abundance in the severe hypoxia scenario following the 40-year initialization period was 91% over years 41–60, 83% over years 61–80, 82% over years 81–100, and 81% over years 101–140.

When we combine the results presented here and the results in the companion paper (Rose et al. 2017a), we conclude that the long-term effect of hypoxia on croaker is about 25% decrease in abundance. We based this on the results presented here for the time series simulations that showed an 11% decrease. This 11% decrease used idealized hypoxia and effective avoidance and therefore represents our minimal estimate of the population-level effects. In Rose et al. (2017a), we used more variable DO values and used sensitivity analysis to make individuals less effective at avoidance, and predicted 10 to 30% reductions. Thus, we conclude that our best estimate of the long-term effects is about a 25% reduction in population abundance.

The reason that the time series simulations presented here were a minimal estimate was because of the oversimplified representation of environmental conditions, our ensuring individuals were effective at avoidance, and carefully setting up the exposure effect submodels and density dependence. In addition to using climatological environmental conditions, we also allowed for effective avoidance behavior that resulted in low exposure to hypoxia because croaker are highly mobile and able to detect and avoid low DO (Wannamaker and Rice 2000; Eby and Crowder 2002; Craig 2012). We developed empirically based submodels for low DO effects on growth, survival, and reproduction that were estimated and tested using laboratory experiments and that accounted for the fluctuating nature of DO exposures. Furthermore, we also included density-dependent juvenile mortality that would act to offset some of the decline in population abundance due to low DO. Our density-dependent mortality generated realistic spawner-recruit relationships. We isolated the DO effect, and we made assumptions that erred on the side of low exposure and realistic effects on individuals, which lead to highly idealized conditions being simulated and some sacrificing of realism. We address some of these key assumptions in Rose et al. (2017a).

Avoidance movement is a critical aspect of determining exposure and therefore effects on individuals and population responses. Simulating avoidance movement is important to determining the exposure of fish to many stressors related to water quality (Kane et al. 2005; Rose et al. 2009). There is no agreed-upon approach, but many examples either use a habitat quality index to direct individuals away from their poor-habitat locations (e.g., Sullivan et al. 2003) or allow individuals to evaluate nearby areas for better conditions (e.g., Karim et al. 2003). The avoidance behavior that we simulated included a threshold of 2.0 mg l⁻¹, a relatively large area for searching for tolerable DO, and consideration of optimal temperatures in the movement to alternative locations. All of these acted to determine the exposure to low DO. Craig (2012) analyzed field data for the GOM and determined that the average low DO avoidance threshold for croaker ranged from 1.24 to 2.68 mg l^-1 across 3 years, with a relatively large amount of variation among individuals in any particular year (range CV 12.2–27.8%). Hence, our use of a 2.0 mg l⁻¹ threshold appears reasonable.

The 81-cell restricted area search for avoidance meant that the simulated croaker were capable of fast swimming for at least 1 h. In the simulations, an individual moved first according to kinesis and then due to avoidance movement. The actual average swimming speed realized in simulations for movement to the first cell with kinesis plus the second cell with avoidance was 3.5 BL s⁻¹, with a few extreme values of about 7–10 BL s⁻¹. Videler and Wardle (1991) reported average maximum sustained swimming speeds (sustained for 200 min) of 3–5 BL s⁻¹ for a variety of species; upper values for prolonged swimming speeds (<200 min) and typical burst swimming speeds approach 10 BL s⁻¹. Thus, our simulated swimming for avoidance is relatively fast but feasible.

We also did not include any additional metabolic costs due to exposure or recovery to low DO nor to changes in swimming behavior due to avoidance movement (Pollock et al. 2007). Such increased energy costs could have increased the effects of hypoxia exposure on individuals. The laboratory results on the metabolic costs associated with swimming (Ohlberger et al. 2005) and specifically to exposure and avoidance of hypoxia by fish are complicated (e.g., van Raaij et al. 1996; Farrell et al. 1998; Vagner et al. 2008; Svendsen et al. 2012) and were not easily extrapolated to croaker. Such considerations are possible by adding a metabolic cost submodel.

One indirect effect associated with avoidance of hypoxia in the model was the movement of croaker away from hypoxic areas (shown in Fig. 7 for severe hypoxia) to cells with adequate DO but potentially less optimal temperatures and lower food resources. After individuals avoided hypoxic areas, movement was determined by kinesis based on optimal temperatures. Because bottom temperatures typically decrease with depth and distance from shore during the summer, this resulted in aggregations of croaker around the offshore edge of the hypoxic area where DO was tolerable and temperatures were cooler. A similar shift in distribution to cooler temperatures and aggregation near the edge of the hypoxic zone has been reported in field studies (Craig and Crowder 2005; Craig 2012). When we repeated the severe hypoxia simulation but individuals avoided low DO by moving to cells with the highest DO (i.e., ignored temperature), age 2 and older abundance was reduced by 32% (versus 19%), demonstrating the potential indirect effect of hypoxia of displacement of individuals to suboptimal conditions.

We also ignored avoidance behavior related to vertical movements in the water column based on empirical and 3-D modeling evidence. The hypoxic zone can range from a thin lens just off of the bottom to more typically 20–50% of the water column (Rabalais and Turner 2006). In our simulations, individuals had to swim horizontally to minimize exposure to low DO, while higher DO water may be available a few meters higher in the water column. Hydroacoustic and trawling studies indicate that fish biomass, not resolvable to the species level, is present in the waters immediately overlaying the top of hypoxic layer suggesting vertical avoidance (Hazen et al. 2009; Zhang et al. 2009). Even so, based on an analysis of paired trawls that sampled different portions of the lower water column, Craig (2012) found no evidence that croaker moved vertically to avoid low DO. Using similar movement dynamics as used here, allowing vertical movement potentially reduced exposure to lethal concentrations, depending on error-prone individuals were, but had relatively no effect on the exposure to sublethal concentrations (LaBone 2016). While assuming that a two-dimensional environment for croaker is a reasonable approximation based on field evidence (also see Rose et al. 2017a), vertical movement should be considered for other species that show less fidelity to a demersal lifestyle.

Next Steps

The next step in the population modeling is to address some of the simplifying assumptions in this analysis reported here. In the companion paper (Rose et al. 2017a), we use output from a three-dimensional hydrodynamics-water model to specify dynamic DO concentrations as input to croaker population model and we covary food availability (chlorophyll-a) and hypoxia to simulate their common source of variation from nutrient loadings. We also perform a sensitivity analysis of key model assumptions including those that control the effectiveness of avoidance movement and the role played by growth, mortality, and reproduction in determining population responses.