Estuarine Dispersion from Tidal Trapping: A New Analytical Framework

Abstract

Observations of tidal trapping in a channel connected to large volumes along its perimeter showed that the exchange between them is driven by advection due to tidal flows. Therefore, quantifying the longitudinal dispersion of scalars in the channel that results from tidal trapping was not possible using traditional frameworks, which assume that the exchange is a diffusive process. This study uses the concentration moment method to solve analytically for the dispersion coefficient of a solute in a tidal channel which exchanges advectively with volumes along its edges. This constitutes a new framework for analyzing the longitudinal dispersion that results from tidal trapping in systems such as a branching tidal channel or the breached salt ponds of San Francisco Bay. A comparison of dispersion coefficients from traditional, diffusion-driven frameworks for tidal trapping, the new advective framework derived in the present study, and observations show that the new formulation is best suited to this environment.

Introduction: Estuarine Dispersion and Tidal Trapping

Exchange between an estuary and its perimeter habitat greatly influences transport and concentrations of scalars throughout the system, and depends on complex interactions between bathymetry, tides, winds, and inputs of freshwater. Supplies of salt, sediment, nutrients, and contaminants to fringe sloughs and marshes have immense ecological implications for the viability of those habitats. Likewise, dispersion of scalar concentrations along the main axis of the estuary is impacted by lateral processes (Fischer 1972; Fischer et al. 1979; Geyer et al. 2008) and is pertinent to the estuary's productivity (Jassby et al. 1995), morphology (Ralston and Stacey 2007), and level of contamination (Smith 1976). This study addresses the physical processes driving lateral exchange between an estuary and its perimeter habitat as well as the implications of this exchange for flow and transport dynamics along the estuary.

Dispersion in Estuaries

The decomposition of estuarine dispersion into longitudinal salt fluxes was formally presented by Fischer (1972, 1976; Fischer et al. 1979). The framework separates velocity and salinity into cross-sectional averages (and variations from the average) and tidal averages (and variations around the average), then averages the product of velocity and salinity over the cross-section and tidally, resulting in a quantitative measure of the contribution of a number of mechanisms to the total longitudinal flux. The decomposition is performed on velocity and salinity values measured (or modeled) throughout a cross-section of an estuary over at least one 25-h period, as done, for example, in the San Francisco Bay by Fram (2005), in the Hudson by Lerczak et al. (2006), and in the Columbia by Hughes and Rattray (1980). Each component of the sum represents a physical transport mechanism: advection by river flow, tidal trapping, Stokes drift, baroclinic steady exchange, and shear dispersion.

Fischer et al. (1979) categorize these mechanisms as either advective or dispersive. Advection by river flow, which represents the salt advected through the estuarine cross-section by freshwater inputs to the landward end of the estuary, is the unique advective term in this framework, while the effects of the remaining terms, which are often coupled, are aggregated by a single dispersion coefficient and treated as a cumulative dispersive process. In this treatment, spreading due to all dispersive terms is represented as a dispersion coefficient multiplied by a salinity gradient, and in a steady balance, this term provides an up-estuary salt flux that balances the down-estuary advective flux from river flow.

The four dispersion terms in this decomposition vary temporally, cross-sectionally, or both. The cross-sectionally averaged, tidally varying terms are tidal trapping and Stokes drift. Tidal trapping occurs when the cross-sectionally averaged velocity and salinity signals are out of quadrature; when maximum cross-sectionally averaged salinity is not reached precisely at the end of the flood tide, the velocity and salinity signals are out of phase by an angle other than 90°. Classically defined, tidal trapping results when dead zones, such as side embayments, small channels, and shoals, trap water and salt on the flood, releasing them on the ebb out of phase with the primary salinity front in the main channel. Traditional treatment of tidal trapping, as well as a new framework for quantifying its effects, will be explored in detail in subsequent sections. Stokes drift is especially important when the tidal range is large compared with the average depth, and arises when the cross-sectionally averaged velocity and the cross-sectional area of the flow are out of quadrature, yielding a non-zero net transport of water. The inertia of a tidal flow can delay slack velocity relative to high or low water as the tidal pressure gradient changes sign. The result is that the cross-sectional area of the flow on floods is greater than ebbs, producing a tidally averaged net landward flux of water. This flux sets up a complimentary barotropic pressure gradient directed down-estuary that balances the net transport of water.

The steady, cross-sectionally variable velocity and salinity fields interact to produce the baroclinic steady exchange term in the salt flux decomposition. This steady flux results from the residual flow and salinity fields and represents the tidally averaged density forcing through the estuary. All remaining variability is encompassed by the shear dispersion term, which is variable in both time and space. This term accounts for an oscillatory, cross-sectionally varying velocity profile acting on the salinity field. Random phenomena that act on time scales shorter than the tidal period are captured by this term, such as rapid changes in wind forcing. In addition, other dispersive mechanisms interact with the shear dispersion term to produce a highly coupled system of fluxes.

The Objective of this Study

Our study explores the salinity dynamics of a tidal slough that exchanges with volumes along its perimeter. This exchange, which is tidally forced, is dynamically equivalent to a branching channel, and the analysis presented here is suitable for both environments. The perimeter volumes (or channel branches), which temporarily retain water and the constituents it carries, alter the phasing of flows and scalar concentrations in the slough's main channel. Longitudinal dispersion in the slough is affected by this exchange largely through the mechanism of tidal trapping. While dispersion due to tidal trapping has been estimated in other studies, most notably by Okubo (1973), for traps that exchange diffusively with the main flow, we have found that the classical formulation misrepresents exchange driven by tidal advection. We propose a distinct formulation to quantify the effects of changes in phasing resulting from perimeter exchange on estuarine dispersion, and we suggest a dimensionless number that helps discern the suitability of these formulations.

In order to explore this new framework, we first summarize the physics that dominate an estuary's exchange with its perimeter and the resulting shifts in phasing of velocities and scalar concentrations. The following section addresses the effects of spatially varying frictional forcing, the interaction of the pressure gradient, velocity, and salinity signals, and the ensuing tidal trapping flux. Subsequently, we present field observations of these phenomena and the ways in which the existing treatment of tidal trapping misrepresents the physics of exchange and dispersion for the present environment. Finally, we derive an alternative formulation for estuarine dispersion driven by perimeter exchange and changes in phasing, and we explore its implications.

The Physics of Tidal Trapping

The phasing of a flow's velocity relative to tidal stage depends on the regional tidal dynamics and the retarding force exerted on the flow by friction. As the tides interact with a basin, the degree of reflection of the tidal wave determines whether the tides are standing waves or progressive waves. Inviscid analysis shows that in standing waves, the velocity and stage are exactly 90° out of phase; in progressive waves, velocity and stage are in phase.

Locally, the effects of friction become important in establishing variability in the phasing of flows. Regions that experience relatively high levels of friction, such as those that are shallow, vegetated, or have an otherwise rough substrate, lose a considerable amount of momentum, and tidal velocities in these regions respond quickly to changes in the barotropic pressure gradient. In comparison, deeper areas exert less friction on the flow, and after reversing, the tidal pressure gradient must increase until it is able to overcome the flow's inertia before changing the flow direction. Equation 1 shows the along-channel balance of momentum from unsteadiness, the barotropic pressure gradient, and the vertical divergence of the Reynolds stress.

$$ \frac{{\partial u}}{{\partial t}} = - g\frac{{\partial \eta }}{{\partial x}} + \frac{\partial }{{\partial z}}\left( {{\nu_t}\frac{{\partial u}}{{\partial z}}} \right) $$

(1)

In the shallow regions, unsteadiness is small, and the along-channel velocity (u) is 90° out of phase with the pressure gradient. In the deep regions, unsteadiness is important, and the pressure gradient and velocity signals are no longer 90° out of phase; in these regions, the velocity's response to tidal forcing is delayed, so that the pressure gradient lags the velocity by less than 90°. The time between a change in forcing and a corresponding change in flow is referred to as the phase lag.

Spatial variation in the amount of friction exerted on a tidal flow will lead to variations in the phasing of the local velocity relative to tidal stage and can cause the cross-sectionally averaged velocity and salinity time series to be out of quadrature. We describe this process using an example of a tidal channel lined by relatively shallow shoals. The channel's response to the changing tidal pressure gradient lags that of the shoals, such that during the flood-to-ebb transition, the main channel continues to carry high-salinity water up-estuary, while the flow over the shoals reverses and freshens. A lateral salinity gradient is thus created. Mixing processes act on this gradient to homogenize the cross-section, which reduces the salinity of the flow in the channel. By the time the velocity changes direction to flow down-estuary, the peak salinity has already passed, and the velocity signal lags the salinity by less than 90°. In this example, the departure from quadrature yields a landward tidal trapping flux of salt.

Fischer et al. (1979) illustrate this phenomenon using an example of a branching tidal channel. The flood waters and a theoretical scalar cloud enter both branches, one small and one large, and upon the transition to the ebb, the flow in the small channel reverses before the flow in the large channel. The result is the fraction of the scalar cloud that traveled into the small channel rejoins the main channel prior to the arrival of the fraction of the scalar cloud that traveled into the large channel. The differential phasing that acts on the two stems of a branching channel divides the original scalar cloud into two portions with differing phase lags, causing both a longitudinal spreading of the scalar as well as a lateral gradient of scalar concentration across the main channel.

There is a subtle, but important, distinction, however, between the examples described in the previous two paragraphs. In the first case, two subregions of the channel are out of phase with one another due to differential effects of friction, but those subregions are continuously exchanging with one another in a diffusive manner. In the second case, the merging channels are out of phase, but now that phase shift directly affects the phasing of the exchange between the two channels. The distinction lies in the process that is providing the exchange between the channel and the storage volume: in the first the two are diffusively coupled; in the second they are advectively coupled but with a variable phase shift.

Observations of Tidal Trapping

South Bay Salt Pond Restoration Project in San Francisco Bay

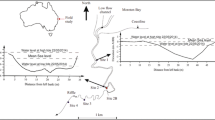
In the South San Francisco Bay, a landscape-scale marsh restoration project under way at the time of this study provided an opportunity to investigate an estuary's exchange with volumes along its perimeter—in this case, breached ponds formerly used for salt production. We conducted field experiments to examine the physics of tidal trapping and estuarine dispersion in a tidal slough connected to former salt ponds through levee breaches. The Island Ponds are a cluster of three adjacent former salt ponds, located in the southeasternmost reach of South San Francisco Bay, as shown in Fig. 1. They are bounded by Coyote Creek on the south and Mud Slough on the north. The levees on their southern border were breached in March 2006, allowing exchange with Coyote Creek for the first time in approximately a century, according to the California Coastal Conservancy, California Department of Fish and Game, and Fish and Wildlife Service, which are the state and federal agencies responsible for the restoration. There were five breaches, two in each of the larger ponds (A21, A19) and one in the smaller pond (A20). The tidal prism within the ponds, which are on average 1 km² in area and 1 m deep, is on the same order as that of the adjacent reach of Coyote Creek: about 10⁶ m³. Coyote Creek is flanked by inter-tidal mudflats to the north and a levee to the south. The total width of the sub- and inter-tidal cross-section is on the order of 150 m. Our study focused on the westernmost breach in Pond A21.

Fig. 1

South San Francisco Bay and the Island Ponds. Breaches, formed in March 2006, allow ponds A19, A20, and A21 to exchange with Coyote Creek

Field Experiments

Field measurements collected in Coyote Creek were used to characterize flow velocity, conductivity, temperature, and depth. We performed a deployment of moored instruments, lasting 2 months (mid-October to mid-December 2006), with sampling frequencies from 3 to 15 min. Four instrument frames were moored in a lateral configuration extending from the thalweg of Coyote Creek, across the channel, through the breach, and into Pond A21 (see Fig. 2). The shallowest stations, inside the pond and inside the breach, were instrumented with two Acoustic Doppler Velocimeters (ADVs, Sontek and Nortek), which measure velocities at a point, with sampling volumes at 0.5 and 1.5 m above the bed. Conductivity–Temperature–Depth (CTD, RBR and Seabird) sensors outfitted with Optical Backscatter (OBS, D&A) sensors to measure conductivity (salinity), temperature, pressure (depth), and backscatter (suspended sediment concentrations) were placed at the same elevations. Acoustic Doppler Current Profilers (ADCPs, RD Instruments), which measure vertical velocity profiles, were deployed at the deeper channel stations, along with CTD/OBSs pairs near the surface and bottom.

Fig. 2

Coyote Creek and Mooring Locations. Moorings are shown by filled black circles

In addition to the moored instrument deployment, boat-mounted profiling and surveying were conducted in Coyote Creek in the spring and fall of 2006, as well as the summer of 2008, to improve spatial resolution over a limited time period. We measured bathymetry and profiles of velocities using a down-looking ADCP, and a CTD/OBS package was mounted to the boat to measure water properties 25 cm below the surface.

Results of Field Experiments

Our measurements yield a picture of flows along Coyote Creek and lateral exchange with the Island Ponds. The experiment duration and sampling frequencies allowed us to capture diurnal and semidiurnal time scales for tides and wind as well as the fortnightly spring–neap tidal frequency. The dominant tidal frequencies are M2 and K1, resulting in twice daily, unequal tides. Coyote Creek is a macro-tidal slough with an average depth in the main channel of 3 m. Tidal range is 2.5 m on neap tides to just over 3 m on springs.

Velocity and Salinity Ranges

In Coyote Creek, depth-averaged along-channel velocities vary over the range of about ±1 m s⁻¹, while cross-channel flows vary within approximately ±0.1 m s⁻¹ (Fig. 3a). In the westernmost breach of Pond A21, depth-averaged along-breach velocities vary over about −1.3 to 1 m s⁻¹, and cross-breach velocities vary from −0.2 to 0.3 m s⁻¹ (Fig. 3b). Noting that the breach is oriented approximately perpendicularly to the axis of Coyote Creek, we define the sign convention as follows: positive along-channel (or cross-breach) velocities are up-estuary (floods), and negative along-channel velocities are down-estuary (ebbs). Positive cross-channel (or along-breach) velocities are directed into the ponds (roughly northward), and negative cross-channel velocities are directed out of the ponds (roughly southward). Salinities varied from about 12 to 28 during this dry weather period (Fig. 3c). The structure of the salinity signal recorded in the breach is quite distinct from that of the channel, and the details of both are discussed in the following sections.

Fig. 3

Conditions at study site: velocities, salinities, and depths. a Coyote Creek velocities (m s⁻¹): gray line along-channel, black line cross-channel. b Breach velocities (m s⁻¹): gray line along-breach, black line cross-breach. c Salinities: gray line Coyote Creek, black line breach. d Breach salinity - Coyote Creek salinity. e Depths (mab): gray line Coyote Creek, black line breach

Lateral Salinity Gradient and Exchange Dynamics

Our observations show a periodically reversing lateral salinity gradient across Coyote Creek on each ebb tide, shown in Fig. 3d as the difference in salinity. The salinity in the channel is essentially symmetric about high and low water, while the pond effluent has a very different salinity structure from the water that enters on the flood. Early in the ebb tide, the pond effluent has a lower salinity than that recorded in the main axis of Coyote Creek, resulting in a negative lateral gradient (for example, at day 294.5 in Fig. 3c, d). Salinity drops quickly as the flow through the breach responds to the reversal in the barotropic pressure gradient, while the salinity in the main channel is sustained as the up-estuary momentum of the deeper flow must be overcome prior to changing direction. This lateral salinity gradient persists for the first half of the tidal cycle and at its maximum has a value of −5 to −3 salinity units per 100 m. Midway through the ebb tide, when the water surface in the pond has reached the elevation of the inter-tidal interior island, the salinity in the channel continues to drop steadily, but the salinity in the pond effluent plateaus at an intermediate value and diminishes only slightly for the remainder of the ebb tide (e.g., days 294.7–294.9). This produces a lateral salinity gradient of the opposite sign and results in higher salinities at the breach relative to the channel flow, with a typical maximum gradient of 6–7 salinity units per 100 m separation between the two mooring stations. In summary, on every ebb tide, a reversing lateral salinity gradient sets up such that early in the ebb, the channel is more saline than the pond effluent, and later, the channel is fresher. The magnitude of this gradient depends on the spring–neap cycle and the daily inequality, where springs and the greater of the daily ebb tides produce the steepest gradients in salinity, as much as 8 salinity units over 100 m.

Phasing in the Channel and Breach

The high-inertia flow in Coyote Creek is slower to respond to the tidal barotropic pressure gradient than the relatively shallow Island Ponds. A lagged correlation of the entire data record of along-channel velocity in Coyote Creek relative to water depth shows that velocity and depth are out of quadrature (where quadrature indicates a perfect standing wave) by 32 min. The phase lag for an individual tide deviates from this average value in response to the daily inequality as well as the spring–neap tidal forcing. The phase lags in the channel between velocity and depth, and velocity and salinity, for one 24-h period are shown in Fig. 4. The phase lags, in days, are shown by the width of the vertical gray bars, and each lag is labeled on the figure in minutes. On this day, high water occurs before high slack tide by 32 and 50 min, while low water leads low slack tide by 22 min, and later lags it by 5 min (Fig. 4a).

Fig. 4

Phasing in Coyote Creek. a Thin black line depth-averaged along-channel velocity (m s⁻¹). Thick black line departure of water depth from the mean, scaled by the tidal range (h*). Solid gray band phase lag between time of slack water and time of maxima/minima of water depth. b Thin black line depth-averaged along-channel velocity (m s⁻¹). Thick black line departure of channel salinity from the mean, scaled by the salinity range (S*)

The maxima and minima in salinity generally precede slack water by 12 min (Fig. 4b) according to a lagged correlation of the salinity and velocity datasets in Coyote Creek. While 15-min salinity data were used to calculate the phasing, Fig. 4b shows the salinity after the application of a 1-h moving average. The elimination of fine-scale fluctuations in the salinity allows the tidal-scale sinusoidal structure and phasing relative to the velocity to be more readily visible in the figure. The observations are consistent with the tendency for the channel to freshen slightly just before high slack tide, as lower-salinity waters transported by the early ebb in low-momentum regions mix laterally, prior to the change in direction of channel flow. Equivalently, just before low slack tide, channel salinity increases as the early flood transports more saline waters first into low-momentum areas, which then mix across the channel.

The flow through the breach, more heavily influenced by friction than the channel, responds more promptly to the tidal pressure gradient, and a lagged correlation shows that slack water lags maxima and minima in the depth by 8 min. Phasing in the breach during the same 24-h period, shown in Fig. 5a, illustrates a range in the magnitude of lags between velocity and depth, from −4 min (where slack tide leads high water) to 34 min. The flood-to-ebb slack tide lags the maxima in velocity by 12 and 7 min during year-day 295, shown in Fig. 5b.

Fig. 5

Phasing in breach. a Thin black line depth-averaged along-breach velocity (m s⁻¹). Thick black line departure of water depth from the mean, scaled by the tidal range (h*). Solid gray band phase lag between time of slack water and time of maxima/minima of water depth. b Thin black line depth-averaged along-breach velocity (m s⁻¹). Thick black line departure of breach salinity from the mean, scaled by the salinity range (S*)

The salinity signal of water in the breach is distinct from that recorded in the channel (see Fig. 3c) because of differences in phasing as well as mixing that takes place within the salt pond. The tidal asymmetries in the breach salinity preclude the use of a lagged correlation to determine the bulk phasing of salt concentration relative to velocity; however, individual phase lags are shown in Fig. 5b. Flood tide salinities that enter the breach are very similar to those recorded in the channel, and the salinity peak occurs within a few minutes of the flood-to-ebb transition in the breach (Fig. 5b). In contrast, the salinity of the pond effluent recorded on the ebb tide shows the effects of mixing within the pond and reaches a plateau of medium salinity by the time the ebb is half over. At the end of the ebb tide, the salinity does not show an ebb-to-flood transition that is coincident with that of the velocity. This is attributed to the storage of late-ebb pond effluent in the broad mudflats that line the north (near-pond) border of Coyote Creek. The early flood tide washes the pond effluent stored on the mudflats up-estuary (and into the pond), and after this water mass has passed by, it is replaced by fresher channel water, and the salinity drops sharply.

Mixing in the Ponds

To explore the mixing that takes place within the ponds, we consider the time series of breach salinity shown in Fig. 5b. As noted in the previous section, by midway through the ebb tide, the salinity of the pond effluent reaches an intermediate value and decreases only minimally from this value for the rest of the ebb (e.g., year-days 295.2 and 295.7 in Fig. 5b). Our data suggest that this transition to well-mixed pond effluent is dependent on pond bathymetry. The Island Ponds were constructed by excavating levee material from the inner perimeter of each pond, resulting in a “borrow ditch” surrounding an interior island. The borrow ditch is subtidal, approximately 25 m wide and 1.65 m deeper than the interior island plane, which itself is inter-tidal (shown schematically in Fig. 6). The sustained medium salinity that we observe exiting the pond in the later portion of the ebb tide starts when water depth is approximately equal to the elevation of the pond's inner island (Fig. 7). Salinities recorded at the three northernmost stations are identical, representing uniform conditions in the borrow ditch and the breach. This signal is distinct from that of the channel thalweg station, where the salinity drops evenly as the ebb decelerates, mirroring the flood tide. This suggests that mixing within the pond varies over the tidal cycle: trapped late-flood waters exit the pond early in the ebb with only slight dilution, effectively unwinding the flood tide, until only the borrow ditch remains full. At this point, the pond effluent is well-mixed, and the salinity exiting the pond departs significantly from salinities measured in the channel.

Fig. 6

Schematic of channel and trap cross-section. Elevation view of Coyote Creek, breach, borrow ditch, and Pond A21. Inset cross-section location. Bathymetry was measured via boat-mounted ADCP for distances up to 200 m and estimated thereafter

Fig. 7

Transition to well-mixed pond effluent: depth and salinity. Thin black line depth (m), thick black line salinity, vertical lines onset of well-mixed pond outflow, horizontal solid line depth coincident with onset of well-mixed conditions. It should be noted that the onset of well-mixed conditions is constant in spite of the daily inequality and the neap-to-spring transition, both of which are evident in the salinity signal

Longitudinal Dispersion

A bulk estimate of the longitudinal spreading of a constituent may be reached by assuming a steady, 1-dimensional balance of advection by freshwater flow and all other mechanisms (Fischer et al. 1979):

$$ {U_{\rm{fresh}}}S = {K_{\rm{bulk}}}\left( {\partial S/\partial x} \right) $$

(2)

MacCready (1999) cautions that the assumption of steady state is ill-advised when an estuary's response to changes in forcing is slow and significant, and we proceed in this case noting that the tidal channel is very shallow and therefore more likely to have a rapid adjustment time. Additionally, this balance is applied to a long (2-month) dataset during which river input was low. Salinity measured as part of the present study was used as the tracer in order to estimate K _bulk, the aggregate dispersion coefficient. S was calculated as the average salinity over each tidal period, and the longitudinal concentration gradient was determined by the maximum change in salinity per tidal cycle divided by the tidal excursion. The freshwater velocity (U _fresh) was estimated using measurements of daily flow rates of freshwater (US Geological Survey 2006) and the cross-sectional area of Coyote Creek (Fig. 8a). This velocity was interpolated onto the approximately twice-daily tidal time scale used for the concentration (Fig. 8b) and concentration gradient (Fig. 8c). The result of this calculation is an average bulk dispersion coefficient on the order of 500 m² s⁻¹ that varies over the range of 300 to 800 m² s⁻¹ with daily and spring–neap tidal forcing, shown in Fig. 8d. The order of magnitude of this value will be referenced in the discussion as we compare dispersion due to tidal trapping to total dispersion in Coyote Creek.

Fig. 8

Bulk dispersion in Coyote Creek. a Fresh water velocity: Q _f/A, (m s⁻¹). b Average salinity per tidal cycle. c Longitudinal salinity gradient (m⁻¹). d Bulk dispersion coefficient (m² s⁻¹). e Depth-averaged along-channel velocity (m s⁻¹), showing spring–neap variability

Application of Traditional Frameworks

Diffusive Exchange

Classical analytical treatment of phase lags and the resulting tidal trapping flux has been directed toward quantifying an effective mass diffusivity coefficient to predict the effect of tidal trapping on longitudinal spreading. Okubo (1973) constructed a model of tidal trapping which predicts longitudinal dispersion in waterways with shoreline irregularities in both a uniform and oscillating flow. In this seminal work, Okubo described these irregularities as temporary traps of water and associated scalars. Okubo represented the exchange between the shoreline irregularity and the main channel as a source/sink term in a 1-dimensional advection–diffusion equation, which is solved for the variance of the contaminant concentration as a function of time. The model, intended to elucidate the apparent diffusivity due to trapping, treats the source/sink term as diffusive, with a functional dependence on the concentration gradient between channel and trap. Okubo's definition of the source/sink term depends on the dimensions of the entrapment region relative to the channel, as well as a time scale which is described as a “characteristic residence time of a contaminant in the trap” (Okubo 1973). Okubo's analysis showed convincingly that this model is well-suited to environments such as the Mersey estuary, and the data Bowden (1965) collected there on observed longitudinal dispersion corroborates that model.

Limitations of the Traditional Framework

Okubo's (1973) effective diffusivity, as reproduced by Fischer et al. (1979), is shown in Eq. 3.

$$ {K_{{\rm{effective,Okubo}}}} = \frac{K}{{1 + r}} + \frac{{r{u_{\rm{C}}}^2}}{{2k{{\left( {1 + r} \right)}^2}\left( {1 + r + \phi /k} \right)}} $$

(3)

K is the diffusivity due to turbulence and processes other than tidal trapping; r is the ratio of trap volume to channel volume; k⁻¹ is the residence time of the trap; φ is 2π/T, where T is the tidal period; and u_C is the amplitude of the velocity in the channel.

Using this model to estimate a diffusion coefficient for a trap that exchanges advectively with the main channel, rather than diffusively, is problematic. For example, we consider a trap that fills and drains with the tides. Any such trap has a characteristic residence time of T, the tidal period, making k equal to T ⁻¹. The strength of the tidal advection which drives the exchange between the channel and trap is not represented in this formulation. The phase lag between the trap's response to the tidal pressure gradient and that of the channel, which has been observed to cause longitudinal scalar spreading as trapped water rejoins channel flow (Blanton and Andrade 2001), is also not captured by Eq. 3.

Development of New Frameworks

Advective Exchange

We propose that there are types of shoreline irregularities for which a distinct model of tidal trapping is better suited than Okubo's (1973) diffusive formulation. In particular, the source/sink term representing the exchange with the trap may be driven by tidal advection rather than diffusion for many environments. The breached Island Ponds in the present study represent such a case, as does the branching channel example discussed by Fischer et al. (1979). Later in this section, we discuss a dimensionless parameter useful for determining the suitability of an advective versus diffusive model.

Following Aris (1956; also Okubo 1973; Young et al. 1982; Wolanski and Ridd 1986), we calculate the time-dependent moments of the distribution of a pulse of solute released in a tidal channel subject to tidal trapping. The effective longitudinal dispersion coefficient in the channel is defined as one half of the derivative of the variance of the distribution with respect to time, and the variance is the ratio of the second to the zeroth moment (Eq. 4). We evaluate the effective dispersion over one tidal cycle, from t = 0 to T, where $\Delta {M_2} = {\left. {{M_2}} \right|_{t = T}} - {\left. {{M_2}} \right|_{t = 0}}$ and $\overline {{M_0}}$ is the tidally averaged zeroth moment in the channel.

$$ {K_{\rm{effective}}} = \frac{1}{2}\frac{{\partial {\sigma^2}}}{{\partial t}} = \frac{1}{2}\frac{\partial }{{\partial t}}\left( {\frac{{{M_2}}}{{{M_0}}}} \right) = \frac{1}{{2T}}\left( {\frac{{\Delta {M_2}}}{{\overline {{M_0}} }}} \right) $$

(4)

Equation 5 represents the 1-dimensional (along-channel) transport equation for solute concentration in a tidal channel. This formulation is distinct from prior analyses (Okubo 1973; Wolanski and Ridd 1986; Ridd et al. 1990) in that the source/sink term employed in our transport equation is advective rather than diffusive. The terms in Eq. 5 are, from left to right, unsteadiness, advection of the solute concentration by an oscillating flow, turbulent diffusion, and an advective source and sink of solute into and out of the trap.

$$ \frac{{\partial S}}{{\partial t}} + {u_{\rm{C}}}\sin \left( {\phi t - \alpha } \right)\frac{{\partial S}}{{\partial x}} - K\frac{{{\partial^2}S}}{{\partial {x^2}}} = - {u_{\rm{T}}}\frac{{{H_{\rm{T}}}}}{{{A_{\rm{C}}}}}\sin \left( {\phi t} \right){S_{\rm{T}}}(t) $$

(5)

S is the concentration of solute in the channel, u_C is the amplitude of the velocity in the channel, which is assumed to be driven by a single tidal constituent; K is the diffusivity for mass due to all other processes, e.g., shear, turbulence; u_T is the amplitude of the velocity into and out of the trap; S_T(t) is the solute concentration entering and exiting the trap; H_T is the depth of flow into and out of the trap; A_C is the cross-sectional area in the channel; φ the inverse of the tidal period (2π/T), and α is the phase lag between flow into the trap and flow in the channel, in radians. On the time interval of 0 to T, the flood occurs from 0 to T/2, and the ebb occurs from T/2 to T. Equation 5 assumes that the main channel width is constant and that the time dependence of depth in the channel and depth in the breach is the same. This assumption is reasonable given the rapid adjustment to a lateral barotropic pressure gradient, which prevents any such gradient from persisting. No assumption is required about the phasing of the tidal pressure gradient relative to the other terms. The only phase lag specified in this 1-dimensional transport equation is that between the main channel flow velocity and the velocity entering and leaving the trap, α. The solute concentration entering and leaving the trap, S_T(t), is not constrained in this transport equation. We first derive a general expression for the effective dispersion due to tidal trapping and then examine particular formulations of S_T(t).

The moments of any distribution may be calculated using Eq. 6.

$$ {M_j} = \int_{ - \infty }^\infty {{x^j}S\left( {x,t} \right)dx} $$

(6)

We differentiate both sides with respect to time, resulting in:

$$ \frac{{\partial {M_j}}}{{\partial t}} = \int_{ - \infty }^\infty {{x^j}\frac{{\partial S\left( {x,t} \right)}}{{\partial t}}dx} $$

(7)

Substituting Eq. 5 into this expression allows us to solve for the moments of the solute distribution without solving for S(x,t) explicitly (Aris 1956). While this integral must be evaluated over all of space, the source/sink term in Eq. 5 exists only within the width of the breach, which we define to be of length 2 l (centered on x = 0 for mathematical simplicity). We therefore evaluate each moment as follows:

$$ \frac{{\partial {M_j}}}{{\partial t}} = - \int_{ - \infty }^\infty {{x^j}{u_{\rm{C}}}\sin \left( {\phi t - \alpha } \right)\frac{{\partial S}}{{\partial x}}dx + \int_{ - \infty }^\infty {{x^j}K\frac{{{\partial^2}S}}{{\partial {t^2}}}dx - \int_{ - l}^l {{x^j}{u_{\rm{T}}}\frac{{{H_{\rm{T}}}}}{{{A_{\rm{C}}}}}\sin \left( {\phi t} \right){S_{\rm{T}}}(t)dx} } } $$

(8)

Integrating Eq. 8 with j = 0 with respect to time yields two terms in the zeroth moment or the total mass of solute: the original amount released into the channel (M ₀(0)), and a fluctuating component resulting from exchange with the trap (Eq. 9). Q _T is defined as the flow rate into and out of the trap: u _T H _T2l.

$$ {M_0}(t) = - \frac{{{Q_{\rm{T}}}}}{{{A_{\rm{C}}}}}\int_0^t {\sin \left( {\phi t} \right){S_{\rm{T}}}(t)dt} + {M_0}(0) $$

(9)

Similar integrations with j = 1 and j = 2 result in the first and second moments, (Eqs. 10 and 11), which represent the location of the centroid of the solute cloud and the variance of the solute distribution, respectively.

$$ {M_1}(t) = {u_{\rm{C}}}\int_0^t {\sin \left( {\phi t - \alpha } \right){M_0}(t)dt} $$

(10)

$$ \Delta {M_2} = 2{u_{\rm{C}}}\int_0^{\rm{T}} {\sin \left( {\phi t - \alpha } \right){M_1}(t)dt} + 2K\int_0^T {{M_0}(t)dt} - \frac{{{l^2}}}{3}\frac{{{Q_{\rm{T}}}}}{{{A_{\rm{C}}}}}\int_0^{\rm{T}} {\sin \left( {\phi t} \right){S_{\rm{T}}}(t)dt} $$

(11)

Equation 11 is the discrete form of the second moment, evaluated over one tidal cycle, which allows us to simplify the effective dispersion coefficient by canceling sinusoidal terms. These terms represent periodic variations within the tidal cycle, while our interest is in the steady growth of the solute cloud over time scales greater than T. With this approach, the total effective diffusion coefficient can be calculated by substituting the equations for the concentration moments: Eqs. 9, 10, and 11, into Eq. 4. The general effective dispersion coefficient is therefore:

$$ \begin{array}{*{20}{c}} {{K_{\rm{effective}}} = - \frac{{{u_C}^2{Q_{\rm{T}}}}}{{\overline {{M_0}} T{A_{\rm{C}}}}}\int_0^{\rm{T}} {\sin \left( {\phi t - \alpha } \right)\left( {\int_0^t {\sin \left( {\phi t - \alpha } \right)\left( {\int_0^t {\sin \left( {\phi t} \right){S_{\rm{T}}}(t)dt} } \right)dt} } \right)dt} } \hfill \\{ - \frac{{{l^2}{Q_{\rm{T}}}}}{{6\overline {{M_0}} T{A_{\rm{C}}}}}\int_0^{\rm{T}} {\sin \left( {\phi t} \right){S_{\rm{T}}}(t)dt} + K} \hfill \\\end{array} $$

(12)

The last term on the right-hand side represents the longitudinal dispersion due to other processes (turbulence, shear) as shown in the diffusive transport term in Eq. 5. The remaining terms in Eq. 12 represent the dispersion due to interaction with the trap, so that K _effective = K _trap + K. The first term in this expression is analogous to the triple integration of Taylor (1953) for shear dispersion, but here the integration is in time rather than in space. The contribution of this term depends on the phase shift of the flow into the trap relative to the tidal flows in the channel. The second term is non-zero only when the concentration in the source/sink term is different during the “sink” (flood) phase and the “source” (ebb) phase, which may result from mixing in the trap. Equation 12 simplifies considerably when we assume a form of S _T(t), which we do in the following section.

Specific Cases

We now consider the effective dispersion for four specific functional forms of S _T(t). We start with two simplistic cases that are helpful for understanding the general equation, and then we examine two slightly more complex cases that approximate a branching channel system and a salt pond system. The structure of the velocities and concentrations in the channel and trap are shown in Fig. 9a–d.

Fig. 9

Theoretical velocities and concentrations for new tidal trapping framework. Concentrations are departures from the average, normalized from −1 to 1. For all panels: thick black line trap concentration, thin black line trap velocity (m s⁻¹), thick gray line channel concentration, thin gray line channel velocity (m s⁻¹). a Case 1: S _T in quadrature with u _T. b Case 2: S _T in quadrature with u _C. c Case 3: no mixing. d Case 4: complete mixing

Both the velocity of flow and solute concentration entering the trap are functions of conditions in the channel (S and u _C); however, in the present analysis, we are treating them as independent. We are able to approximate flows and concentrations in the channel reasonably well, and this approach allows us to solve for the dispersion resulting from exchange with the trap analytically. The soundness of this approach is confirmed by a comparison of the theoretical solutions derived below and a numerical solution to Eq. 12 using field measurements, presented subsequently.

The following scaling groups are helpful in presenting the results of the analytics: a ratio of the volume of flow into and out of the trap to the flow volume in the channel r ∼ Q _T T/A _C u _C T; the tidal excursion L ∼ u _C/φ ∼ u _C T, and the ratio of the mass of solute entering and exiting the trap to that in the channel ε ∼ Q _T S _T L/A _C u _C $\overline {{M_0}}$ ∼ Q _T S _T/A _C u _C S, where we assume that $\overline {{M_0}}$ may be scaled as SL.

S_T in Quadrature with u_T

Although it may not occur naturally, the simplest form of the solute concentration entering and exiting the trap is the case in which S _T is a sinusoid in perfect quadrature with the flow into and out of the trap (u _T), shown in Fig. 9a. While this phasing is realistic—the trap's solute concentration should depend on the velocity entering and exiting the trap—the concentration signal itself for this special case is lacking dependence on the channel concentration, which should be the source of solute during floods. However, this case is illustrative of the main functional relationships that prove consistent for all four specific cases. Evaluating Eq. 12 assuming that S _T(t) = −S _Tcos(φt) yields:

$$ \overline {{M_0}} = \frac{{rL{S_{\rm{T}}}}}{4} + {M_0}(0) $$

(13a)

$$ {K_{\rm{effective}}} = \frac{1}{{2T}}\frac{{\Delta {M_2}}}{{\overline {{M_0}} }} = \varepsilon L{u_{\rm{C}}}\frac{{\cos \alpha \sin \alpha }}{8} + K $$

(13b)

This result provides us with the simplest, clearest, mathematical statement regarding the effective diffusion coefficient due to tidal trapping, which is the first term on the right-hand side of Eq. 13b. Here, we see that the trapping coefficient is proportional to a velocity scale times a length scale (u _C, the tidal velocity scale in the channel, and L, the tidal excursion), as well as the mass trapped relative to the mass in the channel (ε). Finally, the diffusion coefficient due to trapping is proportional to the product of the sine and cosine of the phase lag of the flow into the trap relative to the flow in the channel. At small phase lags, the cosine term is approximately 1, and the trap-induced diffusion coefficient increases linearly with phase lag. When the phase lag is precisely zero, the effect of trapping on dispersion vanishes, and K _effective is simply equal to K.

S_T in Quadrature with u_C

Rather than aligning the concentration in the trap with the exchange flow, in this case it is aligned it in time with flows in the channel. This achieves the opposite trade-off compared with the first special case: the phasing is now dependent on transport in the channel, but the channel can now serve as the source of solute while the trap is filling (Fig. 9b). This is likely to be a correct formulation during the flood (sink) phase, but it will not be correct during the ebb; more realistic cases for that phase will be considered in the next two sections. Evaluating Eq. 12 assuming that the trap concentration is in quadrature with the channel velocity, or S _T(t) = −S _Tcos(φt − α), yields:

$$ \overline {{M_0}} = rL{S_{\rm{T}}}\left( {\frac{{2\pi \sin \alpha + \cos \alpha \sin \alpha }}{{8\pi }}} \right) + {M_0}(0) $$

(14a)

$$ {K_{\rm{effective}}} = \varepsilon L{u_C}\left( {\frac{7}{{16}}{{\cos }^2}\alpha \sin \alpha + \frac{3}{{16}}{{\sin }^3}\alpha - \frac{1}{{12}}\frac{{{l^2}}}{{{L^2}}}\sin \alpha } \right) + K $$

(14b)

Just as in Eq. 13b, the trapping diffusion coefficient is proportional to the tidal velocity scale times the tidal excursion as well as the fractional mass retained in the trap. In this case, the dependence on the phase lag (α) is modified and consists of three terms but is essentially unchanged at small phase lags.

The No-Mixing Case: An Idealized Branching Channel

As a step toward a more physically realistic scenario, we examine the case of an idealized branching channel. The phasing of the trap solute concentration is 90° different from that of the trap velocity (they are in quadrature), but the concentration mimics that of the channel on the flood and then reverses itself on the ebb, effectively unwinding the inflow in a mirror image, symmetric about slack water in the trap, as shown in Fig. 9c. The symmetric structure of the salinity signal results when we invoke the assumption that no mixing occurs within the trap. The trap concentration is therefore described by: S _T(t) = −S _Tcos(φt − α) for 0 < t < T/2, and S _T(t) = S _Tcos(φ(T/2 − t) − α) for T/2 < t < T.

$$ \overline {{M_0}} = rL{S_{\rm{T}}}\left( {\frac{{\cos \alpha - \pi \sin \alpha }}{{8\pi }}} \right) + {M_0}(0) $$

(15a)

$$ {K_{\rm{effective}}} = \varepsilon L{u_{\rm{C}}}\sin \alpha \cos \alpha \left( {\frac{{3\cos \alpha + 32\sin \alpha }}{{24\pi }}} \right) + K $$

(15b)

Once again, εLu _C is the fundamental dimensional group, and the diffusion coefficient increases with phase lag, α.

The Complete-Mixing Case: An Idealized Salt Pond

Exchange with an idealized salt pond is represented by a trap solute concentration in quadrature with the trap velocity. It mimics the channel concentration on the flood, as with the no-mixing case. The ebb for the complete-mixing case, however, is simply the average of the inflow concentration. In other words, the inflow is assumed to be uniformly mixed within the trap as the flood progresses, such that the outflow on the ebb is a constant, average value (Fig. 9d). For this case, the solute concentration in the trap is: S _T(t) = −S _Tcos(φt−α) for 0 < t < T/2, and $S_{T} {\left( t \right)} = \frac{1}{{T \mathord{\left/ {\vphantom {T 2}} \right. \kern-\nulldelimiterspace} 2}}{\int_0^{T \mathord{\left/ {\vphantom {T 2}} \right. \kern-\nulldelimiterspace} 2} { - S_{T} } }\cos {\left( {\varphi t - \alpha } \right)}dt$ for T/2 < t < T.

$$ \overline {{M_0}} = rL{S_{\rm{T}}}\left( {\frac{{\pi \cos \alpha + {\pi^2}\sin \alpha + 16\sin \alpha }}{{16{\pi^2}}}} \right) + {M_0}(0) $$

(16a)

$$ {K_{\rm{effective}}} = \varepsilon L{u_{\rm{C}}}\frac{1}{{3\pi }}{\cos^3}\alpha + \varepsilon L{u_{\rm{C}}}\left( \begin{gathered} \left( {\frac{{21{\pi^2} - 128}}{{96{\pi^2}}}} \right){\cos^2}\alpha \sin \alpha - \frac{5}{{6\pi }}\cos \alpha {\sin^2}\alpha \hfill \\+ \left( {\frac{{9{\pi^2} - 64}}{{96{\pi^2}}}} \right){\sin^3}\alpha + \left( {\frac{{{\pi^2} - 8}}{{24{\pi^2}}}} \right)\frac{{{l^2}}}{{{L^2}}}\sin \alpha \hfill \\\end{gathered} \right) + K $$

(16b)

Note that a ratio of squared length scales appears in this case, in the last sin(α) term on the right hand side, where l/L represents half of the width of the breach or channel opening, scaled by the tidal excursion.

In this final example, the dependence on the phase lag is more complicated, and a new dispersion process is represented. In the five terms that constitute the tidal trapping diffusion coefficient, four of them are proportional to sin(α) and approach zero for small phase shifts; they can be interpreted similarly to the examples in the previous three sections. The first term, however, which depends only on cos(α) is actually due to the diffusive effects of the mixing in the trap itself, which we have assumed here to be complete within the half tidal cycle that the trap is inundated.

Discussion of Frameworks

Advection Versus Diffusion

The difference between the present framework and Okubo's (1973) is the structure of the source/sink term that represents exchange with the trap: this study uses a tidally driven advective flux that accounts for phase lags, while Okubo used a diffusive flux. A comparison of the important scaling groups in the present and traditional frameworks yields a Peclet number that may be useful in elucidating the distinct mechanisms represented in the derivations, as well as the appropriateness of applying one formulation versus the other. The representative time scale for exchange is k ⁻¹ in Okubo's (1973) diffusive framework, and T in the present advective one, as discussed in the “Application of Traditional Frameworks” section. The ratio of these time scales produces Eq. 17:

$$ \frac{{{T^{ - 1}}}}{k}\sim \frac{{{Q_T}{V_{\rm{Prism}}}^{ - 1}}}{{{D_y}{A_{\rm{Trap}}}^{ - 1}}}\sim \frac{{{u_{\rm{T}}}l{H_{\rm{T}}}{{\left( {{A_{\rm{Trap}}}{\eta_0}} \right)}^{ - 1}}}}{{{D_y}{A_{\rm{Trap}}}^{ - 1}}}\sim \frac{{{u_{\rm{T}}}l}}{{{D_y}}}\frac{{{H_{\rm{T}}}}}{{{\eta_0}}} $$

(17)

Exchange in the advective model (in the numerator of Eq. 17) is represented by the time required for the trap to fill or drain the volume of the tidal prism, expressed as the flow rate into and out of the trap (Q _T), divided by the tidal prism of the pond (V _Prism). Diffusive exchange (shown in the denominator) is defined by the time scale for horizontal transport across the trap (A _Trap) driven by lateral diffusion (D _y ). Replacing the flow rate into the trap with a velocity times the area of a rectangular breach (u _T lH _T), and the tidal prism with the trap area times the tidal amplitude (A _Trap η ₀), we can cancel the trap area from the ratio. A Peclet number is reached: u _T l/D _y , scaled by the ratio of the average depth in the trap (H _T) to the tidal amplitude (η ₀) that can be used to discern the relative suitability of each framework for a particular environment. For large Peclet numbers, advection dominates and the framework presented here should be the appropriate one for estimating dispersion from trapping; for small values of the Peclet number, the traditional, diffusion-based formulation should be used.

Variability with Phase Shift

The dependence of the dispersion due to trapping on the phase lag between the breach velocity and the channel velocity, α, is worth exploring (Fig. 10). For each case, the important scaling group in K _trap, εLu _C, is multiplied by a sum of sines and cosines of α. For cases 1–3, where no mixing takes place within the trap, K _trap is 0 when the trap and channel velocities are precisely in phase (α = 0). In these cases, when α = 0, the water removed from the channel on the flood rejoins its original neighbors on the ebb, resulting in no change to the original distribution of concentration in the channel. Contrastingly, when there is no phase lag, the complete-mixing case still alters the concentration distribution in the channel. On the ebb, the pond outflow contains a constant concentration (the volume average of the inflow) and results in the mixing of water masses of different concentrations as they are joined in the channel.

Fig. 10

Theoretical dispersion coefficients as a function of phase lag. Thick black line case 1. Thin black line case 2. Thin gray line case 3. Thick gray line case 4. Asterisk data; numerical evaluation of the theory using measured salinities

We consider case 1, the simplest scenario, to demonstrate the influence of increasing α. As the phase lag grows, the ebb tide joins together water masses with concentrations that are increasingly mismatched. For this scenario, when α equals T/8, the trap returns flow to the channel such that the scalar concentration of trap effluent and that of flow in the channel are as different as possible, producing maximum spreading of the scalar cloud. The opposite is true when α is equal to T/4 or when u _T and u _C are 90° out of phase. In this case, flow is removed from the channel at one location in the symmetric scalar cloud as it advects up- and down-estuary with the tides, and it is returned to the channel in the same location of the opposite side of the scalar cloud, such that the trapped flow rejoins channel flow of the exact same scalar concentration. In this way, no spreading is induced from the phase lags.

By mathematical definition, K _trap for each case is periodic in α, passing through zero and going negative for various values of the phase lag between 0 and T. However, it is important to note that physically, it is impossible to shuffle these water masses in a way that reduces the extent of the scalar cloud, and therefore dispersion from trapping should never be negative. Additionally, there is a physical maximum to α; the difference in response time to the barotropic pressure gradient of the velocity in the channel and the velocity in the trap cannot exceed a few hours. The physically realistic region of the relationship between K _trap and α is limited to low values of α (such as the range shown in Fig. 10).

Comparison with Field Data

While the data collected in this study do not have fine enough temporal or spatial resolution to yield a complete decomposition of dispersive fluxes, it is possible to compare values of dispersion coefficients predicted from the new analytical framework to approximate, but still quantitative, values obtained through the field data. A summary of this comparison is presented in Table 1. Specifically, Eq. 12 is applied discretely to measurements of S _T(t), the concentration of salt recorded at the pond entrance. The integrations are performed numerically by advancing through the data in time. To minimize the effects of higher order tidal harmonics, as only the M2 tide is accounted for in the present study, a repeating window of real data (of duration 12.4 h) was used in this calculation (Fig. 11). The window was selected such that the first point occurs at slack tide between ebb and flood, according to depth-averaged velocities measured at the breach entrance. Parameters representative of the field site are: amplitude of tidal velocities in the channel and into and out of the trap, 1 m s⁻¹; depth in the trap, 2 m; cross-sectional area of the channel, 200 m²; breach width, 20 m; tidal period, 12.4 h; phase lag between trap and channel, 24 min. The initial concentration of solute in the channel, M ₀(0), is scaled as the average concentration of salinity in the channel, 15, times the tidal excursion. The discrete integration of Eq. 12 using measured values of S _T(t) yields a coefficient for dispersion resulting from tidal trapping of 19 m² s⁻¹. This result represents the dispersion due to Coyote Creek's interaction with just one salt pond; accounting for all three Island Ponds would require increasing the values for the flow rate into and out of the ponds, the volume of the ponds, and the width of the combined breaches.

Table 1 Dispersion coefficients from data, existing, and new theoretical models

Fig. 11

Data used in numerical evaluation of theoretical framework. Salinity is used as the solute, and the departure from the average, normalized by the range, is plotted

Using these parameters and the new theoretical models for estimating dispersion from trapping in one salt pond produces values of 9, 30, 15, and 37 m² s⁻¹ for cases 1–4, respectively. The two cases representing no mixing and complete mixing within the trap envelop the estimate of dispersion from the data. The field measurements of S _T(t) lie approximately between the theoretical formulations for S _T(t) in the no-mixing and complete-mixing cases, shown in Fig. 11. The relative structures of these real and contrived time series support the assertion that a salt pond partly mixes the water it receives on the flood tide. As discussed previously, field data suggests that the pond effluent “unwinds,” similar to case 3, until the depth in the pond reaches the surface of the interior island, at which point the remainder of the pond's discharge is well-mixed, as in case 4.

Since we propose that the salt pond environment is better approximated by an advectively driven form of trapping, it is useful to compare the values for K _trap thus obtained to Okubo's (1973) diffusive framework. The geometric parameter r is scaled as the trap volume (A _trap η ₀) to the channel volume (A _C L). The time scale for exchange is T, making k equal to T ⁻¹. Applying Eq. 3 produces a value of K _trap,Okubo of more than 3,000 m² s⁻¹. This unrealistic value, particularly in view of our estimated total diffusion of ∼500 m² s⁻¹, suggests that the diffusive model of exchange between the channel and the trap utilized by Okubo is not the appropriate framework for this environment. This conclusion was, of course, expected based on the strongly advective nature of exchange between the channel and the storage volume or trap.

Other Factors Affecting Longitudinal Dispersion

It is important to note that tidal trapping can set up lateral processes that are not accounted for in either traditional or new frameworks for estimating dispersion. Specifically, in Coyote Creek, very strong, periodic lateral gradients of salinity have been observed, as described in the “Lateral Salinity Gradient and Exchange Dynamics” section. The strongest gradients occur at the end of the ebb tide, where salinities recorded in the channel's thalweg are 2–6 lower than those recorded in the pond effluent over a separation of approximately 100 m. Surface salinity transects demonstrated that this is a frontal gradient, with a sharp change in salinity occurring over a distance of order 10 m. A baroclinically driven lateral circulation would be unsurprising, although depths late in the ebb (1–2 m) made it impossible to resolve such a lateral flow with boat-mounted velocity measurements. If this lateral circulation exists, it would induce rapid cross-sectional mixing, which would diminish dispersion from shear, as discussed by Fischer et al. (1979) and as explored analytically by Smith (1976).

Summary and Conclusions

Measurements of velocities and water properties in a tidal slough connected to former salt ponds in San Francisco Bay showed that tidal trapping is a locally important mechanism driving longitudinal dispersion and fluxes of salt. Observed phase lags between the tidal pressure gradient, velocities in the channel and pond, and salinity signals support the conceptual model of tidal trapping presented by Fischer et al. (1979). Specifically, velocities recorded in the thalweg of the channel lag the exchange flows through the breach by an average of 24 min. Maximum and minimum salinities recorded in the main channel occur before high- and low slack tide, respectively, because of the relatively prompt response of the flow in the shallows to the change in tidal forcing. This serves to bring fresher waters to the channel perimeter around the flood-to-ebb transition (high slack tide) and more saline waters around the ebb-to-flood transition (low slack tide), which mix laterally before the flow in the main channel has changed direction. This process produces the observed phase lags between velocity and salinity in the channel, with the result that those signals are out of quadrature. Additional salinity variation is created by mixing in the interior of the ponds prior to being discharged on the ebb tide.

High barotropic velocities (±1 m s⁻¹) in the main channel and through the breach indicate that exchange between the channel and ponds is driven by tidal advection. Okubo's (1973) classical framework for dispersion from tidal trapping was derived based on diffusive exchange between the trap and channel and, if applied to this system, yields a dispersion coefficient from trapping that is greater than 3,000 m² s⁻¹. Our measurements suggest that the total estuarine dispersion coefficient for this system fluctuates around an average value of 500 m² s⁻¹, reaching a maximum of 800 m² s⁻¹. These disparate estimates indicate that the classical treatment of dispersion from trapping is inappropriate for this advectively driven exchange.

To better assess dispersion from trapping for systems where exchange is forced by tidal advection, such as a branching channel system, as well as perimeter volumes that fill and drain with the tides, we re-derived the expression for the dispersion coefficient replacing the diffusive flux between trap and channel with an advective one. The concentration moment method (following Aris 1956; and later Okubo 1973; Young et al. 1982; and Wolanski and Ridd 1986) was used to solve analytically for the variance of a scalar cloud in the channel due to exchange with a trap as a function of phase lag between flows in the channel and through the breach. This new framework, which is specified for four idealized scenarios, provides a dispersion coefficient from tidal trapping of 15–37 m² s⁻¹ using physical parameters (the phase lag, the ratio of trap volume to channel volume, the tidal excursion, and the ratio of scalar mass in the trap to that in the channel) representative of the study site. Performing the analysis numerically on the observations yields a dispersion coefficient of 19 m² s⁻¹. These results indicate that a framework for dispersion from tidal trapping based on advective exchange is well-suited to the dynamics observed at our study site.