“efforts to develop theories of the way ecosystems or communities are organized must revolve around attempts to discover patterns that can be quantified within systems, and compared across systems” (Levin 1992)

Introduction

Our knowledge of the natural world comes largely from observation, and it is strongly shaped (and biased) by the frequency, duration, and geographic regions of our observations. For example, the earliest observations of marine phytoplankton populations came from studies of the North Atlantic and North Sea (Mills 1989). The spring-bloom paradigm emerged from these early studies and it persists as a canonical pattern of biological oceanography. Implicit in the canonical pattern is the notion that phytoplankton populations fluctuate over a regular seasonal cycle that recurs each year and is the dominant mode of variability (Riley 1947; Sverdrup 1953; Cushing 1959). Satellite observations now provide a global view of phytoplankton biomass that has detected large regional variations in seasonal cycles across the world’s oceans (Longhurst 1995; Platt et al. 2009), and the Continuous Plankton Recorder program has revealed climate-driven changes in seasonal cycles and communities (Edwards and Richardson 2004). Therefore, our knowledge of phytoplankton dynamics in the sea has been refined by expanding the geographic coverage and duration of observations to reveal regional and annual variability not evident from the pioneering studies of plankton populations in the North Atlantic.

Our knowledge of phytoplankton dynamics in estuarine–coastal waters has been built from place-based studies, some of which have now been sustained for a decade or more (see this special issue of Estuaries and Coasts). Collectively, these studies now provide an opportunity to search for canonical patterns of phytoplankton variability in estuarine–coastal waters from observations made across the diversity of marine domains influenced by connectivity to land and capturing processes operating at periods longer than a year. Results from these studies provide reasons to expect that phytoplankton patterns in nearshore waters might be different from those in the ocean (Longhurst 1995). Whereas much of phytoplankton variability in the open ocean is generated by the annual cycles of solar radiation and atmospheric heat input (Sverdrup 1953; Cushing 1959), phytoplankton variability in estuaries and nearshore coastal waters is generated by many additional processes that propagate across their interfaces with land, ocean, atmosphere, and underlying sediments (Cloern 1996). For example, pulses of freshwater inflow can remove phytoplankton from small systems (de Madariaga et al. 1992) or promote phytoplankton growth in large retentive systems by delivering land-derived nitrogen and phosphorus (Paerl et al. 2009). Upwelling in coastal boundary currents can be a source of phytoplankton biomass or nutrients to fuel blooms within rías (Crespo et al. 2007) or estuaries (Brown and Ozretich 2009). Heat waves promote surface blooms in nutrient-rich estuaries by establishing strong thermal stratification (Cloern et al. 2005), and seasonal wind mixing triggers blooms in nutrient-poor bays by mixing high-nutrient bottom waters to the surface (Iverson et al. 1974). Estuaries and shallow bays and lagoons function as tightly linked benthic–pelagic systems where the benthos can be a strong sink for phytoplankton biomass (e.g., grazing by benthic filter feeders; Cloern 1982) or a source as phytoplankton resting stages in sediments develop into vegetative cells that form seasonal blooms (Shikata et al. 2008). Many of these processes fluctuate over a range of timescales, such as the variability of local weather and coastal upwelling with wind events, seasons, El Niño Southern Oscillation cycles, and multidecadal shifts in atmospheric forcing over ocean basins (Di Lorenzo et al. 2008). And many of these processes are modified by humans through river damming (Nixon 2003), flow manipulations (Petersen et al. 2008), habitat transformations (Brush 2009), fishing (Casini et al. 2008), introductions of species (Kideys et al. 2008) that cause ecological regime shifts ramifying across all trophic levels, and disturbances that amplify nutrient inputs from land or remediations that reduce anthropogenic nutrient inputs (Duarte et al. 2009).

Place-based studies have identified the ensemble of processes that can generate phytoplankton variability in estuarine–coastal ecosystems, but their collective observations have not yet been analyzed to measure common patterns of variability, understand how those patterns change with scale, and discover the causes and consequences of pattern—the “fundamental problem of ecology” (Levin 1992). Do canonical phytoplankton patterns even exist in observations from the world’s nearshore coastal ecosystems where so many regulatory processes fluctuate over multiple timescales and where human disturbance is intense (Duarte et al. 2009)? As a step to answer this question, we compiled time series of phytoplankton biomass measured as chlorophyll-a (Chl-a) concentration in estuaries, lagoons, bays, inland seas, nearshore coastal waters, and tidal rivers (which, for brevity, we collectively reference as “estuarine–coastal” ecosystems). Our initial analysis of this compilation focused on the seasonal pattern, and it revealed high diversity in the timing and amplitude of biomass fluctuations, both within and across ecosystems (Cloern and Jassby 2008). Here, we take a next step in the analysis of these time series to measure and compare patterns of phytoplankton variability at different timescales. We present a four-step approach to: (1) illustrate the diverse character of Chl-a time series in these ecosystems; (2) describe a simple method for measuring components of Chl-a variability at ecologically important timescales; (3) apply the approach to quantify patterns within and across estuarine–coastal sites; and (4) develop hypotheses about the processes underlying patterns that emerge from comparative analysis.

What do Phytoplankton Time Series Look Like?

We use time series of Chl-a as a measure of phytoplankton biomass variability because standard methods are established, and Chl-a concentration is routinely measured in research and monitoring programs. Primary production (Cole and Cloern 1987), community respiration (Hopkinson and Smith 2005), condition of cultured mussels (Smaal et al. 2001), and survival of larval fish (Platt et al. 2003) are strongly correlated with Chl-a patterns, so understanding of phytoplankton variability is a key to understanding variability of biogeochemical processes, ecosystem metabolism, and production in food webs supporting fisheries.

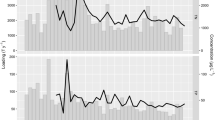
We selected five Chl-a time series (Fig. 1) to illustrate the diverse character of phytoplankton variability observed within individual estuarine–coastal ecosystems. A 12-year record from North Inlet contains a regular seasonal pattern that repeats each year with small annual deviations in timing and amplitude. This recurrence of one pattern is analogous to the canonical spring-bloom pattern of the North Atlantic, and it shows large seasonal (within year) variability but small annual (between year) variability. A contrasting series from Biscayne Bay has biomass fluctuations that appear random and follow no regular seasonal or annual pattern. A series from Chesapeake Bay illustrates complexity that is difficult to decipher by visual inspection. An underlying seasonal pattern may be present in this record, but even if present it is masked by spikiness from irregular events of high biomass. A series from Denmark’s Ringkøbing Fjord illustrates two patterns of long-term variability as a decadal trend of increasing biomass followed by an abrupt and persistent biomass decline. The series from Tampa Bay suggests patterns at different timescales—a long-term decreasing trend, within-year fluctuations that might follow a common seasonal pattern, and irregular bloom events of exceptional biomass that deviate from the trend and seasonal pattern. These examples illustrate patterns of Chl-a variability over timescales from events to decades, and they highlight the challenge of detecting phytoplankton patterns within ecosystems and comparing them across ecosystems. Next, we present a simple method to decompose such time series and extract components of variability associated with years, seasons, and events.

Fig. 1
figure 1

Examples of Chl-a time series in estuarine–coastal ecosystems: North Inlet (from Belle W. Baruch Institute for Marine and Coastal Sciences, http://links.baruch.sc.edu/Data/CoastalData.html); Biscayne Bay site 133 (from SERC-FIU Water Quality Monitoring Network, http://serc.fiu.edu/wqmnetwork/); Chesapeake Bay site 8.1C (from Chesapeake Bay Program, http://www.chesapeakebay.net/data_waterquality.aspx); Ringkøbing Fjord (data provided by J.K. Petersen (Petersen et al. 2008)); and Tampa Bay site 8 (data provided by Ed Sherwood, Tampa Bay Estuary Program)

Full size image

How Can We Extract Patterns from Phytoplankton Time Series?

Long-term time series of Chl-a allow us to examine a variety of phenomena involving different timescales from, for example, the impacts of short-term weather systems over days to those of anthropogenic climate change over decades. But some kind of model is required to describe how a chlorophyll series represents the action of mechanisms at different timescales. Often, this involves isolating underlying components operating at distinct timescales. These components are ultimately constructs that serve a utilitarian purpose, and there is thus no correct model or decomposition method. The various methods reveal and distort scales in different ways, and all are a compromise. The choice of a decomposition method depends on many different factors: the specific question of interest; the dynamics of the series, such as the presence of gradual versus abrupt changes in seasonality; the series length; and details such as the sampling pattern and extent of missing data.

Although chlorophyll time series therefore present a challenge that cannot be addressed with a single solution, we propose a default starting point for decomposition based on examination of series from many different coastal and estuarine ecosystems. We aimed for a method that is intuitively accessible, is easily implemented, and avoids having to select more or less arbitrary parameter values. We compiled time series of near-surface Chl-a concentration provided by individuals or published in reports or online databases; data sources are listed in Supporting Material Table S1. We selected sites for this analysis on the basis of three criteria, trying to balance the need for long time series and unbiased missing data patterns with the need for a wide spectrum of interesting sites. We chose sites that had at least 8 years of data with at least 10 months of data for each year. We further required that each month be represented by at least 6 years of data at each site. This filtering procedure resulted in a total of 84 sites from 51 estuarine–coastal ecosystems. Almost all series were sampled at an approximately monthly frequency, so the few exceptions were first aggregated on a monthly basis using the mean. Unless otherwise stated, R version 2.8.0 and its contributed packages were used for data analysis (R Development Core Team 2007); in particular, the nlme package was used for mixed-effects models (Pinheiro et al. 2007).

Determining an appropriate time series model requires, among other things, an understanding of the relation between the variability of a time series variable and its magnitude. Graphical exploration of the collection of chlorophyll time series suggested that the relation between seasonal variability, expressed as the standard deviation s m of monthly mean observations, and the annual mean Y can be described by \( s_m \propto Y^b \) or, equivalently, \( s_m = a + b\log Y \), where a and b are constant (Fig. 2a). If b = 0, then variability is independent of the overall level and an additive seasonal model is implied; if b = 1, then a multiplicative seasonal model is implied (Chatfield 2004). We determined b and tested whether or not this relationship is site-specific by examining a linear mixed-effects model in which the ith year and kth site is described by:

Fig. 2
figure 2

a Relationship between seasonal variability and annual mean Chl-a for 84 estuarine–coastal sites meeting minimum data requirements (see text). Thick line, Eq. 2. b Relationship between year-to-year variability and long-term mean Chl-a for the same sites as in a. Thick line, Eq. 3

Full size image
$$ \log s_{ik} = \left( {a_0 + a_k } \right) + \left( {b_0 + b_k } \right)\log Y_{ik} + \varepsilon $$
(1)

where a 0 and b 0 are mean values across the population of ecosystems being sampled; a k and b k are random variables representing the respective deviations from these population means for the kth site; and ε is a random variable representing the residual value. The fixed-effects part of the solution, i.e., a 0 and b 0 along with their standard errors, can be summarized as:

$$ \log_{10} s_i = \left( { - 0.23 \pm 0.02} \right) + \left( {1.16 \pm 0.03} \right)\log_{10} Y_i $$
(2)

The mean exponent over this population of ecosystems is therefore slightly greater than 1. Considerable site-specific variation is present, with a k and b k having standard deviations of 0.10 and 0.15, respectively. To test the significance of this site effect, three nested models were examined: (1) the full model (Eq. 1); (2) a model with only the intercept subject to site effects, i.e., b k  = 0; and (3) a site-independent model in which a k  = b k  = 0. An analysis of variance (Pinheiro and Bates 2000) showed that (2) is clearly superior to (3), and (1) is superior to (2) (Table 1). Thus, a and b are indeed site specific.

Table 1 Analysis of variance test for three nested variants of the model in Eq. 1: (1) the full model; (2) b k  = 0 for all k; (3) a k  = b k  = 0 for all k. Based on n = 84 sites
Full size table

A similar relationship appears to hold between the standard deviation s y of annual mean observations and the long-term mean C (Fig. 2b). Indeed, ordinary least-squares regression shows that:

$$ \log_{10} \left( {s_y } \right) = - \left( {0.50 \pm 0.03} \right) + \left( {1.05 \pm 0.04} \right)\log_{10} C $$
(3)

The slope b of this relationship is therefore approximately 1, and interannual variability is directly proportional to the long-term mean.

The site-specific variations found in the relationship between monthly variability and annual mean demonstrate that different time series decomposition models may be suitable for different sites. But Eqs. 2 and 3 show that a multiplicative model is much closer to a correct description than an additive one. Moreover, because the mean exponent for the population differs from 1 by a relatively small amount, the multiplicative seasonal model is an appropriate default model when exploring chlorophyll time series. Population abundances in ecology are often thought to be lognormally distributed, on the basis of both observation and theory (Halley and Inchausti 2002). Direct proportionality between standard deviation and mean is a characteristic of lognormal distributions, so the relationships above may be special cases of a widespread feature of natural populations.

Monthly time series are partitioned here into four components: an overall mean, an annual effect, a seasonal pattern, and residual “events.” Based on the above analysis, either a multiplicative model should be used or the data should be transformed to stabilize the variance and make the components additive. We chose the former to avoid dealing with a transformed variable that has no direct physical interpretation. In particular, we used the multiplicative seasonal model expressed by:

$$ c_{ij} = Cy_i m_j \varepsilon_{ij} $$
(4)

where c ij is chlorophyll concentration in year i (i = 1,…,N) and month j (j = 1,…,12); C is the long-term mean of the series; y i is the annual effect in the ith year; m j is the seasonal (monthly) effect in the jth month; and ε ij is the residual. The annual effect was defined to be simply the annual mean Y i divided by C. Choosing how to estimate the seasonal effect m j is more difficult. Smoothing procedures such as Seasonal-Trend decomposition using Loess (STL; Cleveland et al. 1990) can isolate gradual trends in seasonal pattern (e.g., Fig. 6 of Jassby et al. 1999). But they obscure the timing of abrupt changes in seasonal pattern that may occur in a single year, a phenomenon observed in some of these time series. They also introduce an element of arbitrariness because the greater the smoothing, the greater is the variability that gets attributed to residual events. Here, we define an “average” seasonal pattern by, for each calendar month j, the mean over all years of \( M_{ij} /Y_i \), where M ij is the value for month j in year i, and Y i is again the annual mean for year i. Although this average pattern may not correspond to observed seasonality for systems with large interannual changes in seasonal patterns, it does provide a basis for comparing the general magnitude of the seasonal effect among sites and with the corresponding annual effect at individual sites. The residual series ε ij is then defined by \( \varepsilon_{ij} = c_{ij} /Cy_i m_j \). The residual series can be thought of as a series of “events” that cause a departure from the usual pattern or, if there is no “usual” pattern, as a measure of the stability of the seasonal pattern from year to year. It also includes sampling uncertainty, especially in strongly tidal systems with only one or a few measurements per month. An R function for this partitioning or decomposition procedure is available online as supplementary material.

This model partitions variability into three important components, in addition to the long-term mean C. The annual component y i measures the (multiplicative) deviation of mean Chl-a for an individual year from the long-term mean, where y i  > 1 indicates a year with above-average mean Chl-a. Similarly, the seasonal component m j describes the (multiplicative) deviation of mean Chl-a for a given month from the annual mean, where m j  > 1 indicates a mean monthly Chl-a greater than the annual mean; it provides us with an “average” pattern of seasonal variability. Finally, the residual component ε ij measures (multiplicative) deviations from the average seasonal pattern, where ε ij > 1 indicates an observation greater than the expected value for that month and year. One advantage of this partitioning procedure is that these three components each average 1 and are multipliers of C, so their magnitudes are independent of overall mean biomass and can be directly compared within and across ecosystems. In particular, their standard deviations are also coefficients of variation.

Phytoplankton Patterns Within and Across Estuarine–Coastal Ecosystems

Magnitude of Phytoplankton Variability

Our analysis reveals one striking pattern as the strong correlation between phytoplankton variability and mean biomass at individual sites. This correlation holds at both the monthly (Fig. 2a) and annual (Fig. 2b) timescale, and it has important ecological implications because phytoplankton primary production is proportional to Chl-a biomass in many estuaries (Cole and Cloern 1987). Our previous inventory (Cloern and Jassby 2008) showed a nearly 1,000-fold range of mean Chl-a concentration across 154 estuarine–coastal sites, from < 0.5 μg L−1 in oligotrophic coastal waters such as the Mediterranean Sea and Gulf of Aqaba to >100 μg L−1 in the ultraproductive Cienaga Grande de Santa Marta. The correlations in Fig. 2 imply that variability of primary production within individual ecosystems might therefore span a similar range and so, too, processes associated with primary production: evolution of dissolved oxygen; assimilation of dissolved nutrients, CO2, and contaminants into biomass; and supply of energy and essential biochemicals to consumer organisms from bacteria to larval fish (Cloern 1996). Therefore, mean Chl-a concentration might be more than an index of phytoplankton biomass. It might also be an indicator of the dynamic range of the seasonal and annual variability of emergent ecosystem properties such as water quality, community metabolism, and carrying capacity for fish and shellfish. Our experience tells us that high-biomass systems do indeed have large fluctuations of dissolved oxygen, pH, nutrient concentrations, and food supply to consumers (e.g., Thébault et al. 2008). The patterns in Fig. 2 explain why these attributes might fluctuate in proportion to mean phytoplankton biomass.

Phytoplankton Patterns at Different Scales of Variability

The decomposition method described above extracts patterns of phytoplankton variability as time series of three components, and we illustrate applications to Chl-a series from four ecosystems (Fig. 3). For each system, we show the monthly Chl-a series (top panel, blue lines) and the annual component y (top panel, red bars), residual component ε (middle panel), and seasonal component m (bottom panel, green bars). We selected a series from Moreton Bay to illustrate a coastal site that has weak patterns of variability at all scales (Fig. 3a). Here, Chl-a varies between 0.5 and 5.9 μg L−1, and annual variability is small (y does not deviate much from 1). The residual components are small, and the damped seasonal pattern is peak Chl-a in summer and minimum concentrations in winter. A series from the Sacramento–San Joaquin Delta illustrates very different patterns, with all three components fluctuating over a large range. Here, Chl-a varies from 0.05 to 155 μg L−1 (Fig. 3b), and this range includes large contributions of annual variability (y from 0.2 to 3.9), events of unusually high Chl-a (ε > 3), and a pronounced seasonal pattern with peak biomass in May (m = 2.4) and lowest biomass in winter–spring (m = 0.3 for December). A Chl-a series from the Oosterschelde reveals another set of patterns, with a large seasonal component (peak biomass in June–July) but small ranges of the other components (Fig. 3c). A series from Florida Bay (Fig. 3d) shows the converse, with a large range of the annual component but a weak seasonal pattern. These examples show that the magnitude of phytoplankton variability and the partitioning of that variability into different scales can vary markedly among ecosystems.

Fig. 3
figure 3

Examples of phytoplankton patterns of variability in estuarine–coastal ecosystems. For each site, blue lines are monthly series of Chl-a concentration; red bars are annual components y; purple lines are residual components ε, and green bars are standard seasonal patterns m (Eq. 4). The latter three terms—y, m, and ε—are dimensionless quantities with mean value 1. The examples illustrate: a small variability at all scales (Moreton Bay site 1, data provided by Ray Williams, Moreton Bay Ecosystem Health Monitoring Program); b large variability at all scales (Sacramento–San Joaquin Delta site D26, data from Interagency Ecological Program, Environmental Monitoring Program, http://www.bdat.ca.gov/); c large seasonal variability (Oosterschelde site OS1, data provided by Jacco Kromkamp, Netherlands Institute of Ecology, Center for Estuarine and Coastal Research); and d large annual variability (Florida Bay site 1, data from SERC-FIU Water Quality Monitoring Network, http://serc.fiu.edu/wqmnetwork/)

Full size image

Variability of Phytoplankton Patterns Across Ecosystems

For individual Chl-a series, the standard deviations of y (SD y ) and m (SD m ) are measures of annual and seasonal variability, respectively. We calculated these indices (as population standard deviations) from each of the 84 Chl-a series and show their probability distributions (Fig. 4) as another pattern of phytoplankton variability in estuarine–coastal waters. The standard deviations of y are mostly clustered in a small range of 0.2–0.4 (Fig. 4a). The distribution is skewed, with a few sites having unusually high variability of the annual component—e.g., Florida Bay 1, North San Francisco Bay, Ringkøbing Fjord, Gulf of Naples, and Tampa Bay. Other sites, such as Villefranche Bay and Bedford Basin, have unusually small variability of the annual component. The standard deviations of the seasonal component m are more broadly distributed over the range 0.1–0.6 (Fig. 4b), and a few sites have unusually large seasonal variability—Oosterschelde, Westerschelde, North Inlet, and South San Francisco Bay. These results tell us that seasonal variability is generally higher (median SD m  = 0.39) and distributed over a broader range than annual variability (median SD y  = 0.30) and that some sites stand out with large deviations from central tendencies of annual and seasonal variability. The residual component ε (Fig. 4c) is more variable than the others (median SDε = 0.59), so sources of phytoplankton variability beyond an average seasonal pattern and fluctuations of the annual mean are important. This source is weak in some places, such as the Gulf of Aqaba and Villefranche Bay, but strong in others such as regions around Hong Kong (Deep Bay, Victoria Harbor) and the upper Neuse River Estuary.

Fig. 4
figure 4

Probability distributions of the standard deviations of three components of phytoplankton variability extracted from Chl-a time series at 84 estuarine–coastal sites. The mean value of each (dimensionless) component is 1, so these standard deviations are equivalent to coefficients of variation

Full size image

Results in Fig. 4 show global phytoplankton patterns as distributions of three components of Chl-a variability measured at 84 sites. But they do not tell if these components are interrelated at individual sites. For example, is there a common ratio in the partitioning of Chl-a variability into seasonal and annual components? We compared this partitioning across all sites with a bubble plot (Fig. 5) in which distance along the X- and Y-axis measures annual and seasonal variability, and circle size measures variability of monthly events. This comparison reveals a dispersion of individual patterns. Some ecosystems have low and comparable variability of all components (e.g., sites in Seto Inland Sea, Moreton Bay, Biscayne Bay, and Gironde Estuary); others have high and comparable variability of all components (e.g., sites in the northern coastal Adriatic Sea, Gulf of Naples, Sacramento–San Joaquin Delta, and seaward Neuse River Estuary). Variability in others is dominated by fluctuations of only one component, either seasonal (e.g., Oosterschelde, Bilbao Estuary, Westerschelde, Urdaibai Estuary), annual (e.g., Florida Bay, North San Francisco Bay, Ringkøbing Fjord), or events (e.g., landward Neuse River Estuary, Victoria Harbor, Tolo Harbor). The ratio SD m to SD y varies from 0.17 to 4.5, showing a 25-fold range in the relative importance of seasonal and annual variability. Apparently, there is no universal rule to describe the dominant timescales of phytoplankton variability in these ecosystems.

Fig. 5
figure 5

Bubble plot comparing patterns of chlorophyll-a variability across 84 sites sampled within 51 estuarine–coastal ecosystems. X-axis measures variability of the annual component as standard deviation of y (see Eq. 4), hypothesized to be an index of disturbance from human actions and shifts in the climate system. Y-axis measures variability of the seasonal component as standard deviation of m, hypothesized to be an index of the importance of the annual climate cycle. Circle size measures variability of the residual component as standard deviation of ε, hypothesized to be an index of nutrient enrichment. Data sources are listed in Table S1. Key to sites: 1 Adriatic Sea (North)-SJ103; 2 Adriatic Sea (North)-SJ107; 3 Adriatic Sea (North)-SJ108; 4 Bahia Blanca Estuary-Cuatreros; 5 Baltic (northern)-H03; 6 Baltic (The Sound)-PQ02; 7 Bedford Basin-2; 8 Bilbao Estuary-34-35; 9 Biscayne Bay-123; 10 Biscayne Bay-127; 11 Biscayne Bay-133; 12 rade de Brest-Portzic; 13 Chesapeake Bay-CB1.1; 14 Chesapeake Bay-CB4.1C; 15 Chesapeake Bay-CB8.1; 16 Choptank River Estuary-ET5.1; 17 Deep Bay-DM1; 18 Deep Bay-DM5; 19 English Channel Roscoff-Estacade; 20 Florida Bay-1; 21 Florida Bay-12; 22 Florida Bay-19; 23 Gironde Estuary-Eyrac; 24 Golfe de Lion-Sola; 25 Great Belt-670005; 26 Gulf of Aqaba-Eilat; 27 Gulf of Naples; 28 Gulf of Trieste-000F; 29 Gulf of Trieste-00CZ; 30 James River Estuary-RET5.2; 31 Kattegat-431; 32 Kattegat-925; 33 Long Island Sound-B3; 34 Long Island Sound-H6; 35 Long Island Sound-M3; 36 Moreton Bay site 1; 37 Moreton Bay site 2; 38 Nanticoke River Estuary-ET6.2; 39 Narragansett Bay-2; 40 Neuse River Estuary-160; 41 Neuse River Estuary-30; 42 Neuse River Estuary-70; 43 North Inlet Estuary-OL; 44 Odense Fjord-690001; 45 Oosterschelde-OS1; 46 Oosterschelde-OS5; 47 Oosterschelde-OS8; 48 Patos Lagoon; 49 Patuxent River Estuary-RET1.1; 50 Port Shelter-PM2; 51 Port Shelter-PM8; 52 Potomac River Estuary-RET2.2; 53 Rappahannock Estuary-RET3.2; 54 Rhode River Estuary-3.8; 55 Ringkøbing Fjord; 56 Sacramento–San Joaquin Delta-D26; 57 San Francisco Bay (North)-13&D41; 58 San Francisco Bay (North)-6&D8; 59 San Francisco Bay (South)-21; 60 San Francisco Bay (South)-27; 61 San Francisco Bay (South)-32; 62 Seto Inland Sea-16; 63 Seto Inland Sea-21; 64 Seto Inland Sea-6; 65 Stonehaven, Coastal Atlantic; 66 Tampa Bay-14; 67 Tampa Bay-64; 68 Tampa Bay-8; 69 Tampa Bay-93; 70 Ten Thousand Islands-69; 71 Ten Thousand Islands-73; 72 Tolo Harbor-TM3; 73 Tolo Harbor-TM7; 74 Urdaibai Estuary-30; 75 Urdaibai Estuary-34-35; 76 Victoria Harbor-VM1; 77 Villefranche Bay-B; 78 Wadden Sea; 79 Westerschelde-Bath; 80 Westerschelde-Doel; 81 Westerschelde-Vlissingen; 82 Whitewater Bay-40; 83 Whitewater Bay-49; 84 York River Estuary-RET4.3

Full size image

Processes that Generate Phytoplankton Patterns

We are still in the descriptive natural history phase of phytoplankton research, and our knowledge base is far from that required to explain variability of phytoplankton communities documented in observational records (Smetacek and Cloern 2008). Why does phytoplankton biomass fluctuate mildly in some places and wildly in others? Why do some estuarine–coastal ecosystems have recurrent seasonal patterns that persist from year to year, while others have no seasonal regularity but large variations from year to year? Why is phytoplankton variability in some ecosystems dominated by irregular events? Patterns can provide strong clues about processes of variability, and we conclude with three hypotheses building toward a conceptual framework for explaining the high diversity of phytoplankton patterns illustrated above.

Annual Variability

We examined outliers in the distributions of Fig. 4 to search for clues about processes that give rise to large variability of the individual components. Annual variability at most sites falls within a narrow range, but a few sites have exceptionally large annual variability (Fig. 4a). These sites share a common attribute—disturbance from natural events or human actions. For example, a site in eastern Florida Bay had the largest annual variability. This resulted from an abrupt Chl-a increase during 2005 and 2006, a departure from the low-biomass state during the preceding 13 years (Fig. 3d). This biomass increase was caused by the combined effects of human disturbance (road construction) and passage of three hurricanes that, together, mobilized phosphorus and increased P inputs to this oligotrophic habitat (Rudnick et al. 2006). High annual variability in North San Francisco Bay is the result of a fivefold decline in Chl-a after the introduction and population explosion of a nonindigenous filter feeder, the clam Potamocorbula amurensis (Alpine and Cloern 1992). Mean Chl-a decreased sixfold in the Ringkøbing Fjord after operations of a sluice were modified to increase exchanges with the North Sea, leading to increases in salinity that allowed colonization by the clam Mya arenaria (Petersen et al. 2008). High annual variability in Tampa Bay reflects a trend of decreasing biomass following implementation of policies to reduce anthropogenic inputs of nitrogen and phosphorus (Greening and Janicki 2006). Therefore, disturbances that alter nutrient supply or grazing can cause large, sometimes abrupt, changes in phytoplankton biomass and generate annual variability beyond the narrow range characteristic of estuarine–coastal ecosystems.

Other sites with large components of annual variability had changes in Chl-a associated with shifts or trends of climatic forcing. For example, a trend of declining phytoplankton abundance in the Gulf of Naples occurred during a period of increasing winter cloudiness and intensification of winds (Zingone et al. 2009). Phytoplankton biomass declined in Narragansett Bay (Borkman and Smayda 2009) and nearby Massachusetts Bay (Keller et al. 2001; Hunt et al. 2009) after the North Atlantic Oscillation index shifted from negative to positive. The mechanism appears to be earlier winter warming and control of phytoplankton growth by copepods during the positive phase of the North Atlantic Oscillation. Phytoplankton biomass increased and seasonal patterns changed in South San Francisco Bay after the northeast Pacific shifted from its warm to cold phase after 1998, and the mechanism there was an ocean-derived trophic cascade leading to reduced abundance of bivalves (Cloern et al. 2007). Therefore, observational time series in estuarine–coastal ecosystems are providing compelling evidence that long-term patterns of phytoplankton variability arise from changes in the large-scale climate system and disturbances from human activities. The underlying processes of these patterns are often shifts in top-down control of phytoplankton biomass by pelagic or benthic grazers.

Seasonal Variability

Phytoplankton seasonal variability is more broadly distributed across sites than annual variability but, again, a few sites stand out with exceptionally large seasonal components (Fig. 4b). These sites have a recurrent seasonal pattern with a relatively high amplitude (e.g., Fig. 1a), unlike most others where a regular seasonal pattern is absent (Fig. 1b) or less pronounced or where the seasonal pattern changes over time (see Cloern and Jassby 2008, Fig. 3). As we extend observational records for periods longer than a decade, it is becoming increasingly evident that shifts in phytoplankton seasonal patterns are common in estuarine–coastal ecosystems (e.g., Wasmund et al. 2008; Borkman and Smayda 2009). What attributes, then, allow regular seasonal patterns to persist in places like the Oosterschelde, Westerschelde, and North Inlet (Fig. 4b)?

Recurrence of one pattern, such as the ocean’s canonical spring bloom, implies control by a periodic process tied to astronomical forcings, such as the annual cycles of temperature, solar radiation, and photoperiod. For example, the spring-bloom pattern in South San Francisco Bay is generated by a strong annual cycle of bivalve grazing that peaks in summer–autumn as bivalve biomass grows and temperature-regulated filtration rate increases (Thompson et al. 2009). Regular seasonal patterns at some other sites might also result from strong grazer control that oscillates over the annual temperature cycle. Suspension-feeding bivalves are abundant in the Oosterschelde where cockles and mussels are cultured (Smaal et al. 2001), and the seasonal Chl-a pattern in North Inlet is coherent with seasonal filtration rates by oyster reefs (Dame et al. 1992). Regular seasonal patterns develop at other sites where blooms are triggered by annual cycles of temperature and photoperiod (Shikata et al. 2008), river inflow (Malone et al. 1988), and daily insolation (Sinclair et al. 1981).

If large seasonal components imply strong control of phytoplankton variability by annual climatology, then what determines the relative strength of climatologically driven forcings versus those that fluctuate over shorter and longer timescales? One determinant appears to be latitude, because SD m is strongly positively correlated with the absolute latitude (correlation coefficient \( \rho = 0.40,\ p < 0.001,\ df = 82 \)). This result is consistent with Cushing’s (1959) iconic depiction of phytoplankton seasonal patterns that are damped near the equator but grow in amplitude at high latitudes. However, definitive determination of a latitude effect will require observations from tropical and subtropical sites because our compilation includes no Chl-a series below absolute latitude 22°.

Event-Scale Variability

The largest component of chlorophyll variability is the residual (Fig. 4c), which measures sources of variability that cannot be attributed to an average seasonal pattern or fluctuations in the annual mean. This term can be large where the seasonal pattern changes strongly from year to year. As well as true deviations from a long-term average seasonal pattern, the residual component also includes variability associated with sampling errors that can be large when single measurements are used as estimators of monthly mean Chl-a concentration. Phytoplankton communities and biomass change on many scales at the same time (Li et al. 2009). Large changes can occur at timescales shorter than a month (e.g., Abreu et al. 2009), and monthly scale changes in Chl-a can arise from processes operating at shorter timescales (Lucas and Cloern 2002). Sampling at monthly or even weekly frequency imposes constraints on the scales at which variability can be resolved and provides indices of monthly variability that have potentially large errors (Jassby et al. 2005). A third contribution to the residual component that is not an artifact of sampling frequency is the occurrence of singular events of exceptionally high biomass, such as red tides. These events contribute to the spikiness apparent in some time series (Fig. 1), and the decomposition technique isolates these events so they can be visualized (Fig. 3). Sites having the largest residual component of Chl-a variability (Fig. 4c) are, in fact, high-nutrient habitats in which red tides or other exceptional blooms develop in response to weather events, such as coastal waters of Hong Kong (Yin 2003) and the Neuse River (Paerl et al. 2004). Sites having the smallest residual component are low-nutrient coastal waters such as the Gulf of Aqaba, Villefranche Bay, and rade de Brest. Therefore, although the residual includes multiple sources of variability, it does appear to index exceptional bloom events that can only develop when nutrient stocks are high.

A Conceptual Framework

Ecologists expect to find some common structure to biological dynamics across similar ecosystems, but the dispersion of patterns depicted in Fig. 5 shows little structure to phytoplankton variability in estuarine–coastal ecosystems. Instead, these results show that the relative importance of variability at three timescales follows continuous distributions that cannot be classified into a small set of common behaviors. The three components of variability are uncorrelated, so position of a site along each continuum is independent of position along the others. Position along each continuum is determined by the relative strength of processes operating at timescales of years, months, or events. Case studies presented above suggest the hypotheses that: position of a site along the X-axis of Fig. 5 is a measure of disturbance from human actions or climatic shifts; position along the Y-axis is a measure of the relative strength of forcings associated with the annual climate cycle; and circle size is determined in part by the degree of nutrient enrichment. We propose this conceptual framework as a starting place for the next step of comparative analyses to identify the dominant processes and timescales of phytoplankton variability at individual sites. Ultimately, site-specific mechanistic understanding of phytoplankton dynamics is required to explain why the patterns are so diverse and to understand the ecological significance of this diversity.