The role of persuasion in cultural evolution dynamics

Abstract

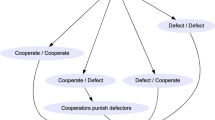
We analyze the evolution of a society in which types evolve not only depending on how much they are fit but also on how much they are able to persuade others about their fitness. This mechanism makes possible to reach equilibria not feasible under standard dynamics. We first provide necessary conditions for a generic matrix and generic class of cultural competition mechanisms in order to observe polymorphic equilibria, comparing it with the standard case. Then, necessary and sufficient conditions for polymorphic equilibrium stability are provided in the case of particular competition rule family, at each competition level. We show that some social dilemmas as prisoner’s dilemma or stag hunt can have their dynamics dramatically changed. We then analyze the prisoner’s dilemma framework finding that also full cooperation is sustainable in equilibrium. Finally we show that this persuasion mechanisms generally increase the equilibrium aggregate production of the society.

Appendices

Appendix 1: Proofs of Propositions

1.1 Proof of Lemma 1

Consider a heterogeneous matching ij with $i\in \{A\}$ and $j\in \{B\}$. Then $\pi _t^{ij}=\beta q_t^{ij}(\bar{\tau }_t)+\gamma (1-q_t^{ji}(\bar{\tau }_t))-c(\tau _t^{i})$, with $\beta q_t^{ij}(\bar{\tau }_t)+\gamma (1-q_t^{ji}(\bar{\tau }_t))$ being the utility of playing a given $\tau _t^{i}$ and $c(\tau _t^{i})$ being the cost. Call $MU(\tau _t^{i})$ the marginal utility of playing $\tau _t^i$. Since Assumption 2a holds, then $MU(\tau _t^{i})\ge 0, \forall \tau _t^{i}>0$ and is monotonic in $\tau _t^{i}$. Thus if $c^{\prime }(\tau _t^{i})|_{\tau _t^{i}=0}=0$ and $c^{\prime }(\tau _t^{i})|_{\tau _t^{i}=1}>(\beta \frac{\partial q_t^{ij}(\bar{\tau }_t)}{\partial \tau _t^{i}}-\gamma \frac{\partial q_t^{ji}(\bar{\tau }_t)}{\partial \tau _t^{i}})|_{\tau _t^{i}=0}$, as Assumption 1 requires, then there exist a unique optimal $\tau _t^{i*}$, and $\tau _t^{i*}\in (0,1)$. The same proof holds for $\tau _t^{j*}$ so that it is also unique and $\tau _t^{j*}\in (0,1)$.

1.2 Proof of Proposition 1

Consider the first part of the proposition. Suppose that Assumption 2b holds so that $\bar{q}_t$ is independent from $p_t$. Given the set of Eq. 1, then also $\pi _t^{ij}$ is independent from $p_t$, $\forall i\ne j$. Consider now the dynamics in Eq. 3. A polymorphic equilibrium exists if and only if there exists a $p^*$ such that $\pi ^A=\pi ^B$. Reminding that $\pi ^A$ and $\pi ^B$ are averages payoffs defined in the set of Eq. 2, then this happen whenever $p\alpha +(1-p)\pi _t^{AB}-p\pi _t^{BA}-(1-p)\delta =0$. Since this is linear in p, then there exists at most one $p^*$ such that this condition is satisfied. Thus, if it exists, the polymorphic equilibrium is unique.

Consider now the second part of the proposition. Since there exists at most one polymorphic equilibrium, then a necessary and sufficient condition for its existence is that the points $p=0$ and $p=1$ are unstable. Call $\Delta _t\equiv \pi _t^{A}-\pi _t^{B}$, then instability conditions of the extreme points can be rewritten as $\Delta _t|_{p=0}>0$ and $\Delta _t|_{p=1}<0$. Given (3) we have that $\Delta _t|_{p=0}=\beta q_t^{AB}+\gamma (1-q_t^{BA})-c(\tau _t^{A})-\delta$ and $\Delta _t|_{p=1}=\alpha -\beta (1-q_t^{A})-\gamma q_t^{B}+c(\tau _t^{B})$.

A necessary condition for $\Delta _t|_{p=0}>0$ is that $c(\tau _t^{A})<\beta q_t^{AB}+\gamma -\gamma q_t^{BA}-\delta$. Since $c(\tau _t^{A})>0$, in order to have this it is necessary that $q_t^{BA}<\frac{\beta q_t^{AB}+\gamma -\delta }{\gamma }$ that, since $q_t^{BA}\in [0,1]$, can be true only if $\frac{\beta q_t^{AB}+\gamma -\delta }{\gamma }>0$. This happens when $q_t^{AB}>\frac{\delta -\gamma }{\beta }$ that, since $q_t^{AB}\in [0,1]$, it is satisfied only if $\frac{\delta -\gamma }{\beta }<1$ and thus $\beta +\gamma >\delta$.

Using the same reasoning, take $\Delta _t|_{p=0}<0$: This is satisfied when $c(\tau _t^{B})<\gamma q_t^{BA}-\alpha +\beta -\beta q_t^{AB}$. Since $c(\tau _t^{B})>0$, the previous condition is satisfied only if $\gamma q_t^{BA}-\alpha +\beta -\beta q_t^{AB}>0$. This happens when $q_t^{AB}<\frac{\gamma q_t^{BA}-\alpha +\beta }{\beta }$ that, since $q_t^{AB}\in [0,1]$, it holds only if $\frac{\gamma q_t^{BA}-\alpha +\beta }{\beta }>0$, that is to say $q_t^{BA}>\frac{\alpha -\beta }{\gamma }$. Since $q_t^{BA}\in [0,1],$ then this happens only if $\frac{\alpha -\beta }{\gamma }<1$ so that only if $\beta +\gamma >\alpha$.

1.3 Proof of Proposition 2

Consider the problem each agent faces. Using Mathematica software, by substituting the q-Rule equations into $\pi _t^{AB}$ and $\pi _t^{BA}$ and solving the first-order conditions we get

$$\begin{aligned} \begin{array}{l} \tau _t^{A^*}=\frac{2\beta ^2(z-1)^2+\gamma (1-z)(2-z\gamma )+\beta (5z-3z^2-2)}{2(1+(\beta -\gamma )^2(z-1)^2)}\\ \tau _t^{B^*}=\frac{\beta ^2(z-1)z+\gamma (z+2\gamma (z-1)^2)+\beta (1-z)(2-2\gamma +3z\gamma )}{2(1+(\beta -\gamma )^2(z-1)^2)}\\ \end{array} \end{aligned}$$

(4)

Substituting now these values into $\pi _t^A$ and $\pi _t^B,$ we are able to compute $\Delta _t=\pi _t^A-\pi _t^B$. We thus have that $p=0$ is unstable if and only if $\Delta _t|_{p_t=0}>0$ and $p=1$ is unstable if and only if $\Delta _t|_{p_t=1}<0$. By solving $\Delta _t|_{p_t=0}=0$ with respect to $\delta,$ we obtain $\bar{\delta }$ and by solving $\Delta _t|_{p_t=1}=0$ by $\alpha$ we obtain $\bar{\alpha }$. What remains is then to check that $\bar{\delta }\in (0,1)$ and $\bar{\alpha }\in (0,1)$.

1.4 Proof of Proposition 3

This proposition is proved just by substituting in $\bar{\delta }$ and $\bar{\alpha }$ the values of $\beta =1$ and $\gamma =0$ and noting that $\bar{\delta }>\bar{\alpha }$ so that all 4 areas are feasible in the space $(\alpha , \delta )\in (0,1)^2$ with $\alpha <\delta$.

1.5 Proof of Proposition 4

Suppose first that the third party is considering the possibility of lowering the competition, so that z becomes higher. We now analyze how this change in z affects $\bar{\alpha }$, $\bar{\delta }$ and the stability properties of equilibria. Now, if $p=1$ is an unstable outcome, an increase in z does not change stability properties of this point. In order to see this, notice, with the help of Fig. 3, that an increase from z to $z^{\prime }$ makes $\bar{\alpha }(z)<\bar{\alpha }(z^{\prime })$ so that if $\alpha <\bar{\alpha }(z)$ then it is also $\alpha <\bar{\alpha }(z^{\prime })$. In this way $p=1$ is unstable under $z^{\prime }$. Following the same reasoning, if $p=1$ is a stable outcome an increase from z to $z^{\prime }$ may make $p=1$ to become unstable since in this case it can happen that $\alpha >\bar{\alpha }(z^{\prime })$. Consider now the point $p=0$. Now, if $z>\bar{z}$ and $p=0$ is unstable, an increase in z can make it stable, while if $p=0$ is stable nothing changes. In fact, in the first case since $\bar{\delta }$ is decreasing in z, it can happen that $\delta <\bar{\delta }(z)$ but $\delta >\bar{\delta }(z^{\prime })$; in the second case if $\delta >\bar{\delta }(z)$ it has to be valid that $\delta >\bar{\delta }(z^{\prime })$. Differently from these cases, by applying the same properties, if $z<\bar{z}$ and $p=0$ is unstable, then an increase in z does not change the stability properties of the point while if $p=0$ is stable an increase in z can make it unstable. Thus, if competition level is low enough ($z>\bar{z}$), then lowering it may have a positive effect on the presence of C agents in the long run, while if $z<\bar{z}$ this policy may induce instability in both extreme points. Consider now the case for an increase in competition level from z to $z^{\prime \prime }$. If $p=1$ is stable, then this policy does not change the stability property of the point, while if $p=1$ is unstable it may make it stable. Consider now $p=0$. If $z>\bar{z}$ and $p=0$ is stable, then a decrease in z can make it unstable, while nothing changes in the case in which $p=0$ is unstable. On the contrary if $z<\bar{z}$ and $p=0$ is stable, then a decrease in z has no effect while if $p=0$ is unstable it may make it stable. Thus we can summarize by saying that if competition is low such that $z>\bar{z}$ making competition higher does not decrease the long-run presence of NC agents in the society, while augmenting it may induce stability in the extreme points. All these results can be summed up in the following statement.

Appendix 2: Areas extensions

We now provide the formulas for the extensions of the 4 areas of Fig. 1 if a PD-like matrix occurs. Notice first that since $\bar{\delta }>\bar{\alpha }$ , then as stated by Proposition 3 all 4 areas are feasible. We define $\Delta i\equiv \frac{\partial Areai}{\partial z}$ $\forall i\in \{I, II, III, IV\}$, $D\bar{\alpha }\equiv \frac{\partial \bar{\alpha }}{\partial z}$ and $D\bar{\delta }\equiv \frac{\partial \bar{\delta }}{\partial z}$. Now,

• Area I: The extension of area I is given by $\bar{\alpha }(1-\bar{\delta })$ so that $\Delta I=(1-\bar{\delta })D\bar{\alpha }-\bar{\alpha }D\bar{\delta }$

• Area II: The extension of area II is given by $\frac{[(1-\bar{\alpha })+(\bar{\delta -\bar{\alpha }})](1-\bar{\delta })}{2}$ so that $\Delta {II}=\bar{\alpha }D\bar{\delta }+\bar{\delta }D\bar{\alpha }-\delta D\bar{\delta }-D\bar{\alpha }$

• Area III: The extension of area III is given by $\frac{(\bar{\delta }-\bar{\alpha })^2}{2}$ so that $\Delta III=(\bar{\delta }-\bar{\alpha })(D\bar{\alpha }-D\bar{\delta })$

• Area IV: The extension of area IV is given by $\frac{[\bar{\delta }+(\bar{\delta }-\bar{\alpha })]\bar{\alpha }}{2}$ so that $\Delta IV=\bar{\alpha }D\bar{\delta }+\bar{\delta }D\bar{\alpha }-\bar{\alpha }D\bar{\alpha }$

Substituting the threshold values and their first derivatives, then Fig. 4 is produced.