1 Introduction

In agriculture, electric fences are predominantly used to keep animals outside or within the area. The fencing of fertile sites or valuable lands as a protection against wildlife is also very important. In recent years, classic steel wires or high-tension plated wires have been replaced by fences made of polymer monofilaments (MFs) and conductive wires in the form of tapes or ropes. Electric fences are designed to create an electrical circuit when touched by a person or animal. The pulse is very short and is then repeated every 1 s. This pulse is commonly referred to as a shock and is felt by the animal or person touching the wire in the fence and the earth during a pulse, which completes an electrical circuit. The animal then remembers the unpleasant experience and will avoid touching the fence again even if it is inactive. The present research is focused on electric tape fencing with respect to the wellbeing of fast-moving animals, especially horses. Safety is, of course, the foremost concern when designing fences. In general, the stronger the fence, the less likely the horse is to escape. Conversely, the stronger the fence, the more likely the horse is to injure himself during a panic. Empirical studies show that a horse trapped in a fence cannot usually free himself. The soft tissues of the front and hind limbs are injured very often. For horses, for example, electric fences with high visibility (e.g., distinctive color and high width) and moderate strength are preferred.

Electric tape fences are made of two components: (a) polymer MFs (usually polyethylene or polypropylene) and (b) metal wires (copper or stainless steel) combined by weaving process. This type of woven fabric is created in full width and arbitrary length using the so-called needlework ribbon fabric technology. Unlike conventional fabrics, fence tapes have only one solid edge, particularly located on the left side. The second edge is usually reinforced by a chain. For tapes of this type, a double weft and different preparations of warp threads are typical. The warp thread is directly fed into the fabric from the creels rather than from the warp drum. The tape is woven by a combination of a plain-weave pattern and plain-weave-derived patterns, such as warp rib, weft rib, and matt rib, which are the strongest and most stable patterns. The metal component, i.e., the wire, is interwoven into the warp of the fabric along with polymer MFs with different flotations. The flotation of wires is woven with a shift due to the fence protection against destructions by, for example, branches. The tape pattern is provided by pattern sheets. For some tapes, the wire is also incorporated into the weft system, which is ensured by the addition of a second feeder. Electric tape fences are strong, durable, and highly visible, and therefore, they are ideal for containing fast-moving animals, such as horses. Electric tapes usually come in three thickness widths: 12, 20, and 40 mm. The narrow tapes should be used to construct an electric tape fence in windy areas, as they have less resistance to wind.

To describe the rheological properties of textile products in general, there have been used various models starting from 1930s as mentioned here [1]. One of the firsts was Voigt–Kelvin’s model followed by Vangheluwe’s model [2] in which a spring with non-linear characteristics is incorporated. Later, Eyring’s dumper was newly introduced to the model [3]. Unfortunately, the output was a non-linear differential equation with no analytic solution. When researching scientific papers over the last 10 years, these interesting papers may be pointed out. For example, the viscoelastic behavior of fibers during woven fabric bagging is investigated and prediction model based on modulus, relaxation time, and weighting constants is proposed in [4]. Simple rheological model consisting of linearly elastic element frictional element was used to study creasing of fabrics in [5, 6]. Kinematic model for a continuum representation of woven fabric was presented and validated with good agreement with experimental data in [7]. A new rheological model describing the compressional behavior of non-woven fabrics is described in [8] together with verification using 19 nonwovens with high level of correlation between theoretical and experimental data set. New rheological model base on theory of plastic-elastic solids was presented in [1]. The model consists of two Hooke’s springs, frictional element and a piston. This model can be used for a description of mechanical behavior of textiles subjected to the tension or compression loads. The presented model was used for the description of relaxation of polypropylene monofilaments subjected to tensile load and rheological properties of non-woven fabrics subjected to the compression loads with no significant difference between theoretical and experimental data. In [9], a numerical model for the evaluation of the mechanical properties of dry MF technical textiles is presented. The tensile and friction properties of single fibers and axial and biaxial behaviors of specimens cut from geotextiles were experimentally studied to calibrate the numerical model. The proposed numerical model could be a tool for the design of various applications of technical textiles. An analytical model for the prediction of mechanical properties of plain weaves and MF technical textiles based on a theory of curved beams is described in [10]. This model takes into consideration the fiber–fiber contact using an elastic spring. The proposed analytical model provides a satisfactory prediction of the mechanical behavior of technical textiles assuming simplifications of the textile geometry. Paper [11] describes the load–extension behavior of ribbon parachute fabrics for cluster sub munitions. The effect of warp density and fiber type on the ribbon fabric performance using strip tensile and tearing tests was studied, and the results show that the breaking load and Young’s modulus increase for strip tensile testing with increasing warp density at the core zone of the fabric. The effect of weave type was found to be insignificant for the tear test [11]. From the point of view of rheological and mechanical properties, electric fences are a nearly undescribed product. Manufacturers have reported the kilogram strength value, material composition, and electrical conductivity of the product and recommend the methods, length, and style of electric fence installation to achieve the highest efficiency in fencing animal farms. However, mechanical properties have not been mentioned or discussed. Related to this is also the need to describe tensile behavior using rheological models. These models can be used both to compare and predict the chosen mechanical characteristics of different fences. To the best of our knowledge, no research has yet been conducted on the rheological and mechanical properties of these types of special hybrid technical textiles, despite the fact that ultimate mechanical characteristics and overall mechanical behavior of fences are of very great importance.

In the present study, nine different specimens of tape electric fences were chosen to explore the material composition, structure, and force–strain responses in the tension of two special component technical textiles. Commonly used tape electric fences were chosen for the horse fencing design. A detailed survey of mechanical properties, including yield point and stiffness coefficient determination, was realized for three representative fences chosen from the main sample set after a quasi-static testing. To characterize the electric tape fence viscoelasticity, dynamic tests and stress–relaxation tests were performed for the same three fence representatives taking into consideration two different deformation rates. Relaxation times and force constants were studied, and a rheological model in generalized form was then proposed.

2 Materials

For the analysis of the materials, structure, and mechanical properties of tape fences, nine samples with different construction parameters were selected from a commercial program of the producers (see Table 1). The thickness of the samples was evaluated using the method proposed in [12], and the width of the sample and diameter of MFs and wires were measured using a digital caliper. The sample coding and main geometrical characteristics are shown in Table 1. Figure 1 shows images of the samples, and Fig. 2 shows the schematic diagrams of the woven tape fences. The material composition of the samples was examined using differential scanning calorimetry, and the results confirmed that all MFs are made of polyethylene and all wires are alloys with the following material composition: 82.3% Cu, 7% Fe, 5.4% Sn, 4.4% Cr, and the remaining percentages with Mn and Mo.

Table 1 Main geometrical characteristics of the electric fence samples
Full size table
Fig. 1
figure 1

Macroscopic images of the electric fence samples

Full size image
Fig. 2
figure 2

Schematic diagrams of the samples. The red and blue colors represent the wires (blue color indicates the wire with a higher diameter), and the black and gray colors represent the MFs (gray color indicates MFs with a higher diameter) (for further details, see Table 1)

Full size image

3 Methods

Because of the large deformation in the geometrical dimensions of the samples during uniaxial loading, conventionally used relationships [Eqs. (1) and (2)] were replaced by Eqs. (3) and (4), which better reflect the essence of the tensile stress of the tape fence samples.

$$\sigma =E\varepsilon ; \sigma =E\varepsilon +{\sigma }_{P } (\mathrm{Elastics};\mathrm{ elasto}-\mathrm{plastic\ element})$$
(1)
$$\tau \dot{\sigma } + \sigma = E\tau \dot{\varepsilon } \, \left( {\text{Maxwells viscoelastic element}} \right)$$
(2)
$$F=kl ; \quad F=kl+{F}_{P}$$
(3)
$$\tau \dot{F}+F=k\tau \dot{l}$$
(4)

where σ is uniaxial stress [Pa], ε is uniaxial strain [−], \(\dot{\varepsilon }\) is strain rate [s−1], E is Young’s modulus [Pa], τ is relaxation time [s], F is uniaxial force [N], \(l\) is uniaxial displacement [m], \(\dot{l}\) is deformation rate [m.s−1], and k is stiffness coefficient [N.m−1].

The chosen approach can avoid the difficult monitoring of changes in the cross sections of fences. However, the obtained empirical results are not always automatically comparable. Considering the goals of this study, the complications are not a major obstacle.

3.1 Quasi-Static Tensile Deformation Test

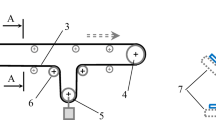
The tensile properties of the tape fence samples, including strength and deformation, were examined under quasi-static loading conditions using the testing systems TIRAtest 2300 and Testometric M-350-5CT with load capacity ranging from 10 to 100 kN according to the ISO 13934 standard [13]. The tests were performed with the full widths of the samples in the warp direction. The measurement conditions were as follows: deformation rate (speed of the clamps) v = 100 mm/min, distance between the clamps of the tensile strength tester l0 = 100 mm, and temperature T = 23 ± 2 °C, RH = 50 ± 5%. The measurement was performed at five different sample locations for a subsequent statistical analysis. A detailed survey of the tensile properties was conducted for the three chosen electric tape fence sample sets, i.e., sample nos. 1, 3, and 5. Load–displacement curves were also further studied. In rheology, this dependence can be described through a combination of two parallel elastic elements (springs) with one St. Venant plastic element (see the first two branches of the model shown in Fig. 4d). Stiffness coefficients (k1, k2) and plasticity limit (P having coordinates [lP, FP]) were determined using the approximation of curves using two straight lines (see Fig. 3). For l ≤ lP, elastic deformation occurs and Eq. (5) can be used. For l > lP, plastic deformation occurs, and Eq. (6) can be used for the description of the tape fence mechanical behavior.

$$F = (k_{1} + k_{2} )l \quad {\text{ for }}l \le l_{P}$$
(5)
$$F = k_{1} (l - l_{P} ) + F_{P}\quad {\text{ for }}l > l_{P}$$
(6)
Fig. 3
figure 3

Schematic diagram of the load–displacement curve

Full size image

3.2 Dynamic Tensile Deformation Test

To characterize the electric tape fence viscoelasticity, dynamic tests and stress–relaxation tests were performed for the same three fence representatives (sample nos. 1, 3, and 5) taking into consideration two different deformation rates. The tests were performed with the full width of samples in the warp direction. The measurement conditions were as follows: testing device = TIRAtest 2300; deformation rates v1 = 100 mm/min and v2 = 200 mm/min; distance between the clamps of the tensile strength tester l0 = 100 mm; and temperature T = 23 ± 2 °C, RH = 50 ± 5%. The measurement was performed at five different sample locations for each deformation rate for the subsequent statistical analysis.

Based on the load–displacement curves gained from the quasi-static deformation test, three interesting deformation levels (expressed as l [mm]) were identified for each sample first (see Table 2). These levels include (a) the state before starting the irreversible deformation (R1), (b) state in the middle of the irreversible deformation (R2), and (c) state before the sample breaks (R3). Stress–relaxation tests were performed according to the scheme presented in Fig. 4a. After reaching the lR1 and lR2 positions, respectively, the relaxation of sample ΔT = 30 s occurs. After reaching the lR3 position, the clamps immediately return to the starting position.

Table 2 Specific deformation levels lRi for the three chosen samples
Full size table
Fig. 4
figure 4

a Scheme of the relaxation test, b load–displacement curve during the stress–relaxation test, c load–time curve during the stress–relaxation test, d proposed rheological model for the electric tape fences

Full size image

The magnitude of F [N] in the sample deformations described by points R1, R2, and R3 using v1 = 100 mm/min (R1’, R2’, R3’ using v2 = 200 mm/min) was extracted from the measured data (Fig. 4b) to check the statistically significant effect of different deformation rates using the hypothesis testing and, more precisely, two-sample t tests.

The relaxation parts of curves F = F (t) were approximated by Eq. (7) using the least squares method (see Fig. 4c). The accuracy of the approximation was evaluated using the mean squared error (MSE).

$$F = F_{A} e^{{ - \frac{t}{{\tau_{3} }}}} + F_{B} e^{{ - \frac{t}{{\tau_{4} }}}} + F_{C} ,$$
(7)

where FA, FB, and FC [N] are the force constants and τ3 and τ4 [s] are the relaxation times.

From a rheological point of view, the relaxation dependence given by Eq. 7 can be described by a combination of two parallel Maxwell’s viscoelastic materials supplemented by an elastic or elastic–plastic component in parallel (see Fig. 4d).

Based on the above-mentioned consequences, the selected electric fences can be viewed as a visco-elasto-plastic material. The following text describes the verification of proposed rheological model consisting of four elastic constants (k1 to k4 [N.m−1]), two viscous constants (τ3, τ4 [s]), and one plastic constant (FP [N] (see Fig. 4d). In this model, the four combinations of simple elements [14] are connected in parallel. The branches containing Maxwell elements described by elastic constant k1 and k2 and sliding element represent together force FC. The branch containing Maxwell element with constant parameter k3 and the dash-pot element described by viscous constant τ3 represents force FA, whereas branch containing Maxwell element with constant parameter k4 and the dash-pot element described by viscous constant τ4 represents force FB, which is consistent with Eq. (7).

4 Results and Discussion

The quasi-static tensile deformation test or strip test was used for the determination of the breaking force and elongation of the electric tape fence samples and detailed survey of the load–extension behavior of the samples. The two types of the load–extension behavior along all nine samples can be distinguished. In the first case, the stress–strain curve is relatively smooth, indicating that both components (i.e., polymer MFs and metal wires) work similarly in terms of mechanical properties. This performance was observed for sample nos. 1, 2, 3, 4, 5, 7, and 9. In Fig. 5a, the stress–strain graphs for sample nos. 1, 3, and 5 are shown to demonstrate this type of behavior. A characteristic change can be observed between the elastic and plastic deformation, where the point is called the plasticity limit (marked by circle) and reversible deformation changes to the irreversible deformation beyond this point. The rupture of the first metal wire (marked by square) can be observed, which does not significantly affect the test because both components have similar rheological and mechanical properties. Thus, the metal component did not carry any significant force in this case. In the second case (sample nos. 6 and 8; Fig. 5b), and the load–extension curve contains a significant peak representing the rupture of a higher number of metallic conductors or the rupture of a significantly stronger metal component (sample no. 6) compared to other samples. In this case, the metal component transmits force during the initial loading of the sample accompanied by a steep increase, followed by a sharp drop of force and subsequent slight increase until the break.

Fig. 5
figure 5

Load–displacement graphs for a sample nos. 1, 3, and 5 and b sample nos. 6 and 8

Full size image

In Fig. 6, a comparison of the samples’ mean values of the breaking load and elongation together with 95% confidence intervals of means is displayed. As expected, the number of MFs, their diameters, and the width of the samples determine the breaking load of the samples. For example, sample no. 6, with the highest width w = 42 mm and total MF cross-sectional area S ÷ 8 mm2, reaches the highest breaking load F = 2769 N and the lowest elongation l/l0 = 14%.

Fig. 6
figure 6

Bar plots of mean values of the a breaking load [N] and b elongation [%] together with 95% confidence intervals of means for all electric tape fence samples

Full size image

This phenomenon was confirmed using multiple linear regression and hypothesis tests (F test and t test). The only statistically significant variable affecting the sample breaking load is the total MF cross-sectional area A [mm2], and a significant linear relationship exists between the response F and predictor variable A (the R2 value of 0.95 is close to 1, and the p value of 1.08E-5 is less than the significance level of 0.05). For further details, see Fig. 7.

Fig. 7
figure 7

Dependence of the breaking load [N] on the total MF cross-sectional area [mm2] for all electric tape fence samples

Full size image

As described above, plasticity limits (P) having coordinates [lP, FP] and stiffness coefficients (k1, k2) were determined for the three representative samples chosen from the electric tape fence sample set. The mean values together with the 95% confidence intervals of the means (in brackets) are shown in Table 3. The results show that the stiffness coefficients are directly connected with the breaking load of the samples. The plasticity limit P is a very interesting change point when observing the mechanical behavior of the product. For displacement l ≤ lP, elastic (or viscoelastic) deformation occurs, which means that the material comes back to its original size and shape when the load is no longer present. By contrast, for l > lP, the material no longer behaves elastically/viscoelastically, but it becomes permanently deformed. In the quasi-static survey, there is no statistically significant difference found between lP for all the three samples, whereas FP differs depending on the deformability and strength of the sample.

Table 3 Stiffness coefficients and plasticity limits for sample nos. 1, 3, and 5
Full size table

The dynamic tensile deformation test provided information on the viscous and plastic behaviors of the electric fence tape samples. As shown in Fig. 5b, where the typical load–displacement curve is shown, the viscous behavior of the samples was confirmed by the fact that there is a relaxation of force in points R1 and R2 (R1’, R2’) and the fact that the load–displacement curve has a hysteresis character because of energy dissipation. The plastic behavior was proven by the fact that points C and C’ do not lie in the origin of the coordinate system.

The two-sample t test was used to check whether the deformation rate has a statistically significant effect on the mechanical behavior of the electric fence samples (H0: R1 = R1’, R2 = R2’, C = C’). The mean values and standard deviations of force F in points R1 and R2 for both rates are shown in Table 4, accompanied with the test statistics (p value). The rates (ranging from 100 to 200 mm/min) of the clamps have no statistically significant effect on the force in point R1 (R1’) because the p values are greater than 0.05. Unfortunately, the device does not offer higher rates. The effect of different deformation rates was confirmed for samples 1 and 5, where the force in the point R2 (R2’) was examined. A lower force was observed using a higher deformation rate for sample 1, which was not expected. This is probably because the fact that the time elapsed between points R1 and R2 was not enough to restore the state of tension. Sample 5 seems to show the greatest difference in the force behavior from the whole sample set and is the most sensitive to the change in rate. When compared with the quasi-static deformation test (above) and based on the relaxation tests (below), a viscous component in the rheological model of the electric fences is ultimately present.

Table 4 Mean values, standard deviations, and p values of the t test for forces and elongations (sample nos. 1, 3, and 5)
Full size table

Table 4 displays the mean values of elongations and the standard deviations and results of the t tests (p value). This investigation also shows that there is no significance difference between elongations at points C and C’, and therefore, the statistically significant effect of the deformation rate on the plastic behavior of the electric tape fence was not confirmed. Thus, it is necessary to emphasize that the results of this study are limited by the use of only two speeds of clamps.

The relaxation curve represents another output of the dynamic tensile deformation test typically with a shape of an exponentially decreasing function at R1 (R1’) and R2 (R2’) points. This function can be approximated by the function F = F (t) (see Eq. (7)). The results are presented in Table 5, where the mean values of force constants FA, FB, and FC [N] and relaxation times τ3 and τ4 [s] and the standard deviations for sample no. 1 are shown. Moreover, in this case, the effect of the deformation rate on all the constants of function F = F (t) was examined using the two-sample t test for equal means. The results show that the different rates (in the range of 100 to 200 mm/min) of the clamps have no statistically significant effect on all the constants of all relaxation curves (points R1, R2; R1’, and R2’) of all the samples (sample nos. 1, 3, and 5) because all the p values are greater than 0.05. However, this difference would be significant over a wider range of deformation rates. The MSE values (see Table 5) ranged between relatively small values from 0.1 to 0.4 N for all fence samples, which means that the model effectively explains a given set of observation. In Fig. 8, the measured relaxation curve and approximated relaxation curve for one of the dynamic tensile deformation measurements of sample no. 1 in the R1 point are compared. The results clearly show that the model with two viscous components seems to be suitable, which is also confirmed by the MSE value of 0.21 N.

Table 5 Mean values of force constants FA, FB, and FC and relaxation times τ3 and τ4 and the standard deviations, p values of the t tests, and MSE values for sample no. 1
Full size table
Fig. 8
figure 8

Dependence of force on the time–measured relaxation curve and approximated relaxation curve for one of the dynamic tensile deformation measurements of sample no. 1 in the R1 point

Full size image

A general rheological model of electric fence was proposed according to the undertaken quasi-static tensile tests and stress–relaxation tests (see Fig. 4d). The spring element describing the elastic behavior and obeying Hooke’s law presents the relationship between a force and deformation. The dash-pot element describing the plastic behavior presents the relationship between a force and the velocity of the deformation. The sliding element as a slip function simply keeps the magnitude of the force below a given threshold value [15]. Here, ki is the stiffness coefficient of the spring elements, τi is the relaxation time of the dash-pot elements, and FP is a sliding force of the sliding (frictional or St. Venant) element. As is apparent from the figure, the proposed rheological model is comprised of spring elements, dash-pot elements, and a sliding element. These elements are used to allow the elastic deformation, viscous deformation, and internal changes in the bodies. The proposed model represents two parts: (a) elasto-plastic and (b) viscous. The elasto-plastic part consists of two spring elements and one sliding element, with the spring elements being connected in parallel. The viscous part consists of two spring elements and two dash-pot elements, with the spring elements being connected in parallel. The use of individual components in the model is in a good agreement with models published for plain woven fabrics made of synthetic materials [7, 16, 17].

This rheological model can be generally described by a second-order differential Eq. (8) using Eq. (3) or (4), which can then be overwritten in a stress–strain configuration (Eq. 9).

$$\ddot{F}+\left({\alpha }_{3}+{\alpha }_{4}\right)\dot{F}+{\alpha }_{3}{\alpha }_{4}F=\left({k}_{12}+{k}_{3}+{k}_{4}\right)\ddot{l}+\left[{k}_{12}\left({\alpha }_{3}+{\alpha }_{4}\right)+{k}_{3}{\alpha }_{4}+{k}_{4}{\alpha }_{3}\right]\dot{l}+{k}_{12}{\alpha }_{3}{\alpha }_{4}l+{C}_{0}{\alpha }_{3}{\alpha }_{4}$$
(8)
$$\ddot{\sigma }+\left({\alpha }_{3}+{\alpha }_{4}\right)\dot{\sigma }+{\alpha }_{3}{\alpha }_{4}\sigma =\left({E}_{12}+{E}_{3}+{E}_{4}\right)\ddot{\varepsilon }+\left[{E}_{12}\left({\alpha }_{3}+{\alpha }_{4}\right)+{E}_{3}{\alpha }_{4}+{E}_{4}{\alpha }_{3}\right]\dot{\varepsilon }+{E}_{12}{\alpha }_{3}{\alpha }_{4}\varepsilon +{C}_{0}{\alpha }_{3}{\alpha }_{4}$$
(9)

where \({k}_{12}={k}_{1}+{k}_{2}, {C}_{0}=0\) for \(l \le l_{P}\) and \({k}_{12}={k}_{1}, {C}_{0}={F}_{P}-{k}_{1}{l}_{P}\) for \(l > l_{P}\), \({E}_{12}={E}_{1}+{E}_{2}, {C}_{0}=0\) for \(l \le l_{P}\) and \({E}_{12}={E}_{1}, {C}_{0}={\sigma }_{P}-{E}_{1}{\varepsilon }_{P}\) for \(l > l_{P}\),

$${\alpha }_{i}=\frac{1}{{\tau }_{i}}.$$

The special shapes of the differential Eq. (8) can be analyzed, which correspond to the experiments performed above, i.e., the quasi-static tensile deformation and dynamic tensile deformation test. A static problem is a trivial case, where all time derivatives of both variables are zero. Equation (8), thus, changes to another form (i.e., Eq. (5) or (6)) depending on the displacement. Thus, the phenomenological constants k1, k2, and FP, and lP, can be determined by static and quasi-static deformation, respectively. The analysis of the time-dependent force on a fixed displacement lR, that is, the analysis of the relaxation test is the second case. F = F (t, lR), and Eq. (8) transforms into Eq. (10).

$$\ddot{F}+\left({\alpha }_{3}+{\alpha }_{4}\right)\dot{F}+{\alpha }_{3}{\alpha }_{4}F={k}_{12}{\alpha }_{3}{\alpha }_{4}{l}_{R}+{C}_{0}{\alpha }_{3}{\alpha }_{4}$$
(10)

On the right side of Eq. (10), there are time-independent constants. It is a second-order linear differential equation with constant coefficients and a special right side. Its general solution (Eq. 11) is given by the sum of the general solutions of the homogeneous equation (with zero in the right side) and the particular solution of the inhomogeneous equation.

$$F\left(t,{l}_{R}\right)={F}_{A}{e}^{-{\alpha }_{3}t}+{F}_{B}{e}^{-{\alpha }_{4}t}+{k}_{12}{l}_{R}+{C}_{0}$$
(11)

Equation (11) corresponds to the approximation function (Eq. 7) of the relaxation characteristics of the electric fence. The coefficients FA and FB (Eq. 11) have integration constants. The last two terms of Eq. (11) represent the constant FC of Eq. 7, giving it a clear physical meaning. It is the force generated in the first two branches of the rheological model (Fig. 5d). If the relaxation test lasts long enough, then Eq. (11) will transform into Eq. (12), which corresponds to relations (5) for \(l = l_{R} \le l_{P}\) and (6) for \(l = l_{R} > l_{P}\).

$$F\left( {t \to \infty ,l_{R} } \right) = k_{12} l_{R} + C_{0}$$
(12)

Using the constants FC, lR and with the knowledge of [lP, FP], the phenomenological constants k1, k2 can be determined using two relaxation tests (\(l_{R1} \le l_{P}\), \(l_{R2} > l_{P}\)). This knowledge can also be used to partially check whether the rheological model corresponds to experimental results. The values from Tables 3 and 4 can be substituted in the right sides of Eqs. (5) and (6). For sample 1, the forces FR1 = 120 N and FR2 = 433 N are obtained. These results agree well with the FC values within the confidence intervals. The displacement rates are shown in Table 5.

Attention remains to be paid on the integration constants FA and FB (Eq. 11) as their size will depend on the nature of the stress definition by which the displacement reaches the point lR, where the relaxation test will take place. If the deformation rate is large enough in the interval [0, lR], i.e., the strain time in this section for l will be an order of magnitude shorter than the respective relaxation times τ3, τ4, then the influence of viscous members in the rheological model can be neglected. The so-called blocking (freezing) of the damper will occur. In this case, the constants k3 and k4 can be directly determined from FA and FB by simply dividing them by the respective displacement lR. By doing this, the procedure for determining all parameters of the rheological model can be completed. It should be mentioned that the constants k3 and k4 were not calculated in this study unfortunately due to not meeting the technical condition of ensuring sufficiently large deformation rate during the experiment.

5 Conclusion

In this study, the mechanical behavior of a sample set containing nine types of electric fences was analyzed. The electric tape fence samples were made of two material components: polyethylene and metal wires via weaving. A combination of plain-weave and plain-weave-derived patterns was used. The metal component was interwoven into the fabric’s warp along with polymer MFs, with different flotations. The mechanical behavior of the sample set was experimentally studied by the following tests: (a) quasi-static tests were performed to gain the full stress–strain responses of the electric tape in tension and (b) dynamic tests and stress–relaxation tests were used to characterize the electric tape fence viscoelasticity. The ultimate characteristics of the fence sample set were examined, and the strength is directly proportional to the total MF cross-section area. Furthermore, the quasi-static test provided information about the stiffness coefficients and plasticity limits of the fences. The dynamic tensile deformation tests proved the viscous and plastic behavior of the samples. The relaxation parts of curves F = F (t) were studied in more detail, they were approximated by a given function, and appropriate constants were extracted.

Based on the detailed findings, a rheological model of the electric fence was compiled. The rheological model is presented to study the mechanical properties of a special type of MF technical textiles, i.e., electric tape fences. The model comprised spring elements, dash-pot elements, and a sliding element. In the end, the validity of the proposed model was verified. The results show that the model appropriately describes the experimentally obtained data. The proposed rheological model investigated the mechanical response of electric fences under various forms of load. Seven constants, which determine the model, can be used as the descriptors of the mechanical properties of fences in comparative studies.

Considering the practical use of electric fences, we can assume that animals cannot exert sufficient force to rupture electric tape fences if they are in a stationary position. Thus, if an animal becomes tangled to the electric fence, it cannot exert enough force to break the fence. For some of the samples, especially sample nos. 6 and 8, which showed a different behavior compared to the rest of the sample set, the animal can develop at least sufficient force to rupture metal components, disrupting the electrical circuit, and the electric fence will not emit electrical impulses. For the remaining samples, where the metal component does not transmit significant force and behaves like the rest of the composite, i.e., polymer filaments, the force required to break the electrical circuit is too high, and the animal cannot develop it statically. In this case, the electric tape fence will still emit electrical impulses to the animal.

As part of further research, it would be appropriate to verify the model for higher deformation rates. It would also be useful to examine samples with a circular cross-section and to determine the influence of cyclic stress and weather conditions on the mechanical properties of fences.