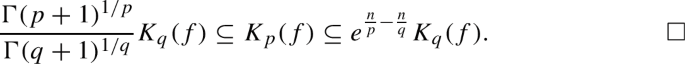Remarks on the Relation of Log-Concave and Contoured Distributions in ${\mathbb {R}}^n$

Abstract

We provide a characterization of those log-concave distributions in ${{\mathbb {R}}}^n$ that are contoured distributions, through the $K_p$-bodies of the distribution, defined by Ball. Our method uses the logarithmic integral for the solution of a Bernstein type approximation problem. In the second part of the paper we state a question for contoured distributions that would provide an alternative approach to the isotropic constant problem.

1 Introduction

In this article we provide a characterization of those log-concave distributions in ${{\mathbb {R}}}^n$ that are contoured distributions. The crucial rôle in this characterization is played by the bodies $K_p(f)$, for $p>0$, of a log-concave function f on ${\mathbb R}^n$ with finite positive integral, introduced by Keith Ball. These bodies are described in the literature as “associated” to the log-concave distribution f, but it is known to the experts that if f is induced by some convex body, in essence they “recover” the norm and/or the original body. More precisely, if f is of the form $h(\Vert x\Vert _K)$ for a convex body K, then $K_p(f)$ is a dilation of K with the magnifying constant depending on $p>0$ and h (see Proposition 3.2 below). The first main result of this article states that the converse also holds true, and so the following characterization for log-concave densities is valid. A probability distribution in ${{\mathbb {R}}}^n$ is called contoured if its probability density function has the form

$$\begin{aligned} f_{K,\phi }(x)=\frac{\omega _n}{|K|}\phi (\Vert x\Vert _K), \quad x\in {\mathbb R}^n, \end{aligned}$$

where K is a star-shaped set in ${\mathbb {R}}^n$ and $\phi :[0,+\infty )\rightarrow [0,+\infty )$ is an integrable function such that $\phi (|x|)$ is a density in ${{\mathbb {R}}}^n$.

Theorem 1.1

Let $f:{{\mathbb {R}}}^n\rightarrow [0,\infty )$ be a log-concave probability density. Then, f defines a contoured distribution if and only if there exist a convex body K in ${{\mathbb {R}}}^n$ and a sequence $(c_p)_{p\in {{\mathbb {N}}}}$ of positive constants such that $K_p(f)=c_pK$ for all $p\in {{\mathbb {N}}}$.

It can be seen that if f is even then the bodies $K_p(f)$ are all equivalent up to constants depending only on p (see Proposition 2.4 below). This shows that in order to provide an example of an even log-concave distribution that is not contoured we need to find an even log-concave function f for which the bodies $K_p(f)$ are not multiples of each other although they are equivalent up to constants that do not depend on the dimension.

The proof of Theorem 1.1 is based on an argument that establishes approximation of a function by polynomials in weighted $L_p$ spaces. Actually, following the same arguments we can also prove that the bodies $K_p$ characterize a log-concave distribution.

Theorem 1.2

Let f, g be two log-concave densities on ${{\mathbb {R}}}^n$. Then, $K_p(f)=K_p(g)$ for all $p\in {{\mathbb {N}}}$ if and only if $f=g$.

Thus, knowing the bodies $K_p(f)$ for all $p\in {{\mathbb {N}}}$ we also know f, since the mapping $f\mapsto (K_p(f))_{p\in {\mathbb {N}}}$ is one-to-one.

In the second part of this article, we associate to any isotropic log-concave distribution a contoured one that distributes the mass isotropically on ${\mathbb {R}}^n$ and we compare their isotropic constants. This shows that the isotropic constant can be controlled by the isotropic constants for contoured distributions.

2 Preliminaries and Notation

We work in ${{\mathbb {R}}}^n$, equipped with a Euclidean structure $\langle \cdot ,\cdot \rangle$. We write $|\cdot |$ for the corresponding Euclidean norm, and $B_2^n$ stands for the Euclidean unit ball, and ${\mathbb {S}}^{n-1}$ for the Euclidean unit sphere. We write $\text {int}(A)$ and $\text {bd}(A)$ for the interior and boundary of a set $A\subseteq {{\mathbb {R}}}^n$ respectively, and |A| for the volume of A in ${\mathbb {R}}^n$, that is its Lebesgue measure. We write $\omega _n$ for the volume of $B_2^n$ and $\sigma =\sigma _n$ for the rotationally invariant probability measure on ${\mathbb {S}}^{n-1}$.

For any integrable function $f:{{\mathbb {R}}}^n\rightarrow {{\mathbb {R}}}$, we denote the Lebesgue integral of f by $\int f(x)\,dx$. Integration in polar coordinates gives that

$$\begin{aligned} \int _{{{\mathbb {R}}}^n}f(x)\,dx =\int _{{\mathbb S}^{n-1}}\int _0^{\infty }f(t\theta )\,t^{n-1}dt\,d\theta =n\omega _n\int _{{\mathbb S}^{n-1}}\int _0^{\infty }f(t\theta )\,t^{n-1}dt\,d\sigma (\theta ). \end{aligned}$$

The letters c, $c_1$, $c_2$ etc, denote absolute positive constants whose value may change from line to line. Whenever we write $a\simeq b$, we mean that there exist absolute constants $c_1,c_2>0$ such that $c_1a\le b\le c_2a$. Similarly, if $A,B\subseteq {\mathbb {R}}^n$ we write $A\simeq B$ if there exist absolute constants $c_1, c_2>0$, independent of the dimension n and any defining parameter of A and B, such that $c_{1}A\subseteq B\subseteq c_{2}A$.

A subset K of ${{\mathbb {R}}}^n$ is called centered if its center of mass lies at the origin i.e. $\int _K\langle x,\theta \rangle dx=0$ for every $\theta \in {\mathbb {S}}^{n-1}$, and it is called symmetric if $-x\in K$ whenever $x\in K$. Moreover, we say that K is star shaped if $\lambda x\in K$ whenever $x\in K$ and $\lambda \in [0,1]$, and that K is a convex body if it is convex and compact in ${{\mathbb {R}}}^n$ with a non-empty interior. The Minkowski functional of a star shaped set $K\subseteq {{\mathbb {R}}}^n$ is the function

$$\begin{aligned} \Vert x\Vert _K:=\inf \big \{\lambda >0:\,x\in \lambda K\big \}, \quad x\in {{\mathbb {R}}}^n. \end{aligned}$$

Note that the Minkowski functional of a symmetric convex body K in ${{\mathbb {R}}}^n$ is a norm in ${{\mathbb {R}}}^n$, and accordingly any norm $\Vert \cdot \Vert$ in ${{\mathbb {R}}}^n$ defines a symmetric convex body K in ${{\mathbb {R}}}^n$ by $K=\{x\in {{\mathbb {R}}}^n:\,\Vert x\Vert \le 1\}$.

A function $u:{\mathbb {R}}^n\rightarrow (-\infty ,+\infty ]$ is convex if

$$\begin{aligned} u((1-\lambda )x+\lambda y)\le (1-\lambda )u(x)+\lambda u(y) \end{aligned}$$

for all x, $y\in {\mathbb {R}}^n$ and all $\lambda \in [0,1]$. It is elementary that every convex function u can be altered on the boundary of the convex set

$$\begin{aligned} \text {dom}(u)=\{x\in {\mathbb {R}}^n:\,u(x)<+\infty \} \end{aligned}$$

so that its epigraph becomes closed, equivalently u is lower-semicontinuous. Such a function is called closed. Moreover, u is continuous on $\text {int}(\text {dom}(f))$. All convex functions in this article will be assumed to be closed.

A convex function is proper if it is not identically $+\infty$. However, in this work we need to also exclude the trivial case where the function is equal to $+\infty$ with the exception of an affine subspace of ${\mathbb {R}}^n$ of dimension strictly less than n (a point if $n=1$). Thus, if $f:{\mathbb {R}}\rightarrow (-\infty ,+\infty ]$ is a proper convex function then the set $\text {dom}(f)$ is a subinterval of ${\mathbb {R}}$, as a non trivial convex subset of ${\mathbb {R}}$. We will also assume that all convex functions in this article are proper in the above sense.

A function $f:{\mathbb {R}}^n\rightarrow [0,\infty )$ is called centered if $\int _{{{\mathbb {R}}}^n}xf(x)\,dx=0$, and f is called log-concave if $\log f$ is concave (or equivalently if $-\log f$ is convex, and so assumed closed and proper throughout this article), that is if $f((1-\lambda )x+\lambda y) \ge (f(x))^{1-\lambda }(f(y))^\lambda$, for all x, $y\in {\mathbb {R}}^n$ and all $\lambda \in (0,1)$.

A basic property of log-concave densities that we will need is that they decay exponentially as $|x|\rightarrow \infty$ (see [1], Lemma 10.6.1). In particular, this implies that a log-concave density has finite moments of all orders.

Lemma 2.1

For every log-concave density f in ${{\mathbb {R}}}^n$, there exist constants $A,B>0$,

such that

$$\begin{aligned} f(x)\le Ae^{-B|x|}, \end{aligned}$$

(1)

for all $x\in {{\mathbb {R}}}^n$. $\square$

The next result is due to Fradelizi [8].

Theorem 2.2

If f is a centered log-concave density in ${{\mathbb {R}}}^n$, then

$$\begin{aligned} f(0)\le \sup _{x\in {{\mathbb {R}}}^n}f(x) \le e^n f(0). \end{aligned}$$

(2)

2.1 Isotropicity

A convex body K in ${{\mathbb {R}}}^n$ is isotropic if it has volume 1, it is centered and its inertia matrix is a multiple of the identity, that is there exists a constant $L_K>0$, called the isotropic constant of K, such that

$$\begin{aligned} \int _K\langle x,\theta \rangle ^2\,dx=L_K^2 \end{aligned}$$

for every $\theta \in {{\mathbb {S}}}^{n-1}$.

More generally, for any probability density function $f:{\mathbb R}^n\rightarrow [0,\infty )$, we define its isotropic constant by

$$\begin{aligned} L_f:=\sup _{x\in {{\mathbb {R}}}^n}f(x)^{1/n} \det {\text {Cov}(f)}^{1/2n}, \end{aligned}$$

where $\text {Cov}(f)$ is the covariance matrix of f with entries

$$\begin{aligned} \text {Cov}(f)_{ij} =\int _{{{\mathbb {R}}}^n}x_ix_jf(x)\,dx - \int _{{{\mathbb {R}}}^n}x_if(x)\,dx\int _{{{\mathbb {R}}}^n}x_jf(x)\,dx. \end{aligned}$$

We say that a probability density function f in ${\mathbb {R}}^n$ distributes the mass isotropically if it is centered and $\text {Cov}(f)$ is a multiple of the identity $n\times n$ matrix. Equivalently the integral

$$\begin{aligned} \int _{{\mathbb {R}}^n}|\langle x,\xi \rangle |^2 f(x)\,dx \end{aligned}$$

is independent of the vector $\xi \in {\mathbb {S}}^{n-1}$. If, in particular, $\text {Cov}(f)$ is the identity, then we say that f is isotropic and we have $L_f=\sup _{x\in {\mathbb R}^n}f(x)^{1/n}$. Note that a convex body K of volume 1 is isotropic if and only if the log-concave function $f_K=L_K^n\mathbb {1}_{L_K^{-1}K}$ is isotropic.

One can check that for every log-concave function $f:{\mathbb R}^n\rightarrow [0,\infty )$ there exist a non-singular affine isomorphism T and a positive number $\alpha$ so that $\alpha f\circ T$ is isotropic.

The hyperplane conjecture is a question in the theory of isotropic log-concave measures, asking if there exists an absolute constant $C>0$ such that

$$\begin{aligned} L_n:=\sup \big \{L_f:\,f \text { is an isotropic log-concave density in } {{\mathbb {R}}}^n\big \}\le C, \end{aligned}$$

for all $n\in {{\mathbb {N}}}$. Bourgain proved in [5] that $L_n \le c\root 4 \of {n}\log {n}$ and later Klartag [11] obtain the bound $L_n \le c\root 4 \of {n}$ (see also [14]). Chen [7] in a breakthrough work proved that for any $\varepsilon >0$ there exists a $n_0(\varepsilon )\in {{\mathbb {N}}}$ such that $L_n\le n^\varepsilon$, for every $n\ge n_0(\varepsilon )$. Klartag and Lehec [13] showed then that $L_n\le c(\log {n})^4$, and shortly after that, Klartag [12] proved that $L_n\le c\sqrt{\log {n}}$, which is the best known upper bound until now.

2.2 Keith Ball’s Bodies

The bodies $K_p(f)$ are defined as follows:

Definition 2.3

(K. Ball) Let $f:{\mathbb {R}}^n\rightarrow [0,+\infty )$ be a measurable function such that $f(0)>0$. For any $p>0$ we define the set $K_p(f)$ as follows:

$$\begin{aligned} K_p(f)=\left\{ x\in {\mathbb {R}}^n:\,\int _0^\infty r^{p-1} f(rx)\,dr\ge \frac{f(0)}{p}\right\} . \end{aligned}$$

If $f_\mu$ is the density of a Borel probability measure $\mu$ and $f_\mu (0)>0$, then we define $K_p(\mu ):=K_p(f_\mu )$.

From the definition it follows that the Minkowski functional of $K_p(f)$ is given by

$$\begin{aligned} \Vert x\Vert _{K_p(f)}=\left( \frac{p}{f(0)}\int _0^\infty r^{p-1}f(rx)\,dr\right) ^{-1/p}. \end{aligned}$$

Ball showed (see [2]) that if $f:\mathbb R^n\rightarrow [0,+\infty )$ is a log-concave function such that $f(0)>0$ and $0<\int _{{\mathbb {R}}^n}f(x)\,dx<+\infty$ then $K_p(f)$ is a convex body for all $p>0$.

Several properties of these bodies are well-known (see for example [1] or [6]). For example, $K_p(\mathbb {1}_K)=K$ for every convex body K in ${\mathbb {R}}^n$, one always has that $0\in K_p(f)$, and $K_p(f)$ is symmetric if f is even. It is also known that the bodies $K_p(f)$ are equivalent:

Proposition 2.4

Let $f:{\mathbb {R}}^n\rightarrow [0,+\infty )$ be a log-concave function such that $f(0)>0$.

• (1) If $0<p\le q$ then

  $$\begin{aligned} \frac{\Gamma (p+1)^{1/p}}{\Gamma (q+1)^{1/q}}K_q(f)\subseteq K_p(f)\subseteq \left( \frac{\Vert f\Vert _\infty }{f(0)}\right) ^{\frac{1}{p}-\frac{1}{q}}K_q(f). \end{aligned}$$

• (2) If f has its barycenter at the origin then, for every $0<p\le q$,

  

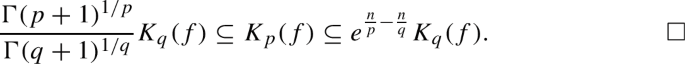
These inclusions imply the following estimate for the volume of $K_p(f)$ for every $p>0$: if f is a centered log-concave density in ${{\mathbb {R}}}^n$, then for every $s>0$ we have

$$\begin{aligned} \frac{1}{e}\le f(0)^{\frac{1}{n}+\frac{1}{s}}\,|K_{n+s}(f)|^{\frac{1}{n}+\frac{1}{s}} \le e\,\frac{n+s}{n}. \end{aligned}$$

(3)

Finally note that if f is even then it is easy to see that $\Vert f\Vert _\infty =f(0)>0$, since by log-concavity $f(0)\ge \sqrt{f(x)}\sqrt{f(-x)}=f(x)$ for every $x\in {\mathbb R}^n$. Then, using the estimate $\Gamma (p+1)^{1/p}\simeq p$, Proposition 2.4 implies that there exists an absolute constant $c>0$ so that if $0<p\le q$ then

$$\begin{aligned} c\frac{p}{q}K_q(f)\subseteq K_p(f)\subseteq K_q(f), \end{aligned}$$

that is, $K_p(f)$ are equivalent up to constants independent of the dimension.

A crucial observation is that through the study of $K_p(f)$ bodies one can provide bounds for the isotropic constant of log-concave probability densities. If $f:{{\mathbb {R}}}^n\rightarrow [0,\infty )$ is an even log-concave function with finite and positive integral, then Ball showed that $K_{n+2}(f)$ is a centrally symmetric convex body in ${{\mathbb {R}}}^n$ such that

$$\begin{aligned} c_1 L_f \le L_{K_{n+2}(f)} \le c_2 L_f, \end{aligned}$$

(4)

where $c_1, c_2 > 0$ are absolute constants. If in addition f is isotropic, then the normalized body $K_{n+2}(f)/|K_{n+2}(f)|^{1/n}$ is an isotropic convex body.

In the general case where $f:{{\mathbb {R}}}^n\rightarrow [0,\infty )$ is a centered log-concave function with finite and positive integral, but not necessarily even, one has that $K_{n+1}(f)$ is a centered convex body in ${{\mathbb {R}}}^n$ with

$$\begin{aligned} c_1 L_f \le L_{K_{n+1}(f)} \le c_2 L_f, \end{aligned}$$

(5)

where $c_1, c_2 > 0$ are absolute constants.

The reader may find more details about the bodies $K_p(f)$ and the geometry of isotropic log-concave measures in the books [1] and [6].

2.3 Contoured Distributions

The contoured distributions were introduced in [10] by Guleryuz et al. A distribution on ${{\mathbb {R}}}^n$ is called contoured if it is absolutely continuous and there exists a decomposition of its probability density function f in the form

$$\begin{aligned} f(x)=c\phi \big (\lambda (x)\big ), \end{aligned}$$

where c is a positive constant, $\phi :[0,+\infty )\rightarrow [0,+\infty )$ is an integrable function and $\lambda :{{\mathbb {R}}}^n\rightarrow [0,\infty )$ is positive away from 0 and positively homogeneous i.e., $\lambda (tx)=t\lambda (x)$, for any $t>0$ and $x\in {{\mathbb {R}}}^n$. We say then that $\lambda$ is a shape function.

Associated to any shape function $\lambda$ is the compact star-shaped body

$$\begin{aligned} K_\lambda =\big \{x\in {{\mathbb {R}}}^n:\,\lambda (x)\le 1\big \}, \end{aligned}$$

and backwards, associated to any compact star-shaped body K is the shape function defined by the Minkowski functional of K (or the norm $\Vert \cdot \Vert _K$ if K is a symmetric convex body),

$$\begin{aligned} \lambda _K(x)=\inf \big \{ t>0:\,x\in tK \big \}. \end{aligned}$$

It is known that there exists a one-to-one correspondence between shape functions and compact star-shaped bodies which leads us to the following notation. We say that the distribution of a random vector in ${{\mathbb {R}}}^n$ is contoured if its probability density function has the form

$$\begin{aligned} f_{K,\phi }(x)=\frac{\omega _n}{|K|}\phi (\Vert x\Vert _K), \quad x\in {\mathbb R}^n, \end{aligned}$$

(6)

where K is a star-shaped set in ${\mathbb {R}}^n$ and $\phi :[0,+\infty )\rightarrow [0,+\infty )$ is an integrable function such that $\phi (|x|)$ is a density in ${{\mathbb {R}}}^n$, which by integration in polar coordinates, is equivalent to

$$\begin{aligned} n\omega _n\int _0^\infty t^{n-1}\,\phi (t)\,dt=1. \end{aligned}$$

(7)

The body K is called the contoured body of the distribution, and $\phi$ is called the radial profile function of the distribution.

In this paper we only consider contoured distributions such that the contoured body K is a centered convex body in ${{\mathbb {R}}}^n$. We refer to the paper [10] for more details about the definition of a contoured distribution and the normalization (7) of its radial profile function.

3 Characterization of Contoured Log-Concave Distributions

Let $W:{{\mathbb {R}}}\rightarrow [1,\infty )$ be an even and continuous function satisfying the condition

$$\begin{aligned} \lim _{|t|\rightarrow +\infty }\frac{\log {W(t)}}{\log {|t|}}=+\infty \end{aligned}$$

(8)

and for each $1\le p<+\infty$, consider the Banach space of measurable functions

$$\begin{aligned} L_W^p=\left\{ f:\int _{\mathbb R}\frac{|f(t)|^p}{W(t)^p}\,dt<+\infty \right\} . \end{aligned}$$

A classical Bernstein type approximation problem is to determine conditions under which the polynomials are dense in $L_W^p$. The following is a well known result in this direction that reduces the answer to the logarithmic integral (see [4, 15] and the references therein).

Theorem 3.1

Let $W:{{\mathbb {R}}}\rightarrow [1,\infty )$ be an even continuous function satisfying (8) such that the map $t\mapsto \log {W(\exp {t})}$ defines a convex function on ${\mathbb R}$. Then, if

$$\begin{aligned} \int _{{\mathbb {R}}}\frac{\log {W(t)}}{t^2+1}\,dt =+\infty , \end{aligned}$$

(9)

the polynomials are dense in $L_W^p$, for any $1\le p<\infty$. Otherwise, if

$$\begin{aligned} \int _{{\mathbb {R}}}\frac{\log {W(t)}}{t^2+1}\,dt <+\infty , \end{aligned}$$

the polynomials are not dense in any $L_W^p$, for $1\le p<\infty$.

It is not hard to see that if f is the density of a contoured distribution in ${{\mathbb {R}}}^n$, then the bodies $K_p(f)$ are all dilations of the distribution’s contoured body. In the next proposition, for the sake of completeness, we quote this well known fact, along with its simple proof.

Proposition 3.2

Let $f(x)=f_{K,\phi }(x)=\frac{\omega _n}{|K|}\phi (\Vert x\Vert _K)$ be the density of a contoured distribution in ${{\mathbb {R}}}^n$, with a radial profile function $\phi$ and a contoured (star-shaped) body K. Then,

$$\begin{aligned} K_p\big (f_{K,\phi }\big )=c_p(\phi )\,K, \quad \forall \,p>0, \end{aligned}$$

(10)

where $\displaystyle { c_p(\phi ):=\frac{1}{\Vert 1\Vert _{K_p(\phi )}} =\left( \frac{p}{\phi (0)}\int _0^\infty t^{p-1} \phi (t)\,dt\right) ^{1/p}}$.

Proof

For all $p>0$, one has that

Thus, in order to prove Theorem 1.1, we need to establish the following reverse statement.

Theorem 3.3

Let f be a log-concave probability density in ${{\mathbb {R}}}^n$ and let K be a convex body in ${{\mathbb {R}}}^n$ with the property that for every $p\in {{\mathbb {N}}}$ there exists a constant $c_p>0$ such that $K_p(f)=c_p K$. Then f defines a contoured distribution.

We first need a couple of technical elementary lemmata. For the first one notice that by convexity, if $x_0<y<z$ then $(z-x_0)f(y)\le (z-y)f(x_0)+(y-x_0)f(z)$. It follows that

$$\begin{aligned} \liminf _{y\rightarrow x_0^+}f(y)\le \limsup _{y\rightarrow x_0^+}f(y)\le f(x_0) \end{aligned}$$

and using lower semi-continuity we readily get the following.

Lemma 3.4

If $f:{\mathbb {R}}\rightarrow (-\infty ,+\infty ]$ is a convex and lower semi-continuous function then $\liminf _{x\rightarrow x_0} f(x)=f(x_0)$ for all $x_0\in {\mathbb {R}}$, and f is continuous at every $x\in \text {dom}(f)$.

For the next lemma, note that if u, w are two convex functions on ${\mathbb {R}}$ and $u(t_0)>w(t_0)$, for some $t_0\in {\mathbb {R}}$, then by Lemma  3.4 we can find $\delta ,\epsilon >0$ and $t_1\in \text {dom}(w)$ with $|t_1-t_0|<\delta$ so that $u(t)\ge \inf _{0<|t-t_0|<\delta }u(t)>w(t_1)+\epsilon$, and by continuity of w at $t_1$ we easily get the following.

Lemma 3.5

Let u, w be two convex functions on ${\mathbb {R}}$ and suppose that there exists $t_0\in {\mathbb {R}}$ so that $u(t_0)>w(t_0)$. Then, we can find $\gamma >0$ and an interval (a, b) so that $u(t)>w(t)+\gamma$ for all $t\in (a,b)$.

Proof of Theorem 3.3

First we prove the following claim, as a consequence of Theorem 3.1.

Claim. Assume that $e^{-u}:{\mathbb R}^n\rightarrow {{\mathbb {R}}}$ is a log-concave density in ${{\mathbb {R}}}^n$ and $x,y\in {{\mathbb {R}}}^n\setminus \{0\}$ satisfy

$$\begin{aligned} \int _{{\mathbb {R}}} e^{-u(tx)}t^{p-1}\,dt = \int _{{\mathbb {R}}} e^{-u(ty)}t^{p-1}\,dt \qquad \forall \,p\in {{\mathbb {N}}}. \end{aligned}$$

(11)

Then $u(tx)=u(ty)$ for every $t\in {{\mathbb {R}}}$.

Proof of the Claim: Consider the function $g(t)=e^{-u(tx)}-e^{-u(ty)}$ and assume that $g(t_0)\ne 0$ for some $t_0\in {{\mathbb {R}}}$. Then by Lemma 3.5 there exist $\gamma >0$ and an interval (a, b) in ${{\mathbb {R}}}$, such that

$$\begin{aligned} g(t)\ge \gamma \quad \text { for all }\, t\in (a,b). \end{aligned}$$

(12)

By Lemma 2.1, there exist constants $A, B>0$ such that $e^{-u(tx)}\le Ae^{-B|x|\,|t|}$ for all $t\in {{\mathbb {R}}}$ and $x\in {{\mathbb {R}}}^n$. Let $c_{x,y}=B\min \{|x|, |y|\}>0$ and define $W:{{\mathbb {R}}}\rightarrow [1,+\infty )$ with

$$\begin{aligned} W(t)=\exp {\big (c_{x,y}|t|\big )}, \end{aligned}$$

Then $\mathbb {1}_{(a,b)}\in L_W^1$, and W satisfies all the conditions of Theorem 3.1. Thus there exists a sequence of polynomials $(p_m)$ such that

$$\begin{aligned} \big \Vert \mathbb {1}_{(a,b)}-p_m\big \Vert _{L_W^1} =\int _{{\mathbb {R}}} \frac{\left| \mathbb {1}_{(a,b)}(t)-p_m(t)\right| }{W(t)}\,dt\rightarrow 0, \end{aligned}$$

(13)

as $m\rightarrow \infty$. Notice now that by (11), (12) and (13) one has

$$\begin{aligned} \gamma (b-a)&\le \left| \int _{{\mathbb {R}}} g(t) \bigl (\mathbb {1}_{(a,b)}(t)-p_m(t)\bigr )\,dt\right| \le \int _{{\mathbb {R}}} |g(t)| \,\bigl |\mathbb {1}_{(a,b)}(t)-p_m(t)\bigr |\,dt \\&\le \int _{{\mathbb {R}}} \bigl (e^{-u(tx)}+e^{-u(ty)}\bigr ) \,\bigl |\mathbb {1}_{(a,b)}(t)-p_m(t)\bigr |\,dt \\&\le \int _{{\mathbb {R}}} \bigl (Ae^{-B|t||x|}+Ae^{-B|t||x|}\bigr ) \,\bigl |\mathbb {1}_{(a,b)}(t)-p_m(t)\bigr |\,dt \\&\le 2A \int _{{\mathbb {R}}} e^{-c_{x,y}|t|} \,\bigl |\mathbb {1}_{(a,b)}(t)-p_m(t)\bigr |\,dt \\&= 2A \int _{{\mathbb {R}}} \frac{\left| \mathbb {1}_{(a,b)}(t)-p_m(t)\right| }{W(t)}\,dt \rightarrow 0, \end{aligned}$$

as $m\rightarrow \infty$ by (13). This is a contradiction and so g must be identically 0.

To finish the proof, write the log-concave density as $f(x)=e^{-u(x)}$, where u is a convex function in ${\mathbb {R}}^n$. By the assumption of the theorem we have that $\Vert x\Vert _{K_p(f)}=c_p^{-1}\Vert x\Vert _K$ for any $p\in {{\mathbb {N}}}$, which implies that

$$\begin{aligned} \frac{p}{c_p f(0)}\int _0^\infty f(rx)r^{p-1}\,dr=\Vert x\Vert _K^{-p}. \end{aligned}$$

Thus for any $p\in {{\mathbb {N}}}$ and any $x\in \text {bd}(K)$, the function

$$\begin{aligned} F_{p}(x)=\frac{p}{c_p f(0)}\int _0^\infty e^{-u(rx)}r^{p-1}\,dr \end{aligned}$$

is constant and in fact it is equal to 1. So by the claim we have that $u(rx)=u(ry)$ for all $r\in {\mathbb {R}}$ and $x, y\in \text {bd}(K)$. To end the proof, fix $x_0\in \text {bd}(K)$ and define $\phi (r)=e^{-u(rx_0)}$. It follows that

$$\begin{aligned} u(x)=u\left( \Vert x\Vert _K\frac{x}{\Vert x\Vert _K}\right) =u(\Vert x\Vert _K x_0)=-\ln \phi (\Vert x\Vert _K) \end{aligned}$$

for every $x\in {\mathbb {R}}^n\setminus \{0\}$, and so $f(x)=e^{-u(x)}=\phi (\Vert x\Vert _K)$ completing the proof. $\square$

Proof of Theorem 1.2

Let $f(x)=e^{-u(x)}$ and $g(x)=e^{-w(x)}$ be two log-concave functions on ${{\mathbb {R}}}^n$, and assume that $K_p(f)=K_p(g)$ for all $p\in {{\mathbb {N}}}$. Thus, by the definition of the bodies $K_p$ we have that, for all $x\in {{\mathbb {R}}}^n$ and $p\in {{\mathbb {N}}}$,

$$\begin{aligned} \int _{{\mathbb {R}}} e^{-u(tx)}t^{p-1}\,dt = \int _{{\mathbb {R}}} e^{-w(tx)}t^{p-1}\,dt. \end{aligned}$$

(14)

Then, the same arguments that we have used in the proof of Theorem 1.1 show that $u(tx)=w(tx)$ for all $t\in {\mathbb R}$ and all $x\in {{\mathbb {R}}}^n$. Thus $f(x)=g(x)$ for all $x\in {{\mathbb {R}}}^n$. The other direction is obvious, and hence the proof is complete. $\square$

3.1 An Example

As discussed in the introduction, if we want to define a log-concave distribution which avoids being a contoured one, we need to find an example for which the bodies $K_p(f)$ avoid being multiples of each other but they are all equivalent, in particular up to constants independent of the dimension in the even case. This may appear to be very delicate and definitely supports a related statement in [10]:

It is worth noting, however, that the class of origin-symmetric convex contoured distributions already contains most, if not all, commonly used explicit examples of multidimensional probability distributions.

Here we provide a simple example of a log-concave distribution that is not contoured. Consider the 1-dimensional log-concave densities $f_1(x)=\frac{1}{2}e^{-|x|}$, $f_2(x)={\mathbb {1}}_{\left[ -\frac{1}{2},\frac{1}{2}\right] }(x)$, $x\in {{\mathbb {R}}}$, and the 2-dimensional log-concave density of their product measure

$$\begin{aligned} f(x,y)=f_1(x)f_2(y)=\frac{1}{2}e^{-|x|}{\mathbb {1}}_{\left[ -\frac{1}{2},\frac{1}{2}\right] }(y), \quad (x,y)\in {{\mathbb {R}}}^2. \end{aligned}$$

For any $p>0$ and any $(x,y)\in {{\mathbb {R}}}^2$, a direct computation leads to the formula

$$\begin{aligned} \Vert (x,y)\Vert _{K_p(f)}=\frac{|x|}{\left( p\int _0^{{|x|}/({2|y|})}t^{p-1}e^{-t}\,dt\right) ^{1/p}}. \end{aligned}$$

Taking (x, y) on the line $x=\alpha y$, we get that for any $\alpha >0$,

$$\begin{aligned} \Vert (\alpha x,x)\Vert _{K_p(f)} =\frac{\alpha |x|}{\left( p\int _0^{{\alpha }/{2}}t^{p-1}e^{-t}\,dt\right) ^{1/p}}, \qquad \forall \,x\in {{\mathbb {R}}}. \end{aligned}$$

Thus

$$\begin{aligned} \frac{\Vert (\alpha x,x)\Vert _{K_p(f)}}{\Vert (\alpha x,x)\Vert _{K_q(f)}} =\frac{\left( q\int _0^{{\alpha }/{2}}t^{q-1}e^{-t}\,dt\right) ^{1/q}}{\left( p\int _0^{{\alpha }/{2}}t^{p-1}e^{-t}\,dt\right) ^{1/p}}, \end{aligned}$$

(15)

for any $p,q,\alpha >0$, and any $x\in {{\mathbb {R}}}$. If f was a contoured density, then by Proposition 3.2 we should have that there exists a constant $C_{p,q}>0$ such that

$$\begin{aligned} \frac{\Vert (x,y)\Vert _{K_p(f)}}{\Vert (x,y)\Vert _{K_q(f)}}=C_{p,q}\qquad \forall \,(x,y)\in {{\mathbb {R}}}^2, \end{aligned}$$

and this is definitely not the case in our example since, as equation (15) shows, the above norm ratio depends also on $(x,y)\in {{\mathbb {R}}}^2$.

4 Isotropic Constant Reduction

In this section, for any log-concave probability density f and every centered convex body K in ${{\mathbb {R}}}^n$, we introduce a contoured probability density that distributes the mass “similarly” to the way f does. The contoured distribution is defined using spherical averages of f.

Definition 4.1

(Spherical average density) Let $f:{\mathbb {R}}^n\rightarrow [0,+\infty )$ be a log-concave probability density. We define a function $\varphi :{\mathbb {R}}\rightarrow [0,+\infty )$ by

$$\begin{aligned} \varphi (t)=\int _{{\mathbb {S}}^{n-1}}f(t\theta )\,d\sigma (\theta ) \end{aligned}$$

and for any centered convex body K in ${{\mathbb {R}}}^n$, we define the spherical average density $h:{\mathbb R}^n\rightarrow [0,\infty )$ by

$$\begin{aligned} h(x)=\frac{\omega _n}{|K|}\varphi (\Vert x\Vert _K). \end{aligned}$$

(16)

Observe that h is a contoured density, since its radial profile function $\varphi$ satisfies the normalization condition (7). Indeed, using polar coordinates we see that

$$\begin{aligned} n\omega _n\int _0^\infty t^{n-1}\,\varphi (t)\,dt&=n\omega _n\int _0^\infty \int _{{\mathbb {S}}^{n-1}} t^{n-1} f(t\theta )\,d\sigma (\theta )dt =\int _{{{\mathbb {R}}}^n} f(x)\,dx=1. \end{aligned}$$

Remark 4.2

Note also that the center of mass of h lies at the origin since its contoured body K is centered. Truthfully, for any $\xi \in {{\mathbb {S}}}^{n-1}$, the definition of h and integration in polar coordinates imply that

$$\begin{aligned} \int _{{{\mathbb {R}}}^n} \langle x,\xi \rangle h(x)\,dx =\frac{\omega _n}{|K|}\,I_1(f) \int _{{{\mathbb {S}}}^{n-1}}\frac{\langle \zeta ,\xi \rangle }{\Vert \zeta \Vert _K^{n+1}}\,d\sigma (\zeta ), \end{aligned}$$

where

$$\begin{aligned} I_1(f)= \int _{{{\mathbb {R}}}^n} |x| f(x)\,dx. \end{aligned}$$

Then, integration in polar coordinates gives

$$\begin{aligned} \frac{n+1}{n}\int _{K} \langle x,\xi \rangle \,dx = \omega _n \int _{{{\mathbb {S}}}^{n-1}}\frac{\langle x,\xi \rangle }{\Vert \zeta \Vert _K^{n+1}}\,d\sigma (\zeta ), \end{aligned}$$

and so

$$\begin{aligned} \int _{{{\mathbb {R}}}^n} \langle x,\xi \rangle h(x)\,dx =\frac{n+1}{n}\,I_1(f)\, \frac{1}{|K|} \int _{K} \langle x,\xi \rangle \,dx=0. \end{aligned}$$

Theorem 4.3

With the above assumptions, if K is an isotropic convex body and f is an isotropic density in ${{\mathbb {R}}}^n$, then so is h and $L_h\simeq L_fL_K$. Moreover, if we choose K to be the isotropic image of $K_{n+1}(f)$, then we get that $L_h\simeq L_f^2$.

Proof

Let f be a log-concave density and K be a centered convex body in ${{\mathbb {R}}}^n$. First note that by Remark 4.2, h is centered. Moreover, for any $\xi \in {{\mathbb {S}}}^{n-1}$, integration in polar coordinates an Fubini’s theorem imply that

$$\begin{aligned}&\int _{{\mathbb {R}}^n}|\langle x,\xi \rangle |^2 h(x)\,dx\\&\quad =\frac{\omega _n}{|K|}\int _{{\mathbb {R}}^n} \int _{{\mathbb {S}}^{n-1}}f(\Vert x\Vert _K\theta )\,d\sigma (\theta )\ |\langle x,\xi \rangle |^2\,dx\\&\quad =\frac{\omega _n}{|K|}\int _{\mathbb S^{n-1}}n\omega _n\int _{{\mathbb {S}}^{n-1}}\int _0^\infty f(\Vert r\zeta \Vert _K\theta )|\langle r\zeta ,\xi \rangle |^2 r^{n-1}\,drd\sigma (\zeta )d\sigma (\theta )\\&\quad =\frac{\omega _n}{|K|} \int _{{\mathbb {S}}^{n-1}} |\langle \zeta ,\xi \rangle |^2 \ n\omega _n \int _{{\mathbb {S}}^{n-1}} \int _0^\infty f(r\Vert \zeta \Vert _K\theta )r^{n+1}\,dr d\sigma (\theta )d\sigma (\zeta ) \\&\quad =\frac{\omega _n}{|K|} \int _{{\mathbb {S}}^{n-1}} \frac{|\langle \zeta ,\xi \rangle |^2}{\Vert \zeta \Vert _K^{n+2}}\,d\sigma (\zeta ) \ n\omega _n \int _{{\mathbb {S}}^{n-1}} \int _0^\infty f(s\theta ) s^{n+1}\,ds d\sigma (\theta ) \\&\quad =\frac{\omega _n}{|K|} \int _{{\mathbb {S}}^{n-1}} \frac{|\langle \zeta ,\xi \rangle |^2}{\Vert \zeta \Vert _K^{n+2}}\,d\sigma (\zeta ) \ \int _{{\mathbb {R}}^n}|x|^2f(x)\,dx, \end{aligned}$$

arriving at

$$\begin{aligned} \int _{{\mathbb {R}}^n}|\langle x,\xi \rangle |^2 h(x)\,dx =\frac{\omega _n}{|K|} I_2(f)^2\int _{{\mathbb {S}}^{n-1}} \frac{|\langle \zeta ,\xi \rangle |^2}{\Vert \zeta \Vert _K^{n+2}}\,d\sigma (\zeta ),\quad \forall \,\xi \in {\mathbb S}^{n-1}. \end{aligned}$$

(17)

If we assume that f distributes the mass isotropically in ${{\mathbb {R}}}^n$, then

$$\begin{aligned} I_2(f)^2=\int _{\mathbb R^n}|x|^2f(x)\,dx=n\frac{L_f^2}{\sup {f^{2/n}}}, \end{aligned}$$

(18)

If moreover K is isotropic, then by computing $\int _K|\langle x,\xi \rangle |^2\,dx$ in polar coordinates, we get that

$$\begin{aligned} \int _{\mathbb S^{n-1}}\frac{|\langle \zeta ,\xi \rangle |^2}{\Vert \zeta \Vert _K^{n+2}}\,d\sigma (\zeta ) =\frac{n+2}{n\omega _n}L_K^2. \end{aligned}$$

(19)

Thus, returning to (17) we finally get

$$\begin{aligned} \int _{{\mathbb {R}}^n}|\langle x,\xi \rangle |^2 h(x)\,dx=\frac{n+2}{n} L_K^2 I_2(f)^2, \end{aligned}$$

that is, the integral on the left is independent of the direction $\xi \in {\mathbb {S}}^{n-1}$, and this means that h distributes the mass in ${\mathbb {R}}^n$ isotropically.

To compute the isotropic constant of h we notice that since f is log-concave, by Theorem 2.2 we have that

$$\begin{aligned} \frac{\omega _n}{|K|} f(0)\le \sup _{x\in {\mathbb {R}}^n}h(x) =\frac{\omega _n}{|K|}\sup _{x\in {\mathbb {R}}^n} \int _{\mathbb S^{n-1}}f(\Vert x\Vert _K\theta )\,d\sigma (\theta ) \le e^n \frac{\omega _n}{|K|}\, f(0) \end{aligned}$$

and so

$$\begin{aligned} \sup _{x\in {\mathbb {R}}^n}h(x)^{1/n} \simeq \left( \frac{\omega _n}{|K|}\right) ^{1/n} f(0)^{1/n} \simeq \left( \frac{\omega _n}{|K|}\right) ^{1/n} \sup _{x\in {\mathbb R}^n}f^{1/n} . \end{aligned}$$

(20)

Now we use the fact that if a density f distributes the mass in ${\mathbb {R}}^n$ isotropically, then

$$\begin{aligned} L_f=\sup _{x\in {\mathbb {R}}^n}f(x)^{1/n} \left( \int _{\mathbb R^n}|\langle x,\xi \rangle |^2 f(x)\,dx\right) ^{1/2}. \end{aligned}$$

Since both f and h distribute the mass isotropically, by (17), (18), (20) and using the estimate $\sqrt{n}\omega _n^{1/n}\simeq 1$, we arrive at the formula

$$\begin{aligned} L_h\simeq \frac{\omega _n^{1/2}}{|K|^{\frac{1}{n}+\frac{1}{2}}} \left( \int _{{\mathbb {S}}^{n-1}} \frac{|\langle \zeta ,\xi \rangle |^2}{\Vert \zeta \Vert _K^{n+2}}\, d\sigma (\zeta )\right) ^{1/2} L_f \end{aligned}$$

(21)

which, for K isotropic and by (19), gives that $L_h\simeq L_K L_f$.

For the second part of the theorem, we assume that f is an isotropic log-concave density in ${{\mathbb {R}}}^n$. Note that if in addition we assume that f is even, then $K_{n+2}(f)$ is centrally symmetric and distributes the mass isotropically in ${{\mathbb {R}}}^n$. Then by (4) we have that $L_K\simeq L_f$ and so $L_h\simeq L_f^2$. Nevertheless, we can prove this result without assuming the evenness of f.

Note that by (5) $K_{n+1}(f)$ is a centered convex body in ${{\mathbb {R}}}^n$ with $L_{K_{n+1}(f)}\simeq L_f$. Then, if T is the isotropic image of $K_{n+1}(f)$, by the affine invariant of the isotropic constant we have that $L_{T}=L_{K_{n+1}(f)}\simeq L_f$. Thus if we take h to be the spherical average density of f with the isotropic body T, by the first part of the Theorem we have that h is also isotropic and

$$\begin{aligned} L_h=L_f\,L_{T}\simeq L_f^2, \end{aligned}$$

completing the proof. $\square$

Remark 4.4

Notice that the spherical average density h in (16) defines always a contoured distribution, but it is not necessarily log-concave. Nevertheless, if one could prove that there exists a log-concave density $f_*$ such that $L_n$ is attained (up to an absolute constant) by $L_{f*}$ and its spherical average density $h_*$ is log-concave, then by Theorem 4.3 we would have that

$$\begin{aligned} L_n^2\simeq L_{f_*}^2\simeq L_{h_*}\le L_n, \end{aligned}$$

and so $L_n$ would be bounded by an absolute constant.

We conclude this section with a remark regarding a question that would allow to use contoured distributions for bounding the isotropic constant. We will say that a (probability density) function $h:{{\mathbb {R}}}^n\rightarrow [0,\infty )$ is sub-log-concave if there exist a log-concave (probability density) function $g:{{\mathbb {R}}}^n\rightarrow [0,\infty )$ and a constant $c>0$ such that $h\le c g$.

Although the spherical average density h in (16) may not be log-concave, since it is defined by a log-concave function f, using Lemma 2.1 we see that it is always sub-log-concave. Define

$$\begin{aligned} L_n^{\textrm{sub}}:=\sup \big \{L_h:\,h \text { is an isotropic { sub-log-concave} density in } {{\mathbb {R}}}^n\big \} \end{aligned}$$

and then obviously $L_n\le L_n^{\textrm{sub}}$. Conversely, if it can be proved that $L_n^{\textrm{sub}}$ is attained (up to an absolute constant) on a log-concave density, say $f_0$, then using a log-concave density that maximizes $L_n$, say $f_{\max }$, by Theorem 4.3 we would get that

$$\begin{aligned} L_n^2\simeq L_{f_{\max }}^2 \simeq L_{h_{\max }} \lesssim L_n^\textrm{sub} \simeq L_{f_0}\le L_{n}, \end{aligned}$$

from which it would follow that $L_n$ is bounded by an absolute constant.

Finally, we note that the same argument also works with the class of contoured distributions. More specifically, we define

$$\begin{aligned} L_n^{\textrm{cont}}:=\sup \big \{L_h:\,h \text { is an isotropic { contoured} density in } {{\mathbb {R}}}^n\big \}, \end{aligned}$$

and similarly to the sub-log-concave case, we see that if $L_n^\textrm{cont}$ is attained (up to an absolute constant) on a log-concave contoured density function, then $L_n$ is bounded by an absolute constant.