On a Formula for All Sets of Constant Width in 3D

Abstract

In the recent paper “On a formula for sets of constant width in 2D, Comm. Pure Appl. Anal. 18 (2019), 2117–2131”, we gave a constructive formula for all 2d sets of constant width. Based on this result we derive here a formula for the parametrization of the boundary of bodies of constant width in 3 dimensions, with the formula depending on one function defined on ${\mathbb {S}}^2$. Each such function gives a minimal value $r_0$ and for all $r\ge r_0$ one finds a body of constant width 2r. Moreover, we show that all bodies of constant width in 3d have such a parametrization. The last result needs a tool that we describe as ‘shadow domain’ and which is explained in an appendix. The construction is explicit and offers a parametrization different from the one given by T. Bayen, T. Lachand-Robert and É. Oudet in “Analytic parametrization of three-dimensional bodies of constant width. Arch. Ration. Mech. Anal., 186 (2007), 225–249”.

1 Introduction

For a compact set $G\subset {\mathbb {R}}^{n}$ one defines its directional width in direction $\omega \in {\mathbb {S}}^{n-1}:=\left\{ x\in {\mathbb {R}} ^{n};\left| x\right| =1\right\}$ by

$$\begin{aligned} {\varvec{d}}_{G}\left( \omega \right) =\max \left\{ \left\langle \omega ,x\right\rangle ;x\in G\right\} -\min \left\{ \left\langle \omega ,x\right\rangle ;x\in G\right\} , \end{aligned}$$

with $\langle \cdot ,\cdot \rangle$ denoting the standard inner product. If G is convex and ${\varvec{d}}_{G}\left( \omega \right) ={\varvec{d}}_{G}$ is constant, then G is called a set of constant width. In 3 dimensions a set of constant width is also called a body of constant width.

The interest in the subject started with Leonhard Euler, who around 1774 considered 2d curves of constant width, which he called ‘curva orbiformis’. He not only studied such sets for 2 dimensions but also gave a formula describing such curves. See §10 of [5]. In 3 dimensions a ball is obviously the classical example of a body of constant width but the famous Meissner bodies also have this property. See [17, 18] or [14]. Quite simple examples can also be constructed by taking a reflection symmetric 2d set of constant width and rotating it around its line of symmetry.

Famous mathematicians such as Minkowski [20] and Hilbert [11] were intrigued by the subject. The first interest of most scholars focused on deriving properties of such domains. A wonderful survey on sets of constant width (up to 1983) was provided by Chakerian and Groemer in [3], and a more recent updated and thorough treatment can be found in the book by Martini, Montejano and Oliveros [16]. Let us recall that the 3d question, motivated by Blaschke’s 2d result [2], as to which body of constant fixed width has the smallest volume or, equivalently, the smallest surface area, is still open. We will not solve that problem, but will give an alternative formula for constructing bodies of constant width that might help.

Let us recall some known facts about sets of constant width. Sets of constant width G in ${\mathbb {R}}^{n}$ are strictly convex and hence any tangential plane touches G in at most one point. Moreover, for every boundary point ${\varvec{X}}$ of G and $r>{\varvec{d}}_G$ there exists even a ball $B_r$ of radius r such that $G\subset B_r$ and $\partial G\cap \partial B_r={\varvec{X}}$. So G slides freely in $B_r$, according to the definition of [12, page 244].

Although the Gauss-map $\partial \Omega \rightarrow {\mathbb {S}}^{n-1}$ (the outward normal on smooth parts of $\partial G$) will not be uniquely defined on edges or corners, the ‘inverse’ $\gamma _{G}:{\mathbb {S}}^{n-1}\rightarrow \partial G$ is well-defined for a strictly convex G and parametrizes $\partial G$. See [15]. In [16, Theorem 11.1.1] one finds, when G is a set of constant width and $\gamma _{G}\in C^{1}\left( {\mathbb {S}}^{n-1}\right)$, that

$$\begin{aligned} \gamma _{G}(\omega )=P_{G}(\omega )\,\omega +\nabla _{P_{G}}(\omega ) \qquad \text { for all }\omega \in {\mathbb {S}}^{n-1}, \end{aligned}$$

(1)

where $P_{G}(\omega ):=\max \left\{ \left\langle \omega ,x\right\rangle ;x\in G\right\}$ is the support function and $\nabla _{P_{G}}$ its gradient along ${\mathbb {S}}^{n-1}$, i.e. $\left\langle \nabla _{P_{G}}(\omega ),v\right\rangle =\left( dP_{G}(\omega )\right) (v)$ for all $\omega \in {\mathbb {S}}^{n-1}$ and $v\in T_{\omega }{\mathbb {S}}^{n-1}$. Howard in [12, Corollary 2.6] states that for a body of constant width the support function $P_G$ is of class $C^{1,1}$ and hence $\gamma _G$ is Lipschitz continuous. A direct proof of this Lipschitz-continuity also follows from Lemma 11 below. Necessary for a set G of constant width ${\varvec{d}}_{G}$ is that

$$\begin{aligned} \gamma _{G}(\omega )-\gamma _{G}(-\omega )={\varvec{d}}_{G}\ \omega \qquad \text { for all }\omega \in {\mathbb {S}}^{n-1}. \end{aligned}$$

(2)

Therefore $P_{G}(\omega )+P_{G}(-\omega )={\varvec{d}}_{G}$ and $\nabla _{P_{G}}(\omega )=\nabla _{P_{G}}(-\omega )$ for all $\omega \in {\mathbb {S}}^{n-1}$.

In [1] a parametrization of sets of constant width is given by using the so-called median surface, which is parametrized by

$$\begin{aligned} M_{G}(\omega ):=\gamma _{G}(\omega )-\tfrac{1}{2}{\varvec{d}}_{G}\ \omega \qquad \text { for all }\omega \in {\mathbb {S}}^{n-1}. \end{aligned}$$

(3)

Writing $x\cdot Y:=\sum _{i}x_{i}Y_{i}$, which may coincide with but will not be restricted just to the inner product $\left\langle \cdot ,\cdot \right\rangle$, the convexity of G leads to

$$\begin{aligned} \left( M_{G}({\hat{\omega }})-M_{G}(\omega )\right) \cdot \omega \le \tfrac{1}{ 4}{\varvec{d}}_{G}\,\left| {\hat{\omega }}-\omega \right| ^{2}\text { for all }\omega ,{\hat{\omega }}\in {\mathbb {S}}^{n-1}, \end{aligned}$$

(4)

while (2) implies

$$\begin{aligned} M_{G}(\omega )=M_{G}(-\omega )\text { for all }\omega \in {\mathbb {S}}^{n-1}. \end{aligned}$$

(5)

The reverse question would be: can one give criteria on a continuous function $\gamma :{\mathbb {S}}^{n-1}\rightarrow {\mathbb {R}}^{n}$ such that $\gamma \left( {\mathbb {S}}^{n-1}\right)$ parametrizes the boundary of a set of constant width? An answer is given by Theorem 2 of [1], where it is stated that for any continuous map $M:{\mathbb {S}}^{n-1}\rightarrow {\mathbb {R}}^{n}$ and $\alpha >0$, which satisfy

$$\begin{aligned} \begin{array}{cl} M(\omega )=M(-\omega )\text { } &{} \text {for all }\omega \in {\mathbb {S}}^{n-1}, \\ \left( M({\hat{\omega }})-M(\omega )\right) \cdot \omega \le \frac{1}{4}\alpha \ \left| {\hat{\omega }}-\omega \right| ^{2} &{} \text {for all } \omega ,{\hat{\omega }}\in {\mathbb {S}}^{n-1}, \end{array} \end{aligned}$$

(6)

the set

$$\begin{aligned} G:=\left\{ M(\omega )+t\omega \;\ \omega \in {\mathbb {S}}^{n-1},0\le t\le \tfrac{1}{2}\alpha \right\} \end{aligned}$$

(7)

is of constant width ${\varvec{d}}_{G}:=\alpha$ and $M_{G}(\omega ):=M(\omega )$. The $\gamma _{G}$ and $M_{G}$ are as in (3).

One finds by continuity of M that

$$\begin{aligned} \partial G\subseteq \left\{ M(\omega )+\tfrac{1}{2}\alpha \ \omega \;\ \omega \in {\mathbb {S}}^{n-1}\right\} \end{aligned}$$

(8)

and even that the identity holds in (8).

Continuity or even differentiability of M by itself is not enough for an $\alpha$ to exist for which (6) holds. The second condition in (6) implies the convexity of G from (7) and as such it gives a monotonicity for directional derivatives, hence a necessary one-sided estimate for second derivatives of M, whenever these exist. In two dimensions, see [13], a few simple conditions on a function in $L^{\infty }( 0,\pi )$ are necessary and sufficient in order to have a curve of constant width. The construction in 2 dimensions is also helpful in 3 dimensions. It will allow us to give a more explicit formula for all bodies of constant width, which is what we want to show here.

2 Two dimensions

In the last century Hammer and Sobczyk described a construction for 2 dimensions in [8,9,10], based on a characterization of what they called ‘outwardly simple line families’. More recently a direct concise formula was given in [13] to describe all those sets in two dimensions starting from any $L^{\infty }( 0,\pi )$-function satisfying 2 equations, namely the ones in (11). Let us recall the 2d formula from [13]:

Theorem 1

([13, Theorem 3.2]) Let ${\varvec{x}}_{0}\in {\mathbb {R}}^{2}$, $r\in {\mathbb {R}}$ and $a\in L^{\infty }\left( {\mathbb {R}}\right)$ satisfy

$$\begin{aligned}&r\ge \left\| a\right\| _{\infty }, \end{aligned}$$

(9)

$$\begin{aligned}&a\left( \varphi +\pi \right) =-a\left( \varphi \right) \text { for all } \varphi , \end{aligned}$$

(10)

$$\begin{aligned}&\int _{0}^{\pi } a\left( s\right) \left( {\begin{array}{c}-\sin s\\ \cos s\end{array}}\right) \ ds=\left( {\begin{array}{c}0\\ 0\end{array}}\right) . \end{aligned}$$

(11)

Define the closed curve ${\varvec{x}}:\left[ 0,2\pi \right] \rightarrow {\mathbb {R}}^{2}$ by

$$\begin{aligned} {\varvec{x}}\left( \varphi \right) ={\varvec{x}}_{0}+\int _{0}^{\varphi }\left( r-a\left( s\right) \right) \left( {\begin{array}{c}-\sin s\\ \cos s\end{array}}\right) ds. \end{aligned}$$

(12)

Then ${\varvec{x}}$ describes the boundary of a set of constant width 2r.

For a simple statement in Theorem 1 the function $a\in L^{\infty }\left( 0,\pi \right)$ is extended to ${\mathbb {R}}$ and such that (9) and (10) are satisfied.

Let us shortly reflect on the differentiability and regularity of the curve given in (12). The formula shows that

$$\begin{aligned} \frac{{\varvec{x}}(\varphi +h)-{\varvec{x}}(\varphi )}{h}=\left( r- \frac{1}{h}\int _{0}^{h}a(\varphi +s)ds\right) \left( \begin{array}{c} -\sin \varphi \\ \cos \varphi \end{array}\right) +{\mathcal {O}}(h) \end{aligned}$$

(13)

and hence ${\varvec{x}}\in C^{0,1}\left( {\mathbb {R}}\right)$, that is, the function ${\varvec{x}}$ is Lipschitz-continuous. For $a\in L^\infty ({\mathbb {R}})$ this is optimal.

One may also consider the graph ${\varvec{x}}(\left[ 0,2\pi \right] )$ as a curve parametrized by arc length. The arc length $\ell$ as a function of $\varphi$ is computed from (13) and with (9) results in

$$\begin{aligned} \ell (\varphi ) = \int _{0}^{\varphi }\left( r-a(s)\right) ds. \end{aligned}$$

This function $\ell$ is also Lipschitz-continuous and we find

$$\begin{aligned} \frac{\ell (\varphi +h)-\ell (\varphi )}{h}\in \left[ r-\left\| a\right\| _{\infty },r+\left\| a\right\| _{\infty }\right] . \end{aligned}$$

For $r>\left\| a\right\| _{\infty }$ it has a Lipschitz-continuous inverse satisfying

$$\begin{aligned} \frac{\ell ^\text {inv}(t+h)-\ell ^\text {inv}(t)}{h}\in \left[ \left( r+\left\| a\right\| _{\infty }\right) ^{-1},\left( r-\left\| a\right\| _{\infty }\right) ^{-1}\right] . \end{aligned}$$

Moreover, for $r>\left\| a\right\| _{\infty }$ one may show that $t\mapsto {\varvec{x}}\circ \ell ^\text {inv}(t)\in C^{1,1}({\mathbb {R}})$. As usual $C^{1,1}({\mathbb {R}})$ are the differentiable functions on ${\mathbb {R}}$ that have a locally Lipschitz-continuous derivative. If $r=\left\| a\right\| _{\infty }$, then the parametrization by arc length in general just lies in $C^{0,1}({\mathbb {R}})$ and nothing more, even when a is smooth.

The formula in (12) describes the boundary of all 2d-domains of constant width:

Theorem 2

([13, Theorem 4.1]) If $G\subset {\mathbb {R}}^{2}$ is a closed convex set of constant width 2r, then there exists ${\varvec{x}}_{0}$ and a as in Theorem 1, such that $\partial G={\varvec{x}}\left( \left[ 0,2\pi \right] \right)$ with ${\varvec{x}}$ as in (12).

The geometric interpretation of the formula in (12) is that ${\varvec{x}}(\varphi )$ and ${\varvec{x}}(\varphi +\pi )$ describe the ends of a rotating stick of length 2r with the varying point of rotation lying on the stick by (9) and determined by $a(\varphi )$. For these ends to coincide for $\varphi \in [0,\pi ]$ with those for $\varphi \in [\pi ,2\pi ]$ one needs condition (10). The two equalities in condition (11) make it a closed curve.

3 A Formula in Three Dimensions

There have been previous attempts to provide an explicit construction of all 3d-bodies of constant width. In [15] Lachand-Robert and Oudet present a geometric construction that generates 3d-bodies of constant width from 2d-sets of constant width. This construction, however, does not capture all 3d-bodies of constant width because a counterexample is provided in the paper [4] by Danzer, who constructs a body of constant width ${\varvec{d}}$, none of whose planar cross-sections have constant width ${\varvec{d}}$ in two dimensions. In [21] Montejano and Roldan-Pensado generalize the construction of Meissner bodies to generate so-called Meissner polyhedra. This construction does not generate all 3d-bodies either, because the rotated Reuleaux triangle is a counterexample. As already mentioned, Bayen, Lachand-Robert and Oudet give a description of (all) n-dimensional sets of constant width in [1, Theorem 2], but the function M has to satisfy a condition at each point of ${\mathbb {S}}^{n-1}$. We provide an alternative construction for $n=3$, based on the method from [13], which gives a condition that is easier to check.

Our approach uses spherical coordinates $(\varphi ,\theta )$ for the parametrization of the surface of the 3d-body of constant width. Indeed, for each fixed angle $\theta$ we apply the 2d-approach to get a curve parametrized by $\varphi$ of constant width 2r. So as a first step the function a from Theorem 1 is now also depending on $\theta$

$$\begin{aligned} \varphi \mapsto a(\varphi ,\theta )\text { for each }\theta , \end{aligned}$$

(14)

and is used to define a curve $\varphi \mapsto {\varvec{x}}(\varphi ,\theta )$ with ${\varvec{x}}$ as in (12), taking ${\varvec{x}}_0=0$ and $\theta$ as a parameter:

$$\begin{aligned} \left( \begin{array}{c} {\varvec{x}}_1\left( \varphi ,\theta \right) \\ {\varvec{x}}_2\left( \varphi , \theta \right) \end{array}\right) =\int _{0}^{\varphi }\left( r-a\left( s,\theta \right) \right) \left( {\begin{array}{c}-\sin s\\ \cos s\end{array}}\right) ds, \end{aligned}$$

We transfer this curve to the plane in ${\mathbb {R}}^3$ through ${\varvec{X}}_0\in {\mathbb {R}}^3$ perpendicular to $(\sin \theta ,-\cos \theta ,0)^T$:

$$\begin{aligned} {\varvec{X}}_0 + {\varvec{x}}_1(\varphi ,\theta )\left( \begin{array}{c} \cos \theta \\ \sin \theta \\ 0 \end{array}\right) +{\varvec{x}}_2(\varphi ,\theta ) \left( \begin{array}{c} 0 \\ 0\\ 1 \end{array}\right) . \end{aligned}$$

This first step however does not yet generate a body of constant width. Whenever $\left\| \partial ^2_\theta a\right\| _\infty$ is bounded and when r is large enough, the second step is to apply a unique shift in the $\left( -\sin \theta ,\cos \theta ,0\right) ^T$-direction for the collection of these rotating 2d-curves. For the magnitude of the shift we will use $h(\varphi ,\theta )$. The combined result of these two steps will yield a 3d-body of constant width. Moreover we will show, that not only the result is a body of constant width but also that each such body can be written this way.

Aside from our results from [13] for two dimensions we will use a result by Hadwiger in [7], which can be roughly described as follows: convex bodies in ${\mathbb {R}}^{n}$ are uniquely determined by the projections in ${\mathbb {R}}^{n-1}$ perpendicular to one fixed direction. The result holds for $n\ge 4$ and, whenever the one fixed direction is regular, also for $n=3$. This last addendum is due to [6]. Regular means here, that the planes perpendicular to that fixed direction which touch the convex domain, do that in precisely one point. Since sets of constant width are necessarily strictly convex, this is obviously the case for those sets and any choice of the fixed direction.

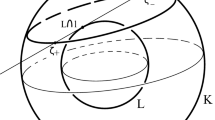
Let us define for $\omega \in {\mathbb {S}}^{2}$ the orthogonal projection $P_{\omega }$ onto the plane $E_{\omega }:=\left\{ x\in {\mathbb {R}}^{3};\langle x,\omega \rangle =0 \right\}$. To exploit the result of Hadwiger we will use for a fixed $u\in {\mathbb {S}}^{2}$ all projections in the directions $\omega \in {\mathbb {S}}^{2}$ with $\left\langle \omega ,u\right\rangle =0$. See Fig. 1. For those $\omega$ we have

$$\begin{aligned} P_{\omega }x=\left\langle u,x\right\rangle u+\left\langle u\times \omega ,x\right\rangle \left( u\times \omega \right) . \end{aligned}$$

(15)

For later use we need to identify the projections onto $E_{\omega }$ with coordinates in ${\mathbb {R}}^{2}$ through

$$\begin{aligned} {\widehat{P}}_{\omega }x=\left( \begin{array}{c} \left\langle u,x\right\rangle \\ \left\langle u\times \omega ,x\right\rangle \end{array} \right) . \end{aligned}$$

(16)

Fig. 1

The plane $E_{\omega }$ for one $\omega$ and ‘all’ planes $E_{\omega }$ with $\omega$ such that $\left\langle \omega ,u\right\rangle =0$. Those $E_{\omega }$ contain u as a common direction

We may now explain the result by Hadwiger in [7] in more detail. He proved that for two convex bodies $G_{1}$ and $G_{2}$ in ${\mathbb {R}}^{3}$ the following holds.

• If $P_{u}G_{1}\simeq P_{u}G_{2}$ and $P_{\omega }G_{1}\simeq P_{\omega }G_{2}$ for all $\omega \in {\mathbb {S}}^{2}$ with $\left\langle \omega ,u\right\rangle =0$, then $G_{1}\simeq G_{2}$.

Here $A\simeq B$ means that A equals B after a translation. In other words, there is a fixed $v\in {\mathbb {R}}^{3}$ such that $A=v+B$. Groemer showed in [6] that one could drop the condition $P_{u}G_{1}\simeq P_{u}G_{2}$, whenever u is a regular direction for $G_{1}$. Here regular means that $\max \left\{ \left\langle u,x\right\rangle ;x\in G_{1}\right\}$ is attained for a unique $x\in G_{1}$. Since domains G of constant width are precisely those domains for which

$$\begin{aligned} G^{*}:=\tfrac{1}{2}G+\tfrac{1}{2}\left( -G\right) :=\left\{ \tfrac{1}{2} x-\tfrac{1}{2}y;x,y\in G\right\} \end{aligned}$$

is a ball, which has only regular directions, one finds that $\big ({\widehat{P}}_{\omega }G\big )^{*}$ is a disc for all $\omega \in {\mathbb {S}}^{2}$ with $\left\langle \omega ,u\right\rangle =0$, if and only if $G^{*}$ is a ball. Necessarily those discs and the ball have the same radius. This implies that a convex closed set $G\subset {\mathbb {R}}^{3}$ is a body of constant width if and only if there is a direction $u\in {\mathbb {S}}^{2}$, such that for some fixed $\rho >0$ one finds

$$\begin{aligned} \big ({\widehat{P}}_{\omega }G\big )^{*}\simeq D_{\rho }:=\left\{ y\in {\mathbb {R}}^{2};\left| y\right| \le \rho \right\} \text { for all } \omega \in {\mathbb {S}}^{2}\text { with }\left\langle \omega ,u\right\rangle =0. \end{aligned}$$

This means that all those $P_{\omega }G$ should be two-dimensional convex sets of constant width $\rho$. So by taking $u=\left( 1,0,0\right)$ we find that the boundary of $P_{\omega }G$ is described by (12) with some a depending on $\omega$. This leads us to the result in Theorem 5.

Notation 3

We parametrize ${\mathbb {S}}^{2}={\varvec{U}}({\mathbb {R}}^{2})$ by

$$\begin{aligned} \omega = {\varvec{U}}\left( \varphi ,\theta \right) :=\left( \begin{array}{c} \sin \varphi \cos \theta \\ \sin \varphi \sin \theta \\ \cos \varphi \end{array} \right) . \end{aligned}$$

(17)

This is the standard parametrization with $\varphi$ the angle between $\omega$ and the positive z-axis and $\theta$ the counterclockwise angle of the projection onto the xy-plane with the x-axis, viewed from the positive z-axis. Obviously this parametrization is not unique as we may restrict $(\varphi ,\theta )$ to some subset of ${\mathbb {R}}^2$.

We may define a convenient $\varphi ,\theta$-dependent orthonormal basis, first for $\sin \varphi \ne 0$,

$$\begin{aligned} \left\{ {\varvec{U}}\left( \varphi ,\theta \right) ,{\varvec{U}} _{\varphi }\left( \varphi ,\theta \right) ,\frac{{\varvec{U}}_{\theta }\left( \varphi ,\theta \right) }{\sin \varphi }\right\}&= \left\{ \left( \begin{array}{c} \sin \varphi \cos \theta \\ \sin \varphi \sin \theta \\ \cos \varphi \end{array} \right) ,\left( \begin{array}{c} \cos \varphi \cos \theta \\ \cos \varphi \sin \theta \\ -\sin \varphi \end{array} \right) ,\left( \begin{array}{c} -\sin \theta \\ \cos \theta \\ 0 \end{array} \right) \right\} \nonumber \\&=: \left\{ {\varvec{U}}\left( \varphi ,\theta \right) ,{\varvec{V}} \left( \varphi ,\theta \right) ,{\varvec{W}}\left( \theta \right) \right\} , \end{aligned}$$

(18)

with the expression in the middle showing the obvious extension when $\sin \varphi =0$.

Any function $(\varphi ,\theta )\mapsto v(\varphi ,\theta ):{\mathbb {R}}^2\rightarrow {\mathbb {R}}$ that is used to define a quantity on ${\mathbb {S}}^2$ necessarily has to possess the obvious periodicity properties as well as some compatibility conditions. The relations, which the function a from (14) has to satisfy, are more subtle. For $\varphi \not \in \left\{ 0,\pi \right\}$ the value $r-a(\varphi ,\theta )$ coincides with the inverse curvature in the $\varphi$-direction. There is however a peculiarity at the north- and southpole, where the curvature in any(!) direction is given by $\left( r-a(0,\theta )\right) ^{-1}$, respectively $\left( r-a(\pi ,\theta ) \right) ^{-1}$, through varying $\theta$. This leads to the following definition with a distinction between pure periodicity and what we call compatibility, both derived from ${\varvec{U}}(\varphi ,\theta )={\varvec{U}}({\hat{\varphi }},{\hat{\theta }})$:

Definition 4

For a function $f:{\mathbb {R}}^2\rightarrow {\mathbb {R}}$ we say that:

• f satisfies the periodicity conditions for ${\mathbb {S}}^2$, if

  $$\begin{aligned} f({\hat{\varphi }},{\hat{\theta }})&=f(\varphi ,\theta )\ \text { for all }\ \hat{ \varphi }-\varphi ,{\hat{\theta }}-\theta \in 2\pi {\mathbb {Z}}\ \text { and} \end{aligned}$$

  (19)
  $$\begin{aligned} f({\hat{\varphi }},{\hat{\theta }})&=f(\varphi ,\theta )\ \text { for all }\ {\hat{\varphi }}+\varphi ,{\hat{\theta }}-\theta +\pi \in 2\pi {\mathbb {Z}}; \end{aligned}$$

  (20)

• f satisfies the compatibility conditions for the poles of ${\mathbb {S}} ^2$, if

  $$\begin{aligned} f(0,\theta )=f(0,0)\ \text { and }\ f(\pi ,\theta )=f(\pi ,0)\ \text { for all }\ \theta \in {\mathbb {R}}. \end{aligned}$$

  (21)

Suppose that $B({\mathbb {R}}^2)$ is some function space. We write:

• $f\in B_{\textrm{p}}({\mathbb {R}}^2)$, whenever $f\in B({\mathbb {R}}^2)$ and satisfies (19) and (20);

• $f\in B_{\textrm{p,c}}({\mathbb {R}}^2)$, whenever $f\in B({\mathbb {R}}^2)$ and satisfies (19), (20) and (21).

With obvious changes we use the similar notations for a vector-valued ${\varvec{F}}:{\mathbb {R}}^2\rightarrow {\mathbb {R}}^3$ whenever $f={\varvec{F}}_i$ satisfies the required properties for all $i\in \{ 1,2,3\}$.

One usually restricts ${\mathbb {R}}^{2}$ to $\left[ 0,\pi \right] \times \left[ 0,2\pi \right]$ to have a unique parametrization at least for the interior points and with some compatibility assumptions at its boundary, but here it will be more convenient to take, see Fig. 2,

$$\begin{aligned} (\varphi ,\theta )\in \left[ 0,2\pi \right] \times \left[ 0,\pi \right] =:{\textsf{S}}. \end{aligned}$$

(22)

Fig. 2

The orientation of $(\varphi ,\theta )\in {\textsf{S}}$ on ${\mathbb {S}}^2$

As in the 2d-case the function a from (14) that we use is such that at opposite points of ${\mathbb {S}}^{2}$ the value is opposite: $a\left( \varphi ,\theta \right) =-a\left( \varphi +\pi ,\theta \right) =-a\left( \pi -\varphi ,\theta +\pi \right)$. Hence a is completely defined by its values on $\left[ 0,\pi \right) \times \left[ 0,\pi \right)$.

Theorem 5

(Constructing bodies of constant width) Suppose that $a\in C_\textrm{p}^2({\mathbb {R}}^2)$ satisfies

$$\begin{aligned}&a\left( \varphi ,\theta \right) =-a\left( \varphi +\pi ,\theta \right) \hspace{5mm}&\text { for all }\left( \varphi ,\theta \right) \in {\mathbb {R}}^2, \end{aligned}$$

(23)

$$\begin{aligned}&\int _{0}^{\pi }a\left( s,\theta \right) \left( {\begin{array}{c}\cos s\\ \sin s\end{array}}\right) \ ds=\left( {\begin{array}{c}0\\ 0\end{array}}\right) \ {}&\text { for all }\theta \in {\mathbb {R}}, \end{aligned}$$

(24)

Let ${\varvec{V}}$ and ${\varvec{W}}$ be as in (18) and suppose that $h:(0,\pi )\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ is defined by:

$$\begin{aligned} h\left( \varphi ,\theta \right) :=-\frac{\int _{0}^{\varphi }\sin \left( \varphi -s\right) ~\partial _{\theta }a(s,\theta )~ds}{\sin \varphi }. \end{aligned}$$

(25)

• 1. Then the definition in (25) can be continuously extended to ${\mathbb {R}}^{2}$. The extended h is such that

  $$\begin{aligned} h(\varphi ,\theta )&=h(\varphi +\pi ,\theta )\ \text { for all }(\varphi ,\theta ) \in {\mathbb {R}}^2, \end{aligned}$$

  (26)
  $$\begin{aligned} h(\varphi ,\theta )&=0\ \text { for all }(\varphi ,\theta )\in \pi {\mathbb {Z}} \times {\mathbb {R}} \end{aligned}$$

  (27)

  and satisfies

  $$\begin{aligned} (\varphi ,\theta )\mapsto h(\varphi ,\theta ){\varvec{W}}(\theta )\in C_{ \textrm{p,c}}^{1}({\mathbb {R}}^{2}). \end{aligned}$$

  (28)

• 2. There exists

  $$\begin{aligned} r_{0}(a)\in \left[ \left\| a\right\| _{\infty },\left\| a\right\| _{\infty }+\left\| \partial _{\theta }a\right\| _{\infty }+\left\| \partial _{\theta }^{2}a\right\| _{\infty }\right] , \end{aligned}$$

  (29)

  such that for all $r\ge r_{0}(a)$ and ${\varvec{X}}_{0}\in {\mathbb {R}}^{3}$, the surface ${\varvec{X}}({\textsf{S}})$, defined by

  $$\begin{aligned} {\varvec{X}}(\varphi ,\theta )={\varvec{X}}_{0}+\int _{0}^{\varphi }\left( r-a\left( s,\theta \right) \right) {\varvec{V}}(s,\theta ) \,ds+h\left( \varphi ,\theta \right) {\varvec{W}}(\theta ), \end{aligned}$$

  (30)

  describes the boundary of a body of constant width 2r. If $r>r_0(a)$, then ${\varvec{X}}$ is a regular parametrization of the boundary.

• 3. Moreover, with $a(\cdot ,\cdot )$ as above, the function h in (25) is the unique possibility in order that ${\varvec{X}}$ in (30) describes the boundary of a body of constant width 2r.

Remark 5.1

A compact surface $M\subset {\mathbb {R}}^3$ is called a $C^1$-manifold, if at each point of M a differentiable local parametrization ${\varvec{Y}}:U\subset {\mathbb {R}}^2\rightarrow M$ exists that is regular (having a strictly positive first fundamental form) with ${\varvec{Y}}\in C^1(U)$ and where U is some open set.

If G is a body of constant width, with $\partial G$ a $C^1$-manifold parametrized by ${\varvec{X}}$, we call ${\varvec{X}}:{\textsf{S}}\rightarrow {\mathbb {R}}^3$ a regular parametrization, if, with ${\varvec{U}}$ as in (17) and

$$\begin{aligned} \varvec{\tilde{X}}:{\mathbb {S}}^{2}\rightarrow \partial G\text { defined by }\varvec{\tilde{X}}\left( \omega \right) :={\varvec{X}}\left( \varphi ,\theta \right) \text { for }\omega ={\varvec{U}}(\varphi ,\theta ) \end{aligned}$$

(31)

lies in $C^{1}({\mathbb {S}}^2)$ and is a diffeomorphism. We will also use ‘regular in a point‘, say in $(\varphi ,\theta )$, when the parametrization $\varvec{\tilde{X}}$ is locally a diffeomorphism near ${\varvec{U}}(\varphi ,\theta )$.

In the theorem above we assumed $a\in C_\textrm{p}^2({\mathbb {R}}^2)$, so that we may use classical derivatives. This will imply that (28) holds and that ${\varvec{X}}$ in (30) is a differentiable parametrization. This parametrization however doesn’t have to be regular in the sense just mentioned and indeed for $r=r_0(a)$ it usually is not.

Moreover, the assumption $a\in C_\textrm{p}^2({\mathbb {R}}^2)$ is too restrictive for general 3d-bodies of constant width. We have seen from the 2d-case that in general $\varphi \mapsto a(\varphi ,\theta )$ lies in $L^\infty ({\mathbb {R}})$ and not even in $C({\mathbb {R}})$. When considering all bodies of constant width, one should assume at most something like $a\in L^\infty _\textrm{p}({\mathbb {R}}^2)$, $a_\theta \in L^\infty ({\mathbb {R}}^2)$ and will find at most that

$$\begin{aligned} \varphi \mapsto {\varvec{X}}(\varphi ,\theta )\in C^{0,1}({\mathbb {R}}), \end{aligned}$$

besides the periodicity conditions. With $a\in L^\infty _\textrm{p}({\mathbb {R}}^2)$, $a_\theta \in L^\infty ({\mathbb {R}}^2)$ the parametrization ${\varvec{X}}:{\textsf{S}}\rightarrow \partial G$ in (30) is still well-defined but not necessarily differentiable. Differentiability is a priori needed to consider regularity of ${\varvec{X}}$.

Our construction will be illustrated by the example in Section 4. The example satisfies all conditions of Theorem 5, except that $a\in C_{\textrm{p}}^{1,1}({\mathbb {R}}^2)$ instead of $C^2({\mathbb {R}}^2)$. One finds ${\varvec{X}}\in C^{0,1}({\mathbb {R}}^2)$. Nevertheless it does supply us with a 3d-set of constant width. There exists $r_0(a)\in [1,\infty )$ and a numerical computation for this example gives $r_0(a)\approx 1.25348$. One may show that for $r=r_{0}(a)$ the surface ${\varvec{X}}({\textsf{S}})$ will not be a $C^{1,1}$-manifold; for $r>r_{0}(a)$ it is. Another example that satisfies all assumptions of Theorem 5 except $a\in C^2({\mathbb {R}}^2)$ is the last one in Fig. 10.

The value of $r_0(a)$ can be computed numerically by finding the smallest $r\ge \left\| a\right\| _\infty$ such that $T(0,r)\ge 0$ and $T(\pi ,r)\ge 0$ in (52) and $D(r,\varphi ,\theta )/\sin \varphi \ge 0$ in (54) holds for all $\varphi \in [0,2\pi ]$, $\theta \in [0,\pi ]$. We will show that, if $r=r_0(a)\ge \left\| a\right\| _\infty$ is admissible, then so are $r>r_0(a)$.

We first prove some results for h that we gather in the next lemma. In fact, Lemma 6 contains the first item of Theorem 5.

Lemma 6

Suppose that $a\in C_{\textrm{p}}^{2}({\mathbb {R}}^{2})$ satisfies (23) and (24). Then h in (25) satisfies the following estimates: for all $(\varphi ,\theta )\in (0,\pi )\times {\mathbb {R}}$

$$\begin{aligned} \left| h\left( \varphi ,\theta \right) \right|&\le \left\| a_{\theta }\right\| _{\infty }\left| \sin \varphi \right| , \end{aligned}$$

(32)

$$\begin{aligned} \left| h_{\varphi }\left( \varphi ,\theta \right) \right|&\le \left\| a_{\theta }\right\| _{\infty }, \end{aligned}$$

(33)

$$\begin{aligned} \left| h_{\theta }\left( \varphi ,\theta \right) \right|&\le \left\| a_{\theta \theta }\right\| _{\infty }\left| \sin \varphi \right| . \end{aligned}$$

(34)

The function h can be continuously extended to ${\mathbb {R}}^{2}$ and the extension is such that (32), (33) and (34) hold for all $(\varphi ,\theta )\in {\mathbb {R}}^2$, as well as that (25) holds for all $\varphi \in {\mathbb {R}}\setminus \pi {\mathbb {Z}}$ and $\theta \in {\mathbb {R}}$. Moreover, one finds that equalities (26) and (27) hold true and that (28) is satisfied.

Proof

A priori h is defined for $\varphi \in \left( 0,\pi \right)$ with the periodicity in the $\theta$-direction being a consequence of the assumption that a satisfies (19) and (20). To consider the extension in the $\varphi$-direction let us first focus on the numerator for h in formula (25). The numerator is $C^1$, since a is $C^2$. By (24) we find that

$$\begin{aligned} \int _{0}^{\pi }\sin \left( \varphi -s\right) ~a_{\theta }(s,\theta )~ds=\partial _{\theta }\left( \int _{0}^{\pi }\sin \left( \varphi -s\right) ~a(s,\theta )~ds\right) =0. \end{aligned}$$

(35)

Moreover, for $\varphi \in \left[ 0,\frac{1}{2}\pi \right]$ we use $1\le 1+\cos \varphi$ and find

$$\begin{aligned} \left| \int _{0}^{\varphi }\sin \left( \varphi -s\right) ~\partial _{\theta }a(s,\theta )~ds\right|\le & {} \left\| \partial _{\theta }a\right\| _{\infty }\int _{0}^{\varphi }\sin \left( \varphi -s\right) ds \\= & {} \left\| \partial _{\theta }a\right\| _{\infty }\left( 1-\cos \varphi \right) \\\le & {} \left\| \partial _{\theta }a\right\| _{\infty }\left( 1-\cos \varphi \right) \left( 1+\cos \varphi \right) \\= & {} \left\| \partial _{\theta }a\right\| _{\infty }\left| \sin \varphi \right| ^{2}, \end{aligned}$$

while for $\varphi \in \left( \frac{1}{2}\pi ,\pi \right]$ we use $1\le 1-\cos \varphi$ and (35) to obtain that

$$\begin{aligned} \left| \int _{0}^{\varphi }\sin \left( \varphi -s\right) ~\partial _{\theta }a(s,\theta )~ds\right|= & {} \left| \int _{\varphi }^{\pi } \sin \left( \varphi -s\right) ~\partial _{\theta }a(s,\theta )~ds\right| \\\le & {} \left\| \partial _{\theta }a\right\| _{\infty }\left| \int _{\varphi }^{\pi }\sin \left( \varphi -s\right) ds\right| \\= & {} \left\| \partial _{\theta }a\right\| _{\infty }\left( 1+\cos \varphi \right) \\\le & {} \left\| \partial _{\theta }a\right\| _{\infty }\left( 1-\cos \varphi \right) \left( 1+\cos \varphi \right) \\= & {} \left\| \partial _{\theta }a\right\| _{\infty }\left| \sin \varphi \right| ^{2}. \end{aligned}$$

Hence we find that h can be continuously extended by 0 for $\varphi \in \left\{ 0,\pi \right\}$ and

$$\begin{aligned} \left| h\left( \varphi ,\theta \right) \right| \le \left\| \partial _{\theta }a\right\| _{\infty }\left| \sin \varphi \right| , \end{aligned}$$

which is (32) at least on $\left[ 0,\pi \right] \times {\mathbb {R}}$.

Taking the formula in (25) for $\varphi +\pi \in (\pi ,2\pi )$, we find by (24), a substitution and (23)

$$\begin{aligned} h\left( \varphi +\pi ,\theta \right)&=-\frac{\int _{0}^{\varphi +\pi }\sin \left( \varphi +\pi -s\right) \partial _{\theta }a\left( s,\theta \right) ds }{\sin \left( \varphi +\pi \right) }\\&=\frac{\int _{\pi }^{\varphi +\pi }\sin \left( \varphi +\pi -s\right) \partial _{\theta }a\left( s,\theta \right) ds }{\sin \varphi } \\&=\frac{\int _{0}^{\varphi }\sin \left( \varphi -s\right) \partial _{\theta }a\left( s-\pi ,\theta \right) ds}{\sin \varphi }\\&=-\frac{\int _{0}^{\varphi }\sin \left( \varphi -s\right) \partial _{\theta }a\left( s,\theta \right) ds }{\sin \varphi }=h\left( \varphi ,\theta \right) \end{aligned}$$

and we find that the definition of h is well-defined on $\left( \pi ,2\pi \right) \times {\mathbb {R}}$ and at least there (26) holds. Then h can be extended continuously by 0 and (32) holds for $\varphi \in \left\{ 0,\pi ,2\pi \right\}$. This allows us to use the definition in (25) for h for all $\varphi$ with $\sin \varphi \ne 0$ and to set $h=0$ whenever $\sin \varphi =0$. Moreover, since $a_{\theta }\in C_{\textrm{p}}^{1}({\mathbb {R}}^{2})$ we find that h and also $h\, {\varvec{W}}$ satisfies (19). One also finds that (27) holds true.

For (20) note that

$$\begin{aligned} h(-\varphi ,\theta +\pi )&=-\frac{\int _{0}^{-\varphi }\sin \left( -\varphi -s\right) ~\partial _{\theta }a(s,\theta +\pi )~ds}{\sin \left( -\varphi \right) }\\&=\frac{\int _{0}^{-\varphi }\sin \left( -\varphi -s\right) ~\partial _{\theta }a(-s,\theta )~ds}{\sin \varphi } \\&=-\frac{\int _{0}^{\varphi }\sin \left( -\varphi +s\right) ~\partial _{\theta }a(s,\theta )~ds}{\sin \varphi }\\&=\frac{\int _{0}^{\varphi }\sin \left( \varphi -s\right) ~\partial _{\theta }a(s,\theta )~ds}{\sin \varphi } =-h(\varphi ,\theta ) \end{aligned}$$

and with

$$\begin{aligned} h(-\varphi ,\theta +\pi ){\varvec{W}}(\theta +\pi )=-h(\varphi ,\theta ) {\varvec{W}}(\theta +\pi )=h(\varphi ,\theta ){\varvec{W}}(\theta ) \end{aligned}$$

we indeed find (20) for $h{\varvec{W}}$. Moreover, $a_{\theta }\in C_{\textrm{p}}^{1}({\mathbb {R}}^{2})$ implies $h\in C^{1}( {\mathbb {R}}^{2})$ and hence (28) holds.

Since the $\theta$-dependence only comes through a the estimate in (34) is proven similarly as for (32). For ( 33) we use a straightforward computation from (25) and using (24) to find

$$\begin{aligned} h_{\varphi }\left( \varphi ,\theta \right)= & {} -\frac{\int _{0}^{\varphi }\sin s~\partial _{\theta }a(s,\theta )~ds}{\left( \sin \varphi \right) ^{2}}\nonumber \\= & {} \frac{\int _{\varphi }^{\pi }\sin s~\partial _{\theta }a(s,\theta )~ds}{\left( \sin \varphi \right) ^{2}}. \end{aligned}$$

(36)

It is sufficient to prove the estimates for $\varphi \in [0,\pi ]$. So we proceed for $\varphi \in [0,\frac{1}{2}\pi ]$ by

$$\begin{aligned} \left| h_{\varphi }\left( \varphi ,\theta \right) \right|\le & {} \frac{\int _{0}^{\varphi }\sin s~ds\left\| a_{\theta }\right\| _{\infty } }{\left( \sin \varphi \right) ^{2}}\\= & {} \frac{1-\cos \varphi }{(\sin \varphi )^2}\left\| a_{\theta }\right\| _{\infty }\\\le & {} \frac{(1-\cos \varphi )(1+\cos \varphi )}{(\sin \varphi )^2}\left\| a_{\theta }\right\| _{\infty }=\left\| a_{\theta }\right\| _{\infty } \end{aligned}$$

and for $\varphi \in [\frac{1}{2}\pi ,\pi ]$ by

$$\begin{aligned} \left| h_{\varphi }\left( \varphi ,\theta \right) \right|\le & {} \frac{\int _{\varphi }^{\pi }\sin s~ds\left\| a_{\theta }\right\| _{\infty } }{\left( \sin \varphi \right) ^{2}}=\frac{1+\cos \varphi }{(\sin \varphi )^2}\left\| a_{\theta }\right\| _{\infty }\\\le & {} \frac{(1-\cos \varphi )(1+\cos \varphi )}{(\sin \varphi )^2}\left\| a_{\theta }\right\| _{\infty }=\left\| a_{\theta }\right\| _{\infty }, \end{aligned}$$

which completes the proof. $\square$

Proofs of Theorem 5 and of the converse result in the next theorem are given in Sect. 5.

Theorem 7

(All bodies of constant width are represented by (30)) Let G be a body of constant width 2r. Then the following holds:

• 1. The boundary $\partial G$ is described by ${\varvec{X}}$ as in (30) for some $a\in L_\textrm{p}^{\infty }({\mathbb {R}}^2)$ with $\left\| a\right\| _\infty \le r$, where $a(\cdot ,\cdot )$ satisfies (23) and (24), and with h such that $h\left( \varphi ,\theta \right) =0$ for $\varphi \in \pi {\mathbb {Z}}$ and

  $$\begin{aligned} h\left( \varphi ,\theta \right) =\frac{\displaystyle \lim _{\varepsilon \rightarrow 0}\int _{0}^{\varphi }\frac{a(s,\theta )-a(s,\theta +\varepsilon )}{ \varepsilon }\sin \left( \varphi -s\right) ds}{\sin \varphi } \text { for }\varphi \not \in \pi {\mathbb {Z}}. \end{aligned}$$

  (37)

• 2. The function h satisfies (26), that is, $h\left( \varphi +\pi ,\theta \right) =h\left( \varphi ,\theta \right)$ for all $( \varphi ,\theta )\in {\mathbb {R}}\times {\mathbb {R}}$, and

  $$\begin{aligned} \left( \varphi ,\theta \right) \mapsto h\left( \varphi ,\theta \right) \left( \begin{array}{c} -\sin \theta \\ \cos \theta \end{array} \right) \in C^{0,1}_{\textrm{p,c}}\left( {\mathbb {R}}^2\right) . \end{aligned}$$

  (38)

  One even finds that the following holds for all $\varphi ,\theta ,\theta _0\in {\mathbb {R}}$:

  $$\begin{aligned} \left| h(\varphi ,\theta )-h(\varphi ,\theta _0)\right| \le 8\pi r \left| \sin \varphi \right| \left| \theta -\theta _0\right| . \end{aligned}$$

  (39)

• 3. Moreover, if $a(\cdot ,\cdot )$ is such that

  • i. $a,\partial _{\theta }a\in C_\textrm{p}^{0}({\mathbb {R}}^2)$, then (25) holds true;

  • ii. $a,\partial _{\theta }a\in C_{\textrm{p}}^{1}({\mathbb {R}}^2)$, then (28) holds true.

4 An Example

The formulas are rather technical and in order to illustrate that (30) does deliver a body of constant width, we give an actual construction in a case that is computable. The example shows a body of constant width connecting two triangular 2d-domains of constant width based on the 2d-formula. In addition to ${\varvec{x}}_{0}=(0,0)$ and $r=1$ we use in Fig. 3:

• for the figure on the left: $a(s)=a_{1}(s):=-\cos (3s)$;

• for the figure in the middle: $a(s)=a_{2}(s):=\sin (3s)$.

One directly checks that conditions (10) and (11) are satisfied for $a_1$ and $a_2$.

The object on the right of Fig. 3 combines these two curves in a 3d-setting in orthogonal planes with the red line as common intersection. In order to find a smooth perturbation from the horizontal to the vertical curve by curves whose projections will be 2d-curves of constant width 1, we use the following:

$$\begin{aligned} a\left( \varphi ,\theta \right) :=\left( \cos \theta \right) ^{2}a_{1}(\varphi )+\left| \sin \theta \right| \sin \theta ~a_{2}(\varphi ). \end{aligned}$$

(40)

Since $a_1$ and $a_2$ satisfy (10) and (11) it follows that a defined in (40) satisfies (23) and (24). The periodicity condition in (19) can be checked directly; the one in (20) follows since $a_1(\varphi )=a_1(-\varphi )$ and $a_2(\varphi )=-a_2(-\varphi )$. One may compute $\left\| a\right\| _\infty = 1$, $\left\| \partial _\theta a\right\| _\infty =\sqrt{2}$ and $\left\| \partial _\theta ^2 a\right\| _\infty = 2\sqrt{2}$.

Fig. 3

The 2d sets with $a_1$ and $a_2$ for $\varvec{x}(0)$ on top, and the combination in 3d by perpendicular planes and joining the red axes

This example does not satisfy the condition of Theorem 5 that $a\in C^2({\mathbb {R}}^2)$, but as we mentioned before, that condition was used to simplify arguments. We will nevertheless find a body of constant width. An argument using smooth approximating functions $a(\cdot ,\cdot )$ should convince the reader.

One has $r_0(a)\ge \max \left( r_0(a_1),r_0(a_2)\right) =1$. Concerning the value of $r_0(a)$ for a in (40) a numerical estimate for the expression in (54) to be positive shows $r_0(a)\approx 1.25348$, which lies inside the interval given in (29).

Fig. 4

On the left the intermediate construction still without the h. It consists of a rotating family of 2d-sets of constant width for each $\theta$. This is not a body of constant width and not even convex. On the right is the corresponding body of constant width as the final result with the shift by h from (25) in the direction ${\varvec{W}}(\theta )$ from (18) as given in (30). Both red curves originate from the curves from Fig. 3. The surface on the right does not look smooth everywhere as indeed here $r=1.25348$, the numerical approximation of $r_0(a)$. These red curves give two planar curves of constant width, since $\partial _\theta a(\varphi ,\theta )=0$ for all $\left( \varphi ,\theta \right) \in {\mathbb {R}}\times \pi {\mathbb {Z}}$

The a in (40) is used to produce the sketch on the left in Fig. 4 using the formula in (30) without the h-term. Each intersection with a plane containing the vertical (red) line $\left\{ \lambda (0,0,1); \lambda \in {\mathbb {R}}\right\}$ will produce a 2d set of constant width. After the modification with the additional h-term in (30) does one indeed find a 3d-body of constant width, which is found on the right of Fig. 4.

Although each body of constant width can be constructed through the formula in (30) it is relatively easy if one connects two curves of constant width as in (40). More examples can be found in Fig. 10.

5 Proofs of the Two Theorems

For the standard inner product of $u,v\in {\mathbb {R}}^{n}$ we use $\left\langle u,v\right\rangle$. The notation $u\cdot v$ is used for componentwise multiplication, which includes but can be more general than the inner product. Let us start by introducing three vectors for a more concise notation:

$$\begin{aligned} \varvec{\Theta }=\left( \begin{array}{c} \cos \theta \\ \sin \theta \\ 0 \end{array} \right) \text {, }\varvec{\Psi }=\left( \begin{array}{c} -\sin \theta \\ \cos \theta \\ 0 \end{array} \right) \text { and }\varvec{\Xi }=\left( \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right) . \end{aligned}$$

(41)

These three directions constitute a $\theta$-dependent orthonormal basis in ${\mathbb {R}}^{3}$ that turns out to be convenient for our parametrization. The following identities hold true:

$$\begin{aligned} \partial _{\theta }\varvec{\Theta }=\varvec{\Psi }\text { and } \partial _{\theta }\varvec{\Psi }=-\varvec{\Theta .} \end{aligned}$$

(42)

Also note that our initial basis (18) can be expressed in terms of (41):

$$\begin{aligned} {\varvec{U}}\left( \varphi ,\theta \right)&=\left( \begin{array}{c} \sin \varphi \cos \theta \\ \sin \varphi \sin \theta \\ \cos \varphi \end{array} \right) =\cos \varphi ~\varvec{\Xi }+\sin \varphi ~\varvec{\Theta } =\left( \begin{array}{c} \sin \varphi \\ \cos \varphi \end{array} \right) \cdot \left( \begin{array}{c} \varvec{\Theta } \\ \varvec{\Xi } \end{array} \right) , \end{aligned}$$

(43)

$$\begin{aligned} {\varvec{V}}\left( \varphi ,\theta \right)&=\left( \begin{array}{c} \cos \varphi \\ -\sin \varphi \end{array} \right) \cdot \left( \begin{array}{c} \varvec{\Theta } \\ \varvec{\Xi } \end{array} \right) \text { and }{\varvec{W}}\left( \theta \right) =\varvec{ \Psi }. \end{aligned}$$

(44)

The dot product $\cdot$ in (43), (44) is a more convenient notation in the following proofs.

Proof of Theorem 5

We will have to show that ${\varvec{X}}$ in (30) is a regular parametrization and secondly, that the resulting surface will yield a body of constant width. For both aspects we need to consider $\partial _{\varphi } {\varvec{X}}\left( \varphi ,\theta \right)$ and $\partial _{\theta } {\varvec{X}}\left( \varphi ,\theta \right)$. Recall that we named ${\varvec{X}}$ a regular parametrization, when in fact $\varvec{\tilde{X}}$ from (31) is.

$\blacktriangleright$ Computation of $\partial _{\varphi }{\varvec{X}}\left( \varphi ,\theta \right)$ and $\partial _{\theta }{\varvec{X}}\left( \varphi ,\theta \right)$. With the notation from (41) we can rewrite (30) as

$$\begin{aligned} {\varvec{X}}\left( \varphi ,\theta \right) ={\varvec{X}} _{0}+\int _{0}^{\varphi }\left( r-a(s,\theta )\right) \left( \begin{array}{c} -\sin s \\ \cos s \end{array} \right) ds\cdot \left( \begin{array}{c} \varvec{\Xi } \\ \varvec{\Theta } \end{array} \right) +h(\varphi ,\theta )\ \varvec{\Psi .} \end{aligned}$$

(45)

One computes that

$$\begin{aligned} \partial _{\varphi }{\varvec{X}}\left( \varphi ,\theta \right) =\left( r-a(\varphi ,\theta )\right) \left( \begin{array}{c} -\sin \varphi \\ \cos \varphi \end{array} \right) \cdot \left( \begin{array}{c} \varvec{\Xi } \\ \varvec{\Theta } \end{array} \right) +\partial _{\varphi }h(\varphi ,\theta )\ \varvec{\Psi } \end{aligned}$$

(46)

and that

$$\begin{aligned} \partial _{\theta }{\varvec{X}}\left( \varphi ,\theta \right)= & {} -\int _{0}^{\varphi }\partial _{\theta }a(s,\theta )\left( \begin{array}{c} -\sin s \\ \cos s \end{array} \right) ds\cdot \left( \begin{array}{c} \varvec{\Xi } \\ \varvec{\Theta } \end{array} \right) -h(\varphi ,\theta )\ \varvec{\Theta }~ \nonumber \\{} & {} \quad + \left( \int _{0}^{\varphi }\left( r-a(s,\theta )\right) \cos s~ds+\partial _{\theta }h(\varphi ,\theta )\right) \varvec{\Psi }. \end{aligned}$$

(47)

Note that from (46) and (47) one may already conclude that for r large enough and $\sin \varphi \ne 0$ one finds that $\partial _{\theta }{\varvec{X}} \left( \varphi ,\theta \right) \times \partial _{\varphi }{\varvec{X}}\left( \varphi ,\theta \right) \ne 0$ and hence for those large r the parametrization is regular away from the ‘poles’ of ${\mathbb {S}}$.

$\blacktriangleright$ Invariant normal direction in regular points. The next step is to show that the outward normal direction at each regular point ${\varvec{X}}(\varphi ,\theta )$, with $\omega ={\varvec{U}}(\varphi ,\theta )$ as in (17), satisfies:

$$\begin{aligned} \nu _{\varvec{\tilde{X}}\left( \omega \right) }=\pm \omega \text { for all } \omega \in {\mathbb {S}}^{2}. \end{aligned}$$

(48)

We will show that $\omega$ is perpendicular to $\partial _{\varphi }{\varvec{X}}\left( \varphi ,\theta \right)$ and $\partial _{\theta }{\varvec{X}}\left( \varphi ,\theta \right)$. Taking h as in (25) is in fact the only possible choice such that

$$\begin{aligned} \omega \cdot \partial _{\theta }{\varvec{X}}\left( \varphi ,\theta \right) =0 \end{aligned}$$

(49)

holds. Indeed with this h we may rewrite (47), at least when $\sin \varphi \ne 0$, to

$$\begin{aligned} \partial _{\theta }{\varvec{X}}\left( \varphi ,\theta \right)= & {} \int _{0}^{\varphi }\partial _{\theta }a(s,\theta )\sin s~ds~\varvec{\Xi }-\frac{\cos \varphi }{\sin \varphi }\int _{0}^{\varphi }\partial _{\theta }a(s,\theta ) \sin s~ds\ \varvec{\Theta }~ \nonumber \\{} & {} +\left( \int _{0}^{\varphi }\left( r-a(s,\theta )\right) \cos s~ds+\partial _{\theta }h(\varphi ,\theta )\right) \varvec{\Psi } \end{aligned}$$

(50)

and using $\omega =\cos \varphi \ \varvec{\Xi }+\sin \varphi \varvec{\ \Theta }$ one directly finds (49). As in the proof of Lemma 6 the factor in front of $\varvec{\Theta }$ in (50) can be continuously extended by 0 when $\sin \varphi =0$. From (46) and again with $\omega =\cos \varphi \ \varvec{\Xi }+\sin \varphi \varvec{\ \Theta }$ we find

$$\begin{aligned} \omega \cdot \partial _{\varphi }{\varvec{X}}\left( \varphi ,\theta \right) =0. \end{aligned}$$

(51)

$\blacktriangleright$ Regular parametrization. For $a\in C_ \textrm{p}^{2}( {\mathbb {R}}^2)$ Lemma 6 implies that the extended h is well-defined and $h{\varvec{W}}$ lies in $C_\textrm{p,c}^{1}({\mathbb {R}}^2)$. From now on, let h be the extended verion. And so with (23) and (24) also the expression in (45) lies in $C^{1}_\textrm{p,c}({\mathbb {R}}^2)$.

In order to have a regular parametrization on ${\mathbb {S}}^2$ it is sufficient that:

• $\partial _{\varphi }{\varvec{X}}\times \partial _{\theta } {\varvec{X}}$ is nontrivial on $\left\{ \left( \varphi ,\theta \right) \in {\mathbb {R}}^{2};\varphi \not \in \pi {\mathbb {Z}}\right\}$, and

• $\partial _{\varphi }{\varvec{X}}\left( \varphi ,0\right) \times \partial _{\varphi }{\varvec{X}}\left( \varphi ,\frac{1}{2}\pi \right)$ is nontrivial for $\varphi \in \left\{ 0,\pi \right\}$.

Let us start with the second case for $\varphi \in \left\{ 0,\pi \right\}$ where we have

$$\begin{aligned} \partial _{\varphi }{\varvec{X}}(\varphi ,0)\times \partial _{\varphi } {\varvec{X}}(\varphi ,\tfrac{1}{2}\pi )=\left( \begin{array}{c} r-a(\varphi ,0) \\ \partial _{\varphi }h\left( \varphi ,0\right) \\ 0 \end{array} \right) \times \left( \begin{array}{c} -\partial _{\varphi }h\left( \varphi ,\frac{1}{2}\pi \right) \\ r-a(\varphi ,\frac{1}{2}\pi ) \\ 0 \end{array} \right) =:\left( \begin{array}{c} 0 \\ 0 \\ T(\varphi ,r) \end{array} \right) . \end{aligned}$$

We find for $T(0,\cdot )$, and similarly for $T(\pi ,\cdot )$, that

$$\begin{aligned} \begin{array}{c} T(0,r)=\left( r-a(0,0)\right) \left( r-a(0,\tfrac{1}{2}\pi )\right) +\partial _{\varphi }h\left( 0,0\right) \partial _{\varphi }h\left( 0,\tfrac{1}{2}\pi \right) , \\ T(\pi ,r)=\left( r-a(\pi ,0)\right) \left( r-a(\pi ,\tfrac{1}{2}\pi )\right) +\partial _{\varphi }h\left( \pi ,0\right) \partial _{\varphi }h\left( \pi ,\tfrac{1}{2}\pi \right) . \end{array} \end{aligned}$$

(52)

Since $\left| h_{\varphi }\left( \varphi ,\theta \right) \right| \le \left\| \partial _{\theta }a \right\| _{\infty }$ holds, see (33), a sufficient condition for $T(0,r)>0$ and $T(\pi ,r)>0$ is

$$\begin{aligned} r>\left\| a\right\| _{\infty }+\left\| \partial _{\theta }a\right\| _{\infty }. \end{aligned}$$

Note that $\partial _r T(0,r)\ge 0$ and $\partial _r T(\pi ,r)\ge 0$ for $r\ge \left\| a\right\| _\infty$. Hence there exists $\tilde{r}_0(a)\ge \left\| a\right\| _\infty$, that is the smallest number such that both terms in (52) are positive for all $r>\tilde{r}_0(a)$ and

$$\begin{aligned} \left\| a\right\| _\infty \le \tilde{r}_0(a)\le \left\| a\right\| _{\infty } +\left\| \partial _{\theta }a\right\| _{\infty }. \end{aligned}$$

(53)

For $\varphi \not \in \pi {\mathbb {Z}}$, using (51) and (49), which state that $\omega$ is perpendicular to $\partial _{\varphi } {\varvec{X}}$ and $\partial _{\theta }{\varvec{X}}$, a simple way of checking that $\partial _{\varphi }{\varvec{X}}\times \partial _{\theta } {\varvec{X}}$ is nontrivial, is to show that ${\varvec{U}}(\varphi ,\theta ) \cdot \left( \partial _{\varphi }{\varvec{X}}\times \partial _{\theta }{\varvec{X}}\right) \ne 0$. Using the orthonormal basis $\left\{ \varvec{\Theta }, \varvec{\Psi ,\Xi }\right\}$ we obtain from (46) and (50):

$$\begin{aligned} D(r,\varphi ,\theta )&:={\varvec{U}}(\varphi ,\theta ) \cdot \left( \partial _{\varphi }{\varvec{X}}(\varphi ,\theta )\times \partial _{\theta }{\varvec{X}}(\varphi ,\theta )\right) \nonumber \\&= \det \left( \begin{array}{ccc} \sin \varphi &{} \left( r-a(\varphi ,\theta )\right) \cos \varphi &{} -\frac{ \cos \varphi }{\sin \varphi }\int _{0}^{\varphi }\partial _{\theta }a(s,\theta )\sin s~ds \\ 0 &{} \partial _{\varphi }h(\varphi ,\theta ) &{} \int _{0}^{\varphi }\left( r-a(s,\theta )\right) \cos s~ds+\partial _{\theta }h(\varphi ,\theta ) \\ \cos \varphi &{} -\left( r-a(\varphi ,\theta )\right) \sin \varphi &{} \int _{0}^{\varphi }\partial _{\theta }a(s,\theta )\sin s~ds \end{array} \right) \nonumber \\&=\left( r-a(\varphi ,\theta )\right) \left( \partial _{\theta }h(\varphi ,\theta )+\int _{0}^{\varphi }\left( r-a(s,\theta )\right) \cos s~ds\right) \nonumber \\&+\partial _{\varphi }h(\varphi ,\theta )\frac{\int _{0}^{\varphi }\sin s\ \partial _{\theta }a(s,\theta )~ds}{\sin \varphi } \nonumber \\&=\left( r-a(\varphi ,\theta )\right) \left( \int _{0}^{\varphi }\left( r-a(s,\theta )\right) \cos s~ds+\partial _{\theta }h(\varphi ,\theta )\right) \nonumber \\&-\left( \partial _{\varphi }h(\varphi ,\theta )\right) ^{2}\sin \varphi . \end{aligned}$$

(54)

In the last step we used (36). Assuming $r\ge \left\| a\right\| _\infty$ and $\varphi \in (0,\pi )$ we have

$$\begin{aligned} \text { for }\varphi \in [0,\tfrac{1}{2}\pi ]:\quad \int _{0}^{\varphi }\left( r-a(s,\theta )\right) \cos s~ds&\ge \left( r-\left\| a\right\| _\infty \right) \sin \varphi ,\\ \text { for }\varphi \in [\tfrac{1}{2}\pi ,\pi ]:\quad \int _{0}^{\varphi }\left( r-a(s,\theta )\right) \cos s~ds&= -\int _{\varphi }^\pi \left( r-a(s,\theta )\right) \cos s~ds\\&\ge \left( r-\left\| a\right\| _\infty \right) \sin \varphi . \end{aligned}$$

Using (33) and (34) from Lemma 6 we get for $\varphi \in (0,\pi )$:

$$\begin{aligned} \frac{D(r,\varphi ,\theta )}{\sin \varphi } \ge \left( \left( r-\left\| a\right\| _{\infty }\right) ^{2}-\left( r-\left\| a\right\| _{\infty }\right) \left\| \partial _{\theta }^{2}a\right\| _{\infty }-\left\| \partial _{\theta }a\right\| _{\infty }^{2}\right) \nonumber \\ \ge \left( r-\left\| a\right\| _{\infty }-\left\| \partial _{\theta }a\right\| _\infty -\left\| \partial _{\theta }^{2}a\right\| _{\infty }\right) \left( r-\left\| a\right\| _{\infty }+\left\| \partial _{\theta }a\right\| _{\infty }\right) , \end{aligned}$$

(55)

which is positive whenever

$$\begin{aligned} r> \left\| a\right\| _{\infty }+\left\| \partial _{\theta }a\right\| _{\infty }+\left\| \partial _{\theta }^{2}a\right\| _{\infty }. \end{aligned}$$

(56)

For $\varphi \in (\pi ,2\pi )$ one obtains (55) from (54) by using $\left| D(r,\varphi ,\theta )\right| =-D(r,\varphi ,\theta )$ and $\left| \sin \varphi \right| =-\sin \varphi$. By (56) there exists

$$\begin{aligned} r_0(a)\in \left[ \left\| a\right\| _{\infty },\left\| a\right\| _{\infty }+ \left\| \partial _{\theta }a\right\| _{\infty }+\left\| \partial _{\theta }^{2}a\right\| _{\infty }\right] . \end{aligned}$$

(57)

defined by

$$\begin{aligned} r_0(a):=\inf \left\{ r\in \left[ \left\| a\right\| _{\infty },\infty \right) ; \frac{D(r,\varphi ,\theta )}{\sin \varphi }>0 \text { for all }\varphi \in (0,\pi )\cup (\pi ,2\pi ),\ \theta \in [0,\pi ]\right\} . \nonumber \\ \end{aligned}$$

(58)

The product on the left hand side of (54) contains two linear terms in r that are increasing for $r\ge \left\| a\right\| _\infty$. The first one is positive for $r> \left\| a\right\| _\infty$. Hence, whenever (54) is positive and $r\ge \left\| a\right\| _\infty$, both these linear terms are positive. Indeed, the expression in (54) is the sum of this product (of two terms linear in r) and a nonpositive term (constant for r). These two linear terms in r are increasing with r and hence, once $D(r_0(a),\varphi ,\theta )/\sin \varphi \ge 0$ for some $r_0(a)\ge \left\| a\right\| _\infty$, one finds for all $r>r_0(a)$ that

$$\begin{aligned} D(r,\varphi ,\theta )/\sin \varphi>0\text { and } \partial _r \left( D(r,\varphi ,\theta )/\sin \varphi \right) >0. \end{aligned}$$

(59)

Since also $r\mapsto T(0,r)$ and $r\mapsto T(\pi ,r)$ are increasing for $r\ge \tilde{r}_0(a)$ as in (53), all $r\in (r_{0}(a),\infty )$ are admissible and the parametrization is well-defined for all $r>r_{0}(a)$. And indeed, if $r_0(a)<\tilde{r}_0(a)$, we will have replaced $r_0(a)$ with $\tilde{r}_0(a)$. For $r=r_{0}(a)$ the parametrization might not be regular.

$\blacktriangleright$ Homotopy to the sphere. The parametrization is well-defined for all $r>r_{0}(a)$ but there is still an argument missing that shows that ${\mathbb {R}}^3\setminus {\varvec{X}}({\textsf{S}})$ consists of two open sets of which the bounded one is topologically homeomorph to an open ball in ${\mathbb {R}}^3$. Here we construct such an homeomorphism through a homotopy from $\omega \mapsto \varvec{\tilde{X}}(\omega )$ to $\omega \mapsto \omega$ by letting $r\rightarrow \infty$ and scaling with 1/r. As a side result we will find that

$$\begin{aligned} \nu _{\varvec{\tilde{X}}\left( \omega \right) }=\omega \text { for all }\omega \in {\mathbb {S}}^2, \end{aligned}$$

so indeed, $\omega$ is the outward normal at $\varvec{\tilde{X}}(\omega )$.

In order to focus on the dependence on r we use an explicit r in the following expression (30) in this paragraph:

$$\begin{aligned} {\varvec{X}}_{e}\left( r,\varphi ,\theta \right) :={\varvec{X}}\left( \varphi ,\theta \right) \text { and } \varvec{\tilde{X}}_{e}\left( r,\omega \right) :=\varvec{\tilde{X}}\left( \omega \right) , \end{aligned}$$

with ${\varvec{X}},\varvec{\tilde{X}}$ from (30) and (31). We define

$$\begin{aligned} (0,1] \times {\mathbb {S}}^{2}\ni \left( \rho ,\omega \right) \mapsto \varvec{\tilde{Y}}\left( \rho ,\omega \right) := \rho \,\varvec{\tilde{X}}_{e}\left( \rho ^{-1}r,\omega \right) \in {\mathbb {R}} ^{3}. \end{aligned}$$

As one may see from (45) one finds that

$$\begin{aligned} \varvec{\tilde{Y}}\left( 1,\omega \right) =\varvec{\tilde{ X}}_{e}\left( r,\omega \right) \text { and }\varvec{\tilde{Y}}\left( 0,\omega \right) :=\lim _{\rho \downarrow 0}\varvec{\tilde{Y}}\left( \rho ,\omega \right) =r\omega \end{aligned}$$

with all $\varvec{\tilde{Y}}\left( \rho ,\cdot \right)$ for $\rho \in [0,1 ]$ being regular parametrizations and their outward normal directions $\nu$ satisfying as in (48)

$$\begin{aligned} \nu _{\varvec{\tilde{Y}}( \rho ,\omega )} =\omega \text { for all }\omega \in {\mathbb {S}}^{2}. \end{aligned}$$

(60)

So ${\mathbb {R}}^{3}{\setminus } \varvec{\tilde{X}}_{e}\left( r,{\mathbb {S}} ^{2}\right)$ has precisely two connected components. We call A the bounded one.

$\blacktriangleright$ Convexity of A. Since the extreme value of $\varvec{\tilde{X}}({\mathbb {S}}^{2})$ in the direction $\omega$ has normal $\omega$, and since by (60) $\nu _{\varvec{\tilde{X}} \left( \omega \right) }=\omega$, that extreme point is indeed $\varvec{ \tilde{X}}\left( \omega \right)$. So for each $\omega \in {\mathbb {S}}^2$ it holds that $\varvec{\tilde{X}}({\mathbb {S}}^{2})$, except for $\varvec{\tilde{X}} \left( \omega \right)$ itself, is on one side of that tangent plane. Hence ${\bar{A}}$ lies on one side of all the tangent planes for $\partial A= \varvec{\tilde{X}}({\mathbb {S}}^{2})$, which implies that ${\bar{A}}$ is convex. See also the proof of Hadamard’s Theorem [19, page 194].

$\blacktriangleright$ Body of constant width. According to the results proved above it is sufficient to show that

$$\begin{aligned} \varvec{\tilde{X}}\left( \omega \right) -\varvec{\tilde{X}}\left( -\omega \right) =2r\omega \text { for all }\omega \in {\mathbb {S}}^{2}. \end{aligned}$$

For the parametrization ${\varvec{X}}$ with ${\varvec{U}}$ as in (17) this coincides with

$$\begin{aligned} {\varvec{X}}(\varphi ,\theta )-{\varvec{X}}(\varphi +\pi ,\theta )=2r\ {\varvec{U}}\left( \varphi ,\theta \right) \text { for all }(\varphi ,\theta )\in {\textsf{S}}. \end{aligned}$$

Indeed, using (45) we find with (23), (24) and (26) that

$$\begin{aligned}&{\varvec{X}}(\varphi +\pi ,\theta )-{\varvec{X}}(\varphi ,\theta ) \\&=\int _{\varphi }^{\varphi +\pi }\left( r-a(s,\theta )\right) \left( \begin{array}{c} -\sin s \\ \cos s \end{array} \right) ds\cdot \left( \begin{array}{c} \varvec{\Xi } \\ \varvec{\Theta } \end{array} \right) +\left( h(\varphi +\pi ,\theta )-h(\varphi ,\theta )\right) \ \varvec{\Psi } \\&=r\left( \begin{array}{c} \cos \left( \varphi +\pi \right) -\cos \varphi \\ \sin \left( \varphi +\pi \right) -\sin \varphi \end{array} \right) \cdot \left( \begin{array}{c} \varvec{\Xi } \\ \varvec{\Theta } \end{array} \right) =-2r\ {\varvec{U}}\left( \varphi ,\theta \right) , \end{aligned}$$

as desired.

$\blacktriangleright$ The limit case. In the proof above we have used that $r>r_0(a)$ in order for the parametrization to be regular. For any $r>r_0(a)$ we found that ${\varvec{X}}$ supplies us with the boundary of a body of constant width. Since ${\varvec{X}}$ is continuously depending on r also the limit for $r\downarrow r_0(a)$ will yield a body of constant width. $\square$

Suppose that G is a body of constant width ${\varvec{d}}_G$. We write ${\varvec{X}}_{0}\in {\mathbb {R}}^{3}$ as the point on $\partial G$ with the largest $x_{3}$ -coordinate. Since a translation of G that maps ${\varvec{X}}_0$ to a fixed point does not meddle with our arguments, we may assume without loss of generality, that

$$\begin{aligned} {\varvec{X}}_0=\left( 0,0,\tfrac{1}{2} {\varvec{d}}_G\right) ^{T}. \end{aligned}$$

(61)

Now G is a body of constant width, for which the point with largest $x_3$-coordinate lies on the $\varvec{\Xi }$-axis. The plane $x_3=\tfrac{1}{2} {\varvec{d}}_G$ is ‘tangential’ to $\partial G$ in the sense that

$$\begin{aligned} \left\langle X,\varvec{\Xi }\right\rangle \le \tfrac{1}{2} {\varvec{d}}_G \text { for all }X \in G \text { and } \left\langle {\varvec{X}}_0,\varvec{\Xi }\right\rangle = \tfrac{1}{2} {\varvec{d}}_G \text { with }{\varvec{X}}_0\in G. \end{aligned}$$

Since G has constant width, it fits precisely between two parallel planes ${\varvec{d}}_G$ apart and hence there is a lowest point ${\varvec{X}}_m\in G$ that has a parallel ‘tangent’ plane below:

$$\begin{aligned} \left\langle X,\varvec{\Xi }\right\rangle \ge -\tfrac{1}{2} {\varvec{d}}_G \text { for all }X \in G \text { and } \left\langle {\varvec{X}}_m,\varvec{\Xi }\right\rangle = -\tfrac{1}{2} {\varvec{d}}_G \text { with }{\varvec{X}}_m\in G. \end{aligned}$$

The only possibility, for this lowest point ${\varvec{X}}_m$ to satisfy $\left| {\varvec{X}}_0-{\varvec{X}}_m\right| \le {\varvec{d}}_G$, is

$$\begin{aligned} {\varvec{X}}_m=\left( 0,0,-\tfrac{1}{2} {\varvec{d}}_G\right) ^{T}. \end{aligned}$$

(62)

Indeed, we may assume without loss of generality that the body of constant width G is such that the ‘highest’ point is (61) and the ‘lowest’ is (62).

Proof of Theorem 7, the derivation of formula (30) for some h

Taking $u=\varvec{\Xi }$ and $\omega =\varvec{\Psi }(\theta )$ the result of Hadwiger, extended by the remark of Groemer that bodies of constant width have only regular boundary points, states that it is sufficient that the projections $P_{\omega }G$ of G, on each of the planes spanned by $\left\{ \varvec{\Theta }(\theta ),\varvec{\Xi }\right\}$ with $\theta \in [0,\pi ]$, are curves of constant width ${\varvec{d}}_{{\widehat{P}}_{\omega }G}=2r$. Thus by Theorem 2 all those sets can be described by (12) with for each $\theta$ some function $a(\cdot ,\theta )$ depending on $\theta$ as a parameter. The value of r is the same for all projections and does not depend on $\theta$. In other words, a fixed r exists and for each $\theta$ a mapping $\varphi \mapsto a(\varphi ,\theta )\in L^{\infty }(0,2\pi )$ such that for the corresponding ${\varvec{x}}$ as in Theorem 1 we have, with ${\widehat{P}}$ as in (16),

$$\begin{aligned} \partial {\widehat{P}}_{\omega }G={\varvec{x}}\left( \left[ 0,2\pi \right] ,\theta \right) \end{aligned}$$

with some ${\varvec{x}}_0(\theta )={\varvec{x}}\left( 0,\theta \right) \in {\mathbb {R}}^{2}$ in accordance with Theorem 1 and

$$\begin{aligned} \sup \left\{ \left| a\left( \varphi ;\theta \right) \right| ;0\le \varphi \le \pi \right\} \le r\ \text { for all }\theta \in \left[ 0,\pi \right] . \end{aligned}$$

Moreover, the mapping $\varphi \mapsto a(\varphi ,\theta )$ satisfies (10) and (11). Hence (23), (24) and $r_{0}(a)\ge \left\| a\right\| _\infty$ are necessary conditions.

Since for each ${\tilde{\omega }}\in {\mathbb {S}}^{2}$ the set G lies in the cylinder perpendicular to its projection, in other words, we have $G\subset P_{{\tilde{\omega }}}G+\left[ {\tilde{\omega }}\right]$ with $\left[ {\tilde{\omega }}\right] =\left\{ \lambda {\tilde{\omega }};\lambda \in {\mathbb {R}}\right\}$. It follows that for each

$$\begin{aligned} X_{*}\in \partial G\cap \left( \partial P_{{\tilde{\omega }}}G+\left[ {\tilde{\omega }}\right] \right) \end{aligned}$$

there is $\left( \varphi ,\theta \right) \in {\textsf{S}}$ with ${\varvec{U}}(\varphi ,\theta )\cdot {\tilde{\omega }}=0$ and a value $h\left( \varphi ,\theta \right) \in {\mathbb {R}}$ such that for ${{\tilde{\omega }}}=\varvec{\Psi }(\theta )$

$$\begin{aligned} X_{*}=P_{{\tilde{\omega }}}(X_{*})+h(\varphi ,\theta )\,{\tilde{\omega }}. \end{aligned}$$

If $X_{**}\in \partial G$ is such that $\left| X_{*}-X_{**}\right| =2r$, with 2r being the width, also $\left| P_{{\tilde{\omega }} }(X_{*})-P_{{\tilde{\omega }}}(X_{**})\right| =2r$ and hence

$$\begin{aligned} X_{**}=P_{{\tilde{\omega }}}(X_{**})+h(\varphi ,\theta )\,{\tilde{\omega }}, \end{aligned}$$

with the same contribution $h(\varphi ,\theta ){{\tilde{\omega }}}$, which implies that

$$\begin{aligned} h\left( \varphi ,\theta \right) =h\left( \varphi +\pi ,\theta \right) \text { for all }\left( \varphi ,\theta \right) \in {\textsf{S}}\text {.} \end{aligned}$$

(63)

Indeed, with the assumptions in (61) and (62), we have

$$\begin{aligned} X_{*}&={\varvec{X}}_0+\varvec{x_1}(\varphi ,\theta )\,\varvec{\Xi }+ \varvec{x_2}(\varphi ,\theta )\,\varvec{\Theta }(\theta ) +h\left( \varphi , \theta \right) \, \varvec{\Psi }(\theta )\nonumber \\&={\varvec{X}}_0+{\varvec{x}}(\varphi ,\theta )\cdot \left( \begin{array}{c} \varvec{\Xi } \\ \varvec{\Theta }(\theta ) \end{array} \right) +h\left( \varphi , \theta \right) \, \varvec{\Psi }(\theta ) \end{aligned}$$

(64)

with

$$\begin{aligned} \left( \begin{array}{c} 0 \\ 0 \end{array} \right) ={\varvec{x}}(0,0)={\varvec{x}}(0,\theta )={\varvec{x}}(2\pi ,\theta )= {\varvec{x}}(\pi ,\theta )+\left( \begin{array}{c} 2r \\ 0 \end{array} \right) . \end{aligned}$$

Here (63) follows from the fact that the line through the points of farthest distance is perpendicular to the plane spanned by $\left\{ \varvec{\Theta }(\theta ),\varvec{\Xi }\right\}$. Since for $\varphi \in \left\{ 0,\pi ,2\pi \right\}$ the $X_{*}$ in (64) does not depend on $\theta$ , one finds for all $\theta \in [0,\pi ]$, that

$$\begin{aligned} h\left( 0,\theta \right) =h\left( \pi ,\theta \right) =h\left( 2\pi ,\theta \right) =0. \end{aligned}$$

The first two terms on the right in (64) inherit the conditions of the two-dimensional formula and so for each $\theta \in [0,\pi ]$ one finds $\varphi \mapsto {\varvec{x}}(\varphi ,\theta )$ as in (12). The formula in (64) describes through ${\varvec{X}}:{\textsf{S}}\rightarrow {\mathbb {R}}^{3}$ all points of $\partial G$ by

$$\begin{aligned} {\varvec{X}}(\varphi ,\theta )= & {} {\varvec{X}}_0+\int _{0}^{\varphi }\left( r-a(s,\theta )\right) \left( \begin{array}{c} -\sin s \\ \cos s \end{array} \right) ds\cdot \left( \begin{array}{c} \varvec{\Xi } \\ \varvec{\Theta }(\theta ) \end{array} \right) \nonumber \\{} & {} +\,\,h\left( \varphi ,\theta \right) \ \varvec{\Psi }(\theta ). \end{aligned}$$

(65)

We will also define

$$\begin{aligned} {\varvec{X}}_{oh}(\varphi ,\theta ):={\varvec{X}}_0+\int _{0}^{\varphi }\left( r-a(s,\theta )\right) \left( \begin{array}{c} -\sin s \\ \cos s \end{array} \right) ds\cdot \left( \begin{array}{c} \varvec{\Xi } \\ \varvec{\Theta }(\theta ) \end{array} \right) , \end{aligned}$$

(66)

and for convenience, similar as for ${\varvec{X}}$ in (31), also

$$\begin{aligned} \omega \mapsto \varvec{\tilde{X}}_{oh}(\omega ):{\mathbb {S}}^2\mapsto {\mathbb {R}}^3\ \text { with } \varvec{\tilde{X}}_{oh}({\varvec{U}}\left( \varphi ,\theta \right) ):={\varvec{X}}_{oh}(\varphi ,\theta ). \end{aligned}$$

(67)

Note that ${\varvec{U}}(\varphi ,\theta )=\cos \varphi ~\varvec{\Xi }+ \sin \varphi ~\varvec{\Theta }(\theta )$ lies in the plane of ${\varvec{X}}_{oh}({\textsf{S}})$ and is perpendicular to the cylinder ${\varvec{X}}_{oh}([0,2\pi ],\theta )+{\mathbb {R}}~\varvec{\Psi }(\theta )$. Since G lies inside this cylinder and ${\varvec{X}}(\varphi ,\theta )$ is a point of $\partial G$ on this cylinder, the vector ${\varvec{U}}(\varphi ,\theta )$ is an outward normal to ${\varvec{X}}({\textsf{S}})$ at ${\varvec{X}}(\varphi ,\theta )$. In other words, writing $\varvec{\tilde{X}}$ as in (31) it follows that

$$\begin{aligned} \omega \mapsto \varvec{\tilde{X}}(\omega ):{\mathbb {S}}^2\rightarrow \partial G\subset {\mathbb {R}}^3 \end{aligned}$$

is the ‘inverse’ of the Gauss map for $\partial G$ and hence Lipschitz-continuous on ${\mathbb {S}}^2$ by Lemma 11. Note that Lemma 10 shows that Lipschitz-continuity of $\varvec{\tilde{X}}$ on ${\mathbb {S}}^2$ implies Lipschitz-continuity of ${\varvec{X}}$ on ${\textsf{S}}$ (but not vice versa!). So we may state, allowing the notation $C^{0,1}_ \textrm{p}({\textsf{S}})$ as a restriction of $C^{0,1}_\textrm{p}({\mathbb {R}}^2)$, that for each coordinate in (65) the Lipschitz-continuity holds for:

$$\begin{aligned} \left( \varphi ,\theta \right)\mapsto & {} \int _{0}^{\varphi }\left( r-a(s,\theta )\right) \sin s\ ds\in C_{\textrm{p}}^{0,1}\left( {\textsf{S}} \right) , \\ \left( \varphi ,\theta \right)\mapsto & {} \int _{0}^{\varphi }\left( r-a(s,\theta )\right) \cos s~ds \cos \theta -h(\varphi ,\theta )\sin \theta \in C_{\textrm{p}}^{0,1}\left( {\textsf{S}}\right) ,\\ \left( \varphi ,\theta \right)\mapsto & {} \int _{0}^{\varphi }\left( r-a(s,\theta )\right) \cos s~ds \sin \theta +h(\varphi ,\theta )\cos \theta \in C_{\textrm{p}}^{0,1}\left( {\textsf{S}}\right) . \end{aligned}$$

Combining the second function above multiplied with $\sin \theta$ and the third multiplied with $\cos \theta$ we find that h is Lipschitz-continuous on ${\textsf{S}}$, which is not sufficient for Lipschitz-continuity on ${\mathbb {S}}^2$. The function $(\varphi ,\theta )\mapsto (\sin \theta ,\cos \theta )$ rephrased in terms of $\omega$ gives a function that is not even continuous on ${\mathbb {S}}^2$. We need another proof that

$$\begin{aligned} \omega \mapsto \tilde{h}(\omega )\text { for }\omega ={\varvec{U}}(\varphi ,\theta ) \text { and }\tilde{h}(\omega )=h(\varphi ,\theta ) \end{aligned}$$

(68)

is Lipschitz-continuous on ${\mathbb {S}}^2$ and for that we will use the next two lemmas. We continue this proof after the proof of Lemma 9 below. $\square$

Note that the sketch on the left of Fig. 4 shows a domain with boundary ${\varvec{X}}_{oh}({\textsf{S}})$.

For the proof that $\omega \mapsto \varvec{\tilde{X}}_{oh}(\omega )$ from (66) is Lipschitz-continuous, we will use the following: if $\varvec{{\tilde{X}}}({\mathbb {S}}^2)$ describes the boundary of G, then $\varvec{{\tilde{X}}}_{oh}({\mathbb {S}}^2)$ gives the boundary of the 3d-shadow domain $Sh_{\varvec{\Xi }}(G)$, when rotating around the central axis $\varvec{\Xi }$. The definition of 3d-shadow domain is found in Appendix C. The function ${\varvec{X}}_{oh}$ does not only parametrize the boundary of that 3d-shadow domain, but since

$$\begin{aligned} {\varvec{X}}_{oh}(\varphi ,\theta )= P_{\varvec{\Psi }(\theta )}\left( {\varvec{X}}_{oh}(\varphi ,\theta )\right) = P_{\varvec{\Psi }(\theta )}\left( {\varvec{X}}(\varphi ,\theta )\right) \end{aligned}$$

we have that each shadow in the direction of $\varvec{\Psi }(\theta )$ has the contour parametrized by $\varphi \mapsto {\varvec{X}}_{oh}(\varphi ,\theta )$.

We start with an a-priori estimate for the position of $\partial G$ in relation with the axes through the highest and lowest point of G.

Lemma 8

Let ${\varvec{X}}$ be as in (65) with ${\varvec{X}}_0$ as in (61). Then for each $(\varphi ,\theta )\in {\textsf{S}}$ one finds with

$$\begin{aligned} {\varvec{Z}}(\varphi ,\theta ):= \left\langle {\varvec{X}}(\varphi ,\theta ),\varvec{\Xi }\right\rangle \varvec{\Xi } \end{aligned}$$

(69)

that

$$\begin{aligned} \left| {\varvec{X}}(\varphi ,\theta )-{\varvec{Z}}(\varphi ,\theta )\right| \le {\varvec{d}}_G\,\left| \sin \varphi \right| . \end{aligned}$$

(70)

Proof

In any horizontal direction the boundary $\partial G$ lies between the extreme cases of two-dimensional curves of constant width. These extreme cases are the Reuleaux triangle pointing left and the one pointing right. See Fig. 5. Rotating the left image around the vertical axis gives the area on the right, where $\partial G$ is located.

Fig. 5

The axis in red with the shaded parts showing the possible areas for the projections in 2d. The shaded parts are the union of two Reuleaux triangles minus their intersection. So with the assumption $r=1$ and $\left| z\right| \le r=1$ we find for the picture on the left $L\in [-\sqrt{3},\sqrt{3}]$. If a body of constant width has $\left( 0,0, \pm 1\right)$ on its boundaries, then the domain lies in the rotated shaded part, which is sketched on the right

So ${\varvec{X}}(\varphi ,\theta )$ is located in the shaded area rotated around the $\varvec{\Xi }$-axis and we will estimate the horizontal differnence to the axis as follows. For the top half we find, using $z\in [-1,1]$ for the relative height $z:=\left( 2/{\varvec{d}}_G\right) {\varvec{Z}}_3(\varphi ,\theta )$ and the circle with center $(0,-1)^T$, that

$$\begin{aligned} \left| {\varvec{X}}(\varphi ,\theta )-{\varvec{Z}}(\varphi ,\theta )\right| \le \tfrac{1}{2} {\varvec{d}}_G \sqrt{4-(1+z)^2} \end{aligned}$$

and for the bottom half, using the circle with center $(0,1)^T$:

$$\begin{aligned} \left| {\varvec{X}}(\varphi ,\theta )-{\varvec{Z}}(\varphi ,\theta )\right| \le \tfrac{1}{2} {\varvec{d}}_G \sqrt{4-(1-z)^2}. \end{aligned}$$

If $\left( \sin {\hat{\varphi }},\cos {\hat{\varphi }}\right) ^T$ denotes the outward normal direction for the circular curves

$$\begin{aligned} z\mapsto \left( \sqrt{4-(1+z)^2},z\right) \text { and }z\mapsto \left( \sqrt{4-(1-z)^2},z\right) , \end{aligned}$$

using the first one for $z\in [0,1]$ and the second for $z\in [-1,0]$, then we have for ${\hat{\varphi }}\in [0,\tfrac{1}{3}\pi ]$, respectively ${\hat{\varphi }}\in [\tfrac{2}{3}\pi ,\pi ]$ that

$$\begin{aligned} \left( \begin{array}{c} \sin {\hat{\varphi }}\\ \cos {\hat{\varphi }} \end{array}\right) =\tfrac{1}{2} \left( \begin{array}{c} \sqrt{4-(1+z)^2}\\ 1+z \end{array}\right) \text { resp. } \left( \begin{array}{c} \sin {\hat{\varphi }}\\ \cos {\hat{\varphi }} \end{array}\right) =\tfrac{1}{2} \left( \begin{array}{c} \sqrt{4-(1-z)^2}\\ z-1 \end{array}\right) . \end{aligned}$$

It follows that

$$\begin{aligned} \left| {\varvec{X}}(\varphi ,\theta )-{\varvec{Z}}(\varphi ,\theta )\right| \le {\varvec{d}}_G \sin {\hat{\varphi }}. \end{aligned}$$

(71)

By the construction we find that ${\varvec{U}}(\varphi ,\theta )$ is an outward normal in ${\varvec{X}}(\varphi ,\theta )$ for $\partial G$. Moreover, see (43), we have ${\varvec{U}}(\varphi ,\theta )=\cos \varphi ~\varvec{\Xi }+\sin \varphi ~\varvec{\Theta }(\theta )$, so ${\varvec{U}}(\varphi ,\theta )$ lies in the $\left\{ \varvec{\Theta }(\theta ),\varvec{\Xi }\right\}$-plane that contains the curve $\varphi \mapsto {\varvec{X}}_{oh}(\varphi ,\theta )$ and is an outward normal to that curve. A sketch of $\varphi \mapsto {\varvec{X}}_{oh}(\varphi ,\theta )$ in the $\left\{ \varvec{\Theta }(\theta ),\varvec{\Xi }\right\}$-plane is found in Fig. 6.

Fig. 6

Comparing the curve $\varphi \mapsto {\varvec{X}}_{oh}(\varphi ,\theta )$ for $\varphi \in [0,\frac{1}{2}\pi ]$ and the two circles parametrized by ${\hat{\varphi }}$ in the $\left\{ \varvec{\Theta }(\theta ),\varvec{\Xi }\right\}$-plane

We have that if $\varphi \in (0,\tfrac{1}{2} \pi ]$, then ${\hat{\varphi }}\in (0,\varphi )$ and if $\varphi \in (\tfrac{1}{2} \pi ,\pi )$, then ${\hat{\varphi }}\in (\varphi ,\pi )$. Both cases imply that $\sin {\hat{\varphi }}\le \sin \varphi$ and we find from (71) that

$$\begin{aligned} \left| {\varvec{X}}(\varphi ,\theta )-{\varvec{Z}}(\varphi ,\theta )\right| \le {\varvec{d}}_G \sin \varphi . \end{aligned}$$

With similar estimates for $\varphi \in (\pi ,2\pi )$ we may conclude that (70) holds. $\square$

Note that ${\varvec{X}}_{oh}(\varphi ,\theta )$ is the perpendicular projection of ${\varvec{X}}(\varphi ,\theta )$ onto the $\left\{ \varvec{\Xi },\varvec{\Theta }\right\}$-plane and hence

$$\begin{aligned} \left| {\varvec{X}}_{oh}(\varphi ,\theta )-\left\langle {\varvec{X}}_{oh}(\varphi ,\theta ), \varvec{\Xi }\right\rangle \varvec{\Xi }\right| \le \left| {\varvec{X}}(\varphi ,\theta )-\left\langle {\varvec{X}}(\varphi ,\theta ), \varvec{\Xi }\right\rangle \varvec{\Xi }\right| , \end{aligned}$$

(72)

implying that the inequality in (70) also holds for ${\varvec{X}}(\varphi ,\theta )$ replaced by ${\varvec{X}}_{oh}(\varphi ,\theta )$, that is, for all $(\varphi ,\theta )\in {\textsf{S}}$:

$$\begin{aligned} \left| {\varvec{X}}_{oh}(\varphi ,\theta )-\left\langle {\varvec{X}}_{oh}(\varphi ,\theta ), \varvec{\Xi }\right\rangle \varvec{\Xi }\right| \le {\varvec{d}}_G\,\left| \sin \varphi \right| . \end{aligned}$$

(73)

This last inequality measures the distance of ${\varvec{X}}_{oh}$ to the axis $\varvec{\Xi }$ and allows us to get a $\sin \varphi$-dependent estimate for the Lipschitz-continuity of $\theta \mapsto {\varvec{X}}_{oh}(\varphi ,\theta )$ by using Lemma 13.

The Lipschitz-continuity of $\varvec{\tilde{X}}$ will follow from Lemma 11. For the Lipschitz-continuity of $\varvec{\tilde{X}}_{oh}$ we will use the concept of shadow domains from Appendix C.

Lemma 9

Suppose that ${\varvec{X}}$ from (65) parametrizes the boundary of G, a body of constant width ${\varvec{d}}_G$, and let ${\varvec{X}}_{oh}$ be as in (66). Then the function $\varvec{\tilde{X}}_{oh}$, defined in (67), is Lipschitz-continuous, for all $\omega ,\omega _0\in {\mathbb {S}}^2$:

$$\begin{aligned} \left| \varvec{\tilde{X}}_{oh}(\omega )-\varvec{\tilde{X}}_{oh}(\omega _0)\right| \le \pi {\varvec{d}}_G \left| \omega -\omega _0\right| , \end{aligned}$$

(74)

and satisfies:

• 1. $P_{\varvec{\Psi }(\theta )}\big (\varvec{\tilde{X}}(\omega ) \big )=\varvec{\tilde{X}}_{oh}(\omega )$ for $\omega ={\varvec{U}}( \varphi ,\theta )\in {\mathbb {S}}^2$, and

• 2. $\partial \left( Sh _{\varvec{\Xi }}(G )\right) =\varvec{\tilde{X}} _{oh}({\mathbb {S}}^{2})$.

Here P is as in (15) with $\varvec{\Psi }(\theta )$ as in (41); $Sh _{\varvec{\Xi }}(\Omega )$ is the 3d-shadow as in Definition 14 and the rotation with respect to the axis $\varvec{\Xi }$.

Proof

We still assume (61). From our construction one finds that the function $\varvec{\tilde{X}}_{oh}:{\mathbb {S}}^{2}\rightarrow {\mathbb {R}}^{3}$ parametrizes the collection of boundaries of ‘2d-shadows’ in the directions $\varvec{\Psi }(\theta )$ for $\theta \in \left[ 0,\pi \right]$ and gives a bounded two-dimensional manifold in ${\mathbb {R}}^{3}$. Each 2d-shadow $P_{\varvec{\Psi }(\theta )}(G)$ for $\theta \in \left[ 0,\pi \right]$ is a two-dimensional set of constant width in the plane spanned by ${\varvec{{\Xi }}}$ and ${\varvec{{\Theta }}}(\theta )$. The 3d-domain $\Omega$ bounded by these curves, that is

$$\begin{aligned} \partial \Omega =\bigcup _{\theta \in \left[ 0,\pi \right] } P_{\varvec{\Psi } (\theta )}\big ({\varvec{X}}(\left[ 0,2\pi \right] ,\theta )\big )=\varvec{\tilde{X}}_{oh}({\mathbb {S}}^2), \end{aligned}$$

is in general not a body of constant width and not even convex. But by rotating a body G of constant width around $\varvec{\Xi }$, we may use that each projection onto the $\left\{ \varvec{\Theta }(\theta ),\varvec{\Xi }\right\}$-plane is a curve of constant width. For each fixed $\varphi$ the function $\theta \mapsto {\varvec{X}}_{oh}(\varphi ,\theta )$ is Lipschitz-continuous according to Lemma 13 and with the estimate in (73) we obtain:

$$\begin{aligned} \left| {\varvec{X}}_{oh}(\varphi ,\theta )-{\varvec{X}}_{oh}(\varphi ,\theta _0)\right| \le {\varvec{d}}_G \left| \theta -\theta _0\right| \left| \sin \varphi \right| \text { for all } \theta ,\theta _0 \text { and }\varphi . \end{aligned}$$

(75)

Lipschitz-continuity of $\varphi \mapsto {\varvec{X}}_{oh}(\varphi ,\theta )$, with constant $L={\varvec{d}}_G$, follows from our 2d-construction:

$$\begin{aligned} \left| {\varvec{X}}_{oh}(\varphi ,\theta )-{\varvec{X}}_{oh}(\varphi _0,\theta )\right| \le {\varvec{d}}_G \left| \varphi -\varphi _0\right| \text { for all } \varphi ,\varphi _0 \text { and }\theta . \end{aligned}$$

(76)

For $\left| \theta -\theta _0\right| \le \frac{1}{2}\pi$ we use a triangle inequality with either $(\varphi ,\theta _0)$ or $(\varphi _0,\theta )$ as an intermediate point and both (75) and (76) to get for all such $(\varphi ,\theta ),(\varphi _0,\theta _0)$:

$$\begin{aligned} \left| {\varvec{X}}_{oh}(\varphi ,\theta )-{\varvec{X}}_{oh}(\varphi _0,\theta _0)\right| \le {\varvec{d}}_G \left( \left| \varphi -\varphi _0\right| + \left| \theta -\theta _0\right| \min \left( \left| \sin \varphi \right| ,\left| \sin \varphi _0\right| \right) \right) ,\nonumber \\ \end{aligned}$$

(77)

which fits with (86) in Lemma 10.

For $\frac{1}{2}\pi <\left| \theta -\theta _0\right| \le \pi$, and $\varphi ,\varphi _0$ both either near 0 or $\pi$, one uses a triangle inequality with $(0,\theta )$ or $(\pi ,\theta )$, corresponding to the poles $\pm e_3$, as an intermediate point and twice (76). Note that one may always choose $\theta ,\theta _0$ such that one of these two cases holds, possibly by extending periodically as in Definition 4 and one obtains estimates as in (87), the second case of Lemma 10. So, with the equivalences in Lemma 10, the function $\varvec{\tilde{X}}_{oh}$ is Lipschitz-continuous on ${\mathbb {S}}^2$. $\square$

Continued proof of Theorem 7, a formula for h and transfer of Lipschitz-continuity

Lemma 11 states that $\omega \mapsto \varvec{\tilde{X}}(\omega )$ is Lipschitz-continuous and Lemma  9 states Lipschitz-continuity for $\omega \mapsto \varvec{\tilde{X}}_{oh}(\omega )$. To show the weighted Lipschitz continuity estimate as in (77) for h, we use the expression

$$\begin{aligned} h(\varphi ,\theta )=\left( {\varvec{X}}(\varphi ,\theta )- {\varvec{X}}_{oh}(\varphi ,\theta )\right) \cdot \varvec{\Psi }(\theta ) \end{aligned}$$

(78)

and the auxiliary term ${\varvec{Z}}(\varphi ,\theta )$ as in (69). We find

$$\begin{aligned}&\left| h(\varphi ,\theta )-h(\varphi _0,\theta _0)\right| \nonumber \\&=\left| \left( \varvec{X}(\varphi ,\theta )- \varvec{X}_{oh}(\varphi ,\theta )\right) \cdot \varvec{\Psi }(\theta )- \left( \varvec{X}(\varphi _0,\theta _0)- \varvec{X}_{oh}(\varphi _0,\theta _0)\right) \cdot \varvec{\Psi }(\theta _0)\right| \nonumber \\&\le \left| \varvec{X}(\varphi ,\theta )-\varvec{X}(\varphi _0,\theta _0)\right| \left| \varvec{\Psi }(\theta )\right| + \left| \varvec{X}_{oh}(\varphi ,\theta )-\varvec{X}_{oh}(\varphi _0,\theta _0)\right| \left| \varvec{\Psi }(\theta )\right| \hspace{3cm}\nonumber \\&\quad + \left( \left| \varvec{X}(\varphi _0,\theta _0)-\varvec{Z}(\varphi _0,\theta _0)\right| + \left| \varvec{Z}(\varphi _0,\theta _0)-\varvec{X}_{oh}(\varphi _0,\theta _0)\right| \right) \left| \varvec{\Psi }(\theta )-\varvec{\Psi }(\theta _0)\right| \nonumber \\&\le \left| \varvec{X}(\varphi ,\theta )-\varvec{X}(\varphi _0,\theta _0)\right| + \left| \varvec{X}_{oh}(\varphi ,\theta )-\varvec{X}_{oh}(\varphi _0,\theta _0)\right| \nonumber \\&\quad + 2\, \varvec{d}_G \left| \sin \varphi _0\right| \pi \left| \theta -\theta _0\right| . \end{aligned}$$

(79)

In the last inequality we used $\left| {\varvec{Z}}(\varphi _0,\theta _0)-{\varvec{X}}_{oh}(\varphi _0,\theta _0)\right| \le \left| {\varvec{Z}}(\varphi _0,\theta _0)-{\varvec{X}}(\varphi _0,\theta _0)\right|$, Lemma 8 and

$$\begin{aligned} \left| \varvec{\Psi }(\theta )-\varvec{\Psi }(\theta _0)\right| \le \left| \theta -\theta _0\right| . \end{aligned}$$

By the symmetry in $\varphi$ and $\varphi _0$, we may show the similar estimate by replacing $\left| \sin \varphi _0\right|$ for $\left| \sin \varphi \right|$ in (79). By Lemma 11 we know that $\varvec{\tilde{X}}$ is Lipschitz-continuous on ${\mathbb {S}}^2$ and by Lemma 9 also that $\varvec{\tilde{X}}_{oh}$ is Lipschitz-continuous on ${\mathbb {S}}^2$. With the transcription of Lipschitz-continuity on ${\mathbb {S}}^2$ and weighted Lipschitz-continuity for $(\varphi ,\theta )$ in Lemma 10 we obtain by (79) the weighted Lipschitz-continuity of h.

For (39) we take $\varphi _0=\varphi$ in (79). By Lemma 11 and Lemma 10 we obtain

$$\begin{aligned} \left| {\varvec{X}}(\varphi ,\theta )-{\varvec{X}}(\varphi ,\theta _0)\right| \le \tfrac{1}{2} \pi \, {\varvec{d}}_G \left| \theta -\theta _0\right| \left| \sin \varphi \right| . \end{aligned}$$

From (74) and Lemma 10 it follows that

$$\begin{aligned} \left| {\varvec{X}}_{oh}(\varphi ,\theta )-{\varvec{X}}_{oh}(\varphi ,\theta _0)\right| \le \pi \, {\varvec{d}}_G\left| \theta -\theta _0\right| \left| \sin \varphi \right| . \end{aligned}$$

Combining these last two inequalities with (79) and using ${\varvec{d}}_G=2r$ we find (39).

Next we will derive formula (25) for h. Note that for $\varvec{\Theta }$ and $\varvec{\Psi }$ as functions of $\theta$:

$$\begin{aligned} \begin{array}{clc} \varvec{\Theta }(\theta +\varepsilon )\hspace{-3mm}&{}=\cos \varepsilon \ \varvec{\Theta }(\theta )+\sin \varepsilon \ \varvec{\Psi }(\theta ) &{} \text {and } \\[1mm] \varvec{\Psi }(\theta +\varepsilon )\hspace{-3mm}&{}=\cos \varepsilon \ \varvec{\Psi }(\theta )-\sin \varepsilon \ \varvec{\Theta }(\theta ). &{} \end{array} \end{aligned}$$

(80)

When there is no misunderstanding we skip the $\theta$-dependence of $\varvec{\Theta }$ and $\varvec{\Psi }$ and use only $\varvec{ \Theta }=\varvec{\Theta }(\theta )$ and $\varvec{\Psi }=\varvec{ \Psi }(\theta )$ . Thus one computes

$$\begin{aligned}&\varvec{X}(\varphi ,\theta +\varepsilon )-\varvec{X}(\varphi ,\theta )= h\left( \varphi ,\theta +\varepsilon \right) \left( \cos \varepsilon \ \varvec{\Psi }-\sin \varepsilon \ \varvec{\Theta }\right) \\&\quad +\int _{0}^{\varphi }\left( r-a(s,\theta +\varepsilon )\right) \left( \begin{array}{c} -\sin s \\ \cos s\end{array}\right) ds\cdot \left( \begin{array}{c} \varvec{\Xi } \\ \cos \varepsilon \ \varvec{\Theta }+\sin \varepsilon \ \varvec{\Psi }\end{array}\right) \\&\quad - h\left( \varphi ,\theta \right) \ \varvec{\Psi } -\int _{0}^{\varphi }\left( r-a(s,\theta )\right) \left( \begin{array}{c} -\sin s \\ \cos s\end{array}\right) ds\cdot \left( \begin{array}{c} \varvec{\Xi } \\ \varvec{\Theta }\end{array}\right) \\&=\left( h\left( \varphi ,\theta +\varepsilon \right) -h\left( \varphi ,\theta \right) \right) \ \varvec{\Psi \ } \\&\quad + \int _{0}^{\varphi }\left( a(s,\theta )-a(s,\theta +\varepsilon )\right) \left( \begin{array}{c} -\sin s \\ \cos s\end{array}\right) ds\cdot \left( \begin{array}{c} \varvec{\Xi } \\ \varvec{\Theta }\end{array}\right) \\&\quad -2\sin (\varepsilon /2)\left( h\left( \varphi ,\theta +\varepsilon \right) \left( \begin{array}{c} \cos (\varepsilon /2) \\ \sin (\varepsilon /2)\end{array}\right) \right. \\&\hspace{1cm}+ \left. \int _{0}^{\varphi }\left( r-a(s,\theta +\varepsilon )\right) \cos s\, ds\left( \begin{array}{c} \sin (\varepsilon /2) \\ -\cos (\varepsilon /2)\end{array}\right) \right) \cdot \left( \begin{array}{c} \varvec{\Theta } \\ \varvec{\Psi }\end{array}\right) . \end{aligned}$$

As ${\varvec{X}}(\varphi ,\theta )$ describes the surface of a body of constant width 2r and

$$\begin{aligned} {\varvec{X}}(\varphi ,\theta )-{\varvec{X}}(\varphi +\pi ,\theta )=2r {\varvec{U}}(\varphi ,\theta ) \end{aligned}$$

we find that for all $t\in {\mathbb {R}}$

$$\begin{aligned} \left| {\varvec{X}}(\varphi ,\theta +t )-{\varvec{X}} (\varphi +\pi ,\theta )\right| \le 2r = \left| {\varvec{X}}(\varphi ,\theta )-{\varvec{X}}(\varphi +\pi ,\theta )\right| . \end{aligned}$$

(81)

Note that

$$\begin{aligned} \left( {\varvec{X}}(\varphi ,\theta +t )-{\varvec{X}}(\varphi +\pi ,\theta )\right) \cdot {\varvec{U}}(\varphi ,\theta )=\left( {\varvec{X}}(\varphi ,\theta +t )-{\varvec{X}}(\varphi ,\theta )\right) \cdot {\varvec{U}}(\varphi ,\theta )+2r \end{aligned}$$

and thus we necessarily have

$$\begin{aligned} \left( {\varvec{X}}(\varphi ,\theta +t )-{\varvec{X}}(\varphi ,\theta )\right) \cdot {\varvec{U}}(\varphi ,\theta )\le 0. \end{aligned}$$

(82)

Since ${\varvec{U}}(\varphi ,\theta )=\cos \varphi \ \varvec{\Xi } +\sin \varphi \ \varvec{\Theta }$ we find, that

$$\begin{aligned}{} & {} \left( {\varvec{X}}(\varphi ,\theta +t )-{\varvec{X}}(\varphi ,\theta )\right) \cdot {\varvec{U}}(\varphi ,\theta )=\int _{0}^{\varphi }\left( a(s,\theta )-a(s,\theta +t )\right) \sin \left( \varphi -s\right) ds \nonumber \\{} & {} \quad -\sin \varphi \left( \sin t \ h\left( \varphi ,\theta +t \right) +2\left( \sin (t /2)\right) ^{2}\int _{0}^{\varphi }\left( r-a(s,\theta +t )\right) \cos s\ ds\right) . \qquad \end{aligned}$$

(83)

Since ${\varvec{X}}$ and h are Lipschitz-continuous we may split (83) in a ‘first order’ and a ‘higher order term’ in t with bounded coefficients, namely

$$\begin{aligned} (83)= & {} t \left( \int _{0}^{\varphi }\frac{a(s,\theta )-a(s,\theta +t )}{t }\sin \left( \varphi -s\right) ds-\sin \varphi \ h\left( \varphi ,\theta \right) \right) \,\\{} & {} + t^2\sin \varphi \frac{\sin t}{t}\frac{h(\varphi ,\theta )-h(\varphi ,\theta +t)}{t}+{\mathcal {O}}( t ^{2}). \end{aligned}$$

For (82) to hold the first order term should be 0, otherwise either for $t>0$ or $t<0$ with $\left| t\right|$ small (82) would be violated, and that means:

$$\begin{aligned} \lim _{t\rightarrow 0}\int _{0}^{\varphi }\frac{a(s,\theta )-a(s,\theta +t )}{t }\sin \left( \varphi -s\right) ds-\sin \varphi \ h\left( \varphi ,\theta \right) = 0. \end{aligned}$$

Hence we find for $\varphi \in (0,\pi )\cup (\pi ,2\pi )$ that

$$\begin{aligned} h\left( \varphi ,\theta \right) =\frac{\lim _{\varepsilon \rightarrow 0}\int _{0}^{\varphi }\frac{a(s,\theta )-a(s,\theta +\varepsilon )}{ \varepsilon }\sin \left( \varphi -s\right) ds}{\sin \varphi }, \end{aligned}$$

(84)

and since h is Lipschitz-continuous with $h(0,\theta )=h(\pi ,\theta )=0$, we may extend h for $\sin \varphi =0$ by 0.

It remains to show the regularity properties stated in the second item of the theorem. These follow rather immediately. Whenever $a,\partial _{\theta }a\in C_{\textrm{p}}^{0}({\mathbb {R}}^2)$ one finds from (84) that

$$\begin{aligned} h\left( \varphi ,\theta \right) =-\frac{\int _{0}^{\varphi }a_{\theta }\left( s,\theta \right) \sin \left( \varphi -s\right) ds}{\sin \varphi } \end{aligned}$$

as in (25). With the extended h being Lipschitz-continuous and satisfying (63) one finds (38) and (26).

For $a,\partial _{\theta }a\in C_{\textrm{p}}^{1}({\mathbb {R}}^2)$ also (28) is satisfied. $\square$

Appendices

On the distance in ${\mathbb {S}}^{2}$

Let $\varvec{\tilde{f}}$ $:{\mathbb {S}}^{2}\rightarrow \mathbb {R }$ be some function. The standard definition for such a function $\varvec{\tilde{f}}$ to be Lipschitz-continuous, is, that there exists $L>0$ such that

$$\begin{aligned} \left| \varvec{\tilde{f}}(\omega )-\varvec{\tilde{f}}(\omega _{0})\right| \le L\left| \omega -\omega _{0}\right| \text { for all }\omega ,\omega _{0}\in {\mathbb {S}}^{2}. \end{aligned}$$

(85)

Since the functions we use are defined in terms of $(\varphi ,\theta )\in {\textsf{S}}$ instead of $\omega \in {\mathbb {S}}^2$, with ${\textsf{S}}$ from (22), we need to reformulate the Lipschitz-condition in (85) to a condition for

$$\begin{aligned} {\varvec{f}}:{\textsf{S}}\rightarrow {\mathbb {R}} \text { for } \omega ={\varvec{U}}( \varphi ,\theta ) \text { and } {\varvec{f}}(\varphi ,\theta )=\varvec{\tilde{f}}(\omega ) \end{aligned}$$

with ${\varvec{U}}$ from (17). In other words, we have to replace $\left| \omega -\omega _0\right|$ with an equivalent expression using $(\varphi ,\theta )$ and $(\varphi _0,\theta _0)$. The corresponding estimates follow next.

Lemma 10

Setting $\omega ={\varvec{U}}\left( \varphi ,\theta \right)$ and $\omega _{0}={\varvec{U}}\left( \varphi _{0},\theta _{0}\right)$, one finds that for all $(\varphi ,\theta )$ and $(\varphi _0,\theta _0)$ in ${\textsf{S}}$:

• if $\varphi ,\varphi _{0}\in \left[ 0,\pi \right]$ or $\varphi ,\varphi _{0}\in \left[ \pi ,2\pi \right]$:

  $$\begin{aligned} \left| \omega -\omega _{0}\right| \le \left| \varphi -\varphi _{0}\right| +\left| \theta -\theta _{0}\right| \min \left( \left| \sin \varphi \right| ,\left| \sin \varphi _{0}\right| \right) \le \pi \left| \omega -\omega _{0}\right| ; \end{aligned}$$

  (86)

• if $\varphi \in \left[ 0,\pi \right]$ and $\varphi _{0}\in \left[ \pi ,2\pi \right]$, or vice versa:

  $$\begin{aligned} \left| \omega -\omega _{0}\right| \le \left| 2\pi -\varphi -\varphi _{0}\right| +\left( \pi -\left| \theta -\theta _{0}\right| \right) \min \left( \left| \sin \varphi \right| ,\left| \sin \varphi _{0}\right| \right) \le \pi \left| \omega -\omega _{0}\right| . \end{aligned}$$

  (87)

Proof

Assuming $\varphi ,\varphi _{0}\in \left[ 0,\pi \right]$ or $\varphi ,\varphi _{0}\in \left[ \pi ,2\pi \right]$ one considers as an intermediate point $\omega _{*}={\varvec{U}}(\varphi _{0},\theta )$ and uses the following estimates:

• The triangle inequality in ${\mathbb {R}}^3$: $\left| \omega -\omega _{0}\right| \le \left| \omega -\omega _{*}\right| +\left| \omega _{*}-\omega _{0}\right|$.

• Comparing the length via the circle with fixed $\varphi _{0}$ on the sphere through the points $\omega$ and $\omega _{*}$ with the straight line in ${\mathbb {R}}^{3}$ through those points gives:

  $$\begin{aligned} \left| \omega -\omega _{*}\right| \le \left| \varphi -\varphi _{0}\right| \le \tfrac{\pi }{2}\left| \omega -\omega _{*}\right| . \end{aligned}$$

• A direct computation shows that

  $$\begin{aligned} \left| \omega _{*}-\omega _{0}\right| =2\left| \sin \varphi _{0}\right| \left| \sin \left( \tfrac{1}{2}\left( \theta -\theta _{0}\right) \right) \right| \end{aligned}$$

  and since $\theta -\theta _{0}\in \left[ -\pi ,\pi \right]$ one finds

  $$\begin{aligned} \tfrac{2}{\pi }\left| \theta -\theta _{0}\right| \le 2\left| \sin \left( \tfrac{1}{2}\left( \theta -\theta _{0}\right) \right) \right| \le \left| \theta -\theta _{0}\right| , \end{aligned}$$

  implying

  $$\begin{aligned} \left| \omega _{*}-\omega _{0}\right| \le \left| \theta -\theta _{0}\right| \left| \sin \varphi _{0}\right| \le \tfrac{ \pi }{2}\left| \omega _{*}-\omega _{0}\right| . \end{aligned}$$

  (88)

  By symmetry we may interchange $\omega$ and $\omega _0$ and hence replace $\left| \sin \varphi _{0}\right|$ with $\left| \sin \varphi \right|$ and hence by $\min \left( \left| \sin \varphi \right| ,\left| \sin \varphi _{0}\right| \right)$ in (88).

• Both $\omega _{*}$ and $\omega _{0}$ lie on the circle on the unit sphere with fixed $\varphi _{0}$. Since $\omega _{*}$ is the point on that circle that is closest to $\omega$, one obtains

  $$\begin{aligned} \left| \omega -\omega _{*}\right| \le \left| \omega -\omega _{0}\right| . \end{aligned}$$

  A similar argument now for the circle on the unit sphere with fixed $\theta _{0}$ shows

  $$\begin{aligned} \left| \omega _{*}-\omega _{0}\right| \le \left| \omega -\omega _{0}\right| . \end{aligned}$$

  (89)

Fig. 7

A sketch of ${\textsf{S}}$ deformed to show a distance equivalent to the one in ${\mathbb {S}}^2$ identifying points at the upper boundary as well as points on the lower boundary. For (86) see left and for (87) see right. The variable $\varphi \in [0,2\pi ]$ moves from left to right; $\theta \left| \sin \varphi \right|$ with $\theta \in [-\frac{1}{2}\pi ,\frac{1}{2} \pi ]$ increases in the vertical direction

Combining these inequalities gives the estimates in (86).

For the second case we assume $\varphi \in \left[ 0,\pi \right]$, $\varphi _{0}\in \left[ \pi ,2\pi \right]$ as in Fig. 7 on the right. We consider the shortest path from $\omega$ to $\omega _{0}$ through $\omega _{*}={\varvec{U}}(2\pi -\varphi _{0},\theta )$ and the top or bottom boundary of ${\textsf{S}}$. Obviously $\left| \omega -\omega _{0}\right| \le \left| \omega -\omega _{*}\right| +\left| \omega _{*}-\omega _{0}\right|$ still holds. As before one finds

$$\begin{aligned} \left| \omega -\omega _{*}\right| \le \left| 2\pi -\varphi _{0}-\varphi \right| \le \tfrac{\pi }{2}\left| \omega -\omega _{*}\right| \end{aligned}$$

and since

$$\begin{aligned} \left| \omega _{*}-\omega _{0}\right| =2\left| \sin \varphi _{0}\right| \sin \left( \frac{\pi -\left| \theta -\theta _{0}\right| }{2}\right) \end{aligned}$$

with $0\le \pi -\left| \theta -\theta _{0}\right| \le \pi$ one obtains

$$\begin{aligned} \left| \omega _{*}-\omega _{0}\right| \le \left( \pi -\left| \theta -\theta _{0}\right| \right) \left| \sin \varphi _{0}\right| \le \tfrac{\pi }{2}\left| \omega _{*}-\omega _{0}\right| . \end{aligned}$$

Also as before we have

$$\begin{aligned} \left| \omega -\omega _{*}\right| \le \left| \omega -\omega _{0}\right| \end{aligned}$$

but the last inequality (89) holds if $\left| \sin \varphi _{0}\right| \le \left| \sin \varphi \right|$. However, by taking the minimum in (87) the result holds true. The different cases are illustrated by Fig. 7. $\square$

The inverse Gauss map for bodies of constant width

As we mentioned in the introduction the Gauss map for bodies of constant width G is not necessarily uniquely defined on $\partial G$, but the inverse is. This ‘inverse’ is even Lipschitz and this can be found as a corollary in [12]. In the next Lemma we will give a short direct proof.

Recall that if G is a body of constant width, then G lies in each direction $\omega \in {\mathbb {S}}^2$ between two parallel planes perpendicular to $\omega$ which have distance ${\varvec{d}}_G$. That means, there are two points ${\varvec{P}}_a,{\varvec{P}}_b\in \partial G$ such that

$$\begin{aligned} \left\langle {\varvec{P}}_a,\omega \right\rangle \le \left\langle x,\omega \right\rangle \le \left\langle {\varvec{P}}_b,\omega \right\rangle \text { for all }x\in G. \end{aligned}$$

(90)

If ${\varvec{P}}_b-{\varvec{P}}_a$ is not a multiple of $\omega$ then $\left| {\varvec{P}}_b-{\varvec{P}}_a\right| >{\varvec{d}}_G$, which violates the assumption that G is a body of constant width. In fact we may use (90) to define an outward normal at ${\varvec{P}}\in \partial G$ by $\omega \in {\mathbb {S}}^2$ that satisfies

$$\begin{aligned} \left\langle x,\omega \right\rangle \le \left\langle {\varvec{P}},\omega \right\rangle \text { for all }x\in G. \end{aligned}$$

(91)

Note that in this way, any ${\varvec{P}}\in \partial G$ has an outward normal but the normal might not be unique.

Lemma 11

If ${\varvec{X}}_1$ and ${\varvec{X}}_2$ are two points on the surface of a body $G\subset {\mathbb {R}}^{3}$ of constant width ${\varvec{d}}_{G}$ and $\omega _{1}$, $\omega _{2}$ are outward normal directions at ${\varvec{X}}_1$, ${\varvec{X}}_2$, then

$$\begin{aligned} \frac{\pi }{2}\left| \omega _{1}-\omega _{2}\right| {\varvec{d}} _{G}\ge \left| {\varvec{X}}_1-{\varvec{X}}_2\right| . \end{aligned}$$

Let us recall a formula for the arc length of the shortest geodesic connecting two points on ${\mathbb {S}}^2$, namely $\ell :{\mathbb {S}}^{2}\times {\mathbb {S}}^{2}\rightarrow \left[ 0,\pi \right]$, defined for $\omega _{\alpha },\omega _{\beta }\in {\mathbb {S}}^{2}$ by

$$\begin{aligned} \ell \left( \omega _{\alpha },\omega _{\beta }\right) =\arccos \left( \omega _{\alpha }\cdot \omega _{\beta }\right) , \end{aligned}$$

which is a natural distance function on the sphere ${\mathbb {S}}^{2}$.

Fig. 8

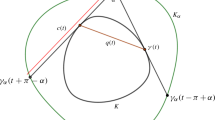
On the left parts of the two spheres from the proof of Lemma 11. G lies below these two spheres and touches them in ${\varvec{X}}_1$ and ${\varvec{X}}_2$. On the right the various $\omega _{...}$ on ${\mathbb {S}}^2$ illustrating $\ell (\omega _1,\omega _2)=\ell (\omega _1,\omega _m)+\ell (\omega _m,\omega _2)\ge \ell (\omega _1,\omega _a)+\ell (\omega _b,\omega _2)$

Proof

Since G is a body of constant width ${\varvec{d}}_{G}$ it holds for any ${\varvec{X}}\in \partial G$ with outward normal $\omega$ that

$$\begin{aligned} x\in G \implies x\in \overline{B_{{\varvec{d}}_G}}\left( {\varvec{X}}-{\varvec{d}}_G\omega \right) . \end{aligned}$$

Here $\overline{B_{r}}({\varvec{M}})$ is the closed ball of radius r and center ${\varvec{M}}$. Let ${\varvec{X}}_1,{\varvec{X}}_2\in \partial G$ with corresponding outward normals $\omega _1,\omega _2$. Set

$$\begin{aligned} B_i:= & {} B_{{\varvec{d}}_{G}}\big ( {\varvec{X}}_i-{\varvec{d}}_{G}\omega _{i}\big ) \text { for }i=1,2,\\ L:= & {} \overline{B_1}\cap \overline{B_2} \text { and }C:=\partial B_1\cap \partial B_2. \end{aligned}$$

These sets are illustrated on the left hand side of Fig. 8. We have ${\varvec{X}}_1,{\varvec{X}}_2\in \partial G\cap \partial L$. Notice that in ${\varvec{X}}_1\in \partial G$ the normal $\omega _1$ is also an outward normal in ${\varvec{X}}_1\in \partial B_1$ on $\partial B_1$, as well as ${\varvec{X}}_2\in \partial G\cap \partial B_2$ is having outward normal $\omega _2$ both on $\partial G$ and $\partial B_2$. Consider a shortest path $t\mapsto \omega (t)$ on ${\mathbb {S}}^2$ connecting $\omega (0)=\omega _1$ with $\omega (1)=\omega _2$. The curve $t\mapsto \omega (t)$ describes a geodesic on ${\mathbb {S}}^2$, which corresponds to the ‘straight’ line connecting $\omega _1$ with $\omega _2$ depicted on the right hand side of Fig. 8.

In that same image on the right one finds the collection of outward normals to $\partial L$ that correspond to the points on C. These outward normals make a band on ${\mathbb {S}}^2$, of which the boundary is marked by the two red circles. A dotted line is defined to be the middle of that band.

Coming back to the geodesic $t\mapsto \omega (t)$, one finds for some $t_m\in (0,1)$ that $\omega _m:=\omega (t_m)$ lies on that dotted line. Not only $\omega _m$ is an outward normal at ${\varvec{P}}$ but also all vectors on the interval in that band through $\omega _m$ perpendicular to the dotted line, which range from $\omega _a$ to $\omega _b$. Here $\omega _a$ is the unique outward normal to $B_1$ at ${\varvec{P}}$ and $\omega _b$ is the unique outward normal to $B_2$ at ${\varvec{P}}$.

Since $\omega _{m}$ lies on the shortest path from $\omega _{1}$ to $\omega _{2}$, we find that

$$\begin{aligned} \ell \left( \omega _{1},\omega _{2}\right) =\ell \left( \omega _{1},\omega _{m}\right) +\ell \left( \omega _{m},\omega _{2}\right) . \end{aligned}$$

Moreover, it holds that

$$\begin{aligned} \ell \left( \omega _{1},\omega _{m}\right) \ge \ell \left( \omega _{1},\omega _{a}\right) \text { and }\ell \left( \omega _{m},\omega _{2}\right) \ge \ell \left( \omega _{b},\omega _{2}\right) . \end{aligned}$$

We now return to the left hand side of Fig. 8. Since

$$\begin{aligned} \left| {\varvec{X}}_1-{\varvec{P}}\right| \le {\varvec{d}}_{G}\, \ell (\omega _1,\omega _a) \text { and } \left| {\varvec{X}}_2-{\varvec{P}}\right| \le {\varvec{d}}_{G}\, \ell (\omega _2,\omega _a), \end{aligned}$$

we obtain

$$\begin{aligned}{} & {} \left| {\varvec{X}}_1-{\varvec{X}}_2\right| \le \left| {\varvec{X}}_1- {\varvec{P}}\right| +\left| {\varvec{P}}- {\varvec{X}}_2\right| \le {\varvec{d}}_{G}\left( \ell \left( \omega _{1},\omega _{a}\right) + \ell \left( \omega _{b},\omega _{2}\right) \right) \\{} & {} \quad \le {\varvec{d}}_{G}\left( \ell \left( \omega _{1},\omega _m\right) + \ell \left( \omega _m,\omega _{2}\right) \right) = {\varvec{d}}_{G}\ \ell \left( \omega _{1},\omega _{2}\right) \le \tfrac{1}{2}\pi \left| \omega _{1}-\omega _{2}\right| {\varvec{d}}_{G}, \end{aligned}$$

which is the claim. $\square$

Shadow domains

In order to show that a body of constant width has some minimal regularity property, namely a kind of Lipschitz-continuity under rotation, we need a geometrical argument. Such an argument follows from ‘observing the shadows’ during rotation. We did not find such a tool in the literature and supply it here.

Definition 12

Suppose that $\Omega \subset {\mathbb {R}}^{2}$ is a bounded, simply connected domain with $0\in \Omega$. We define $R_{\Omega }:\mathbb { R\rightarrow R}^{+}$ by

$$\begin{aligned} R_{\Omega }(\psi ):=\sup \left\{ x\cos \psi +y\sin \psi ;\ \left( {\begin{array}{c}x\\ y\end{array}}\right) \in \Omega \right\} \end{aligned}$$

(92)

and the rotational shadow domain of $\Omega$ by

$$\begin{aligned} Sh (\Omega ):=\left\{ \left( {\begin{array}{c}r\cos \psi \\ r\sin \psi \end{array}}\right) ;0\le r<R_{\Omega }(\psi )\text { and }\psi \in \left[ 0,2\pi \right] \right\} . \end{aligned}$$

The intersection of $Sh (\Omega )$ with the line

$$\begin{aligned} \ell (\psi ):=\left\{ t\left( {\begin{array}{c}\cos \psi \\ \sin \psi \end{array}}\right) ;t\in {\mathbb {R}}\right\} \end{aligned}$$

gives precisely the shadow of $\Omega$ with the light at infinity in the direction $\left( {\begin{array}{c}-\sin \psi \\ \cos \psi \end{array}}\right)$. See Fig. 9 in the case of a triangle.

Fig. 9

On the left a triangle, in the middle $\psi \mapsto R_{\Omega }(\psi )$ as the maximum of the three functions related to the corners under counterclockwise rotation, and on the right the rotational shadow domain of the triangle

Lemma 13

Let $\Omega$ be as in Definition 12. The function $R_{\Omega }$ in (92) is Lipschitz-continuous with Lipschitz-constant at most

$$\begin{aligned} L=\sup \left\{ \left| x\right| ;\ x\in \Omega \right\} . \end{aligned}$$

(93)

Proof

Let $co(\Omega )$ denote the convex hull of $\Omega$. It holds that $R_{co\left( \Omega \right) }(\psi )=R_{\Omega }(\psi )$. Note that taking the convex hull also does not change L. Hence we may assume without loss of generality that $\Omega$ is convex. The boundary of a bounded convex domain in ${\mathbb {R}}^{2}$ with $0\in \Omega$ can be parametrized in polar coordinates with $r(t)>0$ as follows:

$$\begin{aligned} \partial \Omega =\left\{ r(t)\left( {\begin{array}{c}\cos t\\ \sin t\end{array}}\right) ;t\in \left[ 0,2\pi \right] \right\} . \end{aligned}$$

For such a parametrization one finds

$$\begin{aligned} R_{\Omega }(\psi )&=\sup \left\{ r(t)\cos t\cos \psi +r(t)\sin t\sin \psi ;t \in \left[ 0,2\pi \right] \right\} \nonumber \\&=\sup \left\{ r(t)\cos \left( \psi -t\right) ;t \in \left[ 0,2\pi \right] \right\} . \end{aligned}$$

(94)

The function $\psi \mapsto r(t)\cos \left( \psi -t\right)$ is Lipschitz-continuous with constant $\left\| r\right\| _{\infty }=L$ as in (93). A function defined as the supremum of Lipschitz-functions with a uniform constant is Lipschitz-continuous with that same constant. $\square$

Fig. 10

Rotating views of 6 bodies of constant width; each constructed by connecting two simple curves of constant width

Notice that (94) leads to

$$\begin{aligned} R_{\Omega }(\psi )=\sup \left\{ r(\psi -s)\cos \left( s\right) ;\left| s\right| <\tfrac{1}{2}\pi \right\} , \end{aligned}$$

which again explains, why we call $Sh (\Omega )$ the rotational shadow domain. Notice that, since $\cos s<0$ for $s\in [-\pi ,-\frac{1}{2}\pi )\cup (\frac{1}{2}\pi ,\pi ]$ and $0\in \Omega$, only the subinterval $(-\frac{1}{2}\pi ,\frac{1}{2}\pi )$ contributes to this positive supremum.

One may extend this shadow in 2 dimensions to 3d-shadows of a bounded domain $\Omega \subset {\mathbb {R}}^{3}$. With the basis $\left\{ \varvec{\Xi },\varvec{\Theta }(\theta ),\varvec{\Psi }(\theta )\right\}$ as in (41) we define $P_{\varvec{\Psi }(\theta )}: {\mathbb {R}}^{3}\rightarrow {\mathbb {R}}^{3}$, consistent with (15), by

$$\begin{aligned} P_{\varvec{\Psi }(\theta )}\left( \begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array} \right) :=\left\langle \varvec{\Xi },x\right\rangle \varvec{\Xi }+\left\langle \varvec{\Theta }(\theta ),x\right\rangle \varvec{\Theta }(\theta )=\left( \begin{array}{c} \left( \cos \theta \ x_{1}+\sin \theta \ x_{2}\right) \cos \theta \\ \left( \cos \theta \ x_{1}+\sin \theta \ x_{2}\right) \sin \theta \\ x_{3} \end{array} \right) . \end{aligned}$$

With the $\varvec{\Xi }$-axis being fixed the 3d-shadow is constructed as in the 2d-case for each $\varvec{\Xi }$-coordinate being constant. One obtains a 3d-domain by joining the 2d-shadows from rotating around that axis. We use $\varvec{\Xi }$ as before but the 3d-shadow can be defined in any direction.

Definition 14

Suppose that $\Omega \subset {\mathbb {R}}^{3}$ is a bounded domain. Then we define the 3d-shadow domain in the directions perpendicular to the $\varvec{\Xi }$-axis by

$$\begin{aligned} Sh _{\varvec{\Xi }}(\Omega ):=\bigcup \left\{ P_{\varvec{ \Psi }(\theta )}(\Omega );\left| \theta \right| \le \tfrac{1}{2}\pi \right\} . \end{aligned}$$

One may notice that this 3d-shadow domain is related to the 2d-shadows for fixed $x_{3}$. One freezes $x_3=c$, takes the 2d-shadow domain of the intersection of $\Omega$ with the plane defined by $x_3=c$, and joins these shadows in their respective level to obtain again a 3d-domain. Putting this procedure in a formula one obtains:

$$\begin{aligned} Sh _{\varvec{\Xi }}(\Omega )=\bigcup _{ x_{3}\in I}\left( \begin{array}{c} Sh \left( \left\{ \left( \begin{array}{c} x_1 \\ x_2 \end{array}\right) ; (x_1,x_2,x_3)^T\in \Omega \right\} \right) \\ x_3 \end{array} \right) \end{aligned}$$

(95)

for $I:=\left\{ x_3; \exists (x_1,x_2,x_3)\in \Omega \right\}$.