Abstract
We present new estimates in the setting of weighted classical Lorentz spaces for important operators in Harmonic Analysis such as Calderón-Zygmund operators, sparse operators and the Bochner-Riesz operator among others.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Given positive locally integrable functions (called weights)
the main goal of this paper is to prove boundedness of important operators in harmonic analysis on weighted classical Lorentz spaces \(\Lambda ^p_u(w)\), \(p> 0\), defined by those measurable functions f such that
(see [18]) where \(f_u^*\) is the decreasing rearrangement of f defined by
with
This will lead to the unification of classical results about the boundedness of operators on different weighted settings, like the Lebesgue spaces \(L^p(u):= \Lambda ^p_u(1)\) or the classical Lorentz spaces \(\Lambda ^p(w):= \Lambda ^p_1(w)\), resulting into a general framework involving both theories.
Boundedness on weighted classical Lorentz spaces have been already studied for some operators. For instance, let us just mention [3], including the case of the Hilbert transform and the Hilbert maximal operator, and [17] that contains the case of Calderón-Zygmund operators and commutators. Further, we should also consider [18], where the authors study inter alia the characterization of the Hardy-Littlewood maximal operator.
Here, by means of the theory of weighted extrapolation, we present new estimates for operators such as Calderón-Zygmund operators \(T_K\), sparse operators \(A_{{\mathcal {S}}}\) or the Bochner-Riesz operator at the critical index \(B_{\frac{n-1}{2}}\), among many others.
Now, the examples mentioned above share one important property: they all satisfy that, for some (and hence for all) \(p_0 > 1\),
is bounded, where for a given exponent \(p > 1\), \(A_p\) is the class of Muckenhoupt weights defined by those weights v that satisfy
with the supremum being taken overall cubes \(Q \subseteq {\mathbb {R}^n}\). Further, those \(A_p\) weights characterize the boundedness on \(L^p(v)\) of the Hardy-Littlewood maximal operator M defined by
where the supremum is taken overall cubes \(Q \subseteq {\mathbb {R}}^n\) containing x. Moreover, the definition of \(A_p\) can be extended to \(p = 1\), and we say that \(v\in A_1\) if there exists a positive constant C such that
and \(\left\Vert v\right\Vert _{A_1}\) is set to be the infimum of such constants C. We shall point here that the \(A_p\) class of weights increases with the exponent (that is, \(A_p \subseteq A_q\), for \(p \le q\)) so it is natural to define the class of weights
Throughout this paper, an operator T satisfying (1) for some \(p_0\) and with norm constant less than or equal to \(\varphi (\Vert v \Vert _{A_{p_0}})\), and \(\varphi : [1,\infty ) \rightarrow (0,\infty )\) being a nondecreasing function, will be called a Rubio de Francia operator [42]. Those operators satisfy the well-known Rubio de Francia extrapolation theorem.
Theorem 1.1
[29] Given a Rubio de Francia operator T for some exponent \(p_0 \ge 1\). Then, for all \(p_1 > 1\),
with norm constant less than or equal to \(\Phi (\Vert v \Vert _{A_{p_1}})\) where
A Banach function norm \(\rho \) is a mapping \(\rho :\mathcal {M}^{+} \rightarrow [0,\infty ]\), with \(\mathcal {M}^{+}\) being the set of positive measurable functions, such that the following properties hold:
-
(i)
\(\rho (f) = 0 \Leftrightarrow f = 0\) a.e.;
-
(ii)
\(\rho (af) = a\rho (f)\), for \(a \ge 0\);
-
(iii)
\(\rho (f + g) \le \rho (f) + \rho (g)\);
-
(iv)
if \(0 \le f \le g\) a.e., then \(\rho (f)\le \rho (g)\);
-
(v)
if
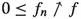 a.e., then
a.e., then 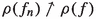 ;
; -
(vi)
if E is a measurable set such that \(|E| < \infty \), then \(\rho (\chi _E) < \infty \) and \(\int _Ef\,dx \le C_E\rho (f)\) for some constant \(0< C_E < \infty \), depending on E and \(\rho \), but independent of f, where \(\chi _E\) represents the characteristic function of E.
The collection \(\mathbb {X} = \mathbb {X}(\rho )\) defined by
is called a Banach function space. Besides, by means of a function norm \(\rho \), we can define its associate norm \(\rho ':\mathcal {M}^{+} \rightarrow [0,\infty ]\) by
which is itself a function norm. This allows us to define the associate space of \(\mathbb {X} = \mathbb {X}(\rho )\) to be the Banach function space \(\mathbb {X}' = \mathbb {X}(\rho ')\) (see [10, Ch. 1-Theorem 2.2]).
A function norm \(\rho \) is called rearrangement invariant (r.i. in short) if \(\rho (f) = \rho (g)\) for every pair of functions f and g that satisfy \(\lambda _f(y) = \lambda _g(y)\) for every \(y > 0\). In this case, we say that \(\mathbb {X} = \mathbb {X}(\rho )\) is a r.i. Banach function space (see [10, 27] for more details on those spaces). For instance, since the decreasing rearrangement on \((0,\infty )\) of f satisfy \(\lambda _{f^*}(y) = \lambda _f(y)\) for every \(y > 0\), in fact it can be obtained a representation of \(\mathbb {X}\) on \((\mathbb {R}^{+}, dt)\) (see [10, Ch. 2-Theorem 4.10]) as follows: there exists a r.i. Banach function space \(\overline{\mathbb {X}}\) over \((\mathbb {R}^{+}, dt)\) such that \(f \in \mathbb {X}\) if and only if \(f^{*} \in \overline{\mathbb {X}}\) with
Moreover, when restricted to a r.i. Banach function space \(\mathbb {X}\) it is possible to define a weighted version of \(\mathbb {X}\) as
for some weight u.
Now, as a consequence of [26, Theorem 4.10], it is known that the Rubio de Francia operators also satisfy boundedness over the weighted version of a r.i. Banach function spaces \(\mathbb {X}\) where, for the sake of simplicity, here we state a different version of that theorem consisting on introducing the maximal operator M and its dual induced by a weight \(u \in A_\infty \) defined as
and where we have kept track of the involved norm constants.
Theorem 1.2
Given a Rubio de Francia operator T for some exponent \(p_0 > 1\). Let \(\mathbb {X}\) be a r.i. Banach function space and let \(u \in A_\infty \) such that
where \(\mathbb {X}(u)'\) is the associate space of \(\mathbb {X}(u)\) defined by those functions f that satisfy
Then,
with constant less than or equal to \(C_1\varphi \left( C_2\left\Vert M_u'\right\Vert _{\mathbb {X}(u)'}\left\Vert M\right\Vert _{\mathbb {X}(u)}^{p_0 - 1}\right) \), where \(\left\Vert M\right\Vert _{\mathbb {X}(u)}\) and \(\left\Vert M_u'\right\Vert _{\mathbb {X}(u)'}\) represent the norm constants of (3) respectively.
The previous result is very useful to prove the boundedness of operators for which condition (1) has been widely studied while this is not the case in other contexts such as, for example, weighted classical Lorentz spaces or more generally r.i. Banach function spaces. However, in order to get estimates over \(\mathbb {X}(u)\) we first must study whether \(\mathbb {X}\) is a r.i. Banach function space and when (3) holds.
For our goal, we will consider \(\mathbb {X}= \Lambda ^p(w)\), for \(p > 0\) and w being a weight in \(\mathbb {R}^{+}\), so that \(\mathbb {X}(u) = \Lambda ^p_u(w)\) and \(\mathbb {X}(u)' = (\Lambda ^p_u(w))'\) is defined by
As a first approach, let us consider the particular case \(u = 1\):
i) Ariño and Muckenhoupt [6] proved that for \(p > 1\),
where
with \(W(t) = \int _0^t w(r)\,dr\). This class of weights has been widely studied (see for instance [7, 8, 13, 39, 40]) and now it is known that the same result in (4) holds for every \(p>0\) (see [19]). Further, although for \(0< p < 1\), \(\Lambda ^p(w)\) is never a Banach function space (see [45, Remark 3.2]) for \(p \ge 1\), \(\Lambda ^p(w)\) is a Banach function space when \(w \in B_p\), and the reciprocal is also true whenever \(p > 1\) (see [15, 43]).
ii) The characterization of the boundedness of M on \((\Lambda ^p(w))'\) (see [8]) is a consequence of the Lorentz-Shimogaki theorem (see, for instance, [10, Ch.3 p. 154]). In particular, if \(w \in B_p\) then
where [39]
From (i) and (ii), we can conclude that for every Rubio de Francia operator T and \(p \ge 1\),
and it is sharp since it is known [43] that
with H being the Hilbert transform, which is a Rubio de Francia operator defined as
whenever this limit exists almost everywhere and where \(\mathcal C_c^\infty ({\mathbb {R}})\) is the set of infinitely differentiable functions with compact support.
Now, take a general \(u \in A_\infty \). In [18, Theorem 3.3.5] it was characterized the weighted strong-type boundedness on \(\Lambda ^{p}_{u}\left( w \right) \) of the Hardy-Littlewood maximal operator for every \(p > 0\) by
where we say that \(w \in B_p(u)\) if there exists some \(\varepsilon > 0\) such that
where the supremum is taken over every finite family of cubes \(\{Q_j\}_{j = 1}^J \subseteq {\mathbb {R}^n}\). (We refer the reader to [1, 18] for more details on this class of weights.)
-
(i)
If \(u = 1\), due to the \(B_p\) class of weights satisfy the \(p - \varepsilon \) property [18, 40] (that is, for \(w \in B_p\) there exists some \(\varepsilon > 0\) such that \(w \in B_{p-\varepsilon }\)) we have that (8) is equivalent to \(w \in B_p\).
-
(ii)
If \(w = 1\) and \(p > 1\), then (8) is equivalent to that there exists some \(0< q < p\) such that
$$\begin{aligned} \frac{u\left( \bigcup _{j = 1}^JQ_j \right) }{u\left( \bigcup _{j = 1}^J E_j \right) } \lesssim \max _{1\le j\le J}\left( \frac{|Q_j|}{|E_j|} \right) ^q, \end{aligned}$$which agrees with \(u \in A_p\) (see, for instance, [22, 33]).
Moreover, \(B_p(u) \subseteq B_p\) for every \(p > 0\) (see [18, Corollary 3.3.4]) so, for \(p \ge 1\) and \(w \in B_p(u)\) then \(\Lambda ^p(w)\) is a r.i. Banach function space.
Therefore, together with (7), if we were able to see when \(M'_u\) is bounded over \((\Lambda ^p_u(w))'\), we could make use of Theorem 1.2 to obtain estimates for a Rubio de Francia operator T on \(\Lambda ^p_u(w)\), at least for \(p \ge 1\) and \(w \in B_p(u)\). Indeed, our main result on this paper says more:
Theorem 1.3
Given a Rubio de Francia operator T for some exponent \(p_0 > 1\). Let \(u \in A_\infty \) and \(p > 0\). Then,
Now, in [4, Theorem 5.5] it was shown that for \(p > 1\),
while for \(0 < p \le 1\) it is just known that
Remark 1.4
At least for \(p > 1\), by means of the Hilbert transform (see (9)) the condition \(B_p(u) \cap {B_{\infty }^{*}}\) on the weight w of Theorem 1.3 is sharp in the sense that it can not be found a greater class for w.
Now, let \(\Lambda ^{p,\infty }_u(w)\), \(p > 0\), be the space defined by those measurable functions f such that
and let \(L^{p,\infty }(u) := \Lambda ^{p,\infty }_u(1)\), \(p \ge 1\). In [20] the authors consider as hypothesis weighted weak-type estimates instead of (1); that is, for some \(p_0 \ge 1\),
and then try to find conditions on p and w for which
holds, so it could be interesting to study the previous to weighted classical Lorentz spaces for a weight \(u \in A_\infty \). However, this is just a consequence of the weighted strong-type extrapolation settled in Theorem 1.3, and the precise result is the following.
Corollary 1.5
If an operator T satisfies (10) for some \(p_0 \ge 1\) and with constant less than or equal to \(\varphi (\left\Vert v\right\Vert _{A_{p_0}})\), where \(\varphi \) is a nonnegative nondecreasing function on \([1, \infty )\), then, for \(p > 0\) and \(u \in A_\infty \),
Again, for \(p > 1\) and by means of the Hilbert transform (see [2, Theorem 1.1]) the condition \(B_p(u) \cap {B_{\infty }^{*}}\) on the weight w of Corollary 1.5 is sharp in the sense that it can not be found a greater class for w.
The paper is organized as follows: in Sect. 2 we study the boundedness of \(M'_u\) over the associate space of \(\Lambda ^p_u(w)\). The proofs of Theorem 1.3 and Corollary 1.5 will be given in Sect. 3, and Sect. 4 will be devoted to applying our results to the boundedness of Calderón-Zygmund operators, sparse operators, the Bochner-Riesz operator and intrinsic square functions.
As usual, we shall use the symbol \(A\lesssim B\) to indicate that there exists a universal positive constant C, independent of all important parameters, such that \(A\le C B\). When \(A\lesssim B\) and \(B\lesssim A\), we will write \(A\approx B\).
2 Boundedness on the Associate Space of \(\Lambda ^p_u(w)\)
Given \(u \in A_\infty \), our goal is to see for which conditions on p and the weight w
holds, where \(M'_u\) is defined in (2).
-
(I)
If \(u = 1\) and \(w \in B_p\), then (11) is equivalent to \(w \in B_\infty ^*\) (see (5)).
-
(II)
If \(w = 1\) and \(p > 1\), then (11) is equivalent to \(M_u': L^{\frac{p}{p-1}}(u) \rightarrow L^{\frac{p}{p-1}}(u)\), which in turn remains true whenever \(u \in A_p\).
In order to see the general setting (see Theorem 2.6), it is necessary to establish a few technical findings initially. In an effort to ensure that the paper is self-contained, we include these results within its contents. First, for a nonnegative measurable function h let
Therefore, by carefully monitoring the constants involved in [5, Theorem 4] (or even [40, Theorem 3.3]), the following result holds.
Proposition 2.1
For every \(p > 0\),
with \(\left\Vert Q\right\Vert _{L^p_{\text {dec}}(w) \rightarrow L^p(w)} \le c_{n,p} \left\Vert w\right\Vert _{{B_{\infty }^{*}}}\) and where \(L^p_{\text {dec}}(w)\) is the set of measurable decreasing functions f satisfying \(\left\Vert f\right\Vert _{L^p(w)} < \infty \).
We also need some technical results related with the Fefferman-Stein maximal operator, which is defined, for every \(h \in L^1_{\text {loc}}({\mathbb {R}^n})\), by
where the supremum is taken over all cubes \(Q\subseteq {\mathbb {R}^n}\) containing the point x (see [30, 41]). Hence, by carefully considering the constants involved in [9, Corollary 4.3 (a)], the following result can be established.
Proposition 2.2
There exists a nondecreasing function \(\varphi _q\) on \([1,\infty )\) such that for every \(t > 0\),
And, as a consequence, the next result follows.
Proposition 2.3
Given \(u \in A_q\), \(q > 1\), and \(w \in {B_{\infty }^{*}}\). If \(\lim _{r\rightarrow \infty } f^*_u(r) = 0\), then
where \(\varphi _q\) is a nonnegative nondecreasing function on \([1,\infty )\).
Proof
By means of Proposition 2.2, there exists a nondecreasing function \(\varphi _q\) on \([1,\infty )\) such that for every \(t > 0\),
Therefore, taking into account Proposition 2.1,
\(\square \)
Furthermore, the Fefferman-Stein maximal operator also satisfy the following statement.
Proposition 2.4
[28] For every \(f \in L^1_{\text {loc}}({\mathbb {R}^n})\), there exists a linear operator \(L_f\) such that
Moreover, the adjoint of \(L_f\), \(\widetilde{L_f}\), satisfies that for every \(g \in L^1_{\text {loc}}({\mathbb {R}^n})\),
Additionally, we will utilize the following result related with weights properties.
Proposition 2.5
Given \(u \in A_q\), \(q > 1\), and \(w \in B_p(u)\), \(p > 0\). Let, for \(N \in \mathbb {N}\), \(u_N = \min (u, N)\). Then,
-
(i)
\(u_N \in A_q\) with
$$\begin{aligned} \left\Vert u_N\right\Vert _{A_q} \le 2^{q + 1}\left\Vert u\right\Vert _{A_q}, \end{aligned}$$ -
(ii)
and there exists some constant \(C_{u,w} > 0\) independent of N such that
$$\begin{aligned} \left\Vert M\right\Vert _{\Lambda ^p_{u_N}(w)} \le C_{u,w}. \end{aligned}$$
Proof
First, taking an arbitrary cube \(Q \subseteq {\mathbb {R}^n}\),
from which (i) follows by taking the supremum overall cubes Q.
To see (ii), let \(f \in \Lambda ^p_{u_N}(w)\) and write
Then,
where in the last estimate we are using that \(w \in B_p(u) \subset B_p\). Now observe that for every \(y > 0\),
and
so that \(\left\Vert f_1\right\Vert _{\Lambda ^p_u(w)} \le \left\Vert f\right\Vert _{\Lambda ^p_{u_N}(w)}\) and \(N\left\Vert f_2\right\Vert _{\Lambda ^p(w)} \le \left\Vert f\right\Vert _{\Lambda ^p_{u_N}(w)}\). Therefore, the results follows by taking \(C_{u,w} = C\left( \left\Vert M\right\Vert _{\Lambda ^p_u(w)}+ \left\Vert M\right\Vert _{\Lambda ^p(w)}\right) \). \(\square \)
Finally, with the previous results at hand, we are able to find conditions so that (11) holds.
Theorem 2.6
Given \(u \in A_{\infty }\). For every \(p > 0\),
Proof
Since \(w \in B_p(u) \subseteq B_p\) we have that \((\Lambda ^p_u(w))'\ne \{0\}\) (see [18]) and, by definition of associate space,
where we can assume that the supremum is taken over all nonnegative functions h satisfying that \(\left\Vert h\right\Vert _{\Lambda ^p_u(w)} \le 1\). We will see that, for such a function h,
from which together with (14), the boundedness of (13) will follow.
First, we observe that h can be chosen to be in \(L^1({\mathbb {R}^n})\). Otherwise, we can take \(h_k = \chi _{{\mathbb {B}}(0,k)}h \in L^1({\mathbb {R}^n})\) (with \({\mathbb {B}}(0,k)\) being the ball of center 0 and radius k) and by the monotone convergence theorem,
so together with \(\left\Vert h_k\right\Vert _{\Lambda ^p_u(w)} \le \left\Vert h\right\Vert _{\Lambda ^p_u(w)}\), we would obtain (15).
Hence, take such a nonnegative function h in (14) satisfying \(h \in L^1({\mathbb {R}^n})\). Further, take \(q > 1\) such that \(u \in A_q\) (since \(u \in A_\infty \)). Then, by Proposition 2.4,
and if we are able to see that
by virtue of Proposition 2.3 and estimate (12) we will deduce that
where \(\left\Vert M\right\Vert _{\Lambda ^p_u(w)} < \infty \) since \(w \in B_p(u)\).
Thus, it all reduces to show that (16) holds. Now, if we assume that u is bounded, that is \(u \le C_u\) for some positive constant \(C_u\), then it is just a consequence of that by construction it is known that \(\widetilde{L_{fu}}(h)\) is bounded in \(L^1({\mathbb {R}^n})\) (see [28]) so for every \(t > 0\),
and hence,
Finally, if u is not bounded, taking \(N \in \mathbb {N}\), we just have to observe that \(u_N = \min (u,N)\) is a bounded weight that satisfy (see Proposition 2.5)
and \(\left\Vert h\right\Vert _{\Lambda ^p_{u_N}(w)} \le 1\), so that by the monotone convergence theorem,
\(\square \)
3 Proof of Main Results
Proof of Theorem 1.3
Suppose first that \(p \ge 1\). Since \(w \in B_p(u) \subseteq B_p\), then \(\Lambda ^p(w)\) is a r.i. Banach function space, and so the result follows by means of Theorems 1.2 and 2.6, together with (7).
Now, assume that \(0< p < 1\). Since \(w \in B_p(u)\), there exists some \(0< \varepsilon < p\) such that \(w \in B_{p - \varepsilon }(u)\), and we can define
to be a version of the function resulting from the Rubio de Francia Algorithm [42], where \(M^0 = Id\) is the identity operator and \(M^k = M \underbrace{\circ \cdots \circ }^k M\) is the k-fold composition of M with itself. Then,
-
(1)
\(f \le \left[ R\left( |f|^{\frac{p}{p - \varepsilon }}\right) \right] ^\frac{p - \varepsilon }{p}\),
-
(2)
\(R\left( |f|^{\frac{p}{p - \varepsilon }}\right) \in A_1\) with \(\left\Vert R\left( |f|^{\frac{p}{p - \varepsilon }}\right) \right\Vert _{A_1} \le 2\left\Vert M\right\Vert _{\Lambda _u^{p - \varepsilon }(w)}\),
-
(3)
and
$$\begin{aligned} \left\Vert \left[ R\left( |f|^{\frac{p}{p - \varepsilon }}\right) \right] ^\frac{p - \varepsilon }{p}\right\Vert _{\Lambda ^p_u(w)} \le \left( \frac{2^{p - \varepsilon }}{2^{p - \varepsilon } - 1}\right) ^\frac{1}{p} \left\Vert f\right\Vert _{\Lambda ^p_u(w)}. \end{aligned}$$
Certainly, since \(B_p(u) \subseteq B_p \subseteq B_1\) then \(\Lambda ^1(w)\) is also a r.i. Banach function space and property (3) can be established as follows:
What’s more, by means of Theorem 2.6 we can define for an arbitrary nonnegative function \(h \in (\Lambda _u^1(w))'\),
so that
-
(1)’
\(h \le S h\),
-
(2)’
\((Sh) u \in A_1\) with \(\left\Vert (Sh) u\right\Vert _{A_1} \le 2\left\Vert M'_u\right\Vert _{(\Lambda _u^1(w))'}\),
-
(3)’
and
$$\begin{aligned} \left\Vert Sh\right\Vert _{(\Lambda ^1_u(w))'} \le 2 \left\Vert h\right\Vert _{(\Lambda ^1_u(w))'}. \end{aligned}$$
Now, \(\Lambda ^1(w)\) is a Banach function space so that for any nonnegative function g (see [10, Ch. 1 Theorem 2.7]),
Then, taking such a nonnegative function h in (17), by Fubini,
Let’s work with \(I_1(h)\) and \(I_2(h)\) separately. First, by Fubini again,
and taking the supremum in \(0 \le h \in \left( \Lambda _u^{1}(w)\right) '\) we have using property (3) that
Now let’s work with \(I_2(h)\). Observe that since \(p_0 \ge 1\), then \(\frac{p(1 - p)}{p_0 - p} \le p.\) Hence, if we take
then, \(p_1 \ge p_0\), \(p_1 > 1\) and \(1 - p_1 = (p - \varepsilon )(1 - p_1/p)\). Therefore, by [29, Lemma 2.1]
with
and, due Theorem 1.1, if we let \(g = |Tf|\),
Therefore,
Thus,
and taking the infimum in \(\gamma >0\),
\(\square \)
Proof of Corollary 1.5
Observe that
implies that for every \(y > 0\),
Fix \(y > 0\) and define \(T_yf := y\chi _{\{|T f| > y\}}\). Hence, by means of Theorem 1.3 we obtain that, for every \(p > 0\) and \(u \in A_\infty \),
Therefore, taking the supremum over all \(y > 0\), we obtain the desired result.
4 Examples and Applications
4.1 Calderón-Zygmund Operators and Commutators
A function K(x, y) on \(\mathbb {R}^n \times \mathbb {R}^n \setminus \{(x,x)\,:\, x \in {\mathbb {R}}^n\}\) is called a standard kernel if there exists \(A, \delta > 0\) satisfying the size condition
and the regularity conditions
when \(|x - x'| \le \frac{1}{2} \max (|x - y|, |x' - y|)\) and
when \(|y - y'| \le \frac{1}{2} \max (|x - y|, |x - y'|)\). Now, given a standard Kernel K, \(T_K\) is called a Calderón-Zygmund operator associated with K if it is defined on the class of Schwartz functions \({\mathcal {S}}({\mathbb {R}}^n)\) (that is, the space of functions in \({\mathcal {C}}^\infty _c({\mathbb {R}}^n)\) that decreases rapidly), which admits a bounded extension on \(L^2({\mathbb {R}}^n)\)
and
for \({\mathcal {C}}^\infty _c({\mathbb {R}}^n)\) being the space of infinitely differentiable functions with compact support (see [31, Ch. 4] for more details on these operators). Also, for a locally integrable function b, the commutator of \(T_K\) and b is defined as
For a general Calderón-Zygmund operator \(T_K\), it is well known that it is bounded on \(L^p(R^n)\), for all \(p > 1\) (see [31, Theorem 4.2.2]). Moreover, R.R. Coifman and C. Fefferman [24] proved that \(T_K\) is bounded on the weighted Lebesgue space \(L^p(v)\) for \(v \in A_p\) and \(p > 1\). Indeed, T.P. Hytönen proved in [32] that
For the commutator, R.R. Coifman, R. Rochberg and G. Weiss [25] proved that \([b,T_K]\) is bounded on \(L^p(\mathbb R^n)\), \(p > 1\), if b is a \(\text {BMO}({\mathbb {R}}^n)\) function, where the space of functions of bounded mean oscillation \(\text {BMO}({\mathbb {R}^n})\) is defined by
where the supremum is taken over all cubes \(Q \in {\mathbb {R}^n}\) with sides parallel to the axes and \(b_Q = \frac{1}{|Q|}\int _Q b(x)\,dx\). An analogue of (18) for the commutator \([b, T_K]\) with a \(\text {BMO}({\mathbb {R}}^n)\) function b is due to D. Chung, C. Pereyra and C. Pérez (see [21]), who proved that
Therefore, as a consequence of Theorem 1.3:
Corollary 4.1
Let K be a standard kernel. Given \(u \in A_\infty \) and \(p > 0\),
and, for \(b \in \text {BMO}(\mathbb {R}^n)\),
Remark 4.2
This extends the results on [17, Theorems 1.1 and 1.2] where the authors saw (19) and (20) for \(p > 1\). Moreover, we recall that an example of a Calderón-Zygmund operator is the Hilbert transform (see (6) for its definition).
4.2 Sparse Operators
These operators have become very popular due to their role in the often-called \(A_2\) conjecture consisting in proving, for instance, (18). This result was first obtained by T.P. Hytönen [32] and then simplified by Lerner [34, 35], who proved that the norm of a Calderón-Zygmund operator in a Banach function space \({\mathbb {X}}\) is dominated by the supremum of the norm in \({\mathbb {X}}\) of all the possible sparse operators, and then proved that every sparse operator is bounded in \(L^2(v)\) for every weight \(v \in A_2\) with sharp constant.
Let us give the precise definition. First, a general dyadic grid \(\mathcal {D}\) is a collection of cubes in \({\mathbb {R}^n}\) satisfying the following properties:
-
(i)
For any cube \(Q \in \mathcal {D}\), its side length is \(2^k\) for some \(k \in \mathbb {Z}\).
-
(ii)
Every two cubes in \(\mathcal {D}\) are either disjoint or one is wholly contained in the other.
-
(iii)
If \(\mathcal {D}_k \subseteq \mathcal {D}\) is the subfamily of cubes formed by the cubes of exactly side length \(2^k\), \(k \in \mathbb {Z}\), then \(\mathcal {D}_k\) form a partition of \({\mathbb {R}^n}\).
Hence, let \(0< \eta < 1\) and let \(\mathcal {D}\) be a family of dyadic cubes. A collection of cubes \(\mathcal {S} \subseteq \mathcal {D}\) is called \(\eta \)-sparse if one can choose pairwise disjoint measurable sets \(E_Q \subseteq Q\) with \(|E_Q| \ge \eta |Q|\), where \(Q\in \mathcal {S}\) (see [30, 37] for more details). Hence, given a \(\eta \)-sparse family of cubes \(\mathcal {S} \subseteq \mathcal {D}\) , the sparse operator \(\mathcal {A}_{\mathcal {S}}\) corresponding to the family \(\mathcal {S}\) is defined by
Therefore, as a consequence of Theorem 1.3:
Corollary 4.3
Given \(u \in A_\infty \) and \(p > 0\),
4.3 Bochner-Riesz Operator
Let \(n > 1\) and
be the Fourier transform of a function \(f \in L^2\left( {\mathbb {R}}^n \right) \). For \(\lambda > 0\), the Bochner-Riesz operator is defined as

These operators were first introduced by Bochner in [11] and, since then, they have been widely studied (see [12, 14, 23, 31, 46]).
When \(\lambda > \frac{n - 1}{2}\), it is well known that \(B_\lambda \) is controlled by the Hardy-Littlewood maximal operator M. As a consequence, all weighted inequalities for M are also satisfied by \(B_{\lambda }\). The value \(\lambda = \frac{n - 1}{2}\) is called the critical index. In this case, Shi and Sun [44] proved that \(B_{\frac{n-1}{2}}\) is bounded in \(L^p(v)\) for every \(p > 1\) and \(v \in A_p\). Moreover, in [38, Theorem 1.6] the authors obtained the following quantitative result.
Proposition 4.4
Let \(n > 1\). Then,
with constant less than or equal to \(C\left\Vert v\right\Vert ^2_{A_2}\).
Therefore, as a consequence of Theorem 1.3:
Corollary 4.5
Let \(\lambda \ge \frac{n-1}{2}\). Given \(u \in A_\infty \) and \(p > 0\),
4.4 Intrinsic Square Functions
For \(0 < \alpha \le 1\), let \(\mathcal {C}_{\alpha }\) be the family of functions \(\phi \) supported in \({\mathbb {B}}(0,1)\) (the n-th dimensional open ball of center 0 and radius 1) such that
Then, given \(f \in L^1_{\text {loc}}({\mathbb {R}^n})\), set
where we are using \(\phi _t\) to denote the usual \(L^1({\mathbb {R}^n})\) dilatation of \(\phi \); that is \(\phi _t(x) = t^{-n}\phi \left( \frac{x}{t} \right) \).
The intrinsic square function (of order \(\alpha \)) introduced by M. Wilson in [47] is defined by
with \(\Gamma _{\alpha }(x) = \{ (y,t) : |x - y| < \alpha t \}\). In [36] it was proved that
Therefore, as a consequence of Theorem 1.3:
Corollary 4.6
Let \(0 < \alpha \le 1\). Given \(u \in A_\infty \) and \(p > 0\),
Remark 4.7
In [47] was proved that \(G_\alpha \) dominates pointwise (modulo constant) operators such as the Lusin area integral, the Littlewood-Paley g-function and the continuous square function (see also [16]). Therefore, analogous results as in Corollary 4.6 can be derived for those operators as well.
References
Agora, E.: Boundedness of the Hilbert Transform on Weighted Lorentz Spaces. PhD thesis, Universitat de Barcelona (2012)
Agora, E., Carro, M. J., Soria, J.: Characterization of the weak-type boundedness of the Hilbert transform on weighted Lorentz spaces. J. Fourier Anal. Appl. 19(4), 712–730 (2013). ISSN 1069-5869. https://doi.org/10.1007/s00041-013-9278-1
Agora, E., Carro, M.J., Soria, J.: Boundedness of the Hilbert transform on weighted Lorentz spaces. J. Math. Anal. Appl. 395(1), 218–229 (2012). ISSN 0022-247X. https://doi.org/10.1016/j.jmaa.2012.05.031
Agora, E., Antezana, J., Carro, M.J., Soria, J.: Lorentz-Shimogaki and Boyd theorems for weighted Lorentz spaces. J. Lond. Math. Soc. (2) 89(2), 321–336, (2014). ISSN 0024-6107. https://doi.org/10.1112/jlms/jdt063
Andersen, K.F.: Weighted generalized Hardy inequalities for nonincreasing functions. Can. J. Math. 43(6), 1121–1135 (1991). ISSN 0008-414X. https://doi.org/10.4153/CJM-1991-065-9
Ariño, M.A., Muckenhoupt, B.: Maximal functions on classical Lorentz spaces and Hardy’s inequality with weights for nonincreasing functions. Trans. Am. Math. Soc. 320(2), 727–735 (1990). ISSN 0002-9947. https://doi.org/10.2307/2001699
Baena-Miret, S., Carro, M.J.: Weighted estimates for Bochner-Riesz operators on Lorentz spaces. In: Proceedings of the Royal Society of Edinburgh: Section A Mathematics, pp. 1–25 (2022). https://doi.org/10.1017/prm.2022.10.
Baena-Miret, S., Carro, M.J.: Boundedness of sparse and rough operators on weighted Lorentz spaces. J. Fourier Anal. Appl. 27(3). Paper No. 43, 22 (2021). ISSN 1069-5869. https://doi.org/10.1007/s00041-021-09842-1
Bagby, R.J., Kurtz, D.S.: Covering lemmas and the sharp function. Proc. Am. Math. Soc. 93(2), 291–296 (1985). ISSN 0002-9939. https://doi.org/10.2307/2044764
Bennett, C., Sharpley, R.: Interpolation of operators. Volume 129 of Pure and Applied Mathematics. Academic Press, Inc., Boston, MA (1988). ISBN 0-12-088730-4
Bochner, S.: Summation of multiple Fourier series by spherical means. Trans. Am. Math. Soc. 40(2), 175–207 (1936). ISSN 0002-9947. https://doi.org/10.2307/1989864
Bourgain, J., Guth, L.: Bounds on oscillatory integral operators based on multilinear estimates. Geom. Funct. Anal. 21(6), 1239–1295 (2011). ISSN 1016-443X. https://doi.org/10.1007/s00039-011-0140-9
Boza, S., Soria, J.: Norm estimates for the Hardy operator in terms of \(B_p\) weights. Proc. Am. Math. Soc. 145(6), 2455–2465 (2017). ISSN 0002-9939. https://doi.org/10.1090/proc/13604
Carleson, L., Sjölin, P.: Oscillatory integrals and a multiplier problem for the disc. Studia Math. 44, 287–299 (errata insert) (1972). ISSN 0039-3223. https://doi.org/10.4064/sm-44-3-287-299
Carro, M.J., García del Amo, A., Soria, J.: Weak-type weights and normable Lorentz spaces. Proc. Am. Math. Soc. 124(3), 849–857 (1996). ISSN 0002-9939. https://doi.org/10.1090/S0002-9939-96-03214-5
Carro, M.J., Grafakos, L., Soria, J.: Weighted weak-type \((1, \,1)\) estimates via Rubio de Francia extrapolation. J. Funct. Anal. 269(5), 1203–1233 (2015). ISSN 0022- 1236. https://doi.org/10.1016/j.jfa.2015.06.005
Carro, M.J., Li, H., Soria, J., Sun, Q.: Calderón-Zygmund operators and commutators on weighted Lorentz spaces. J. Geom. Anal. 31(9), 8979–8990 (2021). ISSN 1050-6926. https://doi.org/10.1007/s12220-020-00560-6
Carro, M.J., Raposo, J.A., Soria, J.: Recent developments in the theory of Lorentz spaces and weighted inequalities. Mem. Am. Math. Soc. 187(877), xii+128 (2007). ISSN 0065-9266. https://doi.org/10.1090/memo/0877
Carro, M.J., Soria, J.: Boundedness of some integral operators. Can. J. Math. 45(6), 1155–1166 (1993). ISSN 0008-414X. https://doi.org/10.4153/CJM-1993-064-2
Carro, M.J., Soria, J., Torres, R.H.: Rubio de Francia’s extrapolation theory: estimates for the distribution function. J. Lond. Math. Soc. (2) 85(2), 430–454 (2012). ISSN 0024-6107. https://doi.org/10.1112/jlms/jdr056
Chung, D., Pereyra, C., Pérez, C.: Sharp bounds for general commutators on weighted Lebesgue spaces. Trans. Am. Math. Soc. 364(3), 1163–1177 (2012). ISSN 0002-9947. https://doi.org/10.1090/S0002-9947-2011-05534-0
Chung, H.M., Hunt, R.A., Kurtz, D.S.: The Hardy-Littlewood maximal function on \(L(p,\, q)\) spaces with weights. Indiana Univ. Math. J. 31(1), 109–120 (1982). ISSN 0022-2518. https://doi.org/10.1512/iumj.1982.31.31012
Christ, M.: On almost everywhere convergence of Bochner-Riesz means in higher dimensions. Proc. Am. Math. Soc. 95(1), 16–20 (1985). ISSN 0002-9939. https://doi.org/10.2307/2045566
Coifman, R.R., Fefferman, C.: Weighted norm inequalities for maximal functions and singular integrals. Studia Math. 51, 241–250 (1974). ISSN 0039-3223. https://doi.org/10.4064/sm-51-3-241-250
Coifman, R.R., Rochberg, R., Weiss, G.: Factorization theorems for Hardy spaces in several variables. Ann. Math. 103, 611–635 (1976). https://doi.org/10.2307/1970954
Cruz-Uribe, D.V., Martell, J.M., Pérez, C.: Weights, extrapolation and the theory of Rubio de Francia. Volume 215 of Operator Theory: Advances and Applications. Birkhäuser/Springer Basel AG, Basel (2011). ISBN 978-3-0348-0071-6. https://doi.org/10.1007/978-3-0348-0072-3
Curbera, G.P., García-Cuerva, J., Martell, J.M., Pérez, C.: Extrapolation with weights, rearrangement-invariant function spaces, modular inequalities and applications to singular integrals. Adv. Math. 203(1), 256–318 (2006). ISSN 0001-8708. https://doi.org/10.1016/j.aim.2005.04.009
de la Torre, A.: On the adjoint of the maximal function. In: Function spaces. Differential Operators and Nonlinear Analysis (Paseky nad Jizerou, 1995), pp. 189–194. Prometheus, Prague (1996)
Duoandikoetxea, J.: Extrapolation of weights revisited: new proofs and sharp bounds. J. Funct. Anal. 260(6), 1886–1901 (2011). ISSN 0022-1236. https://doi.org/10.1016/j.jfa.2010.12.015
Duoandikoetxea, J.: Fourier analysis. Volume 29 of Graduate Studies in Mathematics. American Mathematical Society, Providence, RI (2001). Translated and revised from the 1995 Spanish original by David Cruz-Uribe. ISBN 0-8218-2172-5. https://doi.org/10.1090/gsm/029
Grafakos, L.: Modern Fourier analysis. Volume 250 of Graduate Texts in Mathematics, 3rd edn. Springer, New York (2014). ISBN 978-1-4939-1229-2; 978- 1-4939-1230-8
Hytönen, T.P.: The sharp weighted bound for general Calderón-Zygmund operators.Ann. of Math. (2) 175(3), 1473–1506 (2012). ISSN 0003-486X. https://doi.org/10.4007/annals.2012.175.3.9
Kerman, R.A., Torchinsky, A.: Integral inequalities with weights for the Hardy maximal function. Studia Math. 71(3), 277–284, 1981/82. ISSN 0039-3223. https://doi.org/10.4064/sm-71-3-277-284
Lerner, A.K.: On an estimate of Calderón-Zygmund operators by dyadic positive operators. J. Anal. Math. 121, 141–161 (2013). ISSN 0021-7670. https://doi.org/10.1007/s11854-013-0030-1
Lerner, A.K.: A simple proof of the \(A_2\) conjecture. Int. Math. Res. Not. IMRN (2013)(14), 3159–3170 (2012). ISSN 1073-7928. https://doi.org/10.1093/imrn/rns145
Lerner, A.K.: Sharp weighted norm inequalities for Littlewood-Paley operators and singular integrals. Adv. Math. 226(5), 3912–3926 (2011). ISSN 0001-8708. https://doi.org/10.1016/j.aim.2010.11.009
Lerner, A.K., Nazarov, F.: Intuitive dyadic calculus: the basics. Expo. Math. 37(3), 225–265 (2019). ISSN 0723-0869. https://doi.org/10.1016/j.exmath.2018.01.001
Li, K., Pérez, C., Rivera-Ríos, I.P., Roncal, L.: Weighted norm inequalities for rough singular integral operators. J. Geom. Anal. 29(3), 2526–2564 (2019). ISSN 1050-6926. https://doi.org/10.1007/s12220-018-0085-4
Neugebauer, C.J.: Some classical operators on Lorentz space. Forum Math. 4(2), 135–146 (1992). ISSN 0933-7741. https://doi.org/10.1515/form.1992.4.135
Neugebauer, C.J.: Weighted norm inequalities for averaging operators of monotone functions. Publ. Mat. 35(2), 429–447 (1991). ISSN 0214-1493. https://doi.org/10.5565/PUBLMAT/35291/07
Pérez, C.: Singular integrals and weights. In Harmonic and geometric analysis. Adv. Courses Math. CRM Barcelona, pp. 91–143. Birkhäuser/Springer Basel AG, Basel (2015)
Rubio de Francia, J.L.: Factorization theory and \(A_p\) weights. Am. J. Math. 106(3), 533–547 (1984). ISSN 0002-9327. https://doi.org/10.2307/2374284
Sawyer, E.: Boundedness of classical operators on classical Lorentz spaces. Studia Math. 96(2), 145–158 (1990). ISSN 0039-3223. https://doi.org/10.4064/sm-96-2-145-158
Shi, X.L., Sun, Q.Y.: Weighted norm inequalities for Bochner-Riesz operators and singular integral operators. Proc. Am. Math. Soc. 116(3), 665–673 (1992). ISSN 0002-9939. https://doi.org/10.2307/2159432
Soria, J.: Lorentz spaces of weak-type. Quart. J. Math. Oxford Ser. (2) 49(193), 93–103 (1998). ISSN 0033-5606. https://doi.org/10.1093/qjmath/49.193.93
Vargas, A.M.: Weighted weak type \((1,\, 1)\) bounds for rough operators. J. Lond. Math. Soc. (2), 54(2), 297–310 (1996). ISSN 0024-6107. https://doi.org/10.1112/jlms/54.2.297
Wilson, M.: The intrinsic square function. Rev. Mat. Iberoam. 23(3), 771–791 (2007). ISSN 0213-2230. https://doi.org/10.4171/RMI/512
Acknowledgements
The author expresses gratitude to M.J. Carro for their valuable, thorough, and perceptive feedback on a previous draft of the manuscript. Additionally, the author extends their appreciation to the anonymous referee whose helpful and insightful comments have greatly enhanced the final version of this document.
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The author was partially supported by Grant PID2020-113048GB-I00 funded by MCIN/AEI/10.13039/501100011033.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Baena-Miret, S. Weighted Strong-Type Estimates on Classical Lorentz Spaces. J Geom Anal 34, 86 (2024). https://doi.org/10.1007/s12220-023-01519-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12220-023-01519-z
Keywords
- Weighted classical Lorentz spaces
- Muckenhoupt weights
- Extrapolation theory
- Calderón-Zygmund operators
- Sparse operators
- Bochner-Riesz operator



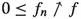 a.e., then
a.e., then 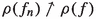 ;
;