A Continuous Transition from $\mathcal {E}$-Sets to R-sets and Beyond

Abstract

The well-known $\mathcal {E}$-set introduced by Hayman in 1960 is a countable collection of Euclidean discs in the complex plane, whose subtending angles at the origin have a finite sum. An important special case of an $\mathcal {E}$-set is known as the R-set, for which the sum of the diameters of the discs is finite. These sets appear in numerous papers in the theories of complex differential and functional equations. A given $\mathcal {E}$-set (hence an R-set) has the property that the set of angles $\theta$ for which the ray $\arg (z)=\theta$ meets infinitely many discs in the $\mathcal {E}$-set has linear measure zero. This paper offers a continuous transition from $\mathcal {E}$-sets to R-sets and then to much thinner sets. In addition to rays, plane curves that originate from the zero distribution theory of exponential polynomials will be considered. It turns out that almost every such curve meets at most finitely many discs in the collection in question. Analogous discussions are provided in the case of the unit disc $\mathbb {D}$, where the curves tend to the boundary $\partial \mathbb {D}$ tangentially or non-tangentially. Finally, these findings will be used for improving well-known estimates for logarithmic derivatives, logarithmic differences and logarithmic q-differences of meromorphic functions, as well as for improving standard results on exceptional sets.

1 Introduction

In 1960,Hayman [8] introduced an $\mathcal {E}$-set as a countable collection of Euclidean discs $D(z_n,r_n)$ not including the origin, for which $z_n\in \mathbb {C}$, $|z_n|\rightarrow \infty$, $r_n>0$, and whose subtending angles at the origin have a finite sum. Any such disc can be seen from the origin at an angle $2\theta _n$, where $\sin \theta _n=r_n/|z_n|$. Thus, by the definition,

$$\begin{aligned} \sum _{n} \frac{r_n}{|z_n|}<\infty . \end{aligned}$$

(1.1)

The circular projection E of such discs onto the interval $[1,\infty )$ has a finite logarithmic measure. This follows from

$$\begin{aligned} \int _E \frac{dx}{x}\le & {} \sum _{n}\int _{|z_n|-r_n}^{|z_n|+r_n}\frac{dx}{x}+O(1) \le \sum _{n} \frac{2r_n}{|z_n|-r_n}+O(1)\\= & {} \sum _{n}\frac{2r_n/|z_n|}{1-r_n/|z_n|}+O(1)<\infty , \end{aligned}$$

because $r_n/|z_n|\rightarrow 0$ as $n\rightarrow \infty$ by (1.1).

A well-known special case of an $\mathcal {E}$-set is an R-set [14, p. 84], which is a collection of Euclidean discs $D(\zeta _n,\rho _n)$, for which $\zeta _n\in \mathbb {C}$, $|\zeta _n|\rightarrow \infty$, $\rho _n>0$, and whose diameters have a finite sum. Thus, the circular projection E of an R-set onto the positive real axis has a finite linear measure: $\int _E dr<\infty$.

If (1.1) holds, then for any $\varepsilon >0$,there exists an $r(\varepsilon )>0$ such that

$$\begin{aligned} \sum _{|z_n|>r(\varepsilon )} \frac{r_n}{|z_n|}<\varepsilon . \end{aligned}$$

This gives rise to the fact that the set of angles $\theta$ for which the ray $\arg (z)=\theta$ meets infinitely many discs of a given $\mathcal {E}$-set has linear measure zero [9, 14]. The same conclusion obviously holds for any R-set.

The next elementary example shows that infinitely many rays can meet infinitely many discs of a given R-set.

Example 1.1

Let $\theta _n=1/n$ for $n\in \mathbb {N}$. For each $n\in \mathbb {N}$ choose any sequence of discs $D(z_{n,k},r_{n,k})$ such that $\arg (z_{n,k})=\theta _n$, $|z_{n,k}|\rightarrow \infty$ as $k\rightarrow \infty$, $r_{n,k}>0$, and that

$$\begin{aligned} \sum _{k=1}^\infty r_{n,k}\le 2^{-n}. \end{aligned}$$

Then the sum of the diameters of the discs in the entire countable collection $\{D(z_{n,k},r_{n,k})\}$ is $\le 2$. Organize the points $z_{n,k}$ in an array such that $z_{n,k}$ lies on the $n\hbox {th}$ row and on the $k\hbox {th}$ column. Then choose those points $z_{n,k}$ that lie in the upper “triangle” of this array using the Cantor diagonal argument. Let $\{w_m\}$ denote the sequence of such points. In the same way,we choose the sequence $\{s_m\}$ from the points $r_{n,k}$. Then the collection $\{D(w_m,s_m)\}$ of discs formed in such a way is an R-set, and each of the rays $\arg (z)=\theta _n$ meets infinitely many discs $D(w_m,s_m)$.

More generally, we will prove that certain plane curves that either drift away or asymptotically approach to a given critical ray $\arg (z)=\phi$ avoid a certain collection of discs. When $\phi =0$, these curves take a simple form

$$\begin{aligned} y=\pm cK(x)\quad \text {or}\quad y=\pm cL(x),\quad c>0, \end{aligned}$$

where K is increasing, continuous, concave and essentially satisfies $1\le K(x)\le x$, while L is decreasing, continuous, convex and $L(x)\rightarrow 0^+$ as $x\rightarrow \infty$. Domains surrounded by curves of either type around finitely many symmetrically separated critical rays are known to contain the majority of zeros of exponential polynomials [10, 11, 17]. This property is, in fact, the motivation for the present paper.

The collections of discs associated with the aforementioned curves depend on the given curve type. In addition, the circular projection E of these discs onto the interval $[1,\infty )$ turns out to satisfy either

$$\begin{aligned} \int _E \frac{dx}{K(x)}<\infty \quad \text {or}\quad \int _E \frac{dx}{L(x)}<\infty . \end{aligned}$$

The former gives a continuous transition from sets of finite logarithmic measure to sets of finite linear measure, while the latter transits the sets of finite linear measure to much thinner sets.

The discussions related to the previous two paragraphs will be carried out in detail in Sect. 2. Analogous situations are then considered in the case of the unit disc $\mathbb {D}$ in Sect. 3. In particular, we will demonstrate that certain collections of Euclidean discs can be avoided with different families of curves that tend to the boundary $\partial \mathbb {D}$ tangentially or non-tangentially. A continuous transition of standard exceptional sets will also be given.

The idea of giving a continuous transition for exceptional sets from finite logarithmic measure to smaller sets is not entirely new neither in the case of $\mathbb {C}$ nor in the case of $\mathbb {D}$. Here, we wish to acknowledge the seminal work by Hinkkanen [12] and Ye [19], in describing the size of the error term in Nevanlinna’s second fundamental theorem.

Gundersen used R-sets and $\mathcal {E}$-sets (but under different terminology) in finding sharp estimates for logarithmic derivatives of meromorphic functions [6]. Applying these findings, Chiang and Feng obtained pointwise estimates for logarithmic differences of meromorphic functions [3], while Wen and Ye estimated logarithmic q-differences of meromorphic functions [18]. Estimates in these directions have had numerous applications in the theories of complex differential equations and complex difference equations. As an application of the continuous transition from sets of finite logarithmic measure to smaller sets, we are able to obtain refined pointwise estimates for logarithmic derivatives, logarithmic differences and logarithmic q-differences of meromorphic functions. The details will be carried out in detail in Sect. 4.

The existing literature contains lemmas to avoid an exceptional set of finite linear measure or of finite logarithmic measure. In Sect. 4, we use the continuous transition method in developing a lemma that allows us to avoid all exceptional sets that are at most of finite logarithmic measure in an optimal way. This approach improves the existing standard approaches.

2 Results for Curves in the Plane

Our construction is based on concavity and convexity of curves, as well as on subadditivity and superadditivity.

2.1 Concave Curves

Let $K:[x_0,\infty )\rightarrow [0,\infty )$ be a strictly increasing, continuous and concave function satisfying $K(x_0)=0$ for some $x_0\ge 0$. Moreover, we suppose that K is subadditive: There exists an $R\ge x_0$ such that

$$\begin{aligned} K(x+y)\le K(x)+K(y),\quad x,y\ge R. \end{aligned}$$

(2.1)

In particular, if $x=y$, then there exists an $R\ge x_0$ such that

$$\begin{aligned} K(2x) \le 2 K(x),\quad x\ge R. \end{aligned}$$

(2.2)

The condition (2.2) is also known as the doubling. For example, the power functions $x\mapsto x^\gamma$, $\gamma \in (0,1]$, and the logarithm $x\mapsto \log (1+x)$ satisfy all of the conditions above for $x_0=0$.

The conditions (2.1) and (2.2) are mainly used for regularity purposes, but they also restrict the growth of K in the following way: If $x\ge R$, then there exists a positive integer N such that $R2^{N-1}\le x\le R2^N$. Thus

$$\begin{aligned} K(x)\le 2 K(x/2)\le 2^2K(x/2^2)\le \cdots \le 2^{N}K(x/2^{N})\le 2^{N} K(R). \end{aligned}$$

This gives rise to

$$\begin{aligned} K(x)= O\left( x\right) , \end{aligned}$$

which is the maximal growth rate for concave functions.

A countable collection of Euclidean discs $D(z_n,r_n)$ for which $z_n\in {\mathbb {C}},|z_n|\rightarrow \infty , r_n>0$, and

$$\begin{aligned} \sum _n \frac{r_n}{K(|z_n|)}<\infty , \end{aligned}$$

(2.3)

is called a K-set. Due to the domain of definition of K, we may restrict to considering those points $z_n$ which satisfy $|z_n|\ge x_0+1$. The case $K(x)=x$ corresponds to the $\mathcal {E}$-set, while the non-permitted case that K is a constant function corresponds to the R-set. Note that (2.3) is not a restriction for the quantity of the points $z_n$.

For any $\phi \in [0,2\pi ]$ and any $c>0$, we denote

$$\begin{aligned} \Lambda (K,\phi ,c)=\left\{ z\in \mathbb {C}: |\Im \left( ze^{-i\phi }\right) |\le cK \left( \Re (ze^{-i\phi })\right) ,\, \Re \left( ze^{-i\phi }\right) \ge x_0\right\} . \end{aligned}$$

In the case $\phi =0$, this domain reduces to

$$\begin{aligned} \Lambda (K,0,c)=\left\{ z\in \mathbb {C}: |y|\le cK(x),\, x\ge x_0\right\} , \end{aligned}$$

and the boundary of it consists of two easily accessible curves of the form

$$\begin{aligned} y=\pm cK(x),\quad x\ge x_0, \end{aligned}$$

(2.4)

around the positive real axis.

We are now ready to state and prove the first of our main results, which contains the $\mathcal {E}$-set as a special case. Indeed, if $K(x)=x$, then the choices $\phi \in \{0,\pi /2,\pi ,3\pi /2\}$ will cover all rays emanating from the origin.

Theorem 2.1

Let U be a K-set, and let $\phi \in [0,2\pi ]$. Then the set $C\subset (0,\infty )$ of values c for which the curve $\partial \Lambda (K,\phi ,c)$ meets infinitely many discs $D(z_n,r_n)$ has measure zero. Moreover, the circular projection E of U onto the interval $[1,\infty )$ satisfies $\int _E\frac{dx}{K(x)}<\infty$.

Proof

By appealing to a rotation, we may suppose that $\phi =0$. Then the boundary $\partial \Lambda (K,\phi ,c)$ consists of the curves in (2.4). It suffices to consider the curves $y=cK(x)$ only, where $c\in I$ and $I\subset (0,\infty )$ is a closed interval. Indeed, we may cover the interval $(0,\infty )$ by countably many closed intervals and by countable additivity of the Lebesgue measure, a countable union of sets of measure zero has measure zero.

Without loss of generality, we may suppose that the points $z_n=x_n+iy_n$ are pairwise distinct and organized by increasing modulus. Due to the global growth restriction $K(x)=O(x)$, we may suppose that $K(x)\le Mx$ for all $x\ge x_0$, where $M>0$ depends only on the set I. Each disc $D_n=D(z_n,r_n)$ can be seen from the origin at an angle $2\theta _n$, where $\sin \theta _n=r_n/|z_n|$. From (2.3), we obtain

$$\begin{aligned} \frac{r_n}{|z_n|}\le \frac{Mr_n}{K(|z_n|)}\rightarrow 0,\quad n\rightarrow \infty . \end{aligned}$$

Thus $\theta _n\rightarrow 0$ as $n\rightarrow \infty$, and we may suppose that the points $z_n$ lie between the lines $y=\pm M x$, and that $x_n\ge x_0\ge 0$ for all n. We denote the associated subsequence of $\{D_n\}$ again by $\{D_n\}$. Since $|z_n|\rightarrow \infty$ as $n\rightarrow \infty$ and $|z_n|\le |x_n|+|y_n|\le (1+M)x_n$ for all n, we see that $x_n\rightarrow \infty$ as $n\rightarrow \infty$.

Let $\varepsilon >0$. By (2.3), we may choose $N(\varepsilon )\in \mathbb {N}$ large enough such that

$$\begin{aligned} \sum _{n=N(\varepsilon )}^\infty \frac{r_n}{K(|z_n|)}<\varepsilon . \end{aligned}$$

(2.5)

Using the monotonicity of K, we obtain

$$\begin{aligned} K(|z_n|)\le K(|x_n|+|y_n|) \le K((1+M)x_n). \end{aligned}$$

If $M\le 1$, then the subadditivity yields

$$\begin{aligned} K(|z_n|)\le K(2x_n)\le 2 K(x_n), \end{aligned}$$

while if $M>1$, then there exists a positive integer N such that $2^{N-1}\le 1+M\le 2^N$, and so

$$\begin{aligned} K(|z_n|)\le 2 K((1+M)x_n/2)\le \cdots \le 2^N K(x_n). \end{aligned}$$

Thus, for all $M>0$, we find that

$$\begin{aligned} \frac{r_n}{K(|z_n|)}\ge \frac{r_n}{2^N K(x_n)}\ge \frac{r_n}{2^N Mx_n}. \end{aligned}$$

(2.6)

Keeping (2.3) in mind, we see that the sequence $\big \{\frac{r_n}{x_n}\big \}$ tends to 0. Hence, by choosing a bigger $N(\varepsilon )$ in (2.5), if necessary, we may suppose that

$$\begin{aligned} x_n-r_n\ge x_n/2> \max \{1,2R\},\quad n\ge N(\varepsilon ). \end{aligned}$$

(2.7)

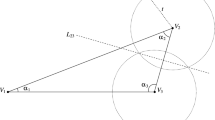
Suppose that a disc $D_n$, $n\ge N(\varepsilon )$, lies tangentially between the increasing curves $y=c_1 K(x)$ and $y=c_2 K(x)$, where $c_1,c_2\in I$ and $c_2>c_1>0$. Let $(a_i,c_i K(a_i))$, $i=1,2$, denote the intersection points, see Fig. 1 below.

Fig. 1

The concave case in the complex plane

Since K(x) is increasing, continuous and concave, the intersection points satisfy

$$\begin{aligned} x_n<a_1<x_n+r_n\quad \text {and}\quad x_n-r_n<a_2<x_n. \end{aligned}$$

(2.8)

Then

$$\begin{aligned} c_2K (x_n-r_n)\le & {} c_2K (a_2)\le y_n+r_n,\\ c_1 K (x_n+r_n)\ge & {} c_1 K (a_1)\ge y_n-r_n, \end{aligned}$$

which give rise to

$$\begin{aligned} c_2-c_1\le \frac{y_n+r_n}{K (x_n-r_n)}-\frac{y_n-r_n}{K (x_n+r_n)}. \end{aligned}$$

(2.9)

Define $c_0=y_n/K (x_n)$. Then the curve $y=c_0K (x)$ travels through the centre point $z_n$ of $D_n$ and $c_1<c_0<c_2$. Note that $c_0\in I$ is uniformly bounded from above and from below.

Set $s_n=\max \{r_n,x_0\}$ and recall that $K(x_0)=0$. From (2.1), (2.7) and the monotonicity of K, we obtain for all $n\ge N(\varepsilon )$ that

$$\begin{aligned} c_0K(x_n+r_n)\le & {} c_0K(x_n+s_n)\le c_0K(x_n)+c_0K(s_n)\le y_n+c_0Mr_n,\\ y_n= & {} c_0K(x_n)\le c_0K(x_n-r_n+s_n)\le c_0K(x_n-r_n)+c_0Mr_n. \end{aligned}$$

Applying these estimates in (2.9) and using (2.2) and (2.7) gives us

$$\begin{aligned} \begin{aligned} c_2-c_1&\le \frac{y_n-c_0Mr_n+(c_0M+1)r_n}{K (x_n-r_n)}-\frac{y_n+c_0Mr_n-(c_0M+1)r_n}{K (x_n+r_n)}\\&\le c_0-c_0+\frac{2(1+c_0M)r_n}{K (x_n-r_n)}\\&\le \frac{2(1+c_0M)r_n}{K (x_n/2)}\le \frac{4(1+c_0M)r_n}{K (x_n)},\quad n\ge N(\varepsilon ). \end{aligned} \end{aligned}$$

(2.10)

Let $\varepsilon >0$, let $N(\varepsilon )\in \mathbb {N}$ be as in (2.7), and let $J_\varepsilon \subset I$ denote the set of values c for which $y=cK(x)$ meets at least one disc $D_n$ with $n\ge N(\varepsilon )$. Then (2.5), (2.6) and (2.10) show that

$$\begin{aligned} \int _{J_\varepsilon }dx\le \sum _{n=N(\varepsilon )}^\infty \frac{4(1+c_0M)r_n}{K (x_n)} \le \sum _{n=N(\varepsilon )}^\infty \frac{2^{N+2}(1+c_0M)r_n}{K (|z_n|)}<2^{N+2}(1+c_0M)\varepsilon . \end{aligned}$$

Here the positive integer N depends only on M, which in turn depends only on the closed interval $I\subset (0,\infty )$. Since $C\cap I$ is clearly contained in $J_\varepsilon$ for every $\varepsilon >0$, it follows that $C\cap I$ has measure zero. The remaining assertion follows from

$$\begin{aligned} \int _E\frac{dx}{K(x)}\le & {} \sum _n\int _{|z_n|-r_n}^{|z_n|+r_n}\frac{dx}{K (x)}+O(1)\le \sum _n \frac{2r_n}{K (|z_n|-r_n)}+O(1)\\\le & {} \sum _n \frac{2r_n}{K (|z_n|/2)}+O(1)\le \sum _n \frac{4 r_n}{K(|z_n|)}+O(1)<\infty , \end{aligned}$$

where we have used (2.2) and (2.7). $\square$

Remark

The closed interval $I\subset (0,\infty )$ in the previous proof is required in the extremal case

$$\begin{aligned} \liminf _{x\rightarrow \infty }\frac{K(x)}{x}>0. \end{aligned}$$

Indeed, we will prove below that

$$\begin{aligned} \liminf _{x\rightarrow \infty }\frac{K(x)}{x}=0 \end{aligned}$$

(2.11)

implies

$$\begin{aligned} \lim _{x\rightarrow \infty }\frac{K(x)}{x}=0. \end{aligned}$$

(2.12)

If (2.12) is valid, then we may suppose that all points $z_n$ lie between the lines $y=\pm x$, in which case we may choose $M=1=N$ in the proof.

Suppose that (2.11) holds, and suppose on the contrary to the assertion in (2.12) that there exists a strictly increasing sequence $\{r_n\}$ of positive real numbers tending to infinity and a constant $\delta >0$ such that $K(r_n)\ge \delta r_n$ for all n. For any fixed $n\in \mathbb {N}$, choose $t\in [r_n,r_{n+1}]$. Then $t=(1-s)r_n+sr_{n+1}$ for some $s\in [0,1]$. Using concavity and the assumption,

$$\begin{aligned} K(t)= & {} K((1-s)r_n+sr_{n+1})\ge (1-s)K(r_n)+sK(r_{n+1})\\\ge & {} (1-s)\delta r_n+s\delta r_{n+1}=\delta t. \end{aligned}$$

Since n was chosen arbitrarily, we obtain $K(t)\ge \delta t$ for all $t\ge r_1$. But this contradicts with the assumption (2.11) and hence proves (2.12).

Remark

Suppose that $K:(x_0,\infty )\rightarrow (0,\infty )$ is an unbounded, strictly increasing, differentiable and concave function satisfying

$$\begin{aligned} \lim _{c\rightarrow 1^-}\liminf _{x\rightarrow \infty }\frac{K(cx)}{K(x)}=1. \end{aligned}$$

The power functions $x\mapsto x^\gamma$, $\gamma \in (0,1]$ and the logarithm $x\mapsto \log (1+x)$ are examples of such functions. Under the conditions above, we may avoid the assumption on subadditivity, and the estimate in (2.10) can be obtained differently. To see this, recall that $r_n/x_n\rightarrow 0^+$ as $n\rightarrow \infty$ and then use [13, Lemma 1] to obtain

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{K(x_n)}{K(x_n\pm r_n)} =\lim _{n\rightarrow \infty }\frac{K(x_n)}{K(x_n(1\pm r_n/x_n))}=1. \end{aligned}$$

Now, from (2.9),

$$\begin{aligned} c_2-c_1\le & {} \frac{2r_n}{K(x_n-r_n)}+y_n\left( \frac{1}{K(x_n-r_n)} -\frac{1}{K(x_n+r_n)}\right) \cdot \frac{K(x_n)^2}{K(x_n)^2}\\= & {} \frac{K(x_n)}{K(x_n-r_n)}\cdot \frac{2r_n}{K(x_n)} +c_0\cdot \frac{K(x_n+r_n)-K(x_n-r_n)}{K(x_n+r_n)K(x_n-r_n)} \cdot \frac{K(x_n)^2}{K(x_n)}\\\sim & {} \frac{2r_n}{K(x_n)}+2c_0\cdot \frac{K(x_n+r_n)-K(x_n-r_n)}{2r_n} \cdot \frac{r_n}{K(x_n)}. \end{aligned}$$

The derivative $K'$ of the concave function K is a decreasing function, and hence $K'(x)\le M$ for all $x>x_0$. By the Mean value theorem, there exists a point $t_n\in (x_n-r_n,x_n+r_n)$ such that

$$\begin{aligned} K(x_n+r_n)-K(x_n-r_n)=2r_nK'(t_n)\le 2r_nM. \end{aligned}$$

Thus we obtain the following alternative for (2.10):

$$\begin{aligned} c_2-c_1 \lesssim (1+c_0M)\cdot \frac{r_n}{K(x_n)}. \end{aligned}$$

This alternative approach may seem unnecessary at this point. However, in the case of the unit disc in Sect. 3 below, a reasoning based on the derivative analogously as in this remark seems to be the most natural choice.

2.2 Convex Curves

Let $L:(x_0,\infty )\rightarrow (0,\infty )$ be a strictly decreasing, continuous and convex function such that $L(x)\rightarrow 0^+$ as $x\rightarrow \infty$. Moreover, we suppose that L satisfies the following reversed doubling condition: There exist constants $\beta \in (0,1)$ and $R> x_0$ such that $L(2x) \ge \beta L(x)$ for all $x\ge R$. For example, the functions $x\mapsto x^{-p}$ satisfy all of the conditions above for all $p>0$.

Remark

Keeping (2.1) in mind, one may wonder if the reversed doubling condition for L could be replaced with superadditivity, meaning that there exists an $R>\max \{x_0,1\}$ such that

$$\begin{aligned} L(x+y)\ge L(x)+L(y),\quad x,y\ge R. \end{aligned}$$

(2.13)

In particular, $L(2x)\ge 2L(x)$ for $x\ge R$. However, such a function cannot satisfy the requirement $L(x)\rightarrow 0^+$ as $x\rightarrow \infty$. Indeed, if $x\ge 2R$, then there exists a positive integer N such that $R2^N\le x\le R2^{N+1}$, and consequently

$$\begin{aligned} L(x)\ge 2L(x/2)\ge \cdots \ge 2^NL(x/2^N)\ge 2^NL(2R)\ge \frac{x}{2R}L(2R). \end{aligned}$$

Superadditivity (2.13) will be needed for rapidly increasing convex curves in Sect. 2.4 below.

The reversed doubling condition induces a restriction on how fast L(x) can tend to zero. Indeed, the reasoning above yields

$$\begin{aligned} L(x)\ge O\left( x^\frac{\log \beta }{\log 2}\right) , \quad \beta \in (0,1). \end{aligned}$$

So, the functions $x\mapsto x^{-p}$, $p>0$, are extremal in this sense.

A countable collection of Euclidean discs $D(z_n,r_n)$ for which $z_n\in {\mathbb {C}},|z_n|\rightarrow \infty , r_n>0$, and

$$\begin{aligned} \sum _n \frac{r_n}{L(|z_n|)}<\infty , \end{aligned}$$

(2.14)

is called an L-set. Due to the domain of definition of L, we may restrict to considering those points $z_n$ which satisfy $|z_n|\ge x_0+1$. The non-permitted case that L is a constant function corresponds to the R-set. In the extremal case $L(x)=x^{-p}$, $p>0$, the radii $r_n$ must tend to zero very fast, which in turn leads to a very thin circular projection set on the interval $[1,\infty )$.

For any $\phi \in [0,2\pi ]$ and any $c>0$, we denote

$$\begin{aligned} \Lambda (L,\phi ,c)=\left\{ z\in \mathbb {C}: |\Im \left( ze^{-i\phi }\right) |\le cL \left( \Re (ze^{-i\phi })\right) ,\, \Re \left( ze^{-i\phi }\right) \ge R\right\} . \end{aligned}$$

In the case $\phi =0$, this domain reduces to

$$\begin{aligned} \Lambda (L,0,c)=\left\{ z\in \mathbb {C}: |y|\le cL(x),\, x\ge R\right\} , \end{aligned}$$

and the boundary of it consists of two easily accessible curves of the form

$$\begin{aligned} y=\pm cL(x),\quad x\ge R, \end{aligned}$$

(2.15)

around the positive real axis.

Theorem 2.2

Let U be an L-set, and let $\phi \in [0,2\pi ]$. Then the set $C\subset (0,\infty )$ of values c for which the boundary $\partial \Lambda (L,\phi ,c)$ meets infinitely many discs $D(z_n,r_n)$ has measure zero. Moreover, the circular projection E of U onto the interval $[1,\infty )$ satisfies $\int _E\frac{dx}{L(x)}<\infty$.

Proof

We follow the same method used in proving Theorem 2.1. We may suppose that $\phi =0$, in which case the boundary curves are of the form (2.15). We may also suppose that the points $z_n=x_n+iy_n$ are pairwise distinct and organized by increasing modulus. Since $L(x)\rightarrow 0$ as $x\rightarrow \infty$ and $r_n\rightarrow 0$ as $n\rightarrow \infty$, we may suppose that the points $z_n$ lie between the horizontal lines $y=\pm M$ for some $M>0$, and that $x_n>0$. Since $|z_n|\rightarrow \infty$, $|y_n|\le M$, and $|z_n|\le |x_n|+|y_n|$, we see that $x_n\rightarrow \infty$ as $n\rightarrow \infty$. In addition, we may directly consider different values of $c\in (0,\infty )$ without having to restrict to one closed subinterval of $(0,\infty )$ at a time.

Since $r_n\rightarrow 0$ and $x_n\rightarrow \infty$, the inequalities in (2.7) require no further convincing in this case. Let $\varepsilon >0$, and choose $N(\varepsilon )\in \mathbb {N}$ large enough satisfying (2.7) and

$$\begin{aligned} \sum _{n=N(\varepsilon )}^\infty \frac{r_n}{L(|z_n|)}<\varepsilon . \end{aligned}$$

(2.16)

This is an analogue of (2.5).

Suppose that a disc $D_n=D_n(z_n,r_n)$ lies tangentially between the decreasing curves $y=c_1 L(x)$ and $y=c_2 L(x)$, where $c_2>c_1>0$. Let $(a_i,c_i L(a_i))$, $i=1,2$, denote the intersection points, see Fig. 2 below.

Fig. 2

The convex case in the complex plane

Since L(x) is decreasing, continuous and convex, the intersection points satisfy

$$\begin{aligned} x_n-r_n<a_1<x_n\quad \text {and}\quad x_n<a_2<x_n+r_n. \end{aligned}$$

Then

$$\begin{aligned} c_2L (x_n+r_n)\le & {} c_2L (a_2)\le y_n+r_n,\\ c_1 L (x_n-r_n)\ge & {} c_1 L (a_1)\ge y_n-r_n, \end{aligned}$$

which gives rise to

$$\begin{aligned} c_2-c_1\le \frac{y_n+r_n}{L(x_n+r_n)}-\frac{y_n-r_n}{L(x_n-r_n)}. \end{aligned}$$

(2.17)

Define $c_0=y_n/L (x_n)$. Then the curve $y=c_0 L(x)$ travels through the centre point $z_n$ of $D_n$ and $c_1<c_0<c_2$. Suppose that

$$\begin{aligned} c_0L(x_n+r_n)<y_n-r_n \end{aligned}$$

(2.18)

for infinitely many indices n, and aim for a contradiction. Denote the subsequences of $\{x_n\}, \{r_n\}, \{y_n\}$ for which (2.18) holds again by $\{x_n\}, \{r_n\}, \{y_n\}$. From (2.18), the average rate of change of the function $c_0L(x)$ on the interval $[x_n,x_n+r_n]$ is

$$\begin{aligned} \frac{c_0L(x_n+r_n)-c_0L(x_n)}{(x_n+r_n)-x_n}< \frac{y_n-r_n-y_n}{r_n}=-1. \end{aligned}$$

(2.19)

By the properties of L(x), the average rate of change of $c_0L(x)$ on the intervals $[x_n,x_n+r_n]$ should tend to zero as $n\rightarrow \infty$, which contradicts with (2.19). In the same way, we see that $y_n+r_n< c_0L(x_n-r_n)$ holds for at most finitely many indices n. Hence we have proved that

$$\begin{aligned} y_n-r_n\le c_0L(x_n+r_n)\le c_0L(x_n-r_n)\le y_n+r_n,\quad n\ge N(\varepsilon ), \end{aligned}$$

by choosing a slightly larger $N(\varepsilon )\in \mathbb {N}$ than in (2.16), if necessary

$$\begin{aligned} \begin{aligned} c_2-c_1&\le \frac{y_n-r_n+2r_n}{L(x_n+r_n)}-\frac{y_n+r_n-2r_n}{L(x_n-r_n)}\\&\le c_0-c_0+\frac{4r_n}{L(x_n+r_n)}\le \frac{4r_n}{L(2x_n)}\\&\le \frac{4r_n}{\beta L(x_n)}\le \frac{4r_n}{\beta L(|z_n|)},\quad n\ge N(\varepsilon ). \end{aligned} \end{aligned}$$

(2.20)

Let $C_\varepsilon \subset (0,\infty )$ denote the set of values c for which the curve $y=cL(x)$ meets at least one of the discs $D_n$, where $n\ge N(\varepsilon )$. By (2.16) and (2.20),

$$\begin{aligned} \int _{C_\varepsilon }dx\le \sum _{n=N(\varepsilon )}^\infty \frac{4r_n}{\beta L(|z_n|)} <\frac{4}{\beta }\varepsilon . \end{aligned}$$

Since C is a subset of $C_\varepsilon$ for any $\varepsilon >0$, we conclude that $\int _Cdx=0$. The remaining assertion follows from

$$\begin{aligned} \int _E\frac{dx}{L(x)}\le & {} \sum _n\int _{|z_n|-r_n}^{|z_n|+r_n}\frac{dx}{L(x)}+O(1)\le \sum _n \frac{2r_n}{L(|z_n|+r_n)}+O(1)\\\le & {} \sum _n \frac{2r_n}{L(2|z_n|)}+O(1)\le \sum _n \frac{2r_n}{\beta L(|z_n|)}+O(1)<\infty , \end{aligned}$$

and the proof is complete. $\square$

Remark

A result similar to Theorem 2.2 but for curves in polar coordinates has been obtained in [11, Lemma 7.1].

2.3 The Constant Case

In order to avoid unnecessary complications in the geometric reasoning, we have intentionally assumed strict monotonicity on K(x) and on L(x). However, either proof goes through if these functions are constant functions. The curves in this situation are just half-lines, and the associated collection of discs constitutes an R-set. This gives rise to the following corollary.

Corollary 2.3

Let $k\in \mathbb {R}$. Then the set $C\subset \mathbb {R}$ of values c for which the line $y=kx+c$ or the line $x=c$ meets infinitely many discs of a given R-set has measure zero.

Fig. 3

The constant case in the complex plane

The following two examples illustrate the sharpness of Corollary 2.3 in regard to the size of the set C.

Example 2.4

We construct an R-set U by modifying the construction for the classical Cantor set $\mathcal {C}$. For brevity, denote $I(x,r)=(x-r,x+r)$. Choose any two open discs in $\mathbb {C}$ whose vertical projections on $\mathbb {R}$ are I(1/6, 2/6) and I(5/6, 2/6) and include them in the collection U. Next, choose any four open discs in $\mathbb {C}$ whose vertical projections on $\mathbb {R}$ are

$$\begin{aligned} I(1/18,2/18),\ I(5/18,2/18),\ I(13/18,2/18),\ I(17/18,2/18), \end{aligned}$$

and include them in U. We continue in this way so that on the kth step,we have $2^k$ open discs whose vertical projections on $\mathbb {R}$ are open intervals of length $2/3^k$ and with the same centre points as the closed intervals that are used in constructing the Cantor set $\mathcal {C}$. The collection U contains all such discs as k tends to infinity, and hence their vertical projections form an open cover for $\mathcal {C}$. The sum of the diameters of the discs in U is

$$\begin{aligned} \sum _{k=1}^\infty 2^k\cdot \frac{2}{3^k}=\frac{4}{3}\sum _{k=0}^\infty \left( \frac{2}{3}\right) ^k=4. \end{aligned}$$

Further, we require that the discs in the collection U are chosen in such a way that their centres $z_n$ satisfy $|z_n|\rightarrow \infty$ as $n\rightarrow \infty$. Hence U is an R-set. Now, if $c\in \mathcal {C}$, then the vertical line $x=c$ meets infinitely many open discs in U. Finally, it is well known that $\mathcal {C}$ is uncountable and has measure zero.

Note that this construction is independent on the density of the centre points $z_n$ of the discs in U because the imaginary parts of $z_n$’s can be chosen arbitrarily, for as long as $|z_n|\rightarrow \infty$ as $n\rightarrow \infty$. Consequently, the exponent of convergence of the sequence $\{z_n\}$ can be arbitrary or even infinite.

Example 2.5

Let $c_n=1/n$ for $n\in \mathbb {N}$. For each $n\in \mathbb {N}$, choose any sequence of discs $D(z_{n,k},r_{n,k})$ such that $\Im (z_{n,k})=c_n$, $|z_{n,k}|\rightarrow \infty$ as $k\rightarrow \infty$, $r_{n,k}>0$, and that

$$\begin{aligned} \sum _{k=1}^\infty r_{n,k}\le 2^{-n}. \end{aligned}$$

Then each vertical line $y=c_n$ meets infinitely many discs, and the sum of the diameters of the discs in the entire collection $\{D(z_{n,k},r_{n,k})\}$ is $\le 2$. Using the Cantor diagonal argument as in Example 1.1, the discs $D(z_{n,k},r_{n,k})$ can be used to form an R-set such that each line in a set of countably many vertical lines meets infinitely many such discs.

2.4 Rapidly Increasing Convex Curves

Let $\mathcal {L}:[0,\infty )\rightarrow [x_0,\infty )$ be a strictly increasing, bijective, continuous and convex function satisfying $\mathcal {L}(0)=x_0$ and

$$\begin{aligned} \lim _{x\rightarrow \infty }\frac{x}{\mathcal {L}(x)}=0. \end{aligned}$$

(2.21)

In addition, we assume that $\mathcal {L}$ satisfies the superadditivity in (2.13), which is known to induce $\mathcal {L}(x)\ge O(x)$. In view of (2.21) and convexity, this lower bound for growth is not an additional restriction. For example, the functions $x\mapsto x^p$, $p>1$, satisfy all of the properties above.

It is clear that $\mathcal {L}$ has a strictly increasing and continuous inverse $\mathcal {L}^{-1}:[x_0,\infty )\rightarrow [0,\infty )$ satisfying $\mathcal {L}^{-1}(x_0)=0$. A countable collection of Euclidean discs $D(z_n,r_n)$ for which $z_n\in {\mathbb {C}},|z_n|\rightarrow \infty , r_n>0$, and

$$\begin{aligned} \sum _{n=1}^\infty \frac{r_n}{\mathcal {L}^{-1}(|z_n|)}<\infty \end{aligned}$$

(2.22)

is called an $\mathcal {L}$-set. Due to the domain of definition of $\mathcal {L}^{-1}$, we may restrict to considering those points $z_n$ for which $|z_n|\ge |x_0|+1$.

Let $R>x_0$ be the constant in (2.13). For any $\phi \in [0,2\pi ]$ and any $c>0$, we denote

$$\begin{aligned} \Lambda (\mathcal {L},\phi ,c)=\left\{ z\in \mathbb {C}: |\Im \left( ze^{-i\phi }\right) |\ge \mathcal {L}\left( c\Re (ze^{-i\phi })\right) ,\, \Re \left( ze^{-i\phi }\right) \ge R\right\} . \end{aligned}$$

In the case $\phi =0$, this domain reduces to

$$\begin{aligned} \Lambda (\mathcal {L},0,c)=\left\{ z=x+iy\in \mathbb {C}: |y|\ge \mathcal {L}(cx),\, x\ge R\right\} . \end{aligned}$$

The relevant part of the boundary consists of two easily accessible curves of the form

$$\begin{aligned} y=\pm \mathcal {L}(cx),\quad x\ge R, \end{aligned}$$

(2.23)

around the positive real axis.

Theorem 2.6

Let U be an $\mathcal {L}$-set, and let $\phi \in [0,2\pi ]$. Then the set $C\subset (0,\infty )$ of values c for which the relevant part of the boundary $\partial \Lambda (\mathcal {L},\phi ,c)$ meets infinitely many discs $D(z_n,r_n)$ has measure zero. Moreover, the circular projection E of U onto the interval $[1,\infty )$ satisfies $\int _E\frac{dx}{\mathcal {L}^{-1}(x)}<\infty$.

Proof

We may suppose that $\phi =0$, in which case the boundary curves are of the form (2.23). It suffices to consider the curves $y=\mathcal {L}(cx)$ only. From [15] and (2.21), it follows that $\mathcal {L}^{-1}$ is a strictly increasing, continuous, concave and subadditive function satisfying

$$\begin{aligned} \lim _{x\rightarrow \infty }\frac{\mathcal {L}^{-1}(x)}{x}=0. \end{aligned}$$

Taking $K=\mathcal {L}^{-1}$ in Theorem 2.1, we find that $\int _E\frac{dx}{\mathcal {L}^{-1}(x)}<\infty$ and that the set $C\subset (0,\infty )$ of values c for which the boundary $\partial \Lambda (K,0,c)$ for $K=\mathcal {L}^{-1}$ meets infinitely many discs $D(z_n,r_n)$ has measure zero. The curves $y=c\mathcal {L}(x)$ and $y=\mathcal {L}^{-1}(x/c)$ are symmetric with respect to the line $y=x$. Hence the boundaries $\partial \Lambda (\mathcal {L}^{-1},0,c)$ and $\partial \Lambda (\mathcal {L},0,1/c)$ are reflected to one another with respect to the line $y=x$. Finally, $0<c<\infty$ if and only if $0<1/c<\infty$, and hence the remaining assertion in the case $\phi =0$ follows. $\square$

3 Results for Curves in the Unit Disc

The continuous transition method presented in Sect. 2 can be formulated in the unit disc $\mathbb {D}$ as well. Just as above, the theory divides into concave and convex situations. We begin with some preparations.

3.1 Preparations

A typical size for an exceptional set $E\subset [0,1)$ in value distribution theory is finite logarithmic measure in the sense of $\int _{E}\frac{dx}{1-x}<\infty$. In particular, if a sequence of Euclidean discs $\Delta (z_n,r_n)\subset \mathbb {D}$ satisfies $|z_n|\rightarrow 1^-$ and

$$\begin{aligned} \sum _n\frac{r_n}{1-|z_n|}<\infty , \end{aligned}$$

(3.1)

then $\frac{r_n}{1-|z_n|}\rightarrow 0$ as $n\rightarrow \infty$, and the circular projection set $E\subset [0,1)$ satisfies

$$\begin{aligned} \int _{E}\frac{dx}{1-x}\le & {} \sum _n\int _{|z_n|-r_n}^{|z_n|+r_n}\frac{dx}{1-x}+O(1)\\\le & {} \sum _n \frac{2r_n}{(1-|z_n|)\left( 1-\frac{r_n}{1-|z_n|}\right) }+O(1)<\infty . \end{aligned}$$

Thus the condition (3.1) is also natural in the value distribution theory.

Recall that a Stolz angle with vertex at $\zeta \in \partial \mathbb {D}$ is a set

$$\begin{aligned} S(\zeta ,c)=\left\{ z\in \mathbb {D}: |1-{\overline{\zeta }}z|\le c(1-|z|)\right\} , \end{aligned}$$

where $c>1$ is some constant [5]. For $c=1$,this set reduces to the line segment $[0,\zeta )$, while for $c<1$,the set is empty. If $z\in S(\zeta ,c)$, then

$$\begin{aligned} 1-|z|\le |1-{\overline{\zeta }}z|\le c(1-|z|). \end{aligned}$$

Hence, if the points $z_n$ are in a Stolz angle with vertex at $z=1$, then the quantities $1-|z_n|$ and $|1-z_n|$ are uniformly comparable. The condition (3.1) then implies that the subtending angles at the point $z=1$ have a finite sum. Thus, for any $\varepsilon >0$ there exists a positive integer $N(\varepsilon )$ such that

$$\begin{aligned} \sum _{n\ge N(\varepsilon )}\frac{r_n}{|1-z_n|}<\varepsilon . \end{aligned}$$

This implies that the set of points $c\in \mathbb {R}$ for which the lines $y=c(x-1)$ (through the point $z=1$) meets infinitely many discs $\Delta (z_n,r_n)$ has linear measure zero. From this point of view, such a collection of discs $\Delta (z_n,r_n)$ is a unit disc analogue for the $\mathcal {E}$-set.

Analogous to R-sets, typical situations when the diameters of a given collection of discs in $\mathbb {D}$ have a finite sum arise, for example, when $\{z_n\}$ is a Blaschke sequence ($r_n=1-|z_n|$) or when $\{z_n\}$ has exponent of convergence $\lambda \ge 0$ ($r_n=(1-|z_n|)^{1+\lambda +\varepsilon }$). These cases are very well known.

As for the curves tending to a boundary point $\zeta \in \partial \mathbb {D}$, the boundaries of Stolz angles are a good starting point. In addition to Stolz angles, we take as our basic model the domains

$$\begin{aligned} R(\zeta ,\gamma ,c)=\left\{ z\in \mathbb {D}: |1-{\overline{\zeta }}z|\le c(1-|z|)^\gamma \right\} , \end{aligned}$$

(3.2)

where $\gamma >0$ and $c>0$ are some constants [1, 5]. The special case $\gamma =1/2$ corresponds to a horodisc at $\zeta$ [5]. In general, $R(\zeta ,\gamma ,c)$ is a tangential domain for $\gamma \in (0,1)$ and a represents a zero angle at $\zeta$ for $\gamma >1$. For example, the angular domain between the curves $y=\pm (1-x)^p$, $p>1$, is a zero angle at $z=1$ because both curves have horizontal tangents at the point (1, 0). If $\zeta =1$, the boundary $\partial R(1,\gamma ,c)$ in the upper half-disc is concave for $0<\gamma <1$ and convex for $\gamma >1$. The extremal case $\gamma =1$ in between these two cases corresponds to the case of lines $y=kx+c$ and $x=c$ in Sect. 2.3.

In what follows, we will generalize the domains in (3.2) by

$$\begin{aligned} \Gamma (k,\zeta ,c)=\left\{ z: |1-{\overline{\zeta }}z|\le ck(1-|z|)\right\} , \end{aligned}$$

where $k:(0,1)\rightarrow (0,1)$ is a strictly increasing function satisfying

$$\begin{aligned} \lim _{x\rightarrow 1^-}\frac{k(1-x)}{k((1-x)(1\pm \delta (x)))}=1 \end{aligned}$$

(3.3)

for every function $\delta :(0,1)\rightarrow (0,1)$ such that $\delta (x)\rightarrow 0$ as $x\rightarrow 1^-$. For example, the functions $k(x)=x^\gamma$ with $\gamma >0$ satisfy (3.3). The remainder of Sect. 3.1 is devoted to classifying functions k satisfying (3.3) in terms of known functions.

To begin with, we say that a function f is regularly varying at the origin if it is real-valued, positive and measurable on $(0,x_0)$, for some $x_0\in (0,\infty ]$, and if there exists a constant $\rho \in \mathbb {R}$ such that for each $\lambda >0$,

$$\begin{aligned} \lim _{x\rightarrow 0^+}\frac{f(\lambda x)}{f(x)}=\lambda ^\rho . \end{aligned}$$

(3.4)

The constant $\rho$ is called the index of regular variation. If $\rho =0$, the function f is called slowly varying at the origin. Functions that are regularly varying at infinity are discussed in [16].

It is easy to see that the function $f_1(x)=x^\gamma$ with $\gamma >0$ is regularly varying of index $\rho =\gamma$ at the origin, while $f_2(x)=\exp (-1/x)$ is not regularly varying at the origin. Thus a function that is regularly varying at the origin may be convex ($\gamma \ge 1$) or concave ($0<\gamma \le 1$). Note that the function $f_3(x)=x^\gamma$ with $\gamma <0$ is regularly varying of negative index $\rho =-\gamma$ at the origin. This gives rise to the following lemma.

Lemma 3.1

Suppose that $f:(0,x_0)\rightarrow (0,\infty )$ is strictly monotonic, continuous and a regularly varying function of index $\rho \ne 0$ at the origin. Then precisely one of the following two cases occurs.

• (1) $\rho >0$, f is strictly increasing and $f(x)\rightarrow 0^+$ as $x\rightarrow 0^+$.

• (2) $\rho <0$, f is strictly decreasing and $f(x)\rightarrow +\infty$ as $x\rightarrow 0^+$.

Proof

Let $\lambda \in (0,1)$, and choose $\varepsilon >0$ small enough such that $\lambda ^\rho +\varepsilon <1$ if $\rho >0$ or $\lambda ^\rho -\varepsilon >1$ if $\rho <0$. Then, by regular variation, there exists a constant $\delta >0$ such that

$$\begin{aligned} \lambda ^\rho -\varepsilon< \frac{f(\lambda x)}{f(x)}< \lambda ^\rho +\varepsilon ,\quad 0<x<\delta . \end{aligned}$$

(3.5)

Suppose next that there exist constants $C_1,C_2,\delta _0>0$ such that

$$\begin{aligned} C_1\le f(x)\le C_2,\quad 0<x<\delta _0, \end{aligned}$$

and aim for a contradiction. By continuity and strict monotonicity, there exists a constant $L\in [C_1,C_2]$ such that $f(x)\rightarrow L$ as $x\rightarrow 0^+$. Likewise, $f(\lambda x)\rightarrow L$ as $x\rightarrow 0^+$. But this violates (3.5). Thus, either f is strictly increasing and satisfies $f(x)\rightarrow 0^+$ as $x\rightarrow 0^+$ or f is strictly decreasing and satisfies $f(x)\rightarrow +\infty$ as $x\rightarrow 0^+$.

Suppose first that f is strictly increasing and satisfies $f(x)\rightarrow 0^+$ as $x\rightarrow 0^+$. Further, suppose on the contrary to the assertion in (1) that $\rho <0$. From the first inequality in (3.5), we have

$$\begin{aligned} \lim _{\lambda \rightarrow 0^+}\frac{f(\lambda x)}{f(x)}=\infty \end{aligned}$$

for any fixed $x\in (0,\delta )$. But this contradicts with the fact that $f(x)\rightarrow 0^+$ as $x\rightarrow 0^+$, and hence $\rho >0$. The proof of (2) can be finished in the same way by relying on the second inequality in (3.5). $\square$

The assumption $\rho \ne 0$ in Lemma 3.1 is necessary. Indeed, $f_1(x)=-\log (x)$ and $f_2(x)=-1/\log (x)$ are both regularly varying functions of index $\rho =0$ at the origin, where $f_1$ is strictly decreasing and $f_2$ strictly increasing.

Next we identify the functions k satisfying (3.3) as functions that are regularly varying at the origin. The proof is based on the reasoning used in proving [13, Lemma 1].

Lemma 3.2

Let $k:(0,1)\rightarrow (0,1)$ be a strictly increasing continuous function, and suppose that $\delta :(0,1)\rightarrow (0,1)$ is any function satisfying $\delta (x)\rightarrow 0$ as $x\rightarrow 1^-$. If k is regularly varying at the origin, then (3.3) holds. Conversely, if k satisfies (3.3), then

$$\begin{aligned} \lim _{\lambda \rightarrow 1^-}\liminf _{t\rightarrow 0^+}\frac{k(\lambda t)}{k(t)}=1. \end{aligned}$$

(3.6)

Proof

Suppose that k is regularly varying of index $\rho \in \mathbb {R}$ at the origin. If $\rho =0$, then from the definition (3.4),

$$\begin{aligned} \lim _{x\rightarrow 1^-}\frac{k(\lambda (1-x))}{k(1-x)}=1 \end{aligned}$$

for every $\lambda >0$. But this implies (3.3). Suppose then that $\rho \ne 0$. From Lemma 3.1 and the fact that $k:(0,1)\rightarrow (0,1)$, we know that $\rho >0$ and that $k(x)\rightarrow 0^+$ as $x\rightarrow 0^+$. Let $\varepsilon >0$ and $\lambda \in (0,1)$. Then there exists a constant $\delta \in (0,1)$ such that

$$\begin{aligned} \lambda ^\rho -\varepsilon \le \frac{k(\lambda (1-x))}{k(1-x)} \le \lambda ^\rho +\varepsilon ,\quad \delta \le x<1. \end{aligned}$$

Moreover, by taking a slightly larger $\delta (0,1)$, if necessary, we find that $\lambda<1\pm \delta (x)<1/\lambda$ for $\delta \le x<1$. Thus

$$\begin{aligned} \lambda ^\rho -\varepsilon\le & {} \liminf _{x\rightarrow 1^-}\frac{k(\lambda (1-x))}{k(1-x)} \le \liminf _{x\rightarrow 1^-}\frac{k((1-x)(1\pm \delta (x))}{k(1-x)}\\\le & {} \limsup _{x\rightarrow 1^-}\frac{k((1-x)(1\pm \delta (x))}{k(1-x)} \le \limsup _{x\rightarrow 1^-}\frac{k((1-x)/\lambda )}{k(1-x)}\\= & {} \lim _{x\rightarrow 1^-}\frac{k((1-x)/\lambda )}{k(1-x)} =\left( \frac{1}{\lambda }\right) ^\rho . \end{aligned}$$

Letting $\varepsilon \rightarrow 0^+$ and then $\lambda \rightarrow 1^-$, the assertion (3.3) follows.

Conversely, suppose that k is a strictly increasing function satisfying (3.3). Since $0<k(\lambda t)/k(t)<1$ for every $0<t<1$ and $0<\lambda <1$, the function

$$\begin{aligned} g(\lambda )=\liminf _{t\rightarrow 0^+}\frac{k(\lambda t)}{k(t)}, \quad 0<\lambda <1, \end{aligned}$$

is non-decreasing in $\lambda$ and satisfies $0\le g(\lambda )\le 1$ for all $0<\lambda <1$. Hence the limit with respect to $\lambda$ in (3.6) exists and is $\le 1$. Suppose on the contrary to the assertion in (3.6) that

$$\begin{aligned} \lim _{\lambda \rightarrow 1^-}\liminf _{t\rightarrow 0^+}\frac{k(\lambda t)}{k(t)}<1. \end{aligned}$$

Let $\{\lambda _n\}$ be any strictly increasing sequence on (0, 1) with $\lambda _n\rightarrow 1^-$ as $n\rightarrow \infty$. Then there exists a strictly increasing sequence $\{x_n\}$ on (0, 1) with $x_n\rightarrow 1^-$ as $n\rightarrow \infty$ and a constant $C\in (0,1)$ such that

$$\begin{aligned} \frac{k(\lambda _n (1-x_n))}{k(1-x_n)}<C,\quad n\in \mathbb {N}. \end{aligned}$$

Define a step function $\delta _0:(0,1)\rightarrow (0,1)$ by

$$\begin{aligned} \delta _0(x)=\left\{ \begin{array}{rl} 1-\lambda _1,\ {} &{} 0<x< x_1,\\ 1-\lambda _n,\ {} &{} x_{n}\le x < x_{n+1},\ n\in \mathbb {N}. \end{array}\right. \end{aligned}$$

Then $\delta _0(x)\rightarrow 0^+$ as $x\rightarrow 1^-$, and

$$\begin{aligned} \liminf _{x\rightarrow 1^-}\frac{k((1-x)(1-\delta _0(x))}{k(1-x)} \le \liminf _{n\rightarrow \infty }\frac{k(\lambda _n(1-x_n))}{k(1-x_n)} \le C<1. \end{aligned}$$

But this violates (3.3), and hence (3.6) holds. $\square$

The assumption that k is regularly varying at the origin is necessary in Lemma 3.2. For example, the function $k(x)=\exp (-1/x)$ is strictly increasing and differentiable, but it doesn’t satisfy (3.3) for $\delta (x)=\sqrt{1-x}$.

The following result may be known, but we offer a proof for the convenience of the reader.

Lemma 3.3

Let $l:(0,1)\rightarrow (0,1)$ be a strictly increasing, continuous and bijective function that is regularly varying of index $\rho >0$ at the origin. Then the inverse $k=l^{-1}$ of l is regularly varying of index $1/\rho$ at the origin.

Proof

It is clear by the assumptions that $l(x)\rightarrow 0^+$ as $x\rightarrow 0^+$. Hence $k(x)\rightarrow 0^+$ as $x\rightarrow 0^+$ as well. Let $\lambda >0$, and suppose that

$$\begin{aligned} \limsup _{x\rightarrow 0^+}\frac{k(\lambda x)}{k(x)}<\lambda ^{1/\rho }. \end{aligned}$$

(3.7)

Then there exist constants $\gamma >0$ and $\delta >0$ such that

$$\begin{aligned} k(\lambda x)<(\lambda ^{1/\rho }-\gamma )k(x),\quad 0<x<\delta . \end{aligned}$$

(3.8)

Choose $\varepsilon >0$ small enough such that

$$\begin{aligned} (\lambda ^{1/\rho }-\gamma )^\rho +\varepsilon <\lambda . \end{aligned}$$

Using the monotonicity of l in (3.8) together with the fact that l is regularly varying of index $\rho$ at the origin, we obtain

$$\begin{aligned} \lambda x<\frac{l((\lambda ^{1/\rho }-\gamma )k(x))}{l(k(x))}\cdot l(k(x))<((\lambda ^{1/\rho }-\gamma )^\rho +\varepsilon )x,\quad 0<x<\delta _0, \end{aligned}$$

where $\delta _0\in (0,\delta )$ is small enough. But this is a contradiction, and hence the inequality < in (3.7) should be $\ge$. Suppose next that

$$\begin{aligned} \limsup _{x\rightarrow 0^+}\frac{k(\lambda x)}{k(x)}>\lambda ^{1/\rho }. \end{aligned}$$

Then there exist a constant $\gamma >0$ and a strictly decreasing sequence $\{x_n\}$ on (0, 1) tending to zero such that

$$\begin{aligned} k(\lambda x_n)>(\lambda ^{1/\rho }+\gamma )k(x_n),\quad n\in \mathbb {N}. \end{aligned}$$

Similarly as above, we arrive at a contradiction. Hence the inequality < in (3.7) should be an equality. A similar proof applies for the limit inferior in place of the limit superior. Since $\lambda >0$ was arbitrarily chosen, this completes the proof. $\square$

Regarding the assumption $\rho >0$ in Lemma 3.3, we note that the function $l(x)=-1/\log (x)$ is regularly varying of index 0 at the origin, but its inverse $k(x)=\exp (-1/x)$ is not regularly varying at the origin.

3.2 Convex Curves

Suppose that $k:(0,1)\rightarrow (0,1)$ is a strictly increasing, differentiable and convex function that is regularly varying at the origin, such that

$$\begin{aligned} \lim _{x\rightarrow 1^-}\frac{k(1-x)}{1-x}=0. \end{aligned}$$

(3.9)

For example, the functions $x\mapsto x^\gamma$ with $\gamma >1$ satisfy all of the conditions above, whereas the identity function satisfies everything else except for (3.9).

A countable collection of Euclidean discs $\Delta (z_n,r_n)\subset \mathbb {D}$ for which $|z_n|\rightarrow 1^-$ and

$$\begin{aligned} \sum _n \frac{r_n}{k(1-|z_n|)}<\infty \end{aligned}$$

(3.10)

is called a k-set. For any $\zeta \in \partial \mathbb {D}$ and any $c>0$, we denote

$$\begin{aligned} \Gamma (k,\zeta ,c)=\left\{ z\in \mathbb {D}:|1-{\overline{\zeta }}z|\le ck(1-|z|)\right\} . \end{aligned}$$

As discussed in Sect. 3.1, the cases $k(x)=x$ and $k(x)=x^\gamma$ with $\gamma >1$ correspond to a Stolz angle and its subset, a zero angle, respectively. For fixed k and $\zeta$, if $c_2>c_1>0$, then $\Gamma (k,\zeta ,c_1)\subset \Gamma (k,\zeta ,c_2)$.

Theorem 3.4

Let U be a k-set, and let $\zeta \in \partial \mathbb {D}$. Then the set $C\subset (0,\infty )$ of values c for which the curve $\partial \Gamma (k,\zeta ,c)$ meets infinitely many discs $\Delta (z_n,r_n)$ has measure zero. Moreover, the circular projection E of U onto the interval [0, 1) satisfies $\int _E\frac{dx}{k(1-x)}<\infty$.

Proof

It suffices to consider the case $\zeta =1$ and the portion of $\partial \Gamma (k,1,c)$ that lies in the upper half-disc, call it $\Gamma ^+(c)$ for short, where $c\in I=[a,b]\subset (0,\infty )$. Indeed, we may cover the interval $(0,\infty )$ by countably many closed intervals, and by countable additivity of the Lebesgue measure, a countable union of sets of measure zero has measure zero.

Suppose that the disc $\Delta (z_n,r_n)$ lies asymptotically between the curves $\Gamma ^+(c_1)$ and $\Gamma ^+(c_2)$, where $a\le c_1<c_2\le b$ and $z_n=x_n+iy_n$. Denote the points of intersection on $\partial \Delta (z_n,r_n)$ by $\zeta _1$ and $\zeta _2$, respectively, see Fig. 4.

Fig. 4

The convex case in the unit disc

We may suppose that the points $z_n$ are pairwise distinct and organized by increasing modulus. Denote $c_0=\frac{|1-z_n|}{k(1-|z_n|)}$. Then the portion of the curve $|1-z|=c_0k(1-|z|)$ that lies in the upper half-disc travels through the centre point $z_n$ of $D_n$ and $a\le c_1<c_0<c_2\le b$.

From (3.9) and (3.10), using monotonicity and convexity of k, we find that

$$\begin{aligned} \frac{r_n}{1-|z_n|}\le \frac{r_n}{k(1-|z_n|)}\rightarrow 0,\quad n\rightarrow \infty . \end{aligned}$$

(3.11)

From Lemma 3.2, we find that (3.3) holds. Furthermore, from (3.3) and (3.11), we obtain

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{k(1-|z_n|)}{k(1-|z_n|\pm r_n)} =\lim _{n\rightarrow \infty }\frac{k(1-|z_n|)}{k\left( (1-|z_n|)\left( 1\pm \frac{r_n}{1-|z_n|}\right) \right) }=1. \end{aligned}$$

(3.12)

Since $k'(x)$ is positive and increasing, there exists a constant $M>0$ such that $0<k'(x)\le M$ for all $x\in (0,1/2)$. Let $N\in \mathbb {N}$ be such that $1/2<|z_n|-r_n<1$ for all $n\ge N$. Now, by the mean value theorem, there exists a point $t_n\in (1-|z_n|-r_n,1-|z_n|+r_n)$ such that

$$\begin{aligned} k(1-|z_n|+r_n)-k(1-|z_n|-r_n)=2r_nk'(t_n)\le 2r_nM,\quad n\ge N. \end{aligned}$$

(3.13)

Then, using (3.12) and (3.13),

$$\begin{aligned} c_2-c_1= & {} \frac{|1-\zeta _2|}{k(1-|\zeta _2|)}-\frac{|1-\zeta _1|}{k(1-|\zeta _1|)} \le \frac{|1-z_n|+r_n}{k(1-|\zeta _2|)}-\frac{|1-z_n|-r_n}{k(1-|\zeta _1|)}\\\le & {} \frac{2r_n}{k(1-|\zeta _2|)}+|1-z_n|\left( \frac{1}{k(1-|\zeta _2|)}-\frac{1}{k(1-|\zeta _1|)}\right) \\\le & {} \frac{2r_n}{k(1-|z_n|-r_n)}+|1-z_n|\left( \frac{1}{k(1-|z_n|-r_n)}-\frac{1}{k(1-|z_n|+r_n)}\right) \\\lesssim & {} \frac{2r_n}{k(1-|z_n|)}+c_0 \frac{k(1-|z_n|+r_n)-k(1-|z_n|-r_n)}{k(1-|z_n|)}\\{} & {} \frac{2r_n(1+c_0M)}{k(1-|z_n|)}\le \frac{2r_n(1+bM)}{k(1-|z_n|)},\quad n\ge N. \end{aligned}$$

The sum of the terms in the upper bound converges by (3.10). The fact that the set C has measure zero can be proved analogously as in Theorem 2.1. The remaining assertion follows from

$$\begin{aligned} \int _{E}\frac{dx}{k(1-x)}\le & {} \sum _n\int _{|z_n|-r_n}^{|z_n|+r_n}\frac{dx}{k(1-x)}+O(1) \le \sum _n \frac{2r_n}{k(1-|z_n|-r_n)}+O(1)\\= & {} \sum _n \frac{2r_n}{k\left( (1-|z_n|)\left( 1-\frac{r_n}{1-|z_n|}\right) \right) }+O(1)<\infty , \end{aligned}$$

where we have used (3.3), (3.10) and (3.11). $\square$

3.3 Concave Curves

Suppose that $l:(0,1)\rightarrow (0,1)$ is a strictly increasing, bijective, differentiable and concave function that is regularly varying of index $\rho \ne 0$ at the origin, such that

$$\begin{aligned} \lim _{x\rightarrow 1^-}\frac{1-x}{l(1-x)}=0. \end{aligned}$$

(3.14)

For example, the functions $x\mapsto x^\gamma$, $0<\gamma <1$, satisfy all of the conditions above.

A countable collection of Euclidean discs $\Delta (z_n,r_n)\subset \mathbb {D}$ for which $|z_n|\rightarrow 1^-$ and

$$\begin{aligned} \sum _n \frac{r_n}{l^{-1}(1-|z_n|)}<\infty , \end{aligned}$$

(3.15)

is called an l-set. For any $\zeta \in \partial \mathbb {D}$ and any $c>0$, we denote

$$\begin{aligned} \Gamma (l,\zeta ,c)=\left\{ z\in \mathbb {D}:~ l(c|1-{\overline{\zeta }}z|)\le 1-|z|\right\} . \end{aligned}$$

Theorem 3.5

Let U be an l-set, and let $\zeta \in \partial \mathbb {D}$. Then the set $C\subset (0,\infty )$ of values c for which the curve $\partial \Gamma (l,\zeta ,c)$ meets infinitely many discs $\Delta (z_n,r_n)$ has measure zero. Moreover, the circular projection E of U onto the interval [0, 1) satisfies $\int _E\frac{dx}{l^{-1}(1-x)}<\infty$.

Proof

We sketch the proof of Theorem 3.5 in the case $\zeta =1$. It suffices to consider the portion of $\partial \Gamma (l,1,c)$ in the upper half-disc, call it $\Gamma ^+(c)$ for short. Suppose that the disc $\Delta (z_n,r_n)$ lies asymptotically between the curves $\Gamma ^+(c_1)$ and $\Gamma ^+(c_2)$, where $c_2>c_1$ and $z_n=x_n+iy_n$. Denote the points of intersection on $\partial \Delta (z_n,r_n)$ by $\zeta _1$ and $\zeta _2$, respectively.

Fig. 5

The concave case in the unit disc

From (3.14), it follows that the inverse $l^{-1}$ of l is strictly increasing, differentiable and convex function such that

$$\begin{aligned} \lim _{x\rightarrow 1^{-}}\frac{l^{-1}(1-x)}{1-x}=0. \end{aligned}$$

The index $\rho$ of regular variation for l is positive by Lemma 3.1. Hence the inverse $k=l^{-1}$ of l is regularly varying of index $1/\rho >0$ at the origin by Lemma 3.3.

Taking $k(x)=l^{-1}(x)$ in Theorem 3.4, we find that $\int _E\frac{dx}{l^{-1}(1-x)}<\infty$ and that the set $C\subset (0,\infty )$ of values c for which the curve $\partial \Gamma (k,1,c)$ for $k(x)=l^{-1}(x)$ meets infinitely many discs $\Delta (z_n,r_n)$ has measure zero. Moreover, the curves $\partial \Gamma (k,1,c)$ and $\partial \Gamma (l,1,1/c)$ are symmetric with respect to the line $x+y=1$. The rest of the proof follows from the fact that $0<c<\infty$ if and only if $0<1/c<\infty$. $\square$

4 Applications

As applications of Sects. 2 and 3, we discuss pointwise estimates for logarithmic derivatives, logarithmic differences and for logarithmic q-differences. In addition, we discuss ways to avoid exceptional sets.

4.1 Logarithmic Derivatives in $\mathbb {C}$

The paper [6] is frequently cited in the theory of complex differential equations. The extremal cases $K(x)\equiv x$ and $K(x)\equiv 1$ in Corollary 4.1 below correspond to Theorems 3 and 4 in [6], respectively. In fact, [6, Theorem 4] is slightly improved because $r^\varepsilon$ in the upper bound is replaced with $\log ^\alpha r$. We remind the reader of Theorem 2.1 according to which a K-set can be avoided by almost every K-curve, and the circular projection E of a K-set on the interval $[1,\infty )$ satisfies $\int _E\frac{dx}{K(x)}<\infty$.

Corollary 4.1

Let f be a meromorphic function in $\mathbb {C}$, let k and j be integers such that $k>j\ge 0$, and let $\alpha >1$ be a given constant. Suppose that $f^{(j)}\not \equiv 0$ and that $K:[0,\infty )\rightarrow [0,\infty )$ is either the constant function $K(x)\equiv 1$ or a strictly increasing, continuous, concave function satisfying the doubling condition (2.2) and $K(x_0)=0$ for some $x_0\ge 0$.

Then there exists a K-set U of discs $D(z_n,r_n)$ satisfying (2.3) and a constant $C>0$ depending only on $\alpha , k, j$ such that for all $z\not \in U$, we have the following estimate (where $r=|z|$):

$$\begin{aligned} \left| \frac{f^{(k)}(z)}{f^{(j)}(z)}\right| \le C\left( \frac{T(\alpha r,f)}{r}+n_j(\alpha r) \log ^+n_j(\alpha r)\frac{\log ^\alpha r}{K(r)}\right) ^{k-j}. \end{aligned}$$

(4.1)

Here $n_j(t)$ is the number of zeros and poles of $f^{(j)}$ in the disc $\{\zeta :|\zeta |\le t\}$, counting multiplicities.

Proof

Let $\{a_m\}$ denote the sequence of zeros and poles of $f^{(j)}$ listed according to multiplicity and ordered by increasing modulus. We follow the proof of [6, Theorem 3] up to (7.7), and set

$$\begin{aligned} \mu _\nu =n_j(\alpha ^{\nu +2})\quad \text {and}\quad d_\nu =\frac{K(\alpha ^\nu )}{(\log (\alpha ^\nu ))^{\alpha }}, \end{aligned}$$

where $\nu \ge \nu _0$ is an integer. We make this choice for the constants $d_\nu$ independently of whether $K(x)\equiv 1$ or not. We also suppose that z is confined to the annulus $\mathcal {A}_\nu =\{\zeta :\alpha ^\nu \le |\zeta |< \alpha ^{\nu +1}\}$, which is equivalent to saying that

$$\begin{aligned} \nu \log \alpha \le \log r<(\nu +1)\log \alpha ,\quad |z|=r. \end{aligned}$$

Since $\alpha >1$ is fixed, there exists an integer $l\ge 1$ such that $\frac{1}{2^l}\le \frac{1}{\alpha }<\frac{1}{2^{l-1}}$. We now make a standard use of Cartan’s lemma as in [6]. Indeed, if z lies outside of Cartan’s discs, then the following analogue of (7.9) in [6] holds:

$$\begin{aligned} \sum _{|a_m|\le \alpha r}\frac{1}{|z-a_m|}\le & {} \sum _{m=1}^{\mu _\nu }\frac{1}{|z-b_m|}<\frac{\mu _\nu (\log \alpha ^\nu )^{\alpha }}{K(\alpha ^\nu )}\sum _{m=1}^{\mu _\nu }\frac{1}{m}\\= & {} \frac{\mu _\nu (\log \alpha ^\nu )^{\alpha }}{K(\frac{1}{\alpha }\alpha ^{\nu +1})}\sum _{m=1}^{\mu _\nu }\frac{1}{m}\le \mu _\nu (1+\log \mu _\nu )\frac{\log ^{\alpha } r}{K(\frac{1}{2^l}\alpha ^{\nu +1})}\\\le & {} 2^l\mu _\nu (1+\log \mu _\nu )\frac{\log ^\alpha r}{K(r)} \le 2^l n_j(\alpha ^2 r)(1+\log n_j(\alpha ^2 r))\frac{\log ^\alpha r}{K(r)}\\\le & {} 2^{l+1} n_j(\alpha ^2 r) \log n_j(\alpha ^2 r)\frac{\log ^\alpha r}{K(r)}. \end{aligned}$$

The assertion (4.1) follows from this similarly as in [6, (7.10)]. Thus (4.1) holds for a fixed $\nu \ge \nu _0$ when z lies outside of Cartan’s discs.

Similarly as in [6], we now consider all $\nu \ge \nu _0$, where $\nu _0\ge 1$ is large enough. Let $A_{\nu ,1},\ldots ,A_{\nu ,l_\nu }$ denote precisely those Cartan discs that intersect the annulus $\mathcal {A}_\nu .$ We mention that for some $\nu$ there might be no discs of this type. It follows from Cartan’s lemma that for each $\nu$ the total sum of the diameters of the discs $A_{\nu ,1},\ldots ,A_{\nu ,l_\nu }$ cannot exceed $4d_\nu$. Since $K(x)=O(x)$, we may choose $\nu _0$ large enough so that the $\alpha ^\nu >4d_\nu$ for all $\nu \ge \nu _0$. Then for $\nu \ge \nu _0$ the origin lies outside of the discs $A_{\nu ,1},\ldots ,A_{\nu ,l_\nu }$.

Now let $D_n=D(z_n,r_n)$ denote the sequence $\{D_n\}$ of all the discs $A_{\nu ,i}$, where $\nu \ge \nu _0$ and $1\le i\le l_\nu$. We have proved that (4.1) holds if z lies outside of the discs $D_n$ and $\{\zeta :|\zeta |\le \alpha ^{\nu _0}\}$. Moreover,

$$\begin{aligned} \sum _{n=1}^\infty \frac{r_n}{K(|z_n|)}= & {} \sum _{\nu =\nu _0}^\infty \sum _{D_n\cap \mathcal {A}_\nu \ne \emptyset }\frac{r_n}{K(|z_n|)}\le \sum _{\nu =\nu _0}^\infty \frac{2d_\nu }{K(\alpha ^\nu -2d_\nu )}\\= & {} \sum _{\nu =\nu _0}^\infty \frac{2d_\nu }{K(\alpha ^\nu (1-2d_\nu /\alpha _\nu ))} \le \sum _{\nu =\nu _0}^\infty \frac{2d_\nu }{K(\alpha ^\nu /2)}\\\le & {} \sum _{\nu =\nu _0}^\infty \frac{4 d_\nu }{K(\alpha ^\nu )} =\sum _{\nu =\nu _0}^\infty \frac{4}{\nu ^\alpha (\log \alpha )^\alpha } <\infty . \end{aligned}$$

This completes the proof. $\square$

4.2 Logarithmic Derivatives in $\mathbb {D}$

The extremal case $k(x)\equiv x$ in Corollary 4.2 below corresponds to [4, Theorem 3.1]. We remind the reader of Theorem 3.4 according to which a k-set can be avoided by almost every k-curve, and the circular projection E of a k-set on the interval [0, 1) satisfies $\int _E\frac{dx}{k(1-x)}<\infty$.

Corollary 4.2

Let f be a meromorphic function in $\mathbb {D}$, let k and j be integers such that $k>j\ge 0$, let $\alpha \in (1,\infty )$ and $b\in (0,1)$ be given constants, and denote $s(r)=1-b(1-r)$. Suppose that $f^{(j)}\not \equiv 0$ and that $k:(0,1)\rightarrow (0,1)$ is either the identity mapping $k(x)=x$ or regularly varying at the origin, strictly increasing, differentiable and convex function satisfying (3.9).

Then there exists a k-set U of discs $D(z_n,r_n)$ satisfying (3.10) and a constant $C>0$ depending only on $\alpha , b,k, j$ such that for all $z\not \in U$, we have the following estimate (where $r=|z|$):

$$\begin{aligned} \left| \frac{f^{(k)}(z)}{f^{(j)}(z)}\right| \le C\left( \frac{T(s(r),f)-\log (1-r)}{(1-r)^2}+W(r)\right) ^{k-j}, \end{aligned}$$

(4.2)

where

$$\begin{aligned} W(r)=\frac{n_j(s(r))}{k(1-r)}\log ^+n_j(s(r))\log ^\alpha \frac{1}{1-r} \end{aligned}$$

and $n_j(t)$ is the number of zeros and poles of $f^{(j)}$ in the disc $\{\zeta :|\zeta |\le t\}$, counting multiplicities.

Proof

Let $\{a_m\}$ denote the sequence of zeros and poles of $f^{(j)}$ listed according to multiplicity and ordered by increasing modulus. We follow the proof of [4, Theorem 3.1], which in turn is reminiscent to the proof of [6, Theorem 3]. In the unit disc case, one just has to be extra careful so that the Cartan discs still remain in $\mathbb {D}$. Set

$$\begin{aligned} \mu _\nu =n_j(1-b^{\nu +2})\quad \text {and}\quad d_\nu =\frac{k(b^{\nu +1})}{\nu ^{\alpha }(-\log b)^\alpha }, \end{aligned}$$

where $\nu \ge \nu _0$ is an integer. We make this choice for the constants $d_\nu$ independently of whether $k(x)=x$ or not. We also suppose that z is confined to the annulus $\mathcal {A}_\nu =\{\zeta :1-b^\nu \le |\zeta |< 1-b^{\nu +1}\}$, which is equivalent to saying that

$$\begin{aligned} \nu (-\log b)\le -\log (1-r)< (\nu +1)(-\log b),\quad |z|=r. \end{aligned}$$

We now make use of Cartan’s lemma as in [4]. Indeed, if z lies outside of Cartan’s discs, and if $\nu _0$ is assumed to be large enough so that $\log \mu _\nu \ge 1$ for all $\nu \ge \nu _0$, then the following analogue of (6.5)–(6.7) in [4] holds:

$$\begin{aligned} \sum _{|a_m|\le s(r)}\frac{1}{|z-a_m|}\le & {} \sum _{m=1}^{\mu _\nu }\frac{1}{|z-b_m|}<\frac{\mu _\nu \nu ^{\alpha }(-\log b)^\alpha }{k(b^\nu )}\sum _{m=1}^{\mu _\nu }\frac{1}{m}\\\le & {} \frac{\mu _\nu \nu ^{\alpha }(-\log b)^\alpha }{k(1-r)}(1+\log \mu _\nu )\\\le & {} \frac{\mu _\nu (1+\log \mu _\nu )}{k(1-r)}\log ^\alpha \frac{1}{1-r}\\\\le & {} 2\frac{n_j(1-b^2(1-r))}{k(1-r)}\log n_j(1-b^2(1-r))\log ^\alpha \frac{1}{1-r}. \end{aligned}$$

The assertion (4.2) follows from this and from [4, (6.1)]. Thus (4.2) holds for a fixed $\nu \ge \nu _0$ when z lies outside of Cartan’s discs.

Similarly as in [4], we now consider all $\nu \ge \nu _0$, where $\nu _0\ge 1$ is large enough. Let $A_{\nu ,1},\ldots ,A_{\nu ,l_\nu }$ denote precisely those Cartan discs that intersect the annulus $\mathcal {A}_\nu .$ We mention that for some $\nu$, there might be no discs of this type. It follows from Cartan’s lemma that for each $\nu$, the total sum of the diameters of the discs $A_{\nu ,1},\ldots ,A_{\nu ,l_\nu }$ cannot exceed $4d_\nu$. Let $\zeta _{\nu ,i}$ and $\xi _{\nu ,i}$ denote the centre and radius of the disc $A_{\nu ,i}$, respectively. It is easy to see that

$$\begin{aligned} |\zeta _{\nu ,i}|+\xi _{\nu ,i}\le 1-b^{\nu +1}+2\xi _{\nu ,i} \le 1-b^{\nu +1}+4d_\nu . \end{aligned}$$

If k is not the identity mapping, then from (3.9), we infer

$$\begin{aligned} \lim _{\nu \rightarrow \infty }\frac{k(b^\nu )}{b^\nu } =\lim _{\nu \rightarrow \infty }\frac{k(1-(1-b^\nu ))}{1-(1-b^\nu )} =0. \end{aligned}$$

Thus we may choose $\nu _0$ large enough so that $4d_\nu <b^{\nu +1}$ for all $\nu \ge \nu _0$. This inequality holds also in the case when $k(x)=x$, but possibly for a different $\nu _0$. Now $|\zeta _{\nu ,i}|+\xi _{\nu ,i}<1$ for all $\nu \ge \nu _0$, which means that $A_{\nu ,1},\ldots ,A_{\nu ,l_\nu }\subset \mathbb {D}$ for all $\nu \ge \nu _0$. Finally, we choose a larger $\nu _0$, if necessary, so that $b^{\nu +1}<1-b^\nu$ for all $\nu \ge \nu _0$. Then $1-b^\nu >4d_\nu$ for all $\nu \ge \nu _0$, which means that the origin lies outside of the discs $A_{\nu ,1},\ldots ,A_{\nu ,l_\nu }$ for all $\nu \ge \nu _0$.

Recall that k satisfies (3.3) by Lemma 3.2. Let $D_n=D(z_n,r_n)$ denote the sequence $\{D_n\}$ of all the discs $A_{\nu ,i}$, where $\nu \ge \nu _0$ and $1\le i\le l_\nu$. We have proved that (4.2) holds if z lies outside of the discs $D_n$ and $\{\zeta :|\zeta |\le 1-b^{\nu _0}\}$. Moreover, since $2d_\nu /b^\nu \rightarrow 0$ as $\nu \rightarrow \infty$, we use (3.3) to find a constant $M>0$ that depends on $b, \alpha , \nu _0$ such that

$$\begin{aligned} \sum _{n=1}^\infty \frac{r_n}{k(1-|z_n|)}= & {} \sum _{\nu =\nu _0}^\infty \sum _{D_n\cap \mathcal {A}_\nu \ne \emptyset }\frac{r_n}{k(1-|z_n|)}\le \sum _{\nu =\nu _0}^\infty \frac{2d_\nu }{k(b^{\nu +1}-2d_\nu )}\\= & {} \sum _{\nu =\nu _0}^\infty \frac{2d_\nu }{k(b^{\nu +1}(1-2d_\nu /b^{\nu +1}))} \le \sum _{\nu =\nu _0}^\infty \frac{M}{\nu ^\alpha } <\infty . \end{aligned}$$

This completes the proof. $\square$

4.3 Logarithmic Differences and q-Differences

A difference counterpart to Gundersen’s pointwise estimates for logarithmic derivatives due to Chiang and Feng, see [3, Theorem 8.2], is also well known. The estimate holds for all z such that |z| lies outside of an exceptional set of finite logarithmic measure. For a K-version of it, all we need is to change the estimate (8.6) in [3] by the reasoning used in proving Theorem 4.1, and use the same constants $d_\nu$. We state the result formally but omit the proof.

Corollary 4.3

Let $f\not \equiv 0$ be a meromorphic function in $\mathbb {C}$, and let $\alpha >1$ and $c\in \mathbb {C}$ be given constants. Suppose that $K:[0,\infty )\rightarrow [0,\infty )$ is as in Corollary 4.1. Then there exists a K-set U of discs $D(z_n,r_n)$ satisfying (2.3) and a constant $C>0$ depending only on $\alpha$ and c such that for all $z\not \in U$, we have the following estimate (where $r=|z|$):

$$\begin{aligned} \left| \log \left| \frac{f(z+c)}{f(z)}\right| \right| \le C\left( \frac{T(\alpha r,f)}{r} +n(\alpha r)\log ^+n(\alpha r)\frac{\log ^{\alpha }r}{K(r)}\right) . \end{aligned}$$

(4.3)

Here n(t) is the number of zeros and poles of f in the disc $\{\zeta :|\zeta |\le t\}$, counting multiplicities.

A q-difference counterpart to Gundersen’s pointwise estimates was discovered by Wen and Ye in [18]. For a K-version of it, all we need is to change the estimate (3.9) in [18] by the reasoning used in proving Theorem 4.1, and use the same constants $d_\nu$, and then [18, Lemma 3.4] yields the following analogue of (4.3):

$$\begin{aligned} \log \frac{f(qz)}{f(z)}= & {} (q-1)z\frac{f'(z)}{f(z)} +O\left( \frac{|q-1|^2m(r^2)}{r^2}\right) +O\left( \frac{|q-1|^2 n(r^2)}{r^2}\right) \\{} & {} +O\left( rn(\alpha r) \log ^ +n_j(\alpha r)\frac{\log ^\alpha r}{K(r)}\right) +O(1), \end{aligned}$$

where $m(r)=m(r,f)+m(r,1/f)$. The details are omitted.

4.4 Exceptional Sets

Suppose that $K:(0,\infty )\rightarrow (0,\infty )$ is one of the following three types of functions: (1) $K(x)\equiv 1$, (2) $K(x)\equiv x$, or (3) $1\le K(x)\le x$ and K is strictly increasing, continuous, concave function satisfying the doubling condition (2.2). Suppose further that $E\subset [1,\infty )$ satisfies $\int _E\frac{dx}{K(x)}<\infty$. The cases (1) and (2) correspond to finite linear measure and finite logarithmic measure, respectively. It is clear that in all three cases,

$$\begin{aligned} \lim _{r\rightarrow \infty }\frac{K(r)}{r}\int _{E\cap [r,\infty )}\frac{dx}{K(x)}=0. \end{aligned}$$

Define the K-density of the set E relative to a given function $\varepsilon :(0,\infty )\rightarrow (0,1]$ by

$$\begin{aligned} \delta (K,\varepsilon )(E)= \limsup _{r\rightarrow \infty }\frac{\frac{K(r)}{r}\int _{E\cap [r,\infty )}\frac{dx}{K(x)}}{\varepsilon (r)}. \end{aligned}$$

If $\delta (K,\varepsilon )(E)\in (0,\infty )$, then it is clear that $\varepsilon (r)$ tends to zero (along a sequence of values r), but not arbitrarily fast.

Special cases of Lemma 4.4 below allow us to avoid exceptional sets of finite linear measure ($K(x)\equiv 1$) or of finite logarithmic measure ($K(x)\equiv x$). The proof is an easy modification of the original results, see [2, Lemma C] and [7, Lemma 5], but the result improves the existing estimates in the sense that a constant $\alpha >1$ is replaced by a function $\alpha (r)>1$ that tends to 1. Indeed, in the original results the function $\varepsilon (r)$ is a constant function $\varepsilon (r)\equiv \varepsilon =\alpha -1$, in which case $\delta (K,\varepsilon )(E)=0$ trivially holds. The K-density introduced above controls how fast $\alpha (r)$ tends to 1.

Lemma 4.4

Let g(r) and h(r) be non-decreasing functions on $(0,\infty )$, and suppose that $g(r)\le h(r)$ for all $r\in (0,\infty ){\setminus } E$, where $\delta (K,\varepsilon )(E)<1/2$, and K and $\varepsilon$ are as above, while $\alpha >0$ is the constant from (2.2). Denote $\alpha (r)=1+\varepsilon (r)$. Then there exists an $R\ge 1$ such that $g(r)\le h(\alpha (r)r)$ for all $r\ge R$.

Proof

There exists a constant $R\ge 1$ such that the doubling condition (2.2) holds for all $x\ge R$, and that

$$\begin{aligned} \varepsilon (r)>2\frac{K(r)}{r}\int _{E\cap [r,\infty )}\frac{dx}{K(x)},\quad r\ge R. \end{aligned}$$

Thus, if $r\ge R$,

$$\begin{aligned} \int _r^{\alpha (r)r}\frac{dx}{K(x)}\ge \frac{(\alpha (r)-1)r}{K(\alpha (r)r)}\ge \frac{\varepsilon (r)r}{K(2r)}\ge \frac{\varepsilon (r)r}{2 K(r)}>\int _{E\cap [r,\infty )}\frac{dx}{K(x)}. \end{aligned}$$

It follows that $[r,\alpha (r)r]\setminus E\ne \emptyset$ for all $r\ge R$. So, if $r\ge R$ is arbitrary, we may choose $t\in [r,\alpha (r)r]{\setminus } E$ such that

$$\begin{aligned} g(r)\le g(t)\le h(t)\le h(\alpha (r)r) \end{aligned}$$

by the monotonicity of g and h. $\square$

Remark

The constant 2 in the assumption $\delta (K,\varepsilon )(E)<1/\alpha$ comes from the doubling condition $K(2x)\le \alpha K(x),\quad x\ge R,$ for some $\alpha >1$.

Next we suppose that $k:(0,1)\rightarrow (0,1)$ is either the identity mapping or regularly varying at the origin, strictly increasing, differentiable and convex function satisfying (3.9). Suppose further that $E\subset [0,1)$ satisfies $\int _E\frac{dx}{k(1-x)}<\infty$. Define the k-density of the set E relative to a given function $b:(0,1)\rightarrow (0,1)$ by

$$\begin{aligned} \delta (k,b)(E)= \limsup _{r\rightarrow 1^-}\frac{\frac{k(1-r)}{1-r}\int _{E\cap [r,1)}\frac{dx}{k(1-x)}}{1-b(r)}. \end{aligned}$$

We state without a proof the following result which reduces to [2, Lemma C] in the case when $k(x)=x$ and when $b(r)=b$ is a constant function.

Lemma 4.5

Let g(r) and h(r) be non-decreasing functions on (0, 1), and suppose that $g(r)\le h(r)$ for all $r\in (0,1){\setminus } E$, where $\delta (k,b)(E)<1$, and k and b are as above. Denote $s(r)=1-b(r)(1-r)$. Then there exists an $R\ge 0$ such that $g(r)\le h(s(r))$ for all $r\ge R$.