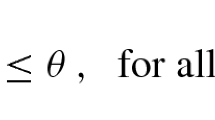Borderline Gradient Continuity for the Normalized p-Parabolic Operator

Abstract

In this paper, we prove gradient continuity estimates for viscosity solutions to $\Delta _{p}^N u - u_t= f$ in terms of the scaling critical $L(n+2,1 )$ norm of f, where $\Delta _{p}^N$ is the game theoretic normalized $p-$Laplacian operator defined in (1.2) below. Our main result, Theorem 2.5 constitutes borderline gradient continuity estimate for u in terms of the modified parabolic Riesz potential $\textbf{P}^{f}_{n+1}$ as defined in (2.9) below. Moreover, for $f \in L^{m}$ with $m>n+2$, we also obtain Hölder continuity of the spatial gradient of the solution u, see Theorem 2.6 below. This improves the gradient Hölder continuity result in Attouchi and Parviainen (Commun Contemp Math 20(4):1750035, 2018) which considers bounded f. Our main results Theorem 2.5 and Theorem 2.6 are parabolic analogues of those in Banerjee and Munive (Commun Contemp Math 22(8):1950069, 2020). Moreover differently from that in Attouchi and Parviainen (Commun Contemp Math 20(4):1750035, 2018), our approach is independent of the Ishii–Lions method which is crucially used in Attouchi and Parviainen (Commun Contemp Math 20(4):1750035, 2018) to obtain Lipschitz estimates for homogeneous perturbed equations as an intermediate step.

1 Introduction

The purpose of this paper is to obtain pointwise gradient continuity estimates for viscosity solutions to

$$\begin{aligned} \Delta _{p}^N u-u_t= f\quad \text {in }Q_1\overset{def}{=} B_1\times (-1,0],\ 1<p<\infty , \end{aligned}$$

(1.1)

in terms of the scaling critical $L(n+2,1)-$norm of f. Here, $\Delta _{p}^N$ denotes the game theoretic normalized $p-$Laplace operator given by

$$\begin{aligned} \Delta _{p}^N u\overset{def}{=} \bigg (\delta _{ij}+ (p-2) \frac{u_i u_j}{ |\nabla u|^2} \bigg ) u_{ij}, \end{aligned}$$

(1.2)

that arises in tug of war games with noise (see [41]) and also image processing (see [17]). More precisely in the context of tug of war games with noise, which has been studied in the interesting paper [41], it turns out that the value functions for these games approximate a solution to the PDE

$$\begin{aligned} \Delta _p^N u = u_t, \end{aligned}$$

(1.3)

when the parameter that controls the size of the possible steps goes to zero. When $p=1$, the Eq. (1.3) formally becomes

$$\begin{aligned} |\nabla u| {\text {div}}\left( \frac{\nabla u}{|\nabla u|}\right) = u_t, \end{aligned}$$

(1.4)

which is the motion of level sets of u by mean curvature. Such an equation has been studied by several authors, see for instance [12, 21]. In [7], it is shown that under some global boundary conditions, the solutions to (1.3) converge to a solution of (1.4) as $p \rightarrow 1$.

Now concerning borderline regularity estimates, we note that it is well known that such estimates play a fundamental role in the theory of elliptic and parabolic partial differential equations. In order to put our main result in the right perspective, we note that in 1981, E. Stein in his work [45] showed the following.

Theorem 1.1

Let L(n, 1) denote the standard Lorentz space, then the following implication holds:

$$\begin{aligned}\nabla v \in L(n,1) \ \implies \ v\ \text {{is continuous}}.\end{aligned}$$

The Lorentz space L(n, 1) appearing in Theorem 1.1 consists of those measurable functions g satisfying the condition

$$\begin{aligned} \int _{0}^{\infty } |\{x: g(x) > t\}|^{1/n} \mathrm{{d}}t < \infty . \end{aligned}$$

Theorem 1.1 can be regarded as the end point case of the Sobolev-Morrey embedding. Moreover, Theorem 1.1 coupled with the standard Calderon-Zygmund theory has the following interesting consequence.

Theorem 1.2

$\Delta u \in L(n,1) \implies \nabla u$ is continuous.

A similar result holds in the parabolic situation for more general variable coefficient operators when $f \in L(n+2, 1)$. As is well known, $"n+2"$ is the right parabolic dimension which is dictated by the one parameter family of parabolic scalings $\{\delta _r\}$ given by $\delta _r(x,t)= (rx, r^2 t)$ that keeps the parabolic structure invariant. The analogue of Theorem 1.2 for general nonlinear and possibly degenerate elliptic and parabolic equations has required the development of a rather sophisticated and powerful nonlinear potential theoretic methods (see for instance [19, 33, 35] and the references therein). The first breakthrough in this direction came up in the work of Kuusi and Mingione in [32] where they showed that the analogue of Theorem 1.2 holds for operators modelled after the variational p-Laplacian. Such a result was subsequently generalized to p-Laplacian type systems by the same authors in [36]. Such results were further extended to degenerate parabolic equations and systems modelled on

$$\begin{aligned} {\text {div}}(|\nabla u|^{p-2} \nabla u) - u_t =f,\ f \in L(n+2, 1) \end{aligned}$$

(1.5)

in [34, 37, 38]. For other local and global borderline gradient continuity results for various kinds of nonlinear equations, we refer to [2, 14, 15, 18, 20, 31]. Very recently, the two of us in [9] obtained a similar borderline gradient continuity result for the following inhomogeneous normalized p-Poisson equation

$$\begin{aligned} \Delta _p^N u = f,\ p>1, f \in L(n,1),\end{aligned}$$

by arguments based on non-divergence form techniques and compactness arguments which have their roots in the fundamental work of Caffarelli in [10]. The results in [9] sharpens the previous results obtained in [4] that dealt with f belonging to subcritical function spaces.

The purpose of this work is to obtain analogous gradient regularity results for solutions to the parabolic normalized $p-$Poisson problem (1.1). Our main results Theorem 2.5 and Theorem 2.6 are parabolic counterparts of those in [9].

We now mention that over the last decade, there has been a growing attention on equations of the type

$$\begin{aligned} \Delta _p^N u-u_t=0, \end{aligned}$$

(1.6)

because of their connections to tug-of-war games with noise. This aspect was first studied in [44] in the stationary case for the infinity Laplacian. In recent times, the parabolic normalized $p-$Laplacian, as well as its degenerate and singular variants, have been studied in a variety of contexts in several papers, see [1, 6,7,8, 17, 24, 28, 29, 41, 43]. See also the recent survey article [42] for a more comprehensive account. As previously mentioned, such equations have also found applications in image processing (see for instance [17]). The gradient Hölder continuity result for solutions to (1.6) was established in [27]. See also [25] for further interesting generalizations. The regularity result in [27] was subsequently extended to equations of the type

$$\begin{aligned} \Delta _p^N u- u_t= f, \ f \in L^{\infty }, \end{aligned}$$

in [3]. Our main results thus further refine the result in [3] by allowing f to belong to more general (and possibly scaling critical) function space.

We would also like to mention that although most of the published works related to the Eq. (1.6) appeared only in recent years, we have seen an unpublished handwritten note by N. Garofalo from 1993 referring to this equation. This is, up to our knowledge, the first time when it was recognized that the Eq. (1.6) should have good regularization properties.

Now a few words regarding our approach: We note that in general, getting $C^{1}-$regularity result amounts to show that the graph of u can be touched by an affine function so that the error is of order o(r) in a parabolic cylinder of size r for every r small enough. The proof of this is based on iterative argument where one ensures improvement of flatness at every successive scale by comparing to a solution of a limiting equation with more regularity. At each step, via rescaling, it reduces to showing that if $\langle p_0,x\rangle +u(x,t)$ solves (1.1) in $Q_1$ (see Sect. 2 for relevant notations), then the oscillation of u is strictly smaller in a smaller cylinder "modulo" a linear function. This is accomplished via compactness arguments which crucially relies on apriori estimates. Such estimates in the context of $\Delta _{p}^N - \partial _t$ come from the Krylov-Safonov theory because the Eq. (1.1) lends itself a uniformly parabolic structure.

Now, for a u that solves (1.1), we have that $v=u-\langle p_0,x\rangle$ is a solution of the following perturbed equation

$$\begin{aligned} \bigg (\delta _{ij} + (p-2) \frac{(v_i +(p_0)_i)(v_j+(p_0)_j)}{|\nabla v + p_0|^2} \bigg ) v_{ij}- v_t=f. \end{aligned}$$

(1.7)

Therefore, in order to obtain improvement of flatness at each scale after a rescaling, it is necessary to get uniform $C^{1}-$type estimates independent of $|p_0|$ for the limiting equations corresponding to the case $f \equiv 0$. This is precisely what has been done in [3] (see also [4]) by an adaptation of the Ishii–Lions approach in [26], using which the authors obtained uniform Lipschitz estimates for solutions to (1.7) for large $|p_0|'s$ when $f=0$. In this paper, we follow an approach which is different from that in [3, 4] and is inspired by ideas in the stationary case developed by the two of us in [9]. Our proofs of Theorems 2.5 and 2.6 are based on separation of the degenerate and the non-degenerate phase, and do not rely on the uniform Lipschitz estimates for equations of the type (1.7). This is inspired by ideas in [47], where an alternate proof of $C^{1, \alpha }-$regularity for the $p-$Laplace equation was given (see also [16, 39, 46] for the first results on $C^{1,\alpha }$ type regularity for p-Laplace type equations). Moreover, in the case when f is bounded, compared to that in [3], our method also provides a different proof of the $C^{1, \alpha }-$ type regularity result for (1.1). Finally we mention that although our proofs follow some key ideas for the stationary case as previously used in [9], nevertheless it entails some delicate adaptations which are intrinsic to the parabolic situation. For instance, the proofs of the main approximation lemmas, i.e. Lemma 3.1 and Lemma 3.3 involve compactness arguments that crucially rely on stability results which are established in the course of this work. It is to be mentioned that the classical stability results for viscosity solutions as in [11] do not apply in our situation because of the non-smooth dependence of the normalized p-Laplace operator on the “gradient” variable. An alternate characterization of viscosity solutions to the homogeneous Eq. (1.6) as in Lemma 2.2 below plays a pervasive role in the proof of such stability arguments. In closing, we refer to [5, 22, 24] for similar regularity results for other variants of the normalized $p-$parabolic operators.

The paper is organized as follows. In Sect. 2, we introduce various notations, notions and gather some preliminary results that are relevant to the present work and then state our main results. In Sect. 3, we prove our main results.

2 Notations, Preliminaries and Statement of the Main Results

A generic point in space time $\mathbb {R}^n \times \mathbb {R}$ will be denoted by (x, t), (y, s) etc. We denote by $B_r(x)$, the Euclidean ball of radius r centered at x. When $x=0$, we will denote such a set by $B_r$. By $\partial B_r(x)$, we will denote the boundary of the set $B_{r}(x)$. For $(x,t)\in \mathbb {R}^{n+1}$, we let

$$\begin{aligned} Q_r(x,t)=Q_r+(x,t),\quad \text {where} \quad Q_r=B_r\times (-r^2,0]. \end{aligned}$$

The parabolic boundary of $Q_r(x,t)$ will be denoted by $\partial _p Q_r(x,t)$. The distance between two points in space time is defined as

$$\begin{aligned} |(x, t) - (y,s)| \overset{def}{=} |x-y| + |t-s|^{1/2}. \end{aligned}$$

(2.1)

For notational ease $\nabla u$ will refer to the quantity $\nabla _x u$. The partial derivative in t will be denoted by $\partial _t u$ and also at times by $u_t$. The partial derivative $\partial _{x_i} u$ will be denoted by $u_i$.

Given $0< \lambda < \Lambda$ and $f \in L^{q}$, $\mathcal {S}(\lambda , \Lambda , f)$ will denote the set of all functions u which solves the following differential inequalities in the $W^{2,q}$ viscosity sense

$$\begin{aligned} u_t-\mathcal {P}_{\lambda , \Lambda }^{+} (\nabla ^2 u) \le f \le u_t-\mathcal {P}_{\lambda , \Lambda }^{-} (\nabla ^2 u). \end{aligned}$$

(2.2)

We refer to [11] for the precise notion of $W^{2,1,q}$ viscosity solutions. The operators $\mathcal {P}_{\lambda , \Lambda }^{-}$ and $\mathcal {P}_{\lambda , \Lambda }^{+}$ appearing in (2.2) are the minimal and maximal Pucci operators, respectively, defined in the following way

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathcal {P}_{\lambda , \Lambda }^{-}( M)= \text {inf}_{\{A \in S(n): \lambda \mathbb {I} \le A \le \Lambda \mathbb {I}\}} \text {trace}\ (AM), \\ \mathcal {P}_{\lambda , \Lambda }^{+}( M)= \text {sup}_{\{A \in S(n): \lambda \mathbb {I} \le A \le \Lambda \mathbb {I}\}} \text {trace}\ (AM), \end{array}\right. } \end{aligned}$$

(2.3)

where S(n) the space of $n \times n$ symmetric matrices.

By $C^{2,1}_{loc}$, we refer to the class of functions $\phi$ such that $\nabla \phi , \nabla ^2 \phi$ and $\phi _t$ exists classically and are locally continuous. Likewise, $W^{2,1,q}_{\hbox { loc}}$ denotes the class of functions $\phi$ such that the distributional $\nabla \phi , \nabla ^2 \phi$ and $\phi _t$ are in $L^q_{\hbox { loc}}$.

We now turn our attention to the relevant notion of solution to (1.1). For $p \in \mathbb {R}^n -\{0\}$ and $X=[m_{ij}] \in S(n)$, following [9], let

$$\begin{aligned} F(q, X)= \bigg (\delta _{ij} + (p-2) \frac{q_i q_j}{|q|^2} \bigg ) m_{ij}. \end{aligned}$$

Then, as in [13], the lower semicontinuous relaxation $F_*$ is defined as follows

$$\begin{aligned} F_*(q,X)={\left\{ \begin{array}{ll} \qquad F(q,X)\quad &{}\hbox {if }q\not =0,\\ \inf _{a\in {{\mathbb {R}}}^n\setminus \{ 0\}}F(a,X)\quad &{}\hbox {if }q=0, \end{array}\right. }\end{aligned}$$

(2.4)

while the upper semicontinuous relaxation $F^{*}$ is defined as

$$\begin{aligned} F^{*}(q,X)={\left\{ \begin{array}{ll} \qquad F(q,X)\quad &{}\hbox {if }q\not =0,\\ \sup _{a\in {{\mathbb {R}}}^n\setminus \{ 0\}}F(a,X)\quad &{}\hbox {if }q=0. \end{array}\right. } \end{aligned}$$

(2.5)

Definition 2.1

We say that u is a $W^{2,1,q}$ viscosity sub-solution of (1.1) in a domain $Q=\Omega \times (0,T]$ in space-time, if given $\phi \in W^{2,1,q}$ such that $u-\phi$ has a local maximum at $(x_0, t_0) \in Q$, then one has

$$\begin{aligned} \text {ess}\limsup _{(x,t) \rightarrow (x_0,t_0)}\left( F^{*} ( \nabla \phi (x,t), \nabla ^2 \phi (x,t))-\varphi _t(x,t) - f(x,t)\right) \ge 0. \end{aligned}$$

(2.6)

In an analogous way, the notion of viscosity supersolution of (1.1) is defined using $F_*$ instead of $F^{*}$, and where $\limsup$ gets replaced by $\liminf$ in the Eq. (2.6) above. Finally, we say that u is a $W^{2,1,q}$ viscosity solution to (1.1) if it is both a subsolution and a supersolution. It is easy to deduce that if u is a $W^{2,1,q}$ viscosity solution to (1.1), then u belongs to the Pucci class $\mathcal {S}(\lambda , \Lambda , f)$ in the $W^{2,1,q}$ viscosity sense where

$$\begin{aligned} \lambda =\text {min}(1, p-1)\quad \hbox {and}\quad \Lambda = \text {max}(1, p-1). \end{aligned}$$

(2.7)

For a historical perspective, we would like to mention that the concept of $W^{2,1,q}$ viscosity solution was introduced in [11] for a general class of fully nonlinear parabolic equations of the type

$$\begin{aligned} F(D^2u, Du, u, x, t)- u_t=f(x,t) \in L^{q}. \end{aligned}$$

(2.8)

In [11], the Krylov-Safonov type Hölder regularity theory developed in [48] for $C^{2}$ viscosity solutions was extended to $W^{2,1,q}$ viscosity solutions of fully nonlinear parabolic equations of the type (2.8) above ( for $q\ge n+1$). Moreover, several existence and uniqueness results for $W^{2,1,q}$ viscosity solutions were established in [11]. It is to be noted that even in the time independent case, uniqueness for Dirichlet problem in general fails when $q < n$. See for instance [23, Notes in Chapter 9, page 254].

Now for the Eq. (1.1), in the case when $f=0$, it follows from Lemma 2.1 in [41] (see also Proposition 2.8 in [7]) that the following equivalent characterisation of viscosity solutions hold. Such an equivalent characterization will play a crucial role in our analysis.

Lemma 2.2

u is a $C^{2,1}$ viscosity solution to

$$\begin{aligned} \Delta _p^N u - u_t =0, \end{aligned}$$

in $\Omega _T \overset{def}{=}\Omega \times (0, T]$ if and only if whenever $(x_0,t_0) \in \Omega _T$ and $\phi \in C^{2,1}(\overline{\Omega _T})$ is such that:

• (a) $u(x_0, t_0) = \phi (x_0, t_0)$,

• (b) $u(x, t) > \phi (x, t)$ for $(x, t) \in \Omega _T$ , $(x, t) \ne (x_0, t_0)$,

then at the point $(x_0, t_0)$, we have:

• (i) $\phi _t \ge \Delta _p^N \phi$ if $\nabla \phi (x_0, t_0) \ne 0$,

• (ii) $\phi _t(x_0, t_0)\ge 0$ if $\nabla \phi (x_0, t_0)=0$, and $\nabla ^2\phi (x_0, t_0)=0.$

Moreover, we require that when testing from above, all the inequalities are reversed.

Lemma 2.2 can be thought of as the parabolic analogue of the following interesting result in [30] which states that for $p-$Laplace equation, i.e.

$$\begin{aligned} {\text {div}}(|\nabla u|^{p-2} \nabla u) =0, \end{aligned}$$

the notion of viscosity solution is only required to be tested at the points where the gradient of the test function does not vanish. This was crucially used in the proof of the corresponding gradient continuity result in [9] for the time independent case. In an entirely analogous way as in [9], Lemma 2.2 plays a critical role in the proof of the corresponding stability result in Lemma 3.3 below which is an important ingredient in the "phase separation" argument in the proof of Theorems 2.5 and 2.6. Note that the stability result in [11] does not apply in our situation because of the singular dependence of the normalized p-Laplacian operator on the gradient variable.

Finally, we mention that the Lorentz space $L(n+2,1)$ consists of those measurable functions $g:\mathbb {R}^{n+1}\rightarrow \mathbb {R}$ satisfying the condition

$$\begin{aligned} \int _{0}^{\infty } |\{(x,t): g(x,t) > s\}|^{\frac{1}{n+2}} \mathrm{{d}}s < \infty . \end{aligned}$$

Remark 2.3

For a function $f: \mathbb {R}^{n+1} \rightarrow \mathbb {R}$, we define the modified Riesz potential $\textbf{P}^f_q(x_0, t_0, r)$ as

(2.9)

where $Q_{\rho }(x_0, t_0) = B_{\rho }(x_0) \times (t_0-\rho ^2, t_0]$ denotes the standard parabolic cylinder with vertex at $(x_0,t_0)$ and width $\rho > 0$.

From Lemma 2.3 in [34] we get that for every $(x_0,t_0)\in \mathbb {R}^{n+1}$

$$\begin{aligned} \textbf{P}^f_q(x_0,t_0,r)\le c_1 \int _{0}^{\omega _n r^{n+2}} \left[ (|f|^q)^{**}(\rho ) \rho ^{\frac{q}{n+2}} \right] ^{\frac{1}{q}} \ \frac{\mathrm{{d}}\rho }{\rho }, \end{aligned}$$

(2.10)

where the constant c depends only on n, $\omega _n$ denotes the measure of the unit-ball, and $(|f|^q)^{**}$ is defined as

$$\begin{aligned} (|f|^q)^{**}(\rho )= \frac{1}{\rho } \int _{0}^{\rho } (|f|^q)^{*}(s) \mathrm{{d}s}, \end{aligned}$$

with $(|f|^q)^{*}(\rho )$ being the radial non-increasing rearrangement of $|f|^q$.

Now, when $f \in L(n+2,1)$, we have from an equivalent characterization of Lorentz spaces that

$$\begin{aligned} \int _{0}^{\infty } \left[ f^{**}(\rho ) \rho ^{\frac{q}{n+2}} \right] ^{\frac{1}{q}} \ \frac{\mathrm{{d}}\rho }{\rho }< \infty , \quad \text {for} q < n+2. \end{aligned}$$

(2.11)

In our subsequent analysis, we will consider the case when $q=n+1$ which ensures the validity of (2.11). It thus follows that

$$\begin{aligned} \textbf{P}^f_q(x_0,t_0,r) \rightarrow 0\ \hbox { as}\ r \rightarrow 0, \end{aligned}$$

(2.12)

when $f \in L(n+2, 1)$ and $q< n+2$.

We now fix a universal parameter which plays a crucial role in our compactness arguments. Let $\beta >0$ be the optimal Hölder exponent such that any arbitrary $C^{2,1}$ viscosity solution u of

$$\begin{aligned} u_t=\Delta ^N_p u\quad \hbox { is in}\ H^{1, \beta }_\mathrm{{loc}}. \end{aligned}$$

The fact that $\beta >0$ follows from the gradient Hölder continuity result established in [27]. We then fix some $\alpha >0$ such that

$$\begin{aligned} \alpha < \beta . \end{aligned}$$

(2.13)

For $\alpha \in (0,1]$ and $k \in {\mathbb {Z}}_+$, we also indicate by $H^{k, \alpha }$, the non isotropic parabolic Hölder space as defined in [40, Chapter 4]. More precisely, for a given domain $\Omega$ in space time, $H^{k, \alpha }(\Omega )$ consists of all functions $f: \Omega \rightarrow \mathbb {R}$ for which the following norm

$$\begin{aligned} ||f||_{H^{k, \alpha }(\Omega )}&:= \sum _{|\beta |+ 2j \le k} || \partial _x^\beta \partial _t^j f||_{L^{\infty }(\Omega )}\nonumber \\&\quad + \sum _{|\beta |+ 2j = k-1} \text {sup}_{\{(x, t_1), (x,t_2) \in \Omega : t_1 \ne t_2\}} \frac{|\partial _x^\beta \partial _t^j f(x, t_1) - \partial _x^\beta \partial _t^j f(x, t_2)|}{|t_1 - t_2|^{\frac{1+\alpha }{2}}} \nonumber \\&\quad + \sum _{|\beta | + 2j= k} \text {sup}_{\{(x_1, t_1), (x_2, t_2) \in \Omega \}} \frac{|\partial _x^\beta \partial _t^j f(x_1, t_1) - \partial _x^\beta \partial _t^j f(x_2, t_2)|}{|x_1-x_2|^{\alpha } +|t_1-t_2|^{\alpha /2}} <\infty . \end{aligned}$$

(2.14)

Over here, $\beta$ is a multi-index of the form $(\beta _1, ..., \beta _n)$ where each $\beta _i \in {\mathbb {Z}}$,, $\beta _i \ge 0$, $|\beta |:=\sum \beta _i$ and $\partial _x^\beta f:= \partial _{x_1}^{\beta _1}\partial _{x_2}^{\beta _2}....\partial _{x_n}^{\beta _n} f$. In our analysis, we will also need the following notion.

Definition 2.4

Given a modulus of continuity $\omega :[0, \infty ) \rightarrow [0, \infty )$ and $\eta \in (0,1]$, we say that $\omega$ is $\eta$-decreasing if

$$\begin{aligned} \frac{\omega (t_1)}{t_1^{\eta }} \ge \frac{\omega (t_2)}{t_2^{\eta }}, \text {for all }t_1 \le t_2.\end{aligned}$$

2.1 Statement of the Main Results

We now state our first main result. This result corresponds to the regularity estimate in the borderline case, i.e., gradient continuity estimates with dependence on the $L(n+2,1)$ norm of f.

Theorem 2.5

For a given $p>1$, let u be a $W^{2,1,n+1}$ viscosity solution of (1.1) in $Q_1$ where $f \in L(n+2,1)$. Then $\nabla u$ is continuous inside of $Q_1$. Moreover, the following borderline estimates hold

$$\begin{aligned} {\left\{ \begin{array}{ll} |\nabla u(x_0,t_0)| \le C( \textbf{P}^{f}_{n+1} (x_0, t_0, 1/2) + \Vert u\Vert _{L^{\infty }(Q_1)})\ \text { {for} }(x_0, t_0) \in Q_{1/2}, \\ |\nabla u(x_1,t_1) - \nabla u(x_2,t_2) | \\ \le C(n, p) ( \Vert u\Vert _{L^{\infty }(Q_{3/4})} |(x_1, t_1) - (x_2, t_2)|^{\alpha /4} + \sup _{(x,t) \in Q_1} \textbf{P}^{f}_{n+1} (x,t, 4 |(x_1, t_1)-(x_2, t_2)|^{1/4})),\\ {\text {sup}}_{\{(x, t_1), (x, t_2) \in Q_{1/2}: t_1 \ne t_2\}} \frac{|u(x, t_1) - u(x, t_2)|}{|t_1-t_2|^{1/2}} \le C({\text {sup}}_{\{(x,t) \in Q_1\}} \textbf{P}^{f}_{n+1} (x,t, 1/2) + \Vert u\Vert _{L^{\infty }(Q_1)}).\end{array}\right. }\nonumber \\ \end{aligned}$$

(2.15)

whenever $(x_1,t_1), (x_2, t_2) \in Q_{1/2}$, and where $\alpha$ is as in (2.13).

Note that the second estimate in (2.15) above provides a modulus of continuity for $\nabla u$ in view of (2.12).

In the case $f \in L^{m}(\mathbb {R}^{n+1})$ with $m>n+2$, we obtain the following regularity result that improves Theorem 1.2 in [3].

Theorem 2.6

For $p>1$ and $m>n+2$, let u be a $W^{2,1,m}$ viscosity solution of (1.1) in $Q_1$, where $f \in L^{m}$. Then, $\nabla u \in C^{\alpha _0}(\overline{Q_{1/2}})$ for some $\alpha _0=\alpha _0(n, p, m)$. Moreover, we have that the following estimates hold

$$\begin{aligned} {\left\{ \begin{array}{ll} \Vert \nabla u\Vert _{H^{\alpha _0}(Q_{1/2})} \le C(n, p, \Vert f\Vert _{L^m}, \Vert u\Vert _{L^{\infty }(Q_1)}), \\ {\text {sup}}_{\{(x, t_1), (x, t_2) \in Q_{1/2}: t_1 \ne t_2\}} \frac{|u(x, t_1) - u(x, t_2)|}{|t_1-t_2|^{\frac{1+\alpha _0}{2}}} \le C(n, p, \Vert f\Vert _{L^m}, \Vert u\Vert _{L^{\infty }(Q_1)}).\end{array}\right. }\nonumber \\\end{aligned}$$

(2.16)

3 Proof of the Main Results

3.1 Proof of Theorem 2.5

Before proceeding further, we would like to alert the reader that in what follows, the number q that appears in Lemmas 3.1, 3.2 and 3.3 equals $n+1$.

We now state our first relevant approximation lemma which plays a very crucial role in the separation of phases. This is the parabolic version of Lemma 3.1 in [9] and corresponds to the non-degenerate phase in our final iteration argument in the proof of Theorem 2.5.

Lemma 3.1

Let u be a $W^{2, 1, q}$ viscosity solution of

$$\begin{aligned} \bigg (\delta _{ij} + (p-2) \frac{(\delta u_i+A_i)(\delta u_j +A_j)}{ |\delta \nabla u+A|^2} \bigg ) u_{ij}-u_t=f\quad \hbox { in}\ Q_1, \end{aligned}$$

(3.1)

with $|u| \le 1$ and $|A| \ge 1$. Given $\tau >0$, there exists $\delta _0=\delta _0(\tau )>0$ such that if

$$\begin{aligned} \max \left( \delta , \left( \frac{1}{|Q_{3/4}|} \int _{Q_{3/4}} |f|^q \right) ^{1/q} \right) \le \delta _0, \end{aligned}$$

then $\Vert w-u\Vert _{L^{\infty }(Q_{1/2})} \le \tau$, for some $w \in C^{2,1}(\overline{Q_{1/2}})$ with universal $C^{2,1}$ bounds depending only on n, p and independent of |A|.

Proof

We argue by contradiction. If not, then there exists $\tau _0>0$ and a sequence of pairs $\{u_k, f_k \}$ that solves (3.1) corresponding to $\{\delta _k, A_k\}$ with $\delta _k \rightarrow 0, f_k \rightarrow 0\ \hbox { in}\ L^q(Q_{3/4})$ as $k \rightarrow \infty$ and such that $u_k's$ are not $\tau _0$ close to any such w. We note that the equation satisfied by $u_k$ can be rewritten as

$$\begin{aligned} \bigg (\delta _{ij} +(p-2) \frac{({\tilde{\delta }}_k (u_k)_i + (\tilde{A}_k)_i ) ({\tilde{\delta }}_k (u_k)_j + ({\tilde{A}}_k)_j)}{ |\tilde{\delta }_k \nabla u_k + {\tilde{A}}_k|^2} \bigg ) (u_k)_{ij}-(u_k)_t =f_k,\nonumber \\ \end{aligned}$$

(3.2)

where ${\tilde{\delta }}_k = \frac{\delta _k}{|A_k|}$ and ${\tilde{A}}_k= \frac{A_k}{|A_k|}$. Since $|A_k| \ge 1$, we have ${\tilde{\delta }}_k \rightarrow 0$ as $k \rightarrow \infty$.

Now it follows that for each k, $u_k \in \mathcal {S}(\lambda , \Lambda , f_k)$ with $\lambda , \Lambda$ as in (2.7) and moreover we have that $\Vert f_k\Vert _{L^{q}(Q_{3/4})}$ is uniformly bounded independent of k. Thus from the Krylov-Safonov-type Hölder estimates as in [11, Lemma 5.1] (see also [48]), we have that $u_k$’s are uniformly Hölder continuous in $\overline{Q_{3/5}}$. Therefore, upto a subsequence, by Arzela-Ascoli we may assume that $u_k \rightarrow u_0$ uniformly on $Q_{3/5}$ and, moreover, we can also assume that ${\tilde{A}}_k \rightarrow A_0$ (by possibly passing to another subsequence) such that $|A_0|=1$.

We now claim that $u_0$ solves

$$\begin{aligned} \bigg (\delta _{ij} + (p-2) (A_0)_i (A_0)_j \bigg ) (u_0)_{ij} -(u_0)_t=0. \end{aligned}$$

(3.3)

By standard theory, it suffices to check that $u_0$ is a $C^{2}-$viscosity solution to the above limiting equation. We note that the stability result in Theorem 6.1 in [11] cannot be directly applied here, because of the singular dependence of the operator in the “gradient” variable. Similar to the elliptic case as in [9], we thus argue as follows.

Let $\phi$ be a $C^{2,1}$ function such that the graph of $\phi$ strictly touches the graph of $u_0$ from above at $(x_0, t_0) \in Q_{1/2}$. We show that at $(x_0,t_0)$

$$\begin{aligned} \bigg (\delta _{ij} + (p-2) (A_0)_i (A_0)_j \bigg ) \phi _{ij}-\phi _t \ge 0. \end{aligned}$$

(3.4)

Suppose that is not the case. Then, there exists $\varepsilon , \eta , r>0$ small enough such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \bigg (\delta _{ij} + (p-2) (A_0)_i (A_0)_j \bigg ) \phi _{ij}-\phi _t \le - \varepsilon \ \hbox { in}\ Q_r(x_0,t_0), \\ \phi - u_0 \ge \eta \ \hbox { on}\ \partial _p Q_r(x_0,t_0). \end{array}\right. } \end{aligned}$$

(3.5)

We now show that for every k, there exists a perturbed test function $\phi + \phi _k$, with $\phi _k \in W^{2,1,q}$, such that

$$\begin{aligned} F_k^{*} ( \nabla (\phi {+}\phi _k), \nabla ^{2} (\phi {+} \phi _k)){-}(\phi {+} \phi _k)_t {\le } f_k - \varepsilon \ \hbox { in}\ Q_r(x_0,t_0),\nonumber \\ \end{aligned}$$

(3.6)

where $F_k^{*}$ is the upper semicontinuous relaxation of the operator in (3.2). Moreover, we can also ensure that $(\phi + \phi _k) - u_k$ has a minimum in $Q_{r}(x_0, t_0) \setminus \partial _p Q_r(x_0, t_0)$ for large enough $k's$. This would then contradict the viscosity formulation for $u_k$ for such $k's$ and hence (3.4) would follow.

Therefore, under the assumption that (3.5) holds, we now show the validity of (3.6). We first observe that from (3.5), the following differential inequality holds

$$\begin{aligned} F_k^{*} ( \nabla (\phi +\phi _k), \nabla ^{2} (\phi + \phi _k)) - (\phi +\phi _k)_t\le & {} \mathcal {P}_{\lambda , \Lambda }^{+} (\nabla ^2 \phi _k) - (\phi _k)_t +C_0 |{\tilde{A}}_k - A_0|\nonumber \\{} & {} + C_0 {\tilde{\delta }}_k |\nabla \phi _k| + C_0 {\tilde{\delta }}_k |\nabla \phi | - \varepsilon , \end{aligned}$$

(3.7)

where $C_0=C_0(\Vert \nabla ^2 \phi \Vert , p, n)$ and $\lambda , \Lambda$ are as in (2.7). Inequality (3.7) will follow by adding and subtracting $\bigg (\delta _{ij} + (p-2) (A_0)_i (A_0)_j \bigg ) \phi _{ij}$, by using (3.5), and then by splitting the considerations depending on whether $\Big |A_0 - ({\tilde{A}}_k + \tilde{\delta }_k (\nabla \phi + \nabla \phi _k))\Big | < 1/2$ or $> 1/2$. This is similar to the argument as in $(3.9)-(3.11)$ in the proof of Lemma 3.1 in [9]. We nevertheless provide the details for the sake of completeness.

Case 1: When $|A_0 - ({\tilde{A}}_k + {\tilde{\delta }}_k (\nabla \phi + \nabla \phi _k))| < 1/2$.

In this case, we first note by triangle inequality that $|(\tilde{A}_k + {\tilde{\delta }}_k (\nabla \phi + \nabla \phi _k)) |>\frac{1}{2}$ since $|A_0| = 1$. Now we have that the function

$$\begin{aligned} a \rightarrow (p-2) \frac{ a_i a_j}{|a|^2},\ \text {for }|a|> 1/2, \end{aligned}$$

is Lipschitz continuous, therefore it follows that

$$\begin{aligned}{} & {} \bigg (\delta _{ij} + (p-2) \frac{{\tilde{A}}_k + {\tilde{\delta }}_k ( \nabla \phi +\nabla \phi _k)}{| {\tilde{A}}_k + {\tilde{\delta }}_k( \nabla \phi + \nabla \phi _k)|^2} \bigg ) (\phi + \phi _k)_{ij}- \bigg (\delta _{ij} + (p-2) (A_0)_i (A_0)_j \bigg ) \phi _{ij} \nonumber \\{} & {} \le \mathcal {P}_{\lambda , \Lambda }^{+} (\nabla ^2 \phi _k) + C \Vert \nabla ^2 \phi \Vert _{L^{\infty }} ( |{\tilde{A}}_k - A_0| + \tilde{\delta }_k |\nabla \phi _k| + {\tilde{\delta }}_k |\nabla \phi |). \end{aligned}$$

(3.8)

Thus by adding and subtracting $\bigg (\delta _{ij} + (p-2) (A_0)_i (A_0)_j \bigg ) \phi _{ij}$ to $F_{k}^*( \nabla (\phi + \phi _k), \nabla ^2(\phi + \phi _k)) - (\phi +\phi _k)_t$ and by using (3.5) and (3.8), we observe that (3.7) follows in this case.

Case 2: When $|A_0 - ({\tilde{A}}_k + {\tilde{\delta }}_k (\nabla \phi + \nabla \phi _k))| >1/2$.

In this case, we note that since

$$\begin{aligned}&F_{k}^*( \nabla (\phi + \phi _k), \nabla ^2(\phi + \phi _k))- \bigg (\delta _{ij} + (p-2) (A_0)_i (A_0)_j \bigg ) \phi _{ij} \nonumber \\&\le \mathcal {P}_{\lambda , \Lambda }^{+} (\nabla ^2 \phi _k) + C \Vert \nabla ^2 \phi \Vert _{L^{\infty }} \nonumber \\&\le \mathcal {P}_{\lambda , \Lambda }^{+} (\nabla ^2 \phi _k) + C\Vert \nabla ^2 \phi \Vert _{L^{\infty }}|A_0 - ({\tilde{A}}_k + {\tilde{\delta }}_k (\nabla \phi + \nabla \phi _k))|\nonumber \\ {}&\text { (using }|A_0 - ({\tilde{A}}_k + {\tilde{\delta }}_k (\nabla \phi + \nabla \phi _k))| >1/2)\nonumber \\&\le \mathcal {P}_{\lambda , \Lambda }^{+} (\nabla ^2 \phi _k) + C\Vert \nabla ^2 \phi \Vert _{L^{\infty }} ( |A_0 - {\tilde{A}}_k| + \tilde{\delta }_k |\nabla \phi | + {\tilde{\delta }}_k |\nabla \phi _k|),\ \text { (by triangle inequality)} \end{aligned}$$

(3.9)

we again obtain by adding and subtracting $\bigg (\delta _{ij} + (p-2) (A_0)_i (A_0)_j \bigg ) \phi _{ij}$ to $F_{k}^*( \nabla (\phi + \phi _k), \nabla ^2(\phi + \phi _k)) - (\phi + \phi _k)_t$ and by using (3.5) that (3.7) follows in this case as well.

Subsequently, we let $\phi _k$ be a strong solution to the following boundary value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathcal {P}_{\lambda , \Lambda }^{+} (\nabla ^2 \phi _k) + C_0 |\tilde{A}_k - A_0| + C_0 {\tilde{\delta }}_k |\nabla \phi _k| + C_0 \tilde{\delta }_k |\nabla \phi | -(\phi _k)_t= f_k\ \hbox { in}\ Q_r(x_0,t_0), \\ \phi _k=0\ \hbox { on}\ \partial _p Q_r(x_0, t_0). \end{array}\right. } \end{aligned}$$

The existence of such strong $W^{2,1,q}$ solution is guaranteed by Theorem 2.8 in [11]. Therefore, with such $\phi _k$, we have that (3.6) holds.

We now observe that since $f_k \rightarrow 0$ in $L^{q}$ and also $\tilde{\delta }_k , |{\tilde{A}}_k - A_0| \rightarrow 0$, from the generalized maximum principle as in [11, Proposition 2.6], we have that

$$\begin{aligned} \Vert \phi _k\Vert _{L^{\infty }(Q_r(x_0, t_0))} \rightarrow 0\ \text {as }k \rightarrow \infty . \end{aligned}$$

Since $\phi - u_0$ has a strict minimum at $(x_0, t_0)$ in $Q_{1/2}$ and consequently in $Q_r(x_0, t_0)$, it follows for large $k's$ that $(\phi + \phi _k) - u_k$ has a minimum in $Q_r(x_0, t_0) \setminus \partial _p Q_r(x_0, t_0)$ (since $\phi _k \equiv 0$ on $\partial _p Q_r(x_0, t_0)$ and $\phi -u_0 \ge \eta$ on $\partial _p Q_r(x_0, t_0)$). From this and in view of the arguments immediately after (3.6) above, we can assert that (3.4) follows.

Now by an analogous argument, we can assert that the opposite inequality holds in (3.4) in the situation when the graph of $\phi$ touches the graph of $u_0$ from below at $x_0$ and consequently it follows that $u_0$ solves (3.3). Moreover, since $|u_0| \le 1$, we have from the classical theory that $u_0$ is smooth with universal $C^{2,1}$ bounds in $Q_{1/2}$. This would then be a contradiction for large enough $k'$s since $u_k \rightarrow u_0$ uniformly. This finishes the proof of the lemma. $\square$

As a consequence of Lemma 3.1, we have the following result on the affine approximation of u at (0, 0), provided there is a sufficiently large non-degenerate slope at a certain scale. As the reader will see, this is ensured by the fast geometric convergence of the approximations.

Lemma 3.2

Let u be a viscosity solution of

$$\begin{aligned} \bigg (\delta _{ij}+ (p-2) \frac{u_i u_j}{|\nabla u|^2} \bigg ) u_{ij}-u_t=f\quad \hbox { in}\ Q_1, \end{aligned}$$

with $u(0,0)=0$. There exists a universal $\delta _0>0$ such that if for some $A \in \mathbb {R}^n$, satisfying $M \ge |A| \ge 2$, we have

$$\begin{aligned} \Vert u- \langle A,x\rangle \Vert _{L^{\infty }(Q_1)} \le \delta _0, \end{aligned}$$

and also

then there exists an affine function $L_0$ with universal bounds depending also on M such that

$$\begin{aligned} |u(x,t)- L_0(x) | \le C(|x|^2+|t|)^{\frac{1}{2}} K((|x|^2+|t|)^{\frac{1}{2}} ). \end{aligned}$$

(3.10)

Here

and $\alpha$ is the universal parameter as in (2.13). In view of Remark 2.3, we note that for $f \in L(n+2, 1)$, we have that $K(r) \rightarrow 0$ as $r \rightarrow 0$.

Proof

We will show that for for every $k=0,1,2, \ldots$, there exist linear functions ${\tilde{L}}_k x\overset{def}{=} \langle A_k, x\rangle$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \Vert u-{\tilde{L}}_k\Vert _{L^{\infty }(Q_{r^k})} \le r^k \omega (r^k), \\ |A_k- A_{k-1}| \le C \omega (r^{k-1}), \end{array}\right. } \end{aligned}$$

(3.11)

for some $r<1$ universal, independent of $\delta _0$. Here we let for a given k,

$$\begin{aligned} \omega (r^k)= \frac{1}{\delta _0} \sum _{i=0}^k r^{i \alpha } \omega _1\left( \frac{3}{4}r^{k-i}\right) , \end{aligned}$$

(3.12)

with $\omega _1$ defined in the following way

We note that $\delta _0$ is to be fixed later. We also let $A_0\overset{def}{=} A$. Now, suppose $A_k$ exists upto some k with the bounds as in (3.11). Then, we observe that

$$\begin{aligned} |A_k|&\ge |A_0| - ( |A_1- A_0| +\ldots + |A_k- A_{k-1}|) \nonumber \\&> 2 - C \sum \omega (r^i)> 2 - \frac{C}{\delta _0} \sum \omega _1 \left( \frac{3}{4}r^i\right) \ \left( \text {using the Cauchy product formula}\right) \nonumber \\&\ge 2 - C_1 \delta _0 > 1\ \left( \text {if }\delta _0\hbox { is small enough}\right) . \end{aligned}$$

(3.13)

In the last inequality in (3.13) above we also used the fact that

(3.14)

Note that the last inequality in (3.14) is a consequence of the following estimate

which in turns follows by breaking the integral in the above expression into integrals over dyadic subintervals of the type $[\frac{3}{4} r^{i}, \frac{3}{4} r^{i-1}]$.

Thus the estimate in (3.13) ensures that the non-degeneracy condition in Lemma 3.1 holds for every k. We prove the claim in (3.11) by induction. From the hypothesis of the lemma, the case when $k=0$ is easily verified with $A_0=A$ with our choice of $\omega$. Let us now assume that the claim as in (3.11) holds upto some k. We then consider

$$\begin{aligned} v= \frac{(u - {\tilde{L}}_k)(r^k x, r^{2k}t)}{ r^k \omega (r^k)}, \end{aligned}$$

which solves

$$\begin{aligned} \bigg (\delta _{ij} + (p-2) \frac{(\omega (r^k) v_i + (A_k)_i)( \omega (r^k) v_j + (A_k)_j)}{| \omega (r^k) \nabla v+ A_k|^2} \bigg ) v_{ij}-v_t= \frac{r^k}{ \omega (r^k)} f(r^k x, r^{2k}t).\nonumber \\ \end{aligned}$$

(3.15)

For ease of notation, by $\tilde{L}(r^k x, r^{2k}t)$ we mean $\tilde{L}(r^kx)$ and from now on we will use this notation provided that there is no ambiguity with it. Now, by a change of variable formula and the definition of $\omega$ it follows that, with

$$\begin{aligned} f_k(x, t)\overset{def}{=} \frac{r^k}{ \omega (r^k)} f(r^k x, r^{2k}t), \end{aligned}$$

we have

(3.16)

Moreover

$$\begin{aligned} \omega (r^k) \le \sum \omega (r^i) \le C_0 \delta _0. \end{aligned}$$

Therefore, v satisfies an equation for which the conditions in Lemma 3.1 are satisfied. Consequently for a given $\tau >0$, we can find $\delta _0>0$ such that for some w with universal $C^{2,1}$ bounds we have that $\Vert w-v\Vert _{L^{\infty }(Q_{1/2})} \le \tau$. Now, given that w has uniform $C^{2,1}$ bound, there exists a universal $C>0$ such that

$$\begin{aligned} |w(x,t)- w(0,0)- Lx| \le C\left( |x|^2+|t|\right) , \end{aligned}$$

(3.17)

where L is the linear approximation for w at (0, 0). We then choose $r>0$ small enough such that

$$\begin{aligned} Cr^2= \frac{r^{1+\alpha }}{2}, \end{aligned}$$

(3.18)

where $\alpha$ is as in (2.13). Subsequently, we let $\tau = \frac{r^{1+\alpha }}{4}$ which decides the choice of $\delta _0$. Then using (3.17) and (3.18), by an application of triangle inequality we have

$$\begin{aligned} \Vert v- L\Vert _{L^{\infty }(Q_r)}&\le \Vert w-v\Vert _{L^{\infty }(Q_r)} + \Vert w-w(0,0) -Lx\Vert _{L^{\infty }(Q_r)} +|w(0,0)|\nonumber \\&\le \frac{r^{1+\alpha }}{2} + 2\tau \le r^{1+\alpha }. \end{aligned}$$

(3.19)

Note that in (3.19) above, we used that $|w(0,0)| \le \tau$ which is a consequence of the fact that $v(0,0)=0$ and also that $\Vert w-v\Vert _{L^{\infty }(Q_{1/2})} \le \tau$.

Consequently, by scaling back to u we obtain

$$\begin{aligned} \Vert u - {\tilde{L}}_{k+1}\Vert _{L^{\infty }(Q_{r^{k+1}})} \le r^{k+1} r^{\alpha } \omega (r^k) \le r^{k+1} \omega (r^{k+1}), \end{aligned}$$

(3.20)

where ${\tilde{L}}_{k+1}(x)\overset{def}{=} {\tilde{L}}_k + r^k \omega (r^k) L\bigg (\frac{x}{r^k} \bigg )$. Note that in the last inequality in (3.20) we also used the following $\alpha -$decreasing property of $\omega$ ( see Definition 2.4)

$$\begin{aligned} r^{\alpha } \omega (r^k) \le \omega (r^{k+1}), \end{aligned}$$

(3.21)

which is easily seen from the expression of $\omega$ as in (3.12). This verifies the induction step. The conclusion now follows by a standard real analysis argument as in the proof of Lemma 4.9 in [2]. $\square$

The next result is an improvement of flatness result that allows to handle the case when the affine approximation have small slopes at a “kth-step”. This corresponds to the degenerate alternative in the iterative argument in the proof of the main result Theorem 2.5.

Lemma 3.3

Let u be a solution to

$$\begin{aligned} \bigg (\delta _{ij}+ (p-2) \frac{u_i u_j}{|\nabla u|^2} \bigg ) u_{ij}-u_t=f\quad \text {in }Q_1, \end{aligned}$$

(3.22)

with $|u| \le 3$ and $u(0,0)=0$. There exists a universal $\varepsilon _0>0$ such that if

(3.23)

then there exists an affine function L, with universal bounds, and a universal $\eta \in (0,1)$ such that

$$\begin{aligned} \Vert u- L\Vert _{L^{\infty }(Q_{\eta })} \le \delta _0 \eta ^{1+\alpha }. \end{aligned}$$

Here $\delta _0>0$ is as in Lemma 3.2 above. Without loss of generality we may take $0<\varepsilon _0 < \delta _0^2$.

Proof

We first show that given $\kappa >0$, there exists $\varepsilon _0>0$ such that if u solves (3.22) and f satisfies the bound in (3.23), then there exists a $C^{2,1}$ viscosity solution w to the normalized p-parabolic equation (1.6) such that

$$\begin{aligned} \Vert w-u\Vert _{L^{\infty }(Q_{1/2})} \le \kappa . \end{aligned}$$

(3.24)

Assume that (3.24) actually holds. It then follows from the $H^{1, \beta }$ regularity result in [27] that there exists an affine function L such that

$$\begin{aligned} |w(x,t) -L(x)| \le C(|x|^2+|t|)^{\frac{1+\beta }{2}}. \end{aligned}$$

We now choose $\eta >0$ such that

$$\begin{aligned} C\eta ^{1+\beta }= \frac{\delta _0}{2} \eta ^{1+\alpha }\ \left( \text {This crucially uses }\alpha < \beta \right) . \end{aligned}$$

Subsequently, we choose $\kappa = \frac{\delta _0}{2} \eta ^{1+\alpha }$, and this decides the choice of $\varepsilon _0$. The conclusion of the lemma now follows by an application of the triangle inequality.

We are now going to prove (3.24). Suppose on the contrary, (3.24) does not hold. Then there exists $\kappa _0>0$ and a sequence of pairs $\{u_k, f_k\}$ which solves (3.22) such that $u_k$ is not $\kappa _0$ close to any such w. Notice that (3.23) implies, for each $k\in \mathbb {N}$, that

$$\begin{aligned} \Vert f_k\Vert _{L^{q}(Q_{3/4})} < \frac{C}{k}. \end{aligned}$$

Then, from uniform Krylov-Safonov-type Hölder estimates as in [11, Lemma 5.1] (see also [48]) and Arzela-Ascoli, it follows that $u_k \rightarrow u_0$ uniformly in $Q_{\frac{1}{2}}$ upto a sub-sequence. We now make the claim that $u_0$ solves (1.6)., i.e.

$$\begin{aligned} \bigg (\delta _{ij}+ (p-2) \frac{(u_0)_i (u_0)_j}{|\nabla u_0|^2} \bigg ) (u_0)_{ij}-(u_0)_t=0\quad \text {in} Q_{\frac{1}{2}}, \end{aligned}$$

(3.25)

in the viscosity sense. Once the claim is established, this would then be a contradiction for large enough k’s and thus (3.24) would follow.

The proof is similar to that of the Claim in Lemma 3.1. As before, we note that the stability result in Theorem 6.1 in [11] cannot be directly applied because the operator $\Delta _{p}^N$ does not satisfy the structural assumptions in [11] because of singular dependence in the “gradient” variable.

Let $\phi$ be a $C^{2,1}$ test function which strictly touches the graph of $u_0$ from above at some point $(x_0, t_0) \in Q_{1/2}$. In view of the equivalent characterization of viscosity solutions to (1.6) as in Lemma 2.2, it suffices to consider the following two cases:

• (1) $\nabla \phi (x_0, t_0) \ne 0$, and

• (2) $\nabla \phi (x_0, t_0)=0, \nabla ^2 \phi (x_0, t_0) = 0$.

For Case (1), we show that

$$\begin{aligned} \Delta _{p}^N \phi (x_0,t_0) -\phi _t(x_0, t_0) \ge 0. \end{aligned}$$

(3.26)

Suppose such is not the case. Then there exists $\varepsilon ,r, \delta >0$ small enough such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta _{p}^N \phi (x) - \phi _t \le - \varepsilon \ \hbox { in}\ Q_r(x_0, t_0), \\ \phi - u_0 > \delta \ \hbox { on}\ \partial Q_r(x_0, t_0). \end{array}\right. } \end{aligned}$$

(3.27)

Moreover, we can also assume that in $Q_r(x_0, t_0)$, we have that

$$\begin{aligned} |\nabla \phi | \ge \kappa >0. \end{aligned}$$

(3.28)

We now show that for every k, there exists perturbed test functions $\phi + \phi _k$ with $\phi _k \in W^{2,1,q}_{loc} (Q_r(x_0, t_0))$ such that

$$\begin{aligned} F^{*} ( \nabla (\phi {+}\phi _k), \nabla ^{2} (\phi {+} \phi _k)) {-} (\phi {+} \phi _k)_t {\le } f_k - \varepsilon \ \hbox { in}\ Q_r(x_0, t_0),\ \text { with} F^{*}\hbox { as in }(2.5).\nonumber \\ \end{aligned}$$

(3.29)

Moreover, we can also ensure that $(\phi + \phi _k) - u_k$ has a minimum in $Q_{r}(x_0,t_0)$ for large enough $k's$. This would then contradict the viscosity formulation for $u_k$, and hence (3.26) would follow.

Hence, under the assumption that (3.27) is valid, we now turn our attention to establish (3.29). We first observe that because of (3.27), (3.28), the following inequality holds,

$$\begin{aligned}&F^{*} ( \nabla (\phi +\phi _k), \nabla ^{2} (\phi + \phi _k)) - (\phi +\phi _k)_t \le \mathcal {P}^{+}_{\lambda , \Lambda } (\nabla ^2 \phi _k) - (\phi _k)_t \nonumber \\&\quad + C(\kappa , \Vert \nabla ^2 \phi \Vert ) |\nabla \phi _k| -\varepsilon , \end{aligned}$$

(3.30)

with $\lambda , \Lambda$ as in (2.7). Here $\mathcal {P}_{\lambda , \Lambda }^{+}$ is the maximal Pucci operator defined as in (2.3). This inequality again follows by an argument similar to that used in deriving (3.7) in the proof of Lemma 3.1 by adding and subtracting $\Delta _{p}^N \phi$, by using (3.27) and then by splitting considerations depending on whether

$$\begin{aligned} |\nabla \phi _k| < \kappa /2\ \text {or}\ > \kappa /2. \end{aligned}$$

At this point, given k, we look for $\phi _k$ which is a strong solution to

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathcal {P}^{+}_{\lambda , \Lambda } (\nabla ^2 \phi _k) + C(\kappa , \Vert \nabla ^2 \phi \Vert ) |\nabla \phi _k|-( \phi _k)_t= f_k\ \hbox { in}\ Q_r(x_0, t_0), \\ \phi _k= 0\ \text {on }\partial _p Q_r(x_0, t_0). \end{array}\right. } \end{aligned}$$

(3.31)

Over here, we remind the reader that $\lambda , \Lambda$ is as in (2.7). The existence of such strong solutions is again guaranteed by Theorem 2.8 in [11]. Moreover since $f_k \rightarrow 0$ in $L^{q}$, therefore from the generalized maximum principle as in [11, Proposition 2.6] we have that

$$\begin{aligned} \Vert \phi _k\Vert _{L^{\infty }(Q_r(x_0,t_0))} \rightarrow 0\ \text {as }k \rightarrow \infty . \end{aligned}$$

Now, since $\phi - u_0$ has a strict minimum at $(x_0, t_0)$, it follows that for large $k's$ that $(\phi + \phi _k) - u_k$ would have a minimum in the inside of $Q_r(x_0,t_0)$ (since $\phi _k \equiv 0$ on $\partial Q_r(x_0, t_0)$ and $\phi -u_0 > \delta$ on $\partial Q_r(x_0, t_0)$). However, because of (3.30) and (3.31) we also have that (3.29) holds which violates the viscosity formulation for $u_k$’s for large enough $k's$. Thus (3.26) holds in this case.

For Case (2), we only need to show that

$$\begin{aligned} \phi _t(x_0, t_0) \le 0, \end{aligned}$$

(3.32)

Suppose that (3.32) does not hold. Then from the continuity of the derivatives of $\phi$, it follows that there exists $\gamma , \delta , r>0$ such that

$$\begin{aligned} \phi _t(x_0,t_0)&{\ge } \gamma \quad \hbox { in}\ Q_r(x_0,t_0),\\ \varphi -u_0&>\delta \quad \text {on }\partial _p Q_r(x_0,t_0)\hbox { and}\\ \mathcal {P}^{+}_{\lambda , \Lambda } (\nabla ^2 \phi )&{<} \frac{\gamma }{2} \quad \text {in }Q_r(x_0,t_0),\hbox { noting that this can be ensured since }\nabla ^2 \phi (x_0, t_0){=}0. \end{aligned}$$

For a given k, we consider $\phi _k$, which is a strong solution to

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathcal {P}^{+}_{\lambda , \Lambda } (\nabla ^2 \phi _k) -(\phi _k)_t= f_k\ \text {in }Q_r(x_0, t_0), \\ \phi _k= 0\ \text {on }\partial Q_r(x_0, t_0). \end{array}\right. } \end{aligned}$$

(3.33)

As before, from the generalized maximum principle we have that

$$\begin{aligned} \Vert \phi _k\Vert _{L^{\infty }(Q_r(x_0,t_0))} \rightarrow 0\ \text {as }k \rightarrow \infty . \end{aligned}$$

Then,

$$\begin{aligned} F^{*} ( \nabla (\phi +\phi _k), \nabla ^{2} (\phi + \phi _k)) - (\phi + \phi _k)_t\le & {} \mathcal {P}^{+}_{\lambda , \Lambda } (\nabla ^2 \phi ) -\phi _t\\{} & {} + \mathcal {P}^{+}_{\lambda , \Lambda } (\nabla ^2 \phi _k) -(\phi _k)_t\\\le & {} \frac{\gamma }{2} -\gamma +f_k\le f_k-\frac{\gamma }{2}. \end{aligned}$$

As before, since $\phi - u_0$ has a strict minimum at $(x_0, t_0)$, it follows that for large $k's$ that $(\phi + \phi _k) - u_k$ would have a minimum in $Q_r(x_0,t_0) \setminus \partial _p Q_r(x_0, t_0)$. On the other hand,

$$\begin{aligned} \limsup _{(x,t) \rightarrow (x_0,t_0)}\left( F^{*} ( \nabla (\phi +\phi _k)(x,t), \nabla ^2 (\phi +\phi _k)(x,t))-(\phi +\phi _k)_t - f_k(x,t)\right) \le -\frac{\gamma }{2}. \end{aligned}$$

This is a contradiction to the viscosity formulation for all such $u_k$’s. Thus (3.32) holds in this case and from Lemma 2.2 we can now assert that $u_0$ is a viscosity subsolution to (1.6). In an analogous way, we can show that $u_0$ is a viscosity supersolution to (1.6) and consequently in view of the arguments after (3.25), the conclusion follows. $\square$

With this Lemma 3.2 and Lemma 3.3 in hand, we now proceed with the proof of our main result. For notational convenience, from now on, sometimes we will denote a point (x, t) in space time by X. Also we set $|X| \overset{def}{=} \text {max} (|x|, |t|^{1/2})$. Note that $|X| \approx |x| + |t|^{1/2}.$

Proof of Theorem 2.5

It suffices to establish the following affine approximation for u at (0, 0). More precisely, we will show there exists an affine function ${\tilde{L}}$ such that

$$\begin{aligned} |u(x,t)- {\tilde{L}}(x)| \le C|X| K_0(4 |X|),\ (x,t) \in Q_{1/2}, \end{aligned}$$

(3.34)

where $K_0(|X|)$ is defined as

and where C is some universal constant.

Likewise a similar affine approximation holds at all points in $Q_{1/2}$ and consequently the estimates in (2.15) follow by a standard real analysis argument.

We may also assume that $u(0,0)=0$. Now with $\eta , \varepsilon _0$ as in Lemma 3.3 and $\delta _0$ as in Lemma 3.2, assume the following hypothesis for a given $i \in \mathbb {N}$,

$$\begin{aligned} {\left\{ \begin{array}{ll} \text {There exists affine function }L_i(x)\overset{def}{=} \langle B_i, x\rangle \hbox { such that}\ \Vert u-L_i\Vert _{L^{\infty }(Q_{\eta ^i})} \le \delta _0 \eta ^i \omega ( \eta ^i) \\ \text {and}\ |B_i| \le 2 \omega (\eta ^i). \\ \end{array}\right. } \end{aligned}$$

Here $\omega$ is defined instead as

$$\begin{aligned} \omega (\eta ^k)\overset{def}{=} \frac{1}{\varepsilon _0} \sum _{i=0}^k \eta ^{i \alpha } \omega _1(\eta ^{k-i}), \end{aligned}$$

(3.35)

where we let $\omega _1$ to be

By multiplying u with a suitable constant we can assume that the Statement [H] holds when $i=0$ with $L_0=0$. Let k be the first integer such that the Statement [H] breaks. Then there are two possibilities.

Case 1: Suppose $k=\infty$. Then given $X=(x,t)$, let $i\in \mathbb {N}$ be such that $|X| \sim \eta ^{i}$. Then from the inequalities in [H] and triangle inequality, it follows that

$$\begin{aligned} |u(x,t)| \!\le \! |u(x,t) \!-\! L_i (x)| \!+\! |L_i (x)| \!\le \! C_1 \eta ^{i} \omega (\eta ^i) \!\!\le \!\! C |X| \omega ( 2|X|)\!\! \le \! \! C |X| K_0( 4 |X|),\nonumber \\ \end{aligned}$$

(3.36)

and thus (3.34) follows with ${\tilde{L}}=0$. The last inequality in (3.36) is seen as follows:

(3.37)

Case 2: Suppose instead that $k < \infty$. Then we have that the Statement [H] is satisfied upto $k-1$. Now let

$$\begin{aligned} v(x,t)\overset{def}{=} \frac{u(\eta ^{k-1}x, \eta ^{2(k-1)} t)}{\eta ^{k-1} \omega (\eta ^{k-1})}, \end{aligned}$$

which solves

$$\begin{aligned} \bigg ( \delta _{ij} +(p-2)\frac{v_i v_j}{|\nabla v|^2} \bigg ) v_{ij} - v_t= \frac{\eta ^{k-1} f(\eta ^{k-1} x, \eta ^{2(k-1)}t)}{\omega (\eta ^{k-1})}. \end{aligned}$$

Moreover, from the estimates in [H] for $i=k-1$ it follows that $|v| \le 2+ \delta _0 \le 3$. Also by change of variable, we have that for

$$\begin{aligned} f_k(x,t)= \frac{\eta ^{k-1} f(\eta ^{k-1} x, \eta ^{2(k-1)} t)}{\omega (\eta ^{k-1})}, \end{aligned}$$

the following holds,

(3.38)

Here we have also used that

Hence, v solves an equation of the type (1.1) such that the hypothesis in Lemma 3.3 is satisfied. Therefore, by applying Lemma 3.3, we obtain that there exists an affine function $Lx= {\tilde{A}} x$ such that

$$\begin{aligned} \Vert v- L\Vert _{L^{\infty }(Q_{\eta })}\le \delta _0 \eta ^{1+\alpha }. \end{aligned}$$

Scaling back to u, we obtain with $L_{k} x\overset{def}{=} \langle B_k, x\rangle$, where $B_k\overset{def}{=}\omega (\eta ^{k-1})\tilde{A}$, that

$$\begin{aligned} \Vert u-L_k\Vert _{L^{\infty }(Q_{\eta ^k})} \le \delta _0 \eta ^k \eta ^{\alpha } \omega ( \eta ^{k-1}) \le \delta _0 \eta ^k \omega ( \eta ^k), \end{aligned}$$

(3.39)

where in the last inequality, we used the $\alpha -$decreasing property of $\omega$ (as in (3.21)). This property is easily seen from the expression of $\omega$ in (3.35) above. However, since the Statement [H] does not hold for $i=k$, we must necessarily have

$$\begin{aligned} |B_k| \ge 2 \omega (\eta ^k). \end{aligned}$$

(3.40)

We now let

$$\begin{aligned} {\tilde{v}}(x,t)= \frac{u(\eta ^k x, \eta ^{2k} t)}{\eta ^k \omega (\eta ^k)}. \end{aligned}$$

Then, we observe that ${\tilde{v}}$ solves

$$\begin{aligned} \bigg (\delta _{ij}+(p-2) \frac{{\tilde{v}}_i {\tilde{v}}_j}{|\nabla {\tilde{v}}|^2} \bigg ){\tilde{v}}_{ij} - {\tilde{v}}_t=\frac{\eta ^k f(\eta ^k x, \eta ^{2k} t)}{\omega (\eta ^k)}. \end{aligned}$$

Moreover, from (3.39) we have, with

$$\begin{aligned} A= \frac{\omega (\eta ^{k-1}){\tilde{A}}}{\omega (\eta ^k)}, \end{aligned}$$

(3.41)

that the following inequality holds

$$\begin{aligned} \Vert {\tilde{v}} - \langle A,x\rangle \Vert _{L^{\infty }(Q_1)} \le \delta _0. \end{aligned}$$

(3.42)

Moreover, using that $|{\tilde{A}}| \le C$, where C is universal, and the $\alpha -$decreasing property of $\omega$, we obtain

$$\begin{aligned} |A| = \frac{|{\tilde{A}}| \eta ^{\alpha } \omega (\eta ^{k-1})}{ \eta ^\alpha \omega (\eta ^{k})} \le \frac{C}{\eta ^{\alpha }}. \end{aligned}$$

(3.43)

Also (3.40) implies

$$\begin{aligned} |A| \ge 2. \end{aligned}$$

Now again by change of variables it is seen that ${\tilde{f}}_k$, defined by

$$\begin{aligned} {\tilde{f}}_k(x,t)\overset{def}{=} \frac{\eta ^k f(\eta ^k x, \eta ^{2k} t)}{ \omega (\eta ^k)}, \end{aligned}$$

(3.44)

satisfies the estimate as in (3.38). Now using the fact that $\varepsilon _0 < \delta _0^2$, we find that ${\tilde{v}}$ satisfies the conditions in Lemma 3.2. Hence, there exists an affine function $L_0 x\overset{def}{=} \langle A_0, x\rangle$, with universal bounds depending on $\eta$, such that

$$\begin{aligned} |{\tilde{v}}(x,t)- L_0(x)| \le C|X| K_{{\tilde{f}}_k}(|X|),\quad |X|<1, \end{aligned}$$

(3.45)

where

with ${\tilde{f}}_k$ as in (3.44). Then, by scaling back to u, we obtain for $|X| \le \eta ^k$ that the following inequality holds by change of variables,

(3.46)

Now, let j be the smallest integer such that $|Y| \le \eta ^{j}$. Then, we have that

(3.47)

where the last inequality in (3.47) follows from a computation as in (3.37). This implies that (3.34) holds with ${\tilde{L}} x\overset{def}{=} \langle \omega (\eta ^k) A_0, x\rangle$, when $|X| \le \eta ^k$.

Now when $|X| \ge \eta ^k$, one can show that

$$\begin{aligned} |u(x,t) | \le C |X| \omega (2|X|) \le C |X| K_0(4 |X|). \end{aligned}$$

(3.48)

This follows from the fact that with $L_ix\overset{def}{=} \langle B_i,x\rangle$ we have for $i=0,\ldots , k-1$,

$$\begin{aligned} \Vert u-L_i\Vert _{L^{\infty }(Q_{\eta ^i})} \le \delta _0 \eta ^i \omega ( \eta ^i), \end{aligned}$$

and

$$\begin{aligned} | B_i| \le 2 \omega (\eta ^i), \end{aligned}$$

because (3.1) holds upto $k-1$. Moreover, for $i=k$, we again have

$$\begin{aligned} \Vert u-L_k\Vert _{L^{\infty }(Q_{\eta ^k})} \le \delta _0 \eta ^k \omega ( \eta ^k). \end{aligned}$$

In this case, instead the following bound holds

$$\begin{aligned} |B_k| \le C \omega (\eta ^{k-1}) \le \frac{C \omega (\eta ^k)}{\eta ^\alpha }\ \text {(using }\alpha -\hbox {decreasing property of }\omega ). \end{aligned}$$

Using these estimates, it is easy to see that (3.48) holds. Now note that with ${\tilde{L}} x\overset{def}{=} \langle {\tilde{B}}, x\rangle$, where ${\tilde{B}}\overset{def}{=} \omega (\eta ^k) A_0$, we also have the following bound

$$\begin{aligned} |{\tilde{B}}| \le C \omega (\eta ^k). \end{aligned}$$

(3.49)

Therefore, it follows from (3.48) and the estimate (3.49) above that

$$\begin{aligned} |u(x,t)- {\tilde{L}}(x) | \le C |X| K_0(4|X|), \end{aligned}$$

(3.50)

also holds when $|X| \ge \eta ^k$, for a possibly different C. Hence the estimate in (3.34) follows with ${\tilde{L}} x\overset{def}{=}\langle {\tilde{B}}, x\rangle$ and this finishes the proof of the theorem. $\square$

3.2 Proof of Theorem 2.6

In this subsection, we assume that u is a $W^{2,1,m}$ viscosity solution to

$$\begin{aligned} \bigg (\delta _{ij} + (p-2) \frac{u_i u_j}{|\nabla u|^2} \bigg ) u_{ij} - u_t =f, \end{aligned}$$

(3.51)

where $f \in L^{m}$ for some $m>n+2$. We now state and prove the counterparts of the approximation lemmas in this situation. The analogue of Lemma 3.1 is as follows.

Lemma 3.4

Let u be a $W^{2,1, m}$ viscosity solution to

$$\begin{aligned} \bigg (\delta _{ij} + (p-2) \frac{(\delta u_i+A_i)(\delta u_j +A_j)}{ |\delta \nabla u+A|^2} \bigg ) u_{ij}- u_t=f\quad \text {in }Q_1, \end{aligned}$$

(3.52)

with $|u| \le 1$ and $|A| \ge 1$. Given $\tau >0$, there exists $\delta _0=\delta _0(\tau )>0$ such that if

$$\begin{aligned} \left( \frac{1}{|Q_{3/4}|} \int _{Q_{3/4}} |f|^m \right) ^{1/m} \le \delta _0, \end{aligned}$$

then $\Vert w-u\Vert _{L^{\infty }(Q_{1/2})} \le \tau$ for some $w \in C^{2,1}(\overline{Q_{1/2}})$ with universal $C^{2,1}$ bounds depending only on n, p and independent of |A|.

Proof

The proof is identical to that of Lemma 3.1 and so we omit the details. $\square$

We now state the counterpart of Lemma 3.2.

Lemma 3.5

Let u be a viscosity solution to

$$\begin{aligned} \bigg (\delta _{ij}+ (p-2) \frac{u_i u_j}{|\nabla u|^2} \bigg ) u_{ij} - u_t=f, \end{aligned}$$

in $Q_1$ with $u(0,0)=0$. There exists a universal $\delta _0>0$, such that if for some $A \in \mathbb {R}^n$ satisfying $M \ge |A| \ge 2$ we have

$$\begin{aligned} \Vert u- \langle A,x\rangle \Vert _{L^{\infty }(Q_1)} \le \delta _0, \end{aligned}$$

and also

$$\begin{aligned} \Vert f\Vert _{L^m(Q_1)} \le \delta _0^2, \end{aligned}$$

then there exists an affine function $L_0$, with universal bounds depending also on M, such that

$$\begin{aligned} |u(x,t)- L_0(x) | \le C|X|^{1+\alpha _0}, \end{aligned}$$

where $\alpha _0 < \min (\alpha , 1-\frac{n+2}{m})$.

Proof

As in the proof of Lemma 3.2, we show that for every $k \in \mathbb {N}$, there exists affine functions ${\tilde{L}}_kx = \langle A_k ,x\rangle$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \Vert u- {\tilde{L}}_k x\Vert _{L^{\infty }(Q_{r^k})}\le \delta _0 r^{k(1+\alpha _0)}, \\ |A_k - A_{k+1}| \le C \delta _0 r^{k\alpha _0}, \end{array}\right. } \end{aligned}$$

(3.53)

for some $r<1$ universal independent of $\delta _0$. The conclusion of the lemma then follows from (3.53) in a standard way. We first observe that (3.53) holds for $k=0$ with $A_0=A$. Moreover the non-degeneracy condition as in (3.13) is easily verified in this situation provided $\delta _0$ is small enough. Now assume (3.53) holds upto some k. We then define

$$\begin{aligned} v= \frac{u-{\tilde{L}}_k (r^k x, r^{2k} t)}{\delta _0r^{k(1+\alpha _0)}}. \end{aligned}$$

Then v solves in $B_1$

$$\begin{aligned} \bigg (\delta _{ij} + (p-2) \frac{ (\delta _0 r^{k \alpha _0} v_i + (A_k)_i) (\delta _0 r^{k \alpha _0} v_j + (A_k)_j)}{| \delta _0 r^{k\alpha _0} \nabla v + A_k|^2} \bigg ) v_{ij} - v_t= f_k, \end{aligned}$$

where $f_k$ is defined as

$$\begin{aligned} f_k(x,t)= r^{k(1-\alpha _0)} \frac{f(r^k x, r^{2k} t)}{\delta _0}. \end{aligned}$$

Now by change of variable it is seen that

$$\begin{aligned} \Vert f_k\Vert _{L^m(Q_1)} = r^{k(1-\frac{n+2}{m} - \alpha _0)} \frac{1}{\delta _0} \Vert f\Vert _{L^m(Q_{r^k})} \le \delta _0. \end{aligned}$$

Note that over here, we crucially used the hypothesis of the lemma i.e,

$$\begin{aligned} \Vert f\Vert _{L^m(Q_1)} \le \delta _0^2, \end{aligned}$$

and the fact that $\alpha _0 < 1-\frac{n+2}{m}$. Therefore, v satisfies the hypothesis of Lemma 3.4 and at this point we can repeat the arguments in the proof of Lemma 3.2 to conclude that there exists ${\tilde{L}}_{k+1}(x) = {\tilde{L}}_k (x) + \delta _0 r^{k(1+\alpha _0)}L( \frac{x}{r^k})$, where L has universal bounds such that (3.53) holds for $k+1$. This verifies the induction step and the conclusion of the lemma thus follows. $\square$

We also have the following lemma which is the analogue of Lemma 3.3.

Lemma 3.6

Let u be a solution of

$$\begin{aligned} \bigg (\delta _{ij}+ (p-2) \frac{u_i u_j}{|\nabla u|^2} \bigg ) u_{ij} - u_t=f \quad \hbox { in}\ Q_1, \end{aligned}$$

(3.54)

with $|u| \le 3$ and $u(0,0)=0$. There exists a universal $\varepsilon _0>0$ such that if

$$\begin{aligned} \Vert f\Vert _{L^m(Q_1)} \le \varepsilon _0, \end{aligned}$$

(3.55)

then there exists an affine function L with universal bounds and a universal $\eta \in (0,1)$ such that

$$\begin{aligned} \Vert u- L\Vert _{L^{\infty }(Q_{\eta })} \le \delta _0 \eta ^{1+\alpha _0}, \end{aligned}$$

where $\delta _0$ is as in Lemma 3.5 above. Without loss of generality we may take $\varepsilon _0 < \delta _0^2$.

Proof

The proof is again identical to that of Lemma 3.3 and thus we skip the details. $\square$

With Lemmas 3.4–3.6 in hand, we now proceed with the proof of Theorem 2.6.

Proof of Theorem 2.6

It suffices to show that at (0, 0), there exists an affine function ${\tilde{L}}$ with universal bounds such that

$$\begin{aligned} |u(x,t)- {\tilde{L}}(x)| \le C|X|^{1+\alpha _0}. \end{aligned}$$

(3.56)

Recall $|X|=\text {max}(|x|, |t|^{1/2})$. We also assume that $u(0,0)=0$. Now with $\eta , \varepsilon _0$ as in Lemma 3.6 and $\delta _0$ as in Lemma 3.5, assume the following hypothesis for a given $i \in \mathbb {N}$,

$$\begin{aligned} {\left\{ \begin{array}{ll} \text {There exists affine function }L_i(x)\overset{def}{=}\ \langle B_i, x\rangle \hbox { such that}\ \Vert u{-}L_i\Vert _{L^{\infty }(Q_{\eta ^i})} {\le } \frac{\delta _0}{\varepsilon _0} \eta ^{i (1{+}\alpha _0)} \\ \text {and}\ |B_i| {\le } \frac{2}{\varepsilon _0} \eta ^{i\alpha _0}. \end{array}\right. }\nonumber \\ \end{aligned}$$

(3.57)

By multiplying u with a suitable constant, we may assume that the hypothesis holds for $i=0$ with $L_0=0$. We can also assume that

$$\begin{aligned} \Vert f\Vert _{L^m(Q_1)} \le 1. \end{aligned}$$

(3.58)

Let k be the smallest integer such that (3.57) fails. Then as in the proof of Theorem 2.5, there are two possibilities.

Case 1: Suppose $k=\infty$. Then in this case, (3.56) is seen to hold with ${\tilde{L}}=0$.

Case 2: Suppose instead that $k<\infty$. Then we have that the hypothesis is satisfied upto $k-1$. As before, we let

$$\begin{aligned} v(x,t)= \varepsilon _0 \frac{u(\eta ^{k-1}x, \eta ^{2(k-1)}t)}{\eta ^{(k-1)(1+\alpha _0)}}, \end{aligned}$$

which solves in $B_1$

$$\begin{aligned} \bigg ( \delta _{ij}+ (p-2) \frac{v_i v_j}{|\nabla v|^2} \bigg ) v_{ij} - v_t = f_k, \end{aligned}$$

where

$$\begin{aligned} f_k(x,t) = \varepsilon _0 \eta ^{(k-1)(1-\alpha _0)} f(\eta ^{k-1} x, \eta ^{2(k-1)} t). \end{aligned}$$

Then by change of variable and (3.58), it is again seen that $\Vert f_k\Vert _{L^m} \le \varepsilon _0$. Moreover, from (3.57) and triangle inequality it follows that $|v| \le 2 + \delta _0 \le 3$. Thus the hypothesis of Lemma 3.6 is satisfied and consequently there exists $L x= \langle {\tilde{A}}, x\rangle$ affine such that

$$\begin{aligned} \Vert v- L\Vert _{L^{\infty }(Q_\eta )} \le \delta _0 \eta ^{1+\alpha _0}. \end{aligned}$$

By scaling back to u, we obtain with $L_k x\overset{def}{=} B_k x$, with $B_k= \frac{\eta ^{(k-1)\alpha _0}}{\varepsilon _0} {\tilde{A}}$, that the following holds,

$$\begin{aligned} \Vert u-L_k\Vert _{L^{\infty }(Q_{\eta ^k})} \le \frac{\delta _0}{\varepsilon _0} \eta ^{k(1+\alpha _0)}. \end{aligned}$$

However since Statement [H1] fails, we must necessarily have

$$\begin{aligned} |B_k| \ge \frac{2}{\varepsilon _0} \eta ^{k\alpha _0}. \end{aligned}$$

If we now let

$$\begin{aligned} {\tilde{v}}(x,t)= \varepsilon _0 \frac{u(\eta ^k x, \eta ^{2k} t)}{\eta ^{k(1+\alpha _0)}}, \end{aligned}$$

then, as in the proof of Theorem 2.5, it can be easily checked that ${\tilde{v}}$ solves an equation of the type (1.1) such that the hypothesis of Lemma 3.5 is verified. Hence there exists an affine function $L_0 x= \langle A_0, x\rangle$, with universal bounds depending on $\eta$, such that

$$\begin{aligned} |{\tilde{v}}- L_0 x| \le C|X|^{1+\alpha _0}. \end{aligned}$$

By scaling back to u we obtain that, with $\tilde{L}(x)\overset{def}{=} \frac{\eta ^{k\alpha _0}}{\varepsilon _0}\langle A_0, x\rangle$, the following estimate holds for $|X| \le \eta ^k$,

$$\begin{aligned} |u(x,t)- {\tilde{L}}(x)| \le C|X|^{1+\alpha _0}. \end{aligned}$$

(3.59)

The rest of the argument is again the same as in the proof of Theorem 2.5, which allows us to conclude that the estimate (3.59) holds also when $|X| \ge \eta ^k$. This finishes the proof of the theorem. $\square$