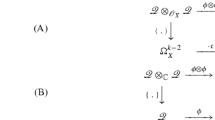Abstract
We define the notions of \(B_{n}\)-generalized pseudo-Hermitian and \(B_{n}\)-generalized pseudo-Kähler structure on an odd exact Courant algebroid E. When E is in the standard form (or of type \(B_{n}\)) we express these notions in terms of classical tensor fields on the base of E. This is analogous to the bi-Hermitian viewpoint on generalized Kähler structures on exact Courant algebroids. We describe left-invariant \(B_{n}\)-generalized pseudo-Kähler structures on Courant algebroids of type \(B_{n}\) over Lie groups of dimension two, three and four.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Generalized complex geometry is a unification of complex and symplectic geometry and represents an active research area in current mathematics at the interface with mathematical physics. The initial idea was to replace the tangent bundle of a manifold M with the generalized tangent bundle \({\mathbb {T}}M:= TM \oplus T^{*}M\) and to include complex and symplectic structures in a more general type of structure, a so called generalized complex structure. Later on, other classical structures (like Kähler, quaternionic, hyper-Kähler etc.) were defined and studied in this general setting.
Generalized tangent bundles are the simplest class of Courant algebroids. They are sometimes called exact Courant algebroids, owing to the fact that they fit into an exact sequence
where \(\pi : {\mathbb {T}}M \rightarrow TM\) is the natural projection (the anchor of \({\mathbb {T}}M\)) and \(\pi ^{*}: T^{*}M \rightarrow {\mathbb {T}}M\) is the dual of \(\pi \) (here \({\mathbb {T}}M\) and \(({\mathbb {T}}M)^{*}\) are identified using the natural scalar product of neutral signature of \({\mathbb {T}}M\)). The notion of a Courant algebroid (see Sect. 2 for its definition) was defined for the first time by Z. J. Liu, A. Weinstein and P. Xu (see [16]) and since then it has been intensively studied. Regular Courant algebroids (i.e. Courant algebroids for which the image of the anchor is a vector bundle) were classified in [3]. This includes a classification of transitive Courant algebroids (i.e. Courant algebroids with surjective anchor). In the context of T-duality, heterotic Courant algebroids (i.e. Courant algebroids for which the associated quadratic Lie algebra bundle is an adjoint bundle) were considered in [1]. To any regular Courant algebroid E one can associate a (regular) quadratic Lie algebroid \(E/ ( \textrm{Ker}\, \pi )^{\perp }\), where \(\perp \) denotes the orthogonal complement with respect to the scalar product of E. Conversely, a regular quadratic Lie algebroid arises in this way from a Courant algebroid if and only if its first Pontryagin class [2, 15] vanishes (see Theorem 1.10 of [3]).
Our setting in this paper are the so called Courant algebroids of type \(B_{n}\) (and their global analogue, the odd exact Courant algebroids), introduced in [13]. The terminology is justified by the fact that the underlying bundle of a Courant algebroid of type \(B_{n}\) is of the form \(TM\oplus T^{*}M \oplus {\mathbb {R}}\) and its scalar product is the natural scalar product of \(TM\oplus T^{*}M \oplus {\mathbb {R}}\) of signature \((n+1, 1)\), where n is the dimension of the manifold M. (Along the same lines, exact Courant algebroids were called in [13] Courant algebroids of type \(D_{n}\), as the natural scalar product of a generalized tangent bundle has neutral signature. One may also define a Courant algebroid of type \(B_{n}\) as a transitive Courant algebroid in the standard form, with quadratic Lie algebra bundle \({\mathcal {Q}} = M\times {\mathbb {R}}\) the trivial line bundle, with positive definite canonical metric, trivial Lie bracket and canonical flat connection. Therefore, from the viewpoint of the classification of transitive Courant algebroids [3], the Courant algebroids of type \(B_{n}\) represent the next simplest class, after generalized tangent bundles.
Courant algebroids of type \(B_{n}\) may be seen as the odd analogue of Courant algebroids of type \(D_{n}\). Following this analogy, generalized complex structures on odd exact Courant algebroids (the so called \(B_{n}\)-generalized complex structures) were introduced and studied systematically in [12, 13]. It is worth mentioning that there are various approaches to define odd dimensional analogues of \(D_{n}\)-generalized geometry (see e.g. [11, 14, 17]). In this paper we adopt the viewpoint of [13] and, in analogy with [8, 9], we define generalized pseudo-Kähler structures on odd exact Courant algebroids as an enrichment of \(B_{n}\)-generalized complex structures.
Structure of the paper and main results. In Sect. 2 we recall basic definitions on Courant algebroids of type \(B_{n}\), odd exact Courant algebroids, generalized metrics and \(B_{n}\)-generalized complex structures.
In Sect. 3 we define the notion of \(B_{n}\)-generalized almost pseudo-Hermitian structure on an odd exact Courant algebroid E as a pair \(({\mathcal {G}}, {\mathcal {F}})\) formed by a generalized metric \({\mathcal {G}}\) and a \(B_{n}\)-generalized almost complex structure \({\mathcal {F}}\) which satisfy \({\mathcal {G}}^{\textrm{end}} {\mathcal {F}} = {\mathcal {F}} {\mathcal {G}}^{\textrm{end}}\). The integrability of \(({\mathcal {G}}, {\mathcal {F}} )\) (and the corresponding notion of \(B_{n}\)-generalized pseudo-Kähler structure) is defined by imposing integrability on \({\mathcal {F}}\) and on the second \(B_{n}\)-generalized almost complex structure \({\mathcal {F}}_{2}:= {\mathcal {F}} {\mathcal {G}}^{\textrm{end}}\).
In analogy with the bi-Hermitian viewpoint on generalized Kähler structures on generalized tangent bundles [8], in Sect. 4 we assume that E is a Courant algebroid of type \(B_{n}\) and we describe \(B_{n}\)-generalized almost pseudo-Hermitian structures on E in terms of classical tensor fields (called “components”) on the base of E. The case when n is odd is described in the next proposition (below ”\(\perp \)” denotes the orthogonal complement with respect to g), cf. Proposition 13 i).
Proposition 1
Let E be a Courant algebroid of type \(B_{n}\) over an n-dimensional manifold M, with Dorfman bracket twisted by (H, F). Assume that n is odd. A \(B_{n}\)-generalized almost pseudo-Hermitian structure \(({\mathcal {G}}, {\mathcal {F}})\) on E is equivalent to the data \((g, J_{+}, J_{-}, X_{+}, X_{-})\) where g is a pseudo-Riemannian metric on M, \(J_{\pm }\in \Gamma ( \textrm{End}\, TM)\) are g-skew-symmetric endomorphisms and \(X_{\pm }\in {{\mathfrak {X}}}(M)\) are vector fields of norm one, such that \(J_{\pm } X_{\pm } =0\) and \(J_{\pm }\vert _{ X_{\pm }^{\perp }}\) are complex structures.
The case when n is even is described in the next proposition, cf. Proposition 13 ii).
Proposition 2
Let E be a Courant algebroid of type \(B_{n}\) over an n-dimensional manifold M, with Dorfman bracket twisted by (H, F). Assume that n is even. A \(B_{n}\)-generalized almost pseudo-Hermitian structure \(({\mathcal {G}}, {\mathcal {F}})\) on E is equivalent to the data \((g, J_{+}, J_{-}, X_{+}, X_{-}, c_{+})\) where g is a pseudo-Riemannian metric on M, \(J_{\pm }\in \Gamma ( \textrm{End}\, TM)\) are g-skew-symmetric endomorphisms, \(X_{\pm }\in {{\mathfrak {X}}}(M)\) are g-orthogonal vector fields and \(c_{+}\in C^{\infty }(M)\) is a function, such that \(J_{-}\) is an almost complex structure on M, \(J_{+}\) satisfies
and \(g(X_{+}, X_{+}) = g(X_{-}, X_{-})= 1-c_{+}^{2}\).
Our aim in Sect. 5 is to express the integrability of a \(B_{n}\)-generalized almost pseudo-Hermitian structure \(({\mathcal {G}}, {\mathcal {F}})\) on a Courant algebroid of type \(B_{n}\) in terms of its components. When n is odd we obtain the following summarized description. (Below \(\nabla \) denotes the Levi-Civita connection of g and \(T^{(1,0)}_{A}M\subset (TM)_{{\mathbb {C}}}\) denotes the i-eigenbundle of an endomorphism A of TM).
Theorem 3
In the setting of Proposition 1, define connections \(\nabla ^\pm \) on TM by
for any \(X\in {{\mathfrak {X}}}(M)\), where we are identifying vectors and co-vectors using the metric g, as explained after equation (18), cf. Notation 15, and \(J_{+} F(X)\) denotes the endomorphism \(J_{+}\) applied to the vector field F(X). Then \(({\mathcal {G}}, {\mathcal {F}})\) is a \(B_{n}\)-generalized pseudo-Kähler structure if and only if \(\nabla ^{\pm } \) preserves \(T_{J_{\pm }}^{(1,0)} M\),
and certain algebraic conditions hold (see Theorem 16 for the precise conditions).
The analogous result for n even is stated as follows.
Theorem 4
In the setting of Proposition 2, assume that \(X_{+}\) and \(X_{-}\) are non-null (at any point), i.e. \(c_{+} (p)^{2} \ne 1\) for any \(p\in M.\) Define connections \(D^\pm \) on TM by
for any \(X\in {{\mathfrak {X}}}(M).\) Then \(({\mathcal {G}}, {\mathcal {F}})\) is a \(B_{n}\)-generalized pseudo-Kähler structure if and only if \(D^{\pm } \) preserves \(T_{J_{\pm }}^{(1,0)} M\), \(X_{+}\) and \(X_{-}\) commute, their covariant derivatives are given by
\(i_{X_{+}} F = dc_{+}\) and certain algebraic conditions hold (see Theorem 20 for the precise conditions).
The proofs of Theorems 3 and 4 are analogues to the proof of Gualtieri on the relation between generalized Kähler structures on exact Courant algebroids and bi-Hermitian data [8]. More precisely, in a first stage we find a criterion for the integrability of a \(B_{n}\)-generalized almost pseudo-Hermitian structure \(({\mathcal {G}}, {\mathcal {F}})\) in terms of the (Dorfman) integrability of the bundles \(L_{1}\), \(L_{1}\cap L_{2}\) and \(L_{1}\cap {\bar{L}}_{2}\) and their invariance under the Dorfman Lie derivative \({{\textbf{L}}}_{u_{0}}\) (where \(L_{1}\) is the (1, 0)-eigenbundle of \({\mathcal {F}}\), \(L_{2}\) is the (1, 0)-eigenbundle of \(G^{\textrm{end}} {\mathcal {F}}\) and \(u_{0} \in \Gamma (\textrm{Ker}\, {\mathcal {F}} )\) is suitably normalized), see Proposition 28. Then the above theorems follow by computing the intersections \(L_{1}\cap L_{2}\) and \(L_{1} \cap {\bar{L}}_{2}\) in terms of the components of \(({\mathcal {G}}, {\mathcal {F}})\) and applying the above-mentioned criterion. The assumption from Theorem 4 that \(X_{\pm }\) are non-null simplifies the argument considerably. Along the way we determine various further properties of the components of \(B_{n}\)-generalized pseudo-Kähler structures as well as a rescaling property for such structures (see Corollary 19 and Corollary 24). Finally, we remark that a generalized Kähler structure on an exact Courant algebroid may be interpreted as a \(B_{n}\)-generalized Kähler structure (see Remark 25).
In Sect. 6 we simplify Theorems 3 and 4 under the assumption that M has small dimension. This section is intended as a preparatory material for Sect. 7, which is devoted to the description of left-invariant \(B_{n}\)-generalized pseudo-Kähler structures \(({\mathcal {G}}, {\mathcal {F}})\) over Lie groups of dimension two, three or four. Let G be a Lie group with Lie algebra \({\mathfrak {g}}\) and E a Courant algebroid of type \(B_{n}\) over G, whose Dorfman bracket is twisted by left-invariant forms (H, F). A \(B_{n}\)-generalized pseudo-Kähler structure on E is called  if its components are left-invariant tensor fields on G (in particular, the function \(c_{+}\) is constant). Our main results from Sect. 7 can be roughly summarized as follows (below \(c_{+}\) and g are part of the components of the corresponding \(B_{n}\)-generalized pseudo-Kähler structure).
if its components are left-invariant tensor fields on G (in particular, the function \(c_{+}\) is constant). Our main results from Sect. 7 can be roughly summarized as follows (below \(c_{+}\) and g are part of the components of the corresponding \(B_{n}\)-generalized pseudo-Kähler structure).
Theorem 5
-
i)
Assume that G is 2-dimensional. There is a left-invariant \(B_{2}\)-generalized pseudo-Kähler structure on E, such that \(c_{\pm } \notin \{ -1, +1\}\), if and only if \({\mathfrak {g}}\) is abelian.
-
ii)
Assume that G is 3-dimensional, unimodular, with canonical operator L (defined in (75)) diagonalizable. There is a left-invariant \(B_{3}\)-generalized pseudo-Kähler structure on E if and only if \({\mathfrak {g}}\) is abelian, \({\mathfrak {g}}= \mathfrak {so} (2) \ltimes {\mathbb {R}}^{2} \) or \({\mathfrak {g}} = \mathfrak {so}(1,1) \ltimes {\mathbb {R}}^{2}\).
-
iii)
Assume that G is 3-dimensional and non-unimodular. Let \({\mathfrak {g}}_{0}\) be the unimodular kernel of \({\mathfrak {g}}\). There is a left-invariant \(B_{3}\)-generalized pseudo-Kähler structure on E such that \(g\vert _{{\mathfrak {g}}_{0} \times {\mathfrak {g}}_{0}}\) is non-degenerate if and only if \({\mathfrak {g}} = {\mathbb {R}} \oplus \mathfrak {sol}_{2}\), where \(\mathfrak {sol}_{2}\) is the unique non-abelian 2-dimensional Lie algebra.
-
iv)
Assume that G is 4-dimensional, non-unimodular, and its unimodular kernel is non-abelian. There is an adapted (see Definition 47) \(B_{4}\)-generalized pseudo-Kähler structure on E such that \(c_{+} \notin \{ -1, 0, 1\}\) if and only if \({\mathfrak {g}} = {\mathbb {R}}\oplus \mathfrak {iso}(2)\), where \(\mathfrak {iso}(2)\) denotes the Lie algebra of the isometry group of the standard (positive definite) metric on \({\mathbb {R}}^{2}.\)
In all cases above E is untwisted (i.e. \(H=0\), \(F=0\)).
The description of the left-invariant \(B_{n}\)-generalized pseudo-Kähler structures which arise in Theorem 5 can be found in Sect. 7.1, Proposition 42, Proposition 44 and Proposition 48. Cases ii) and iii) of Theorem 5 include a description of all left-invariant \(B_{3}\)-generalized Kähler structures on Courant algebroids of type \(B_{3}\) over 3-dimensional Lie groups (see Corollary 45). The various additional assumptions from Theorem 5 were intended to simplify the computations. All examples provided by Theorem 5 live on untwisted Courant algebroids. It would be interesting to find twisted examples.
2 Preliminary Material
For completeness of our exposition we recall the definition of a Courant algebroid (the axioms C2 and C3 are redundant and are only included for convenience).
Definition 6
A  on a manifold M is a vector bundle \(E\rightarrow M\) equipped with a non-degenerate symmetric bilinear form \(\langle \cdot , \cdot \rangle \in \Gamma ( \textrm{Sym}^{2} (E^{*}))\) (called the
on a manifold M is a vector bundle \(E\rightarrow M\) equipped with a non-degenerate symmetric bilinear form \(\langle \cdot , \cdot \rangle \in \Gamma ( \textrm{Sym}^{2} (E^{*}))\) (called the  ), a bilinear operation \([\cdot , \cdot ]\) (called the
), a bilinear operation \([\cdot , \cdot ]\) (called the  ) on the space of smooth sections \(\Gamma (E)\) of E and a homomorphism of vector bundles \(\pi : E \rightarrow TM\) (called the
) on the space of smooth sections \(\Gamma (E)\) of E and a homomorphism of vector bundles \(\pi : E \rightarrow TM\) (called the  ) such that the following conditions are satisfied: for all \(u, v, w\in \Gamma (E)\) and \(f\in C^{\infty }(M)\),
) such that the following conditions are satisfied: for all \(u, v, w\in \Gamma (E)\) and \(f\in C^{\infty }(M)\),
-
C1)
\([ u, [v, w]] = [[ u, v], w] + [v, [u, w]]\),
-
C2)
\(\pi ( [u, v]) = {{\mathcal {L}}}_{\pi (u)} \pi (v) \),
-
C3)
\([u, fv] = \pi (u)(f) v + f [u, v]\),
-
C4)
\(\pi (u) \langle v, w\rangle = \langle [u, v], w\rangle + \langle v, [u, w]\rangle \),
-
C5)
\(2\langle [u, u], v\rangle = \pi (v) \langle u, u\rangle \),
where \({\mathcal {L}}_{\pi (u)} \pi (v)\) denotes the Lie bracket of the vector fields \(\pi (u )\) and \(\pi (v)\).
According to [13], a  over a manifold M of dimension n is the vector bundle \(E = TM \oplus T^{*}M\oplus {\mathbb {R}}\), with scalar product
over a manifold M of dimension n is the vector bundle \(E = TM \oplus T^{*}M\oplus {\mathbb {R}}\), with scalar product
for any \(X, Y\in TM\), \(\xi , \eta \in T^{*}M\) and \(\lambda , \mu \in {\mathbb {R}}\), anchor given by the natural projection \(\pi : E \rightarrow TM\) and Dorfman bracket given by
for any \(X, Y\in {{\mathfrak {X}}}(M)\), \(\xi , \eta \in \Omega ^{1}(M)\) and \(\lambda , \mu \in C^{\infty }(M)\), where \(F\in \Omega ^{2}(M)\) is a closed 2-form and \(H\in \Omega ^{3}(M)\) is such that \( dH + F\wedge F=0\) (we follow the convention of [13], which differs from the convention from our previous works [4] and [5] by a minus sign in the 3-form H). We will refer to (3) as the  . The Courant algebroid of type \(B_{n}\) with Dorfman bracket twisted by (H, F) will be denoted by \(E_{H, F}\) and will be called the
. The Courant algebroid of type \(B_{n}\) with Dorfman bracket twisted by (H, F) will be denoted by \(E_{H, F}\) and will be called the  An
An  is a Courant algebroid isomorphic to a Courant algebroid of type \(B_{n}.\)
is a Courant algebroid isomorphic to a Courant algebroid of type \(B_{n}.\)
2.1 Generalized Metrics
A  on an odd exact Courant algebroid E, with scalar product \(\langle \cdot , \cdot \rangle \) and anchor \(\pi : E \rightarrow TM\), is a subbundle \(E_{-}\subset E\) of rank \(n:=\textrm{dim}\, M\) on which \(\langle \cdot , \cdot \rangle \) is non-degenerate (see e.g. [7]). According to [1], when the restriction \(\pi \vert _{E_{-}}: E_{-} \rightarrow TM\) is an isomorphism, the generalized metric is called
on an odd exact Courant algebroid E, with scalar product \(\langle \cdot , \cdot \rangle \) and anchor \(\pi : E \rightarrow TM\), is a subbundle \(E_{-}\subset E\) of rank \(n:=\textrm{dim}\, M\) on which \(\langle \cdot , \cdot \rangle \) is non-degenerate (see e.g. [7]). According to [1], when the restriction \(\pi \vert _{E_{-}}: E_{-} \rightarrow TM\) is an isomorphism, the generalized metric is called  . Any rank n subbundle \(E_{-}\subset E\) with the property that the restriction \(\langle \cdot , \cdot \rangle \vert _{E_{-}}\) is negative definite is an admissible generalized metric. Such generalized metrics will be called
. Any rank n subbundle \(E_{-}\subset E\) with the property that the restriction \(\langle \cdot , \cdot \rangle \vert _{E_{-}}\) is negative definite is an admissible generalized metric. Such generalized metrics will be called  . All generalized metrics considered in this paper are admissible. For this reason, the word ‘admissible’ will be omitted.
. All generalized metrics considered in this paper are admissible. For this reason, the word ‘admissible’ will be omitted.
A generalized metric \(E_{-}\) on an odd exact Courant algebroid E defines an orthogonal isomorphism \({\mathcal {G}}^{\textrm{end}}\in \Gamma ( \textrm{End}\, E)\) by \({\mathcal {G}}^{\textrm{end}}\vert _{E_{\pm }} = \pm \textrm{Id}\), where \(E_{+}: = E_{-}^{\perp }\) (unless otherwise stated, \(\perp \) will always denote the orthogonal complement with respect to the scalar product of the Courant algebroid). The bilinear form
is given by
It is symmetric and, when \(E_{-}\) is a generalized Riemannian metric, it is positive definite. When referring to a generalized metric we will freely name either the bundle \(E_{-}\) or the bilinear form \({\mathcal {G}}\).
Let \(E_{-}\) be a generalized metric on a Courant algebroid E of type \(B_{n}\) and \(E_{+}:= E_{-}^{\perp }\). Since the restriction of the anchor \(\pi \vert _{E_{-}}: E_{-} \rightarrow TM\) is an isomorphism there is an induced pseudo-Riemannian metric on M, defined by
where \(s: TM \rightarrow E_{-}\) is the inverse of \(\pi \vert _{E_{-}}\). When \(E_{-}\) is a generalized Riemannian metric, g is positive definite. As for generalized metrics on heterotic Courant algebroids (see [1]), the vector bundles \(E_{\pm }\) are given by
where \(A\in \Omega ^{1}(M) \) and \(b\in \Omega ^{2} (M)\).
The next lemma was proved in [1] for heterotic Courant algebroids. The same argument applies to Courant algebroids of type \(B_{n}.\) For completeness of our exposition we include its proof.
Lemma 7
Let \(E_{-}\) be a generalized metric on a Courant algebroid \(E=E_{H, F}\), given by (7). There is an isomorphism between E and another Courant algebroid \({\tilde{E}}\) of type \(B_{n}\) which maps \(E_{-}\) to a generalized metric on \({\tilde{E}}\) of the form (7) with \( A=0\) and \(b =0.\)
Proof
Let \({\tilde{E}}:= E_{{\tilde{H}}, {\tilde{F}}}\) be the Courant algebroid twisted by \(({\tilde{H}}, {\tilde{F}})\), where
(note that \(d{\tilde{H}} + {\tilde{F}}\wedge {\tilde{F}}=0\) and \(d{\tilde{F}} =0\), since \(dH + F\wedge F=0\) and \(dF=0\)). The map \(I: E\rightarrow {\tilde{E}}\) defined by
for \(X\in TM\), \(\eta \in T^{*}M\) and \(\lambda \in {\mathbb {R}}\), is an isomorphism of Courant algebroids which maps \(E_{-}\) to the generalized metric
\(\square \)
Owing to the above lemma we will often assume that a generalized metric on a Courant algebroid of type \(B_{n}\) is given by a subbundle \(E_{-}\) like in (7) with g a pseudo-Riemannian metric, \(b=0\) and \(A=0.\) Such a generalized metric is in the  . For more details on generalized metrics on arbitrary Courant algebroids, see e.g. [7].
. For more details on generalized metrics on arbitrary Courant algebroids, see e.g. [7].
2.2 \(B_{n}\)-Generalized Complex Structures
Following [13], we recall that a  on an odd exact Courant algebroid \((E, \langle \cdot , \cdot \rangle , [\cdot , \cdot ], \pi )\) over a manifold M of dimension n is a complex isotropic rank n subbundle \(L \subset E_{{\mathbb {C}}}\) such that \(L \cap {\bar{L}} =0\). The orthogonal complement \(U_{{\mathbb {C}}}\) of \(L \oplus {\bar{L}}\subset E_{{\mathbb {C}}}\) has rank one. It is generated by a section \(u_{0} \in \Gamma (E)\) (unique up to multiplication by \(\pm 1\)) which satisfies \(\langle u_{0}, u_{0} \rangle = (-1)^{n}\). Let \({\mathcal {F}}\in \Gamma ( \textrm{End}\, E)\) be the endomorphism with i-eigenbundle L, \((-i)\)-eigenbundle \({\bar{L}}\) and \({\mathcal {F}} u_{0} =0.\) It is \(\langle \cdot , \cdot \rangle \)-skew-symmetric and satisfies
on an odd exact Courant algebroid \((E, \langle \cdot , \cdot \rangle , [\cdot , \cdot ], \pi )\) over a manifold M of dimension n is a complex isotropic rank n subbundle \(L \subset E_{{\mathbb {C}}}\) such that \(L \cap {\bar{L}} =0\). The orthogonal complement \(U_{{\mathbb {C}}}\) of \(L \oplus {\bar{L}}\subset E_{{\mathbb {C}}}\) has rank one. It is generated by a section \(u_{0} \in \Gamma (E)\) (unique up to multiplication by \(\pm 1\)) which satisfies \(\langle u_{0}, u_{0} \rangle = (-1)^{n}\). Let \({\mathcal {F}}\in \Gamma ( \textrm{End}\, E)\) be the endomorphism with i-eigenbundle L, \((-i)\)-eigenbundle \({\bar{L}}\) and \({\mathcal {F}} u_{0} =0.\) It is \(\langle \cdot , \cdot \rangle \)-skew-symmetric and satisfies
We will often call \({\mathcal {F}}\) (rather than L) a \(B_{n}\)-generalized almost complex structure. We say that \({\mathcal {F}}\) is a  (or is
(or is  ) if L is integrable. (A subbundle of E or its complexification \(E_{{\mathbb {C}}}\) is called
) if L is integrable. (A subbundle of E or its complexification \(E_{{\mathbb {C}}}\) is called  if its space of sections is closed under the Dorfman bracket). Then L becomes a Lie algebroid with Lie bracket induced by the Dorfman bracket of E.
if its space of sections is closed under the Dorfman bracket). Then L becomes a Lie algebroid with Lie bracket induced by the Dorfman bracket of E.
3 Definition of \(B_{n}\)-Generalized Pseudo-Kähler Structures
Let \((E, \langle \cdot , \cdot \rangle , [\cdot , \cdot ], \pi )\) be an odd exact Courant algebroid over a manifold M of dimension n.
Definition 8
A  \(({\mathcal {G}}, {\mathcal {F}})\) on E is a generalized metric \({\mathcal {G}}\) together with a \(B_{n}\)-generalized almost complex structure \({\mathcal {F}}\) such that \({\mathcal {G}}^{\textrm{end}} {\mathcal {F}} = {\mathcal {F}} {\mathcal {G}}^{\textrm{end}}.\)
\(({\mathcal {G}}, {\mathcal {F}})\) on E is a generalized metric \({\mathcal {G}}\) together with a \(B_{n}\)-generalized almost complex structure \({\mathcal {F}}\) such that \({\mathcal {G}}^{\textrm{end}} {\mathcal {F}} = {\mathcal {F}} {\mathcal {G}}^{\textrm{end}}.\)
The commutativity condition \({\mathcal {G}}^{\textrm{end}} {\mathcal {F}} = {\mathcal {F}} {\mathcal {G}}^{\textrm{end}}\) implies that \({\mathcal {F}}\) preserves the bundles \(E_{\pm }\) determined by the generalized metric. The next lemma summarizes some simple properties of \(B_{n}\)-generalized almost pseudo-Hermitian structures.
Lemma 9
Let \(({\mathcal {G}}, {\mathcal {F}})\) be a \(B_{n}\)-generalized almost pseudo-Hermitian structure on E, \(U:= \textrm{Ker}\, {\mathcal {F}}\) and \(u_{0} \in \Gamma ( U)\) such that \(\langle u_{0}, u_{0} \rangle = (-1)^{n}.\) The following statements hold:
-
i)
\(u_{0}\) is a section of \(E_{+}\) if n is even and a section of \(E_{-}\) if n is odd, i.e.
$$\begin{aligned} {\mathcal {G}}^{\textrm{end}} (u_{0} ) = (-1)^{n} u_{0}. \end{aligned}$$(9) -
ii)
For any \(u, v\in E\),
$$\begin{aligned} {\mathcal {G}}({\mathcal {F}} u, {\mathcal {F}} v)&= {\mathcal {G}}(u, v) -\langle u, u_{0} \rangle \langle v, u_{0}\rangle ,\nonumber \\ {\mathcal {G}}({\mathcal {F}} u, v)&= - {\mathcal {G}}(u, {\mathcal {F}} v) . \end{aligned}$$(10)
Proof
i) Since U has rank one and \({\mathcal {G}}^{\textrm{end}}{\mathcal {F}} = {\mathcal {F}} {\mathcal {G}}^{\textrm{end}}\), we obtain that \({\mathcal {G}}^{\textrm{end}} (u_{0}) = \lambda u_{0}\) for \(\lambda \in C^{\infty }(M)\). From \(({\mathcal {G}}^{\textrm{end}})^{2} = \textrm{Id}\) we obtain that \(\lambda = \pm 1\), i.e. \(u_{0} \in \Gamma ( E_{+})\) or \(u_{0} \in \Gamma (E_{-}).\) On the other hand, \({\mathcal {F}}\) is a complex structure on \(u_{0}^{\perp }\) and preserves \(E_{\pm }\). In particular, \({\mathcal {F}}\) is a complex structure on \(u_{0}^{\perp }\cap E_{\pm }\). If \(u_{0}\in \Gamma (E_{+})\), then \(E_{-} = E_{-} \cap u_{0}^{\perp }\) (because \(E_{\pm }\) are orthogonal) and \({\mathcal {F}}\vert _{E_{-}}\) is a complex structure on \(E_{-}\). This implies that \(n = \textrm{rank}\, E_{-} \) is even. If \(u_{0}\in \Gamma (E_{-})\), then
and \({\mathcal {F}}\) restricts to a complex structure on \(E_{-} \cap u_{0}^{\perp }\). We obtain that n is odd.
ii) Relations (10) are consequences of the properties of \({\mathcal {G}}^{\textrm{end}}\) and \({\mathcal {F}}.\) \(\square \)
In the setting of Lemma 9, let \({\mathcal {F}}_{2}:= {\mathcal {G}}^{\textrm{end}} {\mathcal {F}}.\) Then \({\mathcal {F}}_{2}\) is \(\langle \cdot ,\cdot \rangle \)-skew-symmetric, satisfies relation (8) and \(\textrm{Ker}\, {\mathcal {F}}_{2}= U\). Its i-eigenbundle is given by
where \(L_{1}\) is the i-eigenbundle of \({\mathcal {F}}.\) As
we obtain that \(\textrm{rank}\, L_{2} =\textrm{rank}\, L_{1} =n.\) We deduce that \({\mathcal {F}}_{2}\) is a \(B_{n}\)-generalized almost complex structure. We obtain the following alternative definition of \(B_{n}\)-generalized almost pseudo-Hermitian structures on odd exact Courant algebroids.
Proposition 10
A \(B_{n}\)-generalized almost pseudo-Hermitian structure on E is equivalent to a pair \(({\mathcal {F}}_{1}, {\mathcal {F}}_{2})\) of commuting \(B_{n}\)-generalized almost complex structures such that the bilinear form \((u, v)\mapsto \langle {\mathcal {F}}_{1} {\mathcal {F}}_{2} (u ), v\rangle \) on \(U^{\perp }\) is nondegenerate and
is an isomorphism when n is even while
is an isomorphism when n is odd. Above \(U= \textrm{Ker}\, {\mathcal {F}}_{1} = \textrm{Ker}\, {\mathcal {F}}_{2}\).
Proof
Given \(({\mathcal {F}}_{1}, {\mathcal {F}}_{2})\) as in the statement of the proposition, we recover the generalized metric \({\mathcal {G}}\) from \({\mathcal {G}}^{\textrm{end}}:= -{\mathcal {F}}_{1} {\mathcal {F}}_{2}\) on \(U^{\perp }\) and \({\mathcal {G}}^{\textrm{end}} = (-1)^{n} \textrm{Id}\) on U. The requirement that (12) and (13) are isomorphisms is equivalent to the fact that \({\mathcal {G}}\) is admissible. \(\square \)
Remark 11
In the setting of the above proposition, if \( - \langle {\mathcal {F}}_{1} {\mathcal {F}}_{2} u, u\rangle >0\) for any \(u\in U^{\perp }{\setminus } \{ 0\}\) then \({\mathcal {G}}\) is a generalized Riemannian metric.
Definition 12
A \(B_{n}\)-generalized almost pseudo-Hermitian structure \(({\mathcal {G}}, {\mathcal {F}})\) is called  or a
or a  if \({\mathcal {F}}\) and \({\mathcal {G}}^{\textrm{end}}{\mathcal {F}}\) are \(B_{n}\)-generalized complex structures.
if \({\mathcal {F}}\) and \({\mathcal {G}}^{\textrm{end}}{\mathcal {F}}\) are \(B_{n}\)-generalized complex structures.
4 Components of \(B_{n}\)-Generalized Almost Pseudo-Hermitian Structures
In this section we describe \(B_{n}\)-generalized almost pseudo-Hermitian structures \(({\mathcal {G}}, {\mathcal {F}})\) on a Courant algebroid \(E:= E_{H, F}\) of type \(B_{n}\) over a manifold M of dimension n in terms of tensor fields on M. We assume that the generalized metric \({\mathcal {G}}\) is in standard form. Let \(E= E_{+} \oplus E_{-}\) be the decomposition of E determined by \({\mathcal {G}}\). From the description (7) of \(E_{\pm }\) (with \(b=0\), \(A=0\)) we obtain canonical isomorphisms
where g is the pseudo-Riemannian metric on M induced by \({\mathcal {G}}\), see (6). The second isomorphism (14) maps \(\langle \cdot , \cdot \rangle \vert _{E_{+}}\) to the metric
on \(TM \oplus {\mathbb {R}}\), where \(g_{\textrm{can}} ( \lambda , \mu ):= \lambda \mu .\) Let \(u_{0} \in \Gamma ( \textrm{Ker}\, {\mathcal {F}} )\), normalized by \(\langle u_{0}, u_{0} \rangle = (-1)^{n}\). When n is even, \(u_{0}\in \Gamma (E_{+}) \) and will be denoted by \(u_{+}.\) When n is odd, \(u_{0} \in \Gamma (E_{-})\) and will be denoted by \(u_{-}.\) (See Lemma 9.)
In the next proposition ‘\(\perp \)’ denotes the orthogonal complement in TM with respect to g.
Proposition 13
-
i)
Assume that n is odd. A \(B_{n}\)-generalized almost pseudo-Hermitian structure \(({\mathcal {G}}, {\mathcal {F}})\) on E is equivalent to the data \((g, J_{+}, J_{-}, X_{+}, X_{-})\) where g is a pseudo-Riemannian metric on M, \(J_{\pm }\in \Gamma ( \textrm{End}\, TM)\) are g-skew-symmetric endomorphisms and \(X_{\pm }\in {{\mathfrak {X}}}(M)\) are vector fields, such that \(J_{\pm } X_{\pm } =0\), \(J_{\pm }\vert _{ X_{\pm }^{\perp }}\) are complex structures and \(g(X_{\pm }, X_{\pm }) =1.\)
-
ii)
Assume that n is even. A \(B_{n}\)-generalized almost pseudo-Hermitian structure \(({\mathcal {G}}, {\mathcal {F}})\) on E is equivalent to the data \((g, J_{+}, J_{-}, X_{+}, X_{-}, c_{+})\) where g is a pseudo-Riemannian metric on M, \(J_{\pm }\in \Gamma ( \textrm{End}\, TM)\) are g-skew-symmetric endomorphisms, \(X_{\pm }\in {{\mathfrak {X}}}(M)\) are g-orthogonal vector fields and \(c_{+}\in C^{\infty }(M)\) is a function, such that \(J_{-}\) is an almost complex structure on M, \(J_{+}\) satisfies
$$\begin{aligned} J_{+}X_{+}&= - c_{+} X_{-},\ J_{+}X_{-} = c_{+}X_{+},\\ J_{+}^{2} X&= - X + g(X, X_{+}) X_{+} + g(X, X_{-}) X_{-},\ \forall X\in TM \end{aligned}$$and \(g(X_{+}, X_{+}) = g(X_{-}, X_{-})= 1-c_{+}^{2}\).
-
iii)
In both cases (\(\textrm{dim}\, M\) odd or even), the generalized metric \({\mathcal {G}}\) is given by
$$\begin{aligned} E_{-}= \{ X - i_{X} g\mid X\in TM\} \end{aligned}$$(15)and the \(B_{n}\)-generalized almost complex structures \({\mathcal {F}}_{1} = {\mathcal {F}}\) and \({\mathcal {F}}_{2} = {\mathcal {G}}^{\textrm{end}} {\mathcal {F}}\) are given by
$$\begin{aligned} {\mathcal {F}}_{1} = \left( \begin{array}{ccc} \frac{1}{2} (J_{+}+ J_{-}) &{} \frac{1}{2}(J_{+} - J_{-}) \circ g^{-1} &{} X\\ \frac{1}{2} g \circ (J_{+} - J_{-}) &{} -\frac{1}{2} (J_{+} + J_{-})^{*} &{} i_{X} g\\ -\frac{1}{2} i_{X} g &{} -\frac{1}{2} X &{} 0 \end{array}\right) \end{aligned}$$(16)and
$$\begin{aligned} {\mathcal {F}}_{2} = \left( \begin{array}{ccc} \frac{1}{2} (J_{+}- J_{-}) &{} \frac{1}{2}(J_{+} + J_{-}) \circ g^{-1} &{} X\\ \frac{1}{2} g \circ (J_{+} + J_{-}) &{} -\frac{1}{2} (J_{+} - J_{-})^{*} &{} i_{X} g\\ -\frac{1}{2} i_{X}g &{} -\frac{1}{2} X &{} 0 \end{array}\right) , \end{aligned}$$(17)where \(X:= X_{+}\) when n is odd and \(X:= X_{-}\) when n is even.
Proof
-
i)
The scalar product \(-\langle \cdot , \cdot \rangle \vert _{E_{-}}\) corresponds to g under the first isomorphism (14). Then \(X_{-}:= \pi (u_{-})\) satisfies \(g(X_{-}, X_{-})=1\), since \(\langle u_{-}, u_{-} \rangle =-1.\) By means of the first isomorphism (14), the restriction \({\mathcal {F}}\vert _{E_{-}}\) induces a g-skew-symmetric endomorphism \(J_{-}\) of TM, with \(J_{-}X_{-} =0\) and which is a complex structure on \(X_{-}^{\perp }\). Consider now the second isomorphism (14). By means of this isomorphism, \(\langle \cdot , \cdot \rangle \vert _{E_{+}}\) corresponds to \(g+ g_{\textrm{can}}\) on \(TM\oplus {\mathbb {R}}\) and \({\mathcal {F}}\vert _{E_{+}}\) induces a complex structure \({{\mathcal {J}}}_{+}\) on \(TM\oplus {\mathbb {R}}\), skew-symmetric with respect to \(g+ g_{\textrm{can}}\). An easy computation shows that \({{\mathcal {J}}}_{+}\) is of the form
$$\begin{aligned} {{\mathcal {J}}}_{+} =\left( \begin{array}{cc} J_{+} &{} X_{+}\\ - i_{X_{+}} g &{} 0 \end{array}\right) , \end{aligned}$$where \(X_{+}\in {{\mathfrak {X}}}(M)\) satisfies \(g(X_{+}, X_{+})=1\) and \(J_{+}\in \Gamma ( \textrm{End}\, TM)\) is g-skew-symmetric, \(J_{+}X_{+}=0\) and \(J_{+}\vert _{ X_{+}^{\perp }}\) is a complex structure on \(X_{+}^{\perp }.\)
-
ii)
The restriction \({\mathcal {F}}\vert _{E_{-}}\) induces, under the first isomorphism (14), a g-skew-symmetric almost complex structure \(J_{-}\) on M. Write \(u_{+} = X_{+} + g(X_{+}) + c_{+}\), where \(X_{+}\in {{\mathfrak {X}}}(M)\) and \(c_{+} \in C^{\infty }(M).\) From \(\langle u_{+}, u_{+}\rangle =1\) we obtain \(g(X_{+}, X_{+}) = 1- c_{+}^{2}.\) Under the second isomorphism (14), the restriction \({\mathcal {F}}\vert _{E_{+}}\) induces an endomorphism \({\mathcal {F}}_{+}\in \Gamma ( \textrm{End} (TM\oplus {\mathbb {R}}))\), which satisfies
$$\begin{aligned} {{\mathcal {F}}}_{+}(X_{+}+c_{+} ) =0,\ {\mathcal {F}}_{+}^{2} = -\textrm{Id} + i_{X_{+} + c_{+}}(g + g_{\textrm{can}} )\otimes (X_{+} + c_{+}) \end{aligned}$$and is skew-symmetric with respect to \(g + g_{\textrm{can}}\). Writing \({\mathcal {F}}_{+}\) in block form
$$\begin{aligned} {{\mathcal {F}}}_{+} =\left( \begin{array}{cc} J_{+} &{} X_{-}\\ \omega &{} a \end{array}\right) \end{aligned}$$where \(J_{+}\in \Gamma ( \textrm{End}\, TM)\), \(X_{-}\in {{\mathfrak {X}}}(M)\), \(\omega \in \Omega ^{1}(M)\) and \(a\in C^{\infty }(M)\) an easy check shows that \(a=0\), \(\omega = - i_{X_{-}} g\), \(g(X_{-}, X_{-}) = 1 - c_{+}^{2}\), \( g(X_{+}, X_{-})=0\) and \(J_{+}\) satisfies the required properties.
-
iii)
Relations (16) and (17) follow from i) and ii). For instance, to compute \({\mathcal {F}}\) on a element \(X\in TM\) it suffices to decompose \(X = \frac{1}{2} (X+ i_{X} g) +\frac{1}{2} (X- i_{X} g)\in E_+\oplus E_-\) and to apply the above formulas for \({\mathcal {F}}|_{E_\pm }\). This yields the first column of (16). The second column is obtained similarly after decomposing an element \(\xi \in T^*M\) as \(\xi = \frac{1}{2} (X+i_{X} g) -\frac{1}{2} (X- i_{X} g)\), where \(X=g^{-1}\xi \). \(\square \)
Definition 14
Let \(({\mathcal {G}}, {\mathcal {F}})\) be a \(B_{n}\)-generalized almost pseudo-Hermitian structure on a Courant algebroid \(E_{H, F}\) of type \(B_{n}\) over a manifold M. The tensor fields on M constructed in Proposition 13, are called the  of \(({\mathcal {G}}, {\mathcal {F}} ).\)
of \(({\mathcal {G}}, {\mathcal {F}} ).\)
5 Components of \(B_{n}\)-Generalized Pseudo-Kähler Structures
In this section we express the integrability of a \(B_{n}\)-generalized almost pseudo-Hermitian structure on a Courant algebroid E of type \(B_{n}\) in terms of its components. This is done in Theorems 16 and 20 below. The proofs of these theorems will be presented in Sect. 5.2.
5.1 Statement of Results
Let \(E= E_{H, F}\) be a Courant algebroid of type \(B_{n}\) over a manifold M of dimension n, with Dorfman bracket twisted by (F, H), and \(({\mathcal {G}}, {\mathcal {F}} )\) a \(B_{n}\)-generalized almost pseudo-Hermitian structure on E. As in Sect. 4, we assume that the generalized metric \({\mathcal {G}}\) is in standard form.
Notation 15
-
i)
In analogy with the standard notation for the (1, 0)-bundle of an almost complex structure on a manifold, for any endomorphism \(A\in \Gamma (\textrm{End}\, TM)\), we will denote by \(T^{(1,0)}_{A}M\subset (TM)_{\mathbb {C}}\) its i-eigenbundle.
-
ii)
Let g be the pseudo-Riemannian metric which is part of the components of \(( {\mathcal {G}}, {\mathcal {F}} )\), see Proposition 13. We identify TM with \(T^{*}M\) using g. For \(X, Y\in {\mathfrak {X}}(M)\) we denote by F(X) and H(X, Y) the vector fields identified with the 1-forms \(i_{X}F\) and \(i_{Y} i_{X} H.\) A decomposable tensor \(Z\otimes V\in TM\otimes TM\) with \(Z, V\in TM\) is identified with the endomorphism of TM which assigns to \(X\in TM\) the vector g(Z, X)V. For an endomorphism \(A\in \Gamma (\textrm{End}\, TM)\) we denote by \(A^{\textrm{sym}}\) and \(A^{\textrm{skew}}\) its g-symmetric and g-skew-symmetric parts, respectively.
5.1.1 The Case of Odd n
Assume that n is odd and let \(( g, J_{+}, J_{-}, X_{+}, X_{-})\) be the components of \(({\mathcal {G}}, {\mathcal {F}})\). Define connections \(\nabla ^+\) and \(\nabla ^-\) on TM by
where \(X\in {\mathfrak {X}}(M)\), \(\nabla \) is the Levi-Civita connection of g, H(X) denotes the skew-symmetric endomorphism \(Y\mapsto H(X,Y)\) and the vector field \(J_{+} F(X)\) is metrically identified with a one-form.
Theorem 16
The \(B_{n}\)-generalized almost pseudo-Hermitian structure \(({\mathcal {G}}, {\mathcal {F}} )\) is \(B_{n}\)-generalized pseudo-Kähler if and only if the following conditions hold:
-
i)
The connections \(\nabla ^\pm \) preserve the distributions \(T_{J_\pm }^{(1,0)}M\) (respectively) and
$$\begin{aligned} \nabla _{X}^{-} X_{-} =0,\ \nabla ^{+}_{X} X_{+} = - J_{+} F(X),\ \forall X\in {{\mathfrak {X}}}(M). \end{aligned}$$(19) -
ii)
The forms H and F satisfy the constraints
$$\begin{aligned}&H\vert _{ \Lambda ^{3} T_{J_{\pm }}^{(1,0)}M }=0,\ (i_{X_{+}}H)\vert _{\Lambda ^{2}T_{J_{+}}^{(1,0)}M} = i F\vert _{\Lambda ^{2} T_{J_{+}}^{(1,0)}M},\nonumber \\&(i_{X_{-}}H)\vert _{\Lambda ^{2}T_{J_{-}}^{(1,0)}M} =0,\ F\vert _{\Lambda ^{2} T_{J_{-}}^{(1,0)}M}=0,\ i_{X_{-}} F =0. \end{aligned}$$(20)
We make several comments on the above theorem.
Corollary 17
In terms of the almost contact metric structures \((g, J_{\pm }, \eta _{\pm }:= g ( X_{\pm },\cdot ))\), the conditions from Theorem 16 i) are equivalent to
for any \(X\in {{\mathfrak {X}}}(M)\), together with the facts that \(X_{-}\) is a Killing field and \({{\mathcal {L}}}_{X_{+}} g = - 2 (F\circ J_{+})^{\textrm{sym}}\). (Here the bivector \(F(X)\wedge X_{+}\) is identified with the skew-symmetric endomorphism \(Y \mapsto F(X,Y)X_+ -\eta _+(Y)F(X)\).) In particular, if the Courant algebroid is untwisted (i.e. \(H =0\) and \(F =0\)), the conditions from Theorem 16 reduce to \(\nabla J_{\pm }=0\).
Proof
Assume that the conditions from Theorem 16 hold. In terms of the Levi-Civita connection \(\nabla \), relations (19) become
for any \(X\in {\mathfrak {X}}(M).\) From the above relations we obtain the required expressions for \(d\eta _{\pm }\) and \({\mathcal {L}}_{X_{\pm }} g\). Since \(\nabla ^{\pm }\) preserve the distributions \(T_{J_\pm }^{(1,0)}M\), they also preserve the distributions \(T_{J_\pm }^{(0,1)}M.\) Together with relations (19), they imply that
for any \(X\in {{\mathfrak {X}}}(M)\). Replacing in the above relations \(\nabla ^{\pm }\) with their expressions in terms of \(\nabla \) provided by relations (18), we obtain the required expressions for \(\nabla J_{\pm }\). Reversing the argument we obtain the first statement of the corollary.
When E is untwisted, relations (21) reduce to \(\nabla J_{\pm } =0\). Remark that if \(\nabla J_{\pm } =0\) then \(\nabla X_{\pm } =0\) as \(g(X_{\pm }, X_{\pm }) =1\) and \(\textrm{Ker}\, J_{\pm } = \textrm{span}\{ X_{\pm }\}\). The conditions from Theorem 16 ii) are trivially satisfied. \(\square \)
Corollary 18
In the setting of Theorem 16, if \(({\mathcal {G}}, {\mathcal {F}} )\) is a \(B_{n}\)-generalized pseudo-Kähler structure with components \((g, J_{+}, J_{-}, X_{+}, X_{-})\), then the Killing field \(X_{-}\) commutes with \(X_{+}\) and preserves the endomorphisms \(J_{\pm }\).
Proof
In order to prove that \(X_{+}\) and \(X_{-}\) commute, we write
where we used relations (22) and \(i_{X_{-}} F=0\). The statements \({{\mathcal {L}}}_{X_{-}} J_{\pm } =0\) follow from
together with the first relation (22), \((i_{X_{-}} H)\vert _{\Lambda ^{2} T_{J_{-}}^{(1,0)} M}=0\) (for \({{\mathcal {L}}}_{X_{-}} J_{-}\)) and \(i_{X_{-}} F=0\) (for \({{\mathcal {L}}}_{X_{-}} J_{+}\)). \(\square \)
There is a rescaling property of \(B_{n}\)-generalized pseudo-Kähler structures, which also follows from Theorem 16.
Corollary 19
Let \(({\mathcal {G}}, {\mathcal {F}})\) be a \(B_{n}\)-generalized pseudo-Kähler structure on a Courant algebroid \(E_{H, F}\) of type \(B_{n}\) over an odd dimensional manifold M, with components \((g, J_{+}, J_{-}, X_{+}, X_{-})\). For any \(\lambda \in {\mathbb {R}}{\setminus } \{ 0\}\), the data \(( {\tilde{g}}:= \lambda ^{2} g, {\tilde{J}}_{+}:= J_{+}, {\tilde{J}}_{-}:= J_{-}, {\tilde{X}}_{+}:= \frac{1}{\lambda } X_{+}, {\tilde{X}}_{-}:= \frac{1}{\lambda } X_{-})\) defines a \(B_{n}\)-generalized pseudo-Kähler structure on the Courant algebroid \(E_{{\tilde{H}}, {\tilde{F}}}\), where \({\tilde{H}}:= \lambda ^{2} H\) and \({\tilde{F}}:= \lambda F.\)
Proof
Let us denote by \({\tilde{\nabla }}^\pm \) the connections associated with the rescaled data. Since
for all \(X,Y\in {\mathfrak {X}}(M)\) and \({\tilde{J}}_+=J_+\), we see that \({\tilde{\nabla }}^{\pm } = \nabla ^{\pm }\). Using this fact, it is easy to check that the rescaled data satisfy the conditions from Theorem 16. For instance, we get
where we have used that \({\tilde{F}}(X)= {\tilde{g}}^{-1}{\tilde{F}}(X,\cdot ) = \frac{1}{\lambda }g^{-1}F(X, \cdot ) = \frac{1}{\lambda } F(X)\). \(\square \)
5.1.2 The Case of Even n
Assume that n is even and let \((g, J_{+}, J_{-}, X_{+}, X_{-}, c_{+})\) be the components of \(( {\mathcal {G}}, {\mathcal {F}} )\). To simplify the computations we assume that \(X_{\pm }\) are non-null, i.e. \(g( (X_{\pm })_{p}, (X_{\pm })_{p}) \ne 0\) or \(c_{+}(p)\ne \pm 1\), for any \(p\in M.\) We define the connections
on TM, where \(\nabla \) is the Levi-Civita connection of g.
Theorem 20
The \(B_{n}\)-generalized almost pseudo-Hermitian structure \(( {\mathcal {G}}, {\mathcal {F}} )\) is \(B_{n}\)-generalized pseudo-Kähler if and only if the following conditions hold:
-
i)
\(D^{\pm }\) preserve \(T^{(1,0)}_{J_{\pm }} M\), the vector fields \(\{ X_{+}, X_{-} \}\) commute and their covariant derivatives \(\nabla X_{\pm }\) are given by
$$\begin{aligned} \nabla _{X} X_{+}&= \frac{1}{2}H(X, X_{+}) + c_{+} F(X),\nonumber \\ \nabla _{X} X_{-}&= \frac{1}{2}H(X, X_{-}) - J_{+} F(X), \end{aligned}$$(26)for any \(X\in {{\mathfrak {X}}}(M)\).
-
ii)
The forms F and H satisfy
$$\begin{aligned} F\vert _{\Lambda ^{2} T_{J_{-}}^{(1,0)}M }=0,\quad H\vert _{\Lambda ^{3} T_{J_{\pm }}^{(1,0)}M }=0,\quad (i_{X_{+}+ ic_{+} X_{-}}H)\vert _{\Lambda ^{2} T_{J_{+}}^{(1,0)}M }= 0, \end{aligned}$$(27)and are related by
$$\begin{aligned} F\vert _{\Lambda ^{2} T_{J_{+}}^{(1,0)}M } = - i (i_{X_{-}}H)\vert _{\Lambda ^{2} T_{J_{+}}^{(1,0)}M }. \end{aligned}$$(28) -
iii)
The function \(c_{+}\) is Hamiltonian for the closed 2-form F, with Hamiltonian vector field \(X_{+}\):
$$\begin{aligned} d c_{+} = i_{X_{+}} F. \end{aligned}$$(29)
We make several comments on the above theorem. When the Courant algebroid is untwisted (\(H=0\), \(F=0\)), the conditions simplify considerably.
Corollary 21
In the setting of Theorem 20, assume that E is untwisted. Then \(({\mathcal {G}}, {\mathcal {F}})\) is a \(B_{n}\)-generalized pseudo-Kähler structure if and only if \(\nabla J_{\pm } =0\) and \(\nabla X_{\pm } =0.\) If these conditions hold then the function \(c_{+}\) is constant.
In computations we shall often replace the condition \({\mathcal {L}}_{X_{+} } X_{-} =0\) from the above theorem with a relation between the forms H and F, as follows.
Lemma 22
In the setting of Theorem 20, the commutativity of \(X_{+}\) and \(X_{-}\) can be replaced by the relation
Proof
The statement follows by writing \({{\mathcal {L}}}_{X_{+} } X_{-} =\nabla _{X_{+}} X_{-} -\nabla _{X_{-}} X_{+} \) and using relations (26). \(\square \)
Corollary 23
In the setting of Theorem 20, if \(( {\mathcal {G}}, {\mathcal {F}} )\) is a \(B_{n}\)-generalized pseudo-Kähler structure with components \((g, J_{+}, J_{-}, X_{+}, X_{-}, c_{+})\), then \(X_{+}\) is a Killing field and the almost complex structure \(J_{-}\) is integrable.
Proof
The first relation (26) implies that \(X_{+}\) is a Killing field. The integrability of \(J_{-}\) will follow from the proof of Theorem 20 (see Corollary 33 iii) below). \(\square \)
Another consequence of Theorem 20 is a rescaling property of certain \(B_{n}\)-generalized pseudo-Kähler structures defined on Courant algebroids \(E_{H, F}\) with trivial 2-form F. On such Courant algebroids the function \(c_{+}\) is constant for any \(B_{n}\)-generalized pseudo-Kähler structure (owing to relation (29) above).
Corollary 24
Let \(({\mathcal {G}}, {\mathcal {F}})\) be a \(B_{n}\)-generalized pseudo-Kähler structure on a Courant algebroid \(E_{H}:= E_{H, 0}\) of type \(B_{n}\) over an even dimensional manifold M. Let \((g, J_{+}, J_{-}, X_{+}, X_{-}, c_{+})\) be the components of \(({\mathcal {G}}, {\mathcal {F}})\) and assume that \(c_{+} \not \in \{ -1, 1\}\). Define \({\tilde{g}}:= \epsilon g\) where \(\epsilon := \textrm{sign}\, ( 1- c_{+}^{2})\), \({\tilde{X}}_{\pm }:=\) \(|1- c_{+}^{2}|^{-1/2} X_{\pm }\), and \({\tilde{J}}_{\pm } \in \Gamma ( \textrm{End}\, TM)\) by \({\tilde{J}}_{-}:= J_{-}\), \({\tilde{J}}_+|_{\{ X_{+}, X_{-} \}^{\perp }}:= J_+|_{\{ X_{+}, X_{-} \}^{\perp }}\) and \({\tilde{J}}_{+} X_{+} = {\tilde{J}}_{+} X_{-} =0\). Then \(( {\tilde{g}}, {\tilde{J}}_{+}, {\tilde{J}}_{-}, {\tilde{X}}_{+}, {\tilde{X}}_{-}, {\tilde{c}}_{+}:= 0)\) are the components of a \(B_{n}\)-generalized pseudo-Kähler structure on the Courant algebroid \(E_{{\tilde{H}}}: =E_{{\tilde{H}}, 0}\) where \({\tilde{H}}:= \epsilon H.\)
Remark 25
The formulation and the proof of Theorem 20 can be adapted to the case when the vector fields \(X_{\pm }\) are trivial (see Remark 37). Let \(({\mathcal {G}}, {\mathcal {F}})\) be a \(B_{n}\)-generalized almost pseudo-Hermitian structure on \(E_{H, F}\) with \(X_{+} = X_{-} =0.\) It turns out that \(({\mathcal {G}}, {\mathcal {F}})\) is integrable if and only if \(F =0\) and \(({\mathcal {G}}, {\mathcal {F}} )\) is a generalized pseudo-Kähler structure on the exact Courant algebroid \(TM \oplus T^{*}M\) (trivially extended to \(TM\oplus T^*M \oplus {\mathbb {R}}\)) with Dorfman bracket twisted by the (closed) 3-form H. Such structures were defined in [8] and are deeply studied in the literature (especially for positive definite signature).
5.2 Proofs of Theorems 16 and 20
We start with various general integrability results, which will be used in the proofs of Theorems 16 and 20.
5.2.1 General Integrability Results
Let \(({\mathcal {G}}, {\mathcal {F}} )\) be a \(B_{n}\)-generalized almost pseudo-Hermitian structure on an odd exact Courant algebroid \((E, \langle \cdot , \cdot \rangle , [\cdot , \cdot ], \pi ) \) over a manifold M of dimension n and \(u_{0}\in \Gamma ( \textrm{Ker}\, {\mathcal {F}} )\) such that \(\langle u_{0}, u_{0}\rangle = (-1)^{n}\). For \(u,v\in \Gamma (E)\) and \(A\in \Gamma (\textrm{End} \, E)\) we define \({{\textbf{L}}}_{u} v:= [u,v]\) and \({{\textbf{L}}}_{u}A\in \Gamma ( \textrm{End}\, E)\) by
and refer to it as the  . It is easy to check that \({{\textbf{L}}}_{u}\) acts as a derivation on the \({\mathbb {R}}\)-algebra \(\Gamma (\textrm{End} \, E)\).
. It is easy to check that \({{\textbf{L}}}_{u}\) acts as a derivation on the \({\mathbb {R}}\)-algebra \(\Gamma (\textrm{End} \, E)\).
Lemma 26
If \({\mathcal {F}}\) is integrable, then \({{\textbf{L}}}_{u_{0}}{\mathcal {F}} =0\). If \(({\mathcal {G}}, {\mathcal {F}})\) is integrable, then \({{\textbf{L}}}_{u_{0}}{\mathcal {F}} =0\) and \({{\textbf{L}}}_{u_{0}} {\mathcal {G}}^{\textrm{end}} =0.\)
Proof
The statement \({{\textbf{L}}}_{u_{0} }{\mathcal {F}} =0\) for any \(B_{n}\)-generalized complex structure \({\mathcal {F}}\) and \(u_{0}\in \Gamma ( \textrm{Ker}\, {\mathcal {F}} )\) normalized by \(\langle u_{0}, u_{0} \rangle = (-1)^{n}\) was proved in Lemma 4.13 of [13]. Assume that \(({\mathcal {G}}, {\mathcal {F}})\) is a \(B_{n}\)-generalized pseudo-Kähler structure. Since \({\mathcal {F}}\) and \({\mathcal {F}}_{2}:= {\mathcal {G}}^{\textrm{end}} {\mathcal {F}}\) are integrable, we obtain that \({{\textbf{L}}}_{u_{0} }{\mathcal {F}} = {{\textbf{L}}}_{u_{0} }{\mathcal {F}}_{2} =0\). On the other hand, from \({{\textbf{L}}}_{u_{0}}(u_{0} ) = \frac{1}{2} \pi ^{*} d\langle u_{0}, u_{0} \rangle =0\) we deduce that \({{\textbf{L}}}_{u_{0}}\) preserves \(u_{0}^{\perp }\). Combined with \({\mathcal {G}}^{\textrm{end}} = - {\mathcal {F}} {\mathcal {F}}_{2}\) on \(u_{0}^{\perp }\) we obtain \({{\textbf{L}}}_{u_{0}}{\mathcal {G}}^{\textrm{end}} =0.\) \(\square \)
Let \(L_{1}\subset E_{{\mathbb {C}} }\) be the i-eigenbundle of \({\mathcal {F}}\) and \(E_{\pm }\) the \(\pm 1\)-eigenbundles of \({\mathcal {G}}^{\textrm{end}}.\) From (11),
where \(L_{2}\) is the i-eigenbundle of \({\mathcal {F}}_{2}:= {\mathcal {F}} {\mathcal {G}}^{\textrm{end}}.\) Let \(L_{1}^{+}: =L_{1} \cap L_{2}\) and \(L_{1}^{-}:=L_{1} \cap {\bar{L}}_{2}\).
Lemma 27
Assume that \({\mathcal {F}}\) is integrable. Then the Dorfman Lie derivative \({{\textbf{L}}}_{u_{0}}:\Gamma (E) \rightarrow \Gamma (E)\) preserves \(\Gamma (L_{1}^{+})\) if and only if it preserves \(\Gamma (L_{1}^{-})\).
Proof
We remark that
Assume that \({{\textbf{L}}}_{u_{0} }\) preserves \(\Gamma ( L_{1}^{+})\). Then \({{\textbf{L}}}_{u_{0} }\) preserves also \(\Gamma ( \overline{L_{1}^{+}})\). For any \(v\in \Gamma (L_{1}^{-})\) and \(w\in \Gamma ( \overline{L_{1}^{+}})\),
where we used \(\langle v, w\rangle =0\), \([u_{0}, w]\in \Gamma (\overline{L_{1}^{+}})\) and the first relation (31). Since \({\mathcal {F}}\) is integrable, \([u_{0}, v]\in \Gamma (L_{1})\) (see Lemma 26). The first relation (31) and relation (32) imply that \([u_{0}, v]\in \Gamma ( L_{1}^{-})\). We proved that \({{\textbf{L}}}_{u_{0} }\) preserves \(\Gamma ( L_{1}^{-})\). The converse statement follows in a similar way, by using the second relation (31). \(\square \)
The next proposition is the analogue of Proposition 6.10 of [8].
Proposition 28
Let \(({\mathcal {G}}, {\mathcal {F}})\) be a \(B_{n}\)-generalized almost pseudo-Hermitian structure. Then \(({\mathcal {G}}, {\mathcal {F}})\) is integrable if and only if \(L_{1}\), \(L_{1}^{\pm }\) are integrable and any of the equivalent conditions from Lemma 27 holds.
Proof
If \(({\mathcal {G}}, {\mathcal {F}} )\) is integrable then obviously \(L_{1}^{\pm } \) and \(L_{1}\) are integrable. From Lemma 4.13 of [13], \({{\textbf{L}}}_{u_{0}}\) preserves \(\Gamma (L_{1}^{\pm })\).
For the converse, we need to show that \(L_{2} = L_{1}^{+} \oplus \overline{L_{1}^{-}}\) is integrable, i.e.
The map which assigns to \(X\in {\bar{L}}_{1}\) the covector \(\xi \in L_{1}^{*}\) defined by \(\xi ( Y):= \langle X, Y\rangle \), for any \(Y\in L_{1}\), is an isomorphism, which maps \(\overline{L_{1}^{\pm }}\subset {\bar{L}}_{1}\) onto \(\textrm{Ann}\, (L_{1}^{{\mp }}) \subset L_{1}^{*}\). We identify \({\bar{L}}_{1}\) with \(L_{1}^{*}\) by means of this isomorphism. In particular, \({L}^{*}_{1}\) inherits a Lie algebroid structure from the Lie algebroid structure of \({\bar{L}}_{1}\). As proved in [13] (Section 4.4, page 66), for any \(X\in \Gamma (L_{1})\) and \(\xi \in \Gamma ( L_{1}^{*})\),
where \({\mathcal {L}}_{X}\) denotes the Lie derivative of the Lie algebroid \(L_{1}\), defined by the Cartan formula \({{\mathcal {L}}}_{X}:= i_{X} d_{L_{1} }+ d_{L_{1}} i_{X}\), and
are the exterior derivatives of the Lie algebroids \(L_{1}\) and \(L_{1}^{*}.\) Assume now that \(X\in \Gamma (L_{1}^{+})\) and \(\xi \in \Gamma (\overline{ L_{1}^{-}}).\) Since \({{\textbf{L}}}_{u_{0}}\) preserves \(\Gamma (L_{1}^{+})\), the last term from (34) vanishes and we obtain
where we used \(\xi (X) =0.\) On the other hand, if \({\mathcal {A}}\) is an arbitrary Lie algebroid with a decomposition \({\mathcal {A}} = {\mathcal {A}}_{1} \oplus {\mathcal {A}}_{2}\) where \({\mathcal {A}}_{i}\) are integrable subbundles of \({\mathcal {A}}\), then \( i_{Y} d_{{\mathcal {A}}} \eta \in \Gamma ( \textrm{Ann}\, ({\mathcal {A}}_{1}))\), for any \(Y\in \Gamma ({\mathcal {A}}_{1})\) and \(\eta \in \Gamma ( \textrm{Ann}\, ({\mathcal {A}}_{1})).\) Applying this result to the Lie algebroids \(L_{1} = L_{1}^{+} \oplus L_{1}^{-}\) and
we obtain that \(i_{X} d_{L_{1}} \xi \) is a section of \(\textrm{Ann}\, ( L_{1}^{+}) = \overline{L_{1}^{-}}\) and \(i_{\xi } d_{L_{1}^{*}} X \) is a section of \(L_{1}^{+}\) (in the last statement we identified \(L_{1}^{+}\) with \(\textrm{Ann}\, (\textrm{Ann}\, L_{1}^{+})\) in the natural isomorphism \(L_{1} = (L_{1}^{*})^{*}\)). Relation (33) follows. \(\square \)
Let \(E = E_{H, F}\) be a Courant algebroid of type \(B_{n}\) over a manifold M with Dorfman bracket twisted by (H, F). On M we consider a pseudo-Riemannian metric h, a complex distribution \({\mathcal {D}}\subset (TM)_{{\mathbb {C}}}\) and a vector field \(X_{0}\) (real or complex), h-orthogonal to \({\mathcal {D}}\) and such that \(h(X_{0}, X_{0})=1.\) We define the subbundles of \(E_{{\mathbb {C}}}\) by
Let \(Y_{0}\in {{\mathfrak {X}}}(M)\), \(f\in C^{\infty }(M, {\mathbb {C}})\) and
which are sections of \(E_{\mathbb {C}}\). Let \(\nabla \) be the Levi-Civita connection of h.
Lemma 29
-
i)
The bundle \(L^{h, {\mathcal {D}}}\) is integrable if and only if \({\mathcal {D}}\) is involutive, \(F\vert _{\Lambda ^{2} {\mathcal {D}}} =0\) and, for any \(X, Y\in \Gamma ({\mathcal {D}} )\) and \(Z\in {{\mathfrak {X}}}(M)\),
$$\begin{aligned} h (\nabla _{Z} X, Y) =\frac{1}{2} H(X, Y, Z). \end{aligned}$$(36) -
ii)
The Dorfman Lie derivative \({{\textbf{L}}}_{u^{Y_{0}}}\) preserves \(\Gamma (L^{h,{\mathcal {D}}})\) if and only if
$$\begin{aligned} {{\mathcal {L}}}_{Y_{0}}\Gamma ({\mathcal {D}}) \subset \Gamma ({\mathcal {D}}),\ (i_{Y_{0}} F)\vert _{{\mathcal {D}}} =0 \end{aligned}$$and, for any \( X\in \Gamma ({\mathcal {D}} )\) and \(Z\in {{\mathfrak {X}}}(M)\),
$$\begin{aligned} h (\nabla _{Z} Y_{0}, X) =\frac{1}{2} H(Y_{0}, X, Z). \end{aligned}$$(37) -
iii)
The Dorfman Lie derivative \({{\textbf{L}}}_{u^{Y_{0}, f}}\) preserves \(\Gamma (L^{h,{\mathcal {D}}})\) if and only if
$$\begin{aligned} {{\mathcal {L}}}_{Y_{0}} \Gamma ({\mathcal {D}} )\subset \Gamma ({\mathcal {D}}),\ (i_{Y_{0}} F)\vert _{ {\mathcal {D}}} = (df)\vert _{{\mathcal {D}}} \end{aligned}$$and, for any \(X\in \Gamma ({\mathcal {D}})\) and \(Z\in {{\mathfrak {X}}}(M)\),
$$\begin{aligned} h(\nabla _{X} Y_{0}, Z) =\frac{1}{2}H(Y_{0}, X, Z)- f F(X, Z). \end{aligned}$$(38) -
iv)
The bundle \(L^{h, {\mathcal {D}}, X_{0}}\) is integrable if and only if the following conditions hold:
-
1.
for any \(Y, Z\in \Gamma ({\mathcal {D}} )\),
$$\begin{aligned}&{{\mathcal {L}}}_{Y} Z + i F(Y, Z) X_{0}\in \Gamma ({\mathcal {D}} ),\nonumber \\&{{\mathcal {L}}}_{X_{0}}Y+ i F(X_{0}, Y)X_{0} \in \Gamma ({\mathcal {D}} ) ; \end{aligned}$$(39) -
2.
for any \(Y, Z\in \Gamma ({\mathcal {D}} )\) and \(X\in {{\mathfrak {X}}}(M)\),
$$\begin{aligned} h (\nabla _{X} Y, Z)&=\frac{1}{2} H(X, Y, Z),\nonumber \\ h (\nabla _{X} X_{0}, Y)&=- \frac{1}{2} H (X_{0}, X, Y) + i F(X, Y) . \end{aligned}$$(40)
-
1.
Proof
The proof is a straightforward computation, which uses the expression (3) of the Dorfman bracket. For example, to prove claim i) let \(X, Y\in \Gamma ({\mathcal {D}} )\). Then
is a section of \(L^{h,{\mathcal {D}}}\) if and only if \({{\mathcal {L}}}_{X}Y \in \Gamma ({\mathcal {D}})\), \(F(X, Y)=0\) and
Applying the above relation to \(Z\in {{\mathfrak {X}}}(M)\) and writing it in terms of \(\nabla \) we obtain (36). The other claims can be obtained similarly. \(\square \)
Lemma 30
Let \((E, \langle \cdot , \cdot \rangle , [\cdot , \cdot ], \pi )\) be a Courant algebroid of type \(B_{n}\) over a manifold M, with Dorfman bracket twisted by (H, F), h be a pseudo-Riemannian metric on M and \({\mathcal {D}}_{\pm }\subset (TM)_{{\mathbb {C}}}\) two complex distributions, such that \({\mathcal {D}}_{+}\) is isotropic. Let \(X_{0}\in {{\mathfrak {X}}}(M)_{\mathbb {C}}\) be a complex vector field orthogonal to \({\mathcal {D}}_{+}\), such that \(h ( X_{0}, X_{0}) =1.\) Assume that the following relations hold:
-
i)
for any \(X\in \Gamma ({\mathcal {D}}_{-})\) and \(Y\in \Gamma ({\mathcal {D}}_{+ })\),
$$\begin{aligned} \nabla _{Y}X -\frac{1}{2} H(X, Y) \in \Gamma ({\mathcal {D}}_{-}); \end{aligned}$$(42) -
ii)
for any \(X\in \Gamma ({\mathcal {D}}_{-})\) and \(Y\in \Gamma ({\mathcal {D}}_{+})\),
$$\begin{aligned} \nabla _{X} Y -\frac{1}{2} H(X, Y) \in \Gamma ({\mathcal {D}}_{+}\oplus \textrm{span}_{{\mathbb {C}}}\{ X_{0}\} ); \end{aligned}$$(43) -
iii)
for any \(X\in \Gamma ({\mathcal {D}}_{-})\),
$$\begin{aligned} \nabla _{X_{0}} X + \frac{1}{2} H(X_{0}, X) \in \Gamma ({\mathcal {D}}_{-} ); \end{aligned}$$(44) -
iv)
for any \(X\in \Gamma ({\mathcal {D}}_{-})\),
$$\begin{aligned} \nabla _{X}X_{0} + \frac{1}{2} H(X_{0}, X)- iF(X) \in \Gamma ({\mathcal {D}}_{+} \oplus \textrm{span}_{{\mathbb {C}}}\{ X_{0}\} ); \end{aligned}$$(45) -
v)
for \(X\in \Gamma ({\mathcal {D}}_{-})\),
$$\begin{aligned} F(X) \in \Gamma ({\mathcal {D}}_{-}). \end{aligned}$$(46)
Then
Proof
In order to prove (47) we need to show that \([ X - h(X), Y + h(Y) ] \) and \([ X - h(X), X_{0} + h(X_{0}) + i ] \) are sections of \(L^{-h,{\mathcal {D}}_{-}} \oplus L^{h, {\mathcal {D}}_{+}, X_{0}}\), for any \(X\in \Gamma ({\mathcal {D}}_{-})\) and \(Y\in \Gamma ({\mathcal {D}}_{+})\). Remark that
where we used that \(X_{0}\) is of norm one and orthogonal to \({\mathcal {D}}_{+}.\) Writing \({\mathcal {L}}_{X} Y = {{\mathcal {F}}}^{\prime }_{+}(X, Y) - {{\mathcal {F}}}^{\prime }_{-}(X, Y) \), where
(compare relations (42) and (43)), we obtain
On the other hand, taking the h-inner product with Y of the left hand side of (45) and using that \({\mathcal {D}}_{+}\) is isotropic and \(X_{0}\) is orthogonal to \({\mathcal {D}}_{+}\), we obtain
Using the definition of \({\mathcal {F}}^{\prime }_{\pm }\) it is easy to see that
We deduce that
is a section of \(L^{-h,{\mathcal {D}}_{-}} \oplus L^{h, {\mathcal {D}}_{+}, X_{0}}.\) Similar computations show that
is also a section of \(L^{-h,{\mathcal {D}}_{-}} \oplus L^{h, {\mathcal {D}}_{+}, X_{0}}\), where
(from relations (44), (45) and (46)). \(\square \)
5.2.2 Application of General Integrability Results
We now turn to the setting of Sect. 5.1, and, using the results from the previous section, we prove Theorems 16 and 20. Consider the setting of these theorems. We start by computing the bundles \(L_{1}^{\pm }\) associated to the \(B_{n}\)-generalized pseudo-Hermitian structure \(({\mathcal {G}}, {\mathcal {F}} )\), as in Proposition 28. They turn out to be of the form \(L^{h,{\mathcal {D}}}\) or \(L^{h, {\mathcal {D}}, X_{0}}\) for suitably chosen h, \({\mathcal {D}}\) and \(X_{0}.\)
Lemma 31
-
i)
If n is odd then
$$\begin{aligned} L_{1}^{+}&= \{ X + g(X) \mid X\in T_{J_{+}}^{(1,0)}M\} \oplus \textrm{span}_{{\mathbb {C}}}\{ X_{+} + g(X_{+}) + i\} ,\nonumber \\ L_{1}^{-}&= \{ X - g(X)\mid X\in T_{J_{-}}^{(1,0)}M\} . \end{aligned}$$(52) -
ii)
If n is even then
$$\begin{aligned} L_{1}^{+}&= \{ X + g(X)\mid X\in T^{(1,0)}_{J_{+}}M \}\oplus \textrm{span}_{{\mathbb {C}}} \{ V_{-} + g (V_{-}) + i \} ,\nonumber \\ L_{1}^{-}&= \{ X - g(X)\mid X\in T_{J_{-}}^{(1,0)} M\} , \end{aligned}$$(53)where \(V_{-}:=\frac{1}{ 1- c_{+}^{2} } ( X_{-} - i c_{+} X_{+})\) is of norm one and orthogonal to \(T_{J_{+}}^{(1,0)}M\).
Proof
The proof is straightforward from Proposition 13. In particular, one can easily check from the formulas for \({\mathcal {J}}_+\) and \({\mathcal {F}}_+\) in Proposition 13 that \({\mathcal {J}}_+(X_++i) = i(X_++i)\) and \({\mathcal {F}}_+(V_-+i)=i(V_-+i)\), which are equivalent to \({\mathcal {F}}(X_+ + g(X_+) + i) = i(X_+ + g(X_+) + i)\) and \({\mathcal {F}}(V_-+g(V_-)+i)=i(V_-+g(V_-)+i)\), respectively. \(\square \)
Corollary 32
Assume that n is odd. The following are equivalent:
-
i)
\(( {\mathcal {G}}, {\mathcal {F}} )\) is a \(B_{n}\)-generalized pseudo-Kähler structure;
-
ii)
\(L_{1}^{\pm }\) are integrable and the Dorfman Lie derivative \({{\textbf{L}}}_{u_{-}}\) preserves \(\Gamma ( L_{1}^{-})\), where \(u_{-}:= X_{-} - g(X_{-})\);
-
iii)
\(T_{J_{-}}^{(1,0)}M\) is involutive, \(F\vert _{\Lambda ^{2} T_{J_{-}}^{(1,0)}M}=0\), \(i_{X_{-}} F=0\), the Lie derivative \({{\mathcal {L}}}_{X_{-}}\) preserves \(\Gamma (T_{J_{-}}^{(1,0)}M)\) and the following relations hold:
-
1.
for any \(X, Y\in \Gamma (T_{J_{-}}^{(1,0)}M)\) and \(Z, V\in {{\mathfrak {X}}}(M)\),
$$\begin{aligned} g (\nabla _{Z} X, Y)&=-\frac{1}{2} H(X, Y, Z),\nonumber \\ g(\nabla _{Z} X_{-}, V)&= -\frac{1}{2} H(X_{-}, V, Z); \end{aligned}$$(54) -
2.
for any \(Y, Z\in \Gamma (T_{J_{+}}^{(1,0)}M)\),
$$\begin{aligned}&{{\mathcal {L}}}_{Y} Z + i F(Y, Z) X_{+}\in \Gamma (T_{J_{+}}^{(1,0)}M),\nonumber \\&{{\mathcal {L}}}_{X_{+}} Z + i F(X_{+}, Z) X_{+}\in \Gamma (T_{J_{+}}^{(1,0)}M); \end{aligned}$$(55) -
3.
for any \(Y, Z\in \Gamma (T_{J_{+}}^{(1,0)}M)\) and \(X\in {{\mathfrak {X}}}(M)\),
$$\begin{aligned} g (\nabla _{X} Y, Z)&=\frac{1}{2} H(X, Y, Z),\nonumber \\ g (\nabla _{X} X_{+}, Y)&=- \frac{1}{2}H (X_{+}, X, Y) + i F(X, Y). \end{aligned}$$(56)
-
1.
Proof
The implication i) \(\Longrightarrow \) ii) follows from Proposition 28, while the equivalence between ii) and iii) follows from Lemma 31 i), Lemma 29 i) with \(h:= -g\) and \({\mathcal {D}}:= {T}_{J_{-}}^{(1,0)}M\), Lemma 29 ii) with \(h:= - g\), \({\mathcal {D}}:= T_{J_{-}}^{(1,0)}M\) and \(Y_{0}:= X_{-}\) and Lemma 29 iv) with \(h:= g\), \({\mathcal {D}}:= {T}_{J_{+}}^{(1,0)}M\) and \(X_{0}:= X_{+}\). In order to prove that iii) implies i) we apply again Proposition 28. We need to show that the relations from iii) imply that \(L_{1}\) is integrable, or
The above relation follows from Lemma 30, by noticing that the assumptions from this lemma are implied by the conditions from iii). (The lemma is specialized to \({\mathcal {D}}_\pm = T^{(1,0)}_{J_\pm }M\), \(h=g\) and \(X_0=X_+\)). For example, the first relation (54) implies that \(\nabla _{Y} X - \frac{1}{2} H(X, Y)\) is orthogonal to \({T}_{J_-}^{(1,0)}M\), i.e. is a section of \({T}_{J_{-}}^{(1,0)}M\oplus \textrm{span}_{{\mathbb {C}}}\{ X_{-} \} \), for any \(X\in \Gamma ({T}_{J_{-}}^{(1,0)}M)\) and \(Y\in \Gamma (T_{J_{+}}^{(1,0)}M)\). From the second relation (54), it is also orthogonal to \(X_{-}\). Relation (42) follows. The other relations can be checked similarly. \(\square \)
Corollary 33
Assume that n is even. The following are equivalent:
-
i)
\(({\mathcal {G}}, {\mathcal {F}} )\) is a \(B_{n}\)-generalized pseudo-Kähler structure;
-
ii)
\(L_{1}^{\pm }\) are integrable and the Dorfman Lie derivative \({{\textbf{L}}}_{u_{+}}\) preserves \(\Gamma ( L_{1}^{-})\), where \(u_{+}:= X_{+} + g(X_{+}) +c_{+}\);
-
iii)
\(J_{-}\) is integrable, \(F\vert _{\Lambda ^{2}T^{(1,0)}_{J_{-}}M}=0\) and the following relations hold:
-
1.
for any \(X, Y\in \Gamma ( { T}^{(1,0)}_{J_{-}}M)\) and \(Z\in {{\mathfrak {X}}}(M)\),
$$\begin{aligned} g( \nabla _{Z} X, Y)&=-\frac{1}{2} H(X, Y, Z),\nonumber \\ g(\nabla _{X} X_{+}, Z)&=- \frac{1}{2} H(X_{+}, X, Z) + c_{+} F(X, Z) ; \end{aligned}$$(58) -
2.
for any \(X, Y\in \Gamma (T_{J_{+}}^{(1,0)}M)\),
$$\begin{aligned}&{{\mathcal {L}}}_{X} Y + i F(X, Y) V_{-}\in \Gamma (T^{(1,0)}_{J_{+}}M),\nonumber \\&{{\mathcal {L}}}_{V_{-}}X+ i F(V_{-}, X)V_{-} \in \Gamma (T^{(1,0)}_{J_{+}}M), \end{aligned}$$(59)where, we recall, \(V_{-} =\frac{1}{1- c_{+}^{2}}( X_{-} - i c_{+} X_{+})\);
-
3.
for any \(X, Y\in \Gamma (T_{J_{+}}^{(1,0)}M)\) and \(Z\in {{\mathfrak {X}}}(M)\),
$$\begin{aligned} g(\nabla _{Z} X, Y)&=\frac{1}{2} H(X, Y, Z),\nonumber \\ g (\nabla _{Z} V_{-}, X)&=\frac{1}{2} H(V_{-}, X, Z) - i F(X, Z); \end{aligned}$$(60) -
4.
$$\begin{aligned} i_{X_{+}}F = dc_+. \end{aligned}$$(61)
-
1.
Proof
The claims follow with a similar argument, as in Corollary 32. We only explain the implication ii) \(\Longrightarrow \) iii). We use Lemma 31 ii), Lemma 29 i) with \(h:= -g\) and \({\mathcal {D}}:= T_{J_{-}}^{(1,0)}M\), Lemma 29 iii) with \(h:= - g\), \({\mathcal {D}}:= T_{J_{-}}^{(1,0)}M\), \(Y_{0}:= X_{+}\), \(f:= c_{+}\) and Lemma 29 iv) with \(h:= g\), \({\mathcal {D}}:=T_{J_{+}}^{(1,0)}M\), \(X_{0}:=V_{-}\). We obtain that \(L_{1}^{\pm }\) are integrable and the Dorfman Lie derivative \({{\textbf{L}}}_{u_{+}}\) preserves \(\Gamma ( L_{1}^{-})\) if and only if the relations 1., 2. and 3. from iii) hold, together with \(i_{X_{+}} F = dc_{+}\) on \(T_{J_{-}}^{(1,0)} M\) and \({{\mathcal {L}}}_{X_{+}} \Gamma ( T_{J_{-}}^{(1,0)}M) \subset \Gamma ( T_{J_{-}}^{(1,0)} M)\). However, the real one-form \(i_{X_{+}} F -dc_{+}\) vanishes on \(T_{J_{-}}^{(1,0)} M\) if and only if it is zero, since \(J_-\) is an almost complex structure. Finally, \({{\mathcal {L}}}_{X_{+}} \Gamma ( T_{J_{-}}^{(1,0)}M) \subset \Gamma ( T_{J_{-}}^{(1,0)} M)\) follows by combining the first relation (58) with \(Z:= X_{+}\) with the second relation (58) with \(Z:= Y\) and using that \(F(X, Y)=0\) for any \(X, Y\in \Gamma (T^{(1,0)}_{J_{-}} M)\), since F is of type (1, 1) with respect to \(J_{-}\). \(\square \)
Remark 34
We remark that on the support of the function \(c_+\) the relation (61) is automatically satisfied if the other conditions listed under iii) in Corollary 33 hold. In fact,
and hence (61), follows from the second relation (58), by letting \(Z:= X_{+}\) and using \(g(X_{+}, X_{+}) = 1-c_{+}^{2}.\)
We conclude the proofs of Theorems 16 and 20 by noticing that the conditions from Corollary 32 iii) and 33 iii) are equivalent to the conditions from these theorems. This is done in the next two lemmas.
Lemma 35
Assume that \((g, J_{+}, J_{-}, X_{+}, X_{-})\) are the components of a \(B_{n}\)-generalized almost pseudo-Hermitian structure on a Courant algebroid \(E = E_{H, F}\) of type \(B_{n}\) over an odd dimensional manifold M. The conditions from Corollary 32 iii) are equivalent to the conditions from Theorem 16.
Proof
Assume that the conditions from Corollary 32 iii) are satisfied. Relations (54) imply that \(\nabla ^{-}\) preserves \(T^{(1,0)}_{J_{-}} M\) and \(\nabla ^{-} X_{-}=0\). The second relation (56) implies that
for any \(X\in {{\mathfrak {X}}}(M)\). Using that \(g(X_{+}, X_{+}) =1\) we obtain
Since both, the real and the imaginary parts of the left-hand side of (63) are orthogonal to \(X_{+}\), \(J_{+}\vert _{\textrm{span}\{ X_{+} \}^{\perp }}\) is a complex structure and \(J_{+} X_{+} =0\), we deduce from (63) that
which is equivalent to the second relation (19). We now prove that \(\nabla ^{+}\) preserves \(T^{(1,0)}_{J_{+}} M\). The first relation (56) implies that for any \(X\in {\mathfrak {X}}(M)\) and \(Y\in \Gamma (T^{(1,0)}_{J_{+}}M)\),
It is easy to see that (64) combined with (65) imply that \(\nabla ^{+}\) preserves \(T^{(1,0)}_{J_{+}}M\). The relations from Theorem 16 i) follow.
The relations from Theorem 16 ii) can be obtained by similar computations. To prove that \(H\vert _{\Lambda ^{3} T_{J_{-}}^{(1,0)}M}=0\) let \( X, Y\in \Gamma ( T^{(1,0)}_{J_{-}} M)\) and write
Since \(T^{(1,0)}_{J_{-}}M\) is involutive (from the first condition of Corollary 32 iii)) and \(\nabla ^{-}\) preserves \(T^{(1,0)}_{J_{-}} M\), we obtain that H(X, Y) is a section of \(T^{(1,0)}_{J_{-}} M\). In particular, \(H\vert _{\Lambda ^{3} T_{J_{-}}^{(1,0)}M}=0\). To prove that \(H\vert _{\Lambda ^{3} T_{J_{+}}^{(1,0)}M}=0\) and \((i_{X_{+}}H)= i F\) on \({\Lambda ^{2}T_{J_{+}}^{(1,0)}M}\) we use the first relation (55), together with
for any \(Y, Z\in \Gamma (T^{(1,0)}_{J_{+}} M)\), and the fact that the distribution \(T^{(1,0)}_{J_{+}} M\) is preserved by the connection \(\nabla ^+\). (Recall that \(\nabla ^+\) is related to \(\nabla \) by (18).) Finally, relation \((i_{X_{-}} H)\vert _{\Lambda ^{2} T^{(1,0)}_{J_{-}} M} =0\) follows by writing
and using that \({\mathcal {L}}_{X_{-}}\) and \(\nabla ^{-}\) preserve \(\Gamma ( T^{(1,0)}_{J_{-}} M).\)
In the same vein one proves that conditions from Theorem 16 imply those from Corollary 32 iii). \(\square \)
It remains to explain how Theorem 20 follows from Corollary 33.
Lemma 36
Assume that \((g, J_{+}, J_{-}, X_{+}, X_{-}, c_{+})\) are the components of a \(B_{n}\)-generalized almost pseudo-Hermitian structure on a Courant algebroid \(E = E_{H, F}\) of type \(B_{n}\) over an even dimensional manifold M, such that \(X_{+}\) and \(X_{-}\) are non-null. Then the conditions from Corollary 33 iii) are equivalent to the conditions from Theorem 20.
Proof
Straightforward computations as in the previous lemma show that all conditions from Corollary 33 iii), except the second relation (59), are equivalent to all conditions from Theorem 20, except \({\mathcal {L}}_{X_{+}} X_{-} =0\) (or relation (30), see Lemma 22). Assume that these equivalent conditions hold. Under this hypothesis, we show that the second relation (59) is equivalent to relation (30). Let \(X\in \Gamma ( T^{(1,0)}_{J_{+}} M)\) and recall that \(V_{-} =\frac{1}{ 1- c_{+}^{2}} (X_{-} - i c_{+} X_{+})\). Writing
and using the expressions of \(\nabla _{X} X_{+}\) and \(\nabla _{X} X_{-}\) provided by relations (26), together with the fact that \(D^{+}\) preserves \(T^{(1,0)}_{J_{+}} M\), we obtain that the second relation (59) is equivalent to the statement that the expression
is a section of \(T^{(1,0)}_{J_{+}} M\), for any \(X\in \Gamma (T^{(1,0}_{J_{+}} M).\) Equivalently, \(\textrm{Expr}(X)\) is orthogonal to \(T^{(1,0)}_{J_{+}} M\), \(X_{+}\) and \(X_{-}\). The condition
is equivalent to \((i_{V_{-}} H)\vert _{\Lambda ^{2} T^{(1,0)}_{J_{+}} M}= i F\vert _{\Lambda ^{2} T^{(1,0)}_{J_{+}}M}\), which follows from the third relation (27) and the first relation (28). Similary, one can show that the relations
are equivalent to
for all \(X\in \textrm{span}\{ X_{+}, X_{-}\}^{\perp }.\) Using \(dc_{+} = i_{X_{+}} F\) we obtain that relation (67) is equivalent to relation (30), as needed. \(\square \)
We end this section with a comment which shows that the notion of \(B_{n}\)-generalized Kähler structure includes the notion of generalized Kähler structure on exact Courant algebroids, as defined in [8].
Remark 37
Let \(({\mathcal {G}}, {\mathcal {F}} )\) be a \(B_{n}\)-generalized almost pseudo-Hermitian structure with components \((g, J_{+}, J_{-}, X_{+}, X_{-}, c_{+})\) on a Courant algebroid \(E_{H, F}\) of type \(B_{n}\) over a manifold M of even dimension. Assume that \(X_{+} = X_{-}= 0\) (in particular \(c_{+}\in \{ \pm 1\}\)). Then \(J_{\pm }\) are g-skew-symmetric almost complex structures on M and (in the notation introduced in Sect. 4) \(u_{+} = c_{+}\). The bundles \(L_{1}^{\pm }\) from Proposition 28 are given by
Adapting the above arguments one can show that \(L_{1}^{\pm }\) are integrable and \({{\textbf{L}}}_{ u_{+}}\) preserves \( \Gamma (L_{1}^{\pm })\) if and only if \(F=0\), \(J_{\pm }\) are (integrable) complex structures and the connections \(\nabla _{X} \pm \frac{1}{2} H(X)\) preserve \(J_{{\mp }}.\) These conditions hold if and only if \(({\mathcal {G}}, {\mathcal {F}} )\) is a \(B_{n}\)-generalized pseudo-Kähler structure. When these conditions hold and \({\mathcal {G}}\) is positive definite, \((g, J_{+}, J_{-}, b:=0)\) is the bi-Hermitian structure of a generalized Kähler structure on the exact Courant algebroid \(TM \oplus T^{*}M\) with Dorfman bracket twisted by the closed 3-form H (see Theorem 6.28 of [8]).
6 \(B_{2}\)-, \(B_{3}\)-, \(B_{4}\)-Generalized Pseudo-Kähler Structures
In this section we show that Theorems 16 and 20 simplify considerably when M has dimension two, three or four. Below we denote by \(X^{\flat }\) the 1-form g-dual to a vector field \(X\in {{\mathfrak {X}}}(M).\)
Corollary 38
-
i)
Let \((g, J_{+},J_{-}, X_{+}, X_{-}, c_{+})\) be the components of a \(B_{2}\)-generalized pseudo-Kähler structure \(({\mathcal {G}}, {\mathcal {F}})\) on a Courant algebroid \(E_{F}:= E_{0,F}\) over a 2-dimensional manifold M. The metric g is either positive or negative definite and there is \(\epsilon _{0} \in \{ \pm 1\} \) such that
$$\begin{aligned} J_{-} X_{+} = - \epsilon _{0} X_{-},\ J_{-} X_{-} =\epsilon _{0} X_{+},\ J_{+} = \epsilon _{0} c_{+} J_{-}. \end{aligned}$$(69)If \(c_{+}(p) \ne 0\) for any \(p\in M\) then \(X_{+}\) is a Killing field with \(g(X_{+}, X_{+}) <1\) and \(F=\frac{1}{2c_{+}} d X_{+}^{\flat }\). If \(c_{+}( p) =0\) for any \(p\in M\) then \(X_{+}\) is a parallel unit field and \(F=0.\)
-
ii)
Conversely, any pair \((g, X_{+})\) formed by a pseudo-Riemannian metric g of definite signature and a vector field \(X_{+}\) such that either \(X_{+}\) is a Killing field with \(g(X_{+}, X_{+}) <1\) or \(X_{+}\) is a parallel unit field defines a \(B_{2}\)-generalized pseudo-Kähler structure on \(E_{F} = E_{0, F}\) with F defined as in i). The vector field \(X_{-}\) is arbitrarily chosen, orthogonal to \(X_{+}\) and of the same norm as \(X_{+}\), the endomorphisms \(J_{\pm }\) are defined by (69) and \(c_{+}:= \epsilon _{+} (1- g(X_{+}, X_{+}))^{1/2}\), where \(\epsilon _{+} \in \{ \pm 1\} \).
Proof
-
i)
Since \(J_{-}\) is a g-skew-symmetric complex structure and M is two dimensional, g has signature (2, 0) or (0, 2). The first two relations (69) follow from the fact that \(X_{\pm }\) are orthogonal of the same norm, M is two dimensional and \(J_{-}\) is a g-skew-symmetric complex structure. The last relation (69) follows from \(J_{+} X_{+} =- c_{+} X_{-}\) and \(J_{+} X_{-} = c_{+} X_{+}.\) Since M is 2-dimensional, \(H=0\), F is of type (1, 1) with respect to \(J_{-}\) and the conditions from Theorem 20 (see also Lemma 22) reduce to
$$\begin{aligned} \nabla _{X} X_{+} = c_{+} F(X),\ \nabla _{X} X_{-} = - J_{+} F(X),\ \nabla _{X} J_{-} =0,\ i_{X_{+}} F = d c_{+}, \end{aligned}$$(70)for any \(X\in {{\mathfrak {X}}}(M)\). However, using (69) one can show that the second and third relation (70) are implied by the first and fourth relation. When \(c_{+}(p) \ne 0\), for any \(p\in M\), the first relation (70) implies that \(F = \frac{1}{ 2c_{+}} d X_{+}^{\flat }\) and the last relation (70) is satisfied. When \(c_{+} (p) =0\), for any \(p\in M\), we obtain from the first and last relation (70) that \(\nabla X_{+} =0\) and \(F=0.\)
-
ii)
Reversing the argument from i) we obtain claim ii). \(\square \)
Corollary 39
In the setting of Theorem 16 assume that M is 3-dimensional. Then \(({\mathcal {G}}, {\mathcal {F}} )\) is a \(B_{3}\)-generalized pseudo-Kähler structure if and only if \(i_{X_{-}} F =0\) and
for any \(X\in {{\mathfrak {X}}}(M).\)
Proof
Assume that \(({\mathcal {G}}, {\mathcal {F}} )\) is a \(B_{3}\)-generalized pseudo-Kähler structure. Relations (71) were already obtained in the proof of Corollary 17 (see relations (22)). Since the bundles \(T_{J_{\pm }}^{(1,0)} M\) have rank one, relations (20) reduce to \(i_{X_{-}} F=0.\) We now prove that relations (71) imply that \(\nabla ^{\pm }\) preserve \(T^{(1,0)}_{J_{\pm }}M.\) For this, let \(v_{-}\) be a non-zero local section of \(T^{(1,0)}_{J_{-}} M.\) Since \(\nabla ^{-}g=0\) and \(v_{-}\) is isotropic, \(g(\nabla ^{-}_{X} v_{-}, v_{-})=0\). Moreover,
and we obtain that \(\nabla _{X}^{-} v_{-} \) is a section of \(T^{(1,0)}_{J_{-}} M\), i.e. \(\nabla ^{-}\) preserves \(T^{(1,0)}_{J_{-}} M.\) A similar argument which uses the second relation (71) and the definition (18) of \(\nabla ^{+}\) shows that \(\nabla ^{+}\) preserves \(T^{(1,0)}_{J_{+}} M.\) Reversing the argument we obtain our claim. \(\square \)
Corollary 40
In the setting of Theorem 20, assume that M is four dimensional. Then \(( {\mathcal {G}}, {\mathcal {F}} )\) is \(B_{4}\)-generalized pseudo-Kähler structure if and only if the following conditions hold:
-
i)
the covariant derivatives of \(X_{\pm }\) with respect to the Levi-Civita connection \(\nabla \) of g are given by
$$\begin{aligned} \nabla _{X} X_{+}&= \frac{1}{2} H(X, X_{+}) + c_{+} F(X),\nonumber \\ \nabla _{X} X_{-}&= \frac{1}{2} H(X, X_{-}) - J_{+} F(X), \end{aligned}$$(72)for any \(X\in {{\mathfrak {X}}}(M)\).
-
ii)
the connection \(D^{-} _{X}:=\nabla _{X} +\frac{1}{2} H(X)\) preserves \(J_{-}\);
-
iii)
F is of type (1, 1) with respect to \(J_{-}\), \(i_{X_{+}} F = d c_{+}\) and
$$\begin{aligned} H(X_{+}, X_{-}) = c_{+} F(X_{-}) + J_{+} F(X_{+}). \end{aligned}$$(73)
Proof
Since M has dimension four, \(\textrm{rank}\, T_{J_{+}}^{(1,0)}M =1\) and \(\textrm{rank}\, T_{J_{-}}^{(1,0)}M =2\). Like in the proof of Corollary 39, one can show that relations (26) and \(\textrm{rank}\, T_{J_{+}}^{(1,0)}M =1\) imply that \(D^{+}\) preserves \(T_{J_{+}}^{(1,0)} M\). We deduce that the conditions from Theorem 20 (see also Lemma 22) reduce to the conditions from Corollary 40. \(\square \)
7 Examples Over Lie Groups
In order to illustrate our theory, in this section we construct examples of \(B_{n}\)-generalized pseudo-Kähler structures on Courant algebroids of type \(B_{n}\) over Lie groups of dimension two, three and four.
Definition 41
A Courant algebroid \(E_{H, F}\) of type \(B_{n}\) over a Lie group G is called  if the forms \(H\in \Omega ^{3}(G)\) and \(F\in \Omega ^{2}(G)\) are left-invariant. A \(B_{n}\)-generalized pseudo-Kähler structure is
if the forms \(H\in \Omega ^{3}(G)\) and \(F\in \Omega ^{2}(G)\) are left-invariant. A \(B_{n}\)-generalized pseudo-Kähler structure is  if it is defined on a left-invariant Courant algebroid and its components are left-invariant tensor fields.
if it is defined on a left-invariant Courant algebroid and its components are left-invariant tensor fields.
We identify as usual left-invariant tensor fields on a Lie group G with tensors on the Lie algebra \({\mathfrak {g}}\) of G. In particular, the forms H and F which define a left-invariant Courant algebroid \(E_{H, F}\) over G, as well as the components of a left-invariant \(B_{n}\)-generalized pseudo-Kähler structure on \(E_{H, F}\), will be considered as tensors on the Lie algebra \({\mathfrak {g}}\).
7.1 The Case \(\textrm{dim}\, G=2\)
Let G be a 2-dimensional Lie group with Lie algebra \({\mathfrak {g}}\) and \(({\mathcal {G}}, {\mathcal {F}})\) a left-invariant \(B_{2}\)-generalized pseudo-Kähler structure on a (left-invariant) Courant algebroid \(E_{F}:= E_{0, F}\) of type \(B_{2}\) over G, with components \((g, J_{+}, J_{-}, X_{+}, X_{-}, c_{+}) \). Recall that a 2-dimensional Lie group with a left-invariant metric admits a (non-zero) left-invariant Killing field if and only if it is abelian. Since (under our overall assumption \(c_+^2\ne 1\)) \(X_{+}\) is a Killing field (see Corollary 23) we deduce that G is abelian. From Corollary 38, there is a g-orthonormal basis \(\{ v_{1}, v_{2} \}\) of \({\mathfrak {g}}\) such that
where \(\epsilon _{0}, \epsilon _{+} \in \{ \pm 1 \} \) and \(y\in {\mathbb {R}}{\setminus } \{ 0\} \) is such that \(\epsilon y^{2} \le 1\), where \(\epsilon := g(v_{i}, v_{i})\in \{ \pm 1\}\). The condition \(i_{X_{+}} F = d c_{+}\) together with \(c_{+}\) constant imply \(F=0.\) Note that examples with \(c_+^2=1\) do also exist. These are two-dimensional solvable Kähler Lie groups (G, J, g) considered as generalized Kähler structures on the untwisted generalized tangent bundle of G, which are in turn interpreted as odd exact examples with \(X_+=X_-=0\) as in Remark 37. The Lie algebra \({\mathfrak {g}}\) admits an orthonormal basis \(\{ e_1,e_2\}\) such that \(Je_1=e_2\) and \([e_1,e_2]=\mu e_2\), \(\mu \ge 0\).
7.2 The Case \(\textrm{dim}\, G = 3\)
Let G be a 3-dimensional Lie group with Lie algebra \({\mathfrak {g}}.\) A (non-degenerate) metric g on \({\mathfrak {g}}\) defines a canonical operator \(L\in \textrm{End}\, ({\mathfrak {g}})\), unique up to multiplication by \(\pm 1.\) By choosing an orientation on \({\mathfrak {g}}\), the operator L relates the Lie bracket of \({\mathfrak {g}}\) with the cross product determined by g and the orientation, by
Reversing the orientation, the operator L multiplies by \(-1.\) It is well-known (see [10] for g positive definite and [6] for g of arbitrary signature) that G is unimodular (i.e. \(\textrm{tr}\, ( \textrm{ad}_{X} ) =0\) for any \(X\in {\mathfrak {g}}\)) if and only if L is self-adjoint. In the next proposition we assume for simplicity that L is diagonalizable. This is always the case when g is positive definite and \({\mathfrak {g}}\) is unimodular.
Proposition 42
Let G be a 3-dimensional unimodular Lie group, with Lie algebra \({\mathfrak {g}}.\) There is a left-invariant \(B_{3}\)-generalized pseudo-Kähler structure \(({\mathcal {G}}, {\mathcal {F}} )\) on a Courant algebroid \(E= E_{H, F}\) over G, with components \((g, J_{+}, J_{-}, X_{+}, X_{-})\), such that the operator \(L\in \textrm{End}\, ({\mathfrak {g}})\) associated to g is diagonalizable, if and only if one of the following two cases holds:
-
i)
there is a g-orthonormal basis \(\{ v_{1}, v_{2}, v_{3} \}\) of \({\mathfrak {g}}\), such that \(g(v_{2}, v_{2}) =1\), in which the Lie bracket of \({\mathfrak {g}}\) is given by
$$\begin{aligned}{}[v_{1}, v_{2} ] = \epsilon _{3} \lambda v_{3},\ [ v_{3}, v_{1} ] =0,\ [v_{2}, v_{3} ] = \epsilon _{1}\lambda v_{1}, \end{aligned}$$(76)where \(\epsilon _{i}:= g( v_{i}, v_{i})\in \{ \pm 1\}\) (\(i\in \{ 1,3\}\)), \(\lambda \in {\mathbb {R}}{\setminus } \{ 0\}\), \(X_{-} = v_{2}\) and \(X_{+} = \pm v_{2}.\) In particular, \({\mathfrak {g}}\) is isomorphic to the Lie algebra of Killing fields of Euclidean or Minkowskian 2-space, \({\mathfrak {g}}\cong \mathfrak {iso}(2)= \mathfrak {so}(2) \ltimes {\mathbb {R}}^2\) or \({\mathfrak {g}} \cong \mathfrak {iso}(1,1)=\mathfrak {so}(1,1)\ltimes {\mathbb {R}}^2\), depending on whether \(\epsilon _1\epsilon _3=1\) or \(\epsilon _1\epsilon _3=-1\), cf. Remark 43.
-
ii)
\({\mathfrak {g}}\) is abelian, g is an arbitrary (non-degenerate) metric on \({\mathfrak {g}}\) and \(X_{\pm }\in {\mathfrak {g}}\) are arbitrary space-like unit vectors, i.e. \(g(X_\pm ,X_\pm )=1\).
In both cases \( H =0\), \(F =0\) and \(J_{\pm }\in \textrm{End} ({\mathfrak {g}})\) are arbitrary g-skew-symmetric endomorphisms, which satisfy \(J_{\pm }X_{\pm } =0\) and are complex structures on \(X_{\pm }^{\perp }.\)
Proof
Assume that \({\mathfrak {g}} \) is non-abelian. Since L is diagonalizable, there is a g-orthonormal basis \(\{ v_{1}, v_{2}, v_{3}\}\) in which the Lie bracket of \({\mathfrak {g}}\) is given by
where \(\lambda _{i} \in {\mathbb {R}}\) (not all of them zero) and \(\epsilon _{i}:= g(v_{i}, v_{i})\in \{ \pm 1\}\). The Levi-Civita connection of g is given by
and
Recall, from Corollary 17, that \(X_{-}\) is a Killing field of norm one. It turns out that \({\mathfrak {g}}\) admits such a left-invariant Killing field in the following cases:
-
1)
\(\lambda _{1} \ne \lambda _{2}\), \(\lambda _{3} = \lambda _{1}\) and \(\epsilon _{2} =1\) (up to permutation). Then any space-like left-invariant unit Killing field (in particular, \(X_{-}\)) is of the form \(X_{-} =\pm v_{2}\). Replacing \(v_{2}\) by \(- v_{2}\) (and leaving \(v_{1}\) and \(v_{3}\) unchanged), we may (and will) assume that \(X_{-} = v_{2}.\)
-
2)
\(\lambda _{1} = \lambda _{2} = \lambda _{3} \ne 0\). Any left-invariant vector field is Killing.
Consider case 1) and let \(\{ v_{1}^{*}, v_{2}^{*}, v_{3}^{*}\}\) be the dual basis of \(\{ v_{1}, v_{2}, v_{3}\}\), i.e. \( v_{i}^{*} (v_{j}) = \delta _{ij}.\) The covectors \(v_{i}^{*}\) correspond to \(\epsilon _{i} v_{i}\) in the duality defined by g. From \(i_{X_{-}} F =0\), \(X_{-} = v_{2}\) we deduce that
where \(F_{13}\in {\mathbb {R}}.\) Using relations (78) (with \(\lambda _{3} =\lambda _{1}\)) and relations (79) we obtain from the first relation (71) with \(X_{-} = v_{2}\) that
Recall now, from Corollary 18, that \(X_{+}\) and \(X_{-}\) commute.
When \(\lambda _{3} = \lambda _{1} \ne 0\) the conditions that \(X_{\pm }\) have the same norm and \({\mathcal {L}}_{X_{+}} X_{-} =0\) imply that \(X_{+} = \epsilon X_{-}\) with \(\epsilon \in \{ \pm 1\}\). The second relation (71) reduces to
Using that \(J_{+}\) is g-skew-symmetric, \(J_{+} X_{+} =0\) and \(\textrm{rank} ( \textrm{Ker} \, J_{+}) =1\), together with (80) and (81) we obtain from (82) that \(H =0\), \(F =0\) and \(\lambda _{2} =0.\) This leads to the generalized pseudo-Kähler structure from claim i).
When \(\lambda _{3} = \lambda _{1} =0\), \(X_{-}= v_{2}\) belongs to the center of \({\mathfrak {g}}\) and \({\mathcal {L}}_{X_{-}} X_{+} =0\) does not impose any restrictions on \(X_{+}\) (as it happened when \(\lambda _{3} =\lambda _{1} \ne 0\)). Since \(g(X_{+}, X_{+}) =1\), the vector field \(X_{+}\) is of the form \(X_{+} = \sum a_i v_{i}\), where \(a_1, a_2,a_3\in {\mathbb {R}}\), such that \(\epsilon _{1} a_{1}^{2} + a_{2}^{2} + \epsilon _{3} a_{3}^{2}=1\). The second relation (71) becomes
for any \(X\in {\mathfrak {g}}.\) Since \({\mathfrak {g}}\) is not abelian, \(\lambda _{2} \ne 0.\) Relation (83) with \(X:= v_{1} \) and \(X:= v_{2}\) implies \(a_2=a_3=0\), i.e. \(X_{+} = a_1 v_{1}.\) In particular, as \(J_{+} X_{+} =0\), we obtain that \(J_{_+} v_{1} =0.\) Relation (83) with \(X:= v_{3}\) implies that \(F_{13} J_{+} v_{1} = \epsilon _{1} a_1 \lambda _{2} v_{2}.\) Combined with \(J_{+} v_{1} =0\), this implies that \(a_1 =0\), which is a contradiction. Similar computations show that case 2) leads to a contradiction as well.
In the remaining case, i.e. when \({\mathfrak {g}}\) is abelian, Corollary 39 implies immediately that H and F are zero and the remaining components of \((\mathcal G, \mathcal H)\) are unconstrained. \(\square \)
Remark 43
Consider the \(B_{3}\)-generalized pseudo-Kähler structure \(({\mathcal {G}}, {\mathcal {F}} )\) from Proposition 42 i) and the new basis \(\{ w_{1}:= \frac{1}{\lambda } v_{1}, w_{2}:= \frac{1}{\lambda } v_{2}, w_{3}:= \frac{1}{\lambda } v_{3} \}\) of \({\mathfrak {g}}.\) Rescaling \(({\mathcal {G}}, {\mathcal {F}} )\) by \(\lambda ^{2}\) (according to Corollary 19) we obtain a \(B_{3}\)-generalized pseudo-Kähler structure on the untwisted Courant algebroid of type \(B_{3}\) over G, with components \(({\tilde{g}},{\tilde{J}}_{+}, {\tilde{J}}_{-}, {\tilde{X}}_{+}, {\tilde{X}}_{-})\), such that the basis \(\{ w_{1}, w_{2}, w_{3} \}\) is \({\tilde{g}}\)-orthogonal, and
where \(\epsilon _{i} \in \{ \pm 1\}\) for \(i\in \{ 1, 3\}.\) As above, \({\tilde{J}}_{\pm }\in \textrm{End}\, ( {\mathfrak {g}})\) are arbitrary g-skew-symmetric endomorphisms, such that \({\tilde{J}}_{\pm } w_{2}=0\) and \({\tilde{J}}_{\pm }\) are complex structures on \(\textrm{span}_{{\mathbb {R}}}\{ w_{1}, w_{3}\}.\) In the new basis the structure constants of \({\mathfrak {g}}\) take the standard form (as in [10]):
Let G be a 3-dimensional non-unimodular Lie group, with Lie algebra \({\mathfrak {g}}.\) Since \({\mathfrak {g}}\) is 3-dimensional, its unimodular kernel
is 2-dimensional (and unimodular), hence abelian. Choose a basis \(\{ v_{2}, v_{3 }\}\) of \({\mathfrak {g}}_0\) and a vector \(v_{1}\notin {\mathfrak {g}}_{0}\). In the basis \(\{ v_{1}, v_{2}, v_{3} \}\) the Lie bracket of \({\mathfrak {g}}\) is given by
where \(\alpha , \beta , \gamma , \delta \in {\mathbb {R}}\) and \(\alpha +\delta \ne 0\). Up to a multiplicative factor the constants \(\alpha , \beta , \gamma , \delta \) are independent of the choice of \(v_{1}.\)
Proposition 44
Let G be a 3-dimensional non-unimodular Lie group, with Lie algebra \({\mathfrak {g}} \) and unimodular kernel \({\mathfrak {g}}_{0}.\) There is a left-invariant \(B_{3}\)-generalized pseudo-Kähler structure \(({\mathcal {G}}, {\mathcal {F}} )\) on a Courant algebroid \(E= E_{H, F}\) of type \(B_{3}\) over G, with components \((g, J_{+}, J_{-}, X_{+}, X_{-})\), such that \({\mathfrak {g}}_{0}^{\perp }\cap {\mathfrak {g}}_{0} =0\), if and only if \({\mathfrak {g}}\) is isomorphic to \({\mathbb {R}}\oplus \mathfrak {sol}_2\), where \(\mathfrak {sol}_2\) is the unique non-abelian Lie algebra of dimension 2. If \({\mathfrak {g}}\) is isomorphic to \({\mathbb {R}}\oplus \mathfrak {sol}_2\), then there is a basis \(\{ w_{1}, w_{2}, w_{3} \}\) of \({\mathfrak {g}}\) in which the Lie brackets take the form
the metric g is given by
where \(\delta \in {\mathbb {R}}{\setminus } \{ 0\}\), \(\epsilon , \epsilon ' \in \{ \pm 1\}\) are arbitrary, \(X_{-} = w_{3}\), \(X_{+} = \pm w_{3}\) and \(J_{\pm }\in \textrm{End} ({\mathfrak {g}})\) are arbitrary g-skew-symmetric endomorphisms, which satisfy \(J_{\pm }w_{3} =0\) and are complex structures on \(\textrm{span}_{{\mathbb {R}}}\{ w_{1}, w_{2} \}.\) Moreover, \(H=0\) and \(F=0\).
Proof
Let g be a left-invariant metric on G such that \({\mathfrak {g}}_{0}^{\perp }\cap {\mathfrak {g}}_{0} =0\). Choose a g-orthonormal basis \(\{ v_{1}, v_{2}, v_{3}\}\) of \({\mathfrak {g}}\) such that \(v_{2}, v_{3} \in {\mathfrak {g}}_{0}\). The Lie bracket of \({\mathfrak {g}}\) takes the form (87) in the basis \(\{ v_{1}, v_{2}, v_{3} \}\) and the Levi-Civita connection \(\nabla \) of g is given by
where \(\epsilon _{i}:= g (v_{i}, v_{i}) \in \{ \pm 1\}.\)
From Corollary 17, \(X_{-}\) is a Killing field. It turns out that g admits a non-zero left-invariant Killing field only in the following cases:
-
1)
\(\alpha =0\), \(\delta \ne 0\) and \(\beta \gamma =0\). Any non-zero left-invariant Killing field (in particular \(X_{-}\)) is of the form \(X_{-}= b ( v_{2} -\frac{\beta }{\delta } v_{3})\), where \(b\in {\mathbb {R}}\setminus \{ 0\}\); or
-
2)
\(\alpha \ne 0\), \(\alpha + \delta \ne 0\) and \(\gamma \beta = \delta \alpha \). Any non-zero left-invariant Killing field (in particular \(X_{-}\)) is of the form \(X_{-} = c( -\frac{\gamma }{\alpha } v_{2} + v_{3})\), where \(c\in {\mathbb {R}}{\setminus } \{ 0\}\).
Consider case 1) and let \(\{ v_{1}^{*}, v_{2}^{*}, v_{3}^{*}\}\) be the dual basis. Relation \(i_{X_{-}} F =0\) implies that
where \(F_{13}\in {\mathbb {R}}\). We write \(H = H_{123} v_{1}^{*} \wedge v_{2}^{*} \wedge v_{3}^{*}\), where \(H_{123}\in {\mathbb {R}}.\) Using relations (90) (with \(\alpha =0\)) we obtain that the first relation (71) is equivalent to \(H_{123} = \epsilon _{2} \gamma - \epsilon _{3} \beta \), i.e.
For the second relation (71), let \(X_{+}:= \sum _{i} a_{i} v_{i}\), where \(a_{1}, a_{2}, a_{3} \in {\mathbb {R}}.\) With this notation, the second relation (71) is equivalent to
or, using (91), to
Recall now that \(J_{+} \in \textrm{End} ({\mathfrak {g}})\) is g-skew-symmetric, \(J_{+} X_{+} =0\) and \(J_{+} \) is a complex structure on the orthogonal complement \(X_{+}^{\perp }\). These conditions combined with (93) imply that \(F_{13} = H_{123}=\beta = \gamma = a_{1} = a_{3} =0\). To summarize: case 1) provides a basis \(\{ v_{1}, v_{2}, v_{3}\}\) of \({\mathfrak {g}} \) and a one parameter family (indexed by \(\delta \in {\mathbb {R}}{\setminus } \{ 0\}\), see below) of \(B_{3}\)-generalized pseudo-Kähler structures on the untwisted Courant algebroid (\(H=0\), \(F=0\)), with components \((g, J_{+}, J_{-}, X_{+}, X_{-})\), such that the basis \(\{ v_{1}, v_{2}, v_{3}\}\) is g-orthonormal, the Lie bracket of \({\mathfrak {g}}\) is given by
where \(\delta \in {\mathbb {R}}{\setminus } \{ 0\}\), \(X_{-} = v_{2}\) (replacing, if necessary, \(v_{2}\) by \( -v_{2}\)) and \(X_{+} = \pm v_{2}\). From \(g(X_{\pm }, X_{\pm }) =1\) we obtain that \(g(v_{2}, v_{2} )=1.\) In the new basis \(\{ w_{1}:= \frac{1}{\delta } v_{1}, w_{2}:= v_{3}, w_{3}:= v_{2} \}\) this family takes the form described in the statement of the proposition, where \(\epsilon =\epsilon _1\) and \(\epsilon '=\epsilon _3\).
Similar arguments show that case 2) with \(\gamma \ne 0\) leads to a basis \(\{ v_{1}, v_{2}, v_{3}\}\) of \({\mathfrak {g}}\) and a family of \(B_{3}\)-generalized pseudo-Kähler structures on the untwisted Courant algebroid \((H=0\), \(F=0\)), with components \((g, J_{+}, J_{-}, X_{+}, X_{-})\), such that \(\{ v_{1}, v_{2}, v_{3} \}\) is g-orthonormal, the Lie bracket takes the form
where \(\alpha , \gamma \in {\mathbb {R}}\setminus \{ 0\}\), \(\epsilon _{i}:= g(v_{i}, v_{i}) \in \{ \pm 1\}\), \(X_{-} = c( -\frac{\gamma }{\alpha } v_{2} + v_{3})\) and \(X_{+} = \pm X_{-}\), where \(c\in {\mathbb {R}} \) satisfies \(c^{2} ( \alpha ^{2} \epsilon _{3} + \gamma ^{2} \epsilon _{2})=\alpha ^{2}\). In the new basis
the Lie brackets take the form (88) and the metric g and vector fields \(X_{\pm }\) are given by
Letting \(\delta \) such that \(\delta ^2=\alpha ^2/c^4\) we arrive again at the \(B_{3}\)-generalized pseudo-Kähler structures described in the statement of the proposition, where now \(\epsilon =\epsilon _1\) and \(\epsilon '=\epsilon _{2}\epsilon _{3}\).
Case 2) with \(\gamma =0\) leads to the family of \(B_{3}\)-generalized pseudo-Kähler structures obtained in case 1), but with \(v_{2}\) and \(v_{3}\) interchanged. Therefore, they provide no further \(B_{3}\)-generalized pseudo-Kähler structures besides those described above. \(\square \)
The next corollary summarizes our results from this section in the positive definite case.
Corollary 45
Let \(({\mathcal {G}}, {\mathcal {F}} )\) be a left-invariant \(B_{3}\)-generalized Kähler structure on a Courant algebroid \(E = E_{H, F}\) of type \(B_{3}\) over a 3-dimensional Lie group G with Lie algebra \({\mathfrak {g}}.\) Let \((g, J_{+}, J_{-}, X_{+}, X_{-})\) be the components of \(({\mathcal {G}}, {\mathcal {F}}).\) Up to rescaling of \(({\mathcal {G}}, {\mathcal {F}} )\) one of the following situations holds:
-
i)
there is a g-orthonormal basis \(\{ w_{1}, w_{2}, w_{3} \}\) of \({\mathfrak {g}}\) in which the Lie brackets take the form
$$\begin{aligned}{}[ w_{1}, w_{2} ] = w_{3},\ [ w_{2}, w_{3} ] = w_{1},\ [ w_{3}, w_{1} ]=0 \end{aligned}$$(97)and \(X_{-} = w_{2}\), \( X_{+} = \pm w_{2}.\)
-
ii)
there is a g-orthogonal basis \(\{ w_{1}, w_{2}, w_{3} \}\) of \({\mathfrak {g}}\) in which the Lie brackets take the form
$$\begin{aligned}{}[w_{1}, w_{2} ] = w_{2},\ [w_{1},w_{3} ] = [w_{2}, w_{3} ] = 0, \end{aligned}$$(98)and
$$\begin{aligned} g (w_{1}, w_{1}) = \frac{1}{\delta ^{2}},\ g(w_{2}, w_{2})= 1,\ g(w_{3}, w_{3}) = 1, \end{aligned}$$(99)where \(\delta \in {\mathbb {R}}{\setminus } \{ 0\}\), \(X_{-} = w_{3}\), \(X_{+} = \pm w_{3}\).
-
iii)
the Lie algebra \({\mathfrak {g}}\) is abelian, g is any Riemannian metric on \({\mathfrak {g}}\) and \(X_{\pm }\) are arbitrary vectors from \({\mathfrak {g}}\), of norm one.
In all cases above \(H = 0\), \(F =0\) and \(J_{\pm }\in \textrm{End}\, ( {\mathfrak {g}})\) are g-skew-symmetric endomorphisms, with the properties that \(J_{\pm } X_{\pm }=0\) and \(J_{\pm }\vert _{X_{\pm }^{\perp }}\) are complex structures.
Proof
The claim follows from Propositions 42 and 44 (see also Remark 43), together with the observation that if g is positive definite then the operator L from Proposition 42 is diagonalizable and the assumption \({\mathfrak {g}}_{0}^{\perp }\cap {\mathfrak {g}}_{0} =0\) from Proposition 44 is satisfied. \(\square \)
7.3 The Case \(\textrm{dim}\, G =4\)
Let G be a 4-dimensional Lie group with Lie algebra \({\mathfrak {g}}.\) We assume that \({\mathfrak {g}}\) is of the form
where \({\mathfrak {g}}_{0}\) is a 3-dimensional unimodular non-abelian Lie algebra and \({\mathfrak {u}}\) is 1-dimensional and acts on \({\mathfrak {g}}_{0}\) as a (1-dimensional) family of derivations. Note that such a Lie algebra \({\mathfrak {g}}\) is unimodular if and only if \(\textrm{tr}\, ( \textrm{ad}_X )=0\) for a non-zero element \(X\in {\mathfrak {u}}\).
Example 46
Every non-unimodular Lie algebra \({\mathfrak {g}}\) admits a (unique) codimension one unimodular ideal \({\mathfrak {g}}_0= \textrm{Ker}\, (\textrm{tr}\circ \textrm{ad})\), called the  of \({\mathfrak {g}}\). Choosing a complementary line \({\mathfrak {u}}\) we arrive at a decomposition \({\mathfrak {g}}={\mathfrak {u}} + {\mathfrak {g}}_{0}\). So the assumptions of this section are satisfied by any 4-dimensional non-unimodular Lie algebra with non-abelian unimodular kernel.
of \({\mathfrak {g}}\). Choosing a complementary line \({\mathfrak {u}}\) we arrive at a decomposition \({\mathfrak {g}}={\mathfrak {u}} + {\mathfrak {g}}_{0}\). So the assumptions of this section are satisfied by any 4-dimensional non-unimodular Lie algebra with non-abelian unimodular kernel.
As an application of Corollary 40, we now describe a class (called  ) of left-invariant \(B_{4}\)-generalized pseudo-Kähler structures over G.
) of left-invariant \(B_{4}\)-generalized pseudo-Kähler structures over G.
Definition 47
A left-invariant \(B_{4}\)-generalized pseudo-Hermitian structure \(({\mathcal {G}}, {\mathcal {F}} )\) on a Courant algebroid over G, with components \((g, J_{+}, J_{-}, X_{+}, X_{-}, c_{+})\), is called  if the decomposition \({\mathfrak {g}} = {\mathfrak {u}} + {\mathfrak {g}}_{0}\) is orthogonal with respect to g, the operator L associated to \(({\mathfrak {g}}_{0}, g\vert _{{\mathfrak {g}}_{0}\times {\mathfrak {g}}_{0} })\) is diagonalizable, \(J_{-} ({\mathfrak {u}})\) is included in an eigenspace of L and \({\mathfrak {u}}\) and \(X_{\pm }\) are non-null (i.e. \(c_{+} \in {\mathbb {R}}\setminus \{ \pm 1\}\)).
if the decomposition \({\mathfrak {g}} = {\mathfrak {u}} + {\mathfrak {g}}_{0}\) is orthogonal with respect to g, the operator L associated to \(({\mathfrak {g}}_{0}, g\vert _{{\mathfrak {g}}_{0}\times {\mathfrak {g}}_{0} })\) is diagonalizable, \(J_{-} ({\mathfrak {u}})\) is included in an eigenspace of L and \({\mathfrak {u}}\) and \(X_{\pm }\) are non-null (i.e. \(c_{+} \in {\mathbb {R}}\setminus \{ \pm 1\}\)).
If \((g, J_{+}, J_{-}, X_{+}, X_{-}, c_{+})\) are the components of an adapted \(B_{4}\)-generalized pseudo-Hermitian structure, then there is a g-orthonormal basis of \({\mathfrak {g}}\) (called  ) of the form \(\{ u, e_{1}, e_{2}, e_{3} \}\), where \(u\in {\mathfrak {u}}\) and \(e_{i} \in {\mathfrak {g}}_{0}\),
) of the form \(\{ u, e_{1}, e_{2}, e_{3} \}\), where \(u\in {\mathfrak {u}}\) and \(e_{i} \in {\mathfrak {g}}_{0}\),
in which the Lie bracket takes the form
where \(a_{ij} \in {\mathbb {R}}\) and \(\lambda _{i} \in {\mathbb {R}}\) (at least one non-zero). Since \(\textrm{ad}_{u}\) is a derivation of \({\mathfrak {g}}_{0}\),
where \(\epsilon _{i}:= g( v_{i}, v_{i})\in \{ \pm 1\}\) for any \(i\in \{ 1, 2, 3\}.\) Remark that \(\epsilon _{0}:= g (u, u)= \epsilon _{1}\) and \(\epsilon _{2} = \epsilon _{3}\) since \(J_{-}\) is g-skew-symmetric.
Proposition 48
-
i)
There is an adapted \(B_{4}\)-generalized pseudo-Kähler structure \(({\mathcal {G}}, {\mathcal {F}} )\) on a Courant algebroid \(E = E_{H, F}\) over G, with components \((g, J_{+}, J_{-}, X_{+}, X_{-}, c_{+})\), such that \(c_{+}\ne 0\), if and only if there is an adapted g-orthonormal basis of \(\{ u, e_{1}, e_{2}, e_{3} \}\) of \({\mathfrak {g}}\) such that
$$\begin{aligned}{}[e_{1}, e_{2} ]&= \epsilon _{3} \lambda e_{3},\ [e_{2}, e_{3} ] = 0, \ [e_{3}, e_{1} ] =\epsilon _{2} \lambda e_{2},\nonumber \\ [u, e_{1} ]&=0,\ [ u, e_{2} ]= \beta e_{3},\ [ u, e_{3} ] = - \beta e_{2}, \end{aligned}$$(104)where \(\lambda \in {\mathbb {R}}{\setminus } \{ 0\}\), \(\beta \in {\mathbb {R}}\), \(\epsilon _{i}:= g(e_{i}, e_{i}) \in \{ \pm 1\}\), \(g (u, u)= \epsilon _{1}\) and \(\epsilon _{2} = \epsilon _{3}\). The remaining data are given by: \(X_{+} = a u + b e_{1}\), \(X_{-} = {\tilde{a}} u + {\tilde{b}} e_{1}\), \(J_{+} X_{+} = - c_{+} X_{-}\), \(J_{+} X_{-} = c_{+} X_{+}\), where \(a, b, {\tilde{a}}, {\tilde{b}} \in {\mathbb {R}}\) are such that
$$\begin{aligned} \epsilon _{1} ( a^{2} + b^{2}) = \epsilon _{1} ( {\tilde{a}}^{2} + {\tilde{b}}^{2}) = 1- c_{+}^{2},\ a {\tilde{a}} + b {\tilde{b}} =0, \end{aligned}$$(105)\(c_{+} \in {\mathbb {R}}\setminus \{ -1, 0, 1\}\), the complex structure \(J_{-}\) is given by (101) and \(J_{+} \vert _{\textrm{span}_{{\mathbb {R}}}\{ e_{2}, e_{3} \}}\) is any g-skew-symmetric complex structure. Moreover, \(H =0\) and \(F =0\).
-
ii)
Changing the decomposition \({\mathfrak {g}} = {\mathfrak {u}} + {\mathfrak {g}}_0\) if necessary, the orthonormal vectors \(u, e_1\) can be always chosen such that \(\beta =0\). In particular, \({\mathfrak {g}} \cong {\mathbb {R}} \oplus \mathfrak {iso}(2)\).
We divide the proof of Proposition 48 into several lemmas. Let \(({\mathcal {G}}, {\mathcal {F}})\) be an adapted \(B_{4}\)-generalized pseudo-Hermitian structure on G, with components \((g, J_{+}, J_{-}, X_{+}, X_{-}, c_{+})\), where \(c_{+} \in {\mathbb {R}}\setminus \{ \pm 1\}\) is arbitrary. As above, let \(\{ u, e_{1}, e_{2}, e_{3} \}\) be an adapted basis, \(\epsilon _{i}:= g(e_{i}, e_{i})\) and \(\epsilon _{0}:= g ( u, u).\)
Lemma 49
The Levi-Civita connection of g is given by
Let \(\{ u^{*}, e_{1}^{*}, e_{2}^{*}, e_{3}^{*} \}\) be the dual basis of \( \{ u, e_{1}, e_{2}, e_{3} \}\), i.e.
We write the left-invariant forms H and F as
where \(H_{123}, H_{ij}, F_{ij}, F_{i} \in {\mathbb {R}}\), \(H_{ij} = - H_{ji}\), \(F_{ij} = - F_{ji}\) for any i, j, and to simplify notation we omitted the summation signs. As the pair (H, F) defines a Courant algebroid of type \(B_{4}\), the coefficients of H and F are subject to various constraints which come from \( dF =0\) and \( dH + F\wedge F =0.\)
Lemma 50
-
i)
The equality \( dH + F\wedge F =0\) holds if and only if
$$\begin{aligned} H_{123} (a_{11} + a_{22} + a_{33}) = 2( F_{1} F_{23} + F_{3} F_{12} + F_{2} F_{31}). \end{aligned}$$(107) -
ii)
The 2-form F is closed if and only if
$$\begin{aligned} \epsilon _{1} \lambda _{1} F_{1}&= F_{23} ( a_{22} + a_{33}) + F_{21} a_{31} + F_{13} a_{21},\nonumber \\ \epsilon _{2} \lambda _{2} F_{2}&= F_{31} ( a_{11} + a_{33}) + F_{21} a_{32} + F_{32} a_{12},\nonumber \\ \epsilon _{3} \lambda _{3} F_{3}&= F_{12} ( a_{11} + a_{22}) + F_{32} a_{13} + F_{13} a_{23}. \end{aligned}$$(108)
Proof
The claims follow from a straightforward computation, which uses that the 1-form \(u^{*}\) is closed and the exterior derivatives of the 1-forms \(e_{i}^{*}\) are given by
For instance, these equations imply
and comparing with
yields (107), where \({\mathfrak {S}}\) indicates the sum over cyclic permutations. \(\square \)
We now apply Corollary 40 with \(c_{+}\) a non-zero constant. We consider each condition from this corollary separately.
Lemma 51
The connection \(D^{-} = \nabla +\frac{1}{2} H\) preserves \(J_{-}\) if and only if
Proof
Recall the definition (101) of \(J_{-}.\) Using Lemma 49, one can check that \((D^{-}_{X} J_{-})(u) =0\) for any \(X\in {\mathfrak {g}}\) is equivalent to relations (109). Moreover, these relations imply \( (D^{-}_{X} J_{-})(e_{i}) =0\) for any i. \(\square \)
Since \(c_{+}\ne 0\), from the first relation (72) we obtain that
where \(X_{+}^{\flat }\) is the 1-form g-dual to \(X_{+}.\) The first relation (72) also implies that \(X_{+}\) is a Killing field. On the other hand, remark that if X is a Killing field of constant norm for a pseudo-Riemannian metric h, then \(i_{X} d X^{\flat } =0\) where \(X^{\flat }\) is the h-dual to X. We deduce that the condition \(i_{X_{+}} F =0\) from Corollary 40 is satisfied, once we know that \(X_{+}\) is a Killing field. The next lemma determines the conditions satisfied by the coefficients of Killing fields for g.
Lemma 52
Assume that \(a_{21} = a_{31} =0\) and \(a_{23} + a_{32} =0.\) A vector field \(X_{+}= au + be_{1} + ce_{2} + de_{3}\) is Killing for g if and only if
Lemma 53
Assume that \(a_{21} = a_{31} =0\), \(a_{23} + a_{32} =0\), \(H_{23}=0\), \(H_{12} = - \epsilon _{2} a_{12}\) and \(H_{13} = - \epsilon _{3} a_{13}\). The form F defined by (110) is of type (1, 1) with respect to \(J_{-}\) if and only if the following relations hold:
Proof
From the definition of \(J_{-}\), a 2-form as in (106) is of type (1, 1) with respect to \(J_{-}\) if and only of
Using relation (110), a simple computation shows that
The claim follows from (114) and (113). \(\square \)
Remark 54
For later use, remark that
The next lemma describes the Lie bracket of the Lie algebra \({\mathfrak {g}}\), the Killing field \(X_{+} \), the forms H and F, such that all conditions from Corollary 40 are satisfied, except the normalization \(g(X_{+}, X_{+}) =1- c_{+}^{2}\) and the conditions which involve \(X_{-}\) and \(J_{+}.\)
Lemma 55
Let \(\epsilon _1, \epsilon _2=\epsilon _3\in \{\pm 1\}\) and \(c_+ \in {\mathbb {R}}{\setminus } \{ 0\}\). There are eight classes \((a_{ij}, \lambda _{i}, H_{123}\), \(H_{ij}, F_{ij}, F_{i}, a, b, c, d)\) of solutions of the systems (103), (107), (108), (109), (111), (112), (114), (115) with at least one of the constants a, b, c, d non-zero and excluding the case \(\lambda _1=\lambda _2=\lambda _3=0\), i.e. the case when the ideal \({\mathfrak {g}}_0\subset {\mathfrak {g}}\) is abelian. They are given as follows (below the constants \((H_{123}, H_{ij}, F_{ij}, F_{i}, a\), b, c, d) are incorporated in the corresponding Killing field \(X_{+}\), and forms H and F):
-
1)
\(a_{12} = a_{13} =a_{ii }=0\) for any i, \(a_{23}\in {\mathbb {R}}\), \(\lambda _{1} \in {\mathbb {R}}{\setminus } \{ 0\}\), \( \lambda _{2} =\lambda _{3}\in {\mathbb {R}}{\setminus } \{ \lambda _{1}\}\), \(X_{+} = au + be_{1}\) (with \(a\in {\mathbb {R}}{\setminus } \{ 0\}\) and \(b\in {\mathbb {R}}\)), and
$$\begin{aligned} H = -\lambda _{1} e_{1}^{*}\wedge e^{*}_{2}\wedge e^{*}_{3},\ F = - \frac{b\lambda _{1}}{ c_{+} } e^{*}_{2}\wedge e^{*}_{3}. \end{aligned}$$(116) -
2)
\(a_{12} = a_{13} =a_{ii }=0\) for any i, \(a_{23}\in {\mathbb {R}}\), \(\lambda _{1}= \lambda _{2} =\lambda _{3} \in {\mathbb {R}}{\setminus } \{ 0\}\), \(X_{+} = au + be_{1}\) (with \(a \in {\mathbb {R}}{\setminus } \{ 0\}\) and \(b\in {\mathbb {R}}\)). The forms H and F are given by (116).
-
3)
\(a_{12} = -\frac{d\lambda _{2} \epsilon _{2}}{a}\), \(a_{13} = \frac{ c\lambda _{2}\epsilon _{3}}{a}\), \(a_{ii}=0\) for any i, \(a_{23} \in {\mathbb {R}}\), \(\lambda _{1} =0\), \(\lambda _{2} =\lambda _{3}\in {\mathbb {R}}{\setminus } \{ 0\}\), \(X_{+} = au -\frac{ \epsilon _{3} a a_{23}}{ \lambda _{2}} e_{1} + ce_{2} + de_{3}\) (with \(a\in {\mathbb {R}}{\setminus } \{ 0\}\) and \(c, d\in {\mathbb {R}}\)) and
$$\begin{aligned} H = \frac{\lambda _{2}}{a} u^{*}\wedge ( d e_{1}^{*} \wedge e_{2}^{*} - c e_{1}^{*} \wedge e_{3}^{*}),\ F =0. \end{aligned}$$(117) -
4)
\(a_{12} = a_{13} = a_{ii }=0\) for any i, \(a_{23}\in {\mathbb {R}}\), \(\lambda _{1} =0\), \(\lambda _{2} = \lambda _{3} \in {\mathbb {R}}{\setminus } \{ 0\}\), \(X_{+ } = a u + b e_{1}\) (with \(a\in {\mathbb {R}}{\setminus } \{ 0\} \) and \(b\in {\mathbb {R}}{\setminus } \{ -\frac{\epsilon _{2} a a_{23}}{\lambda _{2}} \}\)). The forms H and F are trivial.
-
5)
\(a_{12} = a_{13} = a_{ii} =0\) for any i, \(a_{23}\in {\mathbb {R}}\), \(\lambda _{1} =\lambda _{2} =\lambda _{3} \in {\mathbb {R}}{\setminus } \{ 0\}\), \(X_{+} = b e_{1}\) (with \(b\in {\mathbb {R}}{\setminus } \{ 0\}\)) and
$$\begin{aligned} H = -\lambda _{1} e_{1}^{*}\wedge e^{*}_{2} \wedge e^{*}_{3},\ F = -\frac{b\lambda _{1}}{ c_{+}} e^{*}_{2} \wedge e^{*}_{3}. \end{aligned}$$(118) -
6)
\(a_{23} =a_{33} =0\), \(a_{11} = -\epsilon _{2} \lambda _{3}\), \(a_{22} = \epsilon _{2} \lambda _{3}\), \(a_{12}, a_{13}\in {\mathbb {R}}\), \(\lambda _{1} = \lambda _{2} =0\), \(\lambda _{3} \in {\mathbb {R}}{\setminus } \{ 0\}\), \(X_{+} = d e_{3}\) (with \(d\in {\mathbb {R}}{\setminus } \{ 0\}\)) and
$$\begin{aligned} H&= \lambda _{3} e^{*}_{1}\wedge e^{*}_{2} \wedge e^{*} _{3}- \epsilon _{2} u^{*} \wedge ( a_{12} e^{*}_{1}\wedge e^{*}_{2} + a_{13} e^{*}_{1}\wedge e^{*}_{3}),\\ F&= -\frac{ \epsilon _{3} d a_{13}}{c_{+}} u^{*}\wedge e^{*}_{1}. \end{aligned}$$ -
7)
\(a_{22} = a_{23} =0\), \(a_{11} = -\epsilon _{3} \lambda _{2}\), \(a_{33} = \epsilon _{3} \lambda _{2}\), \(a_{12}, a_{13}\in {\mathbb {R}}\), \(\lambda _{1} = \lambda _{3} =0\), \(\lambda _{2}\in {\mathbb {R}}{\setminus } \{ 0\}\), \(X_{+} =c e_{2}\) (with \(c\in {\mathbb {R}}{\setminus } \{ 0\}\)) and
$$\begin{aligned} H&= \lambda _{2} e_{1}^{*}\wedge e^{*}_{2} \wedge e^{*}_{3} - \epsilon _{2} u^{*}\wedge ( a_{12} e^{*}_{1} \wedge e_{2}^{*} + a_{13} e^{*}_{1} \wedge e^{*}_{3} ),\\ F&= -\frac{ \epsilon _{2} ca_{12}}{c_{+}} u^{*}\wedge e^{*}_{1}. \end{aligned}$$ -
8)
\(a_{12} = a_{13} = a_{ii} =0\) for any i, \(a_{23}\in {\mathbb {R}}\), \(\lambda _{1} \in {\mathbb {R}}\), \(\lambda _{2} =\lambda _{3} \in {\mathbb {R}} {\setminus } \{ \lambda _{1}\}\), \(X_{+} = b e_{1}\) (with \(b\in {\mathbb {R}}\setminus \{ 0\}\)) and
$$\begin{aligned} H = -\lambda _{1} e^{*}_{1} \wedge e^{*}_{2} \wedge e^{*}_{3},\ F = - \frac{b\lambda _{1}}{c_{+}} e_{2}^{*} \wedge e^{*}_{3}. \end{aligned}$$(119)
In all of the above cases, \(a_{21} = a_{31} =0\) and \(a_{32} = - a_{23}\).
Proof
The claim follows from elementary algebraic computations. When \(a\ne 0\), the second relation (111) implies that \(a_{ii} =0\) for any i and the third and last relation (109) imply that \(\lambda _{2} = \lambda _{3}\) and \(H_{123} =- \lambda _{1}.\) The case \(a\ne 0\) leads to the first four classes of the statement. When \(a =0\), relations (111) imply
In particular, at least two from the \(\lambda _{i}\)’s coincide (otherwise \(X_{+} =0\)). Considering all possibilities (\(\lambda _{1}=\lambda _{2} = \lambda _{3}\), \(\lambda _{1} = \lambda _{2} \ne \lambda _{3}\), \(\lambda _{1} = \lambda _{3} \ne \lambda _{2}\) and \(\lambda _{2} = \lambda _{3} \ne \lambda _{1}\)) we obtain the remaining four cases from the statement. The expressions of H and F follow from (106), (109), (114) and (115). \(\square \)
The next lemma concludes the proof of Proposition 48 i).
Lemma 56
Consider the classes of solutions from Lemma 55 with \(X_{+}\) such that \(0 \ne g(X_{+}, X_{+}) < 1\) and \(c_{+} \in {\mathbb {R}}{\setminus } \{ -1, 0, 1\}\) such that \(c^{2}_{+} = 1 - g(X_{+}, X_{+})\). There is a left-invariant vector field \(X_{-}\) on G and a left-invariant endomorphism \(J_{+}\in \Gamma ( \textrm{End}\, TG)\), such that \(( g, J_{+}, J_{-}, X_{+}, X_{-}, c_{+})\) are the components of an adapted \(B_{4}\)-generalized pseudo-Kähler structure, only in cases 3) (if \(c=d=0\)), 4) and 8) of Lemma 55. The resulting \(B_{4}\)-generalized pseudo-Kähler structures from cases 3), 4) and 8) (with \(a_{23}\) replaced by \(\beta \)) are described in Proposition 48.
Proof
According to Corollary 40 we need to determine \(X_{-}\in {\mathfrak {g}}\) and \(J_{+}\in \textrm{End}\, ( {\mathfrak {g}}) \) such that \(X_{-}\) is orthogonal to \(X_{+}\) and has the same norm as \(X_{+}\), \(J_{+}\) is g-skew-symmetric, \(J_{+} X_{+} = - c_{+} X_{-}\), \(J_{+} X_{-} = c_{+} X_{+}\), \(J_{+}\vert _{ \{ X_{+}, X_{-} \}^{\perp } }\) is a complex structure and
where we used that \(F(X_{+}) =0\). Consider case 1) from Lemma 55. Then \(X_{+} = au + b e_{1}\) with \(a\ne 0\) and
Let \(X_{-}= {\tilde{a}} u + {\tilde{b}} e_{1} +{\tilde{c}}e_{2} +{\tilde{d}}e_{3}\), where \({\tilde{a}}, {\tilde{b}}, {\tilde{c}}, {\tilde{d}}\in {\mathbb {R}}\). We compute
Combining the first relation (121) with (122) and (123), we obtain
Since \(J_{+}\) is g-skew and the basis \(\{ u, e_{1}, e_{2}, e_{3} \}\) is orthonormal, \({\tilde{b}}=0\) and the second line above becomes
On the other hand \({\tilde{b}}=0\) and \(g (X_{+}, X_{-}) =0\) imply that \({\tilde{a}}=0\). Thus \(X_{-}= {\tilde{c}} e_{2} + {\tilde{d}} e_{3}.\) Relation (124) also implies that \(b\ne 0\) (otherwise \(X_{-} =0\)). It is now straightforward to check that relations (124) combined with \(J_{+} X_{-} = c_{+} X_{+}\) and \(c_{+} a\ne 0\) lead to a contradiction. The remaining cases from Lemma 55 can be treated similarly. \(\square \)
It remains to prove Proposition 48 ii). If \(\beta =0\) there is nothing to show. Otherwise, the action of \(\textrm{ad}_{u}\) on the ideal spanned by \(e_2\) and \(e_3\) is always a non-zero multiple of the action of \(\textrm{ad}_{e_1}\) and we can find a linear combination of u and \(e_1\) the adjoint action of which is trivial on the ideal. Rescaling that linear combination we obtain a new unit vector \(u'\in {\mathfrak {g}}\setminus {\mathfrak {g}}_0\), a new line \({\mathfrak {u}}':= {\mathbb {R}}u'\), a new ideal \({\mathfrak {g}}_0':= (u')^\perp \) and a new orthonormal basis \(\{ u',e_1',e_2,e_3\}\) by defining \(e_1':= J_{-} u'\). The decomposition \({\mathfrak {u}}' + {\mathfrak {g}}_0'\) and the basis \(\{ u',e_1',e_2,e_3\}\) have then the claimed properties. The proof of Proposition 48 is now completed.
While this section was concerned with \(B_{4}\)-generalized pseudo-Kähler structures with \(c_{+} \ne 0\), it remains to find examples of such structures with \(c_{+}=0\). Several hints in this direction are given below.
Example 57
-
i)
By rescaling (see Corollary 24), we obtain from Proposition 48 adapted \(B_{4}\)-generalized pseudo-Kähler structures with corresponding vector fields \(X_{\pm }\) of norm one (i.e. \(c_{+}=0\)).
-
ii)
Using similar computations as above, one can construct further left-invariant \(B_{4}\)-generalized pseudo-Kähler structures with \(X_{\pm }\) of norm one. The 2-form F satisfies relations (107), (108) and (113) also in this case, but it is no longer related to \(X_{+}\) by relation (110).
References
Baraglia, D., Hekmati, P.: Transitive Courant algebroids, String structures and \(T\)-duality. Adv. Theor. Math. Phys. 19(3), 613–672 (2015)
Bressler, P.: The first Pontryagin class. Compos. Math. 143(5), 1127–1163 (2007)
Chen, Z., Stiénon, M., Xu, P.: On regular Courant algebroids. J. Sympl. Geom. 11(1), 1–24 (2013)
Cortés, V., David, L.: Generalized connections, spinors and integrability of generalized structures on Courant algebroids. Moscow Math. J. 21(4), 695–736 (2021)
Cortés, V., David, L.: \(T\)-duality for transitive Courant algebroids, to appear in J. Sympl. Geom. 21 (4) (2023); arXiv:2101.07184 [math.DG]
Cortés, V., Krusche, D.: Classification of generalized Einstein metrics on \(3\)-dimensional Lie groups. Can. J. Math. (2023). https://doi.org/10.4153/S0008414X23000056
García-Fernández, M.: Ricci flow, Killing spinors and \(T\)-duality in generalized geometry. Adv. Math. 350, 1059–1108 (2019)
Gualtieri, M.: Generalized complex geometry, Ph.D thesis, University of Oxford, (2004)
Gualtieri, M.: Generalized complex geometry. Ann. Math. 174(1), 75–123 (2011)
Milnor, J.: Curvatures of left invariant metrics on lie groups. Adv. Math. 21, 293–329 (1976)
Poon, Y.S., Wade, A.: Generalized contact structures. J. Lond. Math. Soc. 83(2), 333–392 (2011)
Rubio, R.: \(B_n\)-generalized geometry and \(G^2_2\)-structures. J. Geom. Phys. 73, 150–156 (2013)
Rubio, R.: Generalized Geometry of type \(B_{n}\). Ph.D thesis, University of Oxford (2014)
Sekiya, K.: Generalized almost contact structures and generalized Sasakian structures. Osaka J. Math. 52, 43–58 (2015)
Severa, P.: Letters to Alan Weinstein about Courant algebroids, arXiv:1707.00265 [math.DG]
Liu, Z.J., Weinstein, A., Xu, P.: Manin triples for Lie bialgebroids. J. Differ. Geom. 45, 119–222 (1997)
Wright, K.: Generalized contact geometry as reduced generalized complex geometry. J. Geom. Phys. 130, 331–348 (2018)
Acknowledgements
Research of V.C. was supported by the German Science Foundation (DFG) under Germany’s Excellence Strategy – EXC 2121 “Quantum Universe” – 390833306. V.C. gratefully acknowledges support from the Simons Center for Geometry and Physics, Stony Brook University at which this paper received its last touches. L.D. was partially supported by the UEFISCDI research grant PN-III-P4-ID-PCE-2020-0794, project title “Spectral Methods in Hyperbolic Geometry”.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cortés, V., David, L. \(B_{n}\)-Generalized Pseudo-Kähler Structures. J Geom Anal 33, 261 (2023). https://doi.org/10.1007/s12220-023-01311-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12220-023-01311-z
Keywords
- Generalized Kähler structures
- Odd exact Courant algebroids
- Courant algebroids of type \(B_n\)
- Heterotic Courant algebroids