A Strong-Type Furstenberg–Sárközy Theorem for Sets of Positive Measure

Abstract

For every $\beta \in (0,\infty )$, $\beta \ne 1$, we prove that a positive measure subset A of the unit square contains a point $(x_0,y_0)$ such that A nontrivially intersects curves $y-y_0 = a (x-x_0)^\beta$ for a whole interval $I\subseteq (0,\infty )$ of parameters $a\in I$. A classical Nikodym set counterexample prevents one to take $\beta =1$, which is the case of straight lines. Moreover, for a planar set A of positive density, we show that the interval I can be arbitrarily large on the logarithmic scale. These results can be thought of as Bourgain-style large-set variants of a recent continuous-parameter Sárközy-type theorem by Kuca, Orponen, and Sahlsten.

1 Introduction

Geometric measure theory often tries to identify patters in sufficiently large, but otherwise arbitrary, measurable sets. Recently, nonlinear or curved patterns have begun to attract much attention [1,2,3,4,5,6,7,8,9,10]; most of these references will be discussed below. In this note, we follow one of the many opened lines of research.

Kuca et al. [8] showed that there exists $\varepsilon >0$ with the following property: every compact set $K\subseteq {\mathbb {R}}^2$ with Hausdorff dimension at least $2-\varepsilon$ necessarily contains a pair of points of the form

$$\begin{aligned} (x,y), \ (x,y) + (u,u^2) \end{aligned}$$

(1.1)

for some $u\ne 0$. We can imagine that we started from a point $(x,y)\in K$, translated the parabola $v=u^2$ so that its vertex falls into (x, y), and moved along that parabola to find another point in the set K; see Fig. 1. Their result can be thought of as a continuous-parameter analogue of the classical Furstenberg–Sárközy theorem [11, 12], on ${\mathbb {R}}^2$ instead of ${\mathbb {Z}}$. The parabola cannot be replaced with a vertical straight line (see the comments in [8]); curvature is crucial.

Fig. 1

The two-point pattern inside the set

The authors of [8] mention that a set $A\subseteq [0,1]^2$ of Lebesgue measure at least $0<\delta \leqslant 1/2$ contains a pair of points (1.1) that also satisfy the gap bound

$$\begin{aligned} |u |\geqslant \exp (-\exp (\delta ^{-C})) \end{aligned}$$

for some absolute constant C. This property is seen either by an easy adaptation of Bourgain’s argument from [1] for quadratic progressions

$$\begin{aligned} x, \ x+z, \ x+z^2, \end{aligned}$$

or by merely considering the last two points of the three-point quadratic corner

$$\begin{aligned} (x,y), \ (x+z,y), \ (x,y+z^2), \end{aligned}$$

studied by Christ, Roos, and one of the present authors [4, Theorem 4]. A gap bound is needed in order to have a nontrivial result, as the Steinhaus theorem would identify sufficiently small copies of any finite configuration inside a set of positive measure. Namely, if A has positive measure, then the difference set $A-A$ contains a ball around the origin, so it certainly intersects the parabola $v=u^2$ in a point other than (0, 0). More on polynomial patterns like these can be found in recent preprints [9] and [10].

It is natural to wonder if sets $A\subseteq [0,1]^2$ of positive measure also possess some stronger property of Furstenberg–Sárközy type. For instance, we can consider many parabolas $v=au^2$ with their vertex translated to the point (x, y). Reasoning from the previous paragraph applies equally well for any fixed $a>0$ to the vertically scaled set, giving a well-separated pair of points

$$\begin{aligned} (x,y), \ (x,y)+(u,au^2) \end{aligned}$$

(1.2)

in the set A. However, it is not obvious if there exists a common starting point $(x,y)\in A$ from which we could move along “many” parabolas and always find points in the set A; see Fig. 2. This is the content of our main theorem below and here by many we mean a whole “beam” of parabolas with parameter a running over a non-degenerate interval I. In fact, a parabola can be replaced with any power curve $v=au^\beta$, for a fixed $\beta \ne 1$ and a varying $a>0$.

Fig. 2

Points in the set along many parabolas

Here is the main result of the paper. Let $|E |$ denote the Lebesgue measure of a measurable set $E\subseteq {\mathbb {R}}^2$.

Theorem 1

For a given $\beta \in (0,\infty )$, $\beta \ne 1$, there exists a finite constant $C\geqslant 1$ with the following property: for every $0<\delta \leqslant 1/2$ and every measurable set $A\subseteq [0,1]^2$ of Lebesgue measure $|A |$ at least $\delta$, there exist a point $(x,y)\in A$ and an interval $I\subseteq (0,\infty )$ such that

$$\begin{aligned}{} & {} \exp (-\delta ^{-C})\leqslant \inf I < \sup I\leqslant \exp (\delta ^{-C}), \\{} & {} |I |\geqslant \exp (-\delta ^{-C}), \end{aligned}$$

and that for every $a\in I$, the set A intersects the arc of the power curve

$$\begin{aligned} \big \{ (x,y) + \big (u, a u^\beta \big ): \exp (-\delta ^{-C}) \leqslant u\leqslant \exp (\delta ^{-C}) \big \}. \end{aligned}$$

The following short argument shows that Theorem 1 fails in the limiting case $\beta =1$, i.e., when the power curves are replaced with straight lines through (x, y). Let $N\subseteq [0,1]^2$ be a Nikodym set, which is a set of full Lebesgue measure such that through every point of N, one can draw a line that intersects N only at a single point; let us call such lines exceptional. If ${\mathcal {R}}_{\alpha } :{\mathbb {R}}^2\rightarrow {\mathbb {R}}^2$ denotes the rotation about the point (1/2, 1/2) by the angle $\alpha$, while ${\mathcal {D}}_c:{\mathbb {R}}^2\rightarrow {\mathbb {R}}^2$ denotes the dilation centered at (1/2, 1/2) by the factor $c>0$, then

$$\begin{aligned} A := \bigg ( \bigcap _{\alpha \in [0,2\pi )\cap {\mathbb {Q}}} {\mathcal {D}}_{\sqrt{2}}{\mathcal {R}}_{\alpha } N \bigg )\cap [0,1]^2 \end{aligned}$$

(1.3)

is a Nikodym set such that its exceptional lines determine a dense set of directions through each of its points. In particular, there can be no beam of lines

$$\begin{aligned} \big \{(x,y) + (u,au): u\in {\mathbb {R}}\big \}, \quad a\in I, \quad I\subseteq (0,\infty ) \text { an interval}, \end{aligned}$$

through any point $(x,y)\in A$ that would nontrivially intersect A for each $a\in I$, as required in Theorem 1. In fact, Davies [13] has already constructed a Nikodym set whose exceptional lines though each of its points form both dense and uncountable sets of directions. On the other hand, if we repeat the simple construction (1.3) starting with a Nikodym-type set found by Chang et al. [14, Corollary 1.2], then we can also rule out curves composed of countably many pieces of straight lines.

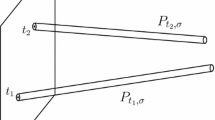
Finally, it is also legitimate to ask if an even stronger result holds for “really large” sets, namely for the sets $A\subseteq {\mathbb {R}}^2$ that occupy a positive “share” of the plane. Recall that the upper Banach density of a measurable set A is defined as

$$\begin{aligned} \overline{\delta }(A):= \limsup _{R\rightarrow \infty } \sup _{(x,y)\in {\mathbb {R}}^2} \frac{ |A \cap \big ([x-R,x+R]\times [y-R,y+R]\big ) |}{ 4R^2 }. \end{aligned}$$

Theorem 2

For a given $\beta >1$ (resp. $0<\beta <1$) and a measurable set $A\subseteq {\mathbb {R}}^2$ with $\overline{\delta }(A)>0$, there is a number $a_0\in (0,\infty )$ with the following property: for every $a_1$ satisfying $0<a_1<a_0$ (resp. $a_1>a_0$), there exists a point $(x,y)\in A$ such that for every $a\in {\mathbb {R}}$ satisfying $a_1\leqslant a\leqslant a_0$ (resp. $a_0\leqslant a\leqslant a_1$) the set A intersects the power curve

$$\begin{aligned} \big \{ (x,y) + \big (u, a u^\beta \big ): u\in (0,\infty ) \big \}. \end{aligned}$$

In comparison with Theorem 1, an improvement coming from Theorem 2 is in the fact that the interval $I=[a_1,a_0]$ (resp. $I=[a_0,a_1]$) can have an arbitrarily small (resp. large) left (resp. right) endpoint $a_1$. It is not clear to us if the latter result also holds with $I=(0,\infty )$; this extension would probably be very difficult to prove. Our proof will rely on Bourgain’s dyadic pigeonholing in the parameter a, and as such, it is unable to assert anything for every single value of $a\in (0,\infty )$. Thus, it is not coincidental that Theorem 2 is quite reminiscent of the so-called pinned distances theorem of Bourgain [15, Theorem 1’]. Our proof will closely follow Bourgain’s proof of that theorem, replacing circles with arcs of the curves $v=a u^\beta$ and also invoking Bourgain’s results on generalized circular maximal functions in the plane [16].

Theorems 1 and 2 might also be interesting because they initiate the study of strong-type (a.k.a. Bourgain-type) results for finite curved Euclidean configurations, asserting their existence in A for a whole interval I of parameters/scales. The two-point pattern (1.2) studied here could possibly be replaced with larger and more complicated configurations in future.

2 Analytical Reformulation

It is sufficient to study the case $\beta >1$. Afterward, one can cover $0<\beta <1$ simply by interchanging the roles of the coordinate axes and applying the previous case to $1/\beta$. Note that all bounds formulated in Theorem 1 and the statement of Theorem 2 are sufficiently symmetric to allow such swapping. Thus, let us fix the parameter $\beta \in (1,\infty )$.

It is geometrically evident that one can realize an arc of the power curve $v=u^\beta$ as a part of a smooth closed simple curve $\Gamma$, which has non-vanishing curvature and which is the boundary of a centrally symmetric convex set in the plane. More precisely, take parameters $0<\eta <\theta$ such that

$$\begin{aligned} \Big (\frac{\theta }{\eta }\Big )^\beta - \beta \frac{\theta }{\eta } < \beta -1. \end{aligned}$$

Figure 3 depicts how the arc

$$\begin{aligned} \big \{ (u,u^\beta ) : \eta \leqslant u\leqslant \theta \big \} \end{aligned}$$

(2.1)

can be extended by its tangents at the endpoints to a boundary of a centrally symmetric convex set. It is then easy to curve and smooth this boundary a little in order to make it $\textrm{C}^\infty$ with non-vanishing curvature while still containing the above arc. The trick of realizing a power arc as a part of the boundary of an appropriate centrally symmetric convex set with intention of applying Bourgain’s results [16] has already been used by Marletta and Ricci [17, Section 1, p. 59].

Fig. 3

The power arc, the reflected arc, and the tangents

Define $\nu$ to be the arc length measure of $\Gamma$. We can also parametrize the curve $\Gamma$ by arc length (i.e., traversing it at unit speed) as

$$\begin{aligned} \Gamma = \{ (\gamma _1(s), \gamma _2(s)): s\in [0,L)\}, \end{aligned}$$

so that we have

$$\begin{aligned} \int _{{\mathbb {R}}^2} f(u,v) \,\textrm{d}\nu (u,v) = \int _{0}^{L} f(\gamma _1(s), \gamma _2(s)) \,\textrm{d}s \end{aligned}$$

for every bounded measurable function f. Now take a nonnegative smooth function $\Psi$ such that its support intersects $\Gamma$ precisely in the arc (2.1), and which is constant 1 on a major part of that arc. Let $\sigma$ be the measure given by

$$\begin{aligned} \textrm{d}\sigma = \frac{\Psi \,\textrm{d}\nu }{\int _\Gamma \Psi \,\textrm{d}\nu }; \end{aligned}$$

note that it is normalized as $\sigma ({\mathbb {R}}^2)=\sigma (\Gamma )=1$. Then

$$\begin{aligned} \int _{{\mathbb {R}}^2} f(u,v) \,\textrm{d}\sigma (u,v) =\int _{{\mathbb {R}}} f(u,u^\beta ) \psi (u) \,\textrm{d}u \end{aligned}$$

for every bounded measurable function f, where $\psi (u)$ is a constant multiple of

$$\begin{aligned} \Psi (u,u^\beta ) (\gamma _1^{-1})'(u). \end{aligned}$$

Thus, $\psi$ is a nonnegative $\textrm{C}^\infty$ function whose support is contained in $[\eta ,\theta ]$. All constants appearing in the proof are allowed to depend on $\Gamma ,\beta ,\eta ,\theta ,\Psi$ without further mention.

If $\sigma _t$ is the dilate of $\sigma$ by a number $t>0$, i.e., $\sigma _t(E):=\sigma (t^{-1}E)$, then we have

$$\begin{aligned} \int _{{\mathbb {R}}^2} f(u,v) \,\textrm{d}\sigma _{t}(u,v) = \frac{1}{t} \int _{{\mathbb {R}}} f \Big (u,\frac{u^{\beta }}{t^{\beta -1}}\Big ) \psi \Big (\frac{u}{t}\Big )\,\textrm{d}u, \end{aligned}$$

so $\sigma _{t}$ is “detects” points on the curve $v=au^\beta$, where

$$\begin{aligned} a = t^{1-\beta }. \end{aligned}$$

(2.2)

Finally, let $\tilde{\sigma }$ be the reflection of $\sigma$, i.e., $\tilde{\sigma }(E):=\sigma (-E)$. Note that

$$\begin{aligned} \big (\tilde{\sigma }_t*f\big )(x,y) = \frac{1}{t} \int _{{\mathbb {R}}} f\Big (x + u, y + \frac{u^{\beta }}{t^{\beta -1}}\Big ) \psi \Big (\frac{u}{t}\Big )\,\textrm{d}u. \end{aligned}$$

(2.3)

Both theorems will be consequences of the following purely analytical result. Let $\mathbbm {1}_E$ denote the indicator function of a set $E\subseteq {\mathbb {R}}^2$.

Proposition 3

Take $0<\delta \leqslant 1/2$ and a measurable set $A\subseteq [0,1]^2$ of measure $|A |\geqslant \delta$. Suppose that there exist dyadic numbers (i.e., elements of $2^{\mathbb {Z}}$)

$$\begin{aligned} 1> b_1> c_1> b_2> c_2> \cdots> b_J> c_J > 0 \end{aligned}$$

having the property

$$\begin{aligned} \inf _{t\in [c_j,b_j]}\big (\tilde{\sigma }_t *\mathbbm {1}_A\big )(x,y)=0 \end{aligned}$$

(2.4)

for every point $(x,y)\in A$ and every index $1\leqslant j\leqslant J$. Then $J\leqslant \delta ^{-C'}$ for some constant $C'\geqslant 1$ independent of $\delta$ or A.

Our main task is to establish Proposition 3 and its proof will span over the next section.

3 Proof of Proposition 3

Let us write $A\lesssim B$ and $B\gtrsim A$ if the inequality $A\leqslant CB$ holds for a constant $C\in (0,\infty )$. This constant C is always understood to depend on $\Gamma ,\beta ,\eta ,\theta ,\Psi$ from previous sections. Let $\tau >0$ be a fixed positive number and $\varrho >0$ a fixed dyadic number; their values will be small and they will be chosen later.

Take a measurable set $A\subseteq [0,1]^2$ with $|A |\geqslant \delta$. We write

$$\begin{aligned} f:=\mathbbm {1}_A \quad \text {and}\quad g:= \mathbbm {1}_{[0,1]^2} - f. \end{aligned}$$

If we take an index j such that

$$\begin{aligned} j > J_0 := \Big \lceil \frac{1}{2} \log _2 \frac{\mathop {\textrm{diam}}\Gamma }{\tau }\Big \rceil , \end{aligned}$$

(3.1)

then

$$\begin{aligned} b_j \frac{\mathop {\textrm{diam}}\Gamma }{2} \leqslant 2^{-2j} \mathop {\textrm{diam}}\Gamma < \tau , \end{aligned}$$

so for every $(x,y)\in A\cap [\tau ,1-\tau ]^2$ and $t\in [c_j,b_j]$, we have

$$\begin{aligned} \big (\tilde{\sigma }_t*\mathbbm {1}_{[0,1]^2} \big )(x,y) = \sigma _t({\mathbb {R}}^2) = \sigma ({\mathbb {R}}^2) = 1. \end{aligned}$$

For such points (x, y), the assumption (2.4) then implies

$$\begin{aligned} f(x,y) \sup _{t\in [c_j,b_j]} \big (\tilde{\sigma }_t *g \big )(x,y) = 1, \end{aligned}$$

which in turn leads to a lower bound

$$\begin{aligned} \int _{{\mathbb {R}}^2}f \cdot \sup _{t\in [c_j,b_j]} (\tilde{\sigma }_t*g)&\geqslant \int _{A\cap [\tau ,1-\tau ]^2} f \cdot \sup _{t\in [c_j,b_j]} \big (\tilde{\sigma }_t*g \big ) \nonumber \\&= |A\cap [\tau ,1-\tau ]^2|\geqslant |A |-4\tau = \int _{{\mathbb {R}}^2} f -4\tau , \end{aligned}$$

(3.2)

provided j is chosen large enough that (3.1) holds.

Let $\varphi _t$ be the Poisson kernel on ${\mathbb {R}}^2$, i.e.,

$$\begin{aligned} {\varphi _t}(x,y):= \frac{t}{2\pi (t^2 + x^2+y^2)^{3/2}} \end{aligned}$$

for every $t>0$, where the normalization is chosen such that $\int _{{\mathbb {R}}^2}\varphi _t = 1$. For a bounded measurable function h we will write

$$\begin{aligned} P_t h = \varphi _t*h. \end{aligned}$$

Also, for $k\in {\mathbb {Z}}$ let ${\mathbb {E}}_k$ denote the martingale averages with respect to the dyadic filtration, i.e.,

$$\begin{aligned} {\mathbb {E}}_k h:= \sum _{|Q |=2^{-2k}} \Big ( |Q|^{-1}\int _Q h \, \Big ) \mathbbm {1}_Q, \end{aligned}$$

where $h\in \textrm{L}^1_{\textrm{loc}}({\mathbb {R}}^2)$ and the sum is taken over all dyadic squares Q in ${\mathbb {R}}^2$ of area $2^{-2k}$ (and side length $2^{-k}$).

Take $t\in [c_j,b_j]$ and $k_j = -\log _2(\varrho c_j)$, which is an integer. We decompose

$$\begin{aligned} \tilde{\sigma }_t *g&= (\tilde{\sigma }_t *g -\tilde{\sigma }_t *{\mathbb {E}}_{k_j} g) \\&\quad +\, (\tilde{\sigma }_t *{\mathbb {E}}_{k_j} g -\tilde{\sigma }_t *P_{\varrho c_j}g) +( \tilde{\sigma }_t *P_{\varrho c_j} g - \tilde{\sigma }_t *P_{\varrho ^{-1} b_j} g ) \\&\quad + (\tilde{\sigma }_t *P_{\varrho ^{-1} b_j} g - P_{\varrho ^{-1} b_j} g)+ P_{\varrho ^{-1} b_j}g . \end{aligned}$$

Taking the triangle inequality and the supremum over t gives

$$\begin{aligned} \int f \cdot \sup _{t \in [c_j,b_j]}\, (\tilde{\sigma }_t *g )&\leqslant \int f \cdot \sup _{t \in [c_j,b_j]}|\tilde{\sigma }_t *( g - {\mathbb {E}}_{k_j} g ) |\end{aligned}$$

(3.3)

$$\begin{aligned}&\quad + \int f \cdot \sup _{t \in [c_j,b_j]} |\tilde{\sigma }_t *{\mathbb {E}}_{k_j} g - \tilde{\sigma }_t *P_{\varrho c_j} g|\end{aligned}$$

(3.4)

$$\begin{aligned}&\quad + \int f \cdot \sup _{t \in [c_j,b_j]} |\tilde{\sigma }_t *P_{\varrho c_j} g -\tilde{\sigma }_t *P_{\varrho ^{-1} b_j} g |\end{aligned}$$

(3.5)

$$\begin{aligned}&\quad + \int f\cdot \sup _{t \in [c_j,b_j]} |\tilde{\sigma }_t *P_{\varrho ^{-1} b_j} g -P_{\varrho ^{-1} b_j} g |\nonumber \\&\quad + \int f \cdot P_{\varrho ^{-1} b_j} g . \end{aligned}$$

(3.6)

We will estimate each of the terms separately, using Hölder’s inequality. For the first term on the right-hand side of (3.3), we will use the bound

$$\begin{aligned} \Big \Vert \sup _{t\in [c_j,1)} |\tilde{\sigma }_t*(g - {\mathbb {E}}_{k_j} g)|\Big \Vert _{\textrm{L}^p ({\mathbb {R}}^2)} \leqslant C_1 \varrho ^\alpha \Vert g\Vert _{\textrm{L}^p({\mathbb {R}}^2)} \end{aligned}$$

(3.7)

whenever $p>2$, where $\alpha$ is a positive constant depending only on p. (Any fixed finite value of p greater than 2 will do.) This bound will follow from the central estimate (10) in Bourgain’s paper [16], which can be written in our notation as

$$\begin{aligned} \Big \Vert \sup _{t \in [2^{-n}, 2^{-n+1})}|\tilde{\sigma }_t *h |\Big \Vert _{\textrm{L}^p({\mathbb {R}}^2)} \lesssim 2^{-\alpha (i-n)} \Vert h\Vert _{\textrm{L}^p({\mathbb {R}}^2)} \end{aligned}$$

(3.8)

whenever ${\mathbb {E}}_i h=0$, while $n\leqslant i$ are positive integers and $p,\alpha$ are as before. Bourgain [16, (10)] actually formulated (3.8) for the full arc length measure $\textrm{d}\nu$, but the very same proof establishes it also for the smooth truncation $\Psi \,\textrm{d}\nu$. In fact, Bourgain has already performed several decompositions of $\nu$ [16, Sections 3–6], and an additional smooth angular finite decomposition of $\Gamma$ can be added freely to the proof of his upper bound [16, (10)], making the proof insusceptible to a smooth truncation by $\Psi$.

In order to prove (3.7), let $d_j=-\log _2(c_j)$. We split $[c_j,1)$ into dyadic intervals $[2^{-n}, 2^{-n+1})$, estimate the maximum in n by the $\ell ^p$-sum, write

$$\begin{aligned} g-{\mathbb {E}}_{k_j}g = \sum _{m=0}^{\infty } \Delta _{m+k_j} g, \end{aligned}$$

where $\Delta _i = {\mathbb {E}}_{i+1} - {\mathbb {E}}_{i}$, and use the triangle inequality, after which it suffices to show

$$\begin{aligned} \bigg \Vert \bigg ( \sum _{n=1}^{d_j} \Big ( \sum _{m=0}^\infty \, \sup _{t \in [2^{-n}, 2^{-n+1})}|\tilde{\sigma }_t *\Delta _{m+k_j} g |\Big )^{p} \bigg ) ^{1/p} \bigg \Vert _{\textrm{L}^p({\mathbb {R}}^2)} \lesssim \varrho ^\alpha \Vert g\Vert _{\textrm{L}^p({\mathbb {R}}^2)}. \end{aligned}$$

The left-hand side can be rewritten as

$$\begin{aligned} \bigg ( \sum _{n=1}^{d_j} \Big \Vert \sum _{m=0}^\infty \sup _{t \in [2^{-n}, 2^{-n+1})} |\tilde{\sigma }_t *\Delta _{m+k_j} g |\Big \Vert _{\textrm{L}^p({\mathbb {R}}^2)}^p \bigg )^{1/p} \end{aligned}$$

and then estimated by Minkowski’s inequality with

$$\begin{aligned} \leqslant \sum _{m=0}^\infty \Big (\sum _{n=1}^{d_j} \Big \Vert \sup _{t \in [2^{-n}, 2^{-n+1})} |\tilde{\sigma }_t *\Delta _{m+k_j} g |\Big \Vert _{\textrm{L}^p({\mathbb {R}}^2)}^p \Big )^{1/p}. \end{aligned}$$

Finally, the inequality (3.8) with $i=m+k_j$ bounds this by

$$\begin{aligned}&\lesssim \sum _{m=0}^\infty \Big (\sum _{n=1}^{d_j} 2^{-p\alpha (m+k_j-n)} \Vert \Delta _{m+k_j}g\Vert _{\textrm{L}^p({\mathbb {R}}^2)}^p \Big )^{1/p} \\&\lesssim \sum _{m=0}^\infty \Big (\sum _{n=1}^{d_j} 2^{-p\alpha (m+k_j-n)} \Vert g\Vert _{\textrm{L}^p({\mathbb {R}}^2)}^p \Big )^{1/p} \\&\lesssim 2^{\alpha (d_j-k_j)}\Vert g\Vert _{\textrm{L}^p({\mathbb {R}}^2)} =\varrho ^\alpha \Vert g\Vert _{\textrm{L}^p({\mathbb {R}}^2)}, \end{aligned}$$

as desired.

To control (3.4) and (3.5), we use Bourgain’s maximal estimate in the plane [16, Theorem 1],

$$\begin{aligned} \Big \Vert \sup _{t\in (0,\infty )} |\tilde{\sigma }_t *h|\Big \Vert _{\textrm{L}^p({\mathbb {R}}^2)} \lesssim \Vert h\Vert _{\textrm{L}^p ({\mathbb {R}}^2)} \end{aligned}$$

for $p>2$. Here, it gives

$$\begin{aligned} \Big \Vert \sup _{t\in [ c_j,b_j ]} |\tilde{\sigma }_t *P_{\varrho c_j} g - \tilde{\sigma }_t *P_{\varrho ^{-1} b_j} g |\Big \Vert _{\textrm{L}^p ({\mathbb {R}}^2)} \leqslant C_2\Vert P_{\varrho ^{-1} b_j} g - P_{\varrho c_j} g \Vert _{\textrm{L}^p({\mathbb {R}}^2)} \nonumber \\ \end{aligned}$$

(3.9)

and

$$\begin{aligned} \Big \Vert \sup _{t\in [ c_j,b_j ]} |\tilde{\sigma }_t *{\mathbb {E}}_{k_j} g - \tilde{\sigma }_t *P_{\varrho c_j} g |\Big \Vert _{\textrm{L}^p ({\mathbb {R}}^2)} \leqslant C_2\Vert P_{\varrho c_j} g - {\mathbb {E}}_{k_j} g \Vert _{\textrm{L}^p({\mathbb {R}}^2)} \end{aligned}$$

(3.10)

for an absolute constant $C_2$.

To estimate (3.6), we claim that for each $(x,y)\in {\mathbb {R}}^2$, j, and $t\leqslant b_j$,

$$\begin{aligned} \big |\big (\tilde{\sigma }_t*P_{\varrho ^{-1} b_j} g \big )(x,y) - \big ( P_{\varrho ^{-1} b_j} g \big )(x,y) \big |\leqslant C_3\varrho \end{aligned}$$

(3.11)

for some absolute constant $C_3$. To see this, we first use that

$$\begin{aligned} \big |\big (\tilde{\sigma }_t*P_{\varrho ^{-1} b_j} g \big )(x,y) - \big ( P_{\varrho ^{-1} b_j} g \big )(x,y) \big |\leqslant \big \Vert ( \tilde{\sigma }_t*\varphi _{\varrho ^{-1} b_j} ) - \varphi _{\varrho ^{-1} b_j} \big \Vert _{\textrm{L}^1({\mathbb {R}}^2)} \Vert g\Vert _{\textrm{L}^\infty ({\mathbb {R}}^2)} \end{aligned}$$

for each $(x,y)\in {\mathbb {R}}^2$. Since $\Vert g\Vert _{\textrm{L}^\infty ({\mathbb {R}}^2)}\leqslant 1$, it only remains to bound, using (2.3),

$$\begin{aligned}&\big \Vert ( \tilde{\sigma }_t*\varphi _{\varrho ^{-1} b_j} ) -\varphi _{\varrho ^{-1} b_j} \big \Vert _{\textrm{L}^{1}({\mathbb {R}}^2)} \\&\quad = \int _{{\mathbb {R}}^2} \bigg |\frac{1}{t}\int _{{\mathbb {R}}} \bigg (\varphi _{\varrho ^{-1} b_j} \Big (x+u, y+\frac{u^\beta }{t^{\beta -1}}\Big ) - \varphi _{\varrho ^{-1} b_j}(x,y) \bigg ) \psi \Big (\frac{u}{t} \Big ) \,\textrm{d}u \bigg |\,\textrm{d}(x,y) \\&\quad \leqslant \int _{{\mathbb {R}}^2} \frac{1}{t}\int _{{\mathbb {R}}} \Big |\varphi _1 \Big (x+\frac{ u \varrho }{ b_j}, y+\frac{u^\beta \varrho }{ b_j t^{\beta -1}}\Big ) - \varphi _1(x,y) \Big |\,\psi \Big (\frac{u}{t} \Big ) \,\textrm{d}u \,\textrm{d}(x,y), \end{aligned}$$

where we also changed variables in x, y. By the mean value theorem, the last display is

$$\begin{aligned} \leqslant \int _{{\mathbb {R}}^2} \frac{1}{t}\int _{{\mathbb {R}}} |\nabla \varphi _1 (z,w) |\Big |\Big (\frac{u\varrho }{ b_j}, \frac{u^\beta \varrho }{ b_j t^{\beta -1}} \Big )\Big |\,\psi \Big ( \frac{u}{t} \Big ) \,\textrm{d}u \,\textrm{d}(x,y) \end{aligned}$$

for

$$\begin{aligned} (z,w)=a(x,y) + (1-a)\Big (x+\frac{u \varrho }{ b_j}, y+\frac{u^\beta \varrho }{ b_j t^{\beta -1}}\Big ) \end{aligned}$$

and some $0<a<1$. This is further bounded by

$$\begin{aligned} \lesssim \int _{{\mathbb {R}}^2} \frac{1}{t}\int _{{\mathbb {R}}} \big (1+|(x,y)|^2\big )^{-3/2} \Big |\Big (\frac{u\varrho }{ b_j}, \frac{u^\beta \varrho }{ b_j t^{\beta -1}} \Big )\Big |\,\psi \Big (\frac{u}{t} \Big ) \,\textrm{d}u \,\textrm{d}(x,y), \end{aligned}$$

where we also used $|u |\lesssim t\leqslant b_j<1$, and dominated a non-centered $|\nabla \varphi _1|$ by a centered integrable function. Integrating in u and (x, y), we obtain a bound by $C_3\varrho$.

Therefore, using (3.2) to obtain a lower bound, estimates (3.7), (3.9), (3.10), (3.11) for upper bounds, and Hölder’s inequality, we obtain

$$\begin{aligned} \int _{{\mathbb {R}}^2} f - 4\tau&\leqslant C_1\varrho ^\alpha + C_2\Vert P_{\varrho c_j} g - {\mathbb {E}}_{k_j} g \Vert _{\textrm{L}^p({\mathbb {R}}^2)} + C_2\Vert P_{\varrho ^{-1} b_j} g - P_{\varrho c_j} g \Vert _{\textrm{L}^p({\mathbb {R}}^2)} \nonumber \\&\quad + C_3 \varrho + \int _{{\mathbb {R}}^2} f \cdot P_{\varrho ^{-1} b_j} g , \end{aligned}$$

(3.12)

provided j is large enough.

Next,

$$\begin{aligned} \int _{{\mathbb {R}}^2} f \cdot P_{\varrho ^{-1} b_j} g =\int _{{\mathbb {R}}^2} f \cdot P_{\varrho ^{-1} b_j} \mathbbm {1}_{[0,1]^2} - \int _{{\mathbb {R}}^2} f \cdot P_{\varrho ^{-1} b_j} f \end{aligned}$$

and we have

$$\begin{aligned} \int _{{\mathbb {R}}^2} f \cdot P_{\varrho ^{-1} b_j} \mathbbm {1}_{[0,1]^2} \leqslant \int _{{\mathbb {R}}^2} f \end{aligned}$$

(3.13)

and

$$\begin{aligned} \int _{{\mathbb {R}}^2} f \cdot P_{\varrho ^{-1} b_j} f \geqslant c_0 \Big ( \int _{{\mathbb {R}}^2} f \Big )^2 \end{aligned}$$

(3.14)

for some absolute constant $c_0>0$. The estimate (3.13) follows by the trivial $\textrm{L}^\infty$ bound for the convolution. To see (3.14), we note that by the Cauchy-Schwarz inequality, for any $k\in {\mathbb {Z}}$,

$$\begin{aligned} \int _{{\mathbb {R}}^2} f \cdot {\mathbb {E}}_k f \geqslant \Big (\int _{{\mathbb {R}}^2} f \Big )^2 \end{aligned}$$

Then it remains to bound the martingale averages from above by the Poisson averages. The reader can find the details in the proof of Lemma 2.1 in [3]. Therefore, from (3.12) and $\int _{{\mathbb {R}}^2}f=|A|\geqslant \delta$, we get

$$\begin{aligned} c_0 \delta ^2 - 4\tau \leqslant C_1\varrho ^\alpha + C_3\varrho + C_2\Vert P_{\varrho c_j} g - {\mathbb {E}}_{k_j} g \Vert _{\textrm{L}^p({\mathbb {R}}^2)} + C_2\Vert P_{\varrho ^{-1} b_j} g - P_{\varrho c_j} g \Vert _{\textrm{L}^p({\mathbb {R}}^2)}, \end{aligned}$$

(3.15)

which will turn out useful provided that $\tau$ is small enough.

Furthermore, we claim that for $p>2$ and for any $J>J_0$, we have

$$\begin{aligned} \sum _{j=J_0+1}^J \Vert P_{\varrho ^{-1} b_j} g - P_{\varrho c_j} g \Vert _{\textrm{L}^p({\mathbb {R}}^2)}^p \leqslant C_4 \big (\log _2\varrho ^{-1}\big )^p \Vert g\Vert ^p_{\textrm{L}^p ({\mathbb {R}}^2)} \leqslant C_4 \big (\log _2\varrho ^{-1}\big )^p \end{aligned}$$

(3.16)

and

$$\begin{aligned} \sum _{j=J_0+1}^J \Vert P_{\varrho c_j} g - {\mathbb {E}}_{k_{j}} g \Vert _{\textrm{L}^p({\mathbb {R}}^2)}^p \leqslant C_4 \Vert g\Vert ^p_{\textrm{L}^p ({\mathbb {R}}^2)} \leqslant C_4 \end{aligned}$$

(3.17)

with the constant $C_4$ independent of $J_0,J$. These will be consequences of boundedness on $\textrm{L}^p({\mathbb {R}}^2)$, $1<p<\infty$, of the square functions

$$\begin{aligned} S_1 h:= \Big ( \sum _{i\in {\mathbb {Z}}} \big |P_{2^{-i+1}} h - P_{2^{-i}} h \big |^2 \Big )^{1/2} \end{aligned}$$

and

$$\begin{aligned} S_2 h:= \Big ( \sum _{i\in {\mathbb {Z}}} \big |P_{2^{-i}} h - {\mathbb {E}}_{i} h\big |^2 \Big )^{1/2}. \end{aligned}$$

Bound for $S_1$ follows from the classical Calderón-Zygmund theory [18, Subsections 6.1.3], while boundedness of $S_2$ was proven by Jones, Seeger, and Wright [19, Sections 3–4]. In fact, the emphasis of the paper [19] was on more general dilation structures and more general martingales, while the square function estimate from the last display is essentially due to Calderón; see [18, Subsection 6.4.4]. Now, (3.16) follows by recalling $p>2$ and writing

$$\begin{aligned}&\bigg ( \sum _{j=J_0+1}^J \Vert P_{\varrho ^{-1} b_j} g - P_{\varrho c_j} g \Vert _{\textrm{L}^p({\mathbb {R}}^2)}^p \bigg )^{1/p} \\&\quad \leqslant (2\log _2\varrho ^{-1}+1) \bigg ( \sum _{i\in {\mathbb {Z}}} \Vert P_{2^{-i+1}} g - P_{2^{-i}} g \Vert _{\textrm{L}^p({\mathbb {R}}^2)}^p \bigg )^{1/p} \\&\quad \lesssim (\log _2\varrho ^{-1}) \bigg \Vert \Big ( \sum _{i\in {\mathbb {Z}}} |P_{2^{-i+1}} g - P_{2^{-i}} g |^p \Big )^{1/p} \bigg \Vert _{\textrm{L}^p({\mathbb {R}}^2)} \\&\quad \leqslant (\log _2\varrho ^{-1}) \Vert S_1 g\Vert _{\textrm{L}^p({\mathbb {R}}^2)} \lesssim (\log _2\varrho ^{-1}) \Vert g\Vert _{\textrm{L}^p({\mathbb {R}}^2)} . \end{aligned}$$

Similarly we deduce (3.17):

$$\begin{aligned} \bigg ( \sum _{j=J_0+1}^J \Vert P_{\varrho c_j} g - {\mathbb {E}}_{k_{j}}g \Vert _{\textrm{L}^p({\mathbb {R}}^2)}^p \bigg )^{1/p} \leqslant \Vert S_2 g\Vert _{\textrm{L}^p({\mathbb {R}}^2)} \lesssim \Vert g\Vert _{\textrm{L}^p({\mathbb {R}}^2)}. \end{aligned}$$

To be completely determined, one can simply take $p=3$. From (3.16) and (3.17), we conclude that there exists $j\in \{J_0+1,\ldots , J\}$ such that

$$\begin{aligned} \Vert P_{\varrho ^{-1} b_j} g - P_{\varrho c_j} g \Vert _{\textrm{L}^3 ({\mathbb {R}}^2)}, \Vert P_{\varrho c_j} g - {\mathbb {E}}_{k_j} g \Vert _{\textrm{L}^3({\mathbb {R}}^2)} \leqslant (2C_4 (J-J_0)^{-1})^{1/3} \log _2\varrho ^{-1}. \end{aligned}$$

Together with (3.15) applied for this particular j and $\tau =c_0\delta ^2/8$ we obtain

$$\begin{aligned} 2^{-1}c_0\delta ^2 \leqslant C_1\varrho ^\alpha + C_3\varrho + 2 C_2(2C_4(J-J_0)^{-1})^{1/3} \log _2\varrho ^{-1}, \end{aligned}$$

i.e.,

$$\begin{aligned} J - J_0 \lesssim \Big (\frac{\log _2\varrho ^{-1}}{2^{-1} c_0\delta ^2-C_1\varrho ^\alpha -C_3\varrho }\Big )^3. \end{aligned}$$

Now we recall that we actually chose $J_0$ in (3.1) at the beginning of the proof, which guarantees that $J_0\leqslant \log _2(C_5 \delta ^{-2})$ for a suitable constant $C_5$. Taking $\varrho$ to be a small multiple of $\min \{\delta ^{2/\alpha }, \delta ^2\}$ we obtain $J \leqslant \delta ^{-C'}$ for a suitable constant $C'$.

4 Proofs of Theorems 1 and 2

In this section, we deduce the two main theorems from Proposition 3. Once again, it is sufficient to consider $\beta \in (1,\infty )$.

Proof of Theorem 1

Set $J=\lfloor \delta ^{-C'}\rfloor +1$, where $C'$ is the constant from Proposition 3. Let us simply choose consecutive dyadic scales, $b_j=2^{-2j+1}$ and $c_j=2^{-2j}$ for every $1\leqslant j\leqslant J$. By the contraposition of Proposition 3 and using formula (2.3), we conclude that there exist a point $(x,y)\in A$ and an index $1\leqslant j\leqslant J$ such that for every $c_j\leqslant t\leqslant b_j$, the set A contains a point of the form

$$\begin{aligned} \Big (x + u, y + \frac{u^{\beta }}{t^{\beta -1}}\Big ), \quad \eta t< u< \theta t. \end{aligned}$$

(4.1)

Substituting (2.2), we get

$$\begin{aligned} c_j\leqslant t\leqslant b_j \quad \Longleftrightarrow \quad b_j^{1-\beta }\leqslant a \leqslant c_j^{1-\beta }, \end{aligned}$$

which now means that for every

$$\begin{aligned} a \in I:= \big [ 2^{(\beta -1)(2j-1)}, 2^{(\beta -1)2j} \big ] \end{aligned}$$

there exists

$$\begin{aligned} \eta a^{-1/(\beta -1)}< u < \theta a^{-1/(\beta -1)} \end{aligned}$$

such that $(x+u,y+au^\beta )\in A$. Observing

$$\begin{aligned}&\inf I \geqslant 1, \\&\sup I \leqslant 2^{2(\beta -1)J} \leqslant 2^{4(\beta -1)\delta ^{-C'}}, \\&|I|\geqslant 2^{\beta -1} - 1, \end{aligned}$$

and that any such u satisfies

$$\begin{aligned}&u \geqslant \eta 2^{-2j} \geqslant \eta 2^{-2J} \geqslant \eta 2^{-2\delta ^{-C'}}, \\&u \leqslant \theta 2^{-2j+1} \leqslant \theta \end{aligned}$$

we finally establish Theorem 1. $\square$

Proof of Theorem 2

Suppose that the claim does not hold for some measurable set $A\subseteq {\mathbb {R}}^2$ with $\overline{\delta }(A)>0$. Take $\delta :=\overline{\delta }(A)/2$ and $J=\lfloor \delta ^{-C'}\rfloor +1$, where $C'$ is the constant from Proposition 3. Inductively, we construct positive numbers

$$\begin{aligned} C_1> B_1> C_2> B_2> \cdots> C_J > B_J \end{aligned}$$

satisfying $C_{j+1}\leqslant B_j/8^{\beta -1}$ and such that for each $j\geqslant 1$ and every point $(x,y)\in A$, there exists $a\in [B_j,C_j]$ with the property that A does not contain a point of the form

$$\begin{aligned} (x+u, y+au^\beta ), \quad u>0. \end{aligned}$$

After the change of variables (2.2), we see that for each $j\geqslant 1$ and every point $(x,y)\in A$, there exists

$$\begin{aligned} C_j^{-1/(\beta -1)} \leqslant t \leqslant B_j^{-1/(\beta -1)} \end{aligned}$$

such that A does not contain a point of the form (4.1), so

$$\begin{aligned} \big (\tilde{\sigma }_t *\mathbbm {1}_A\big )(x,y)=0. \end{aligned}$$

By the definition of the upper Banach density, there exist a number $R\geqslant B_J^{-1/(\beta -1)}$ and a point $(x_0,y_0)\in {\mathbb {R}}^2$ such that

$$\begin{aligned} \big |A\cap \big ([-R,R]^2 + (x_0,y_0)\big ) \big |\geqslant \delta \cdot 4R^2. \end{aligned}$$

Define

$$\begin{aligned} A' := \bigg ( \frac{1}{2R} \big ( A - (x_0,y_0) \big ) +\Big (\frac{1}{2},\frac{1}{2}\Big ) \bigg ) \cap [0,1]^2 \end{aligned}$$

(4.2)

and let $b_j$ and $c_j$,respectively,be the number $B_{J+1-j}^{-1/(\beta -1)}/2R$ rounded up to the nearest dyadic number and the number $C_{J+1-j}^{-1/(\beta -1)}/2R$ rounded down to the nearest dyadic number, i.e.,

$$\begin{aligned} b_j := 2^{\lceil \log _2(B_{J+1-j}^{-1/(\beta -1)}/2R)\rceil }, \quad c_j := 2^{\lfloor \log _2( C_{J+1-j}^{-1/(\beta -1)}/2R)\rfloor } \end{aligned}$$

(4.3)

for every $1\leqslant j\leqslant J$. Finally, for every $(x,y)\in A'$ and every $1\leqslant j\leqslant J$, this implies

$$\begin{aligned} \big (\tilde{\sigma }_t *\mathbbm {1}_{A'}\big )(x,y)=0 \end{aligned}$$

for some $c_j\leqslant t\leqslant b_j$, while we have chosen J so that $J>\delta ^{-C'}$. Note that also $|A'|\geqslant \delta$, so the set (4.2) and the numbers (4.3) violate Proposition 3, which leads us to a contradiction. $\square$