Abstract
In this paper, we consider the semi-classical setting constructed on nilpotent graded Lie groups by means of representation theory. Our aim is to analyze the effects of the pull-back by diffeomorphisms on pseudodifferential operators. We restrict to diffeomorphisms that preserve the filtration and prove that they are uniformly Pansu differentiable. We show that the pull-back of a semi-classical pseudodifferential operator by such a diffeomorphism has a semi-classical symbol that is expressed at leading order in terms of the Pansu differential. Finally, we interpret the geometric meaning of this invariance in the setting of filtered manifolds.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Semi-classical analysis started to develop in the 70s and has proved a flexible tools for the analysis of PDEs [3]. It crucially relies on a microlocal viewpoint and the use of semi-classical pseudodifferential calculus. Such an approach has been recently developed on nilpotent graded Lie groups with the ambition of taking into account the non-commutativity of the group using representation theory and the associated Fourier theory [2, 5, 8]. The symbols of the pseudodifferential operators are then fields of operators on the product \(G\times {\widehat{G}}\) of the group G and its dual space \({\widehat{G}}\). Like in the Euclidean case [15], this semi-classical pseudodifferential calculus enjoys a non-commutative symbolic calculus which describes taking the adjoints and the composition as asymptotic sums of symbols [5, 8]. These tools prove efficient for studying the propagation of oscillations or concentration effects [6] of Schrödinger equations, or related questions in PDEs such as the existence of observability inequalities [7].
In the Euclidean case, invariance to leading order by change of variables is an important property of the semi-classical pseudodifferential calculus. This invariance allows for the identification of the symbol as a function on the cotangent space, and is therefore the foundation of the semi-classical calculus on manifolds [15]. Here we investigate this property for symbols on graded Lie groups: what happens to the semi-classical pseudodifferential operators introduced in [5] when conjugated by the change of variables induced by a local smooth diffeomorphism that preserves the filtration of the group.
It turns out that a smooth function \(\Phi \) between two graded Lie groups G and H that preserves the filtration of the groups is uniformly Pansu differentiable (see Theorem 1.5 below). As a consequence, part of the article consists in revisiting the concept of Pansu differentiability and its link with being filtration preserving. This study allows us to define one-to-one maps between the phase spaces \(G\times {\widehat{G}}\) and \(H\times {\widehat{H}}\) associated with any smooth local diffeomorphisms \(\Phi \) between two nilpotent groups G and H (see Theorem 1.8 below). We investigate the geometric interpretation of these results in the setting of filtered manifolds in the last Sect. 4.
1.1 Graded Groups
A graded group G is a connected simply connected nilpotent Lie group whose (finite dimensional, real) Lie algebra \({\mathfrak {g}}\) admits an \({{\mathbb {N}}}\)-gradation into linear subspaces, i.e.
With this way of describing \({\mathfrak {g}}\), all but a finite number of subspaces \({\mathfrak {g}}_j \) are trivial. We denote by \(j=n_G\) the smallest integer such that all the subspaces \({\mathfrak {g}}_j \), \(j>n_G\), are trivial. If the first stratum \({\mathfrak {g}}_1\) generates the whole Lie algebra, then \({\mathfrak {g}}_{j+1}= [{\mathfrak {g}}_1,{\mathfrak {g}}_j]\) for all \(j\in {{\mathbb {N}}}_0\) and \(n_G\) is the step of the group; the group G is then said to be stratified, and also (after a choice of basis or inner product for \({\mathfrak {g}}_1\)) Carnot.
The product law on G is derived from the exponential map \(\exp _G : {\mathfrak {g}} \rightarrow G\) and the Dynkin formula for the Baker-Campbell-Hausdorff formula (see [8, Theorem 1.3.2])
where the coefficients \(c_{r,s}\) are known:
Above, the sum over \(\ell \) is finite in the nilpotent case. In particular, the term for which \(s_\ell >1\) or \(s_\ell =0\) and \(r_\ell >1\) is zero, while the term \(\textrm{ad}X\textrm{ad}^{-1}Y(Y)\) for \(s_\ell =0, r_\ell =1\) is understood as X. Here \(\ln _G\) denotes the inverse map to \({\exp _G}\); we may drop the subscript G for \(\exp \) and \(\ln \) when the context is clear.
The exponential mapping is a global diffeomorphism from \(\mathfrak g\) onto G. Once a basis \(X_1,\ldots ,X_{n}\) for \({\mathfrak {g}}\) has been chosen, we may identify the points \((x_{1},\ldots ,x_n)\in {\mathbb {R}}^n\) with the points \(x=\exp (x_{1}X_1+\cdots +x_n X_n)\) in G. It allows us to define the (topological vector) spaces \({\mathcal {C}}^\infty (G)\) and \({\mathcal {S}}(G)\) of smooth and Schwartz functions on G identified with \({\mathbb {R}}^n\); note that the resulting spaces are intrinsically defined as spaces of functions on G and do not depend on a choice of basis.
The exponential map induces a Haar measure dx on G which is invariant under left and right translations and defines Lebesgue spaces on G, together with a (non-commutative) convolution for functions \(f_1,f_2\in {\mathcal {S}}(G)\) or in \(L^2(G)\),
We now construct a basis adapted to the gradation. Set \(n_j=\textrm{dim} \, {\mathfrak {g}}_j \) for \(1\le j\le n_G\). We choose a basis \(\{X_1,\ldots , X_{n_1}\}\) of \({\mathfrak {g}}_1\) (this basis is possibly reduced to \(\emptyset \)), then \(\{X_{n_1+1},\ldots , X_{n_1+n_2}\}\) a basis of \({\mathfrak {g}}_2\) (possibly \(\{0\}\)) and so on. Such a basis \({\mathcal {B}}=(X_1, \cdots , X_n)\) of \({\mathfrak {g}}\) is said to be adapted to the gradation; here \(n=\dim {\mathfrak {g}} = n_1+\ldots +n_G\).
The Lie algebra \({\mathfrak {g}}\) is a homogeneous Lie algebra equipped with the family of dilations \(\{\delta _r, r>0\}\), \(\delta _r:{\mathfrak {g}}\rightarrow {\mathfrak {g}}\), defined by \(\delta _r X=r^\ell X\) for every \(X\in {\mathfrak {g}}_\ell \), \(\ell \in {{\mathbb {N}}}\) [8, 9]. We re-write the set of integers \(\ell \in {{\mathbb {N}}}\) such that \({\mathfrak {g}}_\ell \not =\{0\}\) into the increasing sequence of positive integers \(\upsilon _1,\ldots ,\upsilon _n\) counted with multiplicity, the multiplicity of \({\mathfrak {g}}_\ell \) being its dimension. In this way, the integers \(\upsilon _1,\ldots , \upsilon _n\) become the weights of the dilations and we have \(\delta _r X_j =r^{\upsilon _j} X_j\), \(j=1,\ldots , n\), on the chosen basis of \({\mathfrak {g}}\). The associated group dilations are defined by
In a canonical way, this leads to the notions of homogeneity for functions and operators. It also motivates the definition of quasi-norms on G as continuous functions \(|\cdot | : G\rightarrow [0,+\infty )\) homogeneous of degree 1 on G which vanishes only at 0. This often replaces the Euclidean norm in the analysis on homogeneous Lie groups. Any quasi-norm \(|\cdot |\) on G satisfies a triangle inequality up to a constant:
Any two homogeneous quasi-norms \(|\cdot |_1\) and \(|\cdot |_2\) are equivalent in the sense that
For example, the Haar measure is Q-homogeneous where
is called the homogeneous dimension of G.
1.2 Diffeomorphisms Between Graded Groups
1.2.1 Filtration Preserving Maps
In this paragraph, we explain the notion of a (smooth or at least \({\mathcal {C}}^1\)) map preserving the natural filtrations between two graded nilpotent groups G and H. We first need to set some notation. For each \(x\in G\), we denote the differential of the left-translation \(L_x: G \rightarrow G\) by \(x\in G\) at the identity by
For \(y\in H\), we denote by \(\tau _y^H\) the analogue map on H; we may omit the superscript G or H if the context is clear. These maps allow us to view derivatives between Lie groups as acting on the Lie algebras of the groups: if \(\Phi \) is a smooth map from an open set U of G to H, then we define for each \(x\in U\)
By definition, the following diagram commutes :
Note that an equivalent definition for \({\mathfrak {d}}_x\Phi : {\mathfrak {g}} \rightarrow {\mathfrak {h}}\) is given by
In this article, we will use the shorthand:
and for instance (1.2) may be rewritten as
Definition 1.1
Let \(\Phi \) be a smooth function from an open set U of G to H. We say that \(\Phi \) preserves the filtration at \(x\in U\) when we have
1.2.2 Pansu Differentiability
For smooth diffeomorphisms (or at least sufficiently differentiable), the property of preserving the filtration is related to the notion of Pansu differentiability, which we define following [10].
Definition 1.2
Let \(\Phi \) be a map from an open set U of G to H, and let \(x\in U\). The function \(\Phi \) is Pansu differentiable at the point x when for any \(z\in G\), the following limit exists:
The limit is denoted by  ; the map
; the map  is called the Pansu derivative of \(\Phi \) at x.
is called the Pansu derivative of \(\Phi \) at x.
When defining Pansu differentiability on an open set, we add a further hypothesis of uniformity:
Definition 1.3
Let \(\Phi \) be a map from an open set U of G into H. The function \(\Phi \) is uniformly Pansu differentiable on U when
-
(1)
\(\Phi \) is Pansu differentiable at every point \(x\in U\),
-
(2)
the limit in (1.4) holds locally uniformly on \(U\times G.\)
Part (2) of this definition means that for every point \((x,z)\in U\times G\), there exists a compact neighborhood of (x, z) in \(U\times G\) where the limit in (1.4) holds uniformly. Note that this implies that the limit in (1.4) holds uniformly on any compact subset of \(U\times G\). A similar assumption is made in Sect. 4 of [14] with a subtle difference: the limit in (1.4) is supposed to be locally uniform only in \(z\in G\); however, the Pansu derivative at every point is required to be an automorphism of the group G. We will see in Sect. 2 that condition (2) in Definition 1.3 implies that the Pansu derivative is a group morphism, and an automorphism when \(\Phi \) is a diffeomorphism.
Example 1.4
Let \(\Phi : {\mathbb {H}}\rightarrow {\mathbb {R}}^3; \;(p, q, t)\mapsto (p, q, t)\) be the identity map from the Heisenberg group to \(({\mathbb {R}}^3, +)\). Equip both groups with the gradation corresponding to the non-isotropic dilations \(\delta _\varepsilon (p, q, t)=(\varepsilon p, \varepsilon q, \varepsilon ^2 t).\) One computes, for \(x=(p_1, q_1, t_1)\) and \(y=(p_2, q_2, t_2)\),
which converges as \(\varepsilon \rightarrow 0\) if and only if \(p_1q_2=p_2q_1\). In particular, the identity map between \({\mathbb {H}}\) and \(({\mathbb {R}}^3, +)\) is Pansu differentiable at the origin but not in a neighborhood of the origin.
The following property is crucial for our analysis and will be proved in Sect. 2 below. It states that for smooth functions, the notion of uniform Pansu differentiability on an open set coincides with preserving filtration above this set:
Theorem 1.5
Let \(\Phi \) be a smooth function from an open set U of G to H. The map \(\Phi \) is uniformly Pansu differentiable on U if and only if \(\Phi \) preserves the filtration at every point \(x\in U.\) Besides, for such a map \(\Phi \), the Pansu derivative yields a smooth function  on \(U\times G\).
on \(U\times G\).
This result has been proved in [14] in the case of Carnot groups. The filtration preserving maps then are contact maps. The Heisenberg group is a prime example of Warhust’s result [14]. One contribution of this paper is to extend the result to the case of graded groups.
The proof of Theorem 1.5 will also yields the following properties:
Corollary 1.6
We continue with the notation and setting of Theorem 1.5. Let \(\Phi \) be a smooth function from an open set U of G to H which is uniformly Pansu differentiable on U.
-
For each \(x\in U\),
 (resp. \({\mathcal {S}}(G)\)) if \(f\in {\mathcal {C}}^\infty (H)\) (resp. \({\mathcal {S}}(H)\)). The map
(resp. \({\mathcal {S}}(G)\)) if \(f\in {\mathcal {C}}^\infty (H)\) (resp. \({\mathcal {S}}(H)\)). The map 
yields continuous morphisms of topological vector spaces from \({\mathcal {C}}^\infty (H)\) to \({\mathcal {C}}^\infty (U,{\mathcal {C}}^\infty (G))\) and also from \({\mathcal {S}}(H)\) to \({\mathcal {C}}^\infty (U,{\mathcal {S}}(G))\).
-
If \(\Phi \) is a smooth diffeomorphism from U onto its image, then G and H are isomorphic.
1.3 The Dual Set and the Semi-classical Pseudodifferential Calculus
1.3.1 The Dual Set
Recall that a representation \(({\mathcal {H}}_\pi , \, \pi )\) of G is a pair consisting of a Hilbert space \({\mathcal {H}}_\pi \) and a group morphism \(\pi \) from G to the set of unitary transforms on \({\mathcal {H}}_\pi \). In this paper, the representations will always be assumed (unitary) strongly continuous, and their Hilbert spaces separable. A representation is said to be irreducible if the only closed subspaces of \({\mathcal {H}}_\pi \) that are stable under \(\pi \) are \(\{0\}\) and \({\mathcal {H}}_\pi \) itself. Two representations \(\pi _1\) and \(\pi _2\) are equivalent if there exists a unitary transform \({\mathbb {U}}\) called an intertwining map that sends \({\mathcal {H}}_{\pi _1}\) on \({\mathcal {H}}_{\pi _2}\) with
The dual set \({\widehat{G}}\) is obtained by taking the quotient of the set of irreducible representations by this equivalence relation. We may still denote by \(\pi \) the elements of \({\widehat{G}}\) and we keep in mind that different representations of the class are equivalent through intertwining operators. The following properties are straightforwards:
Lemma 1.7
(Pullback of Irreps) Let \(\theta : G\rightarrow H\) be a continuous group homomorphism, and \((\pi , {\mathcal {H}}_\pi )\) be a representation of H. Then
-
\(\pi \circ \theta \) is a representation of G,
-
\(\pi \mapsto \pi \circ \theta \) preserves unitarity and the unitary equivalence class of \(\pi \),
-
\(\pi \mapsto \pi \circ \theta \) preserves irreducibility if \(\theta \) is surjective.
Hence if \(\theta \) is surjective, we have a map
In particular, any automorphism of G induces an automorphism of \(\widehat{G}\), and hence any subgroup of \(\text {Aut}(G)\) acts on \(\widehat{G}\). For instance, the dilations \(\delta _r\), \(r>0\), on a graded Lie group G provide an action of \({\mathbb {R}}^+\) on \({\widehat{G}}\) via
1.3.2 The Fourier Transform
The Fourier transform of an integrable function \(f\in L^1(G)\) at a representation \(\pi \) of G is the operator acting on \({\mathcal {H}}_\pi \) via
Note that \({\mathcal {F}}_G(f)(\pi )\in {\mathcal {L}}({\mathcal {H}}_\pi )\); in this paper, we denote by \({\mathcal {L}}({\mathcal {H}})\) the Banach space of bounded operator on the Hilbert space \({\mathcal {H}}\). Note also that if \(\pi _1,\pi _2\) are two equivalent representations of G with \(\pi _1={\mathbb {U}}^{-1}\circ \pi _2 \circ {\mathbb {U}}\) for some intertwining operator \({\mathbb {U}}\), then
Hence, this defines the measurable field of operators \(\{{{\mathcal {F}}}_G(f)(\pi ), \pi \in \widehat{G}\}\) modulo equivalence. Here, the unitary dual \(\widehat{G}\) is equipped with its natural Borel structure, and the equivalence comes from quotienting the set of irreducible representations of G together with understanding the resulting fields of operators modulo intertwiners.
The Plancherel measure is the unique positive Borel measure \(\mu \) on \({\widehat{G}}\) such that for any \(f\in {{\mathcal {C}}}_c(G)\), we have the Plancherel formula
Here \(\Vert \cdot \Vert _{HS({\mathcal {H}}_\pi )}\) denotes the Hilbert-Schmidt norm on \({\mathcal {H}}_\pi \). This implies that the group Fourier transform extends unitarily from \(L^1(G)\cap L^2(G)\) to \(L^2(G)\) onto \(L^2({\widehat{G}}):=\int _{{\widehat{G}}} {\mathcal {H}}_\pi \otimes {\mathcal {H}}_\pi ^* d\mu (\pi )\) which we identify with the space of \(\mu \)-square integrable fields on \({\widehat{G}}\).
The Plancherel formula also yields an inversion formula for any \( f \in {{\mathcal {S}}}(G)\) and \(x\in G\):
where \(\textrm{Tr}_{{\mathcal {H}}_\pi }\) denotes the trace of operators in \({{\mathcal {L}}}({\mathcal {H}}_\pi )\), the set of bounded linear operators on \({\mathcal {H}}_\pi \). This formula makes sense since, for \(f \in {{\mathcal {S}}}(G)\), the operators \({{\mathcal {F}}}f(\pi )\) are trace-class and \(\int _{{\widehat{G}}} {{\textrm{Tr}}}_{{\mathcal {H}}_\pi } \, \Big | {{\mathcal {F}}}f(\pi ) \Big |d\mu (\pi )\) is finite.
1.3.3 Semiclassical Analysis
For an open set \(U\subset G\), we denote by \({\mathcal {A}}_0(U\times \widehat{G})\) the space of symbols \(\sigma = \{\sigma (x,\pi ) : (x,\pi )\in U\times {\widehat{G}}\}\) of the form
where \(\kappa \in {\mathcal {C}}_c^\infty (U,{\mathcal {S}}( G))\); that is, the map \(x\mapsto \kappa _x\) is compactly supported on U and valued in the set of Schwartz class functions S(G) depending smoothly on \(x\in U\). We call \(x\mapsto \kappa _x\) the convolution kernel of \(\sigma \).
As the Fourier transform is injective, it yields a one-to-one correspondence between \({\mathcal {A}}_0(U\times \widehat{G})\) and \({\mathcal {C}}_c^\infty (U,{\mathcal {S}}( G))\). In this way, \({\mathcal {A}}_0(U\times \widehat{G})\) inherits from \({\mathcal {C}}_c^\infty (U,{\mathcal {S}}( G))\) the structures of topological vector space and smooth compactly supported section of the Schwartz bundle over U. These structures are easier to grasp than being a set of measurable fields of operators on \(U\times \widehat{G}\) modulo intertwiners as described in Sect. 1.3.2. The results of this paper develop a deeper geometric interpretation of the space of symbols, here \({\mathcal {A}}_0(U\times \widehat{G})\), in terms of densities; this will be discussed in Sect. 4.
With the symbol \(\sigma \in {\mathcal {A}}_0(U\times \widehat{G})\), we associate the (family of) semi-classical pseudodifferential operators \(\textrm{Op}_\varepsilon (\sigma )\), \( \varepsilon \in (0,1]\), defined via
or equivalently, in terms of the convolution kernel \(\kappa _x ={\mathcal {F}}^{-1}_G \sigma (x,\cdot )\),
where \(\kappa ^{(\varepsilon )}_x\) is the following rescaling of the convolution kernel:
This second expression for \(\textrm{Op}_\varepsilon (\sigma )\) explains the choice of vocabulary for the convolution kernel of a symbol.
The rescaled convolution kernel is different from the integral kernel of \(\textrm{Op}_\varepsilon (\sigma )\), which is given by:
We emphasize the convolution kernel over the integral kernel, although the latter is used in the pioneer work [11] on pseudodifferential theory on filtered manifolds (see also [12, 13]). The reason is that our approach here is different and aims to be symbolic. It is inspired from semi-classical analysis in Euclidean setting and based on the fact that the symbols obtained via the Fourier transforms of convolution kernels proved a flexible tool for dealing with applications (see [6, 7]).
Our semi-classical pseudodifferential theory may be used to analyze the oscillations of families \((u^\varepsilon )_{\varepsilon >0}\) that are bounded in \(L^2(G)\). One considers the functionals \(\ell _\varepsilon \) defined on \({\mathcal {A}}_0(U\times {\widehat{G}})\) by
The limit points of \(\ell _\varepsilon \) as \(\varepsilon \) goes to 0 have some structures. When the family \((u^\varepsilon )_{\varepsilon >0} \) is \(L^2\)-normalized and after possibly further extraction of subsequences, the limit points of \(\ell _\varepsilon \) define states of the \(C^*\)-algebra \({\mathcal {A}}(U\times {\widehat{G}})\) obtained by completion of \({\mathcal {A}}_0(U\times {\widehat{G}})\) for the norm
For describing the structure of these limit points, we consider the set of pairs \((\gamma ,\Gamma )\) where \(\gamma \) is a positive Radon measure on \(U\times {\widehat{G}}\) and
is a positive \(\gamma \)-measurable field of trace-class operators satisfying
This set is then equipped with the equivalence relation: \((\gamma ,\Gamma ) \sim ( \gamma ',\Gamma ')\) if there exists a measurable function \(f:U\times {\widehat{G}}\rightarrow \mathbb C\setminus \{0\}\) such that
for \(\gamma \)-almost every \((x,\pi )\in U\times {\widehat{G}}\). The equivalence class of \((\gamma ,\Gamma )\) is denoted by \(\Gamma d\gamma \), it is called a positive vector-valued measure. We denote by \({\mathcal {M}}_{ov}^+(U\times {\widehat{G}}) \) the set of these equivalence classes. The positive continuous linear functionals of the \(C^*\)-algebra \({\mathcal {A}}(U\times {\widehat{G}})\) is naturally identified with \({\mathcal {M}}_{ov}^+(U\times {\widehat{G}}) \).
If \((u^\varepsilon )_{\varepsilon >0}\) is a bounded family of \(L^2(U)\), there exist a sequence \((\varepsilon _k)_{k\in {\mathbb {N}}}\) in \((0,+\infty )\) with \(\varepsilon _k\mathop {\longrightarrow }\limits _{k\rightarrow +\infty }0\) and a pair \(\Gamma d\gamma \in {{\mathcal {M}}}_{ov}^+(U\times {\widehat{G}})\) such that we have
Given the sequence \((\varepsilon _k)_{k\in {\mathbb {N}}}\), one has
The positive vector-valued measure \(\Gamma d\gamma \) is called a semi-classical measure of the family \((u^\varepsilon )\) for the sequence \(\varepsilon _k\).
Our aim is to analyze how these notions can be transferred from (an open subset of) a graded group G to another one H via a smooth local diffeomorphism that preserves the filtration of the group.
1.4 Main Result
Let us consider two graded groups, G and H, and a smooth diffeomorphism, \(\Phi \), from an open set U of G to H that is filtration preserving and thus uniformly Pansu differentiable by Theorem 1.5.
We denote by \(J_\Phi \) the Jacobian of \(\Phi \) with respect to Haar measures chosen on G and H, and we consider the operator \(\mathcal {U}_\Phi \) which associates to a function f defined on \(\Phi (U)\subset {H}\) the function
defined on \(U\subset G\). The map \(\mathcal {U}_\Phi \) is a unitary operator from \(L^2(\Phi (U))\) onto \(L^2(U)\).
Conjugation by \(\mathcal {U}_\Phi \) pulls back any \(S\in {\mathcal {L}} (L^2(\Phi (U)))\) to an operator
We want to study the case of \(S=\textrm{Op}_\varepsilon (\sigma )\), \(\sigma \in {\mathcal {A}}_0(\Phi (U)\times \widehat{H})\).
The map \(\Phi \) also induces a transformation \(\mathcal {I}_\Phi \) between convolution kernels. Indeed, for a function \(\kappa :x\mapsto \kappa _x\) in \({\mathcal {C}}_c^\infty (\Phi (U), {\mathcal {S}}(H))\), we associate the function \(\mathcal {I}_\Phi \kappa \) defined via

By Corollary 1.6, \(\mathcal {I}_\Phi \kappa \) is in \({\mathcal {C}}_c^\infty (U, {\mathcal {S}}(G))\) and \(\mathcal {I}_\Phi \) is an isomorphism of topological vector spaces from \({\mathcal {C}}_c^\infty (\Phi (U), {\mathcal {S}}(H))\) onto \({\mathcal {C}}_c^\infty (U, {\mathcal {S}}(G))\). The geometric meaning of this map is discussed in Sect. 4.
By Lemma 1.7, the map

is well-defined. Moreover, it induces an isomorphism of topological vector spaces
defined in the following way: for \(\sigma \in {\mathcal {A}}_0(\Phi (U)\times \widehat{H})\), the symbol \((\widehat{{\mathbb {G}}}\Phi )^*\sigma \) given by

is in \({\mathcal {A}}_0(U\times \widehat{G})\). Indeed, its convolution kernel is \(\mathcal {I}_\Phi \kappa \) when \(\kappa :x\mapsto \kappa _x\) denotes the convolution kernel of \(\sigma \).
Theorem 1.8
Let G and H be two graded groups, and \(\Phi \) a smooth diffeomorphism from an open set U of G to H. Assume that \(\Phi \) is filtration preserving on U (and thus uniformly Pansu differentiable on U). Let \(\sigma \in {\mathcal {A}}_0(\Phi (U)\times \widehat{H})\), then in \({\mathcal {L}}(L^2(U))\),
Note that when we assume that the smooth diffeomorphism \(\Phi \) is uniformly Pansu differentiable on U, this implies that the graded groups G and H are isomorphic (see Corollary 1.6).
Theorem 1.8 is proved in Sect. 3 below. It crucially relies on the Pansu differentiability of filtration preserving maps (see Sect. 2). It also has straightforward consequences on semi-classical measures that we now present. We associate with \(\Phi \) a map from \({\mathcal {M}}^+_{ov}(U\times {\widehat{G}})\) into \({\mathcal {M}}^+_{ov}(\Phi (U)\times {\widehat{H}})\) which maps \(\Gamma d\gamma \in {\mathcal {M}}^+_{ov}(U\times {\widehat{G}})\) on \(\Gamma ^\Phi d\gamma ^\Phi \in {\mathcal {M}}^+_{ov}(\Phi (U)\times {\widehat{H}})\) defined by
Then, the result of Theorem 1.8 implies the next corollary.
Corollary 1.9
Let G and H be two graded groups, and let \(\Phi \) a smooth diffeomorphism from an open set U of G to H. Assume that \(\Phi \) is filtration preserving on U and thus uniformly Pansu differentiable on U. Let \((f^\varepsilon )_{\varepsilon >0}\) be a bounded family in \(L^2(U)\) and \(\Gamma d\gamma \) be a semi-classical measure of \((f^\varepsilon )_{\varepsilon >0}\) for the sequence \(\varepsilon _k\). Then, \(\Gamma ^\Phi d\gamma ^\Phi \) is a semi-classical measure of the family \(\left( \mathcal {U}_\Phi ^* f^\varepsilon \right) _{\varepsilon >0}\) for the sequence \(\varepsilon _k\).
The proof of Theorem 1.8 is developed in Sect. 3 and heavily uses the results of Sect. 2 via Theorem 1.5 and its consequences in Corollary 1.6. Similar results should hold in the microlocal case where no specific scale \(\varepsilon \) is chosen, as developed in [4]. Finally, we develop the geometric interpretation of the convolution kernel in Sect. 4.
2 Filtration Preserving Diffeomorphisms
Our aim in this section is to prove the equivalence between the uniform Pansu differentiability on an open set and the preservation of the filtration above this set, see Theorem 1.5. We will start with introducing some notations and concepts to give a precise meaning to these properties.
2.1 Pansu Differentiability
In this section, we recall basic properties of the Pansu derivative:
Lemma 2.1
Let \(\Phi \) be a map from an open set U of a graded Lie group G to another graded Lie group H.
-
(1)
Let \(x\in U\). If \(\Phi \) is Pansu differentiable at the point x, then the Pansu derivative at x is a 1-homogneous map
 from G to H satisfying
from G to H satisfying  . Moreover, the function \(\Phi \) is continuous at x.
. Moreover, the function \(\Phi \) is continuous at x. -
(2)
If \(\Phi \) is uniformly Pansu differentiable on U, then the Pansu derivative at every point \(x\in U\) is a group morphism from G to H :

Proof
(1) This comes from the definition and the observation that for \(r>0\),
Passing to the limit as \(\varepsilon \) goes to 0, we obtain

Then, fixing a homogeneous quasi-norm on G and using that \(z=\delta _{|z| } \underline{z}\) with \(|\underline{z}|=1\), one writes

Therefore, \(\Phi (x)^{-1} \Phi (xz)\mathop {\longrightarrow }\limits _{|z|\rightarrow 0} 0\), whence the continuity of \(x\mapsto \Phi (x)\).
(2) We write
and use the uniformity of the convergence. \(\square \)
The hypothesis of uniformity for the Pansu differentiability is needed to show that the Pansu derivative is a group morphism [see Part (2) above] but also for the following composition property:
Lemma 2.2
Let F, G, H be three graded Lie groups, let \(\Phi \) be a map from an open set U of G to H, and let \(\Psi \) be a map from an open set \(U'\) of F to G. We assume that \(\Psi (U')\subset U\). If \(\Phi \) and \(\Psi \) are uniformly Pansu differentiable on U and \(U'\) respectively, then their composition \(\Phi \circ \Psi \) is uniformly Pansu differentiable on \(U'\) with

Proof
Write
for (w, z) ranging in a compact subset of \(U'\times F\) and \(\varepsilon \in (0, 1]\). Observe that
By continuity of \(\Phi \), and uniform Pansu differentiability of \(\Psi \), the pair \((\Psi (w), \tilde{z}_\varepsilon )\) ranges in a compact subset of \(\Psi (U')\times G\) on which the map
converges uniformly as \(\varepsilon \rightarrow 0\) (by uniform Pansu differentiability of \(\Phi \)). Since  , the limit of (2.1) as \(\varepsilon \rightarrow 0\) is
, the limit of (2.1) as \(\varepsilon \rightarrow 0\) is  . \(\square \)
. \(\square \)
Remark 2.3
Let us consider a map \(\Phi \) from an open set U of a graded group G to a graded group H such that \(\Phi \) is a bijection from U onto its image \(\Phi (U)\) which is open. If \(\Phi \) and its inverse \(\Phi ^{-1}\) are uniformly Pansu differentiable on U and \(\Phi (U)\) respectively, then we may apply Lemmata 2.1 and 2.2 and use  to obtain
to obtain

In particular, the groups G and H are isomorphic.
2.2 Filtration Preserving Smooth Maps
In this section, we study how to characterize smooth maps that are filtration preserving.
A matrix-valued viewpoint will be helpful for a deeper understanding of Definition 1.1. For a smooth function \(\Phi \) from an open set U of G to H, we denote by \(M_\Phi (x)\) the matrix of \({\mathfrak {d}}_x \Phi \) for the bases
of \({\mathfrak {g}}= \oplus _{j=1}^\infty {\mathfrak {g}}_j \) and \(\mathfrak h = \oplus _{j=1}^\infty {\mathfrak {h}}_j \) adapted to the respective gradations (see Sect. 1.1). This matrix can be written by blocks \(M_{\Phi , i,j}(x)\) associated with the gradation. As the map \({\mathfrak {d}}_x \Phi \) is linear, to identify the blocks \(M_{\Phi ,i,j}(x)\), it is enough to let V vary in \({\mathfrak {g}}_j\) and calculate the projection on \({\mathfrak {h}}_j\) of \(\mathfrak d_x\Phi (V)\). For this, we denote by \(\textrm{pr}_{\mathfrak h,j}\) the projection onto \(\mathfrak h_j\) along \(\oplus _{j'\not = j} \mathfrak h_{j'}\). We may allow ourselves to remove the subscript \(\mathfrak h\) (and write \(\textrm{pr}_{\mathfrak j}\) instead of \(\textrm{pr}_{\mathfrak h,j}\)) when the context is clear.
Let us illustrate this point with the following equivalences.
Lemma 2.4
Let \(\Phi \) be a smooth function from an open set U of G to H, and let \(x\in U\). The following are equivalent:
-
(i)
\(\Phi \) preserves the filtration at x,
-
(ii)
the matrix \(M_\Phi (x)\) defined above is block-upper-diagonal in the sense that all the blocks \(M_{\Phi ,i,j}(x)\), \(i>j\), strictly below the diagonal are 0,
-
(iii)
we have for any \(i>j\)
$$\begin{aligned} \forall \ V\in \mathfrak g_j,\qquad \textrm{pr}_{\mathfrak h,i}( \mathfrak d_x\Phi (V))=0. \end{aligned}$$
We obtain easily the following implication between preserving the filtration and uniform Pansu differentiability.
Lemma 2.5
Let \(\Phi \) be a smooth function from an open set U of G to H, and let \(x\in U\). If \(\Phi \) is Pansu differentiable at x, then \(\Phi \) preserves the filtration at x.
Proof
Let \(V\in \mathfrak g_j\). We have by taking \(t=\varepsilon ^j\) in (1.2),
while the properties of dilations yield
As \(\Phi \) is Pansu differentiable at x, the argument inside \(\textrm{pr}_{\mathfrak h,i}\circ \ln _H\) above has a limit. Hence, if \(i>j\), we have \( \textrm{pr}_{\mathfrak h,i} (\mathfrak d_x\Phi (V))=0\) and we conclude with Lemma 2.4. \(\square \)
In the next sections, we will analyze the reverse implication to the one in Lemma 2.5, using this matrix-valued point of view; this will give Theorem 1.5.
2.3 Characterization of Pansu Differentiability for Smooth Maps
If \(\Phi \) is Pansu differentiable at \(x\in U\), we set

so that we have the following diagram :

This defines the map  . An equivalent definition for this map is given by
. An equivalent definition for this map is given by

for \(V\in \mathfrak g\), having used the shorthand (1.3). Clearly, \(\Phi \) is Pansu differentiable at \(x\in U\) if and only if the limit in (2.2) exists for all \(V\in \mathfrak g\), and it is uniformly Pansu differentiable on U if and only if these limits hold locally uniformly on \(U\times \mathfrak g.\)
The map  may not be linear in general but it will be under mild hypotheses. Indeed, when
may not be linear in general but it will be under mild hypotheses. Indeed, when  is a continuous group morphism, for instance when \(\Phi \) is uniformly Pansu differentiable on an open neighborhood of x, then
is a continuous group morphism, for instance when \(\Phi \) is uniformly Pansu differentiable on an open neighborhood of x, then  is linear with
is linear with

As above, we can adopt a matrix-valued point of view and define  to be the matrix whose columns are the images of \({\mathcal {B}}\) by
to be the matrix whose columns are the images of \({\mathcal {B}}\) by  , that is, the vectors
, that is, the vectors  , \(j=1,\ldots , \dim G\), expressed in the basis \({\mathcal {C}}\). The (rectangular) matrix
, \(j=1,\ldots , \dim G\), expressed in the basis \({\mathcal {C}}\). The (rectangular) matrix  is of the same size as \(M_\Phi (x)\). It makes sense to look at
is of the same size as \(M_\Phi (x)\). It makes sense to look at  and its blocks
and its blocks  associated with the gradation, or rather to the quantities
associated with the gradation, or rather to the quantities  \(V\in \mathfrak g_j\). As a consequence of the definitions of the objects involved and of homogeneous properties, for each \(V\in \mathfrak g_j\) with \(i,j=1,2,\ldots ,\)
\(V\in \mathfrak g_j\). As a consequence of the definitions of the objects involved and of homogeneous properties, for each \(V\in \mathfrak g_j\) with \(i,j=1,2,\ldots ,\)

Actually, very few of the quantities  \(V\in \mathfrak g_j\), are non-zero:
\(V\in \mathfrak g_j\), are non-zero:
Lemma 2.6
Let \(\Phi \) be a smooth function from an open set U of G to H, and let \(x\in U\). We always have (regardless of whether \(\Phi \) is uniformly Pansu differentiable or preserves the filtration) for \(V\in \mathfrak g_j \)
Proof of Lemma 2.6
For each \(x\in U\) and \(V\in \mathfrak g_j\), we have
and the last argument of \(\textrm{pr}_{\mathfrak h,i}\) tends to \(\mathfrak d_x\Phi (V)\) as \(\varepsilon \) goes to 0. \(\square \)
Remark 2.7
-
(1)
By Lemma 2.6 and Eq. (2.3), if \(\Phi \) is Pansu differentiable at x then for each \(V\in \mathfrak g_j\) with \(i,j=1,2,\ldots ,\)

-
(2)
Let us give a matrix interpretation of Part (1). The matrix
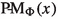 defined above is block-lower-diagonal in the sense that all the blocks
defined above is block-lower-diagonal in the sense that all the blocks  , \(i<j\), strictly above the diagonal are 0. Furthermore, the diagonal blocks coincide with those of \(M_\Phi (x)\). We will see later that one can say more (see Theorem 2.9). This matrix interpretation does not depend on the bases \({\mathcal {B}}\) and \({\mathcal {C}}\) chosen to describe the matrix as long as they are adapted to the gradations.
, \(i<j\), strictly above the diagonal are 0. Furthermore, the diagonal blocks coincide with those of \(M_\Phi (x)\). We will see later that one can say more (see Theorem 2.9). This matrix interpretation does not depend on the bases \({\mathcal {B}}\) and \({\mathcal {C}}\) chosen to describe the matrix as long as they are adapted to the gradations.
The existence of the limits on the left-hand side of (2.3) turns out to also be a sufficient condition for a smooth map to be Pansu differentiable, and thus gives a characterization of smooth Pansu differentiable maps (or at least for \({\mathcal {C}}^k\)-maps for some k large enough).
Proposition 2.8
Let \(\Phi \) be a smooth function from an open set U of G to H. The function \(\Phi \) is uniformly Pansu diffferentiable on U if and only if for each \(x\in U\), \(V\in \mathfrak g_j\), with \(i,j=1,2,\ldots ,\) the limit of
exists as \(\varepsilon \) goes to 0 and, all these limits hold locally uniformly on \(U\times \mathfrak g_j\) for each \(i=1,2,\ldots \)
Proof of Proposition 2.8
We drop the indices of the groups and Lie algebras in the notation for the logarithmic and exponential maps and the projections.
In view of Remark 2.7 (1), it remains to show the reverse implication. Hence, we assume that the limits in (2.4) exist and we aim at proving that for any \(x\in U\), \(V\in \mathfrak g\), \(i=1,2,\ldots \), the limit of \(\textrm{pr}_i \circ \ln _H \delta _{\varepsilon ^{-1}} \left( \Phi _x({\exp }_G(\delta _\varepsilon V))\right) \) exists and that this holds locally uniformly with respect to (x, V) in \(U\times \mathfrak g\). We will prove this recursively on \(i=1,2,\ldots \) First, we need to set some conventions.
Let us recall that the map \(\Theta :{{\mathbb {R}}}^{\dim G} \rightarrow {{\mathbb {R}}}^{\dim G}\) given by the following exponential coordinates of the second kind on \(\mathfrak g\)
is a global diffeomorphism of \({{\mathbb {R}}}^{\dim G}\), and that
We will use the equality
which yields
We will use the star product (1.1) from the Dynkin formula and its properties coming from the gradation property for H via the properties we now describe. Here \(m\ge 2\) is an integer, which will be equal to \(n_G\) below. Consider the star product of m elements \(W_1,\ldots , W_m\) in \(\mathfrak h\) projected onto \(\mathfrak h_i\). This product yields a polynomial map \(\mathfrak h^m\rightarrow \mathfrak h\) whose linear part is the sum \(\textrm{pr}_i (W_1) + \ldots +\textrm{pr}_i (W_m)\). The map \(P_i=P_{i,m} :\mathfrak h^m\rightarrow \mathfrak h\) defined by their difference
is polynomial, valued in \(\mathfrak h_i\) and homogeneous in the sense that
Furthermore, \(P_i\) depends only on the projections of the vectors onto \(\mathfrak h_{j'}\), \(j'<i\). In order to express this technically, for each \(j\in {{\mathbb {N}}}\), we denote by \(\textrm{pr}_{< j} = \textrm{pr}_{1} +\ldots + \textrm{pr}_{j-1}\) the projection onto \(\oplus _{j'< j}\mathfrak h_{j'}\) along \(\oplus _{j' \ge j} \mathfrak h_{j'}\), with the convention \(\textrm{pr}_{<1}:=0\). We have:
Let us come back to (2.5) and set \(m=n_G\). We use a recursive argument and start with \(i=1\); in this case, \(P_1=P_{1,n_G}\) (defined above) is identically zero. Therefore, composing (2.5) with \(\varepsilon ^{-1} \textrm{pr}_1 \circ \ln \) yields the expression
whose limit exists locally uniformly by assumption, see (2.4) for \(i=1\).
The other steps of the recursion are proved in the following manner. At a general recursive step \(i=2,3,\ldots ,\) we have
where
having used the polynomial \(P_i=P_{i, n_G}\) defined above. The properties of \(P_i\) imply
Applying the recursive assumption to each term involving \(\textrm{pr}_{<i}\), the limit of \( \varepsilon ^{-i} Q_{x,i} (\delta _\varepsilon V)\) holds locally uniform as \(\varepsilon \) goes to 0. Therefore, in the expression
the first term on the right-hand side has a locally uniform limit and the other ones too by the hypotheses in (2.4). This shows the i th step and terminates the proof. \(\square \)
2.4 A Refinement on Theorem 1.5
This section is devoted to the statement of the theorem below which implies Theorem 1.5 and Corollary 1.6 but is more technical. It will be shown in Sect. 2.5.
We shall use the following notation: with a subspace \(\mathfrak v\) of \(\mathfrak g\) and an open subset U of G, we associate the open set
and the set
Theorem 2.9
Let \(\Phi \) be a smooth function from an open set U of the graded Lie group G to the graded Lie group H.
-
(i)
The map \(\Phi \) is uniformly Pansu differentiable on U if and only if \(\Phi \) preserves the filtration at every point \(x\in U.\)
-
(ii)
Besides, for such a map \(\Phi \):
-
(1)
The Pansu derivative yields a smooth function
 on \(U\times G\) and the map
on \(U\times G\) and the map  is smooth from U to \(\text {Hom}(G,H)\).
is smooth from U to \(\text {Hom}(G,H)\). -
(2)
For any \(x\in U,\) \(V\in \mathfrak g_j \),

Consequently, the Jacobian \(J_\Phi (x)\) equals the Jacobian of the map
 .
. -
(3)
For any \((x,V)\in U\times \mathfrak g\) and any \(\varepsilon >0\) small enough:

where the function \(\rho \) is valued in \(\mathfrak h\), continuous on \({\mathcal {R}}_{\mathfrak g,U}\) and smooth on the open subset \(\Omega _{\mathfrak g,U}\).
-
(1)
Theorem 1.5 follows from Part (i) while the second part of Corollary 1.6 follows from Part (i) and Remark 2.3. The first Part of Corollary 1.6 is a consequence of Theorem 2.9 (ii) (1).
Before entering into the proof Theorem 2.9, let us give a technical corollary that will be useful in Sect. 3.
Corollary 2.10
Here we fix a homogeneous a quasi-norm \(|\cdot |_G\) on G and we keep the same notation for the function on the underlying Lie algebra \(\mathfrak g\), and similarly for H. We denote by \({\bar{B}}_r\) the corresponding closed balls about 0 of radius \(r>0\).
We continue with the assumptions of Theorem 2.9. We fix a compact subset K of U. Let \(r_0>0\) be so that \(K {\bar{B}}_{r_0}\subset U\). Then there exists a constant \(C>0\) such that for any \((x,V,\varepsilon )\in K\times \mathfrak g \times (0,1]\) satisfying \(\varepsilon |V|_G \le r_0\), we have:
Proof of Corollary 2.10
We set \(V=\delta _{|V|_G} V_0\) and we compute

We deduce
We conclude with the equivalence between homogeneous quasi-norms together with the observation that if \(|\cdot |_G\) denotes the homogeneous quasi-norm given by
then for any \(t\in {{\mathbb {R}}}\) and \(W\in \mathfrak g\), \(|tW|_{G}\le (1+|t|) |W|_G\). \(\square \)
2.5 Proof of Theorem 2.9
2.5.1 A Technical Lemma
The proof of Theorem 2.9 relies on the following property which is of interest on its own, all the more that it holds for any Lie group, not necessarily nilpotent.
Lemma 2.11
Let \(\Phi \) be a smooth function from an open set U of G to H.
-
(1)
For every \(x\in U\) and \(V\in \mathfrak g\), we have for t in a small neighborhood of 0,
$$\begin{aligned} \partial _t \ln _H \circ \Phi _x({\exp _G}(tV) ) = \sum _{p=0}^\infty \, {\widetilde{c}}_{p} \,\textrm{ad}^p\left( \ln _H \Phi _x({\exp _G}(tV) )\right) ( \mathfrak d_{x{\exp _G} (tV)} \Phi (V)), \end{aligned}$$where the coefficients \({\widetilde{c}}_{p}\in {{\mathbb {R}}}\) comes from the Dynkin formula in (1.1). In particular \({\widetilde{c}}_{0}=1\).
-
(2)
We have
$$\begin{aligned} \ln _H \circ \Phi _x({\exp _G}(tV) )|_{t=0}&=0, \\ \partial _{t=0} \ln _H \circ \Phi _x({\exp _G}(tV) )&= \mathfrak d_x \Phi (V), \\ \partial _{t=0}^2 \ln _H \circ \Phi _x({\exp _G}(tV) )&= \partial _{t=0}\mathfrak d_{x{\exp _G}(tV)} \Phi (V), \end{aligned}$$and more generally
$$\begin{aligned}{} & {} \partial _{t=0}^{k+1} \ln _H \circ \Phi _x({\exp _G}(tV) ) \\ {}{} & {} =\partial _{t=0}^{k} \mathfrak d_{x{\exp _G}(tV)} \Phi (V)+\sum _{\begin{array}{c} p,k_2\in {{\mathbb {N}}}\\ p+k_2=k \end{array}} \left( {\begin{array}{c}k_2\\ k\end{array}}\right) {\widetilde{c}}_{p}\, p!\, \textrm{ad}^p ( \mathfrak d_{x} \Phi (V))\partial _{t=0}^{k_2} \mathfrak d_{x{\exp _G}(tV)} \Phi (V) . \end{aligned}$$
Proof
We observe that
where the star product was defined in the introduction [see (1.1)] and
We now apply Dynkin’s formula in (1.1) and notice that since \(Y_0=0\), only two kinds of terms appear. Firstly, there are those with \(\ell \ge 1\), \(s_\ell =1\), \(s_1=\cdots =s_{\ell -1}=0\), \(r_1>0\), ... \(r_{\ell -1}>0\), \(r_\ell \ge 0\). Secondly there are the ones with \(\ell >1\), \(s_\ell =0\), \(s_{\ell -1}=1\), \(s_1=\cdots = s_{\ell -2}=0\), \(r_\ell =1\), \(r_{\ell -1}\ge 0\), \( r_1,\cdots ,r_{\ell -2}>0\). Therefore, the (finite) sum becomes:
Using \(\partial _{u=0}Y_u=\mathfrak d_{x{\exp _G} tV} \Phi (V)\) proves Part 1. Besides, the term \(p=0\) comes from \(n=1\), \(r_1=0\) and \(s_1=1\), whence \({\widetilde{c}}_{0}=c_{0,1}=1\). This shows Part (1).
The first two relations in Part (2) come readily from the definitions of the objects involved. This together with the consequence of Part (1)
implies the rest of Part (2). \(\square \)
2.5.2 Proof of Theorem 2.9
Let us start with the equivalence (i).
Proof of Part (i) in Theorem 2.9
By Lemma 2.5, it suffices to prove the reverse implication: we assume that \(\Phi \) preserves the filtration at every \(x\in U\) and we want to show that it is uniformly Pansu differentiable on U.
Let \(V\in \mathfrak g_j\). By Proposition 2.8, it suffices to show that the limit in (2.4) exists and holds locally uniformly. Here, we will show the existence of the limits as the local uniformity will be a natural consequence of the existence. We only need considering \(j<i\) by Lemma 2.6.
As \(\Phi \) preserves the filtration at every \(x\in U\), by Lemma 2.4, we have in a neighborhood of \(t=0\)
Therefore, differentiating in t, we obtain that in the same neighborhood of \(t=0\)
More precisely, by Lemma 2.4, we also have
and Eq. (2.6) may be generalized into
The latter relation implies that we have for any \(p\in {{\mathbb {N}}}\) and \(\ell =1,2,\ldots \):
The previous fact together with Lemma 2.11 (2) implies for any \(k=2,3,\ldots \)
We now combine these observations with the Taylor expansion of \(t\mapsto \textrm{pr}_{\mathfrak h,i} \circ \ln _H (\Phi _x({\exp _G} (t V )) \) for \(t=\varepsilon ^j\). We push the expansion at a higher order depending on how far j is from i. Indeed, for \(j<i\), we can find an integer \(k\ge 1\) such that \(\frac{i}{k+1}<j< \frac{i}{k-1}\) (with the convention that \(\frac{i}{k-1}=+\infty \) if \(k=1\)) and we push the Taylor expansion up to order k:
By the first part of Lemma 2.11 (2), we have
by (2.6). Therefore, by (2.9), as long as \((k-1)j<i\), we have
This shows the existence of the limits in (2.4) for \(j<i/(k-1)\) such that \(j>i/(k+1)\), and thus recursively for all \(j<i\). Furthermore, one checks easily that they hold locally uniformly, so Part (i) of Theorem 2.9 is proved. \(\square \)
The next points of Theorem 2.9 come from the preceding analysis.
Proof of Part (ii) in Theorem 2.9
Additionally to the limits in (2.4), we have obtained that for any \(V\in \mathfrak g_j\) and \(\textrm{pr}_{\mathfrak h,i}\in \mathfrak h_i\), we have
where the functions \(r_{i,j}\) are valued in \(\mathfrak h_i\), smooth on the open subset \(\Omega _{\mathfrak g_j,U}\) and continuous on \({\mathcal {R}}_{\mathfrak g_j,U}\). This implies Point (2) and that  for any \(j=1,2,\ldots \) Then, the smoothness of
for any \(j=1,2,\ldots \) Then, the smoothness of  stated in Point (1) follows from the Baker-Campbell-Hausdorff formula and the fact that it is a group morphism. Finally, the existence of R in Point (3) follows for general \(V\in \mathfrak g\), using (2.5) and the Baker-Campbell-Hausdorff formula. \(\square \)
stated in Point (1) follows from the Baker-Campbell-Hausdorff formula and the fact that it is a group morphism. Finally, the existence of R in Point (3) follows for general \(V\in \mathfrak g\), using (2.5) and the Baker-Campbell-Hausdorff formula. \(\square \)
3 Invariance of the Semi-classical Calculus on Nilpotent Lie Group
This section is devoted to the proof of Theorem 1.8. We will first recall (see [5, 6]) some properties of the semi-classical calculus that will be useful in the proof.
3.1 \(L^2\)-boundedness in the Semi-classical Calculus
If \(\sigma \in {{\mathcal {A}}}_0(U\times \widehat{G})\), then
and the right-hand side defines the semi-norm \(\Vert \cdot \Vert _{{\mathcal {A}}_0(U\times {\widehat{G}})}\) on \({\mathcal {A}}_0(U\times {\widehat{G}})\). Consequently, the operators \(\textrm{Op}_\varepsilon (\sigma )\) are uniformly bounded on \(L^2(U)\) with bound:
The next lemma shows that the behavior of the integral kernel near the diagonal \(\{(x,x) \ : \ x\in U\}\) in U contains all the information about \(\textrm{Op}_\varepsilon (\sigma )\) at leading order.
Definition 3.1
A cut-off along the diagonal of U is a function \(\chi \in {{\mathcal {C}}}^\infty (U\times U) \) such that for each \(x\in U\), the map \(z\mapsto \chi (x, xz^{-1})\) extends trivially to a smooth function on G that is identically equal to 1 on a neighborhood \(U_1\) of 0 and vanish outside a bounded neighborhood \(U_0\) of 0; moreover, the neighborhoods \(U_1\) and \(U_0\) are assumed to be independent of \(x\in U\). We may call the smallest \(U_0\) the diagonal support of \(\chi \).
For example, if \(\chi _1\in {{\mathcal {C}}}_c^\infty (G)\) is a function equal to 1 close to 0 and with support small enough, then \((x,y)\mapsto \chi _1(xy^{-1})\) is a cut-off along the diagonal of U whose diagonal support is the support of \(\chi \).
Lemma 3.2
Let \(\sigma \in {\mathcal {A}}_0(U\times \widehat{G})\) and let \(\chi \in {{\mathcal {C}}}^\infty (U\times U) \) be a cut-off along the diagonal as introduced in Definition 3.1. Let \(S_\varepsilon \) be the operator with integral kernel
Then, for all \(N\in {{\mathbb {N}}}\), there exists a constant \(C=C_{N,\sigma ,\chi }>0\) such that
Proof
One observes that for all \(N\in {{\mathbb {N}}}\), there exists a bounded function \(\theta \) defined on \(G\times G\) such that, for all \(x,z\in G\)
where \(|\cdot |_G\) is a homogeneous quasi-norm on G. Set \(\widetilde{\kappa }_{x,\varepsilon }(z)= \kappa _x(z) (1-\chi (x,x\delta _\varepsilon z^{-1}))\), then there exists a constant \(c_0>0\) such that
This induces the estimate for the operator \(S_\varepsilon \). \(\square \)
3.2 Proof of Theorem 1.8
Let \(\sigma \in {\mathcal {A}}_0(\Phi (U)\times \widehat{H})\) and denote by \(\kappa :x\mapsto \kappa _x\) its convolution kernel. Set \(\widetilde{\sigma }:= (\widehat{{\mathbb {G}}}\Phi )^*\sigma \in {\mathcal {A}}_0(U\times \widehat{G})\) and denote by \(\widetilde{\kappa }= \mathcal {I}_\Phi \kappa \) its convolution kernel. Note that the x-supports are transported via \(\Phi \):

Let us first proceed to a reduction of the problem using Lemma 3.2. Let \(\chi \in {\mathcal {C}}^\infty (\Phi (U)\times \Phi (U))\) be a cut-off along the diagonal of \(\Phi (U)\). Consider the function \(\widetilde{\chi }\) defined on \(U\times U\) by
Then \(\widetilde{\chi }\) is a cut-off along the diagonal of U.
With the two cut-off functions \(\chi \) and \(\widetilde{\chi }\) in hands, by Lemma 3.2, we can restrict to proving that the operator \(R_\varepsilon \) whose integral kernel is
satisfies \(\Vert R_\varepsilon \Vert _{{\mathcal {L}}(L^2(U))} \le c_0 \,\varepsilon \) for some constant \(c_0>0\).
We observe that the operator \(R_\varepsilon \) may be written in the form
where \(r_{\varepsilon ,x}^{(\varepsilon )} (y) = \varepsilon ^{-Q} r_{\varepsilon ,x}(\delta _\varepsilon ^{-1}y)\) and \(r_{\varepsilon ,x}\) is the function in \({\mathcal {C}}_c^\infty (U, {\mathcal {S}}(G))\) given by

We now aim to prove that
as, by (3.1), this implies \(\Vert R_\varepsilon \Vert _{{\mathcal {L}}(L^2(U))} \le c_0 \varepsilon \).
We observe that the x-support of \(r_{\varepsilon ,x}\) is included in \(K_0\). We may assume that the diagonal support of \(\chi \) is as small as we need below and therefore that the diagonal support of \(\widetilde{\chi }\) is included in a small ball \({\bar{B}}_{r_0}\) of G with a radius \(r_0\) as small as we need; here, we have fixed a homogeneous quasi-norm \(|\cdot |_G\). We can decompose \(I_{\varepsilon } \le I_{1,\varepsilon }+I_{2,\varepsilon }\) with

where
For \(I_{1,\varepsilon }\), we use the Taylor estimates due to Folland and Stein (see [9, Sect. 1.41] or [8, Sect. 3.1.8]): we have for any \(x\in K_0\) and \(z\in \delta _{\varepsilon }^{-1} {\bar{B}}_{r_0}\)
for some compact subset \(K_0'\) of U. Since  , this implies that \(I_{1} \le c_1 \, \varepsilon \) for some constant \(c_1>0\).
, this implies that \(I_{1} \le c_1 \, \varepsilon \) for some constant \(c_1>0\).
For \(I_{2,\varepsilon }\), we apply Theorem 2.9 and Corollary 2.10 with the usual (Euclidean) Taylor estimate to obtain:

for any \(N\in {{\mathbb {N}}}\) and some constant \(D_N>0\), as long as \(x\in K_0\), \(\delta _\varepsilon z^{-1}\in {\bar{B}}_{r_0}\), and \(\varepsilon \in (0,1]\), since \(y\mapsto \kappa _y\in {\mathcal {C}}_c^\infty (U, {\mathcal {S}}(G))\). This implies \(I_2\le c_2 \varepsilon \) for some constant \(c_2>0\), which concludes the proof.
4 Geometric Meaning of the Convolution Kernel
As for the semi-classical calculus in the Euclidean setting, it is important to keep in mind the geometric aspects of the elements that one considers. Indeed, the objects defined using the group Fourier Transform depend on a choice of Haar measure on the graded Lie group G. This makes little difference in the group context, where the Haar measure is determined up to a constant, but will matter more if one wants to extend this non-commutative semi-classical approach on manifolds. In this section, we explain how to avoid choosing a normalization for the Haar measure when defining semi-classical quantization on graded Lie groups. We achieve this by giving a geometrically intrinsic definition of the convolution kernel and thus of the semi-classical symbols.
We will start with well-known geometric considerations and set out their usual conventions. The manifolds (often denoted by M) are assumed to be smooth. If \(F = \cup _{x\in M} F_x\) is a fiber bundle over M, \(\pi _F:F\rightarrow M\) will denote its canonical projection. Here, all the fiber bundles are smooth, and we denote by \(\Gamma (F)\) the space of its smooth sections.
4.1 Generalities on Bundles
Let E be a real vector bundle over a manifold M of rank r.
For \(s\in {\mathbb {R}}^*\), the s-density bundle associated to E is the set \(|\Lambda |^s(E)\) of all maps \(\mu _x: (E_x)^r:=E_x\times \cdots \times E_x\rightarrow {\mathbb {R}} \), for which
When \(E=TM\), we simply write \(|\Lambda |^sM\) for the s-density bundle over M. An s-density \(\mu \) on M is a smooth section of \(|\Lambda |^sM\). When \(s=1\) or \(s=\frac{1}{2}\), we say that \(\mu \) is a density or half-density respectively.
We say that a density \(\mu \) is a positive density when \(\mu _x(v_1, \ldots , v_r)>0\) for all \(x\in M, \, v_i\in E_x\). A nonvanishing n-form \(\omega \) on an open set \(U\subset M\) determines a positive density \(|\omega |\), and identifies s-densities on U with functions via \(\mu =f|\omega |^s\). In particular, an s-density \(\mu \) on M, is written
in local coordinates \((y^i)\).
4.1.1 The canonical \(L^2\) -space
Note that two half-densities determine a 1-density; indeed, given \(u=f\mu ^\frac{1}{2}\) and \(v=g\mu ^\frac{1}{2}\), we have \(uv=fg\mu \). Furthermore, the integral of a 1-density is invariantly defined. Therefore we may define the canonical Hilbert space of half-densities, \(L^2(M)\), as the closure of the set of compactly supported half-densities with respect to
Upon choosing a positive density \(\mu \) on M, we obtain a unitary map between the \(L^2\) space associated to \(\mu \), and the canonical Hilbert space
4.1.2 Densities and mappings
The s-density bundle, \(|\Lambda |^sM\), is a trivial line bundle (though not canonically so), as every smooth manifold has a global positive density. A choice of positive densities \(\mu \) and \(\nu \) on two manifolds M and N respectively allows for the definition of the Jacobian of a smooth map \(\Phi : M\rightarrow N\). Indeed, there exists a positive function \(J_\Phi \) on M, called the Jacobian of \(\Phi \), such that
More generally \(\Phi ^*\left( f\nu ^s \right) =\left( f\circ \Phi \right) J_\Phi ^s\, \mu ^s.\) If in addition, \(\Phi \) is a diffeomorphism, then
where \(\mathcal {U}_\Phi \) is defined as in (1.8) and \(U_\mu \), \(U_\nu \) in (4.1).
4.1.3 Vertical bundles
Consider a fiber bundle \(F = \cup _{x\in M} F_x\) over a manifold M. With \(f\in F\), we associate \(x=\pi _F(f)\) and \(f_x\) the corresponding point in the fiber \(F_x\). The vertical space \({\mathcal {V}}_f(F)\) above a point \(f\in F\) is the tangent space \(T_{f_x} F_x\) to the fiber \(F_x\) at \(f_x\). The resulting vector bundle \({\mathcal {V}}(F) = \cup _{f\in F}{\mathcal {V}}_f(F) \) over F is called the vertical bundle of F; it is given by the kernel of the map \(d\pi _F: TF\rightarrow TM\). Smooth sections of \(|\Lambda |{\mathcal {V}}(F)\) are called vertical densities on F.
Example 4.1
(The vertical bundle of a vector bundle) Suppose \(F=E\) is a vector bundle. Then the vertical space \({\mathcal {V}}_e(E)=T_{e_x} E_x\) above \(e\in E\) (here \(x=\pi _E(e)\)) is naturally identified with \(E_x\). Hence, the vertical bundle \({\mathcal {V}}(E)\) is isomorphic to the pull-back bundle \((\pi _E)^*(E) = \cup _{e\in E} E_{\pi _E(e)}\) of E by the isomorphism of vector bundles \( \text {vert}^E: (\pi _E)^*\left( E\right) \longrightarrow {\mathcal {V}}(E)\):
This example may be generalized to the case of a group bundle:
Example 4.2
(The vertical bundle of a Lie group bundle) Suppose \(F=G=\cup _{x\in M} G_x\) is a Lie group bundle. The vertical space \({{\mathcal {V}}}_{g}(G) = T_{g_x}(G_x)\) above \(g\in G\) (here \(x=\pi _G(g)\)) is naturally isomorphic to the Lie algebra \(\mathfrak g_x\) of the Lie group \(G_x\). Therefore, the vertical bundle \({{\mathcal {V}}}(G)\) is naturally isomorphic to the pull-back bundle \(\cup _{g\in G} {\mathfrak g}_{\pi _G(g)} = (\pi _G)^* (\mathfrak g)\) of the corresponding Lie algebra bundle \({\mathfrak {g}}=\cup _{x\in M} {\mathfrak {g}}_x\). More precisely, the natural isomorphism of vector bundles \( \text {vert}^G: (\pi _{G})^*({\mathfrak {g}})\longrightarrow {\mathcal {V}}(G)\) is given via
4.2 Filtered Manifolds
A filtered manifold is a manifold M equipped with a filtration of the tangent bundle TM by vector bundles
here we are using the convention that \(H^{i} =TM\) for \(i>n_M\). For each \(x\in G\), the quotient
is naturally equipped with a structure of graded Lie algebra, and we denote by \( {\mathbb {G}}_xM\) the corresponding graded Lie group. As explained in [12], the unions
are naturally equipped with a bundle structure that are called the osculating group and Lie algebra bundles over M.
Example 4.3
Equiregular sub-Riemannian manifolds, in particular contact manifolds, are naturally filtered manifolds. Indeed, suppose M is a smooth manifold equipped with a bracket-generating distribution \({\mathcal {D}}\subset TM\). Let \(\Gamma ^1=\Gamma ({\mathcal {D}})\) be the set of smooth sections of \({\mathcal {D}}\), and
As \({\mathcal {D}}\) is bracket generating, there exists i such that \(\Gamma ^i = TM\), and we denote by r the smallest such integer i. If, for every \(i=1, \ldots r\), there exists a subbundle \(H^i\subset TM\) for which \(\Gamma ^i=\Gamma (H^i)\) is the set of smooth sections on \(H^i\), then M is said to have an equiregular sub-Riemannian structure. Clearly, the \(H^i\)’s provide the structure of filtered manifold.
Remark 4.4
Sub-Riemannian (and semi-Riemannian) structures are not in general equiregular. Examples include the Martinet distribution or the Grushin plane. The latter examples also fall outside of the scope of this paper because they are not open subsets of graded Lie groups. An approach to a pseudodifferential calculus on the non-equiregular case is given in [1].
In what follows, it will be helpful to describe a smooth function f on \({\mathbb {G}}M\) by denoting the associated function on the fiber \({\mathbb {G}}_x M\) via
We will thus denote by \({\mathcal {S}}(\mathbb GM):=\cup _{x\in M} {\mathcal {S}}({\mathbb {G}}_xM)\) the (smooth Fréchet) bundle of fiberwise Schwartz functions on the group \({\mathbb {G}}_xM\) over \(x\in M\). The space \(\Gamma _c({\mathcal {S}}({\mathbb {G}}M))\) of compactly supported (smooth) sections of \({\mathcal {S}}({\mathbb {G}}M)\) may be described as the space of smooth function f on \({\mathbb {G}}M\) that are compactly supported in \(x\in M\), and for which the functions \(z_x\mapsto f_x(z_x)\) are Schwartz on \({\mathbb {G}}_xM\) in a way varying smoothly with \(x\in M\).
A morphism of filtered manifolds is a smooth map \(\Phi :M\rightarrow N\) between two filtered manifolds M and N that respects the filtrations. Denoting by \(H^{M,i}\) and \(H^{N,i}\) the vector bundles giving the filtrations of TM and TN respectively, this means that \(d_x\Phi (H_x^{M,i}) \subseteq H_x^{N,i}\) holds at every \(x\in M\) and \(i=0, 1, \ldots \) At every \(x\in M\), we may define a Lie algebra morphism \(\mathfrak G_x \Phi : \mathfrak G_x M \rightarrow \mathfrak G_{\Phi (x)} N\) via
We denote by \({\mathbb {G}}_x \Phi : {\mathbb {G}}_x M \rightarrow \mathbb G_{\Phi (x)} N\) the corresponding group morphism. This induces [12] morphisms between the osculating bundles
that we may call the group and (resp.) Lie algebra osculating maps.
Open sets of graded Lie groups are naturally equipped with a structure of filtered manifolds. The next statement summarizes the main results in Sect. 2:
Lemma 4.5
Let \(\Phi :U\rightarrow H\) be a smooth map from an open set U of a graded group G to a graded group H. The following are equivalent:
-
\(\Phi \) preserves the filtration in the sense of Definition 1.1,
-
\(\Phi \) is locally uniformly Pansu differentiable on U in the sense of Definition 1.3,
-
\(\Phi :U\rightarrow H\) is a morphism of filtered manifolds (as explained above).
Moreover, in this case, the Pansu derivative and the osculating map coincide at every \(x\in U\):

4.3 Densities on Filtered Manifolds
Let M be a filtered manifold.
4.3.1 Haar System
Let us fix a smooth Haar system \(\{\mu _x\}_{x\in M}\) for \({\mathbb {G}}M\), that is, a choice of Haar measure \(\mu _x\) for each of the group fibers \({\mathbb {G}}_xM\) for which
A Haar measure \(\mu _x\) on the group fiber \({\mathbb {G}}_xM\) naturally identifies with a left-invariant density, which we also call \(\mu _x\), on \({\mathbb {G}}_xM\). By left-invariance, each \(\mu _x\) corresponds to a positive element of the one-dimensional vector space \(|\Lambda |\mathfrak {G}_xM\). Indeed, smooth Haar systems for \({\mathbb {G}}M\) correspond in this way to smooth positive sections of \(|\Lambda |\mathfrak {G}M\), which we call Haar densities on M.
4.3.2 Vertical Densities
As in Examples 4.1 and 4.2, the vertical space \({{\mathcal {V}}}_z ( {{\mathbb {G}}}M) = T_{z_x} {{\mathbb {G}}}_xM \) above \(z\in {{\mathbb {G}}}M\) with \(x=\pi _{{{\mathbb {G}}}M}(z)\in M\) identifies naturally with the Lie algebra \(\mathfrak G_xM\). Hence, the vertical bundle \({{\mathcal {V}}}({{\mathbb {G}}}M) \) is naturally isomorphic to the pullback bundle \( (\pi _{{\mathbb {G}}M})^* (\mathfrak {G}M )\) of the osculating Lie algebra bundle. More precisely, the natural isomorphism of vector bundles
is given via:
This isomorphism allows us to lift densities \(x\mapsto \mu _x\) in \(|\Lambda |\mathfrak GM\) to vertical densities \(z\mapsto \check{\mu }_z\) via
This lift yields a map of sections: \( \Gamma \left( |\Lambda |\mathfrak {G}M\right) \rightarrow \Gamma \left( |\Lambda |{\mathcal {V}}({\mathbb {G}}M)\right) \). We shall subsequently blur the distinction between a Haar density on M, its lift to a vertical density on \({\mathbb {G}}M\), and a smooth Haar system on \({\mathbb {G}}M\).
4.3.3 Haar System and Smooth Functions on \({\mathbb {G}}M\)
With respect to a smooth Haar system \(\{\mu _x\}_{x\in M}\) on M, any smooth function \(\widetilde{\kappa }\) on \({\mathbb {G}}M\) yields the vertical density
Conversely, as \(\dim (|\Lambda |\mathfrak {G}_xM) =1\) at every \(x\in M\), any vertical density \(\kappa \) on \({\mathbb {G}}M\) may be written as in (4.2) for a unique smooth function \(\widetilde{\kappa }\) on \({\mathbb {G}}M\). This defines an isomorphism of topological vector spaces
In the next paragraph, we will use the (smooth Fréchet) bundle \({\mathcal {S}}({\mathbb {G}}M, |\Lambda |{\mathcal {V}})\) of fiberwise Schwartz densities; that is, the collection \(\{\kappa _x: z_x\mapsto \kappa _x(z_x)\}_{x\in M}\) of densities on the fibers \({\mathbb {G}}_xM\) for which the function \(z_x\mapsto \tilde{\kappa }(z_x)\) is Schwartz.
4.3.4 Schwartz Vertical Densities
A vertical density \(\kappa \) is said to be a Schwartz vertical density when the corresponding function \(\widetilde{\kappa }\in C^\infty (\mathbb GM)\) from (4.2) is in \(\Gamma _c({\mathcal {S}}({\mathbb {G}}M))\). Although this definition requires the choice of a smooth Haar system \(\mu =\{\mu _x\}_{x\in M}\) on M, the resulting property is independent of \(\mu \) as the x-support of \( x\mapsto \kappa _x\) is assumed to be compact. We denote by \(\Gamma _c({\mathcal {S}}({\mathbb {G}}M, |\Lambda |{\mathcal {V}}))\) the space of vertical Schwartz densities (compactly supported over M). Although these spaces are independent of the choice of Haar system, fixing such a Haar system \(\mu \) establishes an identification between \(\Gamma _c({\mathcal {S}}({\mathbb {G}}M))\) and \(\Gamma _c({\mathcal {S}}({\mathbb {G}}M, |\Lambda |{\mathcal {V}}))\) via the isomorphism of topological vector spaces:
4.4 Convolution Kernels and Semi-classical Symbols as Geometric Items
4.4.1 Convolution Kernels as Vertical Schwartz Densities
We start with the following general observation:
Lemma 4.6
Let \({\mathbb {F}}: {\mathbb {G}}M\rightarrow {\mathbb {G}}N\) be a smooth map. Assume that \({\mathbb {F}}_x:{\mathbb {G}}_xM\rightarrow {\mathbb {G}}_yN\) (with \(y=\pi _{{\mathbb {G}}N}({\mathbb {F}}(z_x)\)) is a group morphism for each \(x\in M\). Then, the differential of \({\mathbb {F}}\) preserves the vertical bundles:
Proof
For each \(z\in \mathbb GM\) and \(V\in \mathfrak {G}_xM\) with \(x=\pi _{\mathbb GM} (z)\), we have:
where \(\mathfrak {F}_x(V):=\frac{d}{dt}\big |_{t=0}{\mathbb {F}}_x\left( \exp _{{\mathbb {G}}_xM}(tV)\right) \). \(\square \)
Given a map \({\mathbb {F}}\) as in Lemma 4.6, we may now define the pullback of a vertical density \(\nu \) on \({\mathbb {G}}N\) to a vertical density \({\mathbb {F}}^*\nu \) on \({\mathbb {G}}M\) via
If in addition \({\mathbb {F}}\) is a diffeomorphism (and hence an isomorphism of filtered manifold), the pushforward is defined by \({\mathbb {F}}_*:=({\mathbb {F}}^{-1})^*\).
Given a morphism of filtered manifolds \(\Phi : M\rightarrow N\), we may apply the above to \({\mathbb {F}}={\mathbb {G}}\Phi \) the osculating map, and define the pullback \(({\mathbb {G}}\Phi )^*\nu \) of a vertical density \(\nu \) on \({\mathbb {G}}N\) to \({\mathbb {G}}M\). If \(\Phi \) is in addition a diffeomorphism, the pushforward yields the following isomorphism of topological vector spaces:
If \(\mu \) and \(\nu \) are vertical densities on M and N respectively, we define the operator
Lemma 4.7
Assume M and N are open subsets of graded Lie groups G and H (resp.). If \(\Phi :M \rightarrow N\) is a diffeomorphism that preserves the filtrations of the group, then it is an isomorphism of filtered manifolds and the map \({\mathcal {I}}_\Phi \) agrees with (1.9).
This result shows that convolution kernels have the geometric structure of vertical Schwartz densities.
Lemma 4.7 motivates \(\Gamma _c\left( {\mathcal {S}}\left( {\mathbb {G}}M, |\Lambda |{\mathcal {V}}\right) \right) \) as the geometric space of convolution kernels for future study of semi-classical pseudodifferential operators on filtered manifolds. It is also interesting to notice that setting \( \kappa ^{(\varepsilon )}:=\left( \delta _\varepsilon \right) _*\kappa \), we have for any smooth Haar system, by homogeneity of Haar measures on graded Lie groups,
where Q is the (constant) homogeneous dimension of the group fibers of \({\mathbb {G}}M\).
Proof of Lemma 4.7
Let G and H be graded Lie groups. We may assume that both groups are modeled on \({\mathbb {R}}^n\), in which case the Lebesgue measure |dz| is a Haar measure for both. If U is an open subset of G, then
and similarly for any open subset of H. With these identifications, the vertical lift of |dz| on \(U\subset G\) to \(|\Lambda |{\mathcal {V}}({\mathbb {G}}U)\) is also written |dz|. By (4.2), any vertical density \(\kappa \) on H has the form
Suppose \(\Phi : U\subset G \rightarrow \Phi (U)\subset H\) is a filtration-preserving diffeomorphism from the open subset \(U\subset G\) to \(\Phi (U)\subset H\). By Lemma 4.5, we have  for any \(z\in {\mathbb {G}}_xU=G\), so
for any \(z\in {\mathbb {G}}_xU=G\), so

Therefore, vertical Schwartz densities on groups transform according to (1.9). \(\square \)
4.4.2 Towards a Set of Semi-classical Symbols on Filtered Manifolds
The fiberwise Fourier transform of \(\kappa \in \Gamma _c\left( {\mathcal {S}}({\mathbb {G}}M, |\Lambda |{\mathcal {V}})\right) \) is defined as
Here \(\widehat{{\mathbb {G}}}_xM\) is the unitary dual to the group fiber \({\mathbb {G}}_xM\) (note that this does not require a choice of Haar system). Then, a natural candidate for the set of semi-classical symbols on M is the image of \(\Gamma _c\left( {\mathcal {S}}({\mathbb {G}}M, |\Lambda |{\mathcal {V}})\right) \) by \({\mathcal {F}}\); we denote it by \({\mathcal {A}}_0(\widehat{{\mathbb {G}}} M)\). Elements of this space are fields of operators on \(\widehat{{\mathbb {G}}} M:=\cup _{x\in M}\widehat{{\mathbb {G}}}_xM\) (modulo intertwiners). In the case where M is an open subset of a graded group G, \({\mathcal {A}}_0(\widehat{{\mathbb {G}}} M)\) coincides with the set \({\mathcal {A}}_0(U\times {\widehat{G}})\) of Sect. 1.3.3.
Given an isomorphism \(\Phi :M\rightarrow N\) of filtered manifolds, the operator defined by
is a generalization of (1.10). Besides, for \(\kappa \in \Gamma _c\left( {\mathcal {S}}({\mathbb {G}}N, |\Lambda |{\mathcal {V}})\right) \) and \(\sigma (x, \pi )={\mathcal {F}}(\kappa )(x, \pi )\) we have
So when M and N are open subsets of graded Lie groups, we are left with (1.11) and the geometric frame is consistent.
References
Androulidakis, I., Mohsen, O., Yuncken, R.: A pseudodifferential calculus for maximally hypoelliptic operators and the Helffer-Nourrigat conjecture. (2022). arXiv preprint arXiv:2201.12060
Bahouri, H., Fermanian-Kammerer, C., Gallagher, I.: Phase space analysis on the Heisenberg group. Astérisque, 345 , 1032–1033 (2012)
Bernard, H.: 30 ans d’analyse semi-classique: bibliographie commentée. https://www.imo.universite-paris-saclay.fr/~helffer/histoire2003.ps
Fermanian-Kammerer, C., Fischer, V.: Defect measures on graded lie groups. Ann. Sc. Norm. Super. Pisa. 21–5, 207–291 (2020)
Fermanian-Kammerer, C., Fischer, V.: Semi-classical analysis on H-type groups. Sci. China Math. 62(6), 1057–1086 (2019)
Fermanian-Kammerer, C., Fischer, V.: Quantum evolution and sub-laplacian operators on groups of Heisenberg type. J. Spectr. Theory 11(3), 1313–1367 (2021)
Fermanian-Kammerer, C., Letrouit, C.: Observability and controllability for the Schroedinger equation on quotients of groups of Heisenberg type, hal:295166262. Journal de l’École Polytechnique, Math 8, 1459–1513 (2021)
Fischer, V., Ruzansky, M.: Quantization on nilpotent Lie groups, Progress in Mathematics, 314, Birkhäuser Basel, (2016)
Folland, G.B., Stein, E.: Hardy spaces on homogeneous groups, Mathematical Notes, 28. Princeton University Press, Princeton (1982)
Pansu, P.: Métriques de Carnot-Carathéodory et quasi-isométries des espaces symétriques de rang un. Ann. Math. Second Ser. 129(1), 1–60 (1989)
Van Erp, E.: The Atiyah-Singer index formula for subelliptic operators on contact manifolds. Part I. Ann. Math. 171, 1647–1681 (2010)
Van Erp, E., Yuncken, R.: On the tangent groupoid of a filtered manifold. Bull. Lond. Math. Soc. 49(6), 1000–1012 (2017)
Van Erp, E., Yuncken, R.: A groupoid approach to pseudodifferential operators. Crelle’s J. 759, 151–182 (2019)
Warhust, B.: Contact and Pansu differentiable maps on Carnot groups. Bull. Austral. Math. Soc. 77, 495–507 (2008)
Zworski, M.: Semiclassical analysis. In: Graduate studies in mathematics, vol. 138. American Mathematical Society, Providence (2012)
Acknowledgements
The authors thank Antoine Julia and Pierre Pansu for inspiring discussions. The authors acknowledge the support of The Leverhulme Trust for this work via Research Project Grant 2020-037, Quantum limits for sub-elliptic operators.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kammerer, C.F., Fischer, V. & Flynn, S. Geometric Invariance of the Semi-classical Calculus on Nilpotent Graded Lie Groups. J Geom Anal 33, 127 (2023). https://doi.org/10.1007/s12220-022-01163-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12220-022-01163-z
Keywords
- Analysis on nilpotent Lie groups
- Semi-classical analysis on nilpotent Lie groups and on filtered manifolds
- Abstract harmonic analysis




 (resp.
(resp. 
 from G to H satisfying
from G to H satisfying  . Moreover, the function
. Moreover, the function 

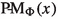 defined above is block-lower-diagonal in the sense that all the blocks
defined above is block-lower-diagonal in the sense that all the blocks  ,
,  on
on  is smooth from U to
is smooth from U to 
 .
.