Abstract
It is known that the study of the boundary behavior of (harmonic or) holomorphic functions, to which N. Sibony has contributed with penetrating work, is linked to the differentiation of integrals. In 1936, R. de Possel observed that, in the general setting of a measure space with no metric structure, certain phenomena, relative to the differentiation of integrals, which are familiar in the Euclidean setting precisely because of the presence of a metric, are devoid of actual meaning. In the first part of this work, we introduce the concept of functional convergence class that provides a unifying framework for various limiting processes and enables us to establish a hierarchy between them, and show that, within this hierarchy, the notion of filter (introduced by H. Cartan just a year after De Possel’s contribution) occupies the position of wider scope. In the second part of this work, we show how to reformulate some of the contributions of de Possel in the language of filters.
Similar content being viewed by others
1 Introduction
In 1936, R. de Possel observed that, in the general setting of a measure space with no metric structure, certain phenomena, relative to the differentiation of integrals, which are familiar in the Euclidean setting precisely because of the presence of a metric, are devoid of actual meaning. In his work, de Possel introduced an axiomatic approach based on a limiting process centered on the preliminary choice of certain sequences of sets. The notion of filter, due to Cartan [8], appeared 1 year after de Possel’s work, and yields another limiting process, which, in the context of the problem of the differentiation of integrals, turns out to be preferable, for specific reasons that will be outlined momentarily.
The purpose of this paper is, first of all, to show that the language of filters yields a notion of limiting process that has wider scope, with respect to other limiting processes. On the basis of this preliminary groundwork, we show how to reinterpret in the language of filters some of the contributions given by de Possel to the problem of the differentiation of integrals in measure spaces.
In order to achieve the first goal, we introduce the concept of functional convergence class and systematize the results on convergence along filters by using a topology on the space of all filters. Moreover, we present a self-contained and fairly complete treatment of the notions centered around the relation between filters and Moore–Smith sequences, encompassing various results not all of which appear to be known, or as well known as they ought to be.
1.1 Background
Let \({{\,\mathrm{{X}}\,}}\equiv ({{\,\mathrm{{X}}\,}},{\mathcal {M}},\omega )\) be a measure space, where \(\omega \) is a measure defined on a \(\sigma \)-algebra \({\mathcal {M}}\) of subsets of \({{\,\mathrm{{X}}\,}}\). The vector space of measurable real-valued functions defined a.e. on \({{\,\mathrm{{X}}\,}}\), whose p th-power is integrable (\(p>0\)), is denoted by \({\mathcal {L}}^p({{\,\mathrm{{X}}\,}})\). The quotient of \({\mathcal {L}}^p({{\,\mathrm{{X}}\,}})\) under a.e. equality is denoted by \({{\,\mathrm{L}\,}}^{p}({{\,\mathrm{{X}}\,}})\). The corresponding projection
maps \(f\in {\mathcal {L}}^p({{\,\mathrm{{X}}\,}})\) to the class of functions which are a.e. equal to \(f\). We denote this class by \({\varvec{f}}\) (in bold font), and say that \(f\in {\mathcal {L}}^p({{\,\mathrm{{X}}\,}})\) is a representative of \({\varvec{f}}\in {{\,\mathrm{L}\,}}^{p}({{\,\mathrm{{X}}\,}})\). The spaces \({\mathcal {L}}^{\infty }({{\,\mathrm{{X}}\,}})\) and \({{\,\mathrm{L}\,}}^{\infty }({{\,\mathrm{{X}}\,}})\) are also defined in the familiar way [29, p. 244].
Similarly, the quotient of \({\mathcal {M}}\) under a.e. equality of measurable sets is denoted by \({{\,\mathrm{M}\,}}\) and is called the measure algebra of \(({{\,\mathrm{{X}}\,}},{\mathcal {M}},\omega )\). The corresponding projection
is called the canonical projection associated to \(({{\,\mathrm{{X}}\,}},{\mathcal {M}},\omega )\), and is a homomorphism of Boolean algebras.
1.1.1 The Mean-Value Operator
Consider the subcollection of \({\mathcal {M}}\) defined as follows:
The sets in (1.2) are called averageable, since for each \({\varvec{f}}\in {{\,\mathrm{L}\,}}^{1}({{\,\mathrm{{X}}\,}})\) and \(Q\in {{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}})\) the mean-value of \({\varvec{f}}\) over \(Q\) may be defined in the familiar way, as follows:
(where \(f\in {\mathcal {L}}^1({{\,\mathrm{{X}}\,}})\) is any representative of \({\varvec{f}}\)). Hence (1.3) defines a function
The mean-value operator for \(({{\,\mathrm{{X}}\,}},{\mathcal {M}},\omega )\) is the linear operator:
defined by
where \(\texttt {hom}_{\texttt {Set}}({{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}}),{{\mathbb {R}}})\) is the collection of all functions from \({{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}})\) to \({{\mathbb {R}}}\). If \(S\subset Q\) then
is the indicator function of S: \({\mathbb {1}}_{S}(x)=1\) if \(x\in {}S\) and \({\mathbb {1}}_{S}(x)=0\) otherwise. Recall that the vertical bar notation is well established in probability theory to denote conditional expectation, of which (1.3) is a particular case. Indeed, if \(f\) is the indicator function of \(R\in {{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}})\), i.e., \(f={\mathbb {1}}_{R}\), then \({\mathbb {1}}_{R}\in {\mathcal {L}}^1({{\,\mathrm{{X}}\,}})\) and instead of \({\left( {\mathbb {1}}_{R}\right) }_{\!\omega }[Q]\) we write \({{\widetilde{\omega }}}\left( R|Q\right) \). Hence
1.1.2 The Problem of the Differentiation of Integrals
The following preliminary observation will help us make a precise statement of the problem.
- (i):
-
The function
$$\begin{aligned} {{\varvec{f}}}_{\!\omega }\in \texttt {hom}_{\texttt {Set}}({{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}}),{{\mathbb {R}}}) \end{aligned}$$(1.6)defined in (1.3) encodes all the mean-values of \({\varvec{f}}\).
- (ii):
-
The Radon–Nykodim theorem says that \({\varvec{f}}\) is uniquely determined by \({{\varvec{f}}}_{\!\omega }\) [29, p. 238].
Observe that \({{\varvec{f}}}_{\!\omega }:{{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}})\rightarrow {{\mathbb {R}}}\) is a bona fide function, defined on \({{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}})\), while \({\varvec{f}}\) is an equivalence class of functions, and that the values \(f(x)\) of a representative of \({\varvec{f}}\) may be recovered only up to a set of measure zero (called the exceptional set of \({\varvec{f}}\)).
The problem of the differentiation of integrals may be described in the following terms:
Find a limiting process that enables us to recapture (a representative of) \({\varvec{f}}\in {{\,\mathrm{L}\,}}^{1}({{\,\mathrm{{X}}\,}})\) from \({{\varvec{f}}}_{\!\omega }\) (i.e., from the mean-values of \({\varvec{f}}\)).
Observe that the notion of limiting process appears in the formulation of the problem in an informal fashion. One of the goals of the present paper is to establish a formal framework for the concept of “limiting process”: This will be achieved by means of the notion of functional convergence class. Another goal, subordinate to the first one, is to identify, within this framework, the notion of limiting process that has wider scope: We will show that the concept of filter has precisely this property.
A solution to the problem of the differentiation of integrals is called a Generalized Lebesgue Differentiation Theorem. Indeed, the Lebesgue differentiation theorem solves the problem of the differentiation of integrals in the case \({{\,\mathrm{{X}}\,}}=({{\mathbb {R}}},{\mathcal {M}},\omega )\), where \(\omega \) is Lebesgue measure and \({\mathcal {M}}\) is the \(\sigma \)-algebra of Lebesgue-measurable subsets of \({{\mathbb {R}}}\), and says that, if \(f\in {\mathcal {L}}^1({{\mathbb {R}}})\), then, for a.e. \(x\in {{\mathbb {R}}}\), its value \(f(x)\) is approximately equal to the mean-value of \(f\) over balls which are, in a certain sense, “close to” x. The prototype result is that, for a.e. \(x\in {{\mathbb {R}}}\),
where \(I_{x}(r)\) is the open interval in \({{\mathbb {R}}}\) of center x and radius r. Observe that the limiting process used in (1.7), to which the function \({{\varvec{f}}}_{\!\omega }\) is subject, rests on the metric structure of \({{\mathbb {R}}}\).
Lebesgue himself has given deep generalizations of his one-dimensional results to higher-dimensional Euclidean space \({{\mathbb {R}}}^n\), where he considered mean-values \({{\varvec{f}}}_{\!\omega }[B]\) of \({\varvec{f}}\) over balls \(B\subset {{\mathbb {R}}}^n\) which are not centered at x, or even balls which do not contain the point x, provided the balls B get “close to” x in a certain manner (which may be described as being of a “nontangential” nature; see [33]). Once more, the metric structure of the ambient space is used to obtain a “limiting value” from the function \({{\varvec{f}}}_{\!\omega }\in \texttt {hom}_{\texttt {Set}}({{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}}),{{\mathbb {R}}})\) defined in (1.3).
In order to achieve his results, Lebesgue had to solve two problems. Firstly, he had to describe what it means for a ball to be “close to” the point x. Secondly, he had to understand which manners of approach of balls to x are compatible with the intended convergence result. The first task, in the context of a metric measure space, such as \({{\mathbb {R}}}^n\), is indeed not a difficult one, since the metric itself, which is used to define the balls, endows the collection of all its nonempty subsets with a pseudometric: The Hausdorff pseudometric. Indeed, in this context, we may say that a sequence
converges to a point \(x\in {{\,\mathrm{{X}}\,}}\) if, for each ball \(B_{x}(r)\) of center x and radius \(r>0\), the set \(\varvec{Q}(n)\) is eventually contained in \(B_{x}(r)\). A similar approach may be adapted, at least in principle, in the context of a topological measure space \(({{\,\mathrm{{X}}\,}}, {\mathcal {M}}, \omega ,\Theta )\) (where \(\omega \) is the measure, defined on a \(\sigma \)-algebra \({\mathcal {M}}\) of subsets of \({{\,\mathrm{{X}}\,}}\), and \(\Theta \) is a topology with \(\Theta \subset {\mathcal {M}}\)).
1.1.3 René de Possel’s Approach
If \(({{\,\mathrm{{X}}\,}}, {\mathcal {M}}, \omega )\) is a measure space with no further structure, then, although it makes sense to consider mean values, as in (1.3), it does not seem possible to define, in this degree of generality, what it means for a sequence \(\varvec{Q}:{\mathbb {N}}\rightarrow {{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}})\) to converge to a point x, especially if the sets \(\varvec{Q}(n)\) are not assumed to contain x. This difficulty was perceived already in 1936 by René de Possel, who observed that only some of the main properties of Lebesgue measure admit d’une manière évidente (in evident ways) an extension to the case of an arbitrary measure space, but others semblent perdre toute signification dès que l’espace n’est plus métrique (appear to lose their meaning as soon as the space is not metric) [9]. Among the latter, he listed the properties related to differentiation of integrals.
It is useful to present the particular solution devised by de Possel in the context of the general underlying problem, which may be formulated by replacing the space \({{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}})\) with a generic set \({{\,\mathrm{{A}}\,}}\) with no further structure. If \(\texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\) denotes the collection of all functions from \({{\,\mathrm{{A}}\,}}\) to \({{\mathbb {R}}}\), then the general underlying problem is that of finding the limiting processes to the which the elements \(\varphi \) of \(\texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\) may be subjected, which yield as a result a “limiting value” \(y\in {{\mathbb {R}}}\) and enable us to write

(where
 denotes the limiting process). Formally, whatever “limiting process” we may be able to devise, its end result is the selection of a collection \({\mathcal {F}}\) of pairs \((y,\varphi )\in {{{\mathbb {R}}}}\times \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\), where
denotes the limiting process). Formally, whatever “limiting process” we may be able to devise, its end result is the selection of a collection \({\mathcal {F}}\) of pairs \((y,\varphi )\in {{{\mathbb {R}}}}\times \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\), where
The particular limiting process devised by de Possel is based on the choice of a nonempty subset V of the collection \(\texttt {hom}_{\texttt {Set}}({\mathbb {N}},{{\,\mathrm{{A}}\,}})\) of all \({{\,\mathrm{{A}}\,}}\)-valued sequences, i.e.,
The limiting process associated to the choice of V in (1.10) is then a natural one: to wit, it is the convergence of \(\varphi \) to \(y\) along each sequence \({\varvec{q}}\) in the collection, i.e.,
The application of this limiting process to the case where \({{\,\mathrm{{A}}\,}}={{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}})\) led de Possel to adopt an axiomatic approach based on the preliminary choice of a function \({\mathcal {V}}\) of the following form:
where \(\texttt {hom}_{\texttt {Set}}({\mathbb {N}},{{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}}))\) is the collection of all \({{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}})\)-valued sequences, with the understanding that the sequences in the collection \({\mathcal {V}}(x)\) are axiomatically assumed to be “convergent” to a given point \(x\in {{\,\mathrm{{X}}\,}}\). In this set-up, de Possel had to solve the following problem: specify conditions on the function \({\mathcal {V}}\) in (1.12) which ensure that
for each \({\varvec{f}}\in \varvec{{\mathcal {R}}}\), where \(\varvec{{\mathcal {R}}}\subset {{\,\mathrm{L}\,}}^{1}({{\,\mathrm{{X}}\,}})\) is a specified class of functions, and a.e. \(x\in {{\,\mathrm{{X}}\,}}\).
1.1.4 Notation from Category Theory
We find it convenient to adapt to our needs the notation from category theory employed in [17], and, whenever it is helpful, we append to an object or a morphism a subscript that specifies in which category it is located. Hence if \(\texttt {C}\) is a given category, we denote by \(\texttt {hom}_{\texttt {C}}(A,Z)\) the collection of morphisms in \(\texttt {C}\) from A to Z. For example, \(\texttt {hom}_{\texttt {Set}}(A,Z)\) [resp. \(\texttt {hom}_{\texttt {BA}}(A,Z)\)] denotes the collection of functions from a set A to a set Z (resp. the collection of Boolean algebra homomorphisms between Boolean algebras A and Z). Moreover, this subscript device will be used as a shorthand for the so-called forgetful functors. For example, if \({{\,\mathrm{{A}}\,}}\) is a topological space, then \({{\,\mathrm{{A}}\,}}_{\texttt {Set}}\) denotes the underlying set. However, we will depart from strict observance of these notational devices whenever they lead to unnecessary notational clutter. For example, we find it useful to write, with a slight abuse of notation, \(\texttt {hom}_{\texttt {Set}}(A,Z)\) instead of \(\texttt {hom}_{\texttt {Set}}(A_{\texttt {Set}},Z_{\texttt {Set}})\), whenever A and Z are objects in some concrete category [recall that an object \(A\equiv (A_{\texttt {Set}},S_{A})\) in a concrete category is a set \(A_{\texttt {Set}}\), called the underlying set, endowed with additional structure \(S_{A}\)]. In the same vein, whenever the precise meaning can be gathered from context, the same symbol will denote an object in a concrete category or its underlying set.
1.2 Foundational Results
The limiting process adopted by de Possel is but one of many that have been conceived. We have already observed that every “limiting process” (1.8) yields, via (1.9), a relation between \({{\mathbb {R}}}\) and \(\texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\), i.e., a subset
1.2.1 Functional Convergence Classes
The first contribution of the present paper is the introduction of a set of axioms which describe the properties which a relation \({\mathcal {F}}\) between \({{\mathbb {R}}}\) and \(\texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\) should satisfy in order to be the outcome of some “reasonable” limiting process which acts, so to say, in the “background.” Indeed, one would hardly expect that every relation \({\mathcal {F}}\) between \({{\mathbb {R}}}\) and \(\texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\) as in (1.14) will be of interest.
A relation \({\mathcal {F}}\) between \({{\mathbb {R}}}\) and \(\texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\) is called a functional convergence class if it has some specific, natural properties, encoded in certain axioms, that will be described momentarily. As far as we know, the notion of functional convergence class is new, although it is inspired by the notion of convergence class [18, p. 73], which has, however, a different character.
The output of a limiting process for real-valued functions is a subset
i.e., a collection of pairs \((y,\varphi )\in {{{\mathbb {R}}}}\times \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\), where \((y,\varphi )\in {\mathcal {F}}\) precisely if  according to the limiting process acting on the background and encoded in \({\mathcal {F}}\). The aim of the abstract notion of functional convergence class is precisely to recapture the natural properties that are expected from \({\mathcal {F}}\).
according to the limiting process acting on the background and encoded in \({\mathcal {F}}\). The aim of the abstract notion of functional convergence class is precisely to recapture the natural properties that are expected from \({\mathcal {F}}\).
The Filter of Neighborhoods of a Point in a Topological Space
Let \({{\,\mathrm{{A}}\,}}\) be a topological space. If \(x\in {{\,\mathrm{{A}}\,}}\), a neighborhood of \(x\) in \({{\,\mathrm{{A}}\,}}\) is a subset of \({{\,\mathrm{{A}}\,}}\) which contains an open set containing \(x\). The set of all neighborhoods of \(x\) in \({{\,\mathrm{{A}}\,}}\) is denoted by
For example, \({{{\textsf {N} }}}_{{{\mathbb {R}}}}(\pi )\) is the collection
We define (with a slight abuse of language)
and \( {{{\textsf {N} }}}_{{{\mathbb {R}}}}(-\infty ){\mathop {=}\limits ^\mathrm{{def}}}\left\{ Q\!:Q\subset {{\mathbb {R}}}\text { and } \exists a\in {{\mathbb {R}}}\text { such that } (-\infty ,a)\subset Q\right\} \).
Definition 1.1
If \({{\,\mathrm{{A}}\,}}\) is nonempty set, a functional convergence relation for real-valued functions on \({{\,\mathrm{{A}}\,}}\) is a subset \({\mathcal {F}}\) of \({{{\mathbb {R}}}}\times \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\) such that, for each \(y\in {{\mathbb {R}}}\),
and
The meaning of (1.18) is that constant functions ought to converge to the constant. The meaning of (1.19) is that it is meant to exclude that every function converges to each value \(y\in {{\mathbb {R}}}\).
Definition 1.2
A functional convergence relation \({\mathcal {F}}\) for real-valued functions defined on \({{\,\mathrm{{A}}\,}}\) is:
-
Translation invariant if, whenever \((y,\varphi )\in {\mathcal {F}}\), for some \((y,\varphi )\in {{{\mathbb {R}}}}\times \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\), and \(r\in {{\mathbb {R}}}\), it follows that \((r+y,r+\varphi )\in {\mathcal {F}}\), where \(r+\varphi \in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\) is defined “pointwise” by \((r+\varphi )(x){\mathop {=}\limits ^\mathrm{{def}}}{}r+\varphi (x)\).
-
Local if, for each \(\beta \in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\), if there exists \(y\in {{\mathbb {R}}}\) such that the following property holds
$$\begin{aligned}&\forall U\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(y)\, \exists V\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(y)\, \exists \varphi \in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}}),\quad (y,\varphi )\in {\mathcal {F}}\quad \text {and}\nonumber \\&\varphi (x)\in {}V \Rightarrow \beta (x)\in {}U \end{aligned}$$(1.20)then \((y,\beta )\in {\mathcal {F}}\).
-
Hereditary if, whenever \(y\in {{\mathbb {R}}}\), \((y,\varphi )\in {\mathcal {F}}\), and \((y,\beta )\in {\mathcal {F}}\), if \(\gamma \in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\) and there exists \(U\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(y)\) such that
$$\begin{aligned} \varphi (x)\in {}U \quad \text {and}\quad \beta (x)\in {}U \Rightarrow \gamma (x)\in \{\varphi (x),\beta (x)\} \end{aligned}$$(1.21)then it follows that \((y,\gamma )\in {\mathcal {F}}\).
Definition 1.3
A functional convergence class for real-valued functions on \({{\,\mathrm{{A}}\,}}\) is a functional convergence relation \({\mathcal {F}}\subset {{{\,\mathrm{{Y}}\,}}}\times \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\,\mathrm{{Y}}\,}})\) which is local, hereditary, and translation invariant. The collection of all functional convergence classes for real-valued functions on \({{\,\mathrm{{A}}\,}}\) is denoted by
The following observations should help the reader to assess the meaning of the axioms that describe the notion of functional convergence class.
(a) These axioms identify a class of subsets of \({{{\mathbb {R}}}}\times \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\).
(b) As we shall see, each \({\mathcal {F}}\) in this class arises from a certain “limiting process,” expressed in purely formal terms by (1.8).
(c) The link between the “limiting process” (acting on the background) and \({\mathcal {F}}\) is given by (1.9).
1.2.2 Examples of Functional Convergence Classes
The following examples will give a first bird’s eye view of the content of this paper and help to clarify the picture. More precisely, we will show that each of the following data entails a limiting process that yields a functional convergence class.
Example (i) The first example of a functional convergence class is the one induced by the choice of a nonempty collection of \({{\,\mathrm{{A}}\,}}\)-valued sequences. In Theorem 3.33 we show that, if \(V\subset \texttt {hom}_{\texttt {Set}}({\mathbb {N}},{{\,\mathrm{{A}}\,}})\) is such a collection and we define \({\mathcal {F}}_{V}\) by
[where \(\lim _{n\rightarrow +\infty }\varphi ({\varvec{q}}(n))=y\) is the familiar notion of convergence for the sequence \(\varphi \circ {\varvec{q}}:{\mathbb {N}}\rightarrow {{\mathbb {R}}}\)] then \({\mathcal {F}}_{V}\) is a functional convergence class.
Example (ii) The second example of a functional convergence class is the one induced by the choice of a direction on \({{\,\mathrm{{A}}\,}}\). In Theorem 3.24 we show that if \(\texttt {R}\) is a direction on \({{\,\mathrm{{A}}\,}}\) (i.e., \(\texttt {R}\) is a preorder on \({{\,\mathrm{{A}}\,}}\) such that for each \(j,k\in {}{{\,\mathrm{{A}}\,}}\), there exists an element \(l\in {{\,\mathrm{{A}}\,}}\) such that \(j\texttt {R}{}{}l\) and \(k\texttt {R}{}{}l\), as explained in Sect. 3.3) and we define \({\mathcal {F}}_{\texttt {R}}\) by

[where
 denotes Moore–Smith convergence of \(\varphi :{{\,\mathrm{{A}}\,}}\rightarrow {{\mathbb {R}}}\) along the direction \(\texttt {R}\), defined in Sect. 3.4], then \({\mathcal {F}}_{\texttt {R}}\) is a functional convergence class.
denotes Moore–Smith convergence of \(\varphi :{{\,\mathrm{{A}}\,}}\rightarrow {{\mathbb {R}}}\) along the direction \(\texttt {R}\), defined in Sect. 3.4], then \({\mathcal {F}}_{\texttt {R}}\) is a functional convergence class.
Example (iii) The third example of a functional convergence class is the one induced by the choice of an \({{\,\mathrm{{A}}\,}}\)-valued Moore–Smith sequence. Theorem 3.33 implies that if \({\varvec{q}}\) is such a sequence (hence \({\varvec{q}}\) is a function \({\varvec{q}}:{{\,\mathrm{D}\,}}\rightarrow {{\,\mathrm{{A}}\,}}\) defined on a directed set, i.e., a set \({{\,\mathrm{D}\,}}\) which is endowed with a direction \(\texttt {R}\)) and we define \({\mathcal {F}}_{{\varvec{q}}}\) by

[where
 denotes Moore–Smith convergence of \(\varphi \circ {\varvec{q}}:{{\,\mathrm{D}\,}}\rightarrow {{\mathbb {R}}}\) along \(\texttt {R}\)], then \({\mathcal {F}}_{{\varvec{q}}}\) is a functional convergence class.
denotes Moore–Smith convergence of \(\varphi \circ {\varvec{q}}:{{\,\mathrm{D}\,}}\rightarrow {{\mathbb {R}}}\) along \(\texttt {R}\)], then \({\mathcal {F}}_{{\varvec{q}}}\) is a functional convergence class.
Example (iv) The fourth example of a functional convergence class is the one induced by the choice of a nonempty collection of \({{\,\mathrm{{A}}\,}}\)-valued Moore–Smith sequences (where different Moore–Smith sequences in the collection are possibly defined on different directed sets). In Theorem 3.33 we show that if V is such a collection and we define \({\mathcal {F}}_{V}\) by

[where, for each \({\varvec{q}}\in {}V\), \(({{\,\mathrm{D}\,}}_{{\varvec{q}}},\texttt {R}_{{\varvec{q}}})\) is the domain of \({\varvec{q}}\), and  denotes Moore–Smith convergence of \(\varphi \circ {\varvec{q}}:{{\,\mathrm{D}\,}}_{{\varvec{q}}}\rightarrow {{\mathbb {R}}}\) along \(\texttt {R}_{{\varvec{q}}}\)] then \({\mathcal {F}}_{V}\) is a functional convergence class.
denotes Moore–Smith convergence of \(\varphi \circ {\varvec{q}}:{{\,\mathrm{D}\,}}_{{\varvec{q}}}\rightarrow {{\mathbb {R}}}\) along \(\texttt {R}_{{\varvec{q}}}\)] then \({\mathcal {F}}_{V}\) is a functional convergence class.
The fifth example of a functional convergence class is the one induced by the choice of a filter on \({{\,\mathrm{{A}}\,}}\).
1.2.3 The Notion of Filter
The notion of filter, due to Henri Cartan, is a tool that helps clarify topological phenomena, and acts as a substitute, in case there is no topology; moreover, it is a precious tool in several mathematical areas.
The key observations leading to the notion of filter are the following. Firstly, observe that if \({{\,\mathrm{{A}}\,}}\) is a topological space and \(x\in {{\,\mathrm{{A}}\,}}\) then the set \( {{{\textsf {N} }}}_{{{\,\mathrm{{A}}\,}}}(x) \), seen as a collection of subset of \({{\,\mathrm{{A}}\,}}\), has the following essential properties:
- (F0):
-
It does not contain the empty set.
- (F1):
-
It is closed under finite intersections.
- (F2):
-
It contains every superset of each of its elements.
Secondly, the familiar \(\epsilon \)–\(\delta \) description of the existence of a limiting value \(\displaystyle \lim \nolimits _{z\rightarrow {}x}{\varphi (z)}\), where \(\varphi \) belongs to \(\texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\) shows that this notion only depends on the values of \(\varphi \) on (set-theoretically) small sets in \({{{\textsf {N} }}}_{{{\,\mathrm{{A}}\,}}}(x)\). In view of the following definition, due to Cartan [8], \({{{\textsf {N} }}}_{{{\,\mathrm{{A}}\,}}}(x)\) is called the neighborhood filter associated to \({{\,\mathrm{{A}}\,}}\) at \(x\).
Definition 1.4
If \({{\,\mathrm{{A}}\,}}\) is a set, a filter on \({{\,\mathrm{{A}}\,}}\) (or filter of subsets of \({{\,\mathrm{{A}}\,}}\)) is a collection of subsets of \({{\,\mathrm{{A}}\,}}\) with the properties (F0), (F1) and (F2). The collection of all filters on \({{\,\mathrm{{A}}\,}}\) is denoted by  .
.
Observe that (F1) is equivalent to the conjunction of the following two axioms:
- (F1.a):
-
The collection contains \({{\,\mathrm{{A}}\,}}\).
- (F1.b):
-
The intersection of two sets in the collection belong to the collection.
There is no filter on the empty set. If  then \({{\,\mathrm{{A}}\,}}\in {{\textsf {Z} }}\), \(\emptyset \not \in {{\textsf {Z} }}\), and, if \({{\textsf {b} }}, {{\textsf {c} }}\in {{\textsf {Z} }}\), then \({{\textsf {b} }}\cap {{\textsf {c} }}\not =\emptyset \).
then \({{\,\mathrm{{A}}\,}}\in {{\textsf {Z} }}\), \(\emptyset \not \in {{\textsf {Z} }}\), and, if \({{\textsf {b} }}, {{\textsf {c} }}\in {{\textsf {Z} }}\), then \({{\textsf {b} }}\cap {{\textsf {c} }}\not =\emptyset \).
Definition 1.5
(Cartan) A filter  is an ultrafilter if
is an ultrafilter if  and \({{\textsf {Z} }}\subset {{\textsf {W} }}\) implies \({{\textsf {Z} }}={{\textsf {W} }}\). The collection of all ultrafilters on a set \({{\,\mathrm{{A}}\,}}\) is denoted by
and \({{\textsf {Z} }}\subset {{\textsf {W} }}\) implies \({{\textsf {Z} }}={{\textsf {W} }}\). The collection of all ultrafilters on a set \({{\,\mathrm{{A}}\,}}\) is denoted by  .
.
1.2.4 The Category of Filtered Sets
Definition 1.6
A filtered set \({{\,\mathrm{{A}}\,}}=({{\,\mathrm{{A}}\,}}_{\texttt {Set}},{{\textsf {Z} }}_{{{\,\mathrm{{A}}\,}}})\) is a set \({{\,\mathrm{{A}}\,}}_{\texttt {Set}}\) endowed with a filter  . The set \({{\,\mathrm{{A}}\,}}_{\texttt {Set}}\) is called the total space of the filtered set \({{\,\mathrm{{A}}\,}}\). A filter-homomorphism \(f:{{\,\mathrm{{A}}\,}}\rightarrow {{\,\mathrm{{A}}\,}}'\) between the filtered set \({{\,\mathrm{{A}}\,}}\) and the filtered set \({{\,\mathrm{{A}}\,}}'\) is a function \(f:{{\,\mathrm{{A}}\,}}_{\texttt {Set}}\rightarrow {{\,\mathrm{{A}}\,}}_{\texttt {Set}}'\) between the underlying sets such that \(\left\{ x\in {{\,\mathrm{{A}}\,}}\!:f(x)\in {{\textsf {b} }}\right\} \in {{\textsf {Z} }}_{{{\,\mathrm{{A}}\,}}}\) for each \({{\textsf {b} }}\in {{\textsf {Z} }}'_{{{\,\mathrm{{A}}\,}}}\).
. The set \({{\,\mathrm{{A}}\,}}_{\texttt {Set}}\) is called the total space of the filtered set \({{\,\mathrm{{A}}\,}}\). A filter-homomorphism \(f:{{\,\mathrm{{A}}\,}}\rightarrow {{\,\mathrm{{A}}\,}}'\) between the filtered set \({{\,\mathrm{{A}}\,}}\) and the filtered set \({{\,\mathrm{{A}}\,}}'\) is a function \(f:{{\,\mathrm{{A}}\,}}_{\texttt {Set}}\rightarrow {{\,\mathrm{{A}}\,}}_{\texttt {Set}}'\) between the underlying sets such that \(\left\{ x\in {{\,\mathrm{{A}}\,}}\!:f(x)\in {{\textsf {b} }}\right\} \in {{\textsf {Z} }}_{{{\,\mathrm{{A}}\,}}}\) for each \({{\textsf {b} }}\in {{\textsf {Z} }}'_{{{\,\mathrm{{A}}\,}}}\).
Filtered sets form the objects of a category, denoted \(\texttt {FSet}\), where morphisms are filter-homomorphisms. We will return momentarily to the notion of filter-homomorphism, in order to achieve a better understanding of its meaning.
Localization We will see that the seemingly simple hypothesis that a certain set belongs to a given filter has great import, and we use the expression the filter \({{\textsf {Z} }}\) is localized in K, where \(K\subset {{\,\mathrm{{A}}\,}}\), as synonym for the set K belongs to the filter  .
.
Definition 1.7
If \(K\subset {{\,\mathrm{{A}}\,}}\), a filter  is weakly localized in K if \(\complement {K}\not \in {{\textsf {Z} }}\). We let
is weakly localized in K if \(\complement {K}\not \in {{\textsf {Z} }}\). We let
Observe that
and
Hence if a filter is localized in K then it is weakly localized in K. The converse implication does not hold, unless the given filter is an ultrafilter, as we will see in Lemma 4.26. Indeed, we will see that a filter is an ultrafilter if and only if equality holds in (1.24).
Example 1.8
If \({{\,\mathrm{{A}}\,}}\) is a topological space and \(x\in {{\,\mathrm{{A}}\,}}\) then \(({{\,\mathrm{{A}}\,}},{{{\textsf {N} }}}_{{{\,\mathrm{{A}}\,}}}(x))\) is a filtered set.
Example 1.9
The collection
is a filter on \({\mathbb {N}}\), called the Fréchet filter on \({\mathbb {N}}\).
Example 1.10
If \({{\,\mathrm{{A}}\,}}\) is a nonempty set then  .
.
Example 1.11
If \(({{\,\mathrm{{X}}\,}},{\mathcal {M}},\omega )\) is a complete probability space then the collection \({{\mathcal {M}}}_{\omega }^{{{\textsf {F} }}}\) of measurable sets of full measure in \({{\,\mathrm{{X}}\,}}\) is a filter on \({{\,\mathrm{{X}}\,}}\).
1.2.5 Limiting Values Along a Filter
Observe that the familiar \(\epsilon \)–\(\delta \) description of the existence of a limiting value \(\displaystyle \lim \nolimits _{z\rightarrow {}x}{\varphi (z)}\), in the case of a real-valued function \(\varphi \) defined on a topological space \({{\,\mathrm{{A}}\,}}\), may be immediately adapted to the case where \(\varphi \) is defined on the underlying set of a filtered set \({{\,\mathrm{{A}}\,}}\).
Definition 1.12
If \({{\,\mathrm{{A}}\,}}\) is a filtered set, \({{\,\mathrm{{Y}}\,}}\) is a topological space, \(\varphi \in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\,\mathrm{{Y}}\,}})\), and \(y\in {{\,\mathrm{{Y}}\,}}\), we say that \(y\) is the limiting value of \(\varphi \) along the filter \({{\textsf {Z} }}\), and write

if \(\varphi :{{\,\mathrm{{A}}\,}}\rightarrow ({{\,\mathrm{{Y}}\,}},{{{\textsf {N} }}}_{{{\,\mathrm{{Y}}\,}}}(y))\) is a filter-homomorphism.
The meaning of the condition that \(\varphi :{{\,\mathrm{{A}}\,}}\rightarrow ({{\,\mathrm{{Y}}\,}},{{{\textsf {N} }}}_{{{\,\mathrm{{Y}}\,}}}(y))\) is a filter-homomorphism is that for each \(U\in {{{\textsf {N} }}}_{{{\,\mathrm{{Y}}\,}}}(y)\), the set \( \left\{ x\in {{\,\mathrm{{A}}\,}}\!: \varphi (x)\in {U}\right\} \) belongs to \({{\textsf {Z} }}\).
Definition 1.13
If \(\varphi :{{\,\mathrm{{A}}\,}}\rightarrow {{\mathbb {R}}}\) is real-valued, we say that  if \(\varphi :{{\,\mathrm{{A}}\,}}\rightarrow ({{\mathbb {R}}},{{{\textsf {N} }}}_{{{\mathbb {R}}}}(\pm \infty ))\) is a filter-homomorphism.
if \(\varphi :{{\,\mathrm{{A}}\,}}\rightarrow ({{\mathbb {R}}},{{{\textsf {N} }}}_{{{\mathbb {R}}}}(\pm \infty ))\) is a filter-homomorphism.
1.2.6 The Functional Convergence Class Induced by a Filter
Example (v) The fifth example of a functional convergence class is the one induced by the choice of a filter on \({{\,\mathrm{{A}}\,}}\). In Theorem 3.2 we show that if \({{\textsf {Z} }}\) is a filter on \({{\,\mathrm{{A}}\,}}\) and we define \({{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})\) by

(where  denotes convergence of \(\varphi :{{\,\mathrm{{A}}\,}}\rightarrow {{\mathbb {R}}}\) along the filter \({{\textsf {Z} }}\), defined in Sect. 1.2.5), then \({{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})\) is a functional convergence class.
denotes convergence of \(\varphi :{{\,\mathrm{{A}}\,}}\rightarrow {{\mathbb {R}}}\) along the filter \({{\textsf {Z} }}\), defined in Sect. 1.2.5), then \({{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})\) is a functional convergence class.
1.3 A Hierarchy of Limiting Processes
The second contribution of this paper is the clarification of the hierarchical relations between the limiting processes described in Examples (i)–(v). More precisely, we will prove the following results.
(Theorem 3.7) Each functional convergence class may be uniquely represented in the form (v). In other words, the limiting process associated to filters recaptures the abstract notion of functional convergence class.
(Theorem 3.34) Each functional convergence class may be represented in the form (iv), albeit not uniquely.
(Theorem 3.37) Each functional convergence class may be represented in the form (iii), albeit not uniquely.
(Theorem 3.36) Not every functional convergence class may be represented in the form (i).
(Theorem 3.29) Not every functional convergence class may be represented in the form (ii). For example, nontangential convergence, that plays a leading role in the study of the boundary behavior of harmonic functions, cannot be represented in this form.
1.4 Applications to the Problem of the Differentiation of Integrals (I)
We are now ready to give a second bird’s eye view of the content of this paper, where we present a reformulation of de Possel’s approach in terms of filters. This reformulation is inspired by the following three implications of the results described in Sect. 1.2.
(A) The lack of uniqueness in Theorem 3.37 means that it is preferable to represent a given functional convergence class in terms of convergence along a filter, as in Sect. 1.2.6 [Example (v)], rather than in terms of convergence along a Moore–Smith sequence, as in (1.22) [Example (iii)], since the exceptional set in the Generalized Lebesgue Differentiation Theorem should not depend on the particular representation (i.e., on the particular Moore–Smith sequence) chosen.
(B) There is no gain in generality in the limiting process described in Example (iv), with respect to the one in Example (iii).
(C) The limiting process produced by filters, described in Example (v), has wider scope than the one produced by collections of sequences, described in Example (i).
The following set-up is based on these implications.
1.4.1 The Set-Up Based on Filters
Since the phenomena of interest in the present work are invariant under rescaling, the results we obtain for complete probability spaces also hold for complete measure spaces endowed with a finite measure (see Sect. 2). Hence, unless otherwise stated, we assume that \(({{\,\mathrm{{X}}\,}},{\mathcal {M}},\omega )\) is a complete probability space.
Denote by  the collection of all filters on \({{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}})\).
the collection of all filters on \({{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}})\).
Definition 1.14
A family of differentiation filters (based on \({{\,\mathrm{{X}}\,}}\)) is a function

which associates to each \(x\in {{\,\mathrm{{X}}\,}}\) a filter  .
.
Definition 1.15
We say that a family of differentiation filters (1.28) differentiates a function \(f\in {\mathcal {L}}^{1}({{\,\mathrm{{X}}\,}}) \) at \(x\in {{\,\mathrm{{X}}\,}}\) if

A family of differentiation filters  as in (1.28) differentiates \({\varvec{f}}\in {{\,\mathrm{L}\,}}^{1}({{\,\mathrm{{X}}\,}})\) if the limiting value
as in (1.28) differentiates \({\varvec{f}}\in {{\,\mathrm{L}\,}}^{1}({{\,\mathrm{{X}}\,}})\) if the limiting value

exists for a.e. \(x\in {{\,\mathrm{{X}}\,}}\) and yields a representative of \({\varvec{f}}\). If \(\varvec{{\mathcal {R}}}\subset {{\,\mathrm{L}\,}}^{1}({{\,\mathrm{{X}}\,}})\), we say that  differentiates \(\varvec{{\mathcal {R}}}\) if
differentiates \(\varvec{{\mathcal {R}}}\) if  differentiates \({\varvec{f}}\) for each \({\varvec{f}}\in \varvec{{\mathcal {R}}}\).
differentiates \({\varvec{f}}\) for each \({\varvec{f}}\in \varvec{{\mathcal {R}}}\).
1.4.2 On the Differentiation of the Class of All Measurable Sets (I)
Perhaps the simplest class of integrable functions is given by the following one, associated to the \(\sigma \)-algebra of measurable sets:
If \(R\in {\mathcal {M}}\) has measure zero, then every family of differentiation filters (1.28) differentiates \({\mathbb {1}}_{R}\). Hence it suffices to restrict attention to \(\left\{ {\mathbb {1}}_{R}\!:R\in {{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}})\right\} \).
Definition 1.16
If  is a family of differentiation filters, as in (1.28), we say that
is a family of differentiation filters, as in (1.28), we say that  differentiates all measurable sets if, for each \(R\in {{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}})\),
differentiates all measurable sets if, for each \(R\in {{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}})\),  differentiates \({\mathbb {1}}_{R}\).
differentiates \({\mathbb {1}}_{R}\).
Definition 1.17
A lifting of \(({{\,\mathrm{{X}}\,}},{\mathcal {M}},\omega )\) is a Boolean homomorphism \(\theta :{{\,\mathrm{M}\,}}\rightarrow {\mathcal {M}}\) which is a right inverse of the canonical projection of \({\mathcal {M}}\) onto \({{\,\mathrm{M}\,}}\), described in (1.1).
Hence a lifting \(\theta :{{\,\mathrm{M}\,}}\rightarrow {\mathcal {M}}\) of \(({{\,\mathrm{{X}}\,}},{\mathcal {M}},\omega )\) amounts to the choice of a representative of the measure class \(\pi (Q)\), for each \(Q\in {\mathcal {M}}\), which preserves the Boolean structure of \({{\,\mathrm{M}\,}}\), and hence establishes a Boolean isomorphism between the measure algebra of \(({{\,\mathrm{{X}}\,}},{\mathcal {M}},\omega )\) and some subalgebra of \({\mathcal {M}}\).
The problem of the differentiation of the class of all integrable functions is clarified by the following result, whose proof may be obtained by adapting the techniques used in [20].
Theorem 1.18
If \(({{\,\mathrm{{X}}\,}},{\mathcal {M}},\omega )\) is a complete probability space, then a necessary and sufficient condition for the existence of a family of differentiation filters  , which differentiates all integrable functions, is the existence of a lifting of \(({{\,\mathrm{{X}}\,}},{\mathcal {M}},\omega )\).
, which differentiates all integrable functions, is the existence of a lifting of \(({{\,\mathrm{{X}}\,}},{\mathcal {M}},\omega )\).
The following result, coupled with Theorem 1.18, shows that there exists a family of differentiation filters  which differentiates all integrable functions.
which differentiates all integrable functions.
Theorem 1.19
(Von Neumann–Maharam) Every complete probability space \(({{\,\mathrm{{X}}\,}},{\mathcal {M}},\omega )\) admits a lifting.
Theorem 1.19 has a “curious history,” as Fremlin puts it, which is recounted in [15, pp. 162–174], where a proof is given. The proof of Theorem 1.19 must necessarily involve the Axiom of Choice [6].
1.4.3 Measurability Issues (I)
In dealing with a general family of differentiation filters  , we are faced with certain measurability issues, as we will see in more detail in Sect. 13. We will treat these difficulties using the same devices which de Possel used in his work.
, we are faced with certain measurability issues, as we will see in more detail in Sect. 13. We will treat these difficulties using the same devices which de Possel used in his work.
For the collection of all subsets of a set \({{\,\mathrm{{A}}\,}}\) we use the standard notation

In the study of filters the empty set is a nuisance, and in order to simplify many statements which otherwise would be too involved, we introduce the following notation for the collection of nonempty subsets of a given set:

Definition 1.20
If \(({{\,\mathrm{{X}}\,}},{\mathcal {M}},\omega )\) is a probability space, the outer measure induced by \(\omega \) is defined by
where, if \(Q\in {{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\), then

The following result is well known.
Lemma 1.21
For each \(Q\in {{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\) there exists a set \(R\in {\mathcal {M}}\) such that \(Q\subset R\) and \(\omega ^*(Q)= \omega (R)\).
Definition 1.22
If \(Q\in {{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\) and \(R\) has the property described in Lemma 1.21, we say that \(R\) is a measurable representative of \(Q\), and write

Definition 1.23

and if \(Q\in {{\mathcal {A}}}^{*}({{{\,\mathrm{{X}}\,}}})\) then

1.4.4 A Criterion for the Differentiation of Integrable Functions
Assume that  is a family of differentiation filters, \(f\in {\mathcal {L}}^1({{\,\mathrm{{X}}\,}})\), \(\alpha \in {{\mathbb {R}}}\), and \(Q\in {{\mathcal {A}}}^{*}({{{\,\mathrm{{X}}\,}}})\).
is a family of differentiation filters, \(f\in {\mathcal {L}}^1({{\,\mathrm{{X}}\,}})\), \(\alpha \in {{\mathbb {R}}}\), and \(Q\in {{\mathcal {A}}}^{*}({{{\,\mathrm{{X}}\,}}})\).
Definition 1.24
We say that  is adapted to \(f\) on \(Q\) above \(\alpha \) (resp. below \(\alpha \)) if
is adapted to \(f\) on \(Q\) above \(\alpha \) (resp. below \(\alpha \)) if
Definition 1.25
We say that the mean-value of f over \(Q\) lies above \(\alpha \) (resp. below \(\alpha \)) if there exists \(Q'\in {\mathcal {M}}[Q]\) such that \({f}_{\!\omega }[Q']>\alpha \) [resp. \({f}_{\!\omega }[Q']<\alpha \)].
Definition 1.26
We say that  and \(f\in {\mathcal {L}}^1({{\,\mathrm{{X}}\,}})\) are compatible if
and \(f\in {\mathcal {L}}^1({{\,\mathrm{{X}}\,}})\) are compatible if
- (a):
-
for all \(Q\in {{\mathcal {A}}}^{*}({{{\,\mathrm{{X}}\,}}})\) and for all \(\alpha \in {{\mathbb {R}}}\), if
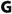 is adapted to \(f\) on \(Q\) above \(\alpha \), then the mean-value of \(f\) on \(Q\) lies above \(\alpha ,\)
is adapted to \(f\) on \(Q\) above \(\alpha \), then the mean-value of \(f\) on \(Q\) lies above \(\alpha ,\) - (b):
-
for all \(Q\in {{\mathcal {A}}}^{*}({{{\,\mathrm{{X}}\,}}})\) and for all \(\alpha \in {{\mathbb {R}}}\), if
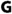 is adapted to \(f\) on \(Q\) below \(\alpha \), then the mean-value of \(f\) on \(Q\) lies below \(\alpha .\)
is adapted to \(f\) on \(Q\) below \(\alpha \), then the mean-value of \(f\) on \(Q\) lies below \(\alpha .\)
Theorem 1.27
If  and \(f\in {\mathcal {L}}^1({{\,\mathrm{{X}}\,}})\) are compatible then
and \(f\in {\mathcal {L}}^1({{\,\mathrm{{X}}\,}})\) are compatible then  differentiates \({\varvec{f}}\).
differentiates \({\varvec{f}}\).
Proof
The proof is given in Sect. 13. \(\square \)
1.4.5 On the Differentiation of the Class of All Measurable Sets (II)
The following theorem is akin to a result due to Busemann and Feller in the context of the so-called differentiation bases [7].
Theorem 1.28
If  is a family of differentiation filters, then the following conditions are equivalent:
is a family of differentiation filters, then the following conditions are equivalent:
- (i):
-
 differentiates \({{\,\mathrm{L}\,}}^{\infty }({{\,\mathrm{{X}}\,}})\).
differentiates \({{\,\mathrm{L}\,}}^{\infty }({{\,\mathrm{{X}}\,}})\). - (ii):
-
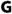 differentiates all measurable sets.
differentiates all measurable sets. - (iii):
-
\(\forall R\in {{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}}),\) for a.e. \(x\in R,\) for each \(\epsilon \in (0,1)\) there exists \({{\textsf {b} }}\in {{\textsf {G} }}(x)\) such that \(\epsilon <{{\widetilde{\omega }}}\left( R|Q\right) \) for each \(Q\in {{\textsf {b} }}\).
Proof
The proof is based on Theorem 1.27 and on an appropriate adaptation of a covering result due to de Possel. Details are omitted. \(\square \)
2 Notation
The sets A, B overlap if \(A\cap {}B\not =\emptyset \). We let \(B\setminus {}A{\mathop {=}\limits ^\mathrm{{def}}}\left\{ x\!:x\in {}B, x\not \in {}A\right\} \) and \(\complement {A}{\mathop {=}\limits ^\mathrm{{def}}}{{\,\mathrm{{X}}\,}}\setminus {}A\). The notation \(A\subset {}B\) (for sets A, B, with \(A,B\subset {{\,\mathrm{{X}}\,}}\)) means that, for all \(x\in {{\,\mathrm{{X}}\,}}\), \(x\in {}A\Rightarrow {}x\in {}B\).
The identity function  is defined by
is defined by  for all \(x\in {{\,\mathrm{{X}}\,}}\).
for all \(x\in {{\,\mathrm{{X}}\,}}\).
The extended real line \(\overline{{{\mathbb {R}}}}\equiv [-\infty ,+\infty ]\) is defined in the familiar way [4, IV.13]. It is a compact topological space which contains \({{\mathbb {R}}}\) as an open subset.
2.1 Sets, Collections, and Families
Since filters are elements of \({{\mathcal {P}}}_{{{\bullet }}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}))\), in order to avoid confusion between the different levels in the hierarchy of powersets, we find it useful to reserve the term set (of points) to a generic element of \({{\mathcal {P}}}({{\,\mathrm{{A}}\,}})\), and call collection (of sets) a generic element of \({{\mathcal {P}}}({{\mathcal {P}}}({{\,\mathrm{{A}}\,}}))\); an element of \({{\mathcal {P}}}({{\mathcal {P}}}({{\mathcal {P}}}({{\,\mathrm{{A}}\,}})))\) is called a family (of collections). We only deal with sets \({{\,\mathrm{{A}}\,}}\) for which \(x,r\in {{\,\mathrm{{A}}\,}}\) \(\Rightarrow \) \(x\not \in r\).
2.1.1 Direct Image and Inverse Image Notation
We also find it useful, for the sake of clarity, to adopt the following notation from [22, p. 154], and write, if \(f\in \texttt {hom}_{\texttt {Set}}(A,Z)\), \(B\in {{\mathcal {P}}}(A)\), and \(C\in {{\mathcal {P}}}(Z)\),

In particular, \({f}_{*}:{{\mathcal {P}}}(A)\rightarrow {{\mathcal {P}}}(Z)\) and, by the same token, \({({f}_{*})}_{*}:{{\mathcal {P}}}({{\mathcal {P}}}(A))\rightarrow {{\mathcal {P}}}({{\mathcal {P}}}(Z))\). The restriction of \({f}_{*}:{{\mathcal {P}}}(A)\rightarrow {{\mathcal {P}}}(Z)\) to \({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\) will also be denoted by \({f}_{*}\) (with a slight abuse of language). Hence
2.2 Measure-Theoretic Notation
A measure space \(({{\,\mathrm{{X}}\,}}, {\mathcal {M}}, \omega )\) is a nonempty set \({{\,\mathrm{{X}}\,}}\) endowed with a \(\sigma \)-algebra \({\mathcal {M}}\subset {{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\) of subsets and a set-function (called a measure) \(\omega :{\mathcal {M}}\rightarrow [0,+\infty ]\) which is countably additive and whose value at \(\emptyset \) is zero [29, p. 217]. The measure \(\omega \) is said to be finite if \(\omega (Q)\in [0,+\infty )\) for all \(Q\in {\mathcal {M}}\). A probability space is a measure space \(({{\,\mathrm{{X}}\,}},{\mathcal {M}},\omega )\) with \(\omega ({{\,\mathrm{{X}}\,}})=1\).
2.2.1 Null Sets and Derived Notions
A null set in a measure space \(({{\,\mathrm{{X}}\,}}, {\mathcal {M}}, \omega )\) is a set \(Q\in {\mathcal {M}}\) such that \(\omega (Q)=0\). The measure space \(({{\,\mathrm{{X}}\,}}, {\mathcal {M}}, \omega )\) is complete if each subset of a null set is also a null set.
In a complete probability space \(({{\,\mathrm{{X}}\,}},{\mathcal {M}},\omega )\), the \(\sigma \)-ideal of null subsets is the collection

The collection \({\mathscr {N}}\) is called a \(\sigma \)-ideal because it has the following properties: (i) it contains the empty set; (ii) if \(Q\in {\mathscr {N}}\) and \(R\subset Q\) then \(R\in {\mathscr {N}}\); (iii) it is closed under countable unions [14, p. 16].
It is useful to introduce the binary relations “\(\varvec{\subset _{\omega }}\)” and  between subsets of a measure space, which are obtained from the inclusion relations “\(\subset \)” and “\(=\)” by replacing the empty set with null sets. If \(Q,R\subset {{\,\mathrm{{X}}\,}}\), we say that \(Q\) is a.e. contained in \(R\), and write \( Q\subset _{\omega }R \) if \(Q\setminus R\in {\mathscr {N}}\): This means that almost all of \(Q\) is a subset of \(R\). We say that the sets \(Q,R\) are almost everywhere equal, and write
between subsets of a measure space, which are obtained from the inclusion relations “\(\subset \)” and “\(=\)” by replacing the empty set with null sets. If \(Q,R\subset {{\,\mathrm{{X}}\,}}\), we say that \(Q\) is a.e. contained in \(R\), and write \( Q\subset _{\omega }R \) if \(Q\setminus R\in {\mathscr {N}}\): This means that almost all of \(Q\) is a subset of \(R\). We say that the sets \(Q,R\) are almost everywhere equal, and write  if \(Q\subset _{\omega }R\) and \( R\subset _{\omega }Q \). Observe that
if \(Q\subset _{\omega }R\) and \( R\subset _{\omega }Q \). Observe that  is an equivalence relation on \({\mathcal {M}}\) and that
is an equivalence relation on \({\mathcal {M}}\) and that  if and only if the symmetric difference
if and only if the symmetric difference  is a null set. We say that \(R\) is a.e. disjoint from \(Q\) if
is a null set. We say that \(R\) is a.e. disjoint from \(Q\) if  , i.e., if \(Q\cap R\) is a null set.
, i.e., if \(Q\cap R\) is a null set.
A set \(Q\subset {{\,\mathrm{{X}}\,}}\) has full measure if \(\complement {Q}\) is a null set. A property holds a.e. (almost everywhere) if it holds on a set of full measure. A set \(Q\subset R\) has full measure in \(R\) if \(Q\cup \complement {R}\) has full measure.
In a complete probability space \(({{\,\mathrm{{X}}\,}},{\mathcal {M}},\omega )\), the collection of measurable sets of full measure is defined as follows:

The collection \({{\mathcal {M}}}_{\omega }^{{{\textsf {F} }}}\) is a filter on \({{\,\mathrm{{X}}\,}}\). Observe that if \(Q,R\in {\mathcal {M}}\), then  if and only if there exists \(F\in {{\mathcal {M}}}_{\omega }^{{{\textsf {F} }}}\) such that \(F\cap Q=F\cap R\).
if and only if there exists \(F\in {{\mathcal {M}}}_{\omega }^{{{\textsf {F} }}}\) such that \(F\cap Q=F\cap R\).
3 Functional Convergence Classes
The goal of this section is to provide some of the proofs of results concerning the abstract notion of functional convergence class, introduced in Sect. 1.2 and show why a priori it is preferable to rephrase the work of R. de Possel in terms of filters rather than in terms of the choice of collections of sequences given in (1.12), as in the original approach by R. de Possel. We will also show that an approach based on the notion of filters appears to be preferable also with respect to a variant of (1.12) where instead of sequences one uses Moore–Smith sequences. Indeed, the lack of a uniqueness (in the representation of a given functional convergence class in terms of convergence along a Moore–Smith sequence) gives rise to ambiguities in the notion of exceptional set.
3.1 Functional Convergence Classes
We now show that the notion of limiting value along a filter on \({{\,\mathrm{{A}}\,}}\) yields a functional convergence class on \({{\,\mathrm{{A}}\,}}\).
Definition 3.1
If \({{\,\mathrm{{A}}\,}}\) is a nonempty set and  , define \({{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})\) as in (1.27).
, define \({{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})\) as in (1.27).
Theorem 3.2
If  then \({{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})\) is a functional convergence class, and hence (1.27) defines a map
then \({{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})\) is a functional convergence class, and hence (1.27) defines a map

Proof
If \(\varphi \in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\) is identically equal to \(y\in {{\mathbb {R}}}\), then \({\varphi }^{*}(U)\equiv {{\,\mathrm{{A}}\,}}\) for each \(U\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(y)\), hence \({{{{{\textbf {{\textsf {lim}}}}} }}}_{{{\textsf {Z} }}}\varphi =y\), i.e., \((y,\varphi )\in {{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})\). If \(y\in {{\mathbb {R}}}\), define \(\varphi \in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\) by \(\varphi (x){\mathop {=}\limits ^\mathrm{{def}}}y+1\) for each \(x\in {{\,\mathrm{{A}}\,}}\). Observe that if \(U{\mathop {=}\limits ^\mathrm{{def}}}\left( y-\frac{1}{2},y+\frac{1}{2}\right) \) then \(U\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(y)\) and \({(\varphi )}^{*}(U)=\emptyset \), thus \({{{{{\textbf {{\textsf {lim}}}}} }}}_{{{\textsf {Z} }}}\varphi =y\) does not hold, hence \((y,\varphi )\not \in {{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})\). We have proved that \({{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})\) is a functional convergence relation.
If \((y,\varphi )\in {{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})\), i.e., \({{{{{\textbf {{\textsf {lim}}}}} }}}_{{{\textsf {Z} }}}\varphi =y\), and \(r\in {{\mathbb {R}}}\), let \(\beta {\mathop {=}\limits ^\mathrm{{def}}}{}r+\varphi \), and \(U\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(r+y)\). Define \(U-r{\mathop {=}\limits ^\mathrm{{def}}}\left\{ x-r\!:x\in {}U\right\} \). Then \(U-r\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(y)\). Observe that \({\beta }^{*}(U)={\varphi }^{*}(U-r)\), since \(\beta (x)=r+\varphi (x)\in {}U\) if and only if \(\varphi (x)\in {}U-r\). Then \({{{{{\textbf {{\textsf {lim}}}}} }}}_{{{\textsf {Z} }}}\varphi =y\) implies that \({\varphi }^{*}(U-r)\in {{\textsf {Z} }}\), and since \({\beta }^{*}(U)={\varphi }^{*}(U-r)\), it follows that \({\beta }^{*}(U)\in {{\textsf {Z} }}\). Since \(U\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(r+y)\) is arbitrary, it follows that \({{{{{\textbf {{\textsf {lim}}}}} }}}_{{{\textsf {Z} }}}\beta =r+y\), i.e., \({{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})\) is translation invariant.
Let \(\beta \in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\) and assume that, for each \(U\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(y)\), there exists \(V\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(y)\) and \(\varphi \in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\) such that \((y,\varphi )\in {{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})\) and \({\varphi }^{*}(V)\subset {\beta }^{*}(U)\). Observe that \({\varphi }^{*}(V)\in {{\textsf {Z} }}\), since \({{{{{\textbf {{\textsf {lim}}}}} }}}_{{{\textsf {Z} }}}\varphi =y\), and hence \({\beta }^{*}(U)\in {{\textsf {Z} }}\). Thus we have proved that \({\beta }^{*}(U)\in {{\textsf {Z} }}\) for each \(U\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(y)\), and this means that \({{{{{\textbf {{\textsf {lim}}}}} }}}_{{{\textsf {Z} }}}\beta =y\), i.e., \((y,\beta )\in {{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})\). Hence \({{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})\) is local.
Assume that \(y\in {{\mathbb {R}}}\), \({{{{{\textbf {{\textsf {lim}}}}} }}}_{{{\textsf {Z} }}}\varphi =y\), \({{{{{\textbf {{\textsf {lim}}}}} }}}_{{{\textsf {Z} }}}\beta =y\), and \(\gamma \in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\). Suppose that \(\gamma \) has the property that, for some \(U\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(y)\), \(\gamma (x)\in \{\varphi (x),\beta (x)\}\) for each \(x\in {\varphi }^{*}(U)\cap {\beta }^{*}(U)\). Let \(V\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(y)\). Then
and since \({\varphi }^{*}(V\cap {}U)\) and \({\varphi }^{*}(V\cap {}U)\) both belong to \({{\textsf {Z} }}\), and \({{\textsf {Z} }}\) is a filter, it follows that \({\gamma }^{*}(V)\in {{\textsf {Z} }}\). Since \(V\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(y)\) is arbitrary, it follows that \({{{{{\textbf {{\textsf {lim}}}}} }}}_{{{\textsf {Z} }}}\gamma =y\). Hence \({{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})\) is hereditary. \(\square \)
In the following section, we will show that the map \({{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}\) in (3.1) is one-to-one and onto.
3.2 A Representation Theorem for Functional Convergence Classes
Definition 3.3
If \({{\,\mathrm{{A}}\,}}\) is a nonempty set and \({\mathcal {F}}\in {\textsf {FCC} }({{{\,\mathrm{{A}}\,}}})\), then define by
Lemma 3.4
If \({\mathcal {F}}\in {\textsf {FCC} }({{{\,\mathrm{{A}}\,}}})\) then \({{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({\mathcal {F}})\) is a filter on \({{\,\mathrm{{A}}\,}},\) and (3.2) defines a function

Proof
It suffices to show that \({{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({\mathcal {F}})\) is a filter. Let \({\mathcal {F}}(0){\mathop {=}\limits ^\mathrm{{def}}}\left\{ \varphi {\in }\texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\!:(0,\varphi ){\in }{\mathcal {F}}\right\} \). Observe that \({\mathcal {F}}(0)\) is not empty, since it contain at least the constant function identically equal to 0. Observe that \({{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({\mathcal {F}})=\left\{ {\varphi }^{*}(U)\!:U\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(0),\varphi \in {\mathcal {F}}(0)\right\} \).
Firstly, observe that \({{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({\mathcal {F}})\) is not empty, since it contains \({{\,\mathrm{{A}}\,}}\), because \({\mathcal {F}}(0)\) contains the constant function identically equal to 0.
Secondly, we show that \(\emptyset \not \in {{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({\mathcal {F}})\). We proceed by contradiction and assume that there exists \(V\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(0)\) and \(\varphi \in {\mathcal {F}}(0)\) such that \({(\varphi )}^{*}(V)=\emptyset \). Let \(\beta \in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\) and observe that (1.20) holds for \(y=0\). Since \({\mathcal {F}}\) is local, it follows that \(\beta \in {\mathcal {F}}(0)\). Hence we have proved that \(\texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})={\mathcal {F}}(0)\). Since \({\mathcal {F}}\) is translation invariant, it follows that \({\mathcal {F}}={{{\mathbb {R}}}}\times \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\), a contradiction.
We now show that
Indeed, if \({{\textsf {b} }}\in {{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({\mathcal {F}})\), there exists \(V\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(0)\) and \(\varphi \in {\mathcal {F}}(0)\) and \({{\textsf {b} }}={\varphi }^{*}(V)\). Observe that, under these hypotheses, \(V\subsetneq {{\mathbb {R}}}\). Choose \(z\in {{\mathbb {R}}}\setminus {}V\). Define \(\beta \in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\) as follows: If \(x\in {{\textsf {c} }}\) then \(\beta (x){\mathop {=}\limits ^\mathrm{{def}}}{}0\); if \(x\in {{\,\mathrm{{A}}\,}}\setminus {{\textsf {c} }}\) then \(\beta (x){\mathop {=}\limits ^\mathrm{{def}}}{}z\). Then \({\beta }^{*}(U)\) is either equal to \({{\textsf {c} }}\) or it is equal to \({{\,\mathrm{{A}}\,}}\). In either case, \({\beta }^{*}(U)\) contains \({{\textsf {b} }}={\varphi }^{*}(V)\). Since \({\mathcal {F}}\) is local, it follows that \((0,\beta )\in {\mathcal {F}}\). Observe that \({\beta }^{*}(V)={{\textsf {c} }}\). Hence \({{\textsf {c} }}\in {{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({\mathcal {F}})\), and the proof of (3.4) is complete.
Now, assume that \(U\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(0)\). We claim that
Indeed, if \(U={{\mathbb {R}}}\) then \({\varphi }^{*}(U)={\beta }^{*}(U)={{\,\mathrm{{A}}\,}}\), hence \({\varphi }^{*}(U)\cap {\beta }^{*}(U)={{\,\mathrm{{A}}\,}}\) and we know already that \({{\,\mathrm{{A}}\,}}\in {{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({\mathcal {F}})\). If \(U\subsetneq {{\mathbb {R}}}\), let \(z\in {{\mathbb {R}}}\setminus {}U\) and define \(\gamma \in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\) as follows: If \(x\in {\varphi }^{*}(U)\cap {\beta }^{*}(U)\) then \(\gamma (x){\mathop {=}\limits ^\mathrm{{def}}}\beta (x)\); if \(x\in {{\,\mathrm{{A}}\,}}\setminus \left( {\varphi }^{*}(U)\cap {\beta }^{*}(U)\right) \) then \(\gamma (x){\mathop {=}\limits ^\mathrm{{def}}}{}z\). Observe that \({\gamma }^{*}(U)={\varphi }^{*}(U)\cap {\beta }^{*}(U)\). Moreover, if \(x\in {\varphi }^{*}(U)\cap {\beta }^{*}(U)\) then \(\gamma (x)\in \{\varphi (x),\beta (x)\}\), hence \(\gamma \in {\mathcal {F}}(0)\), since \({\mathcal {F}}\) is hereditary. It follows that \({\varphi }^{*}(U)\cap {\beta }^{*}(U)\in {{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({\mathcal {F}})\).
Finally, we prove that
Indeed, if \({{\textsf {b} }},{{\textsf {c} }}\in {{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({\mathcal {F}})\) then there exists \(U,V\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(0)\) and \(\varphi ,\beta \in {\mathcal {F}}(0)\) such that \({{\textsf {b} }}={\varphi }^{*}(U)\) and \({{\textsf {c} }}={\beta }^{*}(V)\). Then
Hence (3.6) follows from (3.4) and (3.5). The proof that \({{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({\mathcal {F}})\) is a filter is complete. \(\square \)
Lemma 3.5
The map (3.3) is a left inverse of (3.1).
Proof
We have to show that if  then
then
If \({{\textsf {b} }}\in {{\textsf {Z} }}\) define \(\varphi \in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\) as follows: if \(x\in {{\textsf {b} }}\) then \(\varphi (x){\mathop {=}\limits ^\mathrm{{def}}}{}0\); if \(x\in {{\,\mathrm{{A}}\,}}\setminus {{\textsf {b} }}\) then \(\varphi (x){\mathop {=}\limits ^\mathrm{{def}}}{}1\). Observe that \({{{{{\textbf {{\textsf {lim}}}}} }}}_{{{\textsf {Z} }}}\varphi =0\). Indeed, if \(U\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(0)\) then \({\varphi }^{*}(U)\) is either \({{\textsf {b} }}\) or \({{\,\mathrm{{A}}\,}}\), and hence it belongs to \({{\textsf {Z} }}\). It follows that \((0,\varphi )\in {{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})\). Now observe that \({{\textsf {b} }}={\varphi }^{*}(-1/2,1/2)\), thus \({{\textsf {b} }}\in {{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }}))\). Hence we have proved that \({{\textsf {Z} }}\subset {{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }}))\). Now assume that \({{\textsf {b} }}\in {{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }}))\). Then there exists \(\varphi \) and U, where \((0,\varphi )\in {{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})\) and \(U\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(0)\), such that \({{\textsf {b} }}={\varphi }^{*}(U)\). The fact that \((0,\varphi )\in {{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})\) implies that \({{{{{\textbf {{\textsf {lim}}}}} }}}_{{{\textsf {Z} }}}\varphi =0\), hence it implies that \({\varphi }^{*}(U)\in {{\textsf {Z} }}\), and thus \({{\textsf {b} }}\in {{\textsf {Z} }}\). Hence we have proved that \({{\textsf {Z} }}\supset {{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }}))\), and the proof is complete.\(\square \)
Lemma 3.6
The map (3.3) is a right inverse of (3.1).
Proof
We have to show that if \({\mathcal {F}}\in {\textsf {FCC} }({{{\,\mathrm{{A}}\,}}})\) then
We claim that
Indeed, if \((0,\varphi )\in {\mathcal {F}}\) then, for each \(U\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(0)\), it follows that \({\varphi }^{*}(U)\in {{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({\mathcal {F}})\), hence \(\displaystyle {\mathop {{{{{\textbf {{\textsf {lim}}}}} }}}\nolimits _{{{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({\mathcal {F}})}\varphi =0}\) and thus \((0,\varphi )\in {{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({\mathcal {F}}))\), hence (3.8) holds. Now, if \((y,\varphi )\in {\mathcal {F}}\) then \((0,\varphi -y)\in {\mathcal {F}}\), since \({\mathcal {F}}\) is translation invariant, hence (3.8) implies that \((0,\varphi -y)\in {{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({\mathcal {F}}))\), and since \({{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({\mathcal {F}}))\) is translation invariant, it follows that \((y,\varphi )\in {{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({\mathcal {F}}))\). Hence we have proved that \({\mathcal {F}}\subset {{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({\mathcal {F}}))\).
Assume that \((y,\beta )\in {{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({\mathcal {F}}))\). Then \(\displaystyle {\mathop {{{{{\textbf {{\textsf {lim}}}}} }}}\nolimits _{{{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({\mathcal {F}})} \beta =y}\). Hence \({\beta }^{*}(U)\in {{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({\mathcal {F}})\) for each \(U\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(y)\). This means that for each \(U\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(y)\) there exists \(W\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(0)\) and \(\gamma \in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\) such that \((0,\gamma )\in {\mathcal {F}}\) and \({\gamma }^{*}(W)={\beta }^{*}(U)\). Since \({\mathcal {F}}\) is translation invariant, it follows that for each \(U\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(y)\) there exists \(V\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(y)\) and \(\varphi \in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\) such that \((y,\varphi )\in {\mathcal {F}}\) and \({\varphi }^{*}(V)={\beta }^{*}(U)\). Since \({\mathcal {F}}\) is local, it follows that \((y,\beta )\in {\mathcal {F}}\). Hence we have proved that \({{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {s} }}_{{{\,\mathrm{{A}}\,}}}({\mathcal {F}}))\subset {\mathcal {F}}\), and the proof is complete. \(\square \)
Theorem 3.7
If \({\mathcal {F}}\in {\textsf {FCC} }({{{\,\mathrm{{A}}\,}}})\) then there exists a unique  such that \({{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})={\mathcal {F}}\).
such that \({{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})={\mathcal {F}}\).
Proof
It suffices to apply Lemmas 3.5 and 3.6. \(\square \)
3.3 Moore–Smith Sequences
In 1915 and 1922 Eliakim Hastings Moore and Herman Lyle Smith attempted to subsume different limiting processes under the same notion [23, 24]. They were motivated by the following heuristic principle:
The existence of analogies between central features of various theories implies the existence of a more fundamental general theory embracing the special theories as particular instances and unifying them as to those central features. [23, p. 628]
We now present a list of examples which Moore and Smith had in mind, or which one should keep in mind in order to gain a better appreciation of their contribution. In these examples, marked with their initials, \(\varphi \) denotes a function \({{\,\mathrm{{A}}\,}}\rightarrow {{\mathbb {R}}}\).
(Example MS 1) \({{\,\mathrm{{A}}\,}}={\mathbb {N}}\), hence \(\varphi \) is a sequence of real numbers, and \(\displaystyle {\lim \nolimits _{n\rightarrow +\infty }\varphi (n)}=y\) in the usual sense.
(Example MS 2) \({{\,\mathrm{{A}}\,}}=(-\infty ,a)\cup (a,+\infty )\), with \(a\in {{\mathbb {R}}}\), and \(\displaystyle {\lim \nolimits _{x\rightarrow {}a}\varphi (x)=y}\) in the usual sense
(Example MS 3) \({{\,\mathrm{{A}}\,}}\) is the collection of tagged partitions of the interval [0, 1], \(\varphi \) encodes the Riemann sums of a given function \(f:[0,1]\rightarrow {{\mathbb {R}}}\), and the limiting process to which \(\varphi \) is subject yields as a limiting value the Riemann integral of f, i.e.,  .
.
In their work, they created the notion of Moore–Smith sequence (see below), and, in so doing, they introduced the notion of a direction. As is customary, if \(\texttt {R}\) is a binary relation on a set S, i.e., a subset of \(S\times {}S\), we write \(j\texttt {R}{}k\) instead of \((j,k)\in \texttt {R}\).
Definition 3.8
A preorder \(\texttt {R}\) on a nonempty set S is a reflexive and transitive binary relation on S, i.e., a subset of \(S\times {}S\) with the following properties:
- (R):
-
\(j\texttt {R}{}{}j\) for each \(j\in {}S\) (reflexivity);
- (T):
-
if \(j\texttt {R}{}{}k\) and \(k\texttt {R}{}{}l\) then \(j\texttt {R}{}{}l\) (transitivity).
A preordered set \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\equiv ({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}_{\texttt {Set}},\texttt {R}_{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}})\) is a set \({{\,\mathrm{{A}}\,}}_{\texttt {Set}}\) endowed with a preorder \(\texttt {R}_{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}}\).
Definition 3.9
A partial order \(\texttt {R}\) on a nonempty set S is a preorder \(\texttt {R}\) on S which also satisfies the following condition:
- (A):
-
if \(j\texttt {R}{}{}k\) and \(k\texttt {R}{}{}j\) then \(j=k\) (antisymmetry).
A poset \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is a set \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}_{\texttt {Set}}\) endowed with a partial order \(\texttt {R}_{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}}\).
Example 3.10
\({{\mathcal {P}}}({{\,\mathrm{{A}}\,}})\) is a poset under set inclusion. Every subset of a poset is a poset under the restriction of the binary relation.
Definition 3.11
If \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is a preordered set and \(x\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\), the tail in \({{\,\mathrm{{A}}\,}}\) from \(x\) is the set
A subset \(T\subset {{\,\mathrm{{A}}\,}}\) is called a tail in \({{\,\mathrm{{A}}\,}}\) if \(T=\texttt {tail}_{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}}\!\left( x\right) \) for some \(x\in {{\,\mathrm{{A}}\,}}\).
Definition 3.12
A subset \(T\subset {{\,\mathrm{{A}}\,}}\) is called final in \({{\,\mathrm{{A}}\,}}\) if it contains some tail, and the collection of all final sets in \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is
We may write \({\textsf {Fin} }[{\texttt {R}}]\) instead of \({\textsf {Fin} }[{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}}]\) in case we need to emphasize the role of the direction \(\texttt {R}\).
The notion of tail, and the associated notion of final set, display their full power only if some other assumptions are made on the preorder.
Definition 3.13
A direction on a set S is a preorder \(\texttt {R}{}\) on S such that, for each \(j,k\in {}S\), there exists an element \(l\in {}S\) such that \(j\texttt {R}{}{}l\) and \(k\texttt {R}{}{}l\). We define
A directed set \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}=({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}_{\texttt {Set}},\texttt {R}_{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}})\) is a set \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}_{\texttt {Set}}\) endowed with a direction \(\texttt {R}_{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}}\) on \({{\,\mathrm{{A}}\,}}_{\texttt {Set}}\).
We will see that \({{\,\mathrm{{A}}\,}}\) is a directed set if and only if \({\textsf {Fin} }[{{{\,\mathrm{{A}}\,}}}]\) is a filter on \({{\,\mathrm{{A}}\,}}\).
Example 3.14
\({\mathbb {N}}\) is a directed set under the natural order: \(j\le {}k\) if \(k-j\ge 0\).
The following result shows that reverse inclusion in a filter is a direction.
Example 3.15
If  , then reverse inclusion between sets \((\supset )\) is a direction on \({{\textsf {Z} }}\). In particular, if \(\Theta \) is a topology on \({{\,\mathrm{{A}}\,}}\) and \(x\in {{\,\mathrm{{A}}\,}}\), then \(({{{\textsf {N} }}}_{\Theta }(x),\supset )\) is a directed set.
, then reverse inclusion between sets \((\supset )\) is a direction on \({{\textsf {Z} }}\). In particular, if \(\Theta \) is a topology on \({{\,\mathrm{{A}}\,}}\) and \(x\in {{\,\mathrm{{A}}\,}}\), then \(({{{\textsf {N} }}}_{\Theta }(x),\supset )\) is a directed set.
Directed sets serve as domains of definition of Moore–Smith sequences. It is useful to emphasize the role of the codomain, as in the following definition.
Definition 3.16
If \({{\,\mathrm{{Y}}\,}}\) is a nonempty set, we define

The elements of \({\mathscr {S}}{({{\,\mathrm{{Y}}\,}})}\) are called \({{\,\mathrm{{Y}}\,}}\)-valued Moore–Smith sequences. The directed set which appears in (3.12) is called (with slight abuse of language) the direction of  .
.
Observe that

i.e., each element of \({{\,\mathrm{{Y}}\,}}\) may be seen as a constant sequence, and each sequence is a Moore–Smith sequence.
Lemma 3.17
The map \({{\,\mathrm{{Y}}\,}}\mapsto {\mathscr {S}}{({{\,\mathrm{{Y}}\,}})}\) is the object function of a functor \({\mathscr {S}}:\texttt {Set}\rightarrow \texttt {Set}\). The mapping function of \({\mathscr {S}}\) maps \(f\in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{Y}}\,}},{{\,\mathrm{{Y}}\,}}'),\) where \({{\,\mathrm{{Y}}\,}},{{\,\mathrm{{Y}}\,}}'\) are two sets, to the function \({f}_{\varvec{\circ }}:{\mathscr {S}}{({{\,\mathrm{{Y}}\,}})}\rightarrow {\mathscr {S}}{({{\,\mathrm{{Y}}\,}}')}\) which maps  to
to  where
where  is the composition of functions.
is the composition of functions.
Proof
The proof follows at once from the fact that the composition of functions is associative whenever defined, and  . For background, see [22, p. 501]. \(\square \)
. For background, see [22, p. 501]. \(\square \)
Observe that a direction is not necessarily a partial order, since antisymmetry may fail. An antisymmetric direction on a set \({{\,\mathrm{{A}}\,}}\) is a direction \(\texttt {R}\) on \({{\,\mathrm{{A}}\,}}\) for which if \(j\texttt {R}{}{}k\) and \(k\texttt {R}{}{}j\) then \(j=k\).
3.4 Limiting Values of Moore–Smith Sequences
Definition 3.18
If  is a
is a  -valued Moore–Smith sequence,
-valued Moore–Smith sequence,  is a topology on \({{\,\mathrm{{Y}}\,}}\), \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is the direction of
is a topology on \({{\,\mathrm{{Y}}\,}}\), \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is the direction of  , and \(y\in {{\,\mathrm{{Y}}\,}}\), we say that
, and \(y\in {{\,\mathrm{{Y}}\,}}\), we say that  is the limiting value of.
is the limiting value of.  along \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\), and write
along \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\), and write

if, for each \(O\in {{{\textsf {N} }}}_{\Theta }(y)\),  is final in \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\).
is final in \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\).
Example 3.19
On \({{\mathbb {R}}}\) the preorder \(\le \) [resp. the preorder \(\ge \)] yield the familiar notions  [resp.
[resp.  ] for a \({{\,\mathrm{{Y}}\,}}\)-valued Moore–Smith sequence
] for a \({{\,\mathrm{{Y}}\,}}\)-valued Moore–Smith sequence  .
.
If we need to emphasize more explicitly the preorder \(\texttt {R}\) or the direction \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\), we write

instead of (3.14).
Definition 3.20
If  and \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is the direction of
and \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is the direction of  , we say that
, we say that  if for each \(r\in {{\mathbb {R}}}\) the set
if for each \(r\in {{\mathbb {R}}}\) the set  is final in
is final in  . We say that
. We say that  if
if 
The following elementary remark is useful in topological spaces where points are not necessarily separated. We will see that the set  is endowed with a topology of this kind. Indeed, we will see that
is endowed with a topology of this kind. Indeed, we will see that  is compact but not Hausdorff, while
is compact but not Hausdorff, while  is compact and Hausdorff.
is compact and Hausdorff.
Lemma 3.21
If \(\varvec{{{\,\mathrm{z}\,}}},\varvec{{{\,\mathrm{w}\,}}}\in {{\,\mathrm{{Y}}\,}}\) and \(\Theta \) is a topology on \({{\,\mathrm{{Y}}\,}},\) then the following conditions are equivalent:
- (1):
-
\(,\)
- (2):
-
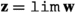 .
.
Remark 3.22
Of course the statement is interesting only if \(\varvec{{{\,\mathrm{z}\,}}}\not =\varvec{{{\,\mathrm{w}\,}}}\). Observe that  is the closure in the given topology, and that (2) rests on the fact that, according to (3.13), we may identify \(\varvec{{{\,\mathrm{w}\,}}}\) with the constant sequence
is the closure in the given topology, and that (2) rests on the fact that, according to (3.13), we may identify \(\varvec{{{\,\mathrm{w}\,}}}\) with the constant sequence  identically equal to \(\varvec{{{\,\mathrm{w}\,}}}\), and indeed (2) says that \(\varvec{{{\,\mathrm{z}\,}}}\) is the limiting value of this sequence.
identically equal to \(\varvec{{{\,\mathrm{w}\,}}}\), and indeed (2) says that \(\varvec{{{\,\mathrm{z}\,}}}\) is the limiting value of this sequence.
Proof
Define  by
by  for each w. Then
for each w. Then  is equal to \({\mathbb {N}}\) for each \(O\in {{{\textsf {N} }}}_{\Theta }(\varvec{{{\,\mathrm{z}\,}}})\), since
is equal to \({\mathbb {N}}\) for each \(O\in {{{\textsf {N} }}}_{\Theta }(\varvec{{{\,\mathrm{z}\,}}})\), since  , hence
, hence  , and (2) follows from the identification of \(\varvec{{{\,\mathrm{w}\,}}}\) with
, and (2) follows from the identification of \(\varvec{{{\,\mathrm{w}\,}}}\) with  in (3.13). \(\square \)
in (3.13). \(\square \)
Lemma 3.21 is a special case of the following, more general, result, due to Garrett Birkhoff [3]. Observe that if \(W\subset {{\,\mathrm{{Y}}\,}}\) then each W-valued Moore–Smith sequence may be seen as a \({{\,\mathrm{{Y}}\,}}\)-valued Moore–Smith sequence:
Lemma 3.23
([3]) If \(({{\,\mathrm{{Y}}\,}},\Theta )\) is a topological space, \(W\subset {{\,\mathrm{{Y}}\,}},\) and \(z\in {{\,\mathrm{{Y}}\,}}\) then the following conditions are equivalent.
- (1):
-
\(,\)
- (2):
-
there exists
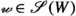 such that
such that  .
.
Proof
If (1) holds, then \({{\textsf {b} }}\cap {}W\not =\emptyset \) for each \({{\textsf {b} }}\in {{{\textsf {N} }}}_{\Theta }(z)\), hence there exists a function  such that
such that  for each \({{\textsf {b} }}\in {{{\textsf {N} }}}_{\Theta }(z)\), and
for each \({{\textsf {b} }}\in {{{\textsf {N} }}}_{\Theta }(z)\), and  is a generalized sequence, by Example 3.15. Let \(O\in {{{\textsf {N} }}}_{\Theta }(z)\) . If \(U\in {{{\textsf {N} }}}_{\Theta }(z)\) and \(O\supset {}U\) then
is a generalized sequence, by Example 3.15. Let \(O\in {{{\textsf {N} }}}_{\Theta }(z)\) . If \(U\in {{{\textsf {N} }}}_{\Theta }(z)\) and \(O\supset {}U\) then  hence
hence  . Hence
. Hence  . Thus
. Thus  . If (2) holds then for each \(O\in {{{\textsf {N} }}}_{\Theta }(z)\) there exists \(x\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) such that
. If (2) holds then for each \(O\in {{{\textsf {N} }}}_{\Theta }(z)\) there exists \(x\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) such that  , thus \(O\cap {}W\) contains
, thus \(O\cap {}W\) contains  for any \(r\in \texttt {tail}_{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}}\!\left( x\right) \). Hence \(O\cap {}W\) is not empty and (1) holds. \(\square \)
for any \(r\in \texttt {tail}_{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}}\!\left( x\right) \). Hence \(O\cap {}W\) is not empty and (1) holds. \(\square \)
Remark on notation In order to facilitate the distinction between the setting of filters and the setting of Moore–Smith sequences, and also to gain a better appreciation of the connection between the two viewpoints, we use bold Sans Serif font to denote limiting notions pertaining to filters, such as \(\varvec{{{{{{\textbf {{\textsf {lim}}}}} }}}}\), \({{{{\textbf {{\textsf {cluster}}}}} }}\), \({{{{\textbf {{\textsf {liminf}}}}} }}\), \({{{{\textbf {{\textsf {limsup}}}}} }}\), and Typewriter font to denote notions pertaining to Moore–Smith sequences, such as  and \(\texttt {ClusterSet}\). Indeed, it seems to us that if we used the same notation for the different notions then the connection between the two viewpoints would be obscured by the uniform notation.
and \(\texttt {ClusterSet}\). Indeed, it seems to us that if we used the same notation for the different notions then the connection between the two viewpoints would be obscured by the uniform notation.
3.5 The Functional Convergence Class Associated to a Direction
The following result says that convergence along a direction, described in Definition 3.18, is a limiting process that yields a functional convergence class, just as the limiting process of convergence along a filter does. However, we will see that the limiting process of convergence along a filter on \({{\,\mathrm{{A}}\,}}\), described in Definition 1.12, has wider scope and higher synthetic power than the limiting process of convergence along a direction on \({{\,\mathrm{{A}}\,}}\), described in Definition 3.18.
Theorem 3.24
If \(\texttt {R}\in {{\,\mathrm{dir}\,}}({{\,\mathrm{{A}}\,}})\) then

is a functional convergence class on \({{\,\mathrm{{A}}\,}}\).
Proof
The proof will be given in Sect. 3.6. \(\square \)
3.6 A Comparison of the Two Notions
In 1938, Herman Lyle Smith considered the following notion of limiting value, due to Arnaud Denjoy [10, p. 165], [32, 13, p. 158]. We say that \(\varphi \) has approximate limiting value equal to \(y\) at \(x_0\) if the following condition holds.
(Example MS 4) \(\varphi :{{\mathbb {R}}}\rightarrow {{\mathbb {R}}}\) is measurable, \(x_0\in {{\mathbb {R}}}\), \(y\in {{\mathbb {R}}}\), and for each \(\epsilon >0\) the set
has density equal to 1 at \(x_0\).
H. L. Smith observed that the limiting notion in (Example MS 4) may be readily subsumed under Definition 1.12 but that it cannot be covered by Definition 3.18 “without a somewhat artificial transformation.”
Observe that the collection of final sets in a directed set is a filter. For example, the filter generated by the natural order on \({\mathbb {N}}\) is the Fréchet filter (see Example 1.9). Indeed, we now show that every directed set \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) yields a filtered set \( {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}_{\texttt {FSet}}{\mathop {=}\limits ^\mathrm{{def}}}({{\,\mathrm{{A}}\,}}_{\texttt {Set}},{\textsf {Fin} }[{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}}])\), whose underlying set is the underlying set of \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) and whose filter is the one generated by the given direction on \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\). In other words, we define a map

Lemma 3.25
If \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is a directed set, then the collection \({\textsf {Fin} }[{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}}]\) of final sets in \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is a filter on \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}},\) called the filter generated by (the tails of) \(\texttt {R}\).
Proof
If \({{\textsf {b} }}_1,{{\textsf {b} }}_2\in {\textsf {Fin} }[{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}}]\) then there exist \(x_1,x_2\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) with \(\texttt {tail}_{{{\,\mathrm{{A}}\,}}}\!\left( x_1\right) \subset {{\textsf {b} }}_1\) and \(\texttt {tail}_{{{\,\mathrm{{A}}\,}}}\!\left( x_2\right) \subset {{\textsf {b} }}_2\), and there exists a majorant \(x\) of \(x_1\), \(x_2\), and therefore \(\texttt {tail}_{{{\,\mathrm{{A}}\,}}}\!\left( x\right) \subset \texttt {tail}_{{{\,\mathrm{{A}}\,}}}\!\left( x_1\right) \cap \texttt {tail}_{{{\,\mathrm{{A}}\,}}}\!\left( x_2\right) \subset {{\textsf {b} }}_1\cap {{\textsf {b} }}_2\). Hence \({{\textsf {b} }}_1\cap {{\textsf {b} }}_2\in {\textsf {Fin} }[{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}}]\). \(\square \)
Lemma 3.25 enables us to subsume Definition 3.18 under Definition 1.12.
Lemma 3.26
If  is a \({{\,\mathrm{{Y}}\,}}\)-valued Moore–Smith sequence, \(\Theta \) is a topology on \({{\,\mathrm{{Y}}\,}},\) \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is the direction of
is a \({{\,\mathrm{{Y}}\,}}\)-valued Moore–Smith sequence, \(\Theta \) is a topology on \({{\,\mathrm{{Y}}\,}},\) \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is the direction of  and \(y\in {{\,\mathrm{{Y}}\,}},\) then the following conditions are equivalent
and \(y\in {{\,\mathrm{{Y}}\,}},\) then the following conditions are equivalent
Proof
Definition 3.18 says precisely that  is a filter-homomorphism. \(\square \)
is a filter-homomorphism. \(\square \)
Proof of Theorem 3.24
Lemma 3.26 says that

and we know from Theorem 3.2 that the right-hand side of (3.17) is a functional convergence class, since \({\textsf {Fin} }[{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}}]\) is a filter on \({{\,\mathrm{{A}}\,}}\). \(\square \)
Hence (3.15) and Theorem 3.24 yield a map
Moreover, the following result also follows immediately from Theorem 3.24.
Theorem 3.27
If \({{\,\mathrm{{A}}\,}}\) is a nonempty set, then the following diagram is commutative

where the map on the top is the one given in (3.16) and the diagonal map is the one given in (3.18).
Proof
The result follows immediately from Lemma 3.26. \(\square \)
Recall that Theorem 3.7 says that \({{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}\) in (3.19) is 1–1 and onto, and this means that every functional convergence class on \({{\,\mathrm{{A}}\,}}\) is associated to a unique filter. One may wonder whether the diagonal map in (3.19) is also onto, i.e., whether every functional convergence class is associated to a direction on \({{\,\mathrm{{A}}\,}}\). As far as we know, the following result is new.
Theorem 3.28
If \({{\,\mathrm{{A}}\,}}\) is equal to the unit disc in \({{\mathbb {C}}},\) then the diagonal map in (3.19) is not onto. Indeed, the functional convergence class associated to nontangential convergence is not associated to any direction.
Proof
We now show that Theorem 3.28 may be reduced to Theorem 3.29, to be stated momentarily. Recall that if \({\mathbb {D}}{\mathop {=}\limits ^\mathrm{{def}}}\left\{ z\!:z\in {{\mathbb {C}}},|z|<1\right\} \) is the unit disc in \({{\mathbb {C}}}\), then there exists a filter  , called the nontangential filter on \({\mathbb {D}}\) ending at 1 (see [11, 12, 33], for background), such that the following result holds.
, called the nontangential filter on \({\mathbb {D}}\) ending at 1 (see [11, 12, 33], for background), such that the following result holds.
(Example MS 5) For each \(\varphi :{\mathbb {D}}\rightarrow {{\mathbb {R}}}\) and each \({z}\in [-\infty ,+\infty ]\), \(\displaystyle {\mathop {{{{{\textbf {{\textsf {lim}}}}} }}}\nolimits _{{{\textsf {S} }}}\varphi }=z\) if and only if \(\displaystyle {\lim \nolimits _{\textsc {t}\ni {}z\rightarrow x}\varphi (z)=z}\) for each open Euclidean triangle \(\textsc {t}\) contained in \({\mathbb {D}}\) and having 1 as a vertex.
A precise definition of the nontangential filter \({{\textsf {S} }}\) will be given in Sect. 5.
Theorem 3.28 follows at once from the following result.
Theorem 3.29
The nontangential filter \({{\textsf {S} }}\) on \({\mathbb {D}}\) is not equal to the filter of tails of any direction on \({\mathbb {D}}\).
The proof of Theorem 3.29 will be given in Sect. 5. \(\square \)
Remark 3.30
We do not know whether an intrinsic characterization of the image of the map (3.16) is known, i.e., whether it is possible to give an intrinsic characterization of those filters which are generated by a direction.
Remark 3.31
Lemma 3.25 shows that every directed set \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) yields a filtered set \( {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}_{\texttt {FSet}}{\mathop {=}\limits ^\mathrm{{def}}}({{\,\mathrm{{A}}\,}}_{\texttt {Set}},{\textsf {Fin} }[{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}}])\), whose underlying set is the underlying set of \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) and whose filter is the filter of tails of the given direction on \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\). We will look at \(\texttt {DSet}\) as a full subcategory of \(\texttt {FSet}\), i.e., we will declare that \(\texttt {DSet}\)-homomorphisms from \({{\,\mathrm{{A}}\,}}\) to \({{\,\mathrm{{A}}\,}}'\), where \({{\,\mathrm{{A}}\,}}\) and \({{\,\mathrm{{A}}\,}}'\) are directed sets, are precisely the \(\texttt {FSet}\)-homomorphisms from \({{\,\mathrm{{A}}\,}}_{\texttt {FSet}}\) to \({{\,\mathrm{{A}}\,}}'_{\texttt {FSet}}\). However, we will not base the notion of Moore–Smith subsequence on this identification, since it would lead to “irregularities” [1, p. 285] and make the subject somewhat “contentious,” as Saitulaa Naranong puts it in Translating between Nets and Filters (2010) (unpublished). We will return to this theme in Sect. 12.
Directed sets form a proper subclass of the objects of the category \(\texttt {FSet}\) of filtered sets, since
(Lemma 3.26) the relevant data in a directed set is the filter of tails of the given direction, and
(Theorem 3.29) The map (3.18) is not necessarily onto.
In his work, R. de Possel used sequences of measurable sets. One may be tempted to employ instead Moore–Smith sequences, and we will do so in Sect. 3.7, but we will see that filters appear to be more flexible and direct. This conclusion may appear to be counterintuitive, since convergence phenomena are based on an idea of movement, and Moore–Smith sequences appear to be especially suited to represent them, because a “dynamic” is encoded in the directed set which acts as their basis, while filters are seemingly “static” objects, in the sense that there is no apparent “sense of direction” in them. In Sect. 9, we will show that this impression is erroneous, since the collection of all filters on a given nonempty set is endowed with a natural topology, which is especially suited to be used in the study of convergence phenomena. Hence, the advantage of filters is that there is no need to rest on the additional structure of a directed set, since a “sense of direction” is encoded in their intrinsic structure.
3.7 The Functional Convergence Class Associated to a Family of Moore–Smith Sequences
We now introduce another method for constructing functional convergence classes.
Definition 3.32
If \({{\,\mathrm{{A}}\,}}\) is a nonempty set and a nonempty set \(V\subset {\mathscr {S}}{({{\,\mathrm{{A}}\,}})}\) is given, then define

Theorem 3.33
If \({{\,\mathrm{{A}}\,}}\) is a nonempty set and a nonempty set \(V\subset {\mathscr {S}}{({{\,\mathrm{{A}}\,}})}\) is given, then \({\mathcal {F}}_{V},\) defined in (3.20), is a functional convergence class.
Proof
The proof will be given in Sect. 7. \(\square \)
Theorem 3.34
If  then there exists \(V\subset {\mathscr {S}}{({{\,\mathrm{{A}}\,}})}\) such that, for each topological space \(({{\,\mathrm{{Y}}\,}},\Theta ),\) every \(y\in {{\,\mathrm{{Y}}\,}},\) and each function \(\varphi :{{\,\mathrm{{A}}\,}}\rightarrow {{\,\mathrm{{Y}}\,}},\) the following conditions are equivalent:
then there exists \(V\subset {\mathscr {S}}{({{\,\mathrm{{A}}\,}})}\) such that, for each topological space \(({{\,\mathrm{{Y}}\,}},\Theta ),\) every \(y\in {{\,\mathrm{{Y}}\,}},\) and each function \(\varphi :{{\,\mathrm{{A}}\,}}\rightarrow {{\,\mathrm{{Y}}\,}},\) the following conditions are equivalent:
- (1):
-

- (2):
-
for each
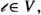
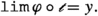
Proof
Define

Observe that \({{\textsf {Z} }}\) is a directed set, by Example 3.15, and hence \(S\subset {\mathscr {S}}{({{\,\mathrm{{A}}\,}})}\). Let  be a topological space, \(\varphi :{{\,\mathrm{{A}}\,}}\rightarrow {{\,\mathrm{{Y}}\,}}\), and \(y\in {{\,\mathrm{{Y}}\,}}\), and assume that (1) holds. If \(U\in {{{\textsf {N} }}}_{\Theta }(y)\) then there exists \({{\textsf {b} }}\equiv {{\textsf {b} }}_U\in {{\textsf {Z} }}\) such that \({{\textsf {b} }}={\varphi }^{*}(U)\). Let
be a topological space, \(\varphi :{{\,\mathrm{{A}}\,}}\rightarrow {{\,\mathrm{{Y}}\,}}\), and \(y\in {{\,\mathrm{{Y}}\,}}\), and assume that (1) holds. If \(U\in {{{\textsf {N} }}}_{\Theta }(y)\) then there exists \({{\textsf {b} }}\equiv {{\textsf {b} }}_U\in {{\textsf {Z} }}\) such that \({{\textsf {b} }}={\varphi }^{*}(U)\). Let  and consider
and consider  , where \({{\textsf {Z} }}\) is seen as a directed set, as in Example 3.15. If \({{\textsf {d} }}\in {{\textsf {Z} }}\) and \({{\textsf {b} }}\supset {{\textsf {d} }}\), then
, where \({{\textsf {Z} }}\) is seen as a directed set, as in Example 3.15. If \({{\textsf {d} }}\in {{\textsf {Z} }}\) and \({{\textsf {b} }}\supset {{\textsf {d} }}\), then  ,
,  , \({{\textsf {d} }}\subset {{\textsf {b} }}\), and \({{\textsf {b} }}={\varphi }^{*}(U)\) imply that
, \({{\textsf {d} }}\subset {{\textsf {b} }}\), and \({{\textsf {b} }}={\varphi }^{*}(U)\) imply that  . Since \(U\in {{{\textsf {N} }}}_{\Theta }(y)\) is arbitrary, it follows that
. Since \(U\in {{{\textsf {N} }}}_{\Theta }(y)\) is arbitrary, it follows that  , and since
, and since  is arbitrary, it follows that (2) holds. If (1) does not hold, then there exists \(U\in {{{\textsf {N} }}}_{\Theta }(y)\) such that \({\varphi }^{*}(U)\not \in {{\textsf {Z} }}\). Hence for each \({{\textsf {b} }}\in {{\textsf {Z} }}\) it is not true that \({{\textsf {b} }}\subset {\varphi }^{*}(U)\) (for otherwise it would follow that \({\varphi }^{*}(U)\in {{\textsf {Z} }}\), since \({{\textsf {Z} }}\) is a filter). Hence for each \({{\textsf {b} }}\in {{\textsf {Z} }}\) there exists \(x_{{{\textsf {b} }}}\in {{\textsf {b} }}\) such that \(x_{{{\textsf {b} }}}\not \in {\varphi }^{*}(U)\), i.e., \(\varphi (x_{{{\textsf {b} }}})\not \in {}U\). Define
is arbitrary, it follows that (2) holds. If (1) does not hold, then there exists \(U\in {{{\textsf {N} }}}_{\Theta }(y)\) such that \({\varphi }^{*}(U)\not \in {{\textsf {Z} }}\). Hence for each \({{\textsf {b} }}\in {{\textsf {Z} }}\) it is not true that \({{\textsf {b} }}\subset {\varphi }^{*}(U)\) (for otherwise it would follow that \({\varphi }^{*}(U)\in {{\textsf {Z} }}\), since \({{\textsf {Z} }}\) is a filter). Hence for each \({{\textsf {b} }}\in {{\textsf {Z} }}\) there exists \(x_{{{\textsf {b} }}}\in {{\textsf {b} }}\) such that \(x_{{{\textsf {b} }}}\not \in {\varphi }^{*}(U)\), i.e., \(\varphi (x_{{{\textsf {b} }}})\not \in {}U\). Define

by letting  . Then
. Then  but it is not true that
but it is not true that  , hence (2) does not hold. \(\square \)
, hence (2) does not hold. \(\square \)
Theorem 3.35
If \({{\,\mathrm{{A}}\,}}\) is a nonempty set, then every functional convergence class on \({{\,\mathrm{{A}}\,}}\) is equal to \({\mathcal {F}}_{V},\) defined in (3.20), for some nonempty \(V\subset {\mathscr {S}}{({{\,\mathrm{{A}}\,}})}\).
Proof
This result follows at once from Theorems 3.7 and 3.34. \(\square \)
We have thus seen that a functional convergence class on \({{\,\mathrm{{A}}\,}}\) may be represented in terms of a unique filter, or in terms of a family V, as in Theorem 3.33. The advantage of the representation in terms of filters is precisely given by uniqueness. Indeed, the lack of uniqueness would cause some difficulties in the determination of the exceptional set for a.e. convergence. Hence the approach based on the notion of filter has higher synthetic power and flexibility.
Theorem 3.34 shows that the functional convergence class \({{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})\) of a given filter \({{\textsf {Z} }}\) on \({{\,\mathrm{{A}}\,}}\) may be described as \({\mathcal {F}}_{V}\), in terms of a set V of \({{\,\mathrm{{A}}\,}}\)-valued Moore–Smith sequences. One may wonder whether it is possible to choose as V a set of \({{\,\mathrm{{A}}\,}}\)-valued sequences, and whether it is possible to choose as V as set consisting of just one Moore–Smith sequence. We will see that the answer to the first question is in the negative, and that the answer to the second question is in the positive.
Theorem 3.36
There exists a nonempty set \({{\,\mathrm{{A}}\,}}\) and a functional convergence class \({\mathcal {F}}\) on \({{\,\mathrm{{A}}\,}}\) such that \({\mathcal {F}}\) cannot be represented in the form \({\mathcal {F}}_{V}\) where V is a collection of \({{\,\mathrm{{A}}\,}}\)-valued sequences.
Proof
Let \({{\,\mathrm{{A}}\,}}={\mathbb {N}}\) and let  be an ultrafilter on \({\mathbb {N}}\) which contains the Fréchet filter. \(\square \)
be an ultrafilter on \({\mathbb {N}}\) which contains the Fréchet filter. \(\square \)
Theorem 3.37
For every nonempty set \({{\,\mathrm{{A}}\,}}\) and each functional convergence class \({\mathcal {F}}\) on \({{\,\mathrm{{A}}\,}}\) there exists an \({{\,\mathrm{{A}}\,}}\)-valued Moore–Smith sequence \({\varvec{q}}\) such that \({\mathcal {F}}={\mathcal {F}}_{{\varvec{q}}}\).
Proof
The proof will be given in Sect. 8. \(\square \)
4 Preliminary Results on Filters
The goal of this section is to give a self-contained presentation of the basic results on filters.
4.1 Basic Lattice-Theoretic Properties of 
A preliminary examination of some lattice-theoretic properties of  will be useful, as we will see, in order to gain a better understanding of the topological implications of the notion of filter. Recall that if \({\mathcal {C}}\) is a family of filters, i.e., if
will be useful, as we will see, in order to gain a better understanding of the topological implications of the notion of filter. Recall that if \({\mathcal {C}}\) is a family of filters, i.e., if  , then
, then
Lemma 4.1
(Cartan [8]) The intersection \(\bigcap {\mathcal {C}}\) of any nonempty family \({\mathcal {C}}\) of filters on a set is not empty and is a filter.
Proof
If  then \({{\,\mathrm{{A}}\,}}\in \bigcap {\mathcal {C}}\), hence \(\bigcap {\mathcal {C}}\not =\emptyset \). If \({{\textsf {b} }}_1,{{\textsf {b} }}_2\in \bigcap {\mathcal {C}}\) then \({{\textsf {b} }}_1,{{\textsf {b} }}_2\in {{\textsf {Z} }}\) for each \({{\textsf {Z} }}\in {\mathcal {C}}\), hence \({{\textsf {b} }}_1\cap {{\textsf {b} }}_2\in {{\textsf {Z} }}\) for each \({{\textsf {Z} }}\in {\mathcal {C}}\), hence \({{\textsf {b} }}_1\cap {{\textsf {b} }}_2\in \bigcap {\mathcal {C}}\). If \({{\textsf {b} }}\in \bigcap {\mathcal {C}}\) and \({{\textsf {b} }}\subset {{\textsf {d} }}\), then \({{\textsf {b} }}\in {{\textsf {Z} }}\) hence \({{\textsf {d} }}\in {{\textsf {Z} }}\) for each \({{\textsf {Z} }}\in {\mathcal {C}}\), thus \({{\textsf {d} }}\in {\mathcal {C}}\). \(\square \)
then \({{\,\mathrm{{A}}\,}}\in \bigcap {\mathcal {C}}\), hence \(\bigcap {\mathcal {C}}\not =\emptyset \). If \({{\textsf {b} }}_1,{{\textsf {b} }}_2\in \bigcap {\mathcal {C}}\) then \({{\textsf {b} }}_1,{{\textsf {b} }}_2\in {{\textsf {Z} }}\) for each \({{\textsf {Z} }}\in {\mathcal {C}}\), hence \({{\textsf {b} }}_1\cap {{\textsf {b} }}_2\in {{\textsf {Z} }}\) for each \({{\textsf {Z} }}\in {\mathcal {C}}\), hence \({{\textsf {b} }}_1\cap {{\textsf {b} }}_2\in \bigcap {\mathcal {C}}\). If \({{\textsf {b} }}\in \bigcap {\mathcal {C}}\) and \({{\textsf {b} }}\subset {{\textsf {d} }}\), then \({{\textsf {b} }}\in {{\textsf {Z} }}\) hence \({{\textsf {d} }}\in {{\textsf {Z} }}\) for each \({{\textsf {Z} }}\in {\mathcal {C}}\), thus \({{\textsf {d} }}\in {\mathcal {C}}\). \(\square \)
Observe that \({{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\) is a poset, hence  is a poset under set inclusion (Example 3.10).
is a poset under set inclusion (Example 3.10).
Definition 4.2
If x, y are elements of a poset \(({{\,\mathrm{{X}}\,}},\texttt {R})\), then an element \(l\in {{\,\mathrm{{X}}\,}}\) is called a lower bound for x and y in \({{\,\mathrm{{X}}\,}}\) if \(l\texttt {R}{}x\) and \(l\texttt {R}{}y\). An element \(l\in {{\,\mathrm{{X}}\,}}\) of a poset \({{\,\mathrm{{X}}\,}}\) is called a meet of x and y, or greatest lower bound (g.l.b.) of x and y, if (i) l is a lower bound of x and y, and (ii) if b is any other lower bound of x and y, then \(b\texttt {R}{}l\). If it exists, a meet of x and y in a poset \({{\,\mathrm{{X}}\,}}\) is denoted by \(x\wedge {}y\).
Observe that antisymmetry of \(\texttt {R}\) implies that, in a poset, a meet of x and y, if it exists, is unique.
The notion of greatest lower bound of a subset S of a poset \({{\,\mathrm{{X}}\,}}\) is defined in a natural way, to wit: If it exists, it is an element \(l\in {{\,\mathrm{{X}}\,}}\) such that (i) l is a lower bound of S (i.e., \(l\texttt {R}{}a\) for each \(a\in {}S\)), and (ii) if b is a lower bound of S, then \(b\texttt {R}{}l\); If it exists, it is unique. If it exists, the greatest lower bound of a subset S is denoted by \(\displaystyle {\bigwedge \nolimits _{s\in {}S}{s}}\).
Proposition 4.3
(Cartan [8]) The infimum (greatest lower bound) \(\displaystyle {\bigwedge \nolimits _{{{\textsf {Z} }}\in {\mathcal {C}}}{{\textsf {Z} }}}\) of any nonempty family \({\mathcal {C}}\) of filters on \({{\,\mathrm{{A}}\,}}\) exists in  . It is the intersection of all the filters in the family.
. It is the intersection of all the filters in the family.
Proof
The statement follows at once from Lemma 4.1. \(\square \)
Definition 4.4
If x, y are elements of a poset \(({{\,\mathrm{{X}}\,}},\mathrm{R})\), an element \(l\in {{\,\mathrm{{X}}\,}}\) is called a upper bound for x and y in \({{\,\mathrm{{X}}\,}}\) if \(x\texttt {R}{}l\) and \(y\texttt {R}{}l\). An element \(l\in {{\,\mathrm{{X}}\,}}\) of a poset \({{\,\mathrm{{X}}\,}}\) is called a join of x and y, or least upper bound (l.u.b.) of x and y, if (i) l is an upper bound of x and y, and (ii) if u is any other upper bound of x and y, then \(l\texttt {R}{}u\). If it exists, a join of x and y in a poset \({{\,\mathrm{{X}}\,}}\) is denoted by \(x\vee {}y\).
Antisymmetry implies that, in a poset, a join of x and y, if it exists, is unique. In Sect. 9.2 we will see that the existence of the join of two filters is more delicate.
4.2 The Operator \(\varvec{{{\,\mathrm{{A}}\,}}^{\uparrow }}\)
In order to present a basic technique for the construction of filters and exhibit more examples of filters, we introduce an operator \({{\,\mathrm{{A}}\,}}^{\uparrow }\) associated to every nonempty set. This operator is actually implicit in the definition of the notion of filter, so it is not surprising that it serves as a useful tool to construct new ones.
The basic building block for the operator \({{\,\mathrm{{A}}\,}}^{\uparrow }\) is contained in the following observation, which shows that  contains a copy of \({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\). Indeed, consider the following diagram
contains a copy of \({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\). Indeed, consider the following diagram

where the function \(\imath :{{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\rightarrow {{\mathcal {P}}}_{{{\bullet }}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}))\) is defined by \(\imath ({{\textsf {b} }}){\mathop {=}\limits ^\mathrm{{def}}}\{{{\textsf {b} }}\}\), for each \({{\textsf {b} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\), and the functions \({{\,\mathrm{{A}}\,}}_{\bullet }\) and \({{\,\mathrm{{A}}\,}}^{\uparrow }\) will be defined momentarily.
Lemma 4.5
If \({{\textsf {b} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\) then the collection
is a filter which contains \({{\textsf {b} }}\) as an element: it is the smallest filter on \({{\,\mathrm{{A}}\,}}\) which contains \({{\textsf {b} }}\) as an element, and is called the principal filter generated by \({{\textsf {b} }}\) on \({{\,\mathrm{{A}}\,}}\).
Proof
(F 0) \({{\textsf {b} }}\not =\emptyset \) \(\Rightarrow \) \(\emptyset \not \in {{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\). (F1.a) \({{\textsf {b} }}\subset {{\,\mathrm{{A}}\,}}\) \(\Rightarrow \) \({{\,\mathrm{{A}}\,}}\in {{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\). (F1.b) \({{\textsf {b} }}_1,{{\textsf {b} }}_2\in {{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\) \(\Rightarrow \) \({{\textsf {b} }}\subset {{\textsf {b} }}_1\) and \({{\textsf {b} }}\subset {{\textsf {b} }}_2\), hence \({{\textsf {b} }}\subset {{\textsf {b} }}_1\cap {{\textsf {b} }}_2\), thus \({{\textsf {b} }}_1\cap {{\textsf {b} }}_2\in {{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\). (F2) If \({{\textsf {c} }}\in {{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\) and \({{\textsf {c} }}\subset {{\textsf {d} }}\) then \({{\textsf {b} }}\subset {{\textsf {c} }}\subset {{\textsf {d} }}\), hence \({{\textsf {b} }}\subset {{\textsf {d} }}\), i.e., \({{\textsf {d} }}\in {{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\). Let \({\mathcal {C}}\) be the family of filters on \({{\,\mathrm{{A}}\,}}\) which contains \({{\textsf {b} }}\) as an element. If \({{\textsf {Z} }}\in {\mathcal {C}}\) and \({{\textsf {c} }}\in {{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\) then \({{\textsf {c} }}\in {{\textsf {Z} }}\), since \({{\textsf {b} }}\in {{\textsf {Z} }}\) and \({{\textsf {Z} }}\) is a filter. Hence \({{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\subset {{\textsf {Z} }}\). The conclusion follows from the fact that \({{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\in {\mathcal {C}}\). \(\square \)
Definition 4.6
Define \({{\,\mathrm{{A}}\,}}_{\bullet }:{{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\rightarrow {{\mathcal {P}}}_{{{\bullet }}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}))\) by \({{\,\mathrm{{A}}\,}}_{\bullet }({{\textsf {b} }}){\mathop {=}\limits ^\mathrm{{def}}}{{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\), for each \({{\textsf {b} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\).
The map \({{\,\mathrm{{A}}\,}}^{\uparrow }\) is designed to make the diagram (4.1) commutative (i.e., to extend \({{\,\mathrm{{A}}\,}}_{\bullet }\) to \({{\mathcal {P}}}_{{{\bullet }}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}))\)) and to commute with the union of collections.
Definition 4.7
A map
commutes with the union of collections if
for each indexed family of collections \({\{{{\textsf {Z} }}_{\alpha }\}}_{\alpha \in {}I}\), where \({{\textsf {Z} }}_{\alpha }\in {{\mathcal {P}}}_{{{\bullet }}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}))\) and I is a nonempty set of indexes.
Lemma 4.8
In diagram (4.1) there exists a unique map \({{\,\mathrm{{A}}\,}}^{\uparrow }\) (dotted arrow) that makes the diagram commute, and which commutes with the union of collections.
Proof
We define the map as follows:
Observe that if \({{\textsf {W} }}=\{{{\textsf {b} }}\}\) where \({{\textsf {b} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\) then \({{\,\mathrm{{A}}\,}}^{\uparrow }[{{\textsf {W} }}]={{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\), hence (4.1) commutes. We now show that \({{\,\mathrm{{A}}\,}}^{\uparrow }\) commutes with the union of collections. Indeed, the statement that \({{{\textsf {b} }}\in {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ \bigcup _{\alpha \in {}I}{{\textsf {Z} }}_{\alpha }\right] }\) means that there exists \(\alpha \in {}I\) and \({{\textsf {c} }}\in {{\textsf {Z} }}_{\alpha }\) such that \({{\textsf {b} }}\supset {{\textsf {c} }}\), and this means precisely that \({{{\textsf {b} }}\in \bigcup _{\alpha \in {}I} {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {Z} }}_{\alpha }\right] }\). In order to show uniqueness, it suffices to observe that \({{\textsf {W} }}=\bigcup _{{{\textsf {b} }}\in {{\textsf {W} }}}\{{{\textsf {b} }}\} =\bigcup _{{{\textsf {b} }}\in {{\textsf {W} }}}\imath ({{\textsf {b} }})\) for each \({{\textsf {W} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})).\) \(\square \)
Lemma 4.9
If \({{\textsf {W} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})) \) then
Proof
If \({{\textsf {b} }}\in {{\textsf {W} }}\) then \({{\textsf {b} }}\subset {{\textsf {b} }}\), hence \({{\textsf {b} }}\in {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \). \(\square \)
Lemma 4.10
If \({{\textsf {W} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})) \) then
Proof
If \({{\textsf {b} }}\in {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \right] \) then \({{\textsf {b} }}\supset {{\textsf {c} }}\) for some \({{\textsf {c} }}\in {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \), i.e., \({{\textsf {c} }}\supset {{\textsf {d} }}\) for some \({{\textsf {d} }}\in {{\textsf {W} }}\). Hence \({{\textsf {b} }}\supset {{\textsf {d} }}\), i.e., \({{\textsf {b} }}\in {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \). We have thus proved that \({{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \right] \subset {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \). The conclusion follows from Lemma 4.9. \(\square \)
4.3 Bases and Subbases
Observe that \({{\textsf {W} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}))\) satisfies (F2) in the axioms of a filter (Sect. 1.2.3) if and only if \({{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] ={{\textsf {W} }}\). Lemma 4.10 then says that \({{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \) satisfies (F2). Lemma 4.5 says that the image of \({{\,\mathrm{{A}}\,}}_{\bullet }\) in (4.1) is contained in  . The same result does not hold for the map \({{\,\mathrm{{A}}\,}}^{\uparrow }\). Indeed, if \({{\textsf {W} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}))\) then the collection \({{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \), defined in (4.4), satisfies (F0) (since \({{\,\mathrm{{A}}\,}}\in {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \)) and (F2) (by Lemma 4.10) but not necessarily (F1) in the definition of filter. For example, if \({{\textsf {W} }}=\{{{\textsf {b} }}_1,{{\textsf {b} }}_2\}\) where \({{\textsf {b} }}_1,{{\textsf {b} }}_2\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\) are disjoint, then \({{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \) is not a filter, since a filter cannot contain disjoint sets.
. The same result does not hold for the map \({{\,\mathrm{{A}}\,}}^{\uparrow }\). Indeed, if \({{\textsf {W} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}))\) then the collection \({{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \), defined in (4.4), satisfies (F0) (since \({{\,\mathrm{{A}}\,}}\in {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \)) and (F2) (by Lemma 4.10) but not necessarily (F1) in the definition of filter. For example, if \({{\textsf {W} }}=\{{{\textsf {b} }}_1,{{\textsf {b} }}_2\}\) where \({{\textsf {b} }}_1,{{\textsf {b} }}_2\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\) are disjoint, then \({{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \) is not a filter, since a filter cannot contain disjoint sets.
Lemma 4.11
(Cartan [8]) If \({{\textsf {W} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}))\) then the following conditions are equivalent:
- (1):
-
\({{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \) is a filter on \({{\,\mathrm{{A}}\,}}\).
- (2):
-
For each \({{\textsf {b} }},{{\textsf {c} }}\in {{\textsf {W} }},\) there exists \({{\textsf {d} }}\in {{\textsf {W} }}\) such that \({{\textsf {d} }}\subset {{\textsf {b} }}\cap {{\textsf {c} }}\).
Proof
If (1) holds and \({{\textsf {b} }},{{\textsf {c} }}\in {{\textsf {W} }}\), then \({{\textsf {b} }}\cap {{\textsf {c} }}\in {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \), hence there exists \({{\textsf {d} }}\in {{\textsf {W} }}\) such that \({{\textsf {b} }}\cap {{\textsf {c} }}\in {}{{\,\mathrm{{A}}\,}}_{{{\textsf {d} }}}\), i.e., \({{\textsf {d} }}\subset {{\textsf {b} }}\cap {{\textsf {c} }}\). If (2) holds and \({{\textsf {b} }},{{\textsf {c} }}\in {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \), then there exist \({{\textsf {b} }}',{{\textsf {c} }}'\in {{\textsf {W} }}\) such that \({{\textsf {b} }}'\subset {{\textsf {b} }}\) and \({{\textsf {c} }}'\subset {{\textsf {c} }}\). Hence there exists \({{\textsf {d} }}\in {{\textsf {W} }}\) with \({{\textsf {d} }}\subset {{\textsf {b} }}'\cap {{\textsf {c} }}'\). Thus \({{\textsf {d} }}\subset {{\textsf {b} }}\cap {{\textsf {c} }}\), i.e., \({{\textsf {b} }}\cap {{\textsf {c} }}\in {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \). \(\square \)
Definition 4.12
If \({{\textsf {W} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}))\) has one of the equivalent properties in Lemma 4.11, we then say that \({{\textsf {W} }}\) is a filter base on \({{\,\mathrm{{A}}\,}}\); the filter \({{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \) defined in (4.4) is the filter generated by \({{\textsf {W} }}\) on \({{\,\mathrm{{A}}\,}}\).
Example 4.13
The collection \({{\textsf {W} }}{\mathop {=}\limits ^\mathrm{{def}}}\left\{ (-x^2,0) \!:x\in {{\mathbb {R}}},x>0\right\} \) is a filter base on \({{\mathbb {R}}}\).
Example 4.14
The collection \({{\textsf {W} }}{\mathop {=}\limits ^\mathrm{{def}}}\left\{ (-\infty ,x^2,)\cup (x^2,+\infty ) \!:x\in {{\mathbb {R}}},x>0\right\} \) is a filter base on \({{\mathbb {R}}}\).
Lemma 4.15
A preorder \(\texttt {R}\) on a set \({{\,\mathrm{{A}}\,}}\) is a direction on \({{\,\mathrm{{A}}\,}}\) if and only if the collection of tails in \(({{\,\mathrm{{A}}\,}},\texttt {R})\) is a filter base.
Proof
If the collection of tails in \(({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}},\texttt {R})\) is a filter base on \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) then, given \(x,r\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\), there exists \(p\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) such that \( \texttt {tail}_{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}}\!\left( p\right) \subset \texttt {tail}_{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}}\!\left( x\right) \cap \texttt {tail}_{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}}\!\left( r\right) \), hence p is a majorant of \(\{x,r\}\). In Lemma 3.26 we proved the converse. \(\square \)
Lemma 4.16
If  and \(f\in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\,\mathrm{{Y}}\,}}),\) then \({({f}_{*})}_{*}({{\textsf {Z} }})\) is a filter base on \({{\,\mathrm{{Y}}\,}}\).
and \(f\in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\,\mathrm{{Y}}\,}}),\) then \({({f}_{*})}_{*}({{\textsf {Z} }})\) is a filter base on \({{\,\mathrm{{Y}}\,}}\).
Proof
Recall that \({({f}_{*})}_{*}:{{\mathcal {P}}}({{\mathcal {P}}}(A))\rightarrow {{\mathcal {P}}}({{\mathcal {P}}}(Y))\) and observe that \({({f}_{*})}_{*}({{\textsf {Z} }}) = \left\{ {f}_{*}({{\textsf {b} }})\!:{{\textsf {b} }}\in {{\textsf {Z} }}\right\} \subset {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}}) \). If \({{\textsf {b} }}_1,{{\textsf {b} }}_2\in {{\textsf {Z} }}\) then \({{\textsf {b} }}_1\cap {{\textsf {b} }}_2\in {{\textsf {Z} }}\) (since \({{\textsf {Z} }}\) is a filter) and \({f}_{*}({{\textsf {b} }}_1\cap {{\textsf {b} }}_2)\subset {f}_{*}({{\textsf {b} }}_1)\cap {f}_{*}({{\textsf {b} }}_2)\), hence (2) in Lemma 4.11 holds. \(\square \)
4.3.1 Generating Bases for a Filter
Lemma 4.17
If \(,\) \({{\textsf {W} }}\subset {{\textsf {Z} }},\) and the following condition holds:
then \({{\textsf {W} }}\) is a filter base on \({{\,\mathrm{{A}}\,}}\) and \( {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] ={{\textsf {Z} }}\).
Proof
\({{\textsf {W} }}\subset {{\textsf {Z} }}\) \(\Rightarrow \) \({{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \subset {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {Z} }}\right] \). Since  , \({{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {Z} }}\right] ={{\textsf {Z} }}\), hence \({{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \subset {{\textsf {Z} }}\). On the other hand, (4.7) and Lemma 4.10 imply that \({{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {Z} }}\right] \subset {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \right] = {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \), hence \({{\textsf {Z} }}\subset {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \). \(\square \)
, \({{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {Z} }}\right] ={{\textsf {Z} }}\), hence \({{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \subset {{\textsf {Z} }}\). On the other hand, (4.7) and Lemma 4.10 imply that \({{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {Z} }}\right] \subset {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \right] = {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \), hence \({{\textsf {Z} }}\subset {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \). \(\square \)
Definition 4.18
If  , \({{\textsf {W} }}\subset {{\textsf {Z} }}\), and (4.7) holds, then we say that \({{\textsf {W} }}\) is generating basis for \({{\textsf {Z} }}\).
, \({{\textsf {W} }}\subset {{\textsf {Z} }}\), and (4.7) holds, then we say that \({{\textsf {W} }}\) is generating basis for \({{\textsf {Z} }}\).
Example 4.19
The collection \({{\textsf {W} }}{\mathop {=}\limits ^\mathrm{{def}}}\left\{ {{\textsf {b} }}\in {{\mathcal {P}}}_{{{\bullet }}}({\mathbb {N}})\!: \exists n\in {\mathbb {N}}\text { such that } {{\textsf {b} }}=\left\{ k\in {\mathbb {N}}\!:k\ge {}n\right\} \right\} \) is a generating basis for the Fréchet filter \({{\textsf {f} }}{\mathbb {N}}\) on \({\mathbb {N}}\), introduced in Example 1.9. Indeed, \( {{\textsf {f} }}{\mathbb {N}}= {{\mathbb {N}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \).
Observe that (4.7) says that for each \({{\textsf {b} }}\in {{\textsf {Z} }}\) there exists \({{\textsf {c} }}\in {{\textsf {W} }}\) such that \({{\textsf {c} }}\subset {{\textsf {b} }}\).
Corollary 4.20
If \({{\textsf {W} }}\) and \({{\textsf {Y} }}\) in \({{\mathcal {P}}}_{{{\bullet }}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}))\) are filter bases on \({{\,\mathrm{{A}}\,}},\) then the following conditions are equivalent:
- (1):
-
\({{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] = {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {Y} }}\right] ,\)
- (2):
-
\({{\textsf {W} }}\subset {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {Y} }}\right] \) and \({{\textsf {Y} }}\subset {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] .\)
If any of these equivalent conditions holds, we say that \({{\textsf {W} }}\) and \({{\textsf {Y} }}\) are equivalent.
4.3.2 Filter Subbases
Observe that if \({{\textsf {W} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}))\) then the collection
satisfies Condition (2) in Lemma 4.11 but it is not necessarily true that \({{\textsf {W} }}^{\cap }\in {{\mathcal {P}}}_{{{\bullet }}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}))\), since it may happen that \(\emptyset \in {{\textsf {W} }}^{\varvec{\cap }}\). However, we have the following result, stated in terms of (4.8).
Lemma 4.21
(Cartan [8]) If \({{\textsf {W} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}))\) then a necessary and sufficient condition for the existence of a filter on \({{\,\mathrm{{A}}\,}}\) which contains \({{\textsf {W} }}\) is that \(\emptyset \not \in {{\textsf {W} }}^{\varvec{\cap }}\). If \(\emptyset \not \in {{\textsf {W} }}^{\varvec{\cap }},\) then \({{\textsf {W} }}^{\varvec{\cap }}\) is a filter base on \({{\,\mathrm{{A}}\,}},\) and the filter \( {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}^{\varvec{\varvec{\cap }}}\right] \) is said to be generated by the subbase \({{\textsf {W} }}\).
Proof
If  with \({{\textsf {W} }}\subset {{\textsf {Y} }}\) and \(\{{{\textsf {b} }}_1,\ldots ,{{\textsf {b} }}_n\}\subset {{\textsf {W} }}\), \(n\in {\mathbb {N}}\), then \(\{{{\textsf {b} }}_1,\ldots ,{{\textsf {b} }}_n\}\subset {{\textsf {Y} }}\), hence \(\bigcap _{j=1}^{n}{{\textsf {b} }}_j\in {{\textsf {Y} }}\) and thus \(\bigcap _{j=1}^{n}{{\textsf {b} }}_j\not =\emptyset \). If \(\emptyset \not \in {{\textsf {W} }}^{\varvec{\cap }}\) then \({{\textsf {W} }}^{\cap }\in {{\mathcal {P}}}_{{{\bullet }}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}))\). Condition (2) in Lemma 4.11 holds for \({{\textsf {W} }}^{\cap }\) by its very construction, and \({{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}^{\varvec{\varvec{\cap }}}\right] \) is a filter which contains \({{\textsf {W} }}\). \(\square \)
with \({{\textsf {W} }}\subset {{\textsf {Y} }}\) and \(\{{{\textsf {b} }}_1,\ldots ,{{\textsf {b} }}_n\}\subset {{\textsf {W} }}\), \(n\in {\mathbb {N}}\), then \(\{{{\textsf {b} }}_1,\ldots ,{{\textsf {b} }}_n\}\subset {{\textsf {Y} }}\), hence \(\bigcap _{j=1}^{n}{{\textsf {b} }}_j\in {{\textsf {Y} }}\) and thus \(\bigcap _{j=1}^{n}{{\textsf {b} }}_j\not =\emptyset \). If \(\emptyset \not \in {{\textsf {W} }}^{\varvec{\cap }}\) then \({{\textsf {W} }}^{\cap }\in {{\mathcal {P}}}_{{{\bullet }}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}))\). Condition (2) in Lemma 4.11 holds for \({{\textsf {W} }}^{\cap }\) by its very construction, and \({{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}^{\varvec{\varvec{\cap }}}\right] \) is a filter which contains \({{\textsf {W} }}\). \(\square \)
Definition 4.22
If \({{\textsf {W} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}))\) and \(\emptyset \not \in {{\textsf {W} }}^{\cap }\), then we then say that \({{\textsf {W} }}\) is a filter subbase on \({{\,\mathrm{{A}}\,}}\), and \({{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}^{\varvec{\varvec{\cap }}}\right] \) is the filter generated by the subbase \({{\textsf {W} }}\) on \({{\,\mathrm{{A}}\,}}\): It is the broadest filter which contains \({{\textsf {W} }}\).
4.4 Ultrafilters and Compactness
If  , then \({{\textsf {Z} }}\subset {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\), and, in particular, if \({{\textsf {b} }}\in {{\textsf {Z} }}\), then \({{\textsf {b} }}\subset {{\,\mathrm{{A}}\,}}\). Thus
, then \({{\textsf {Z} }}\subset {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\), and, in particular, if \({{\textsf {b} }}\in {{\textsf {Z} }}\), then \({{\textsf {b} }}\subset {{\,\mathrm{{A}}\,}}\). Thus

Hence  inherits from \({{\mathcal {P}}}_{{{\bullet }}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}))\) the partial order given by inclusion. The notion of ultrafilter, due to H. Cartan, introduced in Definition 1.5, is useful in several areas: topology, functional analysis, mathematical logic, among many others.
inherits from \({{\mathcal {P}}}_{{{\bullet }}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}))\) the partial order given by inclusion. The notion of ultrafilter, due to H. Cartan, introduced in Definition 1.5, is useful in several areas: topology, functional analysis, mathematical logic, among many others.
Observe that a filter on \({{\,\mathrm{{A}}\,}}\) is an ultrafilter if it is a maximal element of  under inclusion.
under inclusion.
Lemma 4.23
If \({{\textsf {b} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\) then the principal filter \({{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\) is an ultrafilter if and only if \({{\textsf {b} }}\) is a singleton.
Proof
If \({{\textsf {b} }}=\{x\}\), \(x\in {{\,\mathrm{{A}}\,}}\),  , \({{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\subset {{\textsf {Z} }}\), and \({{\textsf {c} }}\in {{\textsf {Z} }}\), then \({{\textsf {b} }}\cap {{\textsf {c} }}\not =\emptyset \), thus \(x\in {{\textsf {c} }}\), hence \({{\textsf {c} }}\in {{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\). If \({{\textsf {b} }}\) is not a singleton, let \(x\in {{\textsf {b} }}\). Then \({{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\subsetneq {{\,\mathrm{{A}}\,}}_{\{x\}}\) since \(\{x\}\in {{\,\mathrm{{A}}\,}}_{\{x\}}\setminus {{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\), hence \({{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\) is not an ultrafilter. \(\square \)
, \({{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\subset {{\textsf {Z} }}\), and \({{\textsf {c} }}\in {{\textsf {Z} }}\), then \({{\textsf {b} }}\cap {{\textsf {c} }}\not =\emptyset \), thus \(x\in {{\textsf {c} }}\), hence \({{\textsf {c} }}\in {{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\). If \({{\textsf {b} }}\) is not a singleton, let \(x\in {{\textsf {b} }}\). Then \({{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\subsetneq {{\,\mathrm{{A}}\,}}_{\{x\}}\) since \(\{x\}\in {{\,\mathrm{{A}}\,}}_{\{x\}}\setminus {{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\), hence \({{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\) is not an ultrafilter. \(\square \)
Lemma 4.24
The collection  is inductive with respect to the partial order induced by \({{\mathcal {P}}}_{{{\bullet }}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}))\).
is inductive with respect to the partial order induced by \({{\mathcal {P}}}_{{{\bullet }}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}))\).
Proof
If  is linearly ordered and \({{\textsf {W} }}{\mathop {=}\limits ^\mathrm{{def}}}\left\{ {{\textsf {b} }}\!: {{\textsf {b} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}), \exists {{\textsf {Z} }}\in {{\textsf {L} }}, {{\textsf {b} }}\in {{\textsf {Z} }}\right\} \) then \({{\textsf {W} }}^{\cap }\) in (4.8) does not contain the empty set, and the filter generated by the subbase \({{\textsf {W} }}\) is an upper bound of \({{\textsf {L} }}\). \(\square \)
is linearly ordered and \({{\textsf {W} }}{\mathop {=}\limits ^\mathrm{{def}}}\left\{ {{\textsf {b} }}\!: {{\textsf {b} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}), \exists {{\textsf {Z} }}\in {{\textsf {L} }}, {{\textsf {b} }}\in {{\textsf {Z} }}\right\} \) then \({{\textsf {W} }}^{\cap }\) in (4.8) does not contain the empty set, and the filter generated by the subbase \({{\textsf {W} }}\) is an upper bound of \({{\textsf {L} }}\). \(\square \)
Theorem 4.25
If  then there exists
then there exists  such that \({{\textsf {Z} }}\subset {{\textsf {W} }}\).
such that \({{\textsf {Z} }}\subset {{\textsf {W} }}\).
Proof
Apply Zorn’s lemma and Lemma 4.24. \(\square \)
Lemma 4.26
If \({{\,\mathrm{{A}}\,}}\not =\emptyset \) then  .
.
Proof
If  , \({{\textsf {b} }}\in {{\mathcal {P}}}({{\,\mathrm{{A}}\,}})\), and \({{\textsf {b} }}\not \in {{\textsf {Z} }}\), then \({{\textsf {Z} }}\subsetneq {{\textsf {Z} }}\cup \{{{\textsf {b} }}\}\), and \({{\textsf {Z} }}\cup \{{{\textsf {b} }}\}\) is not a filter subbase on \({{\,\mathrm{{A}}\,}}\), i.e., there exists \({{\textsf {c} }}\in {{\textsf {Z} }}\) with \({{\textsf {c} }}\cap {{\textsf {b} }}=\emptyset \). Hence \({{\textsf {c} }}\subset \complement {{{\textsf {b} }}}\), thus \(\complement {{{\textsf {b} }}}\in {{\textsf {Z} }}\). If
, \({{\textsf {b} }}\in {{\mathcal {P}}}({{\,\mathrm{{A}}\,}})\), and \({{\textsf {b} }}\not \in {{\textsf {Z} }}\), then \({{\textsf {Z} }}\subsetneq {{\textsf {Z} }}\cup \{{{\textsf {b} }}\}\), and \({{\textsf {Z} }}\cup \{{{\textsf {b} }}\}\) is not a filter subbase on \({{\,\mathrm{{A}}\,}}\), i.e., there exists \({{\textsf {c} }}\in {{\textsf {Z} }}\) with \({{\textsf {c} }}\cap {{\textsf {b} }}=\emptyset \). Hence \({{\textsf {c} }}\subset \complement {{{\textsf {b} }}}\), thus \(\complement {{{\textsf {b} }}}\in {{\textsf {Z} }}\). If  , then there exists \({{\textsf {b} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\setminus {{\textsf {Z} }}\) such that \({{\textsf {Z} }}\cup \{{{\textsf {b} }}\}\) is a filter subbase; hence \({{\textsf {b} }}\cap {{\textsf {c} }}\not =\emptyset \) for each \({{\textsf {c} }}\in {{\textsf {Z} }}\), thus \(\complement {{{\textsf {b} }}}\not \in {{\textsf {Z} }}\). \(\square \)
, then there exists \({{\textsf {b} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\setminus {{\textsf {Z} }}\) such that \({{\textsf {Z} }}\cup \{{{\textsf {b} }}\}\) is a filter subbase; hence \({{\textsf {b} }}\cap {{\textsf {c} }}\not =\emptyset \) for each \({{\textsf {c} }}\in {{\textsf {Z} }}\), thus \(\complement {{{\textsf {b} }}}\not \in {{\textsf {Z} }}\). \(\square \)
Corollary 4.27
If \({{\,\mathrm{{A}}\,}}\not =\emptyset \) then  .
.
Lemma 4.28
If \(,\) \({{\textsf {b} }}\in {{\textsf {Z} }},\) and \({{\textsf {c} }}\subset {{\textsf {b} }},\) then either \({{\textsf {c} }}\in {{\textsf {Z} }}\) or \({{\textsf {b} }}\setminus {{\textsf {c} }}\in {{\textsf {Z} }}\).
Proof
If \({{\textsf {c} }}\not \in {{\textsf {Z} }}\) then \({{\textsf {Z} }}\cup \{{{\textsf {c} }}\}\) is not a filter subbase, hence there exists \({{\textsf {d} }}\in {{\textsf {Z} }}\) with \({{\textsf {d} }}\cap {{\textsf {c} }}=\emptyset \). Hence \({{\textsf {b} }}\cap {{\textsf {d} }}\subset {{\textsf {b} }}\setminus {{\textsf {c} }}\). Thus \({{\textsf {b} }}\setminus {{\textsf {c} }}\in {{\textsf {Z} }}\), since \({{\textsf {b} }}\cap {{\textsf {d} }}\in {{\textsf {Z} }}\). \(\square \)
Observe that, if \(T\in {{\mathcal {P}}}({{\mathcal {P}}}({{\,\mathrm{{A}}\,}}))\) is an open cover of \(K\subset {{\,\mathrm{{A}}\,}}\), then for each \(x\in {}K\) there exists \(O\in {}T\) with \(x\in {}O\), and \(K\subset {}O\cup \complement {O}\).
Lemma 4.29
If \(T\in {{\mathcal {P}}}({{\mathcal {P}}}({{\,\mathrm{{A}}\,}}))\) is an open cover of \(K\subset {{\,\mathrm{{A}}\,}},\) then the collection
is a filter if and only if T has no finite subcover of K.
Proof
Observe that \(\emptyset \in {{\textsf {W} }}^{T}_{K}\) if and only if T has a finite subcover of K, hence it suffices to observe that (i) \({{\,\mathrm{{A}}\,}}\in {{\textsf {W} }}^{T}_{K}\); (ii) \({{\textsf {b} }},{{\textsf {c} }}\in {{\textsf {W} }}^{T}_{K}\Rightarrow {{\textsf {b} }}\cap {{\textsf {c} }}\in {{\textsf {W} }}^{T}_{K}\); (iii) \({{\textsf {b} }}\in {{\textsf {W} }}^{T}_{K}\) and \({{\textsf {b} }}\subset {{\textsf {c} }}\) \(\Rightarrow \) \({{\textsf {c} }}\in {{\textsf {W} }}^{T}_{K}\).
\(\square \)
The following characterization of compactness is useful.
Lemma 4.30
(Cartan [8]) Assume that \(({{\,\mathrm{{A}}\,}},\Theta )\) is a topological space and that \(K\subset {{\,\mathrm{{A}}\,}}\). Then the following conditions are equivalent:
-
K is compact.
-
For each \(,\) if \({{\textsf {Z} }}\) is localized in K, then there exists \(x\in {}K\) such that \({{{\textsf {N} }}}_{\Theta }(x)\subset {{\textsf {Z} }}\).
Proof
If K is not compact, then there exists \(T\subset \Theta \) which is an open cover of K with no finite subcover. Then \({{\textsf {W} }}^{T}_{K}\) in (4.10) is a filter. Observe that \(K\in {{\textsf {W} }}^{T}_{K}\). Theorem 4.25 yields  with \({{\textsf {W} }}^{T}_{K}\subset {{\textsf {Z} }}\). Since T is an open cover of K, for each \(x\in {}K\) there exists \(O\in {}T\) with \(x\in {}O\). We claim that \(O\not \in {{\textsf {Z} }}\). Indeed, \(K\subset {}O\cup \complement {O}\) yields \(\complement {O}\in {{\textsf {W} }}^{T}_{K}\), hence \(\complement {O}\in {{\textsf {Z} }}\), thus \(O\not \in {{\textsf {Z} }}\).
with \({{\textsf {W} }}^{T}_{K}\subset {{\textsf {Z} }}\). Since T is an open cover of K, for each \(x\in {}K\) there exists \(O\in {}T\) with \(x\in {}O\). We claim that \(O\not \in {{\textsf {Z} }}\). Indeed, \(K\subset {}O\cup \complement {O}\) yields \(\complement {O}\in {{\textsf {W} }}^{T}_{K}\), hence \(\complement {O}\in {{\textsf {Z} }}\), thus \(O\not \in {{\textsf {Z} }}\).
If K is compact,  , and \(K\in {{\textsf {Z} }}\), define \(\Theta _{{{\textsf {Z} }}}\subset \Theta \) by \(\Theta _{{{\textsf {Z} }}}{\mathop {=}\limits ^\mathrm{{def}}}\left\{ {{\textsf {b} }}\in \Theta \!:\complement {{{\textsf {b} }}}\in {{\textsf {Z} }}\right\} \). We claim that \(\Theta _{{{\textsf {Z} }}}\) does not cover K, and hence there exists \(x\in {}K\) with \(x\not \in \bigcup \Theta _{{{\textsf {Z} }}}\). If \(U\in \Theta \) and \(x\in {}U\) then \(U\not \in \Theta _{{{\textsf {Z} }}}\), and thus \(\complement {U}\not \in {{\textsf {Z} }}\), hence \(U\in {{\textsf {Z} }}\), by Lemma 4.26. Hence \({{{\textsf {N} }}}_{\Theta }(x)\subset {{\textsf {Z} }}\).
, and \(K\in {{\textsf {Z} }}\), define \(\Theta _{{{\textsf {Z} }}}\subset \Theta \) by \(\Theta _{{{\textsf {Z} }}}{\mathop {=}\limits ^\mathrm{{def}}}\left\{ {{\textsf {b} }}\in \Theta \!:\complement {{{\textsf {b} }}}\in {{\textsf {Z} }}\right\} \). We claim that \(\Theta _{{{\textsf {Z} }}}\) does not cover K, and hence there exists \(x\in {}K\) with \(x\not \in \bigcup \Theta _{{{\textsf {Z} }}}\). If \(U\in \Theta \) and \(x\in {}U\) then \(U\not \in \Theta _{{{\textsf {Z} }}}\), and thus \(\complement {U}\not \in {{\textsf {Z} }}\), hence \(U\in {{\textsf {Z} }}\), by Lemma 4.26. Hence \({{{\textsf {N} }}}_{\Theta }(x)\subset {{\textsf {Z} }}\).
We now prove the claim. If \(\Theta _{{{\textsf {Z} }}}\) covers K, then a finite subcover of \(\Theta _{{{\textsf {Z} }}}\) covers K, and since \(\Theta _{{{\textsf {Z} }}}\) is closed under finite unions, K is contained in one of the sets in \(\Theta _{{{\textsf {Z} }}}\), hence \(\complement {K}\in {{\textsf {Z} }}\), which is impossible since \(K\in {{\textsf {Z} }}\). \(\square \)
4.5 Functorial Properties of Direct Images and Application to Limiting Values
Recall from Lemma 4.16 that if  and \(f\in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\,\mathrm{{Y}}\,}})\), then \({({f}_{*})}_{*}({{\textsf {Z} }})\) is a filter base on \({{\,\mathrm{{Y}}\,}}\).
and \(f\in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\,\mathrm{{Y}}\,}})\), then \({({f}_{*})}_{*}({{\textsf {Z} }})\) is a filter base on \({{\,\mathrm{{Y}}\,}}\).
Definition 4.31
If  and \(f\in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\,\mathrm{{Y}}\,}})\), then the filter generated by \({({f}_{*})}_{*}({{\textsf {Z} }})\) on \({{\,\mathrm{{Y}}\,}}\) is denoted by \({f}_{\varvec{\diamond }}({{\textsf {Z} }})\) and is called the image of \({{\textsf {Z} }}\) by f. Hence
and \(f\in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\,\mathrm{{Y}}\,}})\), then the filter generated by \({({f}_{*})}_{*}({{\textsf {Z} }})\) on \({{\,\mathrm{{Y}}\,}}\) is denoted by \({f}_{\varvec{\diamond }}({{\textsf {Z} }})\) and is called the image of \({{\textsf {Z} }}\) by f. Hence

Lemma 4.32
If \(,\) and \(f\in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\,\mathrm{{Y}}\,}}),\) then
Proof
If \({{\textsf {c} }}\in {f}_{\varvec{\diamond }}({{\textsf {Z} }})\) then there exists \({{\textsf {b} }}\in {{\textsf {Z} }}\) with \({f}_{*}({{\textsf {b} }}) \subset {{\textsf {c} }}\), hence \( {{\textsf {b} }}\subset {f}^{*}({f}_{*}({{\textsf {b} }})) \subset {f}^{*}({{\textsf {c} }})\), thus \({f}^{*}({{\textsf {c} }})\in {{\textsf {Z} }}\). If \({{\textsf {c} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\) then \( {f}_{*}({f}^{*}({{\textsf {c} }})) \subset {{\textsf {c} }}\), and if \({f}^{*}({{\textsf {c} }})\in {{\textsf {Z} }}\) then \({{\textsf {c} }}\in {f}_{\varvec{\diamond }}({{\textsf {Z} }})\). \(\square \)
Proposition 4.33
Assume that \({{\,\mathrm{{A}}\,}}\) and \({{\,\mathrm{{Y}}\,}}\) are filtered spaces, and \(f\in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\,\mathrm{{Y}}\,}})\). Then f is a filter-homomorphism if and only if
Proof
f is a filter-homomorphism iff \({{\textsf {b} }}\in {{\textsf {Z} }}_{{{\,\mathrm{{Y}}\,}}}\) \(\Rightarrow \) \({f}^{*}({{\textsf {b} }})\in {{\textsf {Z} }}_{{{\,\mathrm{{A}}\,}}}\), and Lemma 4.32 says that this is the same as asking that \({{\textsf {b} }}\in {{\textsf {Z} }}_{{{\,\mathrm{{Y}}\,}}}\) \(\Rightarrow \) \({{{\textsf {b} }}}\in {f}_{\varvec{\diamond }}({{\textsf {Z} }}_{{{\,\mathrm{{A}}\,}}})\), i.e., that \({{\textsf {Z} }}_{{{\,\mathrm{{Y}}\,}}}\subset {f}_{\varvec{\diamond }}({{\textsf {Z} }}_{{{\,\mathrm{{A}}\,}}})\). \(\square \)
Corollary 4.34
If \(({{\,\mathrm{{A}}\,}},{{\textsf {Z} }})\) is a filtered set, \(({{\,\mathrm{{Y}}\,}},\Theta )\) is a topological space, \(f:{{\,\mathrm{{A}}\,}}\rightarrow {{\,\mathrm{{Y}}\,}}\) is a function, and \(y\in {{\,\mathrm{{Y}}\,}},\) then the following conditions are equivalent:
- (1):
-
\(\displaystyle {\mathop {{{{{\textbf {{\textsf {lim}}}}} }}}\nolimits _{{{\textsf {Z} }}}f=y},\)
- (2):
-
\({{{\textsf {N} }}}_{\Theta }(y)\subset {f}_{\varvec{\diamond }}({{\textsf {Z} }}).\)
Proof
The result follows at once from Proposition 4.33 and Definition 1.12. \(\square \)
Corollary 4.35
If  and \(f\in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\,\mathrm{{Y}}\,}}),\) then
and \(f\in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\,\mathrm{{Y}}\,}}),\) then  .
.
Proof
Since  , Lemma 4.26 implies that if \({{\textsf {c} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\) then either \({f}^{*}({{\textsf {c} }})\in {{\textsf {Z} }}\) or \(\complement {{f}^{*}({{\textsf {c} }})}\in {{\textsf {Z} }}\), and thus, by Lemma 4.32, either \({{\textsf {c} }}\in {f}_{\varvec{\diamond }}({{\textsf {Z} }})\) or \({{\textsf {c} }}\not \in {f}_{\varvec{\diamond }}({{\textsf {Z} }})\). Hence
, Lemma 4.26 implies that if \({{\textsf {c} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\) then either \({f}^{*}({{\textsf {c} }})\in {{\textsf {Z} }}\) or \(\complement {{f}^{*}({{\textsf {c} }})}\in {{\textsf {Z} }}\), and thus, by Lemma 4.32, either \({{\textsf {c} }}\in {f}_{\varvec{\diamond }}({{\textsf {Z} }})\) or \({{\textsf {c} }}\not \in {f}_{\varvec{\diamond }}({{\textsf {Z} }})\). Hence  by Lemma 4.26. \(\square \)
by Lemma 4.26. \(\square \)
Given a function \(f:{{\,\mathrm{{A}}\,}}\rightarrow {{\,\mathrm{{Y}}\,}}\) we have thus defined the map

Observe that if  and \({{\textsf {Z} }}_1\subset {{\textsf {Z} }}_2\) then \( {f}_{\varvec{\diamond }}({{\textsf {Z} }}_1) \subset {f}_{\varvec{\diamond }}({{\textsf {Z} }}_2)\). Hence we have almost completely proved the following result.
and \({{\textsf {Z} }}_1\subset {{\textsf {Z} }}_2\) then \( {f}_{\varvec{\diamond }}({{\textsf {Z} }}_1) \subset {f}_{\varvec{\diamond }}({{\textsf {Z} }}_2)\). Hence we have almost completely proved the following result.
Lemma 4.36
The assignment  is the object function of a functor from the category of sets to the category of posets. The associated arrow function assigns to each function \(f:{{\,\mathrm{{A}}\,}}\rightarrow {{\,\mathrm{{Y}}\,}}\) the order-preserving function
is the object function of a functor from the category of sets to the category of posets. The associated arrow function assigns to each function \(f:{{\,\mathrm{{A}}\,}}\rightarrow {{\,\mathrm{{Y}}\,}}\) the order-preserving function  .
.
Proof
If  then \({{\textsf {c} }}\in {g}_{\varvec{\diamond }}( {f}_{\varvec{\diamond }}({{\textsf {Z} }}) )\) \(\Leftrightarrow \) \({g}^{*}({{\textsf {c} }})\in {f}_{\varvec{\diamond }}({{\textsf {Z} }}) \) \(\Leftrightarrow \) \( {(g\circ {}f)}^{*}({{\textsf {c} }}) = {f}^{*}( {g}^{*}({{\textsf {c} }}) )\in {{\textsf {Z} }}\) for each \({{\textsf {c} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}'')\), by Lemma 4.32 hence \( {g}_{\varvec{\diamond }}( {f}_{\varvec{\diamond }}({{\textsf {Z} }}) ) = {(g\circ {}f)}_{\varvec{\diamond }}({{\textsf {Z} }})\). \(\square \)
then \({{\textsf {c} }}\in {g}_{\varvec{\diamond }}( {f}_{\varvec{\diamond }}({{\textsf {Z} }}) )\) \(\Leftrightarrow \) \({g}^{*}({{\textsf {c} }})\in {f}_{\varvec{\diamond }}({{\textsf {Z} }}) \) \(\Leftrightarrow \) \( {(g\circ {}f)}^{*}({{\textsf {c} }}) = {f}^{*}( {g}^{*}({{\textsf {c} }}) )\in {{\textsf {Z} }}\) for each \({{\textsf {c} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}'')\), by Lemma 4.32 hence \( {g}_{\varvec{\diamond }}( {f}_{\varvec{\diamond }}({{\textsf {Z} }}) ) = {(g\circ {}f)}_{\varvec{\diamond }}({{\textsf {Z} }})\). \(\square \)
4.6 Extension of Filters from a Subset and Restriction to a Subset
If \(\varOmega \subsetneq {{\,\mathrm{{A}}\,}}\) and \(\imath :\varOmega \rightarrow {{\,\mathrm{{A}}\,}}\) is the standard injection, defined by \(\imath (x){\mathop {=}\limits ^\mathrm{{def}}}{}x\), then the associated map

is injective, as we will see in Lemma 4.38, but this does not mean that if  then
then  . The following result clarifies this point.
. The following result clarifies this point.
Lemma 4.37
If \(\varOmega \subsetneq {{\,\mathrm{{A}}\,}}\) and  then
then  .
.
Proof
Observe that \({{\textsf {Z} }}\) only contains subsets of \(\varOmega \), and  \(\Rightarrow \) \({{\,\mathrm{{A}}\,}}\in {{\textsf {Z} }}\), which is impossible. \(\square \)
\(\Rightarrow \) \({{\,\mathrm{{A}}\,}}\in {{\textsf {Z} }}\), which is impossible. \(\square \)
A precise description of the map (4.13) will now be given.
Lemma 4.38
If \(\varOmega \subsetneq {{\,\mathrm{{A}}\,}}\) and  then \({{\textsf {Z} }}\) is a filter base on \({{\,\mathrm{{A}}\,}},\)
then \({{\textsf {Z} }}\) is a filter base on \({{\,\mathrm{{A}}\,}},\)
and
Proof
The fact that \({{\textsf {Z} }}\) is a filter base on \({{\,\mathrm{{A}}\,}}\) follows at once from  . If \({{\textsf {b} }}\in {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {Z} }}\right] \) and \({{\textsf {b} }}\in {{\,\mathrm{{A}}\,}}_{{{\textsf {d} }}}\) for some \({{\textsf {d} }}\in {{\textsf {Z} }}\), then \({{\textsf {d} }}\subset \varOmega \), \({{\textsf {d} }}\subset {{\textsf {b} }}\), hence \({{\textsf {b} }}\cap \varOmega \in {{\textsf {Z} }}\). Thus \({{\textsf {b} }}= [{{\textsf {b} }}\cap \varOmega ]\,\cup \,[{{\textsf {b} }}\cap ({{\,\mathrm{{A}}\,}}\setminus \varOmega )]\) with \({{\textsf {b} }}\cap \varOmega \in {{\textsf {Z} }}\) since \({{\textsf {d} }}\subset {{\textsf {b} }}\cap \varOmega \subset \varOmega \) and \({{\textsf {d} }}\in {{\textsf {Z} }}\). If \({{\textsf {b} }}={{\textsf {c} }}\cup {{\textsf {d} }}\), \({{\textsf {c} }}\in {{\textsf {Z} }}\), and \({{\textsf {d} }}\in {{\mathcal {P}}}({{\,\mathrm{{A}}\,}}\setminus \varOmega )\), then \({{\textsf {b} }}\in {{\,\mathrm{{A}}\,}}_{{{\textsf {c} }}}\) thus \({{\textsf {b} }}\in {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {Z} }}\right] \). The fact that \({\imath }_{\varvec{\diamond }}\) is injective follows at once from (4.14). Finally, (4.15) follows at once from (4.14). \(\square \)
. If \({{\textsf {b} }}\in {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {Z} }}\right] \) and \({{\textsf {b} }}\in {{\,\mathrm{{A}}\,}}_{{{\textsf {d} }}}\) for some \({{\textsf {d} }}\in {{\textsf {Z} }}\), then \({{\textsf {d} }}\subset \varOmega \), \({{\textsf {d} }}\subset {{\textsf {b} }}\), hence \({{\textsf {b} }}\cap \varOmega \in {{\textsf {Z} }}\). Thus \({{\textsf {b} }}= [{{\textsf {b} }}\cap \varOmega ]\,\cup \,[{{\textsf {b} }}\cap ({{\,\mathrm{{A}}\,}}\setminus \varOmega )]\) with \({{\textsf {b} }}\cap \varOmega \in {{\textsf {Z} }}\) since \({{\textsf {d} }}\subset {{\textsf {b} }}\cap \varOmega \subset \varOmega \) and \({{\textsf {d} }}\in {{\textsf {Z} }}\). If \({{\textsf {b} }}={{\textsf {c} }}\cup {{\textsf {d} }}\), \({{\textsf {c} }}\in {{\textsf {Z} }}\), and \({{\textsf {d} }}\in {{\mathcal {P}}}({{\,\mathrm{{A}}\,}}\setminus \varOmega )\), then \({{\textsf {b} }}\in {{\,\mathrm{{A}}\,}}_{{{\textsf {c} }}}\) thus \({{\textsf {b} }}\in {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {Z} }}\right] \). The fact that \({\imath }_{\varvec{\diamond }}\) is injective follows at once from (4.14). Finally, (4.15) follows at once from (4.14). \(\square \)
Definition 4.39
If \(\varOmega \subsetneq {{\,\mathrm{{A}}\,}}\) and \({{\textsf {Z} }}\) is a filter on \(\varOmega \) then the filter in (4.14) is a filter on \({{\,\mathrm{{A}}\,}}\) called the extension of \({{\textsf {Z} }}\) from \(\varOmega \) to \({{\,\mathrm{{A}}\,}}\).
Proposition 4.40
If  and \(\varOmega \subset {{\,\mathrm{{A}}\,}},\) then the following conditions are equivalent:
and \(\varOmega \subset {{\,\mathrm{{A}}\,}},\) then the following conditions are equivalent:
- (1):
-
\({{\textsf {W} }}\) is weakly localized in \(\varOmega \)
- (2):
-
For each \({{\textsf {d} }}\in {{\textsf {W} }}\), \(\varOmega \cap {{\textsf {d} }}\not =\emptyset \).
- (3):
-
There exists a filter \({\widetilde{{{\textsf {W} }}}}\supset {{\textsf {W} }}\) which is localized in \(\varOmega \).
- (4):
-
The following collection is a filter on \(\varOmega \)
$$\begin{aligned} {{\textsf {Z} }}{\mathop {=}\limits ^\mathrm{{def}}}\left\{ \varOmega \cap {{\textsf {b} }}\!:{{\textsf {b} }}\in {{\textsf {W} }}\right\} . \end{aligned}$$(4.16)
Proof
Let \({{{\textsf {Y} }}}{\mathop {=}\limits ^\mathrm{{def}}}\{{{\textsf {b} }}\}\cup {{\textsf {W} }}\). Since \({{\textsf {W} }}\) is a filter, then \(\emptyset \not \in {{\textsf {Y} }}^{\varvec{\cap }}\) means that \({{\textsf {b} }}\cap {{\textsf {d} }}\not =\emptyset \) for each \({{\textsf {d} }}\in {{\textsf {W} }}\). The equivalence between (2) and (3) then follows at once from Lemma 4.21. We now show that (1) and (2) are equivalent. If (2) does not hold then there exists \({{\textsf {d} }}\in {{\textsf {W} }}\) such that \({{\textsf {b} }}\cap {{\textsf {d} }}=\emptyset \), and this means that \({{\textsf {d} }}\subset \complement {{{\textsf {b} }}}\), hence \(\complement {{{\textsf {b} }}}\in {{\textsf {W} }}\), i.e., (1) does not hold. If (1) does not hold then \(\complement {{{\textsf {b} }}}\in {{\textsf {W} }}\), hence \({{\textsf {b} }}\cap \complement {{{\textsf {b} }}}=\emptyset \), hence (2) does not hold. Observe that (4) implies (2) at once, since no set in a filter can be empty. We now show that (2) implies (4). If \({{\textsf {b} }}_1\in {{\textsf {W} }}\) and \({{\textsf {b} }}_2\in {{\textsf {W} }}\) then \((\varOmega \cap {{\textsf {b} }}_1)\cap (\varOmega \cap {{\textsf {b} }}_2)= \varOmega \cap ({{\textsf {b} }}_1\cap {{\textsf {b} }}_2)\in {{\textsf {Z} }}\). Moreover, if \({{\textsf {b} }}\in {{\textsf {W} }}\) and \(\varOmega \cap {{\textsf {b} }}\subset {{\textsf {d} }}\subset \varOmega \) then \({{\textsf {b} }}\cup {{\textsf {d} }}\supset {{\textsf {b} }}\), hence \({{\textsf {b} }}\cup {{\textsf {d} }}\in {{\textsf {W} }}\), and since \({{\textsf {d} }}=\varOmega \cap ({{\textsf {b} }}\cup {{\textsf {d} }})\), it follows that \({{\textsf {d} }}\in {{\textsf {Z} }}\). \(\square \)
Definition 4.41
If \(\varOmega \subsetneq {{\,\mathrm{{A}}\,}}\), and \({{\textsf {W} }}\) is a filter on \({{\,\mathrm{{A}}\,}}\) which is weakly localized in \(\varOmega \), then the filter in (4.16) is a filter on \(\varOmega \) called the restriction of \({{\textsf {Z} }}\) from \({{\,\mathrm{{A}}\,}}\) to \(\varOmega \).
Theorem 4.42
If \(\varOmega \subsetneq {{\,\mathrm{{A}}\,}}\) and  then the following conditions are equivalent:
then the following conditions are equivalent:
- (1):
-
There exists
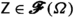 such that \({\imath }_{\varvec{\diamond }}({{\textsf {Z} }})={{\textsf {W} }}.\)
such that \({\imath }_{\varvec{\diamond }}({{\textsf {Z} }})={{\textsf {W} }}.\) - (2):
-
\({{\textsf {W} }}\) is localized in \(\varOmega .\)
Proof
Assume that (1) holds, and observe that \(\varOmega =\varOmega \cup \emptyset \) and \(\varOmega \in {{\textsf {Z} }}\). Hence (4.14) implies that \(\varOmega \in {{\textsf {W} }}\). Assume that (2) holds. Then \({{\textsf {W} }}\) is weakly localized in \(\varOmega \), and Proposition 4.40 implies that the collection in (4.16) is a filter on \(\varOmega \). We claim that \({\imath }_{\varvec{\diamond }}({{\textsf {Z} }})={{\textsf {W} }}\). Let \({{\textsf {d} }}\in {\imath }_{\varvec{\diamond }}({{\textsf {Z} }})\). Then there exists \({{\textsf {b} }}\in {{\textsf {W} }}\) and \({{\textsf {c} }}\in {{\mathcal {P}}}({{\,\mathrm{{A}}\,}}\setminus \varOmega )\) such that \({{\textsf {d} }}=(\varOmega \cap {{\textsf {b} }})\cup {{\textsf {c} }}\). Since \(\varOmega \in {{\textsf {W} }}\), it follows that \(\varOmega \cap {{\textsf {b} }}\in {{\textsf {W} }}\) and hence \({{\textsf {d} }}\in {{\textsf {W} }}\). Hence we have proved that \({\imath }_{\varvec{\diamond }}({{\textsf {Z} }})\subset {{\textsf {W} }}\). Now let \({{\textsf {d} }}\in {{\textsf {W} }}\). Observe that \({{\textsf {d} }}=(\varOmega \cap {{\textsf {d} }})\cup ({{\textsf {d} }}\setminus \varOmega )\). Let \({{\textsf {c} }}{\mathop {=}\limits ^\mathrm{{def}}}\varOmega \cap {{\textsf {d} }}\). Then \({{\textsf {c} }}\in {{\textsf {Z} }}\) and \({{\textsf {d} }}={{\textsf {c} }}\cup ({{\textsf {d} }}\setminus \varOmega )\) with \({{\textsf {c} }}\in {{\textsf {Z} }}\) and \({{\textsf {d} }}\setminus \varOmega \in {{\mathcal {P}}}({{\,\mathrm{{A}}\,}}\setminus \varOmega )\). Hence (4.14) implies that \({{\textsf {d} }}\in {\imath }_{\varvec{\diamond }}({{\textsf {Z} }})\). Hence we have proved that \({\imath }_{\varvec{\diamond }}({{\textsf {Z} }})\supset {{\textsf {W} }}\), and the proof is concluded. \(\square \)
4.7 Separable Filters
Definition 4.43
If there exists a countable generating basis for a filter  , we say that \({{\textsf {Z} }}\) is separable.
, we say that \({{\textsf {Z} }}\) is separable.
In other words, \({{\textsf {Z} }}\) is separable if there exists a countable subcollection \({{\textsf {W} }}\subset {{\textsf {Z} }}\) such that \({{\textsf {Z} }}\subset {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {W} }}\right] \).
Lemma 4.44
If \(,\) \({{\textsf {B} }}\subset {{\textsf {Z} }}\) and \({{\textsf {C} }}\subset {{\textsf {Z} }}\) are generating bases for \({{\textsf {Z} }},\) and \({{\textsf {C} }}\) is countable, then there exists a countable subcollection \({{{\textsf {G} }}}\subset {{\textsf {B} }}\) such that \({{{\textsf {G} }}}\) is a generating basis for \({{\textsf {Z} }}\).
Proof
Corollary 4.20 implies that \({{\textsf {C} }}\subset {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {B} }}\right] \), hence there is a map \(\beta :{{\textsf {C} }}\rightarrow {{\textsf {B} }}\) such that, for each \({{\textsf {c} }}\in {{\textsf {C} }}\), \({{\textsf {c} }}\supset \beta ({{\textsf {c} }})\). Define \({{\textsf {G} }}{\mathop {=}\limits ^\mathrm{{def}}}{\beta }_{*}({{\textsf {C} }})\). Then \({{\textsf {G} }}\) is a countable subcollection of \({{\textsf {B} }}\). Let \({{\textsf {b} }}\in {{\textsf {Z} }}\). Since \({{\textsf {C} }}\) is a generating basis for \({{\textsf {Z} }}\), there exists \({{\textsf {c} }}\in {{\textsf {C} }}\) such that \({{\textsf {b} }}\supset {{\textsf {c} }}\). Since \({{\textsf {c} }}\supset \beta ({{\textsf {c} }})\), it follows that \({{\textsf {b} }}\supset \beta ({{\textsf {c} }})\). Since \(\beta ({{\textsf {c} }})\in {{\textsf {G} }}\) and \({{\textsf {b} }}\in {{\textsf {Z} }}\) is arbitrary, we have proved that \({{\textsf {Z} }}\subset {{{\,\mathrm{{A}}\,}}}^{\uparrow }\!\left[ {{\textsf {G} }}\right] \). Hence \({{{\textsf {G} }}}\) is a generating basis for \({{\textsf {Z} }}\). \(\square \)
5 Proof of Theorem 3.29
If we specialize (3.11) to \({\mathbb {D}}\) we obtain the following:
The goal of this section is to prove Theorem 3.29, a result which deals with the collection \({{\,\mathrm{dir}\,}}({\mathbb {D}})\) of all directions on \({\mathbb {D}}\). In Lemma 3.25 we have defined a function \(\texttt {R}\mapsto {\textsf {Fin} }[{\texttt {R}}]\)

which maps every direction \(\texttt {R}\) on \({\mathbb {D}}\) to the filter of tails of \(\texttt {R}\), denoted by \({\textsf {Fin} }[{\texttt {R}}]\). Recall that there exists  , called the nontangential filter on \({\mathbb {D}}\) ending at 1, which has the following property
, called the nontangential filter on \({\mathbb {D}}\) ending at 1, which has the following property
- (\(\varvec{*}\)):
-
For each
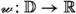 and each \({z}\in \overline{{{\mathbb {R}}}}\),
and each \({z}\in \overline{{{\mathbb {R}}}}\), 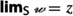 if and only if, for each open Euclidean triangle \(\textsc {t}\) contained in \({\mathbb {D}}\) and having 1 as a vertex,
if and only if, for each open Euclidean triangle \(\textsc {t}\) contained in \({\mathbb {D}}\) and having 1 as a vertex, 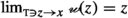 .
.
See [11, 12, 33], for background. It is convenient to replace the open Euclidean triangles which appear in \(\varvec{(*)}\) with the more symmetrical nontangential approach regions in \({\mathbb {D}}\) at 1, as follows. For \(\varrho >0\), let
be the open disc in \({{\mathbb {C}}}\) of center 1 and radius 1.
Definition 5.1
If \({\alpha }>1\) define
Remark
If we used strict inequality in (5.2) (instead of the nonstrict inequality which appears inside the curly brackets) and if we were to omit the intersection with D[1], then we would obtain the same filter, and hence the same notion of convergence, but the proof would become a bit more involved. Indeed, observe that \(\varGamma _{\alpha }\) contains the following set, which will be useful in the proof:
The nontangential filter \({{\textsf {S} }}\) may now be defined as follows. Choose, once and for all, a bijective function
and let \({{\mathbb {Q}}}_+{\mathop {=}\limits ^\mathrm{{def}}}(0,+\infty )\cap {{\mathbb {Q}}}\). The set \(\texttt {hom}_{\texttt {Set}}({\mathbb {N}},{{\mathbb {Q}}}_+)\) parametrizes a filter base on \({\mathbb {D}}\) as follows: For \({{\varvec{r}}}\in \texttt {hom}_{\texttt {Set}}({\mathbb {N}},{{\mathbb {Q}}}_+)\), let
Observe that \({{\,\mathrm{Q}\,}}({{\varvec{r}}})\subset {\mathbb {D}}\). Now define
Lemma 5.2
The collection \({{\textsf {B} }}\) is a filter base on \({\mathbb {D}}\).
Proof
If \({{\varvec{r}}},{{\varvec{s}}}\in \texttt {hom}_{\texttt {Set}}({\mathbb {N}},{{\mathbb {Q}}}_+)\), define \({{\varvec{p}}}\in \texttt {hom}_{\texttt {Set}}({\mathbb {N}},{{\mathbb {Q}}}_+)\) by setting \({{\varvec{p}}}(n){\mathop {=}\limits ^\mathrm{{def}}}{{\varvec{r}}}(n)\wedge {{\varvec{s}}}(n)\). Observe that \({{\,\mathrm{Q}\,}}({{\varvec{p}}})\subset {{\,\mathrm{Q}\,}}({{\varvec{r}}}) \cap {{\,\mathrm{Q}\,}}({{\varvec{s}}})\). Lemma 4.11 implies that the collection \({{\textsf {B} }}\) is a filter base on \({\mathbb {D}}\). \(\square \)
Definition 5.3
The nontangential filter on \({\mathbb {D}}\) ending at 1 is the filter generated by \({{\textsf {B} }}\) on \({\mathbb {D}}\), i.e., \({{\textsf {S} }}{\mathop {=}\limits ^\mathrm{{def}}}{{\mathbb {D}}}^{\uparrow }\!\left[ {{\textsf {B} }}\right] \).
Our goal is to prove the following statement.
- \((\spadesuit )\):
-
There exists no direction \(\texttt {R}\) on \({\mathbb {D}}\) such that the filter of tails of \(\texttt {R}\) is equal to the nontangential filter \({{\textsf {S} }}\).
Indeed, we will prove that \({{\textsf {S} }}\) does not belong to the image of the map (5.1). In other words, we will prove that the following set is empty:
The following useful criterion follows at once from Lemma 3.26.
Lemma 5.4
If \(\texttt {R}\in {{\textsf {Fin} }}^{*}({{\textsf {S} }}),\)  and \(z\in [-\infty ,+\infty ],\) then the following conditions are equivalent.
and \(z\in [-\infty ,+\infty ],\) then the following conditions are equivalent.
- (1):
-
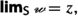
- (2):
-
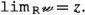
The nontangential filter is related to the nontangential approach regions described in (5.2) as follows.
- (\(\varvec{**}\)):
-
For each
 and each \({z}\in [-\infty ,+\infty ]\),
and each \({z}\in [-\infty ,+\infty ]\),  if and only if
if and only if 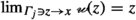 for each \(j\ge 1\).
for each \(j\ge 1\).
Remark
The fact that (\(\varvec{**}\)) holds implies that the choice made in (5.4) does not change the resulting filter. See [11].
If \(\texttt {R}\) is a direction on \({\mathbb {D}}\) and \(x\in {\mathbb {D}}\), the \(\texttt {R}\)-tail in \({\mathbb {D}}\) from \(x\in {\mathbb {D}}\) is defined just as in (3.9), with an emphasis on the direction rather than on the directed set:
We will also need the following notion.
Definition 5.5
If \(Q\in {{\mathcal {P}}}_{{{\bullet }}}({\mathbb {D}})\), we write  if 1 belongs to the topological closure of \(Q\) in \({{\mathbb {R}}}^2\).
if 1 belongs to the topological closure of \(Q\) in \({{\mathbb {R}}}^2\).
Lemma 5.6
If \(Q\rightarrow 1\) then there exists \(f:Q\rightarrow {{\mathbb {R}}}\) such that \(\displaystyle {\lim \nolimits _{Q\ni {}x\rightarrow 1}f(x)}\) does not exist.
Proof
Since \(Q\rightarrow 1\), it is possible to define a sequence \({\left\{ r_j>0\right\} }_{j\ge 0}\) in such a way that \(2=r_0>r_1>\cdots>r_j>r_{j+1}\) for each \(j\ge 0\), \(\displaystyle {\lim \nolimits _{j\rightarrow +\infty }r_j=0}\), and \( Q_j{\mathop {=}\limits ^\mathrm{{def}}}Q\cap \left( D[{r_j}]\setminus {}D[{r_{j+1}}] \right) \not =\emptyset \) for each j. The function \(f:Q\rightarrow {{\mathbb {R}}}\) defined by setting \(f(x)={(-1)}^{j}\) if \(x\in Q_{j}\) has the required property. \(\square \)
Lemma 5.7
If \(\texttt {R}\in {{\textsf {Fin} }}^{*}({{\textsf {S} }}),\) \(x\in {\mathbb {D}},\) \(\alpha >1,\) \(Q\subset \varGamma _{\alpha },\) and \(Q\rightarrow 1,\) then \(Q\cap \texttt {tail}_{\texttt {R}}\!\left( x\right) \not =\emptyset \).
Proof
Assume that \(\texttt {R}\in {{\,\mathrm{dir}\,}}({\mathbb {D}})\), \(x\in {\mathbb {D}}\), \(\alpha >1\), \(Q\subset \varGamma _{\alpha }\), \(Q\rightarrow 1\), and \(Q\cap \texttt {tail}_{\texttt {R}}\!\left( x\right) =\emptyset \). Define  as a function that vanishes identically on \({\mathbb {D}}\setminus {Q}\) and which on \(Q\) is equal to the function described in Lemma 5.6. Then
as a function that vanishes identically on \({\mathbb {D}}\setminus {Q}\) and which on \(Q\) is equal to the function described in Lemma 5.6. Then  does not exist, by \((**)\), but
does not exist, by \((**)\), but  exists. Indeed,
exists. Indeed,  , since for each \(\epsilon >0\) the values of
, since for each \(\epsilon >0\) the values of  on the \(\texttt {R}\)-tail from x all lie in \((-\epsilon ,\epsilon )\). Lemma 5.4 then implies that \(\texttt {R}\not \in {{\textsf {Fin} }}^{*}({{\textsf {S} }})\). \(\square \)
on the \(\texttt {R}\)-tail from x all lie in \((-\epsilon ,\epsilon )\). Lemma 5.4 then implies that \(\texttt {R}\not \in {{\textsf {Fin} }}^{*}({{\textsf {S} }})\). \(\square \)
Lemma 5.8
If \(\texttt {R}\in {{\textsf {Fin} }}^{*}({{\textsf {S} }}),\) then \({\textsf {Fin} }[{\texttt {R}}]\) is separable.
Proof
Let \(q_{n}{\mathop {=}\limits ^\mathrm{{def}}}{}1-\frac{1}{n}\), for each \(n\in {\mathbb {N}}\) with \(n\ge 1\) and let \(Q{\mathop {=}\limits ^\mathrm{{def}}}\left\{ q_{n}\!:n\in {\mathbb {N}},n\ge 1\right\} \). Then \(Q\rightarrow 1\) and \(Q\subset \varGamma _{\alpha }\) for each \(\alpha >1\). Let \({{\textsf {C} }}{\mathop {=}\limits ^\mathrm{{def}}}\left\{ {{\textsf {b} }}\in {{\mathcal {P}}}_{{{\bullet }}}({\mathbb {D}})\!: {{\textsf {b} }}=\texttt {tail}_{\texttt {R}}\!\left( q_{n}\right) \text { for some } n\in {\mathbb {N}}\right\} \). Observe that \({{\textsf {C} }}\) is countable and \({{\textsf {C} }}\subset {\textsf {Fin} }[{\texttt {R}}]\). Lemma 5.7 implies that for each \(x\in {\mathbb {D}}\) there exists \(n\in {\mathbb {N}}\) such that \(q_{n}\in \texttt {tail}_{\texttt {R}}\!\left( x\right) \), i.e., \(\texttt {tail}_{\texttt {R}}\!\left( x\right) \supset \texttt {tail}_{\texttt {R}}\!\left( q_{n}\right) \), and this means that \({\textsf {Fin} }[{\texttt {R}}]\subset {{\mathbb {D}}}^{\uparrow }\!\left[ {{\textsf {C} }}\right] \). Hence \({{\textsf {C} }}\) is a countable generating set for \({\textsf {Fin} }[{\texttt {R}}]\). \(\square \)
Lemma 5.9
If \({{\textsf {G} }}\subset {{\textsf {B} }}\) and \({{\textsf {G} }}\) is countable, then \({{\textsf {S} }}\not \subset {{\mathbb {D}}}^{\uparrow }\!\left[ {{\textsf {G} }}\right] \).
Proof
Let \({{\varvec{r}}}_1,{{\varvec{r}}}_2,\ldots ,{{\varvec{r}}}_k,\ldots \) be a sequence of elements of \(\texttt {hom}_{\texttt {Set}}({\mathbb {N}},{{\mathbb {Q}}}_+)\) such that \({{\textsf {G} }}=\left\{ {{\,\mathrm{Q}\,}}({{\varvec{r}}}_k)\!:k\in {\mathbb {N}}\right\} \). We claim that there exists \({{\varvec{s}}}\in \texttt {hom}_{\texttt {Set}}({\mathbb {N}},{{\mathbb {Q}}}_+)\) such that
Hence \({{\,\mathrm{Q}\,}}({{\varvec{s}}})\not \supset {{\,\mathrm{Q}\,}}({{\varvec{r}}}_k)\) for each \(k\in {\mathbb {N}}\), and since \({{\,\mathrm{Q}\,}}({{\varvec{s}}})\in {{\textsf {S} }}\), this means that \({{\textsf {S} }}\not \subset {{\mathbb {D}}}^{\uparrow }\!\left[ {{\textsf {G} }}\right] \). We will construct \({{\varvec{s}}}\in \texttt {hom}_{\texttt {Set}}({\mathbb {N}},{{\mathbb {Q}}}_+)\) and a sequence \(z_1,z_2,\ldots ,z_k,\ldots \) of points in \({\mathbb {D}}\) in such a way that, for each \(k\in {\mathbb {N}}\),
and
Since \( {{\,\mathrm{Q}\,}}({{\varvec{s}}})= \bigcup _{n\in {\mathbb {N}}}\varGamma _{{\varvec{\alpha }}(n)}\cap D[{{{\varvec{s}}}(n)}]\), in order to ensure that (5.9) holds it is necessary that, for each \(n\in {\mathbb {N}}\),
Recall that \({\varvec{\alpha }}:{\mathbb {N}}\rightarrow (0,+\infty )\cap {{\mathbb {Q}}}\) is an enumeration of the positive rationals larger than 1 chosen in (5.4) once and for all. For \(k=1,2,\ldots \), define an increasing sequence \({\{n_k\}}\) of positive integers with the following property: \({\varvec{\alpha }}(n_1)=2\), \({\varvec{\alpha }}(n_2)>2{\varvec{\alpha }}(n_1)\), and \({\varvec{\alpha }}(n_{k+1})>2{\varvec{\alpha }}(n_k)\) for each \(k\ge 1\). Then define
and, for each integer \(j\ge 2\), define
Then \({\mathbb {N}}=\bigcup _{j=1}^{+\infty }N_j\). Define \({{\varvec{s}}}\in \texttt {hom}_{\texttt {Set}}({\mathbb {N}},{{\mathbb {Q}}}_+)\) in such a way that
The values \(c_j\) will be specified momentarily. Define
and, for each \(k\ge 2\),
Choose
and, for each \(k\ge 1\),
Define \(c_1={|1-z_1|}\). Observe that (5.12) implies that, for each \(k\in {\mathbb {N}}\),
Hence (5.8) holds for each \(k\ge 1\).
In order to show that (5.10) holds for \(k=1\) and each \(n\ge 1\), observe that if \(n\in {}I_1\) then \({\varvec{\alpha }}(n)<{\varvec{\alpha }}(n_1)\), hence (5.13) implies that \(z_1\not \in \varGamma _{{\varvec{\alpha }}(n)}\), hence (5.10) holds for these values of n. If \(n\in {}I_{2}\cup {}I_{3}\cup \cdots \) then (5.11) and (5.13) imply that \({{\varvec{s}}}(n)\le {}c_2<|1-z_1|\), thus \(z_1\not \in {}D[{{\varvec{s}}}(n)]\), hence (5.10) holds also for these values of n.
Now we show that (5.10) holds if \(k=2\) for all \(n\in {\mathbb {N}}\). If \(n\in {}I_1\cup {}I_2\) then \({\varvec{\alpha }}(n)<{\varvec{\alpha }}(n_2)\), and hence (5.14) with \(k=2\) implies (5.10) for these values of n. If \(n\in {}I_3\cup {}I_4\cup \cdots \) then (5.11) implies that \({{\varvec{s}}}(n)\le {}c_3\), and since (5.14) implies that \(c_3<|1-z_2|\), it follows that \({{\varvec{s}}}(n)<|1-z_2|\), hence \(z_2\not \in {}D[{{\varvec{s}}}(n)]\), and (5.10) holds also for these values of n.
The proof of (5.10) for a generic value of k is similar, and is achieved by first showing that it holds if \(n\in {}I_1\cup {}I_2\cup \cdots {}I_k\), and then by showing that it holds for \(n\in {}I_k\cup {}I_{k+1}\cup \cdots \) Indeed, in the first case, observe that \({\varvec{\alpha }}(n)<{\varvec{\alpha }}(n_k)\). Thus (5.14) implies that \(z_k\not \in \varGamma _{{\varvec{\alpha }}(n)}\), hence (5.10) holds. In the second case, (5.11) and (5.14) imply that \({{\varvec{s}}}(n)\le {}c_{k+1}<|1-z_k|\) hence \(z_k\not \in {}D[{{\varvec{s}}}(n)]\), and (5.10) holds also for these values of n.
\(\square \)
Proposition 5.10
The nontangential filter on \({\mathbb {D}}\) ending at 1 is not separable.
Proof
Recall that the collection \({{\textsf {B} }}\), defined in (5.6), is a generating basis for \({{\textsf {S} }}\). Let us assume that \({{\textsf {S} }}\) is separable. Then Lemma 4.44 implies that there exists a countable subcollection \({{\textsf {G} }}\subset {{\textsf {B} }}\) which is a generating basis for \({{\textsf {S} }}\), but this is impossible by Lemma 5.9. \(\square \)
Proof of Theorem 3.29 Assume that the set \({{\textsf {Fin} }}^{*}({{\textsf {S} }})\) is not empty, and let \(\texttt {R}\in {{\textsf {Fin} }}^{*}({{\textsf {S} }})\). Then Lemma 5.8 implies that \({\textsf {Fin} }[{\texttt {R}}]\) is separable. Now \(\texttt {R}\in {{\textsf {Fin} }}^{*}({{\textsf {S} }})\) means that \({\textsf {Fin} }[{\texttt {R}}]={{\textsf {S} }}\), hence it follows that \({{\textsf {S} }}\) is separable, in contradiction with Proposition 5.10.
6 Applications to Set-Valued Moore–Smith Sequences
The goal of this section is to apply the results presented so far to Moore–Smith sequences of nonempty subsets of a given topological space. It seems to us that the topic has an interest of its own, even though its application to the main task of this paper appears to be limited, both because of a lack of a topology, and for the reasons illustrated in Sect. 3.
Since Moore–Smith sequences of points are a special case of Moore–Smith sequences of nonempty subsets of the given topological space, we find it useful to begin with the former case.
6.1 Functorial Properties of the Filter of Tails
The convergence properties of a Moore–Smith sequence are entirely determined by the associated filter of tails, which is encoded in the operator

In Lemma 6.5 we will see that the map  a natural transformation between two functors. Recall that, if \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is a directed set, then \({\textsf {Fin} }[{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}}]\) is the filter of tails of \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\), described in Lemma 3.26.
a natural transformation between two functors. Recall that, if \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is a directed set, then \({\textsf {Fin} }[{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}}]\) is the filter of tails of \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\), described in Lemma 3.26.
Definition 6.1
If  is a \({{\,\mathrm{{Y}}\,}}\)-valued Moore–Smith sequence and \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is the direction of
is a \({{\,\mathrm{{Y}}\,}}\)-valued Moore–Smith sequence and \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is the direction of  , then the filter of tails of
, then the filter of tails of  is the filter on \({{\,\mathrm{{Y}}\,}}\) defined by
is the filter on \({{\,\mathrm{{Y}}\,}}\) defined by

It follows that a filter base of  is
is  , i.e., the collection
, i.e., the collection

The following result says that the convergence properties of a Moore–Smith sequence are entirely determined by the associated filter of tails.
Theorem 6.2
If  is a \({{\,\mathrm{{Y}}\,}}\)-valued Moore–Smith sequence, \(\Theta \) is a topology on \({{\,\mathrm{{Y}}\,}},\) and \(y\in {{\,\mathrm{{Y}}\,}},\) the following conditions are equivalent
is a \({{\,\mathrm{{Y}}\,}}\)-valued Moore–Smith sequence, \(\Theta \) is a topology on \({{\,\mathrm{{Y}}\,}},\) and \(y\in {{\,\mathrm{{Y}}\,}},\) the following conditions are equivalent
Proof
It suffices to apply Lemma 3.26 and Corollary 4.34. \(\square \)
In the following result, due to Bruns and Schmidt [5, p. 171], we show that the map (6.1) is onto, i.e., that for each  there exists
there exists  such that
such that  .
.
Lemma 6.3
If \({{\,\mathrm{{Y}}\,}}\) is a nonempty set, then every filter \({{\textsf {Z} }}\) on \({{\,\mathrm{{Y}}\,}}\) is the filter of tails of a \({{\,\mathrm{{Y}}\,}}\)-valued Moore–Smith sequence  .
.
Proof
Given a filter \({{\textsf {Z} }}\) on \({{\,\mathrm{{Y}}\,}}\), define
consider the direction \(\texttt {R}\) on \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) defined by
and define

by  for each \(({{\textsf {b} }},x)\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\). If \(x\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\), i.e., \(x\equiv ({{\textsf {b} }},x)\), for some \({{\textsf {b} }}\in {{\textsf {Z} }}\) and some \(x\in {{\textsf {b} }}\), then
for each \(({{\textsf {b} }},x)\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\). If \(x\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\), i.e., \(x\equiv ({{\textsf {b} }},x)\), for some \({{\textsf {b} }}\in {{\textsf {Z} }}\) and some \(x\in {{\textsf {b} }}\), then

hence  . \(\square \)
. \(\square \)
Lemma 6.3 may be strengthened so as to yield the following result, due to Bruns and Schmidt [5].
Lemma 6.4
If \({{\,\mathrm{{Y}}\,}}\) is a nonempty set, then every filter \({{\textsf {Z} }}\) on \({{\,\mathrm{{Y}}\,}}\) is the filter of tails of a \({{\,\mathrm{{Y}}\,}}\)-valued Moore–Smith sequence  such that the direction of
such that the direction of  is antisymmetric.
is antisymmetric.
Proof
Instead of (6.3), define
endowed with the lexicographic partial order \(\texttt {R}\) defined by \(({{\textsf {b} }}_1,n_1,x_1) \texttt {R}\, ({{\textsf {b} }}_2,n_2,x_2)\) if and only if
Observe that \(\texttt {R}\) is an antisymmetric direction. Define the Moore–Smith sequence  on \({{\,\mathrm{{A}}\,}}\) by
on \({{\,\mathrm{{A}}\,}}\) by  for each \(({{\textsf {b} }},n,x)\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\). Then
for each \(({{\textsf {b} }},n,x)\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\). Then  . \(\square \)
. \(\square \)
We now show that the function which associates to each nonempty set \({{\,\mathrm{{A}}\,}}\) the map in (6.1) is a natural transformation between the functor in Lemma 3.17 and the one in Lemma 4.36 (see [21] for background on categorical language).
Lemma 6.5
For each pair of nonempty sets \({{\,\mathrm{{Y}}\,}}\) and \({{\,\mathrm{{X}}\,}}\) and every \(f:{{\,\mathrm{{Y}}\,}}\rightarrow {{\,\mathrm{{X}}\,}},\) the diagram (6.4) is commutative.

Proof
If  and
and  , then there exists \(x\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}_{\texttt {Set}}\) such that
, then there exists \(x\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}_{\texttt {Set}}\) such that  , and
, and  . It follows that
. It follows that  and
and  , and this means that
, and this means that  . We have thus proved that
. We have thus proved that  . In order to prove that
. In order to prove that  , it suffices to follow these steps backwards. \(\square \)
, it suffices to follow these steps backwards. \(\square \)
6.2 Set-Valued Moore–Smith Sequences
We will examine not only \({{\,\mathrm{{Y}}\,}}\)-valued Moore–Smith sequences (where \({{\,\mathrm{{Y}}\,}}\) is a given topological space) but also \({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\)-valued Moore–Smith sequences, and show that the latter category of Moore–Smith sequences enjoys properties that are more streamlined with respect to the \({{\,\mathrm{{Y}}\,}}\)-valued Moore–Smith sequences. We now show that the second class of Moore–Smith sequences includes the first one.
Definition 6.6
The injective function
maps  to the function \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\rightarrow {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\) (still denoted by
to the function \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\rightarrow {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\) (still denoted by  ) which maps \(k\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) to
) which maps \(k\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) to  .
.
Observe that the injective map (6.5) is obtained by composition of  with the natural injection \(\imath _{{{\,\mathrm{{Y}}\,}}}:{{\,\mathrm{{Y}}\,}}\rightarrow {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\) given by \(\imath _{{{\,\mathrm{{Y}}\,}}}(x){\mathop {=}\limits ^\mathrm{{def}}}\{x\}\). Hence we will think of \({\mathscr {S}}{({{\,\mathrm{{Y}}\,}})}\) as a subset of \({\mathscr {S}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}}))\), i.e., we will identify
with the natural injection \(\imath _{{{\,\mathrm{{Y}}\,}}}:{{\,\mathrm{{Y}}\,}}\rightarrow {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\) given by \(\imath _{{{\,\mathrm{{Y}}\,}}}(x){\mathop {=}\limits ^\mathrm{{def}}}\{x\}\). Hence we will think of \({\mathscr {S}}{({{\,\mathrm{{Y}}\,}})}\) as a subset of \({\mathscr {S}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}}))\), i.e., we will identify  .
.
Lemma 6.7
The assignment \({{\,\mathrm{{Y}}\,}}\mapsto {\mathscr {S}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}}))\) is the object function of a functor from the category of sets to the category of sets. The associated arrow function assigns to each function \(f:{{\,\mathrm{{Y}}\,}}\rightarrow {{\,\mathrm{{X}}\,}}\) the function \({f}_{\circ }:{\mathscr {S}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})) \rightarrow {\mathscr {S}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{X}}\,}}))\) which maps  to
to  .
.
Proof
The proof follows at once from the fact that the composition of functions is associative. \(\square \)
The function \({f}_{\circ }:{\mathscr {S}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})) \rightarrow {\mathscr {S}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{X}}\,}}))\), restricted to \({\mathscr {S}}{({{\,\mathrm{{Y}}\,}})}\), recaptures the function described in Lemma 3.17. For this reason, it is denoted by the same symbol. Recall that in Sect. 6.1 the map

has been defined, which associates to each  the filter
the filter  , called the filter of tails of
, called the filter of tails of  , and recall the natural injection (6.5)
, and recall the natural injection (6.5)
In Lemma 6.9 we show that the dotted arrow in the following diagram may be defined so as to make it commutative:

Definition 6.8
If  is a \({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\)-valued Moore–Smith sequence, then a tail of
is a \({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\)-valued Moore–Smith sequence, then a tail of  is a subset of \({{\,\mathrm{{Y}}\,}}\) of the form
is a subset of \({{\,\mathrm{{Y}}\,}}\) of the form

where \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is the direction of  and \(j\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}_{\texttt {Set}}\). The collection
and \(j\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}_{\texttt {Set}}\). The collection

is called the filter on \({{\,\mathrm{{Y}}\,}}\) generated by the tails of  . This terminology is justified by the following result.
. This terminology is justified by the following result.
Lemma 6.9
If  is a \({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\)-valued Moore–Smith sequence, then the collection
is a \({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\)-valued Moore–Smith sequence, then the collection  defined in (6.9) is a filter on \({{\,\mathrm{{X}}\,}},\) and the map
defined in (6.9) is a filter on \({{\,\mathrm{{X}}\,}},\) and the map  makes the diagram (6.7) commutative.
makes the diagram (6.7) commutative.
Proof
The first statement follows from the fact that the collection of tails, defined in (6.8), forms a filter base. Indeed, given \(j_1,j_2\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}_{\texttt {Set}}\), there exists \(j_3\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}_{\texttt {Set}}\) such that \(j_1\texttt {R}{}j_3\) and \(j_2\texttt {R}{}j_3\), and then it follows that  . The second statement follows at once from the identification of
. The second statement follows at once from the identification of  with the element of \({\mathscr {S}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}}))\) described in Definition (6.6). \(\square \)
with the element of \({\mathscr {S}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}}))\) described in Definition (6.6). \(\square \)
Hence, for every nonempty set \({{\,\mathrm{{Y}}\,}}\), we have defined a map

Consider the following diagram:

Lemma 6.10
For each nonempty sets \({{\,\mathrm{{Y}}\,}}\) and \({{\,\mathrm{{X}}\,}}\) and every \(f:{{\,\mathrm{{Y}}\,}}\rightarrow {{\,\mathrm{{X}}\,}},\) (6.11) is commutative.
Proof
It suffices to prove that  for each
for each  . Let
. Let  . Then there exists \(Q\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\) such that
. Then there exists \(Q\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\) such that  and \({f}_{*}(Q)\subset {{\textsf {b} }}\). Hence there exists \(j\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}_{\texttt {Set}}\), where \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is the direction of
and \({f}_{*}(Q)\subset {{\textsf {b} }}\). Hence there exists \(j\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}_{\texttt {Set}}\), where \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is the direction of  , such that
, such that  . We claim that
. We claim that  , and hence
, and hence  . In order to prove the claim, observe that if
. In order to prove the claim, observe that if  then
then  for some \(k\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}_{\texttt {Set}}\) with \(j\texttt {R}{}k\). Hence there exists
for some \(k\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}_{\texttt {Set}}\) with \(j\texttt {R}{}k\). Hence there exists  such that \(f(y)=x\). Thus
such that \(f(y)=x\). Thus  (since \(j\texttt {R}{}k\)) and \(y\in {}Q\) (since
(since \(j\texttt {R}{}k\)) and \(y\in {}Q\) (since  ), hence \(x=f(y)\in {{\textsf {b} }}\) (since \({f}_{*}(Q)\subset {{\textsf {b} }}\)).
), hence \(x=f(y)\in {{\textsf {b} }}\) (since \({f}_{*}(Q)\subset {{\textsf {b} }}\)).
If  then there exists \(j\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}_{\texttt {Set}}\) such that
then there exists \(j\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}_{\texttt {Set}}\) such that  . We claim that
. We claim that  , and hence
, and hence  . In order to prove the claim, let
. In order to prove the claim, let  and \(x=f(y)\). Then
and \(x=f(y)\). Then  for some \(k\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}_{\texttt {Set}}\) with \(j\texttt {R}{}k\). Then
for some \(k\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}_{\texttt {Set}}\) with \(j\texttt {R}{}k\). Then  . \(\square \)
. \(\square \)
Observe that Lemma 6.10 says that the assignment  is a natural transformation from the functor \({{\,\mathrm{{A}}\,}}\mapsto {\mathscr {S}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})), f\mapsto {f}_{\circ }\) to the functor
is a natural transformation from the functor \({{\,\mathrm{{A}}\,}}\mapsto {\mathscr {S}}({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})), f\mapsto {f}_{\circ }\) to the functor  .
.
Definition 6.11
If  ,
,  , and
, and  then we say that \({{\textsf {Z} }}\) is represented by
then we say that \({{\textsf {Z} }}\) is represented by  .
.
We now show that every filter on \({{\,\mathrm{{Y}}\,}}\) is the filter generated by the tails of a generalized sequence of nonempty subsets of \({{\,\mathrm{{Y}}\,}}\).
Definition 6.12
From Example 3.15 we obtain a map

as follows: If  , then the natural injection
, then the natural injection
defined, for each \({{\textsf {b} }}\in {{\textsf {Z} }}\), by \(s_{{{\textsf {Z} }}}({{\textsf {b} }}){\mathop {=}\limits ^\mathrm{{def}}}{{\textsf {b} }}\), is a \({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\)-valued Moore–Smith sequence. The proof of the following result is independent of Lemma 6.3.
Lemma 6.13
If  then
then  , hence the map
, hence the map  is onto.
is onto.
Proof
If  consider
consider  described in Definition 6.12, where \(({{\textsf {Z} }},\supset )\) is directed by reverse set inclusion. Then
described in Definition 6.12, where \(({{\textsf {Z} }},\supset )\) is directed by reverse set inclusion. Then  is a \({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\)-valued Moore–Smith sequence. Observe that if \({{\textsf {c} }}\in {{\textsf {Z} }}\) then
is a \({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\)-valued Moore–Smith sequence. Observe that if \({{\textsf {c} }}\in {{\textsf {Z} }}\) then

hence  . \(\square \)
. \(\square \)
Lemma 6.13 says that a filter \({{\textsf {Z} }}\) is represented by the generalized sequence  . The following result follows at once from Lemmas 6.10 and 6.13.
. The following result follows at once from Lemmas 6.10 and 6.13.
Corollary 6.14
If \(f:{{\,\mathrm{{Y}}\,}}\rightarrow {{\,\mathrm{{X}}\,}}\) is a function and  then
then

7 Proof of Theorem 3.33
8 Proof of Theorem 3.37
Let \({\mathcal {F}}\) be a functional convergence class on \({{\,\mathrm{{A}}\,}}\). Theorem 3.7 implies that there exists a filter \({{\textsf {Z} }}\) on \({{\,\mathrm{{A}}\,}}\) such that \({\mathcal {F}}={{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})\). Lemma 6.3 implies that there exists a Moore–Smith sequence  , where D is a directed set, such that
, where D is a directed set, such that  . Recall that
. Recall that  . Let \(\varphi \in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\) and \(y\in {{\mathbb {R}}}\). Then \((y,\varphi )\in {\mathcal {F}}\) if and only if \({{{{{\textbf {{\textsf {lim}}}}} }}}_{{{\textsf {Z} }}}\varphi =y\) (since \({\mathcal {F}}={{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})\)). Corollary 4.34 implies that \({{{{{\textbf {{\textsf {lim}}}}} }}}_{{{\textsf {Z} }}}\varphi =y\) if and only if \({{{\textsf {N} }}}_{{{\mathbb {R}}}}(y)\subset {\varphi }_{\varvec{\diamond }}({{\textsf {Z} }})\). Since
. Let \(\varphi \in \texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {R}}})\) and \(y\in {{\mathbb {R}}}\). Then \((y,\varphi )\in {\mathcal {F}}\) if and only if \({{{{{\textbf {{\textsf {lim}}}}} }}}_{{{\textsf {Z} }}}\varphi =y\) (since \({\mathcal {F}}={{\textsf {c} }}_{{{\,\mathrm{{A}}\,}}}({{\textsf {Z} }})\)). Corollary 4.34 implies that \({{{{{\textbf {{\textsf {lim}}}}} }}}_{{{\textsf {Z} }}}\varphi =y\) if and only if \({{{\textsf {N} }}}_{{{\mathbb {R}}}}(y)\subset {\varphi }_{\varvec{\diamond }}({{\textsf {Z} }})\). Since  , it follows that \({{{\textsf {N} }}}_{{{\mathbb {R}}}}(y)\subset {\varphi }_{\varvec{\diamond }}({{\textsf {Z} }})\) if and only if
, it follows that \({{{\textsf {N} }}}_{{{\mathbb {R}}}}(y)\subset {\varphi }_{\varvec{\diamond }}({{\textsf {Z} }})\) if and only if  . Lemma 4.36 implies that
. Lemma 4.36 implies that  . Hence \((y,\varphi )\in {\mathcal {F}}\) if and only if
. Hence \((y,\varphi )\in {\mathcal {F}}\) if and only if  . Theorem 6.2 implies that
. Theorem 6.2 implies that  if and only if
if and only if  . Hence \((y,\varphi )\in {\mathcal {F}}\) if and only if
. Hence \((y,\varphi )\in {\mathcal {F}}\) if and only if  . \(\square \)
. \(\square \)
9 A Natural Topology on the Collection of Filters
The goal of this section is to show that the collection  of all filters on a given set \({{\,\mathrm{{A}}\,}}\) is naturally endowed with a topology. This result, among many others, indicates that filters are intrinsically associated to the notion of convergence.
of all filters on a given set \({{\,\mathrm{{A}}\,}}\) is naturally endowed with a topology. This result, among many others, indicates that filters are intrinsically associated to the notion of convergence.
9.1 Topological Preliminaries
Observe that, if \(\Theta \) is a topology on a nonempty set \({{\,\mathrm{{X}}\,}}\), then (1.16) defines a function

called the family of (neighborhood) filters associated to \(\Theta \). Observe that the map \(\Theta \mapsto {{{\textsf {N} }}}_{\Theta }\) is injective, i.e., \(\Theta \) may be recaptured from \({{{\textsf {N} }}}_{\Theta }\). Indeed, \( Q\in \Theta \) if and only if for each \(x\in Q\) there exists \(U\in {{{\textsf {N} }}}_{\Theta }(x)\) such that \(x\in {}U\subset Q\).
Definition 9.1
A function  is called a family of filters on \({{\,\mathrm{{X}}\,}}\) based on \({{\,\mathrm{{X}}\,}}\).
is called a family of filters on \({{\,\mathrm{{X}}\,}}\) based on \({{\,\mathrm{{X}}\,}}\).
We now list some properties that a map \(\varphi :{{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\rightarrow {{\mathcal {P}}}({{\,\mathrm{{X}}\,}}) \) may have.
Definition 9.2
A map \( \varphi :{{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\rightarrow {{\mathcal {P}}}({{\,\mathrm{{X}}\,}}) \) may have one or more of the following properties.
-
(pas) (\(\varvec{\varphi }\) preserves the ambient space) \(\varphi ({{\,\mathrm{{X}}\,}})={{\,\mathrm{{X}}\,}}\).
-
(pfi) (\(\varvec{\varphi }\) preserves finite intersections) \(\varphi (Q\cap R)= \varphi (Q)\cap \varphi (R)\) for all \(Q,R\in {{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\).
-
(c) (\(\varvec{\varphi }\) is a contraction) \(\varphi (Q)\subset Q\) for each \(Q\in {{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\).
-
(idem) (\(\varvec{\varphi }\) is idempotent) \(\varphi (\varphi (Q))=\varphi (Q)\) for each \(Q\in {{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\).
-
(mi) (\(\varvec{\varphi }\) is monotone increasing) \(Q\subset R\) \(\implies \) \(\varphi (Q)\subset \varphi (R)\) for all \(Q,R\in {{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\).
-
(d) (\(\varvec{\varphi }\) is deflating) \(\varphi (\varphi (Q))\subset \varphi (Q)\) for each \(Q\in {{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\).
-
(i) (\(\varvec{\varphi }\) is inflating) \(\varphi (Q)\subset \varphi (\varphi (Q))\) for each \(Q\in {{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\).
-
(pfu) (\(\varvec{\varphi }\) preserves finite unions) \(\varphi (Q\cup R)= \varphi (Q)\cup \varphi (R)\) for all \(Q,R\in {{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\).
A map \(\varphi :{{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\rightarrow {{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\) is called regular if it preserves the ambient space and finite intersections, and is an idempotent contraction. Observe that (pas) and (pfi) say that \(\varphi \) is a homomorphism of the multiplicative semigroup of \({{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\) as a Boolean algebra (see Sect. 9.3).
Observe that
Indeed, \(Q\subset R\Rightarrow \varphi (Q)=\varphi (Q\cap R) {\mathop {=}\limits ^{{{\textbf {(pfi)}}}}} \varphi (Q) \cap \varphi (R) \subset \varphi (R)\), while \( (\varphi (Q) {\mathop {\subset }\limits ^{{{\textbf {(c)}}}}} Q) {\mathop {\Rightarrow }\limits ^{{{\textbf {(mi)}}}}} \varphi (\varphi (Q)) \subset \varphi (Q)\).
Lemma 9.3
If \(\Theta \) is a topology on \({{\,\mathrm{{X}}\,}},\) then the associated topological interior operator \( {{{\mathcal {I}}}}_{\Theta }:{{\mathcal {P}}}({{\,\mathrm{{X}}\,}}) \rightarrow {{\mathcal {P}}}({{\,\mathrm{{X}}\,}}) ,\) defined by \( {{\mathcal {I}}}_{\Theta }(Q) {\mathop {=}\limits ^\mathrm{{def}}}\left\{ x\!:x\in Q, \, \exists {\,}U\in \Theta , \, x\in {}U\subset Q\right\} ,\) is a regular map. The map \(\Theta \mapsto {{{\mathcal {I}}}}_{\Theta }\) is injective since \( Q\in \Theta \) if and only if \({{\mathcal {I}}}_{\Theta }(Q)=Q\).
Proof
We omit the proof, which follows immediately from the notion of topology. \(\square \)
Proposition 9.4
([19]) Every regular map \(\texttt {I}:{{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\rightarrow {{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\) is the topological interior operator associated to a (unique) topology.
Proof
Define \( \Theta _{\texttt {I}}{\mathop {=}\limits ^\mathrm{{def}}}\left\{ Q\in {{\mathcal {P}}}({{\,\mathrm{{X}}\,}}) \!: Q=\texttt {I}(Q) \right\} \). Then \(\Theta _{\texttt {I}}\) is a topology on \({{\,\mathrm{{X}}\,}}\) and \(\texttt {I}={{{\mathcal {I}}}}_{\Theta _{\texttt {I}}}\). \(\square \)
To every map  , we associate the map
, we associate the map
defined by \( \mathring{\texttt {N}}(Q) {\mathop {=}\limits ^\mathrm{{def}}}\left\{ x\in {{\,\mathrm{{X}}\,}}\!:Q\in \texttt {N}(x)\right\} \). We may write \(\texttt {N}^{\circ }\) instead of \(\mathring{\texttt {N}}\) for typographical reasons (for example, we do it in the proof of Theorem 9.7). Observe that the map \(\texttt {N}\mapsto \mathring{\texttt {N}}\) is injective, i.e., \(\texttt {N}\) may be recaptured from \(\mathring{\texttt {N}}\). Indeed
Observe that
and that, if \(\Theta \) is a topology on \({{\,\mathrm{{X}}\,}}\), then
Corollary 9.5
For each map \(\texttt {N}:{{\,\mathrm{{X}}\,}}\rightarrow {{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\) the following conditions are equivalent.
- (t):
-
\(\texttt {N}:{{\,\mathrm{{X}}\,}}\rightarrow {{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\) is the family of filters associated to a topology
- (r):
-
\(\mathring{\texttt {N}}:{{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\rightarrow {{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\) is a regular map.
Proof
\(\varvec{{{\textbf {t}}}\Rightarrow {{\textbf {r}}}}\) follows from (9.4) and Lemma 9.3; \(\varvec{{{\textbf {r}}}\Rightarrow {{\textbf {t}}}}\) follows from (9.3) and Proposition 9.4. \(\square \)
Lemma 9.6
For each map \(,\) \(\mathring{\texttt {N}}\) preserves the ambient space and finite intersections.
Proof
The result follows at once from the properties of filters. \(\square \)
Theorem 9.7
([8]) For each map \(,\) the following conditions are equivalent:
- (t):
-
\(\texttt {N}\) is the family of neighborhood filters associated to some topology on \({{\,\mathrm{{X}}\,}}\).
- (r):
-
\(\mathring{\texttt {N}}:{{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\rightarrow {{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\) is an inflating contraction.
Proof
If \(\texttt {N}={{{\textsf {N} }}}_{\Theta }\) for a topology \(\texttt {N}\), then (9.4) implies that \({{{\mathcal {I}}}}_{\Theta } = {({{{\textsf {N} }}}_{\Theta })}^{\circ }=\mathring{\texttt {N}}\), hence Lemma 9.3 yields the result. If \(\mathring{\texttt {N}}:{{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\rightarrow {{\mathcal {P}}}({{\,\mathrm{{X}}\,}})\) is an inflating contraction, then it is a regular map by (9.2) and Lemma 9.6. Proposition 9.4 then implies that \(\mathring{\texttt {N}}\) is the topological interior operator of some topology, say \(\Theta \). Hence (9.3) implies that \(\texttt {N}={{{\textsf {N} }}}_{\Theta }\). \(\square \)
We now wish to express Condition (r) in Theorem 9.7 directly in terms of \(\texttt {N}\).
Proposition 9.8
For each map \(,\) the following conditions are equivalent:
- (t):
-
\(\texttt {N}\) is the family of neighborhood filters associated to some topology on \({{\,\mathrm{{X}}\,}}\).
- (r):
-
\(\mathring{\texttt {N}}\) is an inflating contraction
- \((\varvec{{{\textbf {r}}}^{\prime }})\):
-
\(x\in {{\,\mathrm{{X}}\,}},\) \(Q\in \texttt {N}(x)\Rightarrow {}x\in Q\) and \(\exists \) \(R\in \texttt {N}(x)\) such that \(y\in {}R\) \(\Rightarrow \) \(Q\in \texttt {N}(y)\).
Observe that the set \(R\) is necessarily contained in \(Q\).
Proof
In Theorem 9.7 we proved that (t) and (r) are equivalent, hence it suffices to show that (r) and (r\(\varvec{{}^{\prime }}\)) are equivalent. Assume that (r) holds. Then \(\mathring{\texttt {N}}\) is regular [by Lemma 9.6 and (9.2)]. Hence if \(x\in {{\,\mathrm{{X}}\,}}\) and \(Q\in \texttt {N}(x)\) then \(x\in \mathring{\texttt {N}}(Q) {\mathop {\subset }\limits ^{{{\textbf {(c)}}}}}Q\), hence \(x\in Q\); moreover \(x\in \mathring{\texttt {N}}(Q) {\mathop {=}\limits ^{{{\textbf {(idem)}}}}} \mathring{\texttt {N}}(\mathring{\texttt {N}}(Q)) \) \(\Rightarrow \) \(x\in \mathring{\texttt {N}}(\mathring{\texttt {N}}(Q))\) \(\Rightarrow \) \(\mathring{\texttt {N}}(Q)\in \texttt {N}(x)\) and if \(y\in \mathring{\texttt {N}}(Q)\) then \(Q\in \texttt {N}(y)\), hence \(R{\mathop {=}\limits ^\mathrm{{def}}}\mathring{\texttt {N}}(Q)\) has the property in (r\(\varvec{{}^{\prime }}\)). Assume that (r\(\varvec{{}^{\prime }}\)) holds. Then \(Q\subset {{\,\mathrm{{X}}\,}}\) & \(x\in \mathring{\texttt {N}}(Q)\) \(\Rightarrow \) \(Q\in \texttt {N}(x)\) \({\mathop {\Rightarrow }\limits ^{ { {\textbf {(r}}\varvec{{}^{\prime }}{} {\textbf {)}} }}} x\in Q\), hence \(\mathring{\texttt {N}}(Q)\subset Q\), i.e., \(\mathring{\texttt {N}}\) is a contraction. If \(x\in \mathring{\texttt {N}}(Q)\) then \(Q\in \texttt {N}(x)\) and thus by (r\(\varvec{{}^{\prime }}\)) there exists \(R\in \texttt {N}(x)\) with \(y\in R\Rightarrow Q\in \texttt {N}(y)\), i.e., \(y\in R\Rightarrow {}y\in \mathring{\texttt {N}}(Q)\), i.e., \(R\subset \mathring{\texttt {N}}(Q)\), and since \(R\in \texttt {N}(x)\) and \(\texttt {N}(x)\) is a filter on \({{\,\mathrm{{X}}\,}}\) it follows that \(\mathring{\texttt {N}}(Q)\in \texttt {N}(x)\), i.e., \(x\in \mathring{\texttt {N}}(\mathring{\texttt {N}}(Q))\). Hence \(x\in \mathring{\texttt {N}}(Q) \Rightarrow x\in \mathring{\texttt {N}}(\mathring{\texttt {N}}(Q)) \), i.e., \(\mathring{\texttt {N}}\) is inflating. \(\square \)
Hence in order to describe a topology on  , it suffices to describe a map
, it suffices to describe a map  such that
such that  is an inflating contraction. We first need some more preliminary work.
is an inflating contraction. We first need some more preliminary work.
9.2 Further Lattice-Theoretic Properties of 
We now go back to a question that was left open in Sect. 4.1, to wit: the existence in  , seen as a poset, of the l.u.b. of two given filters
, seen as a poset, of the l.u.b. of two given filters  . Recall from Sect. 4.1 that the l.u.b. of
. Recall from Sect. 4.1 that the l.u.b. of  (called the join of \({{\textsf {Z} }}_1\) and \({{\textsf {Z} }}_2\)), if it exists, is denoted \({{\textsf {Z} }}_1\vee {{\textsf {Z} }}_2\) and has the following two properties: (i) \({{\textsf {Z} }}_1\subset {{\textsf {Z} }}_1\vee {{\textsf {Z} }}_2\) and \({{\textsf {Z} }}_2\subset {{\textsf {Z} }}_1\vee {{\textsf {Z} }}_2\), and (ii) if
(called the join of \({{\textsf {Z} }}_1\) and \({{\textsf {Z} }}_2\)), if it exists, is denoted \({{\textsf {Z} }}_1\vee {{\textsf {Z} }}_2\) and has the following two properties: (i) \({{\textsf {Z} }}_1\subset {{\textsf {Z} }}_1\vee {{\textsf {Z} }}_2\) and \({{\textsf {Z} }}_2\subset {{\textsf {Z} }}_1\vee {{\textsf {Z} }}_2\), and (ii) if  , \({{\textsf {Z} }}_1\subset {{\textsf {W} }}\) and \({{\textsf {Z} }}_2\subset {{\textsf {W} }}\), then \({{\textsf {Z} }}_1\vee {{\textsf {Z} }}_2\subset {{\textsf {W} }}\). We now show that the obstruction to the existence of the join of two filter lies in the existence of a filter which contains both. The following result follows at once from Lemma 4.21. However, it is instructive to provide a direct proof.
, \({{\textsf {Z} }}_1\subset {{\textsf {W} }}\) and \({{\textsf {Z} }}_2\subset {{\textsf {W} }}\), then \({{\textsf {Z} }}_1\vee {{\textsf {Z} }}_2\subset {{\textsf {W} }}\). We now show that the obstruction to the existence of the join of two filter lies in the existence of a filter which contains both. The following result follows at once from Lemma 4.21. However, it is instructive to provide a direct proof.
Lemma 9.9
If \({{\textsf {b} }},{{\textsf {c} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\) and \({{\textsf {b} }}\cap {{\textsf {c} }}=\emptyset \) then there is no filter on \({{\,\mathrm{{A}}\,}}\) which contains both \({{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\) and \({{\,\mathrm{{A}}\,}}_{{{\textsf {c} }}}\).
Proof
If  , \({{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\subset {{\textsf {Z} }}\), and \({{\,\mathrm{{A}}\,}}_{{{\textsf {c} }}}\subset {{\textsf {Z} }}\), then \({{\textsf {b} }},{{\textsf {c} }}\in {{\textsf {Z} }}\) and \({{\textsf {b} }}\cap {{\textsf {c} }}=\emptyset \), which is impossible. \(\square \)
, \({{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\subset {{\textsf {Z} }}\), and \({{\,\mathrm{{A}}\,}}_{{{\textsf {c} }}}\subset {{\textsf {Z} }}\), then \({{\textsf {b} }},{{\textsf {c} }}\in {{\textsf {Z} }}\) and \({{\textsf {b} }}\cap {{\textsf {c} }}=\emptyset \), which is impossible. \(\square \)
These lattice-theoretic issues are actually useful in order to gain a better understanding of the topological implications of the notion of filter, as we will see.
Definition 9.10
If  and \({{\textsf {Z} }}\vee {{\textsf {W} }}\) exists, we write
and \({{\textsf {Z} }}\vee {{\textsf {W} }}\) exists, we write
We read “\({{\textsf {Z} }}\bowtie {{\textsf {W} }}\)” as “\({{\textsf {Z} }}\) and \({{\textsf {W} }}\) intertwine.” If \({{\textsf {b} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\) and \({{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\bowtie {{\textsf {Z} }}\) [where \({{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\) is the principal filter generated by \({{\textsf {b} }}\) over \({{\,\mathrm{{A}}\,}}\), defined in (4.2)] then we write \({{\textsf {b} }}\bowtie {{\textsf {Z} }}\).
Observe that \({{\textsf {Z} }}\bowtie {{\textsf {W} }}\) if and only if, for each \({{\textsf {b} }}\in {{\textsf {Z} }}\), \({{\textsf {b} }}\bowtie {{\textsf {W} }}\).
Definition 9.11
If  and \({{\textsf {Z} }}\vee {{\textsf {W} }}\) does not exist, we write
and \({{\textsf {Z} }}\vee {{\textsf {W} }}\) does not exist, we write
We read “\({{{\textsf {Z} }}}\triangleleft \triangleright {{{\textsf {W} }}}\)” as “\({{\textsf {Z} }}\) and \({{\textsf {W} }}\) are eventually disjoint.”
See [11] for the motivation behind this terminology. In order to clarify this terminology and its meaning, observe that (4.2) defines an injective map

Hence  contains a copy of \({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\).
contains a copy of \({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\).
If \({{\,\mathrm{{A}}\,}}\) is a nonempty set and if \(f:{{\,\mathrm{{A}}\,}}\rightarrow {{\,\mathrm{{Y}}\,}}\) is a function, then we have the following diagram, where \(\epsilon _{{{\,\mathrm{{A}}\,}}}\) and \(\epsilon _{{{\,\mathrm{{Y}}\,}}}\) are given in (9.7), \({f}_{*}\) is given in (2.1), and \({f}_{\varvec{\diamond }}\) in (4.12)

The following result says that the map \({{\,\mathrm{{A}}\,}}\mapsto \epsilon _{{{\,\mathrm{{A}}\,}}}\) is a natural transformation from the functor
to the functor

Lemma 9.12
For each nonempty set \({{\,\mathrm{{A}}\,}}\) and \({{\,\mathrm{{Y}}\,}}\) and every \(f:{{\,\mathrm{{A}}\,}}\rightarrow {{\,\mathrm{{Y}}\,}},\) the diagram (9.8) is commutative.
Proof
If \({{\textsf {c} }}\in {f}_{\varvec{\diamond }}({{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}})\) where \({{\textsf {b} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\), then there exists \({{\textsf {d} }}\in {{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\) and \({f}_{*}({{\textsf {d} }})\subset {{\textsf {c} }}\). Thus \({{\textsf {b} }}\subset {{\textsf {d} }}\), hence \({f}_{*}({{\textsf {b} }})\subset {f}_{*}({{\textsf {d} }})\), so \({f}_{*}({{\textsf {b} }})\subset {{\textsf {c} }}\), i.e., \({{\textsf {c} }}\in {{\,\mathrm{{A}}\,}}_{{f}_{*}({{\textsf {b} }})}\). Hence \({f}_{\varvec{\diamond }}({{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}})\subset {{\,\mathrm{{A}}\,}}_{{f}_{*}({{\textsf {b} }})}\). If \({{\textsf {c} }}\in {{\,\mathrm{{A}}\,}}_{{f}_{*}({{\textsf {b} }})}\) then \({f}_{*}({{\textsf {b} }})\subset {{\textsf {c} }}\). Since \({{\textsf {b} }}\in {{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\), it follows that \({{\textsf {c} }}\in {f}_{\varvec{\diamond }}({{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}})\). Hence \({f}_{\varvec{\diamond }}({{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}})={{\,\mathrm{{A}}\,}}_{{f}_{*}({{\textsf {b} }})}\). \(\square \)
Consider also the natural injection
given by \(\imath _{{{\,\mathrm{{A}}\,}}}(x){\mathop {=}\limits ^\mathrm{{def}}}\{x\}\). Lemma 4.23 says that the composition of (9.9) with (9.7) yields the injection

which maps \(x\in {{\,\mathrm{{A}}\,}}\) to the principal ultrafilter generated by \(x\) over \({{\,\mathrm{{A}}\,}}\).
Lemma 9.13
The injective map (9.7) is order reversing. That is, if \({{\textsf {b} }}_1,{{\textsf {b} }}_2\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\) then
Proof
The fact that if \({{\textsf {b} }}\subset {{\textsf {c} }}\) then \({{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\supset {{\,\mathrm{{A}}\,}}_{{{\textsf {c} }}}\) follows at once from transitivity of inclusion. Observe that \({{\textsf {b} }}_1\cup {{\textsf {b} }}_2\subset {{\textsf {c} }}\) if and only if \({{\textsf {b} }}_1\subset {{\textsf {c} }}\) and \({{\textsf {b} }}_2\subset {{\textsf {c} }}\), hence (9.11) follows at once. \(\square \)
Lemma 9.14
If \({{\textsf {b} }}_1,{{\textsf {b} }}_2\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\) then the following conditions are equivalent:
- (1):
-
\({{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}_1}\bowtie {{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}_2},\)
- (2):
-
\({{\textsf {b} }}_1\) and \({{\textsf {b} }}_2\) overlap (as sets).
If any of these conditions hold, then
Proof
It suffices to apply Lemma 4.21\(\square \)
The following result also follows from Lemma 4.21.
Lemma 9.15
If  then the following conditions are equivalent:
then the following conditions are equivalent:
- (1):
-
\({{\textsf {Z} }}_1\bowtie {{\textsf {Z} }}_2,\)
- (2):
-
\({{\textsf {b} }}_1\cap {{\textsf {b} }}_2\not =\emptyset \) for each \({{\textsf {b} }}_1\in {{\textsf {Z} }}_1\) and each \({{\textsf {b} }}_2\in {{\textsf {Z} }}_2\).
Proof
If (1) holds then \({{\textsf {Z} }}_1\vee {{\textsf {Z} }}_2\) is a filter which contains both \({{\textsf {Z} }}_1\) and \({{\textsf {Z} }}_2\), hence if \({{\textsf {b} }}_1\in {{\textsf {Z} }}_1\) and \({{\textsf {b} }}_2\in {{\textsf {Z} }}_2\) then both \({{\textsf {b} }}_1\) and \({{\textsf {b} }}_2\) belong to \({{\textsf {Z} }}_1\vee {{\textsf {Z} }}_2\) and therefore their intersection cannot be empty. If (2) holds, then \({{\textsf {Z} }}_1\cup {{\textsf {Z} }}_2\) is a filter subbase, and Lemma 4.21 implies that there exists a filter \({{\textsf {Z} }}\) which contains \({{\textsf {Z} }}_1\cup {{\textsf {Z} }}_2\). \(\square \)
Lemma 9.15 says that \({{\textsf {b} }}\) and \({{\textsf {Z} }}\) intertwine if and only if \({{\textsf {b} }}\) and \({{\textsf {c} }}\) overlap for each \({{\textsf {c} }}\in {{\textsf {Z} }}\). This result implies at once the following one.
Corollary 9.16
The filters  are eventually disjoint if and only if there exist sets \({{\textsf {b} }}_1\in {{\textsf {Z} }}_1\) and \({{\textsf {b} }}_2\in {{\textsf {Z} }}_2\) such that \({{\textsf {b} }}_1\cap {{\textsf {b} }}_2=\emptyset \).
are eventually disjoint if and only if there exist sets \({{\textsf {b} }}_1\in {{\textsf {Z} }}_1\) and \({{\textsf {b} }}_2\in {{\textsf {Z} }}_2\) such that \({{\textsf {b} }}_1\cap {{\textsf {b} }}_2=\emptyset \).
9.3 Boolean Algebras
In this section, we prove some useful results which highlight the connection between filters (ultrafilters) and the algebraic structure of a Boolean algebra.
Definition 9.17
A Boolean algebra is a ring R with unity where \(a^2=a\) for each \(a\in {}R\). A function \(f:R_1\rightarrow {}R_2\) between Boolean algebras \(R_1\) and \(R_2\) is called a Boolean algebra homomorphism if \(f(a+b)=f(a)+f(b)\) and \(f({{\textsf {b} }}\cdot {{\textsf {c} }})=f({{\textsf {b} }})\cdot {}f({{\textsf {c} }})\) for all \({{\textsf {b} }},{{\textsf {c} }}\in {}R_1\).
The collection of Boolean algebra homomorphisms from a Boolean algebra \(R_1\) to a Boolean algebra \(R_2\) is denoted by \(\texttt {hom}_{\texttt {BA}}(R_1,R_2)\). The collection of nonzero elements of \(\texttt {hom}_{\texttt {BA}}(R,{{\mathbb {Z}}}_2)\) [resp. \(\texttt {hom}_{\texttt {Set}}(R,{{\mathbb {Z}}}_2)\)] is denoted by \(\texttt {hom}^{*}_{\texttt {BA}}(R,{{\mathbb {Z}}}_2)\) [resp. \(\texttt {hom}^{*}_{\texttt {Set}}(R,{{\mathbb {Z}}}_2)\)].
Lemma 9.18
Every Boolean algebra R is commutative, and \(a+a=0\) holds identically for each \(a\in {}R\).
Proof
See [15]. \(\square \)
9.3.1 Examples of Boolean Algebras
The simplest example of a Boolean algebra is \({\{0,1\}}={{\mathbb {Z}}}_2\), endowed with the usual ring operations of \({{\mathbb {Z}}}_2\equiv {{\mathbb {Z}}}/2\). In order to avoid ambiguities, the sum of \(a,b\in {{\mathbb {Z}}}_2\) is denoted by \(a\,{+_2}\,b\).
A large class of Boolean algebras may be constructed as follows. If S is a set then \(\texttt {hom}_{\texttt {Set}}(S,{{\mathbb {Z}}}_2)\) inherits the algebraic structure from \({{\mathbb {Z}}}_2\) by the familiar procedure of having the operations performed “pointwise.” See [22] for this general technique. Indeed, if \(f,g\in \texttt {hom}_{\texttt {Set}}(S,{{\mathbb {Z}}}_2)\), we define \(f\varvec{+}g\) and \(f\varvec{\cdot }{}g\) as elements of \(\texttt {hom}_{\texttt {Set}}(S,{{\mathbb {Z}}}_2)\) defined by \((f\,\varvec{+_2}g)(s){\mathop {=}\limits ^\mathrm{{def}}}{}f(s)\,{+_2}{\,}g(s)\) and \((f\varvec{\cdot }{}g)(s){\mathop {=}\limits ^\mathrm{{def}}}{}f(s)\cdot {}g(s)\), \(s\in {}S\). Hence \(\texttt {hom}_{\texttt {Set}}(S,{{\mathbb {Z}}}_2)\) inherits from \({{\mathbb {Z}}}_2\) a Boolean algebra structure.
Since a natural identification of \({{\mathcal {P}}}({{\,\mathrm{{A}}\,}})\) with \(\texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {Z}}}_2)\) is established by the map

it follows that \({{\mathcal {P}}}({{\,\mathrm{{A}}\,}})\) inherits the Boolean algebra structure from \(\texttt {hom}_{\texttt {Set}}(A,{{\mathbb {Z}}}_2)\). Observe that, under this identification, the symmetric difference of two elements \({{\textsf {b} }}_1,{{\textsf {b} }}_2\) of \({{\mathcal {P}}}({{\,\mathrm{{A}}\,}})\) corresponds to the sum \({\mathbb {1}}_{{{\textsf {b} }}_1}\varvec{+_2}{\mathbb {1}}_{{{\textsf {b} }}_2}\) in \(\texttt {hom}_{\texttt {Set}}({{\,\mathrm{{A}}\,}},{{\mathbb {Z}}}_2)\), and the intersection of \({{\textsf {b} }}_1\) and \({{\textsf {b} }}_2\) corresponds to the product \({\mathbb {1}}_{{{\textsf {b} }}_1}\varvec{\cdot }{\mathbb {1}}_{{{\textsf {b} }}_2}.\)
9.3.2 Filters, Ultrafilters, and Boolean Algebras
Lemma 9.19
If \({{\,\mathrm{{A}}\,}}\) is not empty, \(\sigma \in \texttt {hom}^{*}_{\texttt {Set}}({{\mathcal {P}}}({{\,\mathrm{{A}}\,}}),{{\mathbb {Z}}}_2),\) and \({{\textsf {Z} }}_{\sigma }{\mathop {=}\limits ^\mathrm{{def}}}\left\{ {{\textsf {b} }}\in {{\mathcal {P}}}({{\,\mathrm{{A}}\,}})\!:\sigma ({{\textsf {b} }})=1\right\} \) then
- (1):
-
\({{\textsf {Z} }}_{\sigma }\) is a filter on \({{\,\mathrm{{A}}\,}}\) if and only if \(\sigma ({{\textsf {b} }}\cap {{\textsf {c} }})=\sigma ({{\textsf {b} }})\sigma ({{\textsf {c} }})\) and \(\sigma (\emptyset )=0\) for all \({{\textsf {b} }},{{\textsf {c} }}\in {{\mathcal {P}}}({{\,\mathrm{{A}}\,}})\).
- (2):
-
\({{\textsf {Z} }}_{\sigma }\) is an ultrafilter on \({{\,\mathrm{{A}}\,}}\) if and only if \(\sigma \in \texttt {hom}^{*}_{\texttt {BA}}({{\mathcal {P}}}({{\,\mathrm{{A}}\,}}),{{\mathbb {Z}}}_2)\).
Proof
(1) (\(\Rightarrow \)) If \({{\textsf {Z} }}_{\sigma }\) is a filter then \(\sigma (\emptyset )=0\) (since a filter does not contain the empty set). Moreover, if \({{\textsf {b} }}\cap {{\textsf {c} }}\not \in {{\textsf {Z} }}_{\sigma }\) then at least one of the sets \({{\textsf {b} }},{{\textsf {c} }}\) does not belong to \({{\textsf {Z} }}_{\sigma }\), hence \(\sigma ({{\textsf {b} }}\cap {{\textsf {c} }})=\sigma ({{\textsf {b} }})\sigma ({{\textsf {c} }})\).
(1) (\(\Leftarrow \)) If \({{\textsf {b} }},{{\textsf {c} }}\in {{\textsf {Z} }}_{\sigma }\) then \(\sigma ({{\textsf {b} }}\cap {{\textsf {c} }})=1\), hence \({{\textsf {b} }}\cap {{\textsf {c} }}\in {{\textsf {Z} }}_{\sigma }\). The empty set does not belong to \({{\textsf {Z} }}_{\sigma }\), since \(\sigma (\emptyset )=0\). If \({{\textsf {b} }}\subset {{\textsf {c} }}\) and \({{\textsf {b} }}\in {{\textsf {Z} }}_{\sigma }\) then \(\sigma ({{\textsf {b} }})=\sigma ({{\textsf {b} }}\cap {{\textsf {c} }}) =\sigma ({{\textsf {b} }})\sigma ({{\textsf {c} }})\), hence \(1=1\cdot \sigma ({{\textsf {c} }})=\sigma ({{\textsf {c} }})\), i.e., \({{\textsf {c} }}\in {{\textsf {Z} }}_{\sigma }\).
(2) (\(\Rightarrow \)) Observe that Lemma 4.28 says that if \(\sigma ({{\textsf {e} }})=1\) and \({{\textsf {d} }}\subset {{\textsf {e} }}\), then \(1=\sigma ({{\textsf {d} }})+_2 \sigma ({{\textsf {e} }}\setminus {{\textsf {d} }})\) (where \(+_2\) denotes sum in \({{\mathbb {Z}}}_2\)), hence if \(\sigma ({{\textsf {b} }}\vartriangle {{\textsf {c} }})=1\) then \((\sigma ({{\textsf {b} }}\setminus {{\textsf {c} }}),\sigma ({{\textsf {c} }}\setminus {{\textsf {b} }}))\) is equal to (1, 0) or (0, 1), and by symmetry it suffices to treat the first case. Hence \(\sigma ({{\textsf {b} }})=1\) (since \({{\textsf {b} }}\setminus {{\textsf {c} }}\subset {{\textsf {b} }}\)) and \(\sigma ({{\textsf {c} }})=0\) (since a filter cannot contain disjoint sets) and thus \(\sigma ({{\textsf {b} }}\vartriangle {{\textsf {c} }})=\sigma ({{\textsf {b} }})+_2\sigma ({{\textsf {c} }})\). If \(\sigma ({{\textsf {b} }}\vartriangle {{\textsf {c} }})=0\) and \(\sigma ({{\textsf {b} }})=1\) then \((\sigma ({{\textsf {b} }}\setminus {{\textsf {c} }}),\sigma ({{\textsf {b} }}\cap {{\textsf {c} }}))\) equals (1, 0) or (0, 1). The first case is impossible, since \(\sigma ({{\textsf {b} }}\setminus {{\textsf {c} }})=1\) \(\Rightarrow \) \(\sigma ({{\textsf {b} }}\vartriangle {{\textsf {c} }})=1\). If instead \((\sigma ({{\textsf {b} }}\setminus {{\textsf {c} }}),\sigma ({{\textsf {b} }}\cap {{\textsf {c} }}))=(0,1)\), then \(\sigma ({{\textsf {c} }})=1\) (since \({{\textsf {b} }}\cap {{\textsf {c} }}\subset {{\textsf {c} }}\)), and thus \(\sigma ({{\textsf {b} }}\vartriangle {{\textsf {c} }})=\sigma ({{\textsf {b} }})+_2\sigma ({{\textsf {c} }})\). The case where \(\sigma ({{\textsf {b} }}\vartriangle {{\textsf {c} }})=0\), \(\sigma ({{\textsf {b} }})=0\), and \(\sigma ({{\textsf {c} }})=1\) is treated by symmetry. If \(\sigma ({{\textsf {b} }}\vartriangle {{\textsf {c} }})=0\), \(\sigma ({{\textsf {b} }})=0\), and \(\sigma ({{\textsf {c} }})=0\) then the conclusion is immediate. Hence \(\sigma ({{\textsf {b} }}\vartriangle {{\textsf {c} }})=\sigma ({{\textsf {b} }})+_2\sigma ({{\textsf {c} }})\) holds for all \({{\textsf {b} }},{{\textsf {c} }}\).
(2) (\(\Leftarrow \)) We know from (1) that \({{\textsf {Z} }}_{\sigma }\) is a filter. Let \({{\textsf {b} }}\subset {{\,\mathrm{{A}}\,}}\), assume that \({{\textsf {b} }}\not \in {{\textsf {Z} }}_{\sigma }\), and observe that \({{\,\mathrm{{A}}\,}}={{\textsf {b} }}\vartriangle \complement {{{\textsf {b} }}}\). The hypotheses imply that \(1=\sigma ({{\textsf {b} }})+_2\sigma (\complement {{{\textsf {b} }}})\), hence \(\sigma (\complement {{{\textsf {b} }}})=1\), i.e., \(\complement {{{\textsf {b} }}}\in {{\textsf {Z} }}_{\sigma }\). Hence \({{\textsf {Z} }}_{\sigma }\) is an ultrafilter by Lemma 4.26. \(\square \)
9.4 The Natural Topology on 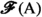
We are now ready to apply Theorem 9.7 and define a map

which satisfies the compatibility condition described in (r) in Theorem 9.7.
Definition 9.20
If \({{\textsf {b} }}\in {{\mathcal {P}}}({{\,\mathrm{{A}}\,}})\) and  define
define

and
Lemma 9.21
If  then
then
is a filter base on  .
.
Proof
If \({{\textsf {b} }}_1,{{\textsf {b} }}_2\in {{\textsf {Z} }}\) let \({{\textsf {b} }}_3{\mathop {=}\limits ^\mathrm{{def}}}{{\textsf {b} }}_1\cap {{\textsf {b} }}_2\). Then \({{\textsf {b} }}_3\in {{\textsf {Z} }}\). Observe that \( {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_3}({{\,\mathrm{{A}}\,}}) = {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1}({{\,\mathrm{{A}}\,}}) \cap {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}}) \). \(\square \)
Definition 9.22
If  , let \(\texttt {N}({{\textsf {Z} }})\) be the filter on
, let \(\texttt {N}({{\textsf {Z} }})\) be the filter on  generated by the filter base \({{\textsf {Z} }}_{\odot }\), i.e.,
generated by the filter base \({{\textsf {Z} }}_{\odot }\), i.e.,

Theorem 9.23
The map \(\texttt {N}\) defined above satisfies the regularity conditions in Theorem 9.7.
Proof
If  and \(Q\in \texttt {N}({{\textsf {Z} }})\) then \(\exists {{\textsf {b} }}\in {{\textsf {Z} }}\) such that \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\subset Q\). Observe that \({{\textsf {b} }}\in {{\textsf {Z} }}\) implies that \({{\textsf {Z} }}\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}}) \). Hence \({{\textsf {Z} }}\in Q\). Now let \(R{\mathop {=}\limits ^\mathrm{{def}}}{{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\) and observe that if \({{\textsf {Y} }}\in R\) then \({{\textsf {b} }}\in {{\textsf {Y} }}\), hence \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\in {{\textsf {Y} }}_{\odot }\), and from \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}}) \subset Q\) it follows that \(Q\in \texttt {N}({{\textsf {Y} }})\). Hence (r\(\varvec{{}^{\prime }}\)) in Proposition 9.8 is satisfied. \(\square \)
and \(Q\in \texttt {N}({{\textsf {Z} }})\) then \(\exists {{\textsf {b} }}\in {{\textsf {Z} }}\) such that \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\subset Q\). Observe that \({{\textsf {b} }}\in {{\textsf {Z} }}\) implies that \({{\textsf {Z} }}\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}}) \). Hence \({{\textsf {Z} }}\in Q\). Now let \(R{\mathop {=}\limits ^\mathrm{{def}}}{{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\) and observe that if \({{\textsf {Y} }}\in R\) then \({{\textsf {b} }}\in {{\textsf {Y} }}\), hence \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\in {{\textsf {Y} }}_{\odot }\), and from \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}}) \subset Q\) it follows that \(Q\in \texttt {N}({{\textsf {Y} }})\). Hence (r\(\varvec{{}^{\prime }}\)) in Proposition 9.8 is satisfied. \(\square \)
Definition 9.24
If \({{\,\mathrm{{A}}\,}}\) is a nonempty set, then the topology on  associated to the map \(\texttt {N}\) defined above is called the natural topology on
associated to the map \(\texttt {N}\) defined above is called the natural topology on  .
.
Lemma 9.25
If  and
and  is the map defined in (9.12) then
is the map defined in (9.12) then

Proof
\({{\textsf {Z} }}\in \mathring{\texttt {N}}(Q)\) \(\Leftrightarrow \) \(Q\in \texttt {N}({{\textsf {Z} }})\) \(\Leftrightarrow \) \(\exists \) \({{\textsf {b} }}\in {{\textsf {Z} }}\) with \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\subset Q\) \(\Leftrightarrow \) \(\exists \) \({{\textsf {b} }}\in {{\textsf {Z} }}\) with \({{\textsf {b} }}\in {}T_{{{\,\mathrm{{A}}\,}}}(Q)\). \(\square \)
Corollary 9.26
A set  is open in the natural topology if and only if
is open in the natural topology if and only if
Proof
It suffices to apply Lemmas 9.3 and 9.25. \(\square \)
The following examples are meant to illustrate these ideas.
Example 9.27
The only open set in the natural topology in  which contains \(\{{{\,\mathrm{{A}}\,}}\}\) is
which contains \(\{{{\,\mathrm{{A}}\,}}\}\) is  .
.
Indeed, if \(\{{{\,\mathrm{{A}}\,}}\}\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\) then \({{\textsf {b} }}\in \{{{\,\mathrm{{A}}\,}}\}\), hence \({{\textsf {b} }}={{\,\mathrm{{A}}\,}}\), thus  .
.
Example 9.28
The set  is open in
is open in  and is not equal to
and is not equal to  .
.
Indeed, if \({{\textsf {Z} }}\in Q\), then there exists \((\alpha ,\beta )\subset (0,1)\) such that \({{\mathbb {R}}}_{(\alpha ,\beta )}\subset {{\textsf {Z} }}\). In particular, \((\alpha ,\beta )\in {{\textsf {Z} }}\). If \({{\textsf {W} }}\in {{{{{\textbf {{\textsf {F}}}}} }}}_{(\alpha ,\beta )}({{\mathbb {R}}})\) then \((\alpha ,\beta )\in {{\textsf {W} }}\) hence \({{\mathbb {R}}}_{(\alpha ,\beta )}\subset {{\textsf {W} }}\) and thus \({{\textsf {W} }}\in Q\). Thus \({{{{{\textbf {{\textsf {F}}}}} }}}_{(\alpha ,\beta )}({{\mathbb {R}}})\subset {}Q\) and \((\alpha ,\beta )\in {{\textsf {Z} }}\,\cap {}\,T_{{{\mathbb {R}}}}(Q)\), i.e., \({{\textsf {Z} }}\in \mathring{\texttt {N}}(Q)\). We have proved that \(Q\subset \mathring{\texttt {N}}(Q)\), hence \(Q\) is open. Observe that \({{\mathbb {R}}}_{(2,3)}\not \in Q\), since a filter cannot contain disjoint sets, hence  .
.
Example 9.29
For each \(x\in {{\,\mathrm{{A}}\,}}\), the set \(U{\mathop {=}\limits ^\mathrm{{def}}}\{{{\,\mathrm{{A}}\,}}_{\{x\}}\}\) is open in  .
.
Indeed, if \(\{{x}\}\in {{\textsf {Z} }}\) and  , then \({{{\,\mathrm{{A}}\,}}}_{\{{x}\}}\subset {{\textsf {Z} }}\) and thus \({{{\,\mathrm{{A}}\,}}}_{\{{x}\}}={{\textsf {Z} }}\), since \({{{\,\mathrm{{A}}\,}}}_{\{{x}\}}\) is an ultrafilter. Hence \({{{{{\textbf {{\textsf {F}}}}} }}}_{\{x\}}({{{\,\mathrm{{A}}\,}}})\subset {}U\), i.e., \(\{{x}\}\in {}T_{{{{\,\mathrm{{A}}\,}}}}(U)\). Since \(\{{x}\}\in {{{\,\mathrm{{A}}\,}}}_{\{{x}\}}\) it follows that \({{{\,\mathrm{{A}}\,}}}_{\{{x}\}}\cap {}T_{{{{\,\mathrm{{A}}\,}}}}(U)\not =\emptyset \), i.e., \({{{\,\mathrm{{A}}\,}}}_{\{{x}\}}\in \mathring{\texttt {N}}(U)\).
, then \({{{\,\mathrm{{A}}\,}}}_{\{{x}\}}\subset {{\textsf {Z} }}\) and thus \({{{\,\mathrm{{A}}\,}}}_{\{{x}\}}={{\textsf {Z} }}\), since \({{{\,\mathrm{{A}}\,}}}_{\{{x}\}}\) is an ultrafilter. Hence \({{{{{\textbf {{\textsf {F}}}}} }}}_{\{x\}}({{{\,\mathrm{{A}}\,}}})\subset {}U\), i.e., \(\{{x}\}\in {}T_{{{{\,\mathrm{{A}}\,}}}}(U)\). Since \(\{{x}\}\in {{{\,\mathrm{{A}}\,}}}_{\{{x}\}}\) it follows that \({{{\,\mathrm{{A}}\,}}}_{\{{x}\}}\cap {}T_{{{{\,\mathrm{{A}}\,}}}}(U)\not =\emptyset \), i.e., \({{{\,\mathrm{{A}}\,}}}_{\{{x}\}}\in \mathring{\texttt {N}}(U)\).
Example 9.30
The set \(Q{\mathop {=}\limits ^\mathrm{{def}}}\{{{\mathbb {R}}}_{\{1,2\}}\}\) is not open in  .
.
Indeed, Theorem 4.25 implies that for each \({{\textsf {b} }}\subset {{\mathbb {R}}}\) with \(\{1,2\}\subset {{\textsf {b} }}\), there exists an ultrafilter  with \({{\textsf {Z} }}\supset {{\mathbb {R}}}_{{{\textsf {b} }}}\). Hence \({{\textsf {Z} }}\not \in Q\), since \({{\mathbb {R}}}_{{{\textsf {b} }}}\) is not an ultrafilter, and this means that \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\mathbb {R}}})\not \subset Q\), i.e., \({{\mathbb {R}}}_{\{1,2\}}\cap \,{}T_{{{\mathbb {R}}}}(Q)=\emptyset \). Hence \({{\mathbb {R}}}_{\{1,2\}}\not \in \mathring{\texttt {N}}(Q)\).
with \({{\textsf {Z} }}\supset {{\mathbb {R}}}_{{{\textsf {b} }}}\). Hence \({{\textsf {Z} }}\not \in Q\), since \({{\mathbb {R}}}_{{{\textsf {b} }}}\) is not an ultrafilter, and this means that \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\mathbb {R}}})\not \subset Q\), i.e., \({{\mathbb {R}}}_{\{1,2\}}\cap \,{}T_{{{\mathbb {R}}}}(Q)=\emptyset \). Hence \({{\mathbb {R}}}_{\{1,2\}}\not \in \mathring{\texttt {N}}(Q)\).
9.5 Basic Properties of the Natural Topology on 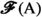
Lemma 9.31
The assignment  is the object function of a functor from the category of sets to the category of topological spaces, where
is the object function of a functor from the category of sets to the category of topological spaces, where  is endowed with the natural topology. The associated arrow function assigns to each function \(f:{{\,\mathrm{{A}}\,}}\rightarrow {{\,\mathrm{{Y}}\,}}\) the continuous function
is endowed with the natural topology. The associated arrow function assigns to each function \(f:{{\,\mathrm{{A}}\,}}\rightarrow {{\,\mathrm{{Y}}\,}}\) the continuous function  .
.
Proof
It suffices to prove that  is continuous with respect to the natural topologies of
is continuous with respect to the natural topologies of  and
and  , since the other statements have been proved in Lemma 4.36. Let
, since the other statements have been proved in Lemma 4.36. Let  , \({{\textsf {W} }}{\mathop {=}\limits ^\mathrm{{def}}}{f}_{\varvec{\diamond }}({{\textsf {Z} }})\), and let
, \({{\textsf {W} }}{\mathop {=}\limits ^\mathrm{{def}}}{f}_{\varvec{\diamond }}({{\textsf {Z} }})\), and let  be a neighborhood of \({{\textsf {W} }}\) in the natural topology of
be a neighborhood of \({{\textsf {W} }}\) in the natural topology of  . Then there exists \({{\textsf {b} }}\in {{\textsf {W} }}\) such that \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{Y}}\,}})\subset Q\). Since \({{\textsf {W} }}{\mathop {=}\limits ^\mathrm{{def}}}{f}_{\varvec{\diamond }}({{\textsf {Z} }})\), \({{\textsf {b} }}\in {{\textsf {W} }}\) implies that there exists \({{\textsf {c} }}\in {{\textsf {Z} }}\) such that \({f}_{*}({{\textsf {c} }})\subset {{\textsf {b} }}\). Observe that \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {c} }}}({{\,\mathrm{{A}}\,}})\) is a neighborhood of \({{\textsf {Z} }}\) in the natural topology of
. Then there exists \({{\textsf {b} }}\in {{\textsf {W} }}\) such that \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{Y}}\,}})\subset Q\). Since \({{\textsf {W} }}{\mathop {=}\limits ^\mathrm{{def}}}{f}_{\varvec{\diamond }}({{\textsf {Z} }})\), \({{\textsf {b} }}\in {{\textsf {W} }}\) implies that there exists \({{\textsf {c} }}\in {{\textsf {Z} }}\) such that \({f}_{*}({{\textsf {c} }})\subset {{\textsf {b} }}\). Observe that \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {c} }}}({{\,\mathrm{{A}}\,}})\) is a neighborhood of \({{\textsf {Z} }}\) in the natural topology of  . If \({{\textsf {V} }}\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {c} }}}({{\,\mathrm{{A}}\,}})\) then \({{\textsf {c} }}\in {{\textsf {V} }}\), and since \({f}_{*}({{\textsf {c} }})\subset {{\textsf {b} }}\), it follows that \({{\textsf {b} }}\in {f}_{\varvec{\diamond }}({{\textsf {V} }})\), i.e., \({f}_{\varvec{\diamond }}({{\textsf {V} }})\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{Y}}\,}})\), and thus \({f}_{\varvec{\diamond }}({{\textsf {V} }})\in Q\). Hence we have proved that \({{\textsf {V} }}\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {c} }}}({{\,\mathrm{{A}}\,}})\) \(\Rightarrow \) \({f}_{\varvec{\diamond }}({{\textsf {V} }})\in Q\). \(\square \)
. If \({{\textsf {V} }}\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {c} }}}({{\,\mathrm{{A}}\,}})\) then \({{\textsf {c} }}\in {{\textsf {V} }}\), and since \({f}_{*}({{\textsf {c} }})\subset {{\textsf {b} }}\), it follows that \({{\textsf {b} }}\in {f}_{\varvec{\diamond }}({{\textsf {V} }})\), i.e., \({f}_{\varvec{\diamond }}({{\textsf {V} }})\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{Y}}\,}})\), and thus \({f}_{\varvec{\diamond }}({{\textsf {V} }})\in Q\). Hence we have proved that \({{\textsf {V} }}\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {c} }}}({{\,\mathrm{{A}}\,}})\) \(\Rightarrow \) \({f}_{\varvec{\diamond }}({{\textsf {V} }})\in Q\). \(\square \)
Proposition 9.32
If \(({{\,\mathrm{{A}}\,}},\Theta )\) is a topological space and  is endowed with the natural topology, then the function
is endowed with the natural topology, then the function  is continuous.
is continuous.
Proof
Let \(x\in {{\,\mathrm{{A}}\,}}\) and let  . Then there exists \({{\textsf {b} }}\in {{{\textsf {N} }}}_{\Theta }(x)\) such that \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\subset {}U\). Since \({{\textsf {b} }}\in {{{\textsf {N} }}}_{\Theta }(x)\), there exists an open set \({{\textsf {c} }}\in \Theta \) such that \(x\in {{\textsf {c} }}\subset {{\textsf {b} }}\). Let \(z\in {{\textsf {c} }}\). Since \({{\textsf {c} }}\in \Theta \) and \({{\textsf {c} }}\subset {{\textsf {b} }}\), then \({{\textsf {b} }}\in {{{\textsf {N} }}}_{\Theta }(z)\), hence \({{{\textsf {N} }}}_{\Theta }(z)\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\), thus \({{{\textsf {N} }}}_{\Theta }(z)\in {}U\). Hence we have proved that if \(z\in {{\textsf {c} }}\) then \({{{\textsf {N} }}}_{\Theta }(z)\in {}U\), i.e., the function \({{{\textsf {N} }}}_{\Theta }\) is continuous at x. Since x is arbitrary, the proof of continuity of \({{{\textsf {N} }}}_{\Theta }\) is complete. \(\square \)
. Then there exists \({{\textsf {b} }}\in {{{\textsf {N} }}}_{\Theta }(x)\) such that \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\subset {}U\). Since \({{\textsf {b} }}\in {{{\textsf {N} }}}_{\Theta }(x)\), there exists an open set \({{\textsf {c} }}\in \Theta \) such that \(x\in {{\textsf {c} }}\subset {{\textsf {b} }}\). Let \(z\in {{\textsf {c} }}\). Since \({{\textsf {c} }}\in \Theta \) and \({{\textsf {c} }}\subset {{\textsf {b} }}\), then \({{\textsf {b} }}\in {{{\textsf {N} }}}_{\Theta }(z)\), hence \({{{\textsf {N} }}}_{\Theta }(z)\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\), thus \({{{\textsf {N} }}}_{\Theta }(z)\in {}U\). Hence we have proved that if \(z\in {{\textsf {c} }}\) then \({{{\textsf {N} }}}_{\Theta }(z)\in {}U\), i.e., the function \({{{\textsf {N} }}}_{\Theta }\) is continuous at x. Since x is arbitrary, the proof of continuity of \({{{\textsf {N} }}}_{\Theta }\) is complete. \(\square \)
Observe that if \(({{\,\mathrm{{A}}\,}},\Theta )\) is Hausdorff then  is injective.
is injective.
The following result will be better appreciated by keeping in mind Lemma 3.21.
Lemma 9.33
If  then the following conditions are equivalent:
then the following conditions are equivalent:
- (1):
-
\({{\textsf {Z} }}\subset {{\textsf {W} }}.\)
- (2):
-
\(,\) where
 is the closure in
is the closure in 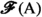 .
. - (3):
-
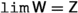 .
.
Proof
If \({{\textsf {Z} }}\subset {{\textsf {W} }}\) and U is an open set in  which contains \({{\textsf {Z} }}\), then there exists \({{\textsf {b} }}\in {{\mathcal {P}}}({{\,\mathrm{{A}}\,}})\) such that \({{\textsf {Z} }}\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\subset {}U\). Then \({{\textsf {b} }}\in {{\textsf {Z} }}\), hence \({{\textsf {b} }}\in {{\textsf {W} }}\), thus \({{\textsf {W} }}\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\). Therefore \({{\textsf {W} }}\in {}U\). These steps are reversible, hence the other implication follows. Hence (1) is equivalent to (2). Recall from Lemma 3.21 that the meaning of (3) is that if we denote by
which contains \({{\textsf {Z} }}\), then there exists \({{\textsf {b} }}\in {{\mathcal {P}}}({{\,\mathrm{{A}}\,}})\) such that \({{\textsf {Z} }}\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\subset {}U\). Then \({{\textsf {b} }}\in {{\textsf {Z} }}\), hence \({{\textsf {b} }}\in {{\textsf {W} }}\), thus \({{\textsf {W} }}\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\). Therefore \({{\textsf {W} }}\in {}U\). These steps are reversible, hence the other implication follows. Hence (1) is equivalent to (2). Recall from Lemma 3.21 that the meaning of (3) is that if we denote by  the constant sequence
the constant sequence  which is identically equal to \({{\textsf {W} }}\) then
which is identically equal to \({{\textsf {W} }}\) then  in the topology of
in the topology of  . Hence (2) and (3) are equivalent, by Lemma 3.23. \(\square \)
. Hence (2) and (3) are equivalent, by Lemma 3.23. \(\square \)
Lemma 9.34
If \({{\,\mathrm{{A}}\,}}\not =\emptyset ,\) then the following conditions are equivalent.
- (1):
-
\({{\,\mathrm{{A}}\,}}\) contains only one point.
- (2):
-
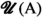 is closed in
is closed in 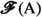 .
. - (3):
-
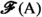 is Hausdorff.
is Hausdorff.
Proof
If (1) holds then  , hence (2) and (3) follow. If \({{\,\mathrm{{A}}\,}}\) contains more than one point, then
, hence (2) and (3) follow. If \({{\,\mathrm{{A}}\,}}\) contains more than one point, then  and by Example 9.27 the only open set in
and by Example 9.27 the only open set in  which contains \(\{{{\,\mathrm{{A}}\,}}\}\) is
which contains \(\{{{\,\mathrm{{A}}\,}}\}\) is  , which is not contained in
, which is not contained in  . Hence (2) \(\Rightarrow \) (1). Lemma 9.33 implies that (3) \(\Rightarrow \) (1). \(\square \)
. Hence (2) \(\Rightarrow \) (1). Lemma 9.33 implies that (3) \(\Rightarrow \) (1). \(\square \)
Proposition 9.35
If \(\varOmega \subsetneq {{\,\mathrm{{A}}\,}}\) then  is continuous.
is continuous.
Proof
Let  and let
and let  . Let
. Let  . Then \({{\textsf {W} }}_0\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\subset {}U\) for some \({{\textsf {b} }}\in {{\textsf {W} }}_0\). Hence \({{\textsf {b} }}={{\textsf {d} }}\cup {{\textsf {c} }}\) for some \({{\textsf {d} }}\in {{\textsf {Z} }}_0\) and some \({{\textsf {c} }}\in {{\mathcal {P}}}({{\,\mathrm{{A}}\,}}\setminus \varOmega )\). We claim that if \({{\textsf {Z} }}\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {d} }}}(\varOmega )\) then \({\imath }_{\varvec{\diamond }}({{\textsf {Z} }})\in {}U\), and this will prove continuity at \({{\textsf {Z} }}_0\), and since \({{\textsf {Z} }}_0\) is arbitrary, it will prove continuity. Let \({{\textsf {Z} }}\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {d} }}}(\varOmega )\). Then
. Then \({{\textsf {W} }}_0\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\subset {}U\) for some \({{\textsf {b} }}\in {{\textsf {W} }}_0\). Hence \({{\textsf {b} }}={{\textsf {d} }}\cup {{\textsf {c} }}\) for some \({{\textsf {d} }}\in {{\textsf {Z} }}_0\) and some \({{\textsf {c} }}\in {{\mathcal {P}}}({{\,\mathrm{{A}}\,}}\setminus \varOmega )\). We claim that if \({{\textsf {Z} }}\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {d} }}}(\varOmega )\) then \({\imath }_{\varvec{\diamond }}({{\textsf {Z} }})\in {}U\), and this will prove continuity at \({{\textsf {Z} }}_0\), and since \({{\textsf {Z} }}_0\) is arbitrary, it will prove continuity. Let \({{\textsf {Z} }}\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {d} }}}(\varOmega )\). Then  and \({{\textsf {d} }}\in {{\textsf {Z} }}\). Since \({{\textsf {b} }}={{\textsf {d} }}\cup {{\textsf {c} }}\) and \({{\textsf {d} }}\in {{\textsf {Z} }}\), it follows that \({{\textsf {b} }}\in {\imath }_{\varvec{\diamond }}({{\textsf {Z} }})\) hence \({\imath }_{\varvec{\diamond }}({{\textsf {Z} }})\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\), and since \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\subset {}U\), it follows that \({\imath }_{\varvec{\diamond }}({{\textsf {Z} }})\in {}U\). \(\square \)
and \({{\textsf {d} }}\in {{\textsf {Z} }}\). Since \({{\textsf {b} }}={{\textsf {d} }}\cup {{\textsf {c} }}\) and \({{\textsf {d} }}\in {{\textsf {Z} }}\), it follows that \({{\textsf {b} }}\in {\imath }_{\varvec{\diamond }}({{\textsf {Z} }})\) hence \({\imath }_{\varvec{\diamond }}({{\textsf {Z} }})\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\), and since \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\subset {}U\), it follows that \({\imath }_{\varvec{\diamond }}({{\textsf {Z} }})\in {}U\). \(\square \)
9.6 Compactness Properties of the Natural Topology
Theorem 9.36
If \({{\,\mathrm{{A}}\,}}\not =\emptyset \) then
- (1):
-
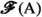 is compact and, for each \({{\textsf {d} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}),\) \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {d} }}}({{\,\mathrm{{A}}\,}})\) is compact in
is compact and, for each \({{\textsf {d} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}}),\) \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {d} }}}({{\,\mathrm{{A}}\,}})\) is compact in 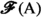 .
. - (2):
-
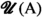 is compact and Hausdorff.
is compact and Hausdorff. - (3):
-
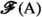 has a basis of open compact sets.
has a basis of open compact sets. 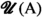 has a basis of closed and open compact sets.
has a basis of closed and open compact sets.
Proof
(1). Since  , it suffices to show that, for each \({{\textsf {d} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\), \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {d} }}}({{\,\mathrm{{A}}\,}})\) is compact. Let \({{\textsf {d} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\),
, it suffices to show that, for each \({{\textsf {d} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\), \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {d} }}}({{\,\mathrm{{A}}\,}})\) is compact. Let \({{\textsf {d} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\),  with \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {d} }}}({{\,\mathrm{{A}}\,}})\in {\mathcal {W}}\), and define
with \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {d} }}}({{\,\mathrm{{A}}\,}})\in {\mathcal {W}}\), and define
by

where \({{\textsf {b} }}\in {{\mathcal {P}}}({{\,\mathrm{{A}}\,}})\). We claim that
and
Hence Lemma 9.19 implies that
is a filter on \({{\,\mathrm{{A}}\,}}\). Now observe that \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {d} }}}({{\,\mathrm{{A}}\,}})\in {\mathcal {W}}\) \(\Rightarrow \) \({\mathcal {W}}^{*}({{\textsf {d} }})=1\) \(\Rightarrow \) \({{\textsf {d} }}\in {{\textsf {Z} }}_{{\mathcal {W}}}\) \(\Rightarrow \) \({{\textsf {Z} }}_{{\mathcal {W}}}\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {d} }}}({{\,\mathrm{{A}}\,}})\). Moreover,

i.e.,  . Lemma 4.30 implies that \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {d} }}}({{\,\mathrm{{A}}\,}})\) is compact.
. Lemma 4.30 implies that \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {d} }}}({{\,\mathrm{{A}}\,}})\) is compact.
We now prove the claim. Observe that  , since a filter cannot contain the empty set. In order to prove (9.14), observe that
, since a filter cannot contain the empty set. In order to prove (9.14), observe that
Let \(v=({\mathcal {W}}^{*}({{\textsf {b} }}_1),{\mathcal {W}}^{*}({{\textsf {b} }}_2))\). If \(v=(1,1)\) then (9.14) is immediate, since \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1\cap {{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}})\in {\mathcal {W}}\) by (9.18). Observe that \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1\cap {{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}}) \subset {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1}({{\,\mathrm{{A}}\,}})\), hence \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1\cap {{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}})\in {\mathcal {W}}\) \(\Rightarrow \) \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1}({{\,\mathrm{{A}}\,}})\in {\mathcal {W}}\). Thus \({\mathcal {W}}^{*}({{\textsf {b} }}_1)=0\) implies that \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1\cap {{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}})\not \in {\mathcal {W}}\), and then both members of (9.14) are equal to 0. A similar result follows if \({\mathcal {W}}^{*}({{\textsf {b} }}_2)=0\).
(2). Let  with
with  . We claim that \({\mathcal {W}}^{*}\in \texttt {Boole} _{*}({{{\mathcal {P}}}({{\,\mathrm{{A}}\,}})},{{{\mathbb {Z}}}_2})\). Lemma 9.19 then implies that \({{\textsf {Z} }}_{{\mathcal {W}}}\), defined in (9.16), belongs to
. We claim that \({\mathcal {W}}^{*}\in \texttt {Boole} _{*}({{{\mathcal {P}}}({{\,\mathrm{{A}}\,}})},{{{\mathbb {Z}}}_2})\). Lemma 9.19 then implies that \({{\textsf {Z} }}_{{\mathcal {W}}}\), defined in (9.16), belongs to  , and (9.17) says that
, and (9.17) says that  , and the proof is concluded by Lemma 4.30. In order to prove that
, and the proof is concluded by Lemma 4.30. In order to prove that
let \(v=({\mathcal {W}}^{*}({{\textsf {b} }}_1),{\mathcal {W}}^{*}({{\textsf {b} }}_2))\). If \(v=(1,1)\) then \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_k}({{\,\mathrm{{A}}\,}})\in {\mathcal {W}}\) (for \(k=1,2\)), hence \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1}({{\,\mathrm{{A}}\,}})\cap {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}})\in {\mathcal {W}}\), thus \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1\cap {{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}})\in {\mathcal {W}}\), by (9.18), and, in particular, \({{\textsf {b} }}_1\cap {{\textsf {b} }}_2\not =\emptyset \). Since \( {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1\vartriangle {{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}}) \cap {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1\cap {{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}}) =\emptyset \), it follows that \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1\vartriangle {{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}})\not \in {\mathcal {W}}\), hence (9.19) holds.
If \(v=(0,1)\) then \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1}({{\,\mathrm{{A}}\,}})\not \in {\mathcal {W}}\) and \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}})\in {\mathcal {W}}\), and, since \({\mathcal {W}}\) is an ultrafilter on  , \(\complement {({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1}({{\,\mathrm{{A}}\,}}))}\in {\mathcal {W}}\).
, \(\complement {({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1}({{\,\mathrm{{A}}\,}}))}\in {\mathcal {W}}\).
Let us assume that \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_2\setminus {{\textsf {b} }}_1}({{\,\mathrm{{A}}\,}})\not \in {\mathcal {W}}\). Since \({\mathcal {W}}\) is an ultrafilter on  , it follows that \(\complement {({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_2\setminus {{\textsf {b} }}_1}({{\,\mathrm{{A}}\,}}))}\in {\mathcal {W}}\) and thus, since
, it follows that \(\complement {({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_2\setminus {{\textsf {b} }}_1}({{\,\mathrm{{A}}\,}}))}\in {\mathcal {W}}\) and thus, since  ,
,

Hence there exists an ultrafilter \({{\textsf {Y} }}\) on \({{\,\mathrm{{A}}\,}}\) such that
Since \({{\textsf {Y} }}\) is an ultrafilter on \({{\,\mathrm{{A}}\,}}\), Lemma 4.26 implies that
thus \( \emptyset ={{\textsf {b} }}_2 \cap \, \complement {({{\textsf {b} }}_2\setminus {{\textsf {b} }}_1)} \in {{\textsf {Y} }}\), which is impossible. It follows that \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_2\setminus {{\textsf {b} }}_1}({{\,\mathrm{{A}}\,}})\in {\mathcal {W}}\), and since \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_2\setminus {{\textsf {b} }}_1}({{\,\mathrm{{A}}\,}}) \subset {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1\vartriangle {{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}})\), it follows that \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1\vartriangle {{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}})\in {\mathcal {W}}\). Thus, if \(v=(0,1)\), both sides of (9.19) are equal to 1. Since the case \(v=(1,0)\) is symmetric, the proof is concluded if we show that (9.19) holds if \(v=(0,0)\). In this case, \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1}({{\,\mathrm{{A}}\,}})\not \in {\mathcal {W}}\) and \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}})\not \in {\mathcal {W}}\). Since \({\mathcal {W}}\) is an ultrafilter on  , it follows that \(\complement {{{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1}({{\,\mathrm{{A}}\,}})}\in {\mathcal {W}}\) and \(\complement {{{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}})}\in {\mathcal {W}}\). Assume that \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1\vartriangle {{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}})\in {\mathcal {W}}\). Since \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1\vartriangle {{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}}) \subset {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1\cup {{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}})\), it follows that \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1\cup {{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}})\in {\mathcal {W}}\). Since
, it follows that \(\complement {{{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1}({{\,\mathrm{{A}}\,}})}\in {\mathcal {W}}\) and \(\complement {{{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}})}\in {\mathcal {W}}\). Assume that \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1\vartriangle {{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}})\in {\mathcal {W}}\). Since \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1\vartriangle {{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}}) \subset {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1\cup {{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}})\), it follows that \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1\cup {{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}})\in {\mathcal {W}}\). Since  , it follows that
, it follows that

Hence there exists an ultrafilter \({{\textsf {Y} }}\) on \({{\,\mathrm{{A}}\,}}\) such that
and since \({{\textsf {Y} }}\) is an ultrafilter on \({{\,\mathrm{{A}}\,}}\), Lemma 4.26 implies that
Thus \( \emptyset =\complement {{{\textsf {b} }}_1} \cap \, \complement {{{\textsf {b} }}_2} \, \cap {({{\textsf {b} }}_1\cup {{\textsf {b} }}_2)} \in {{\textsf {Y} }}\), which is impossible. Hence \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}_1\vartriangle {{\textsf {b} }}_2}({{\,\mathrm{{A}}\,}})\not \in {\mathcal {W}}\), and both sides of (9.19) are equal to 0. Hence  is compact. In order to show that it is Hausdorff, let
is compact. In order to show that it is Hausdorff, let  , with \({{\textsf {Z} }}_1\not ={{\textsf {Z} }}_2\). Then there exists \({{\textsf {b} }}_1\in {{\textsf {Z} }}_1\setminus {{\textsf {Z} }}_2\) and there exists \({{\textsf {b} }}_2\in {{\textsf {W} }}_2\). We claim that \({{\textsf {b} }}_2\setminus {{\textsf {b} }}_1\in {{\textsf {W} }}\). Indeed, Lemma 4.28 and \({{\textsf {b} }}_2\in {{\textsf {Z} }}_2\) imply that either \({{\textsf {b} }}_1\cap {{\textsf {b} }}_2\in {{\textsf {Z} }}_2\), or \({{\textsf {b} }}_2\setminus {{\textsf {b} }}_1\in {{\textsf {Z} }}_2\) but the first possibility is impossible since it implies that \({{\textsf {b} }}_1\in {{\textsf {Z} }}_2\). Hence
, with \({{\textsf {Z} }}_1\not ={{\textsf {Z} }}_2\). Then there exists \({{\textsf {b} }}_1\in {{\textsf {Z} }}_1\setminus {{\textsf {Z} }}_2\) and there exists \({{\textsf {b} }}_2\in {{\textsf {W} }}_2\). We claim that \({{\textsf {b} }}_2\setminus {{\textsf {b} }}_1\in {{\textsf {W} }}\). Indeed, Lemma 4.28 and \({{\textsf {b} }}_2\in {{\textsf {Z} }}_2\) imply that either \({{\textsf {b} }}_1\cap {{\textsf {b} }}_2\in {{\textsf {Z} }}_2\), or \({{\textsf {b} }}_2\setminus {{\textsf {b} }}_1\in {{\textsf {Z} }}_2\) but the first possibility is impossible since it implies that \({{\textsf {b} }}_1\in {{\textsf {Z} }}_2\). Hence  ,
,  ,
,  .
.
(3). The sets \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\), for \({{\textsf {b} }}\in {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{A}}\,}})\), are open, compact, and are a basis for the topology of  . The sets
. The sets  are compact, and since
are compact, and since  is Hausdorff, are closed. Since they are also open in
is Hausdorff, are closed. Since they are also open in  , the proof is complete. \(\square \)
, the proof is complete. \(\square \)
9.7 Other Properties of the Natural Topology
We now show that filters have a dual character. On the one hand, a filter \({{\textsf {W} }}\) on \({{\,\mathrm{{A}}\,}}\) may be seen as a “static” object, i.e., as an element of  , which is endowed, as we have seen, with a natural topology. On the other hand, we may look at \({{\textsf {W} }}\) in various other ways which bring to the forelight a certain dynamic character that is encoded in the intrinsic structure of a filter. Recall from Example 3.15 that if \({{\textsf {W} }}\) is a filter on a nonempty set \({{\,\mathrm{{A}}\,}}\), then \(({{\textsf {W} }},\supset )\) is a directed set, where \(\supset \) is reverse inclusion between sets.
, which is endowed, as we have seen, with a natural topology. On the other hand, we may look at \({{\textsf {W} }}\) in various other ways which bring to the forelight a certain dynamic character that is encoded in the intrinsic structure of a filter. Recall from Example 3.15 that if \({{\textsf {W} }}\) is a filter on a nonempty set \({{\,\mathrm{{A}}\,}}\), then \(({{\textsf {W} }},\supset )\) is a directed set, where \(\supset \) is reverse inclusion between sets.
The following commutative diagram displays the functions which appear in Proposition 9.37.

Recall from Definition 6.12 that \(s_{{{\textsf {W} }}}\) (and hence  ) may be seen as generalized sequences, since \({{\textsf {W} }}\) is directed by reverse set inclusion. Also recall that \(\epsilon _{{{\,\mathrm{{A}}\,}}}\) has been defined in (9.7), and \(\imath _{{{\,\mathrm{{A}}\,}}}\) in (9.9). The maps \(\delta _{{{\,\mathrm{{A}}\,}}}\) and
) may be seen as generalized sequences, since \({{\textsf {W} }}\) is directed by reverse set inclusion. Also recall that \(\epsilon _{{{\,\mathrm{{A}}\,}}}\) has been defined in (9.7), and \(\imath _{{{\,\mathrm{{A}}\,}}}\) in (9.9). The maps \(\delta _{{{\,\mathrm{{A}}\,}}}\) and  are defined by composition: \(\delta _{{{\,\mathrm{{A}}\,}}}=\epsilon _{{{\,\mathrm{{A}}\,}}}\circ \imath _{{{\,\mathrm{{A}}\,}}}\) and
are defined by composition: \(\delta _{{{\,\mathrm{{A}}\,}}}=\epsilon _{{{\,\mathrm{{A}}\,}}}\circ \imath _{{{\,\mathrm{{A}}\,}}}\) and  .
.
Proposition 9.37
If \(,\) then the following conditions are equivalent.
- (1):
-
\(\displaystyle {\mathop {{{{{\textbf {{\textsf {lim}}}}} }}}\nolimits _{{{\textsf {W} }}}{\delta _{{{\,\mathrm{{A}}\,}}}}={{\textsf {Z} }}}.\)
- (2):
-
\(\displaystyle {\mathop {{{{{\textbf {{\textsf {lim}}}}} }}}\nolimits _{{\imath }_{\varvec{\diamond }}({{\textsf {W} }})}\epsilon _{{{\,\mathrm{{A}}\,}}}={{\textsf {Z} }}}.\)
- (3):
-
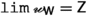 .
. - (4):
-
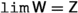 .
. - (5):
-
\({{\textsf {Z} }}\subset {{\textsf {W} }}\).
- (6):
-
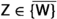 .
.
Proof
In Lemmas 9.33 and 3.21, we have shown that (4), (5), and (6) are equivalent to each other. Observe that Corollary 4.34 says that (1) amounts to asking that

and this means that \(\forall {{\textsf {b} }}\in {{\textsf {Z} }}\) \(\exists {{\textsf {d} }}\in {{\textsf {W} }}\) such that \({(\delta _{{{\,\mathrm{{A}}\,}}})}_{*}({{\textsf {d} }})\subset {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\). Observe that \({(\delta _{{{\,\mathrm{{A}}\,}}})}_{*}({{\textsf {d} }})\subset {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\) means that \(\forall {}x\in {{\textsf {d} }}\), \({{\,\mathrm{{A}}\,}}_{x}\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\), i.e., \({{\textsf {b} }}\in {{\,\mathrm{{A}}\,}}_x\), i.e., \(x\in {{\textsf {b} }}\). Hence \({(\delta _{{{\,\mathrm{{A}}\,}}})}_{*}({{\textsf {d} }})\subset {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\) means that \({{\textsf {d} }}\subset {{\textsf {b} }}\). Thus (1) says that \(\forall {{\textsf {b} }}\in {{\textsf {Z} }}\), \(\exists {{\textsf {d} }}\in {{\textsf {W} }}\) such that \({{\textsf {d} }}\subset {{\textsf {b} }}\), and this condition is equivalent to (5). The diagram on the left side of (9.20) commutes, i.e., \(\delta _{{{\,\mathrm{{A}}\,}}}=\epsilon _{{{\,\mathrm{{A}}\,}}}\circ \imath _{{{\,\mathrm{{A}}\,}}}\), and thus the functoriality properties established in Lemma 4.36 imply that
Hence (1) and (2) are equivalent to each other. Observe that (3) amounts to saying that \(\forall {{\textsf {d} }}\in {{\textsf {Z} }}\) \(\exists {{\textsf {b} }}\in {{\textsf {W} }}\) such that \({{\textsf {c} }}\in {{\textsf {W} }}\) and \({{\textsf {c} }}\subset {{\textsf {b} }}\) implies that \({{\,\mathrm{{A}}\,}}_{{{\textsf {c} }}}\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {d} }}}({{\,\mathrm{{A}}\,}})\). The condition \({{\,\mathrm{{A}}\,}}_{{{\textsf {c} }}}\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {d} }}}({{\,\mathrm{{A}}\,}})\) means that \({{\textsf {d} }}\in {{\,\mathrm{{A}}\,}}_{{{\textsf {c} }}}\), i.e., \({{\textsf {c} }}\subset {{\textsf {d} }}\). Hence (3) says that \(\forall {{\textsf {d} }}\in {{\textsf {Z} }}\) \(\exists {{\textsf {b} }}\in {{\textsf {W} }}\) such that \({{\textsf {c} }}\in {{\textsf {W} }}\) and \({{\textsf {c} }}\subset {{\textsf {b} }}\) implies that \({{\textsf {c} }}\subset {{\textsf {d} }}\), and this means that \(\forall {{\textsf {d} }}\in {{\textsf {Z} }}\) \(\exists {{\textsf {b} }}\in {{\textsf {W} }}\) such that \({{\textsf {b} }}\subset {{\textsf {d} }}\), which is equivalent to (5). \(\square \)
Proposition 9.38
If \(({{\,\mathrm{{A}}\,}},{{\textsf {Z} }})\) is a filtered set, \(({{\,\mathrm{{Y}}\,}},\Theta )\) is a topological space,  is a function, and \(y\in {{\,\mathrm{{Y}}\,}},\) then the following conditions are equivalent:
is a function, and \(y\in {{\,\mathrm{{Y}}\,}},\) then the following conditions are equivalent:
Proof
The result follows at once from Corollary 4.34 and Lemma 9.33. \(\square \)
The meaning of Proposition 9.38 is that the limiting behavior of a function f along a filter \({{\textsf {Z} }}\) is completely determined by the behavior of \({f}_{\varvec{\diamond }}({{\textsf {Z} }})\). Lemma 9.33 enables us to reformulate Theorem 6.2 as follows.
Corollary 9.39
If  is a \({{\,\mathrm{{Y}}\,}}\)-valued Moore–Smith sequence, \(\Theta \) is a topology on \({{\,\mathrm{{Y}}\,}}\), and \(y\in {{\,\mathrm{{Y}}\,}},\) then the following conditions are equivalent:
is a \({{\,\mathrm{{Y}}\,}}\)-valued Moore–Smith sequence, \(\Theta \) is a topology on \({{\,\mathrm{{Y}}\,}}\), and \(y\in {{\,\mathrm{{Y}}\,}},\) then the following conditions are equivalent:
In all these results the same underlying idea emerges, to wit: It is useful to interpret everything in terms of filters and then exploit the natural topology on  . For example, if \(\Theta \) is a topology on \({{\,\mathrm{{Y}}\,}}\), it is customary to say that y is a point of convergence for
. For example, if \(\Theta \) is a topology on \({{\,\mathrm{{Y}}\,}}\), it is customary to say that y is a point of convergence for  if
if  in the natural topology of \({{\,\mathrm{{Y}}\,}}\). We will study other useful applications of this idea in the following sections.
in the natural topology of \({{\,\mathrm{{Y}}\,}}\). We will study other useful applications of this idea in the following sections.
10 Applications of the Natural Topology to Cluster Points of Filters
In this section, we apply the natural topology of  to the study of the notion of cluster point of a filter.
to the study of the notion of cluster point of a filter.
Lemma 10.1
If \(,\) then the following conditions are equivalent:
- (1):
-
\({{\textsf {Z} }}_1\bowtie {{\textsf {Z} }}_2,\)
- (2):
-
There exists
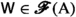 such that
such that 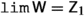 and
and 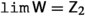 .
.
Proof
The result follows at once from Lemma 9.33. \(\square \)
Lemma 10.2
The collection

is closed in the product topology of  .
.
Proof
If \(({{\textsf {Z} }},{{\textsf {W} }})\not \in {\mathcal {C}}_{{{\,\mathrm{{A}}\,}}}\), then there exist \({{\textsf {b} }}\in {{\textsf {Z} }}\) and \({{\textsf {c} }}\in {{\textsf {W} }}\) such that \({{\textsf {b} }}\cap {{\textsf {c} }}=\emptyset \), by Lemma 9.15. Observe that \({{\textsf {Z} }}\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\), \({{\textsf {W} }}\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {c} }}}({{\,\mathrm{{A}}\,}})\), and \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\) and \({{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {c} }}}({{\,\mathrm{{A}}\,}})\) are disjoint open neighborhoods of \({{\textsf {Z} }}\) and \({{\textsf {W} }}\). Moreover, if \(({{\textsf {Z} }}',{{\textsf {W} }}')\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\,\mathrm{{A}}\,}})\times {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {c} }}}({{\,\mathrm{{A}}\,}})\) then \({{{\textsf {Z} }}'}\triangleleft \triangleright {{{\textsf {W} }}'}\) hence \(({{\textsf {Z} }}',{{\textsf {W} }}')\not \in {\mathcal {C}}_{{{\,\mathrm{{A}}\,}}}\), hence \(\complement {{\mathcal {C}}_{{{\,\mathrm{{A}}\,}}}}\) is open in  . \(\square \)
. \(\square \)
Definition 10.3
If \(\Theta \) is a topology on \({{\,\mathrm{{Y}}\,}}\), the filter  clusters at \(x\in {{\,\mathrm{{Y}}\,}}\) if \({{\textsf {W} }}\bowtie {{{\textsf {N} }}}_{\Theta }(x)\). The cluster set of \({{\textsf {W} }}\) on \({{\,\mathrm{{Y}}\,}}\) is the following subset of \({{\,\mathrm{{Y}}\,}}\):
clusters at \(x\in {{\,\mathrm{{Y}}\,}}\) if \({{\textsf {W} }}\bowtie {{{\textsf {N} }}}_{\Theta }(x)\). The cluster set of \({{\textsf {W} }}\) on \({{\,\mathrm{{Y}}\,}}\) is the following subset of \({{\,\mathrm{{Y}}\,}}\):
The following result says that the search for points of convergence of a filter should be restricted to the cluster set of the filter.
Lemma 10.4
If a filter \({{\textsf {W} }}\) converges to \({{{\textsf {N} }}}_{\Theta }(x)\) then it clusters at \(x\).
Proof
If \({{{\textsf {N} }}}_{\Theta }(x)\subset {{\textsf {W} }}\) then \({{{\textsf {N} }}}_{\Theta }(x)\vee {{\textsf {W} }}={{\textsf {W} }}\), hence \({{{\textsf {N} }}}_{\Theta }(x)\vee {{\textsf {W} }}\) exists. \(\square \)
Lemma 10.5
Let  and let \(\Theta \) be a topology on \({{\,\mathrm{{Y}}\,}}\). Then \({{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {W} }},\Theta ]\) is closed.
and let \(\Theta \) be a topology on \({{\,\mathrm{{Y}}\,}}\). Then \({{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {W} }},\Theta ]\) is closed.
Proof
If \(y\not \in {{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {W} }},\Theta ]\) then \(O\cap {{\textsf {b} }}=\emptyset \) for some \(O\in {{{\textsf {N} }}}_{\Theta }(y)\) and \({{\textsf {b} }}\in {{\textsf {W} }}\), and there exists an open set \(O'\subset {}O\) such that \(y\in {}O'\subset {}O\). Now observe that \(O'\subset {{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {W} }},\Theta ]\), hence \(\complement {({{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {W} }},\Theta ])}\) is open. \(\square \)
10.1 Application to Compactness
We are now ready to obtain a more flexible version of Lemma 4.30.
Proposition 10.6
([8]) If \({{\,\mathrm{{A}}\,}}\) is endowed with a topology \(\Theta \) and \(K\subset {{\,\mathrm{{A}}\,}},\) then the following conditions are equivalent:
- (1):
-
K is compact.
- (2):
-
For each ultrafilter on \({{\,\mathrm{{A}}\,}}\) which is localized in K there exists \(x\in {}K\) such that
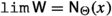 .
. - (3):
-
For each filter \({{\textsf {Z} }}\) on \({{\,\mathrm{{A}}\,}}\) which is localized in K, \(K\cap {{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }},\Theta ]\not =\emptyset \).
Proof
It suffices to prove that (2) and (3) are equivalent, since in Lemma 4.30 we have proved that (1) and (2) are equivalent. Assume that (2) holds, and let  with \(K\in {{\textsf {W} }}\). Theorem 4.25 implies that there exists
with \(K\in {{\textsf {W} }}\). Theorem 4.25 implies that there exists  such that \({{\textsf {Z} }}\subset {{\textsf {W} }}\). Hence (2) implies that there exists \(x\in {}K\) such that \({{{\textsf {N} }}}_{\Theta }(x)\subset {{\textsf {W} }}\). It follows that \({{{\textsf {N} }}}_{\Theta }(x)\vee {{\textsf {Z} }}\) exists, i.e., \(x\in {{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }},\Theta ]\). Assume that (3) holds, and let
such that \({{\textsf {Z} }}\subset {{\textsf {W} }}\). Hence (2) implies that there exists \(x\in {}K\) such that \({{{\textsf {N} }}}_{\Theta }(x)\subset {{\textsf {W} }}\). It follows that \({{{\textsf {N} }}}_{\Theta }(x)\vee {{\textsf {Z} }}\) exists, i.e., \(x\in {{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }},\Theta ]\). Assume that (3) holds, and let  with \(K\in {{\textsf {W} }}\). Then there exists \(x\in {}K\) such that \({{{\textsf {N} }}}_{\Theta }(x)\bowtie {{\textsf {W} }}\), i.e., there exists a filter \({{\textsf {Z} }}\) such that \({{{\textsf {N} }}}_{\Theta }(x)\subset {{\textsf {Z} }}\) and \({{\textsf {W} }}\subset {{\textsf {Z} }}\). Since \({{\textsf {W} }}\) is an ultrafilter, it follows that \({{\textsf {Z} }}={{\textsf {W} }}\), hence \({{{\textsf {N} }}}_{\Theta }(x)\subset {{\textsf {W} }}\). \(\square \)
with \(K\in {{\textsf {W} }}\). Then there exists \(x\in {}K\) such that \({{{\textsf {N} }}}_{\Theta }(x)\bowtie {{\textsf {W} }}\), i.e., there exists a filter \({{\textsf {Z} }}\) such that \({{{\textsf {N} }}}_{\Theta }(x)\subset {{\textsf {Z} }}\) and \({{\textsf {W} }}\subset {{\textsf {Z} }}\). Since \({{\textsf {W} }}\) is an ultrafilter, it follows that \({{\textsf {Z} }}={{\textsf {W} }}\), hence \({{{\textsf {N} }}}_{\Theta }(x)\subset {{\textsf {W} }}\). \(\square \)
The following result follows at once from Lemma 10.5 and Proposition 10.6.
Corollary 10.7
If \(({{\,\mathrm{{A}}\,}},\Theta )\) is a compact topological space and  then \({{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {W} }},\Theta ]\) is a nonempty compact subset of \({{\,\mathrm{{A}}\,}}\).
then \({{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {W} }},\Theta ]\) is a nonempty compact subset of \({{\,\mathrm{{A}}\,}}\).
Lemma 10.8
If \(({{\,\mathrm{{A}}\,}},\Theta )\) is a Hausdorff topological space, \(s,y\in {{\,\mathrm{{A}}\,}},\) and \({{{\textsf {N} }}}_{\Theta }(s)\bowtie {{{\textsf {N} }}}_{\Theta }(y),\) then \(s=y\).
Proof
If \(s\not =y\), there exists \(U\in {{{\textsf {N} }}}_{\Theta }(s)\) and \(V\in {{{\textsf {N} }}}_{\Theta }(y)\) such that \(U\cap {}V=\emptyset \). Hence \({{{{\textsf {N} }}}_{\Theta }(s)}\triangleleft \triangleright {{{{\textsf {N} }}}_{\Theta }(y)}\). \(\square \)
Theorem 10.9
If \(({{\,\mathrm{{A}}\,}},\Theta )\) is a compact Hausdorff topological space, \(,\) and \(y\in {{\,\mathrm{{A}}\,}},\) then the following conditions are equivalent:
- (1):
-
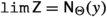 ,
, - (2):
-
\({{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }},\Theta ]=\{y\}.\)
Proof
If (1) holds, then \({{\textsf {Z} }}\supset {{{\textsf {N} }}}_{\Theta }(y)\), hence \(y\in {{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }},\Theta ]\). We now show that \({{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }},\Theta ]\) does not contain other points. Indeed, if \(s\in {{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }},\Theta ]\) then \({{{\textsf {N} }}}_{\Theta }(s)\vee {{\textsf {Z} }}\) exists and, since \({{\textsf {Z} }}\supset {{{\textsf {N} }}}_{\Theta }(y)\), it follows that \({{{\textsf {N} }}}_{\Theta }(s)\vee {{{\textsf {N} }}}_{\Theta }(y)\) exists. Then Lemma 10.8 implies that \(s=y\). Hence (2) holds.
If (1) does not hold, then there exists an open set \(Q\subset {{\,\mathrm{{A}}\,}}\) such that \(y\in Q\) and \(Q\not \in {{\textsf {Z} }}\). Hence \({{\textsf {Z} }}\) is weakly localized in \(\complement {Q}\), and Proposition 4.40 then implies that there exists a filter \({{\textsf {W} }}\) on \({{\,\mathrm{{A}}\,}}\) which is localized in \(\complement {Q}\) and such that \({{\textsf {Z} }}\subset {{\textsf {W} }}\). Since \(Q\) is open and \({{\,\mathrm{{A}}\,}}\) compact, it follows that \(\complement {Q}\) is compact. Hence Proposition 10.6 implies that there exists \(r\in \complement {Q}\) such that \(r\in {{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {W} }},\Theta ]\). Since \({{\textsf {Z} }}\subset {{\textsf {W} }}\), it follows that \(r\in {{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }},\Theta ]\). Since \(r\in \complement {Q}\) and \(y\in Q\), it follows that \(r\not =y\). Hence \({{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }},\Theta ]\) contains more than one point, i.e., (2) does not hold. \(\square \)
11 Filters on the Real Line
The goal of this section is to develop appropriate machinery for the study of convergence properties of filters on \({{\mathbb {R}}}\), since, in view of Corollary 4.34, these filters control the convergence properties of real-valued functions defined on a filtered set.
11.1 The Structure of the Cluster Set of Filters on the Real Line (I)
The main application of the notion of cluster set of a filter, introduced in Definition 10.3, is linked to Lemma 10.4 and Theorem 10.9, which imply that, in order to understand whether a given filter on a compact topological space converges, it suffices to control its cluster set. However, real-valued functions or sequences may very well diverge to \(+\infty \) or \(-\infty \), and indeed, if  , then the statement that
, then the statement that  means that \({{{\textsf {N} }}}_{{{\mathbb {R}}}}(+\infty )\subset {{\textsf {Z} }}\), but then \({{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }},{{\mathbb {R}}}]=\emptyset \). In particular, in this situation, the set \({{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }},{{\mathbb {R}}}]\) does not fully reflect the convergence properties of
means that \({{{\textsf {N} }}}_{{{\mathbb {R}}}}(+\infty )\subset {{\textsf {Z} }}\), but then \({{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }},{{\mathbb {R}}}]=\emptyset \). In particular, in this situation, the set \({{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }},{{\mathbb {R}}}]\) does not fully reflect the convergence properties of  . In order to obtain uniform results, which are useful in dealing with pointwise estimates, as we will see, we set as ambient space the extended real line \(\overline{{{\mathbb {R}}}}\equiv [-\infty ,+\infty ]\), a compact space which allows us to apply Theorem 10.9. Accordingly, we enlarge the ambient space which hosts the filters used in the notion of cluster set. In other words, we move from
. In order to obtain uniform results, which are useful in dealing with pointwise estimates, as we will see, we set as ambient space the extended real line \(\overline{{{\mathbb {R}}}}\equiv [-\infty ,+\infty ]\), a compact space which allows us to apply Theorem 10.9. Accordingly, we enlarge the ambient space which hosts the filters used in the notion of cluster set. In other words, we move from  to
to  .
.
If we specialize Definition 10.3 to \(\overline{{{\mathbb {R}}}}\equiv [-\infty ,+\infty ]\) we obtain, for 

With this definition, if  then \({{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }},\overline{{{\mathbb {R}}}}]=\{+\infty \}\), as one would expect.
then \({{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }},\overline{{{\mathbb {R}}}}]=\{+\infty \}\), as one would expect.
Observe the difference between the neighborhood filter of \(+\infty \) which appears in (11.1), to wit:

and the filter \({{{\textsf {N} }}}_{+\infty }({{\mathbb {R}}})\) defined in (1.17). Indeed, on the one hand,  while, on the other hand,
while, on the other hand,  . We will deal with this difference momentarily.
. We will deal with this difference momentarily.
Recall that closed nonempty intervals in \([-\infty ,+\infty ]\) have the form [a, b] where \(a,b\in \overline{{{\mathbb {R}}}}\) and \(a\le {}b\) (hence possibly \(a=b\)). In particular, \(\{+\infty \}\equiv [+\infty ,+\infty ]\) and \(\{-\infty \}\equiv [-\infty ,-\infty ]\) are closed nonempty intervals in \([-\infty ,+\infty ]\). Similarly, \([0,+\infty ]\) is a closed nonempty interval in \([-\infty ,+\infty ]\).
Theorem 11.1
If \(,\) then \({{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {W} }},\overline{{{\mathbb {R}}}}]\) is a nonempty compact interval of \([-\infty ,+\infty ]\).
Proof
Corollary 10.7 says that \({{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {W} }},\overline{{{\mathbb {R}}}}]\) is a nonempty compact subset of \(\overline{{{\mathbb {R}}}}\). In order to show that it is an interval, assume that \(r,s\in {{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {W} }},\overline{{{\mathbb {R}}}}]\), \(r<s\), and \(u\in (r,s)\). We claim that \(u\in {{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {W} }},\overline{{{\mathbb {R}}}}]\). Seeking a contradiction, assume that \(u\not \in {{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {W} }},\overline{{{\mathbb {R}}}}]\). Then there exists an open interval \((\alpha ,\beta )\subset {{\mathbb {R}}}\) and an element of \({{\textsf {b} }}\in {{\textsf {W} }}\), with \(r<\alpha<u<\beta <s\) and \((\alpha ,\beta )\cap {{\textsf {b} }}=\emptyset \). Then either (i) \({{\textsf {b} }}\subset [\beta ,+\infty ]\) or (ii) \({{\textsf {b} }}\subset [-\infty ,\alpha ]\). If (i) holds then there exists an open neighborhood of r which is disjoint from \({{\textsf {b} }}\), hence \(r\not \in {{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {W} }},\overline{{{\mathbb {R}}}}]\). If (ii) holds then a symmetrical reasoning shows that \(s\not \in {{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {W} }},\overline{{{\mathbb {R}}}}]\). \(\square \)
Given  , in order to be able to apply Corollary 10.7, it is necessary to consider the extension of \({{\textsf {Z} }}\) from \({{\mathbb {R}}}\) to \(\overline{{{\mathbb {R}}}}\), described in Sect. 4.6 and denoted by \({{\textsf {Z} }}'\). Indeed, since
, in order to be able to apply Corollary 10.7, it is necessary to consider the extension of \({{\textsf {Z} }}\) from \({{\mathbb {R}}}\) to \(\overline{{{\mathbb {R}}}}\), described in Sect. 4.6 and denoted by \({{\textsf {Z} }}'\). Indeed, since  , Theorem 11.1 implies that
, Theorem 11.1 implies that
We now go back to the difference between the neighborhood filter of \(+\infty \) which appears in (11.1) and the filter \({{{\textsf {N} }}}_{+\infty }({{\mathbb {R}}})\) defined in (1.17). Since the starting datum is a real filter, i.e., an element  , it would be desirable to express the cluster set of the extension of \({{\textsf {Z} }}\) directly in terms of \({{\textsf {Z} }}\). This task is achieved by the following definition, where we introduce the “extended real cluster set.”
, it would be desirable to express the cluster set of the extension of \({{\textsf {Z} }}\) directly in terms of \({{\textsf {Z} }}\). This task is achieved by the following definition, where we introduce the “extended real cluster set.”
Definition 11.2
If  , the extended cluster set of \({{\textsf {Z} }}\) in \([-\infty ,+\infty ]\) is the following subset of \([-\infty ,+\infty ]\)
, the extended cluster set of \({{\textsf {Z} }}\) in \([-\infty ,+\infty ]\) is the following subset of \([-\infty ,+\infty ]\)
Observe that all filters which appear in (11.3) are filters on \({{\mathbb {R}}}\). However, (11.3) has a slightly spurious appearance, since \({{\textsf {Z} }}\) is a filter on \({{\mathbb {R}}}\), but the resulting cluster set lies inside \(\overline{{{\mathbb {R}}}}\). Indeed, the advantage of Definition (11.2) is that the cluster set is expressed directly in terms of the original filter  and, moreover, the simpler filter (1.17) (a filter on \({{\mathbb {R}}}\)) is used instead of (11.2) (a filter on \(\overline{{{\mathbb {R}}}}\)). This technical convenience has no serious side effects, as shown in the following result.
and, moreover, the simpler filter (1.17) (a filter on \({{\mathbb {R}}}\)) is used instead of (11.2) (a filter on \(\overline{{{\mathbb {R}}}}\)). This technical convenience has no serious side effects, as shown in the following result.
Lemma 11.3
If  then
then
Proof
(Proof of \({{{{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }}',\overline{{{\mathbb {R}}}}] \subset {{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})}}\)). Assume that \(x\in {{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }}',\overline{{{\mathbb {R}}}}]\) and \(x\in {{\mathbb {R}}}\). Then \({{\textsf {Z} }}'\bowtie {{{\textsf {N} }}}_{\overline{{{\mathbb {R}}}}}(x)\) and, for each \(\epsilon >0\) and each \({{\textsf {b} }}'\in {{\textsf {Z} }}'\), the intersection \((x-\epsilon ,x+\epsilon )\cap {{\textsf {b} }}'\) is not empty. If \({{\textsf {b} }}\in {{\textsf {Z} }}\) then \({{\textsf {b} }}\in {{\textsf {Z} }}'\) (by Lemma 4.38) and it follows that \((x-\epsilon ,x+\epsilon )\cap {{\textsf {b} }}\not =\emptyset \). Thus \(x\in {{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})\). Assume that \(+\infty \in {{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }}',\overline{{{\mathbb {R}}}}]\). Then \({{\textsf {Z} }}'\bowtie {{{\textsf {N} }}}_{\overline{{{\mathbb {R}}}}}(+\infty )\). Let \({{\textsf {b} }}\in {{\textsf {Z} }}\). Since  , it follows that \({{\textsf {b} }}\subset {{\mathbb {R}}}\). Moreover, \({{\textsf {b} }}\in {{\textsf {Z} }}'\) (by Lemma 4.38). Let \(a\in {{\mathbb {R}}}\). Then \({{\textsf {b} }}\cap (a,+\infty ]\not =\emptyset \) (since \({{\textsf {Z} }}'\bowtie {{{\textsf {N} }}}_{\overline{{{\mathbb {R}}}}}(+\infty )\)). Since \({{\textsf {b} }}\subset {{\mathbb {R}}}\), it follows that \({{\textsf {b} }}\cap (a,+\infty )\not =\emptyset \). Since \({{\textsf {b} }}\in {{\textsf {Z} }}\) and \(a\in {{\mathbb {R}}}\) are arbitrary, it follows that \({{\textsf {Z} }}\bowtie {{{\textsf {N} }}}_{{{\mathbb {R}}}}(+\infty )\). Hence \(+\infty \in {{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})\). The proof that if \(-\infty \in {{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }}',\overline{{{\mathbb {R}}}}]\) then \(-\infty \in {{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})\) follows by symmetry. Hence we have proved that \({{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }}',\overline{{{\mathbb {R}}}}] \subset {{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})\).
, it follows that \({{\textsf {b} }}\subset {{\mathbb {R}}}\). Moreover, \({{\textsf {b} }}\in {{\textsf {Z} }}'\) (by Lemma 4.38). Let \(a\in {{\mathbb {R}}}\). Then \({{\textsf {b} }}\cap (a,+\infty ]\not =\emptyset \) (since \({{\textsf {Z} }}'\bowtie {{{\textsf {N} }}}_{\overline{{{\mathbb {R}}}}}(+\infty )\)). Since \({{\textsf {b} }}\subset {{\mathbb {R}}}\), it follows that \({{\textsf {b} }}\cap (a,+\infty )\not =\emptyset \). Since \({{\textsf {b} }}\in {{\textsf {Z} }}\) and \(a\in {{\mathbb {R}}}\) are arbitrary, it follows that \({{\textsf {Z} }}\bowtie {{{\textsf {N} }}}_{{{\mathbb {R}}}}(+\infty )\). Hence \(+\infty \in {{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})\). The proof that if \(-\infty \in {{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }}',\overline{{{\mathbb {R}}}}]\) then \(-\infty \in {{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})\) follows by symmetry. Hence we have proved that \({{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }}',\overline{{{\mathbb {R}}}}] \subset {{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})\).
(Proof of \({{{{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }}',\overline{{{\mathbb {R}}}}] \supset {{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})}}\)). Assume that \(x\in {{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})\) and \(x\in {{\mathbb {R}}}\). Hence \({{\textsf {Z} }}\bowtie {{{\textsf {N} }}}_{{{{\mathbb {R}}}}}(x)\). This means that for each \(\epsilon >0\) and each \({{\textsf {b} }}\in {{\textsf {Z} }}\), \({{\textsf {b} }}\cap (x-\epsilon ,x+\epsilon )\not =\emptyset \). Now let \({{\textsf {b} }}'\in {{\textsf {Z} }}\) and \(U\in {{{\textsf {N} }}}_{{\overline{{{\mathbb {R}}}}}}(x)\). Then there exists \(\epsilon >0\), \({{\textsf {b} }}\in {{\textsf {Z} }}\) and \(I\subset \{+\infty ,-\infty \}\) such that \(U\supset (x-\epsilon ,x+\epsilon )\) and \({{\textsf {b} }}'=I\cup {{\textsf {b} }}\). Then \({{\textsf {b} }}\cap (x-\epsilon ,x+\epsilon )\not =\emptyset \) implies that \({{\textsf {b} }}'\cap {}U\not =\emptyset \). Since \({{\textsf {b} }}'\in {{\textsf {Z} }}\) and \(U\in {{{\textsf {N} }}}_{{\overline{{{\mathbb {R}}}}}}(x)\) are arbitrary, it follows that \({{\textsf {Z} }}'\bowtie {{{\textsf {N} }}}_{\overline{{{\mathbb {R}}}}}(x)\), hence \(x\in {{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }}',\overline{{{\mathbb {R}}}}]\). Assume that \(+\infty \in {{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})\). Then \({{\textsf {Z} }}\bowtie {{{\textsf {N} }}}_{{{\mathbb {R}}}}(+\infty )\). This means that, if \({{\textsf {b} }}\in {{\textsf {Z} }}\) and \(a\in {{\mathbb {R}}}\), then \({{\textsf {b} }}\cap (a,+\infty )\not =\emptyset \). Now let \({{\textsf {b} }}'\in {{\textsf {Z} }}'\) and \(U\in {{{\textsf {N} }}}_{\overline{{{\mathbb {R}}}}}(+\infty )\). Then there exists \({{\textsf {b} }}\in {{\textsf {Z} }}\) and \(I\subset \{+\infty ,-\infty \}\) such that \({{\textsf {b} }}'=I\cup {{\textsf {b} }}\). Moreover, there exists \(a\in {{\mathbb {R}}}\) such that \(U\supset (a,+\infty ]\). Since \({{\textsf {b} }}\cap (a,+\infty )\not =\emptyset \), it follows that \({{\textsf {b} }}'\cap {}U\not =\emptyset \). Hence \({{\textsf {Z} }}'\bowtie {{{\textsf {N} }}}_{\overline{{{\mathbb {R}}}}}(+\infty )\), and thus \(+\infty \in {{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }}',\overline{{{\mathbb {R}}}}]\). The proof that if \(-\infty \in {{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})\) then \(-\infty \in {{{\textbf {{\textsf {Cluster}}}}} }[{{\textsf {Z} }}',\overline{{{\mathbb {R}}}}]\) follows by symmetry. \(\square \)
11.2 Cluster Set and Limiting Points
In order to a apply the previous results to  , the following idea is useful.
, the following idea is useful.
Lemma 11.4
If  and \(y\in [-\infty ,+\infty ],\) and \({{\textsf {Z} }}'\) is the extension of \({{\textsf {Z} }}\) from \({{\mathbb {R}}}\) to \(\overline{{{\mathbb {R}}}},\) then the following conditions are equivalent:
and \(y\in [-\infty ,+\infty ],\) and \({{\textsf {Z} }}'\) is the extension of \({{\textsf {Z} }}\) from \({{\mathbb {R}}}\) to \(\overline{{{\mathbb {R}}}},\) then the following conditions are equivalent:
- (1):
-
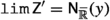 ,
, - (2):
-
 .
.
Proof
(1) \(\Rightarrow \) (2) If \(y\in {{\mathbb {R}}}\), let \(\epsilon >0\) and let \(I{\mathop {=}\limits ^\mathrm{{def}}}(y-\epsilon ,y+\epsilon )\). Then \(I\in {{{\textsf {N} }}}_{\overline{{{\mathbb {R}}}}}(y)\), hence \(I\in {{\textsf {Z} }}'\). Since \({{\textsf {Z} }}'={\imath }_{\varvec{\diamond }}({{\textsf {Z} }})\), where \(\imath :{{\mathbb {R}}}\rightarrow \overline{{{\mathbb {R}}}}\) is the natural injection, Lemma 4.38 implies that \(I\in {{\textsf {Z} }}\). If \(y=\{+\infty \}\), then let \(U\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(+\infty )\). Then there exists \(a\in {{\mathbb {R}}}\) such that \((a,+\infty )\subset {}U\). Observe that \((a,+\infty ]\in {{{\textsf {N} }}}_{\overline{{{\mathbb {R}}}}}(+\infty )\), hence \((a,+\infty ]\in {{\textsf {Z} }}'\). Since \((a,+\infty ]=(a,+\infty )\cup \{+\infty \}\), Lemma 4.38 implies that \((a,+\infty )\in {{\textsf {Z} }}\), hence \(U\in {{\textsf {Z} }}\). The case \(y=-\infty \) is similar.
(2) \(\Rightarrow \) (1) If \(y\in {{\mathbb {R}}}\), let \(U\in {{{\textsf {N} }}}_{\overline{{{\mathbb {R}}}}}(y)\). Then there exists \(\epsilon >0\) such that \((y-\epsilon ,y+\epsilon )\subset {}U\). Hence \((y-\epsilon ,y+\epsilon )\in {{\textsf {Z} }}\), and then (4.15) implies that \((y-\epsilon ,y+\epsilon )\in {{\textsf {Z} }}'\), hence \(U\in {{\textsf {Z} }}'\). If \(y=\{+\infty \}\), let \(U\in {{{\textsf {N} }}}_{\overline{{{\mathbb {R}}}}}(+\infty )\). Then there exists \(a\in {{\mathbb {R}}}\) such that \((a,+\infty ]\subset {}U\). Then \((a,+\infty )\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(+\infty )\), and it follows that \((a,+\infty )\in {{\textsf {Z} }}\), hence \((a,+\infty ]\in {{\textsf {Z} }}'\), thus \(U\in {{\textsf {Z} }}'\). The case \(y=-\infty \) is similar. \(\square \)
Theorem 11.5
If  and \(y\in [-\infty ,+\infty ]\) then the following conditions are equivalent:
and \(y\in [-\infty ,+\infty ]\) then the following conditions are equivalent:
- (1):
-
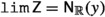 ,
, - (2):
-
\({{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})=\{y\}.\)
Proof
The result follows at once from Lemma 11.3, Theorem 10.9, and Lemma 11.4. \(\square \)
11.3 The Filters \({{{\textsf {N} }}}_{{{\mathbb {R}}}}(\pm \infty )\) from the Viewpoint of the Natural Topology on 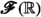
The following result looks at these matters from the viewpoint of the natural topology of  .
.
Lemma 11.6
Consider the  -valued Moore–Smith sequence
-valued Moore–Smith sequence  defined by
defined by

for each \(r\in {{\mathbb {R}}}\). Then

Proof
Let U be a neighborhood of \({{{\textsf {N} }}}_{{{\mathbb {R}}}}(+\infty )\) in  . We may assume, without loss of generality, than \(U={{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\mathbb {R}}})\) for \({{\textsf {b} }}\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(+\infty )\), and that \({{\textsf {b} }}=(x,+\infty )\), where \(x\in {{\mathbb {R}}}\). We claim that
. We may assume, without loss of generality, than \(U={{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\mathbb {R}}})\) for \({{\textsf {b} }}\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(+\infty )\), and that \({{\textsf {b} }}=(x,+\infty )\), where \(x\in {{\mathbb {R}}}\). We claim that

Indeed, if \(x<r\) then \({{\textsf {b} }}\in {{{\textsf {N} }}}_{{{\mathbb {R}}}}(r)\), hence \({{{\textsf {N} }}}_{{{\mathbb {R}}}}(r)\in {{{{{\textbf {{\textsf {F}}}}} }}}_{{{\textsf {b} }}}({{\mathbb {R}}})\), i.e.,  . The proof of the second statement is symmetrical. \(\square \)
. The proof of the second statement is symmetrical. \(\square \)
Corollary 11.7
\({{{\textsf {N} }}}_{{{\mathbb {R}}}}(+\infty )\) and \({{{\textsf {N} }}}_{{{\mathbb {R}}}}(-\infty )\) belong to the closure of \(\left\{ {{{\textsf {N} }}}_{{{\mathbb {R}}}}(r)\!:r\in {{\mathbb {R}}}\right\} \) in the natural topology of  .
.
Proof
It suffices to apply Lemma 3.23. \(\square \)
11.4 The Structure of the Cluster Set of Filters on the Real Line (II)
We now look at the cluster set of  from a more concrete viewpoint, which is useful in dealing with pointwise estimates, and introduce the notion of \(\limsup \) and \(\liminf \) of a filter on \({{\mathbb {R}}}\). These notions are related, as we will see, to the familiar notions of \(\liminf \) and \(\limsup \) of a real-valued sequence or function, but formally different, hence it is convenient to use a different notation. Recall from Sect. 9.2 that if \({{\textsf {Z} }},{{\textsf {W} }}\) are filters on \({{\,\mathrm{{A}}\,}}\) then \({{\textsf {Z} }}\bowtie {{\textsf {W} }}\) means that \({{\textsf {Z} }}\vee {{\textsf {W} }}\) exists in
from a more concrete viewpoint, which is useful in dealing with pointwise estimates, and introduce the notion of \(\limsup \) and \(\liminf \) of a filter on \({{\mathbb {R}}}\). These notions are related, as we will see, to the familiar notions of \(\liminf \) and \(\limsup \) of a real-valued sequence or function, but formally different, hence it is convenient to use a different notation. Recall from Sect. 9.2 that if \({{\textsf {Z} }},{{\textsf {W} }}\) are filters on \({{\,\mathrm{{A}}\,}}\) then \({{\textsf {Z} }}\bowtie {{\textsf {W} }}\) means that \({{\textsf {Z} }}\vee {{\textsf {W} }}\) exists in  , and \({{{\textsf {Z} }}}\triangleleft \triangleright {{{\textsf {W} }}}\) means that \({{\textsf {Z} }}\vee {{\textsf {W} }}\) does not exist in
, and \({{{\textsf {Z} }}}\triangleleft \triangleright {{{\textsf {W} }}}\) means that \({{\textsf {Z} }}\vee {{\textsf {W} }}\) does not exist in  . If \({{\textsf {b} }}\subset {{\,\mathrm{{A}}\,}}\), then \({{\textsf {b} }}\bowtie {{\textsf {W} }}\) [resp. \({{{\textsf {b} }}}\triangleleft \triangleright {{{\textsf {W} }}}\)] means that \({{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\bowtie {{\textsf {W} }}\) [resp. \({{{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}}\triangleleft \triangleright {{{\textsf {W} }}}\)].
. If \({{\textsf {b} }}\subset {{\,\mathrm{{A}}\,}}\), then \({{\textsf {b} }}\bowtie {{\textsf {W} }}\) [resp. \({{{\textsf {b} }}}\triangleleft \triangleright {{{\textsf {W} }}}\)] means that \({{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}\bowtie {{\textsf {W} }}\) [resp. \({{{\,\mathrm{{A}}\,}}_{{{\textsf {b} }}}}\triangleleft \triangleright {{{\textsf {W} }}}\)].
Definition 11.8
If  then we define
then we define

with the understanding that \(\sup \emptyset =-\infty \) and \(\inf \emptyset =+\infty \).
Example 11.9
It is useful to keep in mind the following examples.
- (1):
-
\({{\textsf {Z} }}^+=(-\infty ,0)\) if \({{\textsf {Z} }}\) is the filter generated by the filter base in Example 4.13.
- (2):
-
\({{\textsf {Z} }}^+=(-\infty ,0]\) if \({{\textsf {Z} }}={{{\textsf {N} }}}_{{{\mathbb {R}}}}(0)\).
- (3):
-
\({{\textsf {Z} }}^+={{\mathbb {R}}}\) and \({{\textsf {Z} }}^-=\emptyset \) if \({{\textsf {Z} }}={{{\textsf {N} }}}_{{{\mathbb {R}}}}(+\infty )\).
- (4):
-
\({{\textsf {Z} }}^+=\emptyset \) and \({{\textsf {Z} }}^-={{\mathbb {R}}}\) if \({{\textsf {Z} }}={{{\textsf {N} }}}_{{{\mathbb {R}}}}(-\infty )\).
- (5):
-
\({{\textsf {Z} }}^+={{\textsf {Z} }}^-={{\mathbb {R}}}\) if \({{\textsf {Z} }}\) is the filter generated by the filter base in Example 4.14.
In particular, we observe that \( {{{{\textbf {{\textsf {limsup}}}}}}}\,{{{\textsf {N} }}}_{{{\mathbb {R}}}}(+\infty )= {{{{\textbf {{\textsf {liminf}}}}}}}\,{{{\textsf {N} }}}_{{{\mathbb {R}}}}(+\infty )=+\infty \). In a similar way, one shows that \( {{{{\textbf {{\textsf {limsup}}}}}}}\,{{{\textsf {N} }}}_{{{\mathbb {R}}}}(-\infty )= {{{{\textbf {{\textsf {liminf}}}}}}}\,{{{\textsf {N} }}}_{{{\mathbb {R}}}}(-\infty )=-\infty \).
Definition 11.10
We say that a subset I of \({{\mathbb {R}}}\) is a left-interval in \({{\mathbb {R}}}\) if it has one of the following forms: (i) \(I=(-\infty ,a)\) for some \(a\in {{\mathbb {R}}}\); (ii) \(I=(-\infty ,a]\) for some \(a\in {{\mathbb {R}}}\); (iii) \(I={{\mathbb {R}}}\); (iv) \(I=\emptyset \). The notion of right-interval is defined by symmetry.
Lemma 11.11
If  then \({{\textsf {Z} }}^+\) is a left-interval in \({{\mathbb {R}}},\) and \({{\textsf {Z} }}^-\) is a right-interval in \({{\mathbb {R}}}\).
then \({{\textsf {Z} }}^+\) is a left-interval in \({{\mathbb {R}}},\) and \({{\textsf {Z} }}^-\) is a right-interval in \({{\mathbb {R}}}\).
Proof
The conclusion for \({{\textsf {Z} }}^+\) follows at once from the fact that if \(r\in {{\mathbb {R}}}\), \((r,+\infty )\bowtie {{\textsf {Z} }}\), and \(r'<r\), then \((r',+\infty )\bowtie {{\textsf {Z} }}\). The reasoning for \({{\textsf {Z} }}^-\) is symmetric. \(\square \)
Lemma 11.12
If  and \(x\in {{\mathbb {R}}}\) then
and \(x\in {{\mathbb {R}}}\) then
- (1):
-
If \({{\textsf {Z} }}\subset {{\textsf {W} }}\) then \({{\textsf {Z} }}^+\supset {{\textsf {W} }}^+\) and \({{\textsf {Z} }}^-\supset {{\textsf {W} }}^-\).
- (2):
-
\({{\textsf {Z} }}^+=\emptyset \) if and only if \({{{\textsf {N} }}}_{{{\mathbb {R}}}}(-\infty )\subset {{\textsf {Z} }}\), and \({{\textsf {Z} }}^-=\emptyset \) if and only if \({{{\textsf {N} }}}_{{{\mathbb {R}}}}(+\infty )\subset {{\textsf {Z} }}\).
- (3):
-
\(x\not \in {{\textsf {Z} }}^-\) if and only if \([x,+\infty )\in {{\textsf {Z} }}\), and \(x\not \in {{\textsf {Z} }}^+\) if and only if \((-\infty ,x]\in {{\textsf {Z} }}\).
- (4):
-
If \({{\textsf {Z} }}\subset {{\textsf {W} }}\) then \({{{{\textbf {{\textsf {liminf}}}}}}}\,{{\textsf {Z} }}\le {{{{\textbf {{\textsf {liminf}}}}}}}\,{{\textsf {W} }}\) and \({{{{\textbf {{\textsf {limsup}}}}}}}\,{{\textsf {W} }}\le {{{{\textbf {{\textsf {limsup}}}}}}}\,{{\textsf {Z} }}\).
Proof
By symmetry, it suffices to prove the first statement in each part. (1) If \({{\textsf {Z} }}\subset {{\textsf {W} }}\) and \(r\in {{\textsf {W} }}^+\) then \((r,+\infty )\cap {{\textsf {b} }}\not =\emptyset \) for each \({{\textsf {b} }}\in {{\textsf {W} }}\), hence the same conclusion holds for each \({{\textsf {b} }}\in {{\textsf {Z} }}\). (2) It suffices to observe that (i) the statement \({{\textsf {Z} }}^+=\emptyset \) means that \(\forall \) \(x\in {{\mathbb {R}}}\) \(\exists {{\textsf {b} }}\in {{\textsf {Z} }}\) such that \({{\textsf {b} }}\cap (x,+\infty )=\emptyset \), i.e., \({{\textsf {b} }}\subset (-\infty ,x]\), hence \((-\infty ,x]\in {{\textsf {Z} }}\); (ii) the statement that \(\forall \) \(x\in {{\mathbb {R}}}\) \((-\infty ,x]\in {{\textsf {Z} }}\) is equivalent to \({{{\textsf {N} }}}_{{{\mathbb {R}}}}(-\infty )\subset {{\textsf {Z} }}\). (3) The statement \(x\not \in {{\textsf {Z} }}^-\) means that \(\exists \) \({{\textsf {b} }}\in {{\textsf {Z} }}\) such that \((-\infty ,x)\cap {{\textsf {b} }}=\emptyset \), i.e., \({{\textsf {b} }}\subset [x,+\infty )\), hence \([x,+\infty )\in {{\textsf {Z} }}\), and conversely. (4) Follows at once from (1). \(\square \)
Corollary 11.13
If  and \({{\textsf {Z} }}^+=\emptyset \) then \({{\textsf {Z} }}^-={{\mathbb {R}}},\) and if \({{\textsf {Z} }}^-=\emptyset \) then \({{\textsf {Z} }}^+={{\mathbb {R}}}\)
and \({{\textsf {Z} }}^+=\emptyset \) then \({{\textsf {Z} }}^-={{\mathbb {R}}},\) and if \({{\textsf {Z} }}^-=\emptyset \) then \({{\textsf {Z} }}^+={{\mathbb {R}}}\)
Proof
It suffices to prove the first statement. If \({{\textsf {Z} }}^+=\emptyset \) and \(x\in {{\mathbb {R}}}\setminus {{\textsf {Z} }}^-\) then (2) and (3) in Lemma 11.12 imply that \({{{\textsf {N} }}}_{{{\mathbb {R}}}}(-\infty )\subset {{\textsf {Z} }}\) and \([x,+\infty )\in {{\textsf {Z} }}\), hence \(\emptyset =(-\infty ,x-1)\cap [x,+\infty )\in {{\textsf {Z} }}\), a contradiction. \(\square \)
Lemma 11.14
If \(\alpha ,\beta \in {{\mathbb {R}}},\) \(\alpha <\beta ,\)  and \({{\textsf {c} }}\in {{\textsf {Z} }},\) then
and \({{\textsf {c} }}\in {{\textsf {Z} }},\) then
- (1):
-
If \({{\textsf {c} }}\subset [\beta ,+\infty )\) then \((\alpha ,\beta )\cap {{\textsf {Z} }}^-=\emptyset \).
- (2):
-
If \({{\textsf {c} }}\subset (-\infty ,\alpha ]\) then \((\alpha ,\beta )\cap {{\textsf {Z} }}^+=\emptyset \).
Proof
(1) If \(y\in (\alpha ,\beta )\) and \((-\infty ,y)\bowtie {{\textsf {Z} }}\) then, in particular, \((-\infty ,y)\cap {{\textsf {b} }}\not =\emptyset \), but this is impossible, since \({{\textsf {c} }}\subset [\beta ,+\infty )\). The proof of (2) is similar. \(\square \)
Lemma 11.15
If \(,\) \(x\in {{\mathbb {R}}},\) and \(\epsilon >0,\) then
Proof
If \((x-\epsilon ,x+\epsilon )\cap {{\textsf {Z} }}^-=\emptyset \) then, in particular, \(x+\frac{\epsilon }{2}\not \in {{\textsf {Z} }}^-\). Lemma 11.12 implies that \(\left[ x+\frac{\epsilon }{2},+\infty \right) \in {{\textsf {Z} }}\). Since \(\left( x-\frac{\epsilon }{4},x+\frac{\epsilon }{4}\right) \cap \left[ x+\frac{\epsilon }{2},+\infty \right) =\emptyset \), it follows that \({{{{\textsf {N} }}}_{{{\mathbb {R}}}}(x)}\triangleleft \triangleright {{{\textsf {Z} }}}\), i.e., \(x\not \in {{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})\). If \((x-\epsilon ,x+\epsilon )\cap {{\textsf {Z} }}^+=\emptyset \) then, in particular, \(x-\frac{\epsilon }{2}\not \in {{\textsf {Z} }}^+\). Lemma 11.12 implies that \(\left( -\infty ,x-\frac{\epsilon }{2}\right] \in {{\textsf {Z} }}\). Since \(\left( x-\frac{\epsilon }{4},x+\frac{\epsilon }{4}\right) \cap \left( -\infty ,x-\frac{\epsilon }{2}\right] =\emptyset \), it follows that \({{{{\textsf {N} }}}_{{{\mathbb {R}}}}(x)}\triangleleft \triangleright {{{\textsf {Z} }}}\), i.e., \(x\not \in {{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})\). \(\square \)
Lemma 11.16
If  then
then
with the understanding that \([+\infty ,+\infty ]=\{+\infty \}\) and \([-\infty ,-\infty ]=\{-\infty \}\).
Proof
Theorem 11.1 and Lemma 11.3 imply that it suffices to prove that
By symmetry, it suffices to prove the first statement, which amounts to show that
In order to prove (i), we separately examine the following three cases:
If (i.a) holds, then either \({{\textsf {Z} }}^+=(-\infty ,a)\) or \({{\textsf {Z} }}^+=(-\infty ,a]\), where \(a={{{{\textbf {{\textsf {limsup}}}}}}}\,{{\textsf {Z} }}\in {{\mathbb {R}}}\), but in either case, for each \(\epsilon >0\),
The first statement in (11.7) follows from Lemma 11.12, since \(a+\epsilon \not \in {{\textsf {Z} }}^+\), the second one from the fact that \(a-\epsilon \in {{\textsf {Z} }}^+\). If \({{{{\textsf {N} }}}_{{{\mathbb {R}}}}(a)}\triangleleft \triangleright {{{\textsf {Z} }}}\) then there exists \(r>0\) and \({{\textsf {b} }}\in {{\textsf {Z} }}\) such that \((a-r,a+r)\cap {{\textsf {b} }}=\emptyset \), and this means that
but (11.8) is incompatible with (11.7) with \(\epsilon {\mathop {=}\limits ^\mathrm{{def}}}\frac{r}{2}\). Hence \({{{\textsf {N} }}}_{{{\mathbb {R}}}}(a)\bowtie {{\textsf {Z} }}\), i.e., \(a\in {{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})\), and (i) holds. If (i.b) holds, then \({{\textsf {Z} }}^+=\emptyset \), hence \({{{\textsf {N} }}}_{{{\mathbb {R}}}}(-\infty )\subset {{\textsf {Z} }}\) (by Lemma 11.12), thus \({{{\textsf {N} }}}_{{{\mathbb {R}}}}(-\infty )\bowtie {{\textsf {Z} }}\), and this means that \(-\infty \in {{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})\). If (i.c) holds, then \({{\textsf {Z} }}^+={{\mathbb {R}}}\), i.e., for each \(r\in {{\mathbb {R}}}\), \((r,+\infty )\bowtie {{\textsf {Z} }}\), hence \({{{\textsf {N} }}}_{{{\mathbb {R}}}}(+\infty )\bowtie {{\textsf {Z} }}\), thus \(+\infty \in {{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})\). The proof of (i) is complete.
In order to prove (ii), it suffices to examine the following two cases:
If (ii.a) holds and \({{{{\textbf {{\textsf {limsup}}}}}}}\,{{\textsf {Z} }}<x\), then there exists \(\epsilon >0\) such that \((x-\epsilon ,x+\epsilon )\cap {{\textsf {Z} }}^+=\emptyset \), and Lemma 11.15 implies that \(x\not \in {{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})\). Hence (ii) holds in this case. If (ii.a) holds then \({{\textsf {Z} }}^+=\emptyset \), and Lemma 11.12 implies that \({{\textsf {Z} }}\supset {{{\textsf {N} }}}_{{{\mathbb {R}}}}(-\infty )\), i.e.,  . Then Theorem 11.5 implies that
. Then Theorem 11.5 implies that
hence (ii) holds in this case as well, and the proof is complete. \(\square \)
Corollary 11.17
If  then
then
Theorem 11.18
If  and \(y\in \overline{{{\mathbb {R}}}}\) then the following conditions are equivalent:
and \(y\in \overline{{{\mathbb {R}}}}\) then the following conditions are equivalent:
- (1):
-
\({{{{\textbf {{\textsf {liminf}}}}}}}\,{{{\textsf {Z} }}}={{{{\textbf {{\textsf {limsup}}}}}}}\,{{{\textsf {Z} }}}=y,\)
- (2):
-
\({{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})=\{y\},\)
- (3):
-
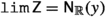 .
.
Proof
The result follows at once from Theorem 11.5 and Lemma 11.16. \(\square \)
We now present a different description of the \({{{{\textbf {{\textsf {limsup}}}}}}}\,{{\textsf {Z} }}\) and \({{{{\textbf {{\textsf {liminf}}}}}}}\,{{\textsf {Z} }}\).
Lemma 11.19
If  then
then
- (1):
-
\( \displaystyle {\mathop {{{{{\textbf {{\textsf {limsup}}}}}}}\,}\limits _{{{\mathbb {R}}}}{{\textsf {Z} }}= \inf \left\{ \sup \left\{ x\!:x\in {{\textsf {b} }}\right\} \!:{{\textsf {b} }}\in {{\textsf {Z} }}\right\} }\)
- (2):
-
\({{{{{\textbf {{\textsf {liminf}}}}}}}\,_{{{\mathbb {R}}}}{{\textsf {Z} }}= \sup \left\{ \inf \left\{ x\!:x\in {{\textsf {b} }}\right\} \!:{{\textsf {b} }}\in {{\textsf {Z} }}\right\} } \)
Proof
It suffices to prove the first statement, by symmetry. If \({{{{\textbf {{\textsf {limsup}}}}}}}\,{{\textsf {Z} }}=+\infty \) then \({{\textsf {Z} }}^+={{\mathbb {R}}}\). Let
If \(\alpha <+\infty \) then there exists \({{\textsf {b} }}\in {{\textsf {Z} }}\) with \(\sup \left\{ x\!:x\in {{\textsf {b} }}\right\} <+\infty \). Let \(\beta {\mathop {=}\limits ^\mathrm{{def}}}\sup \left\{ x\!:x\in {{\textsf {b} }}\right\} \). Then \({{\textsf {b} }}\subset (-\infty ,\beta ]\), hence \(\beta +1\not \in {{\textsf {Z} }}^+\), a contradiction. Hence \(\alpha =+\infty \) and (1) holds. Assume that \({{{{\textbf {{\textsf {limsup}}}}}}}\,{{\textsf {Z} }}=-\infty \). We claim that either \(\alpha =+\infty \) or \(\alpha \in {{\mathbb {R}}}\) lead to a contradiction, and hence \(\alpha =-\infty \). Indeed, if \(\alpha =+\infty \) then \(\sup \left\{ x\!:x\in {{\textsf {b} }}\right\} =+\infty \) for each \({{\textsf {b} }}\in {{\textsf {Z} }}\), hence \((r,+\infty )\bowtie {{\textsf {Z} }}\) for each \(r\in {{\mathbb {R}}}\), thus \({{\textsf {Z} }}^+={{\mathbb {R}}}\) and hence \({{{{\textbf {{\textsf {limsup}}}}}}}\,{{\textsf {Z} }}=+\infty \), a contradiction. On the other hand, if \(\alpha \in {{\mathbb {R}}}\) then \(\alpha -1<\sup \left\{ x\!:x\in {{\textsf {b} }}\right\} \) for each \({{\textsf {b} }}\in {{\textsf {Z} }}\), hence \(\alpha -1\in {{\textsf {Z} }}^+\), i.e., \({{\textsf {Z} }}^+\not =\emptyset \) and hence \({{{{\textbf {{\textsf {limsup}}}}}}}\,{{\textsf {Z} }}>-\infty \), a contradiction. Assume that \(-\infty<{{{{\textbf {{\textsf {limsup}}}}}}}\,{{\textsf {Z} }}<+\infty \) and let \(\beta {\mathop {=}\limits ^\mathrm{{def}}}{{{{\textbf {{\textsf {limsup}}}}}}}\,{{\textsf {Z} }}\). If \(\alpha =+\infty \) then \(\sup \left\{ x\!:x\in {{\textsf {b} }}\right\} =+\infty \) for each \({{\textsf {b} }}\in {{\textsf {Z} }}\), hence \((r,+\infty )\bowtie {{\textsf {Z} }}\) for each \(r\in {{\mathbb {R}}}\), thus \({{\textsf {Z} }}^+={{\mathbb {R}}}\) and hence \({{{{\textbf {{\textsf {limsup}}}}}}}\,{{\textsf {Z} }}=+\infty \), a contradiction. If \(\alpha =-\infty \) then there exists \({{\textsf {b} }}_0\in {{\textsf {Z} }}\) such that \(\sup \left\{ x\!:x\in {{\textsf {b} }}\right\} <\beta -1\), hence \({{\textsf {b} }}_{0}\subset (-\infty ,\beta -1)\), thus \({{\textsf {b} }}_0\cap (\beta -1,\beta +1)=\emptyset \), thus \(\beta \not \in {{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})\), a contradiction, by Lemma 11.16. It follows that \(\alpha \in {{\mathbb {R}}}\). We claim that \(\alpha =\beta \). Assume that \(r\in {{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})\), and \(\epsilon >0\). Then \({{{\textsf {N} }}}_{{{\mathbb {R}}}}(r)\bowtie {{\textsf {Z} }}\), thus \((r-\epsilon ,r+\epsilon )\cap {{\textsf {b} }}\not =\emptyset \) for each \({{\textsf {b} }}\in {{\textsf {Z} }}\). Hence \(r-\epsilon <\sup \left\{ x\!:x\in {{\textsf {b} }}\right\} \) for each \({{\textsf {b} }}\in {{\textsf {Z} }}\), thus \(r-\epsilon \le \alpha \), and since \(\epsilon >0\) is arbitrary, it follows that \(r \le \alpha \). Since this inequality holds for each \(r\in {{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})\), Lemma 11.16 implies that \({{{{\textbf {{\textsf {limsup}}}}}}}\,{{\textsf {Z} }}\le \alpha \). In order to show that equality holds, it suffices to show that \(\alpha \in {{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})\). Suppose not. Then there exists \(\epsilon _0>0\) and \({{\textsf {b} }}_0\in {{\textsf {Z} }}\) with \((\alpha -2\epsilon _0,\alpha +2\epsilon _0)\cap {{\textsf {b} }}_0=\emptyset \). Hence either (i) \({{\textsf {b} }}_0\subset (-\infty ,\alpha -2\epsilon _0]\) or (ii) \({{\textsf {b} }}_0\subset [\alpha +2\epsilon _0,+\infty )\), but (i) would imply that \(\sup \left\{ x\!:x\in {{\textsf {b} }}_0\right\} <\alpha -2\epsilon _0\), which is impossible by (11.10). Hence (ii) holds. However, (11.10) implies that there exists \({{\textsf {b} }}\in {{\textsf {Z} }}\) such that \(\sup \left\{ x\!:x\in {{\textsf {b} }}\right\} <\alpha +\epsilon _0\), and this implies that \({{\textsf {b} }}\cap {{\textsf {b} }}_0=\emptyset \), which is also impossible. Hence \(\alpha \in {{{\textbf {{\textsf {clusterset}}}}} }({{\textsf {Z} }},\overline{{{\mathbb {R}}}})\). \(\square \)
Recall that if \(({{\,\mathrm{{A}}\,}},{{\textsf {Z} }})\) is a filtered set and  . The following result will be useful in applications.
. The following result will be useful in applications.
Theorem 11.20
If \(({{\,\mathrm{{A}}\,}},{{\textsf {Z} }})\) is a filtered set,  is a function, and \(y\in [-\infty ,+\infty ],\) then the following conditions are equivalent:
is a function, and \(y\in [-\infty ,+\infty ],\) then the following conditions are equivalent:
- (1):
-
\(,\)
- (2):
-
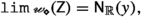
- (3):
-
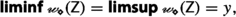
- (4):
-
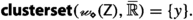
Proof
The equivalence between (1) and (2) is contained in Proposition 9.38. The equivalence between (2), (3), and (4) follows from Theorem 11.18\(\square \)
12 Applications of the Natural Topology to Moore–Smith Sequences of Sets
In this section, we present further results pertaining to Moore–Smith sequences of nonempty subsets of a topological space, which may be obtained as an application of the results on filter presented so far.
12.1 Cofinal Subsets in a Directed Set
The notion of cluster point of a Moore–Smith sequence is based on the notion of cofinal subsets of a directed set. Recall that \({\textsf {Fin} }[{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}}]\) is the collection of all final sets in the directed set \({{\,\mathrm{{A}}\,}}\) and that it is a filter on \({{\,\mathrm{{A}}\,}}_{{\texttt {Set}}}\), by Lemma 3.25.
Definition 12.1
If \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is a directed set then a subset of \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is called cofinal in \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) if it overlaps with each tail of \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\). The collection of all cofinal sets in \({{\,\mathrm{{A}}\,}}\) is denoted by \({\textsf {cof} }({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}})\).
Observe that
since in a directed set each tail overlaps with every other tail, and indeed (recall Definition 1.7)
since the statement that a given set overlaps with each tail of \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is equivalent to the statement that no tail of \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is contained in the complement of the given set, i.e., the complement of the set is not a final set in \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\). In other words, if \(Q\subset {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) then \(Q\in {\textsf {cof} }({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}})\) \(\Leftrightarrow \) \(\complement {Q}\not \in {\textsf {Fin} }[{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}}]\).
Lemma 12.2
If \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is a directed set and \(Q\subset {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) then \(Q\) and \(\complement {Q}\) cannot both fail to be cofinal.
Proof
The result follows from (12.1). Indeed, if \(Q\) and \(\complement {Q}\) both fail to be cofinal, then \(Q\) and \(\complement {Q}\) both belong to \({\textsf {Fin} }[{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}}]\), and this is impossible since \({\textsf {Fin} }[{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}}]\) is a filter. \(\square \)
12.2 The Cluster Set of a Moore–Smith Sequence of Points
Definition 12.3
If  and \(\Theta \) is topology on \({{\,\mathrm{{Y}}\,}}\), we say that
and \(\Theta \) is topology on \({{\,\mathrm{{Y}}\,}}\), we say that  clusters at \(x\) if for each \(U\in {{{\textsf {N} }}}_{\Theta }(x)\) the set
clusters at \(x\) if for each \(U\in {{{\textsf {N} }}}_{\Theta }(x)\) the set  is cofinal in \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\), where \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is the direction of
is cofinal in \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\), where \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is the direction of  , and define
, and define

Lemma 12.4
If  and \(\Theta \) is topology on \({{\,\mathrm{{Y}}\,}},\) then
and \(\Theta \) is topology on \({{\,\mathrm{{Y}}\,}},\) then  is closed.
is closed.
Proof
Assume that  . Then there exists \(U\in {{{\textsf {N} }}}_{\Theta }(x)\) such that the set
. Then there exists \(U\in {{{\textsf {N} }}}_{\Theta }(x)\) such that the set  is not cofinal. Let \(O\in \Theta \) such that \(O\subset {}U\) and \(x\in {}O\). If \(x\in {}O\) then \(O\in {{{\textsf {N} }}}_{\Theta }(x)\) and
is not cofinal. Let \(O\in \Theta \) such that \(O\subset {}U\) and \(x\in {}O\). If \(x\in {}O\) then \(O\in {{{\textsf {N} }}}_{\Theta }(x)\) and  is not cofinal. \(\square \)
is not cofinal. \(\square \)
Observe that if  then
then  , hence the limiting values of a Moore–Smith sequence
, hence the limiting values of a Moore–Smith sequence  belong to the cluster set of
belong to the cluster set of  .
.
12.3 The Cluster Set of Set-Valued Moore–Smith Sequences
Definition 12.5
If  , then the shadow projected by \(U\subset {{\,\mathrm{{Y}}\,}}\) along
, then the shadow projected by \(U\subset {{\,\mathrm{{Y}}\,}}\) along  is the set
is the set

where \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is the direction of  .
.
Definition 12.6
If  , then the inner shadow projected by \(U\subset {{\,\mathrm{{Y}}\,}}\) along
, then the inner shadow projected by \(U\subset {{\,\mathrm{{Y}}\,}}\) along  is the set
is the set

where \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is the direction of  .
.
Observe that  and, if
and, if  , then
, then  .
.
Definition 12.7
If  is a \({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\)-valued Moore–Smith sequence and \(\Theta \) is a topology on \({{\,\mathrm{{Y}}\,}}\), we say that
is a \({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\)-valued Moore–Smith sequence and \(\Theta \) is a topology on \({{\,\mathrm{{Y}}\,}}\), we say that  clusters at \(y\in {{\,\mathrm{{Y}}\,}}\) if, for each \(U\in {{{\textsf {N} }}}_{\Theta }({{y}})\) the shadow
clusters at \(y\in {{\,\mathrm{{Y}}\,}}\) if, for each \(U\in {{{\textsf {N} }}}_{\Theta }({{y}})\) the shadow  is cofinal in \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\), where \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is the direction of
is cofinal in \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\), where \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is the direction of  .
.
If  then this notion recaptures the one introduced in Definition 12.3, and
then this notion recaptures the one introduced in Definition 12.3, and  is defined just as in (12.2).
is defined just as in (12.2).
Definition 12.8
If  is a \({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\)-valued Moore–Smith sequence and \(\Theta \) is a topology on \({{\,\mathrm{{Y}}\,}}\), we say that
is a \({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\)-valued Moore–Smith sequence and \(\Theta \) is a topology on \({{\,\mathrm{{Y}}\,}}\), we say that  converges to \(y\in {{\,\mathrm{{Y}}\,}}\) and write
converges to \(y\in {{\,\mathrm{{Y}}\,}}\) and write

if for each \(U\in {{{\textsf {N} }}}_{\Theta }({{y}})\) the inner shadow  is final in \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\), where \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is the direction of
is final in \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\), where \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is the direction of  . If
. If  then this notion recaptures Definition 3.18.
then this notion recaptures Definition 3.18.
Recall that if  then
then  is the filter of tails of
is the filter of tails of  , introduced in Sect. 6.2. The following result extends Corollary 9.39 to
, introduced in Sect. 6.2. The following result extends Corollary 9.39 to  .
.
Lemma 12.9
If  and \(\Theta \) is a topology on \({{\,\mathrm{{Y}}\,}}\) then the following conditions are equivalent:
and \(\Theta \) is a topology on \({{\,\mathrm{{Y}}\,}}\) then the following conditions are equivalent:
- (1):
-
\(,\)
- (2):
-

Proof
Let \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) be the direction of  . If (1) holds then for each \(U\in {{{\textsf {N} }}}_{\Theta }(y)\) there exists \(j\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) such that if \(k\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) and \(j\texttt {R}_{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}}{}k\) then
. If (1) holds then for each \(U\in {{{\textsf {N} }}}_{\Theta }(y)\) there exists \(j\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) such that if \(k\in {{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) and \(j\texttt {R}_{{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}}{}k\) then  , i.e.,
, i.e.,  , and this means that
, and this means that  , i.e.,
, i.e.,  , hence (2) holds. Since all these steps are reversible, the converse implication holds as well. \(\square \)
, hence (2) holds. Since all these steps are reversible, the converse implication holds as well. \(\square \)
Proposition 12.10
If  and \(\Theta \) is a topology on \({{\,\mathrm{{Y}}\,}}\) then
and \(\Theta \) is a topology on \({{\,\mathrm{{Y}}\,}}\) then

Proof
Let \(y\in {{\,\mathrm{{Y}}\,}}\) and let \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) be the direction of  . Observe that the condition that
. Observe that the condition that  means that for each \(U\in {{{\textsf {N} }}}_{\Theta }({{{y}}})\) and for each \(j\in {}{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) there exists \(k\in {}{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) such that \(j\texttt {R}{}{}k\) and
means that for each \(U\in {{{\textsf {N} }}}_{\Theta }({{{y}}})\) and for each \(j\in {}{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) there exists \(k\in {}{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) such that \(j\texttt {R}{}{}k\) and  , i.e., such that
, i.e., such that  , and since
, and since  , this means that for each \(U\in {{{\textsf {N} }}}_{\Theta }({{{y}}})\) and for each \(j\in {}{{\,\mathrm{{A}}\,}}\) the intersection between
, this means that for each \(U\in {{{\textsf {N} }}}_{\Theta }({{{y}}})\) and for each \(j\in {}{{\,\mathrm{{A}}\,}}\) the intersection between  and U is not empty, and this is equivalent to the condition that
and U is not empty, and this is equivalent to the condition that  . \(\square \)
. \(\square \)
12.4 Applications to the Notion of Moore–Smith Subsequence
There is a close analogy with the situation where  and the one where a sequence \(w={\{w_n\}}_{n\in {\mathbb {N}}}\) is a subsequence of a sequence \(z={\{z_n\}}_{n\in {\mathbb {N}}}\). The following definition makes this analogy more precise.
and the one where a sequence \(w={\{w_n\}}_{n\in {\mathbb {N}}}\) is a subsequence of a sequence \(z={\{z_n\}}_{n\in {\mathbb {N}}}\). The following definition makes this analogy more precise.
Definition 12.11
If  and
and  are \({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\)-valued Moore–Smith sequences, we say that
are \({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\)-valued Moore–Smith sequences, we say that  and
and  are equivalent if
are equivalent if  . We say that
. We say that  is a Moore–Smith subsequence of
is a Moore–Smith subsequence of  if
if  .
.
If  and
and  are \({{\,\mathrm{{Y}}\,}}\)-valued sequences and
are \({{\,\mathrm{{Y}}\,}}\)-valued sequences and  is a subsequence of
is a subsequence of  (in the ordinary sense) then
(in the ordinary sense) then  is a Moore–Smith subsequence of
is a Moore–Smith subsequence of  .
.
Lemma 12.12
If \(,\) \(\Theta \) is a topology on \({{\,\mathrm{{Y}}\,}},\) and  then then the set
then then the set

(where \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is the direction of \()\) is a directed set under the relation \((j,U)\texttt {R}{}(k,V)\) iff \(j\texttt {R}{}{}k\) and \(U\supset {}V\).
Proof
Reflexivity and transitivity are immediate. Assume that (j, U) and (k, V) are elements of  . Since \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is directed, there exists \(l\in {}{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) with \(j\texttt {R}{}{}l\) and \(k\texttt {R}{}{}l\). Since
. Since \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) is directed, there exists \(l\in {}{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) with \(j\texttt {R}{}{}l\) and \(k\texttt {R}{}{}l\). Since  and \(U\cap {}V\in {{{\textsf {N} }}}_{\Theta }({{{y}}})\), there exists \(g\in {}{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) with \(l\texttt {R}{}{}g\) and
and \(U\cap {}V\in {{{\textsf {N} }}}_{\Theta }({{{y}}})\), there exists \(g\in {}{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) with \(l\texttt {R}{}{}g\) and  . Hence
. Hence  , \((j,U)\texttt {R}{}(g,U\cap {}V)\) and \((k,V)\texttt {R}{}(g,U\cap {}V)\). \(\square \)
, \((j,U)\texttt {R}{}(g,U\cap {}V)\) and \((k,V)\texttt {R}{}(g,U\cap {}V)\). \(\square \)
In the following result, we extend to the context of Moore–Smith sequences of sets a familiar fact about sequences of points.
Theorem 12.13
If \(,\) \({{{y}}}\in {{\,\mathrm{{Y}}\,}},\) and \(\Theta \) is a topology on \({{\,\mathrm{{Y}}\,}},\) then the following conditions are equivalent:
- (1):
-
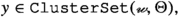
- (2):
-
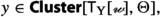
- (3):
-
there exists a \({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\)-valued Moore–Smith sequence
 such that:
such that: - (3.1):
-
 is a Moore–Smith subsequence of
is a Moore–Smith subsequence of 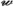 ,
, - (3.2):
-
Proof
Let \({{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) be the direction of  . Since in Proposition 12.10 we proved that (1) and (2) are equivalent, it suffices to show that (3) \(\Rightarrow \) (2) and (1) \(\Rightarrow \) (3) If (3) holds then
. Since in Proposition 12.10 we proved that (1) and (2) are equivalent, it suffices to show that (3) \(\Rightarrow \) (2) and (1) \(\Rightarrow \) (3) If (3) holds then  and, by Lemma 12.9,
and, by Lemma 12.9,  , thus
, thus  exists, hence (2) holds. Finally, we show that (1) implies (3). If (1) holds, apply Lemma 12.12 and obtain the directed set
exists, hence (2) holds. Finally, we show that (1) implies (3). If (1) holds, apply Lemma 12.12 and obtain the directed set  described therein. Now define a \({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\)-valued Moore–Smith sequence whose direction is
described therein. Now define a \({{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{Y}}\,}})\)-valued Moore–Smith sequence whose direction is  as follows:
as follows:

We claim that  is a Moore–Smith subsequence of
is a Moore–Smith subsequence of  and that
and that  .
.
In order to show that  is a Moore–Smith subsequence of
is a Moore–Smith subsequence of  , i.e.,
, i.e.,  , it suffices to show that if \(j\in {}{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) then
, it suffices to show that if \(j\in {}{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) then  . Let \(U\in {{{\textsf {N} }}}_{\Theta }({{{y}}})\). Then there exists \(k\in {}{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) with \(j\texttt {R}{}{}k\) and \(s(k)\cap {}U\not =\emptyset \). We claim that
. Let \(U\in {{{\textsf {N} }}}_{\Theta }({{{y}}})\). Then there exists \(k\in {}{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) with \(j\texttt {R}{}{}k\) and \(s(k)\cap {}U\not =\emptyset \). We claim that

Indeed, if  then there exists
then there exists  with \((k,U)\texttt {R}{}(g,V)\) and
with \((k,U)\texttt {R}{}(g,V)\) and  , i.e.,
, i.e.,  . Since \(j\texttt {R}{}{}k\) and \(k\texttt {R}{}{}g\) we have \(j\texttt {R}{}{}g\). Moreover,
. Since \(j\texttt {R}{}{}k\) and \(k\texttt {R}{}{}g\) we have \(j\texttt {R}{}{}g\). Moreover,  . We have thus proved that
. We have thus proved that  and this means that
and this means that  , i.e.,
, i.e.,  .
.
We now show that  . Let \(U\in {{{\textsf {N} }}}_{\Theta }({{{y}}})\). Since
. Let \(U\in {{{\textsf {N} }}}_{\Theta }({{{y}}})\). Since  , there exists \(j_U\in {}{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) with
, there exists \(j_U\in {}{{\,\mathrm{{{\,\mathrm{{A}}\,}}}\,}}\) with  . Now observe that if
. Now observe that if  then
then  (by definition),
(by definition),  (since
(since  ), and \(V\subset {}U\) (since \((j_U,U)\texttt {R}{}(j,V)\)). Hence
), and \(V\subset {}U\) (since \((j_U,U)\texttt {R}{}(j,V)\)). Hence  . \(\square \)
. \(\square \)
13 Applications to the Problem of the Differentiation of Integrals (II)
Some confusion may arise from the fact that filters on \({{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}})\) takes us one level higher in the hierarchy of powersets, in the following sense: if  and \({{\textsf {b} }}\in {{\textsf {Z} }}\) then \({{\textsf {b} }}\subset {{\,\mathrm{{X}}\,}}\), hence \({{\textsf {Z} }}\) is a collection of subsets of \({{\,\mathrm{{X}}\,}}\); however, if
and \({{\textsf {b} }}\in {{\textsf {Z} }}\) then \({{\textsf {b} }}\subset {{\,\mathrm{{X}}\,}}\), hence \({{\textsf {Z} }}\) is a collection of subsets of \({{\,\mathrm{{X}}\,}}\); however, if  and \({{\textsf {b} }}\in {{\textsf {Z} }}\) then \({{\textsf {b} }}\subset {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{X}}\,}})\) (since \({{\textsf {b} }}\subset {{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}})\)), hence \({{\textsf {b} }}\) is a collection of subsets of \({{\,\mathrm{{X}}\,}}\), and \({{\textsf {Z} }}\) is a family of collections of subsets of \({{\,\mathrm{{X}}\,}}\) (cf. Sect. 2). In particular, one should not confuse a map as in (1.28) (which is, in particular, a map of the form \({{\,\mathrm{{X}}\,}}\rightarrow {{\mathcal {P}}}({{\mathcal {P}}}({{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}})))\)) with a “family of approach regions,” which is a map \({{\,\mathrm{{X}}\,}}\rightarrow {{\mathcal {P}}}({{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}}))\). For more background, see [11].
and \({{\textsf {b} }}\in {{\textsf {Z} }}\) then \({{\textsf {b} }}\subset {{\mathcal {P}}}_{{{\bullet }}}({{\,\mathrm{{X}}\,}})\) (since \({{\textsf {b} }}\subset {{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}})\)), hence \({{\textsf {b} }}\) is a collection of subsets of \({{\,\mathrm{{X}}\,}}\), and \({{\textsf {Z} }}\) is a family of collections of subsets of \({{\,\mathrm{{X}}\,}}\) (cf. Sect. 2). In particular, one should not confuse a map as in (1.28) (which is, in particular, a map of the form \({{\,\mathrm{{X}}\,}}\rightarrow {{\mathcal {P}}}({{\mathcal {P}}}({{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}})))\)) with a “family of approach regions,” which is a map \({{\,\mathrm{{X}}\,}}\rightarrow {{\mathcal {P}}}({{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}}))\). For more background, see [11].
Observe that the expression \(\displaystyle {\mathop {{{{{\textbf {{\textsf {lim}}}}} }}}\nolimits _{{{\textsf {G} }}(x)}{{\varvec{f}}}_{\!\omega }}\) which appears in (1.29) is the limiting value of \({{\varvec{f}}}_{\!\omega }\) along the filter \({{\textsf {G} }}(x)\), introduced in Definition 1.12. We have seen that this limiting value depends on the behavior of the filter  . In order to reduce notational clutter, we will denote the filter \({({{\varvec{f}}}_{\!\omega })}_{\varvec{\diamond }}({{\textsf {G} }}(x))\) by \({{{\textbf {{\textsf {G}}}}} }_{{\varvec{f}}}^{\omega }(x)\), hence we define
. In order to reduce notational clutter, we will denote the filter \({({{\varvec{f}}}_{\!\omega })}_{\varvec{\diamond }}({{\textsf {G} }}(x))\) by \({{{\textbf {{\textsf {G}}}}} }_{{\varvec{f}}}^{\omega }(x)\), hence we define

as follows:
Lemma 13.1
If \({{\textbf {{\textsf {G}}}}} \) is a family of filters on \({{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}})\) based on \({{\,\mathrm{{X}}\,}},\) \(x\in {{\,\mathrm{{X}}\,}},\) and \(f\in {\mathcal {L}}^{1}({{\,\mathrm{{X}}\,}}),\) then the following conditions are equivalent:
- (1):
-
\({{\textbf {{\textsf {G}}}}} \) differentiates \(f\) at \(x,\)
- (2):
-
the following inequalities hold:
$$\begin{aligned} f(x) \le \mathop {{{{{{\textbf {{\textsf {liminf}}}}}}}}}\limits _{{{\mathbb {R}}}} {{{\textbf {{\textsf {G}}}}} }_{f}^{\omega }(x) \le {{{{\textbf {{\textsf {limsup}}}}}}}\,_{{{\mathbb {R}}}} {{{\textbf {{\textsf {G}}}}} }_{f}^{\omega }(x) \le f(x). \end{aligned}$$(13.1)
Proof
It suffices to apply Proposition 9.38 and Theorem 11.18. \(\square \)
Remark 13.2
Observe that, if \({{\textbf {{\textsf {G}}}}} \) is a family of filters on \({{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}})\) based on \({{\,\mathrm{{X}}\,}}\), as in (1.28), and \(f\in {\mathcal {L}}^{1}({{\,\mathrm{{X}}\,}})\), then it is not necessarily true that the functions
are measurable as functions of \(x\in {{\,\mathrm{{X}}\,}}\), unless we impose some conditions on \({{\textbf {{\textsf {G}}}}} \). This problem will be handled in Sect. 13.1 by the same method employed in [9].
13.1 Measurability Issues (II)
Lemma 13.3
If \(f,g:{{\,\mathrm{{X}}\,}}\rightarrow {{\mathbb {R}}}\) are (not necessarily measurable) functions, in order to show that
it suffices to show that
Proof
Assume that \(\omega ^{*}(\{f<g\})>0\). Let \(B_{m,n}{\mathop {=}\limits ^\mathrm{{def}}}\left\{ f<\frac{m-1}{n}<\frac{m}{n}<g\right\} \), where m, n are integers, and observe that \(\displaystyle {\{f<g\}=\bigcup _{m,n}B_{m,n}}\). Then there exist \(m_0,n_0\) such that \(\omega ^{*}(B_{m_0,n_0})>0\), and \(B_{m_0,n_0}\) contradicts (13.2). \(\square \)
Lemma 13.4
If \(f\in {\mathcal {L}}^1({{\,\mathrm{{X}}\,}})\), \(\alpha >0,\) \(Q\in {{\mathcal {A}}}^{*}({{{\,\mathrm{{X}}\,}}}),\) then, in order to show that
it suffices to show that
where \(R'\) is a measurable representative of \(R\).
Proof
If \(R{\mathop {=}\limits ^\mathrm{{def}}}\left\{ x\in Q\!:f(x)\le \alpha \right\} \in {{\mathcal {A}}}^{*}({{{\,\mathrm{{X}}\,}}})\), then \(R\subset \left\{ x\in {{\,\mathrm{{X}}\,}}\!:f(x)\le \alpha \right\} \) and since f is measurable, it follows that there exists a measurable representative \(R'\) of \(R\) such that \(R'\subset \left\{ x\in {{\,\mathrm{{X}}\,}}\!:f(x)\le \alpha \right\} \). Then \({f}_{\!\omega }[R']\le \alpha \), a contradiction with (13.4). \(\square \)
13.2 Proof of Theorem 1.27
Recall from Lemma 13.1 that, in order to show that \({{\textbf {{\textsf {G}}}}} \) differentiates \(f\), it suffices to prove the two inequalities (13.1) for a.e. \(x\in {{\,\mathrm{{X}}\,}}\). Let us examine the inequality on the right. Our task is then to prove that
and apply Lemmas 13.3 and 13.4 with \(g{\mathop {=}\limits ^\mathrm{{def}}}{{{{\textbf {{\textsf {limsup}}}}}}}\,_{{{\mathbb {R}}}} {{{\textbf {{\textsf {G}}}}} }_{f}^{\omega }(x)\). Recall from Lemma 13.3 that, in order to prove that (13.5) holds, it suffices to show that (13.2) holds, where \(g{\mathop {=}\limits ^\mathrm{{def}}}{{{{\textbf {{\textsf {limsup}}}}}}}\,_{{{\mathbb {R}}}} {{{\textbf {{\textsf {G}}}}} }_{f}^{\omega }(x)\). Let us assume that
As we observed in Remark 13.2, the function g is not necessarily measurable. The crucial observation is that \(g(x)>\alpha \), i.e., \({{{{\textbf {{\textsf {limsup}}}}}}}\,_{{{\mathbb {R}}}} {{{\textbf {{\textsf {G}}}}} }_{f}^{\omega }(x)>\alpha \), means, according to Definition 11.8, that there exists \(r\in {{\mathbb {R}}}\) such that \(\alpha <r\) and
Observe that (13.7) means that
and this means that
It follows that (13.6) implies that
and this means that \({{\textbf {{\textsf {G}}}}} \) is adapted to \(f\) on \(Q\) above \(\alpha \). Observe that, a fortiori, this means that, for each \(S\in {{\mathcal {A}}}^{*}({Q})\), \({{\textbf {{\textsf {G}}}}} \) is adapted to \(f\) on S above \(\alpha \). Since \({{\textbf {{\textsf {G}}}}} \) and \(f\) are compatible, it follows that the mean-value of \(f\) over \(R\) lies above \(\alpha \) for each \(R\in {{\mathcal {A}}}^{*}({Q})\). Lemma 13.4 then implies that (13.3) holds, hence
Hence we have shown that (13.2) holds, and Lemma 13.3 then implies (13.5). The other inequality in (13.1) follows along similar lines.
13.3 The Maximal Operator Associated to a Family of Filters
Stein’s theorem on limits of sequences of operators shows that the role played by the boundedness properties of the maximal operator, associated to the study of problems of almost everywhere convergence, is not coincidental but essential; see [11]. It is natural to wonder whether to a given family \({{\textbf {{\textsf {G}}}}} \) of filters on \({{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}})\) based on \({{\,\mathrm{{X}}\,}}\), as in (1.28), it is possible to associate a maximal operator which would play a similar role. As we will see presently, since filters on \({{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}})\) takes us one level higher in the hierarchy of powersets, as observed at the beginning of Sect. 13, the definition of such a maximal operator also depends on the choice of a generating basis for \({{\textsf {G} }}(x)\), for each \(x\in {{\,\mathrm{{X}}\,}}\).
Definition 13.5
If \({{\textbf {{\textsf {G}}}}} \) is a family of filters on \({{\mathcal {A}}}({{{\,\mathrm{{X}}\,}}})\) based on \({{\,\mathrm{{X}}\,}}\), as in (1.28), and if \({{\textsf {W} }}(x)\) is a generating basis for \({{\textsf {G} }}(x)\) for each \(x\in {{\,\mathrm{{X}}\,}}\), we define
Theorem 13.6
If there exists a constant \(C>0\) such that
for each \(\lambda >0\) and each \(f\in {\mathcal {L}}^1({{\,\mathrm{{X}}\,}}),\) and if there exists a dense subset \(C\subset {{\,\mathrm{L}\,}}^{1}({{\,\mathrm{{X}}\,}})\) such that \({{\textbf {{\textsf {G}}}}} \) differentiates C, then \({{\textbf {{\textsf {G}}}}} \) differentiates \({{\,\mathrm{L}\,}}^{1}({{\,\mathrm{{X}}\,}})\).
Proof
The proof follows a standard argument, presented for example in [11, Sect. 5.2.5]. \(\square \)
14 Miscellaneous Notes
The notion of filter is due to Cartan [8]. In 1909, Frigyes Riesz understood the role played by the objects that are now called ultrafilters in the study of the notions of continuum and completeness [26, p. 23], foreshadowing the use of ultrafilters in the construction of a compactification of certain topological spaces, implicitly used by Marshall Harvey Stone in 1937 and Henry Wallman in 1937 and 1938, and explicitly adopted by Samuel [30]. These ideas, as well as those of Felix Hausdorff, who formulated the abstract definition of neighborhoods [16, p. 213], were picked up by Root [27, 28]. In 1938, Herman Lyle Smith also attained the notion of filter, in order to build a theory that could include cases seemingly not covered by the Moore–Smith convergence. More information can be found in [34].
The existing literature has apparently not yet reached a consensus on how the notion of a Moore–Smith subsequence of a given Moore–Smith sequence should be defined. This is a bit surprising, since the “right” definition is virtually contained in an observation made by H. Cartan in 1937, and later in 1955 in the work by Bartle [2] and more conclusively in 1972 in a work by Aarnes and Andenæs [1]. In Sect. 12.4 we have given the “right” notion of Moore–Smith subsequence of a given Moore–Smith sequence. The reason this is the most appropriate notion is fully articulated in [1].
References
Aarnes, J.F., Andenæs, P.R.: On nets and filters. Math. Scand. 31, 285–292 (1972)
Bartle, R.G.: Nets and filters in topology. Am. Math. Mon. 62, 551–557 (1955)
Birkhoff, G.: Moore–Smith convergence in general topology. Ann. Math. 38, 39–56 (1937)
Bourbaki, N.: Chapters 1–4. In: General Topology. Springer, Berlin (1995)
Bruns, G., Schmidt, J.: Zur Äquivalenz von Moore–Smith–Folgen und filters. Math. Nachr. 13, 169–186 (1955)
Burke, M.R.: Liftings and the property of Baire in locally compact groups. Proc. Am. Math. Soc. 117(4), 1075–1082 (1993). https://doi.org/10.2307/2159536
Busemann, H., Feller, W.: Zur Differentiation der Lebesgueschen Integrale. Fundam. Math. 22(1), 226–256 (1934)
Cartan, H.: Theorie des filtres. C. R. Acad. Sci. Paris 595–598, 777–779 (1937)
De Possel, R.: Sur la dérivation abstraite des fonctions d’ensemble. J. Math. Pure Appl. 15, 391–409 (1936)
Denjoy, A.: Sur les fonctions dérivées sommables. Bull. S. M. F. tome 43, 161–248 (1915)
Di Biase, F., Krantz, S.G.: Foundations of Fatou theory and a tribute to the work of E. M. Stein on boundary behavior of holomorphic functions. J. Geom. Anal. 31, 7184–7296 (2021)
Doob, J.L.: Boundary approach filters for analytic functions. Ann. Inst. Fourier 23(3), 187–213 (1973)
Federer, H.: Geometric Measure Theory. Springer, Berlin (1969)
Fremlin, D.H.: Measure Theory, vol. 1, 2nd edn. Torres Fremlin, Colchester (2011)
Fremlin, D.H.: Measure Theory, vol. 3. Torres Fremlin, Colchester (2002)
Hausdorff, F.: Grundzüge der Mengenlehre. Veit & Comp, Leipzig (1914)
Jamneshan, A., Tao, T.: Foundational aspects of uncountable measure theory: Gelfand duality, Riesz representation, canonical models, and canonical disintegration. arXiv:2010.00681v3
Kelley, J.L.: General Topology. Van Nostrand, Princeton (1955)
Kuratowski, K.: Sur l’operation \({\bar{A}}\) de l’Analysis Situs. Fundam. Math. 15, 182–199 (1922)
Lučić, D., Pasqualetto, E.: The Metric-Valued Lebesgue Differentiation Theorem in Measure Spaces and Its Applications. arXiv:2111.08526
Mac Lane, S.: Categories for the Working Mathematicians, 2nd edn. Springer, Berlin (1978)
Mac Lane, S., Birkhoff, G.: Algebra. Chelsea, New York (1988)
Moore, E.H.: Definition of limit in general integral analysis. Proc. Natl Acad. Sci. USA 1(12), 628–632 (1915)
Moore, E.H., Smith, H.L.: A general theory of limits. Am. J. Math. 44(2), 102–121 (1922)
Pettis, B.J.: Cluster sets of nets. Proc. Am. Math. Soc. 22, 386–391 (1969)
Riesz, F.: Stetigkeitsbegriff und abstrakte Mengenlehre. In: Atti del IV Congresso Internazionale dei Matematici, vol. II, pp. 18–24, Roma (1909)
Root, R.E.: Iterated limits of functions on an abstract range. Bull. Am. Math. Soc. 17, 538–539 (1911)
Root, R.E.: Iterated limits in general analysis. Am. J. Math. 36, 79–104 (1914)
Royden, H.L.: Real Analysis, 2nd edn. The Macmillan Company, London (1968)
Samuel, P.: Ultrafilter and compactification of uniform spaces. Trans. Am. Math. Soc. 64(1), 100–132 (1948)
Smiley, M.F.: Filters and equivalent nets. Am. Math. Mon. 64(5), 336–338 (1957)
Smith, H.L.: A general theory of limits. Natl Math. Mag. 12(8), 371–379 (1938). https://doi.org/10.2307/3028618
Stein, E.M., Weiss, G.: Fourier Analysis on Euclidean Spaces. Princeton University Press, Princeton (1971)
Sundström, M.R.: A pedagogical history of compactness. arXiv:1006.4131 [math.HO]
Tukey, J.W.: Convergence and Uniformity in Topology. Princeton University Press, Princeton (1940)
Funding
Open access funding provided by Universitá degli Studi G. D’Annunzio Chieti Pescara within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
There is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Di Biase, F., Krantz, S.G. On the Differentiation of Integrals in Measure Spaces Along Filters. J Geom Anal 33, 29 (2023). https://doi.org/10.1007/s12220-022-01050-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12220-022-01050-7



 is adapted to
is adapted to  is adapted to
is adapted to  differentiates
differentiates 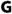 differentiates all measurable sets.
differentiates all measurable sets.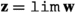 .
.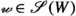 such that
such that  .
.


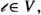
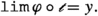

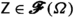 such that
such that 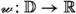 and each
and each 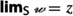 if and only if, for each open Euclidean triangle
if and only if, for each open Euclidean triangle 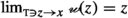 .
.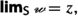
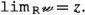
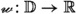 and each
and each  if and only if
if and only if 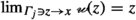 for each
for each 

 , where I is a set of indices and
, where I is a set of indices and  , where
, where 

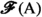
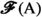
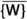 is the closure in
is the closure in 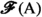 .
.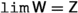 .
.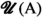 is closed in
is closed in 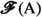 .
.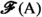 is Hausdorff.
is Hausdorff.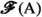 is compact and, for each
is compact and, for each 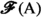 .
.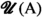 is compact and Hausdorff.
is compact and Hausdorff.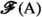 has a basis of open compact sets.
has a basis of open compact sets. 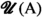 has a basis of closed and open compact sets.
has a basis of closed and open compact sets.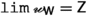 .
.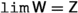 .
.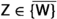 .
.



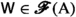 such that
such that 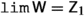 and
and 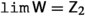 .
.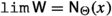 .
.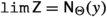 ,
,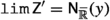 ,
, .
.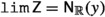 ,
,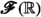
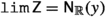 .
.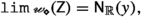
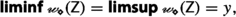
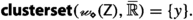

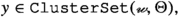
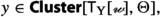
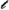 such that:
such that:  is a Moore–Smith subsequence of
is a Moore–Smith subsequence of  ,
,