Computing Nodal Deficiency with a Refined Dirichlet-to-Neumann Map

Abstract

Recent work of the authors and their collaborators has uncovered fundamental connections between the Dirichlet-to-Neumann map, the spectral flow of a certain family of self-adjoint operators, and the nodal deficiency of a Laplacian eigenfunction (or an analogous deficiency associated to a non-bipartite equipartition). Using a refined construction of the Dirichlet-to-Neumann map, we strengthen all of these results, in particular getting improved bounds on the nodal deficiency of degenerate eigenfunctions. Our framework is very general, allowing for non-bipartite partitions, non-simple eigenvalues, and non-smooth nodal sets. Consequently, the results can be used in the general study of spectral minimal partitions, not just nodal partitions of generic Laplacian eigenfunctions.

Appendices

Appendix A: Weights, Cuts and Pair Compatibility Conditions

In this section, we elaborate on some of our constructions and their connection to previous literature. In Sect. A.1, we discuss the relationship between the strong pair compatibility condition in Definition 1.6, and the weak pair compatibility that appeared in earlier works, such as [10], where it was simply referred to as the pair compatibility condition. In Sect. A.2, we describe the cutting construction of [6], and explain how it is related to the valid weights introduced in Definition 1.3.

1.1 A.1 Weak vs Strong Pair Compatibility Conditions

The strong pair compatibility condition (SPCC) was already described in Definition 1.6, which we repeat here for convenience.

Definition A.1

A two-sided, weakly regular partition ${\mathcal {D}}$ is said to satisfy the strong pair compatibility condition (SPCC) if there exists a choice of positive ground states $\{u_i\}_{i=1}^k$ for the Dirichlet Laplacians on $D_i$ such that, for any pair of neighbors $D_i, D_j$, the function $u_{ij}$ defined by

$$\begin{aligned} u_{ij} \big |_{D_i} = u_i, \qquad u_{ij} \big |_{D_j} = -u_j, \end{aligned}$$

(A.1)

is an eigenfunction of the Dirichlet Laplacian on ${{\,\mathrm{Int}\,}}(\overline{D_i\cup D_j})$.

Nodal partitions obviously satisfy the SPCC. The same is true of spectral minimal partitions (see [4]), and in Proposition 2.7 we showed that a partition satisfies the SPCC if and only if it is $\chi$-nodal. A partition satisfying the SPCC is necessarily an equipartition, in the sense that the ground state energy (the smallest eigenvalue of the Dirichlet Laplacian) on each $D_i$ is the same. We denote this common value by $\lambda ({\mathcal {D}})$.

We next recall the weak pair compatibility condition.

Definition A.2

A two-sided, weakly regular equipartition ${\mathcal {D}}$ is said to satisfy the weak pair compatibility condition (WPCC) if for each pair of neighbors $D_i, D_j$, there exists an eigenfunction of the Dirichlet Laplacian on ${{\,\mathrm{Int}\,}}(\overline{D_i\cup D_j})$ with eigenvalue $\lambda ({\mathcal {D}})$ and nodal set $\partial D_i \cap \partial D_j$.

Remark A.3

By [4,  Theorem 2.6] applied to each pair of neighbors, it follows that partitions that satisfy the WPCC also have the equal angle property; cf. Corollary 2.9.

It is obvious that SPCC implies WPCC. When $\Omega$ is simply connected, a bipartite equipartition satisfying WPCC is nodal, and hence satisfies SPCC, by [10,  Theorem 1.3]. If $\Omega$ is not simply connected, however, it is possible to find an equipartition (for a Schrödinger operator with $C^\infty$ potential) that satisfies WPCC but not SPCC, as shown in [10,  Sect. 7].

1.2 A.2 Weights and Cuts

Assuming throughout that ${\mathcal {D}}$ is a two-sided, weakly regular partition, with nodal set $\Gamma$, we first decompose the smooth part of $\Gamma$ into disjoint open curves, labeled $\{C_a\}$, so that $\Gamma = \overline{\cup _a C_a}$. Since ${\mathcal {D}}$ is two-sided, each $C_a$ is contained in $\Gamma _i \cap \Gamma _j$ for some $i \ne j$. Without loss of generality, we can assume $i < j$, and we denote these labels by i(a) and j(a).

Definition A.4

A subset ${\mathcal {C}}\subset \{C_a\}$ is called a valid cut of the partition ${\mathcal {D}}$ if there exists a choice of orientations on the subdomains $\{D_i\}$ such that $C_a \in {\mathcal {C}}$ if and only if $D_{i(a)}$ and $D_{j(a)}$ have the same orientation.

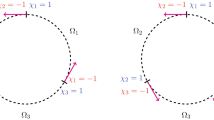
It is sometimes convenient to identity a subset ${\mathcal {C}}= \{C_{a_1}, \ldots , C_{a_p}\} \subset \{C_a\}$ with the corresponding closed subset

$$\begin{aligned} \Gamma ^* := \overline{C_{a_1} \cup \cdots \cup C_{a_p}} \end{aligned}$$

(A.2)

of $\Gamma$ (Fig. 7). We mention that ${\mathcal {C}}\subset \{C_a\}$ is a valid cut if $\Gamma \setminus \Gamma ^*$ is a ${\mathbb {Z}}_2$-homological 1-cycle of $\Omega$ (viewed as a cell complex) relative to the boundary $\partial \Omega$. It is immediate that the empty set is a valid cut of ${\mathcal {D}}$ if and only if ${\mathcal {D}}$ is bipartite.

Fig. 7

Two valid cuts of the same partition are shown in (a) and (b), with the thick line denoting $\Gamma ^*$ and the ± signs indicating the chosen orientations of each $D_i$. In (c) and (d) we show possible choices of $\{\chi _i\}$ for each of these cuts

The maximal cut ${\mathcal {C}}= \{C_a\}$, for which $\Gamma ^* = \Gamma$, is always valid — it corresponds to all subdomains having the same orientation. However, usually one is interested in cuts that are as small as possible. We thus say that a cut is minimal if $\Omega \setminus \Gamma ^*$ is connected.

Proposition A.5

[6,  Prop 4.2] There exists a minimal valid cut ${\mathcal {C}}\subset \{C_a\}$.

Finally, we describe how valid cuts are related to the valid weights $\{\chi _i\}$ in Definition 1.3. Given a set of valid weights $\{\chi _i\}$, we obtain a valid cut ${\mathcal {C}}$ by declaring that $C_a \in {\mathcal {C}}$ if and only if $\chi _{i(a)} = - \chi _{j(a)}$. That is, the cut set $\Gamma ^*$ is the union of all $\Gamma _i \cap \Gamma _j$ along which $\chi _i = - \chi _j$. More precisely, we have the following.

Proposition A.6

Valid cuts are in one-to-one correspondence with edge-equivalence classes of valid weights.

Proof

Given a valid cut, i.e., a choice of orientation for each $D_i$, we get an induced orientation on each $\partial D_i$. Choosing an orientation on each smooth component of $\Gamma$, we obtain a valid set of weights $\{\chi _i\}$ with the property that $\chi _i = -\chi _j$ if and only if $\partial D_i \cap \partial D_j$ is in the cut set $\Gamma ^*$. Changing the orientation on any smooth part of $\Gamma$ will give a different, but edge equivalent, set of weights (recall Definition 2.4), so we get a map from valid cuts to edge-equivalence classes of valid weights. Conversely, a set of valid weights gives an orientation on each $D_i$, and hence a valid cut. It is easily seen that edge-equivalent weights generate the same cut. $\square$

Remark A.7

The proof of Proposition A.6 suggests an equivalent way to define valid cuts and weights: a cut $\Gamma ^*$ is valid if a generic closed path in $\Omega$ intersects $\Gamma \setminus \Gamma ^*$ an even number of times, and a choice of weights $\{\chi _i\}$ is valid if the set $\{C_a : \chi _{i(a)} = - \chi _{j(a)}\}$ defines a valid cut. This alternative definition is not as constructive as Definition 1.3, but it has the advantage of not depending on the manifold structure of $\Omega$, and is thus more convenient for considering partitions on metric graphs.

Remark A.8

Another way of viewing the constructions in this paper is to introduce Aharonov–Bohm operators, as in [6]. Given a set of weights $\chi$ that generates a minimal valid cut, the corresponding $\Delta ^\chi$ is equivalent to a certain Aharonov–Bohm operator, with Aharonov–Bohm solenoids with flux $\pi$ placed at the singular points $x_\ell$ of $\Gamma$ for which $\nu _\ell$ is odd (recall Definition 1.2).

Appendix B: Explicit Construction of the Canonical Solution to (3.2)

In this section, we give an alternate, more explicit proof of the second claim in Theorem 3.1, regarding the existence of a “canonical solution” ${\tilde{u}} \in {{\,\mathrm{dom}\,}}(t^\chi )$ such that $\gamma _{_N}^\chi {\tilde{u}} \in S_\chi$ and ${\tilde{u}}_i$ solves (3.2) for each i. To do this we write the condition $\gamma _{_N}^\chi {\tilde{u}} \in S_\chi$ as a finite system of linear equations and then, by analyzing the corresponding matrix, prove that a solution always exists.

Fix $g \in {{\,\mathrm{dom}\,}}(A)$. For each i, the general solution of (3.2) is given by

$$\begin{aligned} u_i=u_i^g+c_i\varphi _{*,i} \end{aligned}$$

(B.1)

for some $c_i \in \mathbb {R}$. Since $g \in {{\,\mathrm{dom}\,}}(A)$, we know from (3.5) that the two-sided normal derivative $\gamma _{_N}^\chi u$ is a function in $L^2(\Gamma )$, and is given by $\chi _i \partial _{\nu _i}u_i + \chi _j\partial _{\nu _j}u_j$ on $\Gamma _i\cap \Gamma _j$. This will be an element of the subspace $S_\chi$ if and only if

$$\begin{aligned} I_i := \int _{\Gamma _i} \chi _i (\gamma _{_N}^\chi u)\partial _{\nu _i}\varphi _{*,i} = 0 \end{aligned}$$

(B.2)

for each i. Since each point in the smooth part of $\Gamma _i$ is contained in precisely one other $\Gamma _j$, we can rewrite this integral as

$$\begin{aligned} \begin{aligned} I_i&= \sum _{j \ne i} \int _{\Gamma _i\cap \Gamma _j} \big (\partial _{\nu _i}u_i +\chi _{ij} \partial _{\nu _j}u_j\big )\,\partial _{\nu _i}\varphi _{*,i} \\&= \sum _{j \ne i} \int _{\Gamma _i\cap \Gamma _j} \big (\partial _{\nu _i}u^g_i +\chi _{ij} \partial _{\nu _j}u^g_j\big )\,\partial _{\nu _i}\varphi _{*,i}\\&\quad + \sum _{j \ne i} \int _{\Gamma _i\cap \Gamma _j} \big (c_i\partial _{\nu _i}\varphi _{*,i} + \chi _{ij} c_j \partial _{\nu _j}\varphi _{*,j}\big )\,\partial _{\nu _i}\varphi _{*,i}, \end{aligned} \end{aligned}$$

(B.3)

where we have denoted $\chi _{ij} = \chi _i \chi _j$ for convenience. Let us introduce the notations

$$\begin{aligned} \alpha _{i,i} = 0, \qquad \alpha _{i,j} = \int _{\Gamma _i\cap \Gamma _j}|\partial _{\nu _i}\varphi _{*,i}|^2, \quad i \ne j. \end{aligned}$$

It follows from (2.9) that $|\partial _{\nu _i}\varphi _{*,i}| = |\partial _{\nu _j}\varphi _{*,j}|$ on $\Gamma _i \cap \Gamma _j$, and so $\alpha _{i,j} = \alpha _{j,i}$ for all i, j. We similarly get

$$\begin{aligned} \int _{\Gamma _i \cap \Gamma _j} \chi _{ij} (\partial _{\nu _j} \varphi _{*,j})(\partial _{\nu _i} \varphi _{*,i}) = -\alpha _{i,j}, \end{aligned}$$

We then define

$$\begin{aligned} d_i = - \sum _{j \ne i} \int _{\Gamma _i\cap \Gamma _j} \big (\partial _{\nu _i}u^g_i +\chi _{ij} \partial _{\nu _j}u^g_j\big )\,\partial _{\nu _i}\varphi _{*,i} \end{aligned}$$

(B.4)

so the equation (B.3) becomes

$$\begin{aligned} \sum _{j \ne i}(c_i - c_j) \alpha _{i,j} = d_i. \end{aligned}$$

(B.5)

We write the resulting system of equations in matrix form as

$$\begin{aligned} \underbrace{\begin{bmatrix} \sum _j \alpha _{1,j} &{} -\alpha _{1,2} &{} \dots &{} -\alpha _{1,k}\\ -\alpha _{2,1} &{} \sum _j \alpha _{2,j} &{} \dots &{} -\alpha _{2,k}\\ \vdots &{} \vdots &{}\ddots &{} \vdots \\ -\alpha _{k,1} &{} -\alpha _{k,2} &{} \dots &{} \sum _j \alpha _{k,j}\\ \end{bmatrix}}_{=:A} \begin{bmatrix} c_1\\ c_2\\ \vdots \\ c_k\\ \end{bmatrix} = \begin{bmatrix} d_1\\ d_2\\ \vdots \\ d_k\\ \end{bmatrix}, \end{aligned}$$

(B.6)

and observe that the vector $(c_1,c_2,\ldots ,c_k)^t=(1,1,\ldots ,1)^t$ lies in the kernel of the matrix A.

Without loss of generality, we can label the domains $\{D_i\}$ in the partition inductively so that $D_{i+1}$ is a neighbor of at least one of $D_1, \ldots , D_i$, with $D_1$ arbitrary. For the numbers $\alpha _{i,j}$, this means that

$$\begin{aligned}&\alpha _{1,2}>0,\nonumber \\&\alpha _{1,3}+\alpha _{2,3}>0,\nonumber \\&\alpha _{1,4}+\alpha _{2,4}+\alpha _{3,4}>0,\nonumber \\&\vdots \nonumber \\&\alpha _{1,k}+\alpha _{2,k}+\cdots +\alpha _{k-1,k}>0. \end{aligned}$$

(B.7)

Lemma B.1

Let A be the symmetric $k\times k$ matrix in (B.6) and assume that the inequalities in (B.7) hold. Then $\ker A$ is spanned by $(1,1,\ldots ,1)^t$.

Proof

Consider the quadratic form $q[{\mathbf {c}}]=\langle A{\mathbf {c}},{\mathbf {c}}\rangle$ corresponding to the matrix A above, where ${\mathbf {c}}=(c_1,c_2,\ldots ,c_k)^t$. From (B.5), we find that the quadratic form $q[{\mathbf {c}}]$ can be written as

$$\begin{aligned}&\alpha _{1,2}(c_1-c_2)^2\\&\quad +\alpha _{1,3}(c_1-c_3)^2+\alpha _{2,3}(c_2-c_3)^2\\&\quad +\alpha _{1,4}(c_1-c_4)^2+\alpha _{2,4}(c_2-c_4)^2+\alpha _{3,4}(c_3-c_4)^2\\&\quad +\cdots \\&\quad +\alpha _{1,k}(c_1-c_k)^2+\alpha _{2,k}(c_2-c_k)^2+\cdots +\alpha _{k-1,k}(c_{k-1}-c_k)^2. \end{aligned}$$

Since $\alpha _{i,j} \ge 0$ for all i, j, we see that q (and hence A) is non-negative. It remains to identify the kernel. Assume that $q[{\mathbf {c}}]=0$ for some ${\mathbf {c}}$. Then, reading from the top line above, we conclude that $c_2=c_1$ since $\alpha _{1,2}>0$. Inserting $c_1=c_2$, we conclude from the next row that $c_3=c_2$ since $\alpha _{1,3}+\alpha _{2,3}>0$. Continuing in this manner, we conclude that $c_k=c_{k-1}=\cdots =c_2=c_1$. This means that the kernel of A is spanned by the vector $(1,1,\ldots ,1)^t$. $\square$

Finally, from (B.4), we observe that $\sum d_i$ contains a term

$$\begin{aligned} - \int _{\Gamma _i\cap \Gamma _j} \left\{ \big (\partial _{\nu _i}u^g_i +\chi _{ij} \partial _{\nu _j}u^g_j\big )\,\partial _{\nu _i}\varphi _{*,i} + \big (\partial _{\nu _j}u^g_j +\chi _{ij} \partial _{\nu _i}u^g_i\big )\,\partial _{\nu _j}\varphi _{*,j} \right\} \end{aligned}$$

for each pair of neighboring domains, and by (2.9) each of the integrands vanishes. This means $\sum d_i = 0$, so the vector ${\mathbf {d}}=(d_1,d_2,\ldots ,d_k)^t$ is orthogonal to the kernel of A. Thus, the system (B.6) will always be solvable, by the Fredholm alternative for symmetric matrices.