Abstract
We prove a self-improvement property of a capacity density condition for a nonlocal Hajłasz gradient in complete geodesic spaces with a doubling measure. The proof relates the capacity density condition with boundary Poincaré inequalities, adapts Keith–Zhong techniques for establishing local Hardy inequalities and applies Koskela–Zhong arguments for proving self-improvement properties of local Hardy inequalities. This leads to a characterization of the Hajłasz capacity density condition in terms of a strict upper bound on the upper Assouad codimension of the underlying set, which shows the self-improvement property of the Hajłasz capacity density condition.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We introduce a Hajłasz \((\beta ,p)\)-capacity density condition in terms of Hajłasz gradients of order \(0<\beta \le 1\), see Sects. 3 and 4. Our main result, Theorem 9.6, states that this condition is doubly open-ended, that is, a Hajłasz \((\beta ,p)\)-capacity density condition is self-improving both in p and in \(\beta \) if X is a complete geodesic space endowed with a doubling measure. The study of such conditions can be traced back to the seminal work by Lewis [24], who established self-improvement of Riesz \((\beta ,p)\)-capacity density conditions in \({{\mathbb {R}}}^n\). His result has been followed by other works incorporating different techniques often in metric spaces, like nonlinear potential theory [2, 28], and local Hardy inequalities [23].
A distinctive feature of our paper is that we prove the self-improvement of a capacity density condition for a nonlocal gradient for the first time in metric spaces. We make use of a recent advance [19] in Poincaré inequalities, whose self-improvement properties were originally shown by Keith–Zhong in their celebrated work [16]. In this respect, we join the line of research initiated in [20], and continued in [5, 6], for bringing together the seemingly distinct self-improvement properties of capacity density conditions and Poincaré inequalities.
We use various techniques and concepts in the proof of Theorem 9.6. The fundamental idea is to use a geometric concept, more precisely the upper Assouad codimension, and characterize the capacity density with a strict upper bound on this codimension. Here we are motivated by the recent approach from [4], where the Assouad codimension bound is used to give necessary and sufficient conditions for certain fractional Hardy inequalities; we also refer to [22]. The principal difficulty is to prove a strict bound on the codimension. To this end we relate the capacity density condition to boundary Poincaré inequalities, and we show their self-improvement roughly speaking in two steps: (1) Keith–Zhong estimates on maximal functions and (2) Koskela–Zhong estimates on Hardy inequalities. For these purposes, respectively, we adapt the maximal function methods from [19] and the local Hardy arguments from [23].
There is a clear advantage to working with Hajłasz gradients: Poincaré inequalities hold for all measures, see Sect. 3. Other types of gradients, such as p-weak upper gradients [1], do not have this property and therefore corresponding Poincaré inequalities need to be assumed a priori, as was the case in previous works such as [2, 5, 6, 23, 28]. We remark that this requirement already excludes many doubling measures in \({{\mathbb {R}}}\) equipped with Euclidean distance [3].
Our method is to able to overcome the challenges posed by the nonlocal nature of Hajłasz gradients [8]. For example, if a function u is constant in a set \(A\subset X\) and g is a Hajłasz gradient of u, then \(g{\mathbf {1}}_{X\setminus A}\) is not necessarily a Hajłasz gradient of u. This fact makes it impossible to directly use the standard localization techniques for p-weak upper gradients. More specifically, there is no access to neither pointwise glueing lemma nor pointwise Leibniz rule. The Hajłasz gradients do satisfy nonlocal versions of the glueing lemma and the Leibniz rule, both of which we employ in our method.
Standard localization techniques are used in the literature for proving self-improvement properties of capacity density conditions involving p-weak upper gradients. More specifically, the approaches in [2, 28] are based on Wolff potentials, and oscillation estimates for p-harmonic functions and p-energy minimizers near a boundary point. The two papers [5, 6] rely on maximal function techniques and characterizations of pointwise p-Hardy inequalities by curves. The above approaches can not be directly adapted to our setting with Hajłasz gradients of order \(0<\beta \le 1\). The Wannebo approach [31]—that was used as a first half of the argument in [23] to show local p-Hardy inequalities—can not be adapted to our setting either, due to the non-locality. We show that the Wannebo approach can be replaced by Keith–Zhong estimates on maximal functions, and this work constitutes main part of the present paper. We also adapt the second half of [23] for our purposes, namely, the Koskela–Zhong estimates for improving local Hardy inequalities. This last part is translated to the non-local case in a more straightforward way.
Our method also has a disadvantage. We need to assume that X is a complete geodesic space. These assumptions provide us Lemma 5.3, Theorem 3.8, Lemmas 2.6, 2.5, and few other useful properties. We do not know how far these two conditions could be relaxed. In particular, it would be interesting to know if our main result, Theorem 9.6, could be extended to the more general setting of complete and connected metric spaces.
The outline of this paper is as follows. After a brief discussion on notation and preliminary concepts in Sect. 2, Hajłasz gradients are introduced in Sect. 3 along with their calculus and various Poincaré inequalities. Capacity density condition is discussed in Sect. 4, and some preliminary sufficient and necessary bounds on the Assouad codimension are given in Sect. 5. The most technical part of the work is contained in Sects. 6, 7 and 8, in which the analytic framework of the self-improvement is gradually developed. Finally, the main result is given in Sect. 9, in which we show that various geometrical and analytical conditions are equivalent to the capacity density condition. The geometrical conditions are open-ended by definition, and hence all analytical conditions are seen to be self-improving or doubly open-ended.
2 Preliminaries
In this section, we recall the setting from [19]. Our results are based on quantitative estimates and absorption arguments, where it is often crucial to track the dependencies of constants quantitatively. For this purpose, we will use the following notational convention: \(C({*,\ldots ,*})\) denotes a positive constant which quantitatively depends on the quantities indicated by the \(*\)’s but whose actual value can change from one occurrence to another, even within a single line.
2.1 Metric Spaces
Unless otherwise specified, we assume that \(X=(X,d,\mu )\) is a metric measure space equipped with a metric d and a positive complete Borel measure \(\mu \) such that \(0<\mu (B)<\infty \) for all balls \(B\subset X\), each of which is always an open set of the form
with \(x\in X\) and \(r>0\). As in [1, p. 2], we extend \(\mu \) as a Borel regular (outer) measure on X. We remark that the space X is separable under these assumptions, see [1, Proposition 1.6]. We also assume that \(\# X\ge 2\) and that the measure \(\mu \) is doubling, that is, there is a constant \(c_\mu > 1\), called the doubling constant of \(\mu \), such that
for all balls \(B=B(x,r)\) in X. Here we use for \(0<t<\infty \) the notation \(tB=B(x,tr)\). In particular, for all balls \(B=B(x,r)\) that are centered at \(x\in A\subset X\) with radius \(r\le \mathrm {diam}(A)\), we have that
where \(s=\log _2 c_\mu >0\). We refer to [12, p. 31]. If X is connected, then the doubling measure \(\mu \) is also reverse doubling in the sense that there is a constant \(0<c_R=C(c_\mu )<1\) such that
for every \(x\in X\) and \(0<r<{\text {diam}}(X)/2\). See for instance [1, Lemma 3.7].
2.2 Geodesic Spaces
Let X be a metric space satisfying the conditions stated in Sect. 2.1. By a curve we mean a nonconstant, rectifiable, continuous mapping from a compact interval of \({{\mathbb {R}}}\) to X; we tacitly assume that all curves are parametrized by their arc-length. We say that X is a geodesic space, if every pair of points in X can be joined by a curve whose length is equal to the distance between the two points. In particular, it easily follows that
for all balls \(B=B(x,r)\) in a geodesic space X. Since geodesic spaces are connected, the measure \(\mu \) is reverse doubling in a geodesic space X in the sense that inequality (2.3) holds.
The following lemma is [14, Lemma 12.1.2].
Lemma 2.5
Suppose that X is a geodesic space and \(A\subset X\) is a measurable set. Then the function
is continuous whenever \(x\in X\).
The second lemma, in turn, is [19, Lemma 2.5].
Lemma 2.6
Suppose that \(B=B(x,r)\) and \(B'=B(x',r')\) are two balls in a geodesic space X such that \(x'\in B\) and \(0<r'\le \mathrm {diam}(B)\). Then \(\mu (B')\le c_\mu ^3 \mu (B'\cap B)\).
2.3 Hölder and Lipschitz Functions
Let \(A\subset X\). We say that \(u:A\rightarrow {{\mathbb {R}}}\) is a \(\beta \)-Hölder function, with an exponent \(0<\beta \le 1\) and a constant \(0\le \kappa <\infty \), if
If \(u:A\rightarrow {{\mathbb {R}}}\) is a \(\beta \)-Hölder function, with a constant \(\kappa \), then the classical McShane extension
defines a \(\beta \)-Hölder function \(v:X\rightarrow {{\mathbb {R}}}\), with the constant \(\kappa \), which satisfies \(v|_A = u\); we refer to [12, pp. 43–44] and [27]. The set of all \(\beta \)-Hölder functions \(u:A\rightarrow {{\mathbb {R}}}\) is denoted by \({\text {Lip}}_\beta (A)\). The 1-Hölder functions are also called Lipschitz functions.
2.4 Additional Notation
We write \({{\mathbb {N}}}=\{1,2,3,\ldots \}\) and \({{\mathbb {N}}}_0={{\mathbb {N}}}\cup \{0\}\). We use the following familiar notation:

is the integral average of \(u\in L^1(A)\) over a measurable set \(A\subset X\) with \(0<\mu (A)<\infty \). The characteristic function of set \(A\subset X\) is denoted by \({\mathbf {1}}_{A}\); that is, \({\mathbf {1}}_{A}(x)=1\) if \(x\in A\) and \({\mathbf {1}}_{A}(x)=0\) if \(x\in X\setminus A\). The distance between a point \(x\in X\) and a set \(A\subset X\) is denoted by d(x, A). The closure of a set \(A\subset X\) is denoted by  . In particular, if \(B\subset X\) is a ball, then the notation
. In particular, if \(B\subset X\) is a ball, then the notation  refers to the closure of the ball B.
refers to the closure of the ball B.
3 Hajłasz Gradients
We work with Hajłasz \(\beta \)-gradients of order \(0<\beta \le 1\) in a metric space X.
Definition 3.1
For each function \(u:X\rightarrow {{\mathbb {R}}}\), we let \({\mathcal {D}}_H^{\beta }(u)\) be the (possibly empty) family of all measurable functions \(g:X\rightarrow [0,\infty ]\) such that
almost everywhere, i.e., there exists an exceptional set \(N=N(g)\subset X\) for which \(\mu (N)=0\) and inequality (3.2) holds for every \(x,y\in X\setminus N\). A function \(g\in {\mathcal {D}}^\beta _H(u)\) is called a Hajłasz \(\beta \)-gradient of the function u.
The Hajłasz 1-gradients in metric spaces are introduced in [9]. More details on these gradients and their applications can be found, for instance, from [8, 10, 29, 30, 32]. The following basic properties are easy to verify for all \(\beta \)-Hölder functions \(u,v:X\rightarrow {{\mathbb {R}}}\)
-
(D1)
\(|a|g\in {\mathcal {D}}_H^{\beta }(au)\) if \(a\in {{\mathbb {R}}}\) and \(g\in {\mathcal {D}}_H^{\beta }(u)\);
-
(D2)
\(g_u + g_v\in {\mathcal {D}}_H^{\beta }(u+v)\) if \(g_u\in {\mathcal {D}}_H^{\beta }(u)\) and \(g_v\in {\mathcal {D}}_H^{\beta }(v)\);
-
(D3)
If \(f:{{\mathbb {R}}}\rightarrow {{\mathbb {R}}}\) is a Lipschitz function with constant \(\kappa \), then \(\kappa g\in {\mathcal {D}}^\beta _H(f\circ u)\) if \(g\in {\mathcal {D}}^\beta _H(u)\).
There are both disadvantages and advantages to working with Hajłasz gradients. A technical disadvantage is their nonlocality [8]. For instance, if u is constant on some set \(A\subset X\) and \(g\in {\mathcal {D}}^\beta _H(u)\), then \(g{\mathbf {1}}_{X\setminus A}\) need not belong to \({\mathcal {D}}^\beta _H(u)\). By the so-called glueing lemma, see for instance [1, Lemma 2.19], the corresponding localization property holds for so-called p-weak upper gradients, which makes their application more flexible. However, the following nonlocal glueing lemma from [19, Lemma 6.6] holds in the setting of Hajłasz gradients.
We recall the proof for convenience.
Lemma 3.3
Let \(0<\beta \le 1\) and let \(A\subset X\) be a Borel set. Let \(u:X\rightarrow {{\mathbb {R}}}\) be a \(\beta \)-Hölder function and suppose that \(v:X\rightarrow {{\mathbb {R}}}\) is such that \(v|_{X\setminus A} =u|_{X\setminus A}\) and there exists a constant \(\kappa \ge 0\) such that \(|v(x)-v(y)|\le \kappa \, d(x,y)^\beta \) for all \(x,y\in X\). Then
whenever \(g_u\in {\mathcal {D}}_H^{\beta }(u)\).
Proof
Fix a function \(g_u\in {\mathcal {D}}_H^{\beta }(u)\) and let \(N\subset X\) be the exceptional set such that \(\mu (N)=0\) and inequality (3.2) holds for every \(x,y\in X\setminus N\) and with \(g=g_u\).
Fix \(x,y\in X\setminus N\). If \(x,y\in X\setminus A\), then
If \(x\in A\) or \(y\in A\), then
By combining the estimates above, we find that
whenever \(x,y\in X\setminus N\). The desired conclusion \(g_v\in {\mathcal {D}}_H^{\beta }(v)\) follows. \(\square \)
The following nonlocal generalization of the Leibniz rule is from [10]. The proof is recalled for the convenience of the reader. The nonlocality is reflected by the appearence of the two global terms \(\Vert \psi \Vert _\infty \) and \(\kappa \) in the statement below.
Lemma 3.4
Let \(0<\beta \le 1\), let \(u:X\rightarrow {{\mathbb {R}}}\) be a bounded \(\beta \)-Hölder function, and let \(\psi :X\rightarrow {{\mathbb {R}}}\) be a bounded \(\beta \)-Hölder function with a constant \(\kappa \ge 0\). Then \(u\psi :X\rightarrow {{\mathbb {R}}}\) is a \(\beta \)-Hölder function and
for all \(g_u\in {\mathcal {D}}_H^{\beta }(u)\). Here \(\{\psi \not =0\}=\{y\in X: \psi (y)\not =0\}\).
Proof
Fix \(x,y\in X\). Then
Since u and \(\psi \) are both bounded \(\beta \)-Hölder functions in X, it follows that \(u\psi \) is \(\beta \)-Hölder in X.
Fix a function \(g_u\in {\mathcal {D}}_H^{\beta }(u)\) and let \(N\subset X\) be the exceptional set such that \(\mu (N)=0\) and inequality (3.2) holds for every \(x,y\in X\setminus N\) and with \(g=g_u\). Denote \(h=(g_u\Vert \psi \Vert _\infty + \kappa |u|){\mathbf {1}}_{\{\psi \not =0\}}\). Let \(x,y\in X\setminus N\). It suffices to show that
By (3.5), we get
Next we do a case study. If \(x,y\in \{\psi \not =0\}\), then by (3.6) we have
If \(x\in X\setminus \{\psi \not =0\}\) and \(y\in \{\psi \not =0\}\), then
The case \(x\in \{\psi \not =0\}\) and \(y\in X\setminus \{\psi \not =0\}\) is symmetric and the last case is trivial. \(\square \)
A significant advantage of working with Hajłasz gradients is that Poincaré inequalities are always valid [30, 32]. The same is not true for the usual p-weak upper gradients, in which case a Poincaré inequality often has to be assumed.
The following theorem gives a \((\beta ,p,p)\)-Poincaré inequality for any \(1\le p<\infty \). This inequality relates the Hajłasz gradient to the given measure.
Theorem 3.7
Suppose that X is a metric space. Fix exponents \(1\le p<\infty \) and \(0<\beta \le 1\). Suppose that \(u\in \mathrm {Lip}_\beta (X)\) and that \(g\in {\mathcal {D}}_H^{\beta }(u)\). Then

holds whenever \(B\subset X\) is a ball.
Proof
We follow the proof of [12, Theorem 5.15]. Let \(N=N(g)\subset X\) be the exceptional set such that \(\mu (N)=0\) and (3.2) holds for every \(x,y\in X\setminus N\). By Hölder’s inequality

Applying (3.2), we obtain

The claimed inequality follows by combining the above estimates. \(\square \)
In a geodesic space, even a stronger \((\beta ,p,q)\)-Poincaré inequality holds for some \(q<p\). In the context of p-weak upper gradients, this result corresponds to the deep theorem of Keith and Zhong [16]. In our context the proof is simpler, since we have \((\beta ,q,q)\)-Poincaré inequalities for all exponents \(1<q<p\) by Theorem 3.7. It remains to argue that one of these inequalities self-improves to a \((\beta ,p,q)\)-Poincaré inequality when \(q<p\) is sufficiently close to p.
Theorem 3.8
Suppose that X is a geodesic space. Fix exponents \(1< p<\infty \) and \(0<\beta \le 1\). Suppose that \(u\in \mathrm {Lip}_\beta (X)\) and that \(g\in {\mathcal {D}}_H^{\beta }(u)\). Then there exists an exponent \(1<q<p\) and a constant C, both depending on \(c_\mu \), p and \(\beta \), such that

holds whenever \(B\subset X\) is a ball.
Proof
We will apply [19, Theorem 3.6] and for this purpose we need some preparations. Fix \(Q=Q(\beta ,p,c_\mu )\) such that \(Q>\max \{\log _2 c_\mu ,\beta p\}\). Since
there exists \(1<q=q(\beta ,p,c_\mu )<p\) such that \(p<Qq/(Q-\beta q)\) and \(\beta q<Q\). Theorem 3.7 and Hölder’s inequality implies that

whenever \(B\subset X\) is a ball. Now the claim follows from [19, Theorem 3.6], which is based on the covering argument from [11]. We also refer to [7, Lemma 2.2]. \(\square \)
4 Capacity Density Condition
In this section, we define the capacity density condition. This condition is based on the following notion of variational capacity, and it is weaker than the well known measure density condition. We also prove boundary Poincaré inequalities for sets satisfying a capacity density condition. This is done with the aid of so-called Mazya’s inequality, which provides an important link between Poincaré inequalities and capacities.
Definition 4.1
Let \(1\le p<\infty \), \(0<\beta \le 1\), and let \(\Omega \subset X\) be an open set. The variational \((\beta ,p)\)-capacity of a closed subset \(F\subset \Omega \) with \(\mathrm {dist}(F,X\setminus \Omega )>0\) is
where the infimums are taken over all \(\beta \)-Hölder functions u in X, with \(u\ge 1\) in F and \(u=0\) in \(X\setminus \Omega \), and over all \(g\in {\mathcal {D}}_H^{\beta }(u)\).
Remark 4.2
We may take the infimum in Definition 4.1 among all u satisfying additionally \(0\le u\le 1\). This follows by considering the \(\beta \)-Hölder function function \(v=\max \{0,\min \{u,1\}\}\) since \(g\in {\mathcal {D}}^\beta _H(v)\) by Property (D3).
Definition 4.3
A closed set \(E\subset X\) satisfies a \((\beta ,p)\)-capacity density condition, for \(1\le p<\infty \) and \(0<\beta \le 1\), if there exists a constant \(c_0>0\) such that
for all \(x\in E\) and all \(0<r<(1/8){\text {diam}}(E)\).
Example 4.5
We say that a closed set \(E\subset X\) satisfies a measure density condition, if there exists a constant \(c_1\) such that
for all \(x\in E\) and all \(0<r<(1/8){\text {diam}}(E)\). Assume that the metric space X is connected, \(1\le p<\infty \) and \(0<\beta \le 1\), and that a set \(E\subset X\) satisfies a measure density condition. Then it is easy to show that E satisfies a \((\beta ,p)\)-capacity density condition, see below. We remark that the measure density condition has been applied in [17] to study Hajłasz Sobolev spaces with zero boundary values on E.
Fix \(x\in E\) and \(0<r<(1/8){\text {diam}}(E)\). We aim to show that (4.4) holds. For this purpose, we write \(F=E\cap \overline{B(x,r)}\) and \(B=B(x,r)\). Let \(u\in {\text {Lip}}_\beta (X)\) be such that \(0\le u\le 1\), \(u= 1\) in F and \(u=0\) in \(X\setminus 2B\). Let also \(g\in {\mathcal {D}}_H^{\beta }(u)\). Recall that X is connected. Hence, by the properties of u and the reverse doubling inequality (2.3), we obtain

If \(y\in F\), we have \(u(y)=1\) and therefore
Applying the measure density condition (4.6) and the \((\beta ,p,p)\)-Poincaré inequality, see Theorem 3.7, we obtain
By taking infimum over functions u and g as above, we see that
This shows that E satisfies a \((\beta ,p)\)-capacity density condition (4.4).
The following Mazya’s inequality provides a link between capacities and Poincaré inequalities. We refer to [25, Chapter 10] and [26, Chapter 14] for further details on such inequalities.
Theorem 4.7
Let \(1\le p<\infty \), \(0<\beta \le 1\), and let \(B(z,r)\subset X\) be a ball. Assume that u is a \(\beta \)-Hölder function in X and \(g\in {\mathcal {D}}_H^{\beta }(u)\). Then there exists a constant \(C=C(p)\) such that

Here \(\{u=0\}=\{y\in X : u(y)=0\}\).
Proof
We adapt the proof of [18, Theorem 5.47], which in turn is based on [1, Theorem 5.53]. Let \(M=\sup \{|u(x)|: x\in B(z,r)\}<\infty \). By considering \(\min \{M,|u|\}\) instead of u and using (D3), we may assume that u is a bounded \(\beta \)-Hölder function in X and that \(u\ge 0\) in B(z, r). Write \(B=B(z,r)\) and

If \(u_{B,p} = 0\) the claim is true, and thus we may assume that \(u_{B,p} > 0\). Let
for every \(x\in X\). Then \(0\le \psi \le 1\), \(\psi =0\) in \(X\setminus B(z,r)\), \(\psi =1\) in \(\overline{B(z,\tfrac{r}{2})}\), and \(\psi \) is a \(\beta \)-Hölder function in X with a constant \((2r^{-1})^\beta \). Let
Then \(v=1\) in \(\{u=0\}\cap \overline{B(z,\tfrac{r}{2})}\) and \(v=0\) in \(X\setminus B(z,r)\). By Lemma 3.4, and properties (D1) and (D2), the function v is \(\beta \)-Hölder in X and
Here we used the fact that \(g\in {\mathcal {D}}_H^{\beta }(u)\) by assumptions. Now, the pair v and \(g_v\) is admissible for testing the capacity. Thus, we obtain
We use Minkowski’s inequality and the \((\beta ,p,p)\)-Poincaré inequality in Theorem 3.7 to estimate the second term on the right-hand side of (4.8), and obtain

By the triangle inequality and the above Poincaré inequality, we have

Together with (4.9) this gives

and thus
Substituting this to (4.8) and recalling that \(B=B(z,r)\), we arrive at
The claim follows by reorganizing the terms. \(\square \)
The following theorem establishes certain boundary Poincaré inequalities for a set E satisfying a capacity density condition. Mazya’s inequality in Theorem 4.7 is a key tool in the proof.
Theorem 4.10
Let \(1\le p<\infty \) and \(0<\beta \le 1\). Assume that \(E\subset X\) satisfies a \((\beta ,p)\)-capacity density condition with a constant \(c_0\). Then there is a constant \(C=C(p,c_0,c_\mu )\) such that

whenever \(u:X\rightarrow {{\mathbb {R}}}\) is a \(\beta \)-Hölder function in X such that \(u=0\) in E, \(g\in {\mathcal {D}}_H^{\beta }(u)\), and B(x, R) is a ball with \(x\in E\) and \(0<R<{\text {diam}}(E)/4\).
Proof
Let \(x\in E\) and \(0<R<{\text {diam}}(E)/4\). We denote \(r=R/2<{\text {diam}}(E)/8\). Applying the capacity density condition in the ball \(B=B(x,r)\) gives

Write \(\{u=0\}=\{y\in X : u(y)=0\}\supset E\). By the monotonicity of capacity and the doubling condition we have

The desired inequality, for the ball \(B(x,R)=B(x,2 r)=2B\), follows from Theorem 4.7. \(\square \)
5 Necessary and Sufficient Geometrical Conditions
In this section we adapt the approach in [4] by giving necessary and sufficient geometrical conditions for the \((\beta ,p)\)-capacity density condition. These are given in terms of the following upper Assouad codimension [15].
Definition 5.1
When \(E\subset X\) and \(r>0\), the open r-neighbourhood of E is the set
The upper Assouad codimension of \(E\subset X\), denoted by \({{\,\mathrm{\overline{co\,dim}_A}\,}}(E)\), is the infimum of all \(Q\ge 0\) for which there is \(c>0\) such that
for every \(x\in E\) and all \(0<r<R<{\text {diam}}(E)\). If \({\text {diam}}(E)=0\), then the restriction \(R<{\text {diam}}(E)\) is removed.
Observe that a larger set has a smaller Assouad codimension. We need suitable versions of Hausdorff contents from [22].
Definition 5.2
The (\(\rho \)-restricted) Hausdorff content of codimension \(q\ge 0\) of a set \(F\subset X\) is defined by
The following lemma is [22, Lemma 5.1]. It provides a lower bound for the Hausdorff content of a set truncated in a fixed ball in terms of the measure and radius of the truncating ball. The proof uses completeness via construction of a compact Cantor-type set inside E, whose mass is uniformly distributed by a Carathéodory construction.
Lemma 5.3
Assume that X is a complete metric space. Let \(E\subset X\) be a closed set, and assume that \({{\,\mathrm{\overline{co\,dim}_A}\,}}(E)<q\). Then there exists a constant \(C>0\) such that
for every \(x\in E\) and all \(0<r<{\text {diam}}(E)\).
On the other hand, Hausdorff content gives a lower bound for capacity by following lemma. The proof is based on a covering argument, where the covering balls are chosen by chaining. The proof is a more sophisticated variant of the argument given in Example 4.5. Similar covering arguments via chaining have been widely used; see for instance [13].
Lemma 5.5
Assume that X is a connected metric space. Let \(0<\beta \le 1\), \(1\le p<\infty \), and \(0< \eta <p\). Assume that \(B=B(x_0,r)\subset X\) is a ball with \(r<{\text {diam}}(X)/8\), and assume that  is a closed set. Then there is a constant \(C=C(\beta ,p,\eta ,c_\mu )>0\) such that
is a closed set. Then there is a constant \(C=C(\beta ,p,\eta ,c_\mu )>0\) such that
Proof
We adapt the proof of [4, Lemma 4.6] for our purposes. Let \(u\in {\text {Lip}}_\beta (X)\) be such that \(0\le u\le 1\) in X, \(u=1\) in F and \(u=0\) in \(X\setminus 2B\). Let also \(g\in {\mathcal {D}}_H^{\beta }(u)\). We aim to cover the set F by balls that are chosen by chaining. In order to do so, we fix \(x\in F\) and write \(B_0=4B=B(x_0,4 r)\), \(r_0=4 r\), \(r_j=2^{-j+1}r\) and \(B_j=B(x,r_j)\), \(j=1,2,\ldots \). Observe that \(B_{j+1}\subset B_j\) and \(\mu (B_j)\le c_\mu ^3 \mu (B_{j+1})\) if \(j=0,1,2,\ldots \).
By the above properties of u and the reverse doubling inequality (2.3), we obtain

Since \(x\in F\), we find that \(u(x)=1\) and therefore
We write \(\delta =\beta (p-\eta )/p>0\). Using the Poincaré inequality in Theorem 3.7 and abbreviating \(C=C(\beta ,p,\eta ,c_\mu )\), we obtain

By comparing the series in the left- and right-hand side of these inequalities, we see that there exists \(j\in \{0,1,2,\ldots \}\) depending on x such that

Write \(r_x=r_{j}\) and \(B_x=B_{j}\). Then \(x\in B_x\) and straightforward estimates based on (5.6) give
By the 5r-covering lemma [1, Lemma 1.7], we obtain points \(x_k\in F\), \(k=1,2,\ldots \), such that the balls \(B_{x_k}\subset B_0=4B\) with radii \(r_{x_k}\le 4r\) are pairwise disjoint and \(F\subset \bigcup _{k=1}^\infty 5B_{x_k}\). Hence,
where \(C=C(\beta ,p,\eta ,c_\mu )\). We remark that the scale 20r of the Hausdorff content in the left-hand side comes from the fact that radii of the covering balls \(5B_{x_k}\) for F are bounded by 20r. The desired inequality follows by taking infimum over all functions \(g\in {\mathcal {D}}_H^{\beta }(u)\) and then over all functions u as above. \(\square \)
The following theorem gives an upper bound for the upper Assouad codimension for sets satisfying a capacity density condition. We emphasize the strict inequality \({{\,\mathrm{\overline{co\,dim}_A}\,}}(E)<\beta p\), completeness and connectedness in the assumptions below.
Theorem 5.7
Assume that X is a complete and connected metric space. Let \(1\le p<\infty \) and \(0<\beta \le 1\). Let E be a closed set with \({{\,\mathrm{\overline{co\,dim}_A}\,}}(E)<\beta p\). Then E satisfies a \((\beta ,p)\)-capacity density condition.
Proof
Fix \(0<\eta <p\) such that \({{\,\mathrm{\overline{co\,dim}_A}\,}}(E)<\beta \eta \). Let \(x\in E\) and \(0<r<{\text {diam}}(E)/8\), and write \(B=B(x,r)\). By a simple covering argument using the doubling condition, it follows that  with a constant C independent of B. Applying also Lemma 5.5 and then Lemma 5.3 gives
with a constant C independent of B. Applying also Lemma 5.5 and then Lemma 5.3 gives

After simplification, we obtain

and the claim follows. \(\square \)
Conversely, by using boundary Poincaré inequalities, it is easy to show that a capacity density condition implies an upper bound for the upper Assouad codimension.
Theorem 5.8
Let \(1\le p<\infty \) and \(0<\beta \le 1\). Assume that \(E\subset X\) satisfies a \((\beta ,p)\)-capacity density condition. Then \({{\,\mathrm{\overline{co\,dim}_A}\,}}(E)\le \beta p\).
Proof
We adapt the proof of [4, Theorem 5.3] to our setting. By using the doubling condition, it suffices to show that
for all \(w\in E\) and \(0<r<R<{\text {diam}}(E)/4\), where the constant c is independent of w, r and R.
If \(\mu (E_r\cap B(w,R))\ge \frac{1}{2} \mu (B(w,R))\), the claim is clear since \(\bigl (\frac{r}{R}\bigr )^{\beta p}\le 1\). Thus we may assume in the sequel that \(\mu (E_r\cap B(w,R)) < \tfrac{1}{2} \mu (B(w,R))\), whence
We define a \(\beta \)-Hölder function \(u:X\rightarrow {{\mathbb {R}}}\) by
Then \(u=0\) in E, \(u=1\) in \(X\setminus E_{r}\), and
We obtain
where the last step follows from (5.10).
Since \(u=1\) in \(X\setminus E_{r}\) and u is a \(\beta \)-Hölder function with a constant \(r^{-\beta }\), Lemma 3.3 implies that \(g=r^{-\beta }{\mathbf {1}}_{E_{r}}\in {\mathcal {D}}_H^{\beta }(u)\). We observe from (5.11) and Theorem 4.10 that
where the constant C is independent of w, r and R. The claim (5.9) follows from (5.12). \(\square \)
Observe that the upper bound \({{\,\mathrm{\overline{co\,dim}_A}\,}}(E)\le \beta p\) appears in the conclusion of Theorem 5.8. The rest of the paper is devoted to showing the strict inequality \({{\,\mathrm{\overline{co\,dim}_A}\,}}(E)< \beta p\) for \(1<p<\infty \), which leads to a characterization of the \((\beta ,p)\)-capacity density condition in terms of this strict dimensional inequality.
Our strategy is to combine the methods in [19, 23] to prove a significantly stronger variant of the boundary Poincaré inequality, which involves maximal operators, see Theorem 7.4. We use this maximal inequality to prove a Hardy inequality, Theorem 8.4. This variant leads to the characterization in Theorem 9.5 of the \((\beta ,p)\)-capacity density condition in terms of the strict inequality \({{\,\mathrm{\overline{co\,dim}_A}\,}}(E)<\beta p\), among other geometric and analytic conditions. Certain additional geometric assumptions are needed for the proof of Theorem 9.5, namely geodesic property of X. We are not aware, to which extent this geometric assumption can be relaxed.
6 Local Boundary Poincaré Inequality
Our next aim is to show Theorem 7.4, which concerns inequalities localized to a fixed ball \(B_0\) centered at E. The proof of this theorem requires that we first truncate the closed set E to a smaller set \(E_Q\) contained in a Whitney-type ball  such that a local variant of the boundary Poincaré inequality remains valid. The choice of the Whitney-type ball Q and the construction of the set \(E_Q\) are given in this section.
such that a local variant of the boundary Poincaré inequality remains valid. The choice of the Whitney-type ball Q and the construction of the set \(E_Q\) are given in this section.
This truncation construction, that we borrow from [23], is done in such a way that a local Poincaré inequality holds, see Lemma 6.6. This inequality is local in two senses: on one hand, the inequality holds only for balls \(B\subset 4Q \); on the other hand, it holds for functions vanishing on the truncated set \(E_Q\). Due to the subtlety of its consequences, the truncation in this section may seem arbitrary, but it is actually needed for our purposes.
Assume that E is a closed set in a geodesic space X. Fix a ball \(B_0=B(w,R)\subset X\) with \(w\in E\) and \(R<{\text {diam}}(E)\). Define a family of balls
We also need a single Whitney-type ball \(Q=B(w,r_Q)\subset B_0\), where
The 4-dilation of the Whitney-type ball is denoted by \(Q^*=4Q=B(w,4 r_Q)\). Now it holds that \(Q^*\subsetneq X\), since otherwise
The following properties (W1)–(W4) are straightforward to verify. For instance, property (W1) follows from inequality (2.4); we omit the simple proofs.
-
(W1)
If \(B\subset X\) is a ball such that
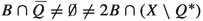 , then \({\text {diam}}(B)\ge 3r_Q/4\);
, then \({\text {diam}}(B)\ge 3r_Q/4\); -
(W2)
If \(B\subset Q^*\) is a ball, then \(B\in {\mathcal {B}}_0\);
-
(W3)
If \(B\subset Q^*\) is a ball, \(x\in B\) and \(0<r\le {\text {diam}}(B)\), then \(B(x,5r)\in {\mathcal {B}}_0\);
-
(W4)
If \(x\in Q^*\) and \(0<r\le 2{\text {diam}}(Q^*)\), then \(B(x,r)\in {\mathcal {B}}_0\).
Observe that there is some overlap between the properties (W2)–(W4). The slightly different formulations will conveniently guide the reader in the sequel.
The following Lemma 6.3 gives us the truncated set \(E_Q\subset {\overline{Q}}\) that contains big pieces of the original set E at small scales. This big pieces property is not always satisfied by \(E\cap Q\), so it cannot be used instead.
Lemma 6.3
Assume that \(E\subset X\) is a closed set in a geodesic space X and that \(Q=B(w,r_Q)\) for \(w\in E\) and \(r_Q>0\). Let \(E_{Q}^0=E\cap \overline{\frac{1}{2} Q}\), define inductively, for every \(j\in {{\mathbb {N}}}\), that
Then the following statements hold:
-
(a)
\(w\in E_{Q}\);
-
(b)
\(E_{Q}\subset E\);
-
(c)
\(E_{Q}\subset {\overline{Q}}\);
-
(d)
\(E^{j-1}_{Q}\subset E^{j}_{Q}\subset E_{Q}\) for every \(j\in {{\mathbb {N}}}\).
The next lemma shows that the truncated set \(E_Q\) in Lemma 6.3 really contains big pieces of the original set E at all small scales. Using these balls we later employ the capacity density condition of E, see the proof of Lemma 6.6 for details.
Lemma 6.4
Let E, Q, and \(E_{Q}\) be as in Lemma 6.3. Suppose that \(m\in {{\mathbb {N}}}_0\) and \(x\in X\) is such that \(d(x,E_{Q}) <2^{-m+1}r_Q\). Then there exists a ball \({\widehat{B}}=B(y_{x,m},2^{-m-1}r_Q)\) such that \(y_{x,m}\in E\),
and \({\widehat{B}}\subset B(x,2^{-m+2}r_Q)\).
We refer to [23] for the proofs of Lemmas 6.3 and 6.4. A similar truncation procedure is a standard technique when proving the self-improvement of different capacity density conditions. It originally appears in [24, p. 180] for Riesz capacities in \({{\mathbb {R}}}^n\), and later also in [28] for \({{\mathbb {R}}}^n\) and in [2] for general metric spaces.
With the aid of big pieces inside the truncated set \(E_Q\), we can show that a localized variant of the boundary Poincaré inequality in Theorem 4.10 holds for the truncated set \(E_Q\), if E satisfies a capacity density condition. Observe that the function u in Lemma 6.6 is assumed to vanish only in the truncated set \(E_Q\), which is a subset of E. This is the key difference when compared to the boundary Poincaré inequality in Theorem 4.10.
Lemma 6.6
Let X be a geodesic space. Assume that \(1\le p<\infty \) and \(0<\beta \le 1\). Suppose that a closed set \(E\subset X\) satisfies the \((\beta ,p)\)-capacity density condition with a constant \(c_0\). Let \(B_0=B(w,R)\subset X\) be a ball with \(w\in E\) and \(R<{\text {diam}}(E)\), and let \(Q=B(w,r_Q)\subset B_0\) be the corresponding Whitney-type ball. Assume that \(B\subset Q^*\) is a ball with a center \(x_B\in E_Q\). Then there is a constant \(K= K(p,c_\mu ,c_0)\) such that

for all \(\beta \)-Hölder functions u in X with \(u=0\) in \(E_Q\), and for all \(g\in {\mathcal {D}}_H^{\beta }(u)\).
Proof
Fix a ball \(B=B(x_B,r_B)\subset Q^*\) with \(x_B\in E_Q\). Recall that \(r_Q=R/128\) as in (6.2). Since \(B\subset Q^*\subsetneq X\), we have
Hence, we can choose \(m\in {{\mathbb {N}}}_0\) such that \(2^{-m+2}r_Q<r_B\le 2^{-m+3}r_Q\). Then
By Lemma 6.4 with \(x=x_B\) there exists a ball \({\widehat{B}}=B(y,2^{-m-1}r_Q)\) such that \(y\in E\),
and \({\widehat{B}}\subset B(x_B,2^{-m+2}r_Q)\subset B(x_B,r_B)=B\). Observe also that \(B\subset 32{\widehat{B}}\).
Fix a \(\beta \)-Hölder function u in X with \(u=0\) in \(E_Q\), and let \(g\in {\mathcal {D}}_H^{\beta }(u)\). We estimate

By the \((\beta ,p,p)\)-Poincaré inequality in Theorem 3.7, we obtain

Using also Hölder’s inequality and the doubling condition, we get

In order to estimate the remaining term \(|u_{{\widehat{B}}}|^p\), we write \( \{u=0\}= \{y\in X : u(y)=0\}\supset E_Q\). Using the monotonicity of capacity, identity (6.8), the assumed capacity density condition, and the doubling condition, we obtain
By Theorem 4.7, we obtain

The proof is completed by combining the above estimates for the three terms. \(\square \)
7 Maximal Boundary Poincaré Inequalities
We formulate and prove our key results, Theorems 7.4 and 7.6. These theorems give improved variants of the local boundary Poincaré inequality (6.7). The improved variants are norm inequalities for a combination of two maximal functions. Hence, we can view Theorems 7.4 and 7.6 as maximal boundary Poincaré inequalities. Our treatment adapts [19] to the setting of boundary Poincaré inequalities.
Definition 7.1
Let X be a geodesic space, \(1<p<\infty \) and \(0<\beta \le 1\). If \({\mathcal {B}}\not =\emptyset \) is a given family of balls in X, then we define a fractional sharp maximal function

whenever \(u:X\rightarrow {{\mathbb {R}}}\) is a \(\beta \)-Hölder function. We also define the maximal function adapted to a given set \(E_Q\subset X\) by

whenever \(u:X\rightarrow {{\mathbb {R}}}\) is a \(\beta \)-Hölder function such that \(u=0\) in \(E_Q\). Here \(x_B\) is the center of the ball \(B\in {\mathcal {B}}\). The suprema in (7.2) and (7.3) are defined to be zero, if there is no ball B in \({\mathcal {B}}\) that contains the point x.
We are mostly interested in maximal functions for the ball family (6.1). The following is the main result in this section.
Theorem 7.4
Let X be a geodesic space. Let \(1<p<\infty \) and \(0<\beta \le 1\). Let \(E\subset X\) be a closed set which satisfies the \((\beta ,p)\)-capacity density condition with a constant \(c_0\). Let \(B_0=B(w,R)\) be a ball with \(w\in E\) and \(R<{\text {diam}}(E)\). Let \(E_Q\) be the truncation of E to the Whitney-type ball Q as in Sect. 6. Then there exists a constant \(C=C(\beta ,p,c_\mu ,c_0)>0\) such that inequality
holds whenever \(u\in \mathrm {Lip}_\beta (X)\) is such that \(u=0\) in \(E_Q\) and \(g\in {\mathcal {D}}_H^{\beta }(u)\).
Proof
We use the following Theorem 7.6 with \(\varepsilon =0\). Observe that the first term on the right-hand side of (7.7) is finite, since u is a \(\beta \)-Hölder function in X such that \(u=0\) in \(E_Q\). Inequality (7.5) is obtained when this term is absorbed to the left-hand side after choosing the number k large enough, depending only on \(\beta \), p, \(c_\mu \) and \(c_0\). \(\square \)
Theorem 7.6
Let X be a geodesic space. Let \(1<q<p<\infty \) and \(0<\beta \le 1\) be such that the \((\beta ,p,q)\)-Poincaré inequality in Theorem 3.8 holds. Let \(E\subset X\) be a closed set satisfying the \((\beta ,p)\)-capacity density condition with a constant \(c_0\). Let \(B_0=B(w,R)\) be a ball with \(w\in E\) and \(R<{\text {diam}}(E)\). Let \(E_Q\) be the truncation of E to the Whitney-type ball \(Q=B(w,r_Q)\subset B_0\) as in Sect. 6. Let \(K=K(p,c_\mu ,c_0)>0\) be the constant for the local boundary Poincaré inequality in Lemma 6.6. Assume that \(k\in {{\mathbb {N}}}\), \(0\le \varepsilon < (p-q)/2\), and \(\alpha =\beta p^2/(2(s+\beta p))>0\) with \(s=\log _2 c_\mu \). Then, inequality
holds for each \(u\in \mathrm {Lip}_\beta (X)\) with \(u=0\) in \(E_Q\) and every \(g\in {\mathcal {D}}_H^{\beta }(u)\). Here \(C_1=C_1(\beta ,p,c_\mu )\), \(C_1=C_1(\beta ,p,c_\mu )\), \( C_3=C(\beta ,p,c_\mu ) \), \(C(k,\varepsilon )=(4^{k\varepsilon }-1)/\varepsilon \) if \(\varepsilon >0\) and \(C(k,0)=k\).
Remark 7.8
Observe that Theorem 7.6 implies a variant of Theorem 7.4 when we choose \(\varepsilon >0\) to be sufficiently small. We omit the formulation of this variant, since we do not use it. This is because of the following defect: one of the terms is the integral of \(g^p\big (M^{\sharp ,p}_{\beta ,{\mathcal {B}}_0}u+M^{E_Q,p}_{\beta ,{\mathcal {B}}_0}u \big )^{-\varepsilon }\) instead of \(g^{p-\varepsilon }\). Because of its independent interest, we have however chosen to formulate Theorem 7.6 such that it incorporates the parameter \(\varepsilon \).
The proof of Theorem 7.6 is completed in Sect. 7.4. For the proof, we need preparations that are treated in Sects. 7.1–7.3. At this stage, we already fix X, E, \(B_0\), Q, \(E_Q\), K, \({\mathcal {B}}_0\), p, \(\beta \), q, \(\varepsilon \), k and u as in the statement of Theorem 7.6. Notice, however, that the \(\beta \)-Hajłasz gradient g of u is not yet fixed. We abbreviate \(M^{\sharp } u=M^{\sharp ,p}_{\beta ,{\mathcal {B}}_0}u\) and \(M^{E_Q}u=M^{E_Q,p}_{\beta ,{\mathcal {B}}_0}u\), and denote
The sets \(U^\lambda \) are open in X. If \(F\subset X\) is a Borel set and \(\lambda >0\), we write \(U^\lambda _F=U^\lambda \cap F\). We refer to these objects throughout Sect. 7 without further notice.
7.1 Localization to Whitney-Type Ball
We need a smaller maximal function that is localized to the Whitney-type ball Q. Consider the ball family
and define
If \(\lambda >0\), we write
We estimate the left-hand side of (7.7) in terms of (7.9) with the aid of the following norm estimate. We will later be able to estimate the smaller maximal function (7.9).
Lemma 7.11
There are constants \(C_1=C(p,c_\mu )\) and \(C_2=C(\beta ,p,c_\mu )\) such that
for all \(g\in {\mathcal {D}}_H^{\beta }(u)\).
Proof
Fix \(g\in {\mathcal {D}}_H^{\beta }(u)\). We have
Let \(x\in B_0\) and let \(B\in {\mathcal {B}}_0\) be such that \(x\in B\). By (6.1) and the \((\beta ,p,q)\)-Poincaré inequality, see Theorem 3.8, we obtain

Here M is the non-centered Hardy–Littlewood maximal function operator. By taking supremum over balls B as above, we obtain
Since \(p-\varepsilon >q\), the Hardy–Littlewood maximal function theorem [1, Theorem 3.13] implies that
Since \(\varepsilon <(p-q)/2\), this provides an estimate for the first term in the right-hand side of (7.12).
In order to estimate the second term in the right-hand side of (7.12), we let \(x\in B_0\setminus Q^*\) and let \(B\in {\mathcal {B}}_0\) be such that \(x\in B\). We will estimate the term

where \(x_B\) is the center of B. Clearly we may assume that  . By condition (W1), we see that \(\mathrm {diam}(B)\ge C{\text {diam}}(B_0)\) and \(\mu (B)\ge C(c_\mu )\mu (B_0)\). Since \(B\in {\mathcal {B}}_0\), we have \(B\subset B_0\). Thus,
. By condition (W1), we see that \(\mathrm {diam}(B)\ge C{\text {diam}}(B_0)\) and \(\mu (B)\ge C(c_\mu )\mu (B_0)\). Since \(B\in {\mathcal {B}}_0\), we have \(B\subset B_0\). Thus,

By taking supremum over balls B as above, we obtain

for all \(x\in B_0\setminus Q^*\). By integrating, we obtain

By the \((\beta ,p,q)\)-Poincaré inequality and Hölder’s inequality with \(q<p-\varepsilon \), we obtain

On the other hand, since \(Q^*=B(w,4r_Q)\) with \(w\in E_Q\) and \(r_Q=R/128\), we have

This concludes the estimate for the integral in (7.13) over \(B_0\setminus Q^*\).
To estimate the integral over the set \(Q^*\), we fix \(x\in Q^*\). Let \(B\in {\mathcal {B}}_0\) be such that \(x\in B\). If \(B\subset Q^*\), then

Next we consider the case \(B\not \subset Q^*\), and again we need to estimate the quantity

We may assume that  . By condition (W1), we obtain \({\text {diam}}(B)\ge C{\text {diam}}(B_0)\) and \(\mu (B)\ge C(c_\mu )\mu (B_0)\). Hence,
. By condition (W1), we obtain \({\text {diam}}(B)\ge C{\text {diam}}(B_0)\) and \(\mu (B)\ge C(c_\mu )\mu (B_0)\). Hence,

By taking supremum over balls B as above, we obtain

for all \(x\in Q^*\). It follows that

We can now estimate as above, and complete the proof. \(\square \)
The following lemma is variant of [19, Lemma 4.12]. We also refer to [10, Lemma 3.6].
Lemma 7.14
Fix \(x,y\in Q^*\). Then
and
Furthermore, assuming that \(\lambda >0\), then the restriction \(u|_{E_Q\cup (Q^*\setminus U^\lambda )}\) is a \(\beta \)-Hölder function in the set \(E_Q\cup (Q^*\setminus U^\lambda )\) with constant \(\kappa =C(\beta ,c_\mu )\lambda \).
Proof
The property (W4) is used below several times without further notice. Let \(z\in Q^*\) and \(0<r\le 2{\text {diam}}(Q^*)\). Write \(B_i=B(z,2^{-i}r)\in {\mathcal {B}}_0\) for each \(i\in \{0,1,\ldots \}\). Then, with the standard ‘telescoping’ argument, see for instance the proof of [10, Lemma 3.6], we obtain

Fix \(x,y\in Q^*\). Since \(0<d=d(x,y)\le {\text {diam}}(Q^*)\), we obtain

It follows that
which is the desired inequality (7.15).
To prove inequality (7.16), we let \(x\in Q^*\). If \(d(x,E_Q)=0\), then \(x\in E_Q\) and we are done since \(u=0\) in \(E_Q\). Therefore we may assume that \(d(x,E_Q)>0\). Then there exists  such that \(d=d(x,y)<\min \{2d(x,E_Q), {\text {diam}}(Q^*)\}\) and we have
such that \(d=d(x,y)<\min \{2d(x,E_Q), {\text {diam}}(Q^*)\}\) and we have

Inequality (7.16) follows.
Fix \(\lambda >0\). Next, we show that \(u|(E_Q\cup (Q^*\setminus U^\lambda ))\) is \(\beta \)-Hölder with constant \(\kappa =C(\beta ,c_\mu )\lambda \). Let \(x,y\in E_Q\cup (Q^*\setminus U^{\lambda })\). There are four cases to be considered. First, if \(x,y\in E_Q\), then
since \(u=0\) in \(E_Q\). If \(x,y\in Q^*\setminus U^\lambda \), then we apply (7.15) and obtain
Here we also used the fact that \(Q^*\subset B_0\). If \(x\in E_Q\) and \(y\in Q^*\setminus U^\lambda \), we apply (7.16) and get
The last case \(x\in Q^*\setminus U^\lambda \) and \(y\in E_Q\) is treated in similar way. \(\square \)
7.2 Stopping Construction
We continue as in [19] and construct a stopping family \({\mathcal {S}}_\lambda (Q)\) of pairwise disjoint balls whose 5-dilations cover the set \(Q^\lambda \subset Q^*=B(w,4r_Q)\); recall (7.10). Let \(B\in {\mathcal {B}}_{Q}\) be a ball centered at  . The parent ball of B is then defined to be \(\pi (B)=2B\) if \(2B\subset Q^*\) and \(\pi (B)=Q^*\) otherwise. Observe that \(B\subset \pi (B)\in {\mathcal {B}}_Q\) and the center of \(\pi (B)\) satisfies \(x_{\pi (B)} \in \{x_B,w\}\subset E_Q\). It follows that all the balls \(B\subset \pi (B)\subset \pi (\pi (B))\subset \cdots \) are well-defined, belong to \({\mathcal {B}}_Q\) and are centered at \(E_Q\). By inequalities (2.1) and (2.4), and property (W1) if needed, we have \(\mu (\pi (B))\le c_\mu ^5 \mu (B)\) and \({\text {diam}}(\pi (B))\le 16{\text {diam}}(B)\).
. The parent ball of B is then defined to be \(\pi (B)=2B\) if \(2B\subset Q^*\) and \(\pi (B)=Q^*\) otherwise. Observe that \(B\subset \pi (B)\in {\mathcal {B}}_Q\) and the center of \(\pi (B)\) satisfies \(x_{\pi (B)} \in \{x_B,w\}\subset E_Q\). It follows that all the balls \(B\subset \pi (B)\subset \pi (\pi (B))\subset \cdots \) are well-defined, belong to \({\mathcal {B}}_Q\) and are centered at \(E_Q\). By inequalities (2.1) and (2.4), and property (W1) if needed, we have \(\mu (\pi (B))\le c_\mu ^5 \mu (B)\) and \({\text {diam}}(\pi (B))\le 16{\text {diam}}(B)\).
Then, we come to the stopping time argument. We will use as a threshold value the number

Fix a level \(\lambda >\lambda _Q/2\). Fix a point \(x\in Q^\lambda \subset Q^*\). If \(\lambda _Q/2<\lambda <\lambda _Q\), then we choose \(B_x=Q^*\in {\mathcal {B}}_{Q}\). If \(\lambda \ge \lambda _Q\), then by using the condition \(x\in Q^\lambda \) we first choose a starting ball B, with \(x\in B\in {\mathcal {B}}_Q\), such that

Observe that  . We continue by looking at the balls \(B\subset \pi (B) \subset \pi (\pi (B))\subset \cdots \) and we stop at the first among them, denoted by \(B_x\in {\mathcal {B}}_{Q}\), that satisfies the following two stopping conditions:
. We continue by looking at the balls \(B\subset \pi (B) \subset \pi (\pi (B))\subset \cdots \) and we stop at the first among them, denoted by \(B_x\in {\mathcal {B}}_{Q}\), that satisfies the following two stopping conditions:

The inequality \(\lambda \ge \lambda _Q\) in combination with the fact that \(Q^*\subsetneq X\) ensures the existence of such a stopping ball.
In any case, the chosen ball \(B_x\in {\mathcal {B}}_Q\) contains the point x, is centered at \(x_{B_x}\in E_Q\), and satisfies inequalities

By the 5r-covering lemma [1, Lemma 1.7], we obtain a countable disjoint family
of stopping balls such that \(Q^\lambda \subset \bigcup _{B\in {\mathcal {S}}_\lambda (Q)} 5B\). Let us remark that, by the condition (W2) and stopping inequality (7.17), we have \(B\subset U^{\lambda }\) if \(B\in {\mathcal {S}}_\lambda (Q)\) and \(\lambda >\lambda _Q/2\).
7.3 Level Set Estimates
Next, we prove two technical results: Lemmas 7.18 and 7.28. We follow the approach in [19] quite closely, but we give details since technical modifications are required. A counterpart of the following lemma can be found also in [16, Lemma 3.1.2]. Recall that \(k\in {{\mathbb {N}}}\) is a fixed number and \(\alpha =\beta p^2/(2(s+\beta p))>0\) with \(s=\log _2 c_\mu > 0\).
Lemma 7.18
Suppose that \(\lambda >\lambda _Q/2\) and let \(B\in {\mathcal {S}}_\lambda (Q)\) be such that \(\mu (U_{B}^{2^k\lambda }) < \mu (B)/2\). Then
Proof
Fix \(x\in U_{B}^{2^k\lambda }\subset B\) and consider the function \(h:(0,\infty )\rightarrow {{\mathbb {R}}}\),
By Lemma 2.5 and the fact that B is open, we find that \(h:(0,\infty )\rightarrow {{\mathbb {R}}}\) is continuous. Observe that \(U_{B}^{2^k\lambda }=U^{2^k\lambda }\cap B\) is also open. Since \(h(r)=1\) for small values of \(r>0\) and \(h(r)<1/2\) for \(r>{\text {diam}}(B)\), we have \(h(r_x)=1/2\) for some \(0<r_x\le {\text {diam}}(B)\). Write \(B'_x=B(x,r_x)\). Then
and
The 5r-covering lemma [1, Lemma 1.7] gives us a countable disjoint family \({\mathcal {G}}_\lambda \subset \{ B'_x\,:\, x\in U_{B}^{2^k\lambda }\}\) such that \(U_{B}^{2^k\lambda }\subset \bigcup _{B'\in {\mathcal {G}}_\lambda } 5B'\). Then (7.20) and (7.21) hold for every ball \(B'\in {\mathcal {G}}_\lambda \); namely, by denoting \(B'_I=U_{B}^{2^k\lambda }\cap B'\) and \({B'_O}=(B\setminus U^{2^k\lambda })\cap B'\), we have the following comparison identities:
where all the measures are strictly positive. These identities are important and they are used several times throughout the remainder of this proof.
We multiply the left-hand side of (7.19) by \({\text {diam}}(B)^{\beta p}\) and then estimate as follows:
By (2.1) and Lemma 2.6, we find that
for all \(B'\in {\mathcal {G}}_\lambda \). Hence, by the comparison identities (7.22),

This concludes our analysis of the ‘easy term’ in (7.23). To treat the remaining term therein, we do need some preparations.
Let us fix a ball \(B'\in {\mathcal {G}}_\lambda \) that satisfies \(\int _{5B'\cap B} |u-u_{{B'_O}}|^p\,d\mu \not =0\). We claim that

In order to prove this inequality, we fix a number \(m\in {{\mathbb {R}}}\) such that

Let us first consider the case \(m< k/2\). Then \(m-k<-k/2\), and since always \(\alpha <p/2\), the desired inequality (7.26) is obtained case as follows:

Next, we consider the case \(k/2\le m\). Observe from (7.24) and the comparison identities (7.22) that

where the last step follows from condition (W3) and the fact that \(5B'\supset {B'_O}\not =\emptyset \). By taking also (7.27) into account, we see that \(2^{mp}\le 2^{p+1} c_\mu ^6 2^{kp}\). On the other hand, we have

where the last step follows from the fact that \(B\in {\mathcal {S}}_\lambda (Q)\) in combination with inequality (7.17). In particular, if \(s=\log _2 c_\mu \) then by inequality (2.2) and Lemma 2.6, we obtain that

This, in turn, implies that
Combining the above estimates, we see that

That is, inequality (7.26) holds also in the present case \(k/2\le m\). This concludes the proof of inequality (7.26).
Using (7.24) and (7.22) and inequality (7.26), we estimate the second term in (7.23) as follows:

Inequality (7.19) follows by collecting the above estimates. \(\square \)
The following lemma is essential for the proof of Theorem 7.6, and it is the only place in the proof where the capacity density condition is needed. Recall from Lemma 6.6 that this condition implies a local boundary Poincaré inequality, which is used here one single time.
Lemma 7.28
Let \(\lambda >\lambda _Q/2\) and \(g\in {\mathcal {D}}_H^{\beta }(u)\). Then
Proof
By the covering property \(Q^\lambda \subset \bigcup _{B\in {\mathcal {S}}_\lambda (Q)} 5B\) and doubling condition (2.1),
Recall also that \(B\subset U^{\lambda }\) if \(B\in {\mathcal {S}}_\lambda (Q)\). Therefore, and using the fact that \({\mathcal {S}}_\lambda (Q)\) is a disjoint family, it suffices to prove that inequality
holds for every \(B\in {\mathcal {S}}_\lambda (Q)\). To this end, let us fix a ball \(B\in {\mathcal {S}}_\lambda (Q)\).
If \(\mu (U_B^{2^k\lambda })\ge \mu (B)/2\), then
which suffices for the required local estimate (7.30). Let us then consider the more difficult case \(\mu (U_B^{2^k\lambda }) < \mu (B)/2\). In this case, by the stopping inequality (7.17),
By Lemma 7.18 it suffices to estimate the integral over the set \(B\setminus U^{2^k\lambda }=B\setminus U^{2^k\lambda }_B\); observe that the measure of this set is strictly positive. We remark that the local boundary Poincaré inequality in Lemma 6.6 will be used to estimate this integral.
Fix a number \(i\in {{\mathbb {N}}}\). Since \(B\subset Q^*\), it follows from Lemma 7.14 that the restriction \(u|_{E_Q\cup (B\setminus U^{2^i \lambda })}\) is a \(\beta \)-Hölder function with a constant \(\kappa _i=C(\beta ,c_\mu )2^i\lambda \). We can now use the McShane extension (2.7) and extend \(u|_{E_Q\cup (B\setminus U^{2^i \lambda })}\) to a function \(u_{2^i \lambda }:X\rightarrow {{\mathbb {R}}}\) that is \(\beta \)-Hölder with the constant \(\kappa _i\) and satisfies the restriction identity
for all \(x\in E_Q\cup (B\setminus U^{2^i \lambda })\). Observe that \(u_{2^i \lambda }=0\) in \(E_Q\), since \(u=0\) in \(E_Q\).
The crucial idea that was originally used by Keith–Zhong in [16] is to consider the function
We want to apply Lemma 3.3. In order to do so, observe that \(u_{2^i \lambda }|_{X\setminus A}=u|_{X\setminus A}\), where
Therefore, by Lemma 3.3 and properties (D1)–(D2), we obtain that
Observe that \(U^{2^k\lambda }_B\supset U^{2^{(k+1)}\lambda }_B \supset \cdots \supset U^{2^{(2k-1)}\lambda }_B\supset U^{4^{k}\lambda }_B\). Using these inclusions it is straightforward to show that the following pointwise estimates are valid in X,
Observe that \(h\in {\text {Lip}}_\beta (X)\) is zero in \(E_Q\) and h coincides with u on \(B\setminus U^{2^k\lambda }\), and recall that \(g_h\in {\mathcal {D}}_H^{\beta }(h)\). Notice also that \(B\subset Q^*\) and \(x_B\in E_Q\). The local boundary Poincaré inequality in Lemma 6.6 implies that
The desired local inequality (7.30) follows by combining the estimates above. \(\square \)
7.4 Completing Proof of Theorem 7.6
We complete the proof as in [19]. Recall that \(u:X\rightarrow {{\mathbb {R}}}\) is a \(\beta \)-Hölder function with \(u=0\) in \(E_Q\) and that
Let us fix a function \(g\in {\mathcal {D}}_H^{\beta }(u)\). Observe that the left-hand side of inequality (7.7) is finite. Without loss of generality, we may further assume that it is nonzero. By Lemma 7.11,
We have
Since \(Q^\lambda =Q^*=Q^{2\lambda }\) for every \(\lambda \in (0,\lambda _Q/2)\), we find that
On the other hand, by Lemma 7.28, for each \(\lambda >\lambda _Q/2\),
Since \(p-\varepsilon >1\), it follows that
where
We estimate these three terms separately. First,
Second,
Third, by Fubini’s theorem,
Combining the estimates above, we arrive at the desired conclusion. \(\square \)
8 Local Hardy Inequalities
We apply Theorem 7.4 to obtain a local Hardy inequality, see (8.2) in Theorem 8.1. This inequality is then shown to be self-improving, see Theorem 8.4, and in this respect we follow the strategy in [23]. However, we remark that the easier Wannebo approach [31] for establishing local Hardy inequalities as in [23] is not available to us, due to absence of pointwise Leibniz and chain rules in the setting of Hajłasz gradients.
Theorem 8.1
Let X be a geodesic space. Let \(1<p<\infty \) and \(0<\beta \le 1\). Let \(E\subset X\) be a closed set which satisfies the \((\beta ,p)\)-capacity density condition with a constant \(c_0\). Let \(B_0=B(w,R)\) be a ball with \(w\in E\) and \(R<{\text {diam}}(E)\). Let \(E_Q\) be the truncation of E to the Whitney-type ball Q as in Sect. 6. Then, there exists a constant \(C=C(\beta ,p,c_\mu ,c_0)\) such that
holds whenever \(u\in \mathrm {Lip}_\beta (X)\) is such that \(u=0\) in \(E_Q\) and \(g\in {\mathcal {D}}_H^{\beta }(u)\).
Proof
Let \(u\in \mathrm {Lip}_\beta (X)\) be such that \(u=0\) in \(E_Q\) and let \(g\in {\mathcal {D}}_H^{\beta }(u)\). Lemma 7.14 implies that
for all \(x\in Q^*\). Therefore
By Theorem 7.4, we obtain
It remains to bound the integral over \(B(w,R) \setminus Q^*\). Since  and \(Q^*=4Q\), we have \(d(x,E_Q)\ge 3r_Q>R/64\) for all \(x\in B(w,R)\setminus Q^*\). Thus, we obtain
and \(Q^*=4Q\), we have \(d(x,E_Q)\ge 3r_Q>R/64\) for all \(x\in B(w,R)\setminus Q^*\). Thus, we obtain
By the \((\beta ,p,p)\)-Poincaré inequality in Lemma 3.7,
For the second term, we have

For the third term, we have \(d(x,E_Q)\le d(x,w)< 4r_Q<R\) for every \(x\in Q^*\). Thus
Applying inequality (8.3), we get
The desired inequality follows by combining the estimates above. \(\square \)
Next, we improve the local Hardy inequality in Theorem 8.1. This is done by adapting the Koskela–Zhong truncation argument from [21] to the setting of Hajłasz gradients; see also [23] and [18, Theorem 7.32] whose proof we modify to our purposes.
Theorem 8.4
Let X be a geodesic space. Let \(1<p<\infty \) and \(0<\beta \le 1\). Let \(E\subset X\) be a closed set which satisfies the \((\beta ,p)\)-capacity density condition with a constant \(c_0\). Let \(B_0=B(w,R)\) be a ball with \(w\in E\) and \(R<{\text {diam}}(E)\). Let \(E_Q\) be the truncation of E to the Whitney-type ball Q as in Sect. 6, and let \(C_1=C_1(\beta ,p,c_\mu ,c_0)\) be the constant in (8.2), see Theorem 8.1. Then there exist \(0< \varepsilon =\varepsilon (p,C_1)<p-1\) and \(C= C(p,C_1)\) such that inequality
holds whenever \(u\in \mathrm {Lip}_\beta (X)\) is such that \(u=0\) in \(E_Q\) and \(g\in {\mathcal {D}}_H^{\beta }(u)\).
Proof
Without loss of generality, we may assume that \(C_1\ge 1\) in (8.2). Let \(u\in \mathrm {Lip}_\beta (X)\) be such that \(u=0\) in \(E_Q\) and let \(g\in {\mathcal {D}}_H^{\beta }(u)\). Let \(\kappa \ge 0\) be the \(\beta \)-Hölder constant of u in X. By redefining \(g=\kappa \) in the exceptional set \(N=N(g)\) of measure zero, we may assume that (3.2) holds for all \(x,y\in X\). Let \(\lambda >0\) and define \(F_\lambda = G_\lambda \cap H_\lambda \), where
and
We show that the restriction of u to \(F_\lambda \cup E_Q\) is a \(\beta \)-Hölder function with a constant \(2\lambda \). Assume that \(x,y\in F_\lambda \). Then (3.2) implies
On the other hand, if \(x\in F_\lambda \) and \(y\in E_Q\), then
The case \(x\in E_Q\) and \(y\in F_\lambda \) is treated in the same way. If \(x,y\in E_Q\), then \(|u(x)-u(y)|=0\). All in all, we see that u is a \(\beta \)-Hölder function in \(F_\lambda \cup E_Q\) with a constant \(2\lambda \).
We apply the McShane extension 2.7 and extend the restriction \(u\vert _{F_\lambda \cup E_Q}\) to a \(\beta \)-Hölder function function v in X with constant \(2\lambda \). Then \(v=u=0\) in \(E_Q\) and \(v=u\) in \(F_\lambda \), thus
by Lemma 3.3.
By applying Theorem 8.1 to the function v and its Hajłasz \(\beta \)-gradient \(g_v\), we obtain
Since \(H_\lambda =F_\lambda \cup (H_\lambda \setminus G_\lambda )\) and \(C_1\ge 1\), it follows that
Here, \(\lambda >0\) was arbitrary, and thus we conclude that (8.6) holds for every \(\lambda >0\).
Next, we multiply (8.6) by \(\lambda ^{-1-\varepsilon }\), where \(0<\varepsilon <p-1\), and integrate with respect to \(\lambda \) over the set \((0,\infty )\). With a change of the order of integration on the left-hand side, this gives
By the definition of \(G_\lambda \), we find that the first term on the right-hand side is dominated by
Using the definitions of \(H_\lambda \) and \(G_\lambda \), the second term on the right-hand side can be estimated from above by
By combining the estimates above, we obtain
where \(C_2 = C_1 2^{p+1} \frac{\varepsilon }{p-\varepsilon }\) and \(C_3 = C_1\bigl (1+2^{p+1}\frac{\varepsilon }{p-\varepsilon }\bigr )\). We choose \(0<\varepsilon =\varepsilon (C_1,p)<p-1\) so small that
This allows us to absorb the first term in the right-hand side of (8.7) to the left-hand side. Observe that this term is finite, since u is \(\beta \)-Hölder in X and \(u=0\) in \(E_Q\). \(\square \)
9 Self-improvement of the Capacity Density Condition
As an application of Theorem 8.4, we strengthen Theorem 5.8 in complete geodesic spaces. This leads to the conclusion that the Hajłasz capacity density condition is self-improving or doubly open-ended in such spaces. In fact, we characterize the Hajłasz capacity density condition in various geometrical and analytical quantities, the latter of which are all shown to be doubly open-ended.
Theorem 9.1
Let X be a geodesic space. Let \(1<p<\infty \) and \(0<\beta \le 1\). Let \(E\subset X\) be a closed set which satisfies the \((\beta ,p)\)-capacity density condition with a constant \(c_0\). Then there exists \(\varepsilon >0\), depending on \(\beta \), p, \(c_\mu \) and \(c_0\), such that \({{\,\mathrm{\overline{co\,dim}_A}\,}}(E)\le \beta (p-\varepsilon )\).
Proof
Let \(w\in E\) and \(0<r<R<{\text {diam}}(E)\). Let \(E_Q\) be the truncation of E to the ball \(Q\subset B_0=B(w,R)\) as in Section 6. Let \(\varepsilon >0\) be as in Theorem 8.4. Observe that
Hence, it suffices to show that
where the constant c is independent of w, r and R.
If \(r\ge R/4\), then the claim is clear since \(\bigl (\frac{r}{R}\bigr )^{\beta (p-\varepsilon )}\le 1\) and
The claim is clear also if \(\mu (E_{Q,r}\cap B(w,R))\ge \frac{1}{2} \mu (B(w,R))\). Thus we may assume that \(r<R/4\) and that \(\mu (E_{Q,r}\cap B(w,R)) < \tfrac{1}{2} \mu (B(w,R))\), whence
Let us now consider the \(\beta \)-Hölder function \(u:X\rightarrow {{\mathbb {R}}}\),
Then \(u=0\) in \(E_Q\), \(u=1\) in \(X\setminus E_{Q,r}\), and
We aim to apply Theorem 8.4. Recall also that \(w\in E_Q\). Thus we obtain
where the last step follows from (9.3).
Since \(u=1\) in \(X\setminus E_{Q,r}\) and u is a \(\beta \)-Hölder function with a constant \(r^{-\beta }\), Lemma 3.3 implies that \(g=r^{-\beta }{\mathbf {1}}_{E_{Q,r}}\in {\mathcal {D}}_H^{\beta }(u)\). Observe that
Hence, the claim (9.2) follows from (9.4) and Theorem 8.4. \(\square \)
The following theorem is a compilation of the results in this paper. It states the equivalence of some geometrical conditions (1)–(2) and analytical conditions (3)–(6), one of which is the capacity density condition. We emphasize that the capacity density condition (3) is characterized in terms of the upper Assouad codimension (1); in fact, this characterization follows immediately from Theorem 5.7 and Theorem 9.1.
Theorem 9.5
Let X be a complete geodesic space. Let \(1<p<\infty \) and \(0<\beta \le 1\). Let \(E\subset X\) be a closed set. Then the following conditions are equivalent:
-
(1)
\({{\,\mathrm{\overline{co\,dim}_A}\,}}(E)<\beta p\).
-
(2)
E satisfies the Hausdorff content density condition (5.4) for some \(0<q<\beta p\).
-
(3)
E satisfies the \((\beta ,p)\)-capacity density condition.
-
(4)
E satisfies the local \((\beta ,p,p)\)-boundary Poincaré inequality (6.7).
-
(5)
E satisfies the maximal \((\beta ,p,p)\)-boundary Poincaré inequality (7.5).
-
(6)
E satisfies the local \((\beta ,p,p)\)-Hardy inequality (8.2).
Proof
The implication from (1) to (2) is a consequence of Lemma 5.3 with \({{\,\mathrm{\overline{co\,dim}_A}\,}}(E)<q<\beta p\). The implication from (2) to (3) follows by adapting the proof of Theorem 5.7 with \(\eta =q/\beta \). The implication from (3) to (4) follows from Theorem 6.6. The implication from (4) to (5) follows from the proof of Theorem 7.4, which remains valid if we assume (4) instead of the \((\beta ,p)\)-capacity density condition. The implication from (5) to (6) follows from the proof of Theorem 8.1. Finally, condition (6) implies the improved local Hardy inequality (8.5) and the proof of Theorem 9.1 then shows the remaining implication from (6) to (1). \(\square \)
Finally, we state the main result of this paper, Theorem 9.6. It is the self-improvement or double open-endedness property of the \((\beta ,p)\)-capacity density condition. Namely, in addition to integrability exponent p, also the order \(\beta \) of fractional differentiability can be lowered. A similar phenomenon is observed in [24] for Riesz capacities in \({{\mathbb {R}}}^n\).
Theorem 9.6
Let X be a complete geodesic space, and let \(1<p<\infty \) and \(0<\beta \le 1\). Assume that a closed set \(E\subset X\) satisfies the \((\beta ,p)\)-capacity density condition. Then there exists \(0<\delta <\min \{\beta ,p-1\}\) such that E satisfies the \((\gamma ,q)\)-capacity density condition for all \(\beta -\delta <\gamma \le 1\) and \(p-\delta<q<\infty \).
Proof
We have \({{\,\mathrm{\overline{co\,dim}_A}\,}}(E)< \beta p\) by Theorem 9.5. Since \(\lim _{\delta \rightarrow 0}(\beta -\delta )(p-\delta )=\beta p\), there exists \(0<\delta <\min \{\beta ,p-1\}\) such that \({{\,\mathrm{\overline{co\,dim}_A}\,}}(E)<(\beta -\delta )(p-\delta )\). Now if \(\beta -\delta <\gamma \le 1\) and \(p-\delta<q<\infty \), then
The claim follows from Theorem 9.5. \(\square \)
A similar argument shows that the analytical conditions (4)–(6) in Theorem 9.5 are also doubly open ended. The geometrical conditions (1)–(2) are open-ended by definition.
References
Björn, A., Björn, J.: Nonlinear Potential Theory on Metric Spaces, Volume 17 of EMS Tracts in Mathematics. European Mathematical Society (EMS), Zürich (2011)
Björn, J., MacManus, P., Shanmugalingam, N.: Fat sets and pointwise boundary estimates for \(p\)-harmonic functions in metric spaces. J. Anal. Math. 85, 339–369 (2001)
Björn, J., Buckley, S.M., Keith, S.: Admissible measures in one dimension. Proc. Am. Math. Soc. 134(3), 703–705 (2006)
Dyda, B., Lehrbäck, J., Vähäkangas, A.V.: Fractional Poincaré and localized Hardy inequalities on metric spaces. Adv. Calc. Var. (2022). https://doi.org/10.1515/acv-2021-0069
Eriksson-Bique, S., Vähäkangas, A.V.: Self-improvement of pointwise Hardy inequality. Trans. Am. Math. Soc. 372(3), 2235–2250 (2019)
Eriksson-Bique, S., Lehrbäck, J., Vähäkangas, A.V.: Self-improvement of weighted pointwise inequalities on open sets. J. Funct. Anal. 279(7), 108691 (2020)
Gogatishvili, A., Koskela, P., Zhou, Y.: Characterizations of Besov and Triebel-Lizorkin spaces on metric measure spaces. Forum Math. 25(4), 787–819 (2013)
Golshtein, V., Troyanov, M.: Axiomatic theory of Sobolev spaces. Expo. Math. 19(4), 289–336 (2001)
Hajłasz, P.: Sobolev spaces on an arbitrary metric space. Potential Anal. 5(4), 403–415 (1996)
Hajłasz, P., Kinnunen, J.: Hölder quasicontinuity of Sobolev functions on metric spaces. Rev. Mat. Iberoamericana 14(3), 601–622 (1998)
Hajłasz, P., Koskela, P.: Sobolev meets Poincaré. C. R. Acad. Sci. Paris Sér. I Math. 320(10), 1211–1215 (1995)
Heinonen, J.: Lectures on Analysis on Metric Spaces. Universitext. Springer, New York (2001)
Heinonen, J., Koskela, P.: Quasiconformal maps in metric spaces with controlled geometry. Acta Math. 181(1), 1–61 (1998)
Heinonen, J., Koskela, P., Shanmugalingam, N., Tyson, J.T.: Sobolev Spaces on Metric Measure Spaces. An Approach Based on Upper Gradients, volume 27 of New Mathematical Monographs. Cambridge University Press, Cambridge (2015)
Käenmäki, A., Lehrbäck, J., Vuorinen, M.: Dimensions, Whitney covers, and tubular neighborhoods. Indiana Univ. Math. J. 62(6), 1861–1889 (2013)
Keith, S., Zhong, X.: The Poincaré inequality is an open ended condition. Ann. Math. (2) 167(2), 575–599 (2008)
Kilpeläinen, T., Kinnunen, J., Martio, O.: Sobolev spaces with zero boundary values on metric spaces. Potential Anal. 12(3), 233–247 (2000)
Kinnunen, J., Lehrbäck, J., Vähäkangas, A.: Maximal Function Methods for Sobolev Spaces, volume 257 of Mathematical Surveys and Monographs. American Mathematical Society (2021)
Kinnunen, J., Lehrbäck, J., Vähäkangas, A.V., Zhong, X.: Maximal function estimates and self-improvement results for Poincaré inequalities. Manuscripta Math. 158(1–2), 119–147 (2019)
Korte, R., Lehrbäck, J., Tuominen, H.: The equivalence between pointwise Hardy inequalities and uniform fatness. Math. Ann. 351(3), 711–731 (2011)
Koskela, P., Zhong, X.: Hardy’s inequality and the boundary size. Proc. Am. Math. Soc. 131(4), 1151–1158 (2003)
Lehrbäck, J.: Hardy inequalities and Assouad dimensions. J. Anal. Math. 131, 367–398 (2017)
Lehrbäck, J., Tuominen, H., Vähäkangas, A.V.: Self-improvement of uniform fatness revisited. Math. Ann. 368(3–4), 1439–1464 (2017)
Lewis, J.L.: Uniformly fat sets. Trans. Am. Math. Soc. 308(1), 177–196 (1988)
Mazya, V.G.: Sobolev Spaces. Springer Series in Soviet Mathematics. Springer, Berlin (1985). (Translated from the Russian by T. O. Shaposhnikova)
Mazya, V.G.: Sobolev spaces with applications to elliptic partial differential equations, volume 342 of Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], agumented Springer, Heidelberg (2011)
McShane, E.J.: Extension of range of functions. Bull. Am. Math. Soc. 40(12), 837–842 (1934)
Mikkonen, P.: On the Wolff potential and quasilinear elliptic equations involving measures. Ann. Acad. Sci. Fenn. Math. Diss. 104, 71 (1996)
Shanmugalingam, N., Yang, D., Yuan, W.: Newton–Besov spaces and Newton–Triebel–Lizorkin spaces on metric measure spaces. Positivity 19(2), 177–220 (2015)
Troyano, M., Goldshtein, V.: An integral characterization of Hajłasz–Sobolev space. C. R. Acad. Sci. Paris Sér. I Math. 333(5), 445–450 (2001)
Wannebo, A.: Hardy inequalities. Proc. Am. Math. Soc. 109(1), 85–95 (1990)
Yang, D.: New characterizations of Hajłasz–Sobolev spaces on metric spaces. Sci. China Ser. A 46(5), 675–689 (2003)
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
J.C. is supported by supported by the Ministerio de Economía y Competitividad (Spain) through Grant Nos. PID2020-113156GB-I00 and SEV-2017-0718, and by Basque Government through Grant Nos. IT-641-13 and BERC 2018-2021 and “Ayuda para la formación de personal investigador no doctor". The authors are grateful to the referees for their comments and suggestions for improving the manuscript.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Canto, J., Vähäkangas, A.V. The Hajłasz Capacity Density Condition is Self-improving. J Geom Anal 32, 276 (2022). https://doi.org/10.1007/s12220-022-00979-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12220-022-00979-z



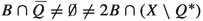 , then
, then