Sampling the Flow of a Bandlimited Function

Abstract

We analyze the problem of reconstruction of a bandlimited function f from the space–time samples of its states $f_t=\phi _t*f$ resulting from the convolution with a kernel $\phi _t$. It is well-known that, in natural phenomena, uniform space–time samples of f are not sufficient to reconstruct f in a stable way. To enable stable reconstruction, a space–time sampling with periodic nonuniformly spaced samples must be used as was shown by Lu and Vetterli. We show that the stability of reconstruction, as measured by a condition number, controls the maximal gap between the spacial samples. We provide a quantitative statement of this result. In addition, instead of irregular space–time samples, we show that uniform dynamical samples at sub-Nyquist spatial rate allow one to stably reconstruct the function $\widehat{f}$ away from certain, explicitly described blind spots. We also consider several classes of finite dimensional subsets of bandlimited functions in which the stable reconstruction is possible, even inside the blind spots. We obtain quantitative estimates for it using Remez-Turán type inequalities. En route, we obtain Remez-Turán inequality for prolate spheroidal wave functions. To illustrate our results, we present some numerics and explicit estimates for the heat flow problem.

Introduction

In this paper, we consider the sampling and reconstruction problem of signals $u = u(t,x)$ that arise as an evolution of an initial signal $f = f(x)$ under the action of convolution operators. The initial signal f is assumed to be in the Paley-Wiener space $PW_c$, $c>0$ (fixed throughout this paper) given by

$$\begin{aligned} PW_{c} := \left\{ f \in L^2({\mathbb {R}}):{\text {supp}}(\widehat{f}) \subseteq [-c,c]\right\} \end{aligned}$$

with the Fourier transform normalized as $\widehat{f}(\xi )=\int _{{\mathbb {R}}}f(t)e^{- it\xi }\,\mathrm {d}t$.

The functions u are solutions of initial value problems stemming from a physical system. Thus, due to the semigroup properties of such solutions, there is a family of kernels $\{\phi _t: t> 0\}$ such that $u(t,x)=\phi _t*f(x)$, $\phi _{t+s}=\phi _t*\phi _s$ for all $t,s\in (0,\infty )$, and $f= \lim \limits _{t\rightarrow 0+}\phi _t*f$, $f\in L^2({{\mathbb {R}}})$.

As we are primarily interested in physical systems, we typically consider the following set of kernels:

$$\begin{aligned} \Phi _c= \{ \phi \in L^1({\mathbb {R}}): \text{ there } \text{ exists } \kappa _\phi >0\;\text{ such } \text{ that } \kappa _\phi \le \widehat{\phi }(\xi ) \le 1 \text { for } |\xi |\le c, \widehat{\phi }(0)=1 \}. \end{aligned}$$

(1.1)

Observe that $\phi \in L^1$ implies that ${\widehat{\phi }}$ is continuous and, therefore, the existence of $\kappa _\phi > 0$ such that $\widehat{\phi }\ge \kappa _\phi$ on $[-c,c]$ is equivalent to $\widehat{\phi }>0$ on $[-c,c]$. We remark that some of our results hold for a less restrictive class of kernels.

Example 1.1

A prototypical example is the diffusion process with ${\widehat{\phi }}_t(\xi ) = e^{-t\sigma ^2\xi ^2}$, $t>0$ It corresponds to the initial value problem (IVP) for the heat equation (with a diffusion parameter $\sigma \not =0$)

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t u(x,t)=\sigma ^2\partial _x^2u(x,t)&{}\text{ for } x\in {\mathbb {R}} \text{ and } t>0\\ u(x,0)=f(x)&{} \end{array}\right. }, \end{aligned}$$

(1.2)

for which the solution is given by $u(x,t)=(\phi _t*f)(x)$.

Other examples include the IVP for the fractional diffusion equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t u(x,t)=(\partial _x^2)^{\alpha /2} u(x,t)&{}\text{ for } x\in {{\mathbb {R}}} \text{ and } t>0\\ u(x,0)=f(x),&{} 0<\alpha \le 1, \end{array}\right. } \end{aligned}$$

for which the solution is given by $u(x,t)=(\phi _t*f)(x)$ with ${\widehat{\phi }}_t(\xi ) = e^{-t|\xi |^\alpha }$, and the IVP for the Laplace equation in the upper half plane

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta u(x,y)=0&{}\text{ for } x\in {{\mathbb {R}}} \text{ and } y>0\\ u(x,0)=f(x)&{} \end{array}\right. }, \end{aligned}$$

for which the solution is given by $u(x,y)=(\phi _y*f)(x)$ with ${\widehat{\phi }}_y(\xi ) := e^{-y|\xi |}$.

The following problem serves as a motivation for this paper.

Problem 1

Let $\phi \in \Phi$, $L>0$, and $\Lambda \subset {{\mathbb {R}}}$ be a discrete subset of ${{\mathbb {R}}}$. What are the conditions that allow one to recover a function $f \in PW_c$ in a stable way from the data set

$$\begin{aligned} \{(f*\phi _t)(\lambda ): \lambda \in \Lambda , 0 \le t \le L\}? \end{aligned}$$

(1.3)

The set of measurements (1.3) is the image of an operator ${\mathcal {T}}:PW_c\rightarrow L^2\big (\Lambda \times [0,L]\big )$. Thus, the stable recovery of f from (1.3) amounts to finding conditions on $\Lambda , \phi$ and L such that ${\mathcal {T}}$ has a bounded inverse from ${\mathcal {T}}(PW_c)$ to $PW_c$ or, equivalently, the existence of $A,B>0$ such that

$$\begin{aligned} A \Vert f\Vert _2^2 \le \int _0^L \sum _{\lambda \in \Lambda } \left| (f*\phi _t)(\lambda ) \right| ^2 dt \le B \Vert f\Vert _2^2, \text { for all } f \in PW_c. \end{aligned}$$

(1.4)

If for a given $\phi$ and L the frame condition (1.4) is satisfied, we say that $\Lambda =\Lambda _{\phi ,L}$ is a stable sampling set.

Remark 1.2

It was shown in [5, Theorem 5.5] that $\Lambda _{\phi ,L}$ is a stable sampling set

for some $L>0$, if and only if $\Lambda _{\phi ,1}$ is a stable sampling set.

Thus, for qualitative results, we will only consider the case of $L=1$. For quantitative results, however, we may keep L in order to estimate the optimal time length of measurements.

Remark 1.3

Whenever (1.4) holds, standard frame methods can be used for the stable reconstruction of f [11].

Let us discuss Problem 1 in more detail in the case of our prototypical example.

Sampling the Heat Flow

Consider the problem of sampling the temperature in a heat diffusion process initiated by a bandlimited function $f \in PW_c$:

$$\begin{aligned} f_t := f * \phi _t, \qquad 0 \le t \le 1, \end{aligned}$$

where $\phi _t$ is the heat kernel at time t:

$$\begin{aligned} \widehat{\phi _t}(\xi ) = e^{-t\sigma ^2\xi ^2}, \end{aligned}$$

(1.5)

with a parameter $\sigma \not =0$. According to Shannon’s sampling theorem, f can be stably reconstructed from equispaced samples $\{f(k/T): k \in {\mathbb {Z}}\}$ if and only if the sampling rate T is bigger than or equal to the critical value $T =\displaystyle \frac{c}{\pi }$, known as the Nyquist rate. The Nyquist bound is universal in the sense that it also applies to irregular sampling patterns: if a bandlimited function can be stably reconstructed from its samples at $\Lambda \subseteq {\mathbb {R}}$, then the lower Beurling density

$$\begin{aligned} D^-(\Lambda ):=\liminf _{r\rightarrow \infty }\inf _{x\in {\mathbb {R}}}\frac{\#(\Lambda \bigcap [x-r,x+r])}{2r} \end{aligned}$$

satisfies $D^{-}(\Lambda ) \ge \displaystyle \frac{c}{\pi }$. Recall that the upper Beurling density is defined by

$$\begin{aligned} D^+(\Lambda ):=\limsup _{r\rightarrow \infty }\sup _{x\in {\mathbb {R}}}\frac{\#(\Lambda \bigcap [x-r,x+r])}{2r}. \end{aligned}$$

We are interested to know if the spatial sampling rate can be reduced by using the information provided by the following spatio-temporal samples:

$$\begin{aligned} \{f_t(k/T): k \in {\mathbb {Z}}, 0 \le t \le 1\}. \end{aligned}$$

(1.6)

Observe that the amount of collected data in (1.6) is not smaller than that in the case of sampling at the Nyquist rate $T=\displaystyle \frac{c}{\pi }$. If $T <\displaystyle \frac{c}{\pi }$, however, the density of sensors is smaller, and thus such a sampling procedure may provide considerable cost savings.

Lu and Vetterli showed [16] that for all $T < \displaystyle \frac{c}{\pi }$ there exist bandlimited signals with norm 1 that almost vanish on the samples (1.6), i.e. stable reconstruction is impossible from (1.6). As a remedy, they introduced periodic, nonuniform sampling patterns $\Lambda \subseteq {\mathbb {R}}$ that do lead to a meaningful spatio-temporal trade-off: there exist sets $\Lambda \subseteq {\mathbb {R}}$ that have sub-Nyquist density and, yet, lead to the frame inequality:

$$\begin{aligned} A \Vert f\Vert _2^2 \le \int _0^1 \sum _{\lambda \in \Lambda } \left| (f_t)(\lambda ) \right| ^2 \mathrm {d}t \le B \Vert f\Vert _2^2, \text { for all } f \in PW_c, \end{aligned}$$

(1.7)

with $A,B>0$; see Example 4.1 for a concrete construction. The emerging field of dynamical sampling investigates such phenomena in great generality (see, e.g., [1,2,3,4,5]).

As follows from Example 4.1, the estimates (1.7) may hold with an arbitrary small sensor density. The meaningful trade-off between spatial and temporal resolution, however, is limited by the desired numerical accuracy. For example, in the following theorem we relate the maximal gap of a stable sampling set to the bounds from (1.7).

Theorem 1.4

Let $\Lambda \subseteq {\mathbb {R}}$ be such that (1.7) holds. Then there exists an absolute constant $K>0$ such that, for $\displaystyle R\ge K\max \left( \frac{B}{A},\frac{1}{c}\right)$ and every $a\in {\mathbb {R}}$, we have $[a-R,a+R]\cap \Lambda \ne \emptyset$. In particular, we have $D^-(\Lambda )\ge K^{-1}\min \left( \frac{A}{B},c\right)$ and $D^+(\Lambda )\le KB$.

Theorem 4.4, which is a more general version of the above result, provides a more explicit dependence of K on the parameters of the problem.

Besides the constraints implied by Theorem 1.4, the special sampling configurations of Lu and Vetterli that lead to (1.7) lack the simplicity of regular sampling patterns. In this article, we explore a different solution to the diffusion sampling problem. We consider sub-Nyquist equispaced spatial sampling patterns (1.6) with $T=\displaystyle \frac{c}{m\pi }$, $m \in \mathbb {N}$, and restrict the sampling/reconstruction problem to a subset $V \subseteq PW_c$, aiming for an inequality of the form:

$$\begin{aligned} A\Vert f\Vert _2^2 \le \int _0^1 \sum _{k\in {\mathbb {Z}}}\left| f_t\left( \frac{m\pi }{c}k\right) \right| ^2\,\mathrm {d}t \le B\Vert f\Vert _2^2, \qquad f \in V. \end{aligned}$$

(1.8)

Specifically, we consider the following signal models.

Away from blind spots. We will identify a set E with measure arbitrarily close to 1 such that (1.8) holds with $V=V_E=\{f\in PW_c: {\text {supp}}\widehat{f} \subseteq E\}$. In effect, E is the set $[-c,c]\setminus {\mathcal {O}}$ where ${\mathcal {O}}$ is a small open neighborhood of a finite set, i.e., E avoids a certain number of “blind spots.”

Theorem 1.5

Let $\phi \in \Phi$ and $m\ge 2$ be an integer. Then for any $r>0$ there exists a certain compact set $E\subseteq [-c,c]$ of measure at least $2c-r$ such that any $f\in V_E$ can be recovered from the samples

$$\begin{aligned} {\mathcal {M}} =\left\{ f_t\left( \frac{m \pi }{c}k\right) : k \in {\mathbb {Z}}, 0 \le t \le 1\right\} \end{aligned}$$

in a stable way.

The set E in the above theorem depends only on $\phi$ and the choice of r. The stable recovery in this case means that (1.8) holds with $B=1$ and some $A > 0$ which is estimated in a more explicit version of the above result, Theorem 2.8.

Prolate spheroidal wave functions. The Prolate Spheroidal Wave Functions (PSWFs) are eigenfunctions of an integral operator known as the time-band liminting operator or sinc-kernel operator

$$\begin{aligned} {\mathcal {Q}}_cf(x)=\int _{-1}^1\frac{\sin \pi c(y-x)}{\pi (y-x)}f(y)\,\text{ d }y. \end{aligned}$$

Using the min-max theorem, we get that $\psi _{n,c}$ is the norm-one solution of the following extremal problem

$$\begin{aligned} \max \left\{ \frac{\Vert f\Vert _{L^2(-1,1)}}{\Vert f\Vert _{L^2({{\mathbb {R}}})}}\,: f\in PW_c,\ f\in {\text {span}}\{\psi _{k,c}:\ k<n\}^\perp \right\} \end{aligned}$$

where the condition $f\in {\text {span}}\{\psi _{k,c}:\ k<n\}^\perp$ is void for $n=0$. The family $(\psi _{n,c})_{n\ge 0}$ forms an orthogonal basis for $PW_c$ and has the property to form an orthonormal sequence in $L^2(-1,1)$.

We consider the N-dimensional space

$$\begin{aligned} V_N=\text{ span }\{\psi ^c_0,\ldots ,\psi ^c_N\}\subset PW_c. \end{aligned}$$

(1.9)

The Landau-Pollak-Slepian theory shows that this subspace provides an optimal approximation of a bandlimited function that is concentrated on $[-1,1]$. More precisely, $V=V_N$ minimizes the approximation error

$$\begin{aligned} \sup _{{\mathop {\Vert f\Vert _2=1}\limits ^{f \in PW_c}}} \inf _{g \in V} \int _{-1}^{1} \left| f(x)-g(x) \right| ^2\, \text{ d }x, \end{aligned}$$

among all N-dimensional subspaces of $PW_c$.

Sparse sinc translates with free nodes. In this model, we let

$$\begin{aligned} V_N =\left\{ \sum _{n=1}^N c_n{\text {sinc}}c(x-\lambda _n)\,: c_1,\ldots ,c_N\in {\mathbb {C}},\ \lambda _1,\ldots ,\lambda _N\in {{\mathbb {R}}}\right\} \end{aligned}$$

(1.10)

be the class of linear combinations of N arbitrary translates of the sinc kernel ${\text {sinc}}(x)=\frac{\sin x}{ x}$ Note that $V_N$ is not a linear space. However, $V_N - V_N \subseteq V_{2N}$. Therefore, (1.8) with $V=V_{2N}$ implies

$$\begin{aligned} A\Vert f-g\Vert _2^2 \le \int _0^1 \sum _{k\in {\mathbb {Z}}}\left| f_t\left( \frac{m\pi }{c}k\right) -g_t\left( \frac{m\pi }{c}k\right) \right| ^2\,\mathrm {d}t \le B\Vert f-g\Vert _2^2, \qquad f,g \in V_N, \end{aligned}$$

which ensures the numerical stability of the sampling problem $f \mapsto \{f_t(m\pi k/c): k \in {\mathbb {Z}}: 0 \le t \le 1 \}$ restricted non-linearly to the class $V_N$. In other words, if (1.8) holds with $V=V_{2N}$ then any $f\in V_N$ can be stably reconstructed from the samples (1.6).

Fourier polynomials. As our last model, we consider the Fourier image of the space of polynomials of degree at most N restricted to the unit interval. Explicitly,

$$\begin{aligned} V_N =\left\{ \sum _{n=0}^N c_n D^n{\text {sinc}}c\cdot : c_0,\ldots ,c_N\in {\mathbb {C}}\right\} , \end{aligned}$$

(1.11)

where $D: PW_c \rightarrow PW_c$ is the differential operator $Df = f^\prime$. Observe that the union of such $V_N$, $N\in {\mathbb {N}}$, is dense in $PW_c$.

In this article, we show that each of the above-mentioned signal models regularizes the diffusion sampling problem, albeit with possibly very large condition numbers.

Theorem 1.6

Let $m \ge 2$ be an integer, $\Phi$ be given by $\widehat{\Phi }(\xi )=e^{-\sigma ^2\xi ^2}$. Let $V=V_N$ be given by (1.9), (1.10), or (1.11). Then (1.8) holds with

$$\begin{aligned} A =\frac{c\kappa _0(c)}{(\sigma c)^2+m} \exp \Bigl (-\kappa _1(c)N-m^2\bigl (-\kappa _2(c)\ln \sigma +\kappa _3(c)\sigma ^2+\ln m\bigr )\Bigr ) , \qquad B=1, \end{aligned}$$

where the $\kappa _j$’s are positive constants that depend on c only.

We provide a more precise expression for the lower frame constant in Theorem 3.5. Note that the lower bound deteriorates when $\sigma ^2 \rightarrow 0$ (no diffusion) and $\sigma ^2 \rightarrow +\infty$ (very rapid diffusion). This agrees with the intuition and numerical experiments for (non-bandlimited) sparse initial conditions presented in [20]: if $\sigma ^2$ is very small, because of spatial undersampling, some components of f may be hidden from the sensors, while for large $\sigma ^2$ the diffusion completely blurs out the signal and no information can be extracted.

Remark 1.7

To simplify the discussion we take $c=1/2$ in this remark. There are instances when Theorem 1.6 applies for a signal $f\in V_N$ which cannot be recovered simply from its samples on, say, $2{{\mathbb {Z}}}$. As an example, we offer $V_1$ given by (1.10) with $\lambda _1 = 1$. The samples at time $t=0$ are not sufficient to identify each signal since ${\text {sinc}}(\cdot -1)\in V_N$ vanishes on $m {\mathbb {Z}}$, $m\ge 2$. Similarly, for Theorem 1.5: the function $\sin (\omega \cdot ) {\text {sinc}}(\frac{\cdot }{a})$, with an appropriately chosen a and $\omega$, belongs to $V_E$ and vanishes on $m{{\mathbb {Z}}}$ for $m\ge 2$. In finite dimensional subspaces $V_N$, e.g., given by (1.9) and (1.11), sampling at time $t=0$ with any $m \in {\mathbb {N}}$ may be sufficient for stable recovery. However, the expected error of reconstruction in the presence of noise will be reduced if temporal samples are used in addition to those at $t=0$. Theorems 1.5 and 1.6 can be used together. For example, a function f can be reconstructed away from the blind spots using Theorem 1.5 and approximated around the blind spots using Theorem 1.6.

Technical Overview

Lu and Vetterli explain the impossibility of subsampling the heat-flow of a bandlimited function on a grid (1.6) as follows [16]. The function with Fourier transform

$$\begin{aligned} \widehat{f} := \delta _{-T} - \delta _{T} \end{aligned}$$

is formally bandlimited to $I =[-c,c]$ if $T<c$, and vanishes on the lattice $\tfrac{\pi }{T} {\mathbb {Z}}$. Moreover, f is an eigenfunction of the diffusion operator since

$$\begin{aligned} \widehat{f}_t = e^{-t\sigma ^2(-T)^2} \delta _{-T} - e^{-t\sigma ^2T^2} \delta _{T} = e^{-t\sigma ^2T^2} \widehat{f}, \end{aligned}$$

see (1.2) and (1.5). Hence, all the diffusion samples (1.6) vanish, although $f \not \equiv 0$. While no Paley-Wiener function is infinitely concentrated at $\{-T,T\}$, a more formal argument can be given by regularization. If $\eta : {\mathbb {R}} \rightarrow {\mathbb {R}}$ is continuous and supported on $[-1,1]$ and $\eta _\varepsilon (x) = \varepsilon ^{-1} \eta (x/\varepsilon )$, then $f \cdot \widehat{\eta }_\varepsilon \in PW_c$ and provides a counterexample to (1.4), provided that $\varepsilon$ is sufficiently small.

As we show below in Sect. 2.1, a similar phenomenon holds for more general diffusion kernels $\phi$ as in (1.1). Indeed, an analysis along the lines of the Papoulis sampling theorem [18] shows that the diffusion samples (1.6) of a function $f \in PW_c$ do not lead to a stable recovery of $\widehat{f}$. However, these samples do allow for the stable recovery away from certain blind spots determined by $\phi$; that is, one can effectively recover $\widehat{f} \cdot \mathbf {1}_{E}$, for a certain subset $E \subseteq I$ of positive measure ($\mathbf {1}_E$ denotes the characteristic function of the set E). If we, furthermore, restrict the sampling problem to one of the finite dimensional spaces $V=V_N$ given by (1.9), (1.10), or (1.11), we may then infer all other values of $\widehat{f}$. The main tools, in this case, are Remez-Turán-like inequalities of the form:

$$\begin{aligned} \Vert \widehat{f}\mathbf {1}_I\Vert \le C_E \Vert \widehat{f}\mathbf {1}_E\Vert , \qquad f \in V. \end{aligned}$$

For Fourier polynomials (1.11) the classical Remez-Turán inequality provides an explicit constant $C_E$, while the case of sparse sinc translates (1.10) is due to Nazarov [17]. The corresponding inequality for prolate spheroidal wave functions (1.9) is new and a contribution of this article (our technique relies on [15]).

Paper Organization and Contributions

In Sect. 2, we show that uniform dynamical samples at sub-Nyquist rate allow one to stably reconstruct the function $\widehat{f}$ away from certain, explicitly described blind spots determined by the kernel $\phi$. We also provide an upper and lower estimate for the lower frame bound in (1.8). The upper estimate relies on the standard formulas for Pick matrices (see, e.g. [7, 10]). The lower estimate is far more intricate and is based on the analysis of certain Vandermonde matrices. We also provide some numerics and explicit estimates in the case of the heat flow problem.

In Sect. 3, we restrict the problem to the sets $V=V_N$ given by (1.9), (1.10), or (1.11). We provide quantitative estimates for the frame bounds in (1.8). En route, we obtain an explicit Remez-Turán inequality for prolate spheroidal wave functions – a result which we find interesting in its own right.

In Sect. 4, we discuss the case of irregular spacial sampling. We recall that a stable reconstruction may be possible with sets $\Lambda$ that have an arbitrarily small (but positive) lower density. Nevertheless, we show that the maximal gap between the spacial samples (and, hence, the lower Beurling density) is controlled by the condition number of the problem (i.e. the ratio $\frac{B}{A}$ of the frame bounds).

Recovering a Bandlimited Function Away from the Blind-Spot

Dynamical Sampling in $PW_c$

In this section, we recall some of the results on dynamical sampling from [4, 5] and adapt them for problems studied in this paper.

For $\phi \in L^1$, consider the function

$$\begin{aligned} {\widehat{\phi }}_p(x)=\sum _{k\in {{\mathbb {Z}}}}{\widehat{\phi }}(x-2ck)\mathbf {1}_{[-c,c)}(x-2ck), \end{aligned}$$

that is, the 2c-periodization of the piece of ${\widehat{\phi }}$ supported in $[-c,c)$. Recall that we consider kernels from the set $\Phi$ given by (1.1). Hence,

$$\begin{aligned} \kappa _\phi \le {\widehat{\phi }}_p(\xi )\le 1, \qquad \xi \in {\mathbb {R}}. \end{aligned}$$

We also write

$$\begin{aligned} \widehat{f_t}(\xi ) := \widehat{f}(\xi ) \widehat{\phi }^t(\xi ), \ f\in PW_c. \end{aligned}$$

Next, we introduce the sampled diffusion matrix, which is the $m\times m$ matrix-valued function given by

$$\begin{aligned} {\mathcal {B}}_m(\xi )= & {} \left( \int \limits ^1_0\overline{(\widehat{\phi })_p^t\left( \frac{2c}{m}(\xi +j)\right) }(\widehat{\phi })_p^t\left( \frac{2c}{m}(\xi +k)\right) \,\mathrm {d}t\right) _{0\le j,k\le m-1} \nonumber \\= & {} \int _0^1{\mathcal {A}}_m^* (\xi ,t){\mathcal {A}}_m(\xi ,t)\,\mathrm {d}t, \end{aligned}$$

(2.12)

where

$$\begin{aligned} {\mathcal {A}}_{m}(\xi ,t)= & {} \begin{pmatrix}\displaystyle (\widehat{\phi })_p^t\left( \frac{2c}{m}(\xi +k)\right) \end{pmatrix}_{k=0,\ldots ,m-1}\\= & {} \begin{pmatrix}\displaystyle (\widehat{\phi })_p^t\left( \frac{2c}{m}\xi \right)&\cdots&\displaystyle (\widehat{\phi })_p^t\left( \frac{2c}{m}(\xi +m-1)\right) \end{pmatrix} \in {\mathcal {M}}_{1,m}(\mathbb {C}). \end{aligned}$$

Remark 2.1

Observe that the matrix function ${\mathcal {B}}_m$ is m-periodic. Its eigenvalues, however, are 1-periodic because the matrices ${\mathcal {B}}_m(\xi )$ and ${\mathcal {B}}_m(\xi +k)$, $k\in {{\mathbb {Z}}}$, are similar via a circular shift matrix.

The following lemma explains the role of the sampled diffusion matrix. In the lemma, we let

$$\begin{aligned} \mathbf{f}(\xi )=\begin{pmatrix}\displaystyle (\widehat{f})_p\left( \frac{2c}{m}(\xi +j)\right) \end{pmatrix}_{j=0,\ldots ,m-1} =\begin{pmatrix}\displaystyle (\widehat{f})_p\left( \frac{2c}{m}\xi \right) \\ \vdots \\ \displaystyle (\widehat{f})_p\left( \frac{2c}{m}(\xi +m-1)\right) \end{pmatrix} \in {\mathcal {M}}_{m,1}(\mathbb {C}). \end{aligned}$$

(2.13)

Note that if we recover $\mathbf{f}(\xi )$ for $\xi \in [0,1]$ then we can recover $f_p$. Observe also that

$$\begin{aligned} \begin{aligned} \int _0^1\Vert \mathbf{f}(\xi )\Vert ^2\,\text{ d }\xi&=\sum _{j=0}^{m-1}\int _0^1\left| (\widehat{f})_p\left( \frac{2c}{m}(\xi +j)\right) \right| ^2\,\text{ d }\xi =\frac{m}{2c}\sum _{j=0}^{m-1}\int _{2cj/m}^{2c(j+1)/m}|(\widehat{f})_p(u)|^2\,\text{ d }u\\&=\frac{m}{2c}\int _{0}^{2c}|(\widehat{f})_p(s)|^2\,\text{ d }s =\frac{m}{2c}\int _{-c}^{c}|\widehat{f}(s)|^2\,\text{ d }s \end{aligned} \end{aligned}$$

(2.14)

In other words, $f\mapsto \sqrt{\frac{2c}{m}}\mathbf{f}: PW_c\rightarrow L^2([0,1],{\mathcal {M}}_{m,1}(\mathbb {C}))$ is an isometric isomorphism.

Lemma 2.2

For $f \in PW_c$,

$$\begin{aligned} \int _0^1 \sum _{k\in {{\mathbb {Z}}}}\left| f_t\left( \frac{m \pi }{c}k\right) \right| ^2\,\mathrm {d}t =\left( \frac{c}{m\pi }\right) ^2\int _0^1\mathbf{f}(\xi )^*{\mathcal {B}}_m(\xi )\mathbf{f}(\xi )\,\mathrm {d}\xi . \end{aligned}$$

(2.15)

Proof

Observe that it suffices to prove the result in $PW_c\cap {\mathcal S}({{\mathbb {R}}})$ (the Schwarz class). Consider the function

$$\begin{aligned} b(\xi ,t)=\sum _{k\in {{\mathbb {Z}}}}f_t\left( \frac{m \pi }{c}k\right) e^{-2i\pi k\xi }. \end{aligned}$$

Using the Poisson summation formula and the definition of $f_t$, we get

$$\begin{aligned} b(\xi ,t)= & {} \frac{c}{m\pi }\sum _{j\in {{\mathbb {Z}}}}\widehat{f_t}\left( \frac{2c}{m}(\xi +j)\right) =\frac{c}{m\pi }\sum _{-\frac{m}{2}-\xi \le j< \frac{m}{2}-\xi } {\widehat{\phi }}^t\left( \frac{2c}{m}(\xi +j)\right) \widehat{f}\left( \frac{2c}{m}(\xi +j)\right) \\= & {} \frac{c}{m\pi }\sum _{j=0}^{m-1} ({\widehat{\phi }})_p^t\left( \frac{2c}{m}(\xi +j)\right) (\widehat{f})_p\left( \frac{2c}{m}(\xi +j)\right) , \end{aligned}$$

Note that the functions $b(\cdot , t)$ are 1-periodic,

$$\begin{aligned} b(\xi ,t)=\frac{c}{m\pi }{\mathcal {A}}_m(\xi ,t)\mathbf{f}(\xi ), \end{aligned}$$

(2.16)

and thus

$$\begin{aligned} \int _0^1|b(\xi ,t)|^2\,\mathrm {d}t=\left( \frac{c}{m\pi }\right) ^2\mathbf{f}(\xi )^*{\mathcal {B}}_m(\xi )\mathbf{f}(\xi ),\ \xi \in {{\mathbb {R}}}. \end{aligned}$$

Combining the last equation with the Parseval’s relation

$$\begin{aligned} \int _0^1|b(\xi ,t)|^2d\xi =\sum _{k\in {{\mathbb {Z}}}}\left| f_t\left( \frac{m \pi }{c}k\right) \right| ^2. \end{aligned}$$

(2.17)

yields the desired conclusion. $\square$

Remark 2.3

Lemma 2.2 shows that the stability of reconstruction from spatio-temporal samples is controlled by the condition number of the self-adjoint matrices ${\mathcal {B}}_m(\xi )$ in (2.12). For symmetric $\phi \in \Phi$ and $m \ge 2$, however,

$$\begin{aligned} \inf _{\xi \in [0,1]} \lambda _{\mathrm {min}} \big ({\mathcal {B}}_m(\xi ) \big ) = \lambda _{\mathrm {min}} \big ({\mathcal {B}}_m(0) \big ) = 0, \end{aligned}$$

which precludes the stable reconstruction of all $f \in PW_c$, see, e.g., [4]. This adds to our explanation of the phenomenon of blind spots in Sect. 1.2. We can nonetheless hope to find a large set $\widetilde{E} \subseteq [0,1]$ such that $\lambda _{\mathrm {min}} \big ({\mathcal {B}}_m(\xi ) \big )\ge \kappa$ for $\xi \in \widetilde{E}$. Then, repeating the computation in (2.14), we get

$$\begin{aligned} \begin{aligned} \int _0^1 \sum _{k\in {{\mathbb {Z}}}}\left| f_t\left( \frac{m \pi }{c}k\right) \right| ^2\,\mathrm {d}t =&\left( \frac{c}{m\pi }\right) ^2\int _0^1\mathbf{f}(\xi )^*{\mathcal {B}}_m(\xi )\mathbf{f}(\xi )\,\mathrm {d}\xi . \ge \kappa \left( \frac{c }{m\pi }\right) ^2\int _{\tilde{E}}\Vert \mathbf{f}(\xi )\Vert ^2\,\mathrm {d}\xi \\ =&\frac{c\kappa }{2m\pi ^2}\int _{E}\Vert \widehat{f}(\xi )\Vert ^2\,\mathrm {d}\xi \end{aligned} \end{aligned}$$

(2.18)

where $E=\displaystyle \left( \frac{2c}{m}(\tilde{E}+{{\mathbb {Z}}})\right) \cap [-c,c]$.

In the following example, we offer some numerics. To simplify the computations, we represent ${\mathcal {B}}_m(\xi )$ in (2.12) as a Pick matrix (see, e.g., [7, 10]). For $\xi \in [-c,c)$, we write $\widehat{\phi }(\xi ) = e^{-\psi (\xi )},$ so that $\psi \ge 0$ and $\psi (0)= 0,$ and obtain for $j, k = 0,\ldots , m-1$,

$$\begin{aligned} ({\mathcal {B}}_m)_{jk}(\xi ) = \int _0^1 \widehat{\phi }^t\left( \frac{2c}{m}(\xi +j^\prime )\right) \, \widehat{\phi }^t \left( \frac{2c}{m}(\xi +k^\prime )\right) \, \mathrm {d}t \end{aligned}$$

where the indices $j^\prime ,k^\prime$ are in the set

$$\begin{aligned} I_\xi =\left\{ n\in {\mathbb {Z}}:\frac{\xi + n}{m} \in [-1/2, 1/2)\right\} , \end{aligned}$$

(2.19)

m divides $|j-j^\prime |$ and $|k-k^\prime |$, and j, k, and $\xi$ are not 0 simultaneously. Thus

$$\begin{aligned} \begin{aligned} ({\mathcal {B}}_m)_{jk}(\xi )&= \int _0^1\ e^{-t\left( \psi \left( \frac{2c}{m}(\xi +j^\prime )\right) + \psi \left( \frac{2c}{m}(\xi +k^\prime )\right) \right) } \,\mathrm {d}t \\&= \left( \psi \left( \frac{2c}{m}(\xi +j^\prime )\right) + \psi \left( \frac{2c}{m}(\xi +k^\prime )\right) \right) ^{-1}\,\left( 1-e^{-\left( \psi \left( \frac{2c}{m}(\xi +j^\prime )\right) + \psi \left( \frac{2c}{m}(\xi +k^\prime )\right) \right) } \right) \end{aligned} \end{aligned}$$

(2.20)

Observe that $({\mathcal {B}}_m)_{00}(0) = 1$.

Example 2.4

Here, we choose $\phi$ to be the Gaussian function, i.e.,

$$\begin{aligned} {\widehat{\phi }}(\xi ) = {\widehat{\phi }}_1(\xi ) = e^{-{{\sigma ^2} \xi ^2}} \end{aligned}$$

for various values of $\sigma \not = 0$. Hence, $\psi (\xi ) = \sigma ^2\xi ^2$, and we get

$$\begin{aligned} ({\mathcal {B}}_m)_{jk}(\xi ) = \frac{m^2}{4c^2\sigma ^2}\cdot \frac{1-e^{ - \left( \frac{\sigma ^2}{m^2} \left( {(\xi +j^\prime )^2} + {(\xi +k^\prime )^2}\right) \right) }}{(\xi +j^\prime )^2+(\xi +k^\prime )^2} \end{aligned}$$

with $j^\prime$, $k^\prime$, and $({\mathcal {B}}_m)_{00}(0)$ as above.

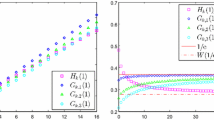
In Figure 1, we show the condition numbers of the matrices ${\mathcal {B}}_m(\xi )$ with $\xi =0.45$, $c=1/2$, $m\in \{2,3,5\}$, and $\sigma$ varying from 1 to 200.

Fig. 1

Condition numbers of ${\mathcal {B}}_m(\xi )$ for $m \in \{2,3,5\}$, $c=1/2$, $\xi =0.45$, and $\sigma \in [1,200]$

In Figure 2, we also show the condition numbers of the matrices ${\mathcal {B}}_m(\xi )$. This time, however, still $c=1/2$, the parameter $\sigma$ is fixed to be 200, whereas the point $\xi$ is allowed to vary from 0.35 to 0.49. We still have $m\in \{2,3,5\}$.

Fig. 2

Condition numbers of ${\mathcal {B}}_m(\xi )$ for $m \in \{2,3,5\}$, $c=1/2$, $\sigma =200$, and $\xi \in [0.35,0.49]$

Estimating the Minimal Eigenvalue of the Sampled Diffusion Matrix

In this subsection, we use Vandermonde matrices to obtain a lower estimate for the eigenvalue $\lambda ^{(m)}_{\min }(\xi )$ of the matrices ${\mathcal {B}}_m(\xi )$ in (2.12). We also present an upper estimate for $\lambda ^{(m)}_{\min }(\xi )$, which follows from the general theory of Pick matrices [7, 10].

We begin with the following auxiliary result.

Lemma 2.5

Let $v_0, v_1, \ldots v_{m-1}$ be m distinct non-zero real numbers and let $\mathbf {v}=(v_0,\ldots ,v_{m-1})$. For $k\in {\mathbb {N}}$, define a function $\Psi _k:{{\mathbb {R}}}\rightarrow {{\mathbb {R}}}$ by $\Psi _k(t)=\tfrac{1-t^2}{1-t^{2/k}}$ if $t\ne 1$ and $\psi _k(1)=k$. For $j=0,\ldots ,m-1$, define

$$\begin{aligned} \sigma _j^2=\sum _{k=0}^{m-1}v_j^{2k}= \Psi _m(v_j^m) = {\left\{ \begin{array}{ll}m&{}\text{ if } v_j=1\\ \frac{1-v_j^{2m}}{1-v_j^2}&{}\text{ otherwise }\end{array}\right. }. \end{aligned}$$

Let $\sigma =\left( \sum _{j=0}^{m-1}\sigma _j^2\right) ^{1/2}$, $\gamma _- = \min _{j} |v_j| >0$, $\gamma _+=\max _{j} |v_j|$ and let

$$\begin{aligned} \alpha = \left( \frac{m-1}{\sigma ^2}\right) ^{\frac{m-1}{2}}\prod _{0\le j< k\le m-1}|v_j-v_k|. \end{aligned}$$

For $N\in \mathbb N$, let $W_N$ be the $(mN)\times m$ Vandermonde matrix associated to $\mathbf {v}_N = (v_0^{\frac{1}{N}}, v_1^{\frac{1}{N}}, \ldots v_{m-1}^{\frac{1}{N}})$, i.e.,

$$\begin{aligned} W_N=\left[ v_j^{\frac{i-1}{N}}\right] _{1\le i\le mN,0\le j\le m-1}. \end{aligned}$$

Then for each $x\in \mathbb {C}^m$, we have

$$\begin{aligned} \alpha ^2 \Psi _N(\gamma _-)\Vert x\Vert ^2 \le \Vert W_N x\Vert ^2 \le \sigma ^2\Psi _N(\gamma _+)\Vert x\Vert ^2. \end{aligned}$$

Proof

let V be the $m\times m$ Vandermonde matrix associated to $\mathbf {v}$:

$$\begin{aligned} V=[v_j^{i}]_{0\le i\le m-1,0\le j\le m-1}. \end{aligned}$$

Note that the Frobenius norm of V and its determinant are given by

$$\begin{aligned} \Vert V\Vert _F=\sigma \quad \text{ and }\quad |\det V|=\prod _{0\le j< k\le m-1}|v_j-v_k|. \end{aligned}$$

Recall from [23] an estimate for the minimal singular value of an $m\times m$ matrix A:

$$\begin{aligned} \sigma _{\min }(A) \ge \left( \frac{m-1}{\Vert A\Vert ^2_F}\right) ^{(m-1)/2}|\det A|. \end{aligned}$$

(2.21)

Specifying this to V we get $\sigma _{\min }(V)\ge \alpha$. As $\Vert V\Vert \le \Vert V\Vert _F$, it follows that, for all $x\in \mathbb {C}^m$,

$$\begin{aligned} \alpha ^2\Vert x\Vert ^2\le \Vert Vx\Vert ^2\le \sigma ^2\Vert x\Vert ^2. \end{aligned}$$

(2.22)

Let $D_N$ be the diagonal matrix with $\mathbf{v}_{N}$ on the main diagonal. Since

$$\begin{aligned} \Vert W_N x\Vert ^2 = \langle W_N^* W_N x, x\rangle = \sum _{\ell =0}^{N-1} \langle (D_N^\ell )^* V^*VD_N^\ell x, x\rangle = \sum _{\ell =0}^{N-1}\Vert VD_N^\ell x\Vert ^2, \end{aligned}$$

we deduce from (2.22) that

$$\begin{aligned} \sum _{\ell =0}^{N-1}\alpha ^2 \Vert D_N^\ell x\Vert ^2\le \Vert W_N x\Vert ^2 \le \sum _{\ell =0}^{N-1}\sigma ^2 \Vert D_N^\ell x\Vert ^2. \end{aligned}$$

Moreover, we have $\gamma _-^{\frac{2\ell }{N}}\Vert x\Vert ^2\le \Vert D_N^\ell x\Vert ^2 \le \gamma _+^{\frac{2\ell }{N}}\Vert x\Vert ^2$ by definition of $D_N$. The conclusion now follows by summing the two geometric sequences. $\square$

Note that the function $\Psi _N$ is increasing on $(0,+\infty )$ and that, for $t\ne 1$, $t>0$

$$\begin{aligned} \lim _{N\rightarrow \infty }\frac{1}{N}\Psi _N(t)=\frac{1-t^2}{\lim _{N\rightarrow \infty }N(1-e^{2\ln t/N})}=\left| \frac{1-t^2}{2\ln t} \right| . \end{aligned}$$

(2.23)

Corollary 2.6

With the notation of Lemma 2.5, assume further that $0<\nu \le v_j\le 1$ and $m\ge 2$. Let

$$\begin{aligned} {\widetilde{\alpha }}=e^{-1/2}m^{-\frac{m-1}{2}}\prod _{0\le j< k\le m-1}|v_j-v_k|. \end{aligned}$$

(2.24)

Then for each $x\in \mathbb {C}^m$, we have

$$\begin{aligned} {\widetilde{\alpha }}^2 \Psi _N(\nu )\Vert x\Vert ^2 \le \Vert W_N x\Vert ^2 \le m^2N\Vert x\Vert ^2. \end{aligned}$$

Proof

Indeed, $\nu \le \gamma _-\le \gamma _+\le 1$ so $\Psi _N(\nu )\le \Psi _N(\gamma _-)$ and $\Psi _N(\gamma _+)\le \Psi _N(1)=N$.

Further, since $v_j\le 1$, $\sigma ^2\le m^2$. Moreover, the derivative of $\left( \frac{t-1}{t}\right) ^{(t-1)/2}=\left( 1-\frac{1}{t}\right) ^{(t-1)/2}$ is

$$\begin{aligned} \frac{1}{2}\left( 1-\frac{1}{t}\right) ^{(t-1)/2}\left( \frac{1}{t}+\ln \left( 1-\frac{1}{t}\right) \right) \le 0 \end{aligned}$$

for $t\ge 1$. Thus,

$$\begin{aligned} \left( \frac{m-1}{m}\right) ^{(m-1)/2}\ge \lim _{t\rightarrow +\infty }\exp \left[ \frac{t-1}{2}\ln \left( 1-\frac{1}{t}\right) \right] =e^{-1/2}. \end{aligned}$$

It follows that $\alpha$ in the statement of Lemma 2.5 satisfies

$$\begin{aligned} \alpha \ge \frac{\prod _{0\le j< k\le m-1}|v_j-v_k|}{\sqrt{e}m^{(m-1)/2}}, \end{aligned}$$

and the result is established. $\square$

Proposition 2.7

Let $\phi \in \Phi$. Define

$$\begin{aligned} \Delta _m(\xi )= \prod _{0\le j< k\le m-1}\left| {\widehat{\phi }}_p\left( \frac{2c}{m}(\xi +j)\right) -{\widehat{\phi }}_p\left( \frac{2c}{m}(\xi +k)\right) \right| . \end{aligned}$$

Then, for each $x\in \mathbb {C}^m$, we have

$$\begin{aligned} \frac{1}{2e m^{m^2}}\Delta _m(\xi )^2 \cdot \frac{1-\kappa _\phi ^{2/m}}{|\ln \kappa _\phi |}\Vert x\Vert ^2\le \langle {\mathcal {B}}_m(\xi ) x, x \rangle \le m\Vert x\Vert ^2. \end{aligned}$$

Proof

We fix $\xi$ and apply Corollary 2.6 to $v_j =\displaystyle ({\widehat{\phi }})_p\left( \frac{2c}{m}(\xi +j)\right) ^{\frac{1}{m}}$. With ${\widetilde{\alpha }}$ given by (2.24),

$$\begin{aligned} {\widetilde{\alpha }}= e^{-1/2}m^{-\frac{m-1}{2}} \prod _{0\le j< k\le m-1}\left| {\widehat{\phi }}_p\left( \frac{2c}{m}(\xi +j)\right) ^{1/m} -{\widehat{\phi }}_p\left( \frac{2c}{m}(\xi +k)\right) ^{1/m} \right| , \end{aligned}$$

we get

$$\begin{aligned} {\widetilde{\alpha }}^2\Psi _N(\kappa _\phi ^{1/m})\Vert x\Vert ^2\le \Vert W_Nx\Vert ^2\le m^2 N \Vert x\Vert ^2. \end{aligned}$$

On the other hand, $\frac{1}{mN} W_N^*W_N$ equals the left-end mN-term Riemann sum for the integral defining ${\mathcal {B}}_m(\xi )$. It follows that

$$\begin{aligned} \langle {\mathcal {B}}_m(\xi ) x, x \rangle = \lim _{N\rightarrow \infty }\frac{1}{mN} \langle W_N^*W_Nx, x \rangle =\lim _{N\rightarrow \infty }\frac{1}{mN} \Vert W_Nx\Vert ^2. \end{aligned}$$

Using (2.23), we get

$$\begin{aligned} {\widetilde{\alpha }}^2\frac{1-\kappa _\phi ^{2/m}}{2m|\ln \kappa _\phi |}\Vert x\Vert ^2\le \langle {\mathcal {B}}_m(\xi ) x, x \rangle \le m\Vert x\Vert ^2. \end{aligned}$$

Finally, note that if $0<a,b\le 1$, using the mean value theorem, there is an $\eta \in (a,b)$ such that

$$\begin{aligned} |a^{1/m}-b^{1/m}|=\frac{1}{m}|a-b|\eta ^{-1+1/m}\ge \frac{1}{m}|a-b|. \end{aligned}$$

Therefore

$$\begin{aligned} {\widetilde{\alpha }}= & {} e^{-1/2}m^{-\frac{m-1}{2}} \prod _{0\le j< k\le m-1}\left| {\widehat{\phi }}_p\left( \frac{2c}{m}(\xi +j)\right) ^{1/m} -{\widehat{\phi }}_p\left( \frac{2c}{m}(\xi +k)\right) ^{1/m} \right| \\\ge & {} e^{-1/2}m^{-\frac{m-1}{2}-\frac{m(m-1)}{2}}\Delta (\xi ) =e^{-1/2}m^{-\frac{m^2-1}{2}}\Delta (\xi ) \end{aligned}$$

establishing the postulated estimates. $\square$

For an upper estimate of the minimal eigenvalue $\lambda ^{(m)}_{\min }(\xi )$ we use the estimates of the singular values of Pick matrices by Beckerman-Townsend [7]. For $p_j\in \mathbb {C}$, $j = 1 , \dots , m$, and $0<a\le x_1< x_2< \dots < x_m \le b$ let

$$\begin{aligned} (P_m)_{jk} = \frac{p_j+ p_k}{x_j+ x_k}, \qquad j,k = 1 , \dots , m, \end{aligned}$$

(2.25)

be the corresponding Pick matrix. Then the smallest singular value $s_{\min }$ of $P_m$ is bounded above by

$$\begin{aligned} s_{\min } \le \min \left\{ 1, 4 \left[ \exp \left( \frac{\pi ^2}{2\ln \left( \frac{4b}{a}\right) } \right) \right] ^{-2\lfloor m/2 \rfloor }\right\} s_{\max }, \end{aligned}$$

(2.26)

where $s_{\max }$ is the largest singular value.

If $(\widetilde{ P}_m)_{jk} = \frac{1-c_jc_k}{x_j+x_k}$, then $\widetilde{P}_m$ is related to a Pick matrix of the form (2.25) via the diagonal matrix $D = \mathrm {diag} (1+c_j)$:

$$\begin{aligned} \frac{1}{2} D ^{-1}\widetilde{P}_m D ^{-1}= P_m \end{aligned}$$

with $p_j = \frac{1-c_j}{1+c_j}$, $c_j\ne -1$.

In our case, see (2.20), $x_j= \psi \left( \frac{2c}{m}(\xi +j)\right)$ and $c_j = e^{-x_j} \in (0,1]$, so $\mathrm {Id}\le D \le 2\mathrm {Id}$ and the singular values of $\mathcal {B}_m (\xi )$ and the corresponding Pick matrix $P_m$ differ at most by a factor 4. Therefore, (2.26) holds with $a (\xi ) = \min \left\{ \psi \left( \frac{2c}{m}(\xi +k)\right) : k\in I_\xi \right\}$ and $b (\xi ) = \max \left\{ \psi \left( \frac{2c}{m}(\xi +k)\right) : k\in I_\xi \right\}$, $I_\xi$ defined in (2.19), and an additional factor 4 provided that $a(\xi ) \ne 0$.

For our main examples, we have $\psi (\xi ) = |\xi |^\alpha$, $\alpha > 0$. This yields

$$\begin{aligned} b(\xi ) \le c^\alpha \quad \text{ and }\quad a(\xi ) \!=\! \min \left\{ \left| \frac{2c}{m}(\xi -k)\right| ^\alpha : \frac{2c}{m}|\xi \!-\! k|\le c,\ |\xi |\le \frac{1}{2}\right\} = \left( \frac{2c}{m}|\xi |\right) ^\alpha \end{aligned}$$

So for the smallest singular value of $\mathcal {B}_m(\xi )$ we obtain the estimate

$$\begin{aligned} \begin{aligned} \lambda ^{(m)}_{\min }(\xi )&\le 4^2\left[ \exp \left( \frac{\pi ^2}{2\ln 4\left( \frac{m}{2|\xi |}\right) ^\alpha } \right) \right] ^{-2\lfloor m/2 \rfloor } m\\&\le 16 m \, \exp \left( -\frac{(m-1)\pi ^2}{\ln 16 + 2\alpha \ln \frac{m}{2|\xi |}} \right) . \end{aligned} \end{aligned}$$

(2.27)

Observe that the Beckerman-Townsend estimate (2.26) holds for all Pick matrices with the same values for $a=\min x_j$ and $b=\max x_j$ and is completely independent of the particular distribution of the $x_j$. Regardless, it shows that the condition number grows nearly exponentially with m, establishing limitations on how well the space–time trade-off can work numerically. Of course, the condition number may be much worse if two values $x_j$ and $x_{j+1}$ are close together (if $x_j = x_{j+1}$, then $P_m$ is singular). Thus, (2.27) is an optimistic upper estimate for $\lambda ^{(m)}_{\min }(\xi )$. By comparison, our lower estimate in Proposition 2.7 depends crucially on the distribution of the parameters $x_j$ and is much harder to obtain. It does, however, establish an upper bound on the condition number and, thus, shows that the space–time trade-off may be useful. A precise result is formulated in the following subsection.

Partial Recoverability

Theorem 2.8

Let $\phi \in \Phi$, $m\ge 2$ an integer and $\widetilde{E}\subseteq I = [0,1]$ be a compact set. Assume that there exists $\delta >0$ such that, for every $0\le j<k\le m-1$ and every $\xi \in \widetilde{E}$

$$\begin{aligned} \left| {\widehat{\phi }}_p\left( \frac{2c}{m}(\xi + j)\right) -{\widehat{\phi }}_p\left( \frac{2c}{m}(\xi +k)\right) \right| \ge \delta . \end{aligned}$$

Let $E=\displaystyle \left( \frac{2c}{m}(\tilde{E}+{{\mathbb {Z}}})\right) \cap [-c,c]$. Then for any $f\in PW_c$, the function $\widehat{f}\mathbf {1}_{ E}$ can be recovered from the samples

$$\begin{aligned} {\mathcal {M}} = \left\{ f_t\left( \frac{m \pi }{c}k\right) : k \in {\mathbb {Z}}, 0 \le t \le 1\right\} \end{aligned}$$

(2.28)

in a stable way. Moreover, we have

$$\begin{aligned} A\Vert \widehat{f}\mathbf {1}_{ E}\Vert ^2 \le \int _0^1 \sum _{k\in {\mathbb {Z}}}\left| f_t\left( \frac{m \pi }{c}k\right) \right| ^2\,\mathrm {d}t \le \frac{c}{2\pi ^2}\Vert \widehat{f}\Vert ^2, \end{aligned}$$

(2.29)

where

$$\begin{aligned}A=\frac{c }{4e\pi ^2}\frac{\delta ^{m(m-1)}}{m^{1+m^2}} \frac{\kappa _\phi ^{2/m}-1}{\ln \kappa _\phi }. \end{aligned}$$

Proof

Recall from (2.15) that we need to estimate

$$\begin{aligned} \int _0^1 \sum _{k\in {\mathbb {Z}}}\left| f_t\left( \frac{m \pi }{c}k\right) \right| ^2\,\mathrm {d}t=\left( \frac{c}{m\pi }\right) ^2\int _0^1\mathbf{f}(\xi )^*{\mathcal {B}}_m(\xi )\mathbf{f}(\xi )\,\mathrm {d}\xi . \end{aligned}$$

The upper bound follows directly from Proposition 2.7, and (2.14):

$$\begin{aligned} \int _0^1\mathbf{f}(\xi )^*{\mathcal {B}}_m(\xi )\mathbf{f}(\xi )\,\mathrm {d}\xi \le m\int _0^1\Vert \mathbf{f}(\xi )\Vert ^2\,\mathrm {d}\xi =\frac{m^2}{2c}\Vert \widehat{f}\Vert ^2. \end{aligned}$$

Let us now prove the lower bound using (2.18). First, $\Delta _m(\xi )\ge \delta ^{\frac{m(m-1)}{2}}$. It follows from Proposition 2.7 that, if $\xi \in \widetilde{E}$ then

$$\begin{aligned} \mathbf{f}(\xi )^*{\mathcal {B}}_m(\xi )\mathbf{f}(\xi ) \ge \frac{\kappa _\phi ^{2/m}-1}{2e m^{m^2}\ln \kappa _\phi } \delta ^{m(m-1)} \Vert \mathbf{f}(\xi )\Vert ^2. \end{aligned}$$

Taking $\displaystyle \kappa =\frac{\kappa _\phi ^{2/m}-1}{2e m^{m^2}\ln \kappa _\phi } \delta ^{m(m-1)}$ in (2.18) gives the result. $\square$

Remark 2.9

The condition number implied by the above theorem is not the best possible one can obtain through this method. For instance, a better estimate for the $\sigma _{\min }$ of a Vandermonde matrix may be used in place of (2.21).

However, the method will always lead to a deteriorating estimate of the condition number as m increases. This follows from the Beckerman-Townsend estimate (2.26) we discussed in the previous subsection.

Corollary 2.10

Assume that $\phi \in \Phi$, ${\widehat{\phi }}$ is even and strictly decreasing on ${{\mathbb {R}}}_+$, and $m\ge 2$ is an integer. Given $\eta \in (0,\frac{1}{4})$, let $\widetilde{E} = [-\frac{1}{2} + \eta , -\eta ]\cup [\eta , \frac{1}{2} -\eta ]$ and $E=\displaystyle \left( \frac{2c}{m}(\tilde{E}+{{\mathbb {Z}}})\right) \cap [-c,c]$. Then there exists $A>0$ such that, for any $f\in PW_c$,

$$\begin{aligned} A\Vert \widehat{f}\mathbf {1}_{ E}\Vert ^2 \le \int _0^1 \sum _{k\in {\mathbb {Z}}}\left| f_t\left( \frac{m \pi }{c}k\right) \right| ^2\,\mathrm {d}t \le \Vert \widehat{f}\Vert ^2. \end{aligned}$$

Proof

We look into the main condition of Theorem 2.8: there exists $\delta >0$ such that, for every $0\le j<k\le m-1$ and every $\xi \in \widetilde{E}$

$$\begin{aligned} \left| {\widehat{\phi }}_p\left( \frac{2c}{m}(\xi +j)\right) - {\widehat{\phi }}_p\left( \frac{2c}{m}(\xi +k)\right) \right| \ge \delta . \end{aligned}$$

(2.30)

For a general $\phi \in \Phi$, the function ${\widehat{\phi }}$ is continuous and, therefore, ${\widehat{\phi }}_p$ is continuous, except possibly on $\displaystyle c+2c{{\mathbb {Z}}}$ where a jump discontinuity occurs if ${\widehat{\phi }}(-c)\ne {\widehat{\phi }}(c)$. Under current assumptions, however, ${\widehat{\phi }}$ is even and, therefore ${\widehat{\phi }}_p$ is continuous everywhere.

For $0\le \ell \le m-1$ and $\xi \in I$, we have $\displaystyle -\frac{1}{2m} \le \frac{\xi + \ell }{m}\le 1- \frac{1}{2m}$ and

$$\begin{aligned} {\widehat{\phi }}_p\left( \frac{2c}{m}(\xi + \ell )\right) ={\left\{ \begin{array}{ll}\displaystyle {\widehat{\phi }}\left( \frac{2c}{m}(\xi + \ell )\right) &{}\text{ if } \displaystyle \frac{\xi + \ell }{m}< 1/2\\ \displaystyle {\widehat{\phi }}\left( \frac{2c}{m}(\xi + \ell -m)\right) &{}\text{ if } \displaystyle \frac{\xi + \ell }{m}\ge 1/2 \end{array}\right. }. \end{aligned}$$

Thus, the condition of Theorem 2.8 would be satisfied with $\widetilde{E}=I$ if $|{\widehat{\phi }}|$ were one-to-one on I, that is, either strictly decreasing or strictly increasing. However, ${\widehat{\phi }}$ is even and strictly decreasing on ${{\mathbb {R}}}_+$, so that ${\widehat{\phi }}_p$ is continuous, strictly decreasing on [0, c] and strictly increasing on $[-c,0]$. It follows that (2.30) may only fail in small intervals around the points $\xi \in I$ where $\displaystyle {\widehat{\phi }}_p\left( \frac{2c}{m}(\xi +j)\right) -{\widehat{\phi }}_p\left( \frac{2c}{m}(\xi + k)\right) = 0$ for some $j,k\in {{\mathbb {Z}}}$. Such points must satisfy

$$\begin{aligned} \frac{\xi + j}{m} = 1-\frac{\xi +\ell }{m},\ 0\le j \le \frac{m-1}{2} < \ell \le m-1. \end{aligned}$$

Thus, we need $\xi = \frac{1}{2}(m-j-\ell )$, i.e. $\xi \in \{0,\pm \frac{1}{2} \}$. In view of the continuity of ${\widehat{\phi }}_p$, it follows that there exists $\eta > 0$ such that (2.30) holds for $\xi \in \widetilde{E} = [-\frac{1}{2} + \eta , -\eta ]\cup [\eta , \frac{1}{2} -\eta ]$. It remains to observe that with any given $\eta \in (0,\frac{1}{4})$ inequality (2.30) will hold for $\delta$ sufficiently small. $\square$

Explicit Quantitative Estimates for the Gaussian

To obtain explicit estimates, we need to establish a precise relation between $\eta$ and $\delta$ in the proof of Corollary 2.10. In other words, we need to estimate $\min \limits _{\xi \in \widetilde{E}} \psi (\xi )$, where, as above, $\widetilde{E} = [-\frac{1}{2} + \eta , -\eta ]\cup [\eta , \frac{1}{2} -\eta ]$, $\eta \in (0, \frac{1}{4})$, and the function $\psi$ is given by

$$\begin{aligned} \omega (\xi ) = \min _{j,k\in {{\mathbb {Z}}}} \left| {\widehat{\phi }}_p\left( \frac{2c}{m}(\xi + j)\right) -{\widehat{\phi }}_p\left( \frac{2c}{m}(\xi +k)\right) \right| . \end{aligned}$$

Lemma 2.11

Let E and $\widetilde{E}$ be as in Corollary 2.10. Assume that the kernel $\phi \in \Phi$ is such that ${\widehat{\phi }}$ is differentiable on E and

$$\begin{aligned} \min _{\xi \in E} \left| {\widehat{\phi }}^\prime (\xi ) \right| \ \ge R. \end{aligned}$$

Then

$$\begin{aligned} \min \limits _{\xi \in \widetilde{E}}\omega (\xi ) \ge \frac{4cR\eta }{m}. \end{aligned}$$

Proof

Observe that

$$\begin{aligned} \min _{\xi \in \widetilde{E}}\min _{j,k\in {{\mathbb {Z}}}} \left| \left| \frac{2c}{m}(\xi + j)\right| -\left| \frac{2c}{m}(\xi + k)\right| \right| = \frac{2c}{m}2\eta . \end{aligned}$$

With this, the assertion of the lemma follows immediately from the mean value theorem. $\square$

The above observation leads to the following explicit estimate for the Gaussian kernel.

Proposition 2.12

Let ${\widehat{\phi }}(\xi )=e^{-\sigma ^2\xi ^2}$, $\sigma \not =0$, and $m\ge 2$ be an integer. Given $\eta \in (0,\frac{1}{4})$, let $\widetilde{E} = [-\frac{1}{2} + \eta , -\eta ]\cup [\eta , \frac{1}{2} -\eta ]$ and $E=\displaystyle \left( \frac{2c}{m}(\tilde{E}+{{\mathbb {Z}}})\right) \cap [-c,c]$. Then, for any $f\in PW_c$, we have

$$\begin{aligned} A\Vert \widehat{f}\mathbf {1}_{E}\Vert ^2 \le \int _0^1 \sum _{k\in {\mathbb {Z}}}\left| f_t\left( \frac{m\pi }{c}k\right) \right| ^2\,\mathrm {d}t \le \Vert \widehat{f}\Vert ^2, \end{aligned}$$

(2.31)

where

$$\begin{aligned} A= \frac{c}{2e\pi ^2(2(\sigma c)^2+m)}\frac{(4cR\eta )^{m(m-1)}}{{m^{1-m+2m^2}}} \quad \text{ with }\quad R = 2\sigma ^2\min \left\{ \eta e^{-(\sigma \eta )^2}, ce^{-(\sigma c)^2}\right\} . \end{aligned}$$

(2.32)

Proof

Observe that Lemma 2.11 applies with R given by (2.32). It remains to apply Theorem 2.8 with $\kappa _\phi = e^{-(\sigma c)^2}$ and $\delta = {4cR\eta /m}$. We deduce that (2.31) holds with

$$\begin{aligned} A&=\frac{c}{4e\pi ^2}\frac{\delta ^{m(m-1)}}{ m^{1+m^2}} \frac{\kappa _\phi ^{2/m}-1}{\ln \kappa _\phi } =\frac{c}{2e\pi ^2}\frac{1-e^{-\tfrac{2(\sigma c)^2}{m}}}{\tfrac{2(\sigma c)^2}{m}}\cdot \frac{(4cR\eta )^{m(m-1)}}{{m^{2-m+2m^2}}}. \end{aligned}$$

Using $\displaystyle \frac{1-e^{-t}}{t}\ge \frac{1}{t+1}$, we obtain the claimed bound. $\square$

We remark that the estimate in the above proposition is quite pessimistic. Our numerical experiments showed that the true bound may be much better.

Remez-Turán Property and Fixing the Blind Spots

In Theorem 2.8, the main issue is that the lower bound is only in terms of $\Vert \widehat{f}\mathbf {1}_{E}\Vert$ and not $\Vert \widehat{f}\Vert$ so that stability is not obtained. In this section, we consider a certain class of subsets of $PW_c$ for which Theorem 2.8 does lead to stable reconstruction.

Remez-Turán Property

Definition 3.1

Let $V\subset PW_c$ and write $\widehat{V}=\{\widehat{f}\,:\ f\in V\}\subset L^2([-c,c])$. We will say that $\widehat{V}$ has the Remez-Turán property if, for every $E\subset [-c,c]$ of positive Lebesgue measure, there exists $C=C(E,V)$ such that, for every $f\in V$,

$$\begin{aligned} \Vert \widehat{f}\mathbf {1}_E\Vert _2\ge C\Vert \widehat{f}\mathbf {1}_{[-c,c]}\Vert _2. \end{aligned}$$

(3.33)

When V is a finite dimensional subspace of $PW_c$ such that $\widehat{V}$ consists of analytic functions (restricted to I), then $\widehat{V}$ has the Remez-Turán property since $\Vert \widehat{f}\mathbf {1}_E\Vert _2$ is then a norm on V which, by finite dimensionality of V, is equivalent to $\Vert \widehat{f}\mathbf {1}_{[-c,c]}\Vert _2$. However, the previous argument does not provide any quantitative estimate on the constant C(E, V). Let us start with two fundamental examples of spaces that have the Remez-Turán property, and for which quantitative estimates are known.

Fourier Polynomials

Let $V_N$ be given by (1.11), so that $\widehat{V}_N=\{P\mathbf {1}_{[-c,c]}, P\in {\mathbb {C}}_N[x]\}$ is the space of polynomials of degree at most N, restricted to I. The quantitative form of the Remez-Turán property for $\widehat{V}_N$ is then known as the Remez Inequality [9]: for every polynomial of degree at most N,

$$\begin{aligned} \Vert P\mathbf {1}_{[-c,c]}\Vert _2 \le \left( \frac{8c}{|E|}\right) ^{N+1/2}\Vert P\mathbf {1}_E\Vert _2. \end{aligned}$$

(3.34)

Sparse Sinc Translates with Free Nodes

Let $V_N$ be given by (1.10), so that $\widehat{V}_N=\displaystyle \left\{ P\mathbf {1}_{[-c,c]}: P(\xi )=\sum _{n=1}^Nc_ne^{2i\pi \lambda _n\xi }\right\}$. Recall that $\widehat{V}_N$ is not a linear subspace. The fact that $\widehat{V}_N$ has the Remez-Turán property is a deep result of Nazarov [17]: for every exponential polynomial of order at most N, i.e. every P of the form $P(\xi )=\sum _{n=1}^Nc_ne^{2i\pi \lambda _n\xi }$ one has

$$\begin{aligned} \Vert P\mathbf {1}_{[-c,c]}\Vert \le \left( \frac{\gamma c}{|E|}\right) ^{N+1/2}\Vert P\mathbf {1}_E\Vert , \end{aligned}$$

(3.35)

where $\gamma$ is an absolute constant.

Prolate Spheroidal Wave Functions (PSWF)

The Prolate spheroidal wave functions (PSWFs) denoted by $(\psi _{n,c}(\cdot ))_{n\ge 0}$, are defined as the bounded eigenfunctions of the Sturm-Liouville differential operator ${\mathcal {L}}_c,$ defined on $C^2([-1,1]),$ by

$$\begin{aligned} \mathcal {L}_c(\psi )=-(1-x^2)\frac{d^2\psi }{d\, x^2}+2 x\frac{d\psi }{d\,x}+c^2x^2\psi . \end{aligned}$$

(3.36)

They are also the eigenfunctions of the finite Fourier transform ${\mathcal {F}}_c$, as well as the ones of the operator $\displaystyle {\mathcal {Q}}_c= \frac{c}{2\pi } {\mathcal {F}}^*_c {\mathcal {F}}_c ,$ which are defined on $L^2([-1,1])$ by

$$\begin{aligned} \mathcal {F}_c(f)(x)= \int _{-1}^1 e^{i\, c\, x\, y} f(y)\,\text{ d }y, \quad \text{ and }\quad {\mathcal {Q}}_c(f)(x)=\int _{-1}^1 \frac{\sin (c(x-y))}{\pi (x-y)} f(y)\,\text{ d }y. \end{aligned}$$

(3.37)

They are normalized so that $\Vert \psi _{n,c}\Vert _{L^2([-1,1])}=1$ and $\psi _{n,c}(1)>0$. We call $(\chi _n(c))_{n\ge 0}$ the corresponding eigenvalues of ${\mathcal {L}}_c$, $\mu _n(c)$ the eigenvalues of $\mathcal {F}_c$

$$\begin{aligned} \mu _n(c)\psi _{n,c}(x)=\int _{-1}^1\psi _{n,c}(y)e^{-icxy}\,\text{ d }y,\ x\in [-1,1]. \end{aligned}$$

(3.38)

and $\lambda _n(c)$ the ones of ${\mathcal {Q}}_c$ which are arranged in decreasing order. They are related by

$$\begin{aligned} \lambda _n(c)=\displaystyle \frac{c}{2\pi }|\mu _n(c)|^2. \end{aligned}$$

A well known property is then that $\Vert \psi _{n,c}\Vert _{L^2({{\mathbb {R}}})}=\frac{1}{\sqrt{\lambda _n(c)}}$. Further, their Fourier transform is given by

$$\begin{aligned} \widehat{\psi _{n,c}}(\xi )= \int _{{{\mathbb {R}}}}\psi _{n,c}(x)e^{-ix\xi }\,\text{ d }x =(-1)^k\frac{2\pi }{c}\frac{\mu _n}{|\mu _n(c)|^2}\psi _{n,c}\left( \frac{\xi }{c}\right) \mathbf {1}_{|\xi |\le c} \end{aligned}$$

(3.39)

The crucial commuting property of ${\mathcal {L}}_c$ and ${\mathcal {Q}}_c$ has been first observed by Slepian and co-authors [21], whose name is closely associated with all properties of PSWFs, the spectrum of the operators ${\mathcal {L}}_c$ and $Q_c$ and almost time- and band-limited functions. Among the basic properties of PSWFs, we cite their analytic extension to the whole real line and their unique properties to form an orthonormal basis of $L^2([-1,1])$ and an orthogonal basis of $PW_c$.

The prolate spheroidal wave functions admit a good representation in terms of the orthonormal basis of Legendre polynomials. In agreement with the standard practice, we will be denoting by $P_k$ the classical Legendre polynomials, defined by the three-term recursion

$$\begin{aligned} P_{k+1}(x) =\frac{2k + 1}{k + 1}x P_k(x) - \frac{k}{k + 1}P_{k-1}(x), \end{aligned}$$

with the initial conditions

$$\begin{aligned} P_0(x) = 1, P_1(x) = x. \end{aligned}$$

These polynomials are orthogonal in $L^2([-c,c])$ and are normalized so that

$$\begin{aligned} P_k(1)=1\quad \text{ and }\quad \int _{-1}^1 P_k(x)^2\,\text{ d }x=\frac{1}{k+1/2}. \end{aligned}$$

We will denote by $P_{k,c}$ the normalized Legendre polynomial $\displaystyle \widetilde{P}_{k,c}(x)=\sqrt{\frac{2k+1}{2c}}P_k\left( \frac{x}{c}\right)$ and the $P_{k,c}$’s then form an orthonormal basis of $L^2([-c,c])$.

We start from the following identity relating Bessel functions of the first kind to the finite Fourier transform of the Legendre polynomials, see [6]: for every $x\in {{\mathbb {R}}}$,

$$\begin{aligned} \int _{-1}^1 e^{i x y} P_k(y)\,\text{ d }y =2i^kj_k(x), \ k\in {\mathbb {N}}, \end{aligned}$$

(3.40)

where $j_k$ is the spherical Bessel function defined by $j_k(x)=\displaystyle (-x)^k\left( \frac{1}{x}\frac{\text{ d }}{\text{ d }x}\right) ^k\frac{\sin x}{x}$. Note that $j_k$ has the same parity as k and recall that, for $x\ge 0$, $j_k(x)=\sqrt{\frac{\pi }{2x}}J_{k+1/2}(x)$ where $J_\alpha$ is the Bessel function of the first kind. In particular, from the well-known bound $|J_{\alpha }(x)|\le \frac{|x|^{\alpha }}{2^{\alpha }\Gamma (\alpha +1)}$, valid for all $x\in {{\mathbb {R}}}$, we deduce that

$$\begin{aligned} |j_k(x)|\le \sqrt{\pi }\frac{|x|^k}{2^{k+1}\Gamma (k+3/2)}, \ k\in {\mathbb {N}}. \end{aligned}$$

Using the bound $\Gamma (x)\ge \sqrt{2\pi }x^{x-1/2}e^{-x}$ we get

$$\begin{aligned} |j_k(x)|\le \frac{e^{k+3/2}}{\sqrt{2}(2k+3)^{k+1}}|x|^k, \ k\in {\mathbb {N}}. \end{aligned}$$

(3.41)

We have the following lemma.

Lemma 3.2

Write $\widehat{\psi _{n,c}}=\sum _{k\ge 0}\beta _k^n(c)P_{k,c}$. Then for every $k,\ell \ge 0$

$$\begin{aligned} |\beta _k^n|\le \frac{10}{c^{3/2}|\lambda _n(c)|}\left( \frac{e}{2k+3}\right) ^{k+1} \end{aligned}$$

This bound is an adaptation of techniques from [15] to improve the proof of the exponential decay from [22].

Proof

Using (3.39), we have

$$\begin{aligned} \beta _k^n(c)= & {} {\left\langle {\psi _{n,c},P_{k,c}}\right\rangle }_{L^2(I)} =\int _{-c}^{c} \widehat{\psi _{n,c}}(x)P_{k,c}(x)\,\text{ d }x\\= & {} (-1)^k\frac{\mu _n(c)}{|\mu _n(c)|^2}\frac{2\pi }{c}\sqrt{\frac{2k+1}{2c}}\int _{-c}^{c} \psi _{n,c}(x/c)P_k\left( \frac{x}{c}\right) \,\text{ d }x\\= & {} (-1)^k\pi \frac{\mu _n(c)}{c^{1/2}|\mu _n(c)|^2}\sqrt{4k+2}\int _{-1}^{1} \psi _{n,c}(x)P_k(x)\,\text{ d }x\\= & {} \frac{(-1)^k\pi \sqrt{4k+2}}{c^{1/2}|\mu _n(c)|^2}\int _{-1}^{1} \int _{-1}^1\psi _{n,c}(y)e^{-icxy}\,\text{ d }y\,P_k(x)\,\text{ d }x \end{aligned}$$

with (3.38). Recalling that $\lambda _n(c)=\displaystyle \frac{c}{2\pi }|\mu _n(c)|^2$ and using Fubini, we get

$$\begin{aligned} \beta _k^n(c)= & {} \frac{(-1)^k 2\sqrt{4k+2}}{c^{3/2}\lambda _n(c)} \int _{-1}^{1}\int _{-1}^1P_k(x)e^{-icxy}\,\text{ d }x\,\psi _{n,c}(y)\,\text{ d }y\\= & {} \frac{(-i)^k 4\sqrt{4k+2}}{c^{3/2}\lambda _n(c)} \int _{-1}^{1} \psi _\ell (y) j_{k}(y)\,\text{ d }y \end{aligned}$$

with (3.40). But then, from (3.41) and Cauchy-Schwarz, we deduce that

$$\begin{aligned} |\beta _k^n(c)|\le & {} \frac{ 4\sqrt{4k+2}}{c^{3/2}\lambda _n(c)} \left( \int _{-1}^{1} j_{k}(y)^2\,\text{ d }y\right) ^{1/2}\\\le & {} \frac{ 4\sqrt{2k+1}e^{k+3/2}}{(2k+3)^{k+1}c^{3/2}\lambda _n(c)} \left( \int _{-1}^{1}|y|^{2k}\,\text{ d }y\right) ^{1/2}\\= & {} 4\sqrt{2e}\frac{1}{c^{3/2}\lambda _n(c)}\left( \frac{e}{2k+3}\right) ^{k+1}. \end{aligned}$$

As $4\sqrt{2e}\le 10$, the result follows. $\square$

We will also need the following estimate.

Lemma 3.3

The eigenvalues (3.38) of ${\mathcal {Q}}_c$ satisfy

$$\begin{aligned} \Lambda _N:=\left( \sum _{n=0}^N \frac{1}{\lambda _n(c)} \right) ^{1/2} \le {\left\{ \begin{array}{ll} \sqrt{3+ec} &{}\text{ if } N \le \max (ec,2)\\ \left( \frac{2(N+1)}{ec}\right) ^{\frac{2N+1}{2}}&{}\text{ if } N\ge \max (ec,2) \end{array}\right. }. \end{aligned}$$

(3.42)

Proof

Precise pointwise estimates of the $\lambda _n(c)$’s have been obtained in [15, Section 4 & Appendix C] and have been further improved in [8] to

$$\begin{aligned} \lambda _n(c)\le \left( \frac{ec}{2(n+1)}\right) ^{2n+1}\qquad \text{ for } n\ge \max \left( n,\frac{ec}{2}\right) . \end{aligned}$$

while we always have $\lambda _n(c)<1$.

It follows that

$$\begin{aligned} \sum _{k=0}^N\frac{1}{\lambda _n(c)}\ge {\left\{ \begin{array}{ll}N+1\le 3+ec&{}\text{ if } N\le \max (ec,2)\\ \frac{1}{\lambda _N(c)}\ge \left( \frac{2(N+1)}{ec}\right) ^{2N+1}&{}\text{ if } N\ge \max (ec,2) \end{array}\right. }. \end{aligned}$$

The result follows. $\square$

We can now prove our Remez lemma for Prolate spheroidal wave functions.

Theorem 3.4

(Remez’s Lemma for PSWF) Let N be an integer and

$$\begin{aligned} V_N=\text{ span }\{\psi _{0,c},\ldots ,\psi _{N,c}\}\subset PW_c. \end{aligned}$$

Then, for every $\psi \in \widehat{V}_N$ and every $E\subseteq [-c,c]$ of positive measure,

$$\begin{aligned} \Vert \psi \Vert \le 2 \left( \frac{8c}{|E|}\right) ^{K(N)}\Vert \widehat{\psi }\mathbf {1}_E\Vert , \end{aligned}$$

(3.43)

where

$$\begin{aligned} K(N) = {\left\{ \begin{array}{ll} \max \left( \left\lceil \frac{3200(3+ec)}{c^3}\right\rceil ,\left\lceil \frac{4ec}{|E|}\right\rceil \right) &{} \text{ if } N \le \max (2,ec),\\ \max \left( 20,N,\left\lceil \frac{8(N+1)}{|E|}\right\rceil \right) &{} \text{ if } N \ge \max (2,ec). \end{array}\right. } \end{aligned}$$

(3.44)

Proof

Let $\psi =\sum _{n=0}^Nc_\ell \psi _{n,c}$ so that, by orthogonality and the fact that $\Vert \psi _{n,c}\Vert =\lambda _n(c)^{-1/2}$,

$$\begin{aligned} \Vert \psi \Vert =\left( \sum _{n=0}^N\frac{|c_n|^2}{\lambda _n(c)}\right) ^{1/2}. \end{aligned}$$

On the other hand

$$\begin{aligned} \widehat{\psi }=\sum _{n=0}^Nc_\ell \widehat{\psi _{n,c}} =\sum _{n=0}^Nc_\ell \sum _{k\ge 0}\beta _k^n(c) P_{k,c}. \end{aligned}$$

Let K be an integer that will be fixed later and write

$$\begin{aligned} \widehat{\psi }=\sum _{n=0}^Nc_\ell \sum _{k=0}^K\beta _k^n(c)P_{k,c} +\sum _{n=0}^Nc_\ell \sum _{k>K}\beta _k^n(c)P_{k,c} :=F_K+R_K. \end{aligned}$$

Note that $F_K$ is a polynomial of degree K so that

$$\begin{aligned} \Vert F_K\mathbf {1}_{[-c,c]}\Vert \le \left( \frac{8c}{|E|}\right) ^{K+\frac{1}{2}}\Vert F_K\mathbf {1}_E\Vert \end{aligned}$$

(3.45)

by (3.34). On the other hand,

$$\begin{aligned} R_K=\sum _{k>K}\left( \sum _{n=0}^Nc_n\beta _k^n(c)\right) P_{k,c} \end{aligned}$$

so that

$$\begin{aligned} \Vert R_K\mathbf {1}_E\Vert \le \Vert R_K\mathbf {1}_{[-c,c]}\Vert =\left( \sum _{k>K}\left| \sum _{n=0}^Nc_n\beta _k^n(c) \right| ^2\right) ^{1/2} \le \left( \sum _{k>K}\sum _{n=0}^N\lambda _n(c)\left| \beta _k^n(c) \right| ^2\right) ^{1/2}\Vert \psi \Vert \end{aligned}$$

by Cauchy-Schwarz. We now apply Lemma 3.2 to get

$$\begin{aligned} \Vert R_K\mathbf {1}_E\Vert\le & {} \frac{10}{c^{3/2}}\left( \sum _{k>K}\sum _{n=0}^N\frac{1}{\lambda _n(c)} \left( \frac{e}{2k+3}\right) ^{2k+2}\right) ^{1/2}\Vert \psi \Vert \\= & {} \frac{10}{c^{3/2}} \left( \sum _{n=0}^N\frac{1}{\lambda _n(c)}\right) ^{1/2} \left( \sum _{k>K}\left( \frac{e}{2k+3}\right) ^{2k+2}\right) ^{1/2}\Vert \psi \Vert \\\le & {} \frac{12}{c^{3/2}} \left( \sum _{n=0}^N\frac{1}{\lambda _n(c)}\right) ^{1/2} \left( \frac{e}{2K+5}\right) ^{K+1}\Vert \psi \Vert . \end{aligned}$$

Using Lemmas 3.3 and 3.2 we can rewrite this in the form $\Vert R_K\mathbf {1}_E\Vert \le \Lambda _N\Phi _K\Vert \psi \Vert$ with

$$\begin{aligned} \Lambda _N:={\left\{ \begin{array}{ll} \sqrt{3+ec} &{}\text{ if } N \le \max (ec,2)\\ \left( \frac{2(N+1)}{ec}\right) ^{N+\frac{1}{2}}&{}\text{ if } N\ge \max (ec,2) \end{array}\right. } \quad \text{ and }\quad \Phi _K=\frac{12}{c^{3/2}}\left( \frac{e}{2K+5}\right) ^{K+1}. \end{aligned}$$

Next

$$\begin{aligned} \Vert \widehat{\psi }\mathbf {1}_E\Vert\ge & {} \Vert F_K\mathbf {1}_E\Vert -\Vert R_K\mathbf {1}_E\Vert \ge \left( \frac{|E|}{8c}\right) ^{K+\frac{1}{2}}\Vert F_K\mathbf {1}_{[-c,c]}\Vert -\Vert R_K\mathbf {1}_{[-c,c]}\Vert \\\ge & {} \left( \frac{|E|}{8c}\right) ^{K+\frac{1}{2}}\Vert \widehat{\psi }\Vert - \left( 1+\left( \frac{|E|}{8c}\right) ^{K+\frac{1}{2}}\right) \Vert R_K\mathbf {1}_{[-c,c]}\Vert \\\ge & {} \left( \frac{|E|}{8c}\right) ^{K+\frac{1}{2}}\Vert \widehat{\psi }\Vert -2\Vert R_K\mathbf {1}_{[-c,c]}\Vert \end{aligned}$$

since $E\subset [-c,c]$ implies $\left( \frac{|E|}{8c}\right) ^{K+\frac{1}{2}}\le 1$. Therefore

$$\begin{aligned} \Vert \widehat{\psi }\mathbf {1}_E\Vert \ge \left( \frac{|E|}{8c}\right) ^{K+\frac{1}{2}}\left( 1-2\Lambda _N\Phi _K \left( \frac{8c}{|E|}\right) ^{K+\frac{1}{2}}\right) \Vert \widehat{\psi }\Vert . \end{aligned}$$

It remains to choose K so that $\displaystyle \Lambda _N\Phi _K\le \frac{1}{4}\left( \frac{|E|}{8c}\right) ^{K+\frac{1}{2}}$.

First, if $N\le \max (ec,2)$, then we want

$$\begin{aligned} \left( \frac{e}{2K+5}\right) ^{1/2}\left( \frac{e}{2K+5}\right) ^{K+1/2}=\left( \frac{e}{2K+5}\right) ^{K+1}\le \frac{c^{3/2}}{48\sqrt{3+ec}} \left( \frac{|E|}{8c}\right) ^{K+\frac{1}{2}} \end{aligned}$$

so that it is enough that $\displaystyle \frac{e}{2K+5}\le \frac{c^3}{48^2(3+ec)}$ and $\displaystyle \frac{e}{2K+5}\le \frac{|E|}{8c}$ so we take

$$\begin{aligned} K=K(N):=\max \left( \left\lceil \frac{3200(3+ec)}{c^3}\right\rceil , \left\lceil \frac{4ec}{|E|}\right\rceil \right) . \end{aligned}$$

On the other hand, if $N\ge \max (ec,2)$, then we want

$$\begin{aligned} \left( \frac{e}{2K+5}\right) ^{1/2}\left( \frac{e}{2K+5}\right) ^{K+1/2} =\left( \frac{e}{2K+5}\right) ^{K+1}\le \frac{1}{4}\left( \frac{ec}{2(N+1)}\right) ^{N+\frac{1}{2}} \left( \frac{|E|}{8c}\right) ^{K+\frac{1}{2}} \end{aligned}$$

Taking $K:=K(N)= \max \left( 20,N,\left\lceil \frac{8(N+1)}{|E|}\right\rceil \right)$, we get

$$\begin{aligned} \left( \frac{e}{2K+5}\right) ^{K+1}\le \frac{1}{4}\left( \frac{e}{2K}\right) ^{K+1/2} \le \frac{1}{4}\left( \frac{ec}{2(N+1)}\frac{|E|}{8c}\right) ^{K+1/2} \end{aligned}$$

which gives the desired estimate since $2(N+1)>ec$ and $K\ge N$. $\square$

Sampling the Heat Flow

Equipped with the Remez-Turán Property, we are ready to close the blind spots in Theorem 2.8. We do it only in the case of heat flow as it should be clear how to obtain similar estimates in the case of other kernels $\phi \in \Phi$.

Theorem 3.5

Let ${\widehat{\phi }}(\xi )=e^{-\sigma ^2\xi ^2}$, $\sigma \not =0$, and $m \ge 2$ be an integer. Let $V=V_N$ be given by (1.9), (1.10), or (1.11). Then, for every $f\in V$,

$$\begin{aligned} \kappa \Vert \widehat{f}\Vert ^2 \le \int _0^1 \sum _{k\in {\mathbb {Z}}}\left| f_t\left( \frac{m\pi }{c}k\right) \right| ^2\,\mathrm {d}t \le \Vert \widehat{f}\Vert ^2, \end{aligned}$$

(3.46)

where

$$\begin{aligned} \kappa = \frac{c\kappa _0(c)}{(\sigma c)^2+m} \exp \Bigl (-\kappa _1(c)N-m^2\bigl (-\kappa _2(c)\ln \sigma +\kappa _3(c)\sigma ^2+\ln m\bigr )\Bigr ) \end{aligned}$$

(3.47)

with $\kappa _j$ positive constants that depend on c only.

Remark 3.6

For $V=V_N$ given by (1.10), (1.11) and for $V=V_N$ given by (1.9) when $N\ge \max (2,ec)$, $\kappa _0,\kappa _1$ do not depend on c.

Proof

To obtain this result, we take $\eta =\displaystyle \frac{1}{8}$ in Proposition 2.12. First note that if $\widetilde{E} = \displaystyle \left[ -\frac{3}{8} ,-\frac{1}{8}\right] \cup \left[ \frac{1}{8}, \frac{3}{8}\right]$ and $E=\displaystyle \left( \frac{2c}{m}(\tilde{E}+{{\mathbb {Z}}})\right) \cap [-c,c]$ then $\displaystyle \frac{c}{|E|}\ge \frac{1}{8}$ (say). Then (2.31) tells us that

$$\begin{aligned} A\Vert \widehat{f}\mathbf {1}_{E}\Vert ^2 \le \int _0^1 \sum _{k\in {\mathbb {Z}}}\left| f_t\left( \frac{m\pi }{c}k\right) \right| ^2\,\mathrm {d}t \le \Vert \widehat{f}\Vert ^2, \end{aligned}$$

(2.31)

for any $f\in PW_c$, where

$$\begin{aligned} A= \frac{c}{2e\pi ^2(2(\sigma c)^2+m)}\frac{(cR/2)^{m(m-1)}}{{m^{1-m+2m^2}}} \quad \text{ with }\quad R = 2\sigma ^2\min \left\{ \frac{1}{8}e^{-(\sigma /8)^2}, ce^{-(\sigma c)^2}\right\} . \end{aligned}$$

Note that

$$\begin{aligned} \frac{cR}{2}=\min \left\{ c\frac{\sigma ^2}{8}e^{-(\sigma /8)^2}, c^2\sigma ^2e^{-(\sigma c)^2}\right\} <1 \end{aligned}$$

so that

$$\begin{aligned} \frac{(cR/2)^{m(m-1)}}{{m^{1-m+2m^2}}}\ge \left( \frac{cR/2}{m}\right) ^{m^2}=\exp \Bigl (-m^2\bigl (-\gamma _1(c)\ln \sigma +\gamma _2(c)\sigma ^2+\ln m\bigr )\Bigr ). \end{aligned}$$

Finally $A\ge \frac{c\gamma _0}{\bigl ((\sigma c)^2+m\bigr )}\exp \Bigl (-m^2\bigl (-\gamma _1(c)\ln \sigma +\gamma _2(c)\sigma ^2+\ln m\bigr )\Bigr )$ where $\gamma _0,\gamma _1(c),\gamma _2(c)$ are constants depending on c only.

It remains to fix the blind spots $\Vert \widehat{f}\mathbf {1}_{E}\Vert ^2$ with the help of a Remez type inequality. For $V=V_N$ given by (1.10), (1.11) and $f\in V_N$, we simply have $\Vert \widehat{f}\mathbf {1}_{E}\Vert ^2\ge \gamma _3^{2N+1}\Vert f\Vert ^2$ where $\gamma _3<1$ is a constant.

For $V=V_N$ given by (1.9), $\Vert \widehat{f}\mathbf {1}_{E}\Vert ^2\ge \gamma _3^{2K(N)}\Vert f\Vert ^2$ where K(N) is given by (3.44)

$$\begin{aligned} K(N) = {\left\{ \begin{array}{ll} \max \left( \left\lceil \frac{3200(3+ec)}{c^3}\right\rceil ,\left\lceil \frac{4ec}{|E|}\right\rceil \right) \le \gamma _4(c) &{} \text{ if } N \le \max (2,ec),\\ \max \left( 20,N,\left\lceil \frac{8(N+1)}{|E|}\right\rceil \right) \le 64(N+1) &{} \text{ if } N \ge \max (2,ec). \end{array}\right. } \end{aligned}$$

Adding the estimates for fixing the blind spot yields (3.47). $\square$

Remark 3.7

Theorem 3.5 immediately implies Theorem 1.6. We also note that if $V=V_N$ is given by (1.9) or (1.11), the reconstruction can be done from measurements at a finite number of spacial locations. Indeed, our results imply that in this case one can find the coefficients of f in its decomposition in a basis of V via simple least squares.

Sensor Density, Maximal Spatial Gaps and Condition Numbers

In this section, we discuss irregular spatio-temporal sampling. We establish that stable reconstruction from dynamical samples may occur when the set $\Lambda$ has an arbitrarily small density. More importantly, however, we show that the density cannot be arbitrarily small for fixed frame bounds in (1.4). In fact, we provide an explicit estimate for the maximal spatial gap in terms of the condition number $\frac{B}{A}$.

Example 4.1

In this example, we take $c=1/2$ to simplify discussion. Assume that $\phi \in \Phi$ is such that $\widehat{\Phi }$ is real, even, and decreasing on [0, 1/2]. Let $\Lambda _0=m {{\mathbb {Z}}}$, with $m \in \mathbb {N}$ odd, $\Lambda _k=mn{{\mathbb {Z}}}+k$, where n is any fixed odd number and $k=1,\dots \frac{m-1}{2}$ . Then $\Lambda =\bigcup \limits _{k=0}^{\frac{m-1}{2}} \Lambda _k$ has density $D^{-}(\Lambda ) \le 1/n+1/m$ and is a stable set of sampling, i.e., (1.7) is satisfied.

The claim in the last example follows by stringing together several theorems on dynamical sampling. Firstly, [4, Theorems 2.4 and 2.5] yield that any $f \in \ell ^2({{\mathbb {Z}}})$ can be recovered from the space–time samples $\{\phi ^j*f(x_k): j=0,\dots ,m-1, \; x_k \in \Lambda \}$ and that the problem of sampling and reconstruction in $PW_c$ on subsets of ${{\mathbb {Z}}}$ is equivalent to the sampling and reconstruction problem of sequences in $\ell ^2({{\mathbb {Z}}})$. Secondly, combining [5, Theorems 5.4 and 5.5] shows that for $\phi \in \Phi$, $f\in PW_c$ can be stably reconstructed from $\{\phi ^j*f(x_k): j=0,\dots ,m-1, \; x_k \in \Lambda \}$ if and only if (1.7) is satisfied.

Example 4.1 thus shows that (1.7) can hold with sets having arbitrarily small densities. The goal of this section is to show that the maximal gap in such sets is controlled by the condition number B/A.

We first establish the following lemma, which parallels [13, Proposition 4.4].

Lemma 4.2

Let $\phi \in \Phi$ be such that ${\widehat{\phi }}$ is $\mathcal {C}^1$-smooth on $I = [-c,c]$. Then there exists a finite constant $C_{\phi , L}$ such that

$$\begin{aligned} \int _{0}^{L}|({\text {sinc}}(c\cdot )*\phi _t)(x)|^2\,\mathrm {d}t\le \frac{C_{\phi , L}}{1+x^2}, \text { for all }x\in {\mathbb {R}}. \end{aligned}$$

(4.48)

On the other hand, setting $c_{\phi ,L}= \frac{2(\kappa _\phi ^{2L}-1)}{\pi ^2\ln \kappa _\phi }>0$, for $|x|\le \pi /2c$, we have

$$\begin{aligned} \int _{0}^{L}|({\text {sinc}}*\phi _t)(x)|^2\,\mathrm {d}t\ge c_{\phi ,L}. \end{aligned}$$

(4.49)

Proof

Firstly, writing the Fourier inversion formula shows that

$$\begin{aligned} ({\text {sinc}}(c\cdot )*\phi _t)(x)=\frac{1}{2c}\int _{-c}^{c}\bigl (\widehat{\phi }(\xi )\bigr )^te^{ix\xi }\,\text{ d }\xi \end{aligned}$$

(4.50)

from which it follows that

$$\begin{aligned} |({\text {sinc}}(c\cdot )*\phi _t)(x)|\le \frac{1}{2c}\int _{-c}^{c}|\widehat{\phi }(\xi )|^t\,\text{ d }\xi \le 1, \end{aligned}$$

(4.51)

due to $|{\widehat{\phi }}|\le 1$.

Secondly, note that, due to its smoothness, ${\widehat{\phi }}^\prime$ is bounded by $E_\Phi :=\sup _{\xi \in [-c,c]}|{\widehat{\phi }}^\prime (\xi )|<+\infty$ on $[-c,c]$ Then, integrating (4.50) by parts leads to

$$\begin{aligned} x({\text {sinc}}(c\cdot )*\phi _t)(x) =\frac{\widehat{\phi }^t(c)e^{i cx}-\widehat{\phi }^t(-c)e^{-i cx}}{2 ic} -\frac{1}{2ic}\int _{-c}^{c}e^{i x\xi }t\widehat{\phi }^{t-1}(\xi )\widehat{\phi }^\prime (\xi )\,\text{ d }\xi , \end{aligned}$$

and, as $\kappa _\phi \le \widehat{\phi }\le 1$ on I, we deduce that

$$\begin{aligned} |x({\text {sinc}}(c\cdot )*\phi _t)(x)|\le \frac{1}{c}+\frac{E_\phi }{\kappa _\phi }t. \end{aligned}$$

Consequently,

$$\begin{aligned} x^2\int _0^L|({\text {sinc}}(c\cdot )*\phi _t)(x)|^2\,\text{ d }t\le \int _0^L\left( \frac{1}{c}+\frac{E_\phi }{\kappa _\phi }t\right) ^2dt =\frac{\kappa _\phi }{3E_\phi }\left( \left( \frac{1}{c}+\frac{E_\phi }{\kappa _\phi }L\right) ^3- \frac{1}{c^3}\right) , \end{aligned}$$

and the estimate (4.48) follows in view of (4.51).

On the other hand (4.50) implies that

$$\begin{aligned} |({\text {sinc}}(c\cdot )*\phi _t)(x)| \ge |\mathfrak {R}({\text {sinc}}(c\cdot )*\phi _t)(x)| = \left| \frac{1}{2c}\int _{-c}^{c}\widehat{\phi }(\xi )^t\cos x\xi \,\text{ d }\xi \right| . \end{aligned}$$

But, for $|\xi |\le c$, we have ${\widehat{\phi }}(\xi )^t\ge \kappa _\phi ^t$. Further, if we also have $|x|\le \pi /2c$, then $\cos 2x\xi \ge 0$. Therefore,

$$\begin{aligned} |({\text {sinc}}(c\cdot )*\phi _t)(x)| \ge \frac{1}{2c}\int _{-c}^{c}\widehat{\phi }(\xi )^t\cos x\xi \,\text{ d }\xi \ge \kappa _\phi ^t\frac{1}{2c}\int _{-c}^{c}\cos x\xi \,\text{ d }\xi =\kappa _\phi ^t{\text {sinc}}(cx)\ge \frac{2}{\pi }\kappa _\phi ^t \end{aligned}$$

since ${\text {sinc}}(cx)$ is decreasing on $[0,\pi /2c]$ and $\displaystyle {\text {sinc}}\left( c\frac{\pi }{2c}\right) =\frac{2}{\pi }$. It follows that

$$\begin{aligned} \int _0^L|({\text {sinc}}*\phi _t)(x)|^2\,\text{ d }t\ge \frac{4}{\pi ^2}\int _0^L \kappa _\phi ^{2t}dt = \frac{2(\kappa _\phi ^{2L}-1)}{\pi ^2\ln \kappa _\phi }> 0, \end{aligned}$$

and we get the desired result. $\square$

Remark 4.3

If ${\widehat{\phi }}(\xi )=e^{-\sigma ^2\xi ^2}$, $\sigma \not =0$, then $\kappa _\phi = e^{-(\sigma c)^2}$ and we may take $E_\phi = \sqrt{\frac{2}{e}}|\sigma |$. Therefore, the constants $c_{\phi ,L}$ and $C_{\phi ,L}$ in the above lemma can be taken as

$$\begin{aligned} C_{\phi ,L} = \frac{1}{c^3}+\bigl (1+\sigma ^2e^{(\sigma c)^2}\bigr ) L^3 \quad \text{ and } \quad c_{\phi ,L} = \frac{2(1-e^{-2L(\sigma c)^2})}{\pi ^2(\sigma c)^2} . \end{aligned}$$

(4.52)

For the estimate of $C_{\phi ,L}$ we have used that

$$\begin{aligned} \frac{1}{3\alpha }(a+\alpha b)=a^2b+\alpha ab^2+\frac{\alpha ^2}{3}b^3 \le a^3+\frac{b^3}{3}(1+2\alpha ^{3/2}+\alpha ^2)\le a^3+b^2(1+\alpha ^2) \end{aligned}$$

with Hölder.

Theorem 4.4

Let $\phi \in \Phi$ and assume that ${\widehat{\phi }}$ is $\mathcal {C}^1$-smooth on $[-c,c]$. Assume that $\Lambda \subseteq {\mathbb {R}}$ is a stable sampling set for Problem 1 with frame bounds A, B (i.e., (1.4) holds:

$$\begin{aligned} A \Vert f\Vert _2^2 \le \int _0^L \sum _{\lambda \in \Lambda } \left| (f*\phi _t)(\lambda ) \right| ^2 dt \le B \Vert f\Vert _2^2, \text { for all } f \in PW_c. \end{aligned}$$

(1.4)

Let $c_{\phi ,L}$ and $C_{\phi ,L}$ be the constants from Lemma 4.2. Then for $R\ge \displaystyle \max \left( \frac{\pi }{c},\frac{8c}{\pi }\frac{B}{A}\frac{C_{\Phi ,L}}{c_{\Phi ,L}}\right)$ and every $a\in {\mathbb {R}}$, we have $[a-R,a+R]\cap \Lambda \ne \emptyset$. Further, we have $D^-(\Lambda )\ge \displaystyle \min \left( \frac{c}{2\pi }, \frac{\pi }{16c}\frac{A}{B}\frac{c_{\Phi ,L}}{C_{\Phi ,L}}\right)$ and $\displaystyle D^+(\Lambda )\le 4\frac{B}{c_{\Phi ,L}}$.

Proof

Denoting $I_a = [a-\pi /4c,a+\pi /4c]$, $a\in {{\mathbb {R}}}$, let us bound the covering number

$$\begin{aligned} n_{\Lambda }:=\sup \limits _{a\in {\mathbb {R}}}\#\left( \Lambda \cap I_a \right) . \end{aligned}$$

We use (4.49), i.e., the fact that $\displaystyle \int _0^L|({\text {sinc}}(c\cdot )*\phi _t)(x)|^2\,\text{ d }t\ge c_{\Phi ,L}$ for $|x|\le \pi /2c$, and our first observation to obtain

$$\begin{aligned} \#\left( \Lambda \cap I_a \right)\le & {} \frac{1}{c_{\Phi ,L}} \sum \limits _{\lambda \in \Lambda \cap I_a}\int _0^L|({\text {sinc}}(c\cdot )*\phi _t)(\lambda -a)|^2\text{ d }t\\\le & {} \frac{1}{c_{\Phi ,L}} \sum \limits _{\lambda \in {{\mathbb {Z}}}}\int _0^L|({\text {sinc}}(c\cdot )*\phi _t)(\lambda -a)|^2\text{ d }t \le \frac{B}{c_{\Phi ,L}}\Vert {\text {sinc}}c(t - a)\Vert ^2 \end{aligned}$$

where we applied (1.4) to $f(t)={\text {sinc}}c(t - a)$ for all $a\in {\mathbb {R}}$. As $\hat{f}(\xi )=\displaystyle \frac{\pi }{c}\mathbf {1}_{[-c,c]}$, Parseval’s relation gives $\Vert f\Vert ^2 =\frac{\pi }{c}$ hence

$$\begin{aligned} n_{\Lambda }\le \frac{\pi }{c}\frac{ B}{c_{\Phi ,L}}. \end{aligned}$$

(4.53)

As a first consequence, this implies that $D^+(\Lambda )\le 4\frac{B}{c_{\Phi ,L}}$.

Now we assume that for some $a_0\in {\mathbb {R}}$, and some $R\ge \displaystyle \frac{\pi }{c}$, $\Lambda \cap [a_0-R,a_0+R]=\emptyset$. As the Paley-Wiener space is invariant under translation, if (1.4) holds for $\Lambda$, it also holds for its translates, so that we may assume that $a_0=0$.

From Lemma 4.2, there exists $C_{\Phi ,L}$ such that $\displaystyle \int _{0}^{L}|({\text {sinc}}(c\cdot )*\phi _t)(x)|^2\mathrm {d}t\le C_{\Phi ,L}/(1+x^2)$. Therefore, we have the following estimates

$$\begin{aligned} \frac{\pi }{c}A\le & {} \sum \limits _{\lambda \in \Lambda }\int _0^L| ({\text {sinc}}(c\cdot )*\phi _t)(\lambda )|^2\,\text{ d }t \le \sum \limits _{\lambda \in \Lambda }\frac{C_{\Phi ,L}}{1+\lambda ^2}\\\le & {} \sum \limits _{k=0}^\infty \sum \limits _{\lambda \in \Lambda \cap [R+k\pi /2c,R+(k+1)\pi /2c]} \frac{C_{\Phi ,L}}{1+\lambda ^2} +\sum \limits _{k=0}^\infty \sum \limits _{\lambda \in \Lambda \cap [-R-(k+1)\pi /2c,-R-k\pi /2c]} \frac{C_{\Phi ,L}}{1+\lambda ^2}\\\le & {} 2n_{\Lambda }\sum \limits _{k=0}^\infty \frac{C_{\Phi ,L}}{1+(R+k\pi /2c)^2} \le 4\frac{C_{\Phi ,L}B}{c_{\Phi ,L}}\int _{R-\pi /2c}^{\infty }\frac{\mathrm {d}x}{1+x^2}\\\le & {} 4\frac{C_{\Phi ,L}B}{c_{\Phi ,L}}\int _{R/2}^{\infty }\frac{\mathrm {d}x}{x^2}=8\frac{C_{\Phi ,L}B}{c_{\Phi ,L}R} \end{aligned}$$

since we assumed that $R\ge \pi /c$. It follows that $R\le \displaystyle \frac{8c}{\pi }\frac{B}{A}\frac{C_{\Phi ,L}}{c_{\Phi ,L}}$. Finally, note that this implies that $D^-(\Lambda )\ge \frac{1}{2R}$. $\square$

Remark 4.5

Computing the explicit estimate for $\frac{C_{\Phi ,L}}{c_{\Phi ,L}}$, we observe that the maximal allowed gap in spacial measurements grows with L, which is to be expected. For the Gaussian, we may take the constant $\frac{C_{\Phi ,L}}{c_{\Phi ,L}}$ to be $O(L^2)$ (see (4.52)). The above results also shows that for $\mathcal {C}^1$-smooth functions $\phi$, stable sampling sets must have positive lower density.

Remark 4.6

Theorem 4.4 immediately implies Theorem 1.4.