Abstract
Extending an example by Colding and Minicozzi (Trans Am Math Soc 356(1):283–289, 2003), we construct a sequence of properly embedded minimal disks \(\Sigma _i\) in an infinite Euclidean cylinder around the \(x_3\)-axis with curvature blow-up at a single point. The sequence converges to a non-smooth and non-proper minimal lamination in the cylinder. Moreover, we show that the disks \(\Sigma _i\) are not properly embedded in a sequence of open subsets of \(\mathbb {R}^3\) that exhausts \(\mathbb {R}^3\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In a series of influential papers [2,3,4,5], Colding and Minicozzi initiated the study of sequences of minimal disks in a 3-manifold. In general, if no restriction on the curvatures of the disks is required, it is known that some wild behaviour should be expected. For instance, in [1] Colding and Minicozzi constructed an example of a sequence of minimal disks in a Euclidean ball for which curvatures blow up at the centre of the ball, and such that the limit lamination is neither smooth nor proper. This result is obtained by a careful analysis of the Weierstrass representation of the minimal disks.
Following this example, a number of similar results have been obtained via analogous methods, in which comparable wild limits are observed with the curvature blowing up at a finite set of points on a line [6], along a closed segment [8], or more generally any compact subset of a line [9]. Using variational methods, Hoffman and White [7] provided examples of minimal disks in an infinite Euclidean cylinder with curvature blow-ups along any prescribed compact subset of the axis of the cylinder.
In this paper, we follow the approach of [1] and show that their example can be extended to create a sequence of properly embedded minimal disks \(\Sigma _i\) in an infinite Euclidean cylinder, displaying the same pathologies. By [5], it is known that these pathologies do not occur if the sequence \(\Sigma _i\) is indeed a sequence of minimal disks properly embedded in a sequence of open sets which invade the whole \(\mathbb {R}^3\).
Here we prove that the disks \(\Sigma _i\), which we obtained by extending the ones constructed in [1], do not give rise to minimal disks properly embedded in a growing family of cylinders which exhaust \(\mathbb {R}^3\).
Our main result is therefore analogous to Theorem 1 in [1] and can be stated as follows; we refer to [1] for the definition of multi-valued graph and pictures.
Theorem 1.1
One can construct a sequence of properly embedded minimal disks \(0\in \Sigma _i\subset \lbrace x_1^2+x_2^2\le 1, x_3\in \mathbb {R}\rbrace \subset \mathbb {R}^3\) containing the \(x_3\)-axis, \(\lbrace (0,0,t)\mid t\in \mathbb {R}\rbrace \subset \Sigma _i\), and such that the following conditions are satisfied:
- (1)
\(\lim _{i\rightarrow \infty }\vert A_{\Sigma _i}\vert ^2(0)=\infty \);
- (2)
\(\sup _i\sup _{\Sigma _i\setminus B_\delta }\vert A_{\Sigma _i}\vert ^2<\infty \) for all \(\delta >0\);
- (3)
\(\Sigma _i\setminus \lbrace x_3\text {-axis}\rbrace =\Sigma _{1,i}\cup \Sigma _{2,i}\), for multi-valued graphs \(\Sigma _{1,i}\) and \(\Sigma _{2,i}\);
- (4)
\(\Sigma _{i}\setminus \lbrace x_3=0\rbrace \) converges to two embedded minimal disks \(\Sigma ^{\pm }\subset \lbrace \pm x_3>0\rbrace \) with \(\overline{\Sigma ^{\pm }}\setminus \Sigma ^{\pm }=\lbrace x_1^2+x_2^2\le 1, x_3=0\rbrace \). Moreover, \(\Sigma ^{\pm }\setminus \lbrace x_3\text {-axis}\rbrace =\Sigma ^{\pm }_1\cup \Sigma ^{\pm }_2\) for multi-valued graphs \(\Sigma ^\pm _1\) and \(\Sigma ^\pm _2\) each of which spirals into \(\lbrace x_3=0\rbrace \).
From (4) we get that \(\Sigma _i\setminus \lbrace 0\rbrace \) converges to a minimal lamination of \(\lbrace x_1^2+x_2^2\le 1,x_3\in \mathbb {R}\rbrace \setminus \lbrace 0\rbrace \) (with leaves \(\Sigma ^-\), \(\Sigma ^+\), and \(\lbrace x_1^2+x_2^2\le 1, x_3=0\rbrace \setminus \lbrace 0\rbrace \)) which does not extend to a lamination of \(\lbrace x_1^2+x_2^2\le 1, x_3\in \mathbb {R}\rbrace \). In other words, 0 is not a removable singularity.
The structure of the paper is as follows: in Sect. 2 we review the definitions and basic results on the Weierstrass representation of minimal surfaces in the Euclidean space \(\mathbb {R}^3\), and set up some notations for the domains and functions that will be used. In Sect. 3, we show that the disks constructed with those data are properly embedded in a fixed infinite Euclidean cylinder around the \(x_3\)-axis, and in Sect. 4 we show that they are not a sequence of properly embedded disks in an exhausting family. Section 5 contains the conclusion of the proof of the main theorem.
2 Preliminaries and Set Up
Let us first fix some notation. Following [1], we will use \((x_1,x_2,x_3)\) as the coordinates in \(\mathbb {R}^3\) and \(z=x+iy\) in \(\mathbb {C}\). Given \(f:\mathbb {C}\rightarrow \mathbb {C}^n\), \(\partial _xf\) and \(\partial _yf\) will denote \(\frac{\partial f}{\partial x}\) and \(\frac{\partial f}{\partial y}\), respectively, and likewise we will have \(\partial _zf=\frac{1}{2}(\partial _xf-i\partial _yf)\). Given a point \(p=(p_1,p_2,p_3)\in \mathbb {R}^3\) and a value \(r>0\), we will denote by \(D_{r}(p)\) the Euclidean disk of radius r, contained in the horizontal plane \(\lbrace x_3=p_3\rbrace \), and centred at the point \(p=(p_1,p_2,p_3)\).
When \(\Sigma \) is a smooth surface embedded in \(\mathbb {R}^3\), we denote by \(\mathbf {K}_\Sigma \) its sectional curvature, and by \(A_\Sigma \) its second fundamental form; so when \(\Sigma \) is minimal we will have \(\vert A_\Sigma \vert ^2=-2 \mathbf {K}_\Sigma \). Moreover, when \(\Sigma \) is oriented, \(\mathbf {n}_\Sigma \) will denote its unit normal.
Let us recall the classical definition of a Weierstrass representation and its role in constructing minimal surfaces (see [10]). Let \(\Omega \subset \mathbb {C}\) be a domain in the complex plane, g a meromorphic function on \(\Omega \) and \(\phi \) a holomorphic 1-form on \(\Omega \); then we refer to the couple \((g,\phi )\) as a Weierstrass representation.
Given a a Weierstrass representation \((g,\phi )\), one can associate to it a conformal minimal immersion \(F:\Omega \rightarrow \mathbb {R}^3\)
Here, \(z_0\in \Omega \) denotes a fixed base point, and the integral is taken along a path \(\gamma _{z_0,z}\) that joins \(z_0\) to z in \(\Omega \). As soon as g has no zeros or poles and \(\Omega \) is simply connected, F will not depend on the choice of the integration path (see [1]). On the other hand the choice of the base point \(z_0\) will change the value of F by an adding constant.
Using the Weierstrass data, one can find explicit formulae for the unit normal \(\mathbf {n} \) and the Gauss curvature \(\mathbf {K}\) (see [10, Sects. 8 and 9]):
As previously pointed out, the main goal of this paper is to provide an unbounded extension of the domain, on which to keep the same choice of the Weierstrass data as in [1]. The map F is guaranteed to be an immersion (that is, \(dF\ne 0\)) as soon as \(\phi \) does not vanish and g has no zeros or poles.
We include the following lemma (see Lemma 1 in [1]), since its results will be useful for some further computations later on.
Lemma 2.1
Let F be as in Eq. (2.1) for the Weierstrass data \((g,\phi )\) given by \(g(z)=e^{i(u(z)+iv(z)}\) and \(\phi =dz\), then
Let us construct the one-parameter family (with parameter \(a\in (0,1/2]\)) of minimal immersions \(F_a\) that we will be using to construct our family of embedded minimal disks \(\Sigma _a\).
Definition 2.2
We choose the same Weierstrass data \((g_a,\phi )\) as in [1], that is
In this case, the two real functions u and v in Lemma 2.1 will then depend on the parameter a: \(h_a=u_a+iv_a\) (see Remark 2.6 for an explicit formulation of both \(u_a\) and \(v_a\)).
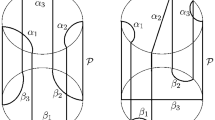
In this paper, we are extending the original bounded domain \(\Omega _a\) defined in [1] to an unbounded one, which will still be denoted by \(\Omega _a\). To do so, we will first introduce the two families of domains \(\mathcal {D}^1_a\) and \(\mathcal {D}^2_a\), as follows (see Fig. 1):
One should notice that the two domains \(\mathcal {D}^1_a\) and \(\mathcal {D}^2_a\) cross at the points where
hence somewhere in the intervals \([\sqrt{3}/2, 1]\) and \([-1,-\sqrt{3}/2]\), depending on the parameter \(a\in (0,1/2]\). One should also notice that for \(x^2>1-a^2\), the second domain \(\mathcal {D}^2_a\) (in red) is strictly contained inside the first domain \(\mathcal {D}^1_a\) (in blue), that is
Vice versa, for \(x^2<1-a^2\), we have the opposite inclusion:
In Colding and Minicozzi’s paper, the domains of definition \(\Omega _a\) are exactly taken as follows (see [1, Eq. (2.1)]):
which always falls into case (2.11), since \(\frac{1}{4}<1-a^2\) for any \(a\in (0,1/2]\).
Let us take into consideration the value \(\frac{1}{\pi }\) (please refer to Remark 3.2 for the reasoning behind the choice of this value). If we divide the interval \([\frac{1}{\pi },\frac{1}{2}]\) into thirds, we get the following two values:
By symmetry, the points \(-x_B\) and \(-x_A\) will divide into thirds the interval \([-\frac{1}{2},-\frac{1}{\pi }]\).
As already pointed out, \(\mathcal {D}^1_a\cap \lbrace (x,y)\mid \vert x \vert \le \frac{1}{2}\rbrace \subset \mathcal {D}^2_a\cap \lbrace (x,y)\mid \vert x \vert \le \frac{1}{2}\rbrace \), which means that if we consider the two boundaries as follows:
we will see jumps (see Fig. 2 for a graphical representation of these jumps) of magnitude equal to \(y_B-y_A\), where
In order to join these two domains:
we can simply take the following line segments:
Using these segments, we are then able to define our domains of definition \(\Omega _a\).
Definition 2.3
Our unbounded domains of definition \(\Omega _a\) for \(a\in (0,1/2]\) are given by
and
where \(\Omega _0^{+}\)and \(\Omega _0^{-}\) are, respectively, the right and left components of \(\Omega _0\).
Remark 2.4
One should notice that Definition 2.3 gives rise to domains \(\Omega _a\) whose boundaries are piecewise smooth. In order to obtain smooth domains, it is sufficient to take the convolution of the boundary with a Friedrich mollifier.
Remark 2.5
Let us notice that, by construction, \(\Omega _a\subset \mathcal {D}_a^2\) for any \(a\in [0,1/2]\).
Remark 2.6
Let us study the explicit formulation of \(h_a=u_a+iv_a\). On a suitable domain of definition we have, using the standard notation \(z=x+iy\), that
Remark 2.7
Let us further notice that the functions \(h_a\) are indeed well defined, since the domains \(\Omega _a\) are simply connected and the points \(\pm ia\notin \Omega _a\). In fact, when \(x=0\), we have \(\vert y\vert \le a^{3/2}/2\), and we have that \(a^{3/2}/2<a\) if and only if \(a<4\) (and by construction we are assuming \(a\le 1/2\)).
Definition 2.8
In order to fix the notation, we will be denoting by \(F_a\) the conformal minimal immersion \(F_a:\Omega _a\rightarrow \mathbb {R}^3\) associated to the Weierstrass representation \((g_a,\phi )\) for any \(a\in (0,1/2]\).
In the following lemma, we will be covering some explicit expressions and bounds that will be useful in the next sections. Unless otherwise stated, from now on we will be working within our domains of definition, that is \(z=x+iy\in \Omega _a\).
Lemma 2.9
Let \(h_a(z)=u_a(z)+iv_a(z)=\frac{1}{a}\arctan \left( \frac{z}{a}\right) \) be as above; then the following holds:
- (1)
\(\partial _z h_a(z)=\dfrac{1}{z^2+a^2}=\dfrac{x^2+a^2-y^2-2ixy}{(x^2+a^2-y^2)^2+4x^2y^2}\,,\)
- (2)
\(\mathbf {K}_a(z)=-\dfrac{\vert \partial _z h_a\vert ^2}{\cosh ^4(v_a)}=-\dfrac{\vert z^2+a^2\vert ^{-2}}{\cosh ^4(Im(\arctan (z/a))/a)}\,,\)
- (3)
\(\partial _y u_a(z)=\dfrac{2xy}{(x^2+a^2-y^2)^2+4x^2y^2}\,,\)
- (4)
\(\partial _y v_a(z)=\dfrac{x^2+a^2-y^2}{(x^2+a^2-y^2)^2+4x^2y^2}\,,\)
- (5)
\(|\partial _y u_a(z)| \le \dfrac{4|xy|}{(x^2+a^2)^2}\,, \)
- (6)
\(\partial _y v_a(z) > \dfrac{3}{8(x^2+a^2)}\,,\)
- (7)
\(v_a(x,y)\ge 0\text { for }y\ge 0\text { and }v_a(x,y)<0\text { for }y<0\,.\)
Proof
(1) and (2) are just computations, and (3) and (4) follow directly from (1) by applying the Cauchy–Riemann equations to \(h_a\) (see equations (2.2), (2.3) and (2.4) in [1]).
Both inequalities (5-6) are obtained using the estimate \(y^2\le \frac{x^2+a^2}{4}\), which holds for every point \((x,y) \in \Omega _a\) (see Remark 2.5). Finally, we obtain (7) by combining (6) with the fact that \(v_a(x,0)=0\). \(\square \)
Remark 2.10
Using the notation in Definition 2.1, we have that for any \(x\in \mathbb {R}\)\(F_a(x,0)=(0,0,x)\). This can be obtain by directly integrating equation (2.4), knowing that \(v_a(x,0)=0\).
Let us further fix the following notation for points on the boundary of \(\Omega _a\).
Definition 2.11
Given fixed values for \(x_0\in \mathbb {R}\) and \(a\in (0,1/2]\), we will denote by \(y_{x_0,a}\) the y value of the point of intersection between the line \(x=x_0\) and the boundary of \(\Omega _a\) in the upper half-plane. Likewise, we will denote by \(-y_{x_0,a}\) the y value of the point of intersection between \(x=x_0\) and the boundary in the lower half-plane.
In other words:
and
Remark 2.12
As already observed in Remark 2.5, we have \(\Omega _a\subset \mathcal D^2_a\). This implies in particular that for all \(x\in \mathbb {R}\) and \(a\in (0,1/2]\) we have \(|y_{x,a}|\le \frac{(x^2+a^2)^{1/2}}{2}\).
3 Lower bound: properly embedded in an infinite cylinder
In this section we want to show that all the minimal disks \(\Sigma _a=F_a(\Omega _a)\) are properly embedded in a fixed infinite cylinder around the \(x_3\)-axis in \(\mathbb {R}^3\). To do this, following [1], we analyse the intersection of \(\Sigma _a\) with the horizontal planes \(\lbrace x_3=x\rbrace \) for varying \(x\in \mathbb {R}\). We will see that there exists some \(R_0>0\) such that for all \(a\in (0,\frac{1}{2}]\) and for all \(x \in \mathbb {R}\), the intersection \(\Sigma _a \cap \{x_3=x\}\) is a smooth curve in the plane \(\{x_3=x\}\) going through the base point \(F_a(x,0)=(0,0,x)\) (see Remark 2.10), whose restriction to the disk \(D_{R_0}((0,0,x))\) is properly embedded in \(D_{R_0}((0,0,x))\).
The following lemmas are the extension of Lemma 3 in [1] to our unbounded domains. Let us fix some notations. We will consider the curves
and use the notation \(\gamma '_{x,a}(y)=\frac{\partial F_a}{\partial y}(x,y)\). Using Eq. (2.5) on the choice of Weierstrass data made in Definition 2.2, this vector can easily be computed to be
so in particular we have that
Lemma 3.1
Using the notations above, the following holds:
- (1)
\(x_3(F_a(x,y))=x\), that is \(\gamma _{x,a}=\Sigma _a \cap \{x_3=x\}\),
- (2)
\(\cos (\gamma '_{x,a}(y),\gamma '_{x,a}(0))=\cos (u_a(x,y)-u_a(x,0))\),
- (3)
the curve \(\gamma _{x,a}\) is a graph over the line with direction \(\gamma '_{x,a}(0)\), contained in a sector of angle \(\theta _0\le \frac{1}{x_A}=\frac{6\pi }{4+\pi }\) (see Eq. (2.13) for the definition of \(x_A\)).
Proof
Statement (1) follows directly from Eq. (2.1), as \(\phi =dz\). Let us prove the other points. Notice that when \(|x|\le x_A\) they are proved in Lemma 3 in [1], so let us focus on the case \(|x|> x_A\). To prove (2), following [1], we consider
so that by the above remarks we get
On the other hand, Eq. (2.5) can also be used to obtain directly that
which proves (2).
To obtain (3) we are going to integrate the inequalities obtained in Lemma 2.9 and use the fact that throughout \(\Omega _a\) we have \(y^2\le \frac{x^2+a^2}{4}\) (see Remark 2.12):
Let us fix an angle \(\theta \in (2, \pi )\). From the last estimate and (2) we get that the absolute value of the angle between \(\gamma '_{x,a}(y)\) and \(\gamma '_{x,a}(0)\) is at most \(\frac{\theta }{2}\) if and only if \(|x|>\frac{1}{\theta }\). We are looking at the case \(|x|>x_A\), so we get that the angle is at most \(\frac{1}{2x_A}\), so that all the tangent vectors \(\gamma '_{x,a}(y)\) live in a sector of angle at most \(\frac{1}{x_A}=\frac{6\pi }{4+\pi }<\pi \) in the direction of \(\gamma '_{x,a}(0)\). In particular \(\gamma _{x,a}\) is a graph over the line in that direction. But by continuity this actually implies that the whole curve is contained in the same sector. \(\square \)
Remark 3.2
For \(|x|\le x_A < \frac{1}{2}\), [1, Eq. (2.11)] proves that \(\gamma _{x,a}\) is contained in a sector of angle 2. In our extension to \(|x|>x_A\), we get a sector of angle \(\theta _0=\frac{1}{x_A}=\frac{6\pi }{4+\pi }\) (see Eq. (2.13) for the definition of \(x_A\)). The reason for this particular choice is as follows: in order to get a convex sector we need \(0<\theta _0=\frac{1}{x_A}<\pi \), i.e. \(\frac{1}{\pi }<x_A\), but in order to get a connected domain \(\Omega _a\) we also need \(x_A<\frac{1}{2}\).
The first third of the interval \([\frac{1}{\pi },\frac{1}{2}]\) turns out to be a geometrically convenient choice to satisfy both conditions, and this is the main reason for the specific choice of \(x_A\) we made above. Any other choice for the value of \(x_A\) in the interval \((\frac{1}{\pi },\frac{1}{2})\) would work.
In Lemma 3 of [1], it is also proved that when \(|x|\le 1/2\), the curves \(\gamma _{x,a}\) have their endpoints outside the disks \(D_{r_0}((0,0,x))\), where \(r_0>0\) does not depend on a or x. We are now going to prove that the same is still true for arbitrarily large values of |x|.
Lemma 3.3
Using the notations above, there exists \( r_0'>0\) such that for any \(|x|>x_A\), and for any \( a \in (0,\frac{1}{2}]\), we have \(||\gamma _{x,a}(y_{x,a})-\gamma _{x,a}(0)||>r_0'\).
Proof
For any \(y\in [-y_{x,a},y_{x,a}]\) we have the following equality:
and we want to find a lower bound for this quantity which is independent of a and x. As observed above, \(||\gamma '_{x,a}(0)||=1\), and of course the cosine term is bounded. So it is enough to bound the numerator of the right-hand side. Reasoning as in the previous lemma, we have the following:
From Lemma 3.1 we get that the absolute value of the argument of the cosine is at most \(\frac{\theta _0}{2}=\frac{1}{2x_A}=\frac{4+\pi }{3\pi }\), so we can get a lower bound for the cosine.
Moreover from Lemma 2.9 we have \(v_a(x,y)\ge 0\) when \(y\ge 0\). This implies that the integrand function is non-negative, and allows us to get
so it is now enough to provide a lower bound for \(v_a\). Integrating the estimate in point (6) of Lemma 2.9, one easily gets that
In the end we get
\(\square \)
We conclude this section with the following statement.
Proposition 3.4
There exists \(R_0>0\) such that, for any \(a \in (0,\frac{1}{2}]\), the surface \(\Sigma _a\cap \{x_1^2+x_2^2\le R_0^2, x_3 \in \mathbb {R}\}\) is a properly embedded minimal disk. Moreover, we have that \(\lbrace 0<x_1^2+x_2^2<R_0^2,\,x_3\in \mathbb {R}\rbrace \cap F_a(\Omega _a)=\tilde{\Sigma }_{1,a}\cup \tilde{\Sigma }_{2,a}\) for multi-valued graphs \(\tilde{\Sigma }_{1,a}\) and \(\tilde{\Sigma }_{2,a}\) over \(D_{R_0}(0)\setminus \lbrace 0\rbrace \).
Proof
By Lemma 3.1 we have that \(F_a\) is an embedding. From Corollary 1 in [1], it follows that there exists a \(r_0>0\) such that for all \(|x|\le x_A\) and \(a\in (0,\frac{1}{2}]\) we have that \(\Sigma _a\cap \{x_3=x\}\) intersects \(D_{r_0}((0,0,x))\) in a properly embedded arc. A similar statement holds when \(|x|>x_A\) for a possibly different \(r_0'>0\) thanks to Lemma 3.3. It is then enough to take \(R_0=\min \{r_0,r_0'\}\).
Furthermore, if we consider Eq. (2.2), we get that \(F_a\) is vertical, that is \(\langle \mathbf {n},(0,0,1)\rangle =0\) when \(\vert g_a\vert =1\). However, \(\vert g_a(x,y)\vert =1\) exactly when \(y=0\), and hence by Remark 2.10, we know that the image is graphical away from the \(x_3\)-axis. Combining this with Lemma 3.3 for \(\vert x\vert \ge x_A\) and [1, Eq. (2.8)] for \(|x|\le x_A\), we finally get our result. \(\square \)
4 Upper bound: not properly embedded in an exhaustion of \(\mathbb {R}^3\)
We are left to prove that our minimal disks \(\Sigma _a\) are not properly embedded in any growing sequence of open sets that exhausts \(\mathbb {R}^3\).
In order to do so, we will show that there exists at least a value \(x\ne 0\) for which the maximal excursion of all helicoids on the horizontal slice \(\lbrace x_3=x\rbrace \) is bounded from above by a constant \(C_x\) depending only on x. This would then imply that one can find an infinite cylinder wide enough (for example, we could take \(\lbrace x_1^2+x^2_2 < 2C_x,\,x_3\in \mathbb {R}\rbrace \)) in which the minimal disks \(\Sigma _a\) are not properly embedded. As we will see in Remark 4.3 this is actually the case for all \(x \ne 0\).
Lemma 4.1
Given an arbitrary value \(x\in \mathbb {R}\setminus \lbrace 0\rbrace \), we have
where \(M_x\) is a constant that depends only on x.
Proof
By construction, as already pointed out in Remark 2.12, we know that \( y^2\le \frac{1}{4}(x^2+a^2)\) for any \((x,y)\in \Omega _a\) and for any \(a\in (0,1/2]\), and hence from Lemma 2.9 we get
Applying this estimate (and knowing \(v_a(x,y)\) is an increasing function in y, see Lemma 2.9), we then obtain
\(\square \)
Lemma 4.2
Given an arbitrary value \(x\in \mathbb {R}\setminus \lbrace 0\rbrace \), we also have
where \(N_x\) is a constant that depends only on x.
Proof
Using the Eqs. (3.3, 3.4), we get
Therefore, since cosine is a bounded function, and using the estimate provided by Lemma 4.1, we obtain
\(\square \)
Remark 4.3
Let us study the behaviour of \(N_x\). As already pointed out before, \(M_x=C\cdot 1/\vert x\vert \), and hence
therefore \(N_x\rightarrow \infty \) both when \(\vert x\vert \rightarrow 0\), and when \(\vert x\vert \rightarrow \infty \). On the other hand, for any x for which \(\vert x\vert \in (0,\infty )\), we have that \(N_x\) is bounded.
Proposition 4.4
The minimal disks \(\Sigma _a\) cannot be properly embedded in any growing sequence of open sets in \(\mathbb {R}^3\) that exhausts \(\mathbb {R}^3\).
Proof
In order to prove this, it is sufficient to show that there exists at least one value of \(x\in \mathbb {R}\) for which the maximal excursion of all the helicoids \(\Sigma _a\) on the horizontal slice \(\lbrace x_3=x\rbrace \) is bounded from above by a constant that depends only on x.
In order to do so, we will be combining the results provided in Lemma 4.2 and Lemma 3.1, so we finally obtain
\(\square \)
5 Proof of Theorem 1.1
This result is analogous to Theorem 1 in Colding and Minicozzi’s paper [1]. In order for this paper to be self-contained, we report the proof below.
Proof of Theorem 1.1
Up to rescaling, it is sufficient to show that there exists a sequence \(\Sigma _i\subset \lbrace x_1^2+x_2^2\le R^2,\,x_3\in \mathbb {R}\rbrace \), for some \(R>0\). Lemma 3.1 gives minimal embeddings \(F_a:\Omega _a\rightarrow \mathbb {R}^3\) with \(F_a(x,0)=(0,0,x)\) for any \(x\in \mathbb {R}\) (see Remark 2.10), so by Proposition 3.4 (3) holds for any \(R\le R_0\).
Let us take \(R=\frac{R_0}{2}\) and \(\Sigma _i=\lbrace x_1^2+x_2^2\le R,\,x_3\in \mathbb {R}\rbrace \cap F_{a_i}(\Omega _{a_i})\), where the sequence \(a_i\) is to be determined.
To get (1), simply notice that, by equation in point (2) of Lemma 2.9, we get \(\vert \mathbf {K}_a\vert (0)=a^{-4}\rightarrow \infty \) as \(a\rightarrow 0\).
Still applying the same equation in point (2) of Lemma 2.9, we get that for all \(\delta >0\), \(\sup _a\sup _{\lbrace \vert x\vert \ge \delta \rbrace \cap \Omega _a}\vert \mathbf {K}_a\vert <\infty \) . Combine this with (3) and Heinz’s curvature estimate for minimal graphs (see [10, Eq. (11.7)]), and we get (2).
In order to get (4), we use Lemma 2 in [1] to choose \(a_i\rightarrow 0\) so the mappings \(F_{a_i}\) converge uniformly in \(C^2\) on compact subsets to \(F_0:\Omega _0\rightarrow \mathbb {R}^3\). Hence, by Lemma 3.1 and Proposition 3.4, the \(\Sigma _i\setminus \lbrace x_3=0\rbrace \) converge to two embedded minimal disks \(\Sigma ^\pm \subset F_0(\Omega _0^\pm )\) with \(\Sigma ^\pm \setminus \lbrace x_3\text {-axis}\rbrace =\Sigma _1^\pm \cup \Sigma _2^\pm \) for multi-valued graphs \(\Sigma _i^\pm \).
To complete the proof, one should notice that in a small enough neighbourhood of the plane \(\{x_3=0\}\), our minimal disks \(\Sigma _i\) coincide with those constructed in [1]. Hence each graph \(\Sigma _i^{\pm }\) is \(\infty \)-valued (and hence spirals into the horizontal plane \(\lbrace x_3=0\rbrace \)), completing point (4). \(\square \)
References
Colding, T.H., Minicozzi II, W.P.: Embedded minimal disks: proper versus nonproper—global versus local. Trans. Am. Math. Soc. 356(1), 283–289 (2003)
Colding, T.H., Minicozzi II, W.P.: The space of embedded minimal surfaces of fixed genus in a 3-manifold I; estimates off the axis for disks. Ann. Math. 160, 27–68 (2004)
Colding, T.H., Minicozzi II, W.P.: The space of embedded minimal surfaces of fixed genus in a 3-manifold II; Multi-valued graphs in disks. Ann. Math. 160, 69–92 (2004)
Colding, T.H., Minicozzi II, W.P.: The space of embedded minimal surfaces of fixed genus in a 3-manifold III; planar domains. Ann. Math. 160, 523–572 (2004)
Colding, T.H., Minicozzi II, W.P.: The space of embedded minimal surfaces of fixed genus in a 3-manifold IV; locally simply-connected. Ann. Math. 160, 573–615 (2004)
Dean, B.: Embedded minimal disks with prescribed curvature blowup. Proc. Am. Math. Soc. 134(4), 1197–1204 (2006)
Hoffman, D., White, B.: Sequences of embedded minimal disks whose curvatures blow up on a prescribed subset of a line. Commun. Anal. Geom. 19(3), 487–502 (2011)
Khan, S.: A minimal lamination of the unit ball with singularities along a line segment. Ill. J. Math. 53.3(2009), 833–855 (2010)
Kleene, S.J.: A minimal lamination with Cantor set-like singularities. Proc. Am. Math. Soc. 140(4), 1423–1436 (2012)
Osserman, R.: A survey of minimal surfaces. Courier SiddiCorporation, Tallahassee (2002)
Acknowledgements
Open access funding provided by University of Jyväskylä (JYU). The authors wish to thank the Department of Mathematics of Bologna University for its kind hospitality during the early stage of this project. This work has been partially supported by the Academy of Finland (Grant 288501 ‘Geometry of subRiemannian groups’), by the European Research Council (ERC Starting Grant 713998 GeoMeG ‘Geometry of Metric Groups’) and by the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie Grant Agreement No 777822 (‘Geometric and Harmonic Analysis with Interdisciplinary Applications’).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ruffoni, L., Tripaldi, F. Extending an Example by Colding and Minicozzi. J Geom Anal 30, 1028–1041 (2020). https://doi.org/10.1007/s12220-019-00177-4
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12220-019-00177-4