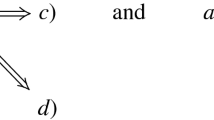On Attractors of Generalized Semiflows with Impulses

Abstract

This paper is devoted to the study of global attractors for problems with state-dependent impulses and possible nonuniqueness of solutions. We provide the criteria under which there exists the global attractor, being on one hand an invariant set, and on the other hand given by the difference of the minimal compact attracting set and the impulsive set M. The new condition (T) used to get the global attractor invariance is discussed and compared with other conditions used in literature for impulsive problems. The theory is illustrated by several examples.

1 Introduction

In the last 20 years, a lot of interest has been attracted to dynamical systems approach to evolutionary problems where the uniqueness of solutions is unknown, or the solution is known to be nonunique for a given initial data. There are several approaches to construct the global attractors for such problems: the approach by multivalued semiflows (or m-semiflows) anticipated by Babin and Vishik [1] and developed by Melnik and Valero [28, 29], the approach by generalized semiflows developed by Ball [3, 4], the one by trajectory attractors developed independently by Chepyzhov and Vishik [11], Málek and Nečas [27], and Sell [32], and finally the approach by the evolutionary systems by Cheskidov and Foiaş [12]. Fairly recent overview of all these approaches can be found in the review paper [2], and some most recent new results for the nonautonomous problems can be found in [17, 18]. In the present paper, we focus on two of those theories, the one of m-semiflows and the one of generalized semiflows (which were related to each other in article [9]) to develop the theory of global attractors for the problems with possible nonuniqueness of solutions and with state-dependent impulses.

The theory of dynamical systems with state-dependent impulses describes the evolution of systems whose continuous development of the process is interrupted by abrupt changes of state. A motivation for considering the dynamical systems with state-dependent impulses comes, for example, from neuroscience. The simplest model of a neuron, the so-called integrate-and-fire neuron, is represented by means of the following ordinary differential equation (ODE)

$$\begin{aligned} u'(t) = -\gamma u(t) + S(t), \end{aligned}$$

with the additional condition

$$\begin{aligned} \text {if}\ \ u(t)= \theta \ \ \text {then}\ \ u(t)\ \ \text {is reset to value}\ \ u_r < \theta . \end{aligned}$$

We are looking for the function u which is the membrane potential of a neuron. It is charged through the excitation, $S(t)\ge 0$, and when it reaches the threshold value $\theta$, the neuron fires and it is reset to the rest potential $u_r$, see [26].

Another impulsive model of a neuron is the Izhikevich model [23] that is based on the following system of two ODEs with the state-dependent impulse

$$\begin{aligned}&v'(t) = 0.04 v^2(t) + 5 v(t) + 140 - u(t) + I(t),\\&u'(t) = a (bv(t) - u(t)),\\&\mathrm {if}\ \ v(t) \ge 30 \ \ \mathrm {then}\ \ v(t) = c\ \text {and}\ u(t) = u(t) + d. \end{aligned}$$

In this model, the membrane potential of a neuron is represented by the variable v and the membrane recovery variable u represents the ionic currents. On one hand, for various values of constants a, b, c, d, the model can mimic various firing patterns of physiological neurons, and, on the other hand, it is computationally simple, as it reduces the number of unknowns from four in the biologically plausible Hodgkin–Huxley model, just to two variables. This simplification without the loss of accuracy in representing the actual physiological behavior is possible due to the presence of impulses in the model [23].

The theory of impulsive dynamical systems with state-dependent impulses, started with Kaul in the paper [24], where he defined the evolution of such systems. Later on, Ciesielski in article [13] presented sufficient conditions to guarantee the continuity of the function that describes the time of reaching impulse points. Moreover, in [14], he obtained the impulsive version of the Ura theorem on stability. Finally, in recent years, Bonotto et al. [5,6,7] obtained the results on existence and upper and lower semicontinuity of attractors for impulsive systems.

In this article, we develop the theory of impulsive dynamical systems for the semigroups without imposing the uniqueness of the state obtained after some time of evolution from the given initial state. We define the impulsive and multivalued dynamical system, which we call impulsive generalized semiflow, and which consists of a generalized semiflow $\mathcal {G}$, an impulsive set M, and an impulsive multifunction I. The set M is the set of states such that if a trajectory of $\mathcal {G}$ reaches the point $x \in M$, then it jumps into a point belonging to I(x). We define the notion of a c-attractor$\mathcal {A}_c$ for this semiflow, i.e., the smallest compact attracting set, without requiring its invariance, and, using the approach of [10] we establish the equivalent conditions for its existence. If $M\cap I(M) = \emptyset$ then the points of M can only be initial points of the trajectories of the impulsive system and, hence, if the intersection $M \cap \mathcal {A}_c$ is nonempty then there is no chance for the set $\mathcal {A}_c$ be invariant. Thus, similar as it is done in the single-valued case in [6], we define the global attractor for the impulsive system as $\mathcal {A}=\mathcal {A}_c{\setminus } M$. The first key results of this paper, Lemma 3.7 and Theorem 3.9 provide the conditions under which this set, although it can possibly be only relatively compact rather than compact, is attracting. This result is new even in the single-valued case as it does not require the tube conditions used in [6] to get the same result. The next key results of this paper, Theorem 4.7 and Corollary 4.8 provide the new condition, called here the condition (T), under which the global attractor $\mathcal {A}$ is invariant. The results are based on the approach of [10, 16, 17], where it is noted that it is enough to obtain the negative invariance of the attractor only for a one given positive time to get its full invariance for all possible times. This approach proves to be convenient for impulsive problems because it allows to restrict to the time length on which at most one jump can occur, and thus it is sufficient to study the situation where the trajectory has only one jump. The results are complemented by the discussion on the continuity of the impact time function, the comparison of our condition (T) with other conditions used for invariance of the attractor for impulsive systems, the criteria for asymptotic compactness, and several examples of impulsive dynamical systems without uniqueness.

We note here that the impulsive dynamical systems for the problems without uniqueness of solutions have already been studied in [20, 30, 31]. The theory developed in the present article complements and extends the results of these papers. First, in addition to them, we obtain the result that the set $\mathcal {A} = \mathcal {A}_c {\setminus } M$ is attracting, and second, similar as [20, 30, 31] we provide the criteria for the global attractor invariance but we show that the condition (24) of [20] is not needed for this invariance which significantly broadens the class of problems, for which our theory works with respect to that of [20, 30, 31], cf. Example 7.8 in Sect. 7.

The structure of the article is as follows. Section 2 is devoted to the definition of the impulsive generalized semiflows. The results on the existence of the global attractor for these semiflows are the subject of Sect. 3 and on their invariance, of Sect. 4. The continuity of the impact time map is studied in Sect. 5, and the criteria which guarantee the asymptotic compactness of generalized impulsive semiflows are provided in Sect. 6. Finally, the comparison of our condition (T) used to obtain the invariance with the other conditions used in literature is contained in Sect. 7, and some examples which illustrate the constructed theory are presented in last Sect. 8.

2 Generalized Impulsive Semiflows

In this section, we remind two useful formalisms for the dynamical systems description of problems without uniqueness of solutions, namely the theory of m-semiflows and the theory of generalized semiflows.

Let (X, d) be a complete metric space. By $\mathcal {P}(X)$ and $\mathcal {B}(X)$ we will denote, respectively, the families of nonempty and nonempty bounded subsets of X. We will also denote ${\mathbb {R}}_+=[0,\infty ),$$\mathbb {N} = \{0,1,2,\ldots \}$ and $\mathbb {N}^+ = \{1,2,\ldots \}$. We denote a sequence $\{x_j\}_{j\in {\mathbb {N}}}$ simply by $\{x_j\}$. By $C([0,\infty );X)$ we mean the set of all continuous functions defined on $[0, \infty )$ taking values in X. We recall the definition of the Hausdorff semidistance between two sets $A,B\subset X$ by $\mathrm {dist}_X(A,B) = \displaystyle \sup _{x\in A}\displaystyle \inf _{y\in B} d(x,y)$.

We start by recalling the theory of generalized semiflows in the sense of Ball [3, 4]. The concept of generalized semiflow will be the base for our formalism of multivalued impulsive systems since it includes in its definition the notion of trajectories and this extra structure is crucial to build the impulsive theory.

Definition 2.1

A family $\mathcal {G}$ of functions $u:{\mathbb {R}}_+\rightarrow X$ will be called a generalized semiflow if the following conditions are satisfied:

(B1):

(Existence) For every $x\in X$ there exists $u\in \mathcal {G}$ such that $u(0) = x$.

(B2):

(Translation property) If $u\in \mathcal {G}$ then for every $\tau \ge 0$ the function $u^\tau$ defined as $u^\tau (t) = u(t+\tau )$ for $t\ge 0$ also belongs to $\mathcal {G}$.

(B3):

(Concatenation property) If $u, v\in \mathcal {G}$ with $v(0)=u(t)$, $t\ge 0$, then the function $w\in \mathcal {G}$, where

$$\begin{aligned} w(s) =&{\left\{ \begin{array}{ll} u(s)\ &{}\text {when}\ s\in [0,t],\\ v(s-t)\ &{}\text {otherwise}. \end{array}\right. } \end{aligned}$$

(B4):

(Uniform upper semicontinuity with respect to initial data) For every sequence $\{u_j\}\subset \mathcal {G}$ with $u_j(0) \rightarrow z$ as $j\rightarrow \infty$, there exist a subsequence $\{u_\mu \} \subset \{ u_j \}$ and $u\in \mathcal {G}$ such that for every compact set $J\subset {\mathbb {R}}_+$

$$\begin{aligned} \lim _{\mu \rightarrow \infty }\sup _{t\in J}d(u_\mu (t),u(t)) = 0. \end{aligned}$$

(B5):

(Continuity) Every trajectory $u\in \mathcal {G}$ is a continuous function from $[0,\infty )$ to X.

The functions $u \in \mathcal {G}$ will be called trajectories of the generalized semiflow $\mathcal {G}$. We will use the notation $\mathcal {G}_x = \{u \in \mathcal {G}: \, u(0)=x\}$.

Next, we recall the definition of upper semicontinuity of multifunctions.

Definition 2.2

Let $X_1, X_2$ be metric spaces. A multifunction $F:X_1\rightarrow \mathcal {P}(X_2)$ is said to be upper semicontinuous at $x\in X_1$, if for every sequence $x_j\rightarrow x$ in $X_1$ and every open set $\mathcal {U}\subset X_2$ such that $F(x)\subset \mathcal {U}$ then there exists $j_0 \in {\mathbb {N}}$ such that for every $j\ge j_0$ we have $F(x_j)\subset \mathcal {U}$.

The following fact is well known in set-valued analysis. Its proof follows the lines of the proof of [21, Proposition 4.1.11], we provide it only for the completeness of exposition.

Lemma 2.3

Let $X_1, X_2$ be metric spaces. The multifunction $F:X_1\rightarrow \mathcal {P}(X_2)$ is upper semicontinuous and compact valued for each $x\in X_1$ if and only if for every sequence $x_j\rightarrow x$ in $X_1$ and every sequence $y_j \in F(x_j)$, $j\in {\mathbb {N}}$, there exists a subsequence $\{ y_\mu \} \subset \{y_j\}$ such that $y_\mu \rightarrow y$ in $X_2$ and $y\in F(x)$.

Proof

We first prove the sufficiency. Take $x_j\rightarrow x$ as $j\rightarrow \infty$ and $y_j\in F(x_j)$, $j\in {\mathbb {N}}$. Suppose that no subsequence of $\{y_j\}$ converges to a point in F(x). This means that for every $y\in F(x)$ there exists $m_0(y)$ and an open neighborhood $\mathcal {U}(y)$ such that $y_j \not \in \mathcal {U}(y)$ for all $j\ge m_0(y)$. The sets $\mathcal {U}(y)$ constitute an open cover of the compact set F(x), whereas $F(x) \subset \bigcup _{i=1}^n \mathcal {U}(\bar{y}_i) = \mathcal {U}$. There exists $m_0$ such that for every $j\ge m_0$ there holds $y_j \not \in \mathcal {U}$. On the other hand, by the upper semicontinuity of F it follows that there exists $j_0$ such that for every $j\ge j_0$ there holds $F(x_j) \subset \mathcal {U}$, whereas $y_j \in \mathcal {U}$, which is a contradiction.

We pass to the proof of necessity. It is clear that F(x) must be a compact set for every $x\in X_1$. Let $x_j \rightarrow x$ in $X_1$ as $j\rightarrow \infty$ and let $\mathcal {U}\subset X_2$ be an open set such that $F(x)\subset \mathcal {U}$. If F is not upper semicontinuous, there must exist a sequence $y_j\in F(x_j)$ and $j_0$ such that $y_j\not \in \mathcal {U}$ for $j\ge j_0$. By hypothesis, for a subsequence, denoted by the same index, $y_j \rightarrow y$ where $y\in F(x)$, which is a contradiction. $\square$

Remark 2.4

If we equip $\mathcal {G} \subset C([0,\infty );X)$ with the following metric of the uniform convergence on compact subsets of $\mathbb {R}_+,$

$$\begin{aligned} d_{\mathcal {G}}(u,v) = \sum _{n=1}^\infty \frac{1}{2^n}\frac{\max _{t\in [0,n]}d(u(t),v(t))}{1+\max _{t \in [0,n]}d(u(t),v(t))}, \end{aligned}$$

then, by Lemma 2.3, it is not difficult to see that condition (B4) actually means that the mapping

$$\begin{aligned} x \,\ni X\mapsto \mathcal {G}_x \subset \mathcal {G} \subset C([0, \infty );X) \end{aligned}$$

is upper semicontinuous and compact valued in $C([0, \infty );X)$.

Remark 2.5

Our definition enforces in the definition of the generalized semiflow conditions (C3) and (C4) presented in [3, 4]. These conditions are needed to build the impulsive theory of generalized semiflows. Note that Ball [3, 4] uses a weaker definition, he does not impose (B5), and in place of (B4) he has a weaker assertion of upper semicontinuity with respect to initial data, not necessarily uniform with respect to t in compact sets, that is, Ball considers the following condition

$(B4')$ For every sequence $\{u_j\}\subset \mathcal {G}$ with $u_j(0) \rightarrow z$ as $j\rightarrow \infty$, there exist a subsequence $\{u_\mu \} \subset \{ u_j \}$ and $u\in \mathcal {G}$ such that $u(0) = z$ and

$$\begin{aligned} \lim _{\mu \rightarrow \infty }d(u_\mu (t),u(t)) = 0. \end{aligned}$$

In our theory, we will need (B4) and (B5) for the global attractor existence, so we incorporate these two assertions in the definition. Our conditions (B4) and (B5) are restrictive; however, they usually hold for generalized semiflows governed by ordinary differential equations (ODEs). They also hold for the weakly damped semilinear wave equation with cubic growth on the nonlinearity (without any growth assumptions on its derivative), cf., [3, Example 2.3].

The theory of generalized semiflows will be the starting point in the construction of the multivalued impulsive dynamical systems. We will, however, also need some notions from an alternative theory, namely multivalued semiflow theory. Hence, following Melnik and Valero [28], we remind the definition of a multivalued semiflow (m-semiflow).

Definition 2.6

A family $\{\pi (t)\}_{t\ge 0}$ of multivalued maps $\pi (t):X\rightarrow \mathcal {P}(X)$ is called an m-semiflow if the following conditions hold:

(A1):

$\pi (0)x = \{x\}$ for every $x\in X$;

(A2):

$\pi (s+t)x\subset \pi (s)\pi (t)x$ for every $t, s\in \mathbb {R}_+$ and $x\in X$.

If in (A2) we have the equality $\pi (s+t)x= \pi (s)\pi (t)x$ in place of the inclusion, then the m-semiflow is said to be strict.

The comparison of the two theories has been done in [9]. From [9, Proposition 2] it follows, that having, from a generalized semiflow $\mathcal {G}$ we can construct a strict m-semiflow by the formula

$$\begin{aligned} y\in \pi (t)x \quad \Leftrightarrow \quad \text {there exists a trajectory}\ u\in \mathcal {G}\ \text {such that}\ u(0) = x\ \text {and} \ u(t) = y, \end{aligned}$$

valid for all $x\in X$ and $t\ge 0$.

Now, we are in position to define an impulsive generalized semiflow.

Definition 2.7

An impulsive generalized semiflow $(\mathcal {G},M,I)$ consists of a generalized semiflow $\mathcal {G}$, a nonempty closed set $M\subset X$ and an upper semicontinuous multifunction $I:M \rightarrow \mathcal {P}(X)$. We assume that for every $x\in M$ there exists $\epsilon _{x} > 0$ such that for every $u\in \mathcal {G}_x$

$$\begin{aligned} \bigcup _{t \in (0, \epsilon _{x})} \{u(t)\} \cap M = \emptyset \end{aligned}$$

(1)

and

$$\begin{aligned} \mathrm {if}\quad u(t_0)=x\quad \text {for some} \quad t_0\in (0,\epsilon _x) \quad \text {and} \quad u \in \mathcal {G} \quad \mathrm {then} \quad \bigcup _{t \in [0,t_0)} \{u(t)\} \cap M = \emptyset .\nonumber \\ \end{aligned}$$

(2)

Let $(\mathcal {G},M,I)$ be an impulsive generalized semiflow. By condition (1), we are able to define the impact time of a trajectory $u\in \mathcal {G}$ by the function

$$\begin{aligned} \phi (u) = \inf \{t> 0\,:\ u(t)\in M\}, \end{aligned}$$

where we use the notation $\phi (u) = \infty$ if $u(t) \notin M$ for all $t>0$.

Remark 2.8

Note that $\phi (u)>0$ for every trajectory $u \in \mathcal {G}$. Indeed, if u is a trajectory in $\mathcal {G}$ with $u(0)\in M$ then it is clear from (1) that $\phi (u)>0$. On the other hand, let $u\in \mathcal {G}$ with $u(0)\not \in M$ and $\phi (u) = 0$. Thus there exists a sequence $t_j \rightarrow 0^+$ as $j\rightarrow \infty$ with $u(t_j) \in M$ for all $j\in {\mathbb {N}}$, whereas due to condition (B5) of Definition 2.1 and closedness of M, it must be that $u(0)\in M$, which is a contradiction.

Remark 2.9

For every trajectory $u\in \mathcal {G}$ such that $\phi (u)\ne \infty$ there holds $u(\phi (u))\in M$. In fact, if we assume that $u(\phi (u))\not \in M$ then there exists a sequence $t_j\rightarrow 0^+$ as $j\rightarrow \infty$ such that $u(\phi (u)+t_j)\in M$ for all $j\in {\mathbb {N}}$. The assertion follows by the continuity of u and closedness of M.

Next, we define the concept of impulsive trajectory of an impulsive generalized semiflow. Let us define ${\mathbb {N}}_k = \{0,1,2,\ldots , k\}$ for $k\in {\mathbb {N}}$ and ${\mathbb {N}}_{\infty } = {\mathbb {N}}$.

Definition 2.10

A mapping $\tilde{u}: [0, \omega ) \rightarrow X$$(0 < \omega \le \infty )$ will be called an impulsive trajectory of an impulsive generalized semiflow $(\mathcal {G},M,I)$ if there exists a division of $[0, \omega )$ into a family of intervals

$$\begin{aligned}{}[0, \omega ) = \displaystyle \bigcup _{n \in {\mathbb {N}}_k}[t_n,t_{n+1}) \quad \text {with}\quad t_0=0, \; t_n < t_{n+1}\quad \text {and}\quad 0\le k \le \infty , \end{aligned}$$

such that for every $n\in {\mathbb {N}}_k$ there exists a trajectory $u_n\in \mathcal {G}$ satisfying:

(i):

either $\phi (u_n) = \infty$ or $\phi (u_n) = t_{n+1}-t_n$;

(ii):

$\tilde{u}(t+t_n) = u_n(t)$ for $t\in [0,\phi (u_n));$

(iii):

if $\phi (u_n) \ne \infty$ then $\tilde{u}(t_{n+1}) \in I(u_n(\phi (u_n)))$.

The time points $t_n$ for $n\in {\mathbb {N}}_k{\setminus } \{ 0\}$ will be called jump points of the impulsive trajectory $\tilde{u}$. The family of impulsive trajectories of an impulsive generalized semiflow will be denoted by $\tilde{\mathcal {G}}$.

Remark 2.11

In Definition 2.10, if $\omega = \infty$ then $t_1 = \infty$ when $k=0$, $t_{k+1} = \infty$ when $1\le k < \infty$ and $\displaystyle \lim _{j\rightarrow \infty } t_j = \infty$ when $k=\infty$. On the other hand, if $\omega < \infty$ then $k = \infty$ as the functions in $\mathcal {G}$ are defined on $[0, \infty )$.

Having the definition of an impulsive trajectory, we may define a new family of multivalued mappings $\{ \tilde{\pi }(t)\}_{t\ge 0}$ with $\tilde{\pi }(t):X\rightarrow \mathcal {P}(X)$ by the formula

$$\begin{aligned} y\in \tilde{\pi }(t)x \quad \Leftrightarrow \quad \text {there exists}\ \tilde{u}\in \tilde{\mathcal {G}}\ \text {such that}\ \tilde{u}(0) = x \ \text {and} \ \tilde{u}(t) = y. \end{aligned}$$

Note that, we first construct the family of trajectories $\tilde{\mathcal {G}}$, and then, from this family, we construct the multivalued mappings $\tilde{\pi }(t)$, $t\ge 0$. This is similar to the construction of an m-semiflow from the generalized semiflow described in [9]. In the sequel, we prove several properties of ${\tilde{\pi }}$ and of $\tilde{\mathcal {G}}$ which will indeed signify that $\tilde{\pi }$ is a strict multivalued semiflow.

Proposition 2.12

Assume that $(\mathcal {G},M,I)$ is an impulsive generalized semiflow. Then for every $x\in X$ there exists $\tilde{u}\in \tilde{\mathcal {G}}$ defined in some interval $J=[0, \omega )$$(\omega$ may be $\infty )$ with $\tilde{u}(0) = x$.

Proof

Let $x\in X$ and $u_0 \in \mathcal {G}_x$. If $\phi (u_0) = \infty$ then the construction is complete. Otherwise, by Remark 2.8 we have $\phi (u_0)>0$. Denote $t_1 = \phi (u_0)$. By Remark 2.9, $u_0(t_1)\in M$. Let $x_1 \in I(u_0(t_1))$. Now, take $u_1 \in \mathcal {G}_{x_1}$. If $\phi (u_1) = \infty$ then we end the construction and define

$$\begin{aligned} \tilde{u}(t) =&{\left\{ \begin{array}{ll} u_0(t)\quad &{}\text {for} \quad t\in [0,t_1)\\ u_1(t-t_1)\quad &{}\text {otherwise}. \end{array}\right. } \end{aligned}$$

If $\phi (u_1)$ is finite, then we denote $t_2 = t_1 + \phi (u_1)$ and we choose $x_2 \in I(u_1(\phi (u_1)))$. Take $u_2 \in \mathcal {G}$, a trajectory with $u_2(0) = x_2$. Again, either $u_2$ does not touch M which allows us to end the construction by taking

$$\begin{aligned} \tilde{u}(t) =&{\left\{ \begin{array}{ll} u_0(t)\quad &{}\text {for} \quad t\in [0,t_1)\\ u_1(t-t_1)\quad &{}\text {for} \quad t\in [t_1,t_2)\\ u_2(t-t_2)\quad &{}\text {otherwise}, \end{array}\right. } \end{aligned}$$

or $\phi (u_2)$ is finite, in which case we continue the construction recursively. Either the construction ends after a finite number of steps, in which case

$$\begin{aligned} \tilde{u}(t) =&{\left\{ \begin{array}{ll} u_n(t-t_n)\quad &{}\text {for} \quad t\in [t_n,t_{n+1}),\quad n\in \{0,\ldots , M-1\}\\ u_{M}(t-t_M)\quad &{}\text {for}\quad t\ge t_M, \end{array}\right. } \end{aligned}$$

or

$$\begin{aligned} \tilde{u}(t) = u_n(t-t_n)\quad \text {for} \quad t\in [t_n,t_{n+1}),\quad n\in \mathbb {N}. \end{aligned}$$

Note that

$$\begin{aligned} \mathrm {either}\quad J = [0, +\infty ) \quad \mathrm {or} \quad J = [0, \omega ) \quad \mathrm {with} \quad \omega = \displaystyle \sum _{j=0}^{\infty } \phi (u_j), \end{aligned}$$

whence we have constructed an impulsive trajectory starting from x which ends the proof. $\square$

In the proof of Proposition 2.12, if we assume that there exists $\xi > 0$ such that $\phi (u)\ge \xi$ for every $u\in \mathcal {G}$ with $u(0)\in I(M)$ and $\phi (u_j) < \infty$ for all $j\in {\mathbb {N}}$, then

$$\begin{aligned} \displaystyle \sum _{j=0}^{\infty } \phi (u_j) = \infty . \end{aligned}$$

Consequently, we have the next result.

Corollary 2.13

Assume that $(\mathcal {G},M,I)$ is an impulsive generalized semiflow and there exists $\xi > 0$ such that $\phi (u)\ge \xi$ for every $u\in \mathcal {G}$ with $u(0)\in I(M)$. Then every trajectory $\tilde{u} \in \tilde{\mathcal {G}}$ is defined in $J= {\mathbb {R}}_+$. Consequently, for every $x\in X$ there exists $\tilde{u} \in \tilde{\mathcal {G}}$ defined in ${\mathbb {R}}_+$ such that $\tilde{u} (0) = x.$

In this way, we shall assume from now on the following condition:

$$\begin{aligned} \mathbf (H) \quad \quad \text {There exists} \ \xi > 0 \ \text {such that} \ \phi (u)\ge \xi \ \text {for every} \ u\in \mathcal {G} \ \text {with} \ u(0)\in I(M). \end{aligned}$$

Lemma 2.14 below shows that $\tilde{\mathcal {G}}$ satisfies the translation and concatenation properties and $\tilde{\pi }$ is a strict multivalued semiflow.

Lemma 2.14

Assume that $(\mathcal {G},M,I)$ is an impulsive generalized semiflow satisfying (H). Then

(i):

$\tilde{\mathcal {G}}$ satisfies the translation and concatenation properties from Definition 2.1.

(ii):

$\{\tilde{\pi }(t)\}_{t\ge 0}$ satisfies $\tilde{\pi }(s+t)x = \tilde{\pi }(s)\tilde{\pi }(t)x$ for every $x\in X$ and every $s,t\ge 0$.

Proof

(i):

Let $\tilde{u} \in \tilde{\mathcal {G}}$ and $\tau \ge 0$. Define the function $\tilde{u}^\tau$ by $\tilde{u}^\tau (t) = \tilde{u}(t+\tau )$ for $t\ge 0$. Assuming without loss of generality that the impulsive trajectory $\tilde{u}$ admits infinite number of impulses, we may write

$$\begin{aligned} \tilde{u}(t) = u_n(t-t_n)\quad \text {for} \quad t\in [t_n,t_{n+1})\quad n\in \mathbb {N}, \end{aligned}$$

where $\{u_n\} \subset \mathcal {G}$, $t_0 = 0$ and $t_n =\phi (u_0) +\ldots + \phi (u_{n-1})$ for every $n \in \mathbb {N}^+$. There exists $k \in \mathbb {N}$ such that $t_{k} \le \tau < t_{k + 1}$. Denote $\tau _0 = 0$, $\tau _n = t_{k+n} - \tau$ for $n\in \mathbb {N}^+$, $v_0 = u_k(\cdot +\tau -t_k)$ and $v_n = u_{n+k}$ for $n\in \mathbb {N}^+$. Then

$$\begin{aligned} \tilde{u}^{\tau }(t) = v_{n}(t - \tau _{n}) \quad \text {for} \quad t\in [\tau _n, \tau _{n+1}) \quad \text {and} \quad n\in \mathbb {N}, \end{aligned}$$

$\phi (v_n) = \tau _{n+1} - \tau _n$, $\tilde{u}(\tau _{n+1}) \in I(v_n(\phi (v_n)))$ and ${\mathbb {R}}_+ = \bigcup _{n\in \mathbb {N}}[\tau _n,\tau _{n+1})$. Hence, $\tilde{u}^{\tau } \in \tilde{\mathcal {G}}$.

We pass to the proof of the concatenation property. Let $\tilde{u}, \tilde{v} \in \tilde{\mathcal {G}}$ be such that $\tilde{u}(t) = \tilde{v}(0)$, $t\ge 0$. Define $\tilde{w}$ by

$$\begin{aligned} \tilde{w}(s) =&{\left\{ \begin{array}{ll} \tilde{u}(s)\ &{}\text {when}\ s\in [0,t],\\ \tilde{v}(s-t)\ &{}\text {otherwise}. \end{array}\right. } \end{aligned}$$

Assuming that $\tilde{u}$ and $\tilde{v}$ admit infinite numbers of impulses, we may write

$$\begin{aligned} \tilde{u}(t) = u_n(t-t_n)\quad \text {for} \quad t\in [t_n,t_{n+1})\quad n\in \mathbb {N}, \end{aligned}$$

and

$$\begin{aligned} \tilde{v}(t) = v_n(t-s_n)\quad \text {for} \quad t\in [s_n,s_{n+1})\quad n\in \mathbb {N}, \end{aligned}$$

where $\{u_n\}, \{v_n\} \subset \mathcal {G}$, $t_0=s_0 = 0$, $t_n =\phi (u_0) +\ldots + \phi (u_{n-1})$ and $s_n =\phi (v_0) +\ldots + \phi (v_{n-1})$ for all $n\in \mathbb {N}^+$. Let $k\in \mathbb {N}$ be such that $t_k \le t < t_{k+1}$. Define the sequence $\{\tau _n\}$ by $\tau _0 = 0$, $\tau _j = t_j$ for $1\le j \le k$, and $\tau _{k+j} = t +s_j$ for $j\in \mathbb {N}^+$. Also, let $w_j = u_j$ for $0 \le j \le k-1$,

$$\begin{aligned} w_{k}(s) =&{\left\{ \begin{array}{ll} u_{k}(s)\ &{}\text {when}\ s\in [0,t - \tau _{k}],\\ v_0(s-t + t_k)\ &{}\text {when}\ s \in [t- \tau _{k}, \tau _{k+1} - \tau _k], \end{array}\right. } \end{aligned}$$

and $w_{k+j} = v_j$ for $j\in \mathbb {N}^+$. Note that $\{w_k\} \subset \mathcal {G}$. Then ${\mathbb {R}}_+ = \bigcup _{n\in \mathbb {N}}[\tau _n,\tau _{n+1})$, $\phi (w_n) = \tau _{n+1}- \tau _n$, $\tilde{w}(t+ \tau _n) = w_n(t)$ for $t\in [0,\phi (w_n))$ and $\tilde{w}(\tau _{n+1}) \in I(w_n(\phi (w_n)))$. Hence, $\tilde{w} \in \tilde{\mathcal {G}}$.

(ii):

Let $y \in \tilde{\pi }(s+t)x$. Then there exists an impulsive trajectory $\tilde{u}\in \tilde{\mathcal {G}}$ such that $\tilde{u}(0) = x$ and $\tilde{u}(t+s) = y$. Let $\tilde{u}(s) = z$ which implies in $z \in \tilde{\pi }(s)x$. Note that

$$\begin{aligned} \tilde{v}(r) = \tilde{u}(s+r), \quad r \ge 0, \end{aligned}$$

belongs to $\tilde{\mathcal {G}}$, $\tilde{v}(0) = z$ and $\tilde{v}(t) = y$. Hence, $y \in \tilde{\pi }(t)z$, that is, $y \in \tilde{\pi }(t)\tilde{\pi }(s)x$.

On the other hand, let $y \in \tilde{\pi }(t)\tilde{\pi }(s)x$. Then there is $z \in \tilde{\pi }(s)x$ such that $y \in \tilde{\pi }(t)z$. Thus, there are impulsive trajectories $\tilde{u}$, $\tilde{v}$ such that $\tilde{u}(0) = x$, $\tilde{u}(s) = z$, $\tilde{v}(0) = z$ and $\tilde{v}(t) = y$. Since

$$\begin{aligned} \tilde{w}(r) =&{\left\{ \begin{array}{ll} \tilde{u}(r)\ &{}\text {when}\ r\in [0,s],\\ \tilde{v}(r-s)\ &{}\text {otherwise}, \end{array}\right. } \end{aligned}$$

belongs to $\tilde{\mathcal {G}}$, $\tilde{w}(0) = x$ and $\tilde{w}(t+s) = y$, we obtain $y \in \tilde{\pi }(s+t)x$. Therefore, $\tilde{\pi }(s+t)x = \tilde{\pi }(s)\tilde{\pi }(t)x$ for every $x\in X$ and every $s,t\ge 0$. $\square$

3 First Results on Attractors

We follow the approach of Chepyzhov, Conti, and Pata who define the global attractor as the smallest compact attracting set, see [10]. Note that in [17] this approach was applied for pullback attractors of nonautonomous multivalued systems, and the same approach was also used in [19], where such type of attractor was called a mini attractor. In [10, 17, 19], no invariance is assumed in the definition of the attractor and no continuity of the underlying semiflow is required for the existence of this object. After obtaining the attractor existence in this “minimal” sense, one tries to recover the attractor invariance (or semi-invariance) after assuming something on the semiflow continuity. Since, in the impulsive case, the semiflow continuity and the attractor invariance are most difficult and delicate to deal with, this approach appears especially well suited in this situation.

3.1 Existence of the Global c-Attractor

Following [5] we define the c-attractor of an impulsive generalized semiflow as its smallest compact attracting set. While the existence of such an object is easy to guarantee under standard assumptions of existence of an absorbing set and asymptotic compactness, this set, in general, will not necessarily be invariant. First, we present the definition of an impulsive $\tilde{\omega }$-limit set which is a generalization to the multivalued case of [6, Definition 3.1].

Definition 3.1

Let $B\in \mathcal {B}(X)$ and $(\mathcal {G},M,I)$ be an impulsive generalized semiflow. The impulsive $\tilde{\omega }$-limit set is defined as

$$\begin{aligned} \tilde{\omega }(B) = \bigcap _{t\ge 0}\overline{\bigcup _{s\ge t}\tilde{\pi }(s)B}. \end{aligned}$$

It is clear that the above definition is equivalent to the following one

$$\begin{aligned} \tilde{\omega }(B) = \{ x\in X\, : \ \text {there exist sequences}\ \{t_j\}\subset {\mathbb {R}}_+ \ \text {and}\ \{\tilde{u}_j\} \subset \tilde{\mathcal {G}} \\ \text {such that}\ \tilde{u}_j(0)\in B, j\in {\mathbb {N}},\ t_j \rightarrow \infty \ \text {and}\ \tilde{u}_j(t_j) \rightarrow x \ \text {as} \ j\rightarrow \infty \}. \end{aligned}$$

We are in position to define the asymptotic compactness of an impulsive generalized semiflow. Similar as in the nonimpulsive situation the asymptotic compactness will turn out to be equivalent to the fact that the $\tilde{\omega }$-limit set of $B\in \mathcal {B}(X)$ is nonempty, compact, and attracts B.

Definition 3.2

An impulsive generalized semiflow $(\mathcal {G},M,I)$ is said to be asymptotically compact if given a set $B\in \mathcal {B}(X)$, a sequence $\{t_j\} \subset {\mathbb {R}}_+$ with $t_j\rightarrow \infty$, a sequence $\{\tilde{u}_j\} \subset \tilde{\mathcal {G}}$ with $\tilde{u}_j(0)\in B$, $j\in {\mathbb {N}}$, then the sequence $\{\tilde{u}_j(t_j)\}$ possesses a convergent subsequence in X.

Lemma 3.3

Let $B\in \mathcal {B}(X)$. Assume that $(\mathcal {G}, M, I)$ is asymptotically compact, satisfies the condition (H) and for each $x \in B$ there exists an impulsive trajectory $\tilde{u} \in \tilde{\mathcal {G}}$ such that $\tilde{u}(0) =x$. Then $\tilde{\omega }(B)$ is nonempty, compact, and attracts the set B.

Proof

The proof is standard and follows by Corollary 2.1 in [25]. $\square$

Definition 3.4

An impulsive generalized semiflow is said to be dissipative if there exists a set $B_0\in \mathcal {B}(X)$ such that for every $B \in \mathcal {B}(X)$ there exists a time $t=t(B) \ge 0$ such that for every $\tilde{u}\in \tilde{\mathcal {G}}$ with $\tilde{u}(0)\in B$ and for every $s\ge t(B)$ there holds $\tilde{u}(s)\in B_0$.

Next, we define the c-attractor of an impulsive generalized semiflow $\tilde{\mathcal {G}}$.

Definition 3.5

A set $\mathcal {A}_c \subset X$ is called a global c-attractor for an impulsive generalized semiflow $(\mathcal {G},M,I)$ if the following properties hold

• $\mathcal {A}_c$ is compact;

• $\mathcal {A}_c$ is attracting, i.e.,

  $$\begin{aligned} \lim _{t\rightarrow \infty }\mathrm {dist}_X(\tilde{\pi }(t)B,\mathcal {A}_c) = 0 \quad \text {for every}\quad B\in \mathcal {B}(X); \end{aligned}$$

• $\mathcal {A}_c$ is minimal in the class of all closed attracting sets.

The next result follows directly from [17, Theorem 3.6].

Theorem 3.6

Let $(\mathcal {G},M,I)$ be an impulsive generalized semiflow satisfying condition (H). Then it has a uniquely defined global c-attractor $\mathcal {A}_c$ if and only if it is asymptotically compact and dissipative. The attractor $\mathcal {A}_c$ is given by

$$\begin{aligned} \mathcal {A}_c = \tilde{\omega }(B_0) = \overline{\bigcup _{B\in \mathcal {B}(X)}\tilde{\omega }(B)}, \end{aligned}$$

where $B_0$ is an absorbing set of $(\mathcal {G},M,I)$.

The notion of global c-attractor was defined for nonautonomous and single-valued case in [5]. This set does not have to be invariant, since it is possible to construct an example where $\mathcal {A}_c$ contains points from M and $I(M)\cap M =\emptyset$, whereas elements of M can only be the initial points of trajectories in $\tilde{\mathcal {G}}$, see [7]. Hence, a natural candidate for the global attractor is the set $\mathcal {A} = \mathcal {A}_c{\setminus } M$. Two questions appear: if the set $\mathcal {A}$ is invariant and if it still attracting. While we postpone the more difficult question of invariance to the next sections, we will first provide the affirmative answer to the second one.

3.2 Existence of Global Attractor

The next property allows us to deduce that if an impulsive generalized semiflow has a c-attractor $\mathcal {A}_c$, then the possibly noncompact set $\mathcal {A}_c{\setminus } M$ is still attracting. This set will be called a global attractor of an impulsive generalized semiflow. Note that the next lemma is a multivalued counterpart of [6, Lemma 3.13].

Lemma 3.7

Let $(\mathcal {G},M,I)$ be an impulsive generalized semiflow which is asymptotically compact and satisfies the condition (H). If $B\in \mathcal {B}(X)$ then

$$\begin{aligned} \tilde{\omega }(B)\cap M \subset \overline{\tilde{\omega }(B){\setminus } M}. \end{aligned}$$

Proof

Take $B\in \mathcal {B}(X)$ and $x\in \tilde{\omega }(B)\cap M$. There exist sequences $\{z_j\} \subset B$ and $t_j\rightarrow \infty$ as $j\rightarrow \infty$, and a sequence of impulsive trajectories $\{\tilde{u}_j\} \subset \tilde{\mathcal {G}}$ such that $\tilde{u}_j(t_j)\rightarrow x$ as $j\rightarrow \infty$ and $\tilde{u}_j(0)=z_j$ for every $j\in {\mathbb {N}}$. For each $j \in {\mathbb {N}}$, there is an integer $n_j\ge 0$ such that $\tau ^j_{n_j} \le t_j < \tau _{n_j+1}^j$ and

$$\begin{aligned} \tilde{u}_{j}(t_{j}) = v_{n_{j}}^j(t_{j} - \tau _{n_j}^j), \end{aligned}$$

where $v_{n_{j}}^j \in \mathcal {G}$ and $\tilde{u}_{j}(t) = v_{n_{j}}^j(t - \tau _{n_j}^j)$ for $\tau _{n_j}^j \le t_j < \tau _{n_j+1}^j$ (if there is no jump in the trajectory $\tilde{u}_j$ for time less than $t_j$, then we may just take $\tau _{n_j}^j = 0$). Let $m\in {\mathbb {N}}$ be such that $\frac{1}{m} < \min \{\epsilon _x,\frac{\xi }{4}\}$, where $\epsilon _x$ comes from Definition 2.7. There exists a subsequence of indexes, which we do not renumber, such that one of the next two assertions hold

(i):

$\tau ^j_{n_j} < t_j - \xi /4$, $j\in {\mathbb {N}}$

(ii):

$t_j + \xi /4 < \tau ^j_{n_j+1}$, $j\in {\mathbb {N}}$.

We continue the proof separately for the two cases.

Case (i). Define $w_j^m= \tilde{u}_j(t_j-\frac{1}{m})$ for $m\in {\mathbb {N}}^+$, $j\in {\mathbb {N}}$. By the asymptotic compactness of the impulsive generalized semiflow, if we fix m, then for a subsequence of j, denoted by the same index and possibly different for each m, there exists $y_m \in \tilde{\omega }(B)$ such that $w_j^m\rightarrow y_m$ as $j\rightarrow \infty$. At first, note that $y_m \not \in M$ for all $m\in {\mathbb {N}}^+$. In fact, let

$$\begin{aligned} \eta _j^m(s) = v_{n_j}^j\left( s + t_{j} - \frac{1}{m} - \tau _{n_j}^j\right) \quad \text {for} \quad s\ge 0. \end{aligned}$$

Since $\eta _j^m(0) \rightarrow y_m$ as $j\rightarrow \infty$, it follows by condition (B4) of Definition 2.1 that there exists $\eta _m\in \mathcal {G}$ with $\eta _m(0) = y_m$ such that for a subsequence of j, which we still denote by the same index, $\eta _j^m \rightarrow \eta _m$ as $j\rightarrow \infty$, uniformly on compact subsets of ${\mathbb {R}}_+$. Hence,

$$\begin{aligned} d(\eta _m(1/m),x)&\le d(\eta _m(1/m),\eta ^m_j(1/m)) + d(\eta ^m_j(1/m),x)\\&\le \sup _{t\in [0,1]}d(\eta _m(t), \eta ^m_j(t))+d(\tilde{u}_j(t_j),x). \end{aligned}$$

The last expression can be made arbitrarily small by taking j large enough, and hence $\eta _m(1/m) = x\in M$. Since $\eta _m(0) = y_m$ and $1/m < \epsilon _x$, we deduce that $y_m\not \in M$, i.e., $y_m\in \tilde{\omega }(B){\setminus } M$ for every $m\in {\mathbb {N}}^+$.

Second, the compactness of $\tilde{\omega }(B)$ implies that $y_m\rightarrow x_0$ as $m\rightarrow \infty$ (passing to a subsequence if necessary). If $x_0\ne x$, then taking another subsequence if necessary, there exists $\eta \in \mathcal {G}$ with $\eta (0) = x_0$ such that $\eta _m \rightarrow \eta$ as $m\rightarrow \infty$, uniformly on compact subsets of ${\mathbb {R}}_+$ (see condition (B4)). Thus,

$$\begin{aligned} d(x,x_0)&= d(\eta _m(1/m),\eta (0)) \le d(\eta _m(1/m), \eta (1/m))+ d(\eta (1/m),\eta (0))\\&\le \sup _{t\in [0,1]}d(\eta _m(t), \eta (t))+ d(\eta (1/m),\eta (0)). \end{aligned}$$

The right-hand side of the last expression can be made as close to zero as we want by taking large m. Hence, it has to be $x=x_0$. It follows that the whole sequence $y_m$ converges to x and the proof for case (i) is complete.

Case (ii). Define $w^m_j= \tilde{u}_j(t_j+\frac{1}{m})$ for $m\in {\mathbb {N}}^+$, $j\in {\mathbb {N}}$. Similarly as in the case (i), using the asymptotic compactness, it follows that for each m there exists $y_m\in \tilde{\omega }(B)$ such that, for a subsequence, still denoted by j, there holds $w^m_j \rightarrow y_m$ as $j\rightarrow \infty$. We will prove that $y_m \not \in M$ for all $m\in {\mathbb {N}}^+$. In fact, let

$$\begin{aligned} \eta _j(s) = v_{n_j}^j\left( s + t_{j} - \tau _{n_j}^j\right) \quad \text {for} \quad s\ge 0. \end{aligned}$$

Since $\eta _j(0) \rightarrow x$ as $j\rightarrow \infty$, it follows by condition (B4) of Definition 2.1 that there exists $\eta \in \mathcal {G}$ with $\eta (0) = x$ such that for a subsequence of j, still denoted by the same index, $\eta _j \rightarrow \eta$ as $j\rightarrow \infty$, uniformly on compact subsets of ${\mathbb {R}}_+$. In particular, $w_j^m = \eta _j(1/m) \rightarrow \eta (1/m)$ as $j\rightarrow \infty$, which means that $y_m = \eta (1/m)$. Since $\eta (0) = x\in M$ and $1/m < \epsilon _x$ we deduce that $y_m\not \in M$, i.e., $y_m\in \tilde{\omega }(B){\setminus } M$ for all $m\in {\mathbb {N}}^+$. Now, since $\eta$ is a continuous function it follows that $y_m = \eta (1/m) \rightarrow \eta (0) = x$ as $m\rightarrow \infty$ and the proof for case (ii) is complete. $\square$

Next, we define the concept of global attractor for an impulsive generalized semiflow.

Definition 3.8

A set $\mathcal {A}\subset X$ is called a global attractor for an impulsive generalized semiflow $(\mathcal {G},M,I)$ if

(i):

$\mathcal {A} = \overline{\mathcal {A}}{\setminus } M$ and $\overline{\mathcal {A}}$ is compact;

(ii):

$\mathcal {A}$ is attracting;

(iii):

$\overline{\mathcal {A}}$ is the smallest closed attracting set.

The difference between the above definition and the definition of the c-attractor stands in the fact that we demand that after we remove elements of M from the smallest closed attracting set, the resulting set should still be attracting.

Theorem 3.9

Let $(\mathcal {G},M,I)$ be an impulsive generalized semiflow which satisfies the condition (H). Then $(\mathcal {G},M,I)$ has a global attractor $\mathcal {A}$ if and only if it is asymptotically compact and dissipative.

Proof

If the global attractor exists then its closure is a c-attractor, consequently the dissipativity and the asymptotic compactness follow from Theorem 3.6. For the proof of the opposite assertion, we assume that the impulsive generalized semiflow is asymptotically compact and dissipative. Theorem 3.6 implies the existence of the c-attractor $\mathcal {A}_c$. Define $\mathcal {A}=\mathcal {A}_c{\setminus } M$. We need to show that $\overline{\mathcal {A}} = \mathcal {A}_c$ and that $\mathcal {A}$ is attracting. By Theorem 3.6 the c-attractor is the impulsive $\omega$-limit of an absorbing set $B_0$, i.e., $\mathcal {A}_c = \tilde{\omega }(B_0)$. It is clear that $\overline{\mathcal {A}} \subset \mathcal {A}_c$. The opposite inclusion follows from Lemma 3.7. Indeed,

$$\begin{aligned} \mathcal {A}_c= & {} (\tilde{\omega }(B_0) {\setminus } M) \cup (\tilde{\omega }(B_0) \cap M) \subset (\tilde{\omega }(B_0) {\setminus } M) \cup \overline{\tilde{\omega }(B_0) {\setminus } M} = \overline{\tilde{\omega }(B_0) {\setminus } M} \\= & {} \overline{\mathcal {A}}. \end{aligned}$$

Now, for $B\in \mathcal {B}(X)$,

$$\begin{aligned} \mathrm {dist}_X(\tilde{\pi }(t)B, \mathcal {A}) = \mathrm {dist}_X(\tilde{\pi }(t)B, \mathcal {A}_c) \rightarrow 0\quad \text {as}\quad t\rightarrow \infty , \end{aligned}$$

and hence $\mathcal {A}$ is attracting, which concludes the proof. $\square$

Remark 3.10

We stress that the statement of the above theorem is similar to [20, Lemma 1]. We note, however, that in [20] the authors do not prove that $\mathcal {A} = \mathcal {A}_c {\setminus } M$ is attracting. So, the result of [20, Lemma 1] is equivalent to our Theorem 3.6 which is the intermediate step to get Theorem 3.9. The novelty of Theorem 3.9 is the proof, that if we remove the elements of the impulse set M from $\mathcal {A}_c$, then the resulting set will still be attracting. We also stress that the above result is the improvement of [6, Lemma 3.13] even for the single-valued case, as we show that the Tube Condition assumed in [6, Lemma 3.13] is in fact not needed for this result to hold.

3.3 Is the Global Attractor Invariant?

The question that remains is, whether the global attractor $\mathcal {A}$ of an impulsive generalized semiflow is an invariant set. Typically, we need to impose some continuity type assumption on the semiflow to recover the attractor invariance. The following example shows that although the underlying generalized semiflow $\mathcal {G}$ satisfies (B4), i.e., it is upper semicontinuous with respect to the initial data, and the jump multifunction I is upper semicontinuous, the global attractor does not have to be invariant.

Example 3.11

Consider the single-valued semiflow given by the solutions of the ODE

$$\begin{aligned}\left\{ \begin{array}{l} x' = x(1-x)(1+x)\\ y' = - y.\end{array} \right. \end{aligned}$$

Let $M = \{ 1/2 \} \times [-1,0]$ and let $I(1/2,y) = \{(3/4 , y)\}$ for $y\in [-1,0]$. It is not hard to verify that $\mathcal {A}_c = [-1,1] \times \{ 0 \}$. Therefore, $\mathcal {A}_c{\setminus } M = ([-1,1] {\setminus } \{1/2\}) \times \{ 0 \}$. This set is attracting but it is neither positively nor negatively invariant. In fact, the largest invariant set included in $\mathcal {A}_c$ is $([-1,1/2) \cup [3/4,1]) \times \{ 0 \}$.

Hence, despite both the semiflow $\mathcal {G}$ is upper semicontinuous with respect to the initial data (in fact, it is single-valued and continuous in the above example) and the jump multifunction is upper semicontinuous (in the above example it is single-valued and continuous), the global attractor does not have to be neither positively nor negatively invariant. This implies that if we want the global attractor to be invariant, then we need some additional assumptions. In the following section, we will provide such assumptions.

4 Invariance of Global Attractor

In Sect. 3, we have proved a result on the existence of the c-attractor $\mathcal {A}_c$ for an impulsive generalized semiflow. This c-attractor could intersect with the set M, thus there was no chance for it to be invariant as in many cases, namely if $I(M)\cap M = \emptyset$, points in M can be only the initial points of the trajectories in $\tilde{\mathcal {G}}$. We have also defined the set $\mathcal {A} = \mathcal {A}_c{\setminus } M$ and we proved that although this set could be no longer compact, it is still attracting. We called this set as the global attractor. This section is devoted to the proof of the invariance of this attractor.

4.1 Definitions and Preliminary Facts

In this subsection, we prove that it is sufficient to obtain the negative semi-invariance of the global attractor on any given time interval. This approach is convenient for problems with impulses as we can restrict our considerations to the short time intervals on which there can occur only at most one jump.

We first remind the definitions of negative and positive semi-invariances for multivalued semiflows (and, equivalently, for impulsive generalized semiflows).

Definition 4.1

A set $S\subset X$ is negatively semi-invariant under the impulsive generalized semiflow $(\mathcal {G},M,I)$ if for every $t\ge 0$ there holds

$$\begin{aligned} S \subset \tilde{\pi }(t)S, \end{aligned}$$

or, in other words, for every $x\in S$ and every $t\ge 0$ there exists an impulsive trajectory $u\in \tilde{\mathcal {G}}$ such that $u(0) \in S$ and $u(t) = x$.

Definition 4.2

A set $S\subset X$ is positively semi-invariant under the impulsive generalized semiflow $(\mathcal {G},M,I)$ if for every $t\ge 0$ there holds

$$\begin{aligned} \tilde{\pi }(t)S \subset S, \end{aligned}$$

or, in other words, for every $x\in S$, every impulsive trajectory $u\in \tilde{\mathcal {G}}$ with $u(0)=x$ and every $t\ge 0$ there holds $u(t)\in S$.

Definition 4.3

A set $S\subset X$ is said to be invariant under the impulsive generalized semiflow $(\mathcal {G},M,I)$ if it is both negatively and positively semi-invariant.

The proof of the next result follows the lines of the proof of [17, Proposition 4.3]. Since impulsive generalized semiflows are strict multivalued semiflows, it states that it is sufficient to prove the negative semi-invariance for some small time $t^*>0$ and, consequently, both negative and positive semi-invariances (and hence the full invariance) will follow for every $t\ge 0$.

Lemma 4.4

Let $(\mathcal {G},M,I)$ be an impulsive generalized semiflow satisfying condition (H) such that $I(M)\cap M = \emptyset$. Assume that $\mathcal {A}$ is the global attractor of this semiflow. If for some $t^*>0$ there holds $\mathcal {A}\subset \tilde{\pi }(t^*)\mathcal {A}$, then $\mathcal {A}$ is invariant.

Proof

Using the fact that $\tilde{\pi }$ is strict, we obtain

$$\begin{aligned} \mathcal {A}\subset \tilde{\pi }(t^*)\mathcal {A} \subset \tilde{\pi }(t^*)\tilde{\pi }(t^*)\mathcal {A} = \tilde{\pi }(2t^*)\mathcal {A} \subset \ldots \subset \tilde{\pi }(nt^*)\mathcal {A} \quad \text {for every}\quad n\in \mathbb {N}^+.\nonumber \\ \end{aligned}$$

(3)

Pick any $s>0$. It follows that

$$\begin{aligned} \mathrm {dist}_X(\tilde{\pi }(s)\mathcal {A},\mathcal {A}) \le \mathrm {dist}_X(\tilde{\pi }(s)\tilde{\pi }(nt^*)\mathcal {A},\mathcal {A}) = \mathrm {dist}_X(\tilde{\pi }(s+nt^*)\mathcal {A},\mathcal {A}). \end{aligned}$$

As $\mathcal {A}$ is attracting, we can pass with n to $\infty$ whence

$$\begin{aligned} \lim _{n\rightarrow \infty }\mathrm {dist}_X(\tilde{\pi }(s+nt^*)\mathcal {A},\mathcal {A}) = 0. \end{aligned}$$

Thus

$$\begin{aligned} \mathrm {dist}_X(\tilde{\pi }(s)\mathcal {A},\mathcal {A}) = 0, \end{aligned}$$

or, in other words,

$$\begin{aligned} \tilde{\pi }(s)\mathcal {A} \subset \overline{\mathcal {A}}. \end{aligned}$$

Since points in M can be only the initial points of the trajectories in $\tilde{\mathcal {G}}$ as $I(M) \cap M = \emptyset$, we deduce that

$$\begin{aligned} \tilde{\pi }(s)\mathcal {A} \subset \overline{\mathcal {A}} {\setminus } M = \mathcal {A}\quad \text {for every}\quad s\ge 0. \end{aligned}$$

(4)

This implies that $\mathcal {A}$ is positively semi-invariant. We pass to the proof of the negative semi-invariance. Using (3) and (4) we deduce that

$$\begin{aligned} \mathcal {A} \subset \tilde{\pi }(nt^*)\mathcal {A} \subset \mathcal {A} \quad \text {for every} \quad n\in \mathbb {N}, \end{aligned}$$

whence

$$\begin{aligned} \mathcal {A} = \tilde{\pi }(nt^*)\mathcal {A} \quad \text {for every} \quad n\in \mathbb {N}. \end{aligned}$$

Let $s\ge 0$ be fixed and choose n such that $s\le nt^*$. Then, by the strictness of $\tilde{\pi }$ and (4) it follows that

$$\begin{aligned} \mathcal {A} = \tilde{\pi }(nt^*)\mathcal {A} = \tilde{\pi }(s)\tilde{\pi }(nt^*-s)\mathcal {A} \subset \tilde{\pi }(s)\mathcal {A}, \end{aligned}$$

whence the assertion follows. $\square$

In the next subsection, we give the criterion for the negative invariance of $\mathcal {A}$ for $t_* = \xi /2$. In consequence, the full invariance for every $t\ge 0$ will follow by Lemma 4.4.

4.2 Negative Invariance of the Global Attractor

It is clear from Example 3.11 that without any additional assumptions the invariance of the global attractor is not true in general. We formulate an additional hypothesis which will guarantee this invariance. The hypothesis relates the set M with the generalized semiflow $\mathcal {G}$:

(T):

If $x \in M$, $\{u_j\} \subset \mathcal {G}$ and $t \in (0,\infty )$ are such that $\{u_j(0)\}$ converges in X and $u_j(t) \rightarrow x$ then there exist a subsequence $\{u_{\mu }\}$ and a sequence $\{\alpha _{\mu }\}\subset {\mathbb {R}}$, $\alpha _{\mu }\rightarrow 0$, such that $t+\alpha _{\mu } \ge 0$ and $u_{\mu }(t+\alpha _{\mu }) \in M$.

Remark 4.5

Since condition (B4) holds, the condition (T) is equivalent to the following condition: if $x \in M$, $\{u_j\} \subset \mathcal {G}$ and $t \in (0,\infty )$ are such that $u_j(t) \rightarrow x$ and

$$\begin{aligned} \lim _{j\rightarrow \infty }\sup _{r\in J}d(u_j(r),u(r))=0\quad \text {on every compact set}\quad J\subset {\mathbb {R}}_+\quad \text {and for some}\quad u\in \mathcal {G}, \end{aligned}$$

then there exist a subsequence $\{u_{\mu }\}$ and a sequence $\{\alpha _{\mu }\}\subset {\mathbb {R}}$, $\alpha _{\mu }\rightarrow 0$, such that $t+\alpha _{\mu } \ge 0$ and $u_{\mu }(t+\alpha _{\mu }) \in M$.

Remark 4.6

We stress that the condition (T) is equivalent to the condition introduced in [20, formula (20), p. 201], as we prove in Sect. 7.2. We remark, however, that in [20] the authors obtain the invariance under this condition, and additional condition given by [20, formula (26), p. 204]. In the following result, we prove that indeed condition (T) guarantees the global attractor invariance, without the need of additional conditions. In Sect. 7.2, we recall [20, formula (26), p. 204] and we give a simple example where this condition is not satisfied and hence the results of [20] cannot be applied, but our next theorem still works.

Theorem 4.7

Let $(\mathcal {G},M,I)$ be an impulsive generalized semiflow satisfying condition (H) such that $I(M) \cap M = \emptyset$. Let $\mathcal {A}$ be the global attractor of $(\mathcal {G},M,I)$. If the condition (T) is satisfied then there holds

$$\begin{aligned} \mathcal {A} \subset \tilde{\pi }(\xi /2)\mathcal {A}. \end{aligned}$$

Proof

Theorem 3.6 and Theorem 3.9 imply that there exists a set $B_0 \in \mathcal {B}(X)$ such that $\mathcal {A} = \tilde{\omega }(B_0){\setminus } M$. Let $x\in \mathcal {A}$. There exist sequences $\{x_j\} \subset B_0$, $t_j\rightarrow \infty$, and $\{\tilde{u}_j\}\subset \tilde{\mathcal {G}}$ such that $\tilde{u}_j(t_j)\rightarrow x$ as $j\rightarrow \infty$ and $\tilde{u}_j(0) = x_j$, $j\in {\mathbb {N}}$. The jump points in the trajectory $\tilde{u}_j$ are denoted by $\{ \tau ^j_i \}_{i=1}^{N_j}$, where we set $\tau ^j_0 = 0$ and either $N_j=\infty$ or $N_j<\infty$ and $\tau ^j_{N_j+1} = \infty$. For each $j\in \mathbb {N}$, let $n_j$ be an integer such that $\tau _{n_j}^j \le t_j < \tau _{n_j+1}^j$. For simplicity, we will write in the remaining part of the proof just $\tau _j$ in place of $\tau _{n_j}^j$. We consider three possibilities.

Case 1. There holds $t_j-\tau _j \rightarrow \xi /2$as$j\rightarrow \infty$. For each $j\in {\mathbb {N}}$, there exist trajectories $v_j,w_j \in \mathcal {G}$ such that $v_j(t) = \tilde{u}_j^{\tau _j-\xi /2}(t)$ for $t\in [0,\xi /2)$ with $v_j(\xi /2) = \displaystyle \lim _{t\rightarrow \xi /2^-} \tilde{u}_j^{\tau _j-\xi /2}(t) \in M$, and $w_j(t) = \tilde{u}_j^{\tau _j}(t)$ for $t\in [0,t_j-\tau _j]$ with $w_j(0) \in I(v_j(\xi /2))$. Asymptotic compactness of $\tilde{\mathcal {G}}$ implies that there exist $y, z\in \tilde{\omega }(B_0)$ such that, for a subsequence of indexes, that we still denote by j, there holds $\tilde{u}_j(\tau _j) = w_j(0)\rightarrow z$ and $\tilde{u}_j(\tau _j-\xi /2) = v_j(0) \rightarrow y$ as $j\rightarrow \infty$. Property (B4) of Definition 2.1 implies that, for another subsequence, there exist trajectories $v,w\in \mathcal {G}$ such that $v_j$ converges to v and $w_j$ converges to w uniformly on compact subsets of $\mathbb {R}_+$. In particular, $v_j(\xi /2) \rightarrow v(\xi /2)$ as $j\rightarrow \infty$. From Lemma 2.3, we have $w(0) = z\in I(v(\xi /2))\subset I(M)$. As $I(M) \cap M = \emptyset$ it follows that $z \in \tilde{\omega }(B_0) {\setminus } M = \mathcal {A}$. Moreover, as $\phi (w) \ge \xi$ it follows that $w(t) \notin M$ for $t\in (0,\xi /2]$. This means that the function $w|_{[0,\xi /2]}$ is a prefix of a trajectory in $\tilde{\mathcal {G}}$. Moreover,

$$\begin{aligned} d\left( w\left( \frac{\xi }{2}\right) ,x\right)&\le d\left( w\left( \frac{\xi }{2}\right) ,w_j(t_j-\tau _j)\right) + d(w_j(t_j-\tau _j),x)\\&\le d\left( w\left( \frac{\xi }{2}\right) ,w(t_j-\tau _j)\right) +d\left( w(t_j-\tau _j),w_j(t_j-\tau _j)\right) \\&\quad + d(\tilde{u}_j(t_j),x), \end{aligned}$$

and, using (B4) and (B5) of Definition 2.1, all sequences on the right-hand side of the last expression converge to zero, whence $w(\xi /2) = x$. Hence, as $w|_{[0,\xi /2]}$ is a prefix of a trajectory in $\tilde{\mathcal {G}}$ with $w(0) \in \mathcal {A}$ and $w(\xi /2) = x$, the proof for this case is complete.

Case 2. There exists$\epsilon > 0$and a subsequence of indexes, still denoted byj, such that$t_j - \tau _j > \xi /2 + \epsilon$. There exist trajectories $v_j \in \mathcal {G}$ such that $v_j(t) = \tilde{u}_j^{t_j-\xi /2-\epsilon }(t)$ for every $t\in [0,\xi /2+\epsilon ]$, $j\in {\mathbb {N}}$. As $v_j(0) = \tilde{u}_j(t_j-\xi /2-\epsilon )$ the asymptotic compactness of $\tilde{\mathcal {G}}$ implies that, for a nonrenumbered subsequence, $v_j(0) \rightarrow z$ as $j\rightarrow \infty$ for some $z\in \tilde{\omega }(B_0)$. Using (B4) of Definition 2.1, there exists a trajectory $v \in \mathcal {G}$ with $v(0) = z$ such that, for another subsequence of indexes, $v_j$ converges to v uniformly on the compact subsets of ${\mathbb {R}}_+$. In particular, $v_j(\epsilon ) = \tilde{u}_j(t_j-\xi /2) \rightarrow v(\epsilon )$ and $\tilde{u}_j(t_j) = v_j(\epsilon +\xi /2) \rightarrow v(\epsilon +\xi /2)$ as $j\rightarrow \infty$. But, as $\tilde{u}_j(t_j) \rightarrow x$ as $j\rightarrow \infty$, it must be that $v(\epsilon +\xi /2) = x$. Now, we show that for every $t\in [\epsilon ,\epsilon +\xi /2)$ there holds $v(t)\notin M$. Indeed, if $v(s)\in M$ for a certain $s\in [\epsilon ,\epsilon +\xi /2)$ then condition (T) implies that, for a subsequence of indexes, still denoted by j, there exists a sequence $\alpha _j \rightarrow 0$ such that $s+\alpha _j \ge 0$ and $v_j(s+\alpha _j) \in M$. But for sufficiently large j, there holds $s+\alpha _j \in (0,\epsilon +\xi /2)$ and hence $\tilde{u}_j(t_j-\xi /2-\epsilon + s + \alpha _j) \in M$. This is impossible since points in M can only be initial point of trajectories in $\tilde{\mathcal {G}}$ as $I(M) \cap M =\emptyset$. Consider the translation $v^\epsilon$. This is a trajectory in $\mathcal {G}$ with $v^\epsilon (0) \in \tilde{\omega }(B_0) {\setminus } M = \mathcal {A}$, $v^\epsilon (\xi /2) = x$ and $v^\epsilon (t) \not \in M$ for $t\in [0,\xi /2]$. It follows that $v^\epsilon |_{[0,\xi /2]}$ is a prefix of a trajectory in $\tilde{\mathcal {G}}$ which makes the proof for this case complete.

Case 3. There exists a subsequence of indexes, still denoted byj, such that$t_j-\tau _j\rightarrow s\in [0,\xi /2)$as$j\rightarrow \infty$. In this case, one may obtain trajectories $v_j\in \mathcal {G}$ such that $v_j(t) = \tilde{u}_j^{t_j-3\xi /4}(t)$ for $t\in [0,\tau _j-t_j+3\xi /4)$ and $v_j(\tau _j-t_j+3\xi /4) \in M$, $j\in {\mathbb {N}}$. As $v_j(0) = \tilde{u}_j(t_j-3\xi /4)$, asymptotic compactness of $\tilde{\mathcal {G}}$ implies that, for a subsequence still denoted by j, $v_j(0) \rightarrow y$ as $j\rightarrow \infty$. From condition (B4) of Definition 2.1, there exists a trajectory $v\in \mathcal {G}$ such that $v(0) = y$ and, for a subsequence, we have the uniform convergence of $v_j$ to v on compact time intervals. Condition (B5) of Definition 2.1 implies the convergence $v_j(\tau _j-t_j+3\xi /4) \rightarrow v(3\xi /4-s)$ as $j\rightarrow \infty$, whence, by the closedness of M we must have $v(3\xi /4-s)\in M$. Moreover, $\tilde{u}_j(\tau _j) = \tilde{u}_j^{t_j-3\xi /4}(\tau _j-t_j+3\xi /4) \in I(v_j(\tau _j-t_j+3\xi /4))$ and, by the asymptotic compactness of $\mathcal {G}$, $\tilde{u}_j(\tau _j) \rightarrow w$ as $j\rightarrow \infty$. From Lemma 2.3, it follows that $w\in I(v(\xi /2-s))\subset I(M)$. Consider the sequence $\{z_j\}\subset \mathcal {G}$ such that $z_j(t) = \tilde{u}_j^{\tau _j}(t)$ for $t\in [0,t_j-\tau _j]$ and $j\in {\mathbb {N}}$. The fact that $\tilde{u}_j(\tau _j) \rightarrow w$ implies that $z_j(0)\rightarrow w$ and by (B4) of Definition 2.1, for a subsequence of indexes, which we do not renumber, we have the uniform convergence $z_j \rightarrow z$ for some $z\in \mathcal {G}_w$ on the compact subsets of ${\mathbb {R}}_+$. This fact, together with continuity of trajectories in $\mathcal {G}$, cf., (B5) of Definition 2.1, implies that $z_j(s) \rightarrow z(s)$ and $z_j(t_j-\tau _j) \rightarrow z(s)$ as $j\rightarrow \infty$. But, since $z_j(t_j-\tau _j) = \tilde{u}_j(t_j)$, we have $z(s) = x$. We construct the trajectory

$$\begin{aligned} \theta (t) =&{\left\{ \begin{array}{ll} v(t+\xi /4) \quad &{}\text {for}\quad t\in [0,\xi /2-s)\\ z(t-\xi /2+s) \quad &{}\text {for}\quad t\in [\xi /2-s,\xi /2]. \end{array}\right. } \end{aligned}$$

First note that $\theta (0) = v(\xi /4)$. Since $v_j(\xi /4) \rightarrow v(\xi /4)$ as $j\rightarrow \infty$, and for sufficiently large j there holds $v_j(\xi /4) = \tilde{u}_j(t_j-\xi /2)$, there must hold $\theta (0) \in \tilde{\omega }(B_0)$. We must show that $\theta$ is a prefix of a trajectory in $\tilde{\mathcal {G}}$ and $\theta (0)\notin M$. Since $z(0) = w \in I(M)$ and $z\in \mathcal {G}$ it is clear that $z(r)\not \in M$ for $r\in [0,s]$ which means that $\theta (t)\not \in M$ for $t\in [\xi /2-s,\xi /2]$. It remains to prove that $v(t+\xi /4)\not \in M$ for $t\in [0,\xi /2-s)$. The proof is analogous to the proof in Case 2. Suppose that $v(r) \in M$ for some $r\in [\xi /4,3\xi /4-s)$. Condition (T) implies that there exists a subsequence of indexes, still denoted by j, and a sequence of real numbers $\{\alpha _j\} \subset {\mathbb {R}}$ such that $\alpha _j \rightarrow 0$ as $j\rightarrow \infty$, $r+\alpha _j \ge 0$ and $v_j(r+\alpha _j) \in M$. There exists ${j_0}\in \mathbb {N}$ such that $0\le r+\alpha _{j_0} < \tau _{j_0}-t_{j_0} + 3\xi /4$. Indeed, suppose that for every $j\in \mathbb {N}$ there holds $r+\alpha _{j} \ge \tau _{j}-t_{j} + 3\xi /4$. We can pass to the limit with j to infinity, whence $r \ge -s + 3\xi /4$, a contradiction with $r \in [\xi /4,3\xi /4-s)$. Hence, as $0\le r+\alpha _{j_0} < \tau _{j_0}-t_{j_0} + 3\xi /4$ it follows that $v_{j_0}(r+\alpha _{j_0}) = \tilde{u}_{j_0}(r+\alpha _{j_0}+t_{j_0}-3\xi /4) \notin M$, a contradiction as $I(M)\cap M = \emptyset$. The proof is complete. $\square$

As a consequence of Theorem 4.7 and Lemma 4.4, we obtain the following result.

Corollary 4.8

Let $(\mathcal {G},M,I)$ be an impulsive generalized semiflow satisfying condition (H) with a global attractor $\mathcal {A}$ such that $I(M)\cap M = \emptyset$. If the condition (T) holds, then the attractor $\mathcal {A}$ is invariant.

5 Continuity of the Impact Time Map

A natural question that appears when studying the theory of impulsive dynamical systems is whether the mapping that defines the impact time, i.e., the time of the first jump for the trajectory, is continuous. It turns out that for multivalued dynamical systems the same condition (T) which guarantees the global attractor invariance is also sufficient for the impact time map continuity. In precise words, we will study the continuity of the mapping $\phi : \mathcal {G} \rightarrow (0, +\infty ]$ given by

$$\begin{aligned} \phi (u) = \inf \{t> 0\,:\ u(t)\in M\}. \end{aligned}$$

In a standard way, we make $(0,+\infty ]$ a locally compact space by defining the neighborhoods of $+\infty$ as the sets $(K,+\infty ]$ for $K>0$. We will also consider a multivalued map $\Phi :X\rightarrow \mathcal {P}((0,+\infty ])$ given by

$$\begin{aligned} \Phi (x) = \{ \phi (u)\,:\ u\in \mathcal {G}_x\}. \end{aligned}$$

For the set $M\subset X$, we denote by $\mathcal {G}_{X {\setminus } M}$ the set of all the trajectories with the initial points not belonging to M. We will show that (T) guarantees the continuity of the function $\phi$ on $\mathcal {G}_{X {\setminus } M}$ and upper semicontinuity of $\Phi$ on $X{\setminus } M$. We remind that $\mathcal {G}$ and $\mathcal {G}_{X {\setminus } M}$ are equipped with the metrics given by the uniform convergence of the compact subsets of $\mathbb {R}_+$. The next example demonstrates that, in general, the function $\phi$ is not continuous on $\mathcal {G}_{X {\setminus } M}$ and the multifunction $\Phi$ is not upper semicontinuous on $X{\setminus } M$.

Example 5.1

Consider the system governed by following ODEs

$$\begin{aligned} \left\{ \begin{array}{l} x' = 0 \\ y' = -1, \end{array} \right. \end{aligned}$$

and let $\mathcal {G}$ be the set of its classical solutions (in fact, these solutions generate a single-valued semiflow). Let $M = [-1,1]\times \{ 0 \}$ be an impulsive set and consider the sequence

$$\begin{aligned} u_j(t) = \left( 1+\frac{1}{j}, 1-t\right) \quad \text {for} \quad t\in {\mathbb {R}}_+ \quad \text {and} \quad j\in {\mathbb {N}}^+. \end{aligned}$$

Then $u_j \rightarrow u$ uniformly on compact subsets of $\mathbb {R}_+,$ where

$$\begin{aligned} u(t) = \left( 1, 1-t\right) \quad \text {for} \quad t\in {\mathbb {R}}_+ . \end{aligned}$$

It is clear that $u_j \in \mathcal {G}_{X {\setminus } M}$ and $u \in \mathcal {G}_{X {\setminus } M}$. Also note that $u_j(0) \rightarrow u(0) = (1,1)$, $\phi (u_j) = \infty$ for all $j\in {\mathbb {N}}^+$ and $\phi (u) = 1.$ Consequently, we have $\displaystyle \liminf _{n\rightarrow \infty } \phi (u_{n}) \ge \phi (u)$, but we do not have $\displaystyle \limsup _{n\rightarrow \infty } \phi (u_n) \le \phi (u)$. Thus $\phi$ is not continuous on $\mathcal {G}_{X {\setminus } M}$ and $\Phi$ (which is single-valued whence upper semicontinuity is just continuity) is not continuous on $X{\setminus } M$.

The next result demonstrates that (T) in fact guarantees the continuity of $\phi$.

Theorem 5.2

Let $\mathcal {G}$ be a generalized semiflow and let $M\subset X$ be a closed set satisfying the condition (T). The mapping $\phi :\mathcal {G}_{X {\setminus } M}\rightarrow (0,+\infty ]$ is continuous.

Proof

Let $z\in X{\setminus } M$, $u\in \mathcal {G}_z$ and $\{u_j\} \subset \mathcal {G}$ be a sequence such that

$$\begin{aligned} \sup _{t\in J} d(u_j(t),u(t)) \rightarrow 0 \quad \text {as} \quad j\rightarrow \infty \end{aligned}$$

(5)

for all compact set $J \subset \mathbb {R}_+$. Since $u(0)=z\notin M$, there is $j_0 \in {\mathbb {N}}$ such that $u_j \in \mathcal {G}_{X {\setminus } M}$ for every $j\ge j_0$. We first prove that

$$\begin{aligned} \phi (u) \le \liminf _{j\rightarrow \infty } \phi (u_j). \end{aligned}$$

If $\displaystyle \liminf _{j\rightarrow \infty } \phi (u_j)=\infty$ then the result follows. Now, let us assume that $\displaystyle \liminf _{j \rightarrow \infty } \phi (u_j) = r \in [0,\infty )$. Using (5) and condition (B5), we may obtain a subsequence $\{u_{\mu }\}$ such that

$$\begin{aligned} u_{\mu }(\phi (u_{\mu }))\rightarrow u(r) \quad \text {as} \quad \mu \rightarrow \infty . \end{aligned}$$

As $u_{\mu }(\phi (u_{\mu }))\in M$ for all $\mu \in \mathbb {N}$, we conclude that $u(r) \in M$, which means that $r\ge \phi (u)$, and the assertion follows.

Now, let us prove that

$$\begin{aligned} \limsup _{j\rightarrow \infty } \phi (u_j) \le \phi (u). \end{aligned}$$

If $\phi (u) = \infty$ then the result is trivial. Otherwise, take a subsequence $\{u_\mu \} \subset \{ u_j\}$ such that $\phi (u_\mu ) \rightarrow c$ as $\mu \rightarrow \infty$. We will prove that $c\le \phi (u)$. As $u(\phi (u)) \in M$, using condition (T) we may assume that there exists a subsequence of indexes $\{ \mu '\}$, a sequence $\{\alpha _{\mu '}\}$ with $\alpha _{\mu '} \rightarrow 0$, such that $u_{\mu '}(\phi (u) + \alpha _{\mu '}) \in M$. Then,

$$\begin{aligned} c = \displaystyle \lim _{\mu '\rightarrow \infty } \phi (u_{\mu '})\le \displaystyle \lim _{\mu '\rightarrow \infty } [ \phi (u) + \alpha _{\mu '}] = \phi (u). \end{aligned}$$

The proof is complete. $\square$

We deduce the following result on the multifunction $\Phi :X{\setminus } M \rightarrow (0,+\infty ]$.

Theorem 5.3

Let $\mathcal {G}$ be a generalized semiflow and let $M\subset X$ be a closed set satisfying the condition (T). If $x_j\rightarrow x$ in $X{\setminus } M$ and $t_j \in \Phi (x_j)$, $j\in {\mathbb {N}}$, then, for a subsequence of indexes we have $t_\mu \rightarrow t \in (0,+\infty ]$, where $t\in \Phi (x)$.

Proof

The result follows immediately from the condition (B4) and Theorem 5.2. $\square$

Remark 5.4

Lemma 2.3 implies that if a closed set M satisfies the condition (T) then the multifunction $\Phi :X{\setminus } M \rightarrow (0,+\infty ]$ is upper semicontinuous and compact valued.

We summarize the results of this section in the following Theorem.

Theorem 5.5

Let $(\mathcal {G}, M, I)$ be an impulsive generalized semiflow satisfying condition (T). Then

• (i) The function $\phi$ is continuous on $\mathcal {G}_{X {\setminus } M}$.

• (ii) If $x_j\rightarrow x$ in $X{\setminus } M$ and $t_j \in \Phi (x_j)$, $j\in {\mathbb {N}}$, then, for a subsequence of indexes, we have $t_\mu \rightarrow t \in (0,+\infty ]$, where $t\in \Phi (x)$.

• (iii) Equivalently to (ii) we may say that the multifunction $\Phi$ is compact valued (in the interval $(0,+\infty ]$ compactified at $+\infty )$ and upper semicontinuous on $X{\setminus } M$.

6 Criteria for Asymptotic Compactness

In the previous sections, we have given conditions which characterize the global attractor existence and its invariance for impulsive generalized semiflows. One of these conditions, given by Definition 3.2 is the asymptotic compactness of an impulsive generalized semiflow. In this section, we prove two results which relate the asymptotic compactness of an impulsive semiflow with the properties of the underlying generalized semiflow $\mathcal {G}$. The first result says that asymptotic compactness of $\mathcal {G}$ and compactness of the set I(M) guarantee the asymptotic compactness of $\tilde{\mathcal {G}}$.

Recall that the definition of asymptotic compactness of $\mathcal {G}$ is the same as presented in Definition 3.2 by replacing $\tilde{\mathcal {G}}$ by $\mathcal {G}$.

Lemma 6.1

Let $(\mathcal {G},M,I)$ be an impulsive generalized semiflow satisfying condition (H). Assume that $\mathcal {G}$ is asymptotically compact and I(M) is compact. Then $\tilde{\mathcal {G}}$ is asymptotically compact.

Proof

Let $B\in \mathcal {B}(X)$, $t_j\rightarrow \infty$ and $\{\tilde{u}_j\} \subset \tilde{\mathcal {G}}$ be such that $\tilde{u}_j(0)\in B$ for every $j\in {\mathbb {N}}$. Denote by $v^j_k \in \mathcal {G}$ the trajectories such that

$$\begin{aligned} v^j_k(t) = \tilde{u}_j(t + \tau _{k}^j)\quad \text {for}\quad t\in [0,\tau _{k+1}^j - \tau _{k}^j). \end{aligned}$$

Clearly, for each $j\in {\mathbb {N}}$, there exists $m_j \in {\mathbb {N}}$ such that $\tau _{m_j}^j \le t_j < \tau _{m_j+1}^j$, with the possibility that $\tau _{m_j+1}^j = \infty$. For simplicity, let us denote $\tau _j = \tau _{m_j}^j$, $\tau _{j+1} = \tau _{m_j+1}^j$ and $v_j = v_{m_j}^{j}$.

Case 1. There exists a subsequence of$\{\tau _j\}$, denoted by the same index, such that$\tau _j = 0$$(m_j=0)$. In this case, $\tilde{u}_j(t_j) = v^j_0(t_j)$ which has a convergent subsequence by the asymptotic compactness of $\mathcal {G}$.

Case 2. For all but finite number of indexes there holds$\tau _j \ne 0$.

We split this case into two separate subcases.

Subcase 2.1. For an infinite number of indexes there holds$t_j = \tau _j$. In this case, $\tilde{u}_j(t_j) \in I(v_{m_j-1}^{j}(t_j)) \subset I(M)$ for an infinite number of indexes, and the result follows by the compactness of I(M).

Subcase 2.2. For all but finite number of indexes there holds$\tau _j< t_j < \tau _{j+1}$. We may assume that there is $j_0\in {\mathbb {N}}$ such that $\tau _j\ne 0$ and $\tau _j< t_j < \tau _{j+1}$ for all $j\ge j_0$. Note that $\tilde{u}_j(t_j) = v_j(t_j- \tau _j)$ and $v_j(0) \in I(M)$ for every $j\ge j_0$. Thus, we may assume that there is $x \in I(M)$ such that

$$\begin{aligned} v_j(0) \rightarrow x \quad \text {as} \quad j\rightarrow \infty . \end{aligned}$$

By condition (B4), there is $u\in \mathcal {G}$ with $u(0) = x$ such that, up to a subsequence,

$$\begin{aligned} \sup _{t\in J} d(v_j(t), u(t)) \rightarrow 0 \quad \text {as} \quad j\rightarrow \infty \end{aligned}$$

(6)

for all compact $J \subset \mathbb {R}_+$. Now, if the sequence $\{t_j- \tau _j\}$ is bounded, we may assume that for a subsequence, still denoted by the same index, $t_j- \tau _j \rightarrow t_0$ as $j\rightarrow \infty$, and then

$$\begin{aligned} \tilde{u}_j(t_j) = v_j(t_j- \tau _j) \rightarrow u(t_0) \in X \quad \text {as} \quad j\rightarrow \infty . \end{aligned}$$

On the other hand, if $t_j- \tau _j \rightarrow \infty$ then $\tilde{u}_j(t_j) = v_j(t_j- \tau _j)$ converges by the asymptotic compactness of $\mathcal {G}$. $\square$

In the second result, we present the criterion for the asymptotic compactness of $(\mathcal {G},M,I)$ for the situation when I(M) is not necessarily a compact set.

Definition 6.2

The generalized semiflow $\mathcal {G}$ is compact if for any sequence $\{u_j\} \subset \mathcal {G}$ with $u_j(0)$ bounded and $t >0$, the sequence $\{u_j(t)\}$ is relatively compact.

Lemma 6.3

Let $(\mathcal {G},M,I)$ be an impulsive generalized semiflow such that the conditions (H) and (T) hold. Assume that $\mathcal {G}$ is compact and $\tilde{\mathcal {G}}$ is dissipative. Then $\tilde{\mathcal {G}}$ is asymptotically compact.

Proof

Let $B\in \mathcal {B}(X)$, $t_j\rightarrow \infty$ and $\{\tilde{u}_j\} \subset \tilde{\mathcal {G}}$ with $\tilde{u}_j(0)\in B$ for every $j\in {\mathbb {N}}$. By the dissipativity of $\tilde{\mathcal {G}}$ there exists a set $B_0 \in \mathcal {B}(X)$ and $t_B \ge 0$ such that $\tilde{u}_j(s) \in B_0$ for all $s \ge t_B$ and $j\in \mathbb {N}$. Let $j_0 \in {\mathbb {N}}$ be such that $t_j \ge t_B + \xi + 1$ for all $j\ge j_0$. Since $\tilde{u}_j \in \tilde{\mathcal {G}}$, for each fixed j, there exists a sequence $\{v_k^j\}_{k=0}^{N_j}\subset \mathcal {G}$$(0\le N_j \le \infty )$ such that

$$\begin{aligned} \tilde{u}_j(t) = v_k^j(t- \tau _k^j)\quad \text {for} \quad t\in [\tau _k^j, \tau _{k+1}^j) \quad \text {and}\quad k\in \{ 0,\ldots , N_j \}, \end{aligned}$$

where $\{ \tau _{k}^j \}_{k=0}^{N_j}$ are the jump times of $\tilde{u}_j$ with $\tau _0^j = 0$. For each $j\in {\mathbb {N}}$ there exists $m_j \in {\mathbb {N}}$ such that $\tau _{m_j}^j \le t_j < \tau _{m_j+1}^j$. Let us denote $\tau _j = \tau _{m_j}^j$, $\tau _{j+1} = \tau _{m_j+1}^j$ and $v_j = v_{m_j}^{j}$.

Case 1. There exists a subsequence, still denoted by$\{t_{j}\}$, such that$t_{j} < \phi (v_0^{j})$for all$j\ge j_0$. Define

$$\begin{aligned} w_j(t) = v_0^{j}(t+t_{j} - 1) \quad \text {for all} \quad t\ge 0, \; j\ge j_0. \end{aligned}$$

Note that $w_j \in \mathcal {G}$ and $w_j(0) = \tilde{u}_{j}(t_{j}-1) \in B_0$ for all $j\ge j_0$. By the compactness of $\mathcal {G}$ there exists a subsequence, which we also denote by $\{w_j\}$, such that $w_{j}(t)$ is convergent for each $t>0$. Consequently,

$$\begin{aligned} \tilde{u}_{j}(t_{j}) = v_0^{j}(t_{j}) = w_{j}(1) \end{aligned}$$

is convergent, and the assertion for this case is proved.

Case 2. For all but finite number of indexes there holds$t_j \ge \tau ^j_1$. Here, we my choose $j_1\ge j_0$ such that $t_j \ge \tau ^j_1$ for all $j\ge j_1$. Since $\tau _{j} \le t_j < \tau _{j+1}$ and condition (ii) holds, it follows that

$$\begin{aligned} \tau _{j+1} - \tau _{j} \ge \xi \quad \text {for every} \quad j\ge j_1. \end{aligned}$$

We split the rest of the proof into three subcases.

Subcase 2.1.$\tau _j < t_B$for all$j\ge j_1$, taking a subsequence if necessary. In this case, we define $w_j(t) = v_{j}(t + t_{j} -\tau _{j} - \xi )$ for $t\ge 0$ and $j\ge j_1$. Since $\tau _{j}< t_B \le t_{j} - \xi < \tau _{j+1}$, it follows that $w_j(0) = \tilde{u}_j(t_{j} - \xi ) \in B_0$ for all $j\ge j_1$. By the compactness of $\mathcal {G}$, we conclude that $\tilde{u}_{j}(t_{j}) = w_j(\xi )$ is relatively compact in X and the assertion follows.

Subcase 2.2. There is$j_2\ge j_1$such that$\tau _{j} \ge t_B$and$t_{j} >\tau _j + \frac{\xi }{2}$, for every$j\ge j_2$. In this case, we define $w_j(t) = v_{j}(t + t_{j} - \xi /2 - \tau _j)$ for $t\ge 0$ and $j\ge j_2$. Using the previous argument, we conclude that $\tilde{u}_{j}(t_{j}) = w_j(\xi /2)$ is relatively compact and the proof is complete.

Subcase 2.3. There is$j_3\ge j_1$such that$\tau _{j} \ge t_B$and$t_{j} \le \tau _{j} + \frac{\xi }{2}$for every$j\ge j_3$. Note that $\tau _{j-1}< t_{j} - \xi < \tau _{j}$, where $\tau _{j-1} = \tau _{m_{j}-1}^{j}$ and $j\ge j_3$. For $j\ge j_3$, set $v_{j-1} = v_{m_{j}-1}^{j}$ and define

$$\begin{aligned} w_j(t) = v_{j-1}(t + t_{j} - \xi - \tau _{j-1}) \quad \text {for every} \quad t \ge 0. \end{aligned}$$

There holds $w_j \in \mathcal {G}$ and $w_j(0) = \tilde{u}_{j}(t_{j} - \xi ) \in B_0$, $j\ge j_3$. By the compactness of $\mathcal {G}$, we may assume that

$$\begin{aligned} \tilde{u}_{j}\left( t_{j} - \frac{7\xi }{8}\right) = v_{j-1}\left( t_{j} - \frac{7\xi }{8}- \tau _{j-1}\right) = w_{j}\left( \frac{\xi }{8}\right) \rightarrow a \quad \text {as} \quad j\rightarrow \infty \end{aligned}$$

for some $a\in X$. Define $z_j = w_j^{\xi /8}$ for $j\ge j_3$, i.e.,

$$\begin{aligned} z_j(t) = w_j\left( t + \frac{\xi }{8}\right) = v_{j-1}\left( t+t_{j} - \frac{7\xi }{8}- \tau _{j-1}\right) \quad \text {for every}\quad t\ge 0. \end{aligned}$$

Condition (B4) of Definition 2.1 implies that, for a subsequence of indexes, still denoted by j, there holds

$$\begin{aligned} \lim _{j \rightarrow \infty } \sup _{s\in J} d(z_j(s),z(s)) = 0\quad \text {for some}\quad z\in \mathcal {G}_a, \end{aligned}$$

(7)

on compact subsets $J\subset {\mathbb {R}}_+$. In particular,

$$\begin{aligned} z_j\left( \frac{\xi }{8}\right) = w_j\left( \frac{\xi }{4}\right) \rightarrow z\left( \frac{\xi }{8}\right) \quad \text {as} \quad j\rightarrow \infty . \end{aligned}$$

We claim that $z\left( \xi /8\right) \notin M$. In fact, suppose to the contrary that $z\left( \xi /8\right) \in M$. By condition (T), there exists a subsequence of $\{z_j\}$, which we denote by the same index, and a sequence $\{\alpha _j\} \subset {\mathbb {R}}$, $\alpha _j \rightarrow 0$ as $j\rightarrow \infty$, such that

$$\begin{aligned} \frac{\xi }{8} + \alpha _j \ge 0 \quad \text {and}\quad z_j\left( \frac{\xi }{8} + \alpha _j\right) \in M. \end{aligned}$$

But, for j sufficiently large, we get $\tau _{j-1}< t_{j} - \frac{3\xi }{4}+ \alpha _j < \tau _{j}$, that is,

$$\begin{aligned} z_j\left( \frac{\xi }{8} + \alpha _j\right)= & {} w_{j}\left( \frac{\xi }{4} + \alpha _j\right) = v_{j-1}\left( t_{j} - \frac{3\xi }{4} + \alpha _j - \tau _{j-1}\right) \\= & {} \tilde{u}_j\left( t_{j} - \frac{3\xi }{4} + \alpha _j \right) \notin M \end{aligned}$$

which is a contradiction. Hence, $z\left( \xi /8\right) \notin M$.

Now, let us define

$$\begin{aligned} \theta _j(t) = z_j^{\xi /8}(t) = z_j\left( t+\frac{\xi }{8}\right) = v_{j-1}\left( t + t_{j} - \frac{3\xi }{4}- \tau _{j-1}\right) \quad \text {for}\quad t\ge 0, \; j\ge j_3. \end{aligned}$$

Then $\theta _j \in \mathcal {G}$ and $\theta _j(0) = z_j(\xi /8)\rightarrow z(\xi /8) \notin M$ as $j\rightarrow \infty$. Moreover, from (7) and Theorem 5.2, it follows that

$$\begin{aligned} \sup _{t\in J} d(\theta _{j}(t), z^{\xi /8}(t))\rightarrow 0 \quad \text {and} \quad \phi (\theta _{j}) \rightarrow \phi (z^{\xi /8}), \quad \text {as} \quad j\rightarrow \infty , \end{aligned}$$

for every compact interval $J \subset \mathbb {R}_+$. Thus,

$$\begin{aligned} \theta _{j}(\phi (\theta _{j})) \rightarrow z^{\xi /8}(\phi (z^{\xi /8})) \quad \text {as} \quad j\rightarrow \infty . \end{aligned}$$

As $v_j(0) \in I(\theta _{j}(\phi (\theta _{j})))$ and I is upper semicontinuous, for a subsequence, still denoted by j, there holds

$$\begin{aligned} v_{j}(0) \rightarrow b \in I(z^{\xi /8}(\phi (z^{\xi /8}))) \quad \text {as} \quad j\rightarrow \infty . \end{aligned}$$

Again, using condition (B4), there exists $w \in \mathcal {G}$ with $w(0)=b$ such that

$$\begin{aligned} \sup _{t\in J} d(v_{j}(t), w(t)) \rightarrow 0 \quad \text {as} \quad j\rightarrow \infty , \end{aligned}$$

for every compact interval $J \subset \mathbb {R}_+$. Note that $t_{j} = \tau _{j} + s_{j}$ for $s_j \in [0,\xi /2]$ and $\tilde{u}_{j}(t_{j}) = v_{j}(s_{j})$, $j\ge j_3$. For a subsequence of indexes, still denoted by j, there holds $s_{j} \rightarrow \lambda \in [0, \xi /2]$, and

$$\begin{aligned} \tilde{u}_{j}(t_{j}) = v_{j}(s_{j}) \rightarrow w(\lambda ) \quad \text {as} \quad j\rightarrow \infty . \end{aligned}$$

The proof is complete. $\square$

7 Comparison Between Condition (T) and Other Conditions used to get Invariance for Impulsive Systems

7.1 Condition (T) and Tube Condition for Single-Valued Systems

For single-valued impulsive semiflows it is proved in [6] that the so-called tube condition guarantees the global attractor invariance. We have proposed the condition (T) which guarantees this invariance in the general multivalued situation and, thus, also in the single-valued one. In this section we prove that the tube condition, in the single-valued case, implies condition (T). In this way, we assume that the generalized semiflow $\mathcal {G}$ is single-valued, i.e., for every $x\in X$ the set $\{u \in \mathcal {G}\, :\ u(0) = x \}$ is a singleton. In such case, we will use the notation

$$\begin{aligned} \mathcal {S}(t)x = u(t) \quad \text {for}\quad u\in \mathcal {G}\quad \text {with}\quad u(0) = x. \end{aligned}$$

For $D\subset X$ and $\Delta \subset [0, \infty )$, we define

$$\begin{aligned} F(D,\Delta ) = \{ y\in X\, : \text {there exists}\ \ \beta \in \Delta \; \text {such that} \; \mathcal {S}(\beta )y \in D \}. \end{aligned}$$

Definition 7.1

Let $\lambda >0$. A closed set S containing $x\in X$ is called a $\lambda$-section through x, if there exists a closed set L such that

• (T1) $F(L,\lambda )=S$;

• (T2) $F(L,[0,2\lambda ])$ contains a neighborhood of x;

• (T3) $F(L,\mu )\cap F(L,\eta ) =\emptyset$, for $0\le \mu <\eta \le 2\lambda$.

The set $F(L,[0,2\lambda ])$ is called a $\lambda$-tube and the set L is called a bar.

We recall the following Lemma, cf. [15, Lemma 1.9].

Lemma 7.2

Let $\{\mathcal {S}(t)\}_{t\ge 0}$ be a single-valued semiflow. If S is a $\lambda$-section through x, then S is a $\mu$-section through x.

The notion of section allows us to define the following property for a tube.

Definition 7.3

Let $M\subset X$ be an impulsive set. We say that a tube $F(L,[0,2\lambda ])$ given by a section S through $x\in M$ is a TC-tube if

$$\begin{aligned} S\subset M\cap F(L,[0,2\lambda ]). \end{aligned}$$

A point $x\in M$ satisfies the Tube Condition (TC) if there exists a TC-tube through x.

As a consequence of Lemma 7.2, we obtain the next result.

Lemma 7.4

Let $x\in X$ be a point satisfying TC with a $\lambda$-section S. Then for any $\eta <\lambda$ the set S is an $\eta$-section with a TC-tube.

In the next result, for single-valued semiflows, we prove that the tube condition implies the condition (T).

Theorem 7.5

Let $(\mathcal {G},M,I)$ be an impulsive generalized semiflow such that the underlying generalized semiflow $\mathcal {G}$ is single-valued. If $x\in X$ satisfies TC then x satisfies the condition (T).

Proof

Let $x \in M$, $t>0$ and $\{u_j\}$ be a sequence of trajectories of the single-valued semiflow $\{\mathcal {S}(t)\}_{t\ge 0}$ such that

$$\begin{aligned} \lim _{j\rightarrow \infty } \sup _{r\in J} d(u_j(r),u(r)) = 0 \quad \text {for every compact}\quad J\subset {\mathbb {R}}_+ \quad \text {and for some}\quad u\in \mathcal {G}, \end{aligned}$$

and that $u_j(t) \rightarrow u(t) = x$ for a certain $t>0$, see Remark 4.5. It is not difficult to see that

$$\begin{aligned} \sup _{r\in J} d(u_{j}^t(r), u^t(r)) \rightarrow 0 \quad \text {as} \quad j\rightarrow \infty , \end{aligned}$$

(8)

for all compact $J \subset \mathbb {R}_+$. By condition (1) from Definition 2.7, there exists $\epsilon _{x} > 0$ such that

$$\begin{aligned} \bigcup _{s \in (0, \epsilon _{x})} \{u^t(s)\} \cap M = \emptyset . \end{aligned}$$

(9)

Now, as x satisfies the condition TC, let $F(L,[0,2\lambda ])$ be a $\lambda$-tube through x given by a section S, with $\lambda < \epsilon _x$. By condition (T2) of a tube, there exists $j_0\in {\mathbb {N}}$ such that

$$\begin{aligned} z_j = u_j(t) \in F(L,[0,2\lambda ]) \quad \text {for all} \quad j \ge j_0. \end{aligned}$$

Then there exists $s_j \in [0, 2\lambda ]$ such that $u_j(t+s_j) \in L$ for every $j\ge j_0$. We may assume that $s_j \rightarrow \bar{s} \in [0, 2\lambda ]$ as $j\rightarrow \infty$.

Case 1. There exists a subsequence, which we denote by the same index, such that$s_j > \lambda$. Since $u_j(t+s_j) = u_j^{t+s_j - \lambda }(\lambda ) \in L$ and $F(L, \lambda )=S$ by (T1), we get $u_j^{t+s_j - \lambda }(0) \in S \subset M$ for every $j\ge j_0$. Set $\alpha _j = s_j - \lambda$, $j\ge j_0$. We claim that $\bar{s} = \lambda$. Indeed, assume that $\bar{s} > \lambda$. Using (8) and (B5), it follows that

$$\begin{aligned} u_j^t(\alpha _j) \rightarrow u^t(\bar{s} - \lambda ) \quad \text {as} \quad j\rightarrow \infty . \end{aligned}$$

But $u_j^t(\alpha _j) \in M$, which implies that $u^t(\bar{s} - \lambda ) \in M$ and it contradicts (9). Thus, for $j\ge j_0,$

$$\begin{aligned} \alpha _j \rightarrow 0, \quad t+\alpha _j > 0 \quad \text {and} \quad u_j(t+\alpha _j) \in M. \end{aligned}$$

Case 2. There exists a subsequence, which we denote by the same index, such that$s_j \le \lambda$. Define $\alpha _j = s_j - \lambda$, $j\ge j_0$. By (8) and (B5) it follows that

$$\begin{aligned} u_j^t(s_j) \rightarrow u^t(\bar{s}) \in L \quad \text {as} \quad j\rightarrow \infty . \end{aligned}$$

But, as $u^t(0)=x\in M\subset S$ and $0\le \bar{s} \le \lambda$, it follows from the definition of the tube that $\bar{s} = \lambda$. Let $j_1\in {\mathbb {N}}$, $j_1 \ge j_0$, be such that $t +\alpha _j > 0$ for all $j\ge j_1$. Then, for $j\ge j_1$,

$$\begin{aligned} u_j^{t+\alpha _j}(\lambda ) \in L \quad \text {whereas}\quad u_j(t+\alpha _j)=u_j^{t+\alpha _j}(0)\in S \subset M. \end{aligned}$$

Hence,

$$\begin{aligned} \alpha _j \rightarrow 0, \quad t+\alpha _j > 0\quad \text {and} \quad u_j(t+\alpha _j) \in M \quad \text {for all} \quad j\ge j_1. \end{aligned}$$

The proof is complete. $\square$

7.2 Condition (T) and Conditions of [20]

The authors in [20, formula (20), p. 201] use the following condition in their proof of the global attractor invariance for generalized impulsive semiflows.

$(T^{*})$:

If $x \in X{\setminus } M$, $\{u_j\} \subset \mathcal {G}$ is such that $u_j(0) \rightarrow x$ and for some $u\in \mathcal {G}_x$ there holds

$$\begin{aligned} \lim _{j\rightarrow \infty }d(u_j(t),u(t)) = 0 \quad \text {for every}\quad t\ge 0, \end{aligned}$$

then $\phi (u) = \infty$ if $\phi (u_j) = \infty$ for infinitely many j, or $\phi (u_j)\rightarrow \phi (u)$ otherwise.

We establish the following result.

Lemma 7.6

The impulsive generalized semiflow $(\mathcal {G},M,I)$ satisfies the condition $(T^{*})$ if and only if it satisfies the condition (T).

Proof

Assume first that $(T^{*})$ is satisfied. In view of Remark 4.5, let $\{u_j\} \subset \mathcal {G}$ be a sequence and $u\in \mathcal {G}$ be such that

$$\begin{aligned} \lim _{j\rightarrow \infty }\sup _{s\in J} d(u_j(s),u(s)) = 0 \end{aligned}$$

for every compact $J\subset {\mathbb {R}}_+$, and $u_j(t)\rightarrow x$ for some $x\in M$ and $t\in (0,\infty )$. Define $\delta = \min \left\{ t, \frac{\epsilon _{x}}{2}\right\}$, where $\epsilon _{x} >0$ comes from condition (1) of Definition 2.7. Consider the sequence $\{u_j^{t-\delta }\}$. Then

$$\begin{aligned} \lim _{j\rightarrow \infty }\sup _{s\in J} d(u_j^{t-\delta }(s),u^{t-\delta }(s)) = 0, \end{aligned}$$

for every compact $J\subset {\mathbb {R}}_+$. Condition (2) from Definition 2.7 implies that for $s\in [0,\delta )$ there holds $u^{t-\delta }(s) \notin M$. In particular, $u^{t-\delta }(0)\notin M$. Hence, as $u^{t-\delta }(\delta ) = u(t) = x\in M$ (thus, $\delta = \phi (u^{t-\delta })$), condition $(T^{*})$ implies that $\phi (u^{t-\delta }_j)\rightarrow \phi (u^{t-\delta })$ as $j\rightarrow \infty$, so we can define $\alpha _j = \phi (u^{t-\delta }_j)-\phi (u^{t-\delta })$ and obtain $j_0\in {\mathbb {N}}$ such that $t + \alpha _j \ge 0$ for every $j\ge j_0$. Thus the assertion follows.

On the other hand, assume that (T) holds. Take $x\in X{\setminus } M$, $\{u_j\}\subset \mathcal {G}$ such that $u_j(0) \rightarrow x$ as $j\rightarrow \infty$, and for some $u\in \mathcal {G}_x$ there holds

$$\begin{aligned} \lim _{j\rightarrow \infty }d(u_j(t),u(t)) = 0 \quad \text {for every}\quad t\ge 0. \end{aligned}$$

As every subsequence of $\{u_j\}$ has another subsequence such that for some $v\in \mathcal {G}_x$ there holds

$$\begin{aligned} \lim _{\mu \rightarrow \infty }\sup _{s\in J} d(u_{\mu }(s),v(s)) = 0\quad \text {for every compact}\quad J\subset {\mathbb {R}}_+, \end{aligned}$$

the uniqueness of the limit implies that $v(s) = u(s)$ for every $s\ge 0$, and the convergence holds for the whole sequence $\{u_j\}$. Thus, the continuity of $\phi$ established in Theorem 5.2 implies that $(T^{*})$ holds. $\square$

Thus we have established that the condition (T) in Corollary 4.8 can be replaced with its equivalent condition $(T^*)$. In consequence, there holds the following result.

Corollary 7.7

Let $(\mathcal {G},M,I)$ be an impulsive generalized semiflow satisfying condition (H) with a global attractor $\mathcal {A}$ such that $I(M)\cap M = \emptyset$. If the condition $(T^*)$ holds, then the attractor $\mathcal {A}$ is invariant.

In [20, Lemma 8], the authors establish the negative invariance for an impulsive generalized semiflow, assuming the condition $(T^{*})$ and the following additional condition, which appears there as [20, formula (26), p. 204]:

$(T^{**})$:

If $x \in M$ and $\{u_j\} \subset \mathcal {G}$ is such that $u_j(0) \rightarrow x$ as $j\rightarrow \infty$, then there exists a subsequence $\{u_{\mu }\}$ such that either $\phi (u_{\mu }) \rightarrow 0$ as $\mu \rightarrow \infty$ or $\phi (u_{\mu }) = \infty$ for infinitely many indexes $\mu$.

We have proved that $(T^*)$ is equivalent to our condition (T) and no additional conditions, such as $(T^{**})$, are needed for the attractor invariance. Next, we exhibit an example where $(T^{**})$ is not satisfied, and the global attractor, being an invariant set, exists by Corollary 7.7.

Example 7.8

Let the generalized semiflow $\mathcal {G}$ (single-valued) be given by the solutions of the following ODE

$$\begin{aligned} x'=-x. \end{aligned}$$

Define $M = \{ 1,2 \}$ and $I(1) = I(2) = 3$. Note that the impulsive generalized semiflow $(\mathcal {G},M,I)$ is also single-valued. It is not difficult to see, that conditions of Corollary 7.7 as well as (T) (or equivalently $(T^*)$) are satisfied. In order to see that $(T^{**})$ does not hold, let us consider the sequence of initial data

$$\begin{aligned} x_j = 2-\frac{1}{j}\quad \text {for}\quad j\ge 2. \end{aligned}$$

It is clear that $x_j \rightarrow 2 \in M$ as $j\rightarrow \infty$. We denote the trajectories that start from $x_j$ by $u_j$. Since

$$\begin{aligned} u_j(t) = \left( 2-\frac{1}{j}\right) e ^{-t}, \end{aligned}$$

by a simple calculation we see that

$$\begin{aligned} \phi (u_j) = \ln \left( \frac{2j-1}{j}\right) , \end{aligned}$$

whereas

$$\begin{aligned} \lim _{j\rightarrow \infty } \phi (u_j) = \ln (2), \end{aligned}$$

and $(T^{**})$ does not hold. It is easy to see that for this example $\mathcal {A}_c = \{ 0 \}\cup [2,3]$, and the global attractor $\mathcal {A} = \{ 0 \}\cup (2,3]$ is an invariant set.

8 Examples

We complement this article by several additional examples that illustrate the obtained results.

Example 8.1

Let $F: \mathbb {R} \rightarrow 2^{\mathbb {R}}$ be given by

$$\begin{aligned} F(x) = \left\{ \begin{array}{ccl} [-1, 1] &{} \text {if} &{} x\in \{-1, 0, 1\}, \\ 1 &{} \text {if} &{} x\in (-\infty , -1)\cup (0, 1), \\ -1 &{} \text {if} &{} x\in (-1, 0)\cup (1, +\infty ). \end{array} \right. \end{aligned}$$

Consider the ordinary differential inclusion

$$\begin{aligned} \dfrac{dx}{dt}(t) \in F(x(t)) \end{aligned}$$

and let $\mathcal {G}$ be the set of its solutions, i.e., absolutely continuous functions $x:{\mathbb {R}}_+\rightarrow {\mathbb {R}}$ which satisfy the inclusion for almost every $t\in {\mathbb {R}}_+$. For the initial data not equal to zero, the solutions are given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \text {if}\ x_0<-1, \ \ x(t) = {\left\{ \begin{array}{ll} x_0+t \ \text {for}\ t\in [0,-1-x_0],\\ -1 \ \text {for}\ t> -1-x_0. \end{array}\right. } \\ \text {if}\ x_0 = -1, \ \ x(t) = -1 \ \text {for}\ t\ge 0.\\ \text {if}\ x_0\in (-1,0), \ \ x(t) = {\left\{ \begin{array}{ll} x_0-t \ \text {for}\ t\in [0,1+x_0],\\ -1 \ \text {for}\ t> 1+x_0. \end{array}\right. } \\ \text {if}\ x_0\in (0,1), \ \ x(t) = {\left\{ \begin{array}{ll} x_0+t \ \text {for}\ t\in [0,1-x_0],\\ 1 \ \text {for}\ t> 1-x_0. \end{array}\right. } \\ \text {if}\ x_0 = 1, \ \ x(t) = 1 \ \text {for}\ t\ge 0.\\ \text {if}\ x_0>1, \ \ x(t) = {\left\{ \begin{array}{ll} x_0-t \ \text {for}\ t\in [0,-1+x_0],\\ 1 \ \text {for}\ t > -1+x_0. \end{array}\right. } \\ \end{array}\right. } \end{aligned}$$

If $x_0 = 0$ we get a family of trajectories originating from $x_0$ given by

$$\begin{aligned} {\left\{ \begin{array}{ll} x(t) = 0\ \text {for}\ t\ge 0.\\ x(t) = {\left\{ \begin{array}{ll} 0 \ \text {for}\ t\in [0,T],\\ T-t \ \text {for}\ t\in [T,T+1],\\ -1 \ \text {for}\ t\ge T+1. \end{array}\right. }\\ x(t) = {\left\{ \begin{array}{ll} 0 \ \text {for}\ t\in [0,T],\\ t-T \ \text {for}\ t\in [T,T+1],\\ 1 \ \text {for}\ t\ge T+1. \end{array}\right. } \end{array}\right. } \end{aligned}$$

Verification that the trajectories of the formulated problem constitute a generalized semiflow according to Definition 2.1 is straightforward. This semiflow is moreover compact. Let $M = \{1/2\}$ be the impulsive set and let $I(1/2) = \{ -1/2 \}$. It is clear that with these defined M and I the problem constitutes an impulsive generalized semiflow. This semiflow is dissipative, and if $x(0)\in I(M)$, then $\phi (x) = \infty$. It is also not hard to see that condition (T) holds, so, according to Lemma 6.3 the constructed impulsive generalized semiflow is asymptotically compact. By Theorem 3.6, it has the global c-attractor. It is also not hard to see that the c-attractor is given by $\mathcal {A}_c = [-1,1/2]\cup \{1\}$, and hence the global attractor is given by $\mathcal {A} = [-1,1/2)\cup \{1\}$. Corollary 4.8 implies that the global attractor is invariant, which is also clearly seen from the explicit formulas for the underlying generalized semiflow.

Example 8.2

Consider the generalized semiflow $\mathcal {G}$ given by the solutions of the ODE $x'= -x$, the set $M = \{1\}$ and $I(1) = \{ 2, 3\}$. Assumptions of Lemma 6.3, Theorem 3.6 and Corollary 4.8 are satisfied, so the global attractor, an invariant set, exists. It is easy to see that the global attractor is $\mathcal {A} = \{ 0\} \cup (1,3]$. Let us show that the impulsive generalized semiflow has an uncountable number of distinct eternal and bounded trajectories. Indeed, let $\{ a_i \}_{i\in \mathbb {Z}}$ be a sequence of zeros and ones, i.e., $\{ a_i \}_{i \in \mathbb {Z}} \in \{ 0,1 \}^{\mathbb {Z}}$. Set $t_0 = 0$ and define a sequence $\{ t_i \}_{i\in \mathbb {Z}}$ by the following recursive formulas

$$\begin{aligned}&t_{i+1} - t_i = \ln 2 \ \ \text {if}\ \ a_i = 1,\\&t_{i+1} - t_i = \ln 3 \ \ \text {if}\ \ a_i = 0. \end{aligned}$$

Now, construct the trajectories of the impulsive generalized semiflow by the formulas

$$\begin{aligned}&x(t) = 2 e^{t_i-t} \ \ \text {if}\ \ a_i = 1 \ \ \text {and}\ \ t\in [t_i,t_{i+1}),\\&x(t) = 3 e^{t_i-t} \ \ \text {if}\ \ a_i = 0 \ \ \text {and}\ \ t\in [t_i,t_{i+1}). \end{aligned}$$

It is visible from the example that introduction of multivalued impulses even in a simple one-dimensional ODE can lead to an uncountable number of distinct nonperiodic complete trajectories in the attractor. Each of these trajectories can be uniquely encoded by an infinite sequence of zeros and ones and each sequence of zeros and ones gives rise to a distinct trajectory. So, the dynamics of the impulsive system can be transformed to the symbolic dynamics over alphabet $\{ 0,1 \}$ with the nonzero topological entropy. Hence, the dynamics of multivalued impulsive problems can potentially be much richer than that of single-valued problems without impulses, in particular it is possible that the dynamics of a one-dimensional impulsive system is topologically chaotic [22]. We stress the fact that it is crucial for the system in this example to be both multivalued and impulsive in order to generate the topologically chaotic symbolic dynamics.

Example 8.3

Consider the phase space $X=L^2(\Omega )$, where $\Omega \subset \mathbb {R}^n$ is an open and bounded set with sufficiently smooth boundary. Consider the problem

$$\begin{aligned}&u_t - \Delta u = 0\ \ \text {for}\ \ (x,t)\in \Omega \times (0,\infty ),\\&u(x,t) = 0 \ \ \text {for}\ \ (x,t)\in \partial \Omega \times (0,\infty ),\\&u(x,0) = u_0(x)\ \ \text {for}\ \ x\in \Omega . \end{aligned}$$

Clearly, if $u_0 \in L^2(\Omega )$, then the problem has a unique weak solution, and the trajectories of the problem constitute a generalized semiflow $\mathcal {G}$, in fact single-valued. Define $M = \{ v\in L^2(\Omega )\, :\ \Vert v\Vert _{L^2(\Omega )} = 1 \}.$ Denote by $\{ e_i \}_{i=1}^\infty$ the orthonormal sequence in $L^2(\Omega )$ of the eigenfunctions of the $-\Delta$ operator with the Dirichlet boundary conditions on $\partial \Omega$, and the corresponding eigenvalues given by

$$\begin{aligned} 0 < \lambda _1 \le \lambda _2 \le \ldots \le \lambda _n \le \ldots \rightarrow \infty . \end{aligned}$$

Every function from $L^2(\Omega )$ can be represented by the Fourier series

$$\begin{aligned} u = \sum _{n=1}^{\infty } (u,e_n)_{L^2(\Omega )} e_n, \end{aligned}$$

where $(u,e_n)_{L^2(\Omega )} = \alpha _n(u)$ is the n-th Fourier coefficient, and $\Vert u\Vert _{L^2(\Omega )}^2 = \sum _{n=1}^\infty \alpha _n^2(u)$. If the initial condition has the decomposition

$$\begin{aligned} u_0 = \sum _{n=1}^{\infty } \alpha _n(u_0) e_n, \end{aligned}$$

then the trajectories of the system are given by

$$\begin{aligned} u(t) = \sum _{n=1}^{\infty } \alpha _n(u_0)e^{-\lambda _n t} e_n. \end{aligned}$$

Now, define

$$\begin{aligned} I(v) = (\alpha _1(v) + [3,4]) e_1 + \sum _{n=2}^\infty \alpha _n(v) e_n \quad \text {for}\ \ v\in M. \end{aligned}$$

The multifunction I is upper semicontinuous and each trajectory of the underlying problem crosses the set M only at most once, hence the problem constitutes an impulsive generalized semiflow.

We show that $I(M) \cap M = \emptyset$. Indeed, let $v\in M$, then $\Vert v\Vert _{L^2(\Omega )}^2 = 1$, i.e., $\sum _{n=1}^\infty \alpha ^2_n(v) = 1$. If $u\in I(v)$, then for some $c\in [3,4]$ there holds

$$\begin{aligned} u = (\alpha _1(v) + c)e_1 + \sum _{n=2}^\infty \alpha _n(v) e_n. \end{aligned}$$

Then, as $|\alpha _1(v)| \le 1$,

$$\begin{aligned} \Vert u\Vert _{L^2(\Omega )}^2= & {} (\alpha _1(v) + c)^2 + \sum _{n=2}^\infty \alpha _n(v)^2 \\= & {} 1 + 2\alpha _1(v) c + c^2 \ge 1 - 2c + c^2 = (c-1)^2 \ge 4, \end{aligned}$$

and $I(M) \cap M = \emptyset .$ Next, we study the quantity

$$\begin{aligned} \phi (u) = \inf \{t > 0: \, u(t) \in M\} \quad \text {for every} \quad u\in \mathcal {G} \quad \text {with} \quad u(0) = u_0\in I(M). \end{aligned}$$

For $u_0 \in I(M)$ there exists $v\in M$ such that $u_0\in I(v)$, and hence for some $c\in [3,4]$

$$\begin{aligned} u_0 = (\alpha _1(v)+c)e_1 + \sum _{n=2}^\infty \alpha _n(v)e_n\quad \text {for}\quad \sum _{n=1}^\infty \alpha _n^2(v) = 1. \end{aligned}$$

We can decompose the dynamics starting from $u_0$ into modes, whence,

$$\begin{aligned} u(t) = (\alpha _1(v)+c)e^{-\lambda _1 t}e_1 + \sum _{n=2}^\infty \alpha _n(v) e^{-\lambda _n t}e_n, \end{aligned}$$

and, since the $\Vert u(t)\Vert _{L^2(\Omega )}^2$ is continuous and decreasing it suffices to find the lower bound on t such that

$$\begin{aligned} (\alpha _1(v)+c)^2e^{-2\lambda _1 t} + \sum _{n=2}^\infty \alpha _n^2(v) e^{-2\lambda _n t} =1. \end{aligned}$$

It follows that

$$\begin{aligned} 2^2 e^{-2\lambda _1 t} \le 1, \end{aligned}$$

whence

$$\begin{aligned} t\ge \frac{1}{2\lambda _1}\ln 4, \end{aligned}$$

and

$$\begin{aligned} \phi (u) \ge \frac{1}{2\lambda _1}\ln 4, \end{aligned}$$

for every $u\in \mathcal {G}$ with $u_0 \in I(M)$. Finally, we demonstrate the condition (T). Let $x\in M$, $\{u_n\}\subset \mathcal {G}$ and $t_0>0$ such that $u_n(t_0) \rightarrow x$ as $n\rightarrow \infty$ and

$$\begin{aligned} \lim _{n\rightarrow \infty } \sup _{r\in J}\Vert u_n(r) - u(r)\Vert _{L^2(\Omega )} =0 \quad \text {for every compact}\quad J\subset {\mathbb {R}}_+ \quad \text {and some} \quad u\in \mathcal {G}. \end{aligned}$$

Let $u_n(0)=u_0^n$ and $u(0) = u_0$, $u_0, u_0^n \in L^2(\Omega ).$ It is clear that $u(t_0) = x$ and $u_0^n \rightarrow u_0$ as $n\rightarrow \infty$. Since $\Vert u(t)\Vert _{L^2(\Omega )}$ is decreasing to zero for any nonzero initial data, in fact

$$\begin{aligned} \Vert u(t)\Vert _{L^2(\Omega )} \le e^{-\lambda _1 t}\Vert u_0\Vert _{L^2(\Omega )}, \end{aligned}$$

(10)

it follows that $\Vert u_0\Vert _{L^2(\Omega )}>1$ and $\Vert u^n_0\Vert _{L^2(\Omega )}>1$ for sufficiently large n. It follows that for every natural n there exists $t_n > 0$ such that $u_n(t_n) \in M$. Moreover, the sequence $\{t_n\}$ is bounded (as $u_n$ satisfies (10)), so, for a subsequence, there holds $t_n \rightarrow {\bar{t}}$ as $n\rightarrow \infty$. It suffices to prove that ${\bar{t}} = t_0$. Indeed, take a compact interval J such that $\{t_n\} \subset J$, then

$$\begin{aligned} \Vert u_n(t_n) - u({\bar{t}})\Vert _{L^2(\Omega )}&\le \Vert u_n(t_n) - u(t_n)\Vert _{L^2(\Omega )} + \Vert u(t_n) - u({\bar{t}})\Vert _{L^2(\Omega )} \\ \ \&\le \sup _{r\in J}\Vert u_n(r) - u(r)\Vert _{L^2(\Omega )} + \Vert u(t_n) - u({\bar{t}})\Vert _{L^2(\Omega )}. \end{aligned}$$

This means that $u_n(t_n) \rightarrow u({\bar{t}})$ as $n\rightarrow \infty$, and, as $u_n(t_n)\in M$ and M is a closed set, it follows that $u({\bar{t}}) \in M$. Since $t_0$ is the only time such that $u(t_0) \in M$ it must be that ${\bar{t}} = t_0$. Finally, take $\alpha _n = t_n - t_0$, which yields $u_n(t_0 + \alpha _n) = u_n(t_n) \in M$ and the proof of condition (T) is complete.

We have proved that assumptions of Lemma 6.3, Theorem 3.6, and Corollary 4.8 are satisfied, which implies the existence of the global attractor, being an invariant set. By studying the behavior of the impulsive generalized semiflow on separate modes, it is not hard to verify that its attractor is given by

$$\begin{aligned} \mathcal {A} = \{ 0 \} \cup \{ c e_1\, : \ c \in (1, 4] \}. \end{aligned}$$

Comparing this example with the examples of [20, 30, 31], the impulsive set M is no longer a part of a hypersurface of codimension one, but a sphere. The dynamics on the attractor is, however, similar as in [20, 30, 31] still reduced to a finite number of first Fourier modes (in fact to the first mode, only). It remains open, to our knowledge, to construct an example of an infinite dimensional impulsive dynamical system such that its attractor contains impulsive trajectories, and the dynamics cannot be reduced to the dynamics on the finite number of first Fourier modes.

Example 8.4

Next, we discuss the example of [20]. We consider the same initial and boundary value problem as in Example 8.3. Consider the impulsive set defined as, cf. formula (34) in [20]

$$\begin{aligned} M = \left\{ v\in L^2(\Omega )\,:\ \alpha _1(v) + \alpha _2(v) = 1\quad \text {and}\quad \alpha _1(v), \alpha _2(v)\ge 0 \right\} . \end{aligned}$$

Then we define the sequence of the initial data

$$\begin{aligned} u_0^n = -\frac{1}{n} e_1 + 2 e_2, \; n\in {\mathbb {N}}^+. \end{aligned}$$

The trajectories of the system are given by

$$\begin{aligned} u_n(t) = -\frac{1}{n} e^{-\lambda _1 t} e_1 + 2 e^{-\lambda _2 t} e_2, \; n\in {\mathbb {N}}^+. \end{aligned}$$

For $n\in \mathbb {N}^+$, $u_n(t)$ will never touch M as $\alpha _1(u_n(t))$ is always negative. Hence, $\phi (u_n) = \infty$. Now $u_0^n\rightarrow u_0$ as $n\rightarrow \infty$, where $u_0 = 2 e_2$. The trajectory that starts from $u_0$ is given by the formula

$$\begin{aligned} u(t) = 2{e^{-\lambda _2 t}}e_2. \end{aligned}$$

Clearly, for every t, we have the uniform convergence $u_n(t)\rightarrow u(t)$ on compact subsets of ${\mathbb {R}}_+$. The trajectory u will hit M at time given by

$$\begin{aligned} 2e^{-\lambda _2 t} = 1, \end{aligned}$$

so

$$\begin{aligned} t= \ln 2 / \lambda _2. \end{aligned}$$

This means that $\phi (u) = \ln 2/ \lambda _2$ and $\phi (u_n) = \infty$ for every $n\in {\mathbb {N}}^+$. Condition $(T^*)$, and equivalently, the condition (T) is violated. Hence, we cannot deduce the invariance of the global attractor from Corollary 7.7. Still, if we fix $\mu >0$ and define, for $v\in M$

$$\begin{aligned} I(v) = \left\{ c_1 e_1 + c_2 e_2 + \sum _{n=3}^\infty \alpha _n(v)e_n\, :\ c_1, c_2\ge 0, c_1+c_2 = 1+\mu \right\} , \end{aligned}$$

it is clear that the constructed impulsive multivalued dynamical system has a global attractor defined as, cf. [20, Lemma 10],

$$\begin{aligned} \mathcal {A}= & {} \left\{ c_1 e^{-\lambda _1 t} e_1 + c_2 e^{-\lambda _2 t} e_2 \,:\ t\in [0,\tau ) , c_1,c_2 \ge 0, c_1+c_2 \right. \\= & {} \left. 1+\mu , c_1 e^{-\lambda _1\tau }+c_2 e^{-\lambda _2\tau } = 1\right\} . \end{aligned}$$

The example shows that the condition (T), and equivalently $(T^*)$, as well as the tube condition, are only sufficient for the global attractor invariance, and there are cases, when the set M has a boundary, for which the global attractor for the impulsive problem exists but its existence is not guaranteed by the conditions known so far. This observation motivates the further work on impulsive problems, to find the condition which would hold for the case such as Example 8.4, but which would exclude the situation such as in Example 3.11, and which would be sufficient for the global attractor existence for the case when the impulsive set M has a boundary.

Example 8.5

In the last example, we come back to the integrate-and-fire neuron model given in the introduction. We assume that the excitation $S>0$ is constant in time but there are two possible reset values. The model is given by the equation

$$\begin{aligned} u'(t) = - \gamma u(t) + S, \end{aligned}$$

(11)

with the reset condition

$$\begin{aligned} \text {if}\quad u(t) = \theta \quad \text {then}\quad u(t) \quad \text {is reset to one of values}\quad u_r^1, u_r^2, \end{aligned}$$

with $u_r^1< u_r^2< \theta$. Indeed, in integrate-and-fire neuron models the reset values can vary for different action potentials, cf. [8, Fig. 1C]. We also assume that $\gamma >0$ and $\theta >0$. We demonstrate that the model satisfies all our assumptions. First, in our case, the family $\mathcal {G}$ are just solutions of the ODE (11), continuous functions, so they constitute, in particular, a generalized semiflow on $X=\mathbb {R}$, according to Definition 2.1. We define $M=\{ \theta \}$ and $I(\theta ) = \{ u^1_r,u^2_r \}$. Now, if only we assume that $S\ne \gamma \theta$, then the triple $(\mathcal {G},M,I)$ constitutes an impulsive generalized semiflow in concordance with Definition 2.7. As $u_1^r< u_2^r<\theta$ it is straightforward to see that the condition $\mathbf (H)$ is satisfied. It is also easy to see that the set

$$\begin{aligned} B_0 = [u_1^r,\theta ] \cup \left[ \frac{S}{\gamma }-1,\frac{S}{\gamma }+1\right] \end{aligned}$$

is absorbing, and so the impulsive generalized semiflow $(\mathcal {G},M,I)$ is dissipative in agreement with Definition 3.4 and asymptotically compact in agreement with Definition 3.2. We can use Theorem 3.9 to deduce the existence of the global attractor $\mathcal {A}$. Since the ODE (11) can easily be integrated exactly, is not hard to see that

$$\begin{aligned}&\mathrm {if}\quad \theta \gamma > S\quad \text {then}\quad \mathcal {A} = \left\{ \frac{S}{\gamma }\right\} , \\&\quad \mathrm {if}\quad \theta \gamma < S\quad \text {then}\quad \mathcal {A} = [u_1^r,\theta ) \cup \left\{ \frac{S}{\gamma }\right\} . \end{aligned}$$

If the excitation S is small, less than the threshold value $\theta \gamma$, then the membrane voltage u always stabilizes to the value $S/\gamma$. On the other hand, under sufficiently large excitation S, the structure of the attractor drastically changes, meaning that the neuron can then generate action potentials. It is also not hard to see that the condition (T) is satisfied, which leads to the attractor invariance. For the case $\theta \gamma < S$, the dynamics in the attractor on the interval $[u_1^r,\theta )$ can be transformed into the symbolic dynamics with positive topological entropy, as in Example 8.2, since each jump from value $\theta$ can occur either to $u^1_r$ or to $u^2_r$. This means that as S passes the value $\theta \gamma$ there occurs the change of the dynamics from the existence of the globally asymptotically stable equilibrium to the dynamics which is topologically chaotic.