Abstract
In a previous article, we generalised the classical four-dimensional Chern–Gauss–Bonnet formula to a class of manifolds with finitely many conformally flat ends and singular points, in particular obtaining the first such formula in a dimension higher than two which allows the underlying manifold to have isolated conical singularities. In the present article, we extend this result to all even dimensions \(n\ge 4\) in the case of a class of conformally flat manifolds.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Among the most fundamental results in differential geometry is the Gauss–Bonnet theorem which relates the Gauss curvature \(K_g\) of a closed and smooth Riemannian surface \((M^2,g)\) with its Euler characteristic \(\chi (M)\) by the formula
Dropping the assumption that the surface is closed, the formula generally requires correction terms as can already be seen by looking at the plane (with \(K=0\) and \(\chi =1\)). Moreover, these correction terms certainly do not only depend on the topology of the underlying surface, but rather on the geometry of its ends. This can be observed by considering a flat cylinder and a catenoid, two surfaces that are topologically equivalent (with Euler characteristic \(\chi =0\)) but satisfy \(K\equiv 0\) and \(K<0\), respectively. Similarly, also when the smoothness assumption is dropped, the Gauss–Bonnet formula requires correction terms. A simple example which illustrates this is the object obtained by cutting out a slice of a two-sphere between two geodesics from its north to its south pole and gluing the resulting bi-gon back together along these geodesics. The “sphere with two conical points” created this way is locally isometric to the round sphere away from the poles (and thus in particular satisfies \(K\equiv 1\)), but due to the fact that we lost area, the Gauss–Bonnet formula cannot hold. In fact, we see that the formula needs a correction term which depends on the area that was cut out, or equivalently on the conical angle at the two singularities. As it turns out, all correction terms can be expressed as isoperimetric ratios at the ends or isoperimetric deficits at the singular points. For only some of the most important results of the extensive literature on such two-dimensional formulas, we refer the reader to [8, 10, 12, 13, 19].
A higher-dimensional analogue of the Gauss–Bonnet formula has been discovered by Chern [9]. In dimension four, it can be expressed as
where \((M^4,g)\) is a smooth closed four-manifold, \(W_g\) is its Weyl curvature, and
is the Paneitz Q-curvature introduced by Branson and Branson-Ørsted [2,3,4]. Here, \(\mathrm {R}_g\) denotes the scalar and \(\mathrm {Rc}_g\) the Ricci curvature of \((M^4,g)\). As in the two-dimensional case, also the four-dimensional formula (1.1) requires correction terms if the smoothness or compactness assumptions are dropped. The most basic situation where this can be observed is for a conformal metric on \(\mathbb {R}^4\setminus \{0\}\) with one end (at infinity) and one singular point (at the origin). For such metrics, we proved the following result in [5].
Theorem 1.1
([5], Theorem 1.1) Let \(g=e^{2w}|\mathrm{{d}}x|^2\) be a metric on \(\mathbb {R}^4\setminus \{0\}\) which is complete at infinity and has finite area over the origin. If g has finite total Q-curvature, \(\int _{\mathbb {R}^4}|Q_{g,4}|\, \mathrm{{d}}V_g<\infty \), and non-negative scalar curvature at infinity and at the origin, then we have
where \(\nu := \lim _{r\rightarrow \infty } C_{3,4}(r)\), \(\mu :=\lim _{r\rightarrow 0} C_{3,4}(r) - 1\), and
denotes the isoperimetric ratio, normalised to be 1 on Euclidean space.
More generally, one can consider four-manifolds \((M^4,g)\) with finitely many conformally flat complete ends and finite area singular points, that is
where (N, g) is a compact manifold with boundary \(\partial N=\big (\bigcup _{i=1}^k \partial E_i\big )\cup \big (\bigcup _{j=1}^{\ell } \partial S_j\big )\), each \(E_i\) is a conformally flat complete simple end satisfying
for some function \(e_i(x)\), and each \(S_j\) is a conformally flat region with finite area and with a point-singularity at some \(p_j\), satisfying
for some function \(s_j(x)\). Here, B denotes the unit ball in \(\mathbb {R}^4\). Localising Theorem 1.1 to such ends and singular regions (obtaining Chern–Gauss–Bonnet formulas with boundary terms), and gluing all the pieces together, we obtained the following more general theorem.
Theorem 1.2
([5], Theorem 1.6) Let \((M^4,g)\) satisfy (1.4)–(1.6) and assume that g has finite total Q-curvature, \(\int _{M}|Q_{g,4}|\, \mathrm{{d}}V_g<\infty \), and non-negative scalar curvature at every singular point and at infinity at each end. Then we have
where in the coordinates of (1.5) and (1.6), we have
and
The Chern–Gauss–Bonnet formulas in the above two theorems, generalising in particular the formulas of Chang et al. [6, 7] for smooth but non-compact four-manifolds, are the first such formulas in a dimension higher than two which allow the underlying manifold to have isolated branch points or conical singularities. It is natural to ask whether Theorems 1.1 and 1.2 can be generalised to higher even dimensions \(n = 2m \ge 4\) using the n-dimensional Q-curvature. In the present article, we give an affirmative answer in the case of Theorem 1.1 and prove an analogue of Theorem 1.2 for a class of conformally flat manifolds.
Restricting to the conformally flat case has two main advantages. On the one hand, the Paneitz operator (see [17]) and its corresponding Q-curvature are not unique for general manifolds but for a conformally flat metric \(g=e^{2w}|\text {d}x|^2\), the n-dimensional Q-curvature is uniquely determined. We define the n-dimensional Q-curvature by the formula
As we only work in even dimensions, this is indeed an n-th order partial differential equation (while it would yield a pseudo-differential equation involving a fractional Laplacian in odd dimensions). Let us remark here that an explicit formula for \(Q_{g,n}\) in terms of the Riemann curvature tensor and its covariant derivatives, similar to (1.2) in the four-dimensional case, is difficult to obtain in higher dimensions and is currently unknown for dimensions higher than 8. On the other hand, a second advantage of restricting to conformally flat manifolds is that in this case the Q-curvature is a multiple of the Pfaffian modulo a divergence term. Thus the Chern–Gauss–Bonnet theorem can be written as
for a smooth and closed (locally) conformally flat n-manifold \((M^n,g)\) with
We first prove the following generalisation of our four-dimensional result from Theorem 1.1.
Theorem 1.3
Let \(n\ge 4\) be an even integer and let \(g=e^{2w}|\mathrm{{d}}x|^2\) be a metric on \(\mathbb {R}^n\setminus \{0\}\) which is complete at infinity and has finite area over the origin. If g has finite total Q-curvature, \(\int _{\mathbb {R}^n}|Q_{g,n}|\, \mathrm{{d}}V_g<\infty \), and non-negative scalar curvature at infinity and at the origin, then we have
where
Here, \(\sigma _n = |\mathbb {S}^{n-1}| = 2\pi ^{n/2} / (\tfrac{n-2}{2})!\) denotes the surface area of the unit \((n-1)\)-sphere.
Remark 1.4
By non-negative scalar curvature at infinity we mean
for some \(0<{r_1}<\infty \). This assumption cannot be replaced by the weaker assumption
as can be seen by considering the metric \(g=e^{2|x|^2}|\text {d}x|^2\), which is complete at infinity, satisfies \(Q_{g,n}\equiv 0\) and
but has asymptotic isoperimetric ratio \(\nu = +\infty \) (and \(\mu =0\), since the metric is smooth at the origin). Similarly, we also require \(\inf _{B_{r_2}(0)} \mathrm {R}_g(x)\ge 0\) for some \(0<{r_2}<\infty \).
Using a partition of unity argument, we then obtain the following more general theorem.
Theorem 1.5
Let \(\Lambda = \{p_1, \ldots , p _k, q _1, \ldots q_\ell \} \subset \mathbb {S}^n\) be a finite (possibly empty) set of points and let \((\Omega = \mathbb {S}^n \setminus \{p_1, \ldots , p _k\},g)\) be such that each \(p_ i\) is a complete end of finite total Q-curvature and non-negative scalar curvature and each \(q _ j\) is a finite area singular point of finite total Q-curvature and non-negative scalar curvature. Then
where
with \(\mathrm {R}_{p}(x)= {{\mathrm{dist}}}(x, p)\), and R is chosen small enough such that the balls \(\{B_R(p)\}_{p\in \Lambda }\) are pairwise disjoint.
To put our results into context, let us compare them with what was previously known. In [11], Fang proved the Chern–Gauss–Bonnet inequality
for smooth locally conformally flat n-manifolds with finitely many ends where the scalar curvature is non-negative. Our Theorems 1.3 and 1.5 do not only generalise this result to manifolds with singularities, but we also get an explicit formula for the error terms in this inequality. Note that for singular manifolds the inequality (1.14) might no longer hold if the conical angle (and hence the isoperimetric ratio) is larger than the Euclidean one. Later, Ndiaye and Xiao [16] obtained a result similar to Theorem 1.3, but again only for smooth metrics. They did not consider the case of manifolds with several ends but only studied conformal metrics on \(\mathbb {R}^n\). Let us remark that their work also contains some small errors which we correct here, in particular in their main theorem they only assume (1.13) and not (1.12), which in view of the counterexample from the above remark is not a sufficiently strong assumption. Nevertheless, we clearly profited from their results and, in fact, some of the ideas in the present article are in parts inspired by [11, 16]—combined with the approach we developed in [5] in order to deal with isolated singularities. Let us also mention here that various normalisations of the Q-curvature exist in the literature and that, in particular, [11, 16] define \(Q_{g,n}\) without the factor 2 in (1.8). We prefer to put this factor to make the results consistent with formula (1.2) and with our earlier work [5] in dimension four.
In the singular case, the problem has previously only been studied for manifolds with edge-cone singularities and V-manifolds, see e.g. [1, 15, 18], but these results are technically very different and none of them allows for isolated singular points.
Let us now describe how this article is organised and how the arguments differ from our previous four-dimensional results in [5]. First, in Sect. 2, we collect some integral estimates which are needed for the arguments in the following sections. Then, in Sects. 3–5, we prove Theorems 1.3 in three steps as follows. In Sect. 3, we prove the result in the special case where \(w=w(r)\) is a radial function on \(\mathbb {R}^n\setminus \{0\}\) and (1.8) reduces to an ODE. To make it easier to deal with all dimensions at once, we do not solve explicitly for the non-linearity in this ODE as we did in [5] but rather prove asymptotic estimates for an abstract kernel (see Lemma 3.1), employing the integral estimates from Sect. 2. In Sect. 4, we introduce an n-dimensional version of our notion of generalised normal metrics from [5] and prove Theorem 1.3 for this class of metrics. Then, in Sect. 5, we show that every metric \(g=e^{2w}|\text {d}x|^2\) on \(\mathbb {R}^n\setminus \{0\}\) satisfying the assumptions of Theorem 1.3 is actually such a generalised normal metric. The necessary singularity removal argument in this section is much more involved than our short argument in dimension \(n=4\) from [5], as we cannot directly apply Bôcher’s Theorem in higher dimensions. Finally, in Sect. 6, we prove Theorem 1.5. As currently no good notion of boundary T-curvature associated to \(Q_{g,n}\) is known in dimensions \(n>4\), we cannot localise Theorem 1.3 as we did in [5]. However, in the special case of domains \(\Omega \) as in Theorem 1.5, we can deduce the desired result from an easy partition of unity argument.
2 Some Integral Estimates
Let \(n\ge 4\) be an even integer. Recall (see e.g. [14, Thm. 6.20]) that \(G_y(x) = \frac{1}{|x-y|^{n-2}}\) is a multiple of the fundamental solution of the Laplacian on \(\mathbb {R}^n\). Indeed, in the sense of distributions, we have
where \(\sigma _n = |\mathbb {S}^{n-1}|\). This has two immediate consequences that are useful for us. First, it shows that in the sense of distributions
where \(\gamma _n\) is given in (1.10). Second, we see that if u is a radial function solving \((-\triangle )^k u=0\) on \(\mathbb {R}^n\setminus \{0\}\), where k is an integer satisfying \(1\le k\le \frac{n}{2}\), then u is given by
for some constants \(c_i\in \mathbb {R}\), where \(c_\ell =0\) for all \(\ell >2k\). Both of these conclusions follow from (2.1) with short calculations, noting that in spherical coordinates \(x=r \sigma \), where \(r>0\) and \(\sigma \in \mathbb {S}^{n-1}\), we have
The goal of this section is to derive some integral estimates which will be useful in the arguments that follow. We denote by

the averaged integral over an \((n-1)\)-sphere of radius r in Euclidean \(\mathbb {R}^n\) and consider the following four integrals:




where \(r = |x|\), \(s=|y|\).
Proposition 2.1
We have the following estimates for the integrals from (2.5)–(2.8).
-
(i)
For any \(r,s > 0\) and even integer \(n\ge 4\), \(I_n(r,s)\) evaluates to
$$\begin{aligned} I_n(r,s) = {\left\{ \begin{array}{ll} \frac{1}{r^{n-2}}, &{} \text { if } s\le r,\\ \frac{1}{s^{n-2}}, &{} \text { if } s> r. \end{array}\right. } \end{aligned}$$(2.9) -
(ii)
There exists \(C>0\) such that for any \(r,s > 0\) and even integer \(n\ge 4\), we have
$$\begin{aligned} \begin{aligned} |r^2 J_n(r,s)-1|&\le C \frac{s^2}{r^2}, \quad \text { if } s \le r,\\ J_n(r,s)&\le C\frac{1}{s^2}, \quad \text { if } s>r. \end{aligned} \end{aligned}$$(2.10)In particular, in both cases, we obtain
$$\begin{aligned} r^2 J_n(r,s) \le C. \end{aligned}$$(2.11) -
(iii)
There exists \(C>0\) such that for any \(r,s > 0\) and even integer \(n\ge 4\), we have
$$\begin{aligned} K_n(r,s)\le C. \end{aligned}$$(2.12) -
(iv)
There exists \(C>0\) such that for any \(r,s > 0\) satisfying \(\frac{1}{2}r\le s\le \frac{3}{2}r\) and any even integer \(n\ge 4\), we have
$$\begin{aligned} |L_n(r,s)| \le C. \end{aligned}$$(2.13)
Proof
(i) This follows analogously to our corresponding estimate in the four-dimensional case [5, (3.17)], but in order to make the article self-contained, we quickly give a proof here. From (2.1), we obtain
Therefore, if \(s \le r\), we have \(y \in B_r(0)\) and hence obtain

Integrating with respect to r, we see that there is a constants \(C_1(s)\) such that

Fixing y (and hence \(|y| = s\)) and letting \(r\rightarrow \infty \), we see that \(C_1(s) = 0\). This proves (2.9) in the first case. If instead we have \(s>r\), (2.14) implies

so that

As \(s > r\), we can fix \(s=|y|\) and let \(r \rightarrow 0\) this time to obtain

This proves (2.9) in the second case.
(ii) If \(n=4\), we have \(J_n(r,s) = I_n(r,s)\), and thus (2.9) yields the desired result. We can therefore assume that n is an even integer satisfying \(n\ge 6\). In the case \(s\le r\), we compute

We therefore obtain
and thus, by (2.3), we have
As \(\lim _{s \rightarrow 0} J_n(r,s) = \frac{1}{r^2}\), we see that \(c_1(r)= \frac{1}{r^2}\) and that all the coefficients in the second sum above have to vanish. This means that
Note that by definition, for any \(t>0\),
so that \(r^2 J_n(r,s) = 1 + p \big (\frac{s^2}{r^2} \big )\), where p is a polynomial of degree \(\frac{n}{2}-2\) with no constant term. Obviously, this is bounded when \(s \le r\), proving the first case of (2.10). If \(s > r\), we simply apply Hölder’s inequality with \(p=\frac{n}{2}-1\), yielding

This proves the second case of (2.10).
(iii) For given \(|y|=s\), let \(A_s:=\{x\in \mathbb {R}^n \mid |x|<\frac{1}{2}|y| \text { or } |x|>2|y|\}\) and notice, by simply plugging in both possible cases, that on \(A_s\) we have
Hence by the triangle inequality \(||x|-|y||\le |x-y|\), we find
On the complement of \(A_s\), we have \(\frac{1}{2}|x| \le |y| \le 2|x|\) and therefore obtain
Using (2.15) and (2.16), we can now estimate

In view of (2.11), the bound (2.12) follows.
iv) Again, we already proved this (in dimension four) in [5], but quickly repeat the short proof here. First, we estimate the integral by

and then estimate the two terms \(L_n^1(r,s)\) and \(L_n^2(r,s)\) separately. In order to estimate the first term, note that combining the assumption \(\frac{1}{2}|x| \le |y| \le \frac{3}{2}|x|\) with \(|x-y| \ge \frac{1}{3} |y|\) implies
which in turn shows that \(\frac{1}{3}\le \frac{|y|}{|x-y|}\le 3\) over the region where we integrate. Hence, we obtain \(L_n^1(r,s) \le \log 3\). For the second integral, we have
Now, the assumption \(\frac{1}{2}r\le |y| \le \frac{3}{2}r\) gives \(\frac{2}{3} \le \frac{r}{|y|} \le 2\). Thus, as \( \log \frac{1}{\left| x-\frac{y}{|y|} \right| }\) is integrable, we have that \(L_n^2(r,s)\) is uniformly bounded on the annulus \(\frac{2}{3} \le \frac{r}{|y|} \le 2\). The uniform bounds for \(L_n^1(r,s)\) and \(L_n^2(r,s)\) imply (2.11). \(\square \)
3 The Rotationally Symmetric Case
In this section, we prove Theorem 1.3 for a conformal metric \(g = e^{2w}|\text {d}x|^2\) on \(\mathbb {R}^n\setminus \{0\}\) when \(w=w(r)\) is a radial function. Here and in the following, we always use the notation \(r=|x|\). In this situation, (1.8) becomes an ODE, but instead of solving for the non-linearity in this ODE as we did in our previous four-dimensional work [5] by an explicit integration, we rather apply the integral estimates derived in the previous section. We first prove the following lemma.
Lemma 3.1
Let \(n\ge 4\) be an even integer and let \(w \in C^\infty (\mathbb {R}^n\setminus \{0\})\) be rotationally symmetric such that \(g = e^{2w}|\mathrm{d}x|^2\) has finite total Q-curvature
For \(\alpha \in \mathbb {R}\), define
Then \(f_\alpha (x) = f_\alpha (r)\) is radially symmetric and satisfies
Moreover, there exists a constant \(C\in \mathbb {R}\) such that
Proof
The radial symmetry of \(f_\alpha \) follows easily from the fact that w and \(\log |x|\) are both radially symmetric. As in Sect. 3 of [5], we have
Hence, using the radial symmetry of w, we obtain

Now, we get that

where \(K_n(r,s)\) is defined in (2.7) and we used Proposition 2.1(iii) as well as the assumption of finite total Q-curvature (3.1) in the last steps. We can therefore apply the dominated convergence theorem, implying
Similarly, as for any fixed y we have
we get, again by the dominated convergence theorem,
which proves (3.2). In order to prove (3.3), we work in spherical coordinates \(x=r \sigma \), where \(r>0\) and \(\sigma \in \mathbb {S}^{n-1}\). In these coordinates, we have \(\nabla = (\frac{\mathrm{d}}{\mathrm{d}r}, \frac{1}{r} \nabla _{\mathbb {S}^{n-1}})\). Therefore, as \(f_\alpha (x)\) is rotationally symmetric, the above yields
and hence the first claim in (3.3). To prove the second claim, we note that, using (2.4), we find
and therefore

where—as above—we used the rotational symmetry of w and hence of \(Q_{g,n}\). Using \(J_n(r,s)\) defined in (2.6) and estimated in (2.11), we then easily get

Therefore \(|x|^2|\triangle f_\alpha (x)|\) is uniformly bounded, thus finishing the proof of the lemma. \(\square \)
Next, we prove that w agrees with some \(f_\alpha \) up to a constant.
Lemma 3.2
Let w be as in Lemma 3.1 and assume in addition either that
for some \(0<r_2\le r_1 < \infty \), or alternatively that for some constant \(C\in \mathbb {R}\)
Then there exist \(\alpha \) and \(C\in \mathbb {R}\) such that
Proof
We first define the function
From (2.2), we see that
Thus, from the definition of Q-curvature in (1.8), we obtain \((-\triangle )^{n/2}(w-f) = 0\). As \((w-f)\) is a radial function, we can use (2.3) to conclude that
Setting \(C:=c_1\) and \(\alpha := c_n\), we can rewrite this as
We need to show that all the coefficients \(c_\ell \) in the above sums vanish. This is done similarly as in the four-dimensional case, see [5, Lemma 2.2], using either the scalar curvature assumption (3.6) or the bounds (3.7). In fact, the formula for the scalar curvature of a conformally flat metric \(g=e^{2w}|\text {d}x|^2\) is
and therefore
By the scalar curvature assumption (3.6), the quantity in (3.10) is non-negative for \(|x|\ge r_1\) as well as for \(|x|\le r_2\). Under the alternative assumption (3.7), this expression does not have a sign, but it is uniformly bounded. We now use the bounds for \(f_\alpha (x)\) from (3.3) to conclude that if any of the odd-index coefficients \(c_{2k+1}\) in (3.8) does not vanish, then the right-hand side of (3.10) will tend to \(-\infty \) as \(|x|\rightarrow \infty \), giving a contradiction. Similarly, if any of the even-index coefficients \(c_{n-2k}\) in (3.8) does not vanish, then the left-hand side of (3.10) tends to \(-\infty \) as \(|x|\rightarrow 0\), yielding again a contradiction. Therefore \(w(x)=f_\alpha (x)+C\). \(\square \)
Remark 3.3
The proof of Lemma 3.2 shows that the scalar curvature assumption (3.6) can be replaced by the (much less geometric) condition that \(|x|^2 \mathrm {R}_g e^{2w}\) is bounded from below. Note that the metric \(g=e^{2|x|^2}|\text {d}x|^2\) from the counterexample stated in Remark 1.4 satisfies \(\mathrm {R}_g\rightarrow 0\) as \(|x|\rightarrow \infty \), but has \(|x|^2 \mathrm {R}_g e^{2w} \rightarrow -\infty \) as \(|x|\rightarrow \infty \). Hence, (the first part of) condition (3.6) cannot be weakened to \(\liminf _{|x|\rightarrow \infty } \mathrm {R}_g(x) \ge 0\) as claimed in [16]. A similar argument shows that also the second part of condition (3.6) cannot be weakened to \(\liminf _{|x|\rightarrow 0} \mathrm {R}_g(x) \ge 0\).
Combining Lemma 3.2 with Eq. (3.2), we immediately obtain the following consequence, which corresponds to [5, Corollary 2.3] in the four-dimensional case.
Corollary 3.4
Let \(g=e^{2w}|\mathrm{d}x|^2\) be as in Lemma 3.2. Then
where
To finish the proof of Theorem 1.3 in the rotationally symmetric case, it remains to express the two limits in Corollary 3.4 as isoperimetric ratios. Let us first recall the mixed volumes \(V_k(\Omega )\) defined by Trudinger [20] for a convex domain \(\Omega \subseteq \mathbb {R}^n\). We can restrict to the special situation where \(\Omega \) is a ball \(B_r(0)\) and \(k=n\) or \(k=n-1\), in which case we obtain the following.
Definition 3.5
We define the k-volumes \(V_k(r)\) for \(k=n\) or \(k=n-1\) by
Moreover, we define the isoperimetric ratio \(C_{n-1,n}(r)\) by
where \(\omega _n = \sigma _n/n = |B_1(0)|\) is the Euclidean volume of a unit ball in \(\mathbb {R}^n\). Note that the normalisation in (3.12) is such that \(C_{n-1,n}(r) \equiv 1\) on Euclidean space.
Theorem 1.3 for rotationally symmetric metrics then follows from Corollary 3.4 combined with the following result.
Lemma 3.6
Let w be as in Lemma 3.2 and assume in addition that g is complete at infinity and has finite area over the origin. Then we have
Proof
Due to the rotational symmetry of w(x), we can rewrite the k-volumes defined in (3.11) as
yielding
Due to the assumption that \(g=e^{2w}|\text {d}x|^2\) has finite area over the origin, we obtain that \(V_n(r)\rightarrow 0\) and \(V_{n-1}(r)\rightarrow 0\) as \(r\rightarrow 0\) and therefore by L’Hôpital’s rule
For \(r\rightarrow \infty \), there are several cases we have to consider.
Since \(V_{n-1}(r)\) is monotone, we have \(r\frac{\mathrm{d}w}{\mathrm{d}r}(r) +1 \ge 0\) for all r by (3.14). In the case where \(\lim _{r\rightarrow \infty } r\frac{\mathrm{d}w}{\mathrm{d}r}(r) + 1> 0\), (3.13)–(3.14) imply that both \(V_n(r)\) and \(V_{n-1}(r)\) tend to infinity and therefore we can again apply L’Hôpital’s rule as above, obtaining
We hence assume that \(\lim _{r\rightarrow \infty } r\frac{\mathrm{d}w}{\mathrm{d}r}(r) +1= 0\) and consider two subcases: If \(V_n(r)\) tends to infinity, then the claim is true (either again by L’Hôpital’s rule if also \(V_{n-1}(r)\) tends to infinity or otherwise we trivially get \(\lim _{r\rightarrow \infty } C_{n-1,n}(r)=0\)). If \(V_n(r)\) is bounded as \(r\rightarrow \infty \), then (3.13) shows that \(e^{nw(r)} \rightarrow 0\) as \(r\rightarrow \infty \), which in turn implies that \(e^{(n-1)w(r)} \rightarrow 0\) and hence again by (3.13) \(V_{n-1}(r)\rightarrow 0\) as \(r\rightarrow \infty \). Therefore, also in this case, we trivially find \(\lim _{r\rightarrow \infty } C_{n-1,n}(r)=0 = \lim _{r\rightarrow \infty } r\frac{\mathrm{d}w}{\mathrm{d}r}(r)+1\).
We have checked all possible cases and thus finished the proof of Lemma 3.6 and in view of Corollary 3.4 also proved Theorem 1.3 for rotationally symmetric metrics.\(\square \)
In the remainder of this section, we study the case where the origin is a second complete end rather than a finite area singular point. This result will be used in Sect. 6.
Lemma 3.7
Let \(n\ge 4\) be an even integer and let \(w \in C^\infty (\mathbb {R}^n\setminus \{0\})\) be rotationally symmetric such that \(g = e^{2w}|\mathrm{{d}}x|^2\) has two complete ends (at infinity and at the origin) satisfying (3.6) or (3.7) and with finite total Q-curvature \(\int _{\mathbb {R}^n} |Q_{g,n}| \mathrm{{d}}V_g < \infty \). Then
where
for an arbitrary \(R>0\).
This lemma in particular has the consequence that no such metric g can have positive Q-curvature everywhere. The proof is almost identical to the above, and we therefore only give a short sketch.
Proof
By Corollary 3.4, subtracting \(\chi (\mathbb {R}^n)=1\) on both sides, we have
where
Following the proof of Lemma 3.6 for the complete end at infinity, we obtain \(\nu = \nu _1\). For the end at the origin, we define
which satisfies
Therefore, denoting
a computation using L’Hôpital’s rule as in Lemma 3.6 implies that
This finishes the proof of Lemma 3.7. \(\square \)
4 Generalised Normal Metrics
In this section, we first define generalised normal metrics on \(\mathbb {R}^n\) as an extension of our definition of generalised normal metrics in \(\mathbb {R}^4\) in [5]. This in turn was a generalisation of normal metrics in [6] and [12]. We then prove Theorem 1.3 for this class of metrics.
Definition 4.1
(Generalised normal metrics) Suppose that \(g=e^{2w}|\text {d}x|^2\) is a metric on \(\mathbb {R}^n \setminus \{0\} \) with finite total Paneitz Q-curvature
We call g a generalised normal metric, if w has the expansion
for some constants \(\alpha ,C\in \mathbb {R}\). For such a generalised normal metric, we then define the averaged metric\(\bar{g}=e^{2\bar{w}}|\text {d}x|^2\) by

Clearly, \(\bar{g}\) is a rotationally symmetric metric.
Proposition 4.2
Suppose that the metric \(g= e ^{2w} |\mathrm{{d}}x|^2 \) on \( \mathbb {R}^n \setminus \{0 \}\) is a generalised normal metric. Then for all \(k > 0\), we have that

where \(o(1)\rightarrow 0\) as \( r\rightarrow \infty \) or \( r \rightarrow 0\).
Proof
The proof of this statement is merely a modification of our four-dimensional version from [5, Lemma 3.4]. The proof for \(r\rightarrow \infty \) was essentially covered in [6, Lemma 3.2] in the four-dimensional case and later generalised in [16, Prop. 3.1 (ii)] to higher dimensions. Note that in [6, 16] the formula (4.3) is proved for normal metrics which differ from our definition of generalised normal metrics by our additional term \(\alpha \log |x|\) in (4.1). But this additional term, the fundamental solution of the \(\frac{n}{2}\)-Laplacian, is rotationally symmetric and thus in Eq. (4.3), \(e^{\alpha \log |x|}\) appears on both sides and hence cancels. For this reason, we only need to prove the proposition for \(r\rightarrow 0\).
Suppose that \(g=e^{2w}|\text {d}x|^2\) is a generalised normal metric. To simplify notation, we denote \(F(y)=Q_g(y)e^{nw(y)}\), which by assumption is in \(L^1\). Then, splitting up \(\mathbb {R}^n\) into three regions, we have
where
We note that \(f(|x|) +\alpha \log |x|+C\) is rotationally symmetric and hence in Eq. (4.3), \(\exp (f(|x|)+\alpha \log |x|+C)\) appears on both sides and thus cancels. Therefore, we need to study only \(w_1(x)\), \(w_2(x)\) and \(w_3(x)\). We first claim the following.
Claim 1
We have
and
Proof
In order to prove (4.4), let \(\eta <\frac{1}{2}\), and estimate
Note that \(|y|\le \eta |x|\) implies
and therefore
We use this to estimate the first integral in (4.6). For the second integral, we then use the bound \(|y|\le \frac{1}{2}|x|\), which by an analogous argument as above yields
Combining the two estimates and using \(\int _{\mathbb {R}^n}|F(y)|\text {d}y < \infty \), we obtain
For \(|x|\rightarrow 0\) and \(\eta \rightarrow 0\), both terms above tend to zero, using again \(\int _{\mathbb {R}^n}|F(y)|\text {d}y < \infty \). This proves (4.4).
The argument to prove (4.5) is dual to what we have just done. For \(\eta >\frac{3}{2}\), we write
Then, we note that \(|y|\ge \eta |x|\) yields
which gives
This can be used to estimate the first integral in (4.7). Similarly, we estimate the second integral, using the bound \(|y|\ge \frac{3}{2}|x|\), which gives
Combining these estimates and using \(\int _{\mathbb {R}^n}|F(y)|\text {d}y < \infty \), we have
For \(|x|\rightarrow 0\), we can send \(\eta \rightarrow \infty \) slow enough such that \(\eta |x|\rightarrow 0\), in which case both terms above tend to zero, using again \(\int _{\mathbb {R}^n}|F(y)|\text {d}y < \infty \). This yields (4.5) and thus finishes the proof of Claim 1. \(\square \)
Claim 2
We have

as well as

Proof
By Fubini’s theorem

where \(L_n(r,s)\) is as in (2.8). By (2.13), we know that \(L_n(r,s)\) is uniformly bounded over the region where we integrate. Therefore, using the assumption of finite total Q-curvature and the dominated convergence theorem, (4.8) follows.
To prove (4.9), we follow the idea of Finn [12] and estimate
Similar to the above, we have
where
Similar to the estimate of \(L_n(r,s)\) in Proposition 2.1, we clearly have \(\tilde{L}_n^1(r,s) \le \log 3 \cdot |E_M|\). We estimate the term \(\tilde{L}_n^2(r,s)\) as follows. Observe that if we have \(|r \sigma - y| \le \frac{|y|}{ 3}\) then
We can thus bound \(\tilde{L}_n^2(r,s)\) by the situation where \(E_M\) is a n-dimensional disc centred at the point \(\frac{y}{r}\) orthogonal to y, in which case we get
Combining these estimates, we have
where \( o(1) \rightarrow 0\) as \( r \rightarrow 0\). This implies
and thus

which finishes the proof of Claim 2. \(\square \)
Using the two claims, it is easy to finish the proof of Proposition 4.2. Combining (4.4), (4.5) and (4.8), as well as Jensen’s inequality, we obtain for \(r\rightarrow 0\)

as \(r \rightarrow 0\). Combining this with (4.9), we find

which is equivalent to (4.3), thus finishing the proof of Proposition 4.2\(\square \)
Proposition 4.2 then immediately implies the following two corollaries.
Corollary 4.3
Let g be a generalised normal metric on \( \mathbb {R}^ n \setminus \{ 0 \} \) with averaged metric \( {\bar{g}}\) and define the mixed volumes \( V_k\) (with respect to g) and \( {\bar{V}} _k \) (with respect to \({\bar{g}}\)) as in Definition 3.5. Then we have
where \(\varepsilon (r) \rightarrow 0\) as \( r \rightarrow 0\) or \( r \rightarrow \infty \).
Corollary 4.4
Suppose that the metric \(g = e^{ 2w }|\mathrm{d}x|^2\) on \( \mathbb {R}^n \setminus \{0\} \) is a generalised normal metric that is complete and has a finite area singularity at \( \{ 0 \} \), then \(\bar{g}=e^{2 \bar{w}} |\mathrm{d}x|^2\) is complete and has a finite area singularity over \( \{ 0 \} \).
In order to conclude that Theorem 1.3 holds for \({\bar{w}}\), we need to either show the geometric property that \({\bar{g}}\) has positive scalar curvature at infinity and the origin, as in (3.6), or alternatively verify the analytical assumption (3.7). These latter bounds are easy to verify for the averaged conformal factor of a generalised normal metric. In fact, we prove a slightly more general result here which we can then also use in the next section.
Lemma 4.5
Suppose that \(g=e^{2w}|\mathrm{d}x|^2\) is a metric on \(\mathbb {R}^n \setminus \{0\} \) with finite total Q-curvature
Define v(x) by
for some constants \(\alpha ,C\in \mathbb {R}\) and set

Then \({\bar{v}}\) satisfies the following bounds
for some constant \(C \in \mathbb {R}\).
Proof
This follows very similarly to the proof of (3.3). From the definition of \( \bar{v}(r)\) we get

Using (3.5) and (4.13), we obtain

Then from (2.11), we see that
as we have finite total Q-curvature. Similarly, using (3.4), we deduce that
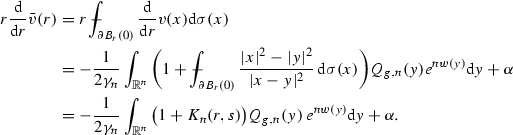
Hence, Eq. (2.12), the assumption of finite total Q-curvature, and the rotational symmetry of \(\bar{v}(r)\) imply
This establishes the lemma. \(\square \)
Obviously, if \(g =e^{2w}|\text {d}x|^2\) is a generalised normal metric on \( \mathbb {R}^n\setminus \{0\}\), then \(v=w\) and hence (4.15) gives the desired bounds for \({\bar{w}}\). This allows us to now prove Theorem 1.3 under the assumption that \(g=e^{2w}|\text {d}x|^2\) is a generalised normal metric.
Proof of Theorem 1.3 for generalised normal metrics
Let g be a generalised normal metric with average metric \({\bar{g}}\) (see Definition 4.1). Corollary 4.4, Lemma 4.5 and the results from the last section show that Theorem 1.3 holds for the rotationally symmetric metric \({\bar{g}}\). Moreover, Corollary 4.3 implies that
where the isoperimetric ratios (given in Definition 3.5) are taken with respect to g and \({\bar{g}}\), respectively. Thus, in order to obtain Theorem 1.3 for the generalised normal metric g, we need to only show that
However, from

this follows immediately. \(\square \)
5 Singularity Removal Theorem
Let \(g = e ^{2w} |\text {d}x|^2\) be a metric on \( \mathbb {R}^n \setminus \{0\} \) satisfying the assumptions of Theorem 1.3. In this section, we show then that g is a generalised normal metric. Together with the results from Sect. 4, this completes the proof of Theorem 1.3.
Proposition 5.1
Suppose that the metric \(g = e^{2w} |\mathrm{{d}}x|^2\) is a complete finite area metric on \(\mathbb {R}^n \setminus \{0\}\) with finite total Q-curvature
and non-negative scalar curvature at infinity and at the origin. Then it is a generalised normal metric in the sense of Definition 4.1
For \(g = e^{2w} |\mathrm{{d}}x|^2\), we define the symmetrisation of w with respect to \( x _0\) by

Clearly \( {\bar{w}}_{ x_0 } \) is rotationally symmetric with respect to \(x_0\). If \( x_0 = 0\) then we will often write \( {\bar{w}} _{ 0}( x ) = {\bar{w}} (x)\).
Lemma 5.2
Let \(g = e^{2w} |\mathrm{{d}}x|^2\) be a complete finite area metric on \(\mathbb {R}^n \setminus \{0\}\) with finite total Q-curvature and non-negative scalar curvature at infinity and at the origin. Then for \(x_0\) close enough to the origin, the symmetrised metric \(\bar{g}_{x_0} = e ^{2 {\bar{w}}_{x_0}} |\mathrm{{d}}x|^ 2\) has finite total Q-curvature and non-negative scalar curvature at infinity and at the origin.
Proof
If \( g = e ^{2w} |\text {d}x|^ 2\) is a metric conformal to the Euclidean metric, then by (3.9) non-negative scalar curvature \( \mathrm {R}_g \ge 0\) is equivalent to
Firstly, note that we have

Furthermore, as \(\nabla = (\frac{\mathrm{{d}}}{\mathrm{d}r}, \frac{1}{r} \nabla _{\mathbb {S}^{n-1}})\) in spherical coordinates around \(x_0\), we have

and therefore

For \(x_0\) and x sufficiently close to the origin, the integrand on the right-hand side of (5.1) is non-positive and hence \(\mathrm {R}_{{\bar{g}}_{x_0}}(x) \ge 0\) if \(x_0\) and x are sufficiently close to the origin. Moreover, \(\mathrm {R}_{{\bar{g}}_{x_0}}(x) \ge 0\) also holds whenever x is sufficiently large. Furthermore \(Q_{ {\bar{g}}_{x_0}, n }\) is absolutely integrable with respect to \(\text {d}V _ {{\bar{g}}_{x_0}}\). This follows from
which implies by Fubini’s theorem

Hence \( {\bar{g}}_{ x_0 }\) has finite total Q-curvature. \(\square \)
Now, let us consider
and its symmetrisation

Then, since \( ( -\triangle ) ^{n/2} v = 2Q _{ n,g } e ^{ nw } = ( -\triangle ) ^{n/2} w\), we also have

Considering first \(x_0=0\), we note that by Lemma 5.2, \(\bar{g} = e^{2 {\bar{w}}} |\text {d}x|^ 2\) has non-negative scalar curvature at infinity and at the origin and by Lemma 4.5, \({\bar{v}}\) satisfies
for some constant \(C \in \mathbb {R}\). Thus, by an argument as in Lemma 3.2, we obtain
for some constants \(C_0\) and \(\alpha \). Further note that for \(x_0 \ne 0\), the Lebesgue differentiation theorem implies that
where \(r = |x - x_0|\). Therefore, we obtain
We can now prove the main result of this section.
Proof of Proposition 5.1
Let v be given by (5.2) and recall from the above that
Over the origin \((-\triangle )^{n/2} ( w - v)\) must equal the sum of Dirac measures and its derivatives as they are the unique distributions supported on a point. In view of (5.3), we conclude that
We first prove the following claim.
Claim 1
\(w ( x) - v ( x ) - \alpha \log |x|\) is harmonic on \(\mathbb {R}^n\setminus \{0\}\).
Proof
For arbitrary \(x_0\), we consider the symmetrisation

where \(r = |x-x_0|\). As the integrand is bounded over the origin by (5.3), \(\psi _{x_0}\) is well defined. Furthermore, \(\psi _{ x_0 }\) is rotationally symmetric about \(x_0\) and by (5.4), we have
Hence, by (2.3), we see that for \(r = |x-x_0|\)
We want to conclude that all coefficients apart from \(c_1\) vanish. As \(\psi _{x_0}\) is bounded at \(x_0\), all the even-index coefficients \(c_{n-2k}\) (including \(c_n\)) have to vanish. For the odd-index coefficients \(c_{2k+1}\), one can easily reproduce the arguments from Lemma 3.2, noting that by Lemma 5.2, \(\bar{g}_{x_0} = e^{2 {\bar{w}}_{x_0}} |\text {d}x|^ 2\) has non-negative scalar curvature at infinity and by an argument as in Lemma 4.5, \({\bar{v}}_{x_0} + \alpha \, \overline{ \log } |x|\) satisfies
for some constant C. This shows that \(\psi _{x_0}(x)\equiv c_1\). (Of course, in view of (5.3), we have \(c_1 = C_0\).) Let us point out here that we do not need that \(\bar{g}_{x_0} = e^{2 {\bar{w}}_{x_0}} |\text {d}x|^ 2\) has non-negative scalar curvature at the origin, and hence smallness of \(|x_0|\) is not needed.
Now we conclude that
As \(x_0\) was arbitrary, this means that \(w(x) - v(x) - \alpha \log |x|\) is harmonic, proving Claim 1. \(\square \)
To complete the proof of the proposition, we show that \(w(x) - v(x) - \alpha \log |x|\) is in fact a constant. This part of the proof is similar to the four-dimensional case [5, Sect. 4].
Since \(w(x) - v(x) - \alpha \log |x|\) is harmonic, it follows that
is also harmonic. Therefore, using the mean value formula, we get

where \( r = |x -x_0|\). Now using the representation formula for v(x) we get that

This is due to the fact that

by (2.11), for any \(y\in \mathbb {R}^n\). Furthermore, using
and \( \triangle w(x) = \triangle v(x) + \alpha \triangle \log |x|\), we obtain from (3.9) that

This shows that

and hence
which by Liouville’s theorem gives that \(w(x) - v(x) - \alpha \log |x|\) is a constant. \(\square \)
6 Multiple Ends and Cone Points
In this section we extend the Chern–Gauss–Bonnet formula to cover the case of a domain conformal to \( \mathbb {S}^n\) with several ends and cone points as in Theorem 1.5.
Proof of Theorem 1.5
Let \( \Lambda = \{p_1, \ldots , p_k, q_1, \ldots , q_\ell \}\) be the set of ends and singular points and pick some arbitrary point \(N \in \mathbb {S}^n \setminus \Lambda \). Then, we consider the stereographic projection \(\pi : \mathbb {S}^n \setminus \{N\} \rightarrow \mathbb {R}^n\) sending N to infinity. We now identify \(\Lambda = \{p_1, \ldots , p_k, q_1, \ldots , q _\ell \} \) with its images in \(\mathbb {R}^n\) under this stereographic projection and interpret the metric g on \(\Omega \) as a metric on \(\mathbb {R}^n \setminus \{p_1,\ldots ,p_k\}\). Hence, there is a function w that is smooth away from \(\Lambda \subset \mathbb {R}^n\) such that
Let us then fix a partition of unity \(\{\varphi _i(x)\}_{i=0,\ldots k+\ell }\) consisting of smooth functions such that \(\varphi _i\) has support in \(B_{2R}(p_i)\) and satisfies \(\varphi _i \equiv 1\) on \(B_R(p_i)\) for \(i =1, \ldots , k\), and \(\varphi _j\) has support in \(B_{2R}(q_j)\) and satisfies \(\varphi _j \equiv 1\) on \(B_R(q_j)\) for \(j = k+1, \ldots k+\ell \). We can make all these balls of radius 2R disjoint by choosing R small enough. The function \(\varphi _0(x)\) is given by the condition
Let \( w _i(x) = w (x) \varphi _ i (x)\) and consider the metrics
By assumption, the metrics \(g_i\), \(i =1, \ldots , k\), are complete with non-negative scalar curvature near the end \(p_i\). Moreover, as \(w_i \equiv 0\) outside \(B_{2R}(p_i)\), we see that \(g_i\) has finite total Q-curvature and is complete at infinity with zero scalar curvature. Fixing some index i, we can assume without loss of generality that \(p_i\) is the origin. We consider the symmetrisation

Clearly, the arguments from Sects. 4 and 5 go through, and we can therefore argue as in Lemma 3.7 to conclude that
where
and where we used the fact that the Euclidean end at infinity has asymptotic isoperimetric ratio 1 and that \(\varphi _i \equiv 1\) on \(B_R(p_i)\).
Similarly for \(j=k+1,\cdots ,k+\ell \), the metrics \(g_j\) have a finite area branched point with non-negative scalar curvature near \(q_j\) and a complete end with vanishing scalar curvature. By an argument as in Theorem 1.3, we therefore find
or equivalently
where
Finally, let us also look at \(g_0 = e^{2w_0}|\text {d}x|^2\). Seen as a metric on \(\mathbb {S}^n\setminus \{N\}\), which agrees with g in a neighbourhood of N and therefore can be smoothly extended to all of \(\mathbb {S}^n\), we obtain by (1.8) and (1.9)
Hence, combining the above formulae (6.1)–(6.3) and using that \( w = \sum _{i=0}^ {k+\ell } w _i\), we obtain
or equivalently
In view of the observation that
Theorem 1.5 then immediately follows.\(\square \)
References
Atiyah, M., LeBrun, C.: Curvature, cones and characteristic numbers. Math. Proc. Camb. Philos. Soc. 155, 13–37 (2013)
Branson, T.P.: Differential operators canonically associated to a conformal structure. Math. Scand. 57, 293–345 (1985)
Branson, T.P.: The Functional Determinant. Global Analysis Research Center Lecture Notes Series, vol. 4. Seoul National University, Seoul (1993)
Branson, T.P., Ørsted, B.: Explicit functional determinants in four dimensions. Proc. Am. Math. Soc. 113, 669–682 (1991)
Buzano, R., Nguyen, H. T.: The Chern–Gauss–Bonnet formula for singular non-compact four-dimensional manifolds. Commun. Anal. Geom. (to appear). Preprint
Chang, S.-Y.A., Qing, J., Yang, P.C.: On the Chern–Gauss–Bonnet integral for conformal metrics on \(R^4\). Duke Math. J. 103(3), 523–544 (2000)
Chang, S.-Y.A., Qing, J., Yang, P.C.: Compactification of a class of conformally flat \(4\)-manifold. Invent. Math. 142, 65–93 (2000)
Chen, W., Li, C.: What kinds of singular surfaces can admit constant curvature? Duke Math. J. 78, 437–451 (1995)
Chern, S.-S.: A simple intrinsic proof of the Gauss–Bonnet formula for closed Riemannian manifolds. Ann. Math. 45, 747–752 (1943)
Cohn-Vossen, S.: Kürzeste Wege und Totalkrümmung auf Flächen. Compos. Math. 2, 69–133 (1935)
Fang, H.: On a conformal Gauss–Bonnet–Chern inequality for LCF manifolds and related topics. Calc. Var. 23, 469–496 (2005)
Finn, R.: On a class of conformal metrics, with applications to differential geometry in the large. Comment. Math. Helv. 40, 1–30 (1965)
Huber, A.: On subharmonic functions and differential geometry in the large. Comment. Math. Helv. 32, 13–72 (1957)
Lieb, E., Loss, M.: Analysis. Graduate Studies in Mathematics, vol. 2, 14th edn. AMS, Providence (2001)
Liu, Z.-D., Shen, Z.: Riemannian geometry of conical singular sets. Ann. Glob. Anal. Geom. 16(1), 29–62 (1998)
Ndiaye, C.B., Xiao, J.: An upper bound of the total \(Q\)-curvature and its isoperimetric deficit for higher-dimensional conformal Euclidean metrics. Calc. Var. 38, 1–27 (2010)
Paneitz, S.: A quartic conformally covariant differential operator for arbitrary pseudo-Riemannian manifolds. Preprint (1983)
Satake, I.: The Gauss–Bonnet theorem for \(V\)-manifolds. J. Math. Soc. Jpn. 9, 464–492 (1957)
Troyanov, M.: Prescribing curvature on compact surfaces with conical singularities. Trans. Am. Math. Soc. 324, 793–821 (1991)
Trudinger, N.S.: On new isoperimetric inequalities and symmetrization. J. Reine Angew. Math. 488, 203–220 (1997)
Acknowledgements
Parts of this work were carried out during a visit of RB at The University of Queensland in Brisbane as well as two visits of HN at Queen Mary University of London. We would like to thank the two universities for their hospitality. These visits have been financially supported by RB’s EPSRC Grant number EP/M011224/1 and HN’s AK Head Travelling Scholarship from the Australian Academy of Science.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Buzano, R., Nguyen, H.T. The Higher-Dimensional Chern–Gauss–Bonnet Formula for Singular Conformally Flat Manifolds. J Geom Anal 29, 1043–1074 (2019). https://doi.org/10.1007/s12220-018-0029-z
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12220-018-0029-z