Phase Separation through Screen Channel Liquid Acquisition Devices in Microgravity

Abstract

To enable future deep space exploration, orbital refueling of spacecraft is essential. However, transferring liquid in a microgravity environment is a complex process dependent on various factors. One of the basic and critical tasks is to separate phases to allow the supply of gas-free liquid from one tank to another. For this purpose, a liquid acquisition device is essential. In this work, a screen channel liquid acquisition device was designed and used to investigate phase separation and liquid removal from an experiment tank in a microgravity environment. The experiments were performed using the drop tower facility at the University of Bremen, with HFE-7500 as the test liquid under isothermal conditions. This investigation explored the interdependent effects of various phenomena, including the reorientation of liquid in the tank, capillary rise between parallel plates, flow through screen pressure variation, and bubble point breakthrough. Under subcritical conditions, the SC-LAD was found to supply gas-free liquid at the outlet, as long as the pressure drop across the screen was lower than the bubble point threshold. At the critical point, the screen started to ingest bubbles, resulting in a sharp peak in the differential pressure signal. The wetted area of the screen was obtained by analyzing images captured with a high-speed camera and used to calculate the analytical pressure drop. The experimental results were compared with the analytical solution and discussed in detail.

Introduction

Technological advancements in the direction of propellant depots and in-orbit refuelling of spacecraft can open up enormous possibilities for future deep space exploration. The duration of missions will no longer be limited by the launch capability of heavy lift vehicles, and a more cost-effective approach can be adopted. There has been growing interest in research and a simultaneous increase in the amount of efforts to conceptualize and evaluate the benefits of propellant depots for several decades (McLean et al. 2011; Gaebler et al. 2009; Zegler and Kutter 2010). The technical ability to perform removal, transfer, and filling of liquid from one tank to another in low gravity is essential. However, the practical realization and maturity of this technology are challenges in themselves.

In a microgravity environment, the removal of gas-free liquid from a propellant tank can be a complex task as the location of the gas-liquid interface is governed primarily by capillary forces. The liquid in the propellant tank adheres to the surface (for contact angles smaller than 90°) and remains closer to the tank wall, while the gaseous phase accumulates in the core of the tank. A dedicated device is essential to separate the phases, control the gas-liquid interface, and allow the withdrawal of gas-free liquid from a tank. Hartwig proposed a liquid acquisition device (or LAD) in his book in 2016 (Hartwig 2016b). A screen channel liquid acquisition device (SC-LAD) is a type of LAD that operates based on the principles of capillary action (Jaekle 1973). A traditional SC-LAD is defined as a closed channel enclosed by three solid sides and one porous side. The porous element enables the phase separation capability by allowing the liquid phase to enter the channel while blocking the entrance of the gaseous phase, as long as the pressure difference across the porous element does not exceed the bubble point pressure. SC-LADs are generally designed using metallic screens as the porous element. They are one of the most promising propellant management devices for long-term applications such as propellant depots (Darr and Hartwig 2014) and have a flight heritage with storable as well as cryogenic liquids (Hartwig 2017). The selection of a screen for an SC-LAD depends on the various factors and requirements of the mission, as discussed in Hartwig and Darr (2014).

The functioning of SC-LAD and bubble point breakthrough under normal gravity conditions, considering various types of screens and test liquids, has been extensively investigated in the literature (Kudlac and Jurns 2006; Hartwig et al. 2014a, b; Hartwig and McQuillen 2015; Hartwig 2016a; Camarotti et al. 2019). Phase separation through a screen-integrated channel was tested on parabolic flight in the work of Bisht and Dreyer (2020), whereas the application of a double screen element in a microgravity environment was explored in a paper by Pingel and Dreyer (2019). However, the number of investigations conducted under microgravity conditions remains limited in comparison. On the other hand, there have been works, such as Rosendahl et al. (2004), Canfield et al. (2013), Grah et al. (2014), and so on, where the behavior of liquid inside open capillary channels was studied to gain a deeper understanding of free surface behavior in low gravity.

There are reported fluid resupply space shuttle experiments in literature, such as FARE-I, FARE-II (Dominick and Driscoll 1993; Dominick et al. 2011) and VTRE (Chato and Martin 2006), where storable fluids were used to test fluid resupply in microgravity. Among the mentioned experiments, FARE-I employed SC-LAD as the primary LAD, whereas FARE-II and VTRE utilized vanes as their primary LAD systems. The main objective of FARE-I was to demonstrate the performance of the SC-LAD, focusing on factors such as expulsion efficiency and liquid refill. The screen type used was DTW 325x2300, and the tested flow rate was in the range of ${44\,\mathrm{\text {mL s}^{-1}}}$ to ${76\,\mathrm{\text {mL s}^{-1}}}$. However, apart from this, no quantitative information was provided regarding pressure drop or bubble point breakthrough. Therefore, in the current experimental investigation, an attempt is made to quantify the phase separation performance of a SC-LAD for removing gas-free liquid from an experiment tank in a microgravity environment.

This investigation aims to explore the interdependent effects of the various phenomena involved, including the reorientation of liquid in the tank, capillary flow between parallel plates, flow through screen pressure, and bubble point breakthrough. The objective of this paper is to contribute to the advancement of refuelling technology by providing experimental data on phase separation and gas-free liquid removal from an experimental tank using a SC-LAD device in a microgravity environment. The experimental results are compared with a simple analytical model, and associated high-speed camera images illustrating the bubble point breakthrough are also presented. These findings aim to enhance our understanding of the phenomena involved and provide valuable insights for future developments in this field.

State of the Art

A SC-LAD screen can separate liquid and gaseous phases as long as the overall pressure difference across the screen does not exceed the bubble point pressure of that screen. Bubble point pressure $\Delta P_{\text {BP}}$ is the maximum pressure difference required across a saturated screen to overcome the surface tension force of the free surface interface at the pores of the screen. This free surface interface prevents the entry of the gaseous phase due to the presence of a localized pressure jump, however, the liquid phase is allowed to enter. The bubble point pressure $\Delta P_{\text {BP}}$ depends on the surface tension of the liquid, the contact angle of the liquid and the solid surface, and the properties of the screen.

$$\begin{aligned} \Delta P_{\text {BP}} = \frac{4 \sigma \cos \theta }{D_{\text {BP}}} \end{aligned}$$

(1)

$D_{\text {BP}}$ is the bubble point diameter of the screen, $\sigma$ is the surface of the liquid, and $\theta$ is the contact angle between liquid and solid surface. The bubble point diameter $D_{\text {BP}}$ is defined as the biggest pore available on the screen surface through which the bubble breakthrough can happen with minimal applied differential pressure. The value of $D_{\text {BP}}$ is accessible only by measuring the bubble point pressure.

In general, the pore size of a screen is commonly expressed as the particle retention diameter $D_{\text {P}}$ which is defined as the maximum diameter of a spherical particle that can pass through the screen. If $D_{\text {P}}$ is used to calculate the bubble point pressure $\Delta P_{\text {BP}}$, it will overestimate the value. The actual shape of the pore is not restricted to a spherical shape. As shown in images from scanning electron microscopy by Hartwig and Darr (2016), pores of a dutch twilled weave have a complex triangular geometry. This means that the radius of the bubble at breakthrough may be larger than the particle retention diameter $D_{\text {P}}$. Therefore, a constant $C_0$ can be used in Eq. 1 which depends on the actual pore geometry and the breakthrough dynamics. The value of $C_0$ was determined experimentally for a dutch twilled weave (DTW) 200 x 1400 by Conrath and Dreyer (2012).

$$\begin{aligned} \Delta P_{\text {BP}} = C_0\frac{4 \sigma \cos \theta }{D_{\text {P}}} \end{aligned}$$

(2)

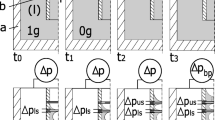
Consider a vertical SCLAD in a liquid bath where the liquid is being removed from the outlet at the top of the SCLAD as shown in Fig. 1. $H_{\text {SC}}$ and $W_{\text {SC}}$ are the height and width of the metallic screen of the SCLAD, respectively. $H_{\text {L}}$ is the height of the screen covered with liquid. In a normal gravity environment on Earth, typical pressure drops associated with such a system are the hydrostatic head $\Delta P_{\text {HS}}$ which depends on the length of the screen exposed to the free surface, the flow through screen pressure drop $\Delta P_{\text {FTS}}$ which accounts for the drop in pressure due to screen resistance, the frictional pressure loss $\Delta P_{\text {FR}}$, the dynamic pressure drop $\Delta P_{\text {DY}}$ which accounts for the pressure loses due to inflow into the channel and other pressure loses due to vibrations, sloshing, and other effects (Hartwig et al. 2014a).

Fig. 1

Schematic of a SCLAD in a partially-filled experiment tank. The origin of the coordinate system is also shown

The sum of all pressure drops can be defined as $\Delta P_{\text {TOT}}$:

$$\begin{aligned} \Delta P_{\text {TOT}} = \Delta P_{\text {HS}} + \Delta P_{\text {FTS}} + \Delta P_{\text {FR}} + \Delta P_{\text {DY}} \end{aligned}$$

(3)

To make sure that a screen allows only liquid to enter into the channel and blocks the gaseous phase, the following condition must be satisfied.

$$\begin{aligned} \Delta P_{\text {TOT}} \le \Delta P_{\text {BP}} \end{aligned}$$

(4)

The flow through screen pressure drop $\Delta P_{\text {FTS}}$ has been defined by many authors in their own interpretation throughout the literature. One of the oldest definitions can be found in the work of Armour and Cannon (1968) where $\Delta P_{\text {FTS}}$ is defined as the sum of viscous and inertial losses as follows:

$$\begin{aligned} \Delta P_{\text {FTS}} = C_1 \left( \frac{\tau B S^2 \mu }{\phi ^2} \right) v_s + C_2 \left( \frac{\tau B \rho }{\phi ^2 D_{\text {BP}}}\right) v_{\text {s}}^2 \end{aligned}$$

(5)

This is reported in Hartwig (2016b) on page 63. The constants $C_1$ and $C_2$ are fitting parameters, B is the screen thickness in the normal direction of the liquid flow, $\tau$ is the tortuosity, S is the surface to volume ratio of the screen, $\phi$ is the porosity, $v_\text {s}$ is the superficial velocity of the liquid, $\rho$ is the liquid density, and $\mu$ is the dynamic viscosity of the liquid.

The superficial velocity $v_\text {s}$ depends on the volumetric flow rate of the liquid $\dot{V_\text {L}}$ and the effective area of the screen covered with liquid $A_\text {L}$.

$$\begin{aligned} v_s = \frac{\dot{V_\text {L}}}{A_\text {L}} \end{aligned}$$

(6)

$\Delta P_{\text {FTS}}$ and $\Delta P_{\text {HS}}$ are the major contributing terms in Eq. 3. Based on the geometry, the dimensions of the SC-LAD, and experiment operating parameters of the current work, other pressure losses are found to be very small in comparison and are neglected. $\Delta P_{\text {HS}}$ becomes insignificant in a microgravity environment, and $\Delta P_{\text {FTS}}$ becomes the most significant pressure loss in the whole system. When the amount of liquid in the tank starts to decrease due to the removal of the liquid, the effective area of the screen $A_\text {L}$ covered with the liquid also decreases. This causes an increase of $\Delta P_{\text {FTS}}$, as shown in Eq. 5. If $\Delta P_{\text {FTS}}$ exceeds the bubble point pressure $\Delta P_{\text {BP}}$, bubbles will get ingested into the SC-LAD. Therefore, $\Delta P_{\text {FTS}}$ is considered one of the main influential parameters to investigate the phase separation performance of a SC-LAD system. At the critical point, the following pressure balance holds:

$$\begin{aligned} \Delta P_{\text {BP}} = \Delta P_{\text {FTS}} \end{aligned}$$

(7)

Equation 5 can be rearranged to obtain a friction factor f with a pore Reynolds number $\text{Re}_\text{P}$ (see Armour and Cannon 1968).

$$\begin{aligned} f = \frac{\phi ^2 D_{\text {BP}}}{\tau B}\frac{\Delta P_{\text {FTS}}}{\rho {v_\text {s}}^2} \end{aligned}$$

(8)

$$\begin{aligned} Re_\text {P} = \frac{\rho v_\text {s}}{\mu S^2 D_{\text {BP}}} \end{aligned}$$

(9)

$$\begin{aligned} f = \frac{C_1}{Re_\text {P}}+ C_2 \end{aligned}$$

(10)

When the value of $\text{Re}_\text{P}$ is below the range of $1 \le \text{Re}_\text{P} \le 10$, the inertial term of the flow through screen pressure drop can be neglected (Bisht and Dreyer (2020)). The values of the fitting parameters $C_1$ and $C_2$ vary from author to author based on different testing conditions and screen types. One can find many different sets of fitting parameters in the literature. Armour and Cannon (1968) have studied and tested five screen weave types and gave common fitting parameters for all weave types. Cady (1973) reported fitting parameters for different screen types. Hartwig worked extensively on different pressure drop models and reported fitting parameters based on cryogenic experiment data. Different fitting parameters for DTW 325 x 2300 were reported by Hartwig et al. (2014a) for different cryogenic liquids, however in Hartwig (2016b) shows group specific fitting parameters along with various screen properties for individual screens. These fitting parameters were further modified and new corrected fitting parameters were reported on pages 234-235 in Hartwig (2016b). Conrath and Dreyer (2012) have worked with DTW 200 x 1400 screens with silicon oil and present fitting parameters under steady-state conditions. 14 different screen meshes from three different metals were tested by Camarotti et al. (2019) at room temperature. It was found that for DTW screens, the fitting parameter used for the whole group does not necessarily fit accurately for all individual screens of the group. Thus, it was recommended to use screen-specific fitting parameters instead of weave type specific whenever possible. In the work of Bisht and Dreyer (2020), they have compared the different analytical solutions with their experiment results.

Table 1 Screen parameters and properties used for DTW 200 x 1400

Experimental Setup

An experiment tank with a SC-LAD was developed for the drop tower experiments to investigate the phase separation capability of the SC-LAD and its limits, the bubble point breakthrough. The drop tower experimental setup was assembled into a drop tower capsule consisting of several platforms carrying a high-speed camera recorder, components from the experiment hydraulic loop, the capsule computer, power units, and batteries.

During free fall, the liquid was removed from the experiment tank through the SC-LAD with the help of a gear pump at a constant flow rate. After a few seconds of liquid removal, based on the initial volume of liquid and removal flow rate, the screen was exposed to the gaseous phase present in the tank. At a certain point in time, when the screen area covered with the liquid became small enough to make the associated flow through screen pressure drop higher than the bubble point pressure, ingestion of bubbles occurred. The pressure and temperature inside the outlet line were recorded for the whole experiment. Two high-speed cameras were placed to observe the tank at all times during the experiment. All the components of the experimental setup are discussed in detail in the following sections.

Fig. 2

Design of the experiment tank and the SC-LAD

Design of the Experiment Tank

A rectangular tank with two sections was designed to host the SC-LAD. A catapult launch creates an initial acceleration of approximately 30 times the normal gravitational acceleration on Earth. The microgravity duration during each flight is around 9.1 seconds. The design of the setup must account for the available time. The final design of the tank and the SC-LAD is shown in Fig. 2.

The tank was made up of two sections. One section contained the SC-LAD and the other section contained eight parallel perforated vanes to withdraw most of the liquid away from the vicinity of the SC-LAD. The vanes ran parallel along the wall and were extended at the bottom of the tank too. The perforation in the vanes served as the communication channel for the liquid between the vanes. The height of the experiment tank was truncated on the side where SC-LAD was present, and an outlet was placed at the top of the SC-LAD. The tank material is PMMA.

The length and width of the experiment tank are $L_\text {T}$ and $W_\text {T}$, respectively. The height of the tank on the side containing the vanes is $H_{\text {T1}}$, and the height of the tank on the truncated side is $H_{\text {T2}}$. The length and width of the outer side of the SC-LAD are $L_0$ and $W_0$, respectively. The height of the SC-LAD is $H_0$. The internal length and width of the channel are $L_\text {CH}$ and $W_\text {CH}$, respectively. The side of the SC-LAD facing the wall of the tank has an opening covered with a metallic screen as shown by dotted lines on the SC-LAD in Fig. 2. The details about the screen used are mentioned in the next section. The vertical dimension of the channel opening is $H_{\text {SC}}$ and the horizontal dimension of the opening is $W_{\text {SC}}$. Every corner of the screen opening has a radius of curvature of ${2\,\textrm{mm}}$ which results in a total approximate open area of the screen $A_{\text {SC}} = {293\,\mathrm{mm^2}}$. The gap between the SC-LAD and the wall of the experiment tank is denoted by a. The maximum volume of liquid that the tank can hold is ${800\,\textrm{ml}}$, but due to the limited microgravity duration, the initial volume of liquid was kept at approximately ${450\,\textrm{ml}}$. Values of the above mentioned parameters are summarized in Table 2.

Table 2 Dimensions of the experiment tank

Screen

The phase separation ability and permissible range of liquid removal flow rate from a SC-LAD depend on the characteristics of the screen. Dutch twilled weave (DTW) screens are most suitable for SC-LAD application according to Darr and Hartwig (2014). These screens are woven with stainless steel wires of two different diameters, called warp and weft wires. We use a DTW 200 x 1400 screen in the SC-LAD of our experiment. A CAD model of a DTW 200 x 1400 screen is shown in Fig. 3. The numbers denote: 200 warp wires per inch and 1400 weft wires per inch. The important screen parameters are given in Table 1. This screen has been used widely in various studies in the literature and has been recommended as one of the five finest DTW screens according to the work of Darr and Hartwig (2014).

Fig. 3

CAD model of DTW 200 x 1400 screen

Test Liquid

The test fluid was $\text {3M}^{\text {TM}}$ $\text {Novec}^{\text {TM}}$ HFE-7500. The contact angle of this liquid with the stainless steel screen material and the acrylic material of the tank is 0°. The liquid properties at different temperatures are given in Table 3, as reported by Bisht 2020 Bisht and Dreyer (2020).

Table 3 Properties of test fluid HFE-7500 Bisht and Dreyer (2020). The contact angle is $\theta = {}{0^{\circ }}{}$

Fluid Loop

The hydraulic loop of the experimental setup consists of the experiment tank ET, a bellow pump BP, the storage tank ST, a flow meter FM, a pump FP, the reserve tank RT, pressure sensors P1 and P2, temperature sensors T1 and T2, and flow control valves V1 to V5 as shown in Fig. 4.

Fig. 4

Hydraulic loop of the drop tower experiment setup

The experimental setup has two important liquid loops. The first loop is a close loop which was used to initialize the pump and flow meter and bring them to a stable working state after turning them on. This loop consists of the FP, the FM, the RT, valve V2, and the FP again. This fluid loop is referred to as the inner loop for convenience in the further text. The other fluid loop is an open loop which was used to perform the experiment in microgravity duration to withdraw liquid from the experiment tank. This loop consists of the ET, sensor T2, P2, and P1, valve V3, the FP, the FM, valve V1, and the ST. This fluid loop is referred to as the outer loop.

A gear pump head from Micropump GA-V21 is used along with a variable speed drive from Ismatec Reglo-Z to pump the liquid around in the loop. The sensor used for flow rate measurement is from SIKA VZ0025. The accuracy of the sensor is ±0.3 % of the measured value as specified in the manufacturer data sheet. A differential pressure sensor (P2) from MEAS company is used to measure the pressure difference in the downstream direction of the SC-LAD. Its measurement range is 0 to 350 hPa with an accuracy of $\pm {0.25\ \mathrm{\%}}$ of full reading, i.e around $\pm {0.9\,\textrm{hPa}}$. An absolute pressure sensor (P1) from company TetraTec is also used with a measurement range of 0 to 0.16 MPa and an accuracy of $\pm {2.1\,\textrm{hPa}}$. The temperature sensors are PCA-type PT100 from JUMO GmbH with an accuracy of $\pm {0.05\,\mathrm{{}^{\circ }\text {C}}}$.

The reserve tank (RT) is an in-house manufactured reservoir that has two compartments separated with a DTW 325 x 2300 screen of ${60\,\mathrm{\text {m}\text {m}}}$ diameter. This tank acts as a liquid supplier to operate the inner loop and also traps the gas bubbles from the liquid lines with the help of the metallic screen. It works on the same principle as the SC-LAD. The accumulated gas in the RT can be removed manually by opening a valve presented at the top of it. RT has a working volume of ${314\,\mathrm{\text {m}\text {L}}}$.

The bellow pump (BP) is an in-house manufactured piece of hardware with a working volume of ${310\,\mathrm{\text {m}\text {L}}}$. It has a bellow made out of Teflon, and a driving screw guides its movement. It is used to do the fine adjustment in the liquid level of the ET before the launch of the drop capsule.

Optics

The optical setup consists of two FASTCAM MH4-10k cameras (CAM1, CAM2) from Photron, a FASTCAM MC2.1 camera recorder, and two Stemmer Imaging LED light panels. The images were recorded at the rate of 500 frames per second for 16.4 seconds with a resolution of 512 x 512 pixels. According to Fig. 2, CAM1 was placed in the y, z-plane facing the SC-LAD at a suitable angle to view the screen inside, and CAM2 was placed in the x, z-plane facing the gap between the SC-LAD and the tank wall. CAM1 was placed to observe the ingested bubble inside the channel after the bubble point breakthrough of the screen, whereas the gap between the SC-LAD and the tank wall, and the movement of the liquid was observed by CAM2. Both cameras were fitted with lenses from the Schneider Kreuznach company. A 1.4/8-0902 C-mount lens with ${8\,\mathrm{\text {m}\text {m}}}$ of focal length and 1.4 manual aperture was used in CAM1, whereas a 2.1/6-0901 lens with ${6\,\mathrm{\text {m}\text {m}}}$ of focus length and 2.1 manual aperture was used in CAM2. The field of view of both the cameras with important labels is shown in Fig. 5a and b.

Fig. 5

The optical setup is shown here. a shows the field of view of CAM1 showing the SC-LAD with ingested bubbles from Exp F5. b shows the field of view of CAM2 showing the screen exposed to liquid and gas from Exp F5

Operations

We used the catapult mode of operation in the Bremen drop tower. During launch, the experiment capsule experiences a brief acceleration of approximately $30 \, g_{\text {E}}$ for around ${300\,\mathrm{\text {m}\text {s}}}$. After that, it travels from the bottom to the top of the tower and back to the ground before landing in the deceleration chamber, resulting in a total microgravity duration of approximately 9.1 seconds.

According to the Bremen Drop Tower payload user’s guide, every drop capsule is equipped with an Inertial Measurement Unit (IMU) type iIMU-FCR-03, manufactured by iMAR Navigation GmbH to measure the angular rate and acceleration of the drop capsule at a sampling rate of ${400\,\mathrm{\text {Hz}}}$. All these data are made available to the experimenters. Figure 6 shows a typical compensated gravity flight profile over time during experiment F5. Microgravity begins at $t={0\,\mathrm{\text {s}}}$ on the time scale. The fluctuation in the acceleration profile before and after the microgravity duration of ${9\,\mathrm{\text {s}}}$ corresponding to the launch and landing of the capsule in the deceleration chamber.

Fig. 6

Acceleration in z-direction versus time plot for experiment F5. The vertical dotted line represents the time of the bubble point breakthrough

The preparation of the experiment capsule was carried out in two phases.

Phase 1: When the capsule was at the ground station and physically accessible, we filled the experiment setup with the necessary amount of test liquid. The reserve tank (RT) was filled using a manual opening at the top. The ET and BP were filled using a liquid refill line through valve V5. All the liquid lines were made sure to be filled with the liquid. It should be noted that the experiment tank and storage tank were kept at ambient pressure during the experiment.

Phase 2: When the capsule was placed inside the drop tower, the activities within the capsule were remotely controlled through a user interface developed using LabVIEW software. An automatic control sequence was programmed to oversee various activities within the experiment, according to the test matrix following the launch of the capsule. The experimenters initiated the launch process through the software interface, and subsequent activities, such as valve operations based on predefined time duration, were executed in accordance with the pre-programmed sequence.

Before the launch of the experiment capsule, the pump was set remotely to a fixed flow rate and kept running in the inner loop. After the launch, as soon as the drop capsule experienced microgravity, the valves V1, V2, and V3 reversed their positions simultaneously through the programmed automatic control sequence, and the removal of liquid started from the ET to the ST via the outer loop. The cameras focused on the experiment were already recording the setup by this time since they were switched on 2 seconds before the commencement of the state of microgravity. The positions of the valves V1, V2, and V3 were reversed again 9 seconds after the setup started experiencing microgravity. The cameras and the pump were then turned off 2 seconds later, following the programmed sequence.

Table 4 Drop tower experiment test matrix and experimental parameters

Test Matrix

The test matrix and experimental parameters of the drop tower experiments are shown in Table 4. The data points for the test matrix have been selected for a combination of different flow rates $\dot{V_{\text {L}}}$ and initial fill levels $h_{\text {IL}}$. The tests are divided into three groups, based on $\dot{V_{\text {L}}}$. The groups are named G1R4, G2R5, and G3R6, where the number after G denotes the group number and the number after R denotes the approximate value of the applied removal flow rate $\dot{V_{\text {L}}}$ in ${\text {mL s}^{-1}}$.

The beginning of the microgravity phase is considered at $t= {0\,\mathrm{\text {s}}}$ on the time scale. $h_{\text {IL}}$ is the fill level of liquid above the top edge of the channel opening covered with the screen, $t_{\text {VO}}$ is the opening time of valves V3 and V1, $t_{\text {VC}}$ is the closing time of valves V3 and V1 after the start of microgravity, $t_\text {B}$ is the time between the start of microgravity and the start of bubbles ingestion, and T is the average liquid temperature in the outlet line measured using temperature sensor T2.

In experiment F8, the liquid removal was paused after the first breakthrough for ${2.75\,\mathrm{\text {s}}}$ and restarted. Therefore $t_{\text {VO}}$ and $t_{\text {VC}}$ have two values corresponding to this test flight along with a reported second breakthrough.

Data Evaluation

We performed 6 drop tower experiments (Table 4) using a catapult in the Drop Tower facility of the University of Bremen. Each flight experienced ${9.1\,\mathrm{\text {s}}}$ of microgravity. The capsule was equipped with various sensors and measurement devices to gather important data throughout the flight, which provided the following data for various measurements during the experiment campaign.

Image Analysis

Two high-speed cameras CAM1 and CAM2 were used to observe the experiment tank during the experiment. The field of view of both the cameras is shown in Fig. 5a and b. The images from the CAM2 were used to analyze and calculate the effective screen area covered with liquid $A_\text {L}$. An LED was placed in the field of view of the camera which got turned on when the SC-LAD was being used to remove liquid from the tank. This LED signal also helped in synchronizing the image data with the output of other sensors like pressure, temperature, etc.

The area calculation was performed using image analysis techniques through ImageJ and Gimp open-source software codes. Due to complex illumination arrangements, automatic edge detection codes and techniques proved to be unhelpful, as the liquid edges were overexposed to the light source. Additionally, the positions of the shadow of the liquid bridge between the SC-LAD and the tank wall move with the movement of the liquid in the gap. Therefore, it was important to analyze each image separately to obtain precise area measurements. The images selected for the area calculations were taken from the time instance when the screen opening started to get partially exposed to the surrounding gaseous phase up to the point of breakthrough. The correlations to calibrate the pixels into length scales were established using reference images with measurement grid stencil on the SC-LAD as shown in Fig. 7d for CAM2. A measuring scale present in the CAM1 field of view was used to obtain its image resolution. The calculated image resolution of CAM1 and CAM2 was 9.25 pixels per ${\text {m}\text {m}}$ and 4.8 pixels per ${\text {m}\text {m}}$, respectively.

Fig. 7

The main steps for the image analysis are explained here. a shows a sample raw image obtained from CAM2 during the experiment in microgravity. b shows the reference image captured from CAM2 on the ground with a stencil on the SC-LAD to highlight the edges of the channel opening covered with the screen. c shows the overlapped image obtained by overlaying the reference image on the raw experiment image. The effective area of the screen covered with the liquid is highlighted along with the dimension of the channel opening. d shows the reference image with the grid used to calculate the image resolution of CAM2. The grid has cell size of ${2.5\,\mathrm{\text {m}\text {m}}}$ x ${2.5\,\mathrm{\text {m}\text {m}}}$

The SC-LAD in the experiment consists of a PMMA channel with an opened side covered by a screen weave. As depicted in the CAD model of the SC-LAD shown in Fig. 2, it is challenging to discern the edges of the channel opening without any external marking since it is concealed by the screen. To accurately identify the edges of the channel opening covered with the screen, several types of stencils were prepared and affixed to the SC-LAD. These stencils aided in capturing the previously obscured channel opening in the images which indirectly helped in the calculation of the wetted area of the screen $A_\text {L}$. The main steps performed for area calculation are described in Fig. 7. Specifically, raw experiment images from CAM2 were superimposed with a reference image taken on the ground to highlight the edges of the channel opening. The selection of $A_\text {L}$ was done manually with care to ensure accurate calculations. For a visual representation, Fig. 8 shows a CAD model highlighting the curvature of the gas-liquid interface present in the gap between the tank wall and the SC-LAD.

Fig. 8

CAD model highlighting the curvature of the gas-liquid interface present in the gap between the SC-LAD and the tank wall

Volumetric Flow rate $\dot{V_L}$ Variation

The flow meter FM measured the removal flow rate $\dot{V_L}$ through the SC-LAD. It was calibrated beforehand to establish a correlation between the measured volumetric flow rate with the voltage output. The measured flow rate was found to vary in the range of $\pm {0.1\,\mathrm{\text{mL s}^{-1}}}$ of the desired flow rate given as voltage input to the pump. The variation of the flow rate $\dot{V_L}$ is shown for all the experiments in Fig. 9. The plot represents the values with a moving average of 100 data points. The sampling rate is ${1000\,\mathrm{\text {Hz}}}$.

Fig. 9

The plot of the volumetric flow rate $\dot{V_L}$ variation with respect to the microgravity time for all the experiments

Temperature Variation

Two temperature sensors (T1 and T2) were used in the experiment setup. T1 was connected to one of the experiment tank walls, and T2 was connected to the outlet line of the SC-LAD. Upon analyzing the data, it was observed that the wall temperature (T1) remains steady, whereas the temperature of the liquid in the outlet line (T2) decreases initially with the liquid flow and reaches a stable state after a few seconds. The average deviation of the T2 readings as compared to the start of the experiment was around ${0.7\,\mathrm{{}^{\circ }\text {C}}}$. The mean average of T2 taken after ${3\,\mathrm{\text {s}}}$ is used to calculate the properties of the test liquid for each experiment. The sampling frequency is ${1000\,\mathrm{\text {Hz}}}$. In the scope of this work, all the experiments are considered to be performed under isothermal conditions.

Pressure Variation

A differential pressure sensor (P2) was utilized to measure the pressure difference in the downstream direction of the SC-LAD. The sensor is located in the liquid line near the outlet of the SC-LAD, as shown in Fig. 4.

The plot in Fig. 10 illustrates the raw values of the differential pressure data $\Delta P_{\text {2R}}$ measured from the P2 sensor for experiment number F5 over time. The beginning of microgravity is indicated at $t={0\,\mathrm{\text {s}}}$, and it lasts until around $t={9.1\,\mathrm{\text {s}}}$. Due to the utilization of a catapult during the launch of the drop capsule, the pressure sensor P2 experienced a high differential pressure for approximately ${300\,\mathrm{\text {m}\text {s}}}$. Consequently, the pressure sensor data reveals a distinct peak, accompanied by several smaller associated pulses, during the capsule’s launch and at the onset of the microgravity period. Furthermore, a notable spike in the pressure signal occurs shortly after 9 seconds, aligning with the impact encountered by the drop capsule as it collides with the deceleration chamber at the conclusion of the flight.

It can be seen from the graph shown in Fig. 10 that the differential pressure $\Delta P_{\text {2R}}$ starts to increase from ${5.5\,\mathrm{\text {s}}}$ for the experiment F5 and reaches a peak value at $t={5.81\,\mathrm{\text {s}}}$. This peak corresponds to the bubble point breakthrough of the SC-LAD. The images captured from the high-speed camera system support the same as shown in Fig. 15. The plot presents the data with a moving average of 100 points. The sampling rate is ${1000\,\mathrm{\text {Hz}}}$.

Differential pressure $\Delta P_{\text {2R}}$ plots with respect to microgravity time are shown for all the experiment groups in Figs. 11, 12, and 13.

Fig. 10

The differential pressure variation over time was measured by sensor P2 for experiment F5. The vertical line represents the time of the bubble point breakthrough at $t={5.81\,\mathrm{\text {s}}}$. The plot also shows the pressure fluctuation during the launch and deceleration of the capsule

Fig. 11

The differential pressure variation with respect to the microgravity time was measured by sensor P2 for experiments group G1R4. The vertical dashed line represents the time of bubble point breakthrough corresponding to each flight

Fig. 12

The differential pressure variation with respect to the microgravity time was measured by sensor P2 for experiments group G2R5. The vertical dashed line represents the time of bubble point breakthrough corresponding to each flight

Fig. 13

The differential pressure variation with respect to the microgravity time was measured by sensor P2 for experiments group G3R6. The vertical dashed line represents the time of bubble point breakthrough corresponding to each flight

Fig. 14

Timeline showing events for experiment F5

Fig. 15

Position of liquid inside the experiment tank at different microgravity time instances from CAM1 and CAM2 during experiment no. F5

Results and Discussion

Phase Separation Result

As discussed in Data Evaluation, six drop tower experiments were performed and categorized into groups based on the applied removal flow rate. Except for experiment no. F8, the liquid removal from the tank was started at $t={0\,\mathrm{\text {s}}}$ and ended at $t={9\,\mathrm{\text {s}}}$. In these experiments, the two-phase flow through the screen continued after the first bubble breakthrough. However, in experiment no. F8, two breakthroughs were observed as the liquid removal was stopped after the first breakthrough and resumed following a pause. Table 4 provides detailed information on all experimental parameters.

The high-speed camera system captured images of the position of the liquid-gas interface inside the tank. The start and stop of liquid removal were controlled by the switching of valves V1, V2, and V3. An LED was connected to the valve control to indicate the start and stop of active liquid removal from the experiment tank. This LED was present in the field of view of CAM2, and all images were synchronized with the sensor data using this output signal from the LED.

A series of images is shown in Fig. 15 for experiment no. F5. An event timeline is provided in Fig. 14 for a better understanding of the experiment progression.

In Fig. 15a, an image taken by CAM2 shows the position of the liquid one second after microgravity commenced. The liquid can be seen rising in the gap between the SC-LAD and the tank wall due to the capillary pressure. In Fig. 15b, the situation of the gap is shown at $t={4\,\mathrm{\text {s}}}$. It can be seen that the gap remains completely filled with liquid, and the supply of liquid to the SC-LAD balances the removal flow rate. In the next image Fig. 15c of the series which was taken at $t={5.5\,\mathrm{\text {s}}}$, the amount of liquid present in the gap can be seen declining as the supply of liquid to the gap from the rest of the tank is not sufficient to fulfill the demand of the SC-LAD. As a result, the screen can be seen partially exposed to the surrounding air. The area of the screen exposed to the air increases further in image Fig. 15d. In the next image at $t={5.75\,\mathrm{\text {s}}}$, both camera views are shown. It can be seen that the area of the screen exposed to air has increased further. We can confirm at the same time from CAM1 view, that the screen is successfully separating the phases and no gaseous bubbles are ingested into the SC-LAD. Finally, in the next image at $t={5.82\,\mathrm{\text {s}}}$, tinny ingested bubbles can be seen after the breakthrough of the screen. This can be inferred from the numerous active pores that can be seen ingesting bubbles in the image from CAM1 in Fig. 15f. The ingested tinny bubbles coalesce into larger bubbles and can be seen in the next image at $t={5.83\,\mathrm{\text {s}}}$. In Fig. 15h, the whole screen is now exposed to air and ingested bubbles have grown even bigger.

This series of aforementioned images and the events they demonstrate are in tune with the differential pressure data shown for experiment no. F5 in Fig. 12. It is observed that the differential pressure starts to increase with the decrease of the effective area of the screen covered with liquid $A_\text {L}$. This starts at around $t={5.5\,\mathrm{\text {s}}}$. The observation can be confirmed by the Eq. 5. As per this correlation, the flow through screen pressure drop $\Delta P_{\text {FTS}}$ increases with any increase in the superficial velocity $v_\text {s}$ and vice versa. Additionally, $v_\text {s}$ is inversely proportional to $A_\text {L}$ as shown in Eq. 6, therefore the $\Delta P_{\text {FTS}}$ increases with any decrease in the value of $A_\text {L}$. At the bubble point breakthrough, the value of $A_\text {L}$ has decreased to the point where the $\Delta P_{\text {FTS}}$ has increased sufficiently to overcome the bubble point pressure of the screen $\Delta P_{\text {BP}}$, and thus the sharp peak in the differential pressure signal is observed in Fig. 10.

Fig. 16

Timeline showing events from experiment F8

Fig. 17

Position of liquid inside the experiment tank at different microgravity time instances from CAM1 and CAM2 in experiment F8. In f, g and h, the LED is off, indicating no active removal of liquid from the SC-LAD

A series of images showing the position of the liquid-gas interface from experiment no. F8 is presented in Fig. 17. To clarify the sequence of events during the experiment, a timeline is provided in Fig. 16. Following the initial breakthrough at $t={4.50\,\mathrm{\text {s}}}$, a significant amount of gas was ingested into the channel, leaving no liquid in the gap. Liquid removal was stopped at $t={5.00\,\mathrm{\text {s}}}$, and the system reached a new equilibrium, with the gap refilled by capillary forces. When the liquid removal was restarted at $t={7.75\,\mathrm{\text {s}}}$, a second bubble point breakthrough of the screen occurred.

The liquid can be seen rising in the gap between the SC-LAD and the tank wall in the image from CAM2 in Fig. 17a. In the next images, at $t={4.00\,\mathrm{\text {s}}}$ and $t={4.25\,\mathrm{\text {s}}}$, the amount of liquid in the gap has decreased due to the constant and continuous removal of the liquid. The liquid-gas interface has moved partially inward exposing the screen to the surrounding air. However, the screen has successfully separated the phases and no gas bubble has been ingested yet. The image at $t={4.52\,\mathrm{\text {s}}}$ shows some tinny ingested bubbles in the CAM1 image which suggests that the first bubble point breakthrough has already occurred. In Fig. 17e, the whole screen is now exposed to air and the channel has ingested a considerable amount of gaseous bubbles. In the next image at $t={5.25\,\mathrm{\text {s}}}$, the liquid removal from the experiment tank is stopped. This can be observed from the off state of the LED display at the top of the image captured by CAM1. Without the external removal force, the screen is again covered with liquid, as indicated by a change in its color at the exposed portion. Additionally, the gap is refilled with liquid due to capillary forces. The next image of the series at $t={6.50\,\mathrm{\text {s}}}$ and $t={7.50\,\mathrm{\text {s}}}$ show that the gap gradually fills with liquid and eventually becomes completely filled. Furthermore, the gaseous bubbles take on a perfectly spherical shape in the absence of the external removal force. At $t={7.75\,\mathrm{\text {s}}}$, the removal of liquid from the experiment tank was restarted. Figure 17i depicts the state of the experiment tank at $t={8.00\,\mathrm{\text {s}}}$, where the liquid-gas interface has moved inward due to the liquid removal. The CAM1 image shows the LED turned on which indicates that the liquid is actively being removed from the experiment tank. Additionally, previously ingested bubbles in the SC-LAD have started to move downstream with the liquid. In the final image of the series, Fig. 17j shows the status of the experiment tank after the second breakthrough, where numerous active pores are ingesting bubbles into the SC-LAD.

As discussed previously for experiment no. F5, the events depicted in the images for experiment no. F8 is also consistent with the differential pressure data displayed in Fig. 13. The occurrence of both the bubble point breakthroughs, as observed in the images, matches with peaks in the differential pressure signal.

The differential pressure sensor data presented in Figs. 11, 12 and 13 is obtained from the differential pressure sensor P2 which is located in the downstream direction after the outlet of the SC-LAD, as represented in Fig. 4. It is located at a distance of around ${150\,\mathrm{\text {m}\text {m}}}$ from the SC-LAD outlet. Due to mechanical limitations, the pressure measurement any closure than this location was not possible. Thus, the pressure sensor detects the frictional losses and additional secondary losses due to the presence of pipe fittings and bends along with the $\Delta P_{\text {FTS}}$. To estimate the $\Delta P_{\text {FTS}}$ from the raw data obtained by the P2 differential pressure sensor $\Delta P_{\text {2R}}$, corrections are necessary for these additional pressure drops. We have calculated the additional minor and major pressure drops in the system for each flight based on experiment conditions and corrected the output of the P2 sensor to estimate the flow through screen pressure drop experimentally to the best of our knowledge. The necessary information regarding location, dimensions, and formulations is presented in Appendix.

As observed from the camera images, the liquid covered the entire surface of the screen at the beginning of all experiments. As the liquid in the tank was removed, the liquid present in the gap decreased, partially exposing the screen to the surrounding air. The decrease in the effective area of the screen covered with liquid $A_\text {L}$ was calculated using image analysis, as described in Image Analysis, with respect to the microgravity time. The variation of $A_\text {L}$ with respect to the microgravity time until the bubble point breakthrough of the screen is presented graphically for each experiment in Figs. 18, 20 and 22 along with the measured differential pressure $\Delta P_{\text {2R}}$ from the pressure sensor P2.

To calculate the flow through screen pressure drop $\Delta P_{\text {FTS}}$ for a given wetted area of the screen $A_\text {L}$, analytical calculations were performed using Eq. 5 and the values given in Table 1. The graphical representation of the correlation between $1/A_L$ and $\Delta P_{\text {FTS}}$ is presented in Figs. 19, 21, and 23, where analytically calculated and experimental data are compared for each experiment group.

The corrected data from the differential sensor P2 is represented as $\Delta P_{\text {2C}}(Fx)$, and the analytically calculated flow through screen pressure drop is represented as $\Delta P_{\text {FTS}}(Fx)$ where x represents the experiment number. The details about the correction introduced in pressure drop measured by sensor P2 can be found in Table 7 of Appendix. The analytical solution is calculated for discrete values of the wetted area $A_{\text {L}}$, but we represent it using continuous lines. This representation allows us to visualize the solution as a smooth line capable of accommodating various values of $A_{\text {L}}$. Regardless of the specific $A_{\text {L}}$ value, the solution consistently lies along the same line.

The results from all the experiments are compared with each other by converting them into dimensionless form, as presented in Fig. 24. ${A_\text {L}}^{\star }$ is the dimensionless form of $A_\text {L}$ obtained after dividing it with the total screen area $A_{\text {SC}}$, and $\Delta {P_{\text {FTS}}}^{\star }$ is the dimensionless form of $\Delta P_{\text {FTS}}$ obtained after divided it with the maximum value of flow through screen pressure drop $\Delta P_{\text {CA}}$ corresponding to the critical area $A_{\text {C}}$.

$$\begin{aligned} {A_\text {L}}^{\star } = A_\text {L}/A_{\text {SC}} \end{aligned}$$

(11)

$$\begin{aligned} \Delta {P_{\text {FTS}}}^{\star } = \Delta P_{\text {FTS}}/\Delta P_{\text {CA}} \end{aligned}$$

(12)

The plot presented in Fig. 24 shows the experimental and analytical data for all the flights of each experiment group. $\Delta {P_{\text {FTS}}}^{\star }$ represents the dimensionless analytical solution and $\Delta {P_{\text {2C}}}^{\star }$ represents the dimensionless corrected values of the experimental data obtained by sensor P2. $\Delta {P_{\text {2C}}}^{\star }$ is obtained by dividing $\Delta P_{\text {2C}}$ with the maximum pressure drop measured at the critical point where breakthrough starts, denoted as $\Delta P_{\text {2CM}}$.

$$\begin{aligned} \Delta {P_{\text {2C}}}^{\star } = \Delta P_{\text {2C}}/\Delta P_{\text {2CM}} \end{aligned}$$

(13)

Fig. 18

Wetted area $A_{\text {L}}$ versus time plot and measured differential pressure $\Delta P_{\text {2C}}$ versus time plot for experiment no. F1 and F3 of group G1R4. The maximum vertical error bar for $A_{\text {L}}$ is $\pm {6.5}\ \textrm{mm}^2$. The vertical line denotes the time of the bubble point breakthrough

Fig. 19

Plot showing $\Delta P_{\text {FTS}}$ with respect to $1/A_{\text {L}}$ for the experiment group no. G1R4. Triangle and circular symbols denote the corrected value of the pressure drop measured during experiment no. F1 and F3, respectively. The analytical $\Delta P_{\text {FTS}}$ is represented as continuous lines $\Delta P_{\text {FTS}}(F1)$ and $\Delta P_{\text {FTS}}(F3)$. The vertical error bar for $\Delta P_{\text {FTS}}$ is $\pm {0.9}\ \textrm{hPa}$ and the maximum horizontal error bar for $1/A_{\text {L}}$ is $\pm {0.08} \times 10^{-2}\ \textrm{mm}^{-2}$

Fig. 20

Wetted area $A_{\text {L}}$ versus time plot and measured differential pressure $\Delta P_{\text {2C}}$ versus time plot for experiment no. F2 and F5 of group G2R5. The maximum vertical error bar for $A_{\text {L}}$ is $\pm {6.5}\ \textrm{mm}^2$. The vertical line denotes the time of the bubble point breakthrough

Fig. 21

Plot showing $\Delta P_{\text {FTS}}$ with respect to $1/A_\text {L}$ for the experiment group no. G2R5. Triangle and circular symbols denote the corrected value of the pressure drop measured during experiment no. F2 and F5, respectively. The analytical $\Delta P_{\text {FTS}}$ is represented as continuous lines $\Delta P_{\text {FTS}}(F2)$ and $\Delta P_{\text {FTS}}(F5)$. The vertical error bar for $\Delta P_{\text {FTS}}$ is $\pm {0.9\,\mathrm{\text {h}\text {Pa}}}$ and the maximum horizontal error bar for $1/A_\text {L}$ is $\pm {0.08} \times 10^{-2}\ \textrm{mm}^{-2}$

Fig. 22

Wetted area $A_{\text {L}}$ versus time plot and measured differential pressure $\Delta P_{\text {2C}}$ versus time plot for experiment no. F6 and F8 of group G3R6. The maximum vertical error bar for $A_{\text {L}}$ is $\pm {6.5}\ \textrm{mm}^2$. The vertical line denotes the time of the bubble point breakthrough

Fig. 23

Plot showing $\Delta P_{\text {FTS}}$ with respect to $1/A_{\text {L}}$ for the experiment group no. G3R6. Square, triangle, and circular symbols denote the corrected value of the pressure drop measured during experiment no. F6 and F8. F8b1 and F8b2 represent the data from the first and second breakthroughs. The analytical $\Delta P_{\text {FTS}}$ is represented as continuous lines $\Delta P_{\text {FTS}}(F6)$ and $\Delta P_{\text {FTS}}(F8)$. The vertical error bar for $\Delta P_{\text {FTS}}$ is $\pm {0.9\,\mathrm{\text {h}\text {Pa}}}$ and the maximum horizontal error bar for $1/A_{\text {L}}$ is $\pm {0.08} \times 10^{-2}\textrm{mm}^{-2}$

Fig. 24

Plot showing $\Delta {P^{\star }}_{\text {FTS}}$ with respect to $1/{A^{\star }}_{\text {L}}$ for all the experiment groups in dimensionless form. $\Delta {P^{\star }}_{2C}$ denotes the dimensionless form of the corrected experimental data measured by pressure sensor P2 and continues lines denoted by $\Delta {P^{\star }}_{FTS}$ represents the dimensionless analytical solutions calculated for different values of wetted area $A_L$ for each experiment group

Analysis of the Maximum Pressure Measured at the Breakthrough Point

It was observed that the pressure sensor P2 showed a peak in the differential pressure measurement corresponding to the breakthrough point for each experiment flight. The time of occurrence of the breakthrough point $t_\text {B}$ depends mainly on factors such as the initial amount of liquid in the tank and the removal flow rate. The maximum pressure measured by the P2 sensor $\Delta P_{\text {2CM}}$ was found to be increasing with the applied flow rate $\dot{V_{\text {L}}}$. We have compared these values with two theoretical formulation of bubble point from literature calculated according to Eq. 1 (Hartwig and Darr 2016) denoted as $\Delta P_{\text {BPH}}$ and Eq. 2 (Conrath and Dreyer 2012) denoted as $\Delta P_{\text {BPC}}$ in Table 5. It is important to note that the theoretical $\Delta P_{\text {BP}}$ is defined for static conditions, while the experiment conditions are dynamic and dependent on the volumetric flow rate.

Some similar observations have been reported in the literature. In the work of Hartwig et al. (2014b), it was found that the breakthrough point of the tested SC-LAD had a second-order dependency on the mass flow rate through the LAD. On the other hand, in the work of Conrath and Dreyer (2012), it was reported that the bubble breakthrough triggered by flow-induced pressure drop across the screen was about 15 % above the static bubble point. For further analysis, an investigation is required with a dedicated experiment design.

Table 5 Comparison of the analytical bubble point $\Delta P_{\text {BPH}}$ and $\Delta P_{\text {BPC}}$ calculation with the maximum measured value of pressure drop at the breakthrough $\Delta P_{\text {2CM}}$ for each experiment. $\Delta P_{\text {BPH}}$ is calculated analytically following Eq. 1 and $\Delta P_{\text {BPC}}$ is calculated using Eq. 2. Values of $C_0$ varies between 0.648 to 0.705 (Conrath and Dreyer 2012), $D_{\text {P}} = {13\pm 1\,\mathrm{\upmu \text {m}}}$ taken from manufacturer Spoerl datasheet Spoerl (2022) and $D_{\text {BP}} = {21.45\,\mathrm{\upmu \text {m}}}$ (Hartwig and Darr 2016). $A_{\text {C}}$ is the value of the critical area corresponding to the breakthrough point and $\Delta P_{\text {CA}}$ is the analytical flow through screen pressure drop calculated corresponding to it. $\Delta P_{\text {2CM}}$ is the maximum value of the corrected data measured by the differential pressure sensor P2 corresponding to the breakthrough point

Conclusion

The experiments were performed to observe and investigate various phenomena associated with the removal of liquid from a tank in microgravity. The experiment tank was designed with an inbuilt screen channel liquid acquisition device SC-LAD to perform the task of phase separation between the gas and liquid phases. The test liquid was HFE-7500 and the working conditions were assumed to be isothermal.

We have presented experimental results from 6 microgravity experiments performed in the drop tower facility of the University of Bremen with a microgravity duration of around 9 seconds for each experiment. The experimental setup was flow rate driven. The experiment tank was initially filled with approximately ${450\,\mathrm{\text {m}\text {L}}}$ of the test liquid, and a fixed removal flow rate was applied to withdraw liquid through the SC-LAD during each experiment. The experiments were grouped into three groups based on the applied removal flow rate $\dot{V_{\text {L}}}$. The pressure drop in the downstream direction of the screen was measured with a differential pressure sensor. As the amount of the liquid present in the experiment tank decreases with time due to constant removal, the area of the screen covered with the liquid $A_\text {L}$ also decreases. This leads to the increase of the superficial velocity and flow through screen pressure drop $\Delta P_{\text {FTS}}$ across the screen. After the critical point, when the differential pressure across the screen surpassed the bubble point pressure limit, the ingestion of gaseous bubbles was observed in the channel with the help of high-speed cameras.

Based on the images obtained during the experiment, the wetted area $A_\text {L}$ of the screen was calculated. The analytical solution for the flow through screen pressure drops $\Delta P_{\text {FTS}}$ was calculated based on the screen properties, fixed volumetric flow rate $\dot{V_{\text {L}}}$ and calculated wetted area $A_\text {L}$ of the screen. The measured differential pressure drop was corrected for minor and major losses, and then compared with the analytically calculated $\Delta P_{\text {FTS}}$.

It was observed that the analytical calculations under-predict the pressure drop for experimental groups with higher flow rates. The difference between the experimentally measured pressure drop values $\Delta P_{\text {2C}}$, and the analytical solutions appears to increase with the volumetric flow rate $\dot{V_{\text {L}}}$. While the experimental and analytical data match well for group G1R4, the difference between the two sets of results is more pronounced for groups with higher $\dot{V_{\text {L}}}$, namely groups G2R5 and G3R6. This discrepancy arises from a possible smaller effective wetted area of the screen than what was calculated from image analysis. Additionally, the curvature of the liquid interface at the edges might also contribute to some deviation. The assumption that the superficial velocity was uniform for the entire wetted area might not hold true for the areas of the screen closer to the edges, which could have a lower velocity than assumed.

The maximum differential pressure reading $\Delta P_{\text {2CM}}$ corresponding to the breakthrough point was also found to be higher in comparison to the theoretical static bubble point $\Delta P_{\text {BP}}$ calculation. The deviation was greater for higher flow rate $\dot{V_{\text {L}}}$. It should be noted that the actual test conditions were dynamic and the system was flow rate driven. Therefore, a direct comparison with the static formulation is not appropriate. For further investigation in this direction, a dedicated experimental design is required.

These experiments reveal the interdependence of various phenomena involved in liquid removal from an experiment tank through a SC-LAD in a microgravity environment. These phenomena include liquid reorientation in the experiment tank, capillary rise of the test liquid between the SC-LAD and the tank wall, a decrease in the wetted area of the screen as the amount of liquid in the tank decreases, and a corresponding increase in pressure drop across the screen, leading to the occurrence of bubble point breakthrough with clear bubbles ingestion.

The results from the experiment campaign showed that the SC-LAD was able to supply gas-free liquid under sub-critical conditions, and bubble ingestion occurred after the system reached the critical point. The effect of the wetted area on the differential pressure drop was clearly observed. The bubble point breakthrough phenomena for different initial conditions were captured using a high-speed camera in the microgravity environment. These results can also be used for numerical simulation and model verification. The presented results demonstrate the successful application of a SC-LAD for phase separation and liquid removal in a microgravity environment.

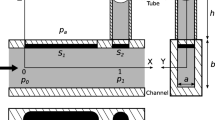
Appendix: Additional Pressure Drop Calculation Due to Location of Differential Pressure Sensor P2

Pressure losses are calculated in the following section between the location of the differential pressure sensor P2 and the screen in the SC-LAD. There are two main categories of pressure losses associated with the flow of liquid in a pipe system: local or minor losses and major losses.

Figure 25 presents a schematic depiction of the components between the screen of the SC-LAD and the location of the differential pressure sensor P2 in the hydraulic loop of the experiment setup. The lengths of the channels and other important dimensions for the calculation of the major and minor losses are also given in the figure and Table 6.

Fig. 25

The schematic representation of the component from the hydraulic loop of the experiment setup between the screen of the SC-LAD and the differential pressure sensor P2

Major Losses

Major losses in pipe flow refer to the pressure losses that occur due to friction when the liquid interacts with the wall surface White (2011). In our experiment, major losses occur along the length of the square channel and the circular pipe.

The pressure loss due in a channel $\Delta P_\text {MAJ}$ is given as

$$\begin{aligned} \Delta P_{\text {MAJ}} = f_{\text {D}}\frac{ L }{D_{\text {H}}} \frac{\rho }{2} v_{\text {m}}^2 \end{aligned}$$

(14)

where $\rho$ is the liquid density, $f_{\text {D}}$ is the Darcy friction factor, L is the length of the channel, $D_{\text {H}}$ is the hydraulic diameter, and $v_{\text {m}}$ is the mean velocity defined as follows.

$$\begin{aligned} v_{\text {m}} = {\frac{\dot{V_{\text {L}}}}{A_{\text {H}}}} \end{aligned}$$

(15)

$\dot{V_{\text {L}}}$ is the volumetric flow rate and $A_{\text {H}}$ is the cross-sectional area.

$$\begin{aligned} \text {Re}_{\text {H}} = \frac{\rho v_{\text {m}} D_{\text {H}}}{\mu } \end{aligned}$$

(16)

The Reynolds $\text {Re}_{\text {H}}$ is build with the hydraulic diameter $D_{\text {H}}$. Its value is important to select the correct $f_{\text {D}}$. Lets consider the section a-b as shown in image Fig. 25. To calculate the major loss $\Delta P_{\text {MAJ}}$ in this section a-b, the parameters given in Table 6 can be used as follows.

$$\begin{aligned} \Delta P_{\text {MAJ}} = \frac{ 56.91 }{\text {Re}_{\text {H}}} \frac{ L }{D_{\text {H}}} \frac{\rho }{2} v_{\text {m}}^2 \end{aligned}$$

(17)

Minor Losses or Local Losses

Minor losses occur at specific locations in the pipe where changes in the flow cross-sectional area or obstructions are present. These pressure losses are often associated with abrupt changes in the flow pattern or localized disturbances.

Local losses $\Delta P_\text {LOC}$ are generally defined as follows

$$\begin{aligned} \Delta P_{\text {LOC}} = K \frac{ \rho }{2} v_{\text {m}}^2 \end{aligned}$$

(18)

where K is the loss coefficient.

The associated parameters and coefficients, along with the source, are given in Table 6. The major and minor losses corresponding to each section can be calculated for all the experiments using Eqs. 14 and 18, along with the parameters given in Table 6. The sum of these losses, denoted as $\Delta P_{\text {2L}}$, for each experiment, needs to be subtracted from the raw pressure data $\Delta P_{\text {2R}}$ of the pressure sensor P2, to obtain the corrected differential pressure data $\Delta P_{\text {2C}}$. These values are summarized in Table 7 for all the experiments

Table 6 Parameters and coefficients used for the calculation of pressure losses for different sections are shown in Fig. 25

Table 7 Calculated major and minor losses for each experiment flight. $\Delta P_{\text {2L}}$ is the total of all the major and minor losses described in the above section. $\Delta P_{\text {2C}} = \Delta P_{\text {2R}} - \Delta P_\text {2L}$