A Model for the Anomalous Velocity-Undercooling Behaviour of Levitated Al-Ni Alloys On-board the International Space Station

Abstract

Al-Ni alloys (for Ni < 45 at.%) show a unique property in that, over at least part of the accessible undercooling range, the recalescence velocity measured in electromagnetically levitated samples is observed to decrease as the undercooling increases. This result has been subject to careful validation, including microgravity experiments utilising the TEMPUS levitation facility on-board the International Space Station (ISS). In these experiments, anomalous growth is observed to coincide with a recalescence morphology comprising multiple circular growth fronts [Herlach et al. Phys. Rev. Mat. 3, 073,402 (2019)], termed “scales”. In this paper we present an analysis of high speed video data from the ISS experiments in which we show that such scale-like growth is consistent with a recalescence front that is initially confined to a thin layer on the surface of the sample. This then nucleates a slower, radial inward growth, which is consistent with microstructures observed in Al-Ni droplets. We show that such surface recalescence would be favoured for samples which were surface enriched in Ni, wherein the recalescence velocity (at fixed nucleation temperature) increases rapidly with Ni-concentration. Moreover, it is shown that the anomalous velocity behaviour can be matched in all compositions studied if the surface enhancement in Ni is a linear function of the nucleation temperature with a gradient of 0.03 at.% K⁻¹. Analysis of historical results from the literature indicates that such surface Ni-enhancement may have been present, but overlooked, in other experiments on Al-rich Al-Ni droplets.

Introduction

The solidification behaviour of deeply undercooled melts and the associated relationship between recalescence (or crystal growth) velocity and undercooling has been extensively studied for more than 70 years. In such studies it has been almost universally found that growth velocity increases monotonically with increasing undercooling (e.g. Cochrane et al. 1991; Bassler et al. 1994; Mullis et al. 2004), even when such measurements are corrected for induced flow effects within the melt (Binder et al. 2014). Indeed, for melts solidifying to a dendritic morphology, the velocity-undercooling relationship is generally found to be of the form V ∝ ΔT^β (e.g. Wilnecker et al. 1989; Battersby et al. 2000; Dragnevski et al. 2004), where V is growth velocity, ΔT is undercooling and the power β is often found to lie in the range 2–4. The mechanisms for such behaviour are well understood and are in accordance with the underlying thermodynamic principles of phase transformations.

There are very few examples of the converse behaviour in which growth velocity is observed to decrease with increasing undercooling. Strong glass forming melts have been predicted to show such behaviour at very high undercooling (Orava and Greer 2014). In such melts the effect of decreasing atomic mobility as the nucleation temperature drops dominates the increase in thermodynamic driving force for crystal growth, wherein a maximum in the growth velocity is predicted. Beyond this, further increases in undercooling lead to decreasing growth velocity. Experimentally, such behaviour has been observed in Cu-Zr (Wang et al. 2014) and Ni-Zr (Kobold et al. 2017) melts. However, another group of materials, namely Al-rich Al-Ni melts have also been observed to show an anomalous growth velocity behaviour in electromagnetic levitation experiments (Lengsdorf et al. 2010). Here a convincing explanation for the behaviour has been lacking.

Lengsdorf et al. (2010) investigated the velocity-undercooling behaviour of 6 Al-Ni alloys ranging in composition from 25 at.% Ni to 45 at.% Ni. In the most dilute alloys (25, 30 and 31.5 at.% Ni) the velocity decreased monotonically with increasing undercooling across the whole undercooling range accessed, which included the low undercooling (ΔT < 100 K) regime. For intermediate Ni content (35 and 40 at.% Ni) the trend was that the velocity first decreased with increasing undercooling eventually displaying a local minimum, after which the velocity increased with increasing undercooling in the conventional manner. Finally, for the most Ni-rich alloy (45 at.% Ni) the velocity appeared to increase monotonically with increasing undercooling. There is one caveat to this, the first data point in the sequence for the 45 at.% Ni alloy was marginally lower than that for its higher undercooling neighbour (V = 0.30 m s⁻¹ at ΔT = 115 K compared to 0.28 m s⁻¹ at ΔT = 128 K). It is not clear, within the expected experimental error, whether the point at ΔT = 128 K represents a true local minimum in the 45 at.% Ni alloy data set, or is just due to scatter in the data. Also unclear from the data of Lengsdorf et al. (2010) is whether the three most dilute alloys would display a local minimum in their growth velocity, followed by conventional V-ΔT behaviour at high undercooling, if sufficiently high undercoolings could be accessed. It would not seem unreasonable to assume that this is the case and indeed subsequent experiments have provided tentative evidence that the velocity may increase in the 25 at.% Ni alloy for undercoolings above 350 K (Herlach et al. 2019).

The phase diagram for the Al-Ni system is shown in Fig. 1. From the phase diagram we would expect the primary solidification phase for the 25 at.% Ni alloy to be Al₃Ni₂, with subsequent peritectic decomposition to Al₃Ni, while for the 5 more concentrated alloys studied by Lengsdorf et al. (2010) the primary solidification phase should be AlNi, with subsequent peritectic decomposition to first Al₃Ni₂ and then Al₃Ni. However, according to in situ synchrotron diffraction experiments conducted on levitated samples, the primary solidification phase is metastable B2-AlNi, even for the 25 at.% Ni alloy. Moreover, unusually for a peritectic reaction, it appears that the conversion of AlNi to Al₃Ni₂ invariably goes to completion, with AlNi rarely observed to survive in the as-solidified sample. This appears to be confirmed by pyrometry data from on-board the International Space Station (ISS) (Herlach et al., 2019) indicating that for the 25 at.% Ni alloy, three episodes of recalescence were observed, which would be consistent with the proposed L + AlNi → L + Al₃Ni₂ → Al₃Ni solidification sequence. The easy peritectic conversion of AlNi to Al₃Ni₂ is usually ascribed to the fact that the Al₃Ni₂ phase is essentially a trigonal extension of the cubic B2 (AlNi) phase, with every third plane of Ni atoms perpendicular to the trigonal axis missing. In line with the argument above that the primary solidification phase for all samples is B2-AlNi, the metastable extensions of the solidus and liquidus lines for this phase are also shown in Fig. 1. These will be required later when we construct a model for the anomalous growth behaviour. These metastable extensions have been calculated using standard CALPHAD methodologies using the assessed thermodynamic data of Du and Calvaguera (1996), Ansara et al. (1997) and Huang and Chang (1998).

Fig. 1

Phase diagram for the Al-rich side of the Al-Ni phase diagram, showing the main phases present, namely α-Al, Al3Ni, Al3Ni2 and B2-AlNi. The metastable extensions of the solidus and liquidus lines for the B2-AlNi phase are shown with dashed lines

The anomalous behaviour displayed by Al-Ni alloys is fundamentally different to that of strong glass formers. Notwithstanding the fact that Al-Ni does not show any unusual tendency towards glass formation, and would therefore be expected to display the behaviour of a fragile, as opposed to strong, undercooled melt, the anomalous behaviour occurs at low undercooling, reverting to conventional behaviour at high undercooling. Various explanations have been proposed to explain the anomalous velocity behaviour observed in Al-Ni alloys, with strong flows in the melt induced by terrestrial electromagnetic levitation being a likely early contender (Herlach et al. 2017). However, careful experiments conducted on the 25 at.% Ni alloy using the TEMPUS facility on-board the ISS have shown that the anomalous velocity behaviour persists in microgravity (Herlach et al. 2019), where the induced flow velocities are calculated to be < 0.001 of those produced during terrestrial levitation experiments. The ISS experiments did however throw up an alternative mechanism for the anomalous velocity behaviour, wherein it may not be a growth phenomenon at all. High speed videos of the recalescence events revealed a series of circular features, termed in Herlach et al. (2019) as scales, that appear to form ahead of the recalescence front. These appear as a series of small, near circular regions at the recalescence front that are distinguished by a bright outer ring and a somewhat darker interior, although the interior is still brighter than the dark area well ahead of the growth front.

In Herlach et al. (2019) scales were associated with nucleation events, wherein it was concluded that multiple nucleation events were occurring ahead of the recalescence front, which were therefore interfering with the normal propagation of the front, causing the anomalous behaviour. This interpretation appears to be supported by two further pieces of evidence. Firstly, analysis of as-solidified Al-Ni samples, both from levitation and from impulse atomization experiments (Ilbagi et al. 2011) show an unusual solidification morphology in which dendrites appear to originate across the whole of the surface of the sample and then grow radially inwards towards the centre. Secondly, the measured growth velocity from Lengsdorf et al. (2010), when plotted as a function of nucleation temperature, T_N, rather than as a function of undercooling, display a single linear trend across all data sets, irrespective of composition (Herlach et al. 2019). Given the very steep slope of the liquidus line, m, (e.g. at C = 31.5 at.% Ni, m = 35 K/at.%) and the consequent large difference in the melting points of the alloys studied by Lengsdorf et al. (2010), such behaviour is incompatible with conventional growth models but could, it is argued in Herlach et al. (2019), be consistent with nucleation dynamics.

In this paper we present a new analysis of the ISS video data which throws doubt on the nucleation interpretation of scales. A model is presented which shows that all of the observational data can be reconciled within the framework of a growth model, albeit one in which the initial growth is confined to a thin surface layer of the sample.

Image Analysis Methods

Of the five growth velocity measurements performed upon the Al-25 at.% Ni alloy on-board the ISS which yielded scale type growth (see Fig. 2 in Herlach et al. 2019), two have been selected for here for detailed analysis. These are Cycle 05 (ΔT = 281.7 K, v = 146 mm s⁻¹) and Cycle 08 (ΔT = 290.8 K, v = 93 mm s⁻¹). These experiments meet the criteria that the first initiation of solidification occurred on the side of the sample facing towards the high speed camera and near the limb of the sample, thereby ensuring that progress of recalescence could be followed across the majority of the sample. In all of the ISS experiments nucleation is allowed to occur spontaneously and it is not therefore guaranteed that these conditions will be met in all experiments. For instance, in Cycle 10 (ΔT = 260.5 K, v = 116 mm s⁻¹), solidification is very clearly initiated on the side of the sample facing away from the camera as the growth front appears more-or-less simultaneously along the whole circumference of the sample and grows towards the middle of the visible face of the sample. The inference here would be that solidification was initiated close to the middle of the reverse face of the sample not viewed by the high speed camera.

Fig. 2

Methodology for locating the leading and trailing edges of the recalescence front. Plot shows the grey level along one column in the rotated image D⁵⁶ . The centre of the recalescence front is located as having an intensity of 81 while the leading and trailing edges are at half this intensity  

For analysis, each movie is converted from the supplied avi format to a collection of still frames, appropriately cropped to remove extraneous background. The movie for Cycle 05 contained 99 frames, each of which were cropped to 431 pixels wide by 461 pixels high. That for Cycle 08 contained 125 frames, cropped to 461 pixels wide by 461 pixels high.

We first take the difference between adjacent frames in each movie. Let frame i within a given movie be denoted by. ${F}^{i}$ The corresponding difference frame is denoted by ${D}^{i}$ :

$${D}^{i}={F}^{i}-{F}^{i-1}$$

(1)

where although the Fⁱ’s are composed of unsigned integers, the Dⁱ’s are stored as signed integers, otherwise information is lost for any pixels in which the difference would be negative. Such frame differencing is useful for tracking recalescence fronts as the progress of the front between frames i—1 and i appears as a bright band due to the change between the two frames. Conversely, the regions both behind and ahead of the front appear dark as the local brightness in both frames is similar. Of course, in the case of the scales morphology it is not clear that any such well-defined front should exist, particularly if the scales represent repeated multiple nucleation events.

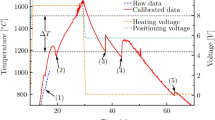
From the difference images, D, we now attempt to track the progress of the solidification front across the sample. We begin by rotating the difference image through an angle θ such that the nucleation point is at the 12 o’clock position. Consequently, the resulting front is approximately horizontal in the image and its direction of propagation is nearly vertically downwards. These angles are a counter-clockwise rotation of 29.7⁰ for Cycle 05 and a clockwise rotation of 37.7⁰ for Cycle 08. We now scan each column of the difference image to find the location of the maximum difference in that column. A plot of the grey level in one such column (column 272 in the rotated image, D⁵⁶ for Cycle 05) is shown in Fig. 2, wherein it can be seen that the maximum value in this case is 81. From the location of the maximum we then scan up and down the column to determine the locations of the leading and trailing edges of the front. These are defined as the position closest to the maximum at which the intensity falls below a threshold level, λ_thr, taken in this instance as. λ_thr = 40 This value is chosen so as to be at least twice the maximum level of noise between frames. The locations of the leading and trailing edges of the recalescence front are also shown in Fig. 2.

By scanning all columns in the difference image the co-ordinates of the locus of the recalescence front can be determined. For display purposes we then mark the leading and trailing edges of the front using coloured markers before rotating the images back to their original orientation. Importantly though, the markers can be imposed not only on the difference images from which they were calculated, but also on the original frames from the movie. In this way we can observe the scale pattern, with the locations of the leading and trailing edges of the recalescence front superimposed.

For the second analysis method a fixed location is selected on the sample and the measured brightness of that location across all frames is monitored, thus building up a time sequence depicting the evolution of the optical signal at that location. However, doing so in a meaningful way requires that the sample is either (i) stationary, or (ii) that its motion can be determined and the ‘fixed’ spot tracked to maintain the same physical location on the sample, accounting for any sample drift. Cycle 08 falls, to a good approximation, within (i), sample drift during filming being limited to ± 2 pixels in both the horizontal and vertical directions. Cycle 05 is though subject to greater drift, to the extent that it necessary to take account of this during point monitoring of the sample brightness. Figure 3 shows both the horizontal and vertical drift of the sample during processing as a function of frame number. This is measured at the location where the limb of the visible sample disc intersects the sample holder, partly obscuring the image towards the top right-hand side of the frame (see e.g. Fig. 4). In both cases the reference position (i.e. the frame in which we define the drift to be zero) has been taken in the middle of the recording, at Frame 51. It is clear from Fig. 3 that during Cycle 05 the sample is subject to considerable drift downwards and to the left during the second half of the filming interval. The fitting curves shown are both order 4 polynomials and these are used to parameterise the drift. It is the displacement from these curves that is actually applied to the spot brightness monitor to maintain a ‘fixed’ physical position on the sample.

Fig. 3

Quantification of sample drift (red and left axis) horizontally and (blue and right axis) vertically in the image plane for recalescence Cycle 05. Zero is taken, by definition, as frame 51, midway through the sequence. Solid curves are order 4 fitting polynomials

Video Analysis Results

One feature of scale like growth that has not previously been commented upon is that during the early stages of recalescence scales are absent, becoming fully developed only as growth continues. This is shown in Fig. 4, in which we compare the morphology of the growth front early in the recalescence phase of solidification, with that later on. In (a), 16 frames after observed nucleation ($\tau=0.24\;\tau_{r}$), the recalescence front is still relatively regular, with only minor indications of the perturbations that will eventually become scales, these not becoming fully developed scales for a further 6 frames (frame 22, $\tau=0.32\;\tau_{r}$ ). However, once initiated, the scales persist throughout the rest of the growth period, as shown in part (b) of the figure which shows the morphology of the recalescence front 36 frames ($\tau=0.55\;\tau_{r}$) after nucleation of solidification. Here $\tau_{r}$ is the fractional recalescence time, i.e. the time since nucleation expressed as a fraction of the total time between the first observation of nucleation and the leading edge of the recalescence front reaching the furthest extent of the sample. The rectangular area of interest in part (b) indicates the magnified area shown in Fig. 5.

Fig. 4

Images (a) 16 ( τ = 0.24 r) and (b) 36 ( τ = 0.55 τ_r) frames after nucleation of solidification in Cycle 05, showing that scales only begin to form after an initial latency in which the recalescence front is scale free

In Herlach et al. (2019), the scales are described as a front of multiple nucleation events, in this section we provide a detailed analysis of the observational evidence from the ISS experiments in order to either confirm or refute this view. Figure 5a shows a magnified view of part of Frame 52 extracted from Cycle 05, with the area shown being highlighted by the rectangular region in Fig. 4b. Figure 5b and c show frames 54 and 56. Two dots have been superimposed for reference and these maintain the same positions in all images. In addition, each scale is numbered, with scales 1–11 already being visible in Frame 52 (Fig. 5a) and each subsequent new scale being numbered sequentially in order of its appearance. In Fig. 5b (Frame 54) three new scales have appeared, these being numbered 12, 13 and 14. Scale number 12 is formed at the junction of existing scales 2 and 3, thereby forming a triple junction between three scales (2 existing + 1 new, green marker), scale 13 also forms at the junction of two existing scales (5 and 7), thereby again forming a triple junction (blue marker), while scale 14 forms in a void between three existing scales; 7, 10 and 11. Meanwhile, the scales numbered 6, 8 and 9 cease to be visible as the contrast between these and the bright background behind the advancing front is decreasing. As time progress, similar patterns are seen in subsequent frames, with new scales appearing at the junctions of existing scales (16 at the junction of 7 and 13 and 17 at the junction 1 and 14, both in Frame 56, Fig. 5c) or in an apparent void between three scales, while scales behind the front eventually merge into the bright background and are lost to view.

Fig. 5

Magnified field of view of three frames (a-52, b-54 and c-56) from Cycle 05. The field of view is as given by the rectangle in Figure 4. The two dots indicate fixed positions on the sample as a reference. Note that new scales always form in contact with existing scales

A further interesting aspect of the growth mode can be elucidated by considering the position of the two marker points. These are positioned in the two triple junctions which first become apparent in Frame 52 (Fig. 5a). What may be observed is that, once formed, the bright triple junctions remain, more-or-less, located where they were initially formed, with the subsequent advancement of the front progressing by means of the new scales initiated. Our view of the progress of a scale-like front may therefore be summarised thus. Scales at the front grow and reach a certain size at which point these “parent” scales spawn “child” scales, most commonly at a junction between two “parent” scales. Thereafter, the “parents” remain essentially immobile and continued growth proceeds by way of the “children” until they reach a certain size and the process repeats. In some cases a “child” appears to fill a gap between three “parent” scales, but as such a gap necessarily contains two junctions between existing scales, it may be that all “children” are uniquely initiated at a single triple junction, with the low resolution of the ISS video obscuring this. Unfortunately, the time resolution of the video is insufficient to determine whether there is any latency between a “parent” scale essentially coming to rest and the “child” scale moving forward, or whether the spawning process is such as to maintain a continuous forward propagation velocity. A significant latency would give rise to growth that proceeds by means of a series of jumps. Such growth has previously been observed in undercooled eutectics and is termed spasmodic growth (Clopet et al. 2013).

We now consider where the visually obvious scale features are located with reference to the advancing front. Figure 6 shows (a) a frame (in this case 48) from the movie from Cycle 08, (b) shows the corresponding frame difference as defined in Eq. (1), (c) shows the leading (green) and trailing (red) edges of the recalescence front superimposed upon the difference image and (d) the same fronts superimposed upon the original image. This particular case has been selected as the front has progressed approximately halfway across the sample, although in other respects these frames are similar to the rest of the movie and the analysis here would not be substantially different should other frames be selected, nor indeed if we had selected Cycle 05, which is only omitted for the sake of brevity. Movies, showing the propagation of the front, for both Cycles 05 and 08, are supplied as part of the supplementary data accompanying this paper. The general conclusion is that the obvious visual features termed scales become most prominent in the region around and behind the trailing edge of the growth front and their presence is much less apparent near the leading edge of the front. Such behaviour does not seem immediately compatible with the behaviour of nucleation events, although further discussion of this is deferred until §4.0.

Fig. 6

(a) Example frame extracted from the high speed video for Cycle 08, (b) corresponding difference image (frame – preceding frame), (c) locations of leading (green) and trailing (red) edges of the recalescence front as calculated from the difference image and (d) leading and trailing edges superimposed upon the original image

Spot brightness measurements have been performed at a number of locations across both samples, with typical results being shown in Fig. 7 for Cycle 08 although, as above, very similar results were obtained for Cycle 05 and are omitted only for the sake of brevity. Three locations were selected as corresponding to the centre of visible scales as the front passes these locations and three locations that correspond to the bright triple junctions at which “child” scales are spawned from their “parents”. The brightness v’s time traces for these are shown in Fig. 7a and b respectively. In both cases, the insert in each figure shows schematically the location at which each measurement was made. For locations selected to fall in the centre of scales, which are also typical of other (random) locations within the sample, the intensity increases rapidly as the front passes, before levelling off to a more gradual, but generally continuing, increase. Conversely, for the locations typical of the triple junctions, the intensity increases rapidly to a maximum before undergoing a small, but distinct decrease in intensity, after which it plateaus.

Fig. 7

Brightness as a function of frame number for various locations on the sample from Cycle 08. Locations were selected so as to be (a) at the centre of scales when fully developed. and (b) at the triple junctions at which new scales were spawned. Inserts shows schematically the locations at which brightness was measured

This behaviour may be explored in more detail by correlating with the location of the front as it passes the point at which the intensity is monitored. This is presented below, although again for the sake of brevity we do this for one location of each type only, those corresponding to curve (b) in both Fig. 7a and b. Three locations are marked on each brightness curve, which correspond to the images shown in Figs. 8a-c and d-f for the scale centres and triple junctions respectively.

Location 1 (curve b in Fig. 7a) corresponds to the leading edge of the scale crossing the point monitored in the image, wherein the brightness has achieved around 40% of the total observed increase. This location is shown in Fig. 8a (Frame 47). Location 2 (corresponding to the image shown in Fig. 8b, Frame 49) is the point at which the centre of the scale occupies the location being monitored. Interestingly, although the leading edge of the scale appears brighter than the interior in both frames, the brightness at the monitoring location increases monotonically during this period. In order for both observations to be consistent, this must imply that during the growth of an individual scale, the brightness of both the leading edge and the interior must be increasing in such a way as to maintain the differential between the edge and the interior. Location 3 corresponds to the point at which (near) maximum brightness is achieved (Frame 60). As can be seen from Fig. 8c, by this time the growth front has long passed the monitoring location and the scale has almost been absorbed into the general bright background behind the front.

Location 4 (curve b in Fig. 7b), corresponds to Frame 38, wherein this is the first time at which a bright triple junction may first be clearly distinguished at the monitored location (Fig. 8d). In contrast to the curve for the scale centre, this location is only marginally behind the advancing growth front and the brightness curve has achieved > 75% of the observed increase, and is at a level comparable to the subsequent plateau. Location 5 is the peak of the intensity curve (Frame 40), wherein a clearly delineated local bright spot, corresponding to the former location of the triple junction, is evident in Fig. 8e at the monitored location. Location 6 is the start (Frame 46) of the plateau region for brightness curve (b). From the corresponding image (Fig. 8f) it is clear that this also conforms to the point at which the feature, in this case the triple junction, is lost in the bright background behind the growth front.

Fig. 8

(a-c) Images of the recalescence front corresponding locations 1-3 on the brightness-time curve given in Fig. 7a, and (d-f) for locations 4-6 on the curve as given in Fig. 7b. Dot on the image indicates the location at which the brightness measurement was taken

Discussion of the Video Analysis

From the above analysis it does not appear that the scale-like growth front conforms to what would normally be considered as either a conventional recalescence front, nor as a series of multiple nucleation events ahead of such a front. The reasons for discounting a conventional recalescence front appear self-evident. The presence of the scales themselves do not suggest such a growth mode, having never previously been observed in the solidification of a deeply undercooled melt. However, there are also more subtle reasons for discounting a conventional recalescence front, most specifically the brightness-time profile for the spot measurements made on the sample surface. Although a conventional recalescence front is preceded by a thermal boundary layer, once the growth front itself passes a given point on a sample surface we would expect the temperature, and hence brightness, of that location on the sample surface to be near constant, with the temperature being close to that of the melting temperature. However, this is not the case here, where we observe the surface brightness continuing to increase, albeit gradually, long after the initial front has passed.

The obvious visual appearance of the scales, combined with the observation of clear radial inward growth of dendrites reported in Herlach et al. (2019), led to the scales being attributed to multiple independent nucleation events. However, this interpretation also has problems. Firstly, careful visual inspection reveals that each new scale is not an independent event ahead of the growth front, but rather is spawned at the junction of two existing scales, from which it then takes over the continued growth of the front. Consequently, if the scales grow out of the front, rather than ahead of the front, it is difficult to see in what sense they can be nucleation events. Secondly, with reference to Fig. 6, it seems that scales actually appear to form behind the leading edge of the growth front. This again is not compatible with a repeated nucleation events as some form of growth front appears to be leading scale formation. Finally, we note that the plots of brightness v’s time at fixed locations on the droplet show some anomalous features. Typically, during recalescence we would expect the brightness to increase rapidly to a level indicative of the liquidus temperature of the melt and plateau, i.e. to show a behaviour more-or-less similar to that shown in Fig. 7a. The behaviour shown in Fig. 7b, in which the initial recalescence is brighter than the subsequent plateau does not fit this model.

This, of course, poses the question, what is the growth mode in these Al-Ni samples? This is discussed in the next section.

A Surface Recalescence Front

In this section we consider the effect of a surface recalescence front, which is a consequence of the solidification rate being much higher for a thin layer at the surface of the sample, than it is through the bulk of the sample. The obvious consequence would be the formation of an intermediate state in which a sample, mostly still comprising the undercooled melt, would be encased in a thin shell of solid, which would itself be a good nucleant for the slower inward radial growth observed in the as-solidified samples. Moreover, such a model could account for the observations in respect of scale growth. Specifically, it is not possible to reconcile single crystal growth along a preferred crystallographic orientation (< 100 > for B2-AlNi) with radial inward growth, the preferred orientation wanting to form a plane interface. Consequently, each scale would represent a colony of dendrites growing approximately towards the centre of the sample with the same crystallographic orientation, with a new scale forming when the misorientation between the planar crystallographic direction and the radial heat flow direction became too large to accommodate.

Such a surface recalescence model is compatible with the video analysis presented above. In this model the leading edge of the recalescence front shown in Fig. 6 is associated with the surface recalescence front, with the scales developing behind this as radial inward growth develops from the surface. Moreover, as latent heat is released from the slower bulk inward phase of growth, this would lead to the slow increase in brightness observed after passage of the initial growth front.

The concept of a surface recalescence front, propagating with velocity V_S, is illustrated schematically in the inset to Fig. 9. Surface growth is accompanied by radial inward growth at the lower bulk growth velocity, V_B, with such growth being initiated immediately subsequent to the passage of the surface front. As the time at which such nucleation of the bulk front is initiated is slightly delayed as one moves further round the surface from the nucleation location, the focus of the inward growing dendrite will be somewhat offset from the centre of the spherical sample. The extent of this offset, q, relative to the sample radius, R, is shown in Fig. 9 as a function of the ratio of the velocities of the surface and bulk growth fronts. Note that for V_S = V_B normal recalescence via a bulk growth mode would be observed and that for surface growth to be observable at all we require V_S > $\frac{\pi}{2}$ V_B, due to the longer path length for a front travelling around the circumference of the sample, rather than through the bulk. The very obvious radial inward growth described by Herlach et al. (2019) requires V_S > > $\frac{\pi }{2}$ V_B.

Fig. 9

The distance, q, for which the focus of the radial dendrites is offset from the centre of the sample as a function of the ratio of solid to bulk recalescence velocities. Bulk growth is observed unless VS >$\frac{\pi}{2}$VB. (Insert) Schematic representation of the development of microstructure through a cross section of a sample with a fast moving surface recalescence front.

In order to clarify this point further, consider Fig. 10, in which we compare the propagation of a bulk front with the propagation of a surface front, as viewed through the cross section of a spherical sample. In the figure, nucleation is assumed to occur at the north pole and in both cases solidification terminates at the south pole, with the cross section taken through these two. The surface of the sample is thus represented by the circumference of the circle and the measured recalescence velocity would be determined by viewing the intersection of the front with the circumference (as viewed in the figure, to the left for a bulk front and to the right for a surface front). What is apparent from the figure is that our normal definition of the recalescence time becomes inadequate when we consider a surface front and that we should actually consider two separate timescales, the visible recalescence time, $\tau_{rv}$ , and the solidification recalescence time $\tau_{rs}$ . Here the visible recalescence time $\tau_{rs}$ is the time taken between nucleation and the point at which the visible recalescence front has fully traversed the sample, which of course in practice means the surface of the sample, this being the only part of the sample that is actually visible. Conversely, the solidification recalescence time is the time between nucleation and the end of the recalescence phase of solidification, i.e. the point at which all of the sample is a semi-solid mush (with a solid fraction given approximately by $\Delta T/\Delta T_{hyp}$ , with $\Delta T_{hyp}$ being the hypercooling limit). Of course, in the case of a bulk front $\tau_{rv}\equiv\tau_{rs}$, and indeed it seems unnecessary to make such a distinction. However, as shown in Fig. 10, in the case of a fast moving surface recalescence front, such a distinction is necessary as $\tau_{rv}\neq\tau_{rs}$.  The four frames in Fig. 10 are given at $\tau=0.25\;\tau_{rv}\;0.50\tau_{rv}\;0.75\mathrm{\;and\;}1.0\tau_{rv}$, respectively, wherein for the bulk front the recalescence stage of solidification is complete as at $\tau_{rv}=\tau_{rs}$  . However, in the case of a surface front this is not the case as, at $\tau=\tau_{rv}$  there is still a significant region of liquid that has not yet undergone recalescence, albeit this is not visible as it is completely enclosed within a solid shell. In this case, $\tau_{rs}$  will be the time between nucleation and the recalescence front reaching the centre of the droplet, which will depend upon the rate of propagation through the bulk, V_B. In Fig. 10 we have taken V_B = V_S/5 for the purpose of illustrating the effect of a surface front that moves much faster than a bulk one.

Fig. 10

Simulated recalescence shown in cross section through a spherical sample for (left) normal bulk propagation and (right) a fast moving surface propagation front with a much slower (VB = VS/5) bulk front. Views given correspond to (a) $\tau=0.25\;\tau_{rv}$ (b) $\tau=0.50\tau_{rv},\;\tau=0.75\tau_{rv}\;\mathrm{and}\;\tau=1.00\tau_{rv}$. Note that in the case of pure bulk propagation recalescence is complete at $\tau=1.00\tau_{rv}$. This is not the case for a surface propagating front, liquid remains in the interior of the sample. Blue represents liquid, yellow the dendritic semi-solid resulting from recalescence

Bulk Growth

For a spherical sample, of radius R, centred on the origin, O(0, 0, 0), the equation for the surface of the sample is:

$${x}^{2}+{y}^{2}+{z}^{2}={R}^{2}$$

(2)

The projection of the sample in the imaging plane, which we take to be x–y, is a circle. Let the observed nucleation point in the imaging plane be (x_n, y_n). Assuming that nucleation occurs on the sample of the surface, which is not unreasonable, the corresponding co-ordinate z_n is given by z_n = z_s, where z_s is the z co-ordinate on the surface of the sphere corresponding to the location (x, y) in the image plane:

$${z}_{\text{s}}=\sqrt{{R}^{2}-{x}^{2}-{y}^{2}}$$

(3)

Solidification proceeds by the propagation of a spherical front growing through the bulk of the undercooled liquid. The origin of this sphere will be (x_n, y_n, z_n) and its radius will be V_Bt, wherein:

$${\left(x-{x}_{\text{n}}\right)}^{2}+{\left(y-{y}_{\text{n}}\right)}^{2}+{\left(z-{z}_{\text{n}}\right)}^{2}={V}_{\text{B}}t$$

(4)

The projection of the recalescence front in the imaging plane is given by the x–y locus of intersection of the growth front with the sample surface. Equating Eq. (4) with Eq. (2) we have:

$$x{x}_{\text{n}}+y{y}_{\text{n}}+z{z}_{\text{n}}={R}^{2}-\frac{1}{2}{\left({V}_{\text{B}}t\right)}^{2}$$

(5)

Using Eq. (3) to eliminate z_n, followed by some relatively straightforward algebra, results in the equation of the recalescence front, projected onto the image plane, as:

$${x}^{2}\left({x}_{\text{n}}^{2}+{z}_{\text{n}}^{2}\right)+{y}^{2}\left({y}_{\text{n}}^{2}+{z}_{\text{n}}^{2}\right)+2xy\left({x}_{\text{n}}{y}_{\text{n}}\right)-2{\psi }^{2}\left(x{x}_{\text{n}}+y{y}_{\text{n}}\right)+\left({\psi }^{4}-{z}_{\text{n}}^{2}{R}^{2}\right)=0$$

(6)

with

$${\psi }^{2}={R}^{2}-\frac{1}{2}{\left({V}_{\text{B}}t\right)}^{2}$$

(7)

Surface Growth

To obtain the projection of a surface growth front in the imaging plane we again assume a spherical sample as defined by Eq. (2), with a surface nucleation point, the projection of which on to the x–y imaging plane is at (x_n, y_n). We define the vectors a and b such that a pass through the origin and the point (x_n, y_n, z_n) while b passes through the origin and an arbitrary point (x, y, z) on the surface of the sphere. The angle, θ, subtended by the intersection of the vectors a and b at O is given by:

$$\mathrm{cos}\theta =\frac{a\cdot b}{\left|a\right|\left|b\right|}$$

(8)

Now, for a front moving outwards from a point on the surface of a sphere at uniform velocity V_S, the angle θ is given by V_St/R. Moreover, as both a and b extend from the origin to the surface of the sphere we have $\vert\boldsymbol a\vert=\vert\boldsymbol b\vert=R$. Therefore, the equation of the recalescence front resulting from a surface front, projected onto the image plane, is given as:

$$x{x}_{\text{n}}+y{y}_{\text{n}}+{z}_{\text{n}}\sqrt{{R}^{2}-{x}^{2}-{y}^{2}}={R}^{2}\mathrm{cos}\left(\frac{{V}_{S}t}{R}\right)$$

(9)

Simulated Recalescence Images

The projection of the ISS TEMPUS samples as observed in the camera image plane are, to a good approximation, circular. By fitting a circle to the image in which the recalescence event is first detectable it is therefore possible to determine the approximate location of the nucleation event. In the co-ordinate system described above, in which the centre of the circle is at (0, 0) and the circle radius is taken as R = ½, the co-ordinates of the observed nucleation events are (0.19, 0.40) for Cycle 05 and (-0.26, 0.35) for Cycle 08. Figure 11 shows as an example the simulated front positions for four times, $\tau=0.2\tau_{rv},\;\tau=0.4\tau_{rv},\;\tau=0.6\tau_{rv}\;\mathrm{and}\;\tau=0.8\tau_{rv}$ for (a) solidification via the growth of a bulk front and (b) solidification via the growth of a surface front for the identified nucleation site in Cycle 08. For solidification via the growth of a bulk front the recalescence solidification time, is the same as the visible recalescence time, as solidification is complete at the end of the observed recalescence. However, for growth of a surface front this is not the case, the interior of the droplet being still partially liquid at the point when the surface front has completely enclosed the droplet in a solid shell. The use of visible recalescence time also implies that the surface velocity required in part (b) of the figure would be $V_{S}=\frac{\pi}{2}V_{B}$, where V_B is the bulk growth velocity appropriate in part (a) of the figure.

Fig. 11

 Simulated images of the recalescence front for (a, left) normal recalescence and (b, right) surface recalescence as a function of visible recalescence time, $\tau_{rv}$. Location of nucleation is as determined experimentally for Cycle 08

What is clear from Fig. 11 is that, although in both cases the visible recalescence time (i.e. the time between the visible front commencing to move across the droplet and completing its passage) is the same, the detail of where the front is at any given instant is different. Specifically, the point on the bulk recalescence front which at any given time will be furthest from the nucleation point will be in the interior of the droplet, on the line joining the nucleation point to the centre. However, the front is only observable where the locus of the 3-dimensional growth front intersects the surface of the sample, which will actually lag significantly behind the point of furthest extent. In contrast the surface front, by its nature, is always visible at its furthest extent from the nucleation event (at least for a nucleation event on the visible side of the sample). Consequently, the surface front appears to propagate faster than the bulk front throughout virtually the whole recalescence time and it should therefore, in principle, be possible to distinguish between these two alternatives by careful analysis of the observed recalescence sequence. This has been conducted for Cycle 08 and the results are presented below. Unfortunately, such an analysis is not possible for Cycle 05 as it appears that more than one nucleation event occurred. This is shown in Fig. 12, in which it is clear that at least two distinct, approximately circular growth fronts can be delineated. One of the nucleation events is clearly observable on the face of the sample facing the camera with its location as given above, although there is a slight uncertainty regarding this as the likely location of the nucleation is on a region of the sample obscured by the sample holder in the upper right-hand corner of the image. We have not been able to determine a location for the second nucleation event and assume that it may be on the side of the sample facing away from the camera.

Fig. 12

Recalescence Cycle 05 towards the end of growth, clearly showing what appear to be two separate recalescence fronts. The most likely cause is thought to be two separate nucleation events occurring with a short interval between

In Fig. 13 we show four views of the sample from Cycle 08 at times corresponding to $0.2\tau_{rv},0.4\tau_{rv},0.6\tau_{rv}\;\mathrm{and}\;0.8\tau_{rv}$. Superimposed upon each is the calculated position for the recalescence front for both pure bulk growth and pure surface growth at the corresponding times. Note that, as above, due to the longer parh travelled by a surface propagating front, the use of visible recalescence times implies that $V_{S}=\frac{\pi}{2}V_{B}$. In fact neither profile fits the observation particularly well. At early time ($\tau=0.2\tau_{rv}$), the observed recalescence front corresponds almost exactly to the calculated position for conventional bulk growth. Thereafter, the observed front appears to catch-up with the surface front which, as explained above, has a higher apparent velocity. However, as described above, the scale-like mode of growth does not start immediately, and our supposition is that the very early stages of growth proceed via a conventional bulk type growth mechanism, which is then overtaken by surface growth. As shown in Fig. 13, a growth front which transitions from bulk, to surface, growth around $\tau=0.25\tau_{rv}$ would seem to fit the observed growth front well over the whole of its visible passage across the sample. We note in regard to Fig. 2 in Herlach et al. (2019), that the measured growth velocity for this sample is very close to the point at which the scale growth morphology transitions to the ‘spikes’ morphology, which we assume is also the point at which the anomalous velocity trend reverses; thereafter the sample shows normal growth behaviour, with the growth velocity increasing with increasing undercooling. We postulate that, close to the transition between anomalous and normal behaviour, $\frac{\pi}{2}$ V_B and V_S are relatively similar and that therefore the transition between initial bulk and subsequent surface growth may be delayed, with the transition occurring here around 0.25. Conversely, at low undercooling, well away from the transition and where the growth velocity is falling steeply with increasing undercooling we postulate that V_S >  > V_B.

Fig. 13

Images of recalescence Cycle 08 at (a) τ = 0.2 $\tau_{rv}$ , (b) τ = 0.4 $\tau_{rv}$, (c) τ = 0.6 $\tau_{rv}$ and (d) τ = 0.8 $\tau_{rv}$. Three calculated front positions are superimposed on each image: blue = pure bulk recalescence, red = pure surface recalescence and green = hybrid, bulk until$\tau=0.25\tau_{rv}$ 

We are not aware of such surface recalescence fronts having previously been reported in the literature pertaining to the solidification of undercooled melts. Nor do accepted theories for the solidification of binary alloys offer any credible mechanism for this phenomenon. The rationale behind this postulate, and more generally the mechanism by which a fast moving surface recalescence front grows in preference to a much slower growing conventional bulk front are explored below.

Calculation of Solidification Velocity in the Al-Ni System

In order to assess the viability of the surface growth mode described above we require a model for the calculation of the growth velocity of the phases involved. Simple analytical models for the calculation of such growth velocities, such as those due to Lipton et al. (1984) or Lipton et al. (1987), hereafter referred to and LGK and LKT respectively, are not considered suitable owing to the unduly restrictive thermodynamic assumptions inherent within such models, particularly the utilisation of the dilute solution approximation which renders the partition coefficient, k, and the gradient of the liquidus line, m, constant. Conversely, 3-dimensional phase-field simulation, using e.g. a model for intermetallic growth such as that presented by Bollada et al. (2020a, b) is considered infeasible due to the computational requirements of such models. As an alternative, we present here a model which, in essence is similar to analytical models such as the LGK and LKT models, but in which the thermodynamic restrictions are relaxed so that a realistic phase diagram for the phase concerned may be incorporated into the model. Full details of the model are provided in Appendix 1.

In line with the discussion of the Al-Ni system presented above, the growth velocity calculations have been performed on the assumption of primary solidification to the B2-AlNi phase, and it is the solidus and liquidus lines for this phase (including their metastable extensions where necessary) that have been used in these calculations. In order to calibrate the model we have used the data of Lengsdorf et al. (2010) for Al-35 at.% Ni and Al-40 at.% Ni. These particular data sets are useful as they display a local minimum in the growth velocity as a function of undercooling, beyond which the velocity-undercooling curve shows normal behaviour, i.e. growth velocity that is increasing with undercooling. It is to these “normal” portions of the velocity-undercooling data that we have fitted the growth model, with the tacit assumption that this represents conventional dendritic growth through the bulk of the sample. The resultant fit is shown by the solid curves in Fig. 14 a and b, with the thermophysical parameters used to obtain the fit being as given by Holland-Moritz et al. (2008). These are reproduced in Table 1, with the parameterisation of the liquidus and solidus curves given in Table 2 (both in Appendix 2). Compared to other deeply undercooled alloy systems (e.g. Castle et al., 2014), the growth velocity for Al-Ni is very low, being just 0.5 m s⁻¹ at a maximum undercooling of $\Delta{T}=300\;K$ for the 35 at.% Ni alloy and just below 1.3 m s⁻¹ at $\Delta{T}=270\;K$  in the 40 at.% Ni alloy, these being the maximum undercoolings achieved for each composition. We note here that this appears to be a natural outcome of the shape of the phase diagram for the B2-AlNi phase, with the calculations performed here showing a large majority of the total undercooling being accounted for by the constitutional undercooling $\Delta{T}_{C}$ , For the 35 at. % Ni alloy $\Delta{T}_{C}=0.89\Delta{T}\;\mathrm{at}\;\Delta{T}=300\;K$, with this fraction dropping monotonically with increasing from a value of in the low undercooling limit. For the 40 at.% Ni alloy the fraction of the undercooling used up in is slightly smaller than for the 35 at.% Ni alloy at all undercoolings, explaining why the growth velocity, although still low, is significantly higher than for the 35 at.% Ni alloy. Again, the fraction decreases monotonically with increasing from a low undercooling limit again around 0.98, reaching $\Delta{T}_{C}=0.83\Delta{T}\;\mathrm{at}\;\Delta{T}=270\;K$. In Herlach et al. (2019) it was noted that, within a standard LKT type growth model, certain unusual combinations of m and k could be contrived to give a velocity-undercooling curve with a negative slope over certain restricted undercooling ranges. However, they also noted that these conditions did not appear to pertain to Al-Ni and so did not constitute an explanation for the anomalous growth behaviour in this system. This conclusion is borne out by growth velocity modelling using a realistic parameterisation of the phase Al-Ni diagram where, for fixed material parameters, the growth velocity is always observed to increase monotonically with increasing undercooling.

Fig. 14

Velocity-undercooling data for (a) Al-35 at% Ni and (b) Al-40 at.% alloys as given by Lengsdorf et al. (2010). Solid curves are model fit to the conventional part of the data set (V increasing), dashed curve is the fit to the anomalous part of the data set (V decreasing) assuming the proposed surface enhancement of Ni concentration

We now turn to what might occur at the surface of the sample to cause an increase in growth velocity confined to a surface layer. As expressed by Eq. (12) in Appendix 1, the product VR is degenerate, with a consequent need for a separate radius selection mechanism, be it marginal stability or a solvability criterion. It has therefore previously been suggested that, although V is decreasing with increasing ∆T, potentially P_T could still be increasing as ∆T increases. Any anomalous increase in V would then be ascribed to a consequent decrease in R. It has for instance been noted previously (see e.g. Galenko and Herlach (2008), Kazak et al. (2017)) that very dilute solutes (present as impurities) can have an effect on growth velocity by affecting the curvature of the dendrite tip, particularly if such solute is strongly partitioning. However, both the extreme purity of material employed in the preparation of the ISS samples and the size of the required effect argue strongly against such a mechanism. Specifically, we might assume that the growth model presented in Fig. 14 represents a correct calculation of P_T over the whole undercooling range, but that some disturbance of the tip selection criteria causes the observed anomalous velocity trend. However, the size of the effect, particularly at low undercooling, would have to be enormous. For the 35 at.% Ni alloy the observed growth velocity at is ∆T = 110 K is V = 0.73 m s⁻¹, nearly 30 times that calculated (V = 0.025 m s⁻¹), requiring a commensurate decreases in R by the same factor. This is much larger than the magnitude of the effect demonstrated in Kazak et al. (2017).

Indeed, the size of the effect required seems to render futile any argument in which the observed velocity decrease with increasing ∆T is reconciled with a monotonically increasing Péclet number. Consequently, we look to other effects that might cause a strong perturbation to the observed growth velocity. In fact, the effect that appears to have the largest effect on the growth velocity is the Ni content of the alloy as shown in Fig. 15. If we were to keep the undercooling fixed (solid curves) but change the alloy concentration the effect is quite modest. For example, the growth velocity of a 35 at.% Ni alloy at an undercooling ∆T = 100 K of is around 2.8 times that of a 25 at.% Ni alloy at the same undercooling. However, this neglects the very steep rate at which the liquidus temperature increases with increasing Ni concentration so that if we consider fixed nucleation temperature (dashed curves), rather than fixed undercooling, the picture is quite different. At a nucleation temperature of T_N = 1284 K (corresponding to ∆T = 100 K in a 25 at.% Ni alloy) the growth velocity in a 35 at.% Ni alloy would be 365 times that in the 25 at.% Ni alloy. Consequently, small enhancements in the Ni concentration at the surface of the sample could have a very significant effect on the observed growth velocity in a surface layer.

Fig. 15

Calculated growth velocity as a function of alloy concentration for (solid curves) fixed undercooling relative to the local liquidus temperature for the indicated concentration and (dashed curves) fixed nucleation temperature corresponding to the indicated undercooling at C = 25 at.% Ni

This is illustrated by returning to Fig. 14, in which the dashed lines show a fit to the portion of the velocity-undercooling data in which the velocity is decreasing with increasing undercooling. The parameters used for these curves are the same as for the respective solid curves, fitted to the portion of the data in which the velocity increases with increasing undercooling, except that the concentration, which we assume to be the concentration of a thin layer at the surface, is allowed to vary linearly with the nucleation temperature T_N. For both alloys the variation is 0.03 at.% K⁻¹, with the alloy returning to its nominal composition at the point where the curves cross. This results in a maximum enhancement in the Ni concentration at the surface of the sample of approximately 4.5 at.% for the 35 at.% Ni alloy and 3.5 at.% for 40 at.% Ni alloy. In fact, as shown in Fig. 16a, all of the Al-Ni data sets displaying an anomalous velocity trend can be reconciled by assuming a similar trend towards surface enhancement of the Ni concentration. In this figure we have taken the anomalous portion of the data from the Al-(25, 30, 31.5, 35, 40) at.% Ni data sets as published by Lengsdorf et al. (2010) and calculated for each V datum the required enhancement in the surface Ni concentration required for the model to match the experimental data. As can be seen from the figure, the maximum surface enhancement in the Ni concentration required to match the experimental velocity determination varies from 7.5 at.% Ni in the more (nominally) dilute alloys to 3.5 at.% in the most (nominally) concentrated alloys. Moreover, each data set displays a gradient close to 0.03 at.% K⁻¹. Consequently, if the data is plotted as the total Ni concentration at the sample surface (Fig. 16b), rather than the excess over nominal, again as a function of nucleation temperature, T_N, the resulting fit is approximately a single straight line for all 5 data sets, mirroring the relationship pointed out in Herlach et al. (2019), wherein it was noted that when plotted against T_N the anomalous growth velocities also adopted a single linear trend. In Herlach et al. (2019) the very different liquidus temperatures of the alloys, ranging from 1384 K for the 25 at.% Ni alloy to 1860 K for the 40 at.% Ni alloy, was taken as evidence that the anomalous velocity data could not be a growth phenomenon. However, the analysis presented here suggests that the anomalous growth trend may be compatible with a purely growth mediated explanation, namely that of an enhanced growth velocity at the sample surface, facilitated by Ni enrichment at the sample surface. Below we consider the mechanism by which such Ni enrichment may occur and ask whether there is any experimental evidence for such enrichment in experiments conducted on Al-rich Al-Ni alloys.

Fig. 16

(a) Proposed surface enhancement in the Ni concentration as a function of (nucleation) temperature required to match the observed anomalous growth velocity data. Note that in all cases the gradient is close to 0.03 at.% per Kelvin, (b) the same data but now expressed as total Ni concentration rather than enhancement over nominal

Surface Ni-Enrichment

The strong affinity of metallic Al for oxygen is well documented. Indeed, the equilibrium constant between Al₂O₃ and liquid Al is estimated to be of the order 10⁷¹ at 1000 K, wherein Al will oxidise for any oxygen partial pressure above 10^–49 Pa (Kaptay 1991), with Hawksworth (2013) estimating initial layer formation in as little as 100 ps. This compares with an oxygen partial pressure inside the TEMPUS facility estimated by Herlach et al. (2017) to be of the order of 10^–2 Pa with a process time of several seconds. The formation, and subsequent efficiency of such an oxide layer as a heterogeneous nucleant is discussed in some detail by Herlach et al. (2017). However, such a layer could potentially also act as a mechanism for the removal of Al, and hence the concentration of Ni, at the sample surface. This would be particularly so if Al₂O₃ is removed from the surface by conversion to the more volatile Al₂O and AlO polymorphs (Hoch and Johnson 1954). Moreover, the concentration gradients established by evaporation from the surface could drive Marangoni flows which serve to reinforce the concentration enhancement (Arangalage 2018). In this respect we note that all TEMPUS experiments on-board the ISS have an allocated dust budget (i.e. maximum generation of dust measured in layer thickness deposited upon the levitation coil) monitored by the Microgravity User Support Center (MUSC). Al-rich samples have been shown to contribute disproportionality to this dust budget due to evaporation of oxides from the sample surface. Indeed one proposed sample (Al₉₆Fe₄) was dropped from the flight schedule due to excessive dust generation, tending to support the hypothesis that Al is lost from the sample surface during processing.

To establish whether an enhanced concentration of Ni at the sample surface is feasible we have looked for information from rapid solidification experiments performed on Al-Ni alloys in the composition range 25–40 at.% Ni. Inhomogeneity of the phase composition of gas atomized Al-27.5 at.% Ni droplets in the size range 212–150 μm has been studied by Mullis et al. (2015). Droplets were analysed by dividing SEM micrographs of the spherical particles, in cross-section, into 6–7 concentric annuli and analysing the prevalence of the main phases (Al₃Ni₂, Al₃Ni and Al-Al₃Ni eutectic) as a function of distance from the droplet centre. In the analysis of Mullis et al. (2015) it was assumed that the composition of the droplets was uniform in the radial co-ordinate r, their purpose being to establish that the distribution of phases was inhomogeneous due to more rapid cooling of the droplet near the surface, which would therefore inhibit the Al₃Ni₂ + L → Al₃Ni peritectic reaction. However, by reanalysing their published data we show that this is also consistent with the Ni concentration being inhomogeneous in r. For each particle we may convert the phase volume fractions given in Fig. 8 in Mullis et al. (2015) to weight fractions. The composition of the Al₃Ni and eutectic are straightforward and may be read from the phase diagram as 25 and 2.7 at.% Ni respectively. The composition of the Al₃Ni₂ phase, being a non-stoichiometric intermetallic, is less straightforward, but as there is only one degree of compositional freedom in the system, this may be fixed by a mass balance on the starting composition of the alloy. This gives the mean composition of the Al₃Ni₂ phase as 39.331 at.% Ni (corresponding to Al₃Ni_1.944), comfortably within the allowed stoichiometry range for the phase. Consequently, with a knowledge of the phases present as a function of radial distance from the particle centre and their composition we can reconstruct the average Ni composition as a function of r. In Fig. 17, we plot the deviation of the composition from its nominal value of 27.5 at.% (positive deviation being a surplus of Ni over nominal, negative a deficiency) against the radial co-ordinate for the centre of each annulus. A clear linear trend is evident, the R² for which is 0.87, the upshot being that we estimate the surface of the droplet (at around r = 100 μm) is around 1.1 at.% richer in Ni than the centre. This is despite the high cooling rates for gas atomized powders, meaning that the time available for migration is likely to be restricted in such samples, cooling rates for gas atomization process normally quoted as being in the range 10²–10⁴ K s⁻¹ (see e.g. Zeoli et al. 2008; Mullis et al. 2013). Consequently, taking a value from the middle of this range (10³ K s⁻¹) and a melt superheat of 200 K as applied during the experiments of Mullis et al. (2015), the typical time between droplet formation and the onset of solidification will be of the order of 0.2 s. This is much shorter than processing times during experiments using the TEMPUS electromagnetic levitator on-board the ISS but still appears to have been sufficient to facilitate chemical separation between the sample surface and the interior. Consequently, the proposed levels of surface Ni-enhancement required to explain the anomalous growth behaviour in Al-Ni alloys may not be unreasonable.

Fig. 17

Calculated surface Ni enhancement in 212-150 μm gas atomised Al-27.5 at.% powders as calculated from the phase analysis data given by Mullis et al. (2015)

Conclusions

The anomalous velocity-undercooling behaviour of Al rich Al-Ni melts has been a puzzle to the solidification community for more than 10 years. Proposed explanations have ranged from mundane instrumental effects, such as strong flow in the melt (Herlach et al. 2017) to invoking exotic new physics such as inverse melting (Herlach et al. 2019). However, none of these have been able to explain all of the observed features during the solidification of these materials. Recently, experiments on-board the ISS have suggested that multiple nucleation events may be occurring just ahead of the recalescence front. It has been suggested by Herlach et al. (2019) that these may be influencing the rate at which the recalescence front propagates, although the details of how this might occur have not been presented. However, here we show that the detail of the experimental results do not appear compatible with such a model. In particular, the scale-like features that were initially associated with such multiple nucleation events do not in fact form ahead of the recalescence front, but rather appear to grow out of the junctions between existing scales and actually become fully developed only once the recalescence front has fully passed over them.

In this paper we propose an alternative mechanism in which recalescence occurs in two stages, a fast growing front which is confined to a thin surface layer on the sample which subsequently nucleates a slower growing dendritic front which propagates radially inwards towards the centre of the sample. In this model, the scale-like features represent the surface signature of colonies of dendrites nucleated with the same crystallographic orientation undertaking such radial growth, with the periodic nucleation of new dendrite colonies occurring so as to maintain (approximate) alignment between the crystallographic growth direction and the direction of heat extraction.

Simulations of recalescence fronts growing on the surface of a sample at constant surface growth rate and through the bulk of the sample at constant bulk growth rate (i.e. in the latter case conventional solidification of an undercooled melt) have been undertaken. These simulations reveal that these two alternatives give rise to distinctly different recalescence images in the 2D imaging plane of the high speed camera being used to monitor solidification of the levitated droplets. Comparison with the actual images captured during the ISS experiments show that the best match is obtained for solidification that occurs via a conventional bulk mechanism for the first 25% of the visible recalescence time and then switches to a surface mode thereafter. This is consistent with the ISS observations that scale-like growth is not evident at the beginning of recalescence.

One route to enhancing the growth velocity sufficiently on the surface of the Al-Ni samples such that surface, rather than conventional bulk, recalescence is observed would be if the surface were enriched slightly in Ni relative to the bulk. Moreover, if this surface enhancement were such that it increased linearly with nucleation temperature, the correct velocity trend is predicted, with the observed anomalous velocity measurements of Lengsdorf et al. (2010) being recovered quantitatively for the case in which the surface enhancement is around 0.03 at.% K⁻¹. One possible route to such surface enhancement of the Ni concentration in undercooled Al-Ni melts would be the preferential loss of aluminium from the surface of the sample, with this effect possibly being magnified by Marangoni flows. However, at this time, this is put forward only tentatively as one possible mechanism and we do not rule out the possibility of other processes either contributing to such a surface Ni-enhancement, or indeed being the dominant mechanism giving rise to it. An analysis of data from Mullis et al. (2015) on gas atomized Al_72.5Ni_27.5 droplets shows that such as surface enhancement of the Ni-concentration may have been present, but overlooked, in these samples, with the possibility that the effect exists overlooked in other studies on this alloy.

As far as we are aware, Al-rich Al-Ni is the only material so far to have been shown to display the type of anomalous velocity-undercooling behaviour described here, although the model proposed above suggests that it may not be the only possible material to do so. In the case that levitated droplets tends towards a surface enhancement of one component of a (say) binary alloy, the primary requirement for this to then lead to solidification via the growth of a surface recalescence front is that the gradient of the liquidus line should be large and positive with respect to the enhanced component. This will lead to a solidification velocity that increases rapidly with concentration at a fixed nucleation temperature, even if that velocity does not increase rapidly with concentration at fixed undercooling. Thereafter, if the mechanism for surface concentration enhancement is that of preferential loss of Al from the surface, such an effect may be limited to other Al-based alloys, with Al–Fe, Al-Mn, Al-Nd and Al-Au all being potential candidate systems. However, if alternative mechanisms are shown to be responsible for the surface concentration enhancement other, potentially non Al-based systems, may also become candidates for study. However, any such system will still require a phase diagram in which m is large and positive (in the direction of the surface concentration enhancement).

Appendices

Appendix 1 – A Growth Velocity Model for an Arbitrary Phase Diagram

The growth velocity model for an arbitrary phase diagram begins with a parameterisation of the solidus and liquidus lines. Within the implementation of the model these parameterisations are placed within subroutines, such that the model can use the phase diagram as a “look up” table, keeping the generality of the model separate from the specifics of the particular system to which it is being applied. That is, for a given temperature the solidus and liquidus concentrations (C_S and C_L) are returned from the phase diagram, or conversely, given a concentration, C, the corresponding solidus and liquidus temperatures may be returned.

As in the models of LGK and LKT we retain the assumption that the dendrite tip propagates as an isothermal paraboloid of revolution with constant velocity V (which below we take to be in the z-direction). Under this assumption, the dimensionless temperature, U_T, (or solute U_C) field around the dendrite tip satisfying $U(\xi = 1) = 1$ and $U(\xi \rightarrow \infty) = 0$ is given by the solution of Ivantsov (1947) as:

$$U=\frac{{\text{Iv}}(P,\xi )}{{\text{Iv}}(P,1)}=\frac{-P{e}^{P}{\text{Ei}}(-P{\xi }^{2})}{-P{e}^{P}{\text{Ei}}(-P)}$$

(10)

Here, Iv is defined as the Ivantsov fuction, Ei is the exponential integral function and $\xi$ is part of the dimensionless, parabolic co-ordinate system given by:

$$\frac{x}{R}=\xi \eta \text{ , }\frac{z-Vt}{R}=\frac{1}{2}\left({\xi }^{2}-{\eta }^{2}\right)$$

(11)

where R is the radius of curvature at the dendrite tip and t is time, wherein the co-ordinate system is co-moving with the growing dendrite. The properties of such a co-ordinate system are explained in Horvay and Cahn (1961). In brief $\xi$ defines a family of parabolæ that are concentric to the freezing front which is $\xi = 1$, with $\xi > 1$ being the region outside of the front. $\eta$ is a co-ordinate that runs along each parabola, measuring distance from the tip, although as both temperature and solute concentration are assumed constant on the dendrite surface $\eta$ does not figure in the diffusion solution. P is the Péclet number, the thermal and solutal variants of which are given respectively by:

$${P}_{T}\text{=}\frac{VR}{2\alpha }\text{ , }{P}_{C}=\frac{VR}{2D}$$

(12)

with $\alpha$ and D being respectively the thermal and solutal diffusivity in the liquid beyond the freezing front.

In order to proceed we assign an initial ‘guess’ to the thermal undercooling, $\Delta{T_T} = \epsilon\Delta{T}$ where $\epsilon$ is a parameter that will be iterated to obtain a self-consistent solution. We also require an initial guess of the Péclet numbers and of the tip radius. Estimates of the Péclet numbers are given by:

$${P}_{T}\text{=}I{v}^{-1}\left(\frac{\Delta {T}_{T}}{L/{c}_{p}},1\right)\text{ , } \, {P}_{C}=\frac{\alpha }{D}{P}_{T}$$

(13)

while the initial tip radius is assumed fixed, irrespective of undercooling. Here L and c_p are the latent and specific heats respectively.

The iterative solution begins by calculation of the growth velocity, V, using Eq. (12) and the curvature and kinetic undercoolings, which are given by:

$$\Delta {T}_{R}=\frac{2\Gamma }{R}\text{ , }\Delta {T}_{K}=\frac{V}{\mu }$$

(14)

where $\Gamma$ is the Gibbs–Thomson coefficient and $\mu$ is a kinetic parameter. We now use the parameterisation of the phase diagram to “look up” the solute concentrations in the solid and liquid, C_S and C_L respectively, corresponding to the dendrite interface temperature, Here the curvature and kinetic undercoolings are accounted for by depressing the solidus and liquidus lines on the phase diagram by $\Delta{T_R} + \Delta{T_K}$.

We now calculate the thermal and solute gradients at the dendrite tip, G_T and G_C respectively, these being given by:

$${G}_{T}=\frac{{{U}^{^{\prime}}}_{T}}{R}\left({T}_{i}-{T}_{\infty }\right)\text{ , }{G}_{C}=\frac{{{U}^{^{\prime}}}_{C}}{R}\left({C}_{L}-{C}_{0}\right)$$

(15)

where U’ is the partial derivative, with respect to z, of the function U defined in Eq. (10):

$${U}^{^{\prime}}={\left.\frac{\partial U}{\partial z}\right|}_{\xi =1}=\frac{-2{e}^{-P}}{{\text{Ei}}(P)}$$

(16)

Once the gradients at the dendrite tip, G_T and G_C, have been evaluated we can then proceed to re-evaluate V and R. The evaluation of R uses the standard expression given by LKT, namely:

$${R}^{2}=\frac{\Gamma }{{\sigma }^{*}\left({\zeta }_{C}m{G}_{C}-{\zeta }_{T}\overline{\kappa }{G}_{T}\right)}$$

(17)

with:

$${\zeta }_{T}=1-\frac{1}{\sqrt{1+{1}/ {{\sigma }^{*}{P}_{T}^{2}}}}, {\zeta }_{C}=1+\frac{2k}{1-2k-\sqrt{1+{1}/{{\sigma }^{*}{P}_{C}^{2}}}}$$

(18)

Here, m is evaluated at the concentration C_L, by differentiation of the parameterised liquidus line on the phase diagram and k is calculated from the previously obtained values of C_S and C_L. $\overline{\kappa }$ is the reduced thermal conductivity, given by:

$$\overline{\kappa }=\frac{{\kappa }_{L}}{{\kappa }_{L}+{\kappa }_{S}}$$

(19)

where $\kappa_L\;\mathrm{and}\;\kappa_S$ are the thermal conductivities of the liquid and solid respectively. $\sigma^*$ is a stability constant which in marginal stability models (Mullins and Sekerka 1964) is generally given the value $1/(4\pi^2) = 0.0253$. More sophisticated theories, such as microscopic solvability (e.g. Kessler et al. 1988), have subsequently shown to be an eigenvalue of the crystalline anisotropy, although the equations for R are otherwise generally of the same form. Given the difficulties in obtaining reliable values for the surface energy anisotropy of crystalline materials, either experimentally or computationally, we have here taken as a fitting parameter.

Finally, we come to the velocity which may be obtained by balancing of heat (solute) flux due to diffusion away from the growing interface with the rate of heat (solute) generation at the interface. The expressions for heat and solute are given by:

$${V}_{T}=\frac{-{\kappa }_{L}{G}_{T}}{L{c}_{p}}\text{ , } \, {V}_{C}=\frac{-{D}_{L}{G}_{C}}{\left({C}_{L}-{C}_{S}\right)}$$

(20)

where V_T and V_C are the velocities calculated from the heat and solute balances respectively. Of course, physically the dendrite must propagate with a single velocity (V_T = V_C), which is the basis upon which we iterate towards a self-consistent solution. V_T > V_C indicates that the thermal undercooling is too high and that ε should be reduced. Conversely, V_T < V_C indicates that the thermal undercooling is too low and that should be increased. In fact, as to a reasonable approximation $V \propto (\Delta{T_T})^2$  it is relatively straightforward to iterate towards a self-consistent solution in which V_T and V_C agree to an arbitrary convergence tolerance, within only a few iterations. The model has been validated against a standard LKT model for the case of arbitrary linear liquidus and solidus lines and found to agree to within whatever convergence tolerance is assigned.

Appendix 2–Parameters for the Al-Ni System

Table 1 Thermophysical parameters used for Al-Ni melts. (source Holland-Moritz et al. 2008)

Table 2 Coefficients for the liquidus and solidus curves for B2-AlNi (order 6 polynomial fit to the solidus and liquidus lines, including metastable extensions, as shown in Fig. 1)