Abstract
For the present study numerical simulations of subcooled flow boiling of FC-72 in microgravity have been conducted to accompany boiling experiments performed in microgravity on the International Space Station (ISS). The numerical domain represents the geometry of the experimental test cell. For all simulations the open source framework OpenFOAM was employed, including extensions to the interFoam solver, which have been developed at the authors’ institute. A reference case has been defined applying intermediate values from the experimental parameter range as system parameters. This case has been examined thoroughly with regards to hydrodynamic phenomena and heat transfer during multiple, successive bubble cycles. Based on this reference case, the system parameters flow velocity, input heat flux, pre-heating time, and subcooling of the liquid bulk have been varied, and the impact of these quantities on bubble growth and movement as well as heat transfer have been studied. It was found, that an increased flow rate as well as increased subcooling lead to smaller bubbles and increased time between subsequent nucleations. A high input heat flux, an increased pre-heating time, and a decreased subcooling lead to a rapid cycle of bubble nucleation and coalescence.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
List of Symbols
\(A_{\mathrm {int}}\) | Interface area | \(\mathrm{m}^{2}\) |
c | Specific heat capacity | J/kg K |
d | Distance between cell center and interface | m |
\(\mathbf {f}_{\sigma }\) | Volumetric surface tension force | \(\mathrm{N}/\mathrm{m}^{3}\) |
F | Volume-of-Fluid indicator variable | - |
\(\mathbf {g}\) | Gravitational acceleration vector | \(\mathrm{m}/\mathrm{s}^{2}\) |
\(\dot{h}\) | Volumetric enthalpy source | \(\mathrm{W}/\mathrm{m}^{3}\) |
\(\mathbf {n}\) | Normal vector | - |
p | Pressure | Pa |
\(\dot{q}_{\mathrm {in}}\) | Input heat flux | \(\mathrm{W}/\mathrm{m}^{2}\) |
t | Time | s |
T | Temperature | \(^\circ \text {C}\), K |
\(\mathbf {u}\) | Velocity vector | m/s |
\(\mathbf {u}_{\mathrm {r}}\) | Compression velocity vector | m/s |
\(\Delta h_{\mathrm {v}}\) | Evaporation enthalpy | \(\mathrm {J/kg}\) |
\(\lambda\) | Thermal conductivity | W/m K |
\(\mu\) | Dynamic viscosity | kg/m s |
\(\rho\) | Density | \(\mathrm{kg}/\mathrm{m}^{3}\) |
\(\dot{\rho }\) | Specific mass source | \(\mathrm{kg}/\mathrm{m}^{3}\,\mathrm{s}\) |
\(\theta\) | Contact angle | \(^\circ\) |
V | Volume | \(\mathrm{m}^{3}\) |
Subscripts
cell | Value in the cell center |
f | Fluid |
s | Solid |
sat | Saturation |
subgrid | Value obtained from the subgrid model |
Introduction
Nucleate boiling is a highly efficient process to transfer high amounts of heat at low wall superheats. The high heat transfer coefficients are of interest not only for terrestrial applications like power generation or refrigeration, but also for the cooling of electronic devices in space applications. However, for the design of heat exchangers in space, it is impossible to employ correlations, which have been obtained under earth gravity conditions (1-g). Local fluid and heat transport phenomena under microgravity conditions are not sufficiently understood. Furthermore, experimental investigations of boiling phenomena in microgravity are used to study the fundamentals of the boiling process in general. The lack of buoyancy, which acts as a detaching force on bubbles, as well as increased time and length scales under microgravity conditions compared to 1-g conditions allow for detailed investigations of processes, which cannot be sufficiently resolved under 1-g conditions. Specifically hydrodynamics and heat transfer in the vicinity of the moving three-phase contact line require a very high resolution.
Boiling in microgravity has been investigated for several decades, both experimentally and numerically, for the above mentioned reasons. Lee and Merte (1999) conducted experiments in long term microgravity varying input heat flux and subcooling. In scenarios of stationary subcooled boiling, when evaporation at the bubble foot and condensation at the bubble cap are in equilibrium, they observed that heat transfer coefficients were enhanced up to 40 % relative to boiling under 1-g conditions, dependent on the level of subcooling. The authors state, that this observation is only valid for low and medium heat fluxes, though, while the value of critical heat flux always decreases in microgravity. Schweizer and Stephan (2009) performed boiling experiments in parabolic flights. They found that in an early stage of bubble growth, subcooling, and gravity have no impact on the ratio between local heat flow at the contact line and the overall heat flow. At later stages of bubble growth however, the ratio strongly increaseds with subcooling and decreases with gravity. Fischer et al. (2012), Fischer et al. (2014) conducted experiments of single successively nucleating bubbles in variable gravity during parabolic flights. They observed bubble shapes with a black and white camera and temperatures at the heater surface with an infrared camera through the infrared transparent heater. From the temperature profiles, the heat flux profiles at the heater surface were calculated numerically. The influence of the heat capacity of the heater substrate was studied in detail. The authors confirmed a temperature drop at the heater surface right below the moving three-phase contact line, which was found in prior studies. The authors concluded, that the temperature drop at the contact line depends on the heat capacity and thus also on the thickness of the heater, since a heater with a higher capacity can more easily compensate the increased heat flux at the contact line. It was concluded, that an accurate boiling model has to include the transient heat transfer characteristics of the wall and that constant heat flux or constant wall temperature boundary conditions at the fluid-wall interface do not properly display the underlying physics.
Special challenges in the numerical simulation of nucleate boiling are the implementation of an accurate phase change model, transport phenomena at extremely small length scales (e.g. contact line motion and contact line evaporation) and transient heat conduction in the solid wall and the liquid thermal boundary layer. Fuchs et al. (2006) developed a model for single bubble nucleate boiling using the finite element method and a moving mesh approach to capture the liquid-vapor interface. The model takes transient heat conduction in wall and liquid into account and includes contact line evaporation according to the work of Stephan and Busse (1992). The drawbacks of this model are that the bubble must be strictly spherical and that no interaction between different bubbles is possible.
During the recent two decades fixed grid methods have been developed, which are able to accurately solve complex multiphase flows. Most of these methods are either of the level-set (LS) or the Volume-of-Fluid (VOF) type. Implementing phase change in these models is a special challenge, because the exact position of the interface and thus the temperature gradient is not known per se. In several works LS is used to simulate nucleate boiling of water, with special attention to contact angle dynamics (Son et al. (1999)), bubble coalescence (Abarajith et al. (2004), Mukherjee and Dhir (2004)), and the influence of gravity (Abarajith et al. (2004), Aktinol and Dhir (2012), Aktinol et al. (2014), Li and Dhir (2007)). All of these works take evaporation in the vicinity of the three-phase contact line into account; however, most of them consider the wall to be isothermal.
Kunkelmann and Stephan (2010) employed a finite volume approach from the open source framework OpenFOAM and its VOF based solver interFoam to simulate pool boiling of refrigerants. They implemented explicit reconstruction of the interface, a boiling model based on the work of Hardt and Wondra (2008), a subgrid model for contact line evaporation according to Stephan and Busse (1992), and transient heat transfer within the wall. They found the results to be in good agreement with analytic and experimental data. Herbert et al. (2013) complemented this model by the capability to account for moving contact lines and validated the solver with experimental data of single drop impingement of FC-72 on a superheated wall. Dietl and Stephan utilized the solver to simulate pool boiling from single reentrant cavities Dietl and Stephan (2014). Rettenmaier et al. complemented the model further by the ability to capture complex hydrodynamic behavior in the vicinity of the three-phase contact line (Rettenmaier (2019)) and enhanced the included capabilities of adaptive mesh refinement and load balancing to account for stable simulations with a high degree of parallelization (Rettenmaier et al. (2019)).
Parallel to experimental research on boiling under microgravity conditions, numerical studies addressing the gravitational influence were published: Aktinol and Dhir (2012) made similar observations as Fischer et al. (2014). They performed simulations of subsequent bubble cycles in pool boiling of water under variable gravitational conditions using the level-set method, taking contact line evaporation and transient heat conduction in the wall into account. They observed a temperature drop in the wall underneath the three-phase contact line and found that the waiting time between bubbles strongly depends on the thickness and on the thermal conductivity of the wall material.
Urbano and co-workers (Urbano et al. (2019)) employed a combined level-set and ghost-fluid approach to perform simulations of subcooled pool boiling of water under microgravity conditions, focusing on a single bubble. They studied the steady state, when evaporation at the wall and condensation to the subcooled bulk are in equilibrium, and used the results to develop an analytical correlation of the equilibrium radius. The authors defined the ratio of the condensation Jacob number and the evaporation Jacob number as a measure between bulk subcooling and wall superheat. They performed parametric studies, varying this Jacob number ratio as well as the static contact angle. They showed, that the equilibrium radius is inversely proportional to the temperature gradient between the superheated wall and the subcooled bulk fluid. Additionally, the equilibrium radius decreased, if the bulk subcooling increased relative to the wall superheat, and it increased for an increasing contact angle. Moreover, they analyzed the Nusselt number in the vicinity of the bubble and found a complex dependency on both contact angle and Jacob number ratio. Transient heat transfer at the wall was included and the strong influence of the wall’s heat transfer capacity on the evaporation mass flow rate and hence the equilibrium radius was highlighted.
The aim of the presented study is to reproduce the experimental setup of the Multiscale Boiling Experiment numerically with the scope to get a detailed insight into quantities, which are difficult or impossible to measure. Subsequent bubble cycles of subcooled flow boiling are simulated. The numerical solver developed by Kunkelmann and Stephan (2010), Herbert et al. (2013) and Rettenmaier (2019) is extended by specific functionalities, which are crucial to model this specific experiment. The geometry of the experimental test cell is used as the system boundary of the numerical mesh. While in the majority of the cited numerical works 2-D simulations of axisymmetric bubbles are performed, for the present work 3-D simulations are conducted in order to cover the physics of moving, non-spherically shaped bubbles in a shear flow in the right way. The impact of physical input quantities is studied within a parameter study. The results will be discussed and presented.
In order to gain more insight into the transport phenomena in microgravity, a reference experiment called Multiscale Boiling, which is running aboard the International Space Station (ISS) since July 2019, has been designed under the coordination of the European Space Agency (ESA). The numerical simulations presented in this paper accompany these space experiments. The experimental setup consists of a boiling cell arranged above a solid substrate. On top of the substrate a thin layer of chromium is sputtered serving as electrical resistance heater. A laminar shear flow of FC-72 streams through the boiling cell and over the substrate, being heated by the chromium layer. In the center of the top of the substrate a cavity has been manufactured to serve as nucleation site for successively nucleating bubbles. During each experimental run, after a specified pre-heating time, the cavity is activated by a laser beam aimed onto the cavity and the continuous boiling process starts. The process is monitored by a black-and-white camera from the side of the test cell and by an infrared camera from below the substrate.
Numerical Model
The numerical method for simulating the boiling flow is based on the finite volume method implemented in the open source toolbox OpenFOAM. The interFoam solver is complemented by a phase change model, a treatment to cover heat and mass transfer in the vicinity of the three-phase contact line as well as conjugate transient heat transfer between wall and fluid. The liquid-vapor interface is tracked by the algebraic VOF approach included in interFoam, extended by a method of explicit interface reconstruction out of the volume fraction field. The model was validated by Kunkelmann and Stephan (2010) against experimental data of nucleate boiling and by Herbert et al. (2013) against experimental data of single drop impingement.
Governing Equations
The equations, which have to be solved by the numerical solver, are the conservation equations of mass, momentum, and energy. Although in an evaporating flow part of the fluid consists of gas, the fluid is considered to be incompressible throughout the numerical domain, which is valid, as long as Mach numbers are sufficiently low. The conservation equations of the fluid are:
The source terms \(\dot{\rho }\) and \(\dot{h}\) in the continuity equation and in the energy equation, respectively, account for phase change. These terms are detailed in Equations 6 and 7 in Chapter 3.3. The terms \(\mathbf {f}_{\sigma }\) and \(\rho \mathbf {g}\) on the right hand side of the momentum equation are volumetric forces due to surface tension and gravity. In the solid domain, the energy equation simplifies to
Multiphase flow is captured by the Volume-of-Fluid method of Hirt and Nichols (1981), which uses an indicator variable F to distinguish between the liquid and the vapor phase. This volume fraction field F is zero for cells completely filled with vapor and unity for cells completely filled with liquid. In cells containing part of the interface, F has values between zero and one. In OpenFOAM, the advection of the volume fraction field is solved by the MULES algorithm:
Again, the term on the right hand side of Equation (5) accounts for phase change. In order to prevent diffusion of the interface, the compression term \(\nabla \cdot (\mathbf {u}_r F (1-F))\) is introduced, which acts in cells containing the interface. The compression vector \(\mathbf {u}_r\) points orthogonal to the interface. While it always scales with the flow velocity in the standard framework of interFoam, it is set to a minimum value of \(|\mathbf {u}_r| = 0.1 m/s\) in the presented simulations due to very small flow velocities.
The fluid and the solid phase are coupled by an iterative Dirichlet-Neumann solution algorithm. On the fluid side the temperature is prescribed as a boundary condition, while on the solid side the heat flux is prescribed. The energy equation is then solved alternating in the fluid and the solid domain until the difference in temperature change between iterations falls below a specified threshold of \(10^{-4}\) K.
Interface Reconstruction
The algebraic VOF approach implemented in OpenFOAM does not provide information about the explicit position of the liquid-vapor interface. Nevertheless, this information is needed by the phase change model. Therefore Kunkelmann (2011) developed an explicit reconstruction of the interface. A surface is created between mesh points holding values of \(F = 0.5\), which results in a piece-wise linear, continuous interface. Furthermore, an accurate calculation of the interface curvature is crucial to avoid spurious currents near the interface. However this turns out to be quite challenging within an VOF approach. Employing the iso-surface interface reconstruction, the accuracy of the curvature calculation can be improved significantly. Rettenmaier (2019) validated the iso-surface curvature calculation against analytical predictions of a sessile drop and a capillary rise between two plates and found it to be about one order of magnitude more accurate than the standard interFoam approach.
Phase Change Model
Phase change at the liquid-vapor interface is modeled by an evaporation model, which has been developed by Kunkelmann and Stephan (2010) and has later been modified by Batzdorf (2015) by an implicit solution algorithm. The interface is assumed to be always at saturation temperature. The heat flux from an arbitrary cell of the volume \(V_{\mathrm {cell}}\) and the temperature \(T_{\mathrm {cell}}\) towards a part of the interface \(A_{\mathrm {int}}\) inside an interface containing cell is calculated by the temperature difference and the distance d. This distance has been determined during interface reconstruction. The resulting density source term in Equation 1 is then
In Equation 6\(\Delta h_{\mathrm {v}}\) is the evaporation enthalpy. In cells adjacent to a wall, which contain part of the three-phase contact line, an extra source term \(\dot{\rho }_{\mathrm {subgrid}}\) is added for evaporation in the microzone, which is obtained by the subgrid model described in the next section. The volumetric enthalpy source term \(\dot{h}\) in Equation 3 is then calculated by
The resulting local mass source terms are then smeared out to a band of cells around the interface according to the method of Hardt and Wondra (2008) in order to assure computational stability. Batzdorf (2015) validated the evaporation model performing a simulation of a growing vapor bubble inside an infinitely extended superheated liquid bulk and found it to be in good agreement with the analytical solution of Scriven (1959), if the mesh resolution is sufficiently small.
Contact Line Evaporation
Hydrodynamics as well as heat transfer in the vicinity of the three-phase contact line, where liquid, vapor, and solid meet, happen at a length scale, which is several orders smaller than the macroscopic boiling process. It would be numerically too expensive to resolve this area with the numerical mesh and to directly simulate the underlying process. Therefore contact line evaporation is treated with a special subgrid scale model. The model calculates the shape of the liquid-vapor interface, the heat flow, and the apparent contact angle \(\theta\) and is based on a formulation by Stephan and Busse (1992). Its implementation is described in detail in Herbert et al. (2013). After the model is solved utilizing Matlabs ode-45 solver, a polynomial regression is made for heat flow, contact angle, and the thickness of the liquid layer in dependence of the wall superheat, and the contact line velocity. The coefficients of this polynomial are then provided as input in the CFD simulation in OpenFOAM.
Acceleration Techniques
The required grid resolution within the fluid domain is strongly diverging. Areas, which contain steep field gradients require a fine grid resolution. Those are the vicinity of the liquid-vapor interface and the thermal boundary layer above the heated wall. On the other hand, liquid and vapor bulk as well as the majority of the solid wall require only a much coarser resolution. Since the liquid-vapor interface is moving due to bubble growth and shear flow, it is necessary, that the grid resolution is permanently refined in those areas, which become the vicinity of the interface, and coarsened, where the interface has moved away from. This technique is commonly referred to as adaptive mesh refinement (AMR) and helps to reduce the overall number of grid cells drastically. Furthermore, parallel computing is used in order to reduce computation time. Because the area of high grid resolution changes through AMR, the distribution of cells on the processors varies significantly throughout the simulation. Therefore, a technique called load balancing (LB) is used to redistribute the cells to the processors during a running simulation, as soon as the imbalance exceeds a defined value. The details of AMR and LB utilized in the present work are outlined in Batzdorf (2015), and Rettenmaier et al. (2019).
Simulation Setup
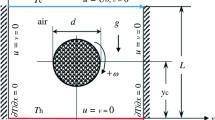
(a) CAD model of the boiling cell, (b) Cross section of 3D computational domain with boundary conditions as defined in Table 1
As outlined in the introduction, the aim of the presented simulations is a numerical reproduction of the Multiscale Boiling Experiment on the ISS. Therefore a number of features specific to the experimental setup have been reproduced within the numeric model as detailed as possible in the numeric framework. Figure 1a shows a CAD model of the boiling cell and Fig. 1b the two numerical domains (fluid and solid) with their boundaries. The fluid domain represents the geometry of the experimental test cell, the solid domain that of the heated wall. A laminar flow of FC-72 enters the fluid domain at the inlet port and flows towards the outlet port in x-direction. This flow is modeled as an ideal Poiseuille flow (i.e. a parabolic velocity profile) with the maximal flow velocity in the middle of the channel and zero at walls. The height of the channel and thus the height of the Poiseuille velocity profile is 5 mm. A complete overview of all numerical boundary conditions is given in table 1.
Three-dimensional simulations are conducted in order to correctly model the hydrodynamics of bubbles affected by a shear flow. It is taken advantage of the plane symmetry in the middle of the boiling cell and the heater, respectively.
At the boundary between the two domains, coupled temperature and heat flux boundary conditions are employed as described in Section 3.1. Additionally, on the solid side of the coupled boundary conditions a heat flux \(\dot{q}_{\mathrm {in}}\) is implemented as a source term, representing the electrical heat source in the experiment. Furthermore, in cells containing part of the three-phase contact line, the contact line evaporation heat flux obtained from the subgrid model is added on the solid side.
In the corresponding experiments a specific pre- heating time is defined before the first nucleation, so that a thermal boundary layer can develop in the flow above the heater. At the end of this pre-heating time, the first nucleation is enforced and the nucleation site is activated by a laser shot focused onto the cavity. According to those experiments, all of the presented simulations start with a single phase liquid flow. The cavity, which serves as nucleation site in the experiment, is not included in the numerical mesh, since including it would be numerically too expensive. Instead, nuclei of vapor are created on the plane surface at the position where the cavity is located in the experiment. During the simulations nuclei are created by manipulating the volume fraction field when one of the two following criteria is met:
-
1.
When a defined waiting times expires
-
2.
After the very first bubble, when a defined wall superheat is reached
The very first bubble in each simulation is created after a simulation time of several seconds, representing the pre-heating time in the experiment. The power of the experimental laser is modeled by increasing the heat flux source term on top of the heater in the cell faces around the nucleation site for a time span according to the experiments, and decreasing it again afterwards. All subsequent bubbles are created as soon as the wall temperature at the nucleation site exceeds a defined superheat criterion. Hsu (1962) developed a model for a necessary wall superheat for incipience of boiling in case of known material properties and cavity features. Based on Hsu’s model, the superheat criterion is set to 7 K throughout all simulations presented. Each time, when a bubble is created by manipulating the volume fraction field, the temperature in the wall cells below the bubble is reduced such that the energy balance is fulfilled taking the evaporation enthalpy of the fluid into account. Figure 2 shows the evolution of the temperature field around the first bubble in a simulation. The decrease of the wall temperature beneath the bubble foot at nucleation can be observed as well as the strong increase in temperature due to the laser power and the following decrease. In the following, in all figures including simulation time, time starts at the first nucleation at the end of the pre-heating time.
Adaptive mesh refinement, as outlined in Section 3.5, is used in the fluid domain in six refinement levels to account for the large size of the computational domain on the one hand and the need for high mesh resolution in the thermal boundary layer and in the vicinity of the liquid-vapor interface on the other hand. Batzdorf (2015) showed, that the evaporation model is in excellent agreement with the analytical solution of Scriven (1959), if the temperature gradient between the liquid-vapor interface and the bulk liquid is resolved with at least four cell layers in case of a 10 K temperature difference. The finest mesh resolution in the present study is chosen such that this condition is fulfilled in the vast majority of the simulation time, which results in cells refined six times compared to the base mesh at the moving interface and a minimum cell size of \(7.5\, \upmu \mathrm{m}\). Figure 3 shows the results of a mesh study, comparing the chosen resolution of \(7.5\, \upmu \mathrm{m}\) cell size with one of \(3.75\, \upmu \mathrm{m}\) cell size for the main growth phase of the vapor bubble in the reference case during the first 20 ms after nucleation. This time span is characterized by the highest temperature gradients and the fastest bubble growth throughout each simulation. It can be observed, that the estimation of the bubble volume is in good agreement for both resolutions, with a slight deviation during the first few ms after nucleation. This deviation originates from the very high temperature gradients in the vicinity of the bubble foot due to the laser power during the first few milliseconds after nucleation. Nevertheless, the deviations have a maximum of only 8.5 % and the bubble diameters start to converge again after approximately 5 ms. The computational effort is approximately three times higher in case of the \(3.75\, \upmu \mathrm{m}\) mesh resolution compared to \(7.5\, \upmu \mathrm{m}\). However, during the observed time span there is only one bubble present in the computational domain, which is comparably small. In some of the cases discussed later, which are characterized by very large or more than one bubble, this factor of computational effort is expected to be even higher due to a much larger liquid-vapor interface. Therefore a minimum cell size of \(7.5\, \upmu \mathrm{m}\) is considered the best compromise between precision and computational effort.
The adaptive mesh refinement in the solid domain is dependent on the refinement in the fluid domain, such that the mesh nodes always coincide at the fluid-solid boundary.
Results and Discussion
A reference case has been defined applying intermediate values from the experimental parameter range and a parameter study has been conducted based on this reference case as shown in table 2. All simulations are performed with the working fluid FC-72 at 0.54 bar or a saturation temperature of \(39.7\,^\circ \text {C}\), respectively. The heat flow resulting from the laser, which activates the nucleation process, is set to 177 mW for 10 ms, beginning with the first nucleation. Gravity is assumed to be 0.01 % of terrestrial gravity. In the following sections, first the reference case will be analyzed in detail in order to gain insight into the hydrodynamic behavior of single vapor bubbles in subcooled flow boiling in microgravity as well as into the connected heat transfer phenomena. Secondly, the influence of flow velocity, input heat flux, pre-heating time and subcooling both on hydrodynamics and heat transfer are analyzed. In the following, to distinguish simulations with different flow velocities, the maximum velocity in the center of the channel is given.
Analysis of the Reference Case
First, we analyzed whether or not the laser pulse has an influence on bubble growth. Secondly, we analyzed the bubble size evolution. Finally, heat transfer characteristics are discussed.
Figure 4 exemplarily shows the vapor bubbles inside the fluid domain in the reference case at a proceeded simulation time of 1.7 s after the very first nucleation. One can clearly observe the third bubble, which is about to merge with the first two ones, which have already merged earlier during the simulation. Figure 5 displays the overall bubble growth process and the influence of laser power on this process. The consideration of the laser power in subcooled boiling only has an effect in the beginning of the growth phase, where it leads to an overshoot in bubble diameter. After approximately 0.3 s, in both cases the bubble strives towards the same equilibrium volume, which is characterized by evaporation at the bubble foot and condensation to the subcooled bulk. The shear flow drags the bubble downstream and a second bubble is created as soon as the wall temperature at the nucleation site reaches the defined superheat. This second bubble grows until it gets in contact with the first bubble and coalescence occurs approximately 1.3 s after the very first nucleation. Figure 6 shows the life cycle of the second bubble in the reference case from nucleation till the end of the coalescence with the first bubble. After the merger, the resulting, larger bubble shrinks until it reaches the equilibrium state again. Nevertheless, due to the momentum of the merger an alternating spreading and receding of the contact line interrupts the shrinking process by a stage of evaporation dominance. Figure 7 shows the evaporation and condensation heat transfer, respectively. While those two effects are in exact equilibrium during stages, when there is no significant change in vapor volume, and evaporation clearly dominates during growth stages, the dominance of either evaporation or condensation alternates during the merger phases. Figure 5 shows the growth phases of a third and a fourth bubble within the evaluated simulation time of 2 s after the pre-heating time. Beginning with the second bubble, the waiting time between successive bubbles decreases and a continuous process of nucleation, growth and coalescence begins. Due to bubble growth times getting shorter, the maximum volume of each successive bubble decreases.
Figure 8 shows the contact line evaporation heat transfer. Relating the values of heat transfer due to contact line evaporation to the overall evaporation heat transfer from Fig. 7, it is striking, that the contact line share is considerably high. During the equilibrium state it is constantly higher than 50 %, while during merger, due to the alternating expanding and contracting bubble foot, the share of contact line evaporation temporarily grows up to almost 60 %. Those values are significantly higher than estimations for the share of contact line heat transfer given in literature for boiling under earth gravity conditions, which are usually in the range of 20 % to 30 % (Kim (2009) and Stephan and Kern (2004)). This higher share of contact line heat flow can be explained by the lack of natural convection in a 0-g environment: Under earth gravity conditions, natural convection causes a significant heat flow through the liquid towards the bubble, enhancing evaporation at the bubble hull. Furthermore, bubble growth shows a more dynamic behavior under earth gravity conditions, causing enhanced evaporation at the bubble hull. Since those two mechanisms are lacking under microgravity conditions, evaporation at the bubble hull is reduced and the overall share of contact line evaporation is increased.
In order to evaluate the sensible heat flow to the fluid, the sensible heat flux to the fluid is integrated over a circle of 2 mm radius around the nucleation site. This way, the heat flow at the majority of the heater surface, where no bubbles are present is cut out of the evaluation in order to focus on the influence of the boiling process on sensible heat transfer. At the same time, a 2 mm radius is sufficient to cover large bubbles, which appear in the cases of high input heat fluxes or low subcooling in the following section. Figure 9 shows the evolution of the sensible heat flow in the reference case over time. One can observe that each nucleation and growth of an additional bubble leads to an increase not only in contact line, but also in sensible heat flow. The reason for this increase is that superheated liquid from the thermal boundary layer is consumed by the evaporating contact line and permanently being replaced by colder liquid. Furthermore, the sensible heat flow shows a strong and short increase every time, when two bubbles coalesce, because in the moment of the merger the successive bubble disappears rapidly and the emerging space is filled with colder bulk liquid, as can be observed in Fig. 6.
Figure 10 shows the evolution of the wall temperature at the nucleation site. One can observe the rapid decrease in temperature every time, when the nucleation temperature of \(46.7^\circ \text {C}\) is reached and a new bubble is created, because the wall temperature is manipulated such that the energy balance is fulfilled. However, due to the very small volume, which is cooled down, compared to the solid volume with a relatively high temperature, the temperature at the nucleation site almost fully recovers in an extremely short time span. Furthermore, a reversible decrease in wall temperature can be observed each time, when the contact line of the sliding bubble passes the location, where the temperature is monitored.
Influence of System Parameters
In this section, we analyze the influence of system parameters on bubble size evolution compared to the reference case and secondly on heat transfer characteristics striking for the specific parameter.
Influence of Flow Velocity
Figure 11 shows the bubble volume evolution for maximum flow velocities lower and higher than in the reference case (0.0375 m/s). Apparently, an increasing flow rate correlates with a decreasing volume of each single bubble. This can be explained by the thermal boundary layer between the superheated wall and the subcooled bulk fluid, which is thinner. Next the maximal wall temperature is lower for higher flow velocities due to the increased convective heat transfer. This also causes prolonged waiting periods between nucleations during the first three bubble cycles in the 0.0625 m/s case. Hence, the first two bubbles do not merge in this case, as indicated in Fig. 12, and the bubble volumes of the first two bubbles permanently add up. For flow velocities lower than in the reference case, the first bubble grows larger and blocks the nucleation site for a longer period of time, such that no subsequent nucleation occurs during the conducted simulation time.
The heat transfer from the wall to the fluid is enhanced for increasing flow velocities: Figures 13 and 14 show the heat transfer due to evaporation at the contact line and the sensible heat flow from the wall to the fluid, respectively. The sensible heat flow is evaluated in the same way as in Section 4.1 within a 2 mm radius around the nucleation site. As Fig. 13 indicates, the contact line heat transfer in case of a single bubble is higher in case of lower flow velocity due to larger bubble volumes and therefore longer contact lines. However, the sensible heat flow is much higher for high flow velocities due to enhanced convection and this effect outweighs the smaller contact line heat transfer. The decrease in sensible heat flow in the 0.0625 m/s case after approximately 1 s is caused by the very first bubble moving out of the evaluated area. Additionally, if the waiting period between two succeeding bubbles is long enough that the bubbles will not merge, the contact line heat transfer and the enhanced sensible heat flow of multiple bubbles add up permanently, as the \(\mathrm{u}_\mathrm{max}\) = 0.0625 m/s case in Figs. 13 and 14 shows. Those findings indicate, that optimum heat transfer during flow boiling in microgravity can be established with relatively high flow velocities combined with parameters such that the waiting time between subsequent bubbles is long enough, that the bubbles will not merge and as many bubbles as possible populate the surface. Figure 15 shows the evolution of wall temperatures for the different flow velocities. Due to the nucleation site being blocked by a slowly or non-moving bubble, the wall temperature eventually increases above the adjusted nucleation temperature in the low velocity cases, while for a higher velocity the evolution of the surface temperature is similar to the reference case.
Influence of Heat Flux and Pre-Heating Time
Process of coalescence with following detachment of vapor and forming of new bubbles in the 2 \(\mathrm{W}/\mathrm{cm}^{2}\) case, which is typically occurring in a fast sequence in high heat flux and high pre-heating time cases, time starting from first nucleation: (a) A subsequent bubble from the nucleation site is coalescing with the first bubble, (b) vapor detaches from the large bubble during the merger process and forms a new bubble upstream of the nucleation site, (c) while the latter bubble is growing, the next bubble nucleates at the defined nucleation site due to the superheat criterion, (d) this bubble again coalesces with the first bubble, (e) again vapor detaches during the merger process, forming another bubble between the nucleation site and the major bubble, (f) another bubble nucleates at the nucleation site due to superheat
As Fig. 16 indicates, the volume of the first bubble increases with increasing heat flux. High heat fluxes as well as increased pre-heating times cause a faster growth and a larger equilibrium size of the first bubble. Furthermore, as soon as this first bubble is dragged downstream sufficiently to give space at the nucleation site for succeeding bubbles, a cycle of rapidly nucleating and merging bubbles begins. During this fast sequence of coalescence between the first and the succeeding bubbles, vapor is repeatedly torn off the major bubble, causing the formation of additional bubbles in the vicinity of the nucleation site, which grow and eventually coalesce with the major bubble again (see Fig. 17). In consequence of this process of “feeding” the first bubble by the succeeding ones, the volume of this bubble grows above its equilibrium size determined by evaporation and condensation at its bubble hull, because the process of nucleation and coalescence is faster than the condensation of the major bubble. Figure 16 depicts, that in every case of high heat fluxes or prolonged waiting times at some point the vapor volume begins to grow without any limit during the conducted simulation time. It is noticeable, that for heat fluxes above 1.5 \(\mathrm{W}/\mathrm{cm}^{2}\), increasing the heat flux even further leads to a smaller global vapor volume after a specific simulation time, because the first bubble grows larger in the beginning and blocks the nucleation site for a longer time, thus the described growing process beyond the equilibrium size begins later. Comparing the effect of an increased input heat flux and an increased pre-heating time compared to the reference case, the same qualitative effect can be observed but with stronger expression for increased heat flux. Increasing the heat flux by the factor 1.5 has the same effect on bubble growth as doubling the pre-heating time to 20 s. Doubling the heat flux has even a slightly stronger effect on the growth of the first bubble than tripling the pre-heating time.
For heat fluxes lower than in the reference case (1 \(\mathrm{W}/\mathrm{cm}^{2}\)), for the prescribed wall superheat criterion of 7 K no nucleation of subsequent bubbles occurs. However, the prescribed superheat criterion is an estimate, based on the model of Hsu (1962) for incipient boiling at a previously inactive cavity. It is possible, that at an activated nucleation site a lower superheat might be sufficient for the nucleation of succeeding bubbles. Figure 18 shows the temporal evolution of the wall temperature at the nucleation site for the reference case and lower heat fluxes, indicating, that decreasing that criterion to appr. 5 K in the case of 0.75 \(\mathrm{W}/\mathrm{cm}^{2}\) or 3 K in the case of 0.5 \(\mathrm{W}/\mathrm{cm}^{2}\) would lead to a stable cycle of subsequent bubbles also for low heat fluxes.
Influence of Subcooling
Figure 19 shows an increase in bubble volume for a decreasing level of subcooling in the bulk fluid. For a very high subcooling of 10 K no successive bubbles appear after the very first, laser induced nucleation for the adjusted wall superheat criterion of 7 K. As discussed in Section 4.2.2, the needed superheat might be lower for successive bubbles at an already active nucleation site. Figure 20 indicates, that successive nucleations would be possible, if the criterion was decreased to approximately 3 K. In case of a subcooling lower than in the reference case, i.e. 2 K, a stable sequence of nucleating bubbles merging with the first one begins after approximately 0.9 s. For saturated boiling (0 K subcooling) the phenomenon of successively nucleating bubbles at the nucleation site and additional bubbles in their vicinity originating from torn off vapor from prior merging processes can be observed, as shown in Fig. 21. This phenomenon is similar to the cases of increased heat flux (Section 4.2.2), but the sequence of nucleation and merger is less rapid. The successive bubbles cannot be explicitly noticed in the representation of vapor volume in Fig. 19, because in case of saturated boiling the very first bubble itself never reaches an equilibrium state and grows infinitely.
Phase interfaces for saturated boiling 0.356 s after first nucleation. Left of the major bubble a subsequent bubble has nucleated, on the most left another bubble has been formed from vapor detached during coalescence. Additionally, a liquid droplet has formed inside the major bubble during a merger
The absolute contact line heat flow (Fig. 22) is larger for decreasing subcooling, since bubbles grow larger and have longer contact lines. Figure 23 shows the sensible heat flow from the wall to the fluid within a 2 mm radius around the nucleation site. During the first few hundred milliseconds after nucleation, i.e. while bubble diameters are still small, the sensible heat flow is higher for high levels of subcooling. This can be explained by the temperature gradient between the wall and the bulk fluid, which is higher in case of higher subcooling. Hence, the pure convective heat transfer to the flowing liquid is enhanced by subcooling. After approximately 0.2 s, when the very first bubbles grow beyond a critical volume in the cases of low subcooling, the effect of increased sensible heat flow in the vicinity of the contact line as described in Section 4.1 outweighs the effect of the higher temperature gradient and an increase in sensible heat flow for a decrease in subcooling can be observed. The decrease in sensible heat flow in the saturated boiling case after approximately 0.6 s can be related to the fact, that the major bubble leaves the evaluated area of 2 mm radius around the nucleation site as it is dragged downstream. However, this observation does not necessarily mean, that low subcooling is correlated with an enhanced sensible heat transfer, since it is only valid in the case, that no subsequent bubbles will nucleate after the very first bubble in case of a high subcooling. As discussed above, it is likely, that lower wall superheats than the adjusted 7 K could be sufficient for subsequent nucleations. The results in Section 4.2.1 show, that if several bubbles populate the heated surface and do not coalesce, the heat transfer due to contact line evaporation as well as the enhanced sensible heat transfer add up. This way, the sensible heat flow in the 10 K subcooling case could be increased beyond the values of 2 K subcooling or saturated boiling. Therefore, it appears desirable to combine a level of subcooling as high as possible with other system parameters such, that several bubbles simultaneously slide on the surface.
Summary and Outlook
In the present study, numerical simulations of subcooled, laminar flow boiling in microgravity have been performed employing a VOF approach implemented in the open source framework OpenFOAM combined with methods to cover phase change, contact line physics, and transient heat transfer with the solid wall, developed at the authors’ institute. The numerical setup as well as the boundary conditions were strongly orientated towards the setup of the accompanying Multiscale Boiling experiment on the International Space Station ISS. Several bubble cycles were covered in each simulation. The first nucleation is set after a pre-defined waiting time, all subsequent nucleations occur, when an adjusted wall superheat at the nucleation site is reached. A reference case has been defined using intermediate values from the experimental parameter range, to examine general hydrodynamic and heat transfer phenomena. The following main observations have been made:
-
The share of contact line heat flow in the total evaporation heat flow is between 50 % and 60 % throughout the process and thus considerably higher as values in literature obtained under earth gravity conditions (e.g. Kim (2009) and Stephan and Kern (2004)). The reason for this observation is the absence of natural convection and the reduced bubble growth dynamics in a 0-g environment, which under earth gravity conditions contribute significantly to the evaporation at the bubble hull.
-
Due to the subcooling of the bulk fluid, each single bubble grows to a volume, where evaporation at the bubble foot and condensation at the upper bubble hull are in equilibrium.
-
With the chosen system parameters, a process of subsequently nucleating and growing bubbles begins, with the succeeding bubbles coalescing with the very first one. After coalescence, the resulting bubble shrinks towards the aforementioned equilibrium volume. During this process, due to strongly alternating bubble deformations, the dominance of evaporation or condensation in the overall process alternates.
-
Additional to the highly increased latent heat transfer at the evaporating contact line, an increased sensible heat flow from the wall to the liquid can be observed next to the contact line in the liquid phase.
-
At the moment of bubble coalescence, sensible heat flow reaches a maximum of short duration, because the subsequent bubble, which is disappearing into the very first one, gives space for colder bulk liquid.
-
The temperature drop inside the wall underneath a newly nucleating bubble as well as the temperature decrease underneath a moving contact line recovers rapidly due to the large thermal capacity of the wall, which is in good agreement with Fischer and co-workers (Fischer et al. (2012), Fischer et al. (2014)).
Based on this reference case, a parameter study has been performed studying the impact of flow velocity, input heat flux, pre-heating time, and subcooling. The most important observations of the parameter study are:
-
An increased flow velocity causes the thermal boundary layer above the wall to be thinner and, due to enhanced convective heat transfer, the wall superheat at the nucleation site to be lower. This causes each single bubble to be smaller and, during the first cycles after the very first bubble, the waiting time between subsequent nucleations to be longer. This makes it more likely, that subsequent bubbles will not coalesce and that the enhanced latent and sensible heat transfer at the bubble foot of several bubbles add up.
-
Low flow velocities cause the very first bubble to grow larger and prevent the nucleation of subsequent bubbles, because the very first bubble blocks the nucleation site.
-
High input heat fluxes as well as increased pre-heating times cause the very first bubble to grow until a larger equilibrium volume compared to the reference case. Additionally, as soon as the very first bubble is dragged down sufficiently to give space at the nucleation site for further nucleations, a cycle of rapidly nucleating bubbles begins, which coalesce immediately with the very first bubble, thus letting it grow infinitely beyond its equilibrium size.
-
The effect of increased input heat flux and increased pre-heating time on bubble growth is similar, but it is stronger for the input heat flux by a factor of approximately 1.5. A possible explanation for this discrepancy could be the relatively low thermal conductivity of the working fluid. However, the impact of thermal conductivity has to be examined in further studies.
-
An increase in subcooling causes the very first bubble to grow to a smaller equilibrium volume and makes subsequent nucleation less likely, dependent on the nucleation criterion. As long as no succeeding bubbles are present on the heated surface due to a high necessary superheat, heat transfer improves with decreasing subcooling, since larger bubbles provide a longer contact line. However, if subsequent bubbles nucleate in a highly subcooled environment and do not coalesce, heat transfer can be enhanced significantly.
For future investigations, a value for the necessary superheat for subsequent nucleations at the activated nucleation site, gained from the accompanying experiment, can be consulted to predict the appearance of bubbles on the heater surface more precisely. With this information, the parameters investigated in the present study can be adjusted in a way, that a large number of bubbles of small diameter are present on the heated surface at the same time. This way an optimal heat transfer can be ensured.
Availability of Data and Material
All secondary data and scripts used to create plots are availabe via Tudatalib: DOI: https://doi.org/10.48328/tudatalib-430
Code Availability
The OpenSource Toolbox OpenFOAM in its developer version OpenFOAM-dev by the OpenFOAM foundation was employed. Additional libraries developed at the authors’ institute were employed, as well.
References
Abarajith, H., Dhir, V., Warrier, G., Son, G.: Numerical simulation and experimental validation of the dynamics of multiple bubble merger during pool boiling under microgravity conditions. Annals of the New York Academy of Sciences 1027, 235–258 (2004)
Aktinol, E., Dhir, V.: Numerical simulation of nucleate boiling phenomenon coupled with thermal response of the solid. Microgravity Science and Technology 24, 255–265 (2012)
Aktinol, E., Warrier, G., Dhir, V.: Single bubble dynamics under microgravity conditions in the presence of dissolved gas in the liquid. International Journal of Heat and Mass Transfer 79, 251–268 (2014)
Batzdorf, S.: Heat transfer and evaporation during single drop impingement onto a superheated wall. Ph.D. thesis, TU Darmstadt (2015)
Dietl, J., Stephan, P.: Numerical simulation of boiling from a single reentrant-cavity. In: Proceedings of the 15th International Heat Transfer Conference, IHTC-15, August 10-15, 2014, Kyoto, Japan (2014)
Fischer, S., Herbert, S., Sielaff, A., Slomski, E., Stephan, P., Oechsner, M.: Experimental investigation of nucleate boiling on a thermal capacitive heater under variable gravity conditions. Microgravity Science and Technology 24(3), 139–146 (2012)
Fischer, S., Herbert, S., Slomski, E., Stephan, P., Oechsner, M.: Local heat flux investigation during pool boiling single bubble cycles under reduced gravity. Heat Transfer Engineering 35(5), 482–491 (2014)
Fuchs, T., Kern, J., Stephan, P.: A transient nucleate boiling model including microscale effects and wall heat transfer. Journal of Heat Transfer 128, 1257–1265 (2006)
Hardt, S., Wondra, F.: Evaporation model for interfacial flows based on a continuum-field representation of the source terms. Journal of Computational Physics 227, 5871–5895 (2008)
Herbert, S., Fischer, S., Gambaryan-Roisman, T., Stephan, P.: Local heat transfer and phase change phenomena during single drop impingement on a hot surface. International Journal of Heat and Mass Transfer 61, 605–614 (2013)
Hirt, C., Nichols, B.: Volume of fluid (vof) method for the dynamics of free boundaries. Journal of Computational Physics 39, 201–225 (1981)
Hsu, Y.Y.: On the size range of active nucleation cavities on a heating surface. Journal of Heat Transfer 84(3), 207–213 (1962)
Kim, J.: Review of nucleate pool boiling bubble heat transfer mechanisms. International Journal of Multiphase Flow 35, 1067–1076 (2009)
Kunkelmann, C.: Numerical model and investigation of boiling phenomena. Ph.D. thesis, TU Darmstadt (2011)
Kunkelmann, C., Stephan, P.: Numerical simulation of the transient heat transfer during nucleate boiling of refrigerant hfe-7000. International Journal of Refrigeration 33, 1221–1228 (2010)
Lee, H., Merte JR., H.: Pool boiling mechanisms in microgravity. Proceedings of the Engineering Foundation Conference on Microgravity Fluid Physics and Heat Transfer, Hawai (1999)
Li, D., Dhir, V.: Numerical study of single bubble dynamics during flow boiling. Journal of Heat Transfer 129, 864–876 (2007)
Mukherjee, A., Dhir, V.: Study of lateral merger of vapor bubbles during nucleate pool boiling. Journal of Heat Transfer 126, (2004)
Rettenmaier, D.: Numerical simulation of shear driven wetting. Ph.D. thesis, TU Darmstadt (2019)
Rettenmaier, D., Deising, D., Ouedraogo, Y., E., G., De Gersem, H., Bothe, D., Tropea, C., Marschall, H.: Load balanced 2d and 3d adaptive mesh refinement in openfoam. SoftwareX 10 (2019)
Schweizer, N., Stephan, P.: Experimental study of bubble behavior and local heat flux in pool boiling under variable gravitational conditions. Multiphase Science and Technology 21, 329–350 (2009)
Scriven, L.E.: On the dynamics of phase growth. Chemical Engineering Science 10, 1–13 (1959)
Son, G., Dhir, V., Ramanujapu, N.: Dynamics and heat transfer associated with a single bubble during nucleate boiling on a horizontal surface. Journal of Heat Transfer 121, 623–631 (1999)
Stephan, P., Busse, C.: Analysis of the heat transfer coefficient of grooved heat pipe evaporator walls. International Journal of Heat and Mass Transfer 35, 383–391 (1992)
Stephan, P., Kern, J.: Evaluation of heat and mass tranfer phenomena in nucleate boiling. International Journal of Heat and Fluid Flow 25, 140–148 (2004)
Urbano, A., Tanguy, S., Colin, C.: Direct numerical simulation of nucleate boiling in zero gravity conditions. International Journal of Heat and Mass Transfer 143, (2019)
Funding
Open Access funding enabled and organized by Projekt DEAL. This research project is funded partially by the European Space Agency (ESA). We would like to thank the German Aerospace Center (DLR) for the financial support in the framework of the “Vapor II project”, grant no. 50WM1959. We kindly acknowledge the financial support by the German Research Foundation (DFG) within the Collaborative Research Centre 1194 “Interaction of Transport and Wetting Processes’
Author information
Authors and Affiliations
Contributions
Benjamin Franz is research assistant at the Institute for Technical Thermodynamics at TU Darmstadt. He performed the simulations and analysis of the data and he drafted the paper. Axel Sielaff is the head of the research group boiling and evaporation and group leader of Mr. Franz at the institute. Peter Stephan is the director of the institute. Mr. Sielaff and Mr. Stephan reviewed the paper and contributed essential suggestions to its content and structure.
Corresponding author
Ethics declarations
Conflicts of Interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Franz, B., Sielaff, A. & Stephan, P. Numerical Investigation of Successively Nucleating Bubbles During Subcooled Flow Boiling of FC-72 in Microgravity. Microgravity Sci. Technol. 33, 27 (2021). https://doi.org/10.1007/s12217-021-09876-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12217-021-09876-6