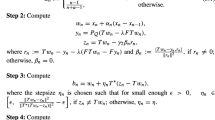Strongly convergent inertial projection and contraction methods for split variational inequality problem

Abstract

In the literature, several methods have been proposed for solving the split variational inequality problems and most of these methods require that the underlying operators are co-coercive while some of them require that the problem is transformed into a product space. These restrictive conditions affect the feasibility of these existing methods. In order to overcome these setbacks, we propose two new inertial projection and contraction methods for solving the split variational inequality problem in real Hilbert spaces without the co-coercive condition and without the product space formulation, which does not fully exploit the attractive splitting structure of the split variational inequality problem. The sequences generated by these methods converge strongly to the solution of the split varitional inequality problems in real Hilbert spaces under the assumptions that the operators are pseudomonotone, Lipschitz continuous and without the sequentially weakly continuity condition. Furthermore, we present several numerical experiments for the proposed methods and compare their performance with other related methods in the literature.

1 Introduction

1.1 Background and literature review

Let ${\mathcal {C}}$ and ${\mathcal {Q}}$ be two nonempty closed and convex subsets of real Hilbert spaces ${\mathcal {H}}_1$ and ${\mathcal {H}}_2$ respectively. Let $T:{\mathcal {H}}_1\rightarrow {\mathcal {H}}_2$ be a bounded linear operator. Let $F:{\mathcal {H}}_1\rightarrow {\mathcal {H}}_1,$ and $A:{\mathcal {H}}_2\rightarrow {\mathcal {H}}_2$ be two operators. The Split Variational Inequality Problem (SVIP) is defined as follows:

Find $x\in {\mathcal {C}}$ such that

$$\begin{aligned} \langle Ax,y-x\rangle \ge 0,~~ \forall ~ y\in {\mathcal {C}} \end{aligned}$$

(1.1)

and $z=Tx \in {\mathcal {Q}}$ solves

$$\begin{aligned} \langle Fz,v-z\rangle \ge 0, ~~\forall ~ v\in {\mathcal {Q}}. \end{aligned}$$

(1.2)

The solution set of the SVIP (1.1)–(1.2) is denoted by $\Gamma :=\Big \{z\in {VI}(A,{\mathcal {C}}): Tz\in {VI}(F,{\mathcal {Q}})\Big \},$ where ${VI}(A,{\mathcal {C}})$ is the solution set of (1.1) and ${VI}(F,{\mathcal {Q}})$ is the solution set of (1.2). Viewing the SVIP separately, we observe that the SVIP comprises of two classical Variational Inequality Problems (VIPs) (1.1)–(1.2). Thus, the SVIP is made up of a pair of VIPs that needs to be solved so that the image of the solution of the VIP $z=Tx$ under a given bounded linear operator T in ${\mathcal {H}}_1$, is a solution of the other VIP in ${\mathcal {H}}_2.$ The SVIP (1.1)–(1.2) is a special model of the following Split Inverse Problem (SIP):

$$\begin{aligned} \text{ Find }~x\in X_1~\text{ that } \text{ solves }~IP_1 \end{aligned}$$

(1.3)

such that

$$\begin{aligned} z=Tx\in X_2~\text{ solves }~IP_2, \end{aligned}$$

(1.4)

where $X_1$ and $X_2$ are two vector spaces, $T:X_1\rightarrow X_2$ is a bounded linear operator, $IP_1$ and $IP_2$ are two inverse problems in $X_1$ and $X_2$, respectively (see [8, 17]). Note that the first known case of the SIP is the following Split Convex Feasibility Problem (SCFP) introduced and studied by Censor and Elfving [15]:

$$\begin{aligned} \text{ Find } ~~x\in {\mathcal {C}}~~\text{ such } \text{ that }~~z=Tx\in {\mathcal {Q}}. \end{aligned}$$

(1.5)

Hence, the SVIP (1.1)–(1.2) can also be viewed as an interesting combination of the classical VIP (1.1) and the SCFP (1.5). Thus, it has wide applications in different fields such as data compression, signal processing, medical treatment of the intensity-modulated radiation therapy (IMRT), medical image reconstruction, phase retrieval, among others (for example, see [6, 7, 21]). Moreover, as special cases, the SVIP includes the split common fixed point problem, the split minimization problem and the split common null point problem (see [26, 36, 38] and references therein).

The classical VIPs have been studied by many researchers due to their applications in diverse fields (see, for example, [10,11,12,13,14, 22, 23, 28, 51]). They have been studied when the assumption on the cost operator is not necessarily co-coercive (see [46]) but very few authors have studied the SVIP when the cost operator is not co-coercive. Censor et al. [16] (see also [17]) proposed an iterative algorithm to solve the SVIP when the cost operators A and F are monotone and Lipschitz continuous. They transformed the SVIP into an equivalent constrained VIP (CVIP) in the product space ${\mathcal {H}}_1\times {\mathcal {H}}_2$ (see [16, Section 4]) and then solved the problem using the well-known subgradient extragradient method [18, 40]. This product space formation has some limitations which include:

• the difficulty encountered when computing the projection onto some new product subspace formulations,

• the difficulty encountered when translating the method back to the original spaces ${\mathcal {H}}_1$ and ${\mathcal {H}}_2,$ and

• the fact that it does not fully exploit the splitting structure of the SVIP (1.1)–(1.2) (see, for example [16, p. 12]).

To circumvent these limitations, Censor et al. [16] proposed a projection-based method that does not require any product space formulation. This makes the projection-based method easier to implement. The proposed projection-based method is presented as follows: For $x_1\in {\mathcal {H}}_1$, the sequence $\{x_n\}$ is generated by

$$\begin{aligned} x_{n+1}=P_{\mathcal {C}}(I-\lambda A)(x_n+\eta T^{*}(P_{\mathcal {Q}}(I-\lambda F)-I)Tx_n),~~ n\ge 1, \end{aligned}$$

(1.6)

where $\eta \in \left( 0,\frac{1}{L}\right)$ with L being the spectral radius of $T^{*}T$ and $T^*$ is the adjoint of T. The identity operator is denoted by I and $P_{{\mathcal {C}}},P_{{\mathcal {Q}}}$ are metric projections onto ${\mathcal {C}},{\mathcal {Q}},$ respectively. They obtained a weak convergence of the sequence $\{x_n\}$ generated by (1.6) to a solution of (1.1)–(1.2) under the condition that the solution set of problem (1.1)–(1.2) is nonempty, A, F are $L_1,L_2$-co-coercive operators respectively, $\lambda \in [0,2\alpha ],$ where $\alpha :=\min \{L_1,L_2\},$ and for all x which are solutions of (1.1),

$$\begin{aligned} \big <Ay,P_{\mathcal {C}}(I-\lambda A)(y)-x\big >\ge 0, ~~ \forall ~y\in {\mathcal {H}}. \end{aligned}$$

(1.7)

Observe that Algorithm (1.6) does not require the product space formation, thus it fully exploits the attractive splitting structure of the SVIP (1.1)–(1.2). However, the authors obtained a weak convergence of this method under some strong assumptions that both mappings are required to be co-coercive and (1.7) holds. Many authors have studied several methods which do not rely on assumption (1.7) for solving SVIP and other related problems (see for example [37]), but their methods also relied on the co-coercivity of the cost operators.

In a quest to overcome these limitations, Tian and Jiang [48] proposed an iterative method and they defined it as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n=P_{{\mathcal {C}}}(x_n-\tau _nT^*(I-S)Tx_n)\\ v_n=P_{{\mathcal {C}}}(y_n-\lambda _n Ay_n)\\ x_{n+1}=P_{{\mathcal {C}}}(y_n-\lambda _n Av_n) \end{array}\right. } \end{aligned}$$

(1.8)

where $\{\tau _n\}\subset [a,b],~~~ \{\lambda _n\}\subset [c,d]$ for some $c,d \in \left( 0,\frac{1}{L}\right) ,~~~ T:{\mathcal {H}}_1\rightarrow {\mathcal {H}}_2$ is a bounded linear operator, $S:{\mathcal {H}}_2\rightarrow {\mathcal {H}}_2$ is a nonexpansive mapping and $A:{\mathcal {C}}\rightarrow {\mathcal {H}}_1$ is a monotone and Lipschitz continuous mapping. They obtained a weak convergence result of the sequence generated by Algorithm (1.8) to the following problem; Find

$$\begin{aligned} x^*\in {\mathcal {C}} \text{ such } \text{ that }\ \langle Ax^*,~x-x^*\rangle ,\ \forall \ x\in {\mathcal {C}}\ \text{ such } \text{ that }\ Tx^*\in F(S) \end{aligned}$$

(1.9)

where F(S) is the set of fixed points of S. Since strong convergence results are more desirable and more applicable than the weak convergence results in infinite dimensional spaces, there is need to develop algorithms that generate strong convergence sequences.

Tian and Jiang [47] modified Algorithm (1.8) into the following viscosity method and they defined it as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n=P_{{\mathcal {C}}}(x_n-\tau _nT^*(I-S)Tx_n)\\ v_n=P_{{\mathcal {C}}}(y_n-\lambda _n Ay_n)\\ t_n=P_{{\mathcal {C}}}(y_n-\lambda _n Av_n)\\ x_{n+1}=\alpha _nhx_n+(1-\alpha _n)t_n \end{array}\right. } \end{aligned}$$

(1.10)

where $\{\tau _n\}\subset [a,b],~~~ \{\lambda _n\}\subset [c,d]$ for some $c,d \in \left( 0,\frac{1}{L}\right) ,~~~ \{\alpha _n\}\subset (0,1),~~~~~ T:{\mathcal {H}}_1\rightarrow {\mathcal {H}}_2$ is a bounded linear operator, $S:{\mathcal {H}}_2\rightarrow {\mathcal {H}}_2$ is a nonexpansive mapping, h is a contraction mapping and $A:{\mathcal {C}}\rightarrow {\mathcal {H}}_1$ is a monotone and Lipschitz continuous mapping. We observe that the conditions on the underlying operators in Algorithms (1.8)–(1.10) does not require the strong co-coercive assumption but it involves computation of many projections which makes them computationally expensive and may affect the efficiency of Algorithms (1.8)–(1.10). Algorithms (1.8)–(1.10) can be used to solve the SVIP (1.1)–(1.2) if we set $S=P_{{\mathcal {Q}}}(I-\lambda F)$ and let A be co-coercive. This implies that when solving the SVIP (1.1)–(1.2), these methods (Algorithm (1.8)–(1.10)) still relies on the co-coercive assumption on the underlying operator A. To weaken the condition on the underlying operators, Pham et al. [42] combined the Halpern method with the subgradient extragradient method for solving the SVIP (1.1)–(1.2) in real Hilbert spaces when the underlying operators A and F are pseudomonotone and Lipschitz continuous. The authors obtained a strong convergence result of their proposed method (see Appendix (6.1)) to a solution of the SVIP (1.1)–(1.2) under the following conditions:

$$\begin{aligned} \limsup \limits _{n\rightarrow \infty } \langle A(x_n), y-y_n\rangle \le \langle A ({\bar{x}}), y-{\bar{y}}\rangle , \end{aligned}$$

for every sequences $\{x_n\}$ and $\{y_n\}$ in ${\mathcal {H}}_1$ converging weakly to ${\bar{x}}$ and ${\bar{y}}$ respectively, and

$$\begin{aligned} \limsup \limits _{n\rightarrow \infty } \langle F(c_n), d-d_n\rangle \le \langle F ({\bar{c}}), d-{\bar{d}}\rangle , \end{aligned}$$

for every sequences $\{c_n\}$ and $\{d_n\}$ in ${\mathcal {H}}_2$ converging weakly to ${\bar{c}}$ and ${\bar{d}}$ respectively. We observe from Appendix (6.1) that the method of Pham et al. [42] involves the computation of two projections onto feasible sets and also two projections per iteration onto half spaces. Also, the knowledge of the bounded linear operator norm is required for the implementation of their method which is usually very difficult to compute and in some cases not known. In this connection, see also [45].

To accelerate the convergence of iterative methods for solving optimization problems, many authors have studied algorithms with inertial extrapolation step due to the improved convergence speed contributed by the presence of the inertial step. These algorithms have been tested in finding solutions of a number of problems and the results showed that the inertial step increases the rate of convergence of these methods (see [9, 31, 32, 50, 52], and other references therein). Recently, Ogwo et al. [39] proposed and studied two new methods with inertial steps for solving the split variational inequality problems in real Hilbert spaces without any product space formulation.

1.2 Motivation

In this paper, we are motivated by a traffic flow network for two cities (see, for example [44]). For City 1, we consider a traffic flow network with $N_1$ number of nodes that are connected by oriented edges. We denote the set of edges of the network and the set of oriented pairs of the nodes by $D_1$ and $W_1$, respectively. Let $w_1=(a_1,b_1)\in W_1$, where $a_1$ and $b_1$ represent the original node and the destination node, respectively, then $P_{w_1}$ is the set of all paths from node $a_1$ to node $b_1$ and $Q_1=\cup _{w_1\in W_1} P_{w_1}$ is the set of all paths in the network. For each path $p_1\in Q_1$, let $z_{p_1}$ be the path flow. We associate each $w_1\in W_1$ with a positive number $d_{w_1}$, which denotes the flow demand from $a_1$ to $b_1$. The feasible set of flows ${\mathcal {C}}$ is defined by

$$\begin{aligned} {\mathcal {C}}=\prod _{w_1\in W_1}{\mathcal {C}}_{w_1}=\{z_1\in {\mathbb {R}}^{|Q_1|}~:~\sum _{p_1\in P_{w_1}} z_{p_1}=d_{w_1},~\forall w_1\in W_1;~z_{p_1}\ge 0,~\forall p_1\in P_{w_1}\}, \end{aligned}$$

where

$$\begin{aligned} {\mathcal {C}}_{w_1}=\{z_1\in {\mathbb {R}}^{|P_{w_1}|}~:~\sum _{p_1\in P_{w_1}} z_{p_1}=d_{w_1},~z_{p_1}\ge 0,~\forall p_1\in P_{w_1}\}. \end{aligned}$$

We can define the value of edge flow $A_{d_1}$ for each edge $d_1\in D_1$ (if the flow vector $z_1$ is known) by

$$\begin{aligned} A_{d_1}=\sum _{p_1\in Q_1} \xi _{p_1d_1} z_{p_1}= \sum _{p_1\in P_{w_1}} \sum _{w_1\in W_1} \xi _{p_1d_1} z_{p_1}, \end{aligned}$$

where

$$\begin{aligned} \xi _{p_1d_1}={\left\{ \begin{array}{ll} 1 &{} \hbox { if}~ d_1 ~\text{ belongs } \text{ to } \text{ path }\ p_1,\\ 0 &{} \text{ otherwise. } \end{array}\right. } \end{aligned}$$

Also, we can define the value of costs for each edge $d_1\in D_1$ by $t_{d_1}=C_{d_1}(A_{d_1})$. Then, the value of costs for each path $p_1$ can be found (see [30]) by

$$\begin{aligned} A_{p_1}(z)=\sum _{d_1\in D_1} \xi _{p_1d_1} t_{d_1}. \end{aligned}$$

Similarly for City 2, the feasible set of flows $\mathcal Q$ is defined by

$$\begin{aligned} {\mathcal {Q}}=\{z_2\in {\mathbb {R}}^{|Q_2|}~:~\sum _{p_2\in P_{w_2}} z_{p_2}=d_{w_2},~\forall w_2\in W_2;~z_{p_2}\ge 0,~\forall p_2\in P_{w_2}\}. \end{aligned}$$

Then, the value of costs for each path $p_2$ can be found by

$$\begin{aligned} F_{p_2}(z)=\sum _{d_2\in D_2} \xi _{p_2d_2} t_{d_2}. \end{aligned}$$

Now, consider $T:{\mathbb {R}}^{|Q_1|}\rightarrow {\mathbb {R}}^{|Q_2|}$, bounded linear operator which connects City 1 to City 2. A feasible flow vector $z_1^*\in {\mathcal {C}}$ is called the equilibrium vector if it satisfies

$$\begin{aligned} \forall q_1\in P_{w_1},~z^*_{q_1}>0 \implies A_{q_1}(z_1^*)=\min _{p_1\in P_{w_1}} A_{p_1}(z_1^*),~\forall w_1\in W_1 \end{aligned}$$

(1.11)

such that $z_2^*=Tz_1^*\in {\mathcal {Q}}$ satisfies

$$\begin{aligned} \forall q_2\in P_{w_2},~z^*_{q_2}>0 \implies F_{q_2}(z_2^*)=\min _{p_2\in P_{w_2}} F_{p_2}(z_2^*),~\forall w_2\in W_2. \end{aligned}$$

(1.12)

This means that when the traffic network is at equilibrium, among all paths of $P_{w_1}$ and $P_{w_1}$, the path with traffic has the lowest cost for each city. It was established in [33] that the feasible flow vector $z_1^*\in {\mathcal {C}}$ satisfies the traffic flow model (1.11)–(1.12) if and only if it solves the SVIP (1.1)–(1.2).

1.3 Contribution

Motivated by the above, our interest in this paper is to introduce and study two new inertial projection and contraction methods for solving the SVIP (1.1)–(1.2) in infinite dimensional real Hilbert spaces when the underlying operators are pseudomonotone and Lipschitz continuous. Our proposed methods for solving the SVIP (1.1)–(1.2) have the following features:

• The choice of the inertial factor in our proposed methods for solving the SVIP (1.1)–(1.2) is new and different from what we have in the literature (see for example [9] and other reference therein).

• Our methods do not require the SVIP (1.1)–(1.2) to be transformed into a product space, rather the methods efficiently and fully exploit the attractive splitting structure of the SVIP (1.1)–(1.2) thereby overcoming potential difficulties posed by the product space formulation.

• Different from the existing methods for solving the SVIP (1.1)–(1.2), our proposed methods only require the underlying operators to be pseudomonotone, Lipschitz continuous and without the sequentially weakly continuity condition often used in the literature.

• Our methods dispense the two extra projections onto half spaces used in [42]. Also, our methods do not depend on the knowledge of the bounded linear operator norm $\Vert T\Vert$ unlike the methods in [16, 42], which require knowledge of the bounded linear operator norm $\Vert T\Vert$. Thus, our methods can be easily implemented since algorithms that depend on the knowledge of the operator norm require computation of the norm of the bounded linear operator, which is difficult to compute and in some cases impossible to compute (see Theorem 2.4).

• The proposed methods include inertial extrapolation step. The inertial step are often employed to increase the convergence speed of algorithms (see [3,4,5, 20, 25] and other references therein).

1.4 Organization of the paper

In Sect. 2, we present certain basic definitions and lemmas that will be required to prove the strong convergence results of our methods. We present and discuss our proposed methods in Sect. 3. In Sect. 4, we present the convergence analysis of these methods. In Sect. 5, we perform some numerical analysis of our methods and compare them with some related methods in the literature and then conclude in Sect. 6.

2 Preliminaries

In this section, we give some lemmas and definitions that will be useful in obtaining our convergence result. We denote the strong and weak convergence by $\rightarrow$ and $\rightharpoonup ,$ respectively. It is known that for a nonempty, closed and convex subset ${\mathcal {C}}$ of ${\mathcal {H}}$, the metric projection denoted by $P_{\mathcal {C}}$ (see [49]), is a map defined on ${\mathcal {H}}$ onto ${\mathcal {C}}$ which assigns to each $x\in {\mathcal {H}}$, the unique point in ${\mathcal {C}}$, denoted by $P_{\mathcal {C}} x$ such that

$$\begin{aligned} ||x-P_{\mathcal {C}}x||=\inf \{||x-y||:~y\in {\mathcal {C}}\}. \end{aligned}$$

The metric projection $P_{\mathcal {C}}$ is characterized by the following inequality:

$$\begin{aligned} \langle x-P_{\mathcal {C}}x, y- P_{\mathcal {C}} x\rangle \le 0,~~\forall ~ y\in {\mathcal {C}}. \end{aligned}$$

Furthermore, the $P_{{\mathcal {C}}}$ is known to possess the following property

$$\begin{aligned} \Vert P_{{\mathcal {C}}}-x\Vert ^2\le \Vert x-y\Vert ^2-\Vert P_{{\mathcal {C}}}x-y\Vert ^2,\hspace{0.2cm} \forall y\in {\mathcal {C}}. \end{aligned}$$

More information on the metric projection can be found, for example, in Section 3 of the book by Goebel and Reich [27] and in the paper by Kopecká and Reich [34].

Lemma 2.1

[1, 41] Let ${\mathcal {H}}$ be a real Hilbert space, then the following assertions hold:

• (1) $2\langle x, y \rangle =\Vert x\Vert ^2+\Vert y\Vert ^2-\Vert x-y\Vert ^2=\Vert x+y\Vert ^2-\Vert x\Vert ^2-\Vert y\Vert ^2,~~\forall x,y \in {\mathcal {H}};$

• (2) $\Vert \alpha x+(1-\alpha )y\Vert ^2 = \alpha \Vert x\Vert ^2+(1-\alpha )\Vert y\Vert ^2-\alpha (1-\alpha )\Vert x-y\Vert ^2,~~\forall x,y \in {\mathcal {H}},~ \alpha \in {\mathbb {R}};$

• (3) $\Vert x-y\Vert ^2 \le \Vert x\Vert ^2+2\langle y, x-y \rangle , ~~\forall x,y \in {\mathcal {H}}.$

Definition 2.2

Let ${\mathcal {H}}$ be a real Hilbert space and $A:{\mathcal {H}}\rightarrow {\mathcal {H}}$ be a mapping. Then, A is said to be

• (i) L-Lipschitz continuous, if there exists $L>0$ such that

  $$\begin{aligned} \Vert Ax-Ay\Vert \le L\Vert x-y\Vert ,~ \forall ~~x,y\in {\mathcal {H}}, \end{aligned}$$

• (ii) L-co-coercive (or L-inverse strongly monotone), if there exists $L>0$ such that

  $$\begin{aligned} \big <Ax-Ay,x-y\big >\ge L\Vert Ax-Ay\Vert ^2,~~ \forall ~x,y \in {\mathcal {H}}, \end{aligned}$$

• (iii) monotone, if

  $$\begin{aligned}\big <Ax-Ay,x-y\big >\ge 0,~~ \forall ~x,y \in {\mathcal {H}}, \end{aligned}$$

• (iv) pseudomonotone, if

  $$\begin{aligned} \big<Ax,y-x \big> \ge 0 \implies ~\big <Ay,y-x \big > \ge 0,~~\forall ~x,y \in {\mathcal {H}}, \end{aligned}$$

• (v) sequentially weakly continuous, if for every sequence $\{x_n\}$ that converges weakly to a point x, the sequence $\{Ax_n\}$ converges weakly to Ax.

We clearly observe that L-co-coercive operators are $\frac{1}{L}$-Lipschitz continuous and monotone but the converse is not always true. We also observe from the definition above that $(ii)\implies (iii)\implies (iv)$ but the converse is not true.

Lemma 2.3

[19] Assume that $A:{\mathcal {H}} \rightarrow {\mathcal {H}}$ is a continuous and pseudomonotone operator. Then, x is a solution of (1.1) if and only if $\langle Ay,y -x \rangle \ge 0,~~ \forall y\in {\mathcal {C}}.$

Theorem 2.4

[29, Theorem 2.3] Let $p\in [1, \infty )$ be a rational number except for $p=1, 2$. Unless $P=NP$, there is no algorithm which computes the p-norm of a matrix with entries in $\{-1, 0, 1\}$ to relative error with running time polynomial in the dimensions.

Lemma 2.5

[43] Let ${\mathcal {C}}\subseteq {\mathcal {H}}$ be a nonempty, closed and convex subset of a real Hilbert space ${\mathcal {H}}.$ Let $u\in {\mathcal {H}}$ be arbitrarily given, $z:=P_{{\mathcal {C}}}u,$ and $\Omega :=\{x\in {\mathcal {H}}:\langle x-u, x-z\rangle \le 0\}.$ Then $\Omega \cap {\mathcal {C}}=\{z\}.$

3 Proposed methods

In this section, we present our proposed methods for solving the SVIP (1.1)–(1.2).

Assumption 3.1

Suppose that the following conditions hold:

• (a) The feasible sets ${\mathcal {C}}$ and ${\mathcal {Q}}$ are nonempty closed and convex subsets of the real Hilbert spaces ${\mathcal {H}}_1$ and ${\mathcal {H}}_2$, respectively.

• (b) $A:{\mathcal {H}}_1 \rightarrow {\mathcal {H}}_1$ and $F:{\mathcal {H}}_2 \rightarrow {\mathcal {H}}_2$ are pseudomonotone and Lipschitz continuous with Lipschitz constants $L_1$ and $L_2$, respectively.

• (c) $A:{\mathcal {H}}_1\rightarrow {\mathcal {H}}_1$ and $F:{\mathcal {H}}_2\rightarrow {\mathcal {H}}_2$ satisfy the following property whenever $\{x_n\}\subset {\mathcal {C}}~~\text {and}~~\{y_n\}\subset {\mathcal {Q}},~~\text {and}~~ x_n\rightharpoonup x,~y_n\rightharpoonup y$ one has $\Vert Ax\Vert \le \liminf \limits _{n\rightarrow \infty }\Vert Ax_n\Vert$ and $\Vert Fy\Vert \le \liminf \limits _{n\rightarrow \infty }\Vert Fy_n\Vert .$

• (d) $T:{\mathcal {H}}_1 \rightarrow {\mathcal {H}}_2$ is a bounded linear operator and the solution set $\Gamma :=\{z\in {{VI}(A,{\mathcal {C}})}: {Tz}\in {{VI}(F,{\mathcal {Q}})}\}$ is nonempty, where ${{VI}(A,{\mathcal {C}})}$ is the solution set of the classical VIP (1.1).

• (e) $\{\alpha _n\}\subset (0,1]$ is non-increasing with $\lim \nolimits _{n\rightarrow \infty }\alpha _n=0$ and $\sum \limits _{n=1}^{\infty }\alpha _n=\infty .$

• (f) $0\le \theta _n\le \theta _{n+1}\le \theta <\frac{1}{3}, \sigma \in (0,\frac{1}{2}].$

• (g) $\{\phi _n\}$ and $\{\psi _n\}$ are non-negative sequences such that $\sum _{n=1}^\infty \phi _n<+\infty$ and $\sum _{n=1}^\infty \psi _n<+\infty .$

When the Lipschitz constants $L_1$ and $L_2$ are known, we present the following method for solving the SVIP (1.1)–(1.2).

Algorithm 3.2

Inertial projection and contraction method with fixed step size.

Step 0: Choose sequences $\{\alpha _n\}^{\infty }_{n=1}$ and $\{\theta _n\}^{\infty }_{n=1}$ such that the conditions from Assumption 3.1(e)–(f) hold and let $\eta \ge 0, \gamma _i\in (0,2),i=1,2,~\mu \in (0,\frac{1}{L_1}),~\lambda \in (0,\frac{1}{L_2}), ~$ and $x_0,x_1 \in {\mathcal {H}}_1$ be given arbitrarily. Set $n:=1.$

Step 1: Given the iterates $x_{n-1}$ and $x_n~~ (n \ge 1),$ $\alpha _n\in (0,1)$ and $\theta _n\in [0,\frac{1}{3}),$ compute

$$\begin{aligned} w_n=\alpha _nx_0+(1-\alpha _n)x_n+\theta _n(x_n-x_{n-1}). \end{aligned}$$

Step 2: Compute

$$\begin{aligned} y_n=P_{\mathcal {Q}}(Tw_n-\lambda FTw_n),\\ z_n=Tw_n-\gamma _2\beta _n r_n, \end{aligned}$$

where $r_n:=Tw_n-y_n-\lambda (FTw_n-Fy_n)$ and $\beta _n:= \frac{\langle Tw_n-y_n,r_n \rangle }{\Vert r_n\Vert ^2},$ if $r_n\ne 0,$ otherwise $\beta _n=0.$

Step 3: Compute

$$\begin{aligned} b_n=w_n+\eta _n T^{*}(z_n-Tw_n), \end{aligned}$$

where the step size $\eta _n$ is chosen such that for some $\epsilon >0,~~~\eta _n\in \Big (\epsilon ,~~ \frac{\Vert Tw_n-z_n\Vert ^2}{\Vert T^{*}(Tw_n-z_n)\Vert ^2}-\epsilon \Big ),$ if $z_n\ne Tw_n;$ otherwise $\eta _n=\eta .$

Step 4: Compute

$$\begin{aligned} u_n= P_{\mathcal {C}} (b_n-\mu Ab_n),\\ t_n=b_n-\gamma _1\gamma _n v_n, \end{aligned}$$

where $v_n:=b_n-u_n-\mu (Ab_n- A u_n)$ and $\gamma _n:=\frac{\langle b_n-u_n,v_n \rangle }{\Vert v_n\Vert ^2},$ if $v_n \ne 0,$ otherwise $\gamma _n=0.$

Step 5: Compute

$$\begin{aligned} x_{n+1}=(1-\sigma )w_n+\sigma t_n. \end{aligned}$$

Set $n:=n+1$ and go back to Step 1.

When the Lipschitz constants $L_1$ and $L_2$ are not known, we present the following method with adaptive step size for solving the SVIP (1.1)–(1.2).

Algorithm 3.3

Inertial projection and contraction method with adaptive step size strategy.

Step 0: Choose the control parameters such that conditions (e)–(g) of Assumption 3.1 hold and let $\eta \ge 0, \gamma _i\in (0,2) ~a_i \in (0,1), i=1,2,$ $\lambda _1>0$, $\mu _1>0$, $\alpha \ge 3$ and $x_0,x_1 \in {\mathcal {H}}_1$ be given arbitrarily. Set $n:=1.$

Step 1: Given the iterates $x_{n-1}$ and $x_n~~ (n \ge 1),$ $\alpha _n\in (0,1)$ and $\theta _n\in [0,\frac{1}{3}),$ compute

$$\begin{aligned} w_n=\alpha _nx_0+(1-\alpha _n)x_n+\theta _n(x_n-x_{n-1}). \end{aligned}$$

Step 2: Compute

$$\begin{aligned} y_n=P_{\mathcal {Q}}(Tw_n-\lambda _n FTw_n),\\ z_n=Tw_n-\gamma _2\beta _n r_n, \end{aligned}$$

where $r_n:=Tw_n-y_n-\lambda _n(FTw_n-Fy_n)$, $\beta _n:= \frac{\langle Tw_n-y_n,r_n \rangle }{\Vert r_n\Vert ^2},$ if $r_n\ne 0,$ otherwise $\beta _n=0;$ and

$$\begin{aligned} \lambda _{n+1}={\left\{ \begin{array}{ll} \min \left\{ \frac{a_2||Tw_n-y_n||}{||FTw_n-Fy_n||},~\lambda _n+\phi _n\right\} ,&{} \text{ if }~FTw_n\ne Fy_n\\ \lambda _n+\phi _n,&{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$

(3.1)

Step 3: Compute

$$\begin{aligned} b_n=w_n+\eta _n T^{*}(z_n-Tw_n), \end{aligned}$$

where the step size $\eta _n$ is chosen such that for some $\epsilon >0,~~~\eta _n\in \Big (\epsilon , ~~\frac{\Vert Tw_n-z_n\Vert ^2}{\Vert T^{*}(Tw_n-z_n)\Vert ^2}-\epsilon \Big ),$ if $z_n\ne Tw_n$; otherwise $\eta _n=\eta .$

Step 4: Compute

$$\begin{aligned} u_n= P_{\mathcal {C}} (b_n-\mu _n Ab_n), \\ t_n=b_n-\gamma _1\gamma _n v_n, \end{aligned}$$

where $v_n:=b_n-u_n-\mu _n(Ab_n- A u_n)$, $\gamma _n=\frac{\langle b_n-u_n,v_n \rangle }{\Vert v_n\Vert ^2},$ if $v_n \ne 0,$ otherwise $\gamma _n=0;$ and

$$\begin{aligned} \mu _{n+1}={\left\{ \begin{array}{ll} \min \left\{ \frac{a_1||b_n-u_n||}{||Au_n-Ab_n||},~\mu _n+\psi _n\right\} ,&{} \text{ if }~Ab_n\ne Au_n\\ \mu _n+\psi _n,&{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$

(3.2)

Step 5: Compute

$$\begin{aligned} x_{n+1}=(1-\sigma )w_n+\sigma t_n. \end{aligned}$$

Set $n:=n+1$ and go back to Step 1.

We outline and discuss some of the properties of our proposed methods.

Remark 3.4

• The choice of the inertial factor $\theta _n\in [0,\frac{1}{3})$ in Algorithms 3.2 and 3.3 is new and different from the choices in literature (see for example [2, 9, 24] and other references therein). As far as we know, this is the first time for which the inertial factor $\theta _n$ is chosen such that $\theta _n\in [0,\frac{1}{3})$ and solves the SVIP when the underlying operators are pseudomonotone and Lipschitz continuous.

• Algorithm 3.3 uses simple step size rules in (3.1) and (3.2), which generate non-monotonic sequences of step sizes. The step sizes are constructed such that the dependence of the algorithm on the initial step sizes $\lambda _1$ and $\mu _1$ is reduced.

• We point out that if the pseudomonotone operators A and F are sequentially weakly continuous, then A and F satisfy condition (c) but the converse is not true. Hence, condition (c) is strictly weaker than the sequentially weakly continuity condition commonly employed in the literature (e.g., see [9, 39]).

• Algorithm 3.2 can be viewed as a modified inertial projection and contraction method involving one projection onto ${\mathcal {C}}$ per iteration for solving the classical VIP in ${\mathcal {H}}_1$. Algorithm 3.3 can be viewed as a modified inertial projection and contraction method involving one projection onto ${\mathcal {Q}}$ per iteration under a bounded linear operator T for solving VIP in ${\mathcal {H}}_2$. Our methods improves other methods in literature which requires extra projections onto half-spaces or feasible sets (see [42] (see Appendix 6.1) and other references therein). In Step 2 of Algorithms 3.2 and 3.3, $r_n$ can be described as weighted average of $(Tw_n-y_n \sim \lambda FTw_n)$ and a hypothetical $(T{\tilde{w}}_n-{\tilde{y}}_n \sim \lambda FT{\tilde{w}}_n)$ in ${\mathcal {H}}_2$, where $T{\tilde{w}}_n=Tw_n-\lambda FTw_n$ and ${\tilde{y}}_n=y_n-\lambda Fy_n$. In Step 4 of Algorithms 3.3 and 3.3, $v_n$ follows similar description. From Step 2 and Step 4 of Algorithms 3.3 and 3.3, we have

  $$\begin{aligned} \beta _n||r_n||^2=\langle Tw_n-y_n, r_n\rangle ,~\forall n\ge 1 \end{aligned}$$

  (3.3)

  holds for both $r_n=0$ and $r_n\ne 0$. Similarly, we have that

  $$\begin{aligned} \gamma _n||v_n||^2=\langle b_n-u_n, v_n\rangle ,~\forall n\ge 1 \end{aligned}$$

  (3.4)

  holds for both $v_n=0$ and $v_n\ne 0$.

• The step sizes $\{\lambda _n\}$ and $\{\mu _n\}$ given by (3.1) and (3.2), respectively are generated at each iteration by some simple computations which makes Algorithm 3.3 easier to implement since it does not require the prior knowledge of the Lipschitz constants $L_1$ and $L_2$.

• Algorithms 3.2 and 3.3 does not require any product space formulation unlike other algorithms in literature which require that the problem be transformed into a product space (see [16] and other references therein). This makes our algorithms easier to implement since they do not encounter the difficulties that might be caused by the product space.

Remark 3.5

[39] The choice of the step size $\eta _n$ in Step 3 of Algorithms 3.2 and 3.3 do not require the prior knowledge of the operator norm $\Vert T\Vert .$ Furthermore, the value of $\eta$ does not influence the algorithms, but it was introduced for the sake of clarity.

Lemma 3.6

[39] The step size $\eta _n$ given in Step 3 of Algorithms 3.2 and 3.3 is well-defined.

4 Convergence analysis

Lemma 4.1

Let $\{x_n\}$ be a sequence generated by Algorithm 3.2 under Assumption 3.1. Then, the following inequality holds:

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2\le \Vert w_n-p\Vert ^2-\Vert x_{n+1}-w_n\Vert ^2,\hspace{0.2cm}\forall ~ p\in \Gamma . \end{aligned}$$

(4.1)

Proof

Let $p\in \Gamma .$ From the definition of $y_n$ and the characteristic property of $P_Q,$ we obtain

$$\begin{aligned} \langle y_n-Tw_n+\lambda FTw_n, ~~y_n-Tp\rangle \le 0. \end{aligned}$$

(4.2)

Since $Tp\in {VI}(F,Q)$ and $y_n\in Q,$ we have

$$\begin{aligned} \langle FTp, y_n-Tp\rangle \ge 0 \end{aligned}$$

and from the pseudomonotonicity of F we have,

$$\begin{aligned} \langle Fy_n, y_n-Tp\rangle \ge 0. \end{aligned}$$

Since $\lambda >0,$ we obtain

$$\begin{aligned} \langle \lambda Fy_n,y_n-Tp\rangle \ge 0. \end{aligned}$$

(4.3)

Adding (4.2) and (4.3), we obtain

$$\begin{aligned} \langle Tw_n-y_n-\lambda (FTw_n-Fy_n),y_n-Tp\rangle \ge 0. \end{aligned}$$

(4.4)

From (4.4) and the definition of $r_n$ in Step 2, we obtain

$$\begin{aligned} \langle Tw_n-Tp, r_n \rangle= & {} \langle Tw_n-y_n, r_n\rangle +\langle y_n-Tp,r_n\rangle \\= & {} \langle Tw_n-y_n,r_n\rangle +\langle y_n-Tp, Tw_n-y_n-\lambda (FTw_n-Fy_n)\rangle \\{} & {} \quad \ge \langle Tw_n-y_n,r_n\rangle , \end{aligned}$$

which implies that

$$\begin{aligned} -\langle Tw_n-Tp, r_n \rangle \le -\langle Tw_n-y_n,r_n\rangle . \end{aligned}$$

(4.5)

From the definition of $z_n$ in Step 2, we have

$$\begin{aligned} ||\beta _n \cdot r_n||^2=\gamma _2^{-2}||z_n-Tw_n||^2. \end{aligned}$$

(4.6)

Hence, from Lemma 2.1 (1), (3.3), (4.5) and (4.6) we obtain

$$\begin{aligned} \Vert z_n-Tp\Vert ^2&=\Vert Tw_n-\gamma _2\beta _nr_n-Tp\Vert ^2\nonumber \\&=\Vert Tw_n-Tp\Vert ^2+\gamma _2^2\beta _n^2\Vert r_n\Vert ^2-2\gamma _2\beta _n\langle Tw_n-Tp, r_n \rangle \nonumber \\&\le \Vert Tw_n-Tp\Vert ^2+\gamma _2^2\beta _n ^2\Vert r_n\Vert ^2-2\gamma _2\beta _n\langle Tw_n-y_n,r_n \rangle \nonumber \\&=\Vert Tw_n-Tp\Vert ^2+\gamma _2^2\beta _n ^2\Vert r_n\Vert ^2-2\gamma _2\beta _n \cdot \beta _n\Vert r_n\Vert ^2\nonumber \\&=\Vert Tw_n-Tp\Vert ^2-\gamma _2(2-\gamma _2)\Vert \beta _n\cdot r_n\Vert ^2\nonumber \\&=\Vert Tw_n-Tp\Vert ^2-\gamma _2^{-1}(2-\gamma _2)||z_n-Tw_n||^2. \end{aligned}$$

(4.7)

Also, from Step 3, Lemma 2.1 and (4.7) we obtain

$$\begin{aligned} \Vert b_n-p\Vert ^2&=\Vert w_n-p\Vert ^2+\eta _n^2\Vert T^{*}(z_n-Tw_n)\Vert ^2+2\eta _n\langle w_n-p, T^{*}(z_n-Tw_n)\rangle \nonumber \\&=\Vert w_n-p\Vert ^2+\eta _n^2\Vert T^{*}(z_n-Tw_n)\Vert ^2+2\eta _n\langle Tw_n-Tp, z_n-Tw_n\rangle \nonumber \\&=\Vert w_n-p\Vert ^2+\eta _n^2\Vert T^{*}(z_n-Tw_n)\Vert ^2\nonumber \\&\quad +\eta _n\left[ \Vert z_n-Tp\Vert ^2 -\Vert Tw_n-Tp\Vert ^2-\Vert z_n-Tw_n\Vert ^2\right] \nonumber \\&\le \Vert w_n-p\Vert ^2+\eta _n^2\Vert T^{*}(z_n-Tw_n)\Vert ^2-\eta _n\Vert z_n-Tw_n\Vert ^2 \nonumber \\&= \Vert w_n-p\Vert ^2-\eta _n\left[ \Vert z_n-Tw_n\Vert ^2-\eta _n\Vert T^{*}(z_n-Tw_n)\Vert ^2\right] . \end{aligned}$$

(4.8)

Thus, by the condition on $\eta _n,$ we obtain that

$$\begin{aligned} \Vert b_n-p\Vert ^2 \le \Vert w_n-p\Vert ^2, \end{aligned}$$

Following similar argument used in obtaining (4.7), we obtain

$$\begin{aligned} \Vert t_n-p\Vert ^2&=\Vert b_n-\gamma _1\gamma _nv_n-p\Vert ^2 \nonumber \\&\le \Vert b_n-p\Vert ^2-\gamma _1^{-1}(2-\gamma _1)\Vert t_n-b_n\Vert ^2. \end{aligned}$$

(4.9)

From Step 5 we have,

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2&=\Vert (1-\sigma )w_n+\sigma t_n-p\Vert ^2\nonumber \\&=\Vert (1-\sigma )(w_n-p)+\sigma (t_n-p)\Vert ^2 \nonumber \\&=(1-\sigma )\Vert w_n-p\Vert ^2+\sigma \Vert t_n-p\Vert ^2-(1-\sigma )\sigma \Vert w_n-t_n\Vert ^2. \end{aligned}$$

(4.10)

Substituting (4.9) into (4.10), we have

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2&\le (1-\sigma )\Vert w_n-p\Vert ^2+\sigma \left( \Vert b_n-p\Vert ^2 -\gamma _1^{-1}(2-\gamma _1)\Vert t_n-b_n\Vert ^2\right) \nonumber \\&-(1-\sigma )\sigma \Vert w_n-t_n\Vert ^2\nonumber \\&=(1-\sigma )\Vert w_n-p\Vert ^2+\sigma \Vert b_n-p\Vert ^2\nonumber \\&-\sigma \gamma _1^{-1}(2-\gamma _1)\Vert t_n-b_n\Vert ^2\nonumber \\&-(1-\sigma )\sigma \Vert w_n-t_n\Vert ^2 \nonumber \\&\le (1-\sigma )\Vert w_n-p\Vert ^2+\sigma \Vert w_n-p\Vert ^2-\sigma \gamma _1^{-1}(2-\gamma _1)\Vert t_n-b_n\Vert ^2\nonumber \\&-(1-\sigma )\sigma \Vert w_n-t_n\Vert ^2 \nonumber \\&=\Vert w_n-p\Vert ^2-\sigma \gamma _1^{-1}(2-\gamma _1)\Vert t_n-b_n\Vert ^2\nonumber \\&-(1-\sigma )\sigma \Vert w_n-t_n\Vert ^2. \end{aligned}$$

(4.11)

From Step 4, we have $t_n-w_n=\frac{1}{\sigma }(x_{n+1}-w_n).$ Substituting this into the previous equality we have,

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2&\le \Vert w_n-p\Vert ^2-\sigma \gamma _1^{-1}(2-\gamma _1)\Vert t_n-b_n\Vert -(1-\sigma )\sigma \cdot \frac{1}{\sigma ^2}\Vert x_{n+1}-w_n\Vert ^2\\&=\Vert w_n-p\Vert ^2-\sigma \gamma _1^{-1}(2-\gamma _1)\Vert t_n-b_n\Vert - \Big (\frac{1}{\sigma }-1\Big )\Vert x_{n+1}-w_n\Vert ^2\\&\le \Vert w_n-p\Vert ^2-\Big (\frac{1}{\sigma }-1\Big )\Vert x_{n+1}-w_n\Vert ^2\\&\le \Vert w_n-p\Vert -\zeta \Vert x_{n+1}-w_n\Vert ^2, \end{aligned}$$

where $\zeta :=\Big (\frac{1}{\sigma }-1\Big ).$ $\square$

Lemma 4.2

Let $\{x_n\}$ be a sequence generated by Algorithm 3.2 under Assumption 3.1. Then $\forall \hspace{0.1cm} p\in \Gamma ,$ we have

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2-\Vert x_n-p\Vert ^2&\le \alpha _n\Vert x_n-x_0\Vert ^2+\theta _n\Vert x_n-p\Vert ^2-\theta _{n-1}\Vert x_{n-1}\nonumber \\&\quad -p\Vert ^2-(1-3\theta _{n+1}-\alpha _n)\Vert x_n-x_{n+1}\Vert ^2 \nonumber \\&\quad -2\alpha _n\langle x_n-p, x_n-x_0\rangle -2\theta _{n+1}\Vert x_{n+1}-x_n\Vert ^2\nonumber \\&\quad +2\theta _n\Vert x_n-x_{n-1}\Vert ^2-\alpha _{n+1}\Vert x_0-x_{n+1}\Vert ^2. \end{aligned}$$

(4.12)

Proof

From the definition of $w_n$ and Lemma (2.1) (1), we have

$$\begin{aligned} \Vert w_n-p\Vert ^2&=\Vert \alpha _nx_0+(1-\alpha _n)x_n+\theta _n(x_n-x_{n-1})-p\Vert ^2 \nonumber \\&=\Vert (x_n-p)+\theta _n(x_n-x_{n-1})-\alpha _n(x_n-x_0)\Vert ^2 \nonumber \\&=\Vert x_n-p\Vert ^2+\Vert \theta _n(x_n-x_{n-1})-\alpha _n(x_n-x_0)\Vert ^2\nonumber \\&\quad +2\langle x_n-p,\theta _n(x_n-x_{n-1})-\alpha _n(x_n-x_0)\rangle \nonumber \\&=\Vert x_n-p\Vert ^2+\Vert \theta _n(x_n-x_{n-1})-\alpha _n(x_n-x_0)\Vert ^2\nonumber \\&\quad +2\theta _n\langle x_n-p, x_n-x_{n-1}\rangle -2\alpha _n\langle x_n-p, x_n-x_0\rangle . \end{aligned}$$

(4.13)

Now, replacing p with $x_{n+1}$ in (4.13), we obtain

$$\begin{aligned} \Vert w_n-x_{n+1}\Vert ^2&=\Vert x_n-x_{n+1}\Vert ^2+\Vert \theta _n(x_n-x_{n-1})-\alpha _n(x_n-x_0)\Vert ^2\nonumber \\&\quad +2\theta _n\langle x_n-x_{n+1}, x_n-x_{n-1}\rangle -2\alpha _n\langle x_n-x_{n+1}, x_n-x_0\rangle . \end{aligned}$$

(4.14)

Substituting (4.13) and (4.14) into (4.1) and from the condition on $\sigma$, we have

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2&\le \Vert x_n-p\Vert ^2+\Vert \theta _n(x_n-x_{n-1})-\alpha _n(x_n-x_0)\Vert ^2\nonumber \\&\quad +2\theta _n\langle x_n-p,x_n-x_{n-1}\rangle \nonumber \\&\quad -2\alpha _n\langle x_n-p, x_n-x_0\rangle \\&\quad -\Vert x_n-x_{n+1}\Vert ^2-\Vert \theta _n(x_n-x_{n-1})-\alpha _n(x_n-x_0)\Vert ^2\nonumber \\&\quad -2\theta _n\langle x_n-x_{n+1}, x_n-x_{n-1}\rangle \\&\quad +2\alpha _n\langle x_n-x_{n+1},x_n-x_0\rangle \\&= \Vert x_n-p\Vert ^2+2\theta _n\langle x_n-p, x_n-x_{n-1}\rangle -2\alpha _n\langle x_n-p, x_n-x_0\rangle \nonumber \\&\quad -2\theta _n\langle x_n-x_{n+1},x_n-x_{n-1}\rangle \\&\quad -\Vert x_n-x_{n+1}\Vert ^2+2\alpha _n\langle x_n-x_{n+1},x_n-x_0\rangle \\&=\Vert x_n-p\Vert ^2+2\theta _n\langle x_n-p, x_n-x_{n-1}\rangle \nonumber \\&\quad -2\alpha _n\langle x_n-p,x_n-x_0\rangle \nonumber \\&\quad +\theta _n\Vert x_n-x_{n+1}\Vert ^2+\theta _n\Vert x_n-x_{n-1}\Vert ^2\\&\quad -\theta _n\Vert (x_n-x_{n+1})+(x_n-x_{n-1})\Vert ^2-\Vert x_n-x_{n+1}\Vert ^2\nonumber \\&\quad +2\alpha _n\langle x_n-x_{n+1},x_n-x_0\rangle . \end{aligned}$$

Hence,

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2-\Vert x_n-p\Vert ^2&\le 2\theta _n\langle x_n-p, x_n-x_{n-1}\rangle -2\alpha _n\langle x_n-p, x_n-x_0\rangle \nonumber \\&\quad -(1-\theta _n)\Vert x_n-x_{n+1}\Vert ^2 {+}\theta _n\Vert x_n-x_{n-1}\Vert ^2{-}\theta _n\Vert (x_n-x_{n+1})\nonumber \\&\quad +(x_n-x_{n-1})\Vert ^2+2\alpha _n\langle x_n-x_{n+1},x_n-x_0\rangle . \end{aligned}$$

(4.15)

Applying Lemma 2.1 (1) to (4.15), we obtain

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2-\Vert x_n-p\Vert ^2&\le \theta _n\Vert x_n-x_{n-1}\Vert ^2-(1-\theta _n)\Vert x_n-x_{n+1}\Vert ^2\nonumber \\&\quad -2\alpha _n\langle x_n-p,x_n-x_0\rangle \\&\quad +2\theta _n\langle x_n-p, x_n-x_{n-1}\rangle \nonumber \\&\quad +2\alpha _n\langle x_n-x_{n+1},x_n-x_0\rangle \\&=\theta _n\Vert x_n-x_{n-1}\Vert ^2-(1-\theta _n)\Vert x_n-x_{n+1}\Vert ^2-\nonumber \\&\qquad 2\alpha _n\langle x_n-p,x_n-x_0\rangle -\theta _n\Vert x_{n-1}-p\Vert ^2\\&\quad +\theta _n\Vert x_n-p\Vert ^2+\theta _n\Vert x_n-x_{n-1}\Vert ^2-\alpha _n\Vert x_0-x_{n+1}\Vert \nonumber \\&\quad +\alpha _n\Vert x_{n+1}-x_n\Vert ^2+\alpha _n\Vert x_n-x_0\Vert ^2, \end{aligned}$$

which implies that

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2-\Vert x_n-p\Vert ^2&\le \alpha _n\Big (\Vert x_n-x_0\Vert ^2-\Vert x_0-x_{n+1}\Vert ^2\Big )\nonumber \\&\quad +\theta _n\Big (\Vert x_n-p\Vert ^2-\Vert x_{n-1}-p\Vert ^2\Big )\nonumber \\&\quad -\Big (1-\theta _n-2\theta _{n+1}-\alpha _n\Big )\Vert x_{n+1}-x_n\Vert ^2\nonumber \\&\quad -2\alpha _n\langle x_n-p, x_n-x_0\rangle \nonumber \\&\quad -2\theta _{n+1}\Vert x_{n+1}-x_n\Vert ^2+2\theta _n\Vert x_n-x_{n-1}\Vert ^2. \end{aligned}$$

(4.16)

Using the fact that $\{\theta _n\}$ is non-decreasing and $\{\alpha _n\}$ is non-increasing on (4.16), we obtain (4.12), which is the desired conclusion. $\square$

Lemma 4.3

Let $\{x_n\}$ be a sequence generated by Algorithm 3.2 under Assumption 3.1. Then $\{x_n\}$ is bounded.

Proof

Let $p\in \Gamma ,$ then from (4.12) and Lemma 2.1, we have

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2-\Vert x_n-p\Vert ^2&\le \alpha _n\Vert x_n-x_0\Vert ^2+\theta _n\Vert x_n-p\Vert ^2-\theta _{n-1}\Vert x_{n-1}\nonumber \\&\quad -p\Vert ^2-(1-3\theta _{n+1}-\alpha _n)\Vert x_n-x_{n+1}\Vert ^2\nonumber \\&\quad -2\theta _{n+1}\Vert x_{n+1}-x_n\Vert ^2+2\theta _n\Vert x_n-x_{n-1}\Vert ^2\nonumber \\&\quad -\alpha _{n+1}\Vert x_0-x_{n+1}\Vert ^2-2\alpha _n\langle x_n-p,x_n-x_0\rangle \nonumber \\&=\alpha _n\Vert x_n-x_0\Vert ^2+\theta _n\Vert x_n-p\Vert ^2-\theta _{n+1}\Vert x_{n-1}-p\Vert ^2\nonumber \\&\quad -(1-3\theta _{n+1}-\alpha _n)\Vert x_n-x_{n+1}\Vert ^2 \nonumber \\&\quad -2\theta _{n+1}\Vert x_{n+1}-x_n\Vert ^2+2\theta _n\Vert x_n-x_{n-1}\Vert ^2\nonumber \\&\quad -\alpha _{n+1}\Vert x_0-x_{n+1}\Vert ^2-\alpha _n\Vert x_n-p\Vert ^2 \nonumber \\&\quad -\alpha _n\Vert x_n-x_0\Vert ^2+\alpha _n\Vert x_0-p\Vert ^2 \nonumber \\&\le \theta _n\Vert x_n-p\Vert ^2-\theta _{n-1}\Vert x_{n-1}-p\Vert ^2\nonumber \\&\quad -(1-3\theta _{n+1}-\alpha _n)\Vert x_n-x_{n+1}\Vert ^2-2\theta _{n+1}\Vert x_{n+1}-x_n\Vert ^2 \nonumber \\&\quad +2\theta _n\Vert x_n-x_{n-1}\Vert ^2-\alpha _n\Vert x_n-p\Vert ^2+\alpha _n\Vert x_0-p\Vert ^2.\nonumber \\ \end{aligned}$$

(4.17)

From this we obtain

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2&-\Vert x_n-p\Vert ^2+\alpha _n\Vert x_n-p\Vert ^2\nonumber \\&\le \theta _n\Vert x_n-p\Vert ^2-\theta _{n-1}\Vert x_{n-1}-p\Vert ^2\nonumber \\&\quad -(1-3\theta _{n+1}-\alpha _n)\Vert x_n-x_{n+1}\Vert ^2-2\theta _{n+1}\Vert x_{n+1}-x_n\Vert ^2\nonumber \\&\quad +2\theta _n\Vert x_n-x_{n-1}\Vert ^2+\alpha _n\Vert x_0-p\Vert ^2. \end{aligned}$$

(4.18)

Let $\rho _j:=e^{\sum \limits _{i=1}^{j}\alpha _i}, j\ge 1.$ Since $e^x\ge x+1$ for all $x\in {\mathbb {R}},$ we have

$$\begin{aligned} \frac{1}{\rho _{n+1}}\Big (\rho _{n+1}\Vert x_{n+1}-p\Vert ^2-\rho _n\Vert x_n-p\Vert ^2\Big )&=\Vert x_{n+1}-p\Vert ^2-\Vert x_n-p\Vert ^2\nonumber \\&\quad +\frac{1}{\rho _{n+1}}\Big (\rho _{n+1}-\rho _n\Big )\Vert x_n-p\Vert ^2\\&\le \Vert x_{n+1}-p\Vert ^2{-}\Vert x_n-p\Vert ^2{+}\alpha _{n+1}\Vert x_n-p\Vert ^2. \end{aligned}$$

Since $\{\alpha _n\}\subset (0,1]$ is non-increasing, we have

$$\begin{aligned}&\frac{1}{\rho _{n+1}}\Big (\rho _{n+1}\Vert x_{n+1}-p\Vert ^2-\rho _n\Vert x_n-p\Vert ^2\Big ) \nonumber \\&\quad \le \Vert x_{n+1}-p\Vert ^2-\Vert x_n-p\Vert ^2+\alpha _n\Vert x_n-p\Vert ^2. \end{aligned}$$

(4.19)

From (4.18) and (4.19), we obtain

$$\begin{aligned} \frac{1}{\rho _{n+1}}\Big [\rho _{n+1}\Vert x_{n+1}-p\Vert ^2-\rho _n\Vert x_n-p\Vert ^2\Big ]&\le \theta _n\Vert x_n-p\Vert ^2-\theta _{n-1}\Vert x_{n-1}-p\Vert ^2\\&\quad -(1-3\theta _{n+1}-\alpha _n)\Vert x_{n+1}-x_n\Vert ^2\\&\quad -2\theta _{n+1}\Vert x_{n+1}-x_n\Vert ^2\\&\quad +2\theta _n\Vert x_n-x_{n-1}\Vert ^2+\alpha _n\Vert x_0-p\Vert ^2. \end{aligned}$$

Since $\rho _n\le \rho _{n+1}, \rho _{n+1}=\rho _ne^{\alpha _{n+1}}$ and $\{\alpha _n\}\subset (0,1]$ is non-increasing, we have

$$\begin{aligned} \rho _{n+1}\Vert x_{n+1}-p\Vert ^2-\rho _n\Vert x_n-p\Vert ^2&\le \rho _{n+1}\theta _n\Vert x_n-p\Vert ^2-\rho _n\theta _{n-1}\Vert x_{n-1}-p\Vert ^2\\&\quad -\rho _{n+1}(1-3\theta _{n+1}-\alpha _n)\Vert x_{n+1}-x_n\Vert ^2\\&\quad -2\rho _{n+1}\theta _{n+1}\Vert x_{n+1}-x_n\Vert ^2\\&\quad +2\rho _n\theta _ne^{\alpha _{n+1}}\Vert x_n-x_{n-1}\Vert ^2+\rho _{n+1}\alpha _n\Vert x_0-p\Vert ^2, \end{aligned}$$

which implies that

$$\begin{aligned}&\rho _{n+1}\Vert x_{n+1}-p\Vert ^2-\rho _n\Vert x_n-p\Vert ^2\\&\quad \le \rho _{n+1}\theta _n\Vert x_n-p\Vert ^2-\rho _n\theta _{n-1}\Vert x_{n-1}-p\Vert ^2\\&\qquad -\rho _{n+1}\big [1-\theta _{n+1}\big (3+2(e^{\alpha _{n+1}}-1)\big )-\alpha _n\big ]\Vert x_{n+1}-x_n\Vert ^2\\&\qquad -2\rho _{n+1}\theta _{n+1}e^{\alpha _{n+1}}\Vert x_{n+1}-x_n\Vert ^2+2\rho _n\theta _ne^{\alpha _n}\Vert x_n-x_{n-1}\Vert ^2\\&\qquad +\rho _{n+1}\alpha _n\Vert x_0-p\Vert ^2. \end{aligned}$$

Since $\{\theta _n\}\subset [0,\theta ],$ we have

$$\begin{aligned} 1-\theta _{n+1}(3+2(e^{\alpha _{n+1}}-1))-\alpha _n\ge 1-\theta (3+2(e^{\alpha _{n+1}}-1))-\alpha _n,\quad \forall n\in {\mathbb {N}}. \end{aligned}$$

(4.20)

Since $\theta \in [0,\frac{1}{3})$ and $\lim \nolimits _{n\rightarrow \infty }\alpha _n=0,$ it follows that the right-hand side of (4.20) is bounded below by a positive number, i.e., there exists a constant $\xi >0$ such that $1-\theta _{n+1}(3+2(e^{\alpha _{n+1}}-1))-\alpha _n \ge \xi ,$ for all $n\in {\mathbb {N}}$ sufficiently large, say for all $n\ge n_0.$ Hence, we have

$$\begin{aligned} \rho _{n+1}\Vert x_{n+1}-p\Vert ^2-\rho _n\Vert x_n-p\Vert ^2&\le \rho _{n+1}\theta _n\Vert x_n-p\Vert ^2-\rho _n\theta _{n-1}\Vert x_{n-1}-p\Vert ^2\\&\quad -\xi \Vert x_{n+1}-x_n\Vert ^2\\&\quad -2\rho _{n+1}\theta _{n+1}e^{\alpha _{n+1}}\Vert x_{n+1}-x_n\Vert ^2\\&\quad +2\rho _n\theta _ne^{\alpha _n}\Vert x_n-x_{n-1}\Vert ^2\\&\quad +\rho _{n+1}\alpha _n\Vert x_0-p\Vert ^2, \end{aligned}$$

which implies that for all $n\ge n_0,$

$$\begin{aligned} \Vert x_0-p\Vert ^2\sum \limits _{k=n_{0}+1}^{n}\rho _{k+1}\alpha _k&\ge \rho _{n+1}\Vert x_{n+1}-p\Vert ^2 + 2\rho _{n+1}\theta _{n+1}e^{\alpha _{n+1}}\Vert x_{n+1}-x_n\Vert ^2\nonumber \\&\quad - \rho _{n+1}\theta _n\Vert x_n-p\Vert ^2-\rho _{n_0+1}\Vert x_{n_0+1}-p\Vert ^2 \nonumber \\&\quad - 2\rho _{n_0+1}\theta _{n_0+1}e^{\alpha _{n_0+1}}\Vert x_{n_0+1}-x_{n_0}\Vert ^2 \nonumber \\&\quad + \rho _{n_0+1}\theta _{n_0}\Vert x_{n_0}-p\Vert ^2. \end{aligned}$$

(4.21)

Dividing the last inequality by $\rho _{n+1}$ and omitting non-positive terms, we have

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2-\theta _n\Vert x_n-p\Vert ^2&\le e^{-t_{n}+1}\Big [\rho _{n_{0}+1}\Vert x_{n_{0}+1}-p\Vert ^2+2\rho _{n_{0}+1}\theta _{n_{0}+1}e^{\alpha _{n_{0}+1}}\nonumber \\&\quad \times \Vert x_{n_{0}+1} -x_{n_0}\Vert ^2-\rho _{n_{0}+1}\theta _{n_0}\Vert x_{n_0}-p\Vert ^2\Big ]\nonumber \\&\quad +\Vert x_0-p\Vert ^2e^{-t_{n}+1}\sum \limits _{k=n_{0}+1}^{n}\alpha _ke^{t_k+1} \end{aligned}$$

(4.22)

where $t_n:=\sum _{i=1}^{n}\alpha _i.$ Since $\alpha _k\in (0,1]$ for all $k\in {\mathbb {N}},$ we observe that $\alpha _ke^{t_k+1}\le e^2(e^{t_k}-e^{t_k-1}),$ for all $k\ge 2,$ so that

$$\begin{aligned} \sum \limits _{k=n_{0}+1}^{n}\rho _{k+1}\alpha _k=\sum \limits _{k=n_{0}+1}^{n}\alpha _ke^{t_k+1}\le e^2(e^{t_n}-e^{t_{n_{0}}})\le e^2e^{t_n}. \end{aligned}$$

Using (4.22), the fact that $\{\theta _n\}\subset [0,\theta ]\subset [0,\frac{1}{3})$ and $e^{-t_n+1}\le 1,$ we have

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2\le&\theta \Vert x_n-p\Vert ^2+\rho _{n_{0}+1}\Vert x_{n_{0}+1}-p\Vert ^2\nonumber \\&+2\rho _{n_{0}+1} \theta _{n_{0}+1}e^{\alpha _{n_{0}+1}}\Vert x_{{n_0}+1}-x_{n_{0}}\Vert ^2+e^2\Vert x_0-p\Vert ^2. \end{aligned}$$

(4.23)

Applying (4.23), $\theta \in [0,1)$ and the convergence of the geometric series, we obtain

$$\begin{aligned} \Vert x_{n+1}&-p\Vert ^2\le \theta ^{n-n_0}\Vert x_{n_{0}+1}-p\Vert ^2\nonumber \\&\quad +\frac{1}{1-\theta }\Big [\rho _{n_{0}+1}\Vert x_{n_{0}+1}\nonumber \\&\quad -p\Vert ^2+2\rho _{n_{0}+1}\theta _{n_{0}+1}e^{\alpha _{n_{0}+1}}\Vert x_{{n_0}+1}-x_{n_{0}}\Vert ^2+e^2\Vert x_0-p\Vert ^2\Big ] \end{aligned}$$

(4.24)

Since $\theta <1,$ it follows that $\{x_n\}$ is bounded.

$\square$

Lemma 4.4

Let $\{x_n\}$ be a sequence generated by Algorithm 3.2 under Assumption 3.1. Suppose

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\Vert x_{n+1}-x_n\Vert =0 \end{aligned}$$

and

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\Big (\Vert x_{n+1}-p\Vert ^2-\theta _n\Vert x_n-p\Vert ^2\Big )=0. \end{aligned}$$

Then $\{x_n\}$ converges strongly to p.

Proof

By the hypothesis of the lemma we have that

$$\begin{aligned} 0&=\lim \limits _{n\rightarrow \infty }\Big (\Vert x_{n+1}-p\Vert ^2-\theta _n\Vert x_n-p\Vert ^2\Big )=\lim \limits _{n\rightarrow \infty }\Big [\Big (\Vert x_{n+1}-p\Vert \nonumber \\&\quad +\sqrt{\theta _n}\Vert x_n-p\Vert \Big )\Big (\Vert x_{n+1}-p\Vert -\sqrt{\theta _n}\Vert x_n-p\Vert \Big )\Big ]. \end{aligned}$$

(4.25)

We claim that this implies

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\Big (\Vert x_{n+1}-p\Vert +\sqrt{\theta _n}\Vert x_n-p\Vert \Big )=0, \end{aligned}$$

and from this it follows that $\{x_n\}$ converges strongly to p. On the contrary, assume that this limit does not hold. Then there exists a subset $K\subseteq {\mathbb {N}}$ and a constant $\beta >0$ such that

$$\begin{aligned} \Vert x_{n+1}-p\Vert +\sqrt{\theta _n}\Vert x_n-p\Vert \ge \beta , \forall ~ n\in K. \end{aligned}$$

(4.26)

Using (4.25) and the fact that $\theta _n\le \theta <1,$ we have

$$\begin{aligned} 0&=\lim \limits _{n\in K}\Big (\Vert x_{n+1}-p\Vert -\sqrt{\theta _n}\Vert x_n-p\Vert \Big )\\&=\limsup \limits _{n\in K}\Big (\Vert x_{n+1}-x_n+x_n-p\Vert -\sqrt{\theta _n}\Vert x_n-p\Vert \Big )\\&\ge \limsup \limits _{n\in K}\Big (\Vert x_n-p\Vert -\Vert x_{n+1}-x_n\Vert -\sqrt{\theta _n}\Vert x_n-p\Vert \Big )\\&\ge \limsup \limits _{n\in K}\Big ( (1-\sqrt{\theta })\Vert x_n-p\Vert -\Vert x_{n+1}-x_n\Vert \Big )\\&=(1-\sqrt{\theta })\limsup \limits _{n\in K}\Vert x_n-p\Vert -\lim \limits _{n\in K}\Vert x_{n+1}-x_n\Vert \\&=(1-\sqrt{\theta })\limsup \limits _{n\in K}\Vert x_n-p\Vert . \end{aligned}$$

Thus, we have $\limsup \limits _{n\in K}\Vert x_n-p\Vert \le 0.$ Since $\liminf \limits _{n\in K}\Vert x_n-p\Vert \ge 0$ holds, it follows that $\lim \nolimits _{n\in K}\Vert x_n-p\Vert =0.$

Applying (4.26), we obtain

$$\begin{aligned} \Vert x_{n+1}-x_n\Vert&\ge \Vert x_{n+1}-p\Vert -\Vert x_n-p\Vert \\&=\Vert x_{n+1}-p\Vert +\sqrt{\theta _n}\Vert x_n-p\Vert -(1+\sqrt{\theta _n})\Vert x_n-p\Vert \\&\ge \frac{\beta }{2} \end{aligned}$$

for all $n\in K$ sufficiently large, which contradicts the assumption that $\lim \nolimits _{n\rightarrow \infty }\Vert x_{n+1}-x_n\Vert =0.$ Hence, the result follows.

$\square$

Lemma 4.5

Let $\{x_n\}$ be a sequence generated by Algorithm 3.2 under Assumption 3.1 such that $\lim \nolimits _{n\rightarrow \infty }\Vert x_{n+1}-x_n\Vert =0.$ Suppose there exists a subsequence $\{x_{n_k}\}$ of $\{x_n\},$ which converges weakly to a point $z\in {\mathcal {H}}_1$ and $\lim \nolimits _{k \rightarrow \infty }\Vert b_{n_k}-w_{n_k}\Vert =0=\lim \limits _{k \rightarrow \infty }\Vert b_{n_k}-t_{n_k}\Vert ,$ then $z\in \Gamma .$

Proof

From the definition of $w_n$ in Step 1 and by the statement of the hypothesis together with the fact that $\lim \nolimits _{n \rightarrow \infty }\alpha _n=0,$ we obtain

$$\begin{aligned} \Vert w_n-x_n\Vert&=\Vert \alpha _n(x_0-x_n)+\theta _n(x_n-x_{n-1})\Vert \nonumber \\&\le \alpha _n\Vert x_0-x_n\Vert +\theta _n\Vert x_n-x_{n-1}\Vert \rightarrow 0, \hspace{0.5cm} \text {as}\hspace{0.2cm} n\rightarrow \infty \end{aligned}$$

(4.27)

Since the subsequence $\{x_{n_k}\}$ of $\{x_n\}$ is weakly convergent to a point $z\in {\mathcal {H}}_1,$ it follows that the subsequence $\{w_{n_k}\}$ of $\{w_n\}$ is also weakly convergent to $z\in {\mathcal {H}}_1.$ Again, since T is a bounded linear operator, we obtain that $\{Tw_{n_k}\}$ converges weakly to Tz.

Without loss of generality, we may assume that $z_n\ne Tw_n,$ then $\eta _n \in \Big (\epsilon , \frac{\Vert z_n-Tw_n\Vert ^2}{\Vert T^{*}(z_n-Tw_n)\Vert ^2}-\epsilon \Big ).$

Hence, we obtain from (4.8) that

$$\begin{aligned} \Vert b_{n_k}-p\Vert ^2&\le \Vert w_{n_k}-p\Vert ^2-\eta _{n_k} \epsilon \Vert T^{*}(z_{n_k}-Tw_{n_k})\Vert ^2 \nonumber \\&\le \Vert w_{n_k}-p\Vert ^2-\epsilon ^2\Vert T^{*}(z_{n_k}-Tw_{n_k})\Vert ^2, \end{aligned}$$

(4.28)

which implies that

$$\begin{aligned} \epsilon ^2\Vert T^{*}(z_{n_k}-Tw_{n_k})\Vert ^2&\le \Vert w_{n_k}-p\Vert ^2-\Vert b_{n_k}-p\Vert ^2\\&\le \Vert w_{n_k}-b_{n_k}\Vert ^2+2\Vert w_{n_k}-b_{n_k}\Vert \Vert b_{n_k}-p\Vert . \end{aligned}$$

From our hypothesis, we have

$$\begin{aligned} \lim \limits _{k \rightarrow \infty }\Vert T^{*}(z_{n_k}-Tw_{n_k})\Vert =0. \end{aligned}$$

(4.29)

From (4.8) and (4.29), we have

$$\begin{aligned} \eta _{n_k}\Vert z_{n_k}-Tw_{n_k}\Vert ^2&\le \Vert w_{n_k}-p\Vert ^2\\&\quad -\Vert b_{n_k}-p\Vert ^2+\eta _{n_k} ^2\Vert T^{*}(z_{n_k}-Tw_{n_k})\Vert ^2\\&\le \Vert w_{n_k}-b_{n_k}\Vert ^2+2\Vert w_{n_k}-b_{n_k}\Vert \Vert b_{n_k}-p\Vert \\&\quad +\eta _{n_k}^2\Vert T^{*}(z_{n_k}-Tw_{n_k})\Vert ^2 \rightarrow 0, ~~\text {as}~~~ k \rightarrow \infty . \end{aligned}$$

Since $\eta _{n_k}>\epsilon >0,$ we obtain

$$\begin{aligned} \lim \limits _{k \rightarrow \infty }\Vert z_{n_k}-Tw_{n_k}\Vert =0. \end{aligned}$$

(4.30)

Using the definition of $r_n$ in Step 2, we observe

$$\begin{aligned} \langle Tw_{n_k}-y_{n_k},r_{n_k}\rangle&=\langle Tw_{n_k}-y_{n_k}, Tw_{n_k}-y_{n_k}-\lambda (FTw_{n_k}-Fy_{n_k})\rangle \nonumber \\&=\Vert Tw_{n_k}-y_{n_k}\Vert ^2-\langle Tw_{n_k}-y_{n_k}, \lambda (FTw_{n_k}-Fy_{n_k})\rangle \nonumber \\&\ge \Vert Tw_{n_k}-y_{n_k}\Vert ^2-\lambda \Vert Tw_{n_k}-y_{n_k}\Vert \Vert FTw_{n_k}-Fy_{n_k}\Vert \nonumber \\&\ge (1-\lambda L_2)\Vert Tw_{n_k}-y_{n_k}\Vert ^2. \end{aligned}$$

(4.31)

Since $\lambda \in (0, \frac{1}{L_2})$, we have that $1-\lambda L_2>0$. Hence, from (4.31), (4.6) and (3.3) we obtain

$$\begin{aligned} \Vert Tw_{n_k}-y_{n_k}\Vert ^2&\le \left( \frac{1}{1-\lambda L_2}\right) \langle Tw_{n_k}-y_{n_k},r_{n_k}\rangle \\&=\left( \frac{1}{1-\lambda L_2}\right) \beta _{n_k}\Vert r_{n_k}\Vert ^2\\&=\left( \frac{1}{1-\lambda L_2}\right) \beta _{n_k}\Vert r_{n_k}\Vert \Vert Tw_{n_k}-y_{n_k}-\lambda (FTw_{n_k}-Fy_{n_k})\Vert \\&=\left( \frac{1}{1-\lambda L_2}\right) \beta _{n_k}\Vert r_{n_k}\Vert \Vert (Tw_{n_k}-y_{n_k})+\lambda (Fy_{n_k}-FTw_{n_k})\Vert \\&\le \left( \frac{1}{1-\lambda L_2}\right) \beta _{n_k}\Vert r_{n_k}\Vert \left( \Vert Tw_{n_k}-y_{n_k}\Vert +\lambda \Vert Fy_{n_k}-FTw_{n_k}\Vert \right) \\&\le \left( \frac{1}{1-\lambda L_2}\right) \beta _{n_k}\Vert r_{n_k}\Vert \left( \Vert Tw_{n_k}-y_{n_k}\Vert +\lambda L_2\Vert y_{n_k}-Tw_{n_k}\Vert \right) \\&= \left( \frac{1+\lambda L_2}{1-\lambda L_2}\right) \Vert Tw_{n_k}-y_{n_k}\Vert \beta _{n_k}\Vert r_{n_k}\Vert \\&=\gamma _2^{-1}\left( \frac{1+\lambda L_2}{1-\lambda L_2}\right) \Vert Tw_{n_k}-y_{n_k}\Vert \Vert z_{n_k}-Tw_{n_k}\Vert , \end{aligned}$$

which implies from (4.30) that

$$\begin{aligned} \Vert Tw_{n_k}-y_{n_k}\Vert \le \gamma _2^{-1} \left( \frac{1+\lambda L_2}{1-\lambda L_2}\right) \Vert Tw_{n_k}-z_{n_k}\Vert \rightarrow 0,~~\text {as}~~ k \rightarrow \infty . \end{aligned}$$

(4.32)

Since $\{Tw_{n_k}\}$ converges weakly to Tz,  then it follows from (4.32) that $\{y_{n_k}\}$ also converges weakly to Tz. Also, since $\{y_{n_k}\}\subset {\mathcal {Q}},$ we have that $Tz\in {\mathcal {Q}}$.

By the characteristic property of $P_{\mathcal {Q}},$ we obtain $\forall ~ x\in {\mathcal {Q}}$ that

$$\begin{aligned} \langle Tw_{n_k}-\lambda FTw_{n_k}-y_{n_k},x-y_{n_k}\rangle \le 0, \end{aligned}$$

which implies

$$\begin{aligned} \frac{1}{\lambda }\langle Tw_{n_k}-y_{n_k},x-y_{n_k}\rangle +\langle FTw_{n_k},y_{n_k}-Tw_{n_k} \rangle \le \langle FTw_{n_k},x-Tw_{n_k}\rangle . \end{aligned}$$

(4.33)

Hence, applying (4.32) in (4.33), we obtain that

$$\begin{aligned} 0\le \liminf \limits _{k \rightarrow \infty }\langle FTw_{n_k},x-Tw_{n_k}\rangle , ~\forall x\in {\mathcal {Q}}. \end{aligned}$$

(4.34)

Observe that

$$\begin{aligned} \langle Fy_{n_k}, x-y_{n_k}\rangle= & {} \langle Fy_{n_k}-FTw_{n_k}, x-Tw_{n_k}\rangle + \langle FTw_{n_k}, x-Tw_{n_k}\rangle \nonumber \\{} & {} +\langle Fy_{n_k}, Tw_{n_k}-y_{n_k}\rangle . \end{aligned}$$

(4.35)

Since F is Lipschitz continuous on ${\mathcal {H}}_2$, we obtain from (4.32) that

$$\begin{aligned} \lim _{k\rightarrow \infty }||FTw_{n_k}-Fy_{n_k}||=0. \end{aligned}$$

Hence, from (4.32), (4.34) and (4.35), we obtain that

$$\begin{aligned} 0\le \liminf \limits _{k \rightarrow \infty }\langle Fy_{n_k},x-y_{n_k}\rangle , ~\forall x\in {\mathcal {Q}}. \end{aligned}$$

(4.36)

Next, we show that $Tz \in \text{ VI }(F,{\mathcal {Q}}).$ Now, we choose a sequence $\{\delta _k\}$ of positive numbers such that $\delta _{k+1}\le \delta _k,~~~\forall ~ k\ge 1$ and $\delta _k \rightarrow 0~~ \text {as}~~~ k \rightarrow \infty .$ From (4.36), we denote by $N_k$ (for each $k\ge 1$), the smallest positive integer such that

$$\begin{aligned} \langle Fy_{n_j},x-y_{n_j}\rangle +\delta _k\ge 0, ~~~\forall j\ge N_k. \end{aligned}$$

(4.37)

Since $\{\delta _k\}$ is decreasing, we have that $\{N_k\}$ is increasing. Also, since $\{y_{N_k}\}\subset {\mathcal {Q}}$ for all $k\ge 1$, we can suppose $Fy_{N_k}\ne 0$ (otherwise, $y_{N_k}$ is a solution). Hence, we can set $q_{N_k}=\frac{Fy_{N_k}}{\Vert Fy_{N_k}\Vert ^2}$ for each $k \ge 1$. Then, $\langle Fy_{N_k}, q_{N_k}\rangle =1$ for each $k\ge 1.$

Therefore, from (4.37) we have

$$\begin{aligned} \langle Fy_{N_k}, x+\delta _kq_{N_k}-y_{N_k}\rangle \ge 0, \end{aligned}$$

which implies from the pseudomonotonicity of F on ${\mathcal {H}}_2$ that

$$\begin{aligned} \langle F(x+\delta _kq_{N_k}),x+\delta _kq_{N_k}-y_{N_k}\rangle \ge 0. \end{aligned}$$

(4.38)

This implies that

$$\begin{aligned} \langle Fx, x-y_{N_k}\rangle \ge \langle Fx-F(x+\delta _kq_{N_k}), x+\delta _kq_{N_k}-y_{N_k}\rangle -\delta _k\langle Fx, q_{N_k}\rangle . \end{aligned}$$

(4.39)

Now, if $FTz=0,$ then $Tz\in {VI}(F,{\mathcal {Q}}).$ So, we may suppose that $FTz\ne 0.$ Since $\{y_{n_k}\}$ converges weakly to Tz,  then by Condition (c) we obtain

$$\begin{aligned} 0< \Vert FTz\Vert \le \liminf \limits _{k \rightarrow \infty }\Vert Fy_{N_k}\Vert . \end{aligned}$$

Since $\{y_{n_k}\}\subset \{y_{N_k}\},$ we obtain that

$$\begin{aligned} 0&\le \limsup \limits _{k \rightarrow \infty }\Vert \delta _kq_{N_k}\Vert =\limsup \limits _{k \rightarrow \infty }\left( \frac{\delta _k}{\Vert Fy_{n_k}\Vert }\right) \le \frac{\limsup \limits _{k \rightarrow \infty }\delta _k}{\liminf \limits _{k\rightarrow \infty }\Vert Fy_{n_k}\Vert } \le \frac{0}{\Vert FTz\Vert }=0. \end{aligned}$$

Therefore, $\lim \nolimits _{k \rightarrow \infty } \delta _kq_{N_k}=0.$ Thus, letting $k\rightarrow \infty$ in (4.39), we have

$$\begin{aligned} \langle Fx, x-Tz\rangle \ge 0, ~~ \forall x\in Q, \end{aligned}$$

(4.40)

which implies by Lemma 2.3 that $Tz\in {VI}(F,Q).$

Next, we show that $z\in {VI}(A, C)$. Following similar method of proof used in obtaining (4.32) and noting our hypothesis $\lim \nolimits _{k\rightarrow \infty }\Vert b_{n_k}-t_{n_k}\Vert =0$, we obtain

$$\begin{aligned} \Vert b_{n_k}-u_{n_k}\Vert \le r_1^{-1} \left( \frac{1+\mu L_1}{1+\mu L_1}\right) \Vert b_{n_k}-t_{n_k}\Vert \rightarrow 0,~~ \text {as}~~~ k\rightarrow \infty . \end{aligned}$$

(4.41)

Following similar method of proof used in obtaining (4.36), we obtain from (4.41), the characteristic property of $P_{\mathcal {C}}$ and the Lipschitz continuity of A on ${\mathcal {H}}_1$ that

$$\begin{aligned} 0\le \liminf \limits _{k \rightarrow \infty }\langle Au_{n_k},y-u_{n_k}\rangle , ~\forall y\in C. \end{aligned}$$

(4.42)

From our hypothesis, (4.41) and the fact that $\{w_{n_k}\}$ converges weakly to z,  we obtain that the subsequences $\{b_{n_k}\}$ and $\{u_{n_k}\}$ of $\{b_n\}$ and $\{u_n\}$ respectively, converge weakly to z. Also, since $\{u_{n_k}\}\subset {\mathcal {C}}$, we have that $z\in {\mathcal {C}}$. Following similar method of proof used in obtaining (4.40), we obtain

$$\begin{aligned} \langle Ay, y-z\rangle \ge 0,~~\forall ~y\in C, \end{aligned}$$

(4.43)

which implies by Lemma 2.3, that $z\in \text{ VI }(A,C).$ Hence, we conclude that $z\in \Gamma .$ $\square$

Lemma 4.6

Let $\{x_n\}$ be a sequence generated by Algorithm 3.2 under Assumption 3.1. Then, for each $n\ge 1$

$$\begin{aligned} v_n:=\Vert x_n-p\Vert ^2+\alpha _n\Vert x_n-x_0\Vert ^2-\theta _{n-1}\Vert x_{n-1}-p\Vert ^2+2\theta _n\Vert x_{n-1}-x_n\Vert ^2\ge 0. \end{aligned}$$

Proof

Since $\{\theta _n\}\in [0,\frac{1}{3})$ is non-decreasing, we have from Lemma 2.1 that

$$\begin{aligned} v_n&=\Vert x_n-p\Vert ^2+\alpha _n\Vert x_n-x_0\Vert ^2-\theta _{n-1}\Vert x_{n-1}-x_n+x_n-p\Vert ^2+2\theta _n\Vert x_{n-1}-x_n\Vert ^2\\&=\Vert x_n-p\Vert ^2+\alpha _n\Vert x_n-x_0\Vert ^2-\theta _{n-1}\Vert x_{n-1}-x_n\Vert ^2-\theta _{n-1}\Vert x_n-p\Vert ^2\\&\quad -2\theta _{n-1}\langle x_{n-1}-x_n,x_n-p\rangle \\&\quad + 2\theta _n\Vert x_{n-1}-x_n\Vert ^2\\&=\Vert x_n-p\Vert ^2+\alpha _n\Vert x_n-x_0\Vert ^2-\theta _{n-1}\Vert x_{n-1}-x_n\Vert ^2-\theta _{n-1}\Vert x_n-p\Vert ^2\\&\quad -\theta _{n-1}\Big [\Vert x_{n-1}-x_n\Vert ^2+\Vert x_n-p\Vert ^2-\Vert x_{n-1}-2x_n+p\Vert ^2\Big ]+2\theta _n\Vert x_{n-1}-x_n\Vert ^2\\&=\Vert x_n-p\Vert ^2+\alpha _n\Vert x_n-x_0\Vert ^2-2\theta _{n-1}\Vert x_{n-1}-x_n\Vert ^2-2\theta _{n-1}\Vert x_n-p\Vert ^2\\&\quad +\theta _{n-1}\Vert x_{n-1}-2x_n+p\Vert ^2\\&\quad +2\theta _n\Vert x_{n-1}-x_n\Vert ^2\\&\ge \Vert x_n-p\Vert ^2+\alpha _n\Vert x_n-x_0\Vert ^2-2\theta _n\Vert x_{n-1}-x_n\Vert ^2-\frac{2}{3}\Vert x_n-p\Vert ^2+\theta _{n-1}\Vert x_{n-1}-2x_n\\&\quad +p\Vert ^2+2\theta _n\Vert x_{n-1}-x_n\Vert ^2\\&=\frac{1}{3}\Vert x_n-p\Vert ^2+\alpha _n\Vert x_n-x_0\Vert ^2+\theta _{n-1}\Vert x_{n-1}-2x_n+p\Vert ^2\\&\ge \frac{1}{3}\Vert x_n-p\Vert ^2+\alpha _n\Vert x_n-x_0\Vert ^2\\&\ge 0, \end{aligned}$$

which is the desired conclusion. $\square$

We are now in a position to prove the main theorem for Algorithm 3.2.

Theorem 4.7

Let $\{x_n\}$ be a sequence generated by Algorithm 3.2 under Assumption 3.1. Then, $\{x_n\}$ converges strongly to $p\in \Gamma ,$ where $p=P_\Gamma x_0.$

Proof

From Lemma 4.6 and (4.12), we obtain

$$\begin{aligned} v_{n+1}-v_n + (1-3\theta _{n-1}-\alpha _n)\Vert x_n-x_{n+1}\Vert ^2\le -2\alpha _n\langle x_n-p,x_n-x_0\rangle . \end{aligned}$$

(4.44)

We consider two cases for our proof.

CASE 1: Let $z\in \Gamma .$ Suppose for some $n_0\in {\mathbb {N}}$ large enough, we have $v_{n+1}\le v_n$ for all $n\ge n_0.$ Then by Lemma 4.6 we have $v_n\ge 0, \forall n\ge 1$ and $\lim \nolimits _{n\rightarrow \infty }v_n=\lim \limits _{n\rightarrow \infty }v_{n+1}$ exists. Since $\{x_n\}$ is bounded, there exists a constant $M>0$ such that $2|\langle x_n-p,x_n-x_0\rangle |\le M.$ Hence, there exists $N\in {\mathbb {N}}$ and $\xi _1>0$ such that $(1-3\theta _{n+1}-\alpha _n)\ge \xi _1, \forall n\ge N.$ Hence, from (4.44) we have that for all $n\ge N$

$$\begin{aligned} \xi _1\Vert x_n-x_{n+1}\Vert ^2&\le v_n - v_{n+1}+\alpha _n M\rightarrow 0,\quad n\rightarrow \infty . \end{aligned}$$

Thus,

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\Vert x_{n+1}-x_n\Vert =0. \end{aligned}$$

(4.45)

From the definition of $w_n$ in Step 1 and by applying (4.45) together with the fact that $\lim \nolimits _{n \rightarrow \infty }\alpha _n=0,$ we have

$$\begin{aligned} \Vert w_n-x_n\Vert&=\Vert \alpha _n(x_0-x_n)+\theta _n(x_n-x_{n-1})\Vert \nonumber \\&\le \alpha _n\Vert x_0-x_n\Vert +\theta _n\Vert x_n-x_{n-1}\Vert \rightarrow 0, \hspace{0.5cm} n\rightarrow \infty \end{aligned}$$

(4.46)

Consequently, we have

$$\begin{aligned} \Vert w_n-x_{n+1}\Vert \rightarrow 0,\quad n\rightarrow \infty . \end{aligned}$$

(4.47)

From (4.11), we have

$$\begin{aligned} \sigma \gamma ^{-1}_1(2-\gamma _1)\Vert t_n-b_n\Vert ^2&\le \Vert w_n-p\Vert ^2-\Vert x_{n+1}-p\Vert ^2\\&=\Big (\Vert w_n-p\Vert -\Vert x_{n+1}-p\Vert \Big )\Big (\Vert w_n-p\Vert +\Vert x_{n+1}-p\Big )\\&\le \Vert w_n-x_{n+1}\Vert \Big (\Vert w_n-p\Vert +\Vert x_{n+1}-p\Big )\\&\le \Vert w_n-x_{n+1}\Vert M_1 \end{aligned}$$

where $M_1:=\sup \nolimits _{n\ge 1}\{\Vert w_n-p\Vert +\Vert x_{n+1}-p\Vert \}.$ Hence

$$\begin{aligned} \Vert t_n-b_n\Vert \rightarrow 0, \hspace{0.2cm} n\rightarrow \infty . \end{aligned}$$

(4.48)

Similarly, we obtain from (4.11) that

$$\begin{aligned} \Vert w_n-t_n\Vert \rightarrow 0, \hspace{0.2cm}n\rightarrow \infty . \end{aligned}$$

Consequently, we have

$$\begin{aligned} \Vert b_n-w_n\Vert \rightarrow 0, \hspace{0.2cm} n\rightarrow \infty . \end{aligned}$$

(4.49)

Using the fact that $\{x_n\}$ is bounded, $\{v_n\}$ is convergent and $\lim \nolimits _{n\rightarrow \infty }\alpha _n=0,$ we obtain from Lemma 4.6 that

$$\begin{aligned} \lambda :=\lim \limits _{n\rightarrow \infty }\Big (\Vert x_{n+1}-p\Vert ^2-\theta _n\Vert x_n-p\Vert ^2\Big )< \infty , \end{aligned}$$

(4.50)

which is the limit of $\lim \nolimits _{n\rightarrow \infty }v_{n+1}.$ Consequently, from Lemma 4.6, we have $\lambda \ge 0.$ We show that $\lambda =0$ holds. So that it follows from Lemma 4.4 that the sequence $\{x_n\}$ converges strongly to the solution p.

Suppose on the contrary $\lambda >0.$ Since $\{x_n\}$ is bounded by Lemma 4.3, there exists a subsequence $\{x_{n_k}\}$ of $\{x_{n}\}$ which converges weakly to z,  such that

$$\begin{aligned} \liminf _{n\rightarrow \infty }\langle x_n-p, p-x_0\rangle =\lim \limits _{k\rightarrow \infty }\langle x_{n_k}-p,p-x_0\rangle =\langle z-p, p-x_0\rangle . \end{aligned}$$

(4.51)

By applying (4.48) and (4.49), it follows from Lemma 4.5 that $z\in \Gamma .$ Since $p=P_\Gamma x_0,$ we obtain from (4.51)

$$\begin{aligned} \liminf \limits _{n\rightarrow \infty }\langle x_{n}-p,p-x_0\rangle =\langle z-p, p-x_0\rangle \ge 0, \end{aligned}$$

(4.52)

which follows from (4.51) that

$$\begin{aligned} \lim \limits _{k\rightarrow \infty }\langle x_{n_k}-p, p-x_0\rangle \ge 0. \end{aligned}$$

From (4.50), we have

$$\begin{aligned} \liminf _{n\rightarrow \infty }\Vert x_{n+1}-p\Vert ^2\ge \lim \limits _{n\rightarrow \infty }\Big (\Vert x_{n+1}-p\Vert ^2-\theta _n\Vert x_n-p\Vert ^2\Big )=\lambda , \end{aligned}$$

and since $\lambda >0,$ we have

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2\ge \frac{1}{2}\lambda ,\quad \forall n\ge n_1 \end{aligned}$$

for some sufficiently large $n_1\in {\mathbb {N}}.$ Observe that

$$\begin{aligned} \langle x_n-p,x_n-x_0\rangle =\Vert x_n-p\Vert ^2+\langle x_n-p,p-x_0\rangle . \end{aligned}$$

Then, by applying (4.52) we have

$$\begin{aligned} \liminf \limits _{n\rightarrow \infty }\langle x_n-p,x_n-x_0\rangle&=\liminf \limits _{n\rightarrow \infty }\Big (\Vert x_n-p\Vert ^2+\langle x_n-p, p-x_0\rangle \Big )\\&\ge \liminf \limits _{n \rightarrow \infty }\Big (\frac{1}{2}\lambda +\langle x_n-p,p-x_0\rangle \Big )\\&=\frac{1}{2}\lambda +\liminf \limits _{n\rightarrow \infty }\langle x_n-p,p-x_0\rangle \\&\ge \frac{1}{2}\lambda . \end{aligned}$$

Again, using the assumption that $\lambda >0,$ we have

$$\begin{aligned} \langle x_n-p,x_n-x_0\rangle \ge \frac{1}{4}\lambda , \hspace{0.2cm} \forall n\ge n_2, \end{aligned}$$

for some sufficiently large $n_2\in {\mathbb {N}}$ such that $n_2\ge n_1.$ From (4.44), we have

$$\begin{aligned} v_{n+1}-v_n\le -\frac{1}{2}\alpha \lambda , \hspace{0.2cm} \forall n\ge n_2. \end{aligned}$$

Applying Lemma 4.6, it follows from the last inequality that

$$\begin{aligned} \frac{1}{2}\lambda \sum \limits _{k=n_2} ^{n}\alpha _k\le v_{n_2}-v_n\le v_{n_2},\hspace{0.2cm} \forall n\ge n_2. \end{aligned}$$

Since $\lambda >0,$ this gives the summability of the sequence $\{\alpha _n\}$ which contradicts $\sum \nolimits _{n=1}^{\infty }\alpha _n=\infty .$ Therefore, we must have $\lambda =0,$ and it follows that the sequence $\{x_n\}$ converges strongly to $p=P_\Gamma x_0$ as required.

CASE 2: Suppose that $\{v_n\}$ is not monotonically decreasing. Let $\tau :{\mathbb {N}}\rightarrow {\mathbb {N}}$ be defined for all $n\ge n_0$ for some $n_0\in {\mathbb {N}}$ large enough by

$$\begin{aligned} \tau _{(n)}:=\text{ max }\{k\in {\mathbb {N}}: k\le n,\hspace{0.1cm} v_k\le v_{k+1}\}. \end{aligned}$$

Observe that $\tau _{(n)}$ is a non-decreasing sequence such that $\tau _{(n)}\rightarrow \infty$ as $n\rightarrow \infty$ and $v_{\tau _{(n)}}\le v_{\tau _{(n)}+1}$ for all $n\ge n_0.$ Similar to CASE 1, for some constant $M>0,$ we obtain from (4.44) that

$$\begin{aligned} \xi _1\Vert x_{\tau _{{(n)}+1}}-x_{\tau _{(n)}}\Vert \le \alpha _{\tau (n)}M\rightarrow 0. \end{aligned}$$

(4.53)

Consequently, we get

$$\begin{aligned} \Vert x_{\tau _{{(n)}+1}}-x_{\tau _{(n)}}\Vert \rightarrow 0, \hspace{0.2cm} n\rightarrow \infty . \end{aligned}$$

(4.54)

Also, following similar procedure as in CASE 1, we obtain

$$\begin{aligned} \Vert x_{\tau _{{(n)}}}-w_{\tau _{(n)}}\Vert \rightarrow 0, \hspace{0.2cm} n\rightarrow \infty . \nonumber \\ \Vert t_{\tau _{{(n)}}}-b_{\tau _{(n)}}\Vert \rightarrow 0, \hspace{0.2cm} n\rightarrow \infty . \nonumber \\ \Vert w_{\tau _{{(n)}}}-t_{\tau _{(n)}}\Vert \rightarrow 0, \hspace{0.2cm} n\rightarrow \infty . \nonumber \\ \Vert b_{\tau _{{(n)}}}-w_{\tau _{(n)}}\Vert \rightarrow 0, \hspace{0.2cm} n\rightarrow \infty . \end{aligned}$$

(4.55)

Observe from (4.44) that for $j\ge 0,$ we have $v_{j+1}<v_j$ when $x_j\notin \Omega :=\{x\in {\mathcal {H}}:\langle x-x_0, x-p\rangle \le 0\}.$ Since $v_{\tau _{(n)}}\le v_{\tau _{(n)}+1},$ we have that $x_{\tau _{(n)}}\in \Omega \hspace{0.1cm} \forall ~ n\ge n_0.$ We have from Lemma 4.3 that $\{x_{\tau _{(n)}}\}$ is bounded, hence there exists a subsequence, again say $\{x_{\tau _{(n)}}\}$ which converges weakly to some $z\in {\mathcal {H}}_1.$ Since $\Omega$ is a closed and convex set, then it is weakly closed and it follows that $z\in \Omega .$ By (4.55), it follows from Lemma 4.5 that $z\in \Gamma .$ Hence, we have $z\in \Omega \cap \Gamma .$ In view of Lemma 2.5, we know that $\Omega \cap \Gamma$ contains only p as its element. Consequently, we have $z=p.$ Moreover, since $x_{\tau _n}\in \Omega$ we have

$$\begin{aligned} \Vert x_{\tau _{(n)}}-p\Vert ^2&=\langle x_{\tau _{(n)}}-x_0, x_{\tau _{(n)}}-p\rangle -\langle p-x_0, x_{\tau _{(n)}}-p\rangle \\&\quad \le -\langle p-x_0, x_{\tau _{(n)}}-p\rangle . \end{aligned}$$

Taking the $\lim \sup$ of the above inequality, we get

$$\begin{aligned} \limsup \limits _{n \rightarrow \infty }\Vert x_{\tau _{(n)}}-p\Vert \le 0. \end{aligned}$$

Thus,

$$\begin{aligned} \Vert x_{\tau _{(n)}}-p\Vert \rightarrow 0,\hspace{.2cm} n\rightarrow \infty . \end{aligned}$$

(4.56)

We claim that this implies $\lim \nolimits _{n \rightarrow \infty }v_{\tau _{(n)}+1}=0.$ From the definition of $v_{\tau _{(n)+1}},$ we have

$$\begin{aligned} v_{\tau _{{(n)}+1}}&=\Vert x_{\tau _{{(n)}+1}}-p\Vert ^2\\&\quad +\alpha _{\tau _{{(n)}+1}}\Vert x_{\tau _{{(n)}+1}} -x_0\Vert ^2-\theta _{\tau _{(n)}}\Vert x_{\tau _{(n)}}-p\Vert ^2\\&\quad +2\theta _{\tau _{{(n)}+1}}\Vert x_{\tau _{{(n)}+1}}-x_{\tau _{(n)}}\Vert ^2\\&=\Vert x_{\tau _{{(n)}+1}}-x_{\tau _{(n)}}+x_{\tau _{(n)}}-p\Vert ^2\\&\quad +\alpha _{\tau _{{(n)}+1}}\Vert x_{\tau _{{(n)}+1}} -x_0\Vert ^2-\theta _{\tau _{(n)}}\Vert x_{\tau _{(n)}}-p\Vert ^2\\&\quad +2\theta _{\tau _{{(n)}+1}}\Vert x_{\tau _{{(n)}+1}}-x_{\tau _{(n)}}\Vert ^2. \end{aligned}$$

Using (4.54), (4.56), the boundedness of $\{\theta _n\}$ and $\{x_n\}$ and the fact that $\lim \nolimits _{n\rightarrow \infty }\alpha _n=0,$ we obtain that $\lim \nolimits _{n\rightarrow \infty }v_{\tau _{{(n)}+1}}=0.$

Next, we show that $\lim \nolimits _{n\rightarrow \infty }v_n=0.$ Observe that for all $n\ge n_0,$ we have $v_{\tau _{(n)}}\le v_{\tau _{{(n)}+1}}$ if $n\ne \tau (n)$ since $v_j>v_{j+1}$ for $\tau (n)+1\le j\le n-1.$ It follows that $\forall n\ge n_0,$ we have

$$\begin{aligned} v_n\le \text{ max }\{v_{\tau _{(n)}},v_{\tau _{{(n)}+1}}\}=v_{\tau _{{(n)}+1}}\rightarrow 0. \end{aligned}$$

Hence,

$$\begin{aligned} \limsup \limits _{n\rightarrow \infty }v_n\le 0. \end{aligned}$$

From Lemma 4.6, we have that

$$\begin{aligned} \liminf \limits _{n\rightarrow \infty }v_n\ge 0. \end{aligned}$$

Thus,

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }v_n=0. \end{aligned}$$

Using the fact that $\{x_n\}$ is bounded, $\lim \nolimits _{n\rightarrow \infty }\alpha _n=0$ and by (4.44), we have

$$\begin{aligned} \Vert x_n-x_{n+1}\Vert \rightarrow 0,\hspace{0.2cm} n\rightarrow \infty , \end{aligned}$$

which implies from the definition of $v_n$ that

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\Big (\Vert x_{n+1}-p\Vert ^2-\theta _n\Vert x_n-p\Vert ^2\Big )=0. \end{aligned}$$

Thus, by Lemma 4.4 we obtain that $\{x_n\}$ converges strongly to $p=P_\Gamma x_0,$ which completes the proof.

$\square$

Remark 4.8

[39]

• Setting ${\mathcal {H}}_1={\mathcal {H}}_2={\mathcal {H}}$, $F=0$ and $T=I_{\mathcal {H}}$ (the identity operator on ${\mathcal {H}}$) in Theorem 4.7, we obtain an inertial projection and contraction method requiring only one projection onto the feasible set ${\mathcal {C}}$ per iteration with fixed step size for solving the classical VIP (1.1) when A is pseudomonotone and Lipschitz continuous as a corollary.

• The conclusions of Lemma 4.1, Lemma 4.5 and Theorem 4.7 still hold even if $\mu \in (0, \frac{1}{L_1})$ and $\lambda \in (0, \frac{1}{L_2})$ in Algorithm 3.2 are replaced with variable step sizes $\mu _n$ and $\lambda _n$, respectively such that

  $$\begin{aligned} 0<\inf _{n\ge 1}\mu _n\le \sup _{n\ge 1} \mu _n<\frac{1}{L_1} ~~\text{ and }~~ 0<\inf _{n\ge 1}\lambda _n\le \sup _{n\ge 1} \lambda _n <\frac{1}{L_2}. \end{aligned}$$

For the convergence analysis of Algorithm 3.3, which does not require the Lipschitz constants of the underlying cost operators to be known, we first state the following lemma on the step size rules derived from [35]. The proof of the lemma is similar to the method of proof in [35]. Hence, we omit the proof here.

Lemma 4.9

Let $\{\lambda _n\}$ and $\{\mu _n\}$ be the sequences generated by (3.1) and (3.2), respectively. Then the sequences $\{\lambda _n\}$ and $\{\mu _n\}$ are well defined, and $\lim \nolimits _{n\rightarrow \infty }\lambda _n=\lambda , \lim \limits _{n\rightarrow \infty }\mu _n=\mu ,$ where $\lambda \in \Big [\min \big \{\frac{a_2}{L_2},\lambda _1\big \}, \lambda _1+\Phi \Big ],$ $\mu \in \Big [\min \big \{\frac{a_1}{L_1},\mu _1\big \}, \mu _1+\Psi \Big ],$ and $\Phi =\sum _{n=1}^{\infty }\phi _n,\Psi =\sum _{n=1}^{\infty }\psi _n.$

Lemma 4.10

Let $\{x_n\}$ be a sequence generated by Algorithm 3.3 under Assumption 3.1. Then,

$$\begin{aligned} ||Tw_n-y_n||\le \gamma _2^{-1} \left( \frac{\lambda _{n+1}+\lambda _n a_2}{\lambda _{n+1}-\lambda _n a_2}\right) ||Tw_n-z_n||,~\forall n\ge 1 \end{aligned}$$

(4.57)

and

$$\begin{aligned} ||b_n-u_n||\le \gamma _1^{-1} \left( \frac{\mu _{n+1}+\mu _n a_1}{\mu _{n+1}-\mu _na_1}\right) ||b_n-t_n||,~\forall n\ge 1. \end{aligned}$$

(4.58)

Proof

From (3.1), we have that

$$\begin{aligned} ||FTw_n-Fy_n||\le \frac{a_2}{\lambda _{n+1}}||Tw_n-y_n||,~\forall n\ge 1, \end{aligned}$$

(4.59)

holds for both $FTw_n=Fy_n$ and $FTw_n\ne Fy_n$. Similar to (4.31), we obtain

$$\begin{aligned} \langle Tw_{n}-y_{n},r_{n}\rangle&\ge \Vert Tw_{n}-y_{n}\Vert ^2-\lambda _{n}\Vert Tw_{n}-y_{n}\Vert \Vert FTw_{n}-Fy_{n}\Vert \\&\ge (1-\lambda _{n}\frac{a_2}{\lambda _{{n}+1}})\Vert Tw_{n}-y_{n}\Vert ^2, \end{aligned}$$

which implies that

$$\begin{aligned} \Vert Tw_{n}-y_{n}\Vert ^2&\le \frac{1}{\left( 1-\lambda _{n}\frac{a_2}{\lambda _{{n}+1}}\right) }\langle Tw_{n}-y_{n}, r_{n}\rangle \\&\le \frac{1}{\left( 1-\lambda _{n}\frac{a_2}{\lambda _{{n}+1}}\right) }\beta _{n}\Vert r_{n}\Vert \left( \Vert Tw_{n}-y_{n}\Vert +\lambda _n\frac{a_2}{\lambda _{n+1}}\Vert Tw_{n}-y_{n}\Vert \right) \\&=\left( \frac{1+\frac{\lambda _{{n}a_2}}{\lambda _{{n}+1}}}{1-\frac{\lambda _{n}a_2}{\lambda _{{n}+1}}}\right) \beta _{n}\Vert r_{n}\Vert \Vert Tw_{n}-y_{n}\Vert \\&=\gamma _2^{-1}\left( \frac{\lambda _{{n}+1}+\lambda _{n}a_2}{\lambda _{{n}+1}-\lambda _{n}a_2}\right) \Vert Tw_{n}-z_{n}\Vert \Vert Tw_{n}-y_{n}\Vert , \end{aligned}$$

which reduces to (4.57) when simplified further. In a similar manner, we get (4.58). $\square$

Remark 4.11

Replacing $\mu$ and $\lambda$ with $\mu _n$ and $\lambda _n$, respectively in Lemma 4.1, we obtain that $\{x_n\}$ is bounded.

By Lemma 4.9, it follows that

$$\begin{aligned} \lim \limits _{n \rightarrow \infty } \left( \frac{\lambda _{{n}+1}+\lambda _{n}a_2}{\lambda _{{n}+1}-\lambda _{n}a_2}\right) =\frac{1+a_2}{1-a_2} \end{aligned}$$

(4.60)

and

$$\begin{aligned} \lim \limits _{n \rightarrow \infty } \left( \frac{\mu _{{n}+1}+\mu _{n}a_1}{\mu _{{n}+1}-\mu _{n}a_1}\right) =\frac{1+a_1}{1-a_1}. \end{aligned}$$

(4.61)

Following the similar procedure used in Theorem 4.7, we obtain the following strong convergence theorem for Algorithm 3.3.

Theorem 4.12

Let $\{x_n\}$ be a sequence generated by Algorithm 3.3 under Assumption 3.1. Then, $\{x_n\}$ converges strongly to $p\in \Gamma ,$ where $p=P_\Gamma x_0.$

Remark 4.13

• The method of proof in this paper is different from the method of proof used in obtaining strong convergence for SVIPs.

• Similar to Remark 4.8, we obtain an inertial projection and contraction method with adaptive step size, requiring only one projection onto the feasible set ${\mathcal {C}}$ per iteration, for solving the classical VIP (1.1) when A is pseudomonotone and Lipschitz continuous as a corollary.

• When the operators A and F are monotone and Lipschitz continuous, we do not need them to satisfy Condition (c). This is because Condition (c) was only used after (4.33) to get the conclusion of Lemma 4.5. But, from (4.33) and the monotonicity oft F, we obtain

  $$\begin{aligned} 0&\le \big<FTw_{n_k},x-Tw_{n_k}\big>+ \frac{1}{\lambda } \big<y_{n_k}-Tw_{n_k},x-y_{n_k}\big>+\big<FTw_{n_k},Tw_{n_k}-y_{n_k}\big>\nonumber \\&\le \left( \big<FTw_{n_k}-Fx,x-Tw_{n_k}\big>+\big<Fx,x-Tw_{n_k}\big>\right) + \frac{1}{\lambda }\Vert y_{n_k}-Tw_{n_k}\Vert \Vert x-y_{n_k}\Vert \\&\quad +\Vert FTw_{n_k}\Vert \Vert Tw_{n_k}-y_{n_k}\Vert \nonumber \\&\le \big <Fx,x-Tw_{n_k}\big >+ \frac{1}{\lambda } \Vert y_{n_k}-Tw_{n_k}\Vert \Vert x-y_{n_k}\Vert {+}\Vert FTw_{n_k}\Vert \Vert Tw_{n_k}{-}y_{n_k}\Vert ,~\forall x\in {\mathcal {Q}}, \end{aligned}$$

  Passing limit as $k\rightarrow \infty ,$ noting that $\{Tw_{n_k}\}$ converges weakly to Tz and applying (4.32), it follows from the last inequality that

  $$\begin{aligned} \langle Fx,x-Tz\rangle \ge 0, ~~ \forall x\in {\mathcal {Q}}. \end{aligned}$$

  Consequently, by Lemma 2.3 we have that $Tz\in {VI}(F,{\mathcal {Q}}).$ Similarly, we obtain that $z\in {VI}(A,{\mathcal {C}}).$ Hence, we conclude that Lemma 4.5 holds.

• Theorem 4.7 and Theorem 4.12 are still true if the operators A and F in finite dimensional spaces are only required to be pseudomonotone and Lipschitz continuous which is an improvement over the results in literature since no product space formulation is required even with the relaxed pseudomonotonicity assumption.

5 numerical experiment

In this section, using some test examples, we discuss the numerical behavior of our methods, Algorithm 3.2 (Proposed Alg. (1) and Algorithm 3.3 (Proposed Alg. (2)), as well as compare them with Algorithm (1.8) (Tian & Jiang Alg. (1)), Algorithm (1.10) (Tian & Jiang Alg. (2)), Appendix 6.1 (Pham et al. Alg.) and Appendix 6.2 (Ogwo et al. Alg.).

In our computations, we randomly choose $x_0, x_1\in {\mathcal {H}}_1$, $\gamma _1 = 1.8,$ $\gamma _2 = 1.1,$ $a_1 = 0.6, a_2 = 0.4,$ $\lambda _1=0.85$ and $\mu _1=0.9$. We choose $\alpha _n=\frac{1}{n+1}, \theta _n=0.29,\sigma =0.45, \phi _n=\frac{1}{(n+1)^2}, \psi _n=\frac{1}{(n+2)^2}$ in Algorithms 3.2 and 3.3. Also, we choose $\delta _n=\frac{1}{n+1}$, $\theta _n=\frac{1}{2}-\delta _n,$ $\alpha _n={\bar{\alpha }}_n,$ $\tau _n=\frac{\delta _n}{n^{0.01}}$ and $\alpha = 3$ in the method of Ogwo et al. [39, Algorithm 3.3]. Using MATLAB 2021(b) and the stopping criterion $||x_{n+1} {-x}_{n}|| < 10^{-2},$ we plot the graphs of errors against the number of iterations in each case. The numerical results are reported in Figs. 1, 2, 3, 4, 5, 6, 7 and 8 and Tables 1 and 2.

Fig. 1

Example 5.1 Case 1

Fig. 2

Example 5.1 Case 2

Fig. 3

Example 5.1 Case 3

Fig. 4

Example 5.1 Case 4

Fig. 5

Example 5.2 Case 1

Fig. 6

Example 5.2 Case 2

Fig. 7

Example 5.2 Case 3

Fig. 8

Example 5.2 Case 4

Example 5.1

Let ${\mathcal {H}}_1={\mathcal {H}}_2 = L_2([0, 2\pi ])$ be equipped with inner product

$$\begin{aligned} \langle x, y\rangle = \int _{0}^{2\pi }x(t)y(t)dt,~~\forall ~x,y \in L_2([0, 2\pi ]) \end{aligned}$$

and norm

$$\begin{aligned} ||x||:= \Big ( \int _{0}^{2\pi }|x(t)|^2dt \Big )^{\frac{1}{2}},~~\forall ~x,y \in L_2([0, 2\pi ]). \end{aligned}$$

Then we define $A:L_2([0, 2\pi ])\rightarrow L_2([0, 2\pi ])$ by

$$\begin{aligned} A(x)(t) = e^{-\Vert x\Vert }\int _{0}^{t}x(s)ds,~~ \forall x\in L_2([0,2\pi ]),~~t\in [0,2\pi ]. \end{aligned}$$

From [46], we have that A is pseudomonotone and Lipschitz continuous but not monotone on $L_2([0,1]).$

Let ${\mathcal {C}} = \{x \in L_2([0, 2\pi ]): \langle y, x\rangle \le v\},$ where $y = t+e^t$ and $v = 1,$ then ${\mathcal {C}}$ is a nonempty closed and convex subset of $L_2([0, 2\pi ])$. We define the metric projection $P_{\mathcal {C}}$ as:

$$\begin{aligned} P_{\mathcal {C}}(x) = {\left\{ \begin{array}{ll} x-\frac{ \langle y, x \rangle -v}{||y||^2}y, &{}\text{ if }~~\langle y, x \rangle > v,\\ x, &{}\text{ if }~~\langle y, x \rangle \le v. \end{array}\right. } \end{aligned}$$

Also, let ${\mathcal {Q}}=\{x\in L_2([0, 2\pi ])~: \Vert x-a\Vert _{ l _2}\le d\},$ where $a=t+3$ and $d=2,$ then ${\mathcal {Q}}$ is a nonempty closed and convex subset of $L_2([0, 2\pi ])$. We define $P_{\mathcal {Q}}$ as:

$$\begin{aligned} P_{\mathcal {Q}}(x) = {\left\{ \begin{array}{ll} x, &{}\text{ if }~~x\in {\mathcal {Q}},\\ \frac{x-a}{\Vert x-a\Vert ^2}d+a, &{}\text{ otherwise }. \end{array}\right. } \end{aligned}$$

We define the operator $F: {\mathcal {Q}}\rightarrow L_2([0,2\pi ])$ by

$$\begin{aligned} F(x)(t):={\mathcal {G}}(x){\mathcal {M}}(x)(t),~~\forall ~x\in {\mathcal {Q}},~~t\in [0,2\pi ], \end{aligned}$$

where ${\mathcal {G}}:{\mathcal {Q}}\rightarrow {\mathbb {R}}$ is defined by $g(x):=\frac{1}{1+\Vert x\Vert ^2}$ and ${\mathcal {M}}:L_2([0,2\pi ])\rightarrow L_2([0,2\pi ])$ is defined by ${\mathcal {M}}(x)(t):=\int _{0}^{t}x(s)ds,~~~\forall ~~ x\in L_2([0,2\pi ]),~~t\in [0,2\pi ]$. We have that ${\mathcal {G}}$ is $\frac{16}{25}$-Lipschitz continuous and $\frac{1}{5}\le {\mathcal {G}}(x)\le 1,~~~\forall ~x\in {\mathcal {C}}$ (see [?]). Hence, from [?], we have that F is pseudomonotone and Lipschitz continuous but not monotone since ${\mathcal {M}}$ is a Volterra intergral mapping which is bounded and linear monotone.

Let $T: L_2([0, 2\pi ]) \rightarrow L_2([0, 2\pi ])$ be defined by

$$\begin{aligned} Tx(s)=\int _{0}^{2\pi } {\mathcal {K}}(s, t)x(t)dt,~\forall ~ x\in L_2([0, 2\pi ]), \end{aligned}$$

where ${\mathcal {K}}$ is a continuous real-valued function on $[0, 2\pi ]\times [0,2\pi ]$. Then, T is a bounded linear operator with adjoint

$$\begin{aligned} T^*x(s)=\int _{0}^{2\pi } {\mathcal {K}}(t, s)x(t)dt,~\forall ~ x\in L_2([0, 2\pi ]). \end{aligned}$$

In particular, we define ${\mathcal {K}}(s, t)=e^{-st}$ for all $s, t \in [0, 2\pi ]$. For Algorithms (1.8) and (1.10), we define the mapping $S: L_2([0,2\pi ])\rightarrow L_2([0,2\pi ])$ by

$$\begin{aligned} Sx(t) = \int _0^{2\pi } tx(s)ds, \quad t\in [0,1]. \end{aligned}$$

Then, S is nonexpansive. For Algorithm (1.10), we define $h: L_2([0, 2\pi ]) \rightarrow L_2([0, 2\pi ])$ by

$$\begin{aligned} hx(t) = \int _0^{2\pi } \frac{t}{2}x(s)ds, \quad x\in [0,1]. \end{aligned}$$

Then, h is a contraction mapping.

We consider the following cases for the numerical experiments of this example.

Case 1 Take $x_0(t)= t + 2$ and $x_1(t)= 0.7e^{-t}$.

Case 2 Take $x_0(t)= 2t + 1$ and $x_1(t)= e^{-3t}$.

Case 3 Take $x_0(t)= 2t + 1$ and $x_1(t)= e^{-t}$.

Case 4 Take $x_0(t)= t^2 + 2t + 1$ and $x_1(t)= e^{-3t}$.

Table 1 Numerical results for example

Table 2 Numerical results for example 5.2

Example 5.2

Let ${\mathcal {H}}_1=\left( l _2({\mathbb {R}}), ~||. ||_{ l _2}\right) ={\mathcal {H}}_2$, where $l _2({\mathbb {R}}):=\{x=(x_1, x_2, x_3, \dots ),~x_i\in {\mathbb {R}}:\sum \limits _{i=1}^\infty |x_i|^2<\infty \}$ and $||x||_{ l _2}:= \left( \sum \limits _{i=1}^\infty |x_i|^2 \right) ^{\frac{1}{2}},~~\forall x \in l _2({\mathbb {R}}).$

Define the operators $A,F: l _2({\mathbb {R}})\rightarrow l _2({\mathbb {R}})$ by $A(x_1, x_2, x_3, \dots )=(3x_1e^{-x_1^2}, 0, 0, \dots )$ and $F(x_1, x_2, x_3, \dots )=(7x_1e^{-x_1^2}, 0, 0, \dots )$ respectively. Then, A, F are pseudo-monotone, Lipschitz continuous and sequentially weakly continuous but not monotone. Let $T: l _2({\mathbb {R}})\rightarrow l _2({\mathbb {R}})$ be defined by $Tx=\left( 0, x_1, \frac{x_2}{2}, \frac{x_3}{3},...\right)$, for all $x\in l _2({\mathbb {R}}).$ Then, T is a bounded linear operator on $\ell _2({\mathbb {R}})$ with adjoint $T^*y=\left( y_2, \frac{y_3}{2}, \frac{y_4}{3},...\right)$ for all $y\in l _2({\mathbb {R}}).$

Now, define ${\mathcal {C}}={\mathcal {Q}}=\{x\in l _2({\mathbb {R}}):||x-a||_{ l _2}\le b\},$ where $a=(1, \frac{1}{2}, \frac{1}{3}, \cdots )$ and $b=3$ for ${\mathcal {C}}$ and $a=(\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \cdots )$, $b=1$ for ${\mathcal {Q}}$. Then $\mathcal {C,Q}$ are nonempty closed and convex subsets of ${ l _2}({\mathbb {R}})$. Thus,

$$\begin{aligned} P_{\mathcal {C}}(x) = {\left\{ \begin{array}{ll} x, &{}\text{ if }~~ ||x-y||_{\ell _2}\le b,\\ \frac{x-y}{||x-y||_{ l _2}}b +a, &{}\text{ otherwise }. \end{array}\right. } \end{aligned}$$

Furthermore, we define the mappings $S, h: l _2({\mathbb {R}})\rightarrow l _2({\mathbb {R}})$ by $Sx=-4(x_1, x_2, x_3, \dots )$ and $hx=\left( \frac{x_1}{2},~\frac{x_2}{2}, \frac{x_3}{2}, \cdots \right)$ for all $x\in l _2({\mathbb {R}})$, and consider the following cases for the starting point:

Case 1 Take $x_0= \left( \frac{1}{5}, \frac{1}{15}, \frac{1}{45}, \cdots \right)$ and $x_1= \left( 1, \frac{1}{2}, \frac{1}{4}, \cdots \right)$.

Case 2 Take $x_0= \left( \frac{2}{5}, \frac{2}{15}, \frac{2}{45}, \cdots \right)$ and $x_1=\left( 2, 1, \frac{1}{2}, \cdots \right)$.

Case 3 Take $x_0= \left( \frac{1}{5} \frac{1}{15}, \frac{1}{45}, \cdots \right)$ and $x_1= \left( \frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \cdots \right) .$

Case 4: Take $x_0= (-3, \frac{3}{2}, -\frac{3}{4}, \cdots )$ and $x_1= (\frac{1}{3}, \frac{2}{9}, \frac{4}{27}\cdots ).$

6 Conclusion

We proposed and studied two new modified inertial projection and contraction methods for solving the SVIP (1.1)–(1.2) in infinite dimensional real Hilbert spaces where the underlying cost operators are pseudomonotone, Lipschitz continuous and without the sequentially weakly continuity condition. The first method is proposed when the Lipschitz constants of the underlying cost operators are known while the latter method involving adaptive step size strategies is proposed when the Lipschitz constants of the underlying cost operators are unknown. The two modified inertial projection and contraction methods proposed in our work require only one projection onto the feasible set per iteration and also do not require the SVIP (1.1)–(1.2) to be transformed into a product space. As far as we know, our choice of the inertial factor $\theta _n\in [0,\frac{1}{3})$ has never been used in obtaining strong convergence result for SVIPs. Thus, our methods seem potentially more applicable than most of the existing methods for solving SVIPs. A direct consequence of our results is that our methods can be reduced to modified inertial projection and contraction methods requiring only one projection onto a feasible set per iteration for solving the classical VIP (1.1) when the underlying operator is pseudomonotone, Lipschitz continuous and without the sequentially weakly continuity condition often used in the literature. Finally, we perform some numerical experiments for our proposed methods and the results show that the inertial technique employed plays a significant role in speeding up the rate of convergence which makes our methods outperform other existing methods compared with for solving the SVIPs.

Appendix

Appendix 6.1 Algorithm 1 of Pham et al. [42].

Step 0.  Choose  $\mu _0, \lambda _0>0, ~~\mu , \lambda \in (0, 1),~\{\tau _n\}\subset [{\underline{\tau }},~ {\bar{\tau }}]\subset \left( 0, \frac{1}{||T||^2+1}\right) , ~\{\alpha _n\} \subset (0, 1) \, {{ such that}}$

$\lim \limits _{n\rightarrow \infty }\alpha _n=0$ ${{ and}} \, \sum _{n=1}^\infty \alpha _n=\infty .$

Step 1. Let   $x_1 \, \in \, {\mathcal {H}}_1. \, {{ Set}}\, n=1$.

Step 2. Compute

$u_n=Tx_n,$

$v_n=P_{\mathcal {Q}}(u_n-\mu _n fu_n),$

$w_n=P_{{\mathcal {Q}}_n}(u_n-\mu _n fv_n),$

where

${\mathcal {Q}}_n=\{w_2\in {\mathcal {H}}_2 : \langle u_n-\mu _n fu_n-v_n, w_2-v_n\rangle \le 0\}$

and

$\mu _{n+1}=\left\{ \begin{array}{lll} \min \left\{ \frac{\mu ||u_n-v_n||}{||fu_n-fv_n||},~\mu _n\right\} ,&{} \text{ if }~fu_n\ne fv_n,\\ \mu _n,&{} {{ otherwise}}. \end{array}\right.$

Step 3. Compute

$y_n=x_n+\tau _n T^*(w_n-u_n),$

$z_n=P_{\mathcal {C}}(y_n-\lambda _n Ay_n),$

$t_n=P_{{\mathcal {C}}_n}(y_n-\lambda _n Az_n),$

where

${\mathcal {C}}_n=\{w_1\in {\mathcal {H}}_1 : \langle y_n-\lambda _n Ay_n-z_n, w_1-z_n\rangle \le 0\}$

and

$\lambda _{n+1}=\left\{ \begin{array}{lll} \min \left\{ \frac{\lambda ||y_n-z_n||}{||Ay_n-Az_n||},~\lambda _n\right\} ,&{} \text{ if }~Ay_n\ne Az_n,\\ \lambda _n,&{} {otherwise}. \end{array} \right.$

Step 4. Compute

$x_{n+1}=\alpha _n x_1+(1-\alpha _n) t_n.$

Set $n:= n+1$ and go back to Step 2.

Appendix 6.2 Algorithm 3.3 of Ogwo et al. [39]

Step 0: Choose sequences $\{\delta _n\}^{\infty }_{n=1}, \{\theta _n\}^{\infty }_{n=1}$ and $\{\tau _n\}^{\infty }_{n=1}$ such that the conditions from Assumption 3.1

(d)–(e) hold and let $\eta \ge 0, \gamma _i\in (0,2), ~a_i \in (0,1), i=1,2, \lambda _1>0, \mu _1>0, \alpha \ge 3$ and $x_0,x_1 \in {\mathcal {H}}_1$

be given arbitrarily. Set n:=1.

Step 1: Given the iterates $x_{n-1}$ and $x_n$ for each $n \ge 1,$ choose $\alpha _n$ such that $0\le \alpha _n \le {\bar{\alpha }}_n,$ where

${\bar{\alpha }}_n:= \left\{ \begin{array}{lll} \min \left\{ \frac{n-1}{n+\alpha -1}, \frac{\tau _n}{\Vert x_n-x_{n-1}\Vert }\right\} , &{} \text{ if } ~ x_n \ne x_{n-1}\\ \frac{n-1}{n+\alpha -1}, &{} {{ otherwise}.} \end{array}\right. \quad \quad \quad \quad (6.1)$

Step 2: Compute

$w_n=x_n+\alpha _n(x_n-x_{n-1}),$

$y_n=P_{\mathcal {Q}}(Tw_n-\lambda _n FTw_n),$

$z_n=Tw_n-\gamma _2\beta _n r_n,$

where $r_n:=Tw_n-y_n-\lambda _n(FTw_n-Fy_n)$, $\beta _n:= \frac{\langle Tw_n-y_n,r_n \rangle }{\Vert r_n\Vert ^2},$ if $r_n\ne 0;$ otherwise, $\beta _n=0;$ and

$\lambda _{n+1}=\left\{ \begin{array}{lll} \min \left\{ \frac{a_2||Tw_n-y_n||}{||FTw_n-Fy_n||},~\lambda _n\right\} ,&{} \textit{if}~FTw_n\ne Fy_n\\ \lambda _n,&{} \textit{otherwise}. \end{array}\right. \quad \quad \quad \quad (6.2)$

Step 3: Compute

$b_n=w_n+\eta _n T^{*}(z_n-Tw_n),$

where the stepsize $\eta _n$ is chosen such that for small enough $\epsilon >0,~~~\eta _n\in \left[ \epsilon , ~~\frac{\Vert Tw_n-z_n\Vert ^2}{\Vert T^{*}(Tw_n-z_n)\Vert ^2}-\epsilon \right] ,$

if $z_n\ne Tw_n$; otherwise, $\eta _n=\eta .$

Step 4: Compute

$u_n= P_{\mathcal {C}} (b_n-\mu _n Ab_n),$

$t_n=b_n-\gamma _1\gamma _n v_n,$

where $v_n:=b_n-u_n-\mu _n(Ab_n- A u_n)$, $\gamma _n=\frac{\langle b_n-u_n,v_n \rangle }{\Vert v_n\Vert ^2},$ if $v_n \ne 0;$ otherwise, $\gamma _n=0;$ and

$\mu _{n+1}=\left\{ \begin{array}{lll} \min \left\{ \frac{a_1||b_n-u_n||}{||Au_n-Ab_n||},~\mu _n\right\} ,&{} \text{ if }~Ab_n\ne Au_n\\ \mu _n,&{} \text{ otherwise }. \end{array}\right. \quad \quad \quad \quad (6.3)$

Step 5: Compute

$x_{n+1}=(1-\theta _n-\delta _n)b_n+\theta _nt_n.$

Set $n:=n+1$ and go back to Step 1.