Equivalent birational embedding IV: reduced varieties

Abstract

Two reduced projective schemes are said to be Cremona equivalent if there is a Cremona map that maps one in the other. In this paper I revise some of the known results about Cremona equivalence and extend the main result of Mella and Polastri (Bull Lond Math Soc 41(1):89–93, 2009) [20] to reducible schemes. This allows to prove a very general contractibility result for union of rational subvarieties.

1 Introduction

The birational geometry of the projective space has always attracted the attention of algebraic geometers. The Cremona group, $Cr(\mathbb {P}^r_k)$, that is the group of birational selfmaps of the projective space, has been intensively studied for well over a century but it is still a quite mysterious object. Here is an extract from the article “Cremona group” in the Encyclopedia of Mathematics, written by V. Iskovskikh in 1982:

One of the most difficult problems in birational geometry is that of describing the structure of the group $Cr(\mathbb {P}^3_k)$, which is no longer generated by the quadratic transformations. Almost all literature on Cremona transformations of three-dimensional space is devoted to concrete examples of such transformations. Finally, practically nothing is known about the structure of the Cremona group for spaces of dimension higher than 3. [14].

Unfortunately after 40 years the situation is not much better. A reasonable set of generators is not known yet. The Cremona groups have been proved to be non simple, [1, 9] and their behavior is wild from many points of view, as an example one can look at the results in [1]. Already the two dimensional Cremona group has many foundational problems that are far from being solved, see [2] for a very nice introduction. Instead of trying to tame this group, in this paper I want to use its wildness to address the following question.

Question: Let $X,Y\subset \mathbb {P}^r$ be birational reduced schemes is there a birational selfmap of the projective space $\omega :\mathbb {P}^r\dasharrow \mathbb {P}^r$ such that $\omega (X)=Y$?

When the answer to the question is positive X and Y are said to be Cremona equivalent. The notion of Cremona equivalence is quite old and already at the end of $\mathrm XIX$th century both Italian and English school of algebraic geometry approached the problem, with special regards to plane curves, [8, 10, 13, 16]. The first result I am aware off in modern times, is due to Jelonek, [15] where the author proved that two irreducible and reduced birational subvarieties of the complex projective space are Cremona equivalent when roughly the dimension is smaller than the codimension. More recently I have been attracted by the problem and dedicated a series of papers to explore the possibility to extend birational maps of projective varieties to the ambient space. The first important improvement has been achieved in [20], see also [7] for an alternative proof, where it is proven that two irreducible and reduced birational projective varieties of codimension at least 2 are Cremona equivalent.

It is not difficult to see that the result is sharp with respect to the codimension. It was classically known the existence of non Cremona equivalent rational plane curves, see for instance Example 3.7. Then stemming from the mentioned result in [20] there are two possible directions: study the Cremona equivalence of divisors, extend the result to reducible and reduced projective varieties. The case of divisors has been fruitfully studied. In [21] and [4] the authors completely described the Cremona equivalence classes of irreducible curves and gave conditions for a plane curve to be of minimal Cremona degree, that is with the smallest degree in the Cremona equivalence class. Partial results have also been obtained for special classes of divisors, [17], and special classes of rational surface, [18, 19].

To the best of my knowledge the only cases of reducible varieties studied in relation to the Cremona equivalence are those concerning the contractibility of set of lines in the projective plane, [5, 6, 8, 11]. Even for this very special class of reducible varieties the answer is really complicate and it is not known yet a complete classification of contractible set of lines in the plane. The problem resting on the different possible configuration of intersection points. Note further that essentially nothing is known about the Cremona equivalence class of non contractible set of lines in the plane. That is given two configurations of lines in the plane nothing is known about their Cremona equivalence.

In this paper I want to address the case of reduced schemes of codimension at least 2. I was really amazed when I realized that also for this class it is possible to extend the result of irreducible subvarieties and give a complete answer to the question.

Theorem 1.1

Let $X,Y\subset \mathbb {P}^r$ be two reduced schemes of dimension at most $r-2$. Then X is Cremona equivalent to Y if and only if X and Y are birational.

To appreciate the result and the amazing flexibility of the Cremona group just think of a bunch of lines $L=\cup _1^s l_i\subset \mathbb {P}^r$, for $n\ge 3$. Then there is a birational map $\omega :\mathbb {P}^r\dasharrow \mathbb {P}^r$ mapping L to a set of s lines passing through a fixed point p. Hence any set of lines in $\mathbb {P}^n$ is contractible by a birational map as soon as $n\ge 3$. No matter how the irreducible components of L intersects we can always contract them to a set of s points with a birational selfmap of $\mathbb {P}^r$. As an application of Theorem 1.1 we’ll prove a similar statement for an arbitrary set of rational varieties.

Despite the proof of the theorem is constructive and algorithmic, it is difficult if not impossible to produce a birational map that realizes the Cremona equivalence of two prescribed subvarieties. This is due to the fact that to follow the proof’s steps one has to produce irreducible monoids with special features and those are difficult to be computed on effective examples. Coming back to the wildness of $Cr(\mathbb{P} ^r_k)$ the positive answer to the Cremona equivalence question for arbitrary subvarieties of codimension at least 2 can be seen as a further confirmation of the difficulty to describe and tame this incredible group of transformations, see also Remark 4.7.

The paper is organized as follows. First I introduce a set of special Cremona birational maps and use them to study the Cremona equivalence of special classes of varieties, in particular an explicit construction of the Cremona equivalence of sets of reduced points is given. Even if this part is not strictly necessary to prove the main result I think it allows to perceive the beauty of Cremona modification and it is also a nice training camp on the birational geometry of projective subvarieties of the projective space. The proof of the main Theorem is then finished in the last section. To do it I adapt the proof in [7] to the case of reducible varieties. This is done improving the computation of the dimension of monoids containing a subvariety, see Lemma 4.4, and avoiding the use of the results in [3] on the Segre locus to produce the chain of double projection needed to complete the argument. Finally as an application it is proven that any set of reduced codimension at least two rational varieties can be contracted by a Cremona transformation.

Many thanks are due to the referee for a careful reading and for suggesting an improvement of Lemma 4.3.

2 Basics on Cremona transformations

we work over the complex field.

Definition 2.1

A Cremona transformation is a birational map $\varphi :\mathbb {P}^r\dasharrow \mathbb {P}^r$ given by equations

$$\begin{aligned}{}[x_0,\ldots ,x_r]\mapsto [F_0(x_0,\ldots ,x_r),\ldots , F_r(x_0,\ldots ,x_r)], \end{aligned}$$

where $F_i(x_0,\ldots ,x_r)$ are homogeneous polynomials of the same degree $\delta >0$, for $i=0,\ldots ,r$.

The inverse map is also a Cremona transformation, and it is defined by homogeneous polynomials $G_i(x_0,\ldots ,x_r)$ of degree $\delta '>0$, for $i=0,\ldots , r$. If the polynomials $\{F_i\}$ are coprime and we choose the $\{G_j\}$ as well coprime we say that $\varphi$ is a $(\delta , \delta ')$--Cremona transformation.

The subscheme

$$\begin{aligned} \textrm{Ind}(\varphi ):=\cap ^r_{i=0}(F_i(x_0,\ldots ,x_r)=0) \end{aligned}$$

is the indeterminacy locus of $\varphi$. Since the composition of $\varphi$ and its inverse is the identity, we have

$$\begin{aligned} G_i(F_0(x_0,\ldots ,x_r), \ldots , F_r(x_0,\ldots ,x_r))=\Phi \cdot x_i,\ \ \hbox { for}\ i=0,\ldots , r\end{aligned}$$

where $\Phi$ is a homogeneous polynomial of degree $\delta \cdot \delta '-1$. The hypersurface $\textrm{Fund}(\varphi ):=\{\Phi =0\}$ is the fundamental locus of $\varphi$ and its support is the reduced fundamental locus $\textrm{Fund}_{\textrm{red}}(\varphi )$. The group of Cremona transformation of $\mathbb {P}^r$ is

$$\begin{aligned} Cr_r:=:Cr(\mathbb {P}^r):=\{\varphi :\mathbb {P}^r\dasharrow \mathbb {P}^r| \text{ the } \text{ map } \varphi \text{ is } \text{ birational }\}. \end{aligned}$$

Remark 2.2

Note that we are not asking for the polynomials $\{F_i\}$ to be coprime. This is quite unusual but useful to prove the main result, indeed this allow us to add fixed components to linear system to produce the birational maps we need.

Let us work out some special cases in details.

Example 2.3

(Quadro-quadric transformation of $\mathbb {P}^r$) Let $Q\subset H\subset \mathbb{P} ^r$ be a codimension 2 reduced quadric and $p\in \mathbb {P}^r{\setminus } H$ a point. Consider the linear system

$$\begin{aligned} \mathcal {L}=|\mathcal {I}_{p\cup Q}(2)| \end{aligned}$$

of quadrics through p and Q. Then $\dim \mathcal {L}=n$ and the scheme theoretic base locus of $\mathcal {L}$ is $Q\cup p$.

Let $\epsilon :Z\rightarrow \mathbb {P}^r$ be the blow up of Q and p with exceptional divisor $E_p$ and $E_Q$ and $\nu :Z\rightarrow \mathbb {P}^{r+1}$ the blow down of the hyperplane H and of the cone $C_p(Q)$ with base Q and vertex p. Then a general conic passing through p and intersecting Q in 2 points is mapped to a line. Therefore $\phi :=\nu \circ \epsilon$ is a Cremona transformation. For a general hyperplane H the restriction $\phi _{|H}$ maps H to a quadric, then the inverse of $\phi$ is again given by quadrics with an isomorphic base locus. This shows that $\phi$ is a quadro-quadric Cremona transformation.

Note that for $n=2$ the map $\phi _\mathcal {L}$ is the standard quadratic Cremona transformation. Moreover for a general linear space $\mathbb {P}^a\cong A\subset \mathbb {P}^r$ containing p, the restriction $\phi _{\mathcal {L}|A}$ is again a quadro-quadric map $\mathbb {P}^a\dasharrow \mathbb {P}^a$.

Recall that Noether–Castelnuovo Theorem shows that $Cr_2$ is generated by the linear automorphisms and the quadro-quadric transformation of $\mathbb {P}^2$. Therefore if we consider a plane $A\cong \mathbb {P}^2$ and any birational map $\omega :A\dasharrow A$ we may write

$$\begin{aligned} \omega =g_1\circ \phi _1\circ \ldots \circ g_h\circ \phi _{h}, \end{aligned}$$

with $\phi _i$ quadro-quadric maps and $g_i$ linear automorphisms of $\mathbb {P}^2$. If $A\subset \mathbb {P}^r$ we may extend both quadro-quadric maps and linear automorphisms to selfmaps of the ambient space. Hence for any map $\omega \in Cr(\mathbb {P}^2)$ there is a birational map $\Omega \in Cr(\mathbb {P}^r)$ such that $\Omega _{|A}=\omega$, as birational maps.

Example 2.4

(Cubo-cubic transformation of $\mathbb {P}^3$) Let $\Gamma \subset \mathbb {P}^3$ be a rational normal curve and $S_1,S_2\in |\mathcal {I}_\Gamma (3)|$ two smooth cubic surfaces containing $\Gamma$. Then we have $S_1\cap S_2=\Gamma \cup R$, for a residual curve R of degree 6 genus 3. It is not difficult to check that

$$\begin{aligned} \dim |\mathcal {I}_R(3)|=3. \end{aligned}$$

and $\Gamma \cdot R=8$, see for instance [23]. This shows that the linear system $|\mathcal {I}_R(3)|$ defines a Cremona transformation $\psi :\mathbb {P}^3\dasharrow \mathbb {P}^3$. that can be described as follows. Let $\epsilon :\mathbb {Z}\rightarrow \mathbb {P}^3$ be the blow up of R and $\nu :Z\rightarrow \mathbb {P}^3$ the blow down of the strict transform of trisecant lines to R. Then we have

$$\begin{aligned} \psi =\nu \circ \epsilon . \end{aligned}$$

Since $\Gamma \cdot R=8$ we have that $\psi (\Gamma )$ is a line, moreover the restriction to a general plane $\psi _{|H}$ maps H to $\mathbb {P}^2$ blown up in 6 points, the intersection points with the curve R. Therefore the inverse of $\phi$ is again defined by cubics and with a bit more of work one can prove that the base locus is of the same type. In particular $\phi$ is a cubo-cubic Cremona transformation

Next we introduce a class of special hypersurfaces that will be of crucial importance in what follows.

Definition 2.5

(Monoids) Let $X\subset \mathbb{P} ^ r$ be a hypersurface of degree d. We say that X is a monoid with vertex $p\in \mathbb{P} ^ r$ if p is a point in X of multiplicity exactly $d-1$. Note that a monoid can have more than one vertex. If we choose projective coordinates in such a way that $p=[1,0,\ldots ,0]$, then

$$\begin{aligned} X=(F_{d-1}(x_1,\ldots ,x_{r})x_{0}+ F_{d}(x_1,\ldots ,x_{r})=0), \end{aligned}$$

where $F_{d-1}$ and $F_d$ are homogeneous polynomials of degree $d-1$ and d respectively and $F_{d-1}$ is nonzero. The hypersurface X is irreducible if and only if $F_{d-1}$ and $F_d$ are coprime.

Construction 2.6

An irreducible monoid X is rational. Indeed, the projection of X from a vertex p onto a hyperplane H not passing through p is a birational map $\pi :X\dasharrow H\cong \mathbb{P} ^ {r-1}$. If H has equation $x_0=0$, then the inverse map $\pi ^ {-1}:\mathbb{P} ^ {r-1} \dasharrow X$ is given by

$$\begin{aligned}{}[x_1,\ldots , x_{r}] \mapsto [-F_{d}(x_0,\ldots ,x_{r-1}),{F_{d-1}(x_1,\ldots ,x_{r})}x_1,\ldots , {F_{d-1}(x_0,\ldots ,x_{r-1})}x_{r}]. \end{aligned}$$

The map $\pi$ is called the stereographic projection of X from p. Its indeterminacy locus is p. Each line through p contained in X gets contracted to a point under $\pi$. The set of all such lines is defined by the equations $\{F_d=F_{d-1}=0\}$. This is the indeterminacy locus of $\pi ^ {-1}$, whereas the hypersurface of H with equation $\{x_0=F_{d-1}=0\}$ is contracted to p by the map $\pi ^ {-1}$.

Monoids are useful to produce an important class of Cremona transformations.

Example 2.7

(de Jonquiéres transformations) A de Jonquiéres transformation of $\mathbb {P}^r$ is a birational map that preserves the family of lines through a point, say p, see [22] for a comprehensive introduction. Let $\omega :\mathbb {P}^r\dasharrow \mathbb {P}^r$ be a de Jonquiéres transformation given by

$$\begin{aligned}{}[x_0,\ldots ,x_n]\mapsto [M_0,\ldots ,M_n]. \end{aligned}$$

Up to a linear automorphisms we may assume that the lines through $[1,0,\ldots ,0]$ are mapped to lines through $[1,0,\ldots ,0]$. Then we may choose the $X_i:=(M_i=0)$ to be monoid with vertex $[1,0,\ldots ,0]$. Moreover $\{X_1,\ldots ,X_n\}$ has to contain a common divisor B, which has to be itself a monoid. This shows that a de Jonquiéres map, up to linear automorphisms, is of the form

$$\begin{aligned}{}[x_0,\ldots ,x_n]\mapsto [x_0F_0+{\tilde{G}}_0,G_1(x_0F_1+{\tilde{G}}_1),\ldots ,G_n(x_0F_1+{\tilde{G}}_1)], \end{aligned}$$

where $G_j\in \mathbb {C}[x_1,\ldots ,x_n]_g$, for $j=1,\ldots n$, and

$$\begin{aligned}{}[x_1,\ldots ,x_n]\mapsto [G_1,\ldots , G_n] \end{aligned}$$

defines a Cremona transformation of $\mathbb {P}^{n-1}$.

We will always be concerned with the subclass of de Jonquiéres maps where $g=1$. That is Cremona transformations that admit the form

$$\begin{aligned}{}[x_0,\ldots ,x_n]\mapsto [x_0F_0+{\tilde{G}}_0,x_1(x_0F_1+{\tilde{G}}_1),\ldots ,x_n(x_0F_1+{\tilde{G}}_1)], \end{aligned}$$

with a slight abuse of language we will also write $\omega$ as the map associated to the linear system

$$\begin{aligned} \{x_0F_0+{\tilde{G}}_0,x_1(x_0F_1+{\tilde{G}}_1),\ldots ,x_n(x_0F_1+{\tilde{G}}_1)\}. \end{aligned}$$

With these notation we have:

• the indeterminacy locus of $\omega$ is $(x_0F_0+{\tilde{G}}_0)\cap (x_0F_1+{\tilde{G}}_1)$,

• the family of lines through $[1,0,\ldots ,0]$ is preserved

• $\omega$ is birational and the inverse is again a de Jonquiéres transformation.

To convince you let me write the map in the following equivalent way

$$\begin{aligned}{}[x_0,\ldots ,x_n]\mapsto \left[ \frac{x_0F_0+G_0}{B},x_1,\ldots ,x_n\right] . \end{aligned}$$

This shows that the lines through $[1,0,\ldots ,0]$ are preserved, the map is birational and its inverse is of the same form.

Let me stress that a de Jonquiéres transformation restricts to a linear automorphism on a general line through the special point p.

The quadro-quadric map described in Example 2.3 is a de Jonquiéres of degree 2, where B is the span of the codimension 2 quadric. The case of $\mathbb {P}^2$ is particularly interesting. A de Jonquiéres map of degree d has $2d-2$ simple base points, maybe infinitely near. The map can be factored via the blow up of the multiple point and then $2d-2$ elementary transformations of Hirzebruch surfaces to finally contract the curve B.

3 Cremona equivalence: definition and first examples

Let us introduce in details the main relation we are going to analyze.

Definition 3.1

Let $X,Y\subset \mathbb {P}^N$ be two birational reduced schemes. We say that X is Cremona equivalent to Y if there is a birational modification $\omega :\mathbb {P}^N\dasharrow \mathbb {P}^N$ that is an isomorphism on the generic points of X, such that $\omega (X)=Y$.

To get acquainted it is useful to have some examples in mind.

Example 3.2

Let $C\subset \mathbb {P}^3$ be a twisted cubic. Let $S_1, S_2$ be two general cubic surfaces containing C. As we saw in Example 2.4 there is a cubo-cubic modification of $\mathbb {P}^3$ that maps the $S_i$ to planes and hence C to a line. So C is Cremona equivalent to a line.

The next is again a cubic curve but reducible

Example 3.3

Consider two sets of three lines in $\mathbb {P}^n$, say $L_1,L_2,L_3$ and $R_1,R_2,R_3$. Let us start assuming that $n=2$. Let $p_{ij}=L_i\cap L_j$ and $q_{hk}=R_h\cap R_k$. Let $\lambda =\sharp \{p_{ij}\}_{i,j\in \{1,2,3\}}$ and $\rho =\sharp \{q_{hk}\}_{h,k\in \{1,2,3\}}$ be the cardinality of the intersection points. If $\lambda =\rho$ then there is a linear automorphism of $\mathbb {P}^2$ realizing the Cremona equivalence. Indeed with the choice of 4 points we can map one configuration to the other.

Assume, without loss of generality, that $\lambda =1$ and $\rho =3$. This time we need a birational modification to put the lines $\{L_1,L_2,L_3\}$ in general position. Let $p_1\in L_1$, $p_2\in L_2$, $q_1,q_2\in L_3$ and $x\in \mathbb {P}^2$ be general points. Consider the linear system

$$\begin{aligned} \mathcal {L}=|\mathcal {I}_{p_1^2\cup p_2^2\cup x^2\cup p_{12}\cup q_1\cup q_2}(4)| \end{aligned}$$

of quartics singular along $p_1,p_2,x$ and passing through the intersection point $p_{12}$ and $q_1$, $q_2$. Then $\phi _\mathcal {L}:\mathbb {P}^2\dasharrow \mathbb {P}^2$ is a Cremona transformation, the composition of two standard Cremona maps,

$$\begin{aligned} \deg \phi _\mathcal {L}(L_i)=4-3=1 \end{aligned}$$

and the lines $\{\phi _\mathcal {L}(L_1),\phi _\mathcal {L}(L_2),\phi _\mathcal {L}(L_3)\}$ are in general position.

We already observed that, thanks to Noether–Castelnuovo Theorem and the quadro quadric transformation of Example 2.3, any Cremona map of $\mathbb {P}^2$ can be extended to an arbitrary $\mathbb {P}^r$. Then for $r\ge 3$ it is enough to prove that any set of three lines is Cremona equivalent to a set of three lines in a plane.

Let $\{L_1,L_2,L_3\}\subset \mathbb {P}^r$ be a set of three lines. Assume first that there is an irreducible quadric $Q\subset \mathbb {P}^r$ containing the set. Let $Y\subset Q$ be a general hyperplane section and $p\in Q$ a general point. Then the quadro-quadric map centered in Y and p maps $\{L_1,L_2,L_3\}$ to a set of three lines in $\mathbb {P}^{r-1}$. Therefore by a recursive argument we may assume that the lines $\{L_1,L_2,L_3\}$ are contained neither in an irreducible quadric nor in a plane and in particular $n=3$.

Here I want to propose two different approaches. First consider a point $p\in \mathbb {P}^3$ and conic $C\subset \mathbb {P}^3$ intersecting the three lines. Let X be a quartic singular along $C\cup p$ and containing $L_1\cup L_2\cup L_3$. By an easy dimensional count X exists and it is mapped to a quadric by a quadro-quadric map centered in $C\cup p$. This is enough to prove that all lines triples are Cremona equivalent.

Then I want to argue in a different way. Without loss of generality, we may assume that $L_1$ is skew to $L_2$ and $L_3$ and $L_2\cap L_3=p$. Pick a general cubic surface S containing $L_1, L_2,L_3$ and let $R\subset S$ be a line intersecting $L_3$ and skew with $L_1$ and $L_2$. Let $\pi :S\rightarrow \mathbb {P}^2$ be the blow down of $L_1, L_2, R$ and three more $(-1)$-curves in S, to points $p_1,p_2,p_3,p_4,p_5, p_6\in \mathbb {P}^2$. Then $\pi (L_3)$ is a line in $\mathbb {P}^2$ spanned by $p_2$ and $p_3$. Let $C\subset \mathbb {P}^2$ be a conic with

$$\begin{aligned} C\cap \{ p_1,p_2,p_3,p_4,p_5, p_6\}=\{p_1,p_2,p_4\}, \end{aligned}$$

then $\Gamma :=\pi ^{-1}_*C$ is a twisted cubic intersecting $L_1, L_2$ and $L_3$ in a point. Let $S_1$ be a general cubic surface containing $\Gamma$ and R the residual intersection

$$\begin{aligned} S\cap S_1=\Gamma \cup R. \end{aligned}$$

Then $R\cap L_i=2$ and the cubo-cubic map $\phi :\mathbb {P}^3\dasharrow \mathbb {P}^3$ centered in R maps S to a plane and the $L_i$ in lines. This is enough to conclude that all triples of lines in $\mathbb {P}^n$ are Cremona equivalent.

Despite the beauty of this constructions it is clearly impossible to proceed in this way for an arbitrary number of lines. Already four lines have many different configurations and one should be able to produce a Cremona modification for all of them. Note further that in $\mathbb {P}^2$ not all line configurations are Cremona equivalent, see [11] for a vast treatment of lines configuration with respect to Cremona equivalence and the problem of contractibility.

Next we consider monoids.

Example 3.4

Irreducible monoids are always Cremona equivalent to a hyperplane. Let $X\subset \mathbb {P}^n$ be a monoid of degree d with vertex $p_0=[1,0,\ldots ,0]$ and Y a monoid of degree $d-1$ with the same vertex. Then the de Jonquiéres transformation given by

$$\begin{aligned} \{X,Yx_1,\ldots ,Yx_n\} \end{aligned}$$

maps X to the hyperplane $(y_0=0)$. Hence any irreducible monoid is Cremona equivalent to a hyperplane.

Example 3.5

Any irreducible rational surface in $\mathbb {P}^3$ of degree at most 3 is Cremona equivalent to a plane. Quadrics and singular cubics are monoids, therefore we conclude with Example 3.4. For smooth cubic we may use the cubo-cubic map to produce the equivalence. Note that non rational irreducible cubics, that is cones over elliptic curves, are not Cremona equivalent to any surface of lower degree, simply because all surfaces of smaller degree are rational.

Already for quartic surfaces in $\mathbb {P}^3$ the situation is much more complicate, but it is still possible to study it, see [18, 19].

Despite this quite long list of explicit examples of Cremona equivalences it is in general quite rare to be able to control birational modification that realizes a Cremona equivalence. On the other hand the Cremona group is so flexible that it is able to realize a huge set of Cremona equivalences. We are ready to appreciate the following theorem.

Theorem 3.6

[7, 20] Let $X,Y\subset \mathbb {P}^r$ be irreducible birational subvarieties and assume that $\dim X\le r-2$. Then X is Cremona equivalent to Y.

Let me spend a few words on this result and its consequences. The Theorem proves that the Cremona group contains, as subsets, the set of birational self map of any subvariety of codimension at least two. Note that in general nothing can be said on the group structure. That is there is no hint that it is possible to realize the group of birational selfmaps of a subvariety as subgroup of some Cremona group. Despite the proof of Theorem 3.6, especially the second one, is quite algorithmic it is in general almost impossible to write down an explicit map that furnishes the Cremona equivalence. On the other hand for few special cases of rational varieties it is possible to describe an explicit linearization, see [7].

It is quite easy to see that the bound on the codimension is sharp.

Example 3.7

Let $C\subset \mathbb{P} ^2$ be an irreducible rational curve of degree 6 with ordinary double points. Note that the pair $(\mathbb {P}^2,\frac{1}{2} C)$ has canonical singularities, therefore, by a standard application of Sarkisov theory, [20], any curve Cremona equivalent to C has degree at least 6, therefore C is not Cremona equivalent to a line.

In a similar fashion it is easy to produce examples in arbitrary dimension, see [20]. It is also possible to see that in general a fixed abstract variety has infinitely many inequivalent birational embeddings with respect to Cremona equivalence, [20].

Definition 3.8

A reduced variety $Z\subset \mathbb {P}^n$ is a cone if there is a point $p\in Z$, called vertex, such that $Z=\cup _{x\in Z{\setminus }\{p\}}\langle x,p\rangle$. The cone with vertex $p\in \mathbb {P}^n$ and base $X\subset \mathbb {P}^n$ is

$$\begin{aligned} C_p(X):=\cup _{x\in X}\langle x,p\rangle . \end{aligned}$$

Example 3.9

(Cones) In [17] it is proven that two divisorial cones $X,Y\subset \mathbb {P}^n$ are Cremona equivalent if their general hyperplane sections are Cremona equivalent. In particular, thanks to Theorem 3.6, a divisorial cone over a rational variety is always Cremona equivalent to a hyperplane.

It is less clear if the irreducibility assumption is needed. On one hand the example of lines, Example 3.3, is not encouraging since the Cremona modification needed depends on the intersection between the irreducible components. On the other hand there are no theoretical limits to extend the proof to reduced schemes. I must say that I was quite surprised when I realized that with few improvements a combination of the proofs in [20] and [7] worked in the reducible case. Before going into this I want to give a last explicit example of Cremona equivalence for reduced schemes: the case of points.

This is the only case in which I am able to provide the Cremona modification in a quite explicit way.

Construction 3.10

Let us consider a de Jonquiéres transformation of degree d,

$$\begin{aligned} \omega :\mathbb {P}^r\rightarrow \mathbb {P}^r \end{aligned}$$

given by

$$\begin{aligned}{}[x_0,\ldots ,x_r]\mapsto [x_0F_0+G_0,x_1(x_0F+G),\ldots ,x_r(x_0F+G)] \end{aligned}$$

Then $p_0=[1,0,\ldots ,0]$ is the vertex of all the monoids and the lines through $p_0$ are preserved. Let $l\ni p_0$ be a line and assume that $\omega$ is defined on the generic point of l. Then we have that either $\omega _{|l}$ is an automorphism or $\omega (l)=p_0$. Moreover $\omega$ is an isomorphism outside the cone with vertex $p_0$ and base

$$\begin{aligned} (x_0F_0+G_0=x_0F+G=0). \end{aligned}$$

As a birational map, we can write $\omega$ as

$$\begin{aligned}{}[x_0,\ldots ,x_r]\mapsto \left[ \frac{x_0F_0+G_0}{x_0F+G}, x_1,\ldots ,x_r\right] . \end{aligned}$$

Let $p=[a_0,\ldots ,a_r], q=[b_0,\ldots ,b_r]\in \mathbb {P}^r{\setminus }\{p_0\}$ be points aligned with $p_0$. Then we may assume that $a_i=b_i$, for $i=1,\ldots ,r$. Hence the condition $\omega (p)=q$ translates into the equation

$$\begin{aligned} a_0F_0(a_1,\ldots ,a_r)+G_0(a_1,\ldots ,a_r)=b_0(a_0F(a_1,\ldots ,a_r)+G(a_1,\ldots , a_r)), \end{aligned}$$

linear in the coefficient of $F_0,G_0,F,G$. Moreover if we choose a map $\omega$ such that $\omega (p)=p$, for a point $p\in \mathbb {P}^r{\setminus }\{p_0\}$ then $\omega$ is an isomorphism in a neighborhood of p.

Let us pick two points, $p,q\subset \mathbb {P}^r$ and a set of a points $\{p_1,\ldots , p_a\}\subset \mathbb {P}^r{\setminus }\langle p,q\rangle$. Then we may choose $p_0\in \langle p,q\rangle {\setminus }\{p,q\}$ such that no pair of points in $\{p_1,\ldots , p_a\}$ is aligned with $p_0$. This shows that there is a d(a) such that for $d\ge d(a)$ there is a de Jonquiéres map, $\omega$, centered in $p_0$ of degree d such that $\omega (p_i)=p_i$, for $i=1,\ldots ,a$ and $\omega (p)=q$. In particular $\omega$ is an isomorphism in a neighborhood of $\{p_1,\ldots , p_a,p,q\}$.

Let us take advantage of this construction to give an explicit version of the Cremona equivalence between reduced sets of points.

Theorem 3.11

Let $Z=\{p_1,\ldots ,p_s\}$ and $Z^\prime =\{p_1^\prime ,\ldots ,p_s^\prime \}$ be reduced sets of s points in $\mathbb{P} ^r$. Then there exists a Cremona transformation $\omega :\mathbb{P} ^r\dasharrow \mathbb{P} ^r$ such that $\omega$ is an isomorphism in a neighborhood of Z and $\omega (Z)=Z^\prime$.

Proof

Let us prove the statement via a recursive argument. We may assume, eventually after a generic quadro-quadric modification, that for any $i=1,\ldots , s$

$$\begin{aligned} \langle p_i,p_i^\prime \rangle \cap \{p_1,\ldots ,p_s,p_1^\prime \ldots ,p_s^\prime \}=\{p_i,p_i^\prime \}. \end{aligned}$$

Then by Construction 3.10 there is a de Jonquiéres map $\phi _1:\mathbb {P}^r\dasharrow \mathbb {P}^r$ such that:

• $\phi _1(p_1)=p_1^\prime$,

• $\phi _1(p_i)=p_i$ and $\phi _1(p_i^\prime )=p_i^\prime$ for $i\ge 2$.

In particular $\phi _1$ is an isomorphism in a neighborhood of $Z\cup Z^\prime$. Set, recursively, $\phi _i:\mathbb {P}^r\dasharrow \mathbb {P}^r$ a de Jonquiéres map such that:

• $\phi _i(p_j^\prime )=p_j^\prime$, for $j<i$,

• $\phi _i(p_i)=p_i^\prime$,

• $\phi _i(p_h)=p_h$ and $\phi _i(p_h^\prime )=p_h^\prime$ for $h>i$.

Then the composition

$$\begin{aligned} \Phi :=\phi _r\circ \cdots \circ \phi _1 \end{aligned}$$

realizes a Cremona equivalence between Z and $Z^\prime$. $\square$

Remark 3.12

Note that Theorem 3.11 proves the Theorem 1.1 for $r=2$. The next section we will devoted to extend it to arbitrary $r\ge 3$.

4 Cremona equivalence for reduced schemes

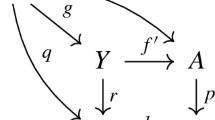
In this section X and Y will be reduced schemes in $\mathbb {P}^r$. Let us start observing a useful way to consider a birational relation between them. The schemes X and Y are birational if exists a smooth scheme Z such that:

• Z has a number of connected components equal to the number of irreducible components of X and Y;

• there are two base point free linear systems $\mathcal {L}_X$ and $\mathcal {L}_Y$ such that the induced morphism $\phi _{\mathcal {L}_X}:Z\rightarrow X$ and $\phi _{\mathcal {L}_Y}:Z\rightarrow Y$ are dominant and birational.

Let ${{\mathcal {M}}}=\mathcal {L}_X+\mathcal {L}_Y$ be the linear system on Z and $\phi _{{\mathcal {M}}}:Z\rightarrow \mathbb {P}^N$ the associated map. We may consider X and Y as linear projections of $\phi _{\mathcal M}(Z)\subset \mathbb {P}^N$. This is essentially the reason we opted in Definition 2.1 to accept non coprime sets of polynomials. With this trick we will be able to factorize a Cremona equivalence between X and Y into steps associated to monoids.

Construction 4.1

(Double projection) Let $X\subset \mathbb{P} ^ r$ be an irreducible monoid of degree d. Let $p_1, p_2\in X$ be two vertices, let $H_1,H_2$ be hyperplanes with $p_i\not \in H_i$, and consider the stereographic projections of X from $p_i$, which is the restriction of the projection $\pi _i:\mathbb{P} ^r\dasharrow H_i$ from $p_i$, with $i=1,2$. The map

$$\begin{aligned} \pi _{X,p_1,p_2}:=\pi _2\circ \pi _1^ {-1}:H_1\dasharrow H_2 \end{aligned}$$

is a Cremona transformation. If $p_1=p_2=p$, then $\pi _{X,p,p}$ does not depend on X and it is a linear automorphism, classically called the perspective with center p of $H_1$ to $H_{2}$.

From now on, we restrict to the case when $p_1\ne p_2$. In this setting, the map $\pi _{X,p_1,p_2}$ is called the double projection and it depends on X and it is in general nonlinear. Assume that $p_r=[0,\ldots ,0,1], p_{r-1}=[0,\ldots , 0,1,0]$ and the hyperplanes $H_1, H_2$ have equations $(x_r=0)$ and $(x_{r-1}=0)$ respectively. Then the defining equation of X has the form

$$\begin{aligned} F_d+x_{r-1}G_{d-1}+x_rF_{d-1}+ x_{r}x_{r-1}F_{d-2}=0, \end{aligned}$$

with $F_i,G_i\in \mathbb {C}[x_0,\ldots ,x_{r-2}]_i$. Then the double projection map $\pi _{X,p_r,p_{r-1}}$ is given by

$$\begin{aligned}{}[x_0,\ldots , x_{r-1}]\mapsto [(F_{d-2}x_{r-1}+F_{d-1})x_0,\ldots , (F_{d-2}x_{r-1}+F_{d-1})x_{r-2},-F_d-x_{r-1}G_{d-1}]. \end{aligned}$$

Observe that the double projection is a de Jonquiéres map of degree d centered in $p_{r-1}\in H_1$.

The main idea to produce the Cremona equivalence between X and Y is borrowed from [20]. Since X and Y are linear projection of the same variety $\phi _{{\mathcal {M}}}(Z)\subset \mathbb {P}^N$ their embedding is determined by functions on Z that are linearly equivalent. Let us see how to use this remark. Let, in this set up, $\phi :Z\dasharrow X\subset \mathbb {P}^r$ be given by equations

$$\begin{aligned} t\mapsto [\phi _0(t),\ldots ,\phi _r(t)] \end{aligned}$$

and $\psi :Z\dasharrow Y\subset \mathbb {P}^r$ by equations

$$\begin{aligned} t\mapsto [\psi _0(t),\ldots ,\psi _r(t)], \end{aligned}$$

with t coordinates on a dense open subset of Z intersecting all connected components. In general $\{(\phi _i=0)\}$ and $\{(\psi _j=0)\}$ have fixed divisorial component but nonetheless they define birational maps to X and Y respectively.

Then we may consider the birational embedding $\eta :Z\dasharrow Z_1\subset \mathbb {P}^{r+1}$ given by equations

$$\begin{aligned} t\mapsto [\phi _0(t),\ldots ,\phi _r(t),\psi _0(t)]. \end{aligned}$$

Assume that there is an irreducible monoid X, with vertices $p_r$ and $p_{r+1}$ and containing $Z_1$. Then the double projection $\pi _{X,p_{r+1},p_r}$ produces a Cremona map $\omega :\mathbb {P}^r\dasharrow \mathbb {P}^r$ such that $\omega (X)$ is associated to the birational embedding

$$\begin{aligned} \phi _1:Z\dasharrow X_1\subset \mathbb {P}^r \end{aligned}$$

given by equations

$$\begin{aligned} t\mapsto [\phi _0(t),\ldots ,\phi _{r-1}(t),\psi _0(t)]. \end{aligned}$$

If further, the monoid X does not contains any of the cones with vertex either $p_r$ or $p_{r+1}$ and base an irreducible component of $Z_1$, then the double projection realizes a Cremona equivalence between X and $\omega (X)$.

Iterating this process we may substitute the functions $\phi _j$ with the functions $\psi _h$ realizing a chain of double projections, that is de Jonquiéres maps, that produces the required Cremona equivalence.

To let this argument work we need to produce the required monoids. Let us start rephrasing [7, Lemma 2.1] to the reducible case, I adopt notation of [12, Chapter 6] for the intersection theory needed.

Remark 4.2

I want to thank the referee for pointing out the following version of the proof that allows to remove the assumption that the projection of Z from $p_r$ is birational.

Lemma 4.3

Let $Z:=\cup _1^h Z_i\subset \mathbb {P}^r{\setminus }\{[0,\ldots ,0,1]\}$ be a reduced scheme, $M_d$ the linear system of monoids with vertex $p_r:=[0,\ldots ,0,1]$ and $M(Z)_d\subset M_d$ those containing the scheme Z. Then, for $d\gg 0$, we have

$$\begin{aligned} \dim (M(Z)_d)\ge \frac{2d^{r-1}}{(r-1)!}+\frac{(r-1-\delta )d^{r-2}}{(r-2)!}+O(d^{r-3}), \end{aligned}$$

where

$$\begin{aligned} \delta =Z\cdot \mathcal{O}_{Z}(1)^{r-2}, \end{aligned}$$

in particular $\delta =0$ if $\dim Z<r-2$.

Proof

Let $\nu :V\rightarrow \mathbb{P} ^ r$ be the blow–up of $\mathbb{P} ^ r$ at $p_r$ with exceptional divisor E. We denote by H the pull back of a general hyperplane of $\mathbb{P} ^ r$ and by $Z'$ the proper transform of Z.

In this notation we have

$$\begin{aligned} M_d \cong \vert dH-(d-1)E\vert = \vert (d-1)(H-E)+H\vert , \end{aligned}$$

and, by a simple dimension count,

$$\begin{aligned} \dim (M_d)=\frac{2d^{r-1}}{(r-1)!}+\frac{(r-1)d^{r-2}}{(r-2)!}+O(d^{r-3}). \end{aligned}$$

(1)

Set $s=\dim Z\le r-2$ by assumption the point $p\not \in Z$, hence

$$\begin{aligned} \mathcal {O}_V(E)\otimes \mathcal {O}_{Z^\prime }\cong \mathcal {O}_{Z^\prime } \end{aligned}$$

and

$$\begin{aligned} \mathcal {O}_{Z^\prime } (dH-rE)\cong \mathcal {O}_{Z^\prime } (dH)\cong \mathcal {O}_{Z}(d), \end{aligned}$$

for any $d,r\in \mathbb {Z}$. In particular, as a polynomial in d

$$\begin{aligned} h^0(\mathcal {O}_{Z^\prime }(dH-rE))=h^0(\mathcal {O}_{Z}(d))=\frac{\delta }{s!}d^s+o(d^{s-1}). \end{aligned}$$

Thus

$$\begin{aligned} \dim (M(Z)_d)\ge \dim (M_d)-h^0(\mathcal {O}_{Z^\prime }(d(H-E)))= \frac{2d^{r-1}}{(r-1)!}+\frac{(r-1-\delta )d^{r-2}}{(r-2)!}+O(d^{r-3}). \end{aligned}$$

$\square$

Next we use Lemma 4.3 to produce monoids.

Lemma 4.4

Let $Z=\cup _1^h Z_j\subset \mathbb{P} ^ r$, with $r\geqslant 3$, be a reduced scheme of dimension $r-2$ and let $p\in \mathbb{P} ^ r{\setminus } Z$ be such that the projection of Z from p is birational to its image. For $d\gg 0$ there is an irreducible monoid of degree d with vertex p, containing Z and not containing the cone $C_p(Z_j)$ over $Z_j$ with vertex p, for $j=1,\ldots h$.

Proof

In the notation of Lemma 4.3 consider $M(Z)_d\subset M_d$ the sublinear system of monoids containing Z.

By Lemma 4.3 we have

$$\begin{aligned} \dim M(Z)_d\ge \frac{2d^{r-1}}{(r-1)!}+\frac{(r-1-\delta )d^{r-2}}{(r-2)!}+O(d^{r-3})>0, \end{aligned}$$

where $\delta$ is the degree of the $(r-2)$-dimensional part of Z. Note that $r\ge 3$ forces $\delta >0$.

Claim 1

For any $j=1,\ldots , s$ and $d\gg 0$ there is a monoid $B_j\in M(Z_j)_d$ such that

$$\begin{aligned} B_j\not \supset C_p(Z_j). \end{aligned}$$

Proof

Let $a=\dim Z_j$ and $\pi _j:\mathbb {P}^{r}\dasharrow \mathbb {P}^{a+2}$ be a general linear projection, if $a=r-2$ we set $\pi _j=id_{\mathbb {P}^r}$. Set $\overline{p}:=\pi _j(p)$, $\overline{Z}:=\pi _j(Z_j)$ and $\alpha =\deg \overline{Z}$.

To prove the claim it is enough to produce a monoid in $\mathbb {P}^{a+2}$ with vertex $\overline{p}$, containing $\overline{Z}$ and not containing the cone $Y:=C_{\overline{p}}(\overline{Z})$.

Let $\overline{M}(\overline{Z})_d$ be the linear system of monoids with vertex $\overline{p}$ in $\mathbb {P}^{a+2}$ and containing $\overline{Z}$.

By Lemma 4.3 we have

$$\begin{aligned} \dim \overline{M}(\overline{Z})_d\ge \frac{2d^{a+1}}{(a+1)!}+\frac{(a+1-\alpha )d^{a}}{a!}+O(d^{a-1})>0. \end{aligned}$$

Let $M'\subset \overline{M}(\overline{Z})_d$ be the sublinear system of divisors containing the cone Y. Note that Y is a hypersurface of degree $\alpha$, i.e. $Y\in |\mathcal{O}_{\mathbb {P}^{a+2}}(\alpha )|$. Hence we have $M'\cong M_{d-\alpha }$ and

$$\begin{aligned} \dim (M')= & {} \frac{2(d-\alpha )^{a+1}}{(a+1)!}+\frac{(a+1)(d-\alpha )^{a}}{a!}+O(d^{a-1})\\= & {} \frac{2d^{a+1}}{(a+1)!}+\frac{(a+1-2\alpha )d^{a}}{a!}+O(d^{a-1}). \end{aligned}$$

Hence

$$\begin{aligned} \dim (\overline{M}(\overline{Z})_d)-\dim (M')=\frac{\alpha d^{a}}{a!}+O(d^{a-1})>0, \quad \text {for}\quad d\gg 0. \end{aligned}$$

This shows the existence of the required monoids. $\square$

Set

• $\pi :\mathbb {P}^{r}\dasharrow \mathbb {P}^{r-1}$ the projection from p

• ${\tilde{Z}}:=\pi (Z)$

• ${\tilde{Z}}_j=\pi (Z_j)$, for any irreducible component $Z_j\subset Z$.

By hypothesis for any $j=1,\ldots ,h$ the variety ${\tilde{Z}}_j$ is an irreducible component of degree $\deg Z_j$ of ${\tilde{Z}}$. In particular $Z_j$ is not contained in the cone over ${\tilde{Z}}{\setminus }\tilde{Z_j}$ with vertex p. Let

$$\begin{aligned} {\tilde{D}}_j\in |\mathcal {I}_{{\tilde{Z}}{\setminus }{\tilde{Z}}_j}(d)| \end{aligned}$$

be a divisor in $\mathbb {P}^{r-1}$ of degree d containing ${\tilde{Z}}{\setminus }{\tilde{Z}}_j$, and $D_j=C_p({\tilde{D}})$ its cone with vertex p.

By Claim 1, for $d\gg 0$, we have $D_j+B_j\in M(Z)_{2d}$. Moreover $D_j+B_j$ does not contain the cone $C_p(Z_j)$. This shows that the general element in $M(Z)_{2d}$ does not contain $C_p(Z_j)$. Hence the general element in $M(Z)_{2d}$ does not contain any of the cones $C_p(Z_j)$, for $j=1,\ldots ,s$. Note that a reducible monoid decomposes in the union of cones, with vertex p, and a single irreducible monoid. Therefore our construction shows that the general element in $M(Z)_{b}$ contains an irreducible monoid X with $X\supset Z$ and $X\not \supset C_p(Z_j)$ for $j=1,\ldots ,h$, for $b\gg 0$. $\square$

The next step is to produce the required double projections.

Lemma 4.5

Let $Z=\cup _1^hZ_j\subset \mathbb{P} ^ r$, with $r\ge 3$, be a reduced scheme of positive dimension $n\leqslant r-3$. Let $p_1,p_2\in \mathbb{P} ^ r{\setminus } Z$ be distinct points such that the projection of Z from the line $\langle p_1,p_2\rangle$ is birational to its image. For $d\gg 0$ there is an irreducible monoid of degree d with vertices $p_1$ and $p_2$, containing Z but not containing any cone $C_{p_i}(Z_j)$, for $i=1,2$ and $j=1,\ldots , h$.

Proof

We start the proof with a reduction to codimension 3 subvarieties.

Claim 2

It suffices to prove the assertion for $n=r-3$.

Proof of the Claim

Consider the projection of $\mathbb{P} ^ r$ to $\mathbb{P} ^ {n+3}$ from a general linear subspace $\Pi$ of dimension $r-n-4$ and call $Z', p'_1,p'_2$ the projections of $Z,p_1,p_2$ respectively. Then $Z'$ is birational to Z and it is still true that the projection of $Z'$ form $\langle {p_1',p_2'}\rangle$ is birational to its image. The dimension of $Z'$ is $n-3$.

Assume the assertion holds for $Z', p'_1,p'_2$ and let $F'\subset \mathbb{P} ^ {n+3}$ be an irreducible monoid of degree $d\gg 0$ with vertices $p'_1,p'_2$ containing $Z'$ but no irreducible components of $C_{p_i^\prime }(Z')$, for $i=1,2$. Let $F\subset \mathbb{P} ^ r$ be the cone over $F'$ with vertex $\Pi$. Then F is an irreducible monoid with vertices $p_1,p_2$ containing Z and no irreducible component of $C_{p_i}(Z)$, for $i=1,2$. $\square$

We can thus assume from now on that $n=r-3$. Fix two hyperplanes $H_1$ and $H_2$, where $p_1\not \in H_1$ and $p_2\not \in H_2$. Let $Z^1$ and $Z^2$ be the birational projections of Z from $p_1$ and $p_2$ to $H_1$ and $H_2$, respectively. Set $p'_{3-i}:=\pi _i(p_{3-i})$, for $i=1,2$. By hypothesis the projection of $Z^i$ from $p^\prime _{3-i}$ is birational, then, by Lemma 4.5, for $i=1,2$ there are irreducible monoids $X_i\subset H_i$ with vertex $p'_{3-i}$ such that:

• $X_i\supset Z^i$

• $X_i$ does not contain any irreducible component of $C_{p^\prime _{3-i}}(Z^i)\subset H_i$,

Set $Y_i:=C_{p_i}(X_i)\subset \mathbb {P}^r$ to be the cone over $X_i$ with vertex $p_i$, then $Y_i$ has the following properties:

• $Y_i$ is a cone with vertex $p_i$

• $Y_i$ is a monoid with vertex $p_{3-i}$,

• $Y_i$ contains the cone $C_{p_i}(Z)$,

• $Y_i$ does not contain any irreducible component of the cone $C_{p_{3-i}}(Z)$.

Then a general linear combination of $Y_1$ and $Y_2$ contains an irreducible monoid with vertices $p_1$ and $p_2$ containing Z and not containing any irreducible component of the cones with vertex $p_1$ and $p_2$ over Z. $\square$

To conclude the proof of Theorem 1.1 we will provide, for $r\ge 3$, the Cremona equivalence via a sequence of double projections as in [20, Theorem 1] and [7, Theorem 2.5]. To do this we plan to use Lemma 4.5. Therefore we need to ensure that projection from the line connecting the vertices of monoids are birational. In [7, Theorem 2.5] this was done via [3, Theorem 1]. Let me spend a few word on this nice Theorem.

Let $X\subset \mathbb {P}^N$ be a non degenerate scheme, the Segre locus of X, ${{\mathcal {S}}}(X)$, is the locus of points from which X is projected in a non birational way. When X is irreducible and reduced Calabri and Ciliberto, [3], proved that this locus has irreducible components of dimension less than $\dim X$, giving a very precise description of its irreducible components. Unfortunately when X is reducible this is no more true. As an example of this behavior consider $X=\cup L_i$ a union of lines, with $L_1\cap L_2\ne \emptyset$. Then any point of the plane spanned by $L_1$ and $L_2$ is in the Segre locus of X.

Therefore the Segre locus of reducible schemes is not well behaved as the one of irreducible varieties and therefore we cannot adapt [3, Theorem 1] for our purposes and we need to substitute it with a finer analysis than the one in [20] of the individual steps of the process. The following is what we need to complete the proof of Theorem 1.1.

Theorem 4.6

Let $X, Y\subset \mathbb{P} ^r$, with $r\geqslant 3$, be two reduced schemes of positive dimension $n<r-1$. Then X, Y are Cremona equivalent if and only if they are birationally equivalent.

Proof

One direction is clear. Assume that X and Y are birational. Then, as observed at the beginning of the section there is a smooth scheme Z and two birational morphisms

$$\begin{aligned} \phi _{\mathcal {L}_X}:Z\rightarrow X\subset \mathbb {P}^r \ \ \textrm{and}\ \ \phi _{\mathcal {L}_Y}:Z\rightarrow Y\subset \mathbb {P}^r, \end{aligned}$$

associated to linearly equivalent linear systems $\mathcal {L}_X\sim \mathcal {L}_Y$.

Claim 3

We may fix basis of $\mathcal {L}_X$ and $\mathcal {L}_Y$ such that the projection of $X=\phi _{\mathcal {L}_X}(Z)$ and $Y=\phi _{\mathcal {L}_Y}(Z)$ from any coordinate subspace of dimension m is birational to its image if $r> n+m+1$ and dominant to $\mathbb{P} ^{r-m-1}$ if $r\le n+m+1$.

Proof of the Claim

It is well known that for any reduced scheme $X\subset \mathbb {P}^r$ of dimension n the projection from a general linear space of dimension less than $r-n-1$ is birational and finite and the projection from a general space of dimension $r-n-1$ is finite. Then it is enough to choose a basis of $\mathcal {L}_X$ and $\mathcal {L}_Y$ in such a way that such linear spaces are coordinate subspaces. $\square$

We may assume that $\phi _{\mathcal {L}_X}$ is given by equations

$$\begin{aligned} t\mapsto [\phi _o(t),\ldots ,\phi _r(t)] \end{aligned}$$

and $\phi _{\mathcal {L}_Y}$ is given by equations

$$\begin{aligned} t\mapsto [\psi _0(t),\ldots ,\psi _r(t)] \end{aligned}$$

where $(\phi _j=0), (\psi _h=0)$ are linearly equivalent divisors on Z and t varies in a suitable dense open subset of Z intersecting all irreducible components of Z.

We prove the theorem by constructing a sequence of birational maps

$$\begin{aligned} \varphi _i: Z\dasharrow Z_i\subset \mathbb{P} ^{r+1}, \end{aligned}$$

and projections

$$\begin{aligned} \eta _i:Z_i\dasharrow X_i,\ \ \nu _i:Z_i\dasharrow X_{i+1}, \end{aligned}$$

for $0\leqslant i\leqslant r$, such that:

• (a) $\eta _0\circ \varphi _0=\phi$ and $\nu _r\circ \varphi _r=\psi$, thus $X_0=X$ and $X_{r+1}=Y$;

• (b) for $0\leqslant i\leqslant r$, there is a Cremona transformation $\omega _i:\mathbb{P} ^ r\dasharrow \mathbb{P} ^ r$, such that $\omega _i$ is an isomorphism in a neighborhood of the generic points of $X_i$, it satisfies $\omega _i(X_i)=X_{i+1}$ and $\omega _{i|X_i}=\nu _i\circ \eta _i^{-1}$.

We may summarize the sequence of maps in the following diagram

The construction is done recursively. For $i=0$ we set

$$\begin{aligned} \varphi _0(t)= [\phi _{0}(t),\ldots ,\phi _{r}(t), \psi _{0}(t)], \\ \eta _0:= \pi _{[0,\ldots ,0,1]|Z_0} \end{aligned}$$

the restriction of the projection from the $(r+1)$th-coordinate point $p_{r+1}:=[0,\ldots ,0,1]$ and

$$\begin{aligned} \nu _0:=\pi _{[0,\ldots ,0,1,0]|Z_0} \end{aligned}$$

the restriction of the projection from the $r$th-coordinate point $p_r:=[0,\ldots ,0,1,0]$. By Claim 3 the projection from $\langle p_r,p_{r+1}\rangle$ is birational. Then by Lemma 4.5 there is a monoid $W\subset \mathbb {P}^{r+1}$ containing $Z_0$ and with vertices in $p_{r+1}$ and $p_r$ such that the double projection $\pi _{W,p_{r+1},p_{r}}$ is an isomorphism on the generic points of $X_0$ and realizes a Cremona equivalence $\omega _0:\mathbb {P}^r\rightarrow \mathbb {P}^r$ such that $\omega _0(X_0)=X_1$.

Assume $0< i\leqslant r-1$. In order to perform the step from i to $i+1$, we have to define the maps $\varphi _{i+1}$, $\eta _{i+1}$, $\nu _{i+1}$ and $\omega _{i+1}$. From the $i$th-step we have the map

$$\begin{aligned} \nu _i\circ \varphi _{i}: Z\dasharrow X_{i+1}\subset \mathbb {P}^ {r} \end{aligned}$$

given by

$$\begin{aligned} t\mapsto [\tilde{\phi }_{i,0}(t),\ldots , \tilde{\phi }_{i,r-i}(t),\psi _{0}(t),\ldots , \psi _i(t)], \end{aligned}$$

for suitable functions $\tilde{\phi }_{i,j}$. Then we define $\varphi _{i+1}:Z\dasharrow Z_{i+1}\subset \mathbb {P}^{r+1}$ as

$$\begin{aligned} t\mapsto [\tilde{\phi }_{i,0}(t),\ldots , \tilde{\phi }_{i,r-i}(t),\psi _{0}(t),\ldots , \psi _i(t),\psi _{i+1}(t)]. \end{aligned}$$

Note that we added the function $\psi _{i+1}$ on the last coordinate, therefore

$$\begin{aligned} \pi _{[0,\ldots ,0,1]}(Z_{i+1})=X_{i+1}. \end{aligned}$$

Therefore we set

$$\begin{aligned} \eta _{i+1}:=\pi _{[0,\ldots ,0,1]|Z_{i+1}}. \end{aligned}$$

To define $\nu _{i+1}$ we need to take a point

$$\begin{aligned} p\in \Pi _{i}:= \{x_{r-i+1}=\ldots =x_{r+1}=0\}\subset \mathbb {P}^{r+1} \end{aligned}$$

and prove that the projection from the line $l_p:=\langle p,[0,\ldots ,0,1]\rangle$ restricts to a birational map on $Z_{i+1}$.

Claim 4

The projection of $Z_{i+1}$ from a general line $l_p$ is birational to its image.

Proof of the Claim

Let $\pi :=\pi _{[0,\ldots ,0,1]}:\mathbb {P}^{r+1}\dasharrow \mathbb {P}^{r}$ be the projection from the point $[0,\ldots ,0,1]$ and ${\tilde{Z}}=\pi (Z_{i+1})$. By construction $\pi _{|Z_{i+1}}$ is birational. Let

$$\begin{aligned} A:=\{x_{r-i+1}=\ldots =x_{r}=0\}\subset \mathbb {P}^{r} \end{aligned}$$

be the linear space we are interested in and $\pi _A:\mathbb {P}^r\dasharrow \mathbb {P}^{i-2}$ the linear projection from A. To prove the claim we have to prove that the projection from a general point of A restricts to a birational map onto ${\tilde{Z}}$.

By Claim 3 the restriction $\pi _{A|{\tilde{Z}}}$ is either birational onto the image or dominant. If $\pi$ is birational the claim is clear.

Assume that $\pi _{A|{\tilde{Z}}}$ is dominant, in particular $i-2\le n$. Let $F\subset {\tilde{Z}}$ be a general fiber of this projection. We have $\dim F_j\le n-i+2$, for all irreducible components $F_j\subset F$. Moreover the fiber F is contained in a linear space $P_F$ of dimension $r-i+2$ and $A\cap P_F$ is a hyperplane. Since

$$\begin{aligned} {{\,\textrm{cod}\,}}_{P_F} F\ge 3 \end{aligned}$$

the general projection from a line in $P_F$ restricts to F as a birational map and being A an hyperplane this shows that the projection, say $\pi _p$, from a general point $p\in A$ restricts to F as a birational map. Let $x\in F$ be a general point and r the line spanned by p and x. By construction we have

$$\begin{aligned} r\cap {\tilde{Z}}=r\cap F=\{x\}. \end{aligned}$$

The scheme F is the general fiber of the linear projection $\pi$ and $x\in F$ is a general point, hence the line r is not tangent to ${\tilde{Z}}$ in x. This shows that the morphism $\pi _{p|{\tilde{Z}}}$ is birational as required. $\square$

Let $p\in \Pi _{i}$ be a general point and $\pi _{p}:\mathbb {P}^{r+1}\dasharrow \mathbb {P}^r$ the projection from p. Set

$$\begin{aligned} \nu _{i+1}:=\pi _{p|Z_{i+1}}. \end{aligned}$$

Thanks to Claim 4 we are in the condition to apply Lemma 4.5 and produce a monoid $W\subset \mathbb {P}^{r+1}$ with the following properties:

• $W\supset Z_{i+1}$

• $p_{r+1}$ and p are vertices of W

• the double projection $\pi _{W,p_{r+1},p}$ is an isomorphism on the generic points of $X_{i+1}$.

Therefore the double projection $\pi _{W,p_{r+1},p}$ realizes a birational map $\omega _{i+1}:\mathbb {P}^r\dasharrow \mathbb {P}^r$ such that $\omega _{i+1}(X_{i+1})=X_{i+2}$ and $\omega _{i+1}$ is an isomorphism in a neighborhood of the generic points of $X_{i+1}$. This proves part (b) of the requirements.

To conclude observe that at the $r$th-step we have

$$\begin{aligned} \varphi _{r}(t)=[\tilde{\phi }_{r,0}(t),\psi _0(t),\ldots ,\psi _r(t)], \end{aligned}$$

therefore, thanks to Claim 3, the restriction of the projection from $p_0:=[1,0,\ldots ,0]$ is automatically birational and the same is true for the projection from the line $\langle [1,0,\ldots ,0],[0,\ldots ,0,1]\rangle$. Therefore we set $\nu _r:=\pi _{[1,0,\ldots ,0]|Z_r}\circ \varphi _r$ to fulfill also the last part of requirement (a).

This chain of double projections realizes the Cremona equivalence between X and Y. $\square$

Remark 4.7

It is interesting to stress the following point. We already observed that double projections are associated to de Jonquiéres Cremona transformations. Therefore all Cremona equivalences of subvarieties of codimension at least 2 can be realized by transformations in the subgroup generated by de Jonquiéres transformations. This is particularly interesting when confronted with [1] where it is proven that the group of de Jonquiéres map is a proper subgroup of $Cr_n$. That is to produce all Cremona equivalences for codimension $\ge 2$ reduced schemes we do not even need the full group $Cr_n$.

As an application of the main result we prove a general contractibility criteria for sets of rational varieties.

Corollary 4.8

Let $Z=\cup _1^s T_i\subset \mathbb {P}^r$ be a reduced scheme all of whose irreducible components are rational varieties of dimension at most $r-2$. Then there is a birational map $\omega :\mathbb {P}^r\dasharrow \mathbb {P}^r$ that contracts Z to a set of s distinct points.

Proof

By Theorem 4.6 there is a birational map $\phi :\mathbb {P}^r\dasharrow \mathbb {P}^r$ such that $\phi (Z)$ is a union of s linear spaces. We are therefore left to study the case of linear spaces. We prove the claim by induction on the dimension of Z. Assume $\dim Z=1$ and

$$\begin{aligned} Z=\cup _1^h l_i\cup \{p_{h+1},\ldots ,p_s\}, \end{aligned}$$

with $l_i$ lines. Then there is a birational map $\omega :\mathbb{P} ^r\dasharrow \mathbb {P}^r$ such that $\cap _1^h\omega (l_i)=p$ is a general point and $\omega (p_i)=p_i$. Consider a quadro-quadric map $\phi :\mathbb {P}^r\dasharrow \mathbb {P}^r$ centered in p and a general codimension 2 quadric Q intersecting the h lines. Then $\phi$ contracts the h lines to a set of h points.

Assume that $\dim Z=i$ and, by induction, that the result is true for sets of linear spaces of dimension at most $i-1\le r-3$.

Set

$$\begin{aligned} Z=\cup _1^h M_i\cup Z^\prime , \end{aligned}$$

with $M_i\cong \mathbb {P}^i$ and $\dim Z^\prime \le i-1$. Fix a general point $p\in \mathbb{P} ^r$, a general codimension 2 quadric $Q\subset H\subset \mathbb{P} ^r$ containing h linear spaces $A_i\subset Q$ of dimension $i-1$. By Theorem 4.6 there is a Cremona equivalence between Z and

$$\begin{aligned} W:=\cup _1^h\langle A_i,p\rangle \cup Z^\prime . \end{aligned}$$

Let $\omega :\mathbb{P} ^r\dasharrow \mathbb {P}^r$ be the quadro-quadric map with base locus $p\cup Q$. Then by construction

$$\begin{aligned} \omega _{|\langle A_i,p\rangle }\cong \mathbb {P}^{i-1}. \end{aligned}$$

Hence $\omega (W)$ is a union of linear spaces of dimension at most $i-1$ and we can conclude by induction that Z is contractible. $\square$