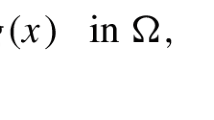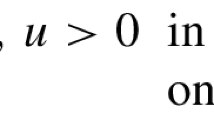Abstract
In this paper we focus on the following nonlocal problem with critical growth:
where \(s\in (0, 1)\), \(N>2s\), \(\Omega \subset \mathbb {R}^{N}\) is a smooth bounded domain, \(\lambda >0\), \((-\Delta )^{s}\) is the fractional Laplacian, \(f= te_{1}+h\) where \(t\in \mathbb {R}\), \(e_{1}\) is the first eigenfunction of \((-\Delta )^{s}\) with homogeneous Dirichlet boundary datum, and \(h\in L^{\infty }(\Omega )\) is such that \(\int _{\Omega } h e_{1}\, dx=0\). According to the interaction of the nonlinear term with the spectrum of \((-\Delta )^{s}\), we establish some existence and multiplicity results for the above problem by means of variational methods.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \(\Omega \subset \mathbb {R}^{N}\) be a smooth bounded domain, \(s\in (0, 1)\) and \(N>2s\). In this paper we deal with the following fractional elliptic problem with critical growth:
where \(2^{*}_{s}:= \frac{2N}{N-2s}\) is the fractional critical Sobolev exponent, \(\lambda >0\) is a constant, and \(u_{+}:= \max \{u, 0\}\). The leading operator \((-\Delta )^{s}\) is the so-called fractional Laplacian operator defined as follows:
We recall that in recent years a great interest has been devoted to the analysis of fractional and non-local operators of elliptic type, both for their interesting theoretical structure and in view of concrete applications in many fields such as, among the others, optimization, finance, phase transitions, anomalous diffusion, crystal dislocation, conservation laws, fractional quantum mechanics, quasi-geostrophic flows; see for instance [4, 24] for more details on this topic.
When \(s\rightarrow 1\), for u smooth enough, \((-\Delta )^{s}u\rightarrow -\Delta u\) and our problem is strictly related to a class of problems which are known as the Ambrosetti–Prodi type. We recall that Ambrosetti and Prodi [2] in 1972 studied the following boundary value problem:
with \(f\in C^{0, \alpha }(\bar{\Omega })\), \(\alpha \in (0, 1)\), \(g\in C^{2}(\mathbb {R})\) is such that \(g(0)=0\), \(g''(t)>0\) for all \(t\in \mathbb {R}\) and
where \(0<\mu _{1}<\mu _{2}\le \dots \le \mu _{n}\le \mu _{n+1}\le \dots\) denote the eigenvalues of \((-\Delta , H^{1}_{0}(\Omega ))\). By using some results on differentiable mappings with singularities, the authors showed that there exists in \(C^{0, \alpha }(\bar{\Omega })\) a closed connected \(C^{1}\) manifold M of codimension 1 such that \(C^{0, \alpha }(\bar{\Omega })\setminus M\) consists exactly of two connected components \(A_{1}\) and \(A_{2}\) with the following properties:
-
(1)
if \(f\in A_{1}\), then (1.2) has no solution,
-
(2)
if \(f\in A_{2}\), then (1.2) has exactly two solutions,
-
(3)
if \(f\in M\), then (1.2) has a unique solution.
Subsequently the the pioneering work by Ambrosetti and Prodi [2], different variants and generalizations of (1.2) have been achieved by many authors; see for instance [1, 5,6,7, 10, 12, 14,15,16,17,18,19,20,21,22, 26]. In particular, Ruf and Srikanth [26] analyzed
with \(1<p<2^{*}-1\) if \(N\ge 3\), where \(2^{*}:=\frac{2N}{N-2}\) is the critical exponent, and \(1<p<\infty\) if \(N= 2\), \(\lambda >\mu _{1}, \lambda \ne \mu _{n}\) for all \(n\in \mathbb {N}\), \(f:=t\varphi _{1}+\bar{f}\), \(t\in \mathbb {R}\), \(\varphi _{1}\) is the positive and normalized first eigenfunction of \((-\Delta , H^{1}_{0}(\Omega ))\), and \(\bar{f}\in C^{0}(\Omega )\) is such that \(\int _{\Omega } \bar{f}\varphi _{1}\, dx=0\). By applying the generalized mountain pass theorem [25], the authors proved that there exists a constant \(T=T(\bar{f})\) such that for \(t>T\) there are at least two solutions of (1.3).
On the other hand, Brezis and Nirenberg [9] in 1983 focused on the existence and non-existence of positive solutions for the following nonlinear critical elliptic problem:
where \(g(\cdot , 0)=0\) and g is some perturbation of lower order of the critical power. When \(g(x, u)=\lambda u\), with \(\lambda >0\), the authors proved that:
-
(A)
if \(N\ge 4\), (1.4) has a positive solution for every \(\lambda \in (0, \mu _{1})\); moreover, (1.4) has no positive solution if \(\lambda \notin (0, \mu _{1})\) and \(\Omega\) is star-shaped,
-
(B)
when \(N=3\) and \(\Omega\) is a ball, (1.4) has a positive solution if and only if \(\lambda \in (\frac{\mu _{1}}{4}, \mu _{1})\).
Later, Deng [18] treated the existence of multiple solutions for the following superlinear problem involving the critical exponent:
where \(g:\bar{\Omega }\times \mathbb {R}\rightarrow \mathbb {R}\in C^{1}\) satisfies \(\lim _{t\rightarrow \pm \infty } \frac{g(x, t)}{|t|^{2^{*}-1}}=0\) uniformly in \(x\in \Omega\), \(f:=t\varphi _{1}+\bar{f}\), \(t\in \mathbb {R}\), and \(\bar{f}\in C^{0, \alpha }(\bar{\Omega })\) is such that \(\int _{\Omega } \bar{f}\varphi _{1}\, dx=0\). Subsequently, motivated by [2, 9, 18, 26], De Figueiredo and Jianfu [16] investigated the existence and the multiplicity of solutions for the following critical Ambrosetti–Prodi type problem:
where \(f:=t \varphi _{1}+\bar{f}\), \(t\in \mathbb {R}\), and \(\bar{f}\in L^{r}(\Omega )\), with \(r>N\), is such that \(\int _{\Omega } \bar{f} \varphi _{1}\, dx=0\). More precisely, they established the following results:
-
(a)
if \(0<\lambda <\mu _{1}\), then there exists \(t_{0}=t_{0}(\bar{f})<0\) such that, if \(t<t_{0}\), (1.5) has a negative solution \(u_{t}\),
-
(b)
if \(\lambda >\mu _{1}\) and \(\bar{f}\) is such that \(\bar{f}\in \ker (-\Delta -\lambda )^{\perp }\) in the case that \(\lambda\) is an eigenvalue of \((-\Delta , H^{1}_{0}(\Omega ))\), then there exists \(t_{0}= t_{0}(\bar{f})>0\) such that, if \(t>t_{0}\), (1.5) has a negative solution \(u_{t}\),
-
(c)
if, in addition to either of the hypotheses above, one assumes that \(\lambda\) is not an eigenvalue of \((-\Delta , H^{1}_{0}(\Omega ))\) and that the dimension \(N>6\), then (1.5) has a second solution,
-
(d)
if \(\lambda =\mu _{1}\), there exists \({{\,\mathrm{\varepsilon }\,}}>0\) such that, if \(\Vert f\Vert _{L^{2}(\Omega )}<{{\,\mathrm{\varepsilon }\,}}\), then (1.5) has a solution.
To our knowledge, the critical fractional Ambrosetti–Prodi problem (1.1) has never been considered in the literature and the goal of this paper is to fill this gap. We underline that an Ambrosetti–Prodi type result for a subcritical problem driven by the fractional spectral Laplacian operator was studied in [3], and that several ideas used in [3] can be easily adapted to deal with the corresponding subcritical problem involving \((-\Delta )^{s}\).
Before stating our main theorems, we introduce some notations and definitions. Denote by
the usual fractional Sobolev space endowed with the norm
where
Let \(\mathbb {H}_{0}^{s}(\Omega )\) be the closed linear subspace given by
equipped with the norm
It is well-known that \(\mathbb {H}_{0}^{s}(\Omega )\) is a Hilbert space with the inner product
\(\mathbb {H}_{0}^{s}(\Omega )\) is continuously embedded in \(L^{r}(\mathbb {R}^{N})\) for all \(r\in [1, 2^{*}_{s}]\) and compactly embedded in \(L^{r}(\mathbb {R}^{N})\) for all \(r\in [1, 2^{*}_{s})\); see [24, Lemma 1.29 and Lemma 1.31]. In order to lighten the notation, in what follows we set \(C(N, s)/2:=1\). With
we indicate the best constant in the Sobolev embedding \(H^{s}(\mathbb {R}^{N})\subset L^{2^{*}_{s}}(\mathbb {R}^{N})\); see [13, Theorem 1.1].
Thanks to the space \(\mathbb {H}_{0}^{s}(\Omega )\), we can correctly encode the variational formulation of problem (1.1). We say that \(u\in \mathbb {H}_{0}^{s}(\Omega )\) is a weak solution to (1.1) if for every \(\phi \in \mathbb {H}_{0}^{s}(\Omega )\) it holds
Denote by \(0<\lambda _{1}<\lambda _{2}\le \dots \le \lambda _{n}\le \lambda _{n+1}\le \dots\) the eigenvalues of \(((-\Delta )^{s}, \mathbb {H}_{0}^{s}(\Omega ))\) with corresponding eigenfunctions \(e_{1}, e_{2}, \dots , e_{n}, e_{n+1}, \dots\) belonging to \(\mathbb {H}_{0}^{s}(\Omega )\). We recall that \(\lambda _{1}\) is simple, \(\lambda _{n}\rightarrow \infty\) as \(n\rightarrow \infty\), \(\{e_{n}\}_{n\in \mathbb {N}}\) is an orthonormal basis of \(L^{2}(\Omega )\) and an orthogonal basis of \(\mathbb {H}_{0}^{s}(\Omega )\), \(e_{n}\in C^{0, \alpha }(\bar{\Omega })\) for some \(\alpha \in (0, 1)\) and \(e_{1}>0\) in \(\Omega\); see [24, Proposition 3.1, Corollary 4.8 and Theorem 5.2].
Our principal results are the following.
Theorem 1
Let \(f:=te_{1}+h\) with \(h\in L^{\infty }(\Omega )\) such that
Suppose \(\lambda \in (\lambda _{k}, \lambda _{k+1})\) for some \(k\in \mathbb {N}\). Then:
-
(i)
there exists \(t_{0}= t_{0}(h)>0\) such that, if \(t>t_{0}\), (1.1) has a nonpositive solution \(u_{t}\in \mathbb {H}_{0}^{s}(\Omega )\),
-
(ii)
if in addition \(N>6s\), (1.1) has a second solution.
Theorem 2
Let \(\lambda =\lambda _{1}\) in (1.1). Suppose
and
where \(M_{1}, M_{2}>0\) are defined as
and
Then (1.1) has a solution.
The proofs of Theorem 1 and Theorem 2 will be obtained by applying suitable variational methods inspired by [16]. More precisely, in order to deduce the existence of a second solution in Theorem 1, we invoke the linking theorem [25] without the Palais–Smale condition. In particular, we use some standard estimates found in [24, 27] to deal with the fractional Brezis–Nirenberg type problem, and we prove some useful lemmas and crucial estimates needed to ensure that the energy functional associated with (1.1) satisfies all geometric assumptions of the linking theorem and that the solution accomplished as weak limit of a Palais–Smale sequence at the linking critical level is not trivial. Clearly, with respect to the local case \(s=1\), a more accurate analysis will be done to overcome some technical difficulties coming from the nonlocal character of \((-\Delta )^{s}\). Finally, we prove Theorem 2 by means of a minimization argument.
The paper is organized as follows. In Sect. 2 we give the proof of Theorem 1 and in Sect. 3 we prove Theorem 2.
2 Proof of Theorem 1
First we claim that (1.1) has a nonpositive solution \(u_{t}\). Let us note that all nonpositive solutions to (1.1) satisfy
By exploiting the Fredholm alternative, it is easy to check that the problem
admits a unique solution \(u_{0}\in \mathbb {H}_{0}^{s}(\Omega )\). From \(h\in L^{\infty }(\Omega )\) and [24, Proposition 4.11], we deduce that \(u_{0}\in L^{\infty }(\Omega )\). On the other hand, \(w_{t}:=\beta _{t} e_{1}\), where \(\beta _{t}:=\frac{t}{\lambda _{1}- \lambda }\), is the unique solution of
Set \(u_{t}:=u_{0}+\beta _{t} e_{1}\). Since \(\lambda >\lambda _{1}\), we get \(u_{t}\le 0\) for \(t>0\) sufficiently large. This implies that (i) of Theorem 1 holds. Let us observe that, if \(\lambda >\lambda _{1}\) is an eigenvalue of \(((-\Delta )^{s}, \mathbb {H}_{0}^{s}(\Omega ))\) and \(h\in \ker ((-\Delta )^{s}-\lambda )^{\perp }\), then we can show that there exists \(t_{0}= t_{0}(h)>0\) such that, if \(t>t_{0}\), (1.1) has a nonpositive solution \(u_{t}\in \mathbb {H}_{0}^{s}(\Omega )\).
From now on, we focus on (ii) of Theorem 1 by finding a second solution to (1.1) of the form \(u=v+u_{t}\), where v solves
To accomplish this purpose, we seek a critical point of the Euler-Lagrange functional \(\mathcal {J}: \mathbb {H}_{0}^{s}(\Omega )\rightarrow \mathbb {R}\) associated with (2.2), that is
We next verify that \(\mathcal {J}\) fulfills all geometric assumptions of the linking theorem (see [25, Theorem 5.3]). Since \(\mathbb {H}_{0}^{s}(\Omega )\) is a Hilbert space, we can consider the direct sum decomposition \(\mathbb {H}_{0}^{s}(\Omega )=\mathbb {H}^{-}\oplus \mathbb {H}^{+}\), where
and
Then it holds (see [24, Proposition 3.1 and Proposition 3.2])
Let \(S_{\varrho }:=\partial B_{\varrho }\cap \mathbb {H}^{+}\) and \(Q:=\{v\in \mathbb {H}_{0}^{s}(\Omega ): v= w+ \zeta \sigma , \, w\in \mathbb {H}^{-}, \, \Vert w\Vert _{\mathbb {H}_{0}^{s}(\Omega )}\le r, \, 0\le \zeta \le R\}\), where \(\sigma \in \mathbb {H}^{+}\), \(0<\varrho <R\) and \(r>0\) will be chosen later so that the following conditions hold:
Lemma 1
There exist \(\varrho >0\) and \(\alpha >0\) such that
Proof
Let \(v\in \mathbb {H}^{+}\). Since \(u_{t}\le 0\) and \(\lambda \in (\lambda _{k}, \lambda _{k+1})\), it follows from (2.3) and the Sobolev inequality [13, Theorem 1.1] that
Define
Observing that
we deduce that \(\omega (\zeta )\) achieve its maximum at \(\zeta = \varrho\) given by
and that
Therefore, \(\mathcal {J}(v)\ge \alpha\) for all \(v\in S_{\varrho }\). The proof of the lemma is complete.
Let \(\eta \in C_{c}^{\infty }(\mathbb {R}^{N})\) be a cut-off function such that \(0\le \eta \le 1\) in \(\mathbb {R}^{N}\), \(\eta =1\) in \(B_{\varsigma }\) and \(\eta =0\) in \(\mathbb {R}^{N}\setminus B_{2\varsigma }\), where \(\varsigma >0\) is such that \(B_{4\varsigma }\subset \Omega\). It is well known (see [13, Theorem 1.1]) that \(S_{*}\) is achieved by
with \(\kappa \in \mathbb {R}\setminus \{0\}\), \(\mu >0\) and \(x_{0}\in \mathbb {R}^{N}\) fixed constants. As in [27], for every \({{\,\mathrm{\varepsilon }\,}}>0\) we define
and set
We recall the following useful estimates (see [27, Proposition 21 and Proposition 22] and [24, Proposition 15.6]).
Lemma 2
Let \(s\in (0, 1)\) and \(N>2s\). Then we have:
Let \(P_{-}: \mathbb {H}_{0}^{s}(\Omega )\rightarrow \mathbb {H}^{-}\) and \(P_{+}: \mathbb {H}_{0}^{s}(\Omega )\rightarrow \mathbb {H}^{+}\) be the orthogonal projections of \(\mathbb {H}_{0}^{s}(\Omega )\) onto \(\mathbb {H}^{-}\) and \(\mathbb {H}^{+}\), respectively. Then, we can prove the next lemma.
Lemma 3
Let \(s\in (0, 1)\) and \(N>2s\). Then the following estimates hold:
Proof
We argue as in [11, Lemma 6]. We write \(u_{{{\,\mathrm{\varepsilon }\,}}}= P_{-}u_{{{\,\mathrm{\varepsilon }\,}}}+P_{+}u_{{{\,\mathrm{\varepsilon }\,}}}\) and
Then, by using (2.12), we can infer
Analogously, we can prove that, for some constant \(C>0\),
that is (2.18) holds. Now, exploiting (2.19), (2.20) and (2.13), we have
and thus (2.15) is satisfied. On the other hand, from (2.12), we see that
Using \(u_{{{\,\mathrm{\varepsilon }\,}}}= P_{-}u_{{{\,\mathrm{\varepsilon }\,}}}+P_{+}u_{{{\,\mathrm{\varepsilon }\,}}}\), \((a+b)^{p}\le 2^{p-1}(a^{p}+b^{p})\) for \(a, b\ge 0\) and \(p\ge 1\), and relations (2.13), (2.20), (2.21), we obtain
Hence, (2.16) is verified. Combining (2.12) and (2.21), we get (2.17). Finally, the estimate (2.14) is a consequence of (2.9). This completes the proof of the lemma.
Fix \(K>0\) and define the set \(\Omega _{{{\,\mathrm{\varepsilon }\,}}, K}:= \{x\in \Omega : P_{+}u_{{{\,\mathrm{\varepsilon }\,}}}(x)>K\}\). By (2.18) we can deduce
which implies that \(P_{+}u_{{{\,\mathrm{\varepsilon }\,}}}(0)\rightarrow \infty\) as \({{\,\mathrm{\varepsilon }\,}}\rightarrow 0\). By the continuity of \(P_{+}u_{{{\,\mathrm{\varepsilon }\,}}}\), there exists \(\nu >0\) such that \(B_{\nu }\subset \Omega _{{{\,\mathrm{\varepsilon }\,}}, K}\). Therefore, we have the result below.
Lemma 4
Let \(s\in (0, 1)\) and \(N>2s\). Then the following estimates hold:
From the fundamental theorem of calculus, we derive the following lemma (see [16, Lemma 2.5]).
Lemma 5
Let \(u, v \in L^{p}(\Omega )\) with \(p\in [2, 2^{*}_{s}]\). If \(\tilde{\Omega }\subset \Omega\) and \(u+v>0\) in \(\tilde{\Omega }\), then there exists a constant \(C>0\), depending on p, such that
Lemma 6
Let \(A, B, C, \nu >0\), and let
Then, \(G_{{{\,\mathrm{\varepsilon }\,}}}\) achieve its maximum at
and it holds
Proof
It is easy to prove that \(G_{{{\,\mathrm{\varepsilon }\,}}}\) achieves its maximum at \(\zeta _{{{\,\mathrm{\varepsilon }\,}}}\) and thus \(G'_{{{\,\mathrm{\varepsilon }\,}}}(\zeta _{{{\,\mathrm{\varepsilon }\,}}})=0\), that is
which yields
Let \(\beta _{{{\,\mathrm{\varepsilon }\,}}}:=\frac{\zeta _{{{\,\mathrm{\varepsilon }\,}}}- \zeta _{0}}{\zeta _{0}}\). Then \(\zeta _{{{\,\mathrm{\varepsilon }\,}}}\rightarrow \zeta _{0}\) and \(\beta _{{{\,\mathrm{\varepsilon }\,}}}\rightarrow 0\) as \({{\,\mathrm{\varepsilon }\,}}\rightarrow 0\). Moreover, by using (2.22) and \(\zeta _{{{\,\mathrm{\varepsilon }\,}}}= (1+ \beta _{{{\,\mathrm{\varepsilon }\,}}}) \zeta _{0}\), we get
Since
we can see that (2.23) becomes
Recalling that \((1+x)^{\alpha }=1+ \alpha x + o(x)\) as \(x\rightarrow 0\), we deduce that
which combined with \(\beta _{{{\,\mathrm{\varepsilon }\,}}}\rightarrow 0\) as \({{\,\mathrm{\varepsilon }\,}}\rightarrow 0\), implies that \(\beta _{{{\,\mathrm{\varepsilon }\,}}}=O({{\,\mathrm{\varepsilon }\,}}^{\nu })\). Finally, as \({{\,\mathrm{\varepsilon }\,}}\rightarrow 0\),
The proof of Lemma 6 is now complete.
Our aim is to select Q and \(\rho\) so that (2.5), (2.6) and (2.7) are satisfied. We also pick \(\sigma\) as function of \({{\,\mathrm{\varepsilon }\,}}\), namely \(\sigma :=P_{+}u_{{{\,\mathrm{\varepsilon }\,}}}\).
Lemma 7
There exist \(r_{0}>0\), \(R_{0}>0\) and \({{\,\mathrm{\varepsilon }\,}}_{0}>0\) such that, for \(r> r_{0}\), \(R> R_{0}\) and \({{\,\mathrm{\varepsilon }\,}}\in (0, {{\,\mathrm{\varepsilon }\,}}_{0})\), we have
for some \(\alpha _{0}<\alpha\), where \(\alpha >0\) is given in (2.8).
Proof
Let us observe that \(\partial Q= \mathcal {Q}_{1}\cup \mathcal {Q}_{2} \cup \mathcal {Q}_{3}\), where
We will study \(\mathcal {J}|_{\mathcal {Q}_{i}}\) for \(i=1,2,3\). We recall that \(\lambda \in (\lambda _{k}, \lambda _{k+1})\). For \(v\in \mathcal {Q}_{1}\), taking into account (2.4), we can see that
Let \(v\in \mathcal {Q}_{2}\). Define
and take
Fix \(0< \zeta \le \tau _{0}\). From (2.4), (2.24) and (2.25), we deduce that
Now, let \(\zeta > \tau _{0}\). Put
Since \(P_{+}u_{{{\,\mathrm{\varepsilon }\,}}}(0)\rightarrow \infty\) as \({{\,\mathrm{\varepsilon }\,}}\rightarrow 0\), there exists \({{\,\mathrm{\varepsilon }\,}}'_{0}>0\) such that, for all \(0<{{\,\mathrm{\varepsilon }\,}}<{{\,\mathrm{\varepsilon }\,}}'_{0}\),
Applying Lemma 5 with \(u=P_{+}u_{{{\,\mathrm{\varepsilon }\,}}}\), \(v=\frac{w+u_{t}}{\zeta }\), \(p=2^{*}_{s}\) and \(\tilde{\Omega }= \Omega _{{{\,\mathrm{\varepsilon }\,}}}\), we get
Then, by using Lemmas 2, 3, 4 and (2.26), we can see that, for \({{\,\mathrm{\varepsilon }\,}}>0\) small enough,
for some \(C_{1}, C_{2}>0\). Invoking Lemma 6, we get
Because
there exists \(r>0\) such that \(\mathcal {J}(v)<0\) for \(v\in \mathcal {Q}_{2}\). In this way we can obtain an \(r_{0}\) satisfying the thesis.
Now, fix \(v\in \mathcal {Q}_{3}\). Then, \(v= w + R P_{+}u_{{{\,\mathrm{\varepsilon }\,}}}\) with \(w\in \bar{B}_{r}\cap \mathbb {H}^{-}\), and it holds
Since \(w\in L^{\infty }(\Omega )\) (note that \(\bar{B}_{r}\cap \mathbb {H}^{-}\) is finite dimensional) and \(u_{t} \in L^{\infty }(\Omega )\) (recall that \(u_{t}=u_{0}+\beta _{t}e_{1}\) and \(u_{0}, e_{1}\in L^{\infty }(\Omega )\)), there exists \(k>0\) such that \(\Vert w+u_{t}\Vert _{L^{\infty }(\Omega )}\le k\). On the other hand, \(P_{+}u_{{{\,\mathrm{\varepsilon }\,}}}(0)\rightarrow \infty\) as \({{\,\mathrm{\varepsilon }\,}}\rightarrow 0\), so we can find \(0<{{\,\mathrm{\varepsilon }\,}}''_{0}<{{\,\mathrm{\varepsilon }\,}}'_{0}\) such that \(P_{+}u_{{{\,\mathrm{\varepsilon }\,}}}(0)>2k\) provided \(0<{{\,\mathrm{\varepsilon }\,}}<{{\,\mathrm{\varepsilon }\,}}''_{0}\). Fix \({{\,\mathrm{\varepsilon }\,}}\in (0, {{\,\mathrm{\varepsilon }\,}}''_{0})\). Then there are \(R_{1}=R_{1}({{\,\mathrm{\varepsilon }\,}})>0\) and \(\eta = \eta ({{\,\mathrm{\varepsilon }\,}})>0\) such that
Consequently, by (2.14), for \(R>R_{1}\),
so there exist \({{\,\mathrm{\varepsilon }\,}}_{0}, R_{0}>0\) such that, for \({{\,\mathrm{\varepsilon }\,}}\in (0, {{\,\mathrm{\varepsilon }\,}}_{0})\) and \(R>R_{0}\), we get \(\mathcal {J}(v)\le 0\) for \(v\in \mathcal {Q}_{3}\). The proof of Lemma 7 is now complete.
Lemma 8
Let \(s\in (0, 1)\) and \(N>6s\). Then the following estimate holds:
Proof
Let \({{\,\mathrm{\varepsilon }\,}}\in (0, {{\,\mathrm{\varepsilon }\,}}_{0})\) be such that the geometry of the linking theorem holds. Take \(w+ \zeta P_{+}u_{{{\,\mathrm{\varepsilon }\,}}} \in Q\). Then,
Let \(\delta\) and \(\tau _{0}\) be defined as in (2.24) and (2.25) respectively. Fix \(0< \zeta \le \tau _{0}\). Arguing as in the proof of Lemma 7 and bearing in mind (2.8), we can see that
Let \(\zeta > \tau _{0}\). As in the proof of Lemma 7, from (2.26), Lemma 2 and Lemma 4, we derive
By Lemma 6 we can infer
Using \(N>6s\), the fact that (2.11) and (2.18) imply
and applying Lemmas 2, 3 and 4, we have
Since \(2s<\frac{N-2s}{2}\) and \(\lambda >0\), the thesis follows by taking \({{\,\mathrm{\varepsilon }\,}}>0\) sufficiently small.
Now we are ready to complete the proof of Theorem 1.
Proof
In view of Lemmas 1, 7 and 8 with \({{\,\mathrm{\varepsilon }\,}}>0\) sufficiently small, it follows from the linking theorem without the Palais–Smale condition (see [23, Theorem 4.3] and [15, Theorem 5.1]) that there exists a sequence \(\{v_{n}\}_{n\in \mathbb {N}}\subset \mathbb {H}_{0}^{s}(\Omega )\) such that
that is, for all \(\phi \in \mathbb {H}_{0}^{s}(\Omega )\),
where c is the linking critical level given by
Now we prove that \(\{v_{n}\}_{n\in \mathbb {N}}\subset \mathbb {H}_{0}^{s}(\Omega )\) is bounded. Let us observe that, since \(u_{t}\le 0\), we have
On the other hand, from (2.27) and (2.28), we obtain
Putting together (2.29) and (2.30), we get
Write \(v_{n}= v_{n}^{-}+v_{n}^{+}\), with \(v_{n}^{\pm }\in \mathbb {H}^{\pm }\). Then, by using (2.3), we can see that
From (2.28), (2.31), (2.32), the Hölder inequality, the Young inequality with \(\eta >0\) (that is \(ab\le \eta a^{2}+C_{\eta }b^{2}\) for \(a, b\ge 0\)) and the Sobolev inequality [13, Theorem 1.1], we have
and choosing \(0<\eta <\frac{1}{C}\left( 1- \frac{\lambda }{\lambda _{k+1}}\right)\) (we recall that \(\lambda \in (\lambda _{k}, \lambda _{k+1})\)) we have
In a similar fashion, we can prove that
Then, (2.33) and (2.34) yield \(\Vert v_{n}\Vert _{\mathbb {H}_{0}^{s}(\Omega )}\le C\) for all \(n\in \mathbb {N}\). Up to a subsequence, we may assume that
Hence, v is a weak solution to
that is, for any \(\phi \in \mathbb {H}_{0}^{s}(\Omega )\) it holds
In particular, taking \(\phi =v\) in (2.37), we get
By applying the Brezis–Lieb lemma [8, Theorem 1], we obtain
and
Then, by using (2.35), (2.39) and (2.40), we deduce
On the other hand, by using (2.35), (2.38), (2.39) and (2.40), we have
Taking into account that \(\langle \mathcal {J}'(v_{n}), v_{n}\rangle \rightarrow 0\) and \(\int _{\Omega } (v_{n}-v)_{+}^{2^{*}_{s}-1} u_{t}\, dx \rightarrow 0\) as \(n\rightarrow \infty\), we deduce
Set \(w_{n}:= v_{n}-v\). Let
If \(\ell =0\), then \(v_{n}\rightarrow v\) in \(\mathbb {H}_{0}^{s}(\Omega )\) as \(n\rightarrow \infty\) and so \(0<\alpha \le c= \mathcal {J}(v)\), that is v is a nontrivial solution to (2.1). Let \(\ell >0\). Our goal is to prove that \(v\not \equiv 0\). Assume by contradiction that \(v=0\). Then, by the Sobolev inequality [13, Theorem 1.1] and (2.42), we can infer
which gives
Now, from (2.41), (2.42), (2.43), \(v=0\) and recalling that \(u_{t}\le 0\), we get
which contradicts Lemma 8. Therefore, \(v\not \equiv 0\). From (2.36) we also derive that \(v\ge 0\) in \(\mathbb {R}^{N}\).
Remark 1
It is also possible to prove that \(\mathcal {J}\) satisfies the Palais-Smale condition at any level \(d\in \mathbb {R}\) such that \(0<d<\frac{s}{N}S_{*}^{\frac{N}{2s}}\).
Remark 2
When \(0<\lambda <\lambda _{1}\), we can argue as at the beginning of Sect. 2 to prove that there exists \(t_{0}=t_{0}(h)<0\) such that, if \(t<t_{0}\), (1.1) has a nonpositive solution \(u_{t}\in \mathbb {H}_{0}^{s}(\Omega )\). If in addition we require that \(N>6s\), we can obtain the existence of a second solution to (1.1) by applying the mountain pass theorem (see [25, Theorem 2.2]).
3 Proof of Theorem 2
Let us consider the problem (1.1) with \(\lambda =\lambda _{1}\), namely
by assuming that (1.6) and (1.7) are satisfied. Let \(\mathbb {H}_{0}^{s}(\Omega )= \mathbb {H}^{-}\oplus \mathbb {H}^{+}\), where \(\mathbb {H}^{-}:= \mathrm{span}\{e_{1}\}\) and \(\mathbb {H}^{+}:=(\mathbb {H}^{-})^{\perp }\). The Euler-Lagrange functional \(\mathcal {J}:\mathbb {H}_{0}^{s}(\Omega )\rightarrow \mathbb {R}\) associated with (3.1) is given by
and its differential is
for \(u, \phi \in \mathbb {H}_{0}^{s}(\Omega )\). For any \(u\in \mathbb {H}_{0}^{s}(\Omega )\) there are \(t\in \mathbb {R}\) and \(v\in \mathbb {H}^{+}\) such that \(u= te_{1}+v\). Then, the functional \(\mathcal {J}\) becomes
where \(u=v+te_{1}\) and \(t= \int _{\Omega } ue_{1}\, dx\).
Lemma 9
For any given \(v\in \mathbb {H}^{+}\), \(\mathcal {J}\) is bounded from above in \(\mathbb {H}^{-}\).
Proof
Fix \(v\in \mathbb {H}^{+}\). Let us define
Note that, for \(t<0\), the Hölder inequality yields
Now, let \(t>0\). We first show that
Put \(M:=\sup _{x\in \Omega } e_{1}(x)\) and choose an open set \(\Omega _{0} \Subset \Omega\) such that \(e_{1}(x)> \frac{M}{4}\) for \(x\in \Omega _{0}\). Let \(\delta := \frac{|\Omega _{0}|}{2}\). Combining Lusin’s theorem with the Tietze extension theorem, we find \(h\in C^{0}(\mathbb {R}^{N})\) such that
Set \(A:=\{x\in \Omega _{0} : h(x)=v(x)\}\) and note that
Put \(L:=\sup _{x\in A} |v(x)|\). For \(x\in A\), we get
and thus there exists \(\kappa >0\) such that
The above inequality implies that (3.2) holds. Using the continuity of \(\psi\) in [0, T], we can infer that \(\mathcal {J}\) is bounded from above in \(\mathbb {H}^{-}\).
It is possible to prove that for each \(v\in \mathbb {H}^{+}\) there exists a unique \(t(v)\in \mathbb {R}\) such that
that is \(\mathcal {J}(v+te_{1})\le \mathcal {J}(v+t(v)e_{1})\) for all \(t\in \mathbb {R}\). By invoking the implicit function theorem, we can define a continuously differentiable map
such that \(\mathcal {J}(v+te_{1})< \mathcal {J}(v+t(v)e_{1})\) for all \(t\in \mathbb {R}\) such that \(t\ne t(v)\). Since, for \(v\in \mathbb {H}^{+}\), \(\psi '(t(v))=0\), we have
Taking \(v=0\) in (3.3), we find
which combined with (1.6) shows that \(t(0)>0\) and
Let us now introduce \(\mathcal {F}:\mathbb {H}^{+}\rightarrow \mathbb {R}\) given by
We claim that \(\mathcal {F}\) attains its minimum on some ball \(B_{\rho }\). It is easy to see that (1.6) and (3.4) give
Lemma 10
There exists \(\beta >0\) such that
where
Proof
Note that, for all \(v\in \mathbb {H}^{+}\), it holds
Using this, the Hölder inequality and the Sobolev inequality [13, Theorem 1.1], we have
Define
Let us compute \(j'(\zeta )\):
Then \(j(\zeta )\) achieve its maximum at \(\varrho _{0}\) given by
Therefore,
and using (1.8) and the first condition in (1.7), we see that
Thus (3.7) yields
provided \(\Vert v\Vert _{\mathbb {H}_{0}^{s}(\Omega )}= \varrho _{0}\). Let us observe that (3.5), the second condition in (1.7) and (1.9) yield
which combined with (3.8) ensures that (3.6) is satisfied.
Proof of Theorem 2
Let us define
We claim that (3.1) has a nontrivial solution \(v_{0}\in B_{\varrho _{0}}\). From (3.9) easily follows that
and in particular
Let \(\{v_{n}\}_{n\in \mathbb {N}}\subset \mathbb {H}_{0}^{s}(\Omega )\) be a minimizing sequence of (3.10). Since \(\Vert v_{n}\Vert _{\mathbb {H}_{0}^{s}(\Omega )}\le \varrho _{0}\), we may assume that, up to a subsequence,
From the weak lower semicontinuity of the norm \(\Vert \cdot \Vert _{\mathbb {H}_{0}^{s}(\Omega )}\), we have
By Ekeland’s variational principle [23, Theorem 4.1], we may assume that
as \(n\rightarrow \infty\). Consequently,
and
From (3.12) we derive that \(v_{0}\) is a weak solution to
Using \(v_{0}\) as test function in the weak formulation of (3.15), we acquire
On the other hand, choosing \(e_{1}\) as test function in the weak formulation of (3.15) and recalling that
we obtain
Next we show that \(v_{0}\not \equiv 0\). We start by observing that
Indeed, if we assume by contradiction that \(t(v_{n})\rightarrow t_{1}\ne t(v_{0})\), using (3.3), we see that
and
imply
that is a contradiction. Set \(w_{n}:= v_{n}- v_{0}\). Using (3.13), (3.14), and the Brezis–Lieb lemma [8, Theorem 1], we get
namely
Analogously, from (3.14), (3.16), (3.17) and the Brezis–Lieb lemma [8, Theorem 1], we have
that is
Let
If \(\ell =0\), then we have done. Suppose \(\ell >0\). By the Sobolev inequality [13, Theorem 1.1], we know that
Passing to the limit as \(n\rightarrow \infty\) in the above inequality, and using (3.19) and \(\ell >0\), we find
Combining (3.11), (3.18), (3.19) and (3.20), we get
which implies that \(\mathcal {F}(v_{0})<0\). This last fact and (3.5) shows that \(v_{0}\not \equiv 0\). Since \(\mathcal {F}(v)\ge \beta >0\) for all \(\Vert v\Vert _{\mathbb {H}_{0}^{s}(\Omega )}= \varrho _{0}\), we can conclude that \(v_{0}\in B_{\varrho _{0}}\). The proof of Theorem 2 is complete.
Remark 3
Following [16], it is also possible to discuss the local bifurcation at \(\lambda =\lambda _{n}\) with \(n>1\).
Remark 4
If we replace \((-\Delta )^{s}\) by the more general nonlocal integro-differential operator \(-\mathcal {L}_{K}\) given by
where \(K:\mathbb {R}^{N}\setminus \{0\}\rightarrow (0, \infty )\) is a function such that:
-
\(mK\in L^{1}(\mathbb {R}^{N})\), where \(m(x):=\min \{|x|^{2}, 1\}\),
-
there exists \(\theta >0\) such that \(K(x)\ge \theta |x|^{-(N+2s)}\) for any \(x\in \mathbb {R}^{N}\setminus \{0\}\),
-
\(K(x)=K(-x)\) for any \(x\in \mathbb {R}^{N}\setminus \{0\}\),
then we can easily adapt our arguments to extend Theorem 1 and Theorem 2 to the following problem:
References
Amann, H., Hess, P.: A multiplicity result for a class of elliptic boundary value problems. Proc. Roy. Soc. Edinburgh Sect. A 84(1–2), 145–151 (1979)
Ambrosetti, A., Prodi, G.: On the inversion of some differentiable mappings with singularities between Banach spaces. Ann. Mat. Pura Appl. (4) 93, 231–246 (1972)
Ambrosio, V.: An Ambrosetti–Prodi type result for fractional spectral problems. Math. Nachr. 293(3), 412–429 (2020)
Ambrosio, V.: Nonlinear Fractional Schrödinger Equations in \(\mathbb{R}^N\), Frontiers in Elliptic and Parabolic Problems. Birkhäuser/Springer, Cham (2021)
Arcoya, D., Ruiz, D.: The Ambrosetti–Prodi problem for the \(p\)-Laplacian operator. Commun. Partial Differ. Equ. 31(4–6), 849–865 (2006)
Berestycki, H., Lions, P.-L.: Sharp existence results for a class of semilinear elliptic problems. Bol. Soc. Brasil. Mat. 12(1), 9–19 (1981)
Berger, M.S., Podolak, E.: On the solutions of a nonlinear Dirichlet problem. Indiana Univ. Math. J. 24 (1974/75), 837–846
Brezis, H., Lieb, E.: A relation between pointwise convergence of functions and convergence of functionals. Proc. Am. Math. Soc. 88(3), 486–490 (1983)
Brezis, H., Nirenberg, L.: Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents. Commun. Pure Appl. Math. 36(4), 437–477 (1983)
Calanchi, M., Ruf, B.: Elliptic equations with one-sided critical growth, Electron. J. Differ. Equ. (2002) No. 89
Chabrowski, J., Yang, J.: Existence theorems for the Schrödinger equation involving a critical Sobolev exponent. Z. Angew. Math. Phys. 49(2), 276–293 (1998)
Chang, K.C.: Ambrosetti–Prodi type results in elliptic systems. Nonlinear Anal. 51(4), 553–566 (2002)
Cotsiolis, A., Tavoularis, N.K.: Best constants for Sobolev inequalities for higher order fractional derivatives. J. Math. Anal. Appl. 295(1), 225–236 (2004)
Dancer, E.N.: On the ranges of certain weakly nonlinear elliptic partial differential equations (9). J. Math. Pures Appl. 57(4), 351–366 (1978)
de Figueiredo, D.G.: Lectures on the Ekeland variational principle with applications and detours, Tata Institute of Fundamental Research Lectures on Mathematics and Physics, 81. Published for the Tata Institute of Fundamental Research, Bombay; by Springer-Verlag, Berlin, 1989. vi+96 pp
De Figueiredo, D.G., Jianfu, Y.: Critical superlinear Ambrosetti–Prodi problems. Topol. Methods Nonlinear Anal. 14(1), 59–80 (1999)
de Morais Filho, D.C., Pereira, F.R.: Critical Ambrosetti–Prodi type problems for systems of elliptic equations. Nonlinear Anal. 68(1), 194–207 (2008)
Deng, Y.-B.: On the superlinear Ambrosetti–Prodi problem involving critical Sobolev exponents. Nonlinear Anal. 17(12), 1111–1124 (1991)
de Paiva, F.O., Montenegro, M.: An Ambrosetti–Prodi-type result for a quasilinear Neumann problem (2). Proc. Edinb. Math. Soc. 55(3), 771–780 (2012)
Hess, P.: On a nonlinear elliptic boundary value problem of the Ambrosetti–Prodi type (5). Boll. Un. Mat. Ital. A 17(1), 187–192 (1980)
Kazdan, J.L., Warner, F.W.: Remarks on some quasilinear elliptic equations. Commun. Pure Appl. Math. 28(5), 567–597 (1975)
Mawhin, J.: The periodic Ambrosetti–Prodi problem for nonlinear perturbations of the \(p\)-Laplacian. J. Eur. Math. Soc. 8(2), 375–388 (2006)
Mawhin, J., Willem, M.: Critical Point Theory and Hamiltonian Systems. Applied Mathematical Sciences, Springer, New York (1989)
Molica Bisci, G., Radulescu, V.D., Servadei, R.: Variational Methods for Nonlocal Fractional Problems. Encyclopedia of Mathematics and its Applications, Cambridge University Press, Cambridge (2016)
Rabinowitz, P.H.: Minimax methods in critical point theory with applications to differential equations. In: CBMS Regional Conference Series in Mathematics, 65. Published for the Conference Board of the Mathematical Sciences, Washington, DC; by the American Mathematical Society, Providence, RI, 1986
Ruf, B., Srikanth, P.N.: Multiplicity results for superlinear elliptic problems with partial interference with the spectrum. J. Math. Anal. Appl. 118(1), 15–23 (1986)
Servadei, R., Valdinoci, E.: The Brezis–Nirenberg result for the fractional Laplacian. Trans. Am. Math. Soc. 367(1), 67–102 (2015)
Funding
Open access funding provided by Università Politecnica delle Marche within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ambrosio, V., Isernia, T. The critical fractional Ambrosetti–Prodi problem. Rend. Circ. Mat. Palermo, II. Ser 71, 1107–1132 (2022). https://doi.org/10.1007/s12215-022-00757-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12215-022-00757-4