Skip to main content
SpringerLink
Log in

Effect of shrinking projection and CQ-methods on two inertial forward–backward algorithms for solving variational inclusion problems

  • Published:
Rendiconti del Circolo Matematico di Palermo Series 2 Aims and scope Submit manuscript

Abstract

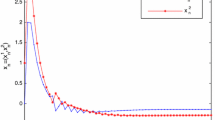
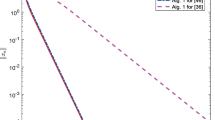
In this paper, we establish the convergence theorems for two projection algorithms for finding a null point of the sum of two monotone operators in Hilbert spaces. Our algorithms are the combination the inertial forward–backward with the shrinking of hybrid projection methods. To clarify the acceleration, effectiveness, and performance of proposed algorithms, numerical contributions have been incorporated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Agarwal, R.P., O’Regan, D., Sahu, D.R.: Fixed Point Theory for Lipschitzian-Type Mappings with Applications. Springer, New York (2009)

    MATH  Google Scholar 

  2. Alvarez, F., Attouch, H.: An inertial proximal method for monotone operators via discretization of a nonlinear oscillator with damping. Set-Valued Anal. 9, 3–11 (2001)

    Article  MathSciNet  Google Scholar 

  3. Bauschke, H.H., Borwein, J.M.: On projection algorithms for solving convex feasibility problems. SIAM Rev. 38, 367–426 (1996)

    Article  MathSciNet  Google Scholar 

  4. Bauschke, H.H., Combettes, P.L.: A weak-to-strong convergence principle for Fejér-monotone methods in Hilbert spaces. Math. Oper. Res. 26, 248–264 (2001)

    Article  MathSciNet  Google Scholar 

  5. Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces. Springer, Berlin (2011)

    Book  Google Scholar 

  6. Bot, R.I., Csetnek, E.R., Hendrich, C.: Inertial Douglas–Rachford splitting for monotone inclusion. Appl. Math. Comput. 256, 472–487 (2015)

    MathSciNet  MATH  Google Scholar 

  7. Bot, R.I., Csetnek, E.R.: An inertial alternating direction method of multipliers. Minimax Theory Appl. 1, 29–49 (2016)

    MathSciNet  MATH  Google Scholar 

  8. Bot, R.I., Csetnek, E.R.: An inertial forward–backward–forward primal-dual splitting algorithm for solving monotone inclusion problems. Numer. Algorithms 71, 519–540 (2016)

    Article  MathSciNet  Google Scholar 

  9. Browder, F.E.: Nonexpansive nonlinear operators in a Banach space. Proc. Natl. Acad. Sci. USA 45, 1041–1044 (1965)

    Article  MathSciNet  Google Scholar 

  10. Bruck, R.E., Reich, S.: Nonexpansive projections and resolvents of accretive operators in Banach spaces. Houston J. Math. 3, 459–470 (1977)

    MathSciNet  MATH  Google Scholar 

  11. Chen, P., Huang, J., Zhang, X.: A primal-dual fixed point algorithm for convex separable minimization with applications to image restoration. Inverse Probl. 29(2), 025011 (2013)

    Article  MathSciNet  Google Scholar 

  12. Combettes, P.L., Wajs, V.R.: Signal recovery by proximal forward–backward splitting. Multiscale Model. Simul. 4, 1168–1200 (2005)

    Article  MathSciNet  Google Scholar 

  13. Dang, Y., Sun, J., Xu, H.: Inertial accelerated algorithms for solving a split feasibility problem. J. Ind. Manag. Optim. 13(3), 1383–1394 (2017)

    MathSciNet  MATH  Google Scholar 

  14. Dong, Q.L., Lu, Y.Y.: A new hybrid algorithm for a nonexpansive mapping. Fixed Point Theroy Appl. 2015, 37 (2015)

    Article  Google Scholar 

  15. Dong, Q., Jiang, D., Cholamjiak, P., Shehu, Y.: A strong convergence result involving an inertial forward–backward algorithm for monotone inclusions. J. Fixed Point Theory Appl. 19, 3097–3118 (2017)

    Article  MathSciNet  Google Scholar 

  16. Dong, Q.L., Cho, Y.J., Rassias, T.M.: General inertial Mann algorithms and their convergence analysis for nonexpansive mappings. Appl. Nonlinear Anal. 134, 175–191 (2018)

    Article  MathSciNet  Google Scholar 

  17. Dong, Q.L., Yuan, H.B., Cho, Y.J., Rassias, T.M.: Modified inertial Mann algorithm and inertial CQ-algorithm for nonexpansive mappings. Optim. Lett. 12, 87–102 (2018)

    Article  MathSciNet  Google Scholar 

  18. Douglas, J., Rachford, H.H.: On the numerical solution of the heat conduction problem in 2 and 3 space variables. Trans. Am. Math. Soc. 82, 421–439 (1956)

    Article  MathSciNet  Google Scholar 

  19. Lions, P.L., Mercier, B.: Splitting algorithms for the sum of two nonlinear operators. SIAM J. Numer. Anal. 16, 964–979 (1979)

    Article  MathSciNet  Google Scholar 

  20. López, G., Martín-Márquez, V., Wang, F., Xu, H.K.: Forward–backward splitting methods for accretive operators in Banach spaces. Abstr. Appl. Anal. (2012). Article ID 109236

  21. Lorenz, D., Pock, T.: An inertial forward–backward algorithm for monotone inclusions. J. Math. Imaging Vis. 51, 311–325 (2015)

    Article  MathSciNet  Google Scholar 

  22. Maingé, P.E.: Inertial iterative process for fixed points of certain quasinonexpansive mappings. Set-Valued Anal. 15, 67–79 (2007)

    Article  MathSciNet  Google Scholar 

  23. Martinez-Yanes, C., Xu, H.K.: Strong convergence of the CQ method for fixed point iteration processes. Nonlinear Anal. 64(11), 2400–2411 (2006)

    Article  MathSciNet  Google Scholar 

  24. Moudafi, A., Oliny, M.: Convergence of a splitting inertial proximal method for monotone operators. J. Comput. Appl. Math. 155, 447–454 (2003)

    Article  MathSciNet  Google Scholar 

  25. Nakajo, K., Takahashi, W.: Strong convergence theorems for nonexpansive mappings and nonexpansive semigroups. J. Math. Anal. Appl. 279(2), 372–379 (2003)

    Article  MathSciNet  Google Scholar 

  26. Nesterov, Y.: A method for solving the convex programming problem with convergence rate \(O(\frac{1}{k^{2}})\). Dokl. Akad. Nauk SSSR 269, 543–547 (1983)

    MathSciNet  Google Scholar 

  27. Parikh, N., Boyd, S.: Proximal algorithms. Found. Trends Optim. 1, 123–231 (2013)

    Google Scholar 

  28. Passty, G.B.: Ergodic convergence to a zero of the sum of monotone operators in Hilbert space. J. Math. Anal. Appl. 72, 383–390 (1979)

    Article  MathSciNet  Google Scholar 

  29. Peaceman, D.H., Rachford, H.H.: The numerical solution of parabolic and elliptic differentials. J. Soc. Ind. Appl. Math. 3, 28–41 (1955)

    Article  MathSciNet  Google Scholar 

  30. Polyak, B.T.: Introduction to Optimization. Optimization Software, New York (1987)

    MATH  Google Scholar 

  31. Polyak, B.T.: Some methods of speeding up the convergence of iterative methods. Zh. Vychisl. Mat. Mat. Fiz. 4, 1–17 (1964)

    MathSciNet  Google Scholar 

  32. Qin, X., Cho, S.Y., Wang, L.: Convergence of splitting algorithms for the sum of two accretive operators with applications. Fixed Point Theory Appl. 2014, 166 (2014)

    Article  MathSciNet  Google Scholar 

  33. Shehu, Y.: Iterative approximations for zeros of sum of accretive operators in Banach spaces. J. Funct. Spaces (2016). Article ID 5973468. https://doi.org/10.1155/2016/5973468

  34. Takahashi, W.: Nonlinear Functional Analysis. Yokohama Publishers, Yokohama (2000)

    MATH  Google Scholar 

  35. Tseng, P.: A modified forward–backward splitting method for maximal monotone mappings. SIAM J. Control. Optim. 38, 431–446 (2000)

    Article  MathSciNet  Google Scholar 

  36. Wang, F., Cui, H.: On the contraction-proximal point algorithms with multiparameters. J. Global Optim. 54, 485–491 (2012)

    Article  MathSciNet  Google Scholar 

  37. Xiu, N., Wang, D., Kong, L.: A note on the gradient projection method with exact stepsize rule. J. Comput. Math. 25, 221–230 (2007)

    MathSciNet  MATH  Google Scholar 

  38. Xu, H.K.: Averaged mappings and the gradient-projection algorithm. J. Optim. Theory Appl. 150(2), 360–378 (2011)

    Article  MathSciNet  Google Scholar 

  39. Yao, Y., Kang, S.M., Jigang, W., Yang, P.X.: A regularized gradient projection method for the minimization problem. J. Appl. Math. (2012). Article ID 259813. https://doi.org/10.1155/2012/259813

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics and Informatics, Thai Nguyen University of Sciences, Thái Nguyên, Vietnam

    Truong Minh Tuyen

  2. Department of Mathematics, Faculty of Science, Sohag University, Sohag, 82524, Egypt

    Hasanen A. Hammad

Authors
  1. Truong Minh Tuyen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hasanen A. Hammad
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hasanen A. Hammad.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tuyen, T.M., Hammad, H.A. Effect of shrinking projection and CQ-methods on two inertial forward–backward algorithms for solving variational inclusion problems. Rend. Circ. Mat. Palermo, II. Ser 70, 1669–1683 (2021). https://doi.org/10.1007/s12215-020-00581-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12215-020-00581-8

Keywords

Mathematics Subject Classification

Search

Navigation