1 Introduction

The theory of modular spaces, introduced by Nakano [59], was extensively studied by Musielak and Orlicz [56, 58], especially for what concerns the special cases of the so-called Orlicz and Musielak–Orlicz spaces.

The notion of modular space \(L_\rho\) is very general and includes in itself several cases of well-know spaces, such as the \({L^p}\)-spaces, the Zygmund (or interpolation) spaces, the Sobolev spaces, and the exponential spaces (see, e.g., [22, 46, 49, 64]).

The main advantages in working in a very abstract setting is that one can obtain the desired results in many settings by a unique and unifying approach.

The study of approximation results in the above context is firstly due to J. Musielak in a number of papers, and subsequently it was carried out by the research group of the University of Perugia in several directions, both for linear and nonlinear approximation. For references of this subject see the monograph [19].

Recently, a family of sampling-type approximation operators, namely the so-called sampling Kantorovich operators, has been introduced and studied in the general setting of Orlicz spaces, which are a particular instance of modular spaces [16, 43].

The above operators are of the form:

$$\begin{aligned} (S^{\chi }_w f)(x):= \sum _{k \in {\mathbb {Z}}} \left[ {w \over \Delta _k} \int _{t_k/w}^{t_{k+1}/w} f(u)\, du\right] \, \chi (wx-t_k), \quad x \in {\mathbb {R}}, \end{aligned}$$
(I)

where \(f{:}\,{\mathbb {R}}\rightarrow {\mathbb {R}}\) is any locally integrable function for which the above series is convergent for every \(x \in {\mathbb {R}}\), \((t_k)_{k \in {\mathbb {Z}}}\) is a suitable sequence of real numbers, with \(0<\Delta _k := t_{k+1}-t_k\), \(k \in {\mathbb {Z}}\), and \(\chi{:}\,{\mathbb {R}}\rightarrow {\mathbb {R}}\) is a kernel function satisfying suitable assumptions, \(w>0\) see, e.g., [6, 18, 32, 33, 50, 60].

The operators in (I) represent the \(L^p\)-version of the generalized sampling operators (see, e.g., [9, 10, 13, 17, 25, 28,29,30, 51, 61]) introduced and studied by P.L. Butzer and his school in the 1980s: both the generalized and the Kantorovich sampling operators are approximate versions of the well-known Wittaker–Kotelnikov–Shannon sampling theorem, see [23].

The main advantages of studying approximation results for the above operators in the setting of Orlicz spaces consists in the possibility of approximating not necessarily continuous functions. This is strongly connected to the expression of \(S^{\chi }_w\) in which we have mean values of the function f on the (not necessarily equally spaced) intervals \([t_k/w, t_{k+1}/w]\), \(w>0\).

The latter fact can be also useful from the point of view of the applications, for instance for digital image processing: indeed, the multivariate version of (I) (see, e.g., [35, 38]) has been successfully applied to several real world problems involving images by the implementation of an optimized algorithm for image reconstruction and enhancement [12, 15, 36].

The study of the above operators in the Orlicz spaces allows to reach a good degree of generality, and to deduce convergence theorems e.g., in \(L^p\)-spaces, and others. However the above approach does not include the cases of the weighted \(L^p\)-spaces, or for instance the weighted Zygmund spaces, and so on.

In order to reach a wide level of generality and to extend the above approximation theorems to a more general setting (including e.g. the above mentioned weighted type spaces), in this paper we study the sampling Kantorovich operators in the general context of modular spaces.

Here, standard assumptions are required on the modular \(\rho\) which generates the spaces \(L_\rho\), together with suitable compatibility conditions among the kernel \(\chi\) and the modulars involved [55]. In this setting, we firstly prove a modular convergence theorem in case of operators \(S^{\chi }_w f\) acting on continuous functions f with compact support. In latter case, if the kernel \(\chi\) has compact support we can also prove that the operators are convergent with respect to the Luxemburg norm.

Then we prove a modular type inequality for the above linear operators, and finally, by exploiting a well-known density result with respect to the modular topology for the space of continuous functions with compact support, we become able to prove a modular convergence theorem in \(L_\rho\).

In the following of the paper, we show some examples of modular spaces in which the above theory holds. In particular, we deeply investigate the case of Musielak–Orlicz spaces: it is well-known that such spaces find applications in the theory of partial differential equations [14, 62] and in operator theory [45, 48, 53, 66]. Here, we show that all the assumptions of the general theory presented are satisfied, providing several examples; among them, the weighted type spaces. We also furnish an example of a modular space, to which our results can be applied, which does not reduce to any Orlicz or Musielak–Orlicz space.

Finally, we also discuss about a number of kernel functions \(\chi\) that satisfy the assumptions here required, such as the Fejér, the Jackson-type, the Bochner–Riesz, the central B-splines kernels, and many others (see e.g., [5, 11, 24, 40]).

2 Notations and basic assumptions

First of all, we begin recalling some basic notions about modular spaces.

Let \(\Omega = (\Omega , \Sigma _\Omega , \mu _\Omega )\) be an arbitrary measure space and let \(X(\Omega )\) be the corresponding vector space of all \(\Sigma _\Omega\)-measurable real-valued functions on \(\Omega\). A functional \(\rho {:}\,X(\Omega ) \rightarrow [0,+\infty ]\) is said to be a modular on \(X(\Omega )\) if the following conditions hold:

(\(\rho 1\)):

\(\rho (f) = 0\) if and only if \(f \equiv 0\) \(\mu _\Omega\)-a.e. in \(\Omega\);

(\(\rho 2\)):

\(\rho (-f)=\rho (f)\) for every \(f \in X(\Omega )\);

(\(\rho 3\)):

\(\rho (\alpha f +\beta g) \le \rho (f)+\rho (g)\) for every f, \(g \in X(\Omega )\) and \(\alpha\), \(\beta \in {\mathbb {R}}^+_0\) with \(\alpha +\beta =1\).

The functional \(\rho\) generates the modular space \(L_\rho (\Omega )\) (see e.g., [19, 52, 56]) defined as follows:

$$\begin{aligned} L_\rho (\Omega ):= \left\{ f \in X(\Omega ){:}\,\lim _{\lambda \rightarrow 0} \rho (\lambda f)=0 \right\} . \end{aligned}$$

It is well-known that \(L_\rho (\Omega )\) is a vector subspace of \(X(\Omega )\), and it is possible to define on it the following (natural) concept of convergence, called modular convergence: we say that a net of functions \((f_w)_{w>0} \subset L_\rho (\Omega )\) is modularly convergent (or \(\rho\)-convergent) to a function \(f \in L_\rho (\Omega )\) if there exist \(\lambda >0\) such that:

$$\begin{aligned} \lim _{w\rightarrow +\infty } \rho (\lambda (f_w-f))= 0. \end{aligned}$$
(1)

Note that, the modular convergence induces a topology called modular topology on \(L_\rho (\Omega )\).

Note that, if (1) holds for every \(\lambda >0\) we will say that the net \((f_w)_{w>0}\) is convergent to f with respect to the Luxemburg-norm.

An other important subspace of \(X(\Omega )\) is given by the so-called space of finite elements, defined by:

$$\begin{aligned} E_\rho (\Omega ):= \left\{ f \in X(\Omega ){:}\,\rho (\lambda f)<+\infty \, \mathrm{for\,every}\,\lambda >0 \right\} . \end{aligned}$$

In particular it is well-known that, if the modular \(\rho\) is a convex functional, one has:

$$\begin{aligned} E_\rho (\Omega ) \subset L_\rho (\Omega ). \end{aligned}$$
(2)

We now recall the following important definitions concerning modular functionals.

We say that a modular \(\rho\) is:

  1. (a)

    monotone if \(\rho (f) \le \rho (g)\) whenever \(|f|\le |g|\), for every f, \(g \in X(\Omega )\);

  2. (b)

    finite if the characteristic function \({\mathbf {1}}_A\) of every measurable set A of finite \(\mu _\Omega\)-measure belongs to \(L_\rho (\Omega )\);

  3. (c)

    strongly finite if every \({\mathbf {1}}_A\) as above belongs to \(E_\rho (\Omega )\);

  4. (d)

    absolutely finite if \(\rho\) is finite and if for every \(\varepsilon\), \(\lambda _0>0\) there exists a \(\delta >0\) such that \(\rho (\lambda _0 {\mathbf {1}}_B)<\varepsilon\) for every \(B \in \Sigma _\Omega\) with \(\mu _\Omega (B)<\delta\);

  5. (e)

    absolutely continuous if there is an \(\alpha >0\) such that for every \(f \in X(\Omega )\) with \(\rho (f)<+\infty\), the following two conditions hold:

    1. (i)

      for every \(\varepsilon >0\) there exists a measurable set \(A \subset \Omega\) with \(\mu _\Omega (A)<+\infty\) such that \(\rho (\alpha f {\mathbf {1}}_{\Omega {\setminus } A})<\varepsilon\);

    2. (ii)

      for every \(\varepsilon >0\) there exists \(\delta >0\) such that \(\rho (\alpha f {\mathbf {1}}_B)<\varepsilon\) for all measurable sets \(B \subset \Omega\) with \(\mu _\Omega (B)<\delta\).

Note that, if \(\rho\) is convex then any strongly finite modular is also finite.

For more details about the above properties, see e.g., [19, 22, 55, 56].

In the present paper, in order to study modular convergence results for a family of discrete sampling-type operators, we will consider \({\mathbb {R}}= ({\mathbb {R}}, \Sigma _{\mathbb {R}}, \mu _{\mathbb {R}})\) and \({\mathbb {Z}}= ({\mathbb {Z}}, \Sigma _{\mathbb {Z}}, \mu _{\mathbb {Z}})\), where \(\mu _{\mathbb {R}}\) and \(\mu _{\mathbb {Z}}\) are the Lebesgue and the counting measures respectively, while \(\Sigma _{\mathbb {R}}\) and \(\Sigma _{\mathbb {Z}}\) are their corresponding \(\sigma\)-algebras, i.e., the families of all measurable sets (with respect to the above measures) which are closed with respect to the operations of countable union and complementary.

Further, by \(\rho _{\mathbb {R}}\) and \(\rho _{\mathbb {Z}}\) we denote two modulars on \(X({\mathbb {R}})\) and \(X({\mathbb {Z}})\) respectively.

Now, we introduce the so-called sampling Kantorovich operators. Let \(\Pi :=(t_k)_{k \in {\mathbb {Z}}} \subset {\mathbb {R}}\) be a sequence such that \(-\infty< t_k< t_{k+1} < +\infty\), for every \(k \in {\mathbb {Z}}\), \(\lim _{k \rightarrow \pm \infty } t_k = \pm \infty\), and there are two positive constants \(\Delta\), \({\bar{\Delta }}\), such that \({\bar{\Delta }} \le \Delta _k := t_{k+1}-t_k \le \Delta\), for every \(k \in {\mathbb {Z}}\).

A function \(\chi {:}\,{\mathbb {R}}\rightarrow {\mathbb {R}}\) will be called a kernel (see also [41]) if it satisfies the following assumptions:

(\(\chi 1\)):

\(\chi \in X({\mathbb {R}})\) and it is bounded in a neighborhood of the origin;

(\(\chi 2\)):

for every \(u \in {\mathbb {R}}\) there holds:

$$\begin{aligned} \sum _{k \in {\mathbb {Z}}} \chi (u-t_k)= 1; \end{aligned}$$
(\(\chi 3\)):

for some \(\beta >0\):

$$\begin{aligned} m_{\beta , \Pi }(\chi ):= \sup _{u \in {\mathbb {R}}} \sum _{k \in {\mathbb {Z}}} |\chi (u-t_k)|\, |u-t_k|^\beta \ <\ +\infty . \end{aligned}$$

For a given kernel \(\chi\) we can recall the definition of the sampling Kantorovich operators (see [16]):

$$\begin{aligned} (S^{\chi }_w f)(x):= \sum _{k \in {\mathbb {Z}}} \left[ {w \over \Delta _k} \int _{t_k/w}^{t_{k+1}/w} f(u)\, du\right] \, \chi (wx-t_k), \quad x \in {\mathbb {R}}, \end{aligned}$$

where \(f{:}\,{\mathbb {R}}\rightarrow {\mathbb {R}}\) is any locally integrable function for which the above series is convergent for every \(x \in {\mathbb {R}}\).

From now on, we will always assume that f belongs to the domain of the above operators.

Note that, assumption \((\chi 3)\) together with assumption \((\chi 1)\) implies that:

$$\begin{aligned} m_{\nu , \Pi }(\chi )\ <\ +\infty , \quad \mathrm{for\,every}\quad 0 \le \nu \le \beta ; \end{aligned}$$

the latter property can be used, e.g., in order to show that the above family of operators is well-defined. Indeed, if we assume that f is a bounded function, it turns out that:

$$\begin{aligned} |(S^{\chi }_w f)(x)|\le \Vert f\Vert _{\infty }\, m_{0, \Pi }(\chi )\ <\ +\infty , \quad x \in {\mathbb {R}}, \end{aligned}$$

where \(\Vert \cdot \Vert _{\infty }\) denotes the usual sup-norm on \({\mathbb {R}}\). Denoting by \(C^0({\mathbb {R}})\) the space of bounded and continuous functions and by \(C({\mathbb {R}})\) the subspace containing the uniformly continuous functions, we can recall the following convergence results.

Theorem 2.1

[16] Let \(f \in C^0({\mathbb {R}})\) be fixed. For every \(x \in {\mathbb {R}}\) we have:

$$\begin{aligned} \lim _{w \rightarrow +\infty }(S^{\chi }_w f)(x)= f(x). \end{aligned}$$

In particular, if \(f \in C({\mathbb {R}})\) there holds:

$$\begin{aligned} \lim _{w \rightarrow +\infty }\Vert S^{\chi }_w f - f\Vert _{\infty }= 0. \end{aligned}$$

Now, we introduce the following compatibility condition.

We will say that the kernel \(\chi\) is compatible with the modulars \(\rho _{\mathbb {R}}\) and \(\rho _{\mathbb {Z}}\) if there exist two positive constants \(D_1\), \(D_2\) and a net \((b_w)_{w>0} \subset {\mathbb {R}}^+_0\), with \(b_w \rightarrow 0\) as \(w \rightarrow +\infty\), such that:

$$\begin{aligned} \rho _{\mathbb {R}}\left( \sum _{k \in {\mathbb {Z}}} g_k\, |\chi (w \cdot - t_k)| \right) \le {1 \over w}\, D_1\, \rho _{\mathbb {Z}}\left( D_2\, g \right) \ +\ b_w \end{aligned}$$
(3)

for any non-negative \(g \in X({\mathbb {Z}})\), \(g=(g_k)_{k \in {\mathbb {Z}}}\), and for sufficiently large \(w>0\).

Remark 2.2

Note that, the above compatibility condition is a particular case of the more general condition originally introduced in [55].

In order to prove the convergence results of the next section, we also need to introduce an additional assumption which relates \(\chi\) with a modular \(\rho _{\mathbb {R}}\).

Let \(\chi\) be a kernel, and \(\rho _{\mathbb {R}}\) be a modular on \(X({\mathbb {R}})\) such that:

  • for any fixed \(\gamma >0\) and \(a >0\) there exist a positive constant T and a measurable set \({{\mathcal {J}}} \subset {\mathbb {R}}\), with \(\mu _{\mathbb {R}}({{\mathcal {J}}})<+\infty\) such that:

    $$\begin{aligned} \rho _{\mathbb {R}}\left( a\ {\mathbf {1}}_{{\mathbb {R}}{\setminus } {{\mathcal {J}}}}(\cdot ) \sum _{k{:}\, t_k \in [-\gamma \, w, +\gamma \, w]}|\chi (w \cdot - t_k)| \right) \le T, \end{aligned}$$
    (4)

    for sufficiently large \(w>0\), where \({\mathbf {1}}_{{\mathbb {R}}{\setminus } {{\mathcal {J}}}}\) denotes the characteristic function of the set \({\mathbb {R}}{\setminus } {{\mathcal {J}}}\).

Note that, any \(\chi (w \cdot - t_k)\) belongs to \(X({\mathbb {R}})\) since \(\chi\) is measurable by the assumption \((\chi 1)\) and therefore the expression in (4) makes sense.

Remark 2.3

Note that, if \(\chi\) has compact support, the assumption (4) is obviously satisfied.

Indeed, let \(\gamma >0\) and \(a>0\) be fixed, and \(supp\, \chi \subset [-L, + L]\), \(L >0\). It is easy to see that for every \(t_k \in [-w\gamma , +w \gamma ]\) it turns out that:

$$\begin{aligned} \chi (wx - t_k)= 0, \quad \quad \mathrm{for\, every} \quad x \notin [- \gamma - L/w, +\gamma + L/w], \quad w>0. \end{aligned}$$

Now, set \({{\mathcal {J}}}:= [- \gamma - L, +\gamma + L]\) and using condition \((\rho 1)\) of the modulars, we have:

$$\begin{aligned} \rho _{\mathbb {R}}\left( a\ {\mathbf {1}}_{{\mathbb {R}}{\setminus } {{\mathcal {J}}}}(\cdot ) \sum _{k:\, t_k \in [-\gamma \, w, +\gamma \, w]}|\chi (w \cdot - t_k)| \right) = 0, \end{aligned}$$

for every \(w \ge 1\).

Moreover, in Sect. 4.1 we give some sufficient conditions in order that (4) is satisfied.

Now, we recall the following theorem which is the analog of the Lebesgue dominated convergence theorem given in the general setting of the modular spaces. This theorem has been originally proved by Musielak [57]; a proof can also be found in the monograph [19].

Theorem 2.4

[57] Let \(\rho _{\mathbb {R}}\) be a monotone, finite and absolutely continuous modular on \(X({\mathbb {R}}).\) Let \((f_w)_{w>0} \subset X({\mathbb {R}})\) a net of functions such that \(f_w \rightarrow 0,\) a.e. in \({\mathbb {R}},\) as \(w \rightarrow +\infty .\) Suppose in addition that there exists a function \(g \in L_{\rho _{\mathbb {R}}}({\mathbb {R}})\) such that \(\rho _{\mathbb {R}}(3\, g)<+\infty\) and \(|f_w(x)| \le g(x),\) a.e. in \({\mathbb {R}},\) for every \(w>0.\) Then \(\rho _{\mathbb {R}}(f_w) \rightarrow 0,\) as \(w\rightarrow +\infty .\)

In conclusion of this section, we recall the following useful result that can be deduced from Theorem 1 of [54].

Theorem 2.5

Let \(\rho _{\mathbb {R}}\) be an absolutely continuous, monotone, and absolutely finite modular on \(X({\mathbb {R}}).\) Then:

$$\begin{aligned} \overline{C_c({\mathbb {R}})}= L_{\rho _{\mathbb {R}}}({\mathbb {R}}), \end{aligned}$$

where \(C_c({\mathbb {R}})\) is the subset of \(C^0({\mathbb {R}})\) of functions with compact support, and the bar represents the closure with respect of the modular topology on \(L_{\rho _{\mathbb {R}}}({\mathbb {R}}).\)

3 Convergence results

We can prove the following theorem.

Theorem 3.1

Let \(\rho _{\mathbb {R}}\) be a convex, monotone, strongly finite and absolutely continuous modular on \(X({\mathbb {R}}).\) Moreover, let \(\chi\) be a kernel which satisfies assumption (4) together with \(\rho _{\mathbb {R}}\). Then for any \(f \in C_c({\mathbb {R}})\) and for every \(\lambda >0,\) with \(0< \lambda \le \alpha /3,\) where \(\alpha\) is the parameter of the absolutely continuity of \(\rho _{\mathbb {R}},\) there holds:

$$\begin{aligned} \lim _{w \rightarrow +\infty } \rho _{\mathbb {R}}\left( \lambda (S^{\chi }_wf-f) \right) = 0. \end{aligned}$$

Proof

Let \({\bar{\gamma }} >0\) such that \(supp\, f \subset [-{\bar{\gamma }}, +{\bar{\gamma }}]=: S\). Now, we can fix \(\gamma > {\bar{\gamma }} + \Delta\) and let us consider the interval \([-\gamma , +\gamma ]\). Then, if \(t_k \notin [-w \gamma , + w \gamma ]\), we have for sufficiently large \(w>0\) that \([-\gamma , +\gamma ] \cap [t_k/w, t_{k+1}/w] = \emptyset\), and so:

$$\begin{aligned} \int _{t_{k}/w}^{t_{k+1}/w}f(u)\, du= 0. \end{aligned}$$

By the above arguments, the definition of the sampling Kantorovich operators reduces to:

$$\begin{aligned} (S^{\chi }_wf)(x)= \sum _{k{:}\, t_k \in [-\gamma w, +\gamma w]}\left[ {w\over \Delta _k} \int _{t_{k}/w}^{t_{k+1}/w}f(u)\, du \right] \, \chi (wx - t_k), \quad x \in {\mathbb {R}}. \end{aligned}$$

Now, it turns out that \(S^{\chi }_wf \in X({\mathbb {R}})\) since \(\chi\) is measurable and \(f \in X({\mathbb {R}})\) since it is continuous, hence \(S^{\chi }_wf - f \in X({\mathbb {R}})\). Further, using the monotonicity of \(\rho _{\mathbb {R}}\) together with the property \((\rho 3)\) of the modulars, we can write what follows:

$$\begin{aligned} \rho _{\mathbb {R}}\left( S^{\chi }_wf - f\right)&\le \rho _{\mathbb {R}}\left( 2\Vert f\Vert _{\infty } \sum _{k{:}\, t_k \in [-\gamma w, +\gamma w]}|\chi (w \cdot - t_k)| \right) + \rho _{\mathbb {R}}(2\, |f|)\\&= \rho _{\mathbb {R}}\left( 2\Vert f\Vert _{\infty } \sum _{k:\, t_k \in [-\gamma w, +\gamma w]}|\chi (w \cdot - t_k)| \right) \, +\, \rho _{\mathbb {R}}(2\, |f |\, {\mathbf {1}}_{S}), \end{aligned}$$

where \({\mathbf {1}}_S\) is the characteristic function of the interval S, with \(\mu _{\mathbb {R}}(S)= 2 {\bar{\gamma }}<+\infty\). Now, applying assumption (4) with \(\gamma\) above fixed and \(a:=4\, \Vert f\Vert _{\infty }\), there exist \(T>0\) and a measurable set \({{\mathcal {J}}} \subset {\mathbb {R}}\) with \(\mu _{\mathbb {R}}({{\mathcal {J}}})<+\infty\) such that:

$$\begin{aligned} \rho _{\mathbb {R}}\left( 4\Vert f\Vert _{\infty }\ {\mathbf {1}}_{{\mathbb {R}}{\setminus } {{\mathcal {J}}}}(\cdot ) \sum _{k:\, t_k \in [-\gamma w, +\gamma w]}|\chi (w \cdot - t_k)| \right) \le T, \end{aligned}$$

for sufficiently large \(w>0\). Recalling that \({\mathbf {1}}_{{{\mathcal {J}}}}\), \({\mathbf {1}}_S \in E_{\rho _{\mathbb {R}}}({\mathbb {R}})\) since \(\rho _{\mathbb {R}}\) is strongly finite, by using again \((\rho 3)\) and the monotonicity of \(\rho _{\mathbb {R}}\), we finally obtain:

$$\begin{aligned} \rho _{\mathbb {R}}\left( S^{\chi }_wf - f \right)&\le \rho _{\mathbb {R}}\left( 4\Vert f\Vert _{\infty }\ {\mathbf {1}}_{{{\mathcal {J}}}}(\cdot ) \sum _{k:\, t_k \in [-\gamma w, +\gamma w]}|\chi (w \cdot - t_k)|\, \right) \\&\quad +\,\rho _{\mathbb {R}}\left( 4\Vert f\Vert _{\infty }\ {\mathbf {1}}_{{\mathbb {R}}{\setminus } {{\mathcal {J}}}}(\cdot ) \sum _{k:\, t_k \in [-\gamma w, +\gamma w]}|\chi (w \cdot - t_k)| \right) \, +\, \rho _{\mathbb {R}}(2\, \Vert f\Vert _{\infty }\, {\mathbf {1}}_{S})\\&\le \rho _{\mathbb {R}}\left( 4\, m_{0, \Pi }(\chi )\, \Vert f\Vert _{\infty }\ {\mathbf {1}}_{{{\mathcal {J}}}}(\cdot ) \right) \ +\ T\ +\ \rho _{\mathbb {R}}(2\, \Vert f\Vert _{\infty }\, {\mathbf {1}}_{S})\ <\ +\infty , \end{aligned}$$

for sufficiently large \(w>0\).

Now, we denote by \(\alpha >0\) the constant of the absolute continuity of \(\rho _{\mathbb {R}}\), and let \(\varepsilon >0\) be fixed. In correspondence to \(\varepsilon / 2\), we have:

  1. (j)

    there exists a measurable subset \(A \subset {\mathbb {R}}\), with \(\mu _{\mathbb {R}}(A)<+\infty\), such that:

    $$\begin{aligned} \rho _{\mathbb {R}}\left( \alpha (S^{\chi }_wf - f)\, {\mathbf {1}}_{{\mathbb {R}}{\setminus } A} \right) < \varepsilon / 2. \end{aligned}$$
    (5)

In particular, since \(\mu _{\mathbb {R}}(A)\) in (j) is finite and \(\rho _{\mathbb {R}}\) is a convex, strongly finite modular (hence in particular it is finite), one has that the characteristic function \({\mathbf {1}}_A \in E_{\rho _{\mathbb {R}}}({\mathbb {R}}) \subset L_{\rho _{\mathbb {R}}}({\mathbb {R}})\), i.e.,

$$\begin{aligned} \lim _{\lambda \rightarrow 0} \rho _{\mathbb {R}}\left( \lambda \, {\mathbf {1}}_A \right) = 0. \end{aligned}$$

Then in correspondence to \(\varepsilon /2\), there exists a sufficiently small \(\lambda _\varepsilon >0\) such that:

$$\begin{aligned} \rho _{\mathbb {R}}\left( \lambda _\varepsilon \, {\mathbf {1}}_A \right) < \varepsilon /2. \end{aligned}$$
(6)

Moreover, since \(f \in C_c({\mathbb {R}})\) and by using Theorem 2.1 we also have:

$$\begin{aligned} \alpha \, \Vert S^{\chi }_w f - f\Vert _{\infty } < \lambda _\varepsilon , \end{aligned}$$
(7)

for sufficiently large \(w>0\).

Now, let \(0< \lambda \le \alpha /2\) arbitrary fixed. We can write what follows:

$$\begin{aligned}&\lambda \, \left| (S^{\chi }_wf)(x) -f(x) \right| \le {\alpha \over 2}\, \left| (S^{\chi }_wf)(x) -f(x) \right| \\&\quad =\ {1 \over 2}\, \left[ \alpha \, \left| (S^{\chi }_wf)(x) -f(x) \right| \, {\mathbf {1}}_{{\mathbb {R}}{\setminus } A}(x)\ +\, \alpha \, \left| (S^{\chi }_wf)(x) -f(x) \right| \, {\mathbf {1}}_{A}(x)\, \right] , \end{aligned}$$

\(x \in {\mathbb {R}}\). Now, by using the property \((\rho 3)\), the monotonicity of \(\rho _{\mathbb {R}}\) and the conditions (5)–(7), we finally obtain:

$$\begin{aligned} \rho _{\mathbb {R}}\left( \lambda \, \left| S^{\chi }_wf -f\right| \right)&\le \rho _{\mathbb {R}}\left( \alpha \, \left| S^{\chi }_wf -f\right| {\mathbf {1}}_{{\mathbb {R}}{\setminus } A}\right) \, +\, \rho _{\mathbb {R}}\left( \alpha \, \left| S^{\chi }_wf -f\right| {\mathbf {1}}_{A}\right) \\&< \varepsilon / 2\, +\, \rho _{\mathbb {R}}\left( \lambda _\varepsilon {\mathbf {1}}_{A}\right) < \varepsilon , \end{aligned}$$

for \(w>0\) sufficiently large. This completes the proof. \(\square\)

Theorem 3.1 is a modular convergence theorem for the family of the sampling Kantorovich operators acting on \(f \in C_c({\mathbb {R}})\).

In what follows, we will show that if the kernel \(\chi\) has compact support, we become able to prove a Luxemburg-norm convergence theorem for the operators \(S^\chi _w f\), when \(f \in C_c({\mathbb {R}})\).

Theorem 3.2

Let \(\rho _{\mathbb {R}}\) be a convex, monotone, strongly finite and absolutely continuous modular on \(X({\mathbb {R}}).\) Moreover, let \(\chi\) be a kernel with compact support. Then for any \(f \in C_c({\mathbb {R}})\) and for every \(\lambda >0\):

$$\begin{aligned} \lim _{w \rightarrow +\infty } \rho _{\mathbb {R}}\left( \lambda (S^{\chi }_wf-f) \right) = 0. \end{aligned}$$

Proof

By using the same notation of Theorem 3.1, we can write what follows:

$$\begin{aligned} (S^{\chi }_wf)(x)= \sum _{k:\, t_k \in [-\gamma w, +\gamma w]}\left[ {w\over \Delta _k} \int _{t_{k}/w}^{t_{k+1}/w}f(u)\, du \right] \, \chi (wx - t_k), \quad x \in {\mathbb {R}}. \end{aligned}$$

Now, since \(supp\, \chi \subset [-L, L]\), with a suitable \(L>0\), proceeding as in Remark 2.3 we obtain that:

$$\begin{aligned} \chi (wx-t_k) = 0, \quad \mathrm{for\,every} \quad x \notin [-L-\gamma ,\, L+\gamma ], \quad t_k \in [-w \gamma , +w \gamma ], \end{aligned}$$

for every \(w\ge 1\), i.e., \(supp\, S^{\chi }_wf \subset [-L-\gamma ,\, L+\gamma ]\), for every \(w\ge 1\). Now, we choose \(N>0\) such that:

$$\begin{aligned}{}[-L-\gamma ,\, L+\gamma ]\, \cup S\ \subset [- N,\, N]=: {{\mathcal {N}}}, \end{aligned}$$

where, as in Theorem 3.1, S denotes the support of f. Thus, for every fixed \(\lambda >0\) we have:

$$\begin{aligned} \lambda \, \left| (S^\chi _w f)(x) - f(x) \right|&= \lambda \, \left| (S^\chi _w f)(x) - f(x) \right| {\mathbf {1}}_{{{\mathcal {N}}}}(x)\\&\le \lambda \, \Vert f\Vert _\infty \left[ m_{0, \Pi }(\chi ) + 1 \right] \, {\mathbf {1}}_{{{\mathcal {N}}}}(x)\ =:\ g(x), \end{aligned}$$

for every \(x \in {\mathbb {R}}\) and w sufficiently large. Now, recalling that the modular \(\rho _{\mathbb {R}}\) is strongly finite and convex, we have that \(g \in E_{\rho _{\mathbb {R}}}({\mathbb {R}}) \subset L_{\rho _{\mathbb {R}}}({\mathbb {R}})\) since \({\mathbf {1}}_{{{\mathcal {N}}}}\in E_{\rho _{\mathbb {R}}}({\mathbb {R}})\), and moreover \(\rho _{\mathbb {R}}(3\, g)<+\infty\). Finally, observing that:

$$\begin{aligned} \lambda \, \left| (S^\chi _w f)(x) - f(x) \right| \rightarrow 0, \quad \text{ as } \quad w \rightarrow +\infty , \end{aligned}$$

for every \(x \in {\mathbb {R}}\) in view of Theorem 2.1, we can apply the modular version of the Lebesgue dominated convergence theorem (Theorem 2.4), obtaining the final assertion. \(\square\)

Now, in order to establish a modular-type inequality for the operators \(S^\chi _w\), we firstly introduce the following subset of \(X({\mathbb {R}})\).

Given the constants E, \(K>0\) and the modulars \(\rho _{\mathbb {R}}\), \(\rho _{\mathbb {Z}}\) on \(X({\mathbb {R}})\) and \(X({\mathbb {Z}})\) respectively, we define the subset \({{\mathcal {L}}}_{E, K}({\mathbb {R}})\) of \(X({\mathbb {R}})\) whose f are locally absolutely integrable and satisfying the following inequality:

$$\begin{aligned} \limsup _{w \rightarrow +\infty }\ {1 \over w}\, \rho _{\mathbb {Z}}\left( \lambda F_w \right) \le E\, \rho _{\mathbb {R}}\left( \lambda \, K\, f \right) , \end{aligned}$$
(8)

for every \(\lambda >0\), where \(F_w=(f_{w,k})_{k \in {\mathbb {Z}}} \in X({\mathbb {Z}})\), \(w>0\), with:

$$\begin{aligned} f_{w,k}:= {w \over \Delta _k }\, \int _{t_k/w}^{t_{k+1}/w}|f(u)|\, du. \end{aligned}$$
(9)

Now we can prove the following.

Theorem 3.3

Let \(\rho _{\mathbb {R}}\) be a monotone modular on \(X({\mathbb {R}})\) and \(\rho _{\mathbb {Z}}\) be a modular on \(X({\mathbb {Z}}).\) Further, let \(\chi\) be a kernel which is compatible with \(\rho _{\mathbb {R}}\) and \(\rho _{\mathbb {Z}}.\) Then, for any function \(f \in {{\mathcal {L}}}_{E,K}({\mathbb {R}}),\) for some E,  \(K>0,\) there holds:

$$\begin{aligned} \limsup _{w \rightarrow +\infty }\ \rho _{\mathbb {R}}\left( c\, S^{\chi }_w f \right) \le E\, D_1\, \rho _{\mathbb {R}}\left( c\, D_2\, K\, f\right) , \end{aligned}$$

for every \(c>0,\) where \(D_1\) and \(D_2\) are the constants of the compatibility condition among \(\chi ,\) \(\rho _{\mathbb {R}}\) and \(\rho _{\mathbb {Z}}\). In particular, if \(f \in L_{\rho _{\mathbb {R}}}({\mathbb {R}})\) it turns out that \(S^{\chi }_w f \in L_{\rho _{\mathbb {R}}}({\mathbb {R}}),\) for every sufficiently large \(w>0.\)

Proof

For every fixed \(c>0\), by using (3), we can write what follows:

$$\begin{aligned} \rho _{\mathbb {R}}\left( c\, S^{\chi }_w f \right)&\le \rho _{\mathbb {R}}\left( c\, \sum _{k \in {\mathbb {Z}}} {w \over \Delta _k }\int _{t_k/w}^{t_{k+1}/w}|f(u)|\, du\, |\chi (w\cdot -t_k)| \right) \\&\le {1 \over w}\, D_1\, \rho _{\mathbb {Z}}\left( D_2\, c\, F_w \right) \, +\, b_w, \end{aligned}$$

for \(w>0\) sufficiently large, with \(D_1\), \(D_2\), and \(F_w\) defined as in (9). Then the first part of the theorem easily follows since \(f \in {{\mathcal {L}}}_{E,K}({\mathbb {R}})\), while the second part is an immediate consequence of the first one. \(\square\)

Now, we are able to prove the main theorem of this section.

Theorem 3.4

Let \(\rho _{\mathbb {R}}\) be a convex, monotone, strongly finite, absolutely finite, and absolutely continuous modular on \(X({\mathbb {R}})\) and \(\rho _{\mathbb {Z}}\) be a modular on \(X({\mathbb {Z}}).\) Further, let \(\chi\) be a kernel compatible with \(\rho _{\mathbb {R}}\) and \(\rho _{\mathbb {Z}},\) and satisfying assumption (4) together with \(\rho _{\mathbb {R}}.\) Then for every \(f \in L_{\rho _{\mathbb {R}}}({\mathbb {R}}),\) such that the space \(f - C_c({\mathbb {R}}) \subset {{\mathcal {L}}}_{E,K}({\mathbb {R}}),\) for some E,  \(K>0,\) there is a constant \(c>0\) such that:

$$\begin{aligned} \lim _{w \rightarrow +\infty } \rho _{\mathbb {R}}\left( c(S^{\chi }_w f - f) \right) = 0. \end{aligned}$$

Proof

Let \(f \in L_{\rho _{\mathbb {R}}}({\mathbb {R}})\) be as in the statement. By Theorem 2.5 there exists \(\lambda >0\) such that, for every \(\varepsilon >0\) there exists \(g \in C_c({\mathbb {R}})\) with:

$$\begin{aligned} \rho _{\mathbb {R}}\left( \lambda (f-g) \right) < \varepsilon . \end{aligned}$$

Let now \(\varepsilon >0\) be fixed and \(g \in C_c({\mathbb {R}})\) as above. Note that, since \(g \in C_c({\mathbb {R}})\), by Theorem 3.1, for every \({\widetilde{\lambda }}>0\) with \({\widetilde{\lambda }} \le \alpha /3\), where \(\alpha\) is the parameter of the absolute continuity of the modular \(\rho _{\mathbb {R}}\), there holds:

$$\begin{aligned} \lim _{w\rightarrow +\infty } \rho _{\mathbb {R}}\left( {\widetilde{\lambda }}(S^{\chi }_w g-g) \right) = 0. \end{aligned}$$
(10)

Now, we can choose a positive constant c such that:

$$\begin{aligned} c \le \min \left\{ {\lambda \over 3 D_2\, K},\, {\alpha \over 9},\, {\lambda \over 3} \right\} , \end{aligned}$$

where \(D_2\) is the constant of the compatibility condition among \(\chi\), \(\rho _{\mathbb {R}}\) and \(\rho _{\mathbb {Z}}\). We now proceed as follows:

$$\begin{aligned} \rho _{\mathbb {R}}\left( c\, (S^{\chi }_w f - f) \right)&\le \rho _{\mathbb {R}}\left( 3\, c\, (S^{\chi }_w f - S^{\chi }_w g) \right) + \rho _{\mathbb {R}}\left( 3\, c\, (S^{\chi }_w g - g) \right) \\&\quad + \rho _{\mathbb {R}}\left( 3\, c\, (g - f) \right) \, =:\ I_1\, +\, I_2\, +\, I_3, \end{aligned}$$

\(w>0\). Recalling that the operator \(S^{\chi }_w\) is linear, \(f-g \in {{\mathcal {L}}}_{E, K}({\mathbb {R}})\), and by applying Theorem 3.3 to \(I_1\), we have that:

$$\begin{aligned} \limsup _{w \rightarrow +\infty }\ \rho _{\mathbb {R}}\left( 3c\, S^{\chi }_w (f -g)\right) \le E\, D_1\, \rho _{\mathbb {R}}\left( 3\, c\, D_2\, K\, (f-g)\right) \le E\, D_1\, \rho _{\mathbb {R}}\left( \lambda \, (f-g)\right) . \end{aligned}$$

For what concerns \(I_2\), by the choice of the constant c and (10) we also have:

$$\begin{aligned} \rho _{\mathbb {R}}\left( 3\, c\, (S^{\chi }_w g - g) \right) \le \rho _{\mathbb {R}}\left( {\alpha \over 3}\, (S^{\chi }_w g - g) \right) < \varepsilon , \end{aligned}$$

for \(w>0\) sufficiently large. In conclusion, we can write:

$$\begin{aligned} \rho _{\mathbb {R}}\left( c\, (S^{\chi }_w f - f) \right) \le \varepsilon + \left( 1 + E\, D_1 \right) \, \rho _{\mathbb {R}}\left( \lambda (f-g) \right) < \left( 2 + E D_1 \right) \, \varepsilon , \end{aligned}$$

for \(w>0\) sufficiently large. This completes the proof. \(\square\)

4 Applications

In this section, we will discuss some concrete examples of modular spaces for which the above results hold. Moreover, also examples of kernels will be presented.

4.1 Convergence in Musielak–Orlicz spaces

Let \(\varphi {:}\,{\mathbb {R}}\times {\mathbb {R}}^+_0 \rightarrow {\mathbb {R}}^+_0\) be a function of two variables which satisfy the following conditions:

\((\varphi 1)\):

\(\varphi (\cdot , u)\) is measurable and locally integrable on \({\mathbb {R}}\) for every \(u \in {\mathbb {R}}^+_0\);

\((\varphi 2)\):

for every \(s \in {\mathbb {R}}\), \(\varphi (s, \cdot )\) is convex on \({\mathbb {R}}^+_0\) with \(\varphi (s, 0)=0\) and \(\varphi (s, u)>0\) for \(u>0\);

\((\varphi 3)\):

\(\varphi\) is \(\tau\)-bounded, i.e., there exist a constant \(C \ge 1\) and a measurable function \(F{:}\,{\mathbb {R}}\times {\mathbb {R}}\rightarrow {\mathbb {R}}^+_0\) such that, for every t, \(s \in {\mathbb {R}}\) and \(u \ge 0\) there holds:

$$\begin{aligned} \varphi (s - t, u) \le \varphi (s, Cu) + F(s,t). \end{aligned}$$
(11)

A function \(\varphi\) as above is said a \(\tau\)-bounded \(\varphi\) -function, and for the sake of simplicity, we will call it simply a \(\varphi\) -function.

The definition of \(\tau\)-boundedness can be found in the monograph of Musielak [56]. We can observe that examples of Musielak–Orlicz spaces which satisfy the \(\tau\)-boundedness with certain \(F \ne 0\) can be constructed following the procedure described in [20].

From now on, we will only consider \(\varphi\)-functions \(\varphi\) which satisfy condition \((\varphi 3)\) with \(F \equiv 0\).

Now, we define the non-negative integral functionals:

$$\begin{aligned} \rho _\varphi (f):= \int _{\mathbb {R}}\varphi (t, |f(t)|)\, dt, \quad \quad \rho ^{\Pi }_{\varphi }(g):= \sum _{k \in {\mathbb {Z}}}\varphi (t_k, |g_k|) \end{aligned}$$
(12)

where \(f \in X({\mathbb {R}})\) and \(g=(g_k)_{k\in {\mathbb {Z}}} \in X({\mathbb {Z}})\), respectively, and \(\Pi =(t_k)_{k \in {\mathbb {Z}}}\) be a sequence with the properties introduced in Sect. 2. It is easy to check that both \(\rho _\varphi\) and \(\rho ^{\Pi }_{\varphi }\) are modulars on \(X({\mathbb {R}})\) and \(X({\mathbb {Z}})\) respectively, which satisfy the properties (a)–(e) given in Sect. 2, see e.g., Example 2.1 (b) and Example 2.2 (a) of pp. 18–19 in [19].

The modular spaces generated by \(\rho _\varphi\) and \(\rho ^{\Pi }_{\varphi }\) are called Musielak–Orlicz spaces (see e.g., [47]) and are defined as follows:

$$\begin{aligned} L^\varphi ({\mathbb {R}}):= L_{\rho _\varphi }({\mathbb {R}})= \left\{ f \in X({\mathbb {R}}){:}\,\lim _{\lambda \rightarrow 0}\rho _\varphi (\lambda f)= 0 \right\} , \end{aligned}$$

and

$$\begin{aligned} L^\varphi ({\mathbb {Z}}):= L_{\rho ^{\Pi }_{\varphi }}({\mathbb {Z}})= \left\{ f \in X({\mathbb {Z}}){:}\,\lim _{\lambda \rightarrow 0}\rho ^{\Pi }_{\varphi }(\lambda f)= 0 \right\} . \end{aligned}$$

The following lemma is related to assumption (4).

Lemma 4.1

Let \(\chi\) be a kernel belonging to \(L^1({\mathbb {R}})\) and \(\varphi\) be a fixed \(\varphi\)-function which satisfies the following additional assumption:

\((\varphi 4)\):

for sufficiently large \(N>0,\) there holds:

$$\begin{aligned} \sup _{|s|>N} \varphi (s, u)=: L_u < +\infty , \quad \quad \mathrm{for\,every}\,u \in {\mathbb {R}}^+_0. \end{aligned}$$
(13)

Then assumption (4) turns out to be satisfied.

Proof

Let \(\gamma >0\) and \(a>0\) be fixed. Moreover, we define \({{\mathcal {J}}}:=[-N, N] \subset {\mathbb {R}}\), where \(N>0\) is the parameter of assumption \((\varphi 4)\), with \(\mu _{\mathbb {R}}({{\mathcal {J}}})=2\, N < +\infty\). Now, by using Jensen inequality (see e.g., [37]) and condition \((\varphi 4)\) we can write what follows:

$$\begin{aligned}&\rho _\varphi \left( a\ {\mathbf {1}}_{{\mathbb {R}}{\setminus } {{\mathcal {J}}}}(\cdot ) \sum _{k:\, t_k \in [-\gamma \, w, +\gamma \, w]}|\chi (w \cdot - t_k)| \right) \\&\qquad = \int _{|t|>N} \varphi \left( t,\, a \sum _{k:\, t_k \in [-\gamma \, w, +\gamma \, w]}|\chi (w t - t_k)| \right) \, dt\\&\qquad \le {1 \over m_{0, \Pi }(\chi )} \int _{|t|>N} \varphi \left( t,\, a\, m_{0, \Pi }(\chi ) \right) \, \sum _{k:\, t_k \in [-\gamma \, w, +\gamma \, w]} |\chi (w t - t_k)|\, dt\\&\qquad \le {L_{a\, m_{0, \Pi }(\chi )} \over m_{0, \Pi }(\chi )} \sum _{k:\, t_k \in [-\gamma \, w, +\gamma \, w]} \int _{|t|>N} |\chi (w t - t_k)|\, dt, \end{aligned}$$

for \(w>0\), where \(L_{a\, m_{0, \Pi }(\chi )} >0\) is the constant of assumption \((\varphi 4)\) with \(u=a\, m_{0, \Pi }(\chi )\). By the change of variable \(y = w t - t_k\) in the above integrals, and observing that in the above sums the number of terms does not exceed \(4\, \gamma \, w / {\bar{\Delta }}\), for \(w>0\) sufficiently large with \({\bar{\Delta }}\) the parameter related to the sequence \((t_k)_{k \in {\mathbb {Z}}}\) (see Sect. 2), we finally have:

$$\begin{aligned}&\rho _\varphi \left( a\ {\mathbf {1}}_{{\mathbb {R}}{\setminus } {{\mathcal {J}}}}(\cdot ) \sum _{k:\, t_k \in [-\gamma \, w, +\gamma \, w]}|\chi (w \cdot - t_k)| \right) \\&\quad \le {L_{a\, m_{0, \Pi }(\chi )} \over w\, m_{0, \Pi }(\chi )}\, \sum _{k:\, t_k \in [-\gamma \, w, +\gamma \, w]} \int _{{\mathbb {R}}} |\chi (y)|\, dy\le {4\, L_{a\, m_{0, \Pi }(\chi )}\, \gamma \over m_{0, \Pi }(\chi )}\, {\bar{\Delta }}^{-1} \Vert \chi \Vert _1, \end{aligned}$$

for \(w>0\) sufficiently large. This completes the proof. \(\square\)

Note that, assumption (4) turns out to be satisfies also in the following case.

Lemma 4.2

Let \(\chi\) be a kernel belonging to \(L^1({\mathbb {R}})\) and \(\varphi\) be a fixed \(\varphi\)-function which satisfies the following additional assumption:

\((\varphi 5)\):

\(\varphi (\cdot , u) \in L^1({\mathbb {R}}),\) for every \(u \in {\mathbb {R}}^+_0.\)

Then assumption (4) turns out to be satisfied.

Proof

Let \(\gamma >0\) and \(a>0\) be fixed. We easily get:

$$\begin{aligned}&\rho _\varphi \left( a\ {\mathbf {1}}_{{\mathbb {R}}{\setminus } {{\mathcal {J}}}}(\cdot ) \sum _{k:\, t_k \in [-\gamma \, w, +\gamma \, w]}|\chi (w \cdot - t_k)| \right) \\&\quad \le \int _{|t|>N} \varphi \left( t,\, a\, m_{0, \Pi }(\chi ) \right) \, dt\le \Vert \varphi \left( \cdot ,\, a\, m_{0, \Pi }(\chi ) \right) \Vert _1\ <\ +\infty , \end{aligned}$$

where \({{\mathcal {J}}}:=[-N, N]\), and \(N>0\) is any fixed positive parameter. \(\square\)

In order to give a complete treatment of the above approximation problem, we can prove the following lemma concerning the space \({{\mathcal {L}}}_{E,K}\), generated by \(\rho _\varphi\) and \(\rho ^{\Pi }_{\varphi }\).

Lemma 4.3

Let \(f \in X({\mathbb {R}})\) be a locally integrable function. Then \(f \in {{\mathcal {L}}}_{E, K}({\mathbb {R}}),\) with \(E:=1/{\bar{\Delta }}\) and \(K:=C,\) where \({\bar{\Delta }}\) is one of the parameter of the sequence \(\Pi\) and C is the constant of the \(\tau\) -boundedness of \(\varphi .\)

In particular, if \(f \in L^\varphi ({\mathbb {R}})\) it turns out that \(S^{\chi }_w f \in L^\varphi ({\mathbb {R}}),\) for every sufficiently large \(w>0.\)

Proof

For every \(\lambda >0\), by assumption \((\varphi 2)\) and using the Jensen inequality and the \(\tau\)-boundedness of \(\varphi\) we can write what follows:

$$\begin{aligned}&{1 \over w}\, \sum _{k \in {\mathbb {Z}}} \varphi \left( t_k,\, \lambda \, \left| {w \over \Delta _k} \int _{t_k/w}^{t_{k+1}/w} f(u)\, du \right| \right) \le {1 \over w}\, \sum _{k \in {\mathbb {Z}}} \varphi \left( t_k,\, \lambda \, {w \over \Delta _k} \int _{t_k/w}^{t_{k+1}/w} \left| f(u)\right| \, du \right) \\&\quad \le {1 \over w}\, \sum _{k \in {\mathbb {Z}}}\, {w \over \Delta _k} \int _{t_k/w}^{t_{k+1}/w} \varphi \left( t_k,\, \lambda \, \left| f(u)\right| \right) \, du \le \ \sum _{k \in {\mathbb {Z}}}\, {1 \over \Delta _k} \int _{t_k/w}^{t_{k+1}/w} \varphi \left( u,\, \lambda \, C\, \left| f(u)\right| \right) \, du\\& \quad \le {\bar{\Delta }}^{-1} \sum _{k \in {\mathbb {Z}}}\, \int _{t_k/w}^{t_{k+1}/w}\varphi \left( u,\, \lambda \, C\, \left| f(u)\right| \right) \, du=, {\bar{\Delta }}^{-1} \int _{\mathbb {R}}\varphi \left( u,\, \lambda \, C\, \left| f(u)\right| \right) \, du. \end{aligned}$$

Now, passing to the \(\limsup\) as \(w \rightarrow +\infty\) we finally obtain the assertion. \(\square\)

Now, we are able to prove the following results in the general setting of Musielak–Orlicz spaces.

Theorem 4.4

Let \(\chi\) be a kernel belonging to \(L^1({\mathbb {R}})\) and \(\varphi\) be a fixed \(\varphi\) -function which satisfies at least one between conditions \((\varphi 4)\) and \((\varphi 5).\) Hence, the following statements hold:

  1. 1.

    for \(f \in C_c({\mathbb {R}})\) :

    $$\begin{aligned} \lim _{w \rightarrow +\infty } \rho _\varphi \left( \lambda \left( S^{\chi }_w f - f \right) \right) = 0, \end{aligned}$$

    for every \(0<\lambda \le \alpha /3,\) where \(\alpha\) is the parameter of the absolute continuity of the modular \(\rho _\varphi .\) In particular, if \(\chi\) has compact support the above convergence result holds for every \(\lambda >0\) ;

  2. 2.

    for any function \(f \in X({\mathbb {R}}),\) there holds:

    $$\begin{aligned} \limsup _{w \rightarrow +\infty }\ \rho _\varphi \left( c\, S^{\chi }_w f \right) \le \left[ \Vert \chi \Vert _1 / {\bar{\Delta }}\, m_{0, \Pi }(\chi )\right] \, \rho _\varphi \left( c\, C^2\, m_{0, \Pi }(\chi )\, f\right) , \end{aligned}$$

    for every \(c>0,\) where \({\bar{\Delta }}\) is one of the parameter of the sequence \(\Pi\) and C is the constant of the \(\tau\) -boundedness of \(\varphi .\) In particular, if \(f \in L^\varphi ({\mathbb {R}})\) it turns out that \(S^{\chi }_w f \in L^\varphi ({\mathbb {R}}),\) for every sufficiently large \(w>0.\)

  3. 3.

    for every function \(f \in L^\varphi ({\mathbb {R}}),\) there is a constant \(c>0\) such that:

    $$\begin{aligned} \lim _{w \rightarrow +\infty } \rho _\varphi \left( c(S^{\chi }_w f - f) \right) = 0. \end{aligned}$$

Theorem 4.4 is a direct consequence of Lemmas 4.1–4.3, Theorems 3.1–3.4.

Concluding this section, we can discuss the case of \(\varphi\)-functions of the form \({\widetilde{\varphi }}(s,u) = {\widetilde{\varphi }}(u)\), \(s \in {\mathbb {R}}\), \(u \in {\mathbb {R}}^+_0\), i.e., when \({\widetilde{\varphi }}\) does not depend by the parameter s.

Here, we consider the following modulars on \(X({\mathbb {R}})\) and \(X({\mathbb {Z}})\) respectively:

$$\begin{aligned} \rho _{{\widetilde{\varphi }}}(f):= \int _{\mathbb {R}}{\widetilde{\varphi }}(|f(t)|)\, dt, \quad \quad \rho _{{\widetilde{\varphi }}}^\Pi (g):= \sum _{k \in {\mathbb {Z}}}{\widetilde{\varphi }}(|g_k|), \end{aligned}$$

and the corresponding modular spaces \(L^{{\widetilde{\varphi }}}({\mathbb {R}})\) and \(L^{{\widetilde{\varphi }}}({\mathbb {Z}})\) are the so-called Orlicz spaces (see e.g., [1, 42, 44]). We point out that in the present case the assumption \((\varphi 3)\) is trivially satisfied with \(F \equiv 0\) and \(C=1\). Moreover, also condition \((\varphi 4)\) holds. Hence we can state the following theorem that match with the theory developed in [16].

Theorem 4.5

Let \(\chi\) be a kernel belonging to \(L^1({\mathbb {R}})\) and \({\widetilde{\varphi }}\) be a fixed \(\varphi\) -function of the form \({\widetilde{\varphi }}(s,u) = {\widetilde{\varphi }}(u),\) \(s \in {\mathbb {R}},\) \(u \in {\mathbb {R}}^+_0.\) Hence, the following statements hold:

  1. 1.

    for \(f \in C_c({\mathbb {R}})\) :

    $$\begin{aligned} \lim _{w \rightarrow +\infty } \rho _{{\widetilde{\varphi }}} \left( \lambda \left( S^{\chi }_w f - f \right) \right) = 0, \end{aligned}$$

    for every \(0<\lambda \le \alpha /3,\) where \(\alpha\) is the parameter of the absolute continuity of the modular \(\rho _{{\widetilde{\varphi }}}.\) In particular, if \(\chi\) has compact support the above convergence result holds for every \(\lambda >0\) ;

  2. 2.

    for any function \(f \in X({\mathbb {R}}),\) there holds:

    $$\begin{aligned} \limsup _{w \rightarrow +\infty }\ \rho _{{\widetilde{\varphi }}}\left( c\, S^{\chi }_w f \right) \le \left[ \Vert \chi \Vert _1 / {\bar{\Delta }}\, m_{0, \Pi }(\chi )\right] \, \rho _{{\widetilde{\varphi }}}\left( c\, m_{0, \Pi }(\chi )\, f\right) , \end{aligned}$$

    for every \(c>0,\) where \({\bar{\Delta }}\) is one of the parameter of the sequence \(\Pi .\) In particular, if \(f \in L^{{\widetilde{\varphi }}}({\mathbb {R}})\) it turns out that \(S^{\chi }_w f \in L^{{\widetilde{\varphi }}}({\mathbb {R}}),\) for every sufficiently large \(w>0.\)

  3. 2.

    for every function \(f \in L^{{\widetilde{\varphi }}}({\mathbb {R}}),\) there is a constant \(c>0\) such that:

    $$\begin{aligned} \lim _{w \rightarrow +\infty } \rho _{{\widetilde{\varphi }}}\left( c(S^{\chi }_w f - f) \right) = 0. \end{aligned}$$

As another particular example of Musielak–Orlicz space, one can consider \(\varphi\)-functions (with respect to the second variable) of the product-type, of the form:

$$\begin{aligned} \varphi (s,u):= \xi (s)\, {\widetilde{\varphi }}(u), \quad s \in {\mathbb {R}}, \quad u \in {\mathbb {R}}^+_0, \end{aligned}$$
(14)

which satisfy the following conditions:

(\({{\mathcal {F}}} 1\)):

\(\xi \in X({\mathbb {R}})\) and there exist \(M \ge m >0\) such that \(m \le \xi (s) \le M\), for every \(s \in {\mathbb {R}}\);

(\({{\mathcal {F}}} 2\)):

\({\widetilde{\varphi }}{:}\,{\mathbb {R}}^+_0 \rightarrow {\mathbb {R}}^+_0\) is a convex function such that \({\widetilde{\varphi }}(0)=0\), and \({\widetilde{\varphi }}(u)>0\) for \(u>0\);

(\({{\mathcal {F}}} 3\)):

for every \(\lambda _1>0\) there exists \(\lambda _2 \ge 1\) such that:

$$\begin{aligned} \lambda _1\, {\widetilde{\varphi }}(u)\le {\widetilde{\varphi }}(\lambda _2\, u), \quad u \in {\mathbb {R}}^+_0. \end{aligned}$$

In this way, it is easy to see that assumptions \((\varphi 1)\) and \((\varphi 2)\) are satisfied. Further, concerning \((\varphi 3)\) we can write what follows:

$$\begin{aligned} \varphi (s-t, u)= \xi (s-t)\, {\widetilde{\varphi }}(u)\le {M \over m}\, \xi (s)\, {\widetilde{\varphi }}(u)\le \xi (s)\, {\widetilde{\varphi }}(\lambda _2\, u)= \varphi (s,\lambda _2\, u), \end{aligned}$$

for every \(u \ge 0\), where \(\lambda _2 \ge 1\) is the parameter of condition (\({{\mathcal {F}}} 3\)) corresponding to \(\lambda _1= M/ m\). The above inequality shows that \(\varphi\)-functions of the form as in (14) are \(\tau\)-bounded with \(F \equiv 0\) and \(C= \lambda _2\). Moreover, it is easy to see that also assumption \((\varphi 4)\) is satisfied. In fact, by the above construction we can consider to have obtained some examples of weighted Orlicz spaces.

Some concrete examples of weighted Orlicz spaces generated by \(\varphi\)-function of the form (14) can be obtained by choosing, for instance,

$$\begin{aligned} \xi (s):= {5 \over s^2 + 1}\, +\, 1, \quad \quad s \in {\mathbb {R}}, \end{aligned}$$
(15)

and as function \({\widetilde{\varphi }}\) one of the following:

$$\begin{aligned} {\widetilde{\varphi }}_1(u):= u^p, \quad \quad {\widetilde{\varphi }}_2(u):= u^\alpha \log ^\beta (u + e), \end{aligned}$$
(16)

for every \(u \ge 0\), where \(1 \le p <+\infty\), \(\alpha \ge 1\), and \(\beta >0\). Obviously, it is easy to show that the above product-type \(\varphi\)-functions satisfy conditions (\({{\mathcal {F}}} 1\)), (\({{\mathcal {F}}} 2\)), and (\({{\mathcal {F}}} 3\)). The Musielak–Orlicz (or weighted Orlicz) spaces generated by \(\varphi = \xi \, {\widetilde{\varphi }}_1\) are the so-called weighted \(L^p\)-spaces, and that ones generated by \(\varphi = \xi \, {\widetilde{\varphi }}_2\) are the weighted Zygmund spaces.

Furthermore, if \(\xi \equiv 1\) in the above examples, i.e., \(\varphi = {\widetilde{\varphi }}\) and does not depend on the parameter s, we found again the case of Orlicz spaces considered in Theorem 4.5. In particular, the functions \({\widetilde{\varphi }}_1\) and \({\widetilde{\varphi }}_2\) generate the well-known \(L^p\)-spaces and Zygmung spaces.

Moreover, we can also consider the following, more interesting (with respect to the previous ones), example of Musielak–Orlicz space generated by the \(\varphi\)-function:

$$\begin{aligned} \varphi _3(s,u):= e^{\psi (s)\, u^\gamma }-1,\ \quad s \in {\mathbb {R}},\ \quad u \in {\mathbb {R}}^+_0, \end{aligned}$$
(17)

\(\gamma >0\), where the function \(\psi\) satisfies the inequality of condition \(({{\mathcal {F}}}1)\) for suitable \(0<m \le M\). By simple computations, it can be shown that also \(\varphi\)-functions of the form as in (17) are \(\tau\)-bounded with \(F \equiv 0\) and \(C= \left( M / m \right) ^{1 / \gamma }\). As an example of function \(\psi\) one can consider again, e.g., the function \(\psi (s)=\xi (s)\) defined in (15).

In the Orlicz-case, when \(\psi (s) = 1\), for every \(s \in {\mathbb {R}}\), we have:

$$\begin{aligned} {\widetilde{\varphi }}_3(u):= e^{u^\gamma }-1, \quad u \in {\mathbb {R}}^+_0, \end{aligned}$$

\(\gamma >0\), which generates the well-known exponential spaces.

Note that, all the above presented examples of modular spaces are generated by modular functionals which has integral form, and reduces to Musielak–Orlicz, weighted Orlicz or Orlicz spaces. However, the theory of modular spaces contains also modulars which are not of integral type and hence, they can not be reduced to the previous cases.

For instance, we can consider the following modulars (see [19, p. 7]):

$$\begin{aligned} \rho ^{\Phi }_{{\mathbb {R}}}(f):= \sup _{\ell \in W} \int _a^ba_\ell (x)\, \left[ \int _{\mathbb {R}}\Phi (x, |f(t)|)\, dt\right] \, dm(x), \end{aligned}$$
(18)

and

$$\begin{aligned} \rho ^{\Phi }_{{\mathbb {Z}}}(g):= \sup _{\ell \in W} \int _a^ba_\ell (x)\, \left[ \sum _{k \in {\mathbb {Z}}} \Phi (x, |g_k|)\right] \, dm(x) \end{aligned}$$
(19)

with \(f \in X({\mathbb {R}})\), \(g=(g_k)_{k \in {\mathbb {Z}}} \in X({\mathbb {Z}})\), and where m is a measure on an interval \([a,b[ \subset {\mathbb {R}}\) (b can be also equal to \(+\infty\)) defined on the \(\sigma\)-algebra of all Lebesgue measurable subset of [a, b[, W be a non-empty set of indices, \(a_\ell :[a,b[ \rightarrow {\mathbb {R}}^+_0\) are measurable functions for every \(\ell \in W\), and \(\Phi {:}\,[a,b[ \times {\mathbb {R}}^+_0 \rightarrow {\mathbb {R}}^+_0\).

Now, if the function \(\Phi\) in the above definitions is convex with respect to the second variable, and satisfies other suitable conditions (see [19, 1–4 p. 7, (b) of p. 19, and (b) of p. 23]) it turns out that \(\rho ^{\Phi }_{{\mathbb {R}}}\) is a convex, monotone, strongly finite, absolutely finite, and absolutely continuous modular on \(X({\mathbb {R}})\) and \(\rho ^{\Phi }_{{\mathbb {Z}}}\) is a modular on \(X({\mathbb {Z}})\). Thus, all the assumptions of Theorem 3.4 required on the modulars are satisfied. Further, considering a given kernel \(\chi\) belonging to \(C_c({\mathbb {R}})\), we immediately have that the compatibility condition (3) hold. Indeed, using Jensen inequality, the change of variable \(y=wt-t_k\), and Fubini–Tonelli theorem, we immediately have:

$$\begin{aligned}&\int _{\mathbb {R}}\Phi (x, \sum _{k \in {\mathbb {Z}}}|g_k|\cdot |\chi (wt-t_k)|)\, dt\\&\quad \le {1 \over m_{0, \Pi }(\chi )}\int _{\mathbb {R}}\sum _{k \in {\mathbb {Z}}} \Phi (x, m_{0, \Pi }(\chi ) |g_k|)\, |\chi (wt-t_k)|\, dt\\&\quad \le {1 \over w\, m_{0, \Pi }(\chi )}\sum _{k \in {\mathbb {Z}}} \Phi (x, m_{0, \Pi }(\chi ) |g_k|)\, \int _{\mathbb {R}}|\chi (y)|\, dy= {\Vert \chi \Vert _1 \over w\, m_{0, \Pi }(\chi )}\sum _{k \in {\mathbb {Z}}} \Phi (x, m_{0, \Pi }(\chi ) |g_k|), \end{aligned}$$

from which (3) follows with \(D_1=\Vert \chi \Vert _1/m_{0, \Pi }(\chi )\), \(D_2=m_{0, \Pi }(\chi )\), and \(b_w=0\). Further, since \(\chi\) has compact support, in view of what has been observed in Remark 2.3, it follows that also (4) holds. Finally, it remains to observe that, any function \(f \in X({\mathbb {R}})\) belongs to the space \({{\mathcal {L}}}_{E, K}({\mathbb {R}})\), with \(E=1/\delta\) and \(K=1\). Indeed, proceeding similarly to above, we immediately have:

$$\begin{aligned}&{1 \over w}\rho ^{\Phi }_{{\mathbb {Z}}}(\lambda F_w)= {1 \over w} \sup _{\ell \in W} \int _a^ba_\ell (x)\, \left[ \sum _{k \in {\mathbb {Z}}} \Phi \left( x, \lambda \, \frac{w}{\Delta _k} \int _{t_k/w}^{t_{k+1}/w}f(u)\, du \right) \right] \, dm(x)\\&\quad \le {1 \over w}\sup _{\ell \in W} \int _a^ba_\ell (x)\, \left[ \sum _{k \in {\mathbb {Z}}} \frac{w}{\Delta _k} \int _{t_k/w}^{t_{k+1}/w} \Phi \left( x, \lambda \,f(u)\right) \, du \right] \, dm(x)\\&\quad \le {1 \over \delta } \sup _{\ell \in W} \int _a^ba_\ell (x)\, \left[ \sum _{k \in {\mathbb {Z}}} \int _{t_k/w}^{t_{k+1}/w} \Phi \left( x, \lambda \, f(u)\right) \, du \right] \, dm(x)\\&\quad = {1 \over \delta } \sup _{\ell \in W} \int _a^ba_\ell (x)\, \left[ \int _{\mathbb {R}}\Phi \left( x, \lambda \, f(u)\right) \, du \right] \, dm(x)= {1 \over \delta }\, \rho ^{\Phi }_{{\mathbb {R}}}(\lambda \, f), \end{aligned}$$

thus choosing \(\lambda >0\) sufficiently small, we get the above claim.

4.2 Examples of kernels

In order to conclude the paper we will present some basic examples of functions that can be used as kernel for the sampling Kantorovich series and that satisfy the assumptions required in the present paper.

Among the most used kernel functions we can mention:

$$\begin{aligned}&\chi _1(x):= \frac{1}{2}\, \left( \frac{\sin (\pi x /2)}{\pi x / 2}\right) ^2, \qquad x \in {\mathbb {R}}, \quad (\mathrm{Fej}{\acute{\mathrm{e}}}{\text {r's}}\,\text {kernel},\,\text {see}\,\text {Fig.}\,{1}\,\text{left}),\\&\chi _2(x):= \frac{3}{2\pi }\, \frac{\sin (x /2)\, \sin (3 x /2)}{3 x^2 / 4}, \qquad x\in {\mathbb {R}}, \quad (\mathrm{de}\,\text {la}\,\text {Vall}{\acute{\mathrm{e}}}\text {e}\,\text {Poussin's}\,\text {kernel}),\\&\chi _3(x):= \frac{\sin (\pi x /2)\, \sin (\pi x)}{\pi ^2 x^2/2}, \qquad x \in {\mathbb {R}}, \end{aligned}$$

see e.g. [24]. The above functions belongs to \(L^1({\mathbb {R}})\), are band-limited and satisfy \((\chi 1)\), \((\chi 2)\) and \((\chi 3)\); for all the details one can see, e.g., [24].

Other important kernels are given by the so-called Jackson-type kernels of order N (see e.g., Fig. 2 left), defined by:

$$\begin{aligned} J_N(x):= c_N\, \text{ sinc}^{2 N}\left( \frac{x}{2 N\pi \alpha }\right) , \quad x \in {\mathbb {R}}, \end{aligned}$$
(20)

with \(N \in {\mathbb {N}}\), \(\alpha \ge 1\), and \(c_N\) is a non-zero normalization coefficient, given by:

$$\begin{aligned} c_N:= \left[ \int _{{\mathbb {R}}} \text{ sinc}^{2 N}\left( \frac{u}{2 N \pi \alpha } \right) \, du \right] ^{-1}. \end{aligned}$$

For the sake of completeness, we recall that the well-known sinc-function is that defined as \(\sin (\pi x)/\pi x\), if \(x \ne 0\), and 1 if \(x=0\), see e.g., [26, 50, 51].

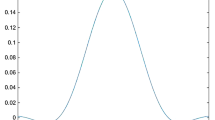
As a further important class of (radial) kernels we can mention the so called Bochner–Riesz kernels of order \(N>0\) (see Fig. 1 right), defined as follows:

$$\begin{aligned} r_N(x):= \frac{2^{N}}{\sqrt{2} \pi }\, \Gamma (N + 1)\, |x|^{-N - 1/2}\, J_{N +1/2}(|x|), \quad x \in {\mathbb {R}}, \end{aligned}$$
(21)

where \(J_\lambda\) is the Bessel function of order \(\lambda\) [27], and \(\Gamma\) is the usual Euler gamma function.

Other examples of band-limited kernels can be generated using the so-called sigmoidal functions (see e.g., [39]). For instance, we can define:

$$\begin{aligned} \sigma _{\gamma }(x):= \left\{ \begin{array}{ll} \displaystyle \frac{1}{|x|^{\gamma }+2}, &{}\quad x<- 2^{1/\gamma },\\ \displaystyle 2^{-(1/\gamma )-2}x+(1/2), &{}\quad - 2^{1/\gamma } \le x \le 2^{1/\gamma },\\ \displaystyle \frac{x^{\gamma }+1}{x^{\gamma }+2}, &{}\quad x > 2^{1/\gamma }, \end{array} \right. \end{aligned}$$
(22)

with \(0 < \gamma \le 1\), and hence the positive functions:

$$\begin{aligned} \chi _{\sigma _{\gamma }}(u):= \frac{1}{2}\, [\sigma _{\gamma }(u+1)-\sigma _{\gamma }(u-1)], \quad u \in {\mathbb {R}}, \end{aligned}$$

belonging to \(L^1({\mathbb {R}})\) and satisfy \((\chi 1)\), \((\chi 2)\) and \((\chi 3)\) [39]. The above examples of kernels have unbounded support. Examples of kernels with compact support can be provided by the well-known central B-splines of order \(n \in {\mathbb {N}}^+\) (see e.g., [7, 8, 63] and Fig. 2 right), defined by:

$$\begin{aligned} M_n(x):= \frac{1}{(n-1)!} \sum ^n_{i=0}(-1)^i \left( {\begin{array}{c}n\\ i\end{array}}\right) \left( \frac{n}{2} + x - i \right) ^{n-1}_+, \quad x \in {\mathbb {R}}, \end{aligned}$$
(23)

where \((x)_+ := \max \left\{ x,0 \right\}\) denotes “the positive part” of \(x \in {\mathbb {R}}\).

For more details concerning the proof of conditions \((\chi 1)\), \((\chi 2)\) and \((\chi 3)\) for the above examples of kernels, see, e.g., [2,3,4, 21, 24, 31, 34, 41, 65].

Fig. 1
figure 1

The Fejér kernel (on the left) and the Bochner–Riesz kernel with \(N=1/2\) (on the right)

Full size image
Fig. 2
figure 2

The Jackson-type kernel with \(N=2\) (on the left) and the central B-spline of order 2 (on the right)

Full size image