1 Introduction

The day the world entered space age—Sputnik-1 was launched on October 4, 1957—was the day when Earth gravity field determination from space started. From the weak radio signals emitted by Sputnik-1 and Sputnik-2 (launched on November 3 the same year), the Earth’s oblateness could be determined in one step and much more accurately than from 150 years of very diligent terrestrial triangulation work by geodesists before (Buchar 1958; Merson and King-Hele 1958; King-Hele 1992). Rapid progress followed during the first 15 years. The Earth’s pear shape was discovered in 1959, followed by the determination of a few additional even and odd zonal spherical harmonics in 1960 (O’Keefe et al. 1959a, b). In 1961, the first attempt was published in identifying a set of tesseral spherical harmonic coefficients (Kozai 1961; Izsak 1963). During this period, more and more satellites with an increasing variety of inclination angles and of altitudes became available for orbit analysis. Camera measurements, dedicated microwave tracking and laser ranging superseded the radio signals of the early years. In the late eighties, the whole development culminated in the availability of spaceborne GPS tracking of satellites in near-Earth orbit, starting with the altimeter satellite Topex/Poseidon (Bertiger et al. 1994; Schutz et al. 1994). The classical astronomical methods of orbit analysis of the pioneering days were quickly replaced by new sophisticated analytical methods (Kaula 1966; Lundquist and Veis 1966) and finally by numerical methods of gravity field determination. Orbit resonance effects were effectively used for complementing and refining the early models and for assessing their accuracy (Balmino and Reigber 1975; Wagner and Klosko 1977). The first standard global gravity models of the Smithsonian Astrophysical Observatory, starting with model SSE-1 (Lundquist and Veis 1966) were followed by the models of the NASA Goddard Space Flight Center, GEM (Lerch et al. 1972) and in Europe by the French–German GRIM series (Balmino et al. 1976). A further major step was the combination of satellite-based orbit perturbations with terrestrial gravity anomalies, and a few years later by the addition of gravity anomalies as derived from satellite altimetry (Kaula 1967; Rapp 1979; Lerch et al. 1979; Wenzel 1999). See also (Nerem et al. 1995). Finally, starting with the launch of the CHAMP satellite in 2000, followed by that of GRACE in 2002 and GOCE in 2009, satellite gravimetry entered a new era. This talk will discuss some of the underlying principles of this new era and the application of gravity models of this new generation in Earth sciences.

2 Freefall and gravitation

To maintain a certain lightness in this article allow me to start with the interpretation of a not very well-known and unnamed painting by Salvador Dali from the year 1948, Fig. 1. What do we see? In the center, there is an apple; the apple is not only an important biblical symbol but as well, since Newton, the classical symbol for gravitation. The apple stands still in the air, obviously kept levitated by some magic forces coming from the four pieces of the marble frame. Maybe inspired by this painting many years back a geodetic instrument has been developed, putting this surrealistic idea into practice (Prothero and Goodkind 1968). Thereby a superconducting sphere—the apple—is kept levitated in perfect rest in a magnetic field. The magnetic field is not only counteracting the gravitational attraction of the Earth, the well-known g ≈ 9.8 m s−2, it also compensates the much smaller temporal variations of gravity. The largest of them are the highs and lows of the tides of sun, moon, and planets. One of these superconducting gravimeters is operating in a laboratory at the satellite observatory Wettzell close to the Czech border. There the instrument is recording tiny phenomena such as the gravitational signal of passing high and low-pressure systems, changes in groundwater level and soil moisture, and even the gravitational effect of rain and snowfall. The magnitude of each of these effects is typically less than one millionth of “g”. The measured time series provide a more representative picture of the local hydrology than data recorded by a so-called lysimeter, specifically developed for this purpose (Creutzfeldt et al. 2008). The strength of this approach is at the same time its weakness. Newton’s law of gravitation tells us that the gravitational attraction of masses decreases very quickly with the square of its distance from the gravimeter. Thus, the measured time series give the changing mass effects only in the immediate surroundings of the instrument. It is impossible, however, to reconstruct a global map of temporal variations of gravity from the few existing instruments, located in places such as Bologna, Brussels, Shanghai, Strasbourg, and Wettzell.

Fig. 1
figure 1

Painting by Salvador Dalí “Sans Titre”, © Salvador Dalí, Fundació Gala-Salvador Dalí, Figueres, 2011

Full size image

The interpretation of the shown painting is ambiguous, however. Even from a closer look, it is impossible to decide whether the apple is standing still or whether the apple together with the four pieces of the marble frame are shown in free fall, just before they hit the ground. With a similar experiment of thought, Einstein explained the principle of equivalence of gravitational and inertial acceleration, his “elevator example” (Falk and Ruppel 1972; Foster and Nightingale 1979). As one would expect, he was very thorough in his explanation, emphasizing that the equivalence only holds if the objects, while falling, share the same center of mass. This is not the case here. Each of the five falling objects occupies a different location relative to all surrounding masses; each will “feel” the gravitational attraction of the surrounding masses slightly differently from the four others. In the language of general relativity, one would say: each of the falling masses follows its world line. For example, the lower two marble pieces are attracted somewhat stronger by the Earth than the apple and even stronger than the upper two masses, just because they are closer to its surface. The differences are very small. It is comparable to studying the gravitational attraction acting on a mass dropped from our left hand as compared to a second one released from our right hand. The difference will be less than one millionth of “g”. However, if one can measure such tiny differences the benefit is that the effect of the surrounding close-by masses is amplified relative to the signal coming from the Earth itself. The latter is essentially identical on all five falling masses and drops out when looking at the differences. We translate this experiment from Dali’s surrealistic painting to a satellite orbiting the Earth. In Fig. 2 we see a satellite and in its interior four cubic test masses, all five, i.e. the four mass probes and the satellite, orbiting the Earth. They are all in free fall in the Earth’s gravitational field. The lower test mass is slightly more attracted, e.g. by a mountain on Earth than the satellite, its mass concentrated in its center of mass in the middle of the four mass probes and more again than the upper mass probe. Also, the test cube in front is attracted in a direction slightly different from that of the masses in the middle and that in the rear. The observer on Earth sees a satellite and four cubes in free fall around the Earth. An observer inside the spacecraft—an astronaut—sees the four mass probes slowly floating in the microgravity environment of the spacecraft interior. When measuring gravitation inside the satellite the main contribution coming from the spherical Earth is not felt at all, while the relative accelerations between the freely floating mass probes will produce an amplified, extremely sensitive measurement series along the orbit of the spatial variations of gravity on Earth. The by far greatest effect, that of the attraction of the spherical Earth, is eliminated leading to a significant accentuation of the small effects produced by mountains and valleys and all other density variations on and inside the Earth. Antonio Marussi (1908–1984), a great geophysicist and geodesist, in a series of wonderful papers explained that these acceleration differences correspond to the curvatures of plumb lines and level surfaces of the Earth’s gravitational field at satellite altitude, see (Marussi 1979, 1984, 1985).

Fig. 2
figure 2

A satellite orbiting the Earth (in free fall) with four cubic test masses in its interior

Full size image

This is the principle of gravitational gradiometry as it was implemented for the first time in space with ESA’s dedicated gravity mission “Gravity field and steady-state Ocean Circulation Explorer” (GOCE). A gravitational gradiometer was the centerpiece of the GOCE satellite, accompanied by a novel and rather complex system of sensors. Of course, in the real experiment, the mass cubes cannot be left floating freely in the satellite’s interior until they hit one of the walls. Instead, each test cube is kept in a fixed position, levitated in an electrostatic feedback system (analogous to the working principle of the superconducting gravimeter). The gradiometer instrument of GOCE comprised three orthogonal one-axis gradiometers, each 50 cm long, with ultrasensitive three-axis accelerometers at its ends and with each one measuring three components of the gravitational gradient along the respective axis. Thus, the GOCE gravitational gradiometer was able to measure all nine elements (3 × 3) of the gradient tensor, the second derivatives of the gravitational potential. GOCE was in orbit from 2009 to 2013. To optimize its sensitivity for gravitational signals on Earth, its orbit altitude was chosen extremely low, only 255 km. During the final measurement cycle, its orbit was lowered further to an altitude of only 225 km. Together with experts from the European Space Agency (ESA), a consortium of scientists from ten institutes of seven European countries developed a processing strategy for data analysis. It was focussing on precise orbit determination, the separation of gravitational gradients from the spacecraft’s angular motion and the determination of the non-gravitational forces acting on the GOCE satellite (Floberghagen et al. 2011; Rummel et al. 2011). Professor Sansò and his team were key partners of the consortium. Already with its first measurement cycle of 62 days, GOCE delivered the most detailed and accurate global geoid map ever produced from space (Pail et al. 2011). Many leading international newspapers were showing the GOCE geoid map on their front pages, compare to, e.g., Fig. 3. The map looks impressive and shows many interesting details. Thus, we will now turn to the question: What does this map tell us, and more importantly, what for is the derived model of the Earth’s gravitational field good? The second part of this article will focus on the role of the Earth’s gravity field in Earth sciences and geodesy.

Fig. 3
figure 3

GOCE gravity model 2009 (© ESA)

Full size image

3 Gravity and Earth sciences

Let us imagine an ocean without any external forcing, no tides, no winds, and no weather. Its surface would have no ripples, no waves, no high tide or low tide, just water at rest. It would be level everywhere, a huge, Earth-encompassing, almost spherical horizontal surface. This “ocean at rest” is hypothetical, for in the real world there are always external forces acting on it. Gill (1982) says on page 46: “If the sea were at rest, its surface would coincide with the geopotential surface”. The surface is called the geoid (Listing 1873). The geoid is shaped by the gravitation of all Earth masses, and superimposed, by the steady effect of the centrifugal force due to the Earth’s rotation. It is an equipotential surface or level surface. In ocean areas, it is close to the sea surface, and we imagine it to be continued also underneath all land areas. It is smooth, mathematically expressed it is infinitely often differentiable. This smoothness does not allow recognizing any variation of the surface’s curvature caused by the Earth’s mass composition. It is “almost spherical”. However, when comparing the geoid with a sphere, one recognizes its oblateness with its radii towards the north and south poles being 21 km shorter than the average radius of the equator. Comparing the geoid with a best fitting ellipsoid [as proposed by Somigliana (1860–1955) and Pizzetti (1860–1918)], many highs and lows get visible. One refers to a Somigliana–Pizzetti ellipsoidal reference field (Moritz 2000). Alternatively, and closer to a geophysical interpretation is a comparison of the geoid with an ellipsoid in hydrostatic equilibrium (Nakiboglu 1982; Chambat et al. 2010). Departures from the ellipsoid are up to − 100 m south of India or + 80 m around Guinea, with a global RMS deviation of ± 30 m, primarily caused by large density anomalies in the Earth’s mantle as shown in Fig. 4. The highs and lows are denoted geoid heights (above/below the best fitting ellipsoid), geoid undulations or geoid anomalies. From what was said above follows the dual role of the geoid (and gravity field) in geodesy and Earth sciences.

Fig. 4
figure 4

Global map of the geoid heights (in meters) referred to a best fitting ellipsoid (Somigliana–Pizzetti)

Full size image

In solid Earth physics, the geoid, or equally well any other functional of the gravity field such as gravity anomalies or gravity disturbances, is the object of study. The posed question is the origin of the observed geoid highs and lows or gravity anomalies and how the weight of the masses above (below) the geoid is balanced in the Earth’s upper layers. In physical oceanography, the object of study is the deviation of the actual or mean ocean surface from the geoid, the geoid serving as physically relevant reference surface, representing the hypothetical ocean surface at rest. The same applies to geodesy where topographic heights are expressed relative to the geoid, in terms of either potential differences or so-called normal or orthometric heights (Heiskanen and Moritz 1967; Sansò et al. 2019). In any application, whether in geodesy, solid Earth physics or oceanography additional information is required. Apart from the ellipsoidal reference model and depending on the application, this may be a terrain model or a model of the sea surface; it may be density information of water, ice or land, and further auxiliary geophysical or oceanographic data sets.

4 Gravity and solid Earth

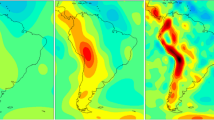
Let us turn first to the role of the geoid in solid Earth physics and consider geoid anomalies, here referenced to an ellipsoid of hydrostatic equilibrium with a flattening of 1:299.63 as shown in Fig. 5. The geoid surface is derived from the latest GOCE gravity model DIR-R6 that is a set of spherical harmonic coefficients up to degree and order (d/o) 300 (Förste et al. 2019; GOCE 2019). This means that the shortest half-wavelength features of this set have a length of about 70 km. Let us concentrate on the general appearance of the highs and lows of this map. They correspond to the deviations of the actual gravity field from its hydrostatic state of equilibrium. Since the late 80s of the last century, the origin of the long-wavelength variations of the geoid is well understood, (Hager et al. 1985; Richards and Hager 1988; Hager and Richards 1989; Anderson 1989). Density contrasts in the Earth’s lower mantle drive viscous flow; the result is dynamic topography at the core/mantle boundary as well as at the surface. The geoid anomalies are the combined effect of interior density contrasts and dynamic topography. The results are in good agreement with seismic tomography. GOCE added an enormous wealth of shorter wavelengths information, with important improvements in places where one would have expected them, such as in parts of South America and Africa, in the Himalayan region and parts of East Asia and Antarctica. The new, globally consistent and accurate results lead to a large number of studies. Some of them deal with the global behavior of the Moho discontinuity, the boundary surface between crust and mantle, some with its regional characteristics. Nowadays, Moho models are primarily derived from seismology and there exist global data sets such as CRUST 1.0 and 2.0 (Mooney et al. 1998; Bassin et al. 2000).

Fig. 5
figure 5

Global map of geoid heights (in meters, up to spherical harmonic degree and order 20), referred to an ellipsoid in hydrostatic equilibrium with f = 1/299.63 (Nakiboglu 1982; Chambat et al. 2010)

Full size image

The GOCE gravity model is of particular importance to a better understanding of the physics of the continents and, in particular, its oldest structures, the Cratons. When comparing GOCE geoid and gravity maps with their predecessors, the improvements in regions such as South America, parts of Africa, Himalaya together with its surroundings and Antarctica are striking. Logically, the greatest progress has been made there (Alvarez et al. 2014; McKenzie et al. 2014). The Trieste group of Carla Braitenberg looked, among others, into the similarities of the tectonics of South America and West Africa, following the footsteps of Wegener (Braitenberg 2015). The Milano group at Polimi used the GOCE geoid model for the improvement of the CRUST 2.0 model, which is based primarily on the analysis of seismic data (Reguzzoni et al. 2013; Sampietro et al. 2014). McKenzie et al. (2014, 2015) focussed his work on the elastic thickness of the lithosphere of the Himalaya and Antarctica. The Himalaya analysis (McKenzie et al. 2014; Shin et al. 2015; Hetényi et al. 2016) is reminding us of the pioneering and still a valuable work of Antonio Marussi et al. in the Karakorum (Marussi 1964). GOCE gave us a look into the tectonics of Antarctica, which is hidden under an ice shield with several kilometers thickness (Ferraccioli et al. 2011; McKenzie et al. 2015). McKenzie et al. (2015) showed that the elastic thickness of Western Antarctica is very different from that of East Antarctica, being 5 km and 21 km, respectively. See also the general studies in (Ebbing et al. 2013; Panet et al. 2014). A very fresh and completely new approach is that taken in (Bouman et al. 2016; Sebera et al. 2017; Ebbing et al. 2018), where the curvature structure of the GOCE gravity model is used for the identification of various crustal structures, in particular, the Cratons.

5 Geodetic ocean topography

As Gill (1982) pointed out, “if the sea were at rest, its surface would coincide with the geopotential surface”. The real ocean is subject to external forces driving the water masses, such as tides, wind, and weather causing the actual sea surface to deviate from the geoid. The height difference between the actual (or mean) ocean surface and the geoid is denoted dynamic ocean topography (DOT). DOT is rather small, typically only 20 or 30 cm, with maxima of up to 1 or 2 m in the centers of the circulation systems. Appropriately, these deviations are denoted ocean topography, in analogy to land topography. For about 30 years, the geometry of the ocean surface, as well as its variation with time, has been measured with great precision from space by the method of satellite altimetry (Fu and Cazenave 2001; Stammer and Cazenave 2018). Taking the height difference between the sea surface and the geoid gives the geodetic DOT. In other words, geodesy succeeded in measuring ocean topography, independent of any oceanographic method and with a precision of a few centimeters. DOT results in pressure gradients. In an ocean with moving water on a rotating Earth, Coriolis force will balance the pressure gradients, the so-called geostrophic balance. The result is the characteristic ocean circulation patterns such as Gulf, Kuroshio, Aghulas or Circumpolar stream (Bingham et al. 2011; Albertella et al. 2012; Janjic et al. 2012; Albertella and Rummel 2014). The availability of the geodetic DOT opened the possibility to invert the process, i.e., to infer from measured ocean topography ocean surface circulation (more accurately: the geostrophic ocean surface velocities), their strength and their patterns. They serve now as a new independent source of information for ocean circulation modeling. There is, however, a second, significantly smaller component of ocean velocities (15% versus 63%) (Sudre et al. 2013; Rio et al. 2013, 2014), called the Ekman surface currents. The Ekman part leaves no trace in ocean topography and has to be deduced from oceanographic measurement techniques. These highly improved methods of ocean surface velocity determination are of significant help for a better understanding of ocean mass and heat transport. Our climate system is largely regulated by the poleward heat transport in the ocean and atmosphere. A prominent example is the mild temperatures at medium and high latitudes of North-Western Europe. Ocean circulation is probably responsible for 30% of the poleward transport of heat, leaving a contribution of 70% for the atmosphere (Wunsch 2005). Mass and heat transport are essential to understanding climate and climate change. High-resolution geoid models as derived from GOCE combined with more than 20 years of excellent ocean and ice altimetry resulted in very accurate estimates of geostrophic ocean velocities as an important new element of ocean modeling. This, in turn, will help to improve our understanding of mass, heat, nutrients, and displacement of matter (Sudre et al. 2013).

6 Height systems

Geodetic heights, sometimes referred to as physical heights, provide an accurate and natural measure of “equally high”, “higher” and “lower”. This implies that heights are closely related to the Earth’s gravity field, or more accurately, to the gravity potential. Points with the same value of gravity potential are equally high; they are located at the same level surface. Ideally, all heights should refer to the geoid, serving as one global geopotential reference surface with height value zero. The height of any arbitrary terrain point is then expressed either by its potential difference relative to the geoid, denoted geopotential number, or when expressed metrically (in meters) as orthometric or normal height (Heiskanen and Moritz 1967; Sansò et al. 2019). Orthometric heights correspond to the length of the plumb line of a terrain point above the geoid. In practice, national height systems refer to mean sea level at a coastal reference point, usually a carefully selected tide gauge. Potential differences are derived from geodetic leveling combined with gravimetry. The method is very precise over shorter distances, say 100 km. Over greater distances, systematic errors tend to enter, growing with the square root of the distance from the starting point. The error accumulation results in undetected deformations on a decimeter to meter level of national and continental height systems. As the mean sea level at the reference point of a height system does very likely not coincide with the geoid because of the DOT (see above), there are offsets between the various national and continental height systems, also at the decimeter to meter level. The situation has fundamentally changed, with the advent, on the one hand, of the dedicated satellite gravimetry missions CHAMP, GRACE and GOCE and, on the other hand with GPS, or more generally GNSS (including the Russian Glonass, the European Galileo and the Chinese Beidou satellite navigation systems).

GNSS is providing precise 3D coordinates of terrain points. Today, under the umbrella of the International Association of Geodesy (IAG), a worldwide valid International Terrestrial Reference System and Frame (ITRS/ITRF) is computed at regular intervals. In its essence, the ITRF is a catalog with coordinates, error standard deviations and temporal coordinate changes of about 1500 terrain points worldwide. The coordinates are based on the combination of GNSS and the complementary geodetic space techniques VLBI, SLR and DORIS (Petit and Luzum 2010; Altamimi et al. 2011, 2017). Also, during the past 30 years, the geometry of the sea surface has been monitored with similar precision by satellite altimetry, see again (Fu and Cazenave 2001; Stammer and Cazenave 2018). Both the vertical component of land and sea elevations are expressed as height above an adopted reference ellipsoid.

It is straightforward, then, to add physical height information, preferably geopotential numbers, to the geometric coordinate triples. They are computed from one of the most recent GOCE or GOCE/GRACE gravity models such as TIM-5, which is a series of spherical harmonic coefficients up to degree and order (d/o) 280 or DIR-5 up to d/o 300 (Brockmann et al. 2014; Bruinsma et al. 2014). However, there is a caveat. The satellite-based gravity models represent only a smoothed version of the actual field, the spherical harmonic series being truncated at 280° or 300°. The short scales, expressed by spherical harmonic coefficients above 280 and 300, respectively, have to come from terrestrial measurements. Currently, this is only possible in regions where modern geodetic infrastructure is available, such as in Europe, North America, Japan, Australia, and New Zealand. Test runs have already shown that with this approach precise and globally consistent height systems are within reach. Furthermore, the method will be able to identify existing offsets between height systems and systematic deformations (Woodworth et al. 2012; Gruber et al. 2013; Rummel and Beutler 2019).

7 Temporal variations of geoid and gravity

As already discussed in Sect. 2, the Earth’s gravity field is changing with time. Prominent examples are the tides of sun, moon, and planets and the effect they have on solid Earth and oceans. Also, certain types of earthquakes are associated with large mass displacements and, as a consequence, with changes in gravity. The focus, nowadays, is however on temporal variations related to the global water cycle, such as sea-level rise, the melting of the ice shields and glaciers, floods, droughts, and the glacial isostatic adjustment (GIA).

Monitoring of processes such as these is of high relevance to the understanding of Earth system and climate change. Temporal variations of gravity are small, typically three orders of magnitude smaller than the spatial variations of the static field. GOCE was not made to measure temporal gravity changes. Its core instrument, the gradiometer, a compact instrument with side lengths of 50 cm, as mentioned above, was designed to measure the Earth’s static field with maximum accuracy and spatial resolution. The GRACE mission (2002–2017) (Tapley et al. 2004), on the other hand, consisted of two satellites following each other along the same orbit at a distance of about 200 km. Their distance variations were measured with a precision of a few micrometers. The gravity signal was extracted from them. The configuration is somehow comparable to a one-axis gradiometer with an arm length of 200 km. This setup allowed GRACE to catch the temporal variations of the field. GRACE measured altogether 163 global monthly solutions of time-varying gravity, out of 187 possible months (Tapley et al. 2019). The signal versus error situation is sketched in Fig. 6. It shows the signal spectrum of the static field, following the “Kaula rule-of-thumb”. It also shows the signal spectrum of a typical set of temporal variation processes, approximately three orders of magnitude smaller. Also included in Fig. 6 are the error spectra of GOCE and GRACE. The GOCE error spectrum intersects the static signal spectrum at about spherical harmonic 220° (ultimately the coefficients up to d/o 300 were recovered), much higher than the GRACE error curve which intersects the signal spectrum at 150°. However, for GOCE the temporal variation signal spectrum remains largely below the error curve, whereas GRACE with its monthly solutions was able to detect the temporal variations up to about 50° or 60°. The GRACE time series of monthly solutions is regarded one of the most important data sources of the World Climate Research Program.

Fig. 6
figure 6

Signal and error spectra between spherical harmonic 2° and 200° (The latter corresponding to length scales of 100 km). The following curves are shown: the dimensionless signal spectrum of the Earth’s gravity field, the corresponding rule-of-thumb and typical spectrum of temporal variations. Also shown are the error spectrum of GOCE, crossing the signal line at 200° and the GRACE error spectrum, crossing the signal line at 150°. The GRACE curves are based on the models EIGEN-5S and EIGEN-5C (Förste et al. 2008)

Full size image

The state-of-the-art of GRACE data analysis is summarized in three wonderful publications (Wouters et al. 2014; Rodell et al. 2018; Tapley et al. 2019). It is all but trivial to separate the various process components from the measured satellite gravimetry signal along the orbits. The geographical location helps as well as rather advanced background prior models of the atmosphere, ocean, ice, hydrology, and solid Earth processes (Dobslaw et al. 2017). The time series is composed of annual, inter-annual and long-term contributions. Highlights, among many achievements, are the quantification of the ice mass loss in Greenland and Antarctica, its regional and long-term pattern of change and its connection to sea-level rise. The total sea-level change, as derived from multi-year satellite altimetry can now be reliably decomposed into the thermal steric component, derived from the global system of Argo floats and the mass component as measured by GRACE. In 2018, the follow-on mission GRACE-FO was launched, successfully continuing the 15-year time series of GRACE (Tapley et al. 2019).

8 Outlook

Satellite gravimetry has turned into an important instrument of the Earth system and climate change research. GRAIL, a mission in principle similar to GRACE, has recovered the gravity field of the moon with unprecedented precision and spatial resolution (Andrews-Hanna et al. 2013; Wieczorek et al. 2013; Zuber et al. 2013). GRAIL suggests that dedicated satellite gravimetry may also be applied for planetary missions. If multi-satellite configurations turn out to be too complex in this case, gradiometry may be the appropriate approach as it is compact and self-contained. For both the Earth and planetary missions, higher accuracy, spatial, and temporal resolution are still desirable. Various studies of mission concepts were already carried out (Panet et al. 2012; Elaska et al. 2014; Pail et al. 2015; Pail 2017). Formation flights with more than one satellite pair may prove to be the right strategy to improve the spatial and temporal resolution. On the sensor side, laser tracking between satellites or between proof masses inside one instrument may be the logical next step and soon quantum gravity and gradiometry (Sheard et al. 2012; Isleif et al. 2016; Abend et al. 2016).