Skip to main content
SpringerLink
Log in

Kinematic and stiffness modelling and performance evaluation of a new PRS-PRU-PUR overconstrained parallel mechanism

  • Original Article
  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

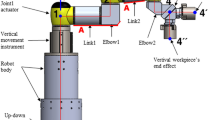
This paper proposes a new 2R1T PRS-PRU-PUR overconstrained parallel mechanism (PM). Firstly, the kinematics and stiffness are studied based on screw theory and strain energy. Compared with a typical 3-PRS PM, the main advantage of the proposed PRS-PRU-PUR PM is that the orientational range β is improved by 50 %. Secondly, the original PM’s kinematic and stiffness performance are evaluated by using the global transmission index and stiffness index, which are 0.675 and 594 respectively, which causes the decrease of the efficiency of some configurations. Finally, the design parameters are optimized to enhance the PM’s kinematic and stiffness performance. The corresponding optimized indices were increased to 0.915 and 2171, respectively, confirming the validity of the optimal design method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

PM :

Parallel mechanism

2R1T :

Two rotations and one translation

DOF :

Degrees of freedom

P :

Prismatic joint

R :

Revolute joint

S :

Spherical joint

U :

Universal joint

O-xyz :

Fixed coordinate frame

O′-x′y′z′ :

Moving coordinate frame

$ ij :

The jth unit screw

\(\$_{ij}^r\) :

The jth wrench for unit constraint

$ Ci :

The ith unit constraint wrench of the PM

\(\$_i^{pm}\) :

The ith unit twist for the moving platform

α :

The rotational angle around the x-axis

β :

The rotational angle around the y′-axis

s :

Sine function

c :

Cosine function

z o :

The operational height of the moving platform

q i :

The ith actuated variable of the P joint

R′ :

Rotation matrix

R x}:

Rotation matrix around the direction of x-axis

R y′ :

Rotation matrix around the direction of y′-axis

p :

Position vector of origin O′

c i}:

Position vector of AiBi

Γ :

Local transmission index (LTI)

$ Ai :

The input twist screw (ITS) of the ith limb

$ Tj :

The transmission wrench screw (TWS)

$ Oi :

The output twist screw (OTS) of the ith limb

λ i :

The input transmissibility of the ith limb

η i :

The output transmissibility of the ith limb

GTW :

Great transmission workspace

σ :

Global transmission index (GTI)

S g :

GTW areas

S :

Areas of overall workspace

E :

Elastic modulus

G :

Shear modulus

A :

Area of cross section

I ly :

Moment of inertia in the y-axis area

J l :

Polar inertia moment

K :

Matrix of the overall stiffness

C :

Matrix of the overall flexibility

W :

Applied external wrench

f ij :

Constraint force

m ij :

Constraint moment

κ :

Virtual-work stiffness index (VSI)

ς :

Global stiffness index (GSI)

B i-x i y i z i :

Limb coordinate frame

References

  1. R. Clavel, A fast robot with parallel geometry, Proceedings of the 18th International Symposium on Industrial Robots, Lausanne, Switzerland (1988) 91–100.

  2. L. M. Xu, Q. H. Chen, L. Y. He and Q. C. Li, Kinematic analysis and design of a novel 3T1R 2-(PRR)2RH hybrid manipulator, Mech. Mach. Theory., 112 (2017) 105–122.

    Article  Google Scholar 

  3. X. Luo, F. G. Xie, X. J. Liu and Z. H. Xie, Kinematic calibration of a 5-axis parallel machining robot based on dimensionless error mapping matrix, Robot. Comput. Integr. Manuf., 70 (2021) 102115.

    Article  Google Scholar 

  4. A. K. Inkulu, M. R. Bahubalendruni, A. Dara and K. Sankarana-rayanaSamy, Challenges and opportunities in human robot collaboration context of Industry 4.0-a state of the art review, Industrial Robot, 49 (2) (2022) 226–239.

    Article  Google Scholar 

  5. J. Wahl, Articulated Tool Head, WO/2000/025976, WIPO Patent (2002).

  6. Z. M. Bi and Y. Jin, Kinematic modeling of exechon parallel kinematic machine, Robot. Comput. Integr. Manuf., 27 (1) (2011) 186–193.

    Article  Google Scholar 

  7. B. Siciliano, The Tricept robot: Inverse kinematics, manipulability analysis and closed-loop direct kinematics algorithm, Robotica, 17 (4) (1999) 437–445.

    Article  Google Scholar 

  8. Q. C. Li and J. M. Hervé, Type synthesis of 3-DOF RPR-equivalent parallel mechanisms, IEEE Transactions on Robotics, 30 (6) (2014) 1333–1343.

    Article  Google Scholar 

  9. L. M. Xu, X. X. Chai, Q. C. Li, L. A. Zhang and W. Ye, Design and experimental investigation of a new 2R1T overconstrained parallel kinematic machine with actuation redundancy, ASME Journal of Mechanisms and Robotics, 11 (3) (2019) 031016.

    Article  Google Scholar 

  10. Z. Chen, Z. M. Chen, Y. W. Li and Z. Huang, Motion characteristics analysis of a novel 2R1T 3-UPU parallel mechanism, ASME J. Mech. Des., 142 (2) (2020) 012302.

    Google Scholar 

  11. Starrag Group, Ecospeed Series, Starrag Group, https://www.starrag.com/zh-cn/series/ecospeed-ecoliner-xi-lie/27/product-range/11, Accessed on June 17 (2021).

  12. Exechon World, Structure Concept of Exechon PKM, Exechon World, http://www.exechonworld.com/document/200804/article34.htm, Accessed on February 10 (2021).

  13. B. B. V. L. Deepak, C. A. Rao and B. M. V. A. Raju, Kinematic Modeling and Simulation of Manipulator for Executing Welding Operations with Arbitrary Weld Joint Profiles, Springer India (2016).

  14. B. B. V. L. Deepak, C. A. Rao and B. M. V. A. Raju, Weld Seam Tracking and Simulation of 3-Axis Robotic Arm for Performing Welding Operation in CAD Environment, Springer India (2016).

  15. S. Zarkandi, Kinematic analysis and optimal design of a novel 3-PRR spherical parallel manipulator, Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 235 (4) (2021) 693–712.

    Google Scholar 

  16. H. Shen, Y. Zhao and G. Wu, Kinematic design of a translational parallel mechanism based on sub-kinematic chain determined workspace superposition, Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 235 (24) (2021).

  17. R. S. Stoughton and T. Arai, A modified stewart platform manipulator with improved dexterity, IEEE Trans. Robot. Autom., 9 (2) (1993) 166–173.

    Article  Google Scholar 

  18. Y. J. Wang, B. Belzile, J. Angeles and Q. C. Li, Kinematic analysis and optimum design of a novel 2PUR-2RPU parallel robot, Mech. Mach. Theory, 139 (2019) 407–423.

    Article  Google Scholar 

  19. J. P. Merlet, Jacobian, manipulability, condition number, and accuracy of parallel robots, ASME J. Mech. Des., 128 (1) (2006) 199–206.

    Article  Google Scholar 

  20. B. Siciliano and O. Khatib, Handbook of Robotics, Springer, Berlin, Heidelberg (2008).

    Book  MATH  Google Scholar 

  21. B. S. El-Khasawneh and P. M. Ferreira, Computation of stiffness and stiffness bounds for parallel link manipulators, Int. J. Mach. Tool. Manuf., 39 (2) (1999) 321–342.

    Article  Google Scholar 

  22. A. Klimchik, A. Pashkevich and D. Chablat, CAD-based approach for identification of elasto-static parameters of robotic manipulators, Finite. Elem. Anal. Des., 75 (6) (2013) 19–30.

    Article  MathSciNet  MATH  Google Scholar 

  23. C. Gosselin, Stiffness mapping for parallel manipulators, IEEE Trans. Robot. Autom., 6 (3) (1990) 377–382.

    Article  Google Scholar 

  24. T. Sun, B. B. Lian and Y. M. Song, Stiffness analysis of a 2-DoF over-constrained RPM with an articulated traveling platform, Mech. Mach. Theory, 96 (2016) 165–178.

    Article  Google Scholar 

  25. A. Pashkevich, D. Chablat and P. Wenger, Stiffness analysis of overconstrained parallel manipulators, Mech. Mach. Theory., 44 (2009) 966–982.

    Article  MATH  Google Scholar 

  26. G. D. L. Soares Júnior, J. C. M. Carvalho and R. S. Goncalves, Stiffness analysis of multibody systems using matrix structural analysis—MSA, Robotica, 34 (10) (2016) 2368–2385.

    Article  Google Scholar 

  27. X. Shan and G. Cheng, Static analysis on a 2(3PUS+S) parallel manipulator with two moving platforms, Journal of Mechanical Science and Technology, 32 (8) (2018) 3869–3876.

    Article  MathSciNet  Google Scholar 

  28. E. Courteille, D. Deblaise and P. Maurine, Design optimization of a delta-like parallel robot through global stiffness performance evaluation, Proceedings of 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, Missouri, USA (2009) 5159–5166.

  29. Q. S. Xu and Y. M. Li, GA-based architecture optimization of a 3-PUU parallel manipulator for stiffness performance, Proceedings of the IEEE 6th World Congress on Intelligent Control and Automation, Dalian, China (2006) 9099–9103.

  30. G. Carbone and M. Ceccarelli, Comparison of indices for stiffness performance evaluation, Front. Mech. Eng., 5 (3) (2010) 270–278.

    Article  Google Scholar 

  31. J. S. Wang, C. Wu and X. J. Liu, Performance evaluation of parallel manipulators: motion/force transmissibility and its index, Mech. Mach. Theory, 45 (10) (2010) 1462–1476.

    Article  MATH  Google Scholar 

  32. F. G. Xie, X. J. Liu and J. S. Wang, A 3-DOF parallel manufacturing module and its kinematic optimization, Robot. Comput. Integr. Manuf., 28 (3) (2012) 334–343.

    Article  Google Scholar 

  33. L. M. Xu, Q. C. Li, J. H. Tong and Q. H. Chen, Tex3: An 2R1T parallel manipulator with minimum DOF of joints and fixed linear actuators, Int. J. Precis. Eng. Man., 19 (2) (2018) 227–238.

    Article  Google Scholar 

  34. S. J. Yan, S. K. Ong and A. Y. C. Nee, Stiffness analysis of parallelogram-type parallel manipulators using a strain energy method, Robot. Comput. Integr. Manuf., 37 (2016) 334–343.

    Article  Google Scholar 

  35. Z. Huang and Q. C. Li, Type synthesis of symmetrical lower-mobility parallel mechanisms using the constraint-synthesis method, Int. J. Rob. Res., 22 (1) (2003) 59–79.

    Google Scholar 

  36. C. Yang, Q. C. Li and Q. H. Chen, Elastostatic stiffness modeling of overconstrained parallel manipulators, Mechanism and Machine Theory (12) (2018) 58–74.

  37. B. Hu, H. Cui and D. Shi, Reachable workspace determination for a spatial hyper-redundant manipulator formed by several parallel manipulators, Journal of Mechanical Science and Technology, 33 (2) (2019) 869–877.

    Article  Google Scholar 

Download references

Acknowledgements

This research work was supported by the National Natural Science Foundation of China under Grant 51935010 and the Fundamental Research Funds of Zhejiang Sci-Tech University under Grant 23242135-Y.

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Zhejiang Sci-Tech University, Hangzhou, 310018, China

    Zhen Wu, Xinxue Chai & Wei Ye

  2. Department of Navigation, Zhejiang Institute of Communications, Hangzhou, 311112, China

    Zhen Wu

Authors
  1. Zhen Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xinxue Chai
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wei Ye
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wei Ye.

Additional information

Zhen Wu received a B.S. degree in ship and ocean engineering from Zhejiang Ocean University, Zhoushan, China in 2013 and received an M.S. degree in ship and ocean engineering from Wuhan University of Technology, Wuhan, China in 2016. He is currently pursuing a Ph.D. degree with the School of Mechanical Engineering, Zhejiang Sci-Tech University. His main research interests are theoretical analysis of parallel robots.

Xinxue Chai received B.S. and Ph.D. degrees in mechanical engineering from Zhejiang Sci-Tech University, Hangzhou, China in 2011 and 2017, respectively. Since 2017, she has been a lecturer with the School of Mechanical Engineering, Zhejiang Sci-Tech University. Her research interest includes mechanism theory using geometric algebra.

Wei Ye received B.S., and Ph.D. degrees in mechanical engineering from Beijing Jiaotong University, Beijing, China, in 2010 and 2016, respectively. He joined the School of Mechanical Engineering, Zhejiang Sci-Tech University, in 2016, where he is currently an Associate Professor. He is the author of one book and more than 20 articles. His research interests include mechanism theory of parallel manipulators and application.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, Z., Chai, X. & Ye, W. Kinematic and stiffness modelling and performance evaluation of a new PRS-PRU-PUR overconstrained parallel mechanism. J Mech Sci Technol 37, 5377–5389 (2023). https://doi.org/10.1007/s12206-023-0938-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-023-0938-z

Keywords

Search

Navigation