Skip to main content
SpringerLink
Log in

Layout optimization of box girder with RBF-NNM-APSO algorithm

  • Original Article
  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

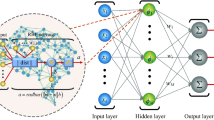
The layout optimization problem of complex box girder structure is solved with a new method RBF-NNM-APSO formed with the digital neural network model (NNM) of radial basis function (RBF) and adaptive particle swarm optimization (APSO) algorithm in this paper. The optimized surrogate model is proposed and applied to the configuration optimization of heavy-duty box girder of casting crane for improving the mechanical properties of the optimized object and expediting proceedings. First, the parametric command flow finite element numerical model of box girder is established. The RBF neural network is trained by constructing a mixed orthogonal experimental table of parameters, and the relationship between the design variables and the maximum stress and deformation is established. Subsequently, the trained RBF neural network design scheme is optimized by APSO algorithm. Finally, on the premise of not increasing the total mass, a new layout form of box girder is obtained.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

X :

Variable matrix

X i :

Particle position

V i :

Particle speed

P i :

Current position of particle

P gb :

Current best position of population

v ij :

Velocity of particle

ω :

Inertia weight

H :

Radial basis vector

C j :

Center vector

B :

Base width vector of RBF neural network

W :

Weight vector

y m :

Output of the network

E :

Performance index function of RBF network

η :

Learning efficiency

α :

Momentum factor

Net1:

Design variable and the maximum stress

Net2:

Design variable and the maximum deformation

σ s :

Yield strength of the material

σ b :

Tensile strength of the material

[Y]:

Allowable deformation of box girder

M t :

Quality before optimization

M :

Quality after optimization

Lb [X]:

Lower bound of a variable

Ub [X]:

Upper bound of a variable

References

  1. Y. Tong, Z. Tang, Y. Wei and Y. Zhen, Research on energy-saving optimization design of bridge crane, Maintenance and Reliability, 15(4) (2013) 449–457.

    Google Scholar 

  2. C. B. Pinca, G. O. Tirian and V. A. Socalicil, Dimensional optimization for the strength structure of a traveling crane, WSEAS Transactions on Applied and Theoretical Mechanics, 4(4) (2005) 147–156.

    Google Scholar 

  3. M. Abid, M. H. Akmal and H. A. Wajid, Design optimization of box type girder of an overhead crane, Iranian J. of Science and Technology: Transactions of Mechanical Engineering, 39(M1) (2015) 106–118.

    Google Scholar 

  4. H. Zhang, Y. Qin and J. Gu, Layout optimization of stiffeners in heavy-duty thin-plate box grider, KSCE J. of Civil Engineering, 25(8) (2021) 3075–3083.

    Article  Google Scholar 

  5. G. L. Putra, M. Kitamura and A. Takezawa, Structural optimization of stiffener layout for stiffened plate using hybrid GA, International J. of Naval Architecture and Ocean Engineering, 11 (2019) 809–818.

    Article  Google Scholar 

  6. A. Ehsani and H. Dalir, Multi-objective design optimization of variable ribs composite grid plates, Structural and Multidisciplinary Optimization, 63(1) (2021) 407–418.

    Article  Google Scholar 

  7. Y. Zhang, Y. Qin and J. Gu, Topology optimization of unsymmetrical complex plate and shell structures bearing multicondition overload, Journal of Mechanical Science and Technology, 35(8) (2021) 1–10.

    Article  Google Scholar 

  8. B. Li, H. Liu and Z. Yang, Stiffness design of plate/shell structures by evolutionary topology optimization, Thin-Walled Structures, 141 (2019) 232–250.

    Article  Google Scholar 

  9. L. Iuspa, Free topology generation of self-stiffened panels using skeleton-based integral soft objects, Computers and Structures, 158 (2015) 184–210.

    Article  Google Scholar 

  10. N. D. Lagaros and M. Papadrakakis, Applied soft computing for optimum design of structures, Structural and Multidisciplinary Optimization, 45(6) (2015) 787–799.

    Article  MATH  Google Scholar 

  11. J. Eason and S. Cremaschi, Adaptive sequential sampling for surrogate model generation with artificial neural networks, Computers and Chemical Engineering, 68 (2014) 220–232.

    Article  Google Scholar 

  12. K. Crombecq, L. D. Tommasi and D. Gorissen, A novel sequential design strategy for global surrogate modeling, Proceedings of the 2009 Winter Simulation Conference (WSC) (2009) 731–742.

  13. M. A. Bezerra et al., Response surface methodology (RSM) as a tool for optimization in analytical chemistry, Talanta, 76(5) (2008) 965–977.

    Article  Google Scholar 

  14. D. Bas and I. H. Boyaci, Modeling and optimization I: usability of response surface methodology, J. of Food Engineering, 78(3) (2007) 836–845.

    Article  Google Scholar 

  15. A. Bhosekar and M. Ierapetritou, Advances in surrogate based modeling, feasibility analysis, and optimization: a review, Computers and Chemical Engineering, 108 (2018) 250–267.

    Article  Google Scholar 

  16. B. Gérard, Neural networks for process control and optimization: two industrial applications, ISA Transactions, 42(1) (2003) 39–51.

    Article  Google Scholar 

  17. S. M. Clarke, J. H. Griebsch and T. W. Simpson, Analysis of support vector regression for approximation of complex engineering analyses, J. of Mechanical Design, 127(6) (2005) 1077–1087.

    Article  Google Scholar 

  18. M. Bjrkman and K. Holmstrm, Global optimization of costly nonconvex functions using radial basis functions, Optimization and Engineering, 1(4) (2000) 373–397.

    Article  MathSciNet  Google Scholar 

  19. F. A. N. Fernandes, Optimization of Fischer-Tropsch synthesis using neural networks, Chemical Engineering and Technology, 29(4) (2006) 449–453.

    Article  Google Scholar 

  20. Z. Mousavi, S. Varahram and M. M. Ettefagh, Deep neural networks-based damage detection using vibration signals of finite element model and real intact state: an evaluation via a lab-scale offshore jacket structure, Structural Health Monitoring—An Internation J., 20(1) (2020) 379–405.

    Article  Google Scholar 

  21. Z. Mousavi, M. M. Ettefagh and M. H. Sadeghi, Developing deep neural network for damage detection of beam-like structures using dynamic response based on FE model and real healthy state, Applied Acoustics, 168 (2020) 107402.

    Article  Google Scholar 

  22. Y. W. Luo, B. Zhang and X. Feng, Pore-affected fatigue life scattering and prediction of additively manufactured inconel 718: an investigation based on miniature specimen testing and machine learning approach, Materials Science and Engineering A, 802 (2021) 140693.

    Article  Google Scholar 

  23. J. Kennedy and R. Eberhart, Particle swarm optimization, Proc. of the IEEE International Conference on Neural Networks, 4 (1995) 1942–1948.

    Article  Google Scholar 

  24. Y. Shi and R. C. Eberhart, Parameter selection in particle swarm optimization, International Conference on Evolutionary Programming (1998) 591–600.

  25. Y. Shi and R. C. Eberhart, Fuzzy adaptive particle swarm optimization, Proc. of the 2001 Congress on Evolutionary Computation, Seoul (2001).

  26. J. Moody and C. Darken, Fast learning in networks of locally-tuned processing units, Neural Computation, 1(2) (1989) 281–294.

    Article  Google Scholar 

  27. H. Y. Cao, X. D. Qin and Z. J. Chen, Enhanced particle swarm optimization for size and shape optimization of truss structures, Engineering Optimization, 49(11) (2017) 1939–1956.

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgments

This work was supported by Shanxi provincial Key Research and Development Project, China (201903D121067), the National Natural Science Foundation of China (51478290) and the Fund for Shanxi ‘1331 Project’ Key Subjects Construction [1331KSC].

Author information

Authors and Affiliations

  1. College of Mechanical Engineering, Taiyuan University of Science and Technology, Taiyuan, 030024, China

    Junle Yang, Yixiao Qin & Qianqian Jiao

Authors
  1. Junle Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yixiao Qin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Qianqian Jiao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yixiao Qin.

Additional information

Junle Yang is a graduate student of Taiyuan University of Science and Technology. His research includes structure optimization and hoisting machinery.

Yixiao Qin is a Professor and doctoral supervisor in Taiyuan University of Science and Technology. He received the Ph.D. from Shanghai Institute of Applied Mathematics and Mechanics. His research interests include optimization design of engineering structure.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, J., Qin, Y. & Jiao, Q. Layout optimization of box girder with RBF-NNM-APSO algorithm. J Mech Sci Technol 36, 5575–5585 (2022). https://doi.org/10.1007/s12206-022-1021-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-022-1021-x

Keywords

Search

Navigation