Skip to main content
SpringerLink
Log in

A numerical study on an infinite linear elastic Bernoulli-Euler beam on a viscoelastic foundation subjected to harmonic line loads

  • Original Article
  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

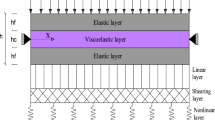
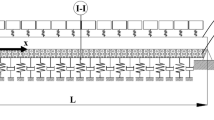
This paper presents a numerical study on the low-amplitude responses of an infinite Bernoulli-Euler beam resting on a viscoelastic foundation subjected to harmonic line loads. To simulate the linear response, a semi-analytical solution procedure that was theoretically proposed by Jang (2016) is utilized and several numerical experiments are conducted to investigate the influence of key model parameters characterizing stiffness and damping. The properties of the viscoelastic foundation are based on theoretical and empirical values for cohesionless sand type foundation. According to the numerical experiments, the obtained responses are compared with those from the closed-form solution and found to have a good agreement with them.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

A :

Cross sectional area

b :

Width of the beam cross-section

C :

Damping coefficient

E :

Young’s modulus of beam

E s :

Young’s modulus of foundation

g :

Gravity acceleration

G,G t :

Kernel function

H :

Half-maximum convention (Heaviside step function)

h :

Height

I :

Second moment of area

K :

Spring coefficient

K p :

Pseudo-spring coefficient

P :

Amplitude of the applied external load

r 0 :

Half-width of the line load

u,v :

Iterative (response) solutions

X 0 :

Constant

W :

External load

α, β, β p :

Parameters

γ :

Rate of the vertical displacement decreasing with depth

γ s :

Unit weight of soil

K :

Loading frequency

V s :

Poisson’s ratio of foundation

ρ :

Density

References

  1. J. T. Kenney, Steady-state vibrations of beam on elastic foundation for moving load, Journal of Applied Mechanics, 21 (1954) 359–364.

    MATH  Google Scholar 

  2. P. M. Mathews, Vibrations of a beam on elastic foundation, Journal of Applied Ma, hema, ics and Mechanics, 35 (1958) 105–115.

    MathSciNet  MATH  Google Scholar 

  3. P. M. Mathews, Vibrations of a beam on elastic foundation II, Journal of Applied Mathematics and Mechanics, 39 (1959) 13–19.

    MathSciNet  MATH  Google Scholar 

  4. W. Stadler and R. W. Shreeves, The transient and steady-state response of the infinite Bernoulli-Euler beam with damping and an elastic foundation, Quarterly Journal of Mechanics and Applied Mathematics, 23 (1970) 197–208.

    Article  Google Scholar 

  5. J. P. Sheehan and L. Debnath, On the dynamic response of an infinite Bernoulli-Euler beam, Pure and Applied Geophysics, 97 (1972) 100–110.

    Article  Google Scholar 

  6. L. Sun, A closed-form solution of a Bernoulli-Euler beam on a viscoelastic foundation under harmonic line loads, Journal of Sound and Vibration, 242 (2001) 619–627.

    Article  Google Scholar 

  7. L. Sun, A closed-form solution of beam on viscoelastic subgrade subjected to moving loads, Computers and Structures, 80 (2002) 1–8.

    Article  Google Scholar 

  8. A. D. Senalp, A. Arikoglu, I. Ozkol and V. Z. Dogan, Dynamic response of a finite length Euler-Bernoulli beam on linear and nonlinear viscoelastic foundations to a concentrated moving force, Journal of Mechanical Science and Technology, 24 (2010) 1957–1961.

    Article  Google Scholar 

  9. D. Basu and N. S. V. Kameswara Rao, Analytical solutions for Euler-Bernoulli beam on visco-elastic foundation subjected to moving load, International Journal for Numerical and Analytical Methods in Geomechanics, 37 (2013) 945–960.

    Article  Google Scholar 

  10. L. Sun, An explicit representation of steady state response of a beam on an elastic foundation to moving harmonic line loads, International Journal for Numerical and Analytical Methods in Geomechanics, 27 (2003) 69–84.

    Article  Google Scholar 

  11. H. Yu and Y. Yuan, Analytical solution for an infinite Euler-Bernoulli beam on a viscoelastic foundation subjected to arbitrary dynamic loads, Journal of Engineering Mechanics, 140 (2014) 542–551.

    Article  Google Scholar 

  12. H. Yu, C. Cai, Y. Yuan and M. Jia, Analytical solutions for Euler-Bernoulli beam on Pasternak foundation subjected to arbitrary dynamic loads, International Journal for Numerical and Analytical Methods in Geomechanics, 41 (2017) 1125–1137.

    Article  Google Scholar 

  13. L. Andersen, S. R. K. Nielsen and P. H. Kirkegaard, Finite element modelling of infinite Euler beams on Kelvin foundations exposed to moving loads in convected coordinates, Journal of Engineering Mechanics, 241 (2001) 587–604.

    MATH  Google Scholar 

  14. V. H. Nguyen and D. Duhamel, Finite element procedures for nonlinear structures in moving coordinates. Part 1: Infinite bar under moving axial loads, Computers and Structures, 84 (2006) 1368–1380.

    Article  Google Scholar 

  15. V. H. Nguyen and D. Duhamel, Finite element procedures for nonlinear structures in moving coordinates. Part II: Infinite beam under moving harmonic loads, Computers and Structures, 86 (2008) 2056–2063.

    Article  Google Scholar 

  16. C. G. Koh, G. H. Chiew and C. C. Lim, A numerical method for moving load on continuum, Journal of Sound and Vibration, 300 (2007) 126–138.

    Article  Google Scholar 

  17. J. Lee, Free vibration analysis of circularly curved multi-span Timoshenko beams by the pseudospectral method, Journal of Mechanical Science and Technology, 21 (2007) 2066–2072.

    Article  Google Scholar 

  18. J. Lee, Free vibration analysis of beams with non-ideal clamped boundary conditions, Journal of Mechanical Science and Technology, 27 (2013) 297–303.

    Article  Google Scholar 

  19. J. Lee, Application of Chebyshev-tau method to the free vibration analysis of stepped beams, International Journal of Mechanical Sciences, 101–102 (2015) 411–420.

    Article  Google Scholar 

  20. B. Akgöz and Ö. Civalek, Buckling analysis of functionally graded microbeams based on the strain gradient theory, Acta Mechanica, 224 (2013) 2185–2201.

    Article  MathSciNet  Google Scholar 

  21. B. Akgöz and Ö. Civalek, A novel microstructure-dependent shear deformable beam model, International Journal of Mechanical Sciences, 99 (2015) 10–20.

    Article  Google Scholar 

  22. H. M. Numanoglu, B. Akgöz and Ö. Civalek, On dynamic analysis of nanorods, International Journal of Engineering Science, 130 (2018) 33–50.

    Article  Google Scholar 

  23. M. Naghinejad and H. R. Ovesy, Viscoelastic free vibration behavior of nano-scaled beams via finite element nonlocal integral elasticity approach, Journal of Vibration and Control, 25 (2019) 445–459.

    Article  MathSciNet  Google Scholar 

  24. T. S. Jang, A new solution procedure for a nonlinear infinite beam equation of motion, Communications in Nonlinear Science and Numerical Simulation, 39 (2016) 321–331.

    Article  MathSciNet  Google Scholar 

  25. T. S. Jang, H. S. Baek and J. K. Paik, A new method for the non-linear deflection analysis of an infinite beam resting on a non-linear elastic foundation, International Journal of NonLinear Mechanics, 46 (2011) 339–346.

    Article  Google Scholar 

  26. T. S. Jang and H. G. Sung, A new semi-analytical method for the non-linear static analysis of an infinite beam on a non-linear elastic foundation: A general approach to a variable beam cross-section, International Journal of Non-Linear Mechanics, 47 (2012) 132–139.

    Article  Google Scholar 

  27. T. S. Jang, A new semi-analytical approach to large deflections of Bernoulli-Euler-v. Karman beams on a linear elastic foundation: Nonlinear analysis of infinite beams, International Journal of Mechanical Sciences, 66 (2013) 22–32.

    Article  Google Scholar 

  28. T. S. Jang, A general method for analyzing moderately large deflections of a non-uniform beam: An infinite Bernoulli-Eulervon Kármán beam on a nonlinear elastic foundation, Acta Mechanica, 225 (2014) 1967–1984.

    Article  MathSciNet  Google Scholar 

  29. F. Ahmad, T. S. Jang, J. A. Carrasco, S. U. Rehman, Z. Ali and N. Ali, An efficient iterative method for computing deflections of Bernoulli-Euler-von Karman beams on a nonlinear elastic foundation, Applied Mathematics and Computation, 334 (2018) 269–287.

    Article  MathSciNet  Google Scholar 

  30. T. S. Jang, A new solution procedure for the nonlinear telegraph equation, Communications in Nonlinear Science and Numerical Simulation, 29 (2015) 307–326.

    Article  MathSciNet  Google Scholar 

  31. T. S. Jang, A new dispersion-relation preserving method for integrating the classical Boussinesq equation, Communications in Nonlinear Science and Numerical Simulation, 43 (2017) 118–138.

    Article  MathSciNet  Google Scholar 

  32. T. S. Jang, A regular integral equation formalism for solving the standard Boussinesq’s equations for variable water depth, Journal of Scientific Computing, 75 (2018) 1721–1756.

    Article  MathSciNet  Google Scholar 

  33. T. S. Jang, A new functional iterative algorithm for the regularized long-wave equation using an integral equation formalism, Journal of Scientific Computing, 74 (2018) 1504–1532.

    Article  MathSciNet  Google Scholar 

  34. T. S. Jang, An improvement of convergence of a dispersionrelation preserving method for the classical Boussinesq equation, Communications in Nonlinear Science and Numerical Simulation, 56 (2018) 144–160.

    Article  MathSciNet  Google Scholar 

  35. MATLAB ver. 9.6.0. Release 2019a, The Mathworks Inc., Natick, Massachusetts, United States (2019).

  36. H. Ding, L. Q. Chen and S. P. Yang, Convergence of Galerkin truncation for dynamic response of finite beams on nonlinear foundations under a moving load, Journal of Sound and Vibration, 331 (2012) 2426–2442.

    Article  Google Scholar 

  37. V. Z. Vlasov and N. N. Leont’ev, Beams, Plates and Shells on Elastic Foundations, Israel Program for Scientific Translations Ltd., Jerusalem, Israel (1966).

    MATH  Google Scholar 

  38. J. Lysmer, Vertical Motion of Rigid Footings, University of Michigan Report to WES Contract Report No. 3-115 under Contract No. DA-22-079-eng-340 (1965).

  39. Y. H. Chen and Y. H. Huang, Dynamic stiffness of infinite Timoshenko beam on viscoelastic foundation in moving coordinate, International Journal for Numerical Methods in Engineering, 48 (2000) 1–18.

    Article  Google Scholar 

  40. J. E. Bowles, Foundation Analysis and Design, McGraw-Hill Book Companies, Inc., Singapore (1997).

    Google Scholar 

  41. A. P. S. Selvadurai, Elastic Analysis of Soil-foundation Interaction, Elsevier Scientific Publishing Company, Amsterdam, The Netherlands (2015).

    Google Scholar 

  42. F. E. Richart, J. R. Hall and R. D. Woods, Vibrations of Soils and Foundations, Prentice Hall Inc., Englewood Cliffs, USA (1970).

    Google Scholar 

Download references

Acknowledgments

The present study was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2018R1D1A1B06049813). And it was also supported by the National Research Foundation of Korea (NRF) Grant funded by the Korean Government (MSIP) (NRF-2017R1A5A1015722 and 2011-0030013).

Author information

Authors and Affiliations

  1. Wessex Institute, Southampton, SO40 7AA, UK

    S. Syngellakis

  2. Department of Naval Architecture and Ocean Engineering, Pusan National University, Busan, 46241, Korea

    Jinsoo Park, Dae Seung Cho & Taek Soo Jang

Authors
  1. S. Syngellakis
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jinsoo Park
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Dae Seung Cho
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Taek Soo Jang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Taek Soo Jang.

Additional information

Stavros Syngellakis is an Adjunct Professor at the Wessex Institute of Technology, Southampton, UK. He received his Ph.D. in Civil Engineering from Princeton University, USA. For most of his academic career, he taught mechanics of solids and structures at the University of Southampton, UK. His research interests include wave propagation in solids, structural stability, fracture and contact mechanics.

Jinsoo Park is a post-doctoral researcher under the supervision of Prof. T.S. Jang at the Department of Naval Architecture and Ocean Engineering, Pusan National University in Busan, Republic of Korea. He is a member of Ocean Engineering Laboratory (Supervisor Prof. TS Jang) and his main fields of research are marine hydrodynamics and its numerical simulation.

Dae Seung Cho is a Professor at the Department of Naval Architecture and Ocean Engineering at Pusan National University in Busan, Republic of Korea. He received his Ph.D degree from Seoul National University. His main fields of research are noise, vibration and radar cross section analysis and control of marine structures.

Taek Soo Jang is a Professor at the Department of Naval Architecture and Ocean Engineering at Pusan National University in Busan, Republic of Korea. He received his Ph.D. degree from Seoul National University. His main fields of research are nonlinear (ocean) system identification (inverse problems), techniques to remedy the ill-posedness, developing nonlinear numerical schemes for ODE & PDE and water waves and wave mechanics.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Syngellakis, S., Park, J., Cho, D.S. et al. A numerical study on an infinite linear elastic Bernoulli-Euler beam on a viscoelastic foundation subjected to harmonic line loads. J Mech Sci Technol 34, 3587–3595 (2020). https://doi.org/10.1007/s12206-020-0810-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-020-0810-3

Keywords

Search

Navigation