Rethinking the encounter probability for direct-to-target nuclear attacks for aviation security

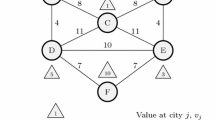
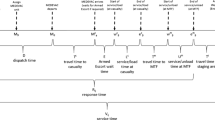
Abstract

The threat of nuclear terrorism has become an important issue for national security. A critical component in preventing a nuclear attack is to prevent nuclear material from being smuggled into the United States via any mode of transportation, including commercial air transportation. Screening baggage on incoming international commercial flights for nuclear material after the flights arrive in the United States makes the system vulnerable to a direct-to-target attack. A direct-to-target attack uses an aircraft to transport a nuclear bomb directly to a particular target prior to United States border screening. The encounter probability has been proposed for capturing the fraction of baggage that has been screened, which indirectly captures screening device utilization. This paper compares and analyzes potential performance measures for analyzing baggage screening systems given the impact of a direct-to-target attack. Seven discrete optimization models are formulated for determining how to screen checked baggage for nuclear material on incoming international flights given the performance measures, including four single-objective models and four goal programming models that analyze the tradeoffs across two performance measures. The models are compared to analyze the tradeoffs across the various performance measures. The results suggest that the encounter probability can be improved by considering one of the proposed performance measures, particularly the performance measure that focuses on targets. The goal programming model results suggest that multiple performance measures can be optimized with minimal trade-offs.

Appendix

Exact algorithms, such as branch and bound, can result in long computation times when solving the integer programming models, since all of the discrete optimization models are NP-hard. Several greedy heuristics are applied to the models introduced in Sections 4 and 5 in order to identify near-optimal solutions in a reduced amount of CPU time. Greedy heuristics for the multidimensional knapsack problem are used, since all of the discrete optimization models considered have a multidimensional knapsack sub-structure. Note that all of the greedy heuristics considered define an efficiency for each flight, e _j , j = 1,2,...,n, or each target e _k , k = 1,2,...,d. As with knapsack greedy heuristics, the flights or targets for all greedy heuristics introduced in this section are covered in non-increasing order of their efficiency values.

First, the two greedy heuristics used for the single objective models are introduced, which adapt the Dobson heuristic and the Toyoda and Senju heuristic (Kellerer et al. 2004) to the single objective discrete optimization models. The reader is referred to Dobson (1982) and Senju and Toyoda (1968) for more details.

The efficiency values of the Dobson heuristic consist of a ratio, whose numerator is the objective function coefficient and whose denominator consists of the sum of the coefficients across all of the constraints. The Dobson heuristic efficiency values for FCP, PCP, and BCP are

$$\begin{array}{lll} e_j &=& \frac{1}{w_j + a_j}, \\ e_j &=& \frac{p_j}{w_j + a_j},\\ e_j &=& \frac{w_j}{w_j + a_j},\end{array}$$

respectively, j = 1,2,...,n. The Dobson heuristic efficiency values for TCP are

$$ e_k = \frac{1}{\sum_{i=1}^{m+1}W_{ik}},\ k=1,2,...,d. $$

Recall that $W_{ik}=\sum_{j \in F_i \cap D_k} w_j$ for knapsacks i = 1,2,...,m (the sum of the baggage going from origin airport i to target k) and $W_{(m+1)k}=\sum_{i=1}^{m} \sum_{j \in F_i \cap D_k} a_j$ for knapsack m + 1 (the total cost to screen the baggage going to target k), k = 1,2,...,d.

The efficiency values of the Toyoda and Senju heuristic capture the relative contribution of the constraints. Let h _ij denote the excess capacity in knapsack i (either a capacity or the budget constraint) if all flights are covered. For FCP, PCP, and BCP,

$$ h_{ij}=\max\left\{0,\ \sum\limits_{j \in F_i} w_{j}-c_i \right\}, i=1,2,...,m $$

and

$$ h_{(m+1)j}=\max\left\{0,\ \sum\limits_{j=1}^n a_j-B \right\}. $$

If there is not some i (i = 1,2,...,m) for each j = 1,2,...,n such that h _ij  > 0, then Toyoda and Senju heuristic efficiency value e _j  = 0, j = 1,2,...,n. Otherwise, the Toyoda and Senju heuristic efficiency values for FCP, PCP, and BCP are

$$\begin{array}{lll} e_j &=& \frac{1}{\sum_{i=1}^m \left(w_j h_{ij}\right)+a_j h_{(m+1)j}},\\ e_j &=& \frac{p_j}{\sum_{i=1}^m \left(w_j h_{ij}\right)+a_j h_{(m+1)j}},\\ e_j &=& \frac{w_j}{\sum_{i=1}^m \left(w_j h_{ij}\right)+a_j h_{(m+1)j}}, \end{array}$$

respectively, j = 1,2,...,n. Note that the Toyoda and Senju heuristic efficiency values are updated after each new flight is covered, which change the remaining capacities c ₁,c ₂,...,c _m and the remaining budget B.

For TCP, let h _ik denote the excess capacity in knapsack i (either a capacity or the budget constraint) if all targets are covered,

$$ h_{ik}=\max\left\{0,\ \sum\limits_{k=1}^d W_{ik}-c_i \right\}, i=1,2,...,m, $$

and

$$ h_{(m+1)k}=\max\left\{0,\ \sum\limits_{k=1}^d W_{(m+1)k}-B \right\}. $$

If there is not some i (i = 1,2,...,m + 1) for each k = 1,2,...,d such that h _ij  > 0, then the Toyoda and Senju heuristic efficiency value e _k  = 0. Otherwise, the Toyoda and Senju heuristic efficiency values for TCP are

$$ e_k = \frac{1}{\sum_{i=1}^{m+1}W_{ik}h_{ik}},$$

k = 1,2,...,d. Note that the Toyoda and Senju heuristic efficiency values are updated after each new target is covered, which change the remaining capacities c ₁,c ₂,...,c _m and the remaining budget B.

Next, consider the goal programming models (TCFCP, TCPCP, TCBCP). The greedy heuristics are applied in two stages. In the first phase, a greedy heuristic for TCP is used to cover targets until T targets are covered (the minimum number of targets to be covered). The three greedy heuristics for TCP include the Dobson heuristic and the Toyoda and Senju heuristic (introduced earlier) as well as the Scaled Dobson heuristic, whose efficiency values are

$$ e_k = \frac{1}{\sum_{i=1}^{m}(W_{ik}/c_i) + W_{(m+1)k}/B},\ k=1,2,...,d. $$

Note that e _k  > 0, k = 1,2,...,d, unless the budget and all origin capacities are zero. The efficiency values are updated after each new target is covered, which change the remaining capacities c ₁,c ₂,...,c _m and the remaining budget B.

In the second stage, one of two greedy heuristics are used (the Dobson heuristic and the Toyoda and Senju heuristic) that correspond to the objective that maximizes either the FC, PC, or BC measure. The adjusted budget and capacities (e.g., after adjusting for the flights that were covered in order to cover T targets) are used to compute the efficiency values for the FCP, PCP, and BCP heuristics. Thus, six greedy heuristics are applied to each goal programming model, each of which uses one of three heuristics for the first stage and one of two heuristics for the second stage.

The long CPU times to solve several PCP, BCP, TCPCP, and TCBCP instances in Section “Computational example” motivate the use of greedy heuristics to efficiently identify near-optimal solutions. All heuristics were run using Matlab 7.9.0.529 (R2009b) on an Intel Xeon X5365 3 GHz processor with 3.25 GB of RAM. The results are illustrated for the scenarios when C = 2,500.

Tables 4, 5, 6 and 7 summarize the solution values for each performance measure from the Dobson heuristics and Toyoda & Senju (abbreviated as T & S) heuristics. Table 4 reports the values of the FC measure using the Dobson heuristic and the Toyoda and Senju heuristic for FCP, PCP, BCP, and TCP. For convenience, the optimal solution values for FCP are listed. Heuristic values that match the optimal solution values are in boldface. Both FCP heuristics identify the optimal solutions for all values of B. The PCP heuristics identify solutions whose FC values are at least a factor of 0.370 of the optimal solution values, the BCP heuristics identify solutions whose FC values are at least a factor of 0.227 of the optimal solution values, and the TCP heuristics identify solutions whose FC values are at least a factor of 0.244 of the optimal solution values. The PCP, BCP, and TCP heuristics all fail to cover many flights.

Table 4 FCP, PCP, BCP, and TCP heuristic results for FC measure.

Table 5 FCP, PCP, BCP, and TCP heuristic results for PC measure.

Table 6 FCP, PCP, BCP, and TCP heuristic results for BC measure.

Table 7 FCP, PCP, BCP, and TCP heuristic results for TC measure.

Table 5 reports the values of the PC measure using the Dobson heuristics and the Toyoda and Senju heuristics for FCP, PCP, BCP, and TCP. The PCP Dobson heuristic identifies one optimal solution (when B = $25K), and the PCP Toyoda and Senju heuristic does not identify any optimal solutions. The PCP Dobson heuristic and the Toyoda and Senju heuristics identify PC solutions whose values are at least a factor of 0.990 of the optimal solution values. The FCP heuristics identify solutions whose PC values are at least a factor of 0.904 of the optimal solution values, the BCP heuristics identify solutions whose PC values are at least a factor of 0.893 of the optimal solution values, and the TCP heuristics identify solutions whose PC values are at least a factor of 0.590 of the optimal solution values.

Table 6 reports the values of the BC measure using the Dobson heuristics and the Toyoda and Senju heuristics for FCP, PCP, BCP, and TCP. The BCP Dobson heuristic identifies two optimal BCP solutions (when B = $100K, $150K), and the BCP Toyoda and Senju heuristic identifies one optimal solution (when B = $100K). The BCP Dobson heuristic and the Toyoda and Senju heuristics identify solutions to BCP whose values are at least a factor of 0.980 of the optimal solution value. The FCP heuristics identify solutions whose BC values are at least a factor of 0.957 of the optimal solution values, the PCP heuristics identify solutions whose BC values are at least a factor of 0.985 of the optimal solution values, and the TCP heuristics identify solutions whose BC values are at least a factor of 0.608 of the optimal solution values. The FCP, PCP, and BCP heuristics tend to nearly fully-utilize the baggage screening capacity.

Table 7 reports the values of the TC measure using the Dobson heuristics and the Toyoda and Senju heuristics for FCP, PCP, BCP, and TCP. It reveals that both the TCP Dobson heuristic and the TCP Toyoda and Senju heuristic identify the optimal TCP solutions for all scenarios considered. The PCP heuristics do not cover any targets, whereas both FCP heuristics cover at most one target, and both BCP heuristics cover at most four targets. The results of Tables 4–7 suggest that the FCP, PCP, and BCP heuristics are effective in covering targets, and that the TCP heuristics are not effective for covering flights, passengers, or bags.

The Dobson heuristics identify solutions whose values are at least as good as the their corresponding Toyoda and Senju heuristic solution values in all but two scenarios across all four models considered (BCP with B = $25K, $175K), which suggests that despite its simplicity, the Dobson heuristic is more effective for FCP, PCP, BCP, and TCP.

Tables 8, 9 and 10 summarize the solution values identified by the heuristics used for the three goal programming models when C = 250), B = $275K, and T varies from 1 to 10. All heuristics cover T targets in the scenarios considered, and hence, only the objective function values are reported (either FC, PC, or BC values). Table 8 reports the FC values for all of the heuristics. The TCFCP heuristics identify FC solution values that are at least 0.985 of the optimal solution values, whereas the TCPCP heuristics identify FC solution values that are at least 0.898 of the optimal solution value, and the TCBCP heuristics identify FC solution values that are at least 0.811 of the optimal solution values. A heuristic dominates the other heuristics if it identifies solution values whose values are at least as good as the those identified by the other heuristics for all scenarios considered (in this case, across all values of T). None of the six TCFCP heuristics dominate the other heuristics in terms of the FC values. However, each of the three TCFCP heuristics that use the Toyoda and Senju heuristic in the FC phase dominate other heuristics in all but two or fewer scenarios, which suggests that the Toyoda and Senju heuristic in the FC phase identifies better solution values than the Dobson heuristic in the FC phase.

Table 8 FC measure for TCFCP, TCPCP, and TCBCP heuristics for B = $275K.

Table 9 PC measure for TCFCP, TCPCP, and TCBCP heuristics for B = $275K.

Table 10 BC measure for TCFCP, TCPCP, and TCBCP heuristics for B = $275K.

Table 9 reports the PC values for the heuristics. The TCPCP heuristics identify PC solution values that are at least 0.983 of the optimal solution values, whereas the TCFCP heuristics identify PC solution values that are at least 0.930 of the optimal solution value and the TCBCP heuristics identify PC solution values that are at least 0.926 of the optimal solution values. None of the six TCPCP heuristics dominate the other heuristics in terms of the PC values.

Table 10 reports the BC values for the heuristics. The TCBCP heuristics identify solution values that are at least 0.955 of the optimal BC solution values, whereas the TCFCP heuristics identify BC solution values that are at least 0.945 of the optimal solution values, and the TCPCP heuristics identify BC solution values that are at least 0.978 of the optimal solution values. The TCBCP heuristic that uses the Scaled Dobson heuristic in the TC phase and then the Toyoda and Senju heuristic in the BC phase dominates all other TCBCP heuristics. The three TCBCP heuristics that use the Toyoda and Senju heuristics in the BC phase identify significantly better BC values than the corresponding TCBCP heuristic that uses the Dobson heuristic in the BC phase. This observation mirrors that of the TCFCP heuristics (and, to a lesser extent, of the TCPCP heuristics), which suggests that the Toyoda and Senju heuristic for the second phase is more effective than using the Dobson heuristic. We also note that the three TCPCP heuristics that use the Dobson heuristic in the BC phase outperform the corresponding TCBCP heuristic in terms of the BC solution values they identify in all thirty instances. The TCPCP heuristics that use the Toyoda and Senju heuristic in the BC phase outperform the corresponding TCBCP heuristics in terms of the BC solution values they identify in fourteen of the thirty instances. This observation is surprising, since it suggests that heuristics aimed at covering the most passengers more fully utilize the baggage screening capacity than heuristics designed to fully utilize the baggage screening capacity. This is largely the result of the TCBCP having a Subset Sum Problem substructure, where the efficiency values are identical across many flights.