A rapidly converging domain decomposition algorithm for a time delayed parabolic problem with mixed type boundary conditions exhibiting boundary layers

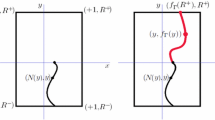
Abstract

A rapidly converging domain decomposition algorithm is introduced for a time delayed parabolic problem with mixed type boundary conditions exhibiting boundary layers. Firstly, a space-time decomposition of the original problem is considered. Subsequently, an iterative process is proposed, wherein the exchange of information to neighboring subdomains is accomplished through the utilization of piecewise-linear interpolation. It is shown that the algorithm provides uniformly convergent numerical approximations to the solution. Our analysis utilizes some novel auxiliary problems, barrier functions, and a new maximum principle result. More importantly, we showed that only one iteration is needed for small values of the perturbation parameter. Some numerical results supporting the theory and demonstrating the effectiveness of the algorithm are presented.

1 Introduction

In the mathematical modeling of various physical phenomena in bioscience and control theory, delay differential equations arise frequently, for instance, in population dynamics [12], immunology [5], physiology [6], and neural networks [11]. The presence of the delay term in these models is due to feedback control because a finite time is required to sense and react to the data like the immune period, the time between a cell is infected and the new virus is produced, the stages of the life cycle, the duration of the infectious period, etc. [28]. In delay models, the evolution of the solution and its derivatives involve the past history also. Singularly perturbed delay differential equations form a significant category among these equations. When the highest order derivative term is multiplied with a small positive parameter, the delay differential equations are called as singularly perturbed delay differential equations. Some applications include modeling of the human pupil-light reflex [17], variational problems in control theory [8], the study of bistable devices [7], and chemical processes [2]. The following Hutchinson’s equation [3]

$$\begin{aligned} u_{t}(y,t)=\epsilon u_{yy}(y,t)+ru(y,t)[1-u(y,t-\tau )], \end{aligned}$$

(1)

is a singularly perturbed differential equation in mathematical ecology, where $\tau$ represents the time lag and $\epsilon$ is the perturbation parameter. This equation serves as a fundamental model for the evolution of a population with density u(y, t). The following singularly perturbed partial differential equation is used to model the processing of metal sheets [3]

$$\begin{aligned} u_{t}=\epsilon u_{y y}+v(f(u(y,t-\tau )))u_{y}+a[g(u(y,t-\tau ))-u(y,t)], \end{aligned}$$

(2)

where u denotes the temperature distribution in the metal sheet with velocity v and heated by a source g. The fixed delay of length $\tau$ is introduced by the controller’s speed.

Consider the singularly perturbed time delayed parabolic problem

(3)

with initial condition

$$\begin{aligned} u(y,t)= g_b(y,t),~~ (y,t)\in \gamma _b=[0,1]\times [-\tau ,0], \end{aligned}$$

and mixed boundary conditions

$$\begin{aligned} \left\{ \begin{array}{ll} \varGamma _{\ell }u(y,t):= \alpha _1u(y,t)-\delta _1\sqrt{\epsilon } u_{y}(y,t)=g_\ell (t), &{}\text {on}~ \gamma _\ell =\{(0,t):0\le t\le T\},\\ \varGamma _{r}u(y,t):= \alpha _2u(y,t)+\delta _2\sqrt{\epsilon } u_{y}(y,t)=g_r(t), &{}\text {on}~ \gamma _r=\{(1,t):0\le t\le T\}, \end{array} \right. \qquad \end{aligned}$$

(4)

where

$$\begin{aligned} Lu(y,t)=u_{t}(y,t)-\epsilon u_{yy}(y,t)+a(y,t)u(y,t). \end{aligned}$$

We define . Suppose $\gamma =\gamma _\ell \cup \gamma _b\cup \gamma _r$ and ${\overline{\gamma }}=\gamma _\ell \cup \gamma _o\cup \gamma _r,$ where $\gamma _o=[0,1]\times \{0\}$. Also, assume that $0<\epsilon \le 1,$ $a(y,t)+b(y,t)\ge \beta >0,$ with $0<\alpha \le a(y,t),~b(y,t)\le 0,$ and $\tau >0.$ Further, the terminal time T is assumed to be $T=\sigma \tau ,$ for some integer $\sigma >1$. We assume that the coefficients of the mixed boundary conditions verify $\alpha _1>0,~\delta _1\ge 0,~\alpha _1\ge \delta _1,$ and $\alpha _2,\delta _2\ge 0$ with $\alpha _2+\delta _2>0$. The data of problem (3)-(4) is supposed to be enough smooth and satisfy appropriate compatibility conditions [31]. With these assumptions, there is a unique solution of (3)-(4) exhibiting boundary layers near $y=0$ and $y=1.$

It is well known that the classical discretization methods are unable to provide satisfactory results for problems with boundary layers, as they require a large number of mesh points to resolve the boundary layers and leads to a high computational cost. To address this issue, a variety of robust/uniform numerical methods have been considered in the literature, see, e.g. [3, 4, 9, 13, 32] for delay differential equations with Dirichlet boundary conditions and [29, 31] for delay differential equations with Robin boundary conditions. Additionally, some new developments addressing singularly perturbed delay differential equations can be observed in [19,20,21,22,23,24,25].

Domain decomposition-based numerical methods have gained significant popularity for solving partial differential equations. Schwarz’s groundbreaking study on domain decomposition in 1870 [30] is acknowledged as the initial work in this field. Domain decomposition enables the application of distinct treatments to each subdomain, allowing the use of different discretization techniques. This approach enables localized handling of singularities within specific subdomains. Additionally, domain decomposition methods offer the advantage of avoiding non-uniform meshes. Furthermore, these methods can be effectively implemented in parallel to enhance the computational efficiency of numerical computations. Most work on domain decomposition for singularly perturbed partial differential equations is restricted to Dirichlet boundary conditions (see [1, 14, 15, 27, 32] and the references therein). For an in-depth exploration of domain decomposition methods, it is recommended to refer to [26, 33]. The existence of a time delay in the differential model and the inclusion of mixed boundary conditions do, indeed, set the theoretical aspect apart. Consequently, problem (3)-(4) has received less attention in the literature.

As far as we are aware, there is no study on domain decomposition for singularly perturbed partial differential equations with a time delay and mixed boundary conditions. So, the purpose of this paper is two-fold: firstly, to develop a novel domain decomposition method for solving problem (3)-(4), and secondly, to provide a comprehensive error analysis of the developed method. We split the domain into three overlapping subdomains (a regular subdomain and two layer subdomains) with the help of a subdomain parameter. Subsequently, an iterative process is proposed, wherein the exchange of information to neighboring subdomains is accomplished through the utilization of piecewise-linear interpolation. It is shown that the algorithm provides uniformly convergent numerical approximations to the solution. More importantly, we showed that only one iteration is needed for very small values of the perturbation parameter $\epsilon .$ Numerical results are presented that support the theory and demonstrate the effectiveness of the algorithm. The current research introduces several novel aspects in terms of analysis. Our analysis utilizes some novel auxiliary problems, barrier functions, and a new maximum principle result.

The work is arranged as follows. The continuous maximum principle and the bounds of the derivatives of the solution are discussed in Sect. 2. In Sect. 3 we introduce an algorithm which is analyzed in Sect. 4. Numerical results are presented in Sect. 5 for two test problems and some concluding remarks are included in Sect. 6.

Notation: C is assumed to be a positive constant independent of the discretization parameters $N_y$, $\varDelta t$, the iteration parameter k and the perturbation parameter $\epsilon$. We define a function $h_{i,n}=h(y_i,t_n)$, for $h \in C([0,1] \times [0,T])$. The norm is defined as discrete maximum norm corresponding to the maximum norm on a bounded and closed subset of $[0,1] \times [0,T]$. And for a mesh function Z, denotes a piecewise linear interpolation at time $t_n$.

2 A priori estimates

We obtain some bounds on the derivatives of the solution of (3)-(4). For this purpose, first we introduce a continuous maximum principle for the operator .

Lemma 1

Let be a sufficiently differentiable function in . Suppose on (0, T] and on $\gamma _b$. Then on implies that on .

Proof

The proof can be obtained using the arguments in [21, 31]. $\square$

Lemma 2

Suppose is a sufficiently differentiable function satisfying on (0, T] and on $\gamma _b$. Then on implies that on .

Proof

We assume that for . Therefore, we have on $(0,\tau ]$, and on $\gamma _b$. Further,

as $b\le 0$ and for . Therefore, for by Lemma 1. Repeating the above arguments and using the fact that for , we can show that , $\forall$ . $\square$

Using the aforementioned maximum principle, we can readily derive the following stability estimate.

Lemma 3

The solution u of problem (3)-(4) satisfies

(5)

Furthermore, the continuous solution u of (3)-(4) satisfies the following estimates.

Lemma 4

Suppose $g_\ell ,~g_r\in C^{\frac{3+\mu }{2}}([0,T])$, $g_b\in C^{(4+\mu ,2+\mu /2)}(\gamma _b)$, $\mu \in (0,1).$ If the compatibility conditions are satisfied up to the second order, then there exists a unique solution to problem (3)-(4) such that . Furthermore, it is true that

(6)

Proof

The first part is proved by using [16]. Now, by using the transformation ${\tilde{y}}=y/\sqrt{\epsilon }$, we transform problem (3)-(4) as follows

(7)

where . Now, we use the result from [16, p. 352] to obtain

$$\begin{aligned} \left\Vert \frac{\partial ^{s_1+s_2}{\tilde{u}}}{\partial {\tilde{y}}^{s_1}\partial t^{s_2}}\right\Vert _{\tilde{D}_\delta }\le C(1+\left\Vert {\tilde{u}}\right\Vert _{\tilde{D}_{2\delta }}), \end{aligned}$$

for all $\tilde{D}_\delta$ in . Here, $0\le s_1+2s_2 \le 4,~s_1,s_2\ge 0,$ and $\tilde{D}_\delta$ is a $\delta -$neighbourhood in of diameter $\delta$.

Transitioning back to the original variable we get

Therefore, the proof is completed using Lemma 3. $\square$

A further decomposition of the solution u is required to prove the convergence analysis of the numerical algorithm. The actual solution u is decomposed as $u=v+w$. The component v is further decomposed as $v=v_0+\epsilon v_1,$ where $v_0$ and $v_1$ are the solutions of the problems

(8)

and

(9)

Thus, the component v solves

The component w solves

(10)

Lemma 5

Suppose , $g_\ell ,~g_r\in C^{\frac{5+\mu }{2}}([0,T])$, $g_b\in C^{(6+\mu ,3+\mu /2)}( \gamma _{b})$, $\mu \in (0,1),$ and appropriate compatibility conditions hold. Then, one can split u as $u=v+w,$ where v and w are the regular and singular components, respectively, satisfying

(11)

(12)

for , $~0\le s_1+2s_2 \le 4,~s_1,s_2\ge 0$.

Proof

The bounds are derived as follows. Note that $v_0$ is the solution of problem (8), which is a problem that does not involve $\epsilon .$ Hence, using a classical argument, we get

Moreover, $v_1$ is the solution to a problem in a form for which Lemma 4 is applicable. Consequently, it holds

Since $v=v_0+\epsilon v_1$, the necessary bounds for the component v and its derivatives follow from the above two bounds. The bounds for the component w and its derivatives can be proved using the arguments in [10]. $\square$

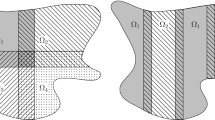
3 The numerical algorithm

The computational domain is divided into three overlapping subdomains , $p=\ell ,m,r,$ where and are the layer subdomains, and is the regular subdomain with

$$\begin{aligned} \rho = \text{ min }\left\{ \frac{1}{4},~~2\sqrt{\frac{\epsilon }{\beta }}\, \ln N_{y}\right\} . \end{aligned}$$

(13)

Here, $\rho$ is the subdomain parameter, which is chosen as the Shishkin transition point. Each subdomain , where , is discretized using a rectangular mesh which is formed by uniform meshes in both directions. We define , where ${\overline{\varOmega }}_o=[-\tau ,0].$ The uniform mesh in the spatial direction is defined as , while $\overline{\varOmega }_o^{m_\tau }$, $\overline{\varOmega }^{M_{t}}$ are the meshes in time direction with uniform length $\varDelta t=T/M_{t}$, which are obtained by dividing $[-\tau ,0]$ and [0, T] in a number of subintervals $m_\tau$ and $M_{t}=\sigma m_\tau ,$ respectively. Defining and $\varOmega ^{M_{t}}=\overline{\varOmega }^{M_{t}}\cap (0,T],$ then on each subdomain, the meshes and $\gamma ^{N_{y},m_\tau }_{b,p}$ are defined as and where $N_{y}$ and $M_{t}$ are the discretization parameters in space and time directions respectively.

On each subdomain , the backward Euler scheme and central differencing are employed to discretize in time and space respectively. Thus, we have

(14)

where

The boundary conditions are discretized with a special second order scheme as follows:

(15)

Here,

In this approach, we discretized the boundary conditions using a combination of spatial and temporal discretizations. It is important to observe that employing the typical upwind discretization for mixed boundary conditions results in linear accuracy. However, with the proposed methodology, we have the possibility to increase this accuracy to a quadratic order by refining the truncation error in both space and time.

Setting , the numerical solution of (3)-(4) is computed using the step by step process defined as follows. Suppose the initial approximation is

and compute for $k\ge 1,$ by solving the following set of equations

(16)

(17)

(18)

The aforementioned process is repeated until the condition is not met, where $\delta$ represents a tolerance specified by the user and the approximate solution of (3)-(4) is defined by

(19)

4 Convergence analysis

To prove the convergence of the proposed method we first introduce the maximum principle for the discrete operators and for . Suppose the operators ${ G}^{N_{y},M_{t}}_p,~p=\ell ,m,r,$ are defined as ${ G}^{N_{y},M_{t}}_{\ell }{ Z}(0,t_n)=\varGamma _{\ell }^{N_{y},M_{t}}{ Z}(0,t_n)$, ${ G}^{N_{y},M_{t}}_r{ Z}(1,t_n)=\varGamma _r^{N_{y},M_{t}} { Z}(1,t_n)$ and ${ G}^{N_{y},M_{t}}_p{ Z}(a,t_n)={ Z}(a,t_n)$ at the points $a=\rho , 1-\rho , 2\rho , 1-2\rho$ for $t_n \in \varOmega ^{M_{t}}$.

Lemma 6

Let ${ Z}_p,~p=\ell ,m,r,$ be a mesh function satisfying ${ G}_{p}^{N_{y},M_{t}}{ Z}_p(y_0,t_n)\ge 0,~{ G}_{p}^{N_{y},M_{t}}{ Z}_p(y_{N_y},t_n)\ge 0,$ $t_n\in \varOmega ^{M_{t}}$ and ${ Z}_p(y_i,t_n)\ge 0$, $(y_i,t_n)\in {\gamma }^{N_{y},m_\tau }_{b,p}$. Then

$L_p^{N_{y},M_{t}}{ Z}_p(y_i,t_n)\ge 0$, implies that ${ Z}_p(y_i,t_n)\ge 0$ for .

Proof

We prove the result for $p=\ell$. A similar argument can be used for $p=m,r$. Suppose the mesh function ${ Z}_\ell$ attains its minimum at $({{\overline{y}}}_i,\overline{t_n})$, that is,

Clearly, $({{\overline{y}}}_i,\overline{t_n})$ is not a member of ${\gamma }^{N_{y},M_{t}}_{b,\ell }$. If , then

$$\begin{aligned} L_\ell ^{N_{y},M_{t}} { Z}_\ell ({{\overline{y}}}_i,\overline{t_n})=({ F}_{t}^-{ Z}_\ell -\epsilon D_{y}{ Z}_\ell +a{ Z}_\ell ) ({{\overline{y}}}_i,\overline{t_n})<0, \end{aligned}$$

since ${ F}_{t}^-{ Z}_\ell ({{\overline{y}}}_i,\overline{t_n})\le 0$ and $D_{y} { Z}_\ell ({{\overline{y}}}_i,\overline{t_n})\ge 0,$ which contradicts the assumption.

Now, suppose $({{\overline{y}}}_i,\overline{t_n}) \in \gamma _{\ell }^{N_{y},M_{t}}$, then

$$\begin{aligned} { G}_{\ell }^{N_{y},M_{t}}{ Z}_\ell ({{\overline{y}}}_i,\overline{t_n})=\left( \alpha _1{ Z}_\ell -\delta _1\sqrt{\epsilon }{ F}_{y}^+{ Z}_\ell +\frac{h_\ell \delta _1}{2 \sqrt{\epsilon }}(a{ Z}_\ell +{ F}_{t}^-{ Z}_\ell )\right) ({{\overline{y}}}_i,\overline{t_n})<0, \end{aligned}$$

since $F_{t}^-{ Z}_\ell ({{\overline{y}}}_i,\overline{t_n})\le 0$ and ${ F}_{y}^+{ Z}_\ell ({{\overline{y}}}_i,\overline{t_n})\ge 0$, which contradicts the assumption. Hence, the proof is complete. $\square$

Lemma 7

Let ${ Y}_p,~p=\ell ,m,r,$ be a mesh function satisfying ${ G}_{p}^{N_{y},M_{t}}{ Y}_p(y_0,t_n)\ge 0,~{ G}_{p}^{N_{y},M_{t}}{ Y}_p(y_{N_y},t_n)\ge 0,$ $t_n\in \varOmega ^{M_{t}}$ and ${ Y}_p(y_i,t_n)\ge 0$, $(y_i,t_n)\in {\gamma }^{N_{y},m_\tau }_{b,p}$. Then implies that ${ Y}_p(y_i,t_n)\ge 0$ for .

Proof

Define , $p=\ell ,m,r,$ $q_1=0,1\dots ,n,$ where $\overline{\varOmega }^{m_\tau }_{q_1}$ is defined by splitting $[(q_1-1)\tau ,q_1\tau ]$ into $m_\tau$ intervals of equal length. Further, we introduce , where $\overline{\varOmega }^{m_\tau }_{q_1,q_2}$ is obtained by splitting the interval $[(q_1-1)\tau ,q_2\tau ]$ into $(q_2-q_1+1)m_\tau$ intervals of equal length.

Assume that ${ Z}_p(y_i,t_n)={ Y}_p(y_i,t_n)$, for . Therefore, we have

$$\begin{aligned} {Z}_p(y_i,t_n)\ge & {} 0,~ (y_i,t_n)\in {\gamma }^{N_y,m_\tau }_{b,p} ~~\text{ and }~~\\ { G}_{p}^{N_{y},M_{t}}{ Z}_p(y_0,t_n)\ge & {} 0,~{ G}_{p}^{N_{y},M_{t}}{ Z}_p(y_{N_y},t_n)\ge 0,~t_n\in \varOmega ^{m_\tau }_1, \end{aligned}$$

and

Hence, Lemma 6 implies that ${ Y}_p(y_i,t_n)={ Z}_p(y_i,t_n)\ge 0$, for . Similarly, for $q_1\ge 2,$ we can establish ${ Y}_p(y_i,t_n)\ge 0$, for using the fact ${ Y}_p(y_i,t_n)\ge 0$ for . $\square$

Next, we define some values that will be used in further analysis.

Further, we define the following auxiliary problems that will be used to prove the convergence of the method.

Lemma 8

Let u be the exact solution of (3)-(4) and the approximate solution provided by the proposed algorithm. Then, it holds that

(20)

Proof

For ,

(21)

Applying Taylor expansions and using the bounds in (6) with $h_\ell \le C\sqrt{\epsilon } N_{y}^{-1}\ln N_{y}$ we obtain

(22)

Next, for $t_n \in \varOmega ^{M_{t}}$ we have and equations (4) and (15) give

Now, using Taylor expansions and the bounds in (6), we get

Further, applying Lemma 7 to the mesh function , we get

Similarly,

Now, we consider two cases to find an estimate for .

Case 1: If $\rho =1/4$, then $h_m=1/(2N_{y})$ and $\epsilon ^{-1}\le C\ln ^2 N_{y}$. Now, using (6) and equation (21), from Taylor expansions we get

Case 2: If $\rho =2\sqrt{\frac{\epsilon }{\alpha }}\ln N_{y}$, then $h_m \le CN_{y}^{-1}$. So by using Taylor expansion and (6), we get

To get a bound of the term $\epsilon \left| \left( D_{y}u-u_{yy}\right) (y_i,t_n)\right|$ we use the solution decomposition $u=v+w$ such that

$$\begin{aligned} \epsilon \left| \left( D_{y}u-u_{yy}\right) (y_i,t_n)\right|\le & {} \epsilon \left| \left( D_{y}v-v_{yy}\right) (y_i,t_n)\right| +\epsilon \left| \left( D_{y}w-w_{y y}\right) (y_i,t_n)\right| .\\ \end{aligned}$$

Now, by using Taylor expansions and the bounds in (11), (12), we get

$$\begin{aligned} \epsilon \left| \left( D_{y}u-u_{yy}\right) u(y_i,t_n)\right|\le & {} C\epsilon h^2_m\left\Vert v_{yyyy}(.,t_n) \right\Vert _{[y_{i-1},y_{i+1}]}+C\epsilon \left\Vert w_{y y}(.,t_n)\right\Vert _{[y_{i-1},y_{i+1}]}\\\le & {} { CN_{y}^{-2}}. \end{aligned}$$

Thus, for , we have

Now, applying Lemma 7 to the mesh function , we get

Therefore, by combining the aforementioned bounds, the desired result can be obtained. $\square$

In the underlying theorem we have shown that the method converges uniformly for $\rho =2\sqrt{\frac{\epsilon }{\beta }}\ln N_{y}$.

Theorem 1

The solution of (3)-(4) and the first iterate of the proposed scheme satisfy

Proof

Suppose

is the mesh function, where $\varPsi _\ell$ is the solution of following problem

(23)

where the operator ${\widetilde{\varGamma }}_\ell ^{N_{y},M_{t}}$ is defined as

$$\begin{aligned} {\widetilde{\varGamma }}_\ell ^{N_{y},M_{t}} \varPsi _\ell (0,t_n)=\alpha _1\varPsi _\ell (0,t_n)-\delta _1\sqrt{\epsilon }{ F}_{y}^+\varPsi _\ell (0,t_n)+\frac{h_\ell \delta _1}{2 \sqrt{\epsilon }}(\beta \varPsi _\ell +{ F}_{t}^-\varPsi _\ell )(0,t_n), \end{aligned}$$

$\varphi _1= 2\alpha _1\sqrt{\epsilon }h_\ell -2\delta _1\epsilon (\zeta _1-1)+\delta _1h_\ell ^2a ~,~ \varphi _2=2\alpha _1\sqrt{\epsilon }h_\ell -2\delta _1\epsilon (\zeta _2-1)+\delta _1h_\ell ^2a$ and $\zeta _1=\beta _1+\beta _2,~\zeta _2=\beta _1-\beta _2$ with

$$\begin{aligned}\beta _1=1+\left( \frac{\rho }{N_{y}}\sqrt{\frac{\beta }{\epsilon }}~\right) ^2,~\beta _2=2\left( \frac{\rho }{N_{y}}\sqrt{\frac{\beta }{\epsilon }}~\right) \sqrt{1+\left( \frac{\rho }{N_{y}}\sqrt{\frac{\beta }{\epsilon }}~\right) ^2},\end{aligned}$$

and satisfies

The solution of problem (23) is

$$\begin{aligned} \varPsi _\ell (y_i,t_n)=\chi ^{[1]} \frac{\varphi _2 \zeta _1^i-\varphi _1\zeta _2^i}{\varphi _2\zeta _1^{N_{y}}-\varphi _1\zeta _2^{N_{y}}}, \end{aligned}$$

(24)

which satisfies and it is monotonically increasing. Also, we have $\varPsi ^\pm (y_i,t_n)\ge 0~~\text{ for }~(y_i,t_n)\in {\gamma }^{N_{y},m_\tau }_{b,\ell },~\varGamma _\ell ^{N_{y},M_{t}}\varPsi ^\pm (0,t_n)\ge 0, \varPsi ^\pm (2\rho ,t_n)\ge 0\,\,\,\text{ for }~t_n\in \varOmega ^{M_{t}},$ and , for . Thus, by applying Lemma 7 to the mesh function $\varPsi ^{\pm }(y_i,t_n),$ we get

Since $y_i \le \rho$ for , equation (24) implies that

$$\begin{aligned} {\varPsi }_{\ell }(y_i,t_n)\le & {} \chi ^{[1]} \frac{\varphi _2 \zeta _1^{N_{y}/2}-\varphi _1\zeta _2^{N_{y}/2}}{\varphi _2\zeta _1^{N_{y}}-\varphi _1\zeta _2^{N_{y}}}=\chi ^{[1]} \frac{\lambda \zeta _1^{N_{y}/2}-\zeta _2^{N_{y}/2}}{\lambda \zeta _1^{N_{y}}-\zeta _2^{N_{y}}}, \text {where}~\lambda =\varphi _2/\varphi _1,\\= & {} \frac{\chi ^{[1]}}{\lambda \zeta _1^{N_{y}/2}+\zeta _2^{N_{y}/2}}\left[ \frac{\lambda ^2\zeta _1^{N_{y}}-\zeta _2^{N_{y}}}{\lambda \zeta _1^{N_{y}}-\zeta _2^{N_{y}}}\right] . \end{aligned}$$

Therefore, we have

$$\begin{aligned} {\varPsi }_{\ell }(y_i,t_n)\le \frac{\chi ^{[1]}}{\lambda \zeta _1^{N_{y}/2}+\zeta _2^{N_{y}/2}}\left[ \frac{\lambda ^2-\zeta _2^{N_{y}}/\zeta _1^{N_{y}}}{\lambda -\zeta _2^{N_{y}}/\zeta _1^{N_{y}}}\right] \le \chi ^{[1]}\frac{C\lambda }{\lambda \zeta _1^{N_{y}/2}+\zeta _2^{N_{y}/2}}, \end{aligned}$$

since $\lambda >1$ and $\zeta _2/\zeta _1<1,$ and hence we get $\left[ \frac{\lambda ^2-\zeta _2^{N_{y}}/\zeta _1^{N_{y}}}{\lambda -\zeta _2^{N_{y}}/\zeta _1^{N_{y}}}\right] \le C\lambda .$ Thus, we have

$$\begin{aligned} {\varPsi }_{\ell }(y_i,t_n)\le \frac{\chi ^{[1]}C}{\zeta _1^{N_y/2}}. \end{aligned}$$

Further, employing the arguments presented in [18, Lemma 5.1] and utilizing the inequality $\chi ^{[1]}\le C$, we can establish that ${\varPsi }_{\ell }(y_i,t_n)\le CN_{y}^{-2}$ for . Thus, it is

(25)

Proceeding in a similar way we can arrive at

(26)

Now, take , which satisfies the following

Thus, Lemma 7 gives

(27)

and hence

$$\begin{aligned} \xi ^{[1]} \le \chi _{\rho }+CN_{y}^{-2}. \end{aligned}$$

(28)

Also, we note that $\chi _{\rho }\le C(\varDelta t + N_{y}^{-2}\ln ^2N_{y})$ using Lemma 8 and , . Thus, we get the result by combining (28) and Lemma 8. $\square$

In the following theorem, for $\rho =1/4$, we find a bound on and then combine it with Lemma 8 to establish a bound on .

Theorem 2

The exact solution of problem (3)-(4) and the approximate solution defined by (19) satisfy

(29)

Proof

Let consider the mesh function

where satisfies

For $t_n \in \varOmega ^{M_{t}}$, we have

i.e. $\varPhi ^{\pm }(y_i,t_n)\ge 0,~~(y_i,t_n)\in \gamma _{b,\ell }^{N_{y},m_\tau }~ \text{ and }~\varGamma _\ell ^{N_{y},M_{t}}\varPhi ^{\pm }(0,t_n)\ge 0,~ \varPhi ^{\pm }(2\rho ,t_n)\ge 0,~t_n\in \varOmega ^{M_{t}}.$

For , it is

Then, Lemma 7 leads to

Hence, for , we get

(30)

Similarly, we can show that

(31)

Since and , we have the following

So, applying Lemma 7, we get

(32)

Next, we calculate a bound of $\xi ^{[2]}$ for which we need to estimate $\chi ^{[2]}$ first. We note that . Consequently

Therefore, we have $\chi ^{[2]}\le \chi _{2\rho }+\chi _{\rho }+5\chi ^{[1]}/6.$ Hence, it is

$$\begin{aligned} \max \{\xi ^{[1]},\chi ^{[2]}\}\le \varUpsilon + 5\chi ^{[1]}/6,~~~\varUpsilon =\chi _{2\rho }+\chi _{\rho }. \end{aligned}$$

By performing the aforementioned procedure, we have

$$\begin{aligned} \max \{\xi ^{[k]},\chi ^{[k+1]}\}\le \varUpsilon +5\chi ^{[k]}/6. \end{aligned}$$

Simplifying the above expression we obtain

$$\begin{aligned} \chi ^{[k]}\le 6\varUpsilon + 5^{k-1}\chi ^{[1]}/6^{k-1}, \end{aligned}$$

and therefore

$$\begin{aligned} \xi ^{[k]}\le 6\varUpsilon +5^{k}\chi ^{[1]}/6^{k}. \end{aligned}$$

(33)

Further, Lemma 8 gives $\varUpsilon \le C(\varDelta t +N_{y}^{-2}\ln ^2N_{y})$, since $(2\rho ,t_n),$ , and and . Also, we have $\chi ^{[1]}\le C.$ Hence, we get the proof by combining (33) and Lemma 8. $\square$

5 Numerical results

Here, two test problems are considered to illustrate the numerical scheme discussed earlier. We compute the uniform error and convergence rate as ${\mathbb {E}}^{N_{y},M_t}=\max _{\epsilon }{\mathbb {E}}^{N_{y},M_t}_\epsilon ~ \text{ and }~{\mathbb {R}}^{N_{y},M_t}=\log _2\left( \frac{{\mathbb {E}}^{N_{y},M_t}}{{\mathbb {E}}^{2N_{y},4M_t}}\right)$, taking $\epsilon \in \{10^{-1},10^{-2},...,10^{-8}\}$ and different values of the discretization parameters $N_{y}, M_t.$ The formula for computation of errors ${\mathbb {E}}^{N_{y},M_t}_\epsilon$ is given below. The approximate solutions are computed using Algorithm 1. The stopping criterion of the algorithm for the considered problems is .

Algorithm 1

Algorithm

Example 1

Consider

where $g_b,~f,~g_\ell$ and $~g_r$ are determined with the help of the exact solution

$u(y,t)=t\left[ \frac{e^{-y/\sqrt{\epsilon }}+e^{(y-1)/\sqrt{\epsilon }}}{1+e^{-1/\sqrt{\epsilon }}}-\cos ^2{\pi y}\right] .$

The maximum pointwise errors for this example are evaluated as ,

where u is the exact solution and is the approximate solution with the proposed scheme.

Table 1 Maximum pointwise errors ${\mathbb {E}}^{N_{y},M_t}_{\epsilon }$, uniform errors ${\mathbb {E}}^{N_{y},M_t}$ and uniform convergence rate ${\mathbb {R}}^{N_{y},M_t}$ for Example 1

Table 2 Required iteration counts to attain the convergence for Example 1

Table 3 Uniform error ${\mathbb {E}}^{N_{y},M_t}$ and uniform convergence rate ${\mathbb {R}}^{N_{y},M_t}$ for Example 1

Table 4 Maximum pointwise errors ${\mathbb {E}}^{N_{y},M_t}_{\epsilon }$, uniform errors ${\mathbb {E}}^{N_{y},M_t}$ and uniform convergence rate ${\mathbb {R}}^{N_{y},M_t}$ for Example 2

Table 5 Required iteration counts to attain the convergence rate ${\mathbb {R}}^{N_{y},M_t}$ for Example 2

Table 6 Maximum pointwise errors ${\mathbb {E}}^{N_{y},M_t}_{\epsilon }$, uniform errors ${\mathbb {E}}^{N_{y},M_t}$ and uniform convergence rate ${\mathbb {R}}_*^{N_{y},M_t}$ for Example 2

Table 7 Required iteration counts to attain the convergence rate ${\mathbb {R}}_*^{N_{y},\varDelta t}$ for Example 2

In Table 1 we present the maximum pointwise errors ${\mathbb {E}}^{N_{y},M_t}_{\epsilon }$, uniform errors ${\mathbb {E}}^{N_{y},M_t}$ and uniform convergence rate ${\mathbb {R}}^{N_{y},M_t}$ for Example 1, which verify the theoretical findings that we have proved earlier in Theorems 1 and 2. The iteration counts mentioned in Table 2 display the number of iteration needed to satisfy the stopping criterion for the algorithm. From Table 2 we can notice that only one iterate is required to stop the iterative procedure for small values of the perturbation parameters, i.e. we can get the desired approximate solution only after one iteration of the algorithm. Further, a comparison between our method and method [31] is given in Table 3. Notably, our method demonstrates lower errors than [31].

Example 2

Consider

where $g_b,~f,~g_\ell$ and $~g_r$ are calculated by the following exact solution

$u(y,t)=(1-e^{-t})\left[ \frac{e^{-y/\sqrt{\epsilon }}+e^{(y-1)/\sqrt{\epsilon }}}{1+e^{-1/\sqrt{\epsilon }}}-\cos ^2{\pi y}\right] .$

Fig. 1

Solution plot for Example 1 with $\epsilon =10^{-7}$ and $N_{y}=64,M_{t}=32$

Fig. 2

Solution plot for Example 2 with $\epsilon =10^{-7}$ and $N_{y}=64,M_{t}=32$

Fig. 3

Error plot corresponding to Example 1

Fig. 4

Error plot corresponding to Example 2

The maximum pointwise errors, uniform errors and uniform rates of convergence are also computed for this example. Table 4 displays the numerical results for Example 2, which agree with the theoretical findings established in Theorems 1 and 2. From this, we can conclude that the rate of convergence of the proposed scheme is almost two. This is evident by the fact that in this case, the space discretization errors dominate the global errors. To indicate the contribution of time discretization errors to global errors the following formula is used

$$\begin{aligned}{\mathbb {R}}_*^{N_{y},M_ t}=\log _2\left( \frac{{\mathbb {E}}^{N_{y},M_t}}{{\mathbb {E}}^{2N_{y},2M_t}}\right) . \end{aligned}$$

The results are collected in Table 6. From this data, we can observe that the rate of convergence is one. Tables 5 and 7 show how many iterations the iterative procedure requires to reach the required accuracy.

The numerical solutions and corresponding loglog plots for Examples 1 and 2 are represented in Figs. 1, 2 and 3, 4 respectively. From Figs. 1 and 2 we can clearly observe the multiscale character of the solutions near the boundary points and that the slope obtained in the error plots validates the convergence order.

6 Conclusion

We developed a rapidly converging domain decomposition algorithm for solving singularly perturbed time delayed parabolic problems with mixed type boundary conditions. The numerical algorithm is proved to be robust convergent, with an accuracy of order one in time and almost two in space. Also, we observed that the numerical results obtained by the proposed numerical algorithm corresponding to the test problems validate the theoretical findings. The data displayed in Tables 2 and 5 illustrate that a single iteration is adequate to meet the specified threshold for low magnitudes of the perturbation parameter.