Utilizing memory effects to enhance resilience in disease-driven prey-predator systems under the influence of global warming

Abstract

This research paper presents an eco-epidemiological model that investigates the intricate dynamics of a predator–prey system, considering the impact of fear-induced stress, hunting cooperation, global warming, and memory effects on species interactions. The model employs fractional-order derivatives to account for temporal dependencies and memory in ecological processes. By incorporating these factors, we aim to provide a more comprehensive understanding of the underlying mechanisms that govern the stability and behavior of ecological systems. Mathematically we investigate system’s existence, equilibria and their stability. Moreover, global stability and hopf bifurcation also analyzed in this study. Numerical simulations have been performed to validate the analytical results. We find that the coexistence equilibrium is stable under specific conditions, along with the predator equilibrium and the disease-free equilibrium. Bifurcation analyses demonstrate the intricate behavior of species densities in response to changes in model parameters. Fear and global warming are found to stabilize the system, while cooperation and additional food for predators lead to destabilization. Additionally, the influence of species memory has been explored. We observe that memory tends to stabilize the system as species memory levels increase.

1 Introduction

Prey-predator models play a crucial role in understanding the dynamics of biological populations and have garnered significant interest in mathematical biology [1]. While chaotic and limit cycle dynamics have been extensively studied in these models, discrete-time models have received relatively less attention, despite their potential to represent nonlinear and chaotic behaviors in non-overlapping organisms like annual plants or insects with single generations per year [2]. To gain a deeper understanding of predator–prey dynamics, several studies have been conducted [3, 4]. Fear’s impact on predator–prey interactions has been a significant focus in ecological and theoretical biology research. Mondal et al. investigated a predator–prey model incorporating fear and additional food, studying equilibrium points’ stability and the presence of Hopf bifurcations [5]. Pal et al. explored the effect of fear in a predator–prey model with the Beddington-DeAngelis functional response, discussing bifurcation, stability, and persistence [6]. Ghosh et al. delved into the memory’s influence using a fractional-order eco-epidemiological model that considered fear, treatment, and hunting cooperation [7]. These investigations contribute to a comprehensive understanding of the complex dynamics in predator–prey systems.

The fields of ecology and epidemiology share common ground, with disease transmission being a significant area of research since Kermac and McKendric’s seminal work on susceptible-infected frameworks [10], which describe the evolution of diseases transmitted upon contact. Subsequently, researchers such as Freedman [11], and Haque [12] have made significant contributions to this field. In 1989, Hadeler and Freedman [13] pioneered the introduction of disease into models of interacting populations. Recent studies in ecological and demographic contexts include those by Mondal et al. [14], Biswas et al. [15]. For instance, Biswas et al. [15] discovered that a longer time lag involved in fear reduces disease transmission, thereby benefiting the system’s dynamics and stability.

The global warming effect can lead to changes in the environment, such as rising temperatures, altered precipitation patterns, and shifts in habitat availability [27, 28]. These changes can directly affect the physiological and metabolic processes of predator species. For example, higher temperatures may lead to increased metabolic rates in predators, which can result in higher energy demands and potentially reduce their growth rates [29]. Moreover, global warming can also influence the availability of prey species for predators. Changes in temperature and climate can impact the distribution and abundance of prey species, affecting the food availability for predators [30]. Reduced prey availability due to global warming can lead to decreased feeding opportunities for predators, leading to slower growth rates. In summary, the global warming effect is an additional factor considered in the predator growth model. It accounts for the potential impacts of environmental changes on predator populations, including changes in metabolic rates and food availability, which can ultimately lead to reduced predator growth rates in the ecosystem [31].

Social interactions are integral to life history traits in many species [16], profoundly affecting population dynamics. Cooperation within populations is widespread and significant in ecological systems, observed in various organisms such as carnivores [18], aquatic organisms [19], and birds [20]. Studies have explored the effects of intra-species cooperation using ecological and mathematical models [21, 22]. Cooperative hunting, for example, can alter the dynamics of predator–prey models [21], leading to complex patterns with multiple periodic cycles [22]. Understanding the role of cooperation in ecological systems is crucial for comprehending population dynamics and species interactions.

In nature, many species exhibit memory, which plays a crucial role in their survival and behavior. For instance, marine organisms like Mysida and Herring display memory-based behaviors to ensure safe living and avoid predation [25, 26]. Traditional dynamical systems described by ordinary differential equations (ODE) lack memory as they represent instantaneous changes in the system. However, fractional-order differential equations (FODE) are associated with memory and are commonly found in biological systems [23, 24]. Fractional derivatives introduce non-local effects, indicating memory influence in the system. Researchers have explored the inclusion of memory in mathematical models using specific power law kernels based on fractional derivatives. Recently, there has been growing interest in studying qualitative properties and numerical solutions of fractional-order biological models due to their inherent memory and relevance in various biological systems [8, 9].

Predator–prey systems have been a subject of significant interest in ecological and mathematical modeling due to their relevance in understanding the dynamics of biological populations. Several computational and mathematical approaches have been employed to analyze and solve nonlinear predator–prey models, with a particular focus on their application in ecological systems [48,49,50,51]. In this context, we draw upon a body of prior research to contextualize our study and highlight the relevance of our work in the face of contemporary challenges such as global warming. The key works presented in [52,53,54,55,56] have contributed to the understanding and analysis of predator–prey systems, providing valuable insights into the dynamics and behavior of these ecological interactions. These studies represent a comprehensive body of work that explores various computational and mathematical techniques for understanding predator–prey dynamics. However, our research takes a unique approach by focusing on the influence of memory effects and global warming on disease-driven prey-predator systems, addressing critical ecological concerns in the contemporary world.

The novelty of the research:

• This research takes a comprehensive approach to understand the complex relationships between ecological processes and disease transmission within the context of global warming.

• The eco-epidemic model integrates various factors, including temperature changes, shifts in predator–prey interactions, and the influence of fear and cooperation-driven adaptive behaviors. This multifactorial approach provides a more realistic representation of the impacts of climate change on ecosystems.

• The research introduces pioneering elements into the eco-epidemic model, including the consideration of global warming, the dynamics of fear, and the effects of hunting cooperation. This combination of elements, specifically global warming, have not been extensively explored in previous models.

• The study investigates the influence of fractional order dynamics, allowing for the observation of species memory effects. This adds a unique and novel dimension to the analysis of eco-epidemic systems.

• Overall, this research represents a significant advancement in the field of ecological modeling by offering a fresh and comprehensive perspective on the intricate interactions between ecological processes, disease transmission, and global environmental changes.

In the following Sect. (Sect. 2), we present formulation of the ecoepidemic model proposed in this study. Section 3 introduces fundamental concepts of fractional calculus. Section 4 addresses the well-posedness and existence of the proposed model, exploring aspects such as positivity, existence, uniqueness, and boundedness of the solution. Section 5 focuses on analyzing the feasible steady states (equilibria) of the model and their stability. In the subsequent Sect. (Sect. 6), we investigate the potential presence of Hopf bifurcation within our system. We validate our analytical findings through numerical simulations and illustrate the complex dynamics of the system in Sect. 7. Finally, the paper concludes in Sect. 8, summarizing the significant outcomes and outlining future research directions.

2 Model formulation

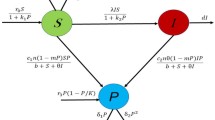
The presented eco-epidemiological model makes several key assumptions to describe the dynamics of the ecological system. In the absence of infection and predators (P), the susceptible prey (S) follows a logistic growth pattern with a growth rate $r_1$. However, the presence of predators induces fear in the prey, leading to a decrease in the prey’s birth rate due to cognitive stress. This fear-induced effect on the birth rate is modeled using the function $\frac{1}{1+k_1P}$ [22, 45], where $k_1$ represents a parameter that captures the influence of fear. This function exhibits a decreasing trend with increasing predator density. Moreover, the model also takes into account the impact of global warming on prey growth. To incorporate this effect, the modified function $\frac{1}{1+k_1P+ g_1S}$ is used, where $g_1$ represents the parameter describing the effect of global warming. Thus, the growth of susceptible prey is influenced not only by predator density but also by the warming conditions.

The death rate of susceptible prey (S) is determined by the term $d_1S$, which accounts for natural mortality in the population. Additionally, the transmission of the disease to susceptible individuals (S) occurs through direct contact with infected individuals (I), represented by the incidence of transmission term $\frac{\beta SI}{S+I}$. Here, $\beta$ represents the disease transmission rate, and transmission only occurs when there is a sufficient level of direct contact between infected and susceptible individuals. It is important to note that the limited mobility of individuals restricts the number of contacts they can make per unit time, thereby impacting disease transmission dynamics. These assumptions together form the basis of the eco-epidemiological model, capturing the intricate interplay between prey, predators, and disease transmission in the ecological system. Therefore, the first equation of the model system is given by

$$\begin{aligned} \frac{d S}{d t}=\frac{r_1 S}{1+k_1P+ g_1S}-d_1S-\alpha _1S^2-\frac{\beta SI}{S+I}. \end{aligned}$$

(1)

For predators to exist, they depend on less dynamic diseased prey as modelled in [17]. To model the interaction between an infected prey and a predator, a generalized type II interaction is used. The encounter rate of the predator population with the infected prey increases with the predator population density, captured by the encounter rate $a(P)=a+bP$, where b represents the level of predator cooperation during hunting. The death rate of infected prey (I) is $d_2$. Thus, the second equation can be written as

$$\begin{aligned} \frac{d I}{d t}=\frac{\beta SI}{S+I} -\frac{(a + b P)IP}{1+e(a + \alpha P)I}-d_2I. \end{aligned}$$

(2)

In this model, the predator is given an alternate food source represented by the biomass L. The interaction between prey and predator involving parasites is modeled by a modified Leslie-Gower type mathematical model. Further, the global warming effect is also taken into account in the predator growth model, leading to reduced predator growth. Hence, the third equation is given by

$$\begin{aligned} \frac{d P}{d t}=P\left\{ \frac{r_2 }{1+ g_2P} -\frac{P}{ e_1 I+L}\right\} . \end{aligned}$$

(3)

The system of nonlinear differential equations resulting from these assumptions is given by

$$\begin{aligned} \frac{d S}{d t}= & {} \frac{r_1 S}{1+k_1P+ g_1S}-d_1S-\alpha _1S^2-\frac{\beta SI}{S+I},\nonumber \\ \frac{d I}{d t}= & {} \frac{\beta SI}{S+I} -\frac{(a + b P)IP}{1+e(a + b P)I}-d_2I,\nonumber \\ \frac{d P}{d t}= & {} P\left( \frac{r_2 }{1+ g_2P} -\frac{P}{ e_1 I+L}\right) , \end{aligned}$$

(4)

with initial conditions

$$\begin{aligned} S(0) = S_0> 0, \ I(0) = I_0> 0, \ P(0) = P_0 > 0. \end{aligned}$$

(5)

The utilization of fractional derivatives enables remarkable methodologies for modeling dynamical systems [32]. Noninteger order derivatives and integrals provide a more intuitive and accurate representation [33]. Noninteger derivatives come in various forms, including the Riemann-Liouville based on power principles laws and the exponential form kernel. The Caputo noninteger order Fabrizio’s differentiation has also been advocated [34]. In their work, Atangana and Baleanu (AB) [35] employed a generalized Mittag-Leffler function (MLF) as the kernel, offering a noninteger differentiation without singularity. The AB noninteger-order differentiation provides an overview of memory [36], and it has been widely used to study many phenomena in nature [37].

However, the influence of a species’ life cycle memory cannot be fully captured by the integer-order scheme (4). Many anti-predator behaviors of prey are not constant over the ecological process; instead, they depend on the temporal memory of both species, and their effects should be examined accordingly. Therefore, the model system (4) has been transformed into the following fractional-order differential equation in the sense of Caputo

$$\begin{aligned} _{t_0}^C D_t^{\eta }S(t)= & {} S \left\{ \frac{r_1 }{1+k_1P+ g_1S}-d_1-\alpha _1S-\frac{\beta I}{S+I}\right\} := y_1(S, I, P),\nonumber \\ _{t_0}^C D_t^{\eta } I(t)= & {} I \left\{ \frac{\beta S}{S+I} -\frac{(a + b P)P}{1+e(a + b P)I}-d_2\right\} := y_2(S, I, P),\nonumber \\ _{t_0}^C D_t^{\eta }P(t)= & {} P\left\{ \frac{r_2 }{1+ g_2P} -\frac{P}{ e_1 I+L}\right\} := y_3(S, I, P). \end{aligned}$$

(6)

In system (6), $_{t_0}^C D_t^{\eta }$ denotes the Caputo fractional derivative of order $\eta$ with the start time $t_0 \ge 0$. This fractional derivative allows us to incorporate memory effects and non-locality into the model dynamics. The parameter $\eta$ represents the fractional order, which lies in the range $0< \eta < 1$. The start time $t_0$ indicates the initial time at which the fractional derivative is applied. Table 1 provides a detailed discussion of each parameter’s biological interpretation and significance within the context of the model.

Table 1 The parameter’s biological descriptions involved in system (6)

3 Fractional calculus foundational concepts

The concept and fundamental characteristics of the Caputo derivative, which will be utilized later in this study, have been briefly introduced in this section. The Caputo derivative is defined as follows.

Definition 1

[38] For a continuous function $y(t) \in C^n ([t_0, +\infty ), R)$, the derivative of fractional order with order $\eta > 0$ is defined as follows:

$$\begin{aligned} _{t_0}^CD_t^\eta y(t)=\frac{1}{\Gamma (n-\eta )} \int _{t_0}^{t} \frac{y^{(n)}(h)}{(t-h)^{\eta -n+1}} \,dh. \end{aligned}$$

For $0 <\eta \le 1$, the Caputo derivative can be expressed in the following form:

$$\begin{aligned} _{t_0}^CD_t^\eta y(t)=\frac{1}{\Gamma (1-\eta )} \int _{t_0}^{t} \frac{y^{'}(h)}{(t-h)^{\eta }} \,dh. \end{aligned}$$

Here, $\eta$ represents the order of the fractional derivative. The function $\Gamma (.)$ refers to the gamma function, n is a positive integer number, and the range of $\eta$ is $n-1< \eta < n$. Additionally, $t \ge t_0$.

Lemma 1

[38] Assume that $0<\eta <1$, $y(t) \in C[a,b]$ and $_{t_0}^CD_t^\eta y(t)$ is continuous in [a, b]. Then

• for any $t\in [a, b], \ y(t)$ is a non-decreasing function when $_{t_0}^CD_t^\eta y(t) \ge 0$.

• for any $t\in [a, b], \ y(t)$ is a non-increasing function when $_{t_0}^CD_t^\eta y(t) \le 0$.

Theorem 1

[39] Assume that y(t) is a continuous function that may be differentiated n-times, and that its Caputo derivative is y(t), i.e., $_{t_0}^CD_t^\eta y(t)$ is piecewise continuous on $[t_0, \infty )$ where $\eta >0$ and $n-1<\eta <n\in N$. The Caputo derivative’s Laplace transform thus becomes

$$\begin{aligned} L{_{t_0}^CD_t^\eta y(t)}=h^{\eta } F (h) - \sum _{i=0}^{n-1} h^{\eta -i-1} h^{i} (t_0), \end{aligned}$$

where $F (y) = L y (t)$. It should be emphasized that for the improper integral connected to the Laplace transformation to converge, $R (h)\ge 0$, the real part of the complex number h must be higher than or equal to zero.

Definition 2

Consider the Caputo fractional order dynamical system represented by the following equation:

$$\begin{aligned} _{t_0}^CD_t^\eta y(t)=\xi (t, y), \end{aligned}$$

where $y(t_0) > 0$. By setting $\xi (t, y) = 0$, the equilibrium points of the system can be determined. Therefore, if $\xi (t, y^*) = 0$, then $y^*$ will be an equilibrium point of the system [40].

Theorem 2

Consider the following system with fractional order

$$\begin{aligned} _{t_0}^CD_t^\eta y(t)=\xi (Y(t), Y(t_0))= \left( y_{t_0}^{(1)}, y_{t_0}^{(2)}, y_{t_0}^{(3)},\ldots , y_{t_0}^{(n)} \right) , \ y_{t_0}^{(i)}>0, \ \forall i \end{aligned}$$

(7)

with $0 < \eta \le 1$, $Y(t) =\left( y^{(1)} (t), y^{(2)} (t ),...,y^{(n)} (t )\right)$ and $\xi (Y): [t_0, \infty ) \rightarrow R^{n \times n}$. If every eigenvalue of the Jacobian matrix $J(Y)=\frac{\partial (\xi _1, \xi _2,\ldots , \xi _n)}{\partial (y_1, y_2,\ldots , y_n)}$ computed at the associated equilibrium point satisfies $| \arg (\lambda _i) | > \frac{\eta \pi }{2}$, the equilibrium points of the dynamical system (7) will be locally asymptotically stable.

4 Well-posedness

Before exploring the dynamical behavior of the proposed model system (6), it is essential to ensure that the underlying model system is physiologically well-posed. To establish this, the model system (6) must possess the following properties.

4.1 Positiveness of solutions

Theorem 3

The model system (6) has solutions starting from $(S_{t_0}, I_{t_0}, P_{t_0})$ that are all non-negative.

Proof

First of all, we assume

$$\begin{aligned} Y(t_0)=\left( S(t_0), I(t_0), P(t_0)\right) \in \Sigma ^+ :=\biggl \{ \left( S(t), I(t), P(t)\right) \in \Sigma ^+ : \ S,I,P \in R^+ \biggl \}, \end{aligned}$$

(8)

which represents the model system’s initial point of solution (6). Let’s now investigate the possibility that there is a constant $t^*$ fulfilling $t_0\le t < t^*$, such that

$$\begin{aligned} \left. \begin{array}{lll} S(t)> 0, \ t_0\le t< t^*\\ S(t^*) =0\\ S(t{^*}^{+}) <0 \end{array}\right\} . \end{aligned}$$

It is clear from the model system (6) that

$$\begin{aligned} _{t_0}^CD_t^\eta S(t)|_{S(t^*)=0}=0. \end{aligned}$$

Lemma 1 leads to the conclusion that $S(t{^*}^{+})=0$, which is the opposite of $S(t{^*}^{+})<0$. As a result, we obtain $S(t)\ge 0, \ \forall \ t\in [t_0, \infty )$. Similar to this, it is easy to demonstrate that $I(t)\ge 0$ and $P(t)\ge 0 \ \forall \ t\in [t_0, \infty )$. As a result, all the model system’s (6) solutions have non-negative outcomes. $\square$

Remarks

Positivity of solutions is a critical aspect in ecological modeling, particularly when studying predator–prey systems. In the context of our research, the positivity of solutions holds profound significance. By ensuring that population densities remain non-negative throughout the simulation of disease-driven prey-predator systems.

4.2 Boundedness of the solutions

Theorem 4

Solutions of the model system (6) starting from $(S_{t_0}, I_{t_0}, P_{t_0})$ remain constrained in the region $\Xi$.

Proof

Consider the following function:

$$\begin{aligned} M(t)=S(t)+ I(t)+ P(t). \end{aligned}$$

The derivative with Caputo sense of M(t) is as follows:

$$\begin{aligned}&_{t_0}^CD_t^\eta M(t)= \frac{r_1 S}{1+k_1P+ g_1S}-d_1S-\alpha _1S^2 -\frac{(a + b P)IP}{1+e(a + b P)I}-d_2I\\&\qquad +P\left\{ \frac{r_2 }{1+ g_2P} -\frac{P}{ e_1 I+L}\right\} \\&\quad \Rightarrow _{t_0}^CD_t^\eta M(t)+d^*M(t) \le r_1 S-\alpha _1S^2+2r_2 P \end{aligned}$$

with $d^*=\min {\{d_1, d_2, r_2\}}$. The maximum value of $r_1 S-\alpha _1S^2$ is $\frac{r_1^2}{4 \alpha _1}$ and we assume the maximum value of P is $P_m$. So,

$$\begin{aligned} _{t_0}^CD_t^\eta M(t)+ d^*M(t) \le L^*, \end{aligned}$$

(9)

where $L^*=\frac{r_1^2}{4 \alpha _1}+2r_2P_m$. Now, using Theorem 1 and the Laplace transform on both sides of inequality (9), we obtain

$$\begin{aligned}{} & {} h^{\eta }Y(h)-h^{\eta -1}M(0)+d^*Y(h)\le \frac{L^*}{s}, \ \text {where} \ Y(h)=L\{M(t)\} \end{aligned}$$

(10)

$$\begin{aligned}{} & {} \quad \Rightarrow {[h^{\eta +1}+d^*h]Y(h)\le \frac{L^*}{sh}+h^{\eta }M(0)}\end{aligned}$$

(11)

$$\begin{aligned}{} & {} \quad \Rightarrow Y(h)\le M(0)\frac{h^{\eta -1}}{h^{\eta }+d^*}+\frac{L^*}{sh(h^{\eta }+d^*)}. \end{aligned}$$

(12)

When we apply the inverse Laplace transform on both sides of (12), we get

$$\begin{aligned} M(t) \le M(0) L^{-1}\biggl \{\frac{h^{\eta -1}}{h^{\eta }+d^*}\biggl \}+L^{-1}\biggl \{\frac{L^*}{sh(h^{\eta }+d^*)}\biggl \}. \end{aligned}$$

(13)

By using Theorem (3.2) provided in [41] on the in Eq. (13), we may now obtain

$$\begin{aligned} M(t) \le M(0) E_{\eta ,1}(-d^*t^{\eta })+L^*t^{\eta } E_{\eta ,\eta +1}(-d^*t^{\eta }). \end{aligned}$$

(14)

The characteristics of the Mittag-Leffer function allow us to

$$\begin{aligned} t^{\eta } E_{\eta ,\eta +1}(-d^*t^{\eta }) =-\frac{1}{d^*} \left[ E_{\eta ,1}(-d^*t^{\eta })-1 \right] . \end{aligned}$$

(15)

As a result, inequality (14) is made to exist using the relation (15)

$$\begin{aligned} M(t) \le \Bigl \{ M(0)-\frac{L^*}{d^*} \Bigl \}E_{\eta ,1}(-d^*t^{\eta }) +\frac{L^*}{d^*}. \end{aligned}$$

Here, the term $E_{\eta ,1} \rightarrow 0$ when $t \rightarrow \infty$. $\square$

So,

$$\begin{aligned} M(t) \le \frac{L^*}{d^*}. \end{aligned}$$

As a result, all of the system’s (6) solutions stay constrained in the region

$$\begin{aligned} \Xi =\biggl \{ (S, I, P) \in \Delta ^+| \ S+I+ P \le \frac{L^*}{d^*}+\sigma , \ \text {(for any arbitrary)}\sigma > 0\biggl \}. \end{aligned}$$

Remarks

Boundedness of solutions is a pivotal aspect of our research, particularly when considering the ecological stability and sustainability of disease-driven prey-predator systems. The concept of boundedness ensures that population dynamics remain within certain limits, preventing unrealistic and ecologically implausible scenarios such as uncontrolled population growth or extinction.

4.3 Existence of the solutions and its uniqueness

Theorem 5

Consider the model system (6) starting with initial point $(S_{t_0}, I_{t_0}, P_{t_0})$, then its always admits a unique solution in the $\Xi ^+$, $\forall \ t \ge t_0$.

Proof

In the beginning, let introduce the time interval $[t_0, t^*], \ t^* < +\infty$ and $\Xi ^+=\biggl \{ (S, I, P) \in R_+^3: \ \max {\Bigl \{|S|, |I|, |P|\Bigl \}} \le {N(\text {say})} \biggl \}$. Let’s think about the map ${\hat{Y}}= \left( y_1(X), y_2(X), y_3(X) \right) ^T$ with $X=(S, I, P)$.

Now, for $X, \ {\hat{X}} \in \Xi ^+$, we have

$$\begin{aligned} || {\hat{Y}} (X) - {\hat{Y}}({\hat{X}}) || = | y_1(X) - y_1 ({\hat{X}}) | + |y_2 (X) - y_2 ({\hat{X}})|+ |y_3 (X) - y_3 ({\hat{X}})|. \end{aligned}$$

To calculate this, we divided it into three parts as follows:

$$\begin{aligned} | y_1(X) - y_1 ({\hat{X}}) |&= \bigg | \frac{r_1S }{1+k_1P+ g_1S}-d_1S-\alpha _1S^2-\frac{\beta SI}{S+I}\\&\quad - \frac{r_1 {\hat{S}} }{1+k_1{\hat{P}}+ g_1{\hat{S}}}+d_1{\hat{S}}+\alpha _1{\hat{S}}^2+\frac{\beta {\hat{S}}{\hat{I}}}{{\hat{S}}+{\hat{I}}} \bigg | \\&= \bigg |\frac{r_1(1+k_1{\hat{P}})(S-{\hat{S}})-r_1k_1{\hat{S}}(P-{\hat{P}})}{(1+k_1P+ g_1S)(1+k_1{\hat{P}}+ g_1{\hat{S}})}\\&\quad -d_1(S-{\hat{S}})-\alpha _1(S+{\hat{S}})(S-{\hat{S}})\\&\quad -\frac{\beta S {\hat{S}}(I-{\hat{I}})+\beta I{\hat{I}}(S-{\hat{S}})}{(S+I)({\hat{S}}+{\hat{I}})}\bigg | \\&\le \{r_1(1+k_1N)+d_1+2\alpha _1N+\beta N^2\}\big |S-{\hat{S}}\big |\\&\quad +r_1k_1N\big |P-{\hat{P}}\big |+\beta N^2\big |I-{\hat{I}}\big |,\\ |y_2 (X) - y_2 ({\hat{X}})|&= \bigg | \frac{\beta SI}{S+I} -\frac{(a + b P)IP}{1+e(a + b P)I}-d_2I- \frac{\beta {\hat{S}}{\hat{I}}}{{\hat{S}}+{\hat{I}}} +\frac{(a + b {\hat{P}}){\hat{I}}{\hat{P}}}{1+e(a + b {\hat{P}}){\hat{I}}}+d_2{\hat{I}}\bigg |\\&= \bigg |\frac{\beta S {\hat{S}}(I-{\hat{I}})+\beta I {\hat{I}}(S-{\hat{S}})}{(S+I)({\hat{S}}+{\hat{I}})}-d_2(I-{\hat{I}})\\&\quad -\frac{\{aI+ea^2I{\hat{I}}+b(PI+{\hat{P}}{\hat{I}})+abeI{\hat{I}}(P+{\hat{P}})+b^2eP{\hat{P}}I{\hat{I}}\}(P-{\hat{P}})+bP{\hat{P}}(I-{\hat{I}})}{\{1+e(a + b P)I\}\{1+e(a + b {\hat{P}}){\hat{I}}\}}\bigg |\\&\le \beta N^2\big |S-{\hat{S}} \big |+(\beta N^2+d_2+b N^2)\big |I-{\hat{I}} \big |\\&\quad +(aN+ea^2N^2+2bN^2+2abeN^3+b^2eN^4)\big |P-{\hat{P}}\big |,\\ |y_3 (X) - y_3 ({\hat{X}})|&= \bigg |\frac{r_2P }{1+ g_2P} -\frac{P^2}{ e_1 I+L} -\frac{r_2 {\hat{P}}}{1+ g_2{\hat{P}}} +\frac{{\hat{P}}^2}{ e_1 {\hat{I}}+L}\bigg |\\&= \bigg | \frac{r_2(P-{\hat{P}})}{(1+ g_2P)(1+ g_2{\hat{P}})}\\&\quad -\frac{\{L(P+{\hat{P}})+e_1({\hat{P}}I+P{\hat{I}})\}(P-{\hat{P}})-P{\hat{P}}(I-{\hat{I}})}{(e_1 I+L)(e_1 {\hat{I}}+L)}\bigg |\\&\le \{r_2+2N(L+e_1N)\}\big |P-{\hat{P}}|+N^2\big |I-{\hat{I}}\big |. \end{aligned}$$

So,

$$\begin{aligned} || {\hat{Y}} (X) - {\hat{Y}}({\hat{X}}) ||&\le D_1\big | S-{\hat{S}}\big |+ D_2\big | I-{\hat{I}}\big |+D_3\big | P-{\hat{P}}\big |\\&\le D|| X - {\hat{X}} ||, \end{aligned}$$

where $D=\max {\bigl \{ D_1, D_2, D_3}\bigl \}$ and $D_1=\{r_1(1+k_1N)+d_1+2\alpha _1N+2\beta N^2\}$, $D_2= (2\beta N^2+d_2+b N^2+N^2)$, $D_3=\{r_1k_1N+aN+ea^2N^2+2bN^2+2abeN^3+b^2eN^4+r_2+2N(L+e_1N)\}$. ${\hat{Y}}(X)$ therefore fulfills the local Lipschitz condition, proving the theorem. $\square$

Remarks

The existence and uniqueness of solutions lie at the heart of our research endeavor, ensuring the rigor and credibility of our investigation into disease-driven prey-predator systems. It is imperative to establish the existence of solutions to confirm that our mathematical model accurately represents the ecological phenomena under study. A unique solution signifies that our model’s predictions are consistent and that there is a single, well-defined trajectory for the evolution of populations within these ecological interactions.

5 Equilibria

We have covered the model system’s (6) steady states in this section. A model system’s steady state represents the constant solutions to the system. The model system’s biologically viable equilibrium points have been identified, and stability of the system dynamics at these points has undergone a thorough analysis.

5.1 Equilibrium points and the requirement for their existence

There are five equilibrium points in the model system (6), and they are as follows:

• 1. The trivial equilibrium point $y_0=(0, 0, 0)$, which is always present and has no parametric space restrictions.

• 2. The susceptible prey equilibrium point $y_S=(S_1, 0, 0)$, where $S_1$ is the root of the quadratic equation: $S^2+\frac{\alpha _1 +g_1 d_1}{g_1 \alpha _1}S+\frac{d_1-r_1}{g_1 \alpha _1}=0$. So, $y_S$ exists and unique when $r_1>d_1$.

• 3. The prey equilibrium point $y_{SI}=(S_2, I_2, 0)$, which can be found by solving the following system of equations

  $$\begin{aligned} \frac{r_1 }{1+ g_1S}-d_1-\alpha _1S-\frac{\beta I}{S+I}&=0,\nonumber \\ \frac{\beta S}{S+I}-d_2&=0. \end{aligned}$$

  (16)

  From second equation, we have $I_2=\frac{\beta -d_2}{d_2}S=\beta ^*S$ (where $\beta ^*=\frac{\beta -d_2}{d_2}$) with $\beta > d_2$. $S_2$ is the positive root(s) of the following quadratic equation which is obtained from first equation of (16):

  $$\begin{aligned} A_2S^2+A_1S+A_0=0, \end{aligned}$$

  where $A_2=g_1(-\beta \beta ^*+\alpha _1+\alpha _1 \beta ^*), A_1=\beta \beta ^*+d_1g_1+d_1g_1\beta ^*+\alpha _1+\alpha _1\beta ^*$ and $A_0= -r_1+d_1-(1-d_1)\beta ^*$. It’s clear that $A_1>0$, then this polynomial has a unique root iff $A_2>0$ and $A_0 < 0$. Thus, $y_{SI}$ exists under the conditions: $\beta > d_2$, $A_2>0$ and $A_0 < 0$.

• 4. The susceptible prey-predator equilibrium point $y_{SP}=(S_3, 0, P_3)$, which can be find by solving the following system of equations

  $$\begin{aligned} \frac{r_1 }{1+k_1P+ g_1S}-d_1-\alpha _1 S&=0,\nonumber \\ \frac{r_2 }{1+ g_2P} -\frac{P}{L}&=0. \end{aligned}$$

  (17)

  From second equation, we have

  $$\begin{aligned} P_3 =\frac{-1+(1+4g_2r_2L)^{1/2}}{2g_2}. \end{aligned}$$

  Substitute $P_3$ in the first equation, we obtain

  $$\begin{aligned} S_3 =\frac{-(\alpha _1+k_1 \alpha _1P_3+d_1g_1)+[(\alpha _1+k_1\alpha _1P_3+d_1g_1)^2-4g_1\alpha _1(d_1+d_1k_1P_3-r_1) ]^{1/2}}{2g_2 \alpha _1}, \end{aligned}$$

  which exists if $r_1 > d_1(1+k_1P_3)$.

• 5. The predator equilibrium point $y_P=(0, 0, P_4)$, where $P_4=\dfrac{-1+\sqrt{1+4g_2r_2L}}{2g_2}$.

• 6. The coexistence equilibrium point $y^*=(S^*, I^*, P^*)$ can be find by solving the following system:

  $$\begin{aligned} \left. \begin{array}{lll} \frac{r_1 }{1+k_1P+ g_1S}-d_1-\alpha _1S-\frac{\beta I}{S+I}&{}=&{}0,\\ \frac{\beta S}{S+I} -\frac{(a + b P)P}{1+e(a + b P)I}-d_2&{}=&{}0,\\ \frac{r_2 }{1+ g_2P} -\frac{P}{ e_1 I+L}&{}=&{}0. \end{array}\right\} \end{aligned}$$

  (18)

  From third equation: $I^*(P)=\frac{g_2P^2+P-r_2L}{r_2e_1}$, by substitute it in first and second equations, the positive intersection of the following two isoclines is represented by $(S^*, P^*)$:

  $$\begin{aligned} \left. \begin{array}{lll} h_1(S, P)=\frac{r_1 }{1+k_1P+ g_1S}-d_1-\alpha _1S-\frac{\beta I^*(P)}{S+I^*(P)}=0,\\ h_2(S, P)=\frac{\beta S}{S+I^*(P)} -\frac{(a + b P)P}{1+e(a + b P)I^*(P)}-d_2=0. \end{array}\right\} \end{aligned}$$

  (19)

  Let $P \rightarrow 0$ (The same when $S \rightarrow 0$) we have

  $$\begin{aligned} \left. \begin{array}{lll} h_1(S, 0)=\frac{r_1}{1+ g_1S}-d_1-\alpha _1S+\frac{\beta L}{e_1S-L}=0,\\ h_2(S, 0)=\frac{e_1\beta S}{e_1S-L} -d_2=0. \end{array}\right\} \end{aligned}$$

  (20)

  By forward computations, from first equation of (20), we obtain the polynomial: $T_3 S^3+T_2S^2+T_1S+T_0=0$ with $T_3=\alpha _1 g_1e_1, \ T_2=d_1g_1e_1+\alpha _1 e_1-\alpha _1 L g_1$, $T_1=-(r_1e_1+\beta Lg_1-d_1e_1+d_1Lg_1+\alpha _1 L)$ and $T_0= r_1L-\beta L-d_1L$. This polynomial has a unique root provided that $d_1g_1+\alpha _1>\alpha _1L g_1$ and $\beta +d_1>r_1$. On other hand, from the second equation of (20), we get $S=\frac{e_1(d_2-\beta )}{L d_2}$, which is positive provided that $d_2>\beta$. If the following sufficient conditions are met

  $$\begin{aligned} \alpha _1 L- d_1< \beta<r_1-d_1, \ \beta < d_2, \end{aligned}$$

  (21)

  then the interior of a positive quadrant in the $S-P$ plane defined by $(S^*, P^*)$, where the above two isoclines have their unique intersection point provided that the following conditions are satisfied

  $$\begin{aligned} \frac{d P}{d S}= - \frac{\partial h_1(S,P)/\partial S }{\partial h_1(S,P)/\partial P} <0, \end{aligned}$$

  (22)
  $$\begin{aligned} \frac{d P}{d S}= - \frac{\partial h_2(S,P)/\partial S }{\partial h_2(S,P)/\partial P}>0. \end{aligned}$$

  (23)

  These necessary conditions ensure that the system (6) has a coexistence equilibrium point.

5.2 Local stability

The behavior of the system’s solutions under a small perturbation in the area surrounding each equilibrium point is referred to as local stability of the model system (6) around each equilibrium point. We looked into the model system’s stability analysis around each equilibrium point. In order to do this, let’s first calculate the Jacobian matrix J(S, I, P) of the model system (6), which is given by

$$\begin{aligned} J(S, I, P)= \left[ j_{iq} \right] _{3 \times 3} = \begin{pmatrix} \frac{\partial y_1(S, I, P)}{\partial S} &{} \frac{\partial y_1(S, I, P)}{\partial I} &{} \frac{\partial y_1(S, I, P)}{\partial P}\\ \frac{\partial y_2(S, I, P)}{\partial S} &{} \frac{\partial y_2(S, I, P)}{\partial I} &{} \frac{\partial y_2(S, I, P)}{\partial P}\\ \frac{\partial y_3(S, I, P)}{\partial S} &{} \frac{\partial y_3(S, I, P)}{\partial I} &{} \frac{\partial y_3(S, I, P)}{\partial P} \end{pmatrix}, \end{aligned}$$

(24)

where $j_{11}=\frac{\partial y_1(S, I, P)}{\partial S}=\frac{r_1 (1+k_1P)}{(1+k_1P+ g_1S)^2}-d_1-2 \alpha _1S-\frac{\beta I^2}{(S+I)^2}$, $j_{12}=\frac{\partial y_1(S, I, P)}{\partial I}= -\frac{\beta S^2}{(S+I)^2}$, $j_{13}=\frac{\partial y_1(S, I, P)}{\partial P}= -\frac{r_1 k_1 S}{(1+k_1P+ g_1S)^2}$, $j_{21}=\frac{\partial y_2(S, I, P)}{\partial S}= \frac{\beta I^2}{(S+I)^2}$, $j_{22}=\frac{\partial y_2(S, I, P)}{\partial I}= \frac{\beta S^2}{(S+I)^2}- \frac{(a + b P)P}{(1+e(a + b P)I)^2}-d_2$, $j_{23}=\frac{\partial y_2(S, I, P)}{\partial P}= -\frac{\left[ (a+2bP)(1+eaI)+eb^2IP^2\right] I}{(1+e(a + b P)I)^2}$, $j_{31}=\frac{\partial y_3(S, I, P)}{\partial S}=0$, $j_{32}=\frac{\partial y_3(S, I, P)}{\partial I}= \frac{e_1 P^2}{ (e_1 I+L)^2}$, $j_{33}=\frac{\partial y_3(S, I, P)}{\partial P}=\frac{r_2 }{(1+ g_2P)^2}-\frac{2P}{ e_1 I+L}$.

Let’s now present, one by one, the dynamical behavior of the model system around each steady state in the subsequent theorems.

Theorem 6

The zero equilibrium point $y_0(0, 0, 0)$ of system (6) is always unstable.

Proof

The eigenvalues of the jacobian matrix (24) around zero equilibrium point $y_0(0, 0, 0)$ are $\lambda _1=r_1-d_1$, $\lambda _2=-d_2$ and $\lambda _3=r_2$. Due to positive sign of the third eigenvalue $\lambda _3=r_2$, $|arg(\lambda _3)|=0< \frac{\eta \pi }{2}$. Hence the zero equilibrium point $y_0(0, 0, 0)$ is saddle point. This implies that, in light of Theorem 2, the equilibrium point $y_0(0, 0, 0)$ is unstable. Hence, the proof is now complete. $\square$

Theorem 7

The behaviour of the model system (6) around the susceptible prey equilibrium point $y_S = (S_1, 0, 0)$ is always unstable.

Proof

The eigenvalues of jacobian matrix (24) around the susceptible prey equilibrium point $y_S = (S_1, 0, 0)$ are $\lambda _1=\frac{r_1}{(1+g_1s_1)^2}-d_1-2\alpha S_1$, $\lambda _2=\beta -d_2$ and $\lambda _3=r_2$. Due to positive sign of third eigenvalue $\lambda _3=r_2$, $|arg(\lambda _3)|=0< \frac{\eta \pi }{2}$. Thus, the susceptible prey equilibrium point $y_S = (S_1, 0, 0)$ is saddle point. This implies that, in light of Theorem 2, the equilibrium point $y_S = (S_1, 0, 0)$ is unstable. The theorem’s proof is now complete. $\square$

Theorem 8

The prey equilibrium point $y_{SI} = (S_2, I_2, 0)$ is always unstable.

Proof

The characteristic equation of jacobian matrix (24) around the prey equilibrium point $y_{SI} = (S_2, I_2, 0)$ is

$$\begin{aligned} (r_2-\lambda ) \Bigl ( \bigl ( j_{11}(S_2, I_2, 0)-\lambda \bigl ) \bigl ( j_{22}(S_2, I_2, 0)-\lambda \bigl )+j_{12} (S_2, I_2, 0)j_{21} (S_2, I_2, 0) \Bigl )=0. \end{aligned}$$

Notice that the sign of first eigenvalue, $\lambda _1=r_2$, is positive. Therefore, $|arg(\lambda _1)|=0< \frac{\eta \pi }{2}$ and hence the prey equilibrium point $y_{SI} = (S_2, I_2, 0)$ is saddle point. Consequently, in light of Theorem 2, the equilibrium point $y_{SI} = (S_2, I_2, 0)$ is unstable. The theorem’s proof is now complete. $\square$

Theorem 9

The susceptible prey-predator equilibrium point $y_{SP} = (S_3,0, P_3)$ is locally asymptotically stable if the following conditions are satisfied

$$\begin{aligned} d_1+2\alpha _1S_3>\frac{r_1(1+k_1P_3))}{(1+k_1P_3+g_1S_3)^2}, \ (a+bP_3)P_3+ d_2>\beta , \ 2\frac{P_3}{L} >\frac{r_2}{(1+g_2P_3)^2}.\nonumber \\ \end{aligned}$$

(25)

Proof

The eigenvalues associated with (24) around the susceptible prey-predator equilibrium point $y_{SP} = (S_3, 0, P_3)$ are $\lambda _1=\frac{r_1(1+k_1P_3))}{(1+k_1P_3+g_1S_3)^2}-d_1-2\alpha _1S_3$, $\lambda _2=\beta -(a+bP_3)P_3-d_2$ and $\lambda _3=\frac{r_2}{(1+g_2P_3)^2}-2\frac{P_3}{L}$. To ensure the local stability of the susceptible prey-predator equilibrium point $y_{SP} = (S_3, 0, P_3)$, conditions given in (25) must hold. If these conditions are satisfied, then the condition $|arg(\lambda _i)|=\pi > \frac{\eta \pi }{2}, \ i=1,2,3$ is also met, and thus the local stability of the susceptible prey-predator equilibrium point $y_{SP} = (S_3, 0, P_3)$ is confirmed. $\square$

Theorem 10

The behaviour of the model system (6) around the predator equilibrium point $y_P = (0, 0, P_4)$ is locally asymptotically stable if the following conditions are satisfied

$$\begin{aligned} \frac{r_1(1+k_1P_4)}{(1+k_1P_4)^2}<d_1, \ \frac{r_2 }{(1+ g_2P_4)^2}<\frac{2P_4}{L}. \end{aligned}$$

(26)

Proof

The eigenvalues of jacobian matrix (24) around the predator equilibrium point $y_P = (0, 0, P_4)$ are $\lambda _1=\frac{r_1 (1+k_1P_4)}{(1+k_1P_4)^2}-d_1$, $\lambda _2=- (a+bP_4)P_4-d_2$ and $\lambda _3=\frac{r_2 }{(1+ g_2P_4)^2}-\frac{2P_4}{L}$. If conditions given in (26) hold, $|arg(\lambda _i)|=\pi > \frac{\eta \pi }{2}, \ i=1,2,3$ is also met, and thus the local stability of the predator equilibrium point $y_{P} = (0, 0, P_4)$ is validated. $\square$

In order to discuss the local stability of the coexistence equilibrium point, we need to refer to the reference [42] for “Definition (1)” and “Proposition (1).” These definition and proposition likely contain the necessary mathematical framework and conditions to analyze the stability of the coexistence equilibrium point in the context of the model under consideration.

Theorem 11

The coexistence equilibrium point $y^{*} = (S^{*}, I^{*}, P^{*})$ if exists, is locally asymptotically stable if any one of the following circumstances occurs:

• If $Q(f)> 0, \ A^*> 0, \ C^* > 0$ and $A^{*} B^{*}- C^{*} > 0$, for $0< \eta < 1$.

• If $Q(f)< 0, \ A^* \ge 0, \ B^* \ge 0$ and $C^* > 0$, for $0< \eta < 2/3$.

• If $Q(f)< 0, \ A^*> 0, \ B^* > 0$ and $A^* B^*=C^*$, for $0< \eta < 1$.

All symbols used here are well-defined in the proof.

Proof

The jacobian matrix around the coexistence equilibrium point $y^{*} = (S^{*}, I^{*}, P^{*})$ is

$$\begin{aligned} J(S^{*}, I^{*}, P^{*})=[j_{iq}^*]_{3 \times 3}, \end{aligned}$$

(27)

and the characteristic equation of it will be

$$\begin{aligned} f(\lambda )= \lambda ^3+A^* \lambda ^2+ B^*\lambda + C^*=0, \end{aligned}$$

(28)

where

$$\begin{aligned} A^*&= -(j_{11}^*+j_{22}^*+j_{33}^*),\\ {B^*}&= {j_{11}^*j_{22}^*+j_{11}^*j_{33}^*+j_{22}^*j_{33}^*-j_{12}^*j_{21}^*-j_{23}^*j_{32}^*,}\\ {C^*}&={ j_{12}^*j_{21}^*j_{33}^* + j_{11}^*j_{23}^*j_{32}^* - j_{13}^*j_{21}^*j_{32}^* - j_{11}^*j_{22}^*j_{33}^*.} \end{aligned}$$

Consequently, the discriminant associated with the cubic polynomial $f(\lambda )$ is

$$\begin{aligned} Q(f)= 18 A^* B^* C^*+ (A^* B^*)^2-4(A^*)^3 C^*-4 (B^*)^3-27(C^*)^2. \end{aligned}$$

(29)

$\square$

Remarks

Analyzing the local stability of the equilibria is essential for understanding the dynamics and behavior of these complex ecological interactions. The trivial equilibrium, where all populations are at zero, is always a saddle point. It signifies a state of instability and dynamic interactions within the ecosystem. An unstable equilibrium point where only susceptible prey is present, with neither infected prey nor predators, has specific ecological implications. In practical terms, the instability of this equilibrium point highlights the ecological importance of predators in regulating prey populations and maintaining the balance within ecosystems. An unstable equilibrium point with both susceptible and infected prey but without predators ecologically indicates a situation where disease transmission within the prey population is not effectively controlled. This situation can lead to concerns about disease outbreaks, population declines, and potential disruptions within the ecosystem. A conditionally stable equilibrium point where susceptible prey and predator populations coexist while the infected prey population is absent ecologically signifies a balanced and sustainable state. It highlights the role of predators and other ecological factors in controlling disease spread and maintaining ecological stability within the system. A conditionally stable equilibrium where only the predator population exists, with no prey population, carries specific ecological implications. It represents an imbalanced state within the ecosystem and signifies the potential vulnerability of the predator population to food scarcity. A conditionally stable coexistence equilibrium where all susceptible prey, infected prey, and predators are present holds several ecological significance. Ecologically, this equilibrium suggests that there is a balanced coexistence of susceptible prey, infected prey, and predators. The presence of infected prey indicates that the disease is not driving the prey population to extinction but is being regulated by predators. This equilibrium showcases the ability of predators to control disease transmission within the prey population, preventing disease outbreaks.

6 Hopf-bifurcation

In this section, we go over the system’s Hopf bifurcation analysis. We now take into account the following fractional-order system:

$$\begin{aligned} _{t_0}^C D_t^{\eta }Y(t)=y(\beta , S, I, P), \end{aligned}$$

(30)

where $y^*$ is the system’s equilibrium point, and where $0< \eta <1, y \in R^3$. As a bifurcation parameter, we select $\beta$. Keeping in mind that the characteristic equation of $J(S^*, I^*, P^*)$ is

$$\begin{aligned} \lambda ^3+A^* \lambda ^2+ B^*\lambda + C^*=0. \end{aligned}$$

(31)

Where $A^*, B^*$ and $C^*$ are given in (29). Then, according to Ghosh et al. [47], if the conditions listed below are met, system (6) experiences a Hopf bifurcation around $y^*$ when $\beta$ crosses a critical value $\beta ^*$.

• 1. $A^*(\beta ^*), B^*(\beta ^*)$ and $C^*(\beta ^*)$ are greater than zero.

• 2. $A^*(\beta ^*) B^*(\beta ^*)- C^*(\beta ^*)=0$.

• 3. $Re(\frac{d \lambda _i}{d \beta })_{\beta =\beta ^*} \ne 0$.

Then there are three eigenvalues admits the characteristic equation of Jacobian matrix of system (6) at $y^*$, two of them are complex-conjugated eigenvalues such as $\lambda _{1,2}=\phi _{1,2} (\beta ) \pm i \rho (\beta )$ and third eigenvalue is $\lambda _3=-\phi$. The system may experience a Hopf-bifurcation with respect to this parameter because it is now known that the fractional-order derivative $\eta$ plays a significant role in regulating the stability of the system dynamics with respect to $\eta$, we now define a function by

$$\begin{aligned} \Gamma (\eta )=\frac{\eta \pi }{2}-\min _{1\le \eta \le 2}|arg(\lambda _{i})|. \end{aligned}$$

As the derivative order crosses a critical value, we now present the prerequisites for the occurrence of a Hopf bifurcation at the endemic equilibrium point.

Remarks

The existence of Hopf bifurcation in ecological modeling has specific ecological implications. Generally, Hopf bifurcation in ecological systems indicates a transition from a stable equilibrium to a periodic or oscillatory behavior. These oscillations may have implications for ecosystem resilience, predator–prey interactions, and the response of the ecosystem to changing environmental conditions. Understanding the ecological significance of Hopf bifurcation is essential for making informed decisions about conservation and management strategies in real-world ecosystems.

7 Numerical simulation

In our numerical simulations, we adopted a set of hypothetical parameter values as follows:

$$\begin{aligned}{} & {} r_1=1.1, \ k_1= 0.95, \ g_1=0.7, \ d_1= 0.01, \ \alpha _1= 0.002, \ \beta =0.52, \ a=0.9,\nonumber \\{} & {} b=0.85, \ e=0.25, \ d_2=0.02, \ r_2=0.18, \ g_2=0.2, \ L=0.7, \ e_1=0.65. \end{aligned}$$

(32)

It’s important to note that these values were not derived from any experimental real-world data. While these parameter values were informed by references in existing literature [17, 45, 46], they are not meant to represent a specific real-world example. Rather, they were selected to illustrate and test the principles and concepts presented in the theoretical framework.

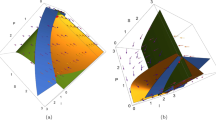
From analytical calculation, it is hard to say the existence of coexistence equilibrium $y^*$. As a result, we numerically verify the existence of coexistence equilibrium first. To do this, we plot system of Eq. (18) in $S-I-P$ space as illustrated in Fig. 1. It is clear in figure that three planes intersect at pink color at positive octant, which is the coexistence equilibrium $y^*$.

Fig. 1

Coexistence equilibrium $y^*$. Parameters values are specified in (32) except $r_1=0.7$

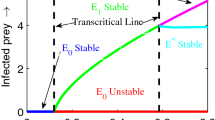
To verify analytical conditions numerically, we first check local stability of system’s different steady states. Analytically we find that the equilibria $y_0$, $y_S$ and $y_{SI}$ are always unstable. As a result numerically also we did not get stability of these equilibria. On the other hand, $y_P$, $y_{SP}$ and $y^*$ are stable under specific conditions. Numerically, we also verify stability of these equilibria, Fig. 2. It is clear from Fig. 2a that $y^*$ is stable and the parameter used in this figure satisfies stability condition of $y^*$. Similarly, $y_P$ is stable in Fig. 2b and $y_{SP}$ is stable in Fig. 2c, the parameter used in these figures satisfy respective conditions of stability of these equilibria. Ecologically, stability of equilibria refers to the capacity of an ecosystem or population to maintain a relatively constant or balanced state over time. This concept is crucial in ecology because it helps us understand how ecosystems and populations respond to changes in their environment and whether they are resilient to disruptions.

Fig. 2

Stability of different steady states through time series solutions. a Coexistence equilibrium $y^*$ stable; b predator equilibrium $y_P$ stable; c susceptible prey-predator equilibrium $y_{SP}$ stable. Parameters values are specified in (32) except the parameters mentioned in the respective figures

Next, we verify global stability of coexistence equilibrium $y^*$ and disease-free equilibrium $y_{SP}$. Analytically, we have seen that $y^*$ is globally asymptotically stable. Numerically, in Fig. 3a, we observe that whatever be the initial conditions solution trajectories converge to $y^*$ implying global stability of $y^*$. Similarly, in Fig. 3b, we have seen that all the solution trajectories initiating from different positions ultimately converge to the equilibrium $y_{SP}$. Thus, $y_{SP}$ is also globally asymptotically stable. A globally stable equilibrium point serves as an ecological "attractor." This means that, regardless of how far the ecosystem or population deviates from this equilibrium due to disturbances or fluctuations, it will eventually return to this stable state. This property reflects the system’s resilience, its ability to absorb shocks, and its capacity to maintain ecological balance over time.

Fig. 3

Global stability of a endemic equilibrium $y^*$ and b disease-free equilibrium $y_{SP}$. Parameters values are specified in (32) except the parameters mentioned in the respective figures

In Figs. 4 and 5, we plot bifurcation diagrams. In these figures, species maximum and minimum densities are plotted varying a model parameter. Blue dots represent system’s stable behaviour whereas red curves illustrate system’s unstable behavior (in this case species density fluctuate within an interval). It is apparent from Fig. 4a that species densities stabilized from fluctuation due to increased fear of predator. Similar effect can be observed due to the effect of global warming as shown in Fig. 4b. However, infection rate can destabilize as well as stabilize the system as illustrated in Fig. 4c. That is species densities remain fixed for higher and lower values of it whereas they fluctuate for moderate values. Hunting cooperation destabilize the system, i.e, for lower level of cooperation system is in stable mode whereas system oscillates around the coexistence equilibrium for higher level of cooperation, Fig. 5a. Moreover, species densities increase as cooperation levels enhance. Further, the effect of global warming act upon predator growth stabilize the destabilized system (see Fig. 5b). Similar as cooperation additional food for predator destabilized the system as shown in Fig. 5c. From this bifurcation analysis we conclude that cooperation and additional food destabilize the system whereas global warming and fear stabilize the system. Thus, each of these phenomena are well connected for species stable behavior. Understanding Hopf bifurcation is crucial for assessing the resilience and stability of ecosystems. This may manifest as population cycles, where predator and prey populations, for example, exhibit regular fluctuations.

Fig. 4

One parameter bifurcation diagram with respect to the important model parameters. Parameters values are specified in (32)

Fig. 5

One parameter bifurcation diagram with respect to the important model parameters. Parameters values are specified in (32) except $r_1=0.9$

Next, we observe the effect of memory on system’s dynamics by plotting bifurcation diagrams as depicted in Fig. 6(a,b,c). In each row, we plot only predator population by varying model parameters for different memory levels. Other species exhibit same behavior so do no plot all species because it is meaningless. We notice in each row that as species memory level increases, i.e., the value of memory parameter $\eta$ decreases, length of stable branch increases and unstable branch decreases. Thus, one can conclude that species memory has tendency to stabilize an unstable system. Moreover, in Fig. 7, we plot above bifurcations in 3d plane by incorporating memory parameter to see the effect of memory on continuous change of it. From these figures, we observe that how length of unstable branch decrease on increasing species memory level, i.e., decreasing the value of memory parameter $\eta$. Ultimately, higher memory stabilizes the system by eliminating limit cycles (i.e., population oscillations). Memory effect in ecology emphasizes the enduring impact of past events and interactions on the current and future state of ecosystems. It underscores the complexity of ecological systems and their capacity to adapt and maintain stability over time.

Fig. 6

One parameter bifurcation diagrams for different values memory parameter $\eta$. Parameters values are specified in (32) except in b $r_1=0.9$

Fig. 7

Bifurcation diagrams with respect to a model parameter with memory parameter. Parameters are same as in (32)

8 Conclusion

The eco-epidemiological model under examination delves into the dynamics of a predator–prey system influenced by various factors, including stress induced by fear, the impact of global warming, and the transmission of diseases. It also considers the cooperation or coordination among individual predators during their hunting activities. Fractional-order derivatives are integrated into the model to account for memory-related effects within the system. Through a combination of analytical and numerical simulations, several crucial insights have emerged. The system exhibits multiple equilibria, including coexistence equilibrium ($y^*$), predator equilibrium ($y_P$), and disease-free equilibrium ($y_{SP}$), each of which demonstrates stability under certain conditions. On the other hand, other equilibria ($y_0$, $y_S$, and $y_{SI}$) are found to be unstable. Both the coexistence equilibrium ($y^*$) and the disease-free equilibrium ($y_{SP}$) are globally asymptotically stable, signifying that the system tends to converge towards these equilibria, regardless of its initial conditions. Bifurcation diagrams provide insights into how changes in model parameters affect the densities of species. Specifically, factors like fear and global warming tend to stabilize the system, while cooperation and an increase in food resources have a destabilizing influence. Consequently, the impact of global warming in warmer environments enhances stability, aligning with prior research findings (Sohlstrom et al., [29]). The infection rate can either promote stability or induce instability, depending on its value. Additionally, the memory parameter $\eta$ plays a pivotal role in system stability. As species’ memory levels increase (i.e., as $\eta$ decreases), unstable branches in the bifurcation diagrams shorten, indicating that memory tends to stabilize the system. This observation consistently supports prior research findings [7, 44, 47], highlighting the influence of memory on system stability and resilience of ecosystems.

In summary, this research sheds light on the intricate interplay of fear, global warming, cooperation, and memory in shaping the stability and dynamics of the eco-epidemiological system. The adoption of a fractional-order approach allows for a more precise representation of real-world ecological processes characterized by temporal dependencies and memory effects. These findings enhance our comprehension of complex ecological interactions and can provide valuable insights for designing effective management and conservation strategies in ecosystems affected by fear, cooperation, disease, and environmental changes.

Some potential future directions for our research:

• Spatial Considerations: Extend our model to incorporate spatial dynamics. Ecological systems often have spatial components, and incorporating spatial considerations can lead to a more realistic understanding of how populations and epidemics spread.

• Climate Scenarios: Explore different climate change scenarios to understand how variations in temperature and precipitation patterns may impact the ecoepidemic dynamics. This could involve incorporating stochasticity into our model.

• Multispecies Interactions: Consider expanding our model to include interactions with multiple species. Ecological systems are often characterized by complex interactions between multiple species, and understanding these interactions can provide a more comprehensive view of ecosystem dynamics.