Skip to main content
SpringerLink
Log in

Scenario decomposable subgradient projection method for two-stage stochastic programming with convex risk measures

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

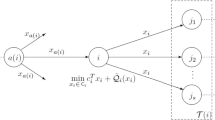
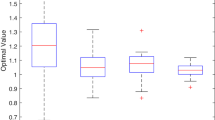
We consider the general two-stage convex stochastic programs with discrete distribution, in which the risk measure is only assumed to be convex and monotonic, not necessarily to be coherent or have special structures. We propose a scenario decomposition framework which incorporates subgradient computation and the incremental constraint projection steps. The decomposition of the algorithm is based on the scenario-wise separability of these computations. We analyze the convergence and local rate of convergence of the proposed method under mild conditions. This method is further applied to a class of distributionally robust two-stage stochastic programs. Numerical results of a practical multi-product assembly model are reported to demonstrate the effectiveness of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Ruszczyńki, A.: Decomposition methods. In: Shapiro, A., Ruszczyńki, A. (eds.) Stochastic Programming, vol 10 of Handbooks in Operations Research and Management Science, pp. 141–211. Elsevier, Heidelberg (2003)

    Google Scholar 

  2. Pereira, M.V.F., Pinto, L.M.: Multi-stage stochastic optimization applied to energy planning. Math. Program. 52, 359–375 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  3. Philpott, A.B., Guan, Z.: On the convergence of stochastic dual dynamic programming and related methods. Oper. Res. Lett. 36(4), 450–455 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  4. Kelley, J.E., Jr.: The cutting-plane method for solving convex programs. J. Soc. Ind. Appl. Math. 8(4), 703–712 (1960)

    Article  MathSciNet  MATH  Google Scholar 

  5. Shapiro, A.: Topics in Stochastic Programming. CORE Lecture Series. Universite Catholique de Louvain, Louvain-la-Neuve (2011)

    Google Scholar 

  6. Rockafellar, R.T., Wets, R.J.B.: Scenario and policy aggregation in optimization under uncertainty. Math. Op. Res. 16, 119–147 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  7. Rockafellar, R.T., Sun, J.: Solving monotone stochastic variational inequalities and complementarity problems by progressive hedging. Math. Program. 174(1), 453–471 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  8. Zhang, M., Sun, J., Xu, H.: Two-stage quadratic games under uncertainty and their solution by progressive hedging algorithms. SIAM J. Optim. 29(3), 1799–1818 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  9. Artzner, P., Delbaen, F., Eber, J.M., Heath, D.: Coherent measures of risk. Math. Financ. 9(3), 203–228 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  10. Föllmer, H., Schied, A.: Stochastic Finance: An Introduction in Discrete Time. Walter de Gruyter, Berlin (2004)

    Book  MATH  Google Scholar 

  11. Ang, M., Sun, J., Yao, Q.: On the dual representation of coherent risk measures. Ann. Op. Res. 262(1), 29–46 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  12. Philpott, A., de Matos, V.: Dynamic sampling algorithms for multi-stage stochastic programs with risk aversion. Eur. J. Op. Res. 218(2), 470–483 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  13. Sun, J., Liao, L., Rodrigues, B.: Quadratic two-stage stochastic optimization with coherent measures of risk. Math. Program. 168, 599–613 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  14. Philpott, A., de Matos, V., Finardi, E.: On solving multistage stochastic programs with coherent risk measures. Op. Res. 61(4), 957–970 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  15. Guigues, V., Rmisch, W.: Sampling-based decomposition methods for multistage stochastic programs based on extended polyhedral risk measures. SIAM J. Optim. 22(2), 286–312 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  16. Rockafellar, R.T.: Solving stochastic programming problems with risk measures by progressive hedging. Set-Valued Var. Anal. 26(4), 759–768 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  17. Sun, J., Yang, X., Yao, Q., Zhang, M.: Risk minimization, regret minimization and progressive hedging algorithms. Math. Program. 181, 509–530 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  18. Collado, R.A., Papp, D., Ruszczyński, A.: Scenario decomposition of risk-averse multistage stochastic programming problems. Ann. Op. Res. 200(1), 147–170 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  19. Bauschke, H.H. (1996): Projection algorithms and monotone operators [PhD thesis] Canada. Simon Fraser University. Burnaby

  20. Wang, M., Bertsekas, D.P.: Incremental constraint projection methods for variational inequalities. Math. Program. 150(2), 321–363 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  21. Xia, F.Q., Ansari, Q.H., Yao, J.C.: A new incremental constraint projection method for solving monotone variational inequalities. Optim. Methods Softw. 32(3), 470–502 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  22. Iusem, A.N., Jofré, A., Thompson, P.: Incremental constraint projection methods for monotone stochastic variational inequalities. Math. Op. Res. 44(1), 236–263 (2019)

    MathSciNet  MATH  Google Scholar 

  23. Wang, M., Bertsekas, D.P.: Incremental constraint projection-proximal methods for non-smooth convex optimization. Cambridge (MA): Massachusetts Institute of Technology, Lab for Information and Decision Systems Report LIDS-P-2907. (2013)

  24. Shapiro, A., Dentcheva, D., Ruszczyńki, A.: Lectures on Stochastic Programming: Modeling and Theory. SIAM, Philadelphia (2009)

    Book  Google Scholar 

  25. Bertsekas, D.P.: Convex Optimization Algorithms. Athena Scientific, Belmont (2015)

    MATH  Google Scholar 

  26. Deutsch, F., Hundal, H.: The rate of convergence for the cyclic projections algorithm iii: regularity of convex sets. J. Approx. Theory 155, 155–184 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  27. Robbins, H., Siegmund, D.: A convergence theorem for nonnegative almost supermartingales and some applications. In: Rustagi, J.S. (ed.) Optimizing Methods in Statistics, pp. 233–257. Academic Press, New York (1971)

    Google Scholar 

  28. Nedić, A., Bertsekas, D.P.: Convergence rate of the incremental subgradient algorithm. In: Uryasev, S., Pardalos, P.M. (eds.) Stochastic Optimization: Algorithms and Applications, pp. 263–304. Springer, Dordrecht (2000)

    Google Scholar 

  29. Bertsekas, D.P.: Constrained Optimization and Lagrange Multiplier Methods. Academic Press, New York (2014)

    MATH  Google Scholar 

  30. Jiang, R., Guan, Y.: Risk-averse two-stage stochastic program with distributional ambiguity. Op. Res. 66(5), 1390–1405 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  31. Hanasusanto, G.A., Kuhn, D.: Conic programming reformulations of two-stage distributionally robust linear programs over wasserstein balls. Op. Res. 66(3), 849–869 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  32. Chen, Y., Sun, H., Xu, H.: Decomposition and discrete approximation methods for solving two-stage distributionally robust optimization problems. Comput. Optim. Appl. 78(1), 205–238 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  33. Ben-Tal, A., Teboulle, M.: Penalty functions and duality in stochastic programming via \(\phi \)-divergence functionals. Math. Op. Res. 12(2), 224–240 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  34. Bayraksan, G., Love, D.K.: Data-driven stochastic programming using phi-divergences. In: Aleman, M., Aurélie, C., Thiele (eds.) Tutorials in Operations Research, INFORMS Catonsville (2015)

  35. Higle, J.L., Sen, S.: Stochastic Decomposition: A Statistical Method for Large Scale Stochastic Linear Programming. Springer, Dordrecht (2013)

    MATH  Google Scholar 

  36. Bareilles, G., Laguel, Y., Grishchenko, D., Iutzeler, F., Malick, J.: Randomized progressive hedging methods for multi-stage stochastic programming. Ann. Op. Res. 295(2), 535–560 (2020)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Statistics and Mathematics, Shanghai Lixin University of Accounting and Finance, Shanghai, China

    Haodong Yu

Authors
  1. Haodong Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Haodong Yu.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yu, H. Scenario decomposable subgradient projection method for two-stage stochastic programming with convex risk measures. J. Appl. Math. Comput. 69, 2389–2419 (2023). https://doi.org/10.1007/s12190-023-01840-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-023-01840-4

Keywords

Search

Navigation