1 Introduction

As is known to all, the catastrophic influences of infectious diseases on the development of the world cannot be ignored, and the struggle between human beings and infectious diseases has never stopped. Since Kermack and McKendrick [1] pioneered the SIR (susceptible-infected-removed) epidemic compartmental model, various mathematical models have been widely established, and quite a few scholars have achieved many good results which are useful for the control and prevention of the spread of the epidemic [2,3,4,5,6,7,8,9,10,11]. It is worth noting that many diseases, such as mumps, HIV etc., have a latent period, which is the period of time between the exposure to a disease-causing agent and the onset of disease the agent causes. It is reasonable to consider the SEIR model, which introduces the latent period by using a compartmental approach. There are intensive literatures about kinds of SEIR models with the efforts of many researchers [2, 6, 9]. Generally speaking, classic SEIR models assume that the latent individuals are not contagious, and the susceptible individuals may become contagious only through contact with the infective individuals. However, this assumption is quite different from features of some transmitted diseases (such as SARS [12] and COVID-19 [13]) with infectivity in the latent period. This fact has been concerned by some scholars and SEIR models with infectivity in the latent period have also been considered, see [12, 14, 15].

The COVID-19, which is a highly contagious and lethal respiratory virus with a similar incubation time and generation time as SARS coronavirus (see [16]), has spread throughout almost every nation on our planet to become a pandemic since 2019. The time between infections and developing the symptoms is within 2–14 days, and the infected person’s latent period is infectious. To date, COVID-19 has ravaged more than two hundred countries around the world and has caused enormous economic and human losses. The worst scenario is that there was no specific treatment or vaccine available to prevent at the early stages of the outbreak. For this reason, we have to rely on traditional public health measures to respond to the outbreak, such as isolation, quarantine, social distance and community containment [16,17,18]. Many of these were implemented successfully as effective measures during SARS in 2003, providing impetus to continue such stringent measures for COVID-19. China drew useful lessons learnt from SARS outbreak almost 20 years ago and issued unprecedented gigantic interventions to prevent the propagation of COVID-19, including household quarantine, wearing masks, lockdown and strict constant tracing [19,20,21,22,23,24]. In a recent investigation, an SEIR epidemic model of deterministic differential equations

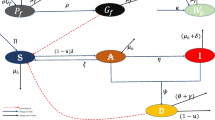
$$\begin{aligned} \left\{ \begin{array}{lll} {\dot{S}}(t)=\Lambda -\beta (1-\eta _1)S(t)[I(t)+\eta _2E(t)]-\mu S(t),\\ {\dot{E}}(t)=\beta (1-\eta _1)S(t)[I(t)+\eta _2E(t)]-(\delta +\mu )E(t),\\ {\dot{I}}(t)=\delta E(t)-(\theta +\alpha +\mu )I(t),\\ {\dot{R}}(t)=(\theta +\eta _{3}\alpha )I(t)-\mu R(t) \end{array} \right. \end{aligned}$$
(1.1)

has been used by Jiao et al. [25] to model the spread of the epidemic with infectivity in the latent period and household quarantine on the susceptible by focusing on the transmitting features of COVID-19, where \(\Lambda >0\) represents the recruitment rate; \(\beta >0\) is the infective rate from S to E; \(\eta _1(0<\eta _1<1)\) stands for the household quarantine rate of the susceptible; \(\eta _2(0<\eta _2<1)\) is the rate at which the exposed individuals become infectious in the latent period; \(\delta >0\) stands for the transition rate of becoming infectious after a latent period (\(\delta >\eta _2(\theta +\alpha +\mu )\)); \(\mu >0\) is the natural death rate; the hospitalized rate of I is given by \(\alpha >0\); \(\theta >0\) can be regarded as the rate that I become R; \(\eta _3>0\) is the recovery rate of I. The schematic diagram of model (1.1) is shown in Fig. 1 below.

Fig. 1
figure 1

The schematic diagram of the deterministic model (1.1)

Full size image

Consider the absence of R(t) in other equations, Jiao et al. [25] only focused on the following three-dimensional model

$$\begin{aligned} \left\{ \begin{array}{lll} {\dot{S}}(t)=\Lambda -\beta (1-\eta _1)S(t)[I(t)+\eta _2E(t)]-\mu S(t),\\ {\dot{E}}(t)=\beta (1-\eta _1)S(t)[I(t)+\eta _2E(t)]-(\delta +\mu )E(t),\\ {\dot{I}}(t)=\delta E(t)-(\theta +\alpha +\mu )I(t), \end{array} \right. \end{aligned}$$
(1.2)

and obtained the basic reproduction number \(R_0=\frac{\Lambda \beta (1-\eta _1)[\delta +\eta _2(\theta +\alpha +\mu )]}{\mu (\theta +\alpha +\mu )(\delta +\mu )}\). Furthermore, they proved that model (1.2) admits a globally asymptotically stable disease-free equilibrium if \(R_0<1\), while the positive equilibrium of model (1.2) is globally asymptotically stable if \(R_0>1\).

Due to the existence of random phenomena in an ecosystem, epidemic models are unavoidably subjected to the environmental fluctuations. In fact, temperature changes, humidity and media coverage inevitably affect the spread of epidemic. To better explain these phenomena, many researchers have included stochastic perturbations in the process of epidemic modelling and achieved numerous good results [26,27,28,29,30,31,32,33,34,35,36]. Keeping in mind such an idea, Shangguan and Liu et al. [37] recently incorporated white noises into model (1.2) and assumed that stochastic perturbations on the individuals are proportional to S(t), E(t), I(t), and derived a new stochastic version as follows

$$\begin{aligned} \left\{ \begin{array}{lll} dS(t)=[\Lambda -\beta (1-\eta _1)S(t)(I(t)+\eta _2E(t))-\mu S(t)]dt+\sigma _{1}S(t)dB_{1}(t),\\ dE(t)=[\beta (1-\eta _1)S(t)(I(t)+\eta _2E(t))-(\delta +\mu )E(t)]dt+\sigma _{2}E(t)dB_{2}(t),\\ dI(t)=[\delta E(t)-(\theta +\alpha +\mu )I(t)]dt+\sigma _{3}I(t)dB_{3}(t), \end{array} \right. \nonumber \\ \end{aligned}$$
(1.3)

where \(B_i(t)\) represent independent standard Brownian motions with \(B_i(0)=0\), and \(\sigma _i^2>0\) represent the intensities of noises, \(i=1,2,3\). They investigated the above model’s stochastic dynamics such as extinction, persistence in the mean and ergodic stationary distribution (ESD), and compared with model (1.2) and revealed the effect of white noises on the spread of the disease.

Note that periodicity is also an important factor and a quantity of human infectious diseases similarly fluctuate over time and often seasonally spread. The birth rate, death rate, recovery rate and other parameters appear more or less periodicity rather than keeping constant, and hence it is reasonable to further take periodic variation into account in the process of investigating the stochastic epidemic model. The existence of periodic solutions is important for understanding and controlling the transmissibility of the diseases, and is extensively researched as a key point in many literatures [38,39,40,41,42,43,44]. For instance, Lin et al. [39] researched a stochastic non-autonomous periodic SIR model and established the threshold of the disease to occur and also verified the existence of periodic solutions. The existence of periodic solutions for a stochastic periodic SIS model with general nonlinear incidence proposed by Ramziya et al. [41] was discussed. Inspired by the arguments above, we focus on the stochastic model (1.3) and further investigate a corresponding model with periodic variable coefficients, which yields

$$\begin{aligned} \left\{ \begin{array}{lll} dS(t)=[\Lambda (t)-\beta (t)(1-\eta _1)S(t)(I(t)+\eta _2E(t))-\mu (t)S(t)]dt+\sigma _{1}(t)S(t)dB_{1}(t),\\ dE(t)=[\beta (t)(1-\eta _1)S(t)(I(t)+\eta _2E(t))-(\delta (t)+\mu (t))E(t)]dt+\sigma _{2}(t)E(t)dB_{2}(t),\\ dI(t)=[\delta (t)E(t)-(\theta (t)+\alpha (t)+\mu (t))I(t)]dt+\sigma _{3}(t)I(t)dB_{3}(t), \end{array} \right. \nonumber \\ \end{aligned}$$
(1.4)

where the parameters \(\Lambda (t)\), \(\beta (t)\), \(\mu (t)\), \(\delta (t)\), \(\theta (t)\), \(\alpha (t)\) and \(\sigma _i(t) (i=1,2,3)\) involved with the above model (1.4) are positive continuous T-periodic functions.

Recalling the stochastic model (1.3), we find that white noises are incorporated into the deterministic model (1.2). Next, based on model (1.3), we take a further step to investigate the influence of telephone noises which can be described as a switching between (finite) regimes of environment. The switching is without memory with exponential distribution waiting times and the waiting time for the next switch has an exponential distribution [45], which can be modeled by a finite-state Markov chain. The analysis of stochastic epidemic models with Markov switching has received considerable attention, see [35, 42, 44, 46, 47] and the references therein. Motivated by this good idea, we suppose that there exist N regimes and a corresponding version is governed by

$$\begin{aligned} \left\{ \begin{array}{lll} dS(t)=[\Lambda (k)-\beta (k)(1-\eta _1)S(t)(I(t)+\eta _2E(t))-\mu (k)S(t)]dt+\sigma _{1}(k)S(t)dB_{1}(t),\\ dE(t)=[\beta (k)(1-\eta _1)S(t)(I(t)+\eta _2E(t))-(\delta (k))+\mu (k))E(t)]dt+\sigma _{2}(k)E(t)dB_{2}(t),\\ dI(t)=[\delta (k)E(t)-(\theta (k))+\alpha (k))+\mu (k))I(t)]dt+\sigma _{3}(k)I(t)dB_{3}(t). \end{array} \right. \nonumber \\ \end{aligned}$$
(1.5)

The switching between these N regimes is given by a Markov chain on the state space \({{\mathbb {S}}}=\{1, 2, \ldots , N\}\). This model evolves to a stochastic model with regime switching as follows

$$\begin{aligned} \left\{ \begin{array}{lll} dS(t)=\{\Lambda (\xi (t))-\beta (\xi (t))(1-\eta _1)S(t)[I(t)+\eta _2E(t)]-\mu (\xi (t))S(t)\}dt\\ \qquad \qquad +\,\,\sigma _{1}(\xi (t))S(t)dB_{1}(t),\\ dE(t)=\{\beta (\xi (t))(1-\eta _1)S(t)[I(t)+\eta _2E(t)]-[\delta (\xi (t))+\mu (\xi (t))]E(t)\}dt\\ \qquad \qquad +\,\,\sigma _{2}(\xi (t))E(t)dB_{2}(t),\\ dI(t)=\{\delta (\xi (t))E(t)-[\theta (\xi (t))+\alpha (\xi (t))+\mu (\xi (t))]I(t)\}dt\\ \qquad \qquad +\,\,\sigma _{3}(\xi (t))I(t)dB_{3}(t), \end{array} \right. \nonumber \\ \end{aligned}$$
(1.6)

where \(\xi (t)\) is a right-continuous time Markov chain with values in finite state space \({{\mathbb {S}}}\). We assume that the Brownian motions \(B_i(\cdot )\) are dependent of the Markov chain \(\xi (\cdot )\). For each \(k\in {{\mathbb {S}}}\), the parameters \(\Lambda (k),\beta (k),\delta (k),\theta (k),\alpha (k),\mu (k)\) and \(\sigma _i(k)(i = 1, 2, 3)\) are positive constants. Model (1.5) is called a subsystem of model (1.6) and model (1.6) can be regarded as model (1.5) switching from one to another by the law of the Markov chain for all \(k\in {{\mathbb {S}}}\).

For the convenience of subsequent sections, we list the following preliminaries. In details, assign \({{\mathbb {R}}}_+=[0,\infty ),{{\mathbb {R}}}_+^3=\{(x_1,x_2,x_3)\in {{\mathbb {R}}}^3:x_i>0,i=1,2,3\}\) and let a complete probability space \((\Omega ,{\mathcal {F}},\{{\mathcal {F}}_t\}_{t\ge 0},{{\mathbb {P}}})\) with a filtration \(\{{\mathcal {F}}_t\}_{t\ge 0}\) satisfy the usual conditions. For an integral function \(\aleph (t)\) defined for \(t\in {{\mathbb {R}}}_+\), we denote \(\langle \aleph \rangle _t=\frac{1}{t}\int _0^t\aleph (s)ds\), \(\aleph ^l=\inf _{t\in {{\mathbb {R}}}_+}\aleph (t)\) and \(\aleph ^u=\sup _{t\in {{\mathbb {R}}}_+}\aleph (t)\). For each vector \(\pounds =(\pounds (1), . . . , \pounds (N))\), we define that \({\hat{\pounds }}=\min _{k\in {{\mathbb {S}}}}\{\pounds (k)\}\) and \(\check{\pounds }=\max _{k\in {{\mathbb {S}}}}\{\pounds (k)\}\). The generator for \(\xi (t)\) is defined as \(\Gamma =(\gamma _{ij})_{N\times N}\), where \(\gamma _{ij}=-\sum _{j=1}^N\gamma _{ij}\), and \(\gamma _{ij}\ge 0\ (i\ne j)\) is the transition rate from i to j, that is

$$\begin{aligned} {{\mathbb {P}}}(\xi (t+\Delta )=j|\xi (t)=i)=\left\{ \begin{array}{lll} \gamma _{ij}\Delta +o(\Delta ),\ \ \ \ \ \ \ \ \text {if}\ \ i\ne j,\\ 1+\gamma _{ij}\Delta +o(\Delta ),\ \ \ \text {if}\ \ i=j, \end{array} \right. \end{aligned}$$

where \(\Delta >0\). Assume that \(\xi (t)\) is irreducible, which implies that it has a unique stationary distribution \(\pi =\{\pi _1, \pi _2,\ldots ,\pi _N\}\) which can be governed by the equation \(\pi \Gamma =0\) subject to \(\sum _{h=1}^N\pi _h=1\) and \(\pi _h>0\) for any \(h\in {{\mathbb {S}}}\).

As a continuation of our previous work [37], the object of the present paper is to examine the effect of environmental variability on the dynamics of disease transmission of models (1.4) and (1.6). The rest sections of this work are summarized as follows. We discuss the existence of a positive periodic solution of model (1.4) in Sect. 2. Section 3 establishes sharp sufficient criteria for the ESD of model (1.6). In Sect. 4, several specific numerical examples are presented to substantiate our analytic results. Lastly, a series of concluding remarks are contained in Sect. 5.

2 Existence of positive periodic solution of (1.4)

The part of this paper, we proceed to discuss the existence of positive periodic solutions of model (1.4). In what follows, let us first prepare the following definition and two lemmas.

Definition 2.1

[49] A stochastic process \(\zeta (t)=\zeta (t,\omega )(-\infty<t<+\infty )\) is T-period if for every finite sequence of numbers \(t_1, t_2,\cdots , t_n\) the joint distribution of random variables \(\zeta (t_1+h),\zeta (t_2+h),\cdots ,\zeta (t_n+h)\) is independent of h, where \(h = kT\), \(k=\pm 1,\pm 2,\cdots \).

A periodic stochastic system is given by

$$\begin{aligned} dx(t)=h(x(t),t)dt+g(x(t),t)dB(t),\ \ x\in {{\mathbb {R}}}^n, \end{aligned}$$
(2.1)

where both functions h(t) and g(t) are T-periodic in t.

Lemma 2.1

[49] Suppose that the coefficients involved with (2.1) are T-periodic and system (2.1) owns a unique global solution. Also, there is a function \(W(t,x)\in C^2\) in \({{\mathbb {R}}}\) which is T-periodic in t and satisfies

\((\mathbf{A}_1)\):

\(\inf _{|x|>{{\mathbb {R}}}}W(t,x)\rightarrow +\infty \) as \({{\mathbb {R}}}\rightarrow +\infty \),

\((\mathbf{A}_2)\):

\(LW(t,x)\le -1\) outside some compact set.

Then system (2.1) has a T-periodic solution.

Lemma 2.2

For any initial value \((S(0),E(0),I(0))\in {{\mathbb {R}}}_+^3\), there is a unique globally positive solution \((S(t),E(t),I(t))\in {{\mathbb {R}}}_+^3\) of model (1.4) for \(t\ge 0\) almost surely.

Proof

Define a \(C^2\)-function \(V:{{\mathbb {R}}}_+^3\rightarrow {{\mathbb {R}}}_+\) as follows

$$\begin{aligned} V(S,E,I)=\left( S-q_1-q_1\ln \frac{S}{q_1}\right) +(E-1-\ln E)+q_2(I-1-\ln I), \end{aligned}$$

where

$$\begin{aligned} q_1=\frac{\delta ^l+\mu ^l}{\beta ^u(1-\eta _1)[\eta _2+\frac{\delta ^u}{\mu ^l+\alpha ^l+\theta ^l}]},\ \ q_2=\frac{q_1\beta ^u(1-\eta _1)}{\mu ^l+\alpha ^l+\theta ^l}. \end{aligned}$$
(2.2)

By Itô’s formula, we derive that

$$\begin{aligned} dV=LVdt+\sigma _1(t)(S-q_1)dB_1(t)+\sigma _2(t)(E-1)dB_2(t)+q_2\sigma _3(t)(I-1)dB_3(t), \end{aligned}$$

where

$$\begin{aligned} \begin{array}{lll} LV=\Lambda (t)-\beta (t)(1-\eta _1)S(I+\eta _2E)-\mu (t)S-q_1\Lambda (t)\frac{1}{S}+q_1\beta (t)(1-\eta _1)I\\ \qquad \qquad +q_1\beta (t)(1-\eta _1)\eta _2E+q_1\mu (t)+\frac{1}{2}q_1\sigma _1^2(t)+\beta (t)(1-\eta _1)S(I+\eta _2E)\\ \qquad \qquad -(\delta (t)+\mu (t))E-\beta (t)(1-\eta _1)\eta _2S+\mu (t)+\delta (t)+q_2\delta (t)E+\frac{1}{2}\sigma _2^2(t)\\ \qquad \qquad -q_2(\alpha (t)+\mu (t)+\theta (t))I-q_2\delta (t)\frac{E}{I}-\beta (t)(1-\eta _1)\frac{SI}{E}\\ \qquad \qquad +q_2(\alpha (t)+\mu (t)+\theta (t))+\frac{1}{2}q_2\sigma _3^2(t)\\ \qquad \le \Lambda ^u+q_1\beta ^u(1-\eta _1)I+q_1\beta ^u(1-\eta _1)\eta _2E+q_1\mu ^u+\frac{1}{2}q_1(\sigma _1^2)^u-(\delta ^l+\mu ^l)E\\ \qquad \qquad +\mu ^u+\delta ^u+\frac{1}{2}(\sigma _2^2)^u+q_2\delta ^uE-q_2(\alpha ^l+\mu ^l+\theta ^l)I+q_2(\alpha ^u+\mu ^u+\theta ^u) +\frac{1}{2}q_2(\sigma _3^2)^u\\ \qquad =\Lambda ^u+(q_1+1)\mu ^u+\delta ^u+q_2(\alpha ^u+\mu ^u+\theta ^u)+\frac{1}{2}q_1(\sigma _1^2)^u+\frac{1}{2}(\sigma _2^2)^u +\frac{1}{2}q_2(\sigma _3^2)^u\\ \qquad \qquad +[q_1\beta ^u(1-\eta _1)-q_2(\alpha ^l+\mu ^l+\theta ^l)]I+[q_1\beta ^u(1-\eta _1)\eta _2+q_2\delta ^u-(\delta ^l+\mu ^l)]E. \end{array} \end{aligned}$$

Recalling (2.2), we can easily get

$$\begin{aligned} q_1\beta ^u(1-\eta _1)-q_2(\alpha ^l+\mu ^l+\theta ^l)=0,\ \ q_1\beta ^u(1-\eta _1)\eta _2+q_2\delta ^u-(\delta ^l+\mu ^l)=0. \end{aligned}$$

Then

$$\begin{aligned} LV\le \Lambda ^u+(q_1+1)\mu ^u+\delta ^u+q_2(\alpha ^u+\mu ^u+\theta ^u)+\frac{1}{2}q_1(\sigma _1^2)^u +\frac{1}{2}(\sigma _2^2)^u+\frac{1}{2}q_2(\sigma _3^2)^u={\mathcal {K}}, \end{aligned}$$

where \({\mathcal {K}}>0\) is a constant. Since the rest part can be proved in the same way as in the proof of Theorem 2.1 in [48], the details are omitted. \(\square \)

Assign

$$\begin{aligned} {\mathfrak {R}}=\frac{\langle \beta (1-\eta _1)\Lambda \delta \rangle _T}{\langle \mu +\frac{1}{2}\sigma _1^2\rangle _T \langle \delta +\mu +\frac{1}{2}\sigma _2^2\rangle _T\langle \theta +\alpha +\mu +\frac{1}{2}\sigma _3^2\rangle _T}. \end{aligned}$$

Let us now begin to state our principal conclusion on the existence of a positive periodic solution of model (1.4).

Theorem 2.1

Model (1.4) owns a positive T-periodic solution if \({\mathfrak {R}}>1\).

Proof

Let us consider a \(C^2\)-function \(W:[0,+\infty )\times {{\mathbb {R}}}_+^3\rightarrow {{\mathbb {R}}}_+\) with the form

$$\begin{aligned} \begin{array}{lll} W(S,E,I,t)={\mathcal {M}}_1(-\ln S-a_1\ln E-a_2\ln I-vI+w(t))+\frac{1}{p+1}(S+E+I)^{p+1}\\ -\ln S-\ln E, \end{array} \end{aligned}$$

where

$$\begin{aligned} \begin{array}{lll} a_1=\frac{\langle \beta (1-\eta _1)\delta \Lambda \rangle _T}{\langle \delta +\mu +\frac{1}{2}\sigma _2^2\rangle _T^2 \langle \theta +\alpha +\mu +\frac{1}{2}\sigma _3^2\rangle _T},\ a_2=\frac{\langle \beta (1-\eta _1)\delta \Lambda \rangle _T}{\langle \delta +\mu +\frac{1}{2}\sigma _2^2\rangle _T \langle \theta +\alpha +\mu +\frac{1}{2}\sigma _3^2\rangle _T^2},\\ v={\beta ^u(1-\eta _1)\eta _2}/{\delta ^l}, \end{array} \end{aligned}$$

and w(t) is a T-periodic function with

$$\begin{aligned} w'(t)=\langle \mathfrak {{\mathfrak {R}}}_0\rangle _T-{\mathfrak {R}}_0(t), \end{aligned}$$
(2.3)

where \({\mathfrak {R}}_0(t)\) will be provided later. Let \(p>0\) and \({\mathcal {M}}_1>0\) is a sufficiently large constant satisfying

$$\begin{aligned} p<{2\mu ^l}/{((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)},\ \ -\vartheta {\mathcal {M}}_1+f_2\le -2, \end{aligned}$$

where \(\vartheta :=\langle \mu +\frac{1}{2}\sigma _1^2\rangle _T({\mathfrak {R}}-1)\) and \(f_2\) will be supplied later.

We can easily derive that W(S, E, I, t) is T-periodic in t, and

$$\begin{aligned} \lim _{\kappa \rightarrow +\infty ,(S,E,I)\in {{\mathbb {R}}}_+^3\setminus U_\kappa }W(S,E,I,t)=+\infty , \end{aligned}$$

where \(U_\kappa =({1}/{\kappa },\kappa )\times ({1}/{\kappa },\kappa )\times ({1}/{\kappa },\kappa )\) and the number \(\kappa >1\) is sufficiently large, which implies that the assumption \((\mathbf{A}_1)\) in Lemma 2.1 verified.

Now, we continue to confirm that the assumption \((\mathbf{A}_2)\) in Lemma 2.1. Assign

$$\begin{aligned} W(S,E,I,t)={\mathcal {M}}_1(W_1+w(t))+W_2+W_3, \end{aligned}$$

where \(W_1=-\ln S-a_1\ln E-a_2\ln I-vI,W_2=\frac{1}{p+1}(S+E+I)^{p+1},W_3=-\ln S-\ln E\).

Making use of Itô’s formula to \(W_1\) yields

$$\begin{aligned}&\begin{array}{lll} LW_1=-\frac{\Lambda (t)}{S}+\beta (t)(1-\eta _1)(I+\eta _2E)+\mu (t)+\frac{1}{2}\sigma _1^2(t)-a_1\beta (t)(1-\eta _1)\frac{SI}{E}\\ \qquad \qquad -\,\,a_1\beta (t)(1-\eta _1)\eta _2S+a_1(\mu (t)+\delta (t)+\frac{1}{2}\sigma _2^2(t))-a_2\delta (t)\frac{E}{I}\\ \qquad \qquad +\,a_2(\theta (t)+\alpha (t)+\mu (t)+\frac{1}{2}\sigma _3^2(t))-v\delta (t)E+v(\theta (t)+\alpha (t)+\mu (t))I\\ \end{array}\nonumber \\&\quad \begin{array}{lll} \qquad \le -\,\,3\root 3 \of {a_1a_2\Lambda (t)\beta (t)(1-\eta _1)\delta (t)}+a_1(\mu (t)+\delta (t)+\frac{1}{2}\sigma _2^2(t))\\ \qquad \qquad +\,\,a_2(\theta (t)+\alpha (t)+\mu (t)+\frac{1}{2}\sigma _3^2(t))+\mu (t)+\frac{1}{2}\sigma _1^2(t)+\beta ^u(1-\eta _1)I\\ \qquad \qquad +\,\,v(\theta ^u+\alpha ^u+\mu ^u)I\\ \qquad ={\mathfrak {R}}_0(t)+[\beta ^u(1-\eta _1)+v(\theta ^u+\alpha ^u+\mu ^u)]I, \end{array}\nonumber \\ \end{aligned}$$
(2.4)

where

$$\begin{aligned} \begin{array}{lll} {\mathfrak {R}}_0(t)=-3\root 3 \of {a_1a_2\Lambda (t)\beta (t)(1-\eta _1)\delta (t)}+a_1(\mu (t)+\delta (t)+\frac{1}{2}\sigma _2^2(t))\\ \qquad \qquad +a_2(\theta (t)+\alpha (t)+\mu (t)+\frac{1}{2}\sigma _3^2(t))+\frac{1}{2}\sigma _1^2(t)+\mu (t). \end{array} \end{aligned}$$

It follows from (2.3) and (2.4) that

$$\begin{aligned} \begin{array}{lll} L(W_1+w(t))\le \langle {\mathfrak {R}}_0\rangle _T+[\beta ^u(1-\eta _1)+v(\theta ^u+\alpha ^u+\mu ^u)]I\\ \qquad \qquad \qquad \qquad =-\langle \mu +\frac{1}{2}\sigma _1^2\rangle _T({\mathfrak {R}}-1)+[\beta ^u(1-\eta _1)+v(\theta ^u+\alpha ^u+\mu ^u)]I\\ \qquad \qquad \qquad \qquad :=-\vartheta +[\beta ^u(1-\eta _1)+v(\theta ^u+\alpha ^u+\mu ^u)]I. \end{array}\nonumber \\ \end{aligned}$$
(2.5)

Applying Itô’s formula to \(W_2\) leads to

$$\begin{aligned} \begin{array}{lll} \displaystyle LW_2=[\Lambda (t)-\mu (t)(S+E+I)-(\theta (t)+\alpha (t))I](S+E+I)^p\\ \qquad \qquad +\frac{p}{2}[\sigma _1^2(t)S^2+\sigma _2^2(t)E^2+\sigma _3^2(t)I^2](S+E+I)^{p-1}\\ \quad \qquad \le \Lambda ^u(S+E+I)^p-\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] (S+E+I)^{p+1}\\ \quad \qquad \le -\frac{1}{2}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] (S^{p+1}+E^{p+1}+I^{p+1})+J, \end{array}\nonumber \\ \end{aligned}$$
(2.6)

where

$$\begin{aligned} J=\sup _{(S,E,I)\in {{\mathbb {R}}}_+^3}\left\{ -\frac{1}{2}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] (S+E+I)^{p+1} +\Lambda ^u(S+E+I)^p\right\} . \end{aligned}$$

Similar to \(LW_2\), we can obtain

$$\begin{aligned} \begin{array}{lll} LW_3=-\frac{\Lambda (t)}{S}+\beta (t)(1-\eta _1)I+\beta (t)(1-\eta _1)\eta _2E-\beta (t)(1-\eta _1)\frac{SI}{E}\\ \qquad \qquad -\beta (t)(1-\eta _1)\eta _2S+\delta (t)+2\mu (t)+\frac{1}{2}\sigma _1^2(t)+\frac{1}{2}\sigma _2^2(t)\\ \quad \qquad \le -\frac{\Lambda ^l}{S}+\beta ^u(1-\eta _1)I+\beta ^u(1-\eta _1)\eta _2E-\beta ^l(1-\eta _1)\frac{SI}{E}+2\mu ^u\\ \qquad \qquad +\delta ^u+\frac{1}{2}(\sigma _1^2)^u+\frac{1}{2}(\sigma _2^2)^u. \end{array} \end{aligned}$$
(2.7)

By virtue of (2.5)-(2.7), we have

$$\begin{aligned} \begin{array}{lll} LW\le -\vartheta {\mathcal {M}}_1+\{{\mathcal {M}}_1[\beta ^u(1-\eta _1)+v(\theta ^u+\alpha ^u+\mu ^u)]+\beta ^u(1-\eta _1)\}I\\ \qquad \qquad -\frac{1}{2}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] (S^{p+1}+E^{p+1}+I^{p+1})\\ \qquad \qquad +\beta ^u(1-\eta _1)\eta _2E-\beta ^l(1-\eta _1)\frac{SI}{E}-\frac{\Lambda ^l}{S}+\frac{1}{2}(\sigma _1^2)^u+\frac{1}{2}(\sigma _2^2)^u\\ \qquad \qquad +J+2\mu ^u+\delta ^u\\ \quad \qquad =-\vartheta {\mathcal {M}}_1-\frac{1}{2}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] (S^{p+1}+E^{p+1}+I^{p+1})\\ \qquad \qquad +HI+\beta ^u(1-\eta _1)\eta _2E-\beta ^l(1-\eta _1)\frac{SI}{E}-\frac{\Lambda ^l}{S}+\frac{1}{2}(\sigma _1^2)^u+\frac{1}{2}(\sigma _2^2)^u\\ \qquad \qquad +J+2\mu ^u+\delta ^u, \end{array} \end{aligned}$$
(2.8)

where \(H={\mathcal {M}}_1[\beta ^u(1-\eta _1)+v(\theta ^u+\alpha ^u+\mu ^u)]+\beta ^u(1-\eta _1)\).

Define a bounded closed set with the form

$$\begin{aligned} U=\left\{ \varepsilon \le S\le \frac{1}{\varepsilon },\ \ \varepsilon ^3\le E\le \frac{1}{\varepsilon ^3},\ \ \varepsilon \le I\le \frac{1}{\varepsilon }\right\} , \end{aligned}$$

where the constant \(\varepsilon >0\) is suitably small such that

$$\begin{aligned}&\displaystyle -\frac{\Lambda ^l}{\varepsilon }+f_1\le -1, \end{aligned}$$
(2.9)
$$\begin{aligned}&\displaystyle -\beta ^l(1-\eta _1)\frac{1}{\varepsilon }+f_1\le -1, \end{aligned}$$
(2.10)
$$\begin{aligned}&\displaystyle -\vartheta {\mathcal {M}}_1+H\varepsilon +f_2\le -1, \end{aligned}$$
(2.11)
$$\begin{aligned}&\displaystyle -\frac{1}{4}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] \frac{1}{\varepsilon ^{p+1}}+f_3\le -1, \end{aligned}$$
(2.12)
$$\begin{aligned}&\displaystyle -\frac{1}{4}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] \frac{1}{\varepsilon ^{3(p+1)}}+f_4\le -1, \end{aligned}$$
(2.13)
$$\begin{aligned}&\displaystyle -\frac{1}{4}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] \frac{1}{\varepsilon ^{p+1}}+f_5\le -1, \end{aligned}$$
(2.14)

where \(f_1,f_2,f_3,f_4,f_5\) are positive constants which can be determined in (2.15)-(2.19), respectively. For convenience, we divide \({{\mathbb {R}}}_+^3\setminus U\) into six domains with the following forms

$$\begin{aligned} \begin{array}{lll} U_1=\{(S,E,I)\in {{\mathbb {R}}}_+^3|0<S<\varepsilon \},\ \ U_2=\{(S,E,I)\in {{\mathbb {R}}}_+^3|S>\varepsilon ,I>\varepsilon ,0<E<\varepsilon ^3\},\\ U_3=\{(S,E,I)\in {{\mathbb {R}}}_+^3|0<I<\varepsilon \},\ \ U_4=\{(S,E,I)\in {{\mathbb {R}}}_+^3|S>\frac{1}{\varepsilon }\},\\ U_5=\{(S,E,I)\in {{\mathbb {R}}}_+^3|I>\frac{1}{\varepsilon }\},\ \ U_6=\{(S,E,I)\in {{\mathbb {R}}}_+^3|E>\frac{1}{\varepsilon ^3}\}. \end{array} \end{aligned}$$

Obviously, \({{\mathbb {R}}}_+^3\setminus U=U_1\cup U_2\cup U_3\cup U_4\cup U_5\cup U_6\). Next we will prove, by verifying the above six cases, that \(LW\le -1\) on \({{\mathbb {R}}}_+^3\setminus U\).

Case 1 If \((S,E,I)\in U_1\), then one derives, by (2.8) and (2.9), that

$$\begin{aligned} \begin{array}{lll} LW\le -\frac{\Lambda ^l}{S}-\frac{1}{2}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] (S^{p+1}+E^{p+1}+I^{p+1})\\ \qquad \qquad +\beta ^u(1-\eta _1)\eta _2E+HI+J+2\mu ^u+\delta ^u+\frac{1}{2}(\sigma _1^2)^u+\frac{1}{2}(\sigma _2^2)^u\\ \qquad \quad \le -\frac{\Lambda ^l}{S}+f_1\le -\frac{\Lambda ^l}{\varepsilon }+f_1\le -1, \end{array} \end{aligned}$$

where

$$\begin{aligned} \begin{array}{lll} f_1=\sup _{(S,E,I)\in {{\mathbb {R}}}_+^3}\left\{ -\frac{1}{2}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] (S^{p+1}+E^{p+1}+I^{p+1})\right. \\ \left. \qquad \qquad +HI+\beta ^u(1-\eta _1)\eta _2E+J+2\mu ^u+\delta ^u+\frac{1}{2}(\sigma _1^2)^u+\frac{1}{2}(\sigma _2^2)^u\right\} . \end{array}\nonumber \\ \end{aligned}$$
(2.15)

Case 2 If \((S,E,I)\in U_2\), then we have from (2.8) and (2.11) that

$$\begin{aligned} \begin{array}{lll} \displaystyle LW\le -\beta ^l(1-\eta _1)\frac{SI}{E}-\frac{1}{2}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] (S^{p+1}+E^{p+1}+I^{p+1})\\ \qquad \qquad +HI+\beta ^u(1-\eta _1)\eta _2E+J+2\mu ^u+\delta ^u+\frac{1}{2}(\sigma _1^2)^u+\frac{1}{2}(\sigma _2^2)^u\\ \qquad \quad \le -\beta ^l(1-\eta _1)\frac{SI}{E}+f_1\le -\beta ^l(1-\eta _1)\frac{1}{\varepsilon }+f_1\le -1. \end{array} \end{aligned}$$

Case 3 If \((S,E,I)\in U_3\), then combining (2.8) with (2.12) results in

$$\begin{aligned} \begin{array}{lll} \displaystyle LW\le -\vartheta {\mathcal {M}}_1+HI-\frac{1}{2}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] (S^{p+1}+E^{p+1}+I^{p+1})\\ \qquad \qquad +\beta ^u(1-\eta _1)\eta _2E+J+2\mu ^u+\delta ^u+\frac{1}{2}(\sigma _1^2)^u+\frac{1}{2}(\sigma _2^2)^u\\ \qquad \quad \le -\vartheta {\mathcal {M}}_1+HI+f_2\le -\vartheta {\mathcal {M}}_1+H\varepsilon +f_2\le -1, \end{array} \end{aligned}$$

where

$$\begin{aligned} \begin{array}{lll} f_2=\sup _{(S,E,I)\in {{\mathbb {R}}}_+^3}\left\{ -\frac{1}{2}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] (S^{p+1}+E^{p+1}+I^{p+1})\right. \\ \left. \qquad \qquad +\beta ^u(1-\eta _1)\eta _2E+J+2\mu ^u+\delta ^u+\frac{1}{2}(\sigma _1^2)^u+\frac{1}{2}(\sigma _2^2)^u\right\} . \end{array} \end{aligned}$$
(2.16)

Case 4 If \((S,E,I)\in U_4\), then using (2.8) and (2.12) yields

$$\begin{aligned} \begin{array}{lll} LW\le -\frac{1}{4}\left[ \mu ^l-\frac{p}{2}(\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] S^{p+1} -\frac{1}{4}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] S^{p+1}\\ \qquad \qquad -\frac{1}{2}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] (E^{p+1}+I^{p+1})+\beta ^u(1-\eta _1)\eta _2E\\ \qquad \qquad +HI+J+2\mu ^u+\delta ^u+\frac{1}{2}(\sigma _1^2)^u+\frac{1}{2}(\sigma _2^2)^u\\ \qquad \quad \le -\frac{1}{4}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] S^{p+1}+f_3\\ \qquad \quad \le -\frac{1}{4}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] \frac{1}{\varepsilon ^{p+1}}+f_3\le -1, \end{array} \end{aligned}$$

where

$$\begin{aligned} \begin{array}{lll} f_3=\sup _{(S,E,I)\in {{\mathbb {R}}}_+^3}\left\{ -\frac{1}{4}\left[ \mu ^l-\frac{p}{2}(\sigma _1^2)^u\vee (\sigma _2^2)^u \vee (\sigma _3^2)^u)\right] S^{p+1}+\beta ^u(1-\eta _1)\eta _2E\right. \\ \left. \qquad \qquad -\frac{1}{2}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] (E^{p+1}+I^{p+1})+2\mu ^u+HI\right. \\ \left. \qquad \qquad +J+\delta ^u+\frac{1}{2}(\sigma _1^2)^u+\frac{1}{2}(\sigma _2^2)^u\right\} . \end{array}\nonumber \\ \end{aligned}$$
(2.17)

Case 5 If \((S,E,I)\in U_5\), then one can know from (2.8) and (2.13) that

$$\begin{aligned} \begin{array}{lll} \displaystyle LW\le -\frac{1}{4}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] I^{p+1} -\frac{1}{4}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] I^{p+1}\\ \qquad \qquad -\frac{1}{2}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] (S^{p+1}+E^{p+1})+\beta ^u(1-\eta _1)\eta _2E+HI+J\\ \qquad \qquad +2\mu ^u+\delta ^u+\frac{1}{2}(\sigma _1^2)^u+\frac{1}{2}(\sigma _2^2)^u\\ \qquad \quad \le -\frac{1}{4}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] I^{p+1}+f_4\\ \qquad \quad \le -\frac{1}{4}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] \frac{1}{\varepsilon ^{3(p+1)}}+f_4\le -1, \end{array} \end{aligned}$$

where

$$\begin{aligned} \begin{array}{lll} \displaystyle f_4=\sup _{(S,E,I)\in {{\mathbb {R}}}_+^3}\left\{ -\frac{1}{4}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] I^{p+1} \qquad \qquad +\beta ^u(1-\eta _1)\eta _2E\right. \\ \left. \qquad \qquad -\frac{1}{2}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] (S^{p+1}+E^{p+1}) +2\mu ^u+\delta ^u+HI\right. \\ \left. \qquad \qquad +J+\frac{1}{2}(\sigma _1^2)^u+\frac{1}{2}(\sigma _2^2)^u\right\} . \end{array} \end{aligned}$$
(2.18)

Case 6 If \((S,E,I)\in U_6\), then by (2.8) and (2.14) we have

$$\begin{aligned} \begin{array}{lll} \displaystyle LW\le -\frac{1}{4}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] E^{p+1} -\frac{1}{4}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] E^{p+1}\\ \qquad \qquad -\frac{1}{2}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] (S^{p+1}+I^{p+1})+\beta ^u(1-\eta _1)\eta _2E+HI+J\\ \qquad \qquad +2\mu ^u+\delta ^u+\frac{1}{2}(\sigma _1^2)^u+\frac{1}{2}(\sigma _2^2)^u\\ \qquad \quad \le -\frac{1}{4}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] E^{p+1}+f_5\\ \qquad \quad \le -\frac{1}{4}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] \frac{1}{\varepsilon ^{p+1}}+f_5\le -1, \end{array} \end{aligned}$$

where

$$\begin{aligned} \begin{array}{lll} f_5=\sup _{(S,E,I)\in {{\mathbb {R}}}_+^3}\left\{ -\frac{1}{4}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] E^{p+1}+\beta ^u(1-\eta _1)\eta _2E\right. \\ \left. \qquad \qquad -\frac{1}{2}\left[ \mu ^l-\frac{p}{2}((\sigma _1^2)^u\vee (\sigma _2^2)^u\vee (\sigma _3^2)^u)\right] (S^{p+1}+I^{p+1})+2\mu ^u +\delta ^u+HI\right. \\ \left. \qquad \qquad +J+\frac{1}{2}(\sigma _1^2)^u+\frac{1}{2}(\sigma _2^2)^u\right\} . \end{array} \end{aligned}$$
(2.19)

The above discussions of six cases show that \(LW\le -1\), \((S,E,I)\in {{\mathbb {R}}}_+^3\setminus U\), which means that the assumption \((\mathbf{A}_2)\) in Lemma 2.1 also holds. Thus model (1.4) owns a positive T-periodic solution. \(\square \)

3 Ergodic stationary distribution of (1.6)

Our purpose in this section is to analyze the ESD of model (1.6). We first give some lemmas which are important for subsequent discussions.

Let \((X(t),\xi (t))\) be the diffusion process governed by

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle dX(t)=b(X(t),\xi (t))dt+\sigma (X(t),\xi (t))dB(t),\\ X(0)=x_0,\ \ \ \xi (0)=\xi , \end{array} \right. \end{aligned}$$
(2.1)

where \(b(\cdot , \cdot ) : {{\mathbb {R}}}^n\times {{\mathbb {S}}}\rightarrow {{\mathbb {R}}}^n, \sigma (\cdot , \cdot ) : {{\mathbb {R}}}^n\times {{\mathbb {S}}}\rightarrow {{\mathbb {R}}}^{n\times n}\) and \(D(x, k)=\sigma (x, k)\sigma ^\top (x, k)=(d_{ij}(x,k))\). For each \(k\in {{\mathbb {S}}}\), we assume that \({\mathcal {W}}(\cdot , k)\) is any twice continuously differentiable function, and the operator L can be described by

$$\begin{aligned} L{\mathcal {W}}(x,k)=\sum b_i(x,t)\frac{\partial {\mathcal {W}}(x,k)}{\partial x_i}+\frac{1}{2}\sum _{i,j=1}^nd_{ij}(x,k)\frac{\partial ^2{\mathcal {W}}(x,k)}{\partial x_i\partial x_j}+\sum _{l=1}^N\gamma _{kl}{\mathcal {W}}(x,l). \end{aligned}$$

Lemma 3.1

[49] Assume that the following three assumptions hold

\(\mathrm{(B_1)}\):

for \(i\ne j\), \(\gamma _{ij}>0\), \(i,j\in {{\mathbb {S}}}\),

\(\mathrm{(B_2)}\):

for each \(k\in {{\mathbb {S}}}\),

$$\begin{aligned} \psi |\zeta |^2\le \langle D(x,k)\zeta ,\zeta \rangle \le \psi ^{-1}|\zeta |^2,\ \ \ \zeta \in {{\mathbb {R}}}^n, \end{aligned}$$

with some constant \(\psi \in (0,1]\) for all \(x\in {{\mathbb {R}}}^n\),

\(\mathrm{(B_3)}\):

there exists a nonempty open set D with compact closure, satisfying that, for each \(k\in {{\mathbb {S}}}\), there is a nonnegative function \({\mathcal {W}}(\cdot , k):D^c\rightarrow {{\mathbb {R}}}\) such that \({\mathcal {W}}(\cdot , k)\) is twice continuously differentiable and that for some \(\alpha >0\),

$$\begin{aligned} L{\mathcal {W}}(x,k)\le -\alpha ,\ (x,k)\in D^c\times {{\mathbb {S}}}, \end{aligned}$$

then system (2.1) is ergodic and positive recurrent. Namely, there exists a unique stationary distribution \(\pi (\cdot , \cdot )\) such that for any Broel measurable function \(h(\cdot , \cdot ):{{\mathbb {R}}}^n\times {{\mathbb {S}}}\rightarrow {{\mathbb {R}}}\) satisfying

$$\begin{aligned} \sum _{k=1}^N\int _{{{\mathbb {R}}}^n}|h(x,k)|\pi (dx,k)<\infty , \end{aligned}$$

one has

$$\begin{aligned} P\big (\lim _{t\rightarrow \infty }\frac{1}{t}\int _0^th(X(s),\xi (s))ds=\sum _{k=1}^N\int _{{{\mathbb {R}}}^n}|h(x,k)|\pi (dx,k)\big )=1. \end{aligned}$$

Lemma 3.2

For any initial value \((S(0),E(0),I(0),\xi (0))\in {{\mathbb {R}}}_+^3\times {{\mathbb {S}}}\), model (1.6) has a unique globally positive solution \((S(t),E(t),I(t),\xi (t))\) on \(t\ge 0\) almost sure.

Proof

Since the procedure to prove this lemma is very similar to that of Lemma 2.2, we only give the formulas which are different from those in Lemma 2.2. Assign

$$\begin{aligned} U(S,E,I)=(S-b_1-b_1\ln \frac{S}{b_1})+(E-1-\ln E)+b_2(I-1-\ln I), \end{aligned}$$

where \(b_1={({\hat{\delta }}+{\hat{\mu }})}/{\check{\beta }(1-\eta _1)[\eta _2+{\check{\delta }}/{({\hat{\mu }}+{\hat{\alpha }}+{\hat{\theta }})}]}\) and \(b_2={b_1\check{\beta }(1-\eta _1)}/{({\hat{\mu }}+{\hat{\alpha }}+{\hat{\theta }})}\). Based on the idea of the proof of Lemma 2.2, the remaining proof can be similarly validated. \(\square \)

Denote

$$\begin{aligned} {\mathfrak {R}}_0^s=\frac{\sum \nolimits _{k=1}^N\pi _k(\beta (k)(1-\eta _1)\Lambda \delta )}{\sum \nolimits _{k=1}^N\pi _k(\mu (k)+\frac{1}{2}\sigma _1^2(k))\sum \nolimits _{k=1}^N\pi _k(\delta (k)+\mu (k)+\frac{1}{2}\sigma _2^2(k))\sum \nolimits _{k=1}^N\pi _k(\theta (k)+\alpha (k)+\mu (k)+\frac{1}{2}\sigma _3^2(k))}. \end{aligned}$$

Next, we focus on the existence of a unique ESD of model (1.6).

Theorem 3.1

For any initial value \((S(0),E(0),I(0),\xi (0))\in {{\mathbb {R}}}_+^3\times {{\mathbb {S}}}\), the solution \((S(t),E(t),I(t),\xi (t))\) of model (1.6) owns a unique ESD if \({\mathfrak {R}}_0^s>1\).

Proof

First, the condition \(\gamma _{ij}>0\) (\(i\ne j\)) is given by Sect. 1, which is the required assertion of the assumption \((\mathbf{B}_1)\) in Lemma 3.1.

Next, let us verify the assumption \((\mathbf{B}_2)\) in Lemma 3.1. One can derive the following diffusion matrix of model (1.6)

$$\begin{aligned} A=(a_{ij}(S,E,I,k))=\left( \begin{array}{ccc} \sigma _1^2(k)S^2&{} 0 &{} 0\\ 0 &{} \sigma _2^2(k)E^2 &{} 0\\ 0 &{} 0 &{} \sigma _3^2(k)I^2\\ \end{array} \right) . \end{aligned}$$

We have

$$\begin{aligned} \sum _{i,j=1}^3a_{ij}(S,E,I,k)\zeta _i\zeta _j=\sigma _1^2(k)S^2\zeta _1^2+\sigma _2^2(k)E^2\zeta _2^2+\sigma _3^2(k)I^2\zeta _3^3 \ge M||\zeta ||^2 \end{aligned}$$

for any \((S,E,I)\in D^c\times {{\mathbb {S}}},\zeta =(\zeta _1,\zeta _2,\zeta _3)\in {{\mathbb {R}}}^3\), where

$$\begin{aligned} M=\min _{(S,E,I)\in D^c\times {{\mathbb {S}}}}\{\sigma _1^2(k)S^2,\sigma _2^2(k)E^2,\sigma _3^2(k)I^2\}, \end{aligned}$$

\(D=[\epsilon ,{1}/{\epsilon }]\times [\epsilon ,{1}/{\epsilon }]\times [\epsilon ,{1}/{\epsilon }]\) and the constant \(\epsilon >0\) is sufficiently small. Thus, we can obtain that the assumption \((\mathbf{B}_2)\) in Lemma 3.1 is valid.

At last, we need to prove that the assumption \((\mathbf{B}_3)\) holds. In the same way as in the above proof of the assumption \((\mathbf{A}_2)\) in Theorem 2.1, hence we only give the formulas which are different from those in Sect. 2.

A \(C^2\)-function is constructed as follows

$$\begin{aligned} \begin{array}{lll} \displaystyle {\tilde{W}}(S,E,I,k) ={\mathcal {M}}_2(-\ln S-c_1\ln E-c_2\ln I-\frac{\check{\beta }(1-\eta _1)\eta _2}{{\hat{\delta }}}I+\lambda (k))\\ \qquad \qquad \qquad \qquad +\frac{1}{\varrho +1}(S+E+I)^{\varrho +1}-\ln S-\ln E, \end{array} \end{aligned}$$

where

$$\begin{aligned} \root 3 \of {c_1}= & {} \frac{\sum \nolimits _{k=1}^N\pi _k\root 3 \of {\beta (k)(1-\eta _1)\delta (k)\Lambda (k)}}{\big (\sum \nolimits _{k=1}^N\pi _k\root 3 \of {\mu (k)+\delta (k) +\frac{1}{2}\sigma _2^2(k)}\big )^2\big (\sum \nolimits _{k=1}^N\pi _k\root 3 \of {\theta (k)+\alpha (k)+\mu (k)+\frac{1}{2}\sigma _3^2(k)}\big )},\\ \root 3 \of {c_2}= & {} \frac{\sum \nolimits _{k=1}^N\pi _k\root 3 \of {\beta (k)(1-\eta _1)\delta (k)\Lambda (k)}}{\big (\sum \nolimits _{k=1}^N\pi _k\root 3 \of {\mu (k)+\delta (k) +\frac{1}{2}\sigma _2^2(k)}\big )\big (\sum \nolimits _{k=1}^N\pi _k\root 3 \of {\theta (k)+\alpha (k)+\mu (k)+\frac{1}{2}\sigma _3^2(k)}\big )^2}, \end{aligned}$$

\(\lambda (k)\) will be determined later, \(\varrho >0\) and \({\mathcal {M}}_2>0\) such that

$$\begin{aligned} \varrho <2\check{\mu }/({\hat{\sigma }}_1^2\vee {\hat{\sigma }}_2^2\vee {\hat{\sigma }}_3^2),\ \ -{\tilde{\vartheta }}{\mathcal {M}}_2+{\tilde{C}}_2\le -2, \end{aligned}$$

where \({\tilde{\vartheta }}=\sum _{k=1}^{N}\pi _k(\mu (k)+\frac{1}{2}\sigma _1^2(k))(\tilde{{\mathfrak {R}}}_0-1)\) and

$$\begin{aligned} {\tilde{C}}_2= & {} \sup _{(S,E,I)\in {{\mathbb {R}}}_+^3}\left\{ -\frac{1}{2}[\check{\mu }-\frac{p}{2}({\hat{\sigma }}_1^2\vee {\hat{\sigma }}_2^2\vee {\hat{\sigma }}_3^2)] (S^{p+1}+E^{p+1}+I^{p+1})\right. \\&\quad \left. +{\hat{\beta }}(1-\eta _1)\eta _2E+J+2{\hat{\mu }}+{\hat{\delta }}+\frac{1}{2}{\hat{\sigma }}_1^2+\frac{1}{2}{\hat{\sigma }}_2^2\right\} . \end{aligned}$$

Obviously, \({\tilde{W}}(S,E,I,k)\) admits a minimum value point \((S_*,E_*,I_*,k)\) in the interior of \({{\mathbb {R}}}_+^3\times {{\mathbb {S}}}\). Consider a nonnegative \(C^2\)-function as follows

$$\begin{aligned} \begin{array}{lll} {\mathcal {W}}(S,E,I,k)={\tilde{W}}(S,E,I,k)-{\tilde{W}}(S_*,E_*,I_*,k)\\ \qquad \qquad \qquad \qquad ={\mathcal {M}}_2(-\ln S-c_1\ln E-c_2\ln I-\frac{1}{{\hat{\delta }}}\check{\beta }(1-\eta _1)\eta _2I+\lambda (k))\\ \qquad \qquad \qquad \qquad \qquad +\frac{1}{\varrho +1}(S+E+I)^{\varrho +1}-\ln S-\ln E-{\tilde{W}}(S_*,E_*,I_*,k)\\ \qquad \qquad \qquad \qquad ={\mathcal {M}}_2({\mathcal {W}}_1+\lambda (k))+{\mathcal {W}}_2+{\mathcal {W}}_3, \end{array} \end{aligned}$$

where \({\mathcal {W}}_1=-\ln S-c_1\ln E-c_2\ln I-\frac{\check{\beta }(1-\eta _1)\eta _2}{{\hat{\delta }}}I,{\mathcal {W}}_2=\frac{1}{\varrho +1}(S+E+I)^{\varrho +1}, {\mathcal {W}}_3=-\ln S-\ln E-{\tilde{W}}(S_*,E_*,I_*,k)\). One derives, by Itô’s formula to \({\mathcal {W}}_1\), that

$$\begin{aligned} \begin{array}{lll} L{\mathcal {W}}_1=-\frac{\Lambda (k)}{S}+\beta (k)(1-\eta _1)I+\beta (k)(1-\eta _1)\eta _2E+\mu +\frac{1}{2}\sigma _1^2(k)\\ \qquad \qquad -c_1\beta (k)(1-\eta _1)\frac{SI}{E}-c_1\beta (k)(1-\eta _1)\eta _2S+c_1(\mu (k)+\delta (k)+\frac{1}{2}\sigma _2^2(k))\\ \qquad \qquad -c_2\delta (k)\frac{E}{I}+c_2(\theta (k)+\alpha (k)+\mu (k)+\frac{1}{2}\sigma _3^2(k))-\frac{1}{{\hat{\delta }}}\check{\beta }(1-\eta _1)\eta _2\delta (k)E\\ \qquad \qquad +\frac{1}{{\hat{\delta }}}\check{\beta }(1-\eta _1)\eta _2(\theta (k)+\mu (k)+\alpha (k))I\\ \qquad \quad \le -3\root 3 \of {c_1c_2\Lambda (k)\beta (k)(1-\eta _1)\delta (k)}+c_1(\mu (k)+\delta (k)+\frac{1}{2}\sigma _2^2(k))\\ \qquad \qquad +c_2(\theta (k)+\alpha (k)+\mu (k)+\frac{1}{2}\sigma _3^2(k))+\mu (k)+\frac{1}{2}\sigma _1^2(k)\\ \qquad \qquad +\check{\beta }(1-\eta _1)[1+\frac{1}{{\hat{\delta }}}\eta _2(\check{\theta }+\check{\alpha }+\check{\mu })]I\\ \qquad \quad ={\bar{R}}_0(k)+\check{\beta }(1-\eta _1)[1+\frac{1}{{\hat{\delta }}}\eta _2(\check{\theta }+\check{\alpha }+\check{\mu })]I, \end{array} \end{aligned}$$

where

$$\begin{aligned} \begin{array}{lll} {\bar{R}}_0(k)=-3\root 3 \of {c_1c_2\Lambda (k)\beta (k)(1-\eta _1)\delta (k)}+c_1(\mu (k)+\delta (k)+\frac{1}{2}\sigma _2^2(k))\\ \qquad \qquad +c_2(\theta (k)+\alpha (k)+\mu (k)+\frac{1}{2}\sigma _3^2(k))+\mu (k)+\frac{1}{2}\sigma _1^2(k). \end{array} \end{aligned}$$

Now, we define \({\bar{R}}_0=({\bar{R}}_0(1),{\bar{R}}_0(2),\ldots ,{\bar{R}}_0(N))^\top \), and since the generator matrix \(\Gamma \), so there exists a solution \(\lambda =(\lambda (1),\lambda (2),\ldots ,\lambda (N))^\top \) for the following Poisson system

$$\begin{aligned} \Gamma \lambda =\sum _{h=1}^N\pi _h{\bar{R}}_0(h)-{\bar{R}}_0. \end{aligned}$$

This shows that

$$\begin{aligned} \sum _{l\in {{\mathbb {S}}}}\gamma _{kl}\lambda (l)+{\bar{R}}_0(k)=\sum _{k=1}^N\pi _k{\bar{R}}_0(k), \end{aligned}$$

which together with the definitions of \(c_1\) and \(c_2\) leads to

$$\begin{aligned} \begin{array}{lll} L({\mathcal {W}}_1+\lambda (k)) \le {\bar{R}}_0(k)+\check{\beta }(1-\eta _1)[1+\frac{1}{{\hat{\delta }}}\eta _2(\check{\theta }+\check{\alpha }+\check{\mu })]I +\sum _{l\in {{\mathbb {S}}}}\gamma _{kl}\lambda (l)\\ \qquad \qquad \qquad \qquad =\sum _{k=1}^N\pi _k{\bar{R}}_0(k)+\check{\beta }(1-\eta _1)[1+\frac{1}{{\hat{\delta }}}\eta _2(\check{\theta }+\check{\alpha }+\check{\mu })]I\\ \qquad \qquad \qquad \qquad =-\sum _{k=1}^N\pi _k(\mu (k)+\frac{\sigma _1^2(k)}{2})({\mathfrak {R}}_0^s-1)\\ \qquad \qquad \qquad \qquad \quad +\check{\beta }(1-\eta _1) [1+\frac{1}{{\hat{\delta }}}\eta _2(\check{\theta }+\check{\alpha }+\check{\mu })]I. \end{array} \end{aligned}$$

The remaining proof is similar to (2.6)-(2.19), and hence is omitted. So model (1.6) admits a unique ESD. \(\square \)

4 Numerical simulations

In this sequel, we will focus on illustrating the feasibility of theoretical results on models (1.4) and (1.6) by two numerical examples. Assume that initial values of models (1.4) and (1.6) are given by \((S(0),E(0),I(0))=(0.3,0.4,0.2)\).

Fig. 2
figure 2

a Periodic solution of the stochastic model (1.4) with \(\sigma _1(t)=\sigma _2(t)=\sigma _3(t)\equiv 0\). b Periodic solution of the stochastic model (1.4). c The phase portraits of S(t) and I(t) of model (1.4) and its corresponding deterministic model. d The phase portraits of a and b

Full size image

Example 1

In model (1.4), we fix the parameters \(\Lambda (t)=1+0.1\sin \pi t\), \(\mu (t)=0.2+0.1\sin \pi t\), \(\eta _1=0.2\), \(\eta _2=0.2\), \(\beta (t)=0.5+0.1\sin \pi t\), \(\theta (t)=0.15+0.1\sin \pi t\), \(\delta (t)=0.5+0.1\sin \pi t\), \(\alpha (t)=0.25+0.1\sin \pi t\), \(\sigma _1(t)=\sigma _2(t)=\sigma _3(t)=0.01+0.05\sin \pi t\). A calculation shows that \({\mathfrak {R}}\approx 2.462713>1\). So it follows from Theorem 2.1 that model (1.4) has a T-periodic solution, we can clearly see Fig. 2. Moreover Fig. 2a, b show that S(t), E(t), I(t) fluctuate periodically.

Example 2

In model (1.6), we assume that the Markov chain \(\xi (t)\) switches among these states \({{\mathbb {S}}}=\{1,2\}\) with the generator

$$\begin{aligned} \Gamma =\left( \begin{array}{ccc} -6&{} 6\\ 4 &{} -4\\ \end{array} \right) , \end{aligned}$$

and the corresponding stationary distribution \(\pi =(\pi _1,\pi _2)=(0.4,0.6)\). Select \(\Lambda (1)=0.9\), \(\beta (1)=0.4\), \(\alpha (1)=0.25\), \(\mu (1)=0.2\), \(\theta (1)=0.15\), \(\eta _1=0.2\), \(\eta _2=0.2\), \(\sigma _1(1)=0.05\), \(\sigma _2(1)=0.05\), \(\sigma _3(1)=0.05\), \(\Lambda (2)=1\), \(\beta (2)=0.6\), \(\alpha (2)=0.3\), \(\mu (2)=0.3\), \(\theta (2)=0.25\), \(\eta _1=0.2\), \(\eta _2=0.2\), \(\sigma _1(2)=0.1\), \(\sigma _2(2)=0.1\), \(\sigma _3(2)=0.1\), and then \({\mathfrak {R}}_0^s=1.0528286>1\). So we know from Theorem 3.1 that model (1.6) owns a unique ESD, this result is illustrated by Fig. 3.

Fig. 3
figure 3

a Markov chain. b A stationary distribution of the stochastic model (1.6). c–e The probability density functions (PDF) of S(t), E(t), and I(t) in model (1.6), respectively.

Full size image

5 Discussions

As a continuation of our previous work [37], based on the stochastic model (1.3) with infectivity in the latent period and household quarantine, we continue to consider two types of stochastic models, in which the periodic variation and telephone noise are respectively considered (see models (1.4) and (1.6)). Two sets of sufficient criteria are respectively established for the T-periodic solution and the existence of a unique ESD, see Theorems 2.1 and 3.1. From the above theoretical results, the conclusions are summarised below.

  • We can conclude that, by Theorem 2.1, model (1.4) has a positive T-periodic solution if \({\mathfrak {R}}>1\). Recalling the expression of \({\mathfrak {R}}\), we find that low noise intensities \(\sigma _i^2(i=1,2,3)\) and inadequate cooperation from the household quarantine rate \(\eta _1\) can prevent the disease from dying out, in other words, the disease will fluctuate periodically.

  • We have shown that, under Theorem 3.1, model (1.6) owns a unique ESD if \({\mathfrak {R}}_0^s>1\). This implies that decreasing the noise intensities \(\sigma _i^2(i=1,2,3)\) and the household quarantine rate \(\eta _1\) can lead to a prevalence level of the disease. It is evident that household quarantine, if it is strictly implemented by the government, plays a crucial role in controlling the disease spread, which is consistent with that of Refs. [25, 37]. It’s necessary to point out that China has accomplished an unprecedented gigantic achievement, which benefits from the whole government’s swift and decisive response in a short time, including the detection of cases to immediate isolation, strict contact tracing, medical observation of all contacts, as well as household quarantine. Particular emphasis is that both household quarantine and the latent individuals tracing have significant influences on the control of the epidemic.

Finally, we should point out that our present work is only considered the stochastic dynamics of the three-dimensional models (1.4) and (1.6) with variables S, E and I. In fact, it will deserve to respectively incorporate the periodic variation and telephone noise into the variable R in four-dimensional model. Also, some interesting topics deserve further investigation. We can explore the effects of delay [36] or impulse [30] on periodic model (1.4), and may study model (1.6) driven by Lévy jumps [29]. We leave these issues for future consideration.