Skip to main content

Advertisement

SpringerLink
Log in

Stability analysis of a logistic growth epidemic model with two explicit time-delays, the nonlinear incidence and treatment rates

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

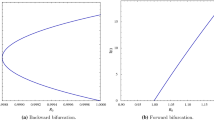
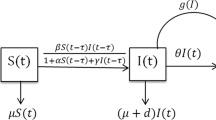
In the present study, a time-delayed SIR epidemic model with a logistic growth of susceptibles, Crowley–Martin type incidence, and Holling type III treatment rates is proposed and analyzed mathematically. We consider two explicit time-delays: one in the incidence rate of new infection to measuring the impact of the latent period, and another in the treatment rate of infectives to analyzing the effect of late treatment availability. The stability behavior of the model is analyzed for two equilibria: the disease-free equilibrium (DFE) and the endemic equilibrium (EE). We derive the threshold quantity, the basic reproduction number \(R_0\), which determines the eradication or persistence of infectious diseases in the host population. Using the basic reproduction number, we show that the DFE is locally asymptotically stable when \(R_0< 1\), linearly neutrally stable when \(R_0= 1\), and unstable when \(R_0> 1\) for the time-delayed system. We analyze the system without a latent period, revealing the forward bifurcation at \(R_0= 1\), which implies that keeping \(R_0\) below unity can diminish the disease. Further, the stability behavior for the EE is investigated, demonstrating the occurrence of oscillatory and periodic solutions through Hopf bifurcation concerning every possible grouping of two time-delays as the bifurcation parameter. To conclude, the numerical simulations in support of the theoretical findings are carried out.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Owolabi, K.M.: Mathematical study of two-variable systems with adaptive numerical methods. Numer. Anal. Appl. 9, 218–230 (2016)

    Article  MathSciNet  Google Scholar 

  2. Owolabi, K.M.: Numerical solution of diffusive HBV model in a fractional medium. SpringerPlus 5, 1643 (2016)

    Article  Google Scholar 

  3. Owolabi, K.M., Patidar, K.C.: Numerical simulations of multicomponent ecological models with adaptive methods. Theor. Biol. Med. Model. 13, 1 (2016)

    Article  Google Scholar 

  4. Owolabi, K.M., Patidar, K.C., Shikongo, A.: Mathematical analysis and numerical simulation of a tumor-host model with chemotherapy application. Commun. Math. Biol. Neurosci. 2018, 21 (2018)

    Google Scholar 

  5. Owolabi, K.M., Patidar, K.C., Shikongo, A.: Efficient numerical method for a model arising in biological stoichiometry of tumour dynamics. Discrete Contin. Dyn. Syst.S 12(3), 591–613 (2019)

    Article  MathSciNet  Google Scholar 

  6. Owolabi, K.M., Atangana, A.: Mathematical analysis and computational experiments for an epidemic system with nonlocal and nonsingular derivative. Chaos Solitons Fract. 126, 41–49 (2019)

    Article  MathSciNet  Google Scholar 

  7. Owolabi, K.M., Shikongo, A.: Mathematical modelling of multi-mutation and drug resistance model with fractional derivative. Alex. Eng. J. 59(4), 2291–2304 (2020)

    Article  Google Scholar 

  8. Mishra, A.M., Purohit, S.D., Owolabi, K.M., Sharma, Y.D.: A nonlinear epidemiological model considering asymptotic and quarantine classes for SARS CoV-2 virus. Chaos Solitons Fract. 138, 109953 (2020)

    Article  MathSciNet  Google Scholar 

  9. Kermack, W.O., Mckendrick, A.G.: A contribution to the mathematical theory of epidemic. Proc. R. Soc. Lond. 115(772), 700–721 (1927)

    MATH  Google Scholar 

  10. Hethcote, H.W., van den Driessche, P.: An SIS epidemic model with variable population size and a delay. J. Math. Biol. 34, 177–194 (1995)

    Article  MathSciNet  Google Scholar 

  11. d’Onofrio, A., Manfredi, P., Salinelli, E.: Vaccinating behaviour, information, and the dynamics of SIR vaccine preventable diseases. Theor. Popul. Biol. 71(3), 301–317 (2007)

    Article  Google Scholar 

  12. Zhang, J.Z., Jin, Z., Liu, Q.X., Zhang, Z.Y.: Analysis of a delayed SIR model with nonlinear incidence rate. Discrete Dyn. Nat. Soc. 2008, 636153 (2009)

    MathSciNet  MATH  Google Scholar 

  13. Wang, J.J., Zhang, J.Z., Jin, Z.: Analysis of an SIR model with bilinear incidence rate. Nonlinear Anal. Real World Appl. 11(4), 2390–2402 (2010)

    Article  MathSciNet  Google Scholar 

  14. Xue, Y., Li, T.: Stability and Hopf bifurcation for a delayed SIR epidemic model with logistic growth. Abstr. Appl. Anal. 2013, 916130 (2013)

    Article  MathSciNet  Google Scholar 

  15. Kumar, A., Nilam: Dynamic Behavior of an SIR epidemic model along with time delay; Crowley–Martin type incidence rate and Holling type II treatment rate. Int. J. Nonlinear Sci. Numer. Simul. 20(7–8), 757–771 (2019)

  16. Goel, K., Nilam: Stability behavior of a nonlinear mathematical epidemic transmission model with time delay. Nonlinear Dyn. 98, 1501–1518 (2019)

  17. Mena-Lorca, J., Hethcote, H.W.: Dynamic models of infectious disease as regulators of population size. J. Math. Biol. 30(7), 693–716 (1992)

    MathSciNet  MATH  Google Scholar 

  18. Gumel, A.B., McCluskey, C.C., Watmough, J.: An SVEIR model for assessing potential impact of an imperfect anti-SARS vaccine. Math. Biosci. Eng. 3(3), 485–512 (2007)

    MathSciNet  MATH  Google Scholar 

  19. Tipsri, S., Chinviriyasit, W.: Stability analysis of SEIR model with saturated incidence and time delay. Int. J. Appl. Phys. Math. 4(1), 42–45 (2014)

    Article  Google Scholar 

  20. Goel, K., Kumar, A., Nilam: A deterministic time-delayed SVIRS epidemic model with incidences and saturated treatment. J. Eng. Math. 121, 19–38 (2020)

  21. Goel, K., Kumar, A., Nilam: Nonlinear dynamics of a time-delayed epidemic model with two explicit aware classes, saturated incidences, and treatment. Nonlinear Dyn. 101, 1693–1715 (2020)

  22. Kumar, A.: Stability of a fractional-order epidemic model with nonlinear incidences and treatment rates. Iran. J. Sci. Technol. Trans. A Sci. 44, 1505–1517 (2020)

    Article  MathSciNet  Google Scholar 

  23. Liu, W., Levin, S.A., Iwasa, Y.: Influence of nonlinear incidence rates upon the behavior of SIRS epidemiological models. J. Math. Biol. 23, 187–204 (1986)

    Article  MathSciNet  Google Scholar 

  24. Dubey, B., Patra, A., Srivastava, P.K., Dubey, U.S.: Modeling and analysis of an SEIR model with different types of nonlinear treatment rates. J. Biol. Syst. 21(03), 1350023 (2013)

    Article  MathSciNet  Google Scholar 

  25. Dubey, P., Dubey, B., Dubey, U.S.: An SIR model with nonlinear incidence rate and Holling type III treatment rate. In: Cushing, J., Saleem, M., Srivastava, H., Khan, M., Merajuddin, M. (eds.) Applied Analysis in Biological and Physical Sciences. Springer Proceedings in Mathematics and Statistics 186, Springer, New Delhi (2016)

    MATH  Google Scholar 

  26. Crowley, P.H., Martin, E.K.: Functional responses and interference within and between year classes of a dragonfly population. J. N. Am. Benthol. Soc. 8(3), 211–221 (1989)

    Article  Google Scholar 

  27. Song, X., Cheng, S.: A delay-differential equation model of HIV infection of CD4+ T-cells. J. Korean Math. Soc. 42(5), 1071–1086 (2005)

    Article  MathSciNet  Google Scholar 

  28. Xu, R., Ma, Z.: Stability of a delayed SIRS epidemic model with a nonlinear incidence rate. Chaos Solitons Fract. 41(5), 2319–2325 (2009)

    Article  MathSciNet  Google Scholar 

  29. Shan, C., Zhu, H.: Bifurcations and complex dynamics of an SIR model with the impact of the number of hospital beds. J. Differ. Equ. 257(5), 1662–1688 (2014)

    Article  MathSciNet  Google Scholar 

  30. Wang, W., Ruan, S.: Bifurcation in an epidemic model with constant removal rates of the infectives. J. Math. Anal. Appl. 21, 775–793 (2004)

    Article  MathSciNet  Google Scholar 

  31. Wang, W.: Backward bifurcation of an epidemic model with treatment. Math. Biosci. 201, 58–71 (2006)

    Article  MathSciNet  Google Scholar 

  32. Zhou, L., Fan, M.: Dynamics of an SIR epidemic model with limited medical resources revisited. Nonlinear Anal. Real World Appl. 13(1), 312–324 (2012)

    Article  MathSciNet  Google Scholar 

  33. Wu, K., Darcet, D., Wang, Q., Sornette, D.: Generalized logistic growth modeling of the COVID-19 outbreak: comparing the dynamics in the 29 provinces in China and in the rest of the world. Nonlinear Dyn. 101, 1561–1581 (2020)

    Article  Google Scholar 

  34. Li, J., Teng, Z., Wang, G., Zhang, L., Hu, C.: Stability and bifurcation analysis of an SIR epidemic model with logistic growth and saturated treatment. Chaos Solitons Fract. 99, 63–71 (2017)

    Article  MathSciNet  Google Scholar 

  35. Avila-Vales, E., Pérez, Á.G.C.: Dynamics of a time-delayed SIR epidemic model with logistic growth and saturated treatment. Chaos Solitons Fract. 127, 55–69 (2019)

    Article  MathSciNet  Google Scholar 

  36. Hale, J.K., Lunel, S.M.V.: Introduction to Functional Differential Equations. Springer, New York (1993)

    Book  Google Scholar 

  37. van den Driessche, P., Watmough, J.: Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180(1–2), 29–48 (2002)

    Article  MathSciNet  Google Scholar 

  38. Guckenheimer, J., Holmes, P.: Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields. Springer, Berlin (1983)

    Book  Google Scholar 

  39. Castillo-Chavez, C., Song, B.: Dynamical models of tuberculosis and their applications. Math. Biosci. Eng. 1(2), 361–404 (2004)

    Article  MathSciNet  Google Scholar 

  40. Wang, X.: A simple proof of Descartes’s rule of signs. Am. Math. Mon. 111(6), 525–526 (2004)

    Article  Google Scholar 

  41. Hassard, B.D., Kazarinoff, N.D., Wan, Y.H.: Theory Applications of Hopf Bifurcation. Cambridge University Press, Cambridge (1981)

    MATH  Google Scholar 

  42. Shampine L.F., Thompson S.: Numerical solution of delay differential equations. In: Delay Differential Equations. Springer, Boston (2009). https://doi.org/10.1007/978-0-387-85595-0_9

  43. Rebenda, J., Šmarda, Z.: Numerical algorithm for nonlinear delayed differential systems of nth order. Adv. Differ. Equ. 2019, 26 (2019)

    Article  Google Scholar 

Download references

Acknowledgements

The authors are grateful to the Delhi Technological University, Delhi, India, for providing financial support to carry out this research work. They are also indebted to the handling editor and the anonymous reviewers for their constructive comments and suggestions, which led to an improvement in the original manuscript.

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, Delhi Technological University, Delhi, 110042, India

    Kanica Goel &  Nilam

  2. Department of Mathematics, School of Basic Sciences and Research, Sharda University, Greater Noida, 201310, India

    Abhishek Kumar

Authors
  1. Kanica Goel
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Abhishek Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Nilam
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Abhishek Kumar or Nilam.

Ethics declarations

Conflict of interest

The authors have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Goel, K., Kumar, A. & Nilam Stability analysis of a logistic growth epidemic model with two explicit time-delays, the nonlinear incidence and treatment rates. J. Appl. Math. Comput. 68, 1901–1928 (2022). https://doi.org/10.1007/s12190-021-01601-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-021-01601-1

Keywords

Mathematics Subject Classification

Search

Navigation