Solving the Cauchy problem for the Helmholtz equation using cubic smoothing splines

Abstract

We consider the Cauchy problem for the Helmholtz equation defined in a rectangular domain. The Cauchy data are prescribed on a part of the boundary and the aim is to find the solution in the entire domain. The problem occurs in applications related to acoustics and is illposed in the sense of Hadamard. In our work we consider regularizing the problem by introducing a bounded approximation of the second derivative by using Cubic smoothing splines. We derive a bound for the approximate derivative and show how to obtain stability estimates for the method. Numerical tests show that the method works well and can produce accurate results. We also demonstrate that the method can be extended to more complicated domains.

1 Introduction

The Cauchy problem for the Helmholtz equation arises in many areas of applied science in relation to wave propagation, vibration and electromagnetic wave scattering. The commonly considered waves being water, sound and electromagnetic waves. It is often used in the determination of acoustic cavities [5] or the detection of the source of acoustical noise [6, 23]. Other applications include the description of underwater waves [10], the determination of the radiation field surrounding a source of radiation [21], the localization of a tumor in a human brain [13], the identification and location of vibratory sources [15, 16] and the detection of surface vibrations from interior acoustical pressure [7].

The Cauchy problem for the Helmholtz equation is ill-posed, in the sense of Hadamard, see [9], and therefore regularization is needed. In the literature, different regularization methods have been applied to the Cauchy problem for the Helmholtz equation. In [25] the problem was treated in the frequency domain, and an a priori bound $\Vert u(\cdot ,a)\Vert _2$ was used to stabilize the problem. A similar approach was used in [14], where the problem was stabilized using Meyer wavelets, which are compactly supported in the frequency domain, and also in [12]. In [24], the problem was regularized using a modified Tikhonov method. We also refer to [1,2,3,4, 19, 26], and the references therein, for more regularization techniques that have been successfully applied to the problem.

In this paper, we develop a novel regularization method for the Cauchy problem for the Helmholtz equation. In our previous work [18] we have shown that approximating a derivative by a bounded approximation based on Cubic smoothing splines has a stabilizing effect for the inverse heat conduction problem. Here we apply the same technique to the Helmholtz equation and are able to derive stability estimates. Also, we implement the method numerically and demonstrate that the method works well. Finally, we extend the method to the case of a modified Helmholtz equation, $\Delta u+\alpha u=0$, where $\alpha :=\alpha (x,y)>0$ is a function. The modified Helmholtz equation appears in situations where the problem is solved in more complicated domains .

2 The Helmholtz equation and ill-posedness

We consider the following Cauchy problem for the Helmholtz equation, in the rectangular domain $\Omega = [0,1] \times [0,a]$: Find $u \in C^2(\Omega ) \cap C^1(\bar{\Omega })$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{xx} + u_{yy} + k^2u = 0,\quad &{} 0\le x\le 1,\,0< y < a, \\ u(x,0) = g(x), &{} 0\le x\le 1,\\ u_y(x,0)= \eta (x), &{} 0 \le x \le 1, \\ u(0,y)= u(1,y) = 0 &{} 0 \le y \le a, \end{array}\right. } \end{aligned}$$

(2.1)

where $k^2$ represents the wave number and g(x) and $\eta (x)$ are the Cauchy data, available on part of the boundary of the domain.

The solution to (2.1), computed by the method of separation of variables, is

$$\begin{aligned} u(x,y) = \sum _{j=1}^\infty \sin (j\pi x)\left( {\widehat{g}}_j\cosh \left( \omega _j y\right) + \frac{{\widehat{\eta }}_j}{\omega _j}\sinh \left( \omega _j y\right) \right) , \end{aligned}$$

(2.2)

where $\omega _j= (j^2\pi ^2-k^2)^{1/2}$ is a frequency, and

$$\begin{aligned} {\widehat{g}}_j = 2\int _0^1g(x)\sin (j\pi x)\quad dx\quad \text{ and }\quad \widehat{\eta }_j = 2\int _0^1\eta (x)\sin (j\pi x) \quad dx, \end{aligned}$$

are the Fourier–Sine coefficients. Note that the frequencies $\omega _j$ may be either real or complex.

The series (2.2) is convergent for the case of exact Cauchy data $[g,\eta ]$. If we instead have noisy data $[g^\delta , \eta ^\delta ]$, such that $\Vert g^\delta -g\Vert _2$ and $\Vert \eta ^\delta -\eta \Vert _2\le \delta$, where $\delta$ is a bound on the error, then there is no guarantee that the solution exists. This is because the magnification factors, e.g. $|\cosh (\omega _j y)|$ and $|\sinh (\omega _j y)/\omega _j|$, for a fixed $y>0$, grows exponentially as $j\rightarrow \infty$. Thus a small error in the Fourier coefficients, i.e. $\widehat{g}_j$ and $\widehat{\eta }_j$, for large values of j, are blown-up and may destroy the solution. This means that the problem is severely ill-posed, and stabilization is needed [9].

We remark that while the Cauchy problem (2.1) has a unique solution the same is not necessarily true for the boundary value problem obtained by replacing the Cauchy data, at $y=0$, by Dirichlet data $u(x,a)=f(x)$ and $u(x,0)=g(x)$. This can easily be seen by considering the function,

$$\begin{aligned} u_0(x,y)=\sin (\pi x)\sin (\pi a^{-1} y), \end{aligned}$$

(2.3)

which satisfies the Helmholtz equation in the domain $\Omega$, with the wave number $k^2=\pi ^2+(\pi /a)^2$ and zero Dirichlet data. Similar solutions can be constructed for the case of zero Neumann, or Robin boundary, conditions. For our work we avoid issues related to non-uniqueness of the solution by only considering small values of the wave-number, i.e. $k^2\le \pi ^2(1+1/a^2)$, see [1].

2.1 Stabilization by discretizing the x-axis

In this section we stabilize the Cauchy problem for the Helmholtz equation by discretizing the x-variable. We replace the second derivative $\partial _x^2$ by a matrix $D^2$ in order to regularize the problem. For this purpose we rewrite (2.1) as an initial-value problem

$$\begin{aligned} \left( \begin{array}{c} u \\ u_y \end{array}\right) _y= \left( \begin{array}{cc} 0 &{} 1 \\ -(k^2 + \partial _x^2) &{} 0 \end{array}\right) \left( \begin{array}{c} u \\ u_y \end{array}\right) ,\quad 0 \le y \le a, \end{aligned}$$

(2.4)

with initial-boundary data

$$\begin{aligned} u(x,0)=g(x),\,u_y(x,0)=\eta (x),\quad \text{ for } \quad 0 \le x \le 1, \end{aligned}$$

(2.5)

and

$$\begin{aligned} u(0,y)= u(1,y) =0,\quad \text{ for }\quad 0\le y \le a. \end{aligned}$$

(2.6)

We discretize (2.4) on a uniform grid $0=x_1< \dots <x_n=1$. For simplicity we introduce an operator that samples the functions on the grid such that, e.g

$$\begin{aligned} g_\Delta =(g(x))_\Delta =(g(x_1),\dots , g(x_n))^T. \end{aligned}$$

By introducing semi-discrete representations of the solution and its derivative, i.e.

$$\begin{aligned} U(y)=(u(\cdot , y))_\Delta \quad \text{ and }\quad U_y(y)=(u_y(\cdot ,y))_\Delta , \end{aligned}$$

we obtain the initial value problem,

$$\begin{aligned} \left( \begin{array}{c} U \\ U_y \end{array}\right) _y= \left( \begin{array}{cc} 0 &{} I \\ -(k^2I + D^2) &{} 0 \end{array}\right) \left( \begin{array}{c} U \\ U_y \end{array}\right) , \quad 0 \le y \le a, \end{aligned}$$

(2.7)

with initial data $U(0)=g_\Delta$ and $U_y(0)=\eta _\Delta$. The solution to (2.7) can formally be written as

$$\begin{aligned} \left( \begin{array}{c} U \\ U_y \end{array}\right) = e^{\mathcal {B}y}\left( \begin{array}{c} {g}_\Delta \\ {\eta }_\Delta \end{array}\right) ,\quad \text{ where } \quad \mathcal {B} = \left( \begin{array}{cc}0 &{} I \\ -(k^2I + D^2) &{} 0 \end{array}\right) . \end{aligned}$$

(2.8)

In [8] it was observed that since for any matrix the $\Vert D^2\Vert _2$ is bounded. Thus the system of ordinary differential equations (2.7) is well-posed and the solution depends in a stable way on the used data. By controlling the accuracy of the approximation $D^2$ the degree of stability can be adjusted to be suitable for a problem with a specific noise level.

3 Regularization by cubic smoothing splines

In this section we demonstrate that the Cauchy Problem for the Helmholtz equation can be regularized by using a cubic smoothing spline. We show how the approximation of $\partial _x^2 \approx D^2$ is achieved using a cubic smoothing spline and also develop and prove Lemmas on the stability of the resulting regularized solution.

3.1 Differentiation by cubic smoothing splines

We adopt the basic notation about splines and introduce the second derivative matrix $D_{\lambda }^2$, show its properties and derive its bound in the Euclidean norm. We use a uniform grid, with grid parameter h. We work in an $L^2$ setting and introduce the Sobolev space

$$\begin{aligned} W^2[0,1]=\{u\,:\,u,u^\prime \,\text { abs. cont. on }[0,1] \text { and } u^{\prime \prime }\in L^2[0,1]\,\}, \end{aligned}$$

(3.9)

together with the standard norms and semi-norms as defined in [20].

Let $y = (y_1, y_2,\ldots ,y_n)^T$ be a vector of data values on the grid. The cubic smoothing spline that approximates y on the grid is defined as follows:

Definition 3.1

Let $y\in {\mathbb {R}}^n$ be a vector. The cubic smoothing spline $s_\lambda [y]$ is obtained by solving

$$\begin{aligned} \min _{u \in W^2[0,1]} h\Vert y - u_\Delta \Vert _2^2 + \lambda |u|_2^2, \end{aligned}$$

(3.10)

where $\lambda >0$ is the regularization parameter and $|u|_2$ denotes the semi-norm.

It is known that the solution to (3.10) is a natural cubic spline and the corresponding operator, mapping $y\in \mathbb {R}^n$ onto $s_\lambda [y]\in W^2([0,1])$, is linear, see [20, 22]. Thus we can introduce a matrix approximating the second derivative as follows:

Definition 3.2

The matrix $D_\lambda ^2 \in \mathbb {R}^{n \times n}$ is defined by

$$\begin{aligned} D_\lambda ^2 y = (s_\lambda ''[y](x))_\Delta ,\quad \text { for all }y\in \mathbb {R}^n. \end{aligned}$$

(3.11)

The following properties of the matrix are useful:

Lemma 3.3

The matrix $D_{\lambda }^2$ is real and symmetric.

Proof

The matrix $D_\lambda ^2$ can be represented as $D_\lambda ^2=EWA^T$, where the matrix $W=h(hA^TA+\lambda B)^{-1}$, with $(B)_{ij} = (\beta _i, \beta _j)_2$ is symmetric, $(A)_{ij}=\beta _j(x_i)$, and $(E)_{ij}=\beta _j^{\prime \prime }(x_i)$, see [18]. A direct computation shows that

$$\begin{aligned} (D_\lambda ^2)_{i,j}=\sum _{l=1}^{n+1}\sum _{k=1}^{n+1} \beta _l^{\prime \prime }(x_i)w_{lk}\beta _k(x_j). \end{aligned}$$

(3.12)

Since both $\beta _k(x)$ and $\beta _k^{\prime \prime }(x)$ are even functions, with respect to $x=x_k$, then we have $\beta _l^{\prime \prime }(x_i)\beta _k(x_j)=\beta _l^{\prime \prime }(x_j)\beta _k(x_i)$. Hence rearranging the indicies shows that $(D_\lambda ^2)_{ij}=(D_\lambda ^2)_{ji}$, and the matrix is symmetric with real entries. $\square$

Proposition 3.4

The matrix $D_{\lambda }^2$ satisfies

$$\begin{aligned} \Vert D_{\lambda }^2\Vert \le c_3 \lambda ^{-1/2}, \end{aligned}$$

(3.13)

where $c_3$ is a constant.

Proof

Since the second derivative of a cubic spline u is piecewise linear, with respect to the grid $\Delta$, we have $h\Vert (u^{\prime \prime })_\Delta \Vert _2^2\le c_1^2|u^{\prime \prime }|_0^2$, where $c_1$ is a constant. Then from the definition of $D_\lambda ^2$ we have

$$\begin{aligned} \Vert D_\lambda ^2 y\Vert _2^2 = \Vert (u^{\prime \prime })_\Delta \Vert _2^2 \le \frac{c_1^2}{h}|u^{\prime \prime }|_0^2=\frac{c_1^2}{h}|u|_2^2, \end{aligned}$$

(3.14)

where $u(x)=s_\lambda [y](x)$ is the smoothing cubic spline corresponding to the vector $y\in {\mathbb {R}}^n$. Let $y=y-u_\Delta +u_\Delta$, then we can expand $\Vert y\Vert _2^2$ as

$$\begin{aligned} \Vert y\Vert _2^2=(y-u_\Delta +u_\Delta )^T(y-u_\Delta +u_\Delta )= \Vert y-u_\Delta \Vert _2^2+2(y-u_\Delta )^Tu_\Delta +\Vert u_\Delta \Vert _2^2. \end{aligned}$$

(3.15)

A consequence of the fact that u(x) solves the least squares problem (3.10), is that $h(y-u_\Delta )^Tu_\Delta = \lambda |u|_2^2$, see [18, Lemma 3.7]. Inserting into (3.15), we obtain the estimate

$$\begin{aligned} |u|_2^2 \le \frac{h}{2\lambda }\Vert y\Vert _2^2. \end{aligned}$$

(3.16)

By using (3.16) in (3.14) we obtain the desired bound. $\square$

3.2 Stability analysis

In this section we establish stability results, for the initial value problem (2.7), when the approximation $\partial _x^2 \approx D_\lambda ^2$ is used. The proofs are based on the idea that, since $D_\lambda ^2$ is a real symmetric matrix, there exists a unitary matrix X such that

$$\begin{aligned} D_{\lambda }^2=X\Lambda _\lambda X^T,\quad (\Lambda _\lambda )_{j,j}=\mu _j, \quad j=1,2,\dots , n, \end{aligned}$$

(3.17)

where the eigenvalues $\mu _j$ are real. The stability results are established by a sequence of Lemmas:

Lemma 3.5

Let $D^2= D_\lambda ^2$ , where $\lambda$ is the regularization parameter, and let $U_1$ and $U_2$ be two different solutions to (2.7), corresponding to Cauchy data $[(g_1)_\Delta ,\eta _\Delta ]$ and $[(g_2)_\Delta , \eta _\Delta ]$, respectively. Then, if $\sigma = \sqrt{\Vert D_\lambda ^2\Vert _2 - k^2} > 0$,

$$\begin{aligned} \Vert U_1 - U_2\Vert _2 \le \cosh \left( \sigma y\right) \Vert (g_1 - g_2)_\Delta \Vert _2. \end{aligned}$$

(3.18)

Proof

Let X be as defined in (3.17) and introduce a new variable $V(y)=X^T(U_1-U_2)$. The system (2.7) simplifies to

$$\begin{aligned} V_{yy}(y)+(k^2I + \Lambda _\lambda )V(y) = 0,\qquad 0<y<a, \end{aligned}$$

(3.19)

with boundary conditions $V(0)=X^T(g_1-g_2)_\Delta$ and $V_y(0) = X^T(\eta -\eta )_\Delta =0$. Since $\Lambda _\lambda$ is a diagonal matrix, the problem (3.19) can be solved for each eigenvalue $\mu _j$ individually,

$$\begin{aligned} V_{yy}(\mu _j,y) + (k^2 +\mu _j)V(\mu _j,y)= 0, \end{aligned}$$

(3.20)

with known boundary conditions $V(\mu _j, 0)$ and $V_y(\mu _j,0)=0$. We identify two distinct cases:

Case 1 If $\mu _j + k^2 > 0$, we have the general solution as

$$\begin{aligned} V(\mu _j,y)=C_1\cos \left( \sqrt{|k^2+\mu _j|}y\right) + C_2\sin \left( \sqrt{|k^2+\mu _j|}y\right) , \end{aligned}$$

(3.21)

where we write $|k^2+\mu _j|$ to emphasize the fact that we take the square root of a positive number. The constants $C_1$ and $C_2$ are computed by using the boundary conditions and we obtain the solution

$$\begin{aligned} V(\mu _j,y)=\cos \left( \sqrt{|k^2+\mu _j|}y\right) V(\mu _j,0),\quad \text {and}\quad |V(\mu _j,y)| \le |V(\mu _j,0)|. \end{aligned}$$

(3.22)

Hence this case does not contribute to the instability of the problem.

Case 2 If $\mu _j + k^2 < 0$, we have the general solution as

$$\begin{aligned} V(\mu _j,y)=C_1e^{\sqrt{|k^2+\mu _j|}y} + C_2e^{-\sqrt{|k^2+\mu _j|}y}. \end{aligned}$$

(3.23)

Again $C_1$ and $C_2$ are computed by making use of the boundary conditions and the solution is

$$\begin{aligned} V(\mu _j,y)=\cosh \left( \sqrt{|\mu _j+k^2|}y\right) V(\mu _j,0). \end{aligned}$$

(3.24)

Now, since $k^2$ is positive and $\mu _j+k^2$ is assumed to be negative, we see that $|\mu _j + k^2| \le \Vert D_\lambda ^2\Vert _2-k^2=\sigma ^2$. Thus, due to $\cosh$ being a monotonically increasing function on the interval $[0,\infty )$, we have

$$\begin{aligned} |V(\mu _j,y)|^2\le \cosh ^2(\sigma y)|V(\mu _j,0)|^2. \end{aligned}$$

(3.25)

Here the magnification factor $\cosh (\sigma y)$ grows as $\mu _j \rightarrow -\infty$ and thus these components contribute to the instability of the problem.

Finally, since X is orthogonal, we have $\Vert V\Vert _2=\Vert U_1-U_2\Vert _2$ and

$$\begin{aligned} \Vert V\Vert _2^2 =\sum _{j=1}^n|V(\mu _j,y)|^2 \le \cosh ^2(\sigma y)\sum _{j=1}^n\left| V(\mu _j,0)\right| ^2 = \cosh ^2(\sigma y)\Vert V(0)\Vert _2^2, \end{aligned}$$

(3.26)

with $\Vert V(0)\Vert _2 =\Vert (g_1-g_2)_\Delta \Vert _2$. The proof is complete. $\square$

Lemma 3.6

Let $D^2= D_\lambda ^2$, with $\lambda$ as the regularization parameter, and let $U_1$ and $U_2$ be two different solutions to (2.7), corresponding to Cauchy data $[g_\Delta ,(\eta _1)_\Delta ]$ and $[g_\Delta , (\eta _2)_\Delta ]$. Then, if $\sigma =\sqrt{\Vert D_\lambda ^2\Vert _2 - k^2}>0$,

$$\begin{aligned} \Vert U_1 - U_2\Vert _2 \le \sigma ^{-1}\sinh \left( \sigma y\right) \Vert (\eta _1 -\eta _2)_\Delta \Vert _2. \end{aligned}$$

(3.27)

Proof

The proof is similar to that of the previous Lemma. Introduce a new variable $V(\mu _j,y)=X^T(U_1-U_2)$, and note that $V(0)=X^T(g-g)_\Delta =0$ and $V_y(0)=X^T(\eta _1-\eta _2)_\Delta$. The problem is solved for one eigenvalue at a time,

$$\begin{aligned} V_{yy}(\mu _j,y) + (k^2 +\mu _j)V(\mu _j,y)=0, \end{aligned}$$

(3.28)

with known boundary conditions $V_y(\mu _j,0)$ and $V(\mu _j,0)=0$. Again, we have two cases and if $\mu _j+k^2 > 0$ the solution can be written

$$\begin{aligned} V(\mu _j,y)=\frac{\sin \left( \sqrt{|\mu _j+k^2|}y\right) }{\sqrt{|\mu _j+k^2|}}V_y(\mu _j,0)= \frac{\sin \left( \sqrt{|\mu _j+k^2|}y\right) }{\sqrt{|\mu _j+k^2|}y}yV_y(\mu _j,0). \end{aligned}$$

(3.29)

By making use of the fact that $|\sin (\alpha )/\alpha |\le 1$ we obtain

$$\begin{aligned} |V(\mu _j,y)|\le y|V_y(\mu _j,0)|. \end{aligned}$$

(3.30)

Thus the solution components satisfying $\mu _j+k^2 > 0$ are stable.

For the case $\mu _j+k^2<0$, the solution can be verified to be

$$\begin{aligned} V(\mu _j,y)=\frac{\sinh (\sqrt{|\mu _j + k^2|}y)}{\sqrt{|\mu _j+ k^2|}}V_y(\mu _j,0). \end{aligned}$$

(3.31)

Since $k^2>0$ and $\mu _j>-\Vert D_\lambda ^2\Vert _2$ we have $|\mu _j+k^2|\le \sigma ^2$. Hence, by making use of the monotonicity of $\sinh (\alpha )/\alpha$, see [18, Lemma 2.5], we obtain

$$\begin{aligned} |V(\mu _j,y)|=\frac{\sinh (\sqrt{|\mu _j+k^2|}y)}{\sqrt{|\mu _j+k^2|}}|V_y(\mu _j,0)| \le \frac{\sinh (\sigma y)}{\sigma }|V_y(\mu _j,0)|. \end{aligned}$$

(3.32)

Since, $\sinh (\sigma y)/\sigma >y$, for $\sigma ,y>0$, the estimate (3.30), obtained for the case $\mu _j+k^2 > 0$, also satisfies (3.32). Thus both cases can be combined.

Finally, since X is orthogonal, we have

$$\begin{aligned} \Vert U_1(y)-U_2(y)\Vert _2=\Vert V(y)\Vert _2\le \sigma ^{-1}\!\sinh (\sigma y)\Vert V_y(0)\Vert _2. \end{aligned}$$

(3.33)

The final result follows by noting that $V_y(0)=(\eta _1-\eta _2)_\Delta$. $\square$

Proposition 3.7

Suppose that $U_\lambda$ is the regularized solution to (2.7), with exact data $[g,\eta ]$, and that $U_\lambda ^\delta$ is the regularized solution with noisy data $[g^\delta , \eta ^\delta ]$, where $\lambda$ is the regularization parameter. Then, if $D^2 = D_\lambda ^2$ and $\sigma =\sqrt{ \Vert D_\lambda ^2\Vert _2 - k^2}>0$,

$$\begin{aligned} \Vert U_\lambda ^\delta - U_\lambda \Vert _2 \le \cosh (\sigma y)\Vert ( g^\delta -g)_\Delta \Vert _2 + \sigma ^{-1}\sinh (\sigma y)\Vert (\eta ^\delta -\eta )_\Delta \Vert _2. \end{aligned}$$

(3.34)

Proof

Let $U_1$ be the regularized solution to (2.7) with data $[g, \eta ^\delta ]$. We have by the triangle inequality

$$\begin{aligned} \Vert U_\lambda ^\delta - U_\lambda \Vert _2 \le \Vert U_\lambda ^\delta - U_1\Vert _2 + \Vert U_1 - U_\lambda \Vert _2 \end{aligned}$$

The result then follows by applying Lemma 3.5 and Lemma 3.6 to the respective terms. $\square$

The above proposition means that the approximation $D^2\approx D_\lambda ^2$ does stabalize the computations.

4 Simulated numerical examples

The numerical implementation of the splines based approach consists of implementing the procedure for computing the matrix-vector product $D_\lambda ^2y$, for a given vector $y \in {\mathbb {R}}^n$. With the procedure in place, we are able to solve the initial value problem (2.7) using a standard Runge–Kutta method, i.e. ode23 in Matlab, with automatic step size control.

For all numerical experiments we used a uniform grid of size $n=500$ in the x-variable. Note that we do not need to specify a grid in the y-direction since this is dealt with implicitly by the Runge–Kutta code. The specific tests are detailed below.

Fig. 1

The analytical solution u(x, y) used for the tests. The wavenumber is $k^2=12$ and the domain is $\Omega =[0,1]\times [0,0.2]$. We display the function u(x, y) evaluated on a uniform grid (left graph) and also the corresponding Cauchy data, i.e. $g(x)=u(x,0)$ (right,blue/dashed) and $\eta (x)=u_y(x,0)$ (right,black/solid)

Test 1 For the first test we used $k^2=12$, $a=0.2$, and the analytical solution

$$\begin{aligned} u(x,y)= & {} \sin (\pi x)\cosh \left( \sqrt{\pi -k^2}y\right) +\sin (2\pi x)\sinh \left( \sqrt{4\pi ^2-k^2}y\right) \\&+ \sin (3\pi x)\cosh \left( \sqrt{9\pi ^2-k^2}y\right) , \end{aligned}$$

which satisfies the Helmholtz equation in the domain $\Omega =[0,1]\times [0,a]$. By evaluating the function u(x, y), and its derivative, for $y=0$, we obtain the Cauchy data $g(x)=u(x,0)$ and $\eta (x)=u_y(x,0)$, for $0<x<1$. The analytical solution, for the case $k^2=12$ and $a=0.2$, is illustrated in Fig. 1.

Fig. 2

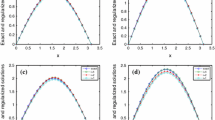
We display the L-curve (top-left) and the error $\Vert f^\delta _\lambda -f\Vert _2$, as a function of $\lambda$ (top-right). The L-curve suggests the parameter $\lambda =2.5\cdot 10^{-7}$ and the minimum error is obtained for $\lambda =6.3\cdot 10^{-7}$. We also show the solutions obtained by using the $\lambda$ value predicted by the L-curve (middle-left) and the $\lambda$ value which gives the smallest error (middle-right). Finally, we show the solution obtained using $\lambda =2\cdot 10^{-8}$ (bottom-left), which adds too little regularization, and $\lambda =1\cdot 10^{-4}$ (bottom-right), which results in a too smooth solution. In all cases both the exact solution f(x) (black/solid-curves) and the inverse solution $f^\delta _\lambda (x)$ (blue/dashed-curves) are shown

In order to investigate the ill-posedness of the inverse problem we added normally distributed noise of size $\delta = 10^{-3}$ to the Cauchy data giving us noisy vectors $[g^\delta ,\eta ^\delta ]$. The inverse problem was solved for a wide range of regularization parameters $\lambda$, i.e. $10^{-7} \le \lambda \le 10^{-5}$. For each value of the regularization parameter we computed a regularized solution $f^\delta _\lambda (x):=u^\delta _\lambda (x,a)$ and also the error $\Vert f^\delta _\lambda -f\Vert _2$. In Fig. 2 we illustrate how the error depends on the parameter $\lambda$. We see that there is a trade-off between enforcing stability, i.e. a large regularization parameter $\lambda$, and solving the Helmholtz equation accurately, i.e. computing the second derivative accurately which means a small parameter $\lambda$. The conclusion is that by selecting an appropriate value for $\lambda$ we are able to find a good regularized solution.

In actual applications the exact solution to the problem is unknown and we cannot compute the error $\Vert f_\lambda ^\delta - f\Vert _2$. Thus another method for finding a good regularization parameter is needed. The L-curve, originally introduced in [17], is a plot of the norm of the approximate solution versus the residual in a $\log \!-\!\log$ scale. Since our algorithm uses the semi-norm $|u|_2$ as the penalty term it is natural to measure the solution norm by the second derivative, $\Vert (f_\lambda ^\delta )^{\prime \prime })_\Delta \Vert _2$. In our implementation the second derivative is approximated using the standard, centered, second order accurate, finite difference quotient. In order to define a residual we recall that the purpose of the residual is to measure the missmatch between an approximate solution and the available data. For our tests we define the residual as follows: Let v(x, t) satisfy the Helmholtz equation, with Dirichlet data $v(x,a)=f^\delta _\lambda (x)$ and Neumann data $v_y(0,x)=\eta ^\delta (x)$. The residual is then defined as $\Vert v(x,0) - g^\delta \Vert _2$. Note that this means that the residual is zero for the exact solution and data. However the residual does not necessarily tend to zero as $\lambda \rightarrow 0$. In our work we compute the function v(x, t) by a standard finite difference scheme, see [1, 2] for details. The computed L–curve is displayed in Fig. 2. We pick the regularization parameter $\lambda$ that correspond to the point closest to the lower-left corner of the L-curve where both the solution norm and the residual is small. We see that the solution, obtained by using the parameter $\lambda$ suggested by the L–curve, is nearly optimal.

Fig. 3

The optimal regularization parameter $\lambda$ as a function of the noise level $\delta$ present in the available Cauchy data (left graph). Also the error in the computed solution, when the optimal $\lambda$ is used, as a function of the noise level (right graph). Here $a=0.2$ and $k^2=12$

Test 2 In order to further investigate the properties of the smoothing spline regularization method we carry out tests and find the optimal value of $\lambda$, and also the corresponding errors, as a function of the noise level. For this test the analytic solution from Test 1 was used with $a=0.2$ and $k^2=12$. In the experiment we picked a large range of noise levels, i.e. $10^{-4}\le \delta \le 10^{-1}$, and for each level of noise we determined the optimal value of $\lambda$, i.e. the one that minimize the error $\Vert f_{\lambda (\delta )}^\delta -f\Vert _2$. The results are shown in Fig. 3. We see that a smaller amount of noise $\delta$ means that we can use a smaller regularization parameter $\lambda$. This is consistent with the stability results derived in Sect. 3.2.

5 A modified Helmholtz equation

In this Section we look into solving the Cauchy problem for a modified Helmholz equation in the rectangle $\Omega =[0,1]\times [0,a]$. Find $u \in C^2(\Omega ) \cap C^1(\bar{\Omega })$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta u + \alpha u = 0,\qquad &{} 0<x<1, 0<y<a,\\ u(x,0)=g(x), &{} 0\le x \le 1, \\ u_y(x,0)=\eta (x),&{} 0\le x \le 1, \\ u(0,y)=u(1,y)=0, &{} 0<y<a, \end{array}\right. } \end{aligned}$$

(5.35)

where $\alpha :=\alpha (x,y)$ is a positive, real valued function defined on the domain $\Omega$. The goal is to demonstrate that our Cubic spline regularization method can be used for solving this more general case.

Fig. 4

A domain $\Omega ^\prime$ is transformed into the rectangle $\Omega =[0,1]\times [0,a]$ by a conformal mapping $\phi$. The Cauchy data is available on $\Gamma _1^\prime$, which is mapped onto $\Gamma _1=[0,1]\times \{0\}$

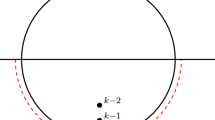
The modified Helmholtz equation is important in applications since it models wave propagation in a material with variable density. Also, consider a sitution where a function v satisfies the Helmholtz equation, with a constant wave number $k^2$, in a more complicated domain $\Omega ^\prime$, as illustrated in Fig. 4. For simplicity of notation we identify ${\mathbb {R}}^2$, with the complex plane ${\mathbb {C}}$. If $\phi :\Omega ^\prime \mapsto \Omega$ is the conformal mapping that transforms the domain $\Omega ^\prime$ into the rectangle $\Omega$ then $u(z)=v(\phi ^{-1}(z))$, satisfies

$$\begin{aligned} |(\phi ^{-1})^\prime |^2\Delta u + k^2 u=0,\text { or }\Delta u + \alpha u=0, \end{aligned}$$

(5.36)

where $\alpha =k^2/|(\phi ^{-1})^\prime (z)|^2$, and $(\phi ^{-1})^\prime$ is understood as the derivative of an inverse function of a complex variable z. Thus, solving the modified Helmholtz equation in the rectangular domain $\Omega$ is equivalent to solving the ordinary Helmholtz equation in the more complicated domain $\Omega ^\prime$. Note that it is essential that the domains $\Omega$ and $\Omega ^\prime$ are topologically equivalent in the sense that corners are mapped onto corners and smooth boundary segments are mapped onto the sides of the rectangle. Otherwise we would introduce singularities in the derivative boundary conditions, which is something the algorithm could not handle.

In order to demonstrate that the cubic spline regularization method can be applied to the problem (5.35) we select a function

$$\begin{aligned} \alpha (x,y)=7+\sin (x/3)\cos (y/2)+3xy^2, \end{aligned}$$

(5.37)

Fig. 5

The numerically constructed test solution u(x, y) (left graph), for the case of the modified Helmholtz equation. The domain is $\Omega =[0,1]\times [0,0.2]$. We also display the Cauchy data, i.e. $g(x)=u(x,0)$ (right,blue/dashed) and $\eta (x)=u_y(x,0)$ (right,black/solid)

Fig. 6

We display the error $\Vert f^\delta _\lambda -f\Vert _2$, as a function of $\lambda$ (top-left). The error is minimized for $\lambda =2\cdot 10^{-7}$ and the corresponding regularized solution $f_\lambda ^\delta (x)$ is also displayed (top-right,blue curve) together with the exact solution f(x) (top-right,black-curve). The ill-posedness of the problem is illustrated by plotting the solution corresponding to $\lambda =5\cdot 10^{-8}$ (bottom-left) which adds to little regularization. We also display the solution corresponding to $\lambda =8\cdot 10^{-6}$ (bottom-right) which means too much added stability. In both cases the regularized solution $f_\lambda ^\delta$ (blue/dashed curves) and the exact solution f (black/solid curves) are shown

and also suitable Dirichlet data $u(x,0)=g(x)$ and $u(x,a)=f(x)$, with $a=0.2$. The corresponding Neumann Data $\eta (x)=u_y(x,0)$ was computed by solving the equation $\Delta u + \alpha u=0$, in the rectangle $[0,1]\times [0,0.2]$, with appropriate Dirichlet data on the boundary, using a uniform grid of size $n=501$ in the x–direction and $m=101$ in the y-direction. The code used for this purpose is a standard ${\mathcal {O}}(\Delta x^2)$ accurate finite difference solver. The computed solution u(x, y), and also the Cauchy data $[f,\eta ]$, are illustrated in Fig. 5.

Test 3 For this test the numerical test solution illustrated in Fig. 5 was used. Noisy Cauchy data was created by adding normally distributed random noise, with variance $10^{-3}$ to the exact data vectors. We then solved the inverse problem for a wide range of regularization parameter values $\lambda$. The results are shown in Fig. 6. Again we see that there is an optimal regularization parameter, that represents the appropriate compromise between stability and accuracy. By using this parameter value we are able to reconstruct the solution accurately.

We also remark that experiments with different noise levels and different parameter values show that our method works well for the modified Helmholtz equation. The problem is severely ill-posed but still it is relatively easy to find a value for $\lambda$ that works well.

6 Concluding remarks

In this paper we have developed a regularization method for solving the Cauchy problem for the Helmholtz equation based on Cubic smoothing splines. In our work we have developed a stability theory for the discrete problem that is solved numerically. One of the results is a matrix approximation of the second derivative for which we have obtained a norm-bound. The stability results are comparable to those obtained by different authors using similar methods.

Numerical experiments show that the method works well and can produce accurate results. For the experiments we have also introduced a residual that allows us to find appropriate regularization parameters by using the L–curve method. In our tests the parameters obtained from the L–curve are close to the optimal ones. We remark that the residual definition is clearly not optimal. Since we have to solve a well-posed boundary value problem to compute the residual we will have numerical errors. Thus, for a fixed step size for the discretization, the residual will not tend to zero as the noise level tends to zero. Also, since the Cauchy problem for the Helmholtz equation is severely ill-posed the results are quite sensitive with respect to the regularization parameter $\lambda$. More work is needed to obtain a good, and practical, parameter selection strategy.

The derived stability results, see Sect. 3.2, essentially show that as long as $\exp ( a c_3 \lambda ^{-1/4} )\delta \rightarrow 0$, as $\delta \rightarrow 0$, then the propagated data error satisfies $\Vert U_{\lambda (\delta )}-U_{\lambda (\delta )}^\delta \Vert _2\rightarrow 0$. One potential parameter choice rule is

$$\begin{aligned} \lambda (\delta )=\left( -\frac{1}{ac_3}\log \sqrt{\delta }\right) ^{-4}, \end{aligned}$$

(6.38)

which means $\exp ( a c_3 \lambda ^{-1/4} )\delta =\delta ^{1/2}$. Since, by this rule, $\lambda (\delta )\rightarrow 0$ as $\delta \rightarrow 0$, we apply less and less regularization as the noise level is reduced, and thus it is resonable to expect that the appxoximation error $\Vert U_\lambda -U\Vert _2$ also tends to zero. A formal proof of convergence for the above parameter choice rule is something we intend to do in future work.

For our work we have primarily considered rectangular domains but in actual applications it is often the case that the Helmholtz equation is valid in a more complicated domain. Thus we extend our method to also treat the modified Helmholtz equation, i.e $\Delta u +\alpha u =0$, where $\alpha (x,y) > 0$ is a function. This allows us to use a conformal mapping, or orthogonal mapping, to transform the domain under consideration to a rectangle. In this paper we only have initial numerical tests but this is something we intend to develop further in the future.

In the future we intend to apply our method to similar problems and make more systematic comparisons with the work of others, e.g. [3, 11, 14]. We also hope to apply the method to medical problems with measured data.