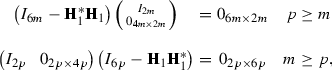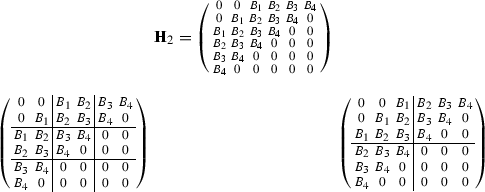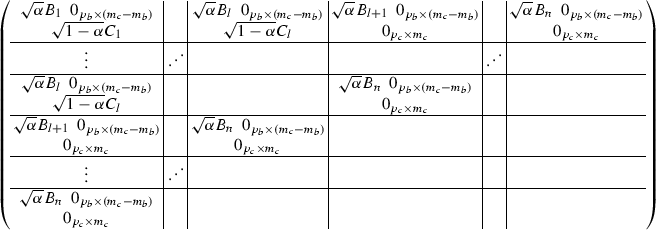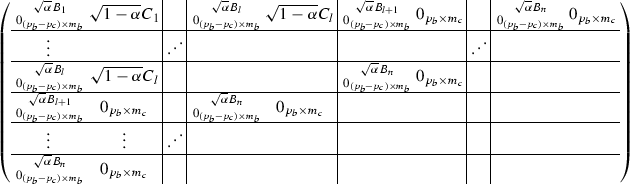Abstract
We here study finite impulse response (FIR) rectangular, not necessarily causal, systems which are (para)-unitary on the unit circle (=the class \(\mathcal {U}\)). First, we offer three characterizations of these systems. Then, introduce a description of all FIRs in \(\mathcal {U}\), as copies of a real polytope, parametrized by the dimensions and the McMillan degree of the FIRs. Finally, we present six simple ways (along with their combinations) to construct, from any FIR, a large family of FIRs, of various dimensions and McMillan degrees, so that whenever the original system is in \(\mathcal {U}\), so is the whole family. A key role is played by Hankel matrices.
Similar content being viewed by others
Notes
Passive electrical circuits are either dissipative or lossless.
For example, in studying classical filters a “high-pass” could be viewed as an “all-pass” minus a “low-pass”.
= Bounded at infinity and in engineering called causal or colloquially proper.
In the sequel, boldface characters will stand for block-structured matrices.
In general, the Hankel operator is infinite, but since we here focus on F(z) in (2.2) with a FIR, the corresponding Hankel matrix is finite and no truncation is needed.
For given n and \(\rho \), one can always find \(\zeta \in [0, \rho -1]\) so that \(\frac{n+\zeta }{\rho }\) is natural. Then, the last part of \({\mathbf B_{\frac{n}{\rho }}}\) in (2.15) is comprized of zeros.
References
Alpay, D., Gohberg, I.: Unitary rational matrix functions. In: Gohberg, I. (ed.) Topics in Interpolation Theory of Rational Matrix-Valued Functions, Operator Theory: Advances and Applications, vol. 33, pp. 175–222. Birkhäuser Verlag, Basel (1988)
Alpay, D., Gohberg, I.: On orthogonal matrix polynomial. In: Gohberg, I. (ed.) Orthogonal Matrix-Valued Polynomials and Applications, Operator Theory: Advances and Applications, vol. 34, pp. 25–46. Birkhäuser Verlag, Basel (1988)
Alpay, D., Jorgensen, P.E.T, Lewkowicz, I.: Extending wavelet filters. Infinite-dimensions, the non-rational case and Indefinite-inner product spaces. In: Excursions in Harmonic Analysis Book Series, vol. 2, Chap 5, pp. 71-113, Springer-Birkhäuser, New York (2012)
Alpay, D., Jorgensen, P., Lewkowicz, I.: Extending wavelet filters. Infinite dimensions, the non-rational case and indefinite-inner product spaces. In: Excursions in Harmonic Analysis Book Series, vol. 2, Chap. 5, pp. 71-113, Springer-Birkhäuser, New York (2012)
Alpay, D., Jorgensen, P.E.T., Lewkowicz, I.: Parameterization of all wavelet filters: Input-output and State Space. Sampl. Theory Signal Image Process. 12, 159–188 (2013)
Alpay, D., Jorgensen, P.E.T., Lewkowicz, I.: Characterizations of rectangular, (para)-unitary rational functions. a manuscript
Alpay, D., Jorgensen, P.E.T, Lewkowicz, I.: Filter banks—an interpolation approach. A manuscript
Alpay, D., Jorgensen, P., Lewkowicz, I., Marziano, I.: Representation formulas for hardy space functions through the Cuntz relations and new interpolation problems. In: Shen, X., Zayed, A.I. (eds.) Multiscale Signal Analysis and Modeling. In the series Lecture Notes in Electrical Engineering, Springer. http://arxiv.org/abs/1104.0621
Alpay, D., Rakowski, M.: Co-Isometrically Valued Matrix Functions Operator Theory: advances & Application, vol. 80. Birkhäuser, Basel (1995)
Bart, H., Gohberg, I., Kaashoek, M.: Minimal Factorization of Matrix and Operator and Functions, Operator Theory: advances and Applications, vol. 1. Birkhäuser, Basel (1979)
Bratteli, O., Jorgensen, P.E.T.: Wavelet filters and infinite-dimensional unitary groups. In: Proceedings of the International Conference on Wavelet Analysis and Applications (Guangzhou, China 1999), AMS/IP Stud. Adv. Math., Amer. Math. Soc. 25, pp. 35–65 (2002)
Bratteli, O., Jorgensen, P.E.T.: Wavelets Through the Looking Glass. Birkhäuser, Basel (2002)
Cescato, D., Bölcskei, H.: QR decomposition of Laurent polynomial matrices sampled on the unit circle. IEEE Trans. Inf. Theory 56, 4754–4761 (2010)
Cescato, D., Bölcskei, H.: Algorithms for interpolation-based QR decomposition in MIMO-OFDM systems. IEEE Trans. Signal Proc. 59, 1719–1733 (2011)
Chai, L., Zhang, J., Zhang, C., Mosca, E.: Optimal noise reduction in oversampled PR filter banks. IEEE Trans. Signal Proc. 57, 3844–3857 (2009)
Davidson, T.N.: Enriching the art of FIR filter design via convex optimization (efficient evaluation of inherent tradeoffs). IEEE Signal Proc. Mag. 27, 89–101 (2010)
Genin, Y., Van Dooren, P., Kailath, T., Delosme, J.M., Morf, Martin: On \(\Sigma -\)Lossless transfer functions and related questions. Linear Algebr. & Appl. 50, 251–275 (1983)
Gohberg, I., Lancaster, P., Rodman, L.: Representations and divisibility of operator polynomials. Can. J. Math. 30, 1045–1069 (1978)
Hassibi, B., Sayed, A.H., Kailath, T.: Indefinite-Quadratic Estimation and Control, A Unified Approach to \(H^2\) and \(H^{\infty }\) Theories. SIAM, Englewood Cliffs (1999)
Hoang, H.G., Tuan, H.D., Nguyen, T.Q.: Frequency selective KYP lemma, IIR filter and filter bank design. IEEE Trans. Signal Proc. 57, 956–965 (2009)
Horn, R.A., Johnson, C.R.: Matrix Analysis. Cambridge University Press, Cambridge (1985)
Horn, R.A., Johnson, C.R.: Topics in Matrix Analysis. Cambridge University Press, Cambridge (1991)
Icart, S.: Matrices polynomiales et égaliation de canal. In: Mémoire d’Habilitation à diriger des recherches, Polytech’Nice- Sophia Antipolis Département Électronique, (In French) (2013)
Jorgensen, P.E.T.: Matrix factorizations, algorithms, wavelets. Not. Am. Math. Soc. 50, 880–894 (2003)
Jorgensen, P.E.T.: Analysis and Probability: wavelets, Signals, Fractals, Graduate Texts in Mathematics, vol. 234. Springer, New York (2006)
Jorgensen, P.E.T.: Unitary matrix functions, wavelet algorithms, and structural properties of wavelets. In: Gabor and Wavelet Frames, Lect. Notes Ser. Inst. Math. Sci. Natl. Univ. Singap., 10, pp. 107–166, World Science Publisher, Hackensack (2007)
Levinson, Y., Mirkin, L.: FIR stabilization in discrete one-sided model matching problem. Automatica 48, 2990–2992 (2012)
Levinson, Y., Mirkin, L.: \(L^2\) Optimization in discrete FIR estimation: exploiting dtate-space structure. SIAM J. Control Optim. 51, 419–441 (2013)
Mallat, S.: A Wavelet Tour of Signal Processing, 3rd edn. Academic Press, Paris (2009)
McWhirter, J.G., Baxter, P.D., Cooper, T., Redif, S., Foster, J.: An EVD algorithm for para-hermitian polynomial matrices. IEEE Trans. Signal Proc. 55, 2158–2169 (2007)
Olivi, M.: Parametrization of rational lossless matrices with applications to linear system theory. Université De Nice Sophia Antipolis, Mthématique, Mémoire d’Habilitation à Diriger des Recherches (2010)
Oraintara, S., Tran, T.D., Heller, P.N., Nguyen, T.Q.: Lattice structure for regular para-unitary linear-phase filter-banks and \(M\)-band orthogonal symmetric wavelets. IEEE Trans. Signal Proc. 49, 2659–2672 (2001)
Potapov, V.P.: Multiplicative structure of J-nonexpansive matrix functions. Trudy Mosk. Math. Ob. 4 (1955), pp. 125236 [Russian]; English Translation: AMS Translations, Series 2, 15, pp. 131–243 (1960)
Redif, S., McWhirter, J.G., Weiss, S.: Design of FIR paraunitary filter banks for subband coding using polynomial eigenvalue decomposition. IEEE Trans. Signal Proc. 59, 5253–5264 (2011)
Rissanen, J.: Algorithms for triangular decomposition of block Hankel and Toeplitz matrices with applications to factoring positive matrix polynomials. Math. Comput. 27(121), 147–154 (1973)
Sørensen, M., De Lathauwer, L., Icart, S., Deneire, L.: On Jacobi-type methods for blind equalization of paraunitary channels. Signal Process. 92, 617–625 (2012)
Strang, G., Nguyen, T.: Wavelets and Filter Banks. Wellesley-Cambridge Press, Cambridge (1996)
Tohidan, M., Amindavar, H., Reza, A.M.: A DFT-based approximate eigenvalue and singular value decompositiob of polynomial matrices. EURASIP J. Adv. Signal Process. 93, 1–16 (2013)
Tuqan, J., Vaidyanathan, P.P.: A state space approach to the design of globally optimal FIR energy compaction filters. IEEE Trans. Signal Proc. 48, 2822–2838 (2000)
Vaidyanathan, P.P.: Multirate Systems and Filter Banks. Prentice-Hall, Englewood Cliffs (1993). Signal Processing Series
Valli, G.: Interpolation theory, loop groups and instantons. J. Reine Math. 446, 137–163 (1994)
Vikalo, H., Hassibi, B., Erdogan, A., Kailath, T.: On robust signal reconstruction in noisy filter banks. Eurasip Signal Process. 85, 1–14 (2005)
Yang, G., Zheng, N.: An optimization algorithm for biorthogonal wavelet filter banks design. Int. J. Wavelets Multiresolut. Inf. Process. 6, 51–63 (2008)
Acknowledgments
This research is partially supported by the BSF Grant no. 2010117. D. Alpay: the Earl Katz family for endowing the chair which supported his research.
Author information
Authors and Affiliations
Corresponding author
Appendix: Construction of families of FIRs
Appendix: Construction of families of FIRs
For each of the items I through VI from Subsect. 2.2 we here fill-in the following details:
-
1.
Construct new polynomials from the original one.
-
2.
Show that whenever the original polynomial was in \(\mathcal {U}\), so are the newly constructed polynomials.
I. Reverse polynomial
Using \({\mathbf T}\) from (2.18),
The realtion with the corresponding Hankel matrix is straightforward and thus omitted.
II. Preserving the McMillan degree.
For simplicity of exposition we consider as an illustrative example the polynomial F(z) in (2.1) with \(n=4\) and the parameter q attaining the values \(-1\) and \(-2\).
-
a. For \(q=-1\) the corresponding Hankel matrix, \({\mathbf H_1}\) from (2.8) can be, without loss of generality, extended with a row and a column of zeros so it is \(6p\times 6m\). Now the resulting Hankel matrix may be partitioned in two forms,
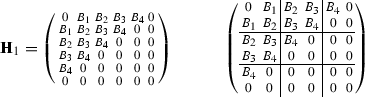
which produce the two polynomials in item II a.
Following Theorem 4.1 note that
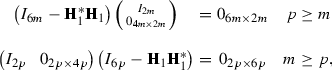
so indeed the polynoial is in \(\mathcal {U}\).
-
b. Substituting in F(z) in (2.12) \(q=-2\) yield a Hankel matrix \({\mathbf H}_2\) with three partitionings
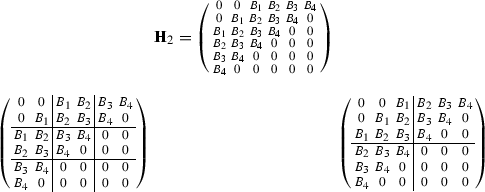
so that the three polynomials in item II b are obtained.
These three polynomials are in \(\mathcal {U}\), as following Theorem 4.1 one obtains,

To make the last construction more realistic take for example, \(m=p=2\) and

In items III through VI we produce more elaborate structures out of a given Hankel matrix. To this end, we find it convenient to introduce the following notation. Let \(\alpha ,\beta \ge 0\) and \(\eta ,\delta >0\) be integers. One can construct the following \((\alpha +\beta +\eta )\delta \times \eta \delta \) isometry, i.e. \(U_\mathrm{Iso}^*U_\mathrm{Iso}=I_{\eta \delta }\),

Similarly, \(U_\mathrm{Coiso}\) is the following \(\eta \delta \times (\alpha +\beta +\eta )\delta \) coisometry, i.e. \(U_\mathrm{Coiso}U_\mathrm{Coiso}^*=I_{\eta \delta }\),

Let \(\rho \in \{1,~2,~\ldots ~,~n\}\) be so that \(\frac{n}{\rho }\) is natural. Substitute in \(~U_\mathrm{Iso}\) and in \(~U_\mathrm{Coiso}\) see (5.1), (5.2) respectively: \(\alpha =a\rho {p}\), \(\beta =b\rho {p}\), with \(a, b\ge 0\) integers, \(\eta =\frac{n}{\rho }\), \(\delta =\rho {p}~\) and consider the pair of products,

and

Both cases yield the same \((a+b+1)np\times (a+b+1)nm\) Hankel matrix, denoted by \({\mathbf H}(a, b, \rho )\). For example,

or

or for \(~n=6\)

III. Doubling the powers.
First note that \({\mathbf H}(a, b, 1)\) (i.e. when \(\rho =1\)) corresponds to \(p\times m\)-valued polynomial in (2.13) with \(\gamma :=a+b+1\).
As another example, the above Hankel matrix \({\mathbf H}(0,~1,~3)\) is associated with the polynomial F(z) in (2.14).
IV. Rectangular polynomials.
Another sample of a Hankel matrix associated with \(U_\mathrm{Iso}{\mathbf B_o}~\) in (5.3) (or \(\hat{{\mathbf {B}}}_{o} U_\mathrm{Coiso}\) in (5.4)) is obtained when the parameters are \(~a=2\), \(b=2\) \(\rho =2\), i.e. Now, multiplying \({\mathbf H}(a,~b,~\rho )\) from the right by \(U_\mathrm{Iso}\) in (5.1) with the parameters \(\alpha =(\rho -1)m\), \(\beta =0\), \(\eta =\frac{n}{\rho }(a+b+1)\) and \(\delta =m\) yields the following \((a+b+1)np\times (a+b+1)\frac{n}{\rho }m\) Hankel matrix (here \(a=2, b=2, \rho =2\))

which corresponds to the \(p\rho \times m\)-valued polynomial in IV a.
Similarly, multiplying \({\mathbf H}(a,~b,~\rho )\) from the left by \(U_\mathrm{Coiso}\) in (5.2) with the parameters \(~\alpha =(\rho -1)p\), \(\beta =0\), \(\eta =\frac{n}{\rho }(a+b+1)\) and \(\delta =p~\) yields the following \((a+b+1)\frac{n}{\rho }p\times (a+b+1)nm\) Hankel matrix (here \(a=2, b=2, \rho =2\))

which corresponds to the \(p\times \rho {m}\)-valued polynomial in IV b.
It is easy to verify that if \({\mathbf H_o}\) satisfies the first line in (4.5) then so do all Hankel matrices of the form \({\mathbf H}_0U_\mathrm{Iso}\) (5.7).
Similarly, if \({\mathbf H}_0\) satisfies the second line in (4.5) then so do all Hankel matrices of the form \(U_\mathrm{Coiso}{\mathbf H}_0\) (5.8).
In the sequel, we shall adjust our previous notation in (2.8) of the Hankel matrix associated with
to \(~ {\mathbf H}_{\mathbf {B}, n, \eta } \) (in (2.8) the subscricts B and n were omitted, as so far they were evident from the context). For example, with the polynomial
one can associate the \((l+\eta )p_c\times (l+\eta )m_c\) Hankel matrix,

V. Composition of polynomials.
With the pair of poynomilas in (2.16) one can associated the Hankel matrices \({\mathbf H}_{\mathbf {B}, n, 0}\) and \({\mathbf H}_{\mathbf {C}, l, 0}\), which are of dimensions \(np_b\times nm_b\) and \(lp_c\times nm_c\), respectively.
Out of this pair, one can construct (at least) the three following Hankel matrices, all of the form \({\mathbf H}_{\mathbf {D}, n, 0}~\):
-
a. A \(~n(p_b+p_c)\times n(m_b+m_c)\) Hankel matrix

or another \(~n(p_b+p_c)\times n(m_b+m_c)\) Hankel matrix

-
b. For \(m_c\ge m_b~\) a \(~n(p_b+p_c)\times nm_c\) Hankel matrix
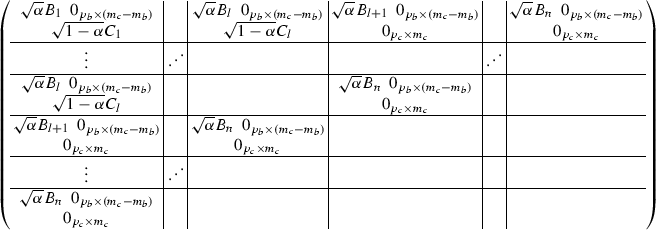
-
c. For \(p_b\ge p_c\) a \({ np}_{ b}\times (m_b+m_c)n\) Hankel matrix
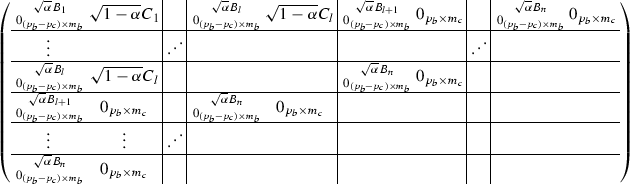
VI. Product of polynomials
Recall that out of
the following \(~p_b\times m_c\)-valued polynomial was obtained
where the coefficients \(D_1~,~\ldots ~,~D_{n+l-1}~\) were explicitely given in (2.17).
Expressing, (2.17) in terms of corresponding Hankel matrices yields
where the Hankel matrices \({\mathbf H}_{\mathbf {B}, n, l}\), \({\mathbf H}_{\mathbf {C}, l, n}~\) and \(~{\mathbf H}_{\mathbf {D}, n+l-1, 1}~\) are \((n+l)p_b\times (n+l)\rho \), \((n+l)\rho \times (n+l)m_c~\) and \(~(n+l)p_b\times (n+l)m_c~\) respectively, while \(~{\mathbf T}_{m+l, \rho }\) is the permutation matrix as in (2.18).
Next, to establish the fact that \(F_d(z)\) is in \(~\mathcal {U}\), we go through the following steps.
First, from (5.10) note that
Assuming now that \(~F_b\in \mathcal {U}\), it follows from (4.5) that
where \(\Delta _{(n-1)\rho }\) is \(~(n-1)\rho \times (n-1)\rho ~\) positive semi-definite (weak) contraction.
Assuming now that also \(~F_c\in \mathcal {U}\), (carefully following the dimensions) it follows from (4.5) that
where \(\hat{\Delta }_{(n+l-2)p_b}\) is a \(~(n+l-1)p_b\times (n+l-1)p_b~\) positive semi-definite (weak) contraction, this part is estabilished and indeed \(F_d\in \mathcal {U}\).
Showing the relation for \({\mathbf H}_{\mathbf {D}, n+l-1, 1} {\mathbf H}_{\mathbf {D}, n+l-1, 1}^*\) is quite similar and thus omitted. \(\square \)
Rights and permissions
About this article
Cite this article
Alpay, D., Jorgensen, P. & Lewkowicz, I. Characterizations of families of rectangular, finite impulse response, para-unitary systems. J. Appl. Math. Comput. 54, 395–423 (2017). https://doi.org/10.1007/s12190-016-1015-x
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12190-016-1015-x
Keywords
- Finite impulse response
- Laurent polynomials
- Isometry
- Co-isometry
- Realization
- Blaschke–Potapov
- Hankel operator