1 Introduction

High-level radioactive nuclear waste generally refers to the waste products containing high-level radioactive materials which are generated by the nuclear power industry and are inevitable by-products due to nuclear power plants. As they may seriously threaten the health of human and other forms of life, countries across the globe have attached great importance to their safe disposal (Guo et al. 2001). The disposal technology normally includes marine disposal, island disposal, etc. At present, one widely adopted scheme for safe disposal of high-level radioactive nuclear waste is supposed to be deep geological disposal (Alberdi et al. 2000), which, in other words, means that the high-level radioactive nuclear waste is buried within a stable geological body at a depth of 500–1000 m to separate them from the biosphere permanently (Su et al. 2011). The engineered underground facility for burying the nuclear waste is called geological disposal repository. In various countries, different types of rocks would be selected for such repositories. China mainly focuses on the large granite masses (Wang et al. 2006).

For a comprehensive assessment of one target granite body, synthetical studies of the tectonics, hydrology, and geophysics are required. Active source seismic exploration is one of the most important technical approaches (Chen et al. 2017).

On one pre-selected geological disposal repository located on the eastern edge of the Badanjilin Desert, our seismic exploration work was carried out. The objectives of the proposed exploration were to answer the following questions: whether the rock is thin, where the rock’s boundaries are and their spatial distribution, if the faults interpreted by remote sensing technology (Fig. 1) exist.

Fig. 1
figure 1

Graph of remote sensing interpretation of the seismic work area

Full size image

The seismic exploration research focusing on one large high-velocity granitic pluton is uncommon. During the research, we found that the study area was with complex landforms which included three distinct types: semi-desert grasslands, areas of shifting dunes, and areas of outcrops (Fig. 2). In addition, the elevations along the seismic lines change dramatically (Fig. 3). Thus, in the course of seismic data acquisition and processing, we encountered difficulties (Chen et al. 2015) of crossing obstacles, removing harmful scattered waves, and building complex near-surface velocity models. To address those problems, targeted techniques such as cross-obstacle seismic geometry design, angle-domain vector resolution based scattered wave removal (Liu 2013; He et al. 2015), and an acoustic wave equation-based inversion method jointly utilizing both the travel time and waveform of first arrival waves (Luo and Schuster 1991; Jiang and Zhang 2016; Yao et al. 2019), were adopted.

Fig. 2
figure 2

Pictures of landforms along the seismic lines

Full size image
Fig. 3
figure 3

Elevations along the TMS1 (a) and TMS2 (b) lines

Full size image

2 Seismic acquisition and the cross-obstacle seismic geometry design

Based on the seismic exploration objectives, the main seismic working parameters were set as: 4 m trace interval, 24 m shot interval, 300 traces receiving (the receiver array length of one single-shot was 1.2 km), fold number ≥ 25, 1 ms sampling rate, and 3 s record length.

In the course of seismic acquisition, seismic spread must overcome certain obstacles. As shown in Fig. 2d, one large rock outcrop emerges from the ground (stake 4748–5084 m of the TMS2 seismic line). If its negative influences were ignored, it would engender the lack of seismic data, and there would be a gap existing between stake 4750–5100 m in the final reflection imaging profile. Given this realization, we presented a patent for invention (Li et al. ZL201710342906.5) whose function aims at mitigating the harmful effect of obstacles on the seismic line via redesigning the routine seismic geometry. As shown in Fig. 4a, new shot and receiver positions were set (Fig. 4a). One of the rules for setting those new positions was to assure the real fold numbers on each Common Mid-Point (red points) always above the mean level (blue points) in the most economical way. As shown in Fig. 4b, there was no gap in the relevant position, thus the negative influence of the obstacle was effectively weakened. It was due to this technique, the geological task of continuously tracking the rock’s top interface could be realized.

Fig. 4
figure 4

The redesigned cross-obstacle seismic geometry (a) and the final profile (b) utilizing the new geometry

Full size image

3 Removing complex near-surface scattered waves via an angle-domain vector resolution de-noising method

When active source seismic exploration work is carried out in a complex near-surface area, the acquired seismic records normally contain many harmful scattered waves. The Tamusu research area is also a case in point. The scattered waves are usually mixed with the effective signal (Fig. 5a), and by our research, they could not be reasonably filtered out via the traditional filtering methods of the time and frequency domain or wavelet domain (Li et al. 2016).

Fig. 5
figure 5

Results of removing scattered noises: original common-shot gather (a), de-noised common-shot gather (b), and the separated noises (c)

Full size image

To de-noise the harmful complex near-surface scattered waves, an angle-domain vector resolution de-noising method was adopted. This method could make use of the difference of emergence angles between reflected waves and scattered waves to de-noise. In addition, it could be used in pre-stack processing.

After applying the abovementioned method on common-shot-gathers, the useful reflected waves and the harmful scattered waves were separated satisfactorily (Fig. 5b, c). Consequently, the quality of the seismic imaging profile, especially the left and top portion of the profile, was improved significantly (Fig. 6).

Fig. 6
figure 6

The top portion of the reflection imaging profiles obtained from the original common-shot gathers (a) and the de-noised common-shot gathers (b)

Full size image

4 Building complex near-surface velocity models utilizing both the travel time and waveform of first arrival waves

According to previous experience, the accuracy of near-surface velocity would influence the total quality of seismic profiles (Xia 2014), especially in a study area with complex surface conditions.

Thus, an acoustic wave equation-based high-resolution near-surface velocity inversion method, which could jointly utilize both the travel time and waveform of first arrival waves, was adopted in the present research. The fundamental theory of this method was proposed by Luo and Schuster in 1991. Its basic procedure includes: firstly, get simulated data (Yao et al. 2016) by solving acoustic wave equation and work out a kind of pseudo-residual data via a link function which relates the simulated data and the observed data; secondly, we are supposed to minimize the pseudo-residual data with the classical full-waveform inversion engine (Yao and Wu 2017; Li et al. 2020; Liu et al. 2020).

The abovementioned method has been applied to crosshole seismic data effectively. In the present research, we adopt it to process ground-observation seismic data on the complex near-surface area. The detailed algorithm is elaborated as follows:

  1. 1.

    Calculate the simulated seismic data via solving the acoustic wave equation;

  2. 2.

    Calculate the pseudo-residual data of first arrival waves via the following equations,

    $$d_{{{\text{pres}}}} \left( {x_{{\text{r}}} ,t;x_{{\text{s}}} } \right) = - \frac{2}{E}\frac{{\partial d_{{{\text{cal}}}} \left( {x_{{\text{r}}} ,t;x_{{\text{s}}} } \right)}}{\partial t}\Delta \tau \left( {x_{{\text{r}}} ;x_{{\text{s}}} } \right)$$
    (1)

    and

    $$E = \int {\frac{{\partial d_{{_{{{\text{obs}}}} }} \left( {x_{{\text{r}}} ,t + \Delta \tau ;x_{{\text{s}}} } \right)}}{\partial t}\frac{{\partial d_{{_{{{\text{cal}}}} }} \left( {x_{{\text{r}}} ,t;x_{{\text{s}}} } \right)}}{\partial t}{\text{d}}t}$$
    (2)

    where \(\Delta \tau \left( {x_{{\text{r}}} ;x_{{\text{s}}} } \right)\) is the time difference of the first arrival waves of observed data and simulated data. \(d_{{{\text{cal}}}} \left( {x_{{\text{r}}} ,t;x_{{\text{s}}} } \right)\) represents the calculated simulated data. \(d_{{{\text{obs}}}} \left( {x_{{\text{r}}} ,t + \Delta \tau ;x_{{\text{s}}} } \right)\) represents the observed data, which have been corrected by \(\Delta \tau\). \(d_{{{\text{pres}}}} \left( {x_{{\text{r}}} ,t;x_{{\text{s}}} } \right)\) represents the pseudo-residual data. \(E\) is the energy term related to the time derivative of \(d_{{{\text{cal}}}} \left( {x_{{\text{r}}} ,t;x_{{\text{s}}} } \right)\) and \(d_{{{\text{obs}}}} \left( {x_{{\text{r}}} ,t + \Delta \tau ;x_{{\text{s}}} } \right)\);

  3. 3.

    Backward-propagate the pseudo-residual data to calculate the pseudo-residual wavefield, meanwhile reconstruct the source wavefield;

  4. 4.

    Calculate the correction gradient direction \(g\left( {\mathbf{x}} \right)\) of the velocity model via Eq. (3), and calculate the update direction via a kind of conjugate gradient method (e.g., Conjugate Descent scheme, Fletcher–Reeves scheme, Hestenes–Stiefel scheme, etc.);

    $$g\left( {\mathbf{x}} \right) = - \frac{1}{{v^{3} \left( {\mathbf{x}} \right)}}\sum\limits_{s \in S} {\int_{0}^{T} {\frac{{\partial p_{{\text{s}}} \left( {{\mathbf{x}},t;x_{{\text{s}}} } \right)}}{\partial t}} \frac{{\partial p_{\text{r}} \left( {{\mathbf{x}},t;x_{{\text{s}}} } \right)}}{\partial t}{\text{d}}t}$$
    (3)

    where \(p_{{\text{s}}} \left( {{\mathbf{x}},t;x_{{\text{s}}} } \right)\) is the reconstructed forward-propagating source wavefield. \(p_{{\text{r}}} \left( {{\mathbf{x}},t;x_{{\text{s}}} } \right)\) is the backward-propagating pseudo residual wavefield. \(v\left( {\mathbf{x}} \right)\) represents the current velocity model;

  5. 5.

    Take the sum of the square of the pseudo-residual data of all the shots as the objective function, which is mathematically expressed as,

    $$C = \sum\limits_{s \in S} {\int_{0}^{T} {d_{{{\text{pres}}}}^{2} \left( {x_{{\text{r}}} ,t;x_{{\text{s}}} } \right){\text{d}}t} }$$
    (4)

    and calculate the iteration step length via a three-point parabola method.

  6. 6.

    Update the model and go to the next iteration.

As shown in Fig. 3, the ground surface of the Tamusu area is rugged. To address the issue of an irregular free-surface, we adopt an algorithm called the acoustic-elastic boundary approach (Xu et al. 2007) which deals with the model’s top free-surface by modifying the density and lame constants on special positions. As shown in Fig. 7, the red and blue triangles separately indicate the positions on which \(\rho_{x}\) and \(\rho_{z}\) should be modified (\(\rho_{x} = 0.5\rho ,\rho_{z} = 0.5\rho\)) in a staggered-grid finite-difference model. The black points indicate where \(\lambda\) should be set 0 (\(\lambda = 0\)).

Fig. 7
figure 7

Model parameter modification scheme for irregular free-surface of acoustic-elastic boundary approach

Full size image

In addition to the above, there were some details required manual intervention when real data were processed. The total processing procedure of the seismic data of Tamusu is described below.

4.1 Pick up the travel time of first arrival waves

In the total inversion process, travel time of first arrival waves of the observed data needs to be picked up once. But because real data normally includes a mass of noises and abnormal values, this process needs human intervention to ensure the results’ quality. The travel time of first arrival waves of the TMS1 and TMS2 seismic lines are shown in Fig. 8a, b.

Fig. 8
figure 8

Manually picked travel time of the first arrival waves of the TMS1 (a) and TMS2 (b) lines

Full size image

4.2 Waveform data preparation

The frequency band of the raw data of Tamusu is about 16–80 Hz, which is slightly higher for the waveform inversion research. Hence, the filtering work should be done to extract the low-frequency components of the observed data.

According to the research, we finally chose a band-pass filter with the parameters of (4.8–24.48 Hz). To avoid the disturbance that came from background noises and late-arrival waves, we only left the first arrival wave. The typical data processing results of seismic data of TMS1 (FFID = 101) and TMS2 (FFID = 201) are shown in Fig. 9.

Fig. 9
figure 9

Examples of filtering and extracting first arrival waves: single shot of TMS1 (a), single shot of TMS2 (b). Left: raw data; middle: filted data; right: first arrival waves; cyan line: travel time picked by manual

Full size image

4.3 Initial models’ building

To carry out the joint inversion of travel time and waveform of first arrival waves, initial velocity models were built via an MSFM (multi-stencil fast marching) based ray-tracing inversion algorithm (Lu et al. 2013). The initial models built for the TMS1 and TMS2 seismic lines are displayed in Fig. 10a, b.

Fig. 10
figure 10

Initial velocity models for the TMS1 (a) and TMS2 (b) lines

Full size image

4.4 Velocity model updating process

Started with the initial models mentioned above, the inversion calculation of the TMS1 line stopped after 68 iterations, and the calculation of the TMS2 line stopped after 71 iterations. The updated velocity models obtained in the first, middle, and last iterations are displayed separately in Fig. 11.

Fig. 11
figure 11

Velocity model updating processes of the TMS1 (a) and TMS2 (b) lines

Full size image

4.5 Analysis of the pseudo-residual of first arrival waves

To check the inversion processing, parts of pseudo-residual data and the corresponding observed data and simulated data are displayed in Fig. 12. It could be found that the value of initial velocity models built via the ray-tracing inversion algorithm tended to be small, because in the first iteration, the arrival-time of the simulated data (blue line) felled behind that of the real data (red line). As iteration went on, the difference between the red line and the blue line decreased gradually.

Fig. 12
figure 12

Example analysis of the pseudo-residual of first arrival waves of the TMS1 (a) and TMS2 (b) lines left: observed data; middle: simulated data; right: pseudo-residual data; red line: first break of observed data; green line: first break of simulated data; cyan line: waveform marching result

Full size image

The green line represents the waveform matching results which were obtained through the calculation of waveform cross-correlation. In the first iteration, they were not continuous and regular enough. This phenomenon could be attributed to the waveform of first arrival waves of the observed data and the simulated data had large differences. As the iteration continued, the continuity and regularity of the green line were improved. What's more, it could also be observed that the amplitude of the pseudo-residuals became smaller until hardly could be seen. All of these indicate the model’s updating was in the right direction for reducing the travel time and waveform residuals.

4.6 Analysis of the evolution of the objective function

As mentioned above, we have taken the sum of the square of pseudo-residual data of all the shots as the objective function. Figure 13 shows the evolution of the objective function, in which we could see the value decreases with the iteration number increasing. The reason why the curve heightens at some points is due to the fact that we have set the top and bottom limitations for the velocity model, when some value excesses the limits, the value would be clipped and the model would be smoothed again to remove the sharp interfaces.

Fig. 13
figure 13

Evolution curves of the objective function of the TMS1 (a) and TMS2 (b) lines

Full size image

Based on the features shown in Figs. 12 and 13, the final updated models of TMS1 and TMS2 could be deemed reliable. The obtained near-surface velocity models could be used as important references for the seismic interpretation. Meanwhile, the subsequent seismic processing steps, such as tomographic static correction, migration, etc., could benefit from the models as well.

5 Seismic interpretation

For seismic interpretation in the present research, it is important to take distinctions into consideration between the high-velocity rock seismic exploration and those carried out on sedimentary environments (Yuan et al. 2017). Few studies of seismic imaging profiles on granite body have been published in China. But generally speaking, because the velocity of granite would normally exceed the values of its surrounding rocks, the seismic events from rock boundaries, e.g., the side or top boundary, would be characterized by strong amplitude and good continuation. However, the seismic events within the rock are normally disordered and with low-frequency, intermittent, worm-like forms. The unconformable contact relationships may be observed on the flanks of the granite rock or between the rock with its overlying strata.

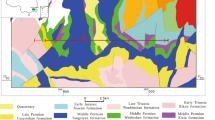
According to regional geological research (Wang et al. 1998; Liu and Zhang 2014), the study area could be divided into two geologic zones: a Late Paleozoic plutonic zone in the northwest and a Mesozoic–Cenozoic basin in the southeast (Fig. 14). The Late Paleozoic plutonic zone consists primarily of Late Paleozoic plutonic rocks. And there are a few residues of Early Paleozoic plutonic rocks and Precambrian metamorphic crystalline basement, as well as some Indo-Chinese plutonic rocks. The deposits of the Mesozoic–Cenozoic basin are composed primarily of Jurassic–Cretaceous sandy conglomerate. In the study area, the granite rock mass is always NEE extension and there are almost no fold structures. The major structural features of the study area consist of faults with different strikes and ductile shear zones (Fig. 14).

Fig. 14
figure 14

Regional geological map of the seismic work area

Full size image

5.1 TMS1 seismic line

Figure 15 shows the interpretation results of the TMS1 seismic line, based on the near-surface velocity profile (Fig. 15a) and the reflection profile (Fig. 15b).

Fig. 15
figure 15

Seismic interpretation of the TMS1 line: near-surface velocity profile (a); reflection profile (b)

Full size image

On the top of Fig. 15b, there is a high-energy reflection wave group composed of two seismic events with good lateral continuation. In Fig. 15a, at the depth of 40–50 m below ground surface, the velocity value increases rapidly from 2000 m/s to about 4200 m/s. As can be seen, the upper boundary of the high-velocity part in Fig. 15a is consistent with the lateral variation of the strong seismic events on the top of Fig. 15b. Comprehensively speaking, it could be speculated that the high-energy reflections on the top of Fig. 15b derive from the top interface of the granite rock. Above the granite, there exist sedimentary and weathered strata, which shows low-speed. Below the top interface of the rock, the reflection events are weak and irregular (Fig. 15b), which could represent that the wave impedance differences within the rock are small.

Based on the regional geology findings (Fig. 14), there was one fault (named Yihe Erbeng fault) across the middle part of the TMS1 seismic line. It could be observed that the strong reflection wave group on the top of Fig. 15b obviously disconnects beneath the stack 4599 m. In Fig. 15a, the high-speed portion nearly emerged from the ground at the corresponding position. With all the above evidence considered, a southward-dipping reverse fault (labeled FP1) was interpreted.

Beyond that, the other three fault points (labeled FP2–FP4) could be interpreted in TMS1 profiles. There is a low-speed anomaly beneath the stack 6100–7100 m in Fig. 15a. Comparing this phenomenon with the reflection imaging profile (Fig. 15b), we could speculate that a northward-dipping fault (labeled FP2) and a southward-dipping fault (labeled FP3) exist. FP2 extended downward to FP3, and the FP2, FP3 faults commonly controlled the Quaternary sedimentary sequence between them. In addition to this, there was a velocity reversal between FP2 and FP3 in Fig. 15a. Meanwhile, there are phenomena of distortions or interruptions of reflection events at the corresponding position in Fig. 15b. These phenomena could indicate the presence of a small fracture labeled as FP4.

Based on the position of the faults, FP3 is speculated to control the southeastern boundary of the Haizi Adergen ductile shear zone (Fig. 14), and FP2 is speculated to control the southern boundary of the shallow graben which is filled with Quaternary. The FP3 fault has been revealed as a normal fault in its upper part and a reverse fault in its lower part, which is considered to be related to multistage tectonization under a stress environment that had changed.

A few arcuate reflection events such as R1 and R2 are recognized in Fig. 15b, the phenomenon of which is considered to be related to the nonuniform property inside the rock.

5.2 TMS2 seismic line

Figure 16 shows the interpretation results of TMS2 seismic line, based on the near-surface velocity profile (Fig. 16a) and the reflection profile (Fig. 16b).

Fig. 16
figure 16

Seismic interpretation of the TMS2 line: near-surface velocity profile (a); reflection profile (b)

Full size image

What is interpreted at first is the southern unconformity (labeled AU3) of the target granite. We could see there is a clear color edge below the stack 4240 m in Fig. 16a. Besides, there is a group of strong, steep reflection events in Fig. 16b. On south of AU3, the reflections are numerous. What's more, the neighboring reflections generally exhibit parallel or subparallel, all of which reveal that the reflection events on the south side of AU3 derive from a sedimentary environment. But on the north of AU3, the number of reflections decreases obviously, meanwhile most of them seem disordered and weak. With the regional geological findings considered, AU3 is interpreted as the southern boundary of the target granite, the south of which is the Mesozoic–Cenozoic basin.

Furthermore, it could be inferred that two unconformities (labeled AU1 and AU2) and two faults (labeled FP5 and FP6) exist within the Mesozoic–Cenozoic basin. As shown in Fig. 16b, the neighboring reflections are usually parallel in local regions. However, on both sides of AU1 and AU2, clear crossing angles between the overlying and the nether reflection events are demonstrated. This phenomenon is a typical characteristic of the angular unconformity on reflection imaging profiles. In addition, Fig. 16a exhibits rapid changes of velocity at the corresponding locations of AU1 and AU2. Based on the research of regional tectonics, AU3 reflects the unconformable contact between the lower-middle Jurassic Jijigou Formation (J1–2j) and the middle Permian quartz diorite (P2δο). AU2 represents the unconformity between the nether lower-middle Jurassic Jijigou Formation (J1–2j) and the overlying lower Cretaceous Bayingebi Formation (K1b). AU1 represents the unconformity between the nether strata (K1b) and the overlying widespread proluvial series of Pleistocene (Qp3pl). As the old strata (K1b) crops out the ground, AU1 is discontinuous.

On the north side of AU3, there is a group of high-energy reflections with good lateral continuation on the top portion of Fig. 16b. It could be speculated that the reflections derive from the top of the granite. The fluctuation changes of this reflection group are in perfect accordance with the color edge of the high-speed portion in Fig. 16a. Meanwhile, there is good correspondence between the continuations of the top reflection with the changes of outcrops’ lithology as shown in Fig. 14.

There are some groups of arcuate reflection events (labeled R1–R3), which could be recognized in Fig. 16b. This phenomenon may be related to the nonuniform property within the rock mass.

Near the north end of the TMS2, based on Fig. 16a and b, three faults (labeled as FP7–FP9) are interpreted.

There is a distinct low-speed zone in Fig. 16a. As well as a distinct dislocation phenomenon of reflections exists beneath the stack 16,440 m in Fig. 16b. Meanwhile, the distortions and interruptions phenomena of reflections could be observed. All of these phenomena reveal that one southward-dipping fault (FP8) exists beneath the TMS2 seismic line.

According to the reflection wave features and the velocity reversal phenomenon next to FP8, we could infer that two small northward-dipping faults (labeled FP7 and FP9) exist, and they merge downward with FP8. As shown in the regional tectonic map (Fig. 14), the north of the TMS2 seismic line crosses the southwest corner of the Cretaceous Yihetukemu basin which is covered by Quaternary. Thus, FP7 and FP8 faults just correspond to the two boundaries of the southwest corner of the basin.

The reason why FP8 shows normal property in its upper part and demonstrates reverse property in its lower part is considered to be related to multistage tectonization under different stress environments.

6 Conclusions

The present research adopts seismic exploration technology, which has a long history for serving the petroleum industry, to address the issue of siting a geological disposal repository for high-level radioactive nuclear waste in the nuclear industry. The techniques presented in the paper, e.g., cross-obstacle seismic geometry design, angle-domain near-surface scattered wave removal, and acoustic wave equation-based inversion method jointly utilizing both the and waveform of first arrival waves, have reference value for seismic exploration on complex near-surface areas in Western or Southern China. Based on the practice of seismic exploration on target granite rock mass, the following conclusions could be developed:travel time

  1. 1.

    To address the problems include crossing obstacles seismic acquisition, harmful scattered wave removal, and complex near-surface area velocity inversion, several targeted techniques were adopted. It could be considered that the experience derived from the present research is beneficial and worthy of reference for future studies. Some geotectonic phenomena, such as rock’s top interface and side boundaries, as well as local fractures within the rock, were revealed by the velocity and reflection imaging profiles separately. The features on different kinds of profiles had good coincidence.

  2. 2.

    The AU3 on the TMS2 seismic line is a significant boundary between the target granite body and the Mesozoic–Cenozoic basin. Combined with previous geological research, it could be inferred that AU3 separates the lower–middle Jurassic Jijigou Group (J1–2j) on its south side from the middle Permian quartz diorite (P2δο) on its north side.

  3. 3.

    In accordance with the “Safety guide for siting of geological disposal repository for nuclear waste (HAD401/06)” (China National Nuclear Safety Administration 2013), section 3.2.2, “The host rock must be adequately deep and extensive. The fractures that can offer a migration pathway for radioactive nuclide should be kept away in the site selection.” The results of the active source seismic exploration at Tamusu area indicate that: ① the target rock is not thin or has been transported by geological process from somewhere else, but a native and massive rock; ② a few small-scale local fractures whose space distribution and characteristics were revealed by the seismic profiles exist, and then keeping away from these fractures is needed to be taken into account.