EMT simulation and effect of TTI anisotropic media in EMT signal

Abstract

An axisymmetric finite difference method is employed for the simulations of electromagnetic telemetry in the homogeneous and layered underground formation. In this method, we defined the anisotropy property using extensive 2D conductivity tensor and solved it in the transverse magnetic mode. Significant simplification arises in the decoupling of the anisotropic parameter. The developed method is cost-efficient, more straightforward in modeling anisotropic media, and easy to be implemented. In addition, we solved the integral operation in the estimation of measured surface voltage using Gaussian quadrature technique. We performed a series of numerical modeling of EM telemetry signals in both isotropic and anisotropic models. Experiment with 2D tilt transverse isotropic media characterized by the tilt axis and anisotropy parameters shows an increase in the EMT signal with an increase in the angle of tilt of the principal axis for a moderate coefficient of anisotropy. We show that the effect of the tilt of the subsurface medium can be observed with sufficient accuracy and that it is an order of magnitude of 5 over the tilt of 90 degrees. Lastly, consistent results with existing field data were obtained by employing the Gaussian quadrature rule for the computation of surface measured signal.

1 Introduction

In borehole drilling, effective geosteering and accurate well landing require quick access to point scale data about formation being drilled, bit trajectory, well condition and lots more. Borehole telemetry is defined as the two-way transfer of such data from the bottom hole assembly (BHA) to the rig and the return of instructions from the rig to the borehole. Borehole data transmission could be useful in geothermal exploration, mineral exploration but are mostly used by the oil and gas industry. Borehole telemetry has been an essential part of industrial drilling for oil and gas resources in recent decades, especially in an unconventional reservoir and during horizontal drilling.

It provides considerable time savings and minimizes the risks associated with geosteering and accurate well landing. This technique has been successfully applied in the drilling of several oil wells (Schnitger and Macpherson 2009; Baker Hughes 2014). Telemetry methods can be classified based on the physical property considered in relation to the data propagation, such as mud pulse telemetry, electromagnetic telemetry and acoustic telemetry or combination of different techniques, e.g., acoustic–electromagnetic technique.

Electromagnetic telemetry (EMT) uses transmitted electromagnetic waves from bottom hole assembly (BHA) to the surface through the drill string, well and adjacent formations as a means of data transfer. Borehole telemetry aids in accurate core point access to formation properties acquired close to the drill bit by logging while drilling (LWD) in real time, to fully assist in timely identification of zones of interest. EMT measurements can be acquired continuously without the risk of data unavailability or insufficiency due to challenges with drilling fluid conditions as observed in mud pulse telemetry. However, electromagnetic telemetry is profoundly affected by formation properties. Therefore, effective simulation of the EMT response requires the consideration of the effect of formation anisotropy on the current distribution pattern and, in turn, the voltage measured at the surface with respect to the source location.

In EM study, formation anisotropy causes currents to depart from the direction of an exciting electric field within the formation of interest (Lu et al. 2002). Therefore, accurate estimation of EMT signals at the rig floor can be marred by the effect of anisotropy on acquired data. Anisotropy is a phenomenon that describes the variation in earth physical properties as it occurs on various scales in a variety of geophysical applications. The measured earth properties could differ along the different measurement axes. Previous applications of electromagnetic telemetry include marine controlled-source electromagnetic (CSEM) studies, reservoir characterization, SeaBed Logging (SBL), etc. (Brown et al. 2012; Cuevas 2019; He et al. 2019; Constable et al. 2019; Li et al. 2019). For several decades, studies have been carried out on electrical anisotropy as part of induction logging in efforts to better quantify hydrocarbon reservoir potential (Moran and Gianzero 1979; Anderson et al. 1998; Wilson 2015). In reservoir evaluation, electrical anisotropy measurements may improve the estimate of hydrocarbons in place. The conductivity tensor that relates the induced current to the applied electric field has three principal values, each corresponding to a direction of maximal conductivity. The resistivity of shale mostly controls the horizontal resistivity $\left( {\rho_{h} } \right)$ of the laminae, whereas the resistivity of hydrocarbon-bearing sands dictates the vertical resistivity $\left( {\rho_{t} } \right)$ (Klein 1993; Tabanou et al. 1999). Electrical anisotropy is caused by many different mechanisms such as conductive fluids filling in fractured formations with voids, and laminated deposition of substances of different electrical properties (e.g., sands and clays). In general, electrical anisotropy arises from the presence of sedimentary structures whose length scale is far smaller than the resolving power of measuring equipment, for example, shales and intercalation of thin layer of shale with sandstone are common phenomena resulting in formation anisotropy (Klein et al. 1995).

The effect of anisotropy on EMT data can be investigated via forward modeling using the finite difference method (FDM), the finite element method, etc. In this study, we considered how formation anisotropy affects the current distribution pattern within the drill string and, in turn, the voltage measured at the surface with respect to the source location during EMT. Emphasis was placed on investigating the effect of change in the orientation of the axis of symmetry of formation property in an anisotropic medium. We pay no attention to fluid invasion, but we consider the effect of the casing on the current distribution at specified distances from the source and measured voltage at the surface. For modeling of an electromagnetic telemetry system in an anisotropic environment, and considering the accuracy requirement for practical application and the implemented complexity of the schemes, we intend to apply FDM to model EM propagation tools in axisymmetric formation with anisotropy. FDM can take all the features in an electromagnetic telemetry system, such as drill pipes, drilling fluid in the borehole and multiple layers earth formation into consideration.

In this paper, we developed a scheme to model the EMT response in a 2D underground formation by employing a FD algorithm in the cylindrical coordinate system, to make use of the 2D structure to reduce the number of unknowns.

2 Methodology

2.1 Isotropic medium

Consider a homogenous and isotropic medium which is fully characterized by the constant parameters for magnetic permeability μ and electric permittivity ɛ. Next, assume that the source function and all the field variables exhibit the common time dependence $e^{{j\left( {\omega t - kr} \right)}}$, where ω is the angular frequency and k is the wave vector. Then, in terms of the fundamental field vectors, the electric intensity $E$ and the magnetic intensity $H$ are continuous and possess continuous derivatives at ordinary points, such that

$$\nabla \times E = - i\omega \mu H - J_{m}^{s}$$

(1)

$$\nabla \times H = + i\omega k_{\varepsilon } E + J_{e}^{s}$$

(2)

where $k_{\varepsilon } = i\omega \left( {\varepsilon - i{\raise0.7ex\hbox{${\sigma_{t} }$} \!\mathord{\left/ {\vphantom {{\sigma_{t} } \omega }}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$\omega $}}} \right)$, $\varepsilon$ is the dielectric permittivity, and $J_{e}^{s}$ and $J_{m}^{s}$ are the electric and magnetic source terms, respectively. $\sigma_{t}$ in Eq. (2) is the electrical conductivity tensor, and it is defined as follows:

$$\sigma_{t} = \left( {\begin{array}{*{20}c} {\sigma_{\rho } } & 0 & 0 \\ 0 & {\sigma_{\phi } } & 0 \\ 0 & 0 & {\sigma_{z} } \\ \end{array} } \right),$$

(3)

where $\sigma_{\rho }$, $\sigma_{\phi }$ and $\sigma_{z}$ are principle conductivities.

Furthermore, considering a cylindrical coordinate system, an electromagnetic telemetry system is characterized by EM signals propagated using an insulating gap source on the drill string surrounded by a uniform vertical column of either conductive or resistive drilling fluid, and an outer column of either layered formation and/or borehole casing (Fig. 1). The system, as defined radially outward from the center of the borehole, is solved as an axisymmetric and transverse magnetic problem. With the input voltage at the gap given and the magnetic current circulating the drill string specified at the source position, the governing equation for transmission of the radial magnetic field $H_{\phi }$ is given as

$$\frac{\partial }{\partial \rho }\left( {\frac{1}{{\rho k_{\varepsilon } }}\frac{\partial }{\partial \rho }\left( {\rho H_{\phi } } \right)} \right) + \frac{\partial }{\partial z}\left( {\frac{1}{{k_{\varepsilon } }}\frac{{\partial H_{\phi } }}{\partial z}} \right) + k_{0}^{2} \mu_{r} H_{\phi } = - J_{m}^{s},$$

(4)

Fig. 1

Diagram of a borehole with a telemetry system (modified after Ribeiro and Carrasquilla 2014). (Jiang et al. 2017; Anderson 2001)

where $J_{m}^{s} = i\omega \mu M_{\phi }$, and $M_{\phi }$ is the magnetic current density. The isotropic medium is characterized by a “radial conductivity” $\sigma_{\rho }$ which has the same value as the “vertical conductivity” $\sigma_{z}$ at any point within the given layer, such that $\sigma_{\rho } = \sigma_{z}$. Relative permittivity value of 1 was used in this study.

The current flowing along the drill string is given as $J = 2\pi \rho H_{\phi }$ (Chen et al. 2017); therefore, Eq. (4) becomes

$$\frac{1}{2\pi }\left( {\frac{\partial }{\partial \rho }\left( {\frac{1}{{\rho^{2} k_{\varepsilon } }}\frac{\partial }{\partial \rho }\left( {\rho J_{z} } \right)} \right) + \frac{\partial }{\partial z}\left( {\frac{1}{{\rho k_{\varepsilon } }}\frac{{\partial J_{z} }}{\partial z}} \right) + \frac{{k_{0}^{2} }}{\rho }\mu_{r} J_{z} } \right) = - J_{m}^{s}.$$

(5)

2.2 2D Anisotropy

Considering an electromagnetic telemetry system as described above and displayed in Fig. 1, the governing equation for EM propagation in full anisotropic media with conductivity tensor $\sigma_{t}$ in the cylindrical coordinate system is given as

$$\begin{gathered} \frac{1}{r}D_{\phi}^{h } E_{z} - D_{z}^{h} E_{\phi } = - i\omega \mu H_{r} - J_{r}^{m} \hfill \\ D_{z}^{h} E_{r} - D_{r}^{h} E_{z} = - i\omega \mu H_{\phi } - J_{\phi }^{m} \hfill \\ D_{r}^{h} E_{\phi } - \frac{1}{r}D_{\phi }^{h} E_{r} + \frac{{E_{\phi } }}{r} = - i\omega \mu H_{z} - J_{z}^{m} \hfill \\ \end{gathered}$$

(6)

$$\begin{gathered} \frac{1}{r}D_{\varphi}^{h} H_{z} - D_{z}^{h} H_{\phi } = k_{rr} E_{r} - k_{r\phi } E_{\phi } - k_{rz} E_{z} - J_{r}^{e} \hfill \\ D_{z}^{h} H_{r} - D_{r}^{h} H_{z} = k_{\phi r} E_{r} - k_{\phi \phi } E_{\phi } - k_{\phi z} E_{z} - J_{\phi }^{e} \hfill \\ D_{r}^{h} H_{\phi } - \frac{1}{r}D_{\phi }^{h} H_{r} + \frac{{H_{\phi } }}{r} = k_{zr} E_{r} - k_{z\phi } E_{\phi } - k_{zz} E_{z} - J_{z}^{e} . \hfill \\ \end{gathered}$$

(7)

Even though 3D forward modeling (Wang and Fang 2001; Weiss and Newman 2002; Davydycheva et al. 2003), combining high-performance computing, is available both in academic researches and in commercial software, full 3D methods are still prohibitively expensive for fast forward modeling. An intermediate solution between the 1D model and fully 3D model is the 2D model which has uniform property along the strike axis and is less computationally intensive.

In this study, a representative formation with anticlinal structure, which shows uniformity in the phi-direction but layering in the “r” and “z” plane, is considered. Generally, the transmitter of the EM tool consists of a very thin insulating gap along the drill string, generating controlled voltage difference along the conductive drill string. The source transmission of the EM tool consists of radially transmitted magnetic current. So the electric current transmission is majorly in the vertical direction along the drill string (which serves like air duct in guided waves). Even considering geological deformation, it is reasonable to assume that within the propagation range of a typical EMT system in a vertical or pseudo-vertical well (centimeters to tens of meters), the geological formation is an asymmetrical 2D structure, which exhibits uniform EM properties in phi direction. A depth slice of formation with anticlinal structure, which shows uniformity in the phi-direction but inhomogeneity in the r-z plane, is shown in Fig. 2 using a coordinate system image.

Fig. 2

Diagram of depth slice from an axisymmetric anticlinal structure. Each depth slice shows different layers within a given radial distance $r = 10$ m from the center (0). The radial distance is projected on the axis for $\phi$ equal to 0°and 180°. The change in sign marks opposite sides of the radial length from negative to positive

Therefore, consider an axisymmetric problem (that is, the physical properties are radially isotropic) for an anisotropic media, whose conductivity tensor is expressed as in a cylindrical coordinate system $\left( {r,\phi ,z} \right)$ as

$$\sigma_{t} = \left( {\begin{array}{*{20}c} {\sigma_{rr} } & 0 & {\sigma_{rz} } \\ 0 & {\sigma_{\phi \phi } } & 0 \\ {\sigma_{zr} } & 0 & {\sigma_{zz} } \\ \end{array} } \right).$$

(8)

The medium is characterized by a “radial conductivity” $\sigma_{rr}$ which is constant in the horizontal directions and varies in the vertical direction for “vertical conductivity” $\sigma_{zz}$ , such that $\sigma_{rr} \ne \sigma_{zz}$. The values of the subsurface conductivity tensor used in this study were defined using the anisotropy factor ${\uplambda }$, longitudinal conductivity $\sigma_{h}$, transverse conductivity $\sigma_{t}$ and dip angle θ. (See “Appendix 1” for details.) The principal conductivity $\sigma_{m}$ is defined by the dip and resultant of the longitudinal conductivity and transverse conductivity. For simplicity, the uniform dielectric constant value of 1 was used in this study. Therefore, Eqs. (6) and (7) are reduced to

$$\begin{gathered} - D_{z}^{h} E_{\phi } = - i\omega \mu H_{r} - J_{r}^{m} \hfill \\ D_{z}^{h} E_{r} - D_{r}^{h} E_{z} = - i\omega \mu H_{\phi } - J_{\phi }^{m} \hfill \\ D_{r}^{h} E_{\phi } + \frac{{E_{\phi } }}{r} = - i\omega \mu H_{z} - J_{z}^{m} \hfill \\ \end{gathered}$$

(9)

and

$$\begin{gathered} - D_{z}^{h} H_{\phi } = k_{rr} E_{r} - k_{rz} E_{z} - J_{r}^{e} \hfill \\ D_{z}^{h} H_{r} - D_{r}^{h} H_{z} = - k_{\phi \phi } E_{\phi } - J_{\phi }^{e} \hfill \\ D_{r}^{h} H_{\phi } + \frac{{H_{\phi } }}{r} = k_{zr} E_{r} - k_{zz} E_{z} - J_{z}^{e} .\hfill \\ \end{gathered}$$

(10)

Thus, as for 2D (TM) with 2D anisotropic problems, the curl–curl operator cannot simply be replaced by the Laplacian operator. However, the simplified off-diagonal elements of the conductivity tensor make it possible to couple these equations into pure TM modes as in the 2D isotropic case. Therefore, solving the transverse magnetic (TM) problem, the reduced 2D equation is given as

$$\begin{gathered} - D_{z}^{h} H_{\phi } = k_{rr} E_{r} - k_{rz} E_{z} \hfill \\ D_{z}^{h} E_{r} - D_{r}^{h} E_{z} = - i\omega \mu H_{\phi } - J_{\phi }^{m} \hfill \\ D_{r}^{h} H_{\phi } + \frac{{H_{\phi } }}{r} = k_{zr} E_{r} - k_{zz} E_{z}. \hfill \\ \end{gathered}$$

(11)

By solving for E_r and E_z in the first and last terms in Eq. (11), respectively, and substituting the obtained values in the second term, the following is obtained:

$$\begin{gathered} - k_{rr} k_{zz} \overline{U} H_{\phi } - k_{rr} k_{zz} \overline{U} J_{\phi }^{m} = - D_{z} k_{zz} H_{\phi } - D_{r} k_{rr} H_{\phi } \hfill \\ + D_{r}^{e} k_{rr} \frac{1}{r}H_{\phi } + D_{r}^{e} k_{rr} k_{zr} E_{r} - D_{z}^{e} k_{zz} k_{rz} E_{z} \hfill \\ \end{gathered}$$

(12)

where $\overline{U} = i\omega \mu .$ Eliminating $k_{rz} E_{z}$ and $k_{zz} E_{z}$ from the equations for E_r and E_z, respectively, and substituting the resulting equations into Eq. (12), one can derive a system for estimating the radial magnetic field

$$\left( \begin{gathered} D_{z} k_{zz} U + D_{r} k_{rr} U - \hfill \\ D_{r}^{e} \frac{1}{r}k_{rr} U - \overline{U} + D_{z}^{e} D_{r}^{h} k_{rz} U + \hfill \\ D_{r}^{e} D_{z}^{h} k_{zr} U - D_{z}^{e} \frac{1}{r}k_{rz} U \hfill \\ \end{gathered} \right)H_{\phi } = \overline{U} J_{\phi }^{m}$$

(13)

where $U = k_{rr} k_{zz} - k_{rz}^{2}.$

We note in Eq. (13) that the upper term is identical to and represents the 2D equation for isotropic medium, while the lower terms are indicative of the anisotropic effect. Considering Eq. (13), the upper terms can be considered as the primary term, while the lower term can be considered for anisotropy, the secondary term which can be updated for varying anisotropy conditions and effect.

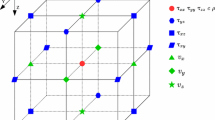
Furthermore, we approximate the ordinary differential equations in terms of a series of numerical operators representing higher-order forward and backward difference approximations and averaging operators; the higher-order central difference approximation can be obtained by combining forward and backward difference operators. The above equation can be discretized and solved by the conventional first-order finite difference method. However, for better efficiency in this paper, we used third-order forward and backward difference approximations, and fifth-order central difference approximation for the finite difference method. The discrete approximation of Eqs. (5) to (13) is formulated on a staggered 2D grid. In this formulation, the electric components were located on cell faces, while the magnetic components were located on cell nodes. For the isotropic part, the above implementation is direct and requires N faces and N + 2 nodes for every vertical discrete layer/discretization. However, for the anisotropic term, a slight complication arises from implementing the update parameters from the conductivity functions. In our implementation of this term, we averaged the update parameters onto the nodes/cell faces using a four-plane average matrix (Guo et al. 2018);

$${\text{AFZ } = \text{ }}\left[ {\begin{array}{*{20}c} {1/4} & {1/4} & m & {1/4} & {1/4} & 0 & 0 \\ 0 & {1/4} & {1/4} & m & {1/4} & m & 0 \\ 0 & 0 & {1/4} & {1/4} & m & m & 0 \\ n & n & n & 0 & n & n & n \\ 0 & 0 & 0 & m & {1/4} & m & {1/4} \\ \end{array} } \right]$$

(14)

to ensure continuity.

With mapping operators and mapped model parameters, discretizing Eqs. (13) and (14) term by term, the complete matrix form for the magnetic phi-components on a staggered grid can then be represented as

$$\left( \begin{gathered} D_{z} {\text{aup}} + D_{r} {\text{bup}} - D_{r}^{e} {\text{arup}} + \hfill \\ \overline{D}_{zr} \cdot \left( {{\text{AFZ}} * {\text{crup}}} \right) + \hfill \\ \overline{D}_{rz} \cdot \left( {{\text{AFZ}} * {\text{cup}}} \right) - \hfill \\ D_{z}^{e} \cdot \left( {{\text{AFZ}} * {\text{crup}}} \right) - \overline{U} \hfill \\ \end{gathered} \right)H_{\phi } = \overline{U} J_{\phi }^{m}$$

(15)

where ${\text{aup}} = k_{zz} U,$ ${\text{bup}} = k_{rr} U,$ ${\text{arup}} = \frac{1}{r}k_{rr} U,$ ${\text{crup}} = \frac{1}{r}k_{rz} U,$ and ${\text{cup}} = k_{rz} U.$

The results of this investigation were assessed by comparing the plots of the current distribution along the drill string and the measured EMT signal on the surface. To obtain the nodal values, the radial magnetic field value was interpolated as the dot product of the face calculated radial magnetic field with the AFZ transpose matrix.

3 Modeling

In this study, we used these standard model parameters unless specified otherwise: frequency range of 5–10 Hz, drill string inner radius of 0.25 m, while the outer radius is 0.3 m, and the casing inner and outer radius of 0.4 m and 0.45 m, respectively. Uniform conductivity value of 5 × 10⁶ S/m was used for the casing and drill string, while the drilling fluid conductivity was set as 1 S/m. The relative magnetic permeability of the casing, borehole fluid and the formation is assumed to be unity.

We first consider a vertical well in a homogeneous underground formation with a resistivity value of 10 Ω.m. Solid drill string with a radius of 0.25 m and casing with an inner and outer radius of 0.35 m and 0.4 m, respectively, were used in this model. The total length of the drill string and the casing is 1200 m and 800 m, respectively. The voltage source with a value of 1 v and propagating frequency of 10 Hz were set 15 m away from the base of the drill string. To assess the accuracy of the FD code, we compared the current distribution along the drill string obtained from the FD method with the one obtained from the numerical simulation software (COMSOL vs. 5.3a 2017), which is designed based on the finite element method (Fig. 3).

Fig. 3

Comparison of amplitude of current flow along the drill string in a homogeneous formation obtained from the FD method and FEM method in COMSOL Multiphysics software

A conventional decrease in the amplitude of current along the drill string away from the source is recorded. Also, a decrease in amplitude is recorded across the 800 m depth mark due to the presence of casing in the vertical well. We can see that current flow along the drill pipe calculated by both the FD method and the FEM method from COMSOL suite agrees relatively well with the exception of the depths below 1000 m where the FEM data show no definite trend and are less fitting.

We further consider a vertical well in a homogeneous underground formation with a resistivity of 10 Ω.m, and a two-layered earth model with resistivity 1 Ω.m and 10 Ω.m, respectively. The length of the drill string is constant, while the length of the borehole casing varied between 800 and 920 m depth, for both the homogeneous formation and two-layer earth model, respectively. The diameters of the drill pipe and the borehole are 0.3 m and 0.45 m, respectively. The resistivity of the drilling fluid is set as 1 Ω.m, and the conductivity of both drilling pipe and borehole casing is assumed to be 5 × 10⁶ S/m. The downhole transmitter with 1v voltage source is set at 50 m behind the drill bit.

Figure 4a shows the simulated magnitude of the current flowing through the drill string with a transmitting frequency of 5 Hz. The magnitude of the current flowing through the drill string gradually decreases with an increase in distance from the source; this reflects the change in current density with loss of current into the adjacent formations. Comparison of current distribution result for cased borehole (black) and non-cased borehole (red) shows a decrease in the magnitude of the current flowing along the drill string from the depth of 800 m due to the presence of steel casing. In the case of layered medium (Fig. 4b), with transmitting frequency of 10 Hz, slight deflection (reduction in current magnitude) due to borehole casing was recorded at a depth of 920 m. However, the most notable perturbation is the current loss in the adjacent conductive layer at a depth of 550 m in the cased well.

Fig. 4

Amplitude of current flow along the drill string in; a a homogeneous formation and b 2-layered earth model. The current flow, as indicated above, is attenuated in the presence of both conductive adjacent formation and well casing. These form the major challenges encountered in EM telemetry

The general feature one might observe from these figures is that the current distribution along the drill string is much stronger without casing than with casing. The disparity in the magnitude of the current distribution might be explained by the fact that a single metal cylinder in a given model can support a guided wave theory (Stratton 1941). In other words, the current induced by the current/voltage source at the insulating gap along the drill string flows majorly vertically along the drill string. However, with the second highly conductive metal cylinder included, more current gets attenuated by the adjacent steel, leading to a reduction in the surface measured EMT signal.

As mentioned above, the current density will produce a pattern of vertical distribution within the drill string and near-vertical distribution along the inner annulus. When compared to the current flow in a cased well, a similar flow pattern is expected for current within the drill string, while the magnitude of current within the annulus is reduced because there is a current loss to the conductive casing. These flow patterns are shown in Fig. 5, representing the current distributions in the vertical plane (r-z plane) for cases with and without a steel casing. The difference between the current distributions of these two cases can be seen clearly with the current being weak along the borehole direction within the cased region.

Fig. 5

Current flow distribution in a homogeneous formation with; a non-cased well and b cased well

4 Recorded voltage estimation

The recorded voltage at the surface can be obtained by calculating the integral of the electric field calculated from the obtained current distribution. (See “Appendix 2”) In practice, the integrand is seldom smooth. However, this issue is addressed in Gaussian quadrature by using weighting function, which results in removal of integrable singularities (Mahesh and Sucharitha 2018; Piqueras et al., 2019; Hassan et al. 2020). Therefore, for higher accuracy calculation, we used the explicit Legendre–Gauss–Lobatto (LGL), Legendre–Gauss–Radau (LGR), Gauss–Lobatto (GLo) and Gauss–Legendre (GLe) quadrature techniques, which converge accurately to estimate the potential across two measuring points (−1,1). The integral form of the quadrature techniques is given in “Appendix 2.” When using the Gaussian quadrature techniques, selecting an appropriate bandwidth for a kernel density estimator is important. Several techniques have been used to select the smoothing parameter for reasonable density estimate. These are categorized as either plug-in bandwidth estimators, which tend to select larger bandwidths and could produce over-smoothed results, classical estimators which on the other hand could produce under smoothed results when the smoothing problem is severe (Loader 1999), or nonparametric estimation (Marron and Chung 2001; Chan et al. 2010; Golyandina et al. 2012), which considers a family of smooths with a broad range of bandwidths, instead of a single estimated function. Noting that the goal is to decide on selecting the smoothing parameter purely from the data, we used the nonparametric technique.

Figure 6 shows an example of voltage responses generated from a mixture of a Gaussian variable using the homogenous earth model and 10 Hz propagating frequency. The kernel density was estimated using n (number of data points observed from a realization of the random variables) that varies from 2 to 150, thereby varying the bandwidths. The wide range of smoothing considered allows a contrast of estimated features and possible point of convergence. In comparison, the accuracy of the estimated values increases with an increase in the value of n and at a different rate for most of the techniques. However, with n equal to 150, the different techniques converge to given stable values.

Fig. 6

Estimated voltage responses with several bandwidths initiated by changing the number of data point value from 2 to 150

Using n equal to 150, the comparison of voltage measured at the surface using both homogeneous earth and the three-layer earth model, with background resistivity of 10 Ω.m, middle layer resistivity value of 2 Ω.m, and source location varying from 200 to 1350 m depth at an interval of 45 m, is shown in Figs. 7 and 8. The confined conductive layer was set between the depths of 440 m and 580 m. A small difference in the value of the measured voltage at the surface is obtained by comparing the results from Gauss quadrature algorithms with the direct method between the depth of 200–300 m for transmitting frequency of 10 Hz, and 300 m to 700 m for transmitting frequency of 5 Hz. Below these depths, the results from the different techniques are similar. In general, an increase in measured voltage at the surface is obtained between the depths of 440 m and 600 m, as the source is located within the conductive layer. As the source depth increases, the magnitude of the EMT signal recorded at the surface reduces as the rate of attenuation of the current flowing through the drill string increases within the conductive layer.

Fig. 7

Simulated measured EMT signal for BHA transmitted signal at 10 Hz frequency set at depths ranging from 200 to 1370 m in a homogeneous formation and b layered earth model

Fig. 8

Simulated measured EMT signal for BHA transmitted signal at 5 Hz frequency set at depths ranging from 200 to 1440 m in a homogeneous formation and b layered earth model

Furthermore, we used an example of a field telemetry data acquired in Shandong Province, China. The resistivity log and constructed earth resistivity model are shown in Fig. 9. The drilling fluid resistivity value of 1 Ω.m was used in this case. The working frequency and output/input current of the downhole source were 10 Hz and 1.4 A, respectively. The diameter of the drill pipe was set as 0.35 m, while the borehole diameter was set as 0.5 m. In the case of the cased well simulation, the casing diameter was set as 0.6 m. *Note that the resistivity of the first layer was set as 30 Ω.m considering the inconsistency in the resistivity log and the high value of the measured field data within this depth. Also, the coefficients of anisotropy values of 1.8, 0.6, 0.8, 2 and 1.5 were used to define the longitudinal conductivity values at depths [320 366] m, [367 440] m, [441 480] m, [481 520] m and [667 760] m, respectively. The measured EMT signal was simulated at depths ranging from 150 to 1080 m.

Fig. 9

Resistivity well logging data (a) and respective earth resistivity model (b) used in EMT signal simulation (units in Ω.m). Established baselines with deterministic linear trends along the resistivity log were used to represent average vertical resistivity within each of the representative units

Figure 10 shows the comparison of the simulated surface recorded telemetry signal using the different integral techniques with the field-measured data. The obtained plots show that the simulated responses follow the same trend as the field measurements over a large depth range. The simulated EMT signal in a cased well (Fig. 10b) shows a more pronounced representation of the low-magnitude field data with the exception of a significant difference between the depths of 300 m and 480 m, as observed in the result for the non-cased well signal as well (Fig. 10a). In general, the magnitude of the measured EMT signal simulated without borehole casing is higher with the given model. The simulated EMT signal is a close match with high-magnitude field data within the first 300 m and at subsequent depths.

Fig. 10

Comparison of measured EMT signal (Mag high—maximum value in black, and Mag low—minimum value in red) with simulated EMT signal for BHA transmitted signal at 10 Hz frequency set at depths ranging from 150 to 1080 m in; a non-cased well, b cased well, and c 1D representation of the transverse resistivity model. LGL, LGR, GLe and GLo are the integral results obtained from using Legendre–Gauss–Lobatto, Legendre–Gauss–Radau, Gauss–Lobatto and Gauss–Legendre quadrature techniques

Furthermore, we compared the EMT response from the isotropic model with the final response of transverse anisotropy (Fig. 11). Introducing anisotropy into some of the layers results in better representation of the recorded voltage at the different source depths. The simulated EMT signal with anisotropic model gave a better representation of the field data between the depths of 150–280 m and 400–1080 m. The similarity between the measured voltage and the simulated voltage plots shows that these techniques can be used as an effective method for the calculation of surface recorded voltage in cases where high-order accuracy is required, especially when the order of noise magnitude is close to that of the expected signal.

Fig. 11

Comparison of simulated EMT signal from the isotropic model with the result from the anisotropic model. a The result from the isotropic model, b result from the anisotropic model and c 1D representation of the isotropic resistivity model

However, the uncertainties between the earth model used and the resistivity log, as well as other cultural and drilling conditions, will lead to discrepancies between numerical simulation results and actual measurements. For example, the resistivity distribution near the surface is subject to larger variation due to moisture; and the mud resistivity in borehole may change with depth. Although the formation resistivity is considered as anisotropic due to successive intercalation of resistive and conductive earth material in each purported layer, the value of the anisotropic factor is at best an estimate. Therefore, later in the study, we considered the effect of change in the angle of orientation of the axis of symmetry of the conductivity principal axis on the surface measured EMT signal.

In addition, we considered the effect of change in conductivity of the drill string on both the current distribution along the string. We measured the EMT signal, using a three-layer earth model, with background resistivity of 10 Ω.m and middle layer resistivity value of 2 Ω.m. The conductivity of the casing was set as 5 × 10⁵ S/m. The source location was set at a depth of 1480 m, 280 m ahead of the casing and 20 m behind the drill bit. The confined conductive layer was set between the depths of 440 m and 580 m. The obtained results are shown in Fig. 12. The result shows an initial non-appreciable increase in the magnitude of the current flowing along the drill string with a decrease in the conductivity of the drill string. However, the current flow via the drill string increases rapidly as the conductivity value reduces to 1 × 10⁴ S/m. A plot of voltage recorded at the surface shows an initial relatively constant voltage value with a decrease in the conductivity of the drill string. However, when the conductivity value of the drill string is reduced from 1 × 10⁶ to 1 × 10⁴ S/m, the simulated EMT signal increases exponentially. The drill string conductivity values of 1 × 10⁴ S/m give the highest voltage of 2.53 mV at the surface. In contrast, the conductivity value of 1 × 10⁷ S/m gives the lowest surface measured voltage of 0.11 mV, with a dipole distance of 100 m. Therefore, the development of hybrid drill string material with low conductivity will be favorable in the application of electromagnetic telemetry in general.

Fig. 12

Comparison of simulated EMT signal with a change in the conductivity of the drill string; a current density along the drill string and b measured voltage at the surface

Lastly, we considered a two-layer earth model where part of the first layer has anisotropic property. Given that (1) a broad range of value of anisotropy factor from 0.5 to about 30 could exist in a sedimentary environment, though the values are usually within 1 and 5, and (2) an increase in anisotropy factor represents either decrease in the transverse conductivity or increase in longitudinal conductivity, and assuming that the model is radially isotropic, changes in surface recorded voltage with change in the dip of the principal axis of subsurface material property (conductivity), with respect to a given anisotropy value, are considered. Here, we consider an axisymmetric model in which the resistivity parameters do not change in the phi-direction. The model properties may be described with reference to either a cylindrical (measurement) coordinate frame involving the tensor elements ρ_rr, ρ_rz, ρ_zz or a principal axis frame involving the components ρ_h, ρ_t and θ^o. Here, ρ_h is the longitudinal resistivity, ρ_t is the transverse resistivity, and θ° is the angle of the symmetry axis relative to the vertical, which is physically meaningful since eigenvectors are aligned with the natural rock frame. The angle of the symmetry axis is illustrated schematically in Fig. 13a.

Fig. 13

a Simplified diagram of anisotropic 2-D TTI media, showing the axis of symmetry and principal resistivities. b 1D representation of the resistivity model. The geographic coordinate frame is r, z, while the principal axis frame (or natural rock frame) is tilted away from this direction. The directions of the principal axes are the corresponding eigenvectors

By rearranging the orthogonal anisotropic resistivity model parameters (ρ_h and ρ_t), we may introduce an alternative form of description for the media, namely the mean resistivity ρ_m and the coefficient of anisotropy λ, given by:

$$\rho_{m} = \sqrt {\rho_{t} \rho_{h} } \;\;{\text{and}}\;\;\lambda = \sqrt {{\raise0.7ex\hbox{${\rho_{t} }$} \!\mathord{\left/ {\vphantom {{\rho_{t} } {\rho_{h} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\rho_{h} }$}}}.$$

(16)

The quantity ρ_m is the geometric mean of the longitudinal and transverse resistivities. It is equal to surface measured apparent resistivity. In this section, we focused on incorporating the coefficient of anisotropy with the model parameters and the orientation of the axis of symmetry and considering its effect on electromagnetic telemetry signal.

As an instructive preliminary investigation, we computed current distribution along the drill string and the surface measured signal, at a dipole length of 100 m, for the different axes of symmetry, θ (°), and fixed value of ρ_h, λ. The current distribution along the drill string was calculated for a two-layered anisotropic model with an anisotropic value of λ = 5, ρ_h of 1 Ω.m and 10 Ω.m for the top and lower layers, respectively. The anisotropic column was between the depths of 220 m and 440 m, and θ (°) varies from 2° to 90°.

The simulated surface measurement related to θ = 90° is five orders of magnitude higher than θ = 2° (Table 1). The existence of resistive anisotropic medium confined by conductive isotropic materials (great simplifications arise in the decoupling of the anisotropy parameters) results in a significant reduction in the magnitude of surface recorded EMT signal. The rose diagram in Fig. 13a shows that the sensitivities to change in θ angle increase with a decrease in θ and very rapidly for angles below 60°. The source of the amplitude difference in the sensitivity stems from the difference in the model parameters θ (°), leading to an increase in the value of ρ_r (Ω m) as θ increases, and its value tends toward the value of the major principal axis ρ_z (Ω m).

Table 1 Surface measure voltage for electromagnetic telemetry

To illustrate the differences with the change in the dip of the principal axis, the currents have been plotted. Since the horizontal conductivity is fixed in this study, plots of the current distribution along the drill string exhibit the same patterns as those of surface measured voltage. The plot of the current distribution along the drill string (Fig. 14b) shows an increase in the magnitude of the current flowing along the drill string with an increase in the angle of orientation of the axis of symmetry. At low angle (θ = 30° and 15°), the magnitude of the current distribution along the drill string decreases very fast within the anisotropic layer, and the z-plane becomes almost entirely vertical (Figs. 13 and 14b). When θ is between 45° and 75°, slight variation in the magnitude of the current distribution along the drill string was observed, and at θ > 75° no significant change in current density was recorded. In comparison with the result from the isotropic medium, the value of current flowing along the drill string with θ = 45° has almost the same value as that of the isotropic medium, while for θ > 45°, the current density is higher. (The horizontal component is dominant.)

Fig. 14

Comparison of simulated EMT signal with the change in the angle of the principal axis of symmetry of the subsurface property; a rose diagram showing the change in EMT signal magnitude with a change in the angle of the principal axis of symmetry and b current density along the drill string at different angles of principal axis of symmetry

Although EM telemetry is used in subsurface wireless communication, it is not as a quantitative well logging tool, a substantial level of accuracy should be of priority for modeling of EM telemetry. This study shows the complexity in an accurate simulation of EMT measured signal and the extensive effect of anisotropy which could be of significant influence even if for a short section. Hence, a combination of mud-pulse and EM telemetry could be useful in ensuring a continuous transmission of measurable signal with high magnitude.

5 Conclusion

In this paper, we presented an efficient FDM scheme for simulations of electromagnetic telemetry in the axisymmetric model. In terms of application, homogeneous and layered earth models were used as examples. The current density along the drill string and surface measured voltages were solved to understand the effect of change in drill string conductivity and angle of axisymmetry of the earth physical property on electromagnetic telemetry. The algorithm and model used straightforwardly assimilates the 2D anisotropy and allows the computation of the anisotropy effect as an update field. Also, we considered the Gaussian quadrature techniques in the effective estimation of measured EMT signal. A field case was also given showing that the calculated results by the proposed method agree with the measured data. Lastly, the effect of change in axis of symmetry of earth layering and occurrence of confined resistive layers should be taken into account in considering the effectiveness of EM telemetry. In general, we found that the accuracy of the 2D FDM scheme presented in this study is suitable for practical applications and that the computational efficiency is much higher than for 3D modeling. It is believed that simulations in this paper will facilitate the feasibility study of an electromagnetic system for real field jobs.

Appendices

Appendix 1

In this section, the anisotropic parameters defining a homogeneous TTI medium $\sigma_{h}$, $\sigma_{t}$ or $\sigma_{m}$, ${\uplambda }$, azimuth $\phi$ and the dip angle θ were used in deriving the conductivity values for TTI medium in a cylindrical coordinate system, where ${\uplambda }$ is the anisotropy factor, ${\sigma }_{h}$ represents the longitudinal conductivity, ${\sigma }_{t}$ represents the transverse conductivity and $\sigma_{m}$ is the geometric mean of the principal conductivities and is defined by the dip and resultant of the longitudinal conductivity and transverse conductivity. Given the diagonalized conductivity matrix in Cartesian coordinate which represents the three eigenvalues σ₁, σ₂, σ₃ as

$$\sigma_{T} = \left( {\begin{array}{*{20}c} {\sigma_{xx} } & 0 & 0 \\ 0 & {\sigma_{yy} } & 0 \\ 0 & 0 & {\sigma_{zz} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\sigma_{1} } & 0 & 0 \\ 0 & {\sigma_{2} } & 0 \\ 0 & 0 & {\sigma_{3} } \\ \end{array} } \right),$$

(17)

we define the relationship between the geometric mean, the principal conductivities and coefficient of anisotropy as $\sigma_{xx} = \sigma_{yy} = \sigma_{h}$, $\sigma_{zz} = \sigma_{t}$, $\sigma_{m} = \sqrt {\sigma_{h} \sigma_{t} }$ and $\lambda^{2} = {{\sigma_{h} } \mathord{\left/ {\vphantom {{\sigma_{h} } {\sigma_{t} }}} \right. \kern-\nulldelimiterspace} {\sigma_{t} }}$ for transverse anisotropic (VTI) medium. Compared to the VTI medium, the conductivity tensor of TTI medium in the Cartesian coordinate system can be expressed as

$$\sigma_{T} = R^{ - 1} \left( {\begin{array}{*{20}c} {\sigma_{1} } & 0 & 0 \\ 0 & {\sigma_{2} } & 0 \\ 0 & 0 & {\sigma_{2} } \\ \end{array} } \right)R ,$$

(18)

where

$$R = \left( {\begin{array}{*{20}c} {\cos \phi \cos \theta } & {\sin \phi \cos \theta } & { - \sin \theta } \\ { - \sin \phi } & {\cos \phi } & 0 \\ {\cos \phi \sin \theta } & {\sin \phi \sin \theta } & {\cos \theta } \\ \end{array} } \right) .$$

The anisotropic medium can thus be described by six independent components writing in Cartesian coordinate or recording frame as:

$$\left( {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{xy} } \\ {\sigma_{xz} } \\ {\sigma_{yy} } \\ {\sigma_{yz} } \\ {\sigma_{zz} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\sigma_{h} \cos^{2} \theta \cos^{2} \phi + \sigma_{h} \sin^{2} \phi + \sigma_{t} \sin^{2} \theta \cos^{2} \phi } \\ {0.5\left( { - \sigma_{h} + \sigma_{t} } \right)\sin^{2} \theta \sin 2\phi } \\ {0.5\left( { - \sigma_{h} + \sigma_{t} } \right)\cos \phi \sin 2\theta \,} \\ {\left( { - \sigma_{h} + \sigma_{t} } \right)\sin^{2} \theta \sin^{2} \phi + \sigma_{h} } \\ {0.5\left( { - \sigma_{h} + \sigma_{t} } \right)\sin \phi \sin 2\theta } \\ {\sigma_{h} \sin^{2} \theta + \sigma_{t} \cos^{2} \theta } \\ \end{array} } \right)$$

(19)

where $\sigma_{1} = \sigma_{2} = \sigma_{h}$ and $\sigma_{3} = \sigma_{t}$.

However, for the general 2/2.5-D case where $\phi = 0$, that is, there is no dependency on the azimuth, we obtain:

$$\left( {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{xz} } \\ {\sigma_{yy} } \\ {\sigma_{zz} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\sigma_{h} \cos^{2} \theta + \sigma_{t} \sin^{2} \theta } \\ {0.5\left( { - \sigma_{h} + \sigma_{t} } \right)\sin 2\theta } \\ {\sigma_{h} } \\ {\sigma_{h} \sin^{2} \theta + \sigma_{t} \cos^{2} \theta } \\ \end{array} } \right) .$$

(20)

To translate these results into a cylindrical coordinate system with situations where the axis of symmetry is tilted along the dip, we used the following expression:

$$\sigma_{Tc} = Rc^{ - 1} \left( {\begin{array}{*{20}c} {\sigma_{h} \cos^{2} \theta + \sigma_{t} \sin^{2} \theta } & 0 & {0.5\left( { - \sigma_{h} + \sigma_{t} } \right)\sin 2\theta } \\ 0 & {\sigma_{h} } & 0 \\ {0.5\left( { - \sigma_{h} + \sigma_{t} } \right)\sin 2\theta } & 0 & {\sigma_{h} \sin^{2} \theta + \sigma_{t} \cos^{2} \theta } \\ \end{array} } \right)$$

(21)

where $\sigma_{Tc}$ is the conductivity tensor in the cylindrical coordinate system and $Rc^{ - 1}$ is the conversion matrix. The matrix expression for the conversion matrix is given as

$$Rc^{ - 1} = \left( {\begin{array}{*{20}c} {\cos \phi } & {\sin \phi } & 0 \\ { - \sin \phi } & {\cos \phi } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right) .$$

(22)

Finally, the TTI conductivity tensor is given as

$$\left( {\begin{array}{*{20}c} {\sigma_{rr} } \\ {\sigma_{rz} } \\ {\sigma_{\phi \phi } } \\ {\sigma_{zz} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\cos \phi \left( {\sigma_{h} \cos^{2} \theta + \sigma_{t} \sin^{2} \theta } \right)} \\ {\cos \phi \left( {0.5\left( { - \sigma_{h} + \sigma_{t} } \right)\sin 2\theta } \right)} \\ {\sigma_{h} \cos \phi } \\ {\sigma_{h} \sin^{2} \theta + \sigma_{t} \cos^{2} \theta } \\ \end{array} } \right).$$

(23)

Note that there is no dependence on the axial direction with $\phi = 0$. Therefore, the conductivity parameter for the TTI model considered in this study can be presented in a 3 × 3 matrix form as

$$\sigma_{Tc} = \left( {\begin{array}{*{20}c} {\sigma_{rr} } & 0 & {\sigma_{rz} } \\ 0 & {\sigma_{\phi \phi } } & 0 \\ {\sigma_{rz} } & 0 & {\sigma_{zz} } \\ \end{array} } \right) .$$

(24)

Appendix 2

In electromagnetic telemetry, the recorded voltage at the surface can be obtained by calculating the integral of the electric field calculated from the obtained current distribution as

$$V_{{{\text{received}}}} = \int_{{r_{0} }}^{r} {E_{r} \partial r = } \int_{{r_{0} }}^{r} {\frac{{J_{r} }}{{\sigma_{h} }}\partial r} .$$

(25)

Considering a vertical dipole system, the measured EMT signal is calculated using the z-component of the current density as

$$V_{{{\text{received}}}} = \int_{{z_{0} }}^{z} {E_{z} \partial z = } \int_{{z_{0} }}^{z} {\frac{{J_{z} }}{{\sigma_{t} }}\partial z} .$$

(26)

However, in this study, we considered only the conventional surface measurement of EMT signal, where r₀ is the position on the blowout preventer and r represents second position tens of meters to over a hundred meters from $r_{0}$.

To solve the integrand, we adopted Gaussian quadrature techniques using weighing function through which integrable singularities are removed. Conventionally, the domain of integration is taken as [a,b], whereas in Gaussian quadrature, the domain is reduced to [−1,1]. The general Gaussian quadrature can be represented as

$$\int\limits_{ - 1}^{1} {f\left( x \right)} dx = \int\limits_{ - 1}^{1} {W\left( x \right)} g(x)dx \approx \sum\limits_{i = 1}^{n - 1} {w_{i} g\left( {x_{i} } \right)} .$$

(27)

In this study, we used the explicit Legendre–Gauss–Lobatto (LGL), Gauss–Lobatto (GLo), Legendre–Gauss–Radau (LGR) and Gauss–Legendre (GLe) quadrature techniques, which converge accurately to estimate the potential across two measuring points (−1,1). The integral form of the quadrature techniques is given as

$$\textbf {GLo}\, \text{-}\,\,\,\,\int\limits_{ - 1}^{1} {f\left( x \right)} dx \approx \frac{2}{{n\left( {n - 1} \right)}}\left( {f\left( { - 1} \right){ + }f\left( 1 \right)} \right){ + }\sum\limits_{i = 2}^{n - 1} {w_{i} g\left( {x_{i} } \right)} ,$$

(28)

$$\textbf{LGL}\, \text{-}\,\,\,\,\int\limits_{ - 1}^{1} {f\left( x \right)} dx \approx \frac{h}{2}\sum\limits_{i = 1}^{n} {w_{i} g\left( {x_{i} } \right)} ,$$

(29)

$$\textbf{LGR}\, \text{-}\,\,\,\,\int\limits_{ - 1}^{1} {f\left( x \right)} dx \approx w_{1} f\left( { - 1} \right){ + }\sum\limits_{i = 2}^{n} {w_{i} g\left( {x_{i} } \right)} ,$$

(30)

and

$$\textbf{GLe}\, \text{-}\,\,\,\, \int\limits_{a}^{b} {f\left( x \right)} dx \approx \sum\limits_{i = 1}^{n} {w_{i} \frac{b - a}{2}g\left( {\frac{{a{\text{ } + \text{ b}}}}{2} - \frac{b - a}{2}x_{i} } \right)} ,$$

(31)

$$\text{with weights;}\, \textbf{LGL}\,\text{-}\,\,\,\,w_{i} \,{ = }\,\frac{2}{{n\left( {n - 1} \right)\left[ {P_{n - 1} \left( {x_{i} } \right)} \right]^{2} }} ,$$

(32)

$$\textbf{GLo}\, \text{-}\,\,\,\,w_{i} \,{ = }\,\frac{2}{{n\left( {n - 1} \right)\left[ {P_{n - 1} \left( {x_{i} } \right)} \right]^{2} }} ,$$

(33)

$$\textbf{GLe}\, \text{-}\,\,\,\,w_{i} \,{ = }\,\frac{2}{{\left( {1 - x_{i}^{2} } \right)\left[ {P^{\prime}_{n} \left( {x_{i} } \right)} \right]^{2} }} ,$$

(34)

$$\text{and}\,\textbf{LGR}\, \text{-}\,\,\,\,w_{i}\, { = }\,\frac{2}{{\left( {1 - x_{i} } \right)\left[ {P_{n - 1}^{\prime} \left( {x_{i} } \right)} \right]^{2} }} ,$$

(35)

where n is the number of function values $f_{1} , \ldots ,f_{n}$ at a distinct set of points $x_{1} , \ldots ,x_{n}$. P_n(x_i) denotes the Legendre polynomials with the nth polynomial normalized to be monic, and x_i is the ith root of P_n. More on the nodes and weights of the Gaussian quadrature techniques can be found in the literature (Canuto et al. 1987; Mathew and Fink 2004; Abbott 2005; Mahesh and Sucharitha 2018). The voltage between the two measuring points is set by initially introducing the two terminals as the domain points [−1,1] in the calculation of the weight and polynomial nodes. Then, the actual point values [a,b] are used to re-calibrate the weights and nodes.