Abstract
Equivalent staggered-grid (ESG) as a new family of schemes has been utilized in seismic modeling, imaging, and inversion. Traditionally, the Taylor series expansion is often applied to calculate finite-difference (FD) coefficients on spatial derivatives, but the simulation results suffer serious numerical dispersion on a large frequency zone. We develop an optimized equivalent staggered-grid (OESG) FD method that can simultaneously suppress temporal and spatial dispersion for solving the second-order system of the 3D elastic wave equation. On the one hand, we consider the coupling relations between wave speeds and spatial derivatives in the elastic wave equation and give three sets of FD coefficients with respect to the P-wave, S-wave, and converted-wave (C-wave) terms. On the other hand, a novel plane wave solution for the 3D elastic wave equation is derived from the matrix decomposition method to construct the time–space dispersion relations. FD coefficients of the OESG method can be acquired by solving the new dispersion equations based on the Newton iteration method. Finally, we construct a new objective function to analyze P-wave, S-wave, and C-wave dispersion concerning frequencies. The dispersion analyses show that the presented method produces less modeling errors than the traditional ESG method. The synthetic examples demonstrate the effectiveness and superiority of the presented method.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Numerical modeling for elastic wave propagation is a powerful tool in seismic data processing and interpretation (Duan et al. 2013). The numerical modeling has extensive applications in 2D seismic exploration, but it suffers inherent weaknesses and certain limitations for complex media. In recent years, seismic explorations have gradually shifted to areas with complex geological conditions, such as regions with mountains, deserts, faulted basins (Yang et al. 2015). As a result, 3D numerical modeling has attracted growing attention for high-precision seismic exploration. 3D wave equations can comprehensively describe seismic wavefield characteristics and propagation laws, and provide the theoretical basis for the acquisition, processing, interpretation (Xia et al. 2004). In addition, the elastic wavefield carries rich information related to the earth media, which means that it may provide more underground geological and structural information (Yong et al. 2016; Yang et al. 2018). Therefore, the high-precision simulation of the 3D elastic waveform plays a pivotal role in seismic exploration technologies.
Many numerical methods have been developed to solve wave equations, including the finite-difference (FD) methods, pseudo-spectral methods (Reshef et al. 1988), finite element methods (Marfurt 1984), spectral element methods (Zhu et al. 2011), etc. FD methods are generally popular in seismic numerical modeling because of their small computational cost and easy implementation (Alford et al. 1974; Dablain 1986; Etgen 2007; Moczo et al. 2007), while they suffer the inherent numerical dispersion because we have to approximate the differential operators with the truncated difference operators. In addition, there will lead to strong dispersion artifacts for modeling high-frequency wave propagations with large spatial spacing (Holberg 1987; Zhang and Yao 2012, 2013). Numerical dispersion is an inevitable problem in FD methods, which directly affects the accuracy of the wavefield simulation. To reduce the numerical dispersion, we can adopt a finer mesh or a lower wavelet frequency, but a thinner grid means high computational cost, reducing computing efficiency and increasing the storage burden on the computer. Optimizing FD coefficients is an effective approach to suppress numerical dispersion without increasing the computational cost and memory storage.
So far, various methods of optimizing FD coefficients have been developed, which can be mainly divided into two categories: Taylor expansion methods (Jastram and Behle 1993; Finkelstein and Kastner 2007; Liu and Sen 2009), optimization-based methods (Chen et al. 2010; Liu and Sen 2011; Wang et al. 2014). The first category consumes a lower computational cost than the other one for solving the dispersion equations, and it usually provides high accuracy on a small frequency zone (Ren and Liu 2015). The second category acquires FD coefficients by minimizing phase velocity errors, which possesses a broad effective frequency band but sacrifices computational efficiency and still has the potential of not convergence (Liu 2013). In addition, FD coefficients can be optimized by truncating window functions. The conventional window functions mainly include Hanning windows (Zhou and Greenhalgh 1992), Gauss windows (Igel et al. 1995) and modified binomial windows (Chu and Stoffa 2012). Recently, several new truncation windows have gradually been developed, such as a Chebyshev’s auto-convolution window (Wang et al. 2015) and a truncation window based on the least-squares algorithm (Ren et al. 2018). These methods based on truncated windows can partially suppress numerical dispersion.
The staggered-grid (SG) scheme introduced by Yee (1966) is an alternative approach to solve the elastic wave equation. Virieux (1986) applies this scheme with second-order accuracy in both time and space to solve the P-SV wave equation in heterogenous media. Levander (1988) develops a fourth-order accuracy in space and second-order accuracy in time FD scheme based on the staggered-grid scheme. Afterward, some optimized FD methods based on the staggered-grid scheme are gradually applied to solve the elastic wave equation (Ma and Zhu 2003; Kosloff et al. 2010; Yang et al. 2014). The SG scheme is often applied to solve first-order velocity–stress equations, which is not conducive to memory storage because of the existence of intermediate variables. Bartolo et al. (2012) develop an equivalent SG scheme (ESG) to solve the second-order system of the acoustic equation, obtaining the same level of accuracy and stability as the conventional SG scheme. Based on previous methods, we construct an optimized equivalent staggered-grid scheme (OESG) to improve the accuracy of elastic wave simulation. Different from the acoustic wave equation, the spatial derivatives are coupled with the velocity terms in the elastic wave equation, which affects the weight distribution of the grid points when the spatial derivatives are approximated with the truncated difference operators. In this paper, we take P-wave, S-wave, and C-wave into account and obtain the optimized FD coefficients of 3D elastic wave modeling.
We start by deriving the plane wave solutions of the 3D elastic wave equation to construct the dispersion relationships. Then we give three sets of FD coefficients to make up the OESG scheme. Moreover, the Newton iteration method is used to solve the new dispersion equations by minimizing the relative phase velocity error in the time–space domain. Finally, we analyze the dispersion characteristics and give several results of numerical modeling, proving the validity and superiority of the presented method.
2 Methodology
2.1 The OESG scheme for the 3D elastic wave equation
The first-order velocity–stress elastic wave equation is popular in seismic forward modeling, but there are nine variables (three particle velocities and six stresses) propagated in 3D cases, increasing the storage demands (Li et al. 2018). Therefore, we will adopt the second-order elastic wave equation to simulate in this study. In the 3D Cartesian coordinate system, the second-order elastic wave equation with constant P- and S-wave speed in the isotropic media can be approximately expressed as
where u, v, w are the particle displacement vectors in x-, y- and z-direction, respectively. t is the travel time. α and β denote P-wave and S-wave speeds, respectively, where we have α2 = (λ +2 μ)/ρ, β2 = μ/ρ. λ and μ are the Lamé parameters, and ρ is the medium density. Note that Eq. 1 is derived from the constant velocity media, where the model parameters λ, μ, ρ are assumed to be constant. To extend the new method from homogeneous model to heterogeneous model, we need to assume the local constant velocity, which is reasonable according to the numerical results of a two-layer model with large velocity variations given by Liu (2014). Hence, Eq. 1 can also handle heterogeneous models with this assumption.
We set three sets of FD coefficients with respect to wave speeds and write out the OESG scheme of Eq. 1 as
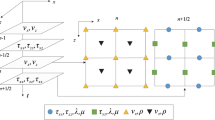
where \( \left( {u,v,w} \right)_{i,j,k}^{n} \) are displacement components at discrete positions (x, y, z) = (ih, jh, kh) in discrete times t = n∆t. h and ∆t denote spatial and temporal sampling intervals, respectively. M represents half of the spatial operator lengths. i, j, k are discrete points on different directions, and a, b, c are the FD coefficients associated with P-wave, S-wave and C-wave terms, respectively. We also display the 3D OESG stencil to help understand, as shown in Fig. 1.
2.2 Plane wave solution of the 3D elastic wave equation
Applying the spatial Fourier transform to Eq. 1, we have
where \( \left( {\hat{u},\hat{v},\hat{w}} \right)\left( {\varvec{k},t} \right) \) denote displacement components in the wavenumber domain, and k = (kx, ky, kz) = (kcosθcosϕ, kcosθsinϕ, ksinθ) denotes the wavenumber vector. θ and ϕ are the dip angle and azimuth angle, respectively. In a matrix form, Eq. 3 can be written in the following form, as
where L is the second-order derivative of displacement components, as
T denotes the transpose symbol. A is the coefficients matrix with
It turns out that the matrix A is a real symmetric matrix, concluding that there exists an orthogonal matrix P that makes A = P\( \varLambda \)P−1. Eigenvalues of the matrix A is λ1 = − α2k2, λ2 = λ3 = − β2k2. According to the theory of linear algebra, we can derive the orthogonal matrix P, as
Therefore, Eq. 4 can be rewritten as
For the above equations, we can easily find the general solution of Eq. 4, as
where \( \left( {\hat{u},\hat{v},\hat{w}} \right)\left( {\varvec{k},0} \right) \) denote the initial values of displacement components. Finally, we can acquire the plane wave solution of the 3D elastic wave by writing Eq. 9 as an expression form of Eq. 10.
2.3 Solving FD coefficients based on the time–space dispersion relations with Newton’s method
With the spatial Fourier transform on both sides of Eqs. 2a–2c, then substituting Eq. 10 and simplifying, we obtain three dispersion relations, as
Detailed derivations can be found in “Appendix 1”. Equations 11a and 11b have the same forms, only with different wave speeds. Therefore, we can compute FD coefficients associated with the P- and S-wave speeds by solving Eq. 11a. Equation 11a cannot be solved directly because of its nonlinearity. Therefore, we need to construct the objective function based on the L2 norm theory, as
where
and ke denotes the effective wavenumber range. r is the CFL (Courant–Friedrichs–Lewy) number, which can be represented as r = α∆t/h. We adopt the iterative format of Newton’s method to solve Eq. 11a, as
where a represents FD coefficients, and k is the number of iterations. We can acquire the Hessian matrix H and gradient vector g of the objective function by taking first-order and second-order derivatives of Eq. 12. Details of the derivations are shown in “Appendix 2”. As a result, we can get the FD coefficients a and b by Eq. 13. To accelerate the convergence, the initial iteration values should be set as the conventional SG FD coefficients, and the error limit is set to 1% as the termination condition (Yong et al. 2017). Due to the fast convergence speed of Newton’s method, it usually takes only a few iterations to get a satisfactory result.
As for solving Eq. 11c, there is a trouble that the denominator could be zero if we just divide it by sin2(0.5αk∆t) − sin2(0.5βk∆t), resulting in non-convergence of the algorithm. Thus, we choose to break this term down into two terms by matching the terms of α and β, as
where
Similarly, the detailed derivations of first-order and second-order derivatives for Eq. 11c are contained in “Appendix 2”. Therefore, we can also get the FD coefficients c by Eq. 13.
2.4 Numerical dispersion analysis
It can be seen from the above analyses that three kinds of FD coefficients are solved separately, indicating that the dispersion analyses for them should also be separate. As a result, using the relation \( f = kv/2\pi \), we construct three dispersion equations taking the frequency as an independent variable, as
where
For Eq. 15, it is worth noting that the new independent variable of the dispersion equations is the frequency f instead of kh. Next, based on Eqs. 15, we give several dispersion curves in the homogeneous media. The first test is a low-speed medium, whose parameters are α = 2000 m/s, β =1154 m/s, h = 15 m, ∆t = 0.5 ms, M = 5, shown in Fig. 2. Note that all simulation parameters should meet the stability condition, whose governing equation will be given below.
Note that the effective frequency range in Fig. 2 is about 0-38 Hz, which can be calculated by the spatial domain sampling theorem f < β/2 h. Figure 2 shows the dispersion curves of three wave terms with the ESG and OESG methods in a constant velocity medium. One can see that all the curves in Fig. 2 almost lie underneath the ideal one for all frequency ranges, indicating that there suffers the spatial dispersion. In addition, the dispersion errors of the three wave terms are different under the same medium parameters, indicating that it is necessary to analyze the three wave terms separately. As can be seen from Fig. 2, the P-wave term suffers the smallest dispersion errors among the three terms, and the S-wave term has the largest errors.
Comparing Fig. 2a with d, we can conclude that the OESG method performs fewer errors of P-wave than the traditional ESG method, which reveals the advantage of the presented method. For the errors of S-wave and C-wave, the OESG method also can reduce dispersion errors compared with the ESG method in the same frequency range, shown in Fig. 2b–c and e–f. Figure 2 also displays the error values of three wave terms when f = 30 Hz, θ = ϕ = 0 (See the black arrows), providing a piece of evidence for the above conclusions. In addition, the dispersion errors vary with different propagation angles. There is a maximal dispersion error on the condition of θ = ϕ = 0 and minimal dispersion error on the condition of θ = ϕ = π/4, indicating that the propagation angles are the factor that affects the numerical dispersion. In general, the OESG method can effectively suppress spatial dispersion and has higher simulation precision than the traditional ESG method.
To test the presented method’s accuracy in a high-velocity medium, we increase the P-wave and S-wave speed to α = 4000 m/s, β =2309 m/s, shown in Fig. 3. Comparing with Fig. 3a–c, d–f shows weaker spatial dispersion of three wave terms in the same frequency values, indicating that the presented can also effectively reduce spatial dispersion compared to the traditional ESG method in high-velocity media. Figure 3 also marks the percentage error values at some points, providing a piece of evidence for verifying the superiority of the OESG method in suppressing spatial dispersion. In addition, temporal dispersion occurs in a high-speed medium even though the time step is small, shown in Fig. 3a (see the red box). To further investigate the ability of our method to suppress temporal dispersion for the elastic wave equation modeling, we move ∆t = 0.5 ms to ∆t = 1 ms, and then introduce an optimal method based on least-squares (LS) algorithm (Yang et al. 2014). As a result, the three wave terms suffer severe temporal dispersion, shown in Fig. 4.
The black arrows in Fig. 4 indicate the temporal dispersion errors of the three methods when f = 60 Hz, θ = ϕ = π/4. By comparison, we know that the OESG method has the minimum temporal dispersion errors among the three methods. Comparing Fig. 4h–i with b–c, it can be seen that the OESG method also effectively suppress spatial dispersion compared to the traditional ESG method. In Fig. 4e–f and h–i, one can see that the LS method based on spatial domain optimization has less spatial dispersive error than the OESG method when frequency is high. Note that the OESG method based on time–space domain optimization can simultaneously suppress spatial and temporal dispersion to attain an optimal result, which leads to an average effect between the spatial dispersion and temporal dispersion. Therefore, the OESG method is slightly weaker than the LS method in suppressing spatial dispersion, while the LS method performs poor in suppressing temporal dispersion.
In addition, the P- to S-wave speed ratio (α/β) is also a factor affecting the numerical dispersion. In some special media such as sedimentary basins, α/β is as large as five and even larger (Moczo et al. 2010). Based on Fig. 2d–f, we move α = 2000 m/s, β = 1143 m/s to α= 2000 m/s, β =400 m/s, and obtain corresponding dispersion error curves, shown in Fig. 5. The maximum frequency f decreases to about 13 Hz according to the spatial domain sampling theorem, which means that the FD method suffers the severe numerical dispersion using a wavelet with high frequency. The numerical dispersion can be reduced effectively by shortening mesh spacing. Therefore, for the high α/β ratio areas, fine space girds are used.
2.5 Stability analysis and boundary conditions
When solving wave equations, it is very important that the solution of the discrete difference equation is stable or not. There are two main reasons for the instability in the process of numerical simulation. On the one hand, FD coefficients are sensitive to the optimized wavenumber range. FD methods will be unstable when the optimized wavenumber range is too small. According to the sampling theorem, we have kmax= π/h, which is maximal wavenumber. We define fmax= 2.5 f0 and take kcon= 2πfmax/vmax (where, kcon< kmax) as the wavenumber range to optimize FD coefficients, while the iterative process will be unstable when k is too small. In this paper, we adopt Yong’s (2017) method to modify the wavenumber range. The new wavenumber ke can be defined as
where vph, vreal denote the phase and real velocities, respectively. τ is the relative phase velocity error, and kopt is the optimized wavenumber. We will choose the optimized wavenumber range strictly according to Eq. 16 in the following numerical examples.
On the other hand, improper calculation parameters will also lead to the instability of algorithms. At present, the Fourier analysis and matrix analysis are mainly used to qualitatively and quantitatively study stability conditions for different elastic wave equations. We derive the stability condition of the presented method by the matrix analysis method, as
The detailed derivation process is included in “Appendix 3”. Subsequent algorithm tests show that the presented method has almost the same stability as the traditional ESG method. Besides, we adopt absorption boundary conditions, whose attenuation function can be written as (Cerjan et al. 1985)
where npd is the thickness of the absorption layer, and i denotes spatial coordinates.
3 Numerical examples
In this section, we test some models, including several homogeneous models, the two-layer model and the salt-dome model in the 3D case. The main objective of these simulations is to prove the validity and superiority of the OESG method compared with the traditional methods. In these examples, we will use a Ricker wavelet source that is simultaneously added to three displacement components. In addition, we consider the previously mentioned absorbing boundary condition and give npd =30 in all the simulations. Finally, for the 3D elastic wave equation, there are three displacement components. Here, we can draw our conclusions by analyzing one of the three components.
3.1 The homogeneous model
The first model is a homogeneous model with lower velocity (α = 2000 m/s, β =1154 m/s), which is modeled using the numerical parameters h = 15 m and ∆t = 0.5 ms in the grid dimensions of 200 × 200 × 200. The source whose peak frequency is 14 Hz is located at the center of the model. Figure 6 displays the snapshots of different sections with the ESG and OESG methods. It exhibits a strong spatial dispersion for the S-wave term with the ESG method in Fig. 6a. We can shrink the sampling intervals or increase the spatial FD order to improve the simulation results, but there are all sorts of problems such as oversize computational cost and the instability of the algorithm. The OESG method based on time–space domain optimization can effectively reduce numerical dispersion, shown in Fig. 6b.
To further investigate the simulation accuracy of the OESG method, we reduce the spatial FD order of the OESG method to M = 3, shown in Fig. 6c. It can be seen that Fig. 6c performs the similar modeling accuracy to Fig. 6a, which suggests that the presented method with the low spatial FD order can achieve the accuracy requirement of the traditional ESG method with the high spatial FD order.
Besides, we extract single vertical slices of snapshots and adopt the reference method (see Fig. 6d) with the minimum possible dispersion errors by reducing the mesh step. As shown in Fig. 7, the reference method matches well with the OESG method with M = 5, but poor with the ESG method with M = 5. Table 1 gives a statistic of relative amplitude errors in Fig. 7. From Table 1, we know that the OESG method with M = 3 has smaller relative amplitude errors than the ESG method with M = 5, which means that forward modeling using the OESG method can save the computational cost of FD operator lengths compared to the traditional ESG method. The relative amplitude errors can be calculated by
Vertical slice of snapshots at x = 1500 m, y = 1500 m, z = 600 m-1035 m in Fig. 6. a The ESG method with M = 5; b The OESG method with M = 3; c The OESG method with M = 5
where Ucal, Uref denote the calculated wavefield values and reference values along the z-direction, respectively. N is the total number of the calculated wavefields.
We continue to test the accuracy of the presented method in a high-speed medium. We give the snapshots of the ESG and OESG methods, where α = 4000 m/s, β =2309 m/s, f = 30 Hz, shown in Fig. 8. Comparing Fig. 8a with b, the traditional ESG method suffers severer numerical dispersion than the OESG method, indicating that the presented method can effectively suppress numerical dispersion in high-speed media. In general, the presented method can suppress the numerical dispersion in the low- and high-speed media, which is also consistent with the above dispersion analyses.
3.2 The two-layer model
It can be known from the above analyses that the FD coefficients of the OESG method are calculated in the time–space domain and correspond to the wave speed values one to one. As a result, the OESG method has higher simulation accuracy in the heterogeneous media than the traditional ESG method. Therefore, we first test a two-layer model, shown in Fig. 9. The gird dimensions are 201 × 201 × 201. The spatial and temporal sampling intervals are h = 15 m, ∆t = 0.5 ms. The P-wave velocities in the first and second layers are 2000 m/s and 2500 m/s, respectively. The S-wave speed is obtained by the ratio α/β = 1.73. The source whose peak frequency is 14 Hz is located at the location (1500 m, 1500 m, 1500 m). For the two-layer model in Fig. 9, we give its FD coefficients according to P-wave speeds, listed in Table 2.
Figure 10 shows the simulation results of different methods. In Fig. 10, we can observe the reflections, transmissions of P-wave, S-wave, and C-wave:
-
A, B, and C denote the direct S-wave, the reflected S-wave, and the transmitted S-wave, respectively;
-
D, E, and F denote the direct P-wave, the reflected P-wave and the transmitted P-wave, respectively;
-
G and H denote the reflection and transmission for the converted SP-wave, respectively;
-
I and J denote the reflection and transmission for the converted PS-wave,
which illustrates that the OESG method is effective for numerical forward modeling of the heterogeneous medium. In addition, comparing Fig. 10b with Fig. 10a, we know that the traditional ESG method suffers the severer spatial dispersion for the S-wave term than the OESG method (see black arrows).
3.3 The 3D salt-dome model
Next, we consider the 3D salt-dome model whose velocity range is 1500 to 4482 m/s, shown in Fig. 11. The model dimensions are 225 × 225 × 201. The spatial and temporal sampling intervals are h = 15 m, ∆t = 0.5 ms. The S-wave speeds are obtained by the ratio α/β = 1.73. The source whose peak frequency is 14 Hz is located at the location (1680 m, 1680 m, 0 m). For the 3D salt-dome model, we need to discretize the velocity model with a sampling interval. Given a sampling interval of 5 m/s, about 600 sets of FD coefficients are required, but we can store them in the computer before starting numerical simulations. Table 3 lists the partial FD coefficients for simulations of the 3D salt-dome model.
Figure 12 shows the snapshots of the 3D salt-dome model at 0.9 s with different methods. On the one hand, the reflections from the salt-dome are distinct and the location of salt-dome anomalies in Fig. 11 can be well matched in Fig. 12, proving the validity of the OESG method in the heterogeneous media. On the other hand, from the black arrows and red boxes in Fig. 12a–c, we can see that the traditional ESG method can lead to severer numerical dispersion than the OESG and LS methods.
To facilitate analysis, we extract some single traces from common-shot gathers with a time record of 1.5 s (common-shot gathers are found in “Appendix 4”) and adopt the reference method (a)
with the lowest possible dispersion errors by increasing the order of the FD scheme, shown in Fig. 13. One can see that the OESG method is very close to the reference method (See red dashed in Fig. 13), while there is always a mismatch between the LS method and the reference method (See green dashed in Fig. 13). The blue dashed represents the traditional method, which has the biggest amplitude errors among the three methods. Table 4 shows the relative amplitude errors of seismograms in Fig. 13. By comparison, the OESG method has lower relative amplitude errors than the other two methods. From the above analyses, it can be concluded that the OESG method is superior to the other two methods for 3D elastic waveform modeling in complex med.
4 Discussions
FD methods have always been used to solve partial differential equations (acoustic wave and elastic wave equations) on seismic exploration (Keiiti and Larner 1970; Kindelan et al. 1990), but it suffers the dispersion errors because of the inherent characteristics of its algorithm. In this paper, we adopt the second-order elastic wave equation in terms of pressure only, avoiding the first-order derivative variables and thus reducing memory requirements. To improve simulation accuracy, we obtain the optimized FD coefficients by minimizing the relative phase velocity error.
There are two different points from other optimized methods. On the one hand, we get new plane wave solutions of the 3D elastic wave equation, as shown in Eq. 10. On the other hand, we consider the coupling between P-wave and S-wave when computing the second-order spatial derivatives, and then adopt three sets of coefficients with respect to the three sets of wave terms shown in Eq. 2. Intending to eliminate the instability caused by too narrow wavenumber range, we modify the optimized wavenumber range, which makes the algorithm more robust. In addition, we also derive the stability condition of the presented method, concluding that the OESG method has almost the same stability as the traditional ESG method.
Naturally, there are some drawbacks to the new method, such as the complexity of formula derivations. In this aspect, subsequent researchers can choose other iterative methods or objective functions to simplify the formula according to the requirements. Besides, the computational efficiency of the algorithm has not been improved, which limits its promotion and application in seismic imaging and inversion. For this problem, we plan to take the work of imaging and inversion to further work by GPU’s method.
5 Conclusions
The OESG method for the 3D elastic wave equation is developed to simultaneously suppress temporal and spatial dispersion. Different from the traditional FD methods, the OESG method possesses the new plane wave solution that is more appropriate to construct the time–space dispersion relationships. As a result, we obtain FD coefficients using the Newton iteration method based on new time–space dispersion equations. In addition, we also modify the wavenumber range and objective function, obtaining more satisfactory results. With a local constant velocity assumption, we simulate the propagation of elastic waves in the 3D homogeneous and heterogeneous media using the OESG method.
The presented method’s advantages mainly include three aspects. Firstly, the presented method has a lower spatial dispersion error than the traditional ESG method. Numerical examples show that the OESG method with M = 3 can achieve the simulation accuracy of the traditional ESG method with M = 5, which is conducive to save the amount of computation. Secondly, compared with the LS method, the presented method performs well in suppressing temporal dispersion, while it is slightly weaker than the LS method in suppressing spatial dispersion. However, the presented method has smaller relative amplitude errors than the LS method in 3D salt-dome model, shown in Table 4, indicating that the OESG method is superior to the LS method in complex media. Thirdly, FD coefficients of the presented method are calculated from medium velocities, meaning that it is more accurate to heterogeneous media than the LS and traditional ESG methods whose FD coefficients are the constant. Numerical examples prove that the presented method is superior to the LS and traditional ESG methods.
References
Alford RM, Kelly KR, Boore DM. Accuracy of finite-difference modeling of the acoustic wave equation. Geophysics. 1974;39(6):834–42. https://doi.org/10.1190/1.1440470.
Bartolo LD, Dors C, Mansur WJ. A new family of finite-difference schemes to solve the heterogeneous acoustic wave equation. Geophysics. 2012;77(5):T187–99. https://doi.org/10.1190/geo2011-0345.1.
Cerjan C, Kosloff D, Kosloff R, et al. A nonreflecting boundary condition for discrete acoustic and elastic wave equations. Geophysics. 1985;50(4):705–8. https://doi.org/10.1190/1.1441945.
Chen S, Yang DH, Deng XY. A weighted Runge–Kutta method with weak numerical dispersion for solving wave equations. Commun Comput Phys. 2010;7(5):1027–48. https://doi.org/10.4208/cicp.2009.09.088.
Chu C, Stoffa PL. Determination of finite-difference weights using scaled binomial windows. Geophysics. 2012;77(3):W17–26. https://doi.org/10.4208/cicp.2009.09.088.
Dablain MA. The application of high-order differencing to the scalar wave equation. Geophysics. 1986;51(1):54–66. https://doi.org/10.1190/1.1442040.
Duan YT, Hu TY, Yao FC, et al. 3D elastic wave equation forward modeling based on the precise integration method. Appl Geophys. 2013;10(1):71–8. https://doi.org/10.1007/s11770-013-0370-8.
Etgen JT. A tutorial on optimizing time domain finite-difference schemes: “Beyond Holberg”. Stanf Expl Proj Rep. 2007;129:33–43.
Finkelstein B, Kastner R. Finite difference time domain dispersion reduction schemes. J Comput Phys. 2007;221(1):422–38. https://doi.org/10.1016/j.jcp.2006.06.016.
Holberg O. Computational aspects of the choice of operator and sampling interval for numerical differentiation in large-scale simulation of wave phenomena. Geophys Prospect. 1987;35(6):629–55. https://doi.org/10.1111/j.1365-2478.1987.tb00841.x.
Igel H, Mora P, Riollet B. Anisotropic wave propagation through finite-difference grids. Geophysics. 1995;60(4):1203–16. https://doi.org/10.1190/1.1443849.
Jastram C, Behle A. Accurate finite-difference operators for modelling the elastic wave equation. Geophys Prospect. 1993;41(4):453–8. https://doi.org/10.1111/j.1365-2478.1993.tb00579.x.
Keiiti A, Larner KL. Surface motion of a layered medium having an irregular interface due to incident plane SH waves. J Geophys Res. 1970;75(5):933–54. https://doi.org/10.1029/jb075i005p00933.
Kindelan M, Kamel A, Sguazzero P. On the construction and efficiency of staggered numerical differentiators for the wave equation. Geophysics. 1990;55(1):107–10. https://doi.org/10.1190/1.1442763.
Kosloff D, Pestana RC, Tal-Ezer H. Acoustic and elastic numerical wave simulations by recursive spatial derivative operators. Geophysics. 2010;75(6):T167–74. https://doi.org/10.1190/1.3485217.
Levander AR. Fourth-order finite-difference P-SV seismograms. Geophysics. 1988;53(11):1425–36. https://doi.org/10.1190/1.1442422.
Liu Y, Sen MK. A new time-space domain high-order finite-difference method for the acoustic wave equation. J Comput Phys. 2009;228(23):8779–806. https://doi.org/10.1016/j.jcp.2009.08.027.
Liu Y, Sen MK. Scalar wave equation modeling with time-space domain dispersion-relation-based staggered-grid finite-difference schemes. Bull Seismol Soc Am. 2011;101(1):141–59. https://doi.org/10.1785/0120100041.
Liu Y. Globally optimal finite-difference schemes based on least squares. Geophysics. 2013;78(4):T113–32. https://doi.org/10.1190/geo2012-0480.1.
Liu Y. Optimal staggered-grid finite-difference schemes based on least-squares for wave equation modelling. Geophys J Int. 2014;197(2):1033–47. https://doi.org/10.1093/gji/ggu032.
Li YY, Du Y, Yang JD, et al. Elastic reverse time migration using acoustic propagators. Geophysics. 2018;83(5):S399–408. https://doi.org/10.1190/geo2017-0687.1.
Marfurt K. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations. Geophysics. 1984;49(4):533–49. https://doi.org/10.1190/1.1441689.
Ma DT, Zhu GM. Numerical modeling of P-wave and S-wave separation in elastic wavefield. Oil Geophys Prospect. 2003;38(5):482–6. https://doi.org/10.3321/j.issn:1000-7210.2003.05.005(in Chinese).
Moczo P, Robertsson JOA, Eisner L. The finite-difference time-domain method for modeling of seismic wave propagation. Adv Geophys. 2007;48:421–516. https://doi.org/10.1016/s0065-2687(06)48008-0.
Moczo P, Kristek J, Galis M, Pazak P. On accuracy of the finite-difference and finite-element schemes with respect to P-wave to S-wave speed ratio. Geophys. J. Int. 2010. https://doi.org/10.1111/j.1365-246X.2010.04639.x.
Reshef M, Kosloff D, Edwards M, et al. Three-dimension acoustic modeling by the Fourier method. Geophysics. 1988;53(9):1175–83. https://doi.org/10.1190/1.1442557.
Ren ZM, Liu Y. Acoustic and elastic modeling by optimal time-space-domain staggered-grid finite-difference schemes. Geophysics. 2015;80(1):T17–40. https://doi.org/10.1190/geo2014-0269.1.
Ren YJ, Huang JP, Liu M, et al. Window functions and optimized staggered-grid finite-difference operators. Appl Geophys. 2018;15(2):253–60. https://doi.org/10.1007/s11770-018-0668-7.
Virieux J. P-SV wave propagation in heterogeneous media: velocity-stress finite-difference method. Geophysics. 1986;51(4):889–901. https://doi.org/10.1016/0148-9062(86)92435-6.
Wang YF, Liang WQ, Nashed Z, et al. Seismic modeling by optimizing regularized staggered-grid finite-difference operators using a time-space-domain dispersion-relationship-preserving method. Geophysics. 2014;79(5):T277–85. https://doi.org/10.1190/geo2014-0078.1.
Wang ZH, Liu H, Tang XD, et al. Optimized finite-difference operators based on Chebyshev auto-convolution combined window function. Chin J Geophys. 2015;58(2):628–42. https://doi.org/10.1002/cjg2.20166(in Chinese).
Xia F, Dong LG, Ma ZT. The numerical modeling of 3-D elastic wave equation using a high-order, staggered-grid, finite difference scheme. Appl Geophys. 2004;1(1):38–41. https://doi.org/10.1007/s11770-004-0028-7.
Yee K. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. IEEE Trans Antennas Propag. 1966;14:302–7. https://doi.org/10.1109/tap.1966.1138693.
Yang L, Yan HY, Liu H. Least squares staggered-grid finite-difference for elastic wave modelling. Explor Geophys. 2014;45(4):255–60. https://doi.org/10.1071/eg13087.
Yang JD, Huang JP, Wang X, et al. An amplitude-preserved adaptive focused beam seismic migration method. Pet Sci. 2015;12(3):417–27. https://doi.org/10.1007/s12182-015-0044-7.
Yong P, Huang JP, Li ZC, et al. Elastic-wave reverse-time migration based on decoupled elastic-wave equations and inner-product imaging condition. J Geophys Eng. 2016;13(6):953–63. https://doi.org/10.1088/1742-2132/13/6/953.
Yong P, Huang JP, Li ZC, et al. Forward modeling by optimized equivalent staggered-grid finite-difference method. J Chin Univ Pet. 2017;41(6):71–8. https://doi.org/10.3969/j.issn.1673-5005.2017.06.008(in Chinese).
Yang JD, Zhu HJ, Huang JP, et al. 2D isotropic elastic Gaussian beam migration for common-shot multicomponent records. Geophysics. 2018;83(2):S127–40. https://doi.org/10.1190/geo2017-0078.1.
Zhou B, Greenhalgh SA. Seismic scalar wave equation modeling by a convolutional differentiator. Bull Seismol Soc Am. 1992;82(1):289–303.
Zhu CY, Qin GL, Zhang JZ. Implicit Chebyshev spectral element method for acoustics wave equations. Finite Elem Anal Des. 2011;47(2):184–94. https://doi.org/10.1016/j.finel.2010.09.004.
Zhang JH, Yao ZX. Optimized finite-difference operator for broadband seismic wave modeling. Geophysics. 2012;78(1):A13–8. https://doi.org/10.1190/geo2012-0277.1.
Zhang JH, Yao ZX. Optimized explicit finite-difference schemes for spatial derivatives using maximum norm. J Comput Phys. 2013;250:511–26. https://doi.org/10.1016/j.jcp.2013.04.029.
Author information
Authors and Affiliations
Corresponding author
Additional information
Edited by Jie Hao
Appendices
Appendix 1: The derivation of dispersion relations
With the temporal Fourier transform of the left-hand side for Eqs. 2a–2c, then substituting Eq. 10 and simplifying, we have
Similarly, taking spatial Fourier transform of the right-hand side of Eqs. 2a–2c, we have
Note that the item of 1/2 is eliminated when constructing the dispersion relations. That is to say, we do not need to consider this item in the above calculations. Combining with Eqs.~20 and 21, we can get the dispersion relations as Eqs. 11a–11c.
Appendix 2: The calculation steps of Newton’s method
Taking the first-order and second-order derivatives of Eq. 12, we have
Similarly, taking the first-order and second-order derivatives of Eq. 14, we have
Appendix 3: The derivation of stability conditions
For Eq. 5, we have
Combining Eq. 20, we have
where
we define \( \vartheta \) = sin(0.5αk∆t), γ = sin(0.5βk∆t). Obviously, the matrix B can be written as \( B = P\varLambda^{{\prime }} P^{ - 1} \). The eigenvalues of the matrix B are \( \lambda_{1}^{{\prime }} = - \vartheta^{2} k^{2} ,\lambda_{2}^{{\prime }} = \lambda_{3}^{{\prime }} = - \gamma^{2} k^{2} . \) So Eq. 25 can be transformed into
which means
So we can get two equations, as
Using the relation \( - 1 \le \sin^{2} \left( {0.5\alpha k\Delta t} \right) \le 1,\alpha > \beta , \) we have
According to Eq. 21, we can easily derive the maximum value of k. Finally, we can get stability condition using the inequality in Eq. 30, shown in Eq. 31.
Appendix 4: The other results for elastic wave numerical modeling
See Fig. 14.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zou, Q., Huang, JP., Yong, P. et al. 3D elastic waveform modeling with an optimized equivalent staggered-grid finite-difference method. Pet. Sci. 17, 967–989 (2020). https://doi.org/10.1007/s12182-020-00477-3
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12182-020-00477-3