1 Introduction

The risk of pre-existing faults and fractures reactivating in current stress fields is of great importance in gas production/injection activities. The possible consequences of such reactivation have been investigated by many researchers in the past decade (e.g., Rutqvist et al. 2007; Kulikowski et al. 2016; Vilarrasa et al. 2016; Rutqvist et al. 2017). Breaching the hydraulic integrity of the caprock by creating or enhancing leakage conduits (Wiprut and Zoback 2002; Hawkes et al. 2005; Langhi et al. 2010) and induced seismicity in the area (Hsieh and Bredehoft 1981; Zoback and Gorelick 2012; Rutqvist et al. 2013, 2017) are two examples of such consequences. On the other hand, the economic benefits of gas injection for enhanced oil recovery (EOR) and profitable results derived from greenhouse gases mitigation through CO2 sequestration cannot be neglected (Shukla et al. 2010). The evaluation of the stability of pre-existing faults and estimating the maximum safe pore pressure are conducted through geomechanical studies of reservoir and caprock in sedimentary basins. These data are crucial for reservoir stimulation procedures in EOR activities (Konstantinovskaya et al. 2012). Therefore, in order to carry out safe gas injection and storage, critically stressed fractures in the current stress field should be identified, and the maximum sustainable pore pressure created by this injection should be calculated using analytical or numerical methods (Morris et al. 1996; Reynolds et al. 2003; Streit and Hillis 2004; Hawkes et al. 2005; Mildren et al. 2005; Rutqvist et al. 2007; Teatini et al. 2014). Slip tendency analysis introduced by Morris et al. (1996) considers that the propensity of a fault surface to slip in a given stress field depends on the surface frictional characteristics, and was defined as the ratio of shear to normal stress acting on the surface. Rutqvist et al. (2007) showed that the maximum sustainable injection pressure or critical pore pressure (PC) required to induce slip, can be estimated from slip tendency parameters. The intent of this study is to estimate the present-day stress magnitudes and orientations in Gachsaran oilfield and investigating the fault stability in both current and after-injection stress fields needed for oil recovery in the Asmari reservoir. These goals were achieved by plotting 3D Mohr diagrams and calculating the slip tendency factors introduced by Morris et al. (1996) and Hawkes et al. (2005). The maximum sustainable pore pressure was also estimated by these methods. Finally, the effect of pore pressure increase on stress magnitude is shown by stress polygons.

2 Geological setting

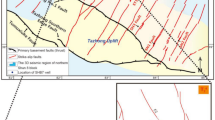
Gachsaran oilfield is situated in the Iranian section of the Zagros fold-thrust belt, a belt which stretches from the Anatolian fault in eastern Turkey to the Minab fault near the Makran region in the southeast of Iran. This fold-thrust belt is a part of an active foreland basin complex, which was initiated in the late Tertiary time by the collision between the Iranian and Arabian Plates (Stocklin 1974; Berberian and King 1981). This field is an elongated doubly plunging anticlinal structure with dimensions of 65 km in length and 4–8 km in width and is considered one of the most important productive oilfields in the Oligocene–Lower Miocene carbonate horizons (Asmari formation) and the Middle Cretaceous carbonate horizons (Sarvak formation) (Shaban et al. 2011). The Asmari reservoir, which is characterized by its 30° API and low sulfur content oil, produces almost 85 percent of total Iranian crude oil and is one of the most known reservoirs in the world (Rezaie and Nogole-Sadat 2004). This reservoir first was discovered by Anglo-Persian Oil Company in 1931 and had a peak production of 180 thousand barrels per day in 1976. The Asmari formation consists of cream to gray limestone, dolomitic limestone, and dolomite and its thickness in the type section is 314 m (Darvishzadeh 2009). The caprock of this oilfield is a Miocene aged formation called the Gachsaran formation, which consists of seven members. This formation is composed of anhydrite, limestone, and bituminous shale, and its oldest and the lowermost member, which is the caprock of the Asmari reservoir, is called member 1 (James and Wynd 1965). The average thickness of member 1 in this field is about 40 m (Darvishzadeh 2009). The lower contact of the Asmari formation is the Pabdeh formation, which is the source rock with the age of Paleocene to Eocene. The location of Gachsaran oilfield and the Cenozoic era of stratigraphic column in Zagros fold-thrust belt are shown in Fig. 1.

Fig. 1
figure 1

a The location of the Gachsaran oilfield in the Zagros fold-thrust belt (Shaban et al. 2011), b the stratigraphic column of the field (Geological Society of Iran, GSI)

Full size image

The four faults F1, F2, F3, and F4 have been analyzed in this study (Fig. 2). All of them are normal faults, and there is no information about their cohesion strength (C) and the coefficient of static friction (μ). Since the cohesion of the weakness (pre-existing fault) can be neglected, they were considered cohesionless (i.e., C = 0). Byerlee (1978) demonstrated that the coefficient of static friction is between 0.85 when confining pressure is less than 200 MPa and 0.6 for more than 200 MPa. It is recommended that in the absence of such data, the coefficient of static friction can be set to 0.6 (Rutqvist et al. 2007; Zoback 2007). The structural and mechanical characteristics of the faults are summarized in Table 1.

Fig. 2
figure 2

UGC map of the Asmari reservoir showing the location of the faults. (C.R. is Caprock and As. is Asmari Formation)

Full size image
Table 1 Structural and mechanical properties of faults
Full size table

3 Methodology

In order to investigate the reactivation tendency of these faults, some of the geomechanical parameters and the current stress field were calculated using well logs. For this goal, P- and S-wave velocities were used to estimate the dynamic elastic properties of rocks such as Young’s modulus and Poisson’s ratio. Then the static elastic properties were calculated using relationships derived in the National Iranian South Oil Company (NISOC) laboratory. Since these relationships were not published before, their accuracy was tested by an equation derived in another oilfield from the same reservoir in the area. In the next step, the vertical stress magnitude was calculated by using the density log (RHOB) at the desired depth. The orientations of the minimum and the maximum horizontal stresses were identified by interpreting image logs, and their magnitudes were estimated using poroelastic equations. Pore pressure estimations were made based on Eaton’s (1975) empirical relationship modified for an Iranian field, and its accuracy was controlled by in situ pore pressure measurements carried out in a well. In order to investigate the possibility of fault slippage, 3D Mohr diagrams were applied to determine the present state of each fault in the stress field. Using Morris et al. (1996) and Hawkes et al. (2005) equations, the slip tendency and modified slip tendency for the current stress state and pore pressure, for each of the faults, were calculated, and the maximum sustainable pore pressure increase caused by injection was also computed. Finally, by plotting stress polygons, the effect of pore pressure increase on the stress field is shown in an illustrative manner.

4 Theory and background

4.1 Elastic properties

The speed of elastic waves in solids is linked to the elastic moduli and bulk density \(\rho\) by the wave equation (Mavko et al. 2009). In order to estimate the magnitude of elastic moduli in rocks, knowing the magnitude of seismic velocities (VP and VS) is essential. Since the dipole shear sonic imager (DSI) was not available in the field, VS magnitude was estimated using the rock physical model introduced by Xu and Payne (2009). In this method, for predicting the S-wave log, both matrix and porosity of rock will be modeled. At the beginning, the VP log was modeled, and then the best match between the modeled VP and the directly measured VP from the dt log was used to estimate VS. After that, the dynamic Poisson’s ratio and Young’s modulus were calculated as follows:

$$\upsilon_{\text{d}} = \frac{1}{2}\frac{{(V_{\text{P}} /V_{\text{S}} )^{2} - 2}}{{\left( {V_{\text{P}} /V_{\text{S}} } \right)^{2} - 1}}$$
(1)
$$E_{\text{d}} = 2\rho V_{\text{S}}^{2} \left( {1 + \upsilon } \right)$$
(2)

where VP and VS are the P-wave and S-wave velocities, \(\nu_{\text{d}}\) is the dynamic Poisson’s ratio, and Ed is the dynamic Young’s modulus.

In most cases, the static moduli are different from the dynamic ones. One reason is that stress–strain relations for rocks are often nonlinear. Another reason is that rocks are often inelastic. Also, there are no universal relationships between static and dynamic moduli, since the conditions of measurements (e.g., effective pressure and pore fluid) affect the elastic wave velocity and the derived elastic moduli in a sample (Mavko et al. 2009). In this article, an equation derived by NISOC laboratory (Eq. 3) was used to convert a dynamic Young’s modulus to a static one. In order to evaluate the validity of this relationship, the Seyed Sajadi and Aghighi (2015) equation (Eq. 5) was used to calculate the static Young’s modulus.

$$E_{\text{s}} = 0.7 \times E_{\text{d}} \quad {\text{NISOC}}\;{\text{laboratory}}\;\left( {\text{unpublished}} \right)$$
(3)
$$\nu_{\text{s}} = \nu_{\text{d}}$$
(4)
$$E_{\text{s}} = \left( {0.731 \times E_{\text{d}} } \right) - 2.337\quad {\text{Seyed}}\,{\text{Sajadi}}\,{\text{and}}\,{\text{Aghighi}}\,\left( {2015} \right)$$
(5)

In these equations, ES is the static Young’s modulus, and νS is the static Poisson’s ratio. Figure 3 shows the elastic moduli calculated by Eqs. 3–5. As it can be seen, the static Young’s moduli estimated by Eqs. 3 and 5 (ES1 and ES2) show a good overlap.

Fig. 3
figure 3

Logs of density (RHOB), velocity (real VP and modeled VS), static Young’s modulus (Es), and Poisson’s ratio (ν) for the Asmari reservoir in a well. ES1 and ES2 are calculated by the NISOC and Seyed Sajadi and Aghighi equations, respectively

Full size image

4.2 In situ stresses magnitudes and orientations

Determining the magnitudes and orientations of the principal stresses is imperative in any fault reactivation analysis. The regional stress field at any given depth consists of three principal stress magnitudes: the vertical stress (σV) usually considered to be solely due to the weight of the overburden, the minimum horizontal stress (σhmin), and the maximum horizontal stress (σHmax) (Kidambi and Kumar 2016). Mathematically, the magnitude of vertical stress σV can be calculated by integration of rock densities from the surface to the depth of interest, z (Zoback et al. 2003):

$$\sigma_{\text{V}} = \mathop \int \limits_{0}^{z} \rho \left( z \right)g {\text{d}}z \approx \bar{\rho }gz$$
(6)

where \(\rho \left( z \right)\) is the density as a function of depth, \(g\) is the gravitational acceleration constant, and \(\bar{\rho }\) is the mean overburden density. As the available density logs were collected from a certain depth in the reservoir, an average density of about 2.3 g/cm3 was considered for calculating σV to the ground surface.

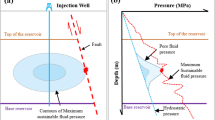
A typical approach to estimate the least principal stress is called the leak-off test (LOT). LOTs are conducted after the casing has been cemented in place and the casing shoe is drilled out a short distance (~ 5 m) (Zoback et al. 2003). By pumping at a constant rate into a well, the pressure will increase linearly with time, as the volume of the system is fixed. The point at which a distinct deviation occurs from the linear increase of wellbore pressure with time is called the leak-off point (LOP). At LOP, a hydraulic fracture must exist. If the LOP is not reached, a limited test, which is called formation integrity test (LT or FIT) is conducted. Such tests simply indicate that at the maximum pressure achieved, the fluid did not propagate away from the wellbore wall, and this pressure was not enough to create a fracture or did not exceed the least principal stress if a fracture was initiated (Zoback et al. 2003). The FIT does not provide any information about the magnitude of the least principal stress (Konstantinovskaya et al. 2012); however, it can be used as an indicator of the lower bound of σhmin, because the pressure at FIT will always be less than the least principal stress (Fig. 4). Since the FIT was carried out in the field, the magnitudes of the minimum and maximum horizontal stresses were also calculated by the poroelastic horizontal strain model Fjaer et al. (2008), as follows:

$$\sigma_{\text{hmin}} = \frac{\nu }{1 - \nu }\sigma_{\text{V}} + \frac{1 - 2\nu }{1 - \nu }P_{\text{P}} \left( \alpha \right) + \frac{E}{{1 - \nu^{2} }}\varepsilon_{x} + \frac{\nu E}{{1 - \nu^{2} }}\varepsilon_{y}$$
(7)
$$\sigma_{\text{Hmax}} = \frac{\nu }{1 - \nu }\sigma_{\text{V}} + \frac{1 - 2\nu }{1 - \nu }P_{\text{P}} \left( \alpha \right) + \frac{E}{{1 - \nu^{2} }}\varepsilon_{y} + \frac{\nu E}{{1 - \nu^{2} }}\varepsilon_{x}$$
(8)

In these equations, σV is the vertical stress, PP is pore pressure (in MPa), α is the Biot’s coefficient (which was considered 1 to account for the brittle failure of rocks), E is the static Young’s modulus (in GPa), and ν is Poisson’s ratio. εx and εy are the magnitudes of the rock deformation in the x and y planes, which can be calculated as a function of the overburden stress as Eqs. 9 and 10:

$$\varepsilon_{x} = \frac{{\sigma_{\text{V}} \times \nu }}{E} \times \left( {\frac{1}{1 - \nu } - 1} \right)$$
(9)
$$\varepsilon_{y} = \frac{{\sigma_{\text{V}} \times \nu }}{E} \times \left( {1 - \frac{{\nu^{2} }}{1 - \nu }} \right)$$
(10)

Observations of stress-induced breakouts are a very effective technique for determining stress orientation in wells and boreholes. The most reliable way to observe these features in a well is through the use of ultrasonic image logs. The borehole breakouts and the drilling-induced tensile fractures are caused by hoop stress and radial stress, respectively (Zoback 2007). In vertical wells, the breakouts form at the azimuth of the minimum horizontal compressive stress, and drilling-induced tensile fractures form in the wall of the borehole at the azimuth of the maximum horizontal compressive stress when the circumferential stress acting around the well locally goes into tension. According to Wiprut et al. (2000), drilling-induced tensile fractures can define stress orientations with great detail and precision. In this research, an image log was interpreted to find the stress orientations in the field. Based on the drilling-induced fractures observed in the image log, the azimuth of σHmax was determined. A total number of 32 fractures were observed in the studied well, with a prevailing azimuth of 52° (the existence of drilling-induced tensile fractures is 90° from the breakouts). The interpreted image log showing the drilling-induced tensile fractures and the rose diagram of identified fractures in the studied well are illustrated in Figs. 5 and 6, respectively. Figure 7 shows the fault planes and in situ stresses orientations in the lower hemisphere stereographic projection.

Fig. 4
figure 4

An extended LOT schematic illustration (adapted from Konstantinovskaya et al. 2012). The magnitude of the least principal stress is nearly equal to leak-off test (LOP) or instantaneous shut-in pressure (ISIP) (LOP ≈ ISIP ≈ σhmin). The formation integrity test (FIT) does not yield any specific information about the σhmin, but it is always lower than σhmin

Full size image
Fig. 5
figure 5

Image log of a well with drilling-induced tensile fractures (pink lines), the prevailed azimuth of σHmax is nearly 52°

Full size image
Fig. 6
figure 6

Rose diagram showing the orientation of drilling-induced tensile fractures observed in the studied well

Full size image
Fig. 7
figure 7

Stereographic projection of fault planes and in situ stresses orientations

Full size image

4.3 Pore pressure

A good estimation of pore pressure by using cost-effective predicting methods is essential for reservoir simulation studies. The Terzaghi hypothesis, which describes the compaction of soil due to overburden stress, is the basis of formation pore pressure prediction (Azadpour et al. 2015). In this study, the pore pressure was estimated by the modified Eaton (1975) method, delivered by Azadpour et al. (2015). The modified Eaton’s equation is as follows:

$$P_{\text{pg}} = S_{\text{g}} - \left( {S_{\text{g}} - P_{\text{ng}} } \right)\left( {\frac{{50 + \left( {185 - 50} \right)e^{ - 0.00137z} }}{{\Delta t}}} \right)^{x}$$
(11)

where Ppg is the formation pressure gradient, Png is the hydrostatic pore pressure gradient which is suggested 1.049 × 10−2 MPa/m (0.464 psi/ft) for Iran, Δt is the measured sonic transit time by well logging, z is depth, and x is the exponent constant, which was determined as 0.5 by Azadpour et al. (2015) for a field in Iran. The overburden pressure gradient Sg can be calculated by the following equation:

$$S_{\text{g}} = 0.433 \times \rho_{\text{b}}$$
(12)

where the ρb is the bulk density.

After calculating the pore pressure using Eqs. 11 and 12, the accuracy of this method was investigated by the direct measurements of formation fluid pressure obtained by a Repeat Formation Tester (RFT) in a limited number of wells in the field. Figure 8 is the stress-depth plot showing the general stress state of the field (left) and a well faulted by F2.

Fig. 8
figure 8

Stress-depth plots showing the stress state in the Gachsaran oilfield (with the line of best fit) (left), and a well faulted by F2 (right). The gray points represent the formation fluid pressures (RFT), and triangles indicate FIT pressure (the stresses are calculated using the elastic moduli estimated by the NISOC equation)

Full size image

As it can be seen in Fig. 8, in this field the maximum principal stress (σ1) is σV, and the intermediate and minimum principal stresses (σ2 and σ3) are σHmax and σhmin, respectively. So, according to Anderson’s faulting theory (Anderson 1951), this field is in a normal faulting regime (i.e., σ1 > σ2 > σ3). The estimated (red line) and directly measured Pp (gray points in Fig. 8) shows a maximum difference of 2 MPa, which confirms an acceptable range for the accuracy of the Azadpour et al. (2015) method. The results of the measured geomechanical parameters for this well are also summarized in Table 2. As it can be seen in both Fig. 8 and Table 2, the horizontal stresses in some depth are higher than the vertical stress, which is caused by stress perturbation resulted from faulting.

Table 2 Minimum, maximum, and average magnitudes of the geomechanical parameters for a well
Full size table

5 Three-dimensional Mohr diagrams

One of the best ways to show the shear and normal stresses acting on arbitrarily oriented faults in three dimensions is Mohr diagrams (Zoback 2007). These diagrams are also used to explain the mechanism of faulting and reactivation of pre-existing faults (Yin and Ranalli 1992; Jolly and Sanderson 1997; McKeagney et al. 2004; Streit and Hillis 2004; Xu et al. 2010). In 3D Mohr diagrams, the values of three principal stress σ1, σ2, and σ3 are used to define three Mohr circles. Faults can be shown by a point, located in the space between the two small Mohr circles (defined by the differences between σ1 and σ2, and σ2 and σ3, respectively), and the big Mohr circle (defined by the difference between σ1 and σ3) (Zoback 2007). The position of this point defines the shear and normal stresses on the fault plane. These stresses can be readily calculated using the following equations:

$$\sigma_{\text{n}} = \sigma_{\text{V}} \left( {\cos \beta_{1} } \right)^{2} + \sigma_{\text{H}} \left( {\cos \beta_{2} } \right)^{2} + \sigma_{\text{h}} \left( {\cos \beta_{3} } \right)^{2}$$
(13)
$$\tau = \sqrt {\sigma_{\text{V}}^{2} \left( {\cos \beta_{1} } \right)^{2} + \sigma_{\text{H}}^{2} \left( {\cos \beta_{2} } \right)^{2} + \sigma_{\text{h}}^{2} \left( {\cos \beta_{3} } \right)^{2} - \sigma_{\text{n}}^{2} }$$
(14)

where σn is the normal stress and τ is the shear stress. β1, β2, and β3 are the angles between the surface normal (n) and the axes of the greatest, the intermediate, and the least principal stresses, respectively. Figure 9 shows the normal and shear stresses acting on a plane, and the orientation of this plane in the stress field defined by three angles of β1, β2, and β3. In this study, we used the open source MohrPlotter software to calculate these angles and the stresses on the fault planes.

Fig. 9
figure 9

Adopted from Schmitt (2014)

a Resolved normal (σ) and shear (τ) stress on plane A. b Orientation of the potential slip plane A in terms of three angles β1, β2, and β3 from the coordinate axes of the principal stresses.

Full size image

Estimating the maximum sustainable pore pressure can be achieved by calculating the fluid pressure increase required to induce failure on faults. In a Mohr diagram, this pore pressure increase is the difference between the effective normal stress acting on a fault segment and the effective normal stress required to cause failure on this segment (Streit and Hillis 2004). In this research, the 3D Mohr diagrams were plotted for the faults (Fig. 10), and the effective normal and shear stresses on their planes were calculated \(\left( {\sigma_{\text{ni}}^{{\prime }} , \, \tau } \right)\). In the next step, the maximum sustainable pore pressure (Ppmax) due to gas injection and the corresponding effective normal stress at the failure point \(\left( {\sigma_{\text{nf}}^{{\prime }} } \right)\) for each fault were obtained by moving the Mohr circle to the left as much as possible until it touched the failure envelope (Fig. 11). The results are summarized in Table 3.

Fig. 10
figure 10

3D Mohr diagrams of four faults F1, F2, F3, and F4 (using the NISOC equation). As can be seen, none of the faults is critically stressed, and all of them are stable in the current stress field and pore pressure

Full size image
Fig. 11
figure 11

Mohr diagram plotted for F1 for estimating critically stressed pore pressure. The pore pressure increase to cause failure (ΔPp) for this fault is about 24.9 MPa

Full size image
Table 3 Effective normal and shear stress, initial pore pressure (Ppi), the maximum sustainable pore pressure (Ppmax), pore pressure increase (ΔPp), and normal stress at failure point \(\left( {\sigma_{\text{nf}}^{{\prime }} } \right)\) for the faults
Full size table

As Fig. 10 shows, none of the faults is critically stressed in the current stress field. According to these diagrams, F1, F3, and F4 are on the large Mohr circle (σ1–σ3) and are parallel to σ2, which in this case is σHmax. F2 is on the small circle (σ2–σ3) and is nearly parallel to σ1, which is σV in this field. According to the results presented in Table 3, the highest pore pressure increase required for reactivation is for F2 (ΔPp = 35.4 MPa).

6 Slip tendency parameter

Reactivation of pre-existing faults may create leakage conduits that will risk the seal capacity in an injection project. The slip will occur on a fault when the maximum shear stress acting on the fault plane exceeds the shear strength of the fault. Slip tendency is a method that allows quick assessment of stress states and related potential fault activity (Morris et al. 1996). Using two-dimensional stress equations given by Jaeger and Cook (1969), the values of shear and normal stresses on the fault plane can be calculated as follows:

$$\sigma_{\text{n}} = \frac{{\left( {\sigma_{1} + \sigma_{3} } \right)}}{2} - \frac{{\left( {\sigma_{1} - \sigma_{3} } \right)}}{2}\cos 2\theta$$
(15)
$$\tau = \frac{{\left( {\sigma_{1} - \sigma_{3} } \right)}}{2}\sin 2\theta$$
(16)

Slip tendency is defined as the ratio of shear to normal stress acting on the surface as follows:

$$T_{\text{s}} = {\raise0.7ex\hbox{$\tau $} \!\mathord{\left/ {\vphantom {\tau {\sigma_{\text{n}}^{{\prime }} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sigma_{\text{n}}^{{\prime }} }$}}$$
(17)

where τ is the shear stress, \(\sigma_{\text{n}}^{{\prime }}\) is the effective normal stress (σn − PP), and Ts is the slip tendency. For a cohesionless fault (C = 0), slip will be induced when \(\tau /\sigma_{\text{n}}^{{\prime }} \ge \mu\) (Rutqvist et al. 2007). Although using a frictional coefficient of 0.6 gives a conservative estimate of the maximum sustainable pore pressure during injection, it is a common assumption used in many similar studies (e.g., Rutqvist et al. 2007; Zoback 2007; Hung and Wu 2012; Konstantinovskaya et al. 2012; Figueiredo et al. 2015).

Hawkes et al. (2005) introduced the modified slip tendency (Tsm) (Eq. 18) and demonstrated that fault slip risk is a function of the in situ stress magnitudes, pore pressure in the fault plane, orientation of the fault plane, and fault friction angle, as follows:

$$T_{\text{sm}} = \frac{{\left( {\sigma_{1} - \sigma_{3} } \right)\sin 2\delta }}{{\left[ {\left( {\sigma_{1} + \sigma_{3} } \right) + \left( {\sigma_{1} - \sigma_{3} } \right)\cos 2\delta - 2P_{\text{p}} } \right]\tan \phi_{\text{fault}} }}$$
(18)

where σ1 is the maximum principal in situ stress, σ3 is the minimum principal in situ stress. δ is dip angle of the fault (with respect to horizontal) for a normal fault stress regime (in radians), Φfault is the fault friction angle (in radians) (31° = 0.54 radians), and Pp is pore pressure in the fault plane. When Tsm ≥ 1, fault reactivation is expected. It is noteworthy that for all the methods used here (i.e., Mohr diagrams, slip tendency and modified slip tendency) the principal stresses were considered within a specified range (e.g., 10 m) of the middle part of the fault planes.

According to Rutqvist et al. (2007) and Figueiredo et al. (2015), whenever the maximum principal effective stress exceeds three times the minimum compressive effective stress, shear slip will be induced. So, the critical pore pressure (PC), which is required to induce slip on an arbitrarily oriented fault can be calculated as:

$$P_{\text{C}} = \frac{{3\sigma_{3} - \sigma_{1} }}{2}$$
(19)

After calculating the slip tendency for each fault in the current stress field and pore pressure using Eqs. 17 and 18, the critical pore pressure (PCr) was also calculated by Eq. 18 considering Tsm = 1 (limit equilibrium) and Eq. 19 (Table 3).

According to Hawkes et al. (2005), in a normal fault stress regime, the faults that are most likely to slip first in any setting, tend to be those that strike sub-parallel to the intermediate in situ principal stress (σ2 = σHmax) and dip at roughly 60°. In the field F1, F3 and F4 have strikes nearly parallel to the σHmax orientation, but only the dip of F3 is 59° (Fig. 7 and Table 1). Based on the results of both 3D Mohr diagrams (Table 3) and slip tendency equations (Table 4), F3 is more likely to reactivate, since its ΔPp and Ppmax are lower than the other faults. It also has the highest slip tendency value, which means it can reactivate with a lower pore pressure increase. On the other hand, F2 is the most stable fault, because it has the lowest Ts and Tsm and can undergo an average maximum pore pressure of 55–57 MPa.

Table 4 Slip tendencies calculated using Morris et al. (1996) (Ts) and Hawkes et al. (2005) (Tsm) equations; critical pore pressures calculated from the Rutqvist et al. (2007) (Pc) and Hawkes et al. (2005) (PCr) equations
Full size table

7 Stress polygon

The stress polygon, which was introduced by Zoback et al. (1986) and Moos and Zoback (1990), is a method for visualizing the relationships between the magnitudes of overburden stress, and maximum and minimum horizontal stresses (Enderlin 2008). These polygons define the possible stress magnitudes at a given depth, a known pore pressure, and an assumed coefficient of friction (Zoback 2007). These polygons can also be used to demonstrate the stability of a fault in the current stress field if the values of three principal stresses are known. The horizontal stresses can be anywhere in the triangles, indicating a specific stress regime (i.e., normal, strike-slip and reverse). If the horizontal stresses are right on the edge, it is showing a Mohr circle touching the failure line, and the minimum horizontal stress and effective vertical stress are such that the fault is in the critical state. In case of normal faulting regime, σV is the maximum principal stress, σHmax is less than or equal to σV, and σhmin cannot be below a value determined by the frictional strength of crust. For this part, we also used a frictional coefficient of μ = 0.6, which corresponds to a \(f\left( \mu \right) = 3.1\). An example of a stress polygon and the formulations needed for plotting its different regions is shown in Fig. 12.

Fig. 12
figure 12

Stress polygon showing different regions of stress regimes and formulations needed

Full size image

For inactive faults (not critically stressed), the horizontal stresses are within the normal faulting triangle (NF), and its Mohr circle does not touch the failure line, but when the horizontal stresses are on the left vertical edge of the normal faulting triangle, the fault is critically stressed (active fault) and the Mohr circle reaches the failure line. In this study, stress polygons were plotted for two states of current stress field and the critical pore pressure obtained by 3D Mohr diagrams (Fig. 13).

Fig. 13
figure 13

Stress polygons plotted for the four faults. Three triangles NF, SS, and RF represent the normal, strike-slip and reverse faulting regimes, respectively. The blue solid lines represent the current stress field and pore pressure. Black dashed lines represent the stress field in critical pore pressure obtained by 3D Mohr diagrams. Circle and diamond shaped points represent the NISOC and Seyed Sajadi and Aghighi (2015) equations for obtaining elastic moduli used for estimating the horizontal stresses magnitudes

Full size image

As Fig. 13 shows, all the faults are inactive at the present stress state, and the estimated horizontal stresses fall within the normal faulting triangle (triangle with solid lines). By increasing pore pressure to its critical value, horizontal stresses will be positioned on the left edge of the smaller triangle (triangle with dashed lines) showing the risk of reactivation. The NISOC equation (Eq. 3) shows a very close agreement to the Seyed Sajadi and Aghighi (2015) equation (Eq. 5), which confirms their validity for estimating elastic moduli in the reservoir.

8 Conclusions

Gachsaran oilfield, which is one of the most productive fields in Iran, requires primary EOR techniques such as gas injection to increase the amount of crude oil extraction. Reactivation of pre-existing faults is one of the major risks related to the use of such methods in reservoirs that can result in severe damage to the wellbores and other infrastructure. In this paper, the reactivation tendency of four faults in the Asmari reservoir in the field was analyzed using two analytical methods of 3D Mohr diagrams and slip tendency parameters. For this purpose, by using the equation derived in the NISOC laboratory, static elastic moduli were calculated to estimate the current stress regime of the field, and then the accuracy of the results was examined by the Seyed Sajadi and Aghighi (2015) equation. Results demonstrated that both equations are in accordance with each other. After that, 3D Mohr diagrams of the faults were plotted, which showed that all faults are stable in today’s stress field and pore pressure. In order to evaluate the results of the 3D Mohr diagrams, the slip tendency factor was also calculated, and then the critical pore pressure of the faults due to gas injection was estimated. Results of all three methods of 3D Mohr diagrams, slip tendency and modified slip tendency, confirmed that F2 is the most stable fault in the field, and it can sustain a maximum pore pressure of 55–57 MPa. In the field F1, F3, and F4 have strikes sub-parallel to the σHmax orientation, but only the dip of F3 is appropriate for reactivation. These results show that F3 is more prone to reactivation (Ppmax = 38.8 MPa). According to the results, the best location for an injection well in EOR and geosequestration activities will be the NW side of F2. Since the slip tendency factor can estimate the critical pore pressure with a good precision and without knowing the stress orientation, it will be more cost-effective in such studies, because of costliness and difficult interpretation of image logs.